五年级陈杯模拟题一学生版
五年级陈杯模拟

五年级考前模拟(二)一、填空:1、计算+151151515154040404151515303031515202++= 2、计算10981543143213211⨯⨯++⨯⨯+⨯⨯+⨯⨯ = 3、a,b,c,d,e 五个字母自左至右有 种排列4、能同时被2,3,4,5,6,7,8,9整除的最小五位数是5、p,q 均为质数,且5p+7q=29,则p+q=6、小明将20.0.6乘以一个数,误写成20.06乘以一个数,结果与正确答案正好相差20.06,则正确答案应该是7、将15个整数分成甲、乙两组。
甲组6个数的平均数是乙组9个数的平均数的2倍,而两组数的平均数的和为48,那么这15个数的平均数是8、规定:a *b=2a+b,则(1*2.5)*(21*1.2)= 9、如果A@B=BA AB ⨯-,那么1@2+2@3+3@4+…+99@100= 10、甲、乙两件商品的成本共600元,已知甲按45%的利润定价,乙按40%的利润定价。
后来,甲打8折出售,乙打9折出售,结果共获利110元,则甲商品的成本是11、原计划项目组25人一起来完成一项工程,工作6天后,调走5人干其他工作,这样,完成这项工程就比原计划多用了4天。
原计划完成这项工程用 天12、甲队完成一项工程,一天完成125,要超出53共需 天 13、某工厂预计用30天完成一批加工零件。
先由18名工人干了12天,完成了任务的31,现因任务紧急,需要提前6天完成全部加工任务,则需要增加工人 名14、一项工程甲、乙合作完成了全工程的107,剩下的由甲单独完成,甲一共做了2110天。
若这项工程由甲单独做,需15天,如果有一单独做,需 天。
15、一辆汽车从甲地到乙地,行驶前一半路程的平均速度是每小时30千米,行驶后一半路程的平均速度是每小时60千米,那么,汽车从甲地到乙地的平均速度是每小时 千米。
16、一个六位自然数200 8能被12整除,中间两位共有 种不同的填法17、图中阴影部分的面积是1006008平方厘米,则长方形ABCD 的面积是18、长方形ABCD 被线段DE 分成一个三角形和一个梯形,其中AE=3EB,BC=7厘米,所分成的两个图形的面积差为21平方厘米,则长方形ABCD的周长是19、一个牧场长满青草,牛在吃草儿草又在不断生长,27头牛6天可以把牧场的草全部吃完;23头牛吃完全部牧场的草则要9天。
五年级计算数阵图与数字谜学生版

数阵图与数字谜知识要点解决数阵类问题可以采取从局部到整体再到局部的方法入手:第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.数字谜问题往往综合了数字的整除特征、质数与合数、分解质因数、个位数字、余数、分数与小数互化、方程、估算、找规律等题型,因此要求同学们能够很好地掌握上述知识点,并加以灵活运用.数字谜一般分为横式数字谜和竖式数字谜.横式数字谜经常和数论里面的知识结合考察,有些时候也可以转化为竖式数字谜;竖式数字谜通常有如下突破口:末位和首位、进位和借位、个位数字、位数的差别等.数字谜的常用分析方法有:个位数字分析法、高位数字分析法、数字大小估算分析法、进位错位分析法、分解质因数法、奇偶分析法等.数论知识【例1】(第一届“华罗庚金杯”少年数学邀请赛决赛一试)如图,4个小三角形的顶点处有6个圆圈。
如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形3个顶点上的数之和相等。
问这6个质数的积是多少?【例2】 一个整数乘以13后,乘积的最后三位数是123,这样的整数中最小的是多少?【例3】 红、黄、蓝和白色卡片各一张,每张上写有一个数字。
小明将这4张卡片如图放置,使它们构成一个四位数,并计算这个四位数与它的数字之和的10倍的差。
结果小明发现,无论白色卡片上是什么数字,计算结果都是1998。
问:红、黄、蓝3张卡片上各是什么数字?蓝白黄红【例4】 如图算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字,请求出这个算式。
春夏秋冬四季季年年年年年年【例5】 将1~9分别填入这九个区域,使得每个圆里的数字和相等。
【例6】已知76⨯=⨯,相同的字母代表相同的数字,不同的字母代表不同的数字,求ABCXYZ XYZABCABCXYZ是多少?【例7】三位数AAA乘三位数AAB等于六位数CCCDDD,求A,B,C,D分别是多少?【例8】(第二届“华罗庚金杯”少年数学邀请赛复赛)试将1,2,3,4,5,6,7分别填入下面的方框中,每个数字只用一次:(这是一个三位数)、(这是一个三位数)、(这是一个一位数),使得这三个数中任意两个都互质。
五年级组“陈省身杯”模拟题答案

五年级组“陈省身杯”模拟题测试时间60分钟姓名:成绩:(1)计算:28.67×67+3.2×286.7+573.4×0.05=_2867____。
(2)如果10+9-8×7÷□+6-5×4+3-2=1,那么记号“□”所表示的数是_11.2___。
(3)在下面的算式中,不同的汉字代表不同的数字.那么.陈+省+杯+数+学+活+动+周= _37___ _。
陈省杯数学活动周×9111111111(4) 五(1)班有46人,喜欢打乒乓球的有32人,喜欢打羽毛球的有26人。
有2人两种运动都不喜欢。
既喜欢打乒乓球,又喜欢打羽毛球的至少有___14_____人。
(5)有四张卡片它们是①⑨⑨⑧, 用这四张卡片组成最大的四位数是___9981___最小的四位数是 1899 。
(6)请你把15个苹果分装在四个盒子里,使得无论要拿几个苹果都有不用再打开盒子。
这四个盒子的苹果分别是 1.2.4.8 。
(7)今年姐妹俩年龄的和是50岁,若干年前,当姐姐的年龄只有妹妹现在这么大时,妹妹的年龄恰好是姐姐年龄的一半,姐姐今年__30___岁。
(8)平行四边形ABCD内有任意一点E(右图)。
已知三角形AED和BEC的面积分别是15.8平方厘米和35.2平方厘米,AB的长是17厘米,平行四边形的高DF= 6__厘米。
(9)一把钥匙只能开的把锁,现在有10把钥匙和10把锁,但不知哪把钥匙开哪把锁,最多试___45__次可以确定那把钥匙开那把锁。
(10)两块地共收皮棉14000千克,平均每公顷收1750千克,已知第一块地每公顷收2500千克。
比第二块多收1000千克,两块地的面积分别是___2__公顷和__6___公顷。
(11)甲、乙两人从底楼开始比赛爬楼梯,甲跑到第四层时,乙恰好到第三层,照这样计算,甲跑到第十六层,乙跑到第_11__。
(12)四个小孩在校园内踢球,“砰”的一声,不知是谁踢球把教室窗户的玻璃打破了。
2010陈省身杯数学邀请赛五年级答案
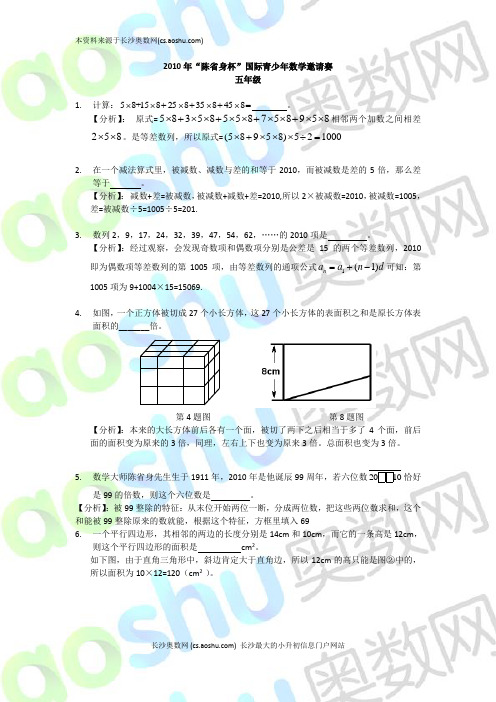
2010年“陈省身杯”国际青少年数学邀请赛五年级1. 计算:58+15⨯⨯8+25⨯8+35⨯8+45⨯8= 。
【分析】: 原式=58358558758958⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯相邻两个加数之间相差258⨯⨯。
是等差数列,所以原式=(58958)521000⨯+⨯⨯⨯÷=2. 在一个减法算式里,被减数、减数与差的和等于2010,而被减数是差的5倍,那么差等于 。
【分析】: 减数+差=被减数,被减数+减数+差=2010,所以2×被减数=2010,被减数=1005,差=被减数÷5=1005÷5=201.3. 数列2,9,17,24,32,39,47,54,62,……的2010项是 。
【分析】:经过观察,会发现奇数项和偶数项分别是公差是15的两个等差数列,2010即为偶数项等差数列的第1005项,由等差数列的通项公式1(1)n a a n d =+-可知:第1005项为9+1004×15=15069.4. 如图,一个正方体被切成27个小长方体,这27个小长方体的表面积之和是原长方体表面积的_______倍。
第4题图 第8题图【分析】:本来的大长方体前后各有一个面,被切了两下之后相当于多了4个面,前后面的面积变为原来的3倍,同理,左右上下也变为原来3倍。
总面积也变为3倍。
5. 数学大师陈省身先生生于1911年,2010年是他诞辰99周年,若六位数2010恰好是99的倍数,则这个六位数是 。
【分析】:被99整除的特征:从末位开始两位一断,分成两位数,把这些两位数求和,这个和能被99整除原来的数就能,根据这个特征,方框里填入696. 一个平行四边形,其相邻的两边的长度分别是14cm 和10cm ,而它的一条高是12cm ,则这个平行四边形的面积是 cm 2。
如下图,由于直角三角形中,斜边肯定大于直角边,所以12cm 的高只能是图②中的,所以面积为10×12=120(cm 2 )。
新人教版五年级下册数学竞赛模拟试题

新人教版五年级下册数学竞赛模拟试题1.一个长方体木料的长和宽都是4米,高是8米,求这根木料的体积。
答案是128立方米。
如果把这根木料锯成两个正方体,求这两个正方体的表面积之和。
答案是96平方米。
2.一个长方形的长和宽都扩大2倍,它的周长扩大2倍,面积扩大4倍。
3.一个长方形至少旋转180度,与原来的图形重合;一个等边三角形至少旋转120度与原来的图形重合;一个正六边形至少旋转60度与原来的图形重合。
4.能同时被2、3、5整除的最大的三位数是990.5.把一张纸连续对折三次,所得长度是这张纸的1/8,对折四次,所得长度是这张纸的1/16.6.把两个棱长为5厘米的正方体木板粘合成一个长方体,这个长方体的表面积是250平方厘米,体积是250立方厘米。
7.甲乙两数的和为8.5,如果甲数的小数点向右移动一位,就正好等于乙数的7倍。
求乙数。
答案是5.8.用体积为1立方厘米的小正方体,堆成一个体积为1立方米的大正方体,需要xxxxxxx个小正方体木块。
如果把这些小正方体木块一个挨一个地排成一行,长度为10千米。
9.橡皮的体积约为10立方厘米,集装箱的体积约为40立方米。
10.50÷7商的小数点后面第4个数字是8,小数点后面第30个数字是7.11.XXX家的贮藏室长16米,宽12米,如果用边长为4米的正方形地砖把贮藏室的地面铺满,使用的地砖都是整块,可以选择边长为4米的地砖。
12.观察一个正方体时,一次最多能看到3个面。
13.一根6.4米长的彩带,每1.4米剪一段包扎一个礼盒,这根彩带可以包扎4个礼盒。
14.按规律填数:2、3、5、7、11,下一个数是13.二.明辨是非。
(10分)1.被除数÷(除数×商)= 1.(√)2.如果a与b是互质数,那么一定是最简分数。
(√)3.左图梯形中两个阴影的三角形面积一定相等。
(√)4.一个分数的分母含有质因数2或5,这个数一定能化成有限小数。
(×)5.一个长方体,它的长、宽、高都扩大2倍,它的体积扩大8倍。
五年级陈杯模拟题一学生版

五年级陈杯模拟题第一套1.72×108+108×46-(118×142-118×134)= 。
2.修路队修一条路,如果每天修48米,需15天修完。
现在每天多修12米,需要______天修完。
3.婷婷到游乐园游玩,游乐园有一张价目表:“骑木马,每10分钟1元;蹦床,每10分钟2元;电动车,每10分钟5元;碰碰车,每10分钟8元。
”爸爸只让婷婷玩20分钟,那么买票的钱共有_______种可能。
4.在1—9中最多能排出______个数,使得这些数中没有一个数是另一个数的整数倍。
5.有三张卡片,正、反面各写有1个数字,第一张写有0和1。
第二张写有2和3,第三张写有4和5。
从这三张卡片中取出两张,放成一排,那么一共可以组成_____个不同的两位数。
6.在下边的乘法算式中,被乘数是。
口口口口×口=8888口7.若干个球分别放在甲、乙、丙、丁4个盒子中。
甲盒中的球最多,甲盒比乙盒多4个球,乙盒与丙盒相差3个球,丙盒与丁盒相差2个球。
甲盒比放球最少的盒最少多放个球。
8.一列由三个数组成的数组,依次是(1,2,4),(2,4,8),(3,6,12)……第100组中的三个数之和是。
9.有一个自然数,若从中连续减去1,3,5……若干个相邻奇数后剩10,若从中连续减去2,4,6……同样多个相邻偶数后剩3,这个自然数是。
10.下图中,等腰直角三角形ABC的面积是8,AE=CF,四边形BEOF的面积比三角形AOC的面积大4,AE= 。
11.有一个怪钟,一圈共有20个格,每过7分钟指针跳一次,每跳一次要跳过3个格。
上午10点整时指针刚从0跳到3,昨天晚上10点整时指针指向第格。
12.小明和小红只有1分和2分的硬币。
小明的1分硬币是小红1分硬币的2倍,小红的2分硬币比小明的2分硬币多26枚。
小明有134枚硬币,比小红多13枚。
小明和小红的硬币的币值共分。
13.某裁缝做1件上衣的时间能做3条短裤或5个背心,他一天能做1件上衣、2条短裤、3个背心。
决胜陈杯讲座五年级

五年级陈杯三个月冲刺规划
建议时间:10月—11月中旬 1、优先关注薄弱专题 2、翻看错题本和以前的讲义 3、做好复习计划,具体到天 建议时间:11月中旬—12月中旬 1、09、10两年MO试题 2、重点关注和陈杯相似的杯赛 建议时间:12月中下旬 1、陈杯近三年五年级真题 2、适当练习六年级陈杯真题 3、针对性地陈杯模拟题演练
Page 16
行程真题赏析
华华和英英分别从A、B两地同时出发相向而行。当华华经过A、B两 地的中点C地100米后,两人第一次相遇;然后两人又继续前进,当华 华到达B地后立即返回,又经过C地300米后他追上了英英,则AB两地 相距_______米。 小强从家里步行到考场参加“2010年陈省身数学周活动”,如果每分 钟走50米,就要迟到3分钟,如果每分钟走60米,就可以提前2分钟到 考场,那么从小强家到学校的路程是 米。 A、B两地相距4800米,甲在A地,乙丙在B地,第一天,甲向B出发, 乙丙向A出发,甲乙相遇后乙掉头,10分钟后乙和丙相遇;第二天, 甲向B的反方向出发,乙丙向A出发,乙追上甲后掉头,20分钟后乙和 丙相遇。甲的速度为每分钟45米,求丙的速度。
Page 27
近期活动
Page 28
感谢您的关注
29
A D
FB GC来自Page 19几何真题赏析
如图,已知CD=5cm,DE=4cm,EF=9cm,FG=3cm。直线AB将图形分 成两部分,左边部分面积是42cm2,右边的面积是62cm2,那么三角形 ADG面积是 cm2
一个平行四边形,其相邻的两边的长度分别是14cm和10cm,而它的 一条高是12cm,则这个平行四边形的面积是 cm2。
时间
2010年 2011年
五年级陈杯模拟1(精品)
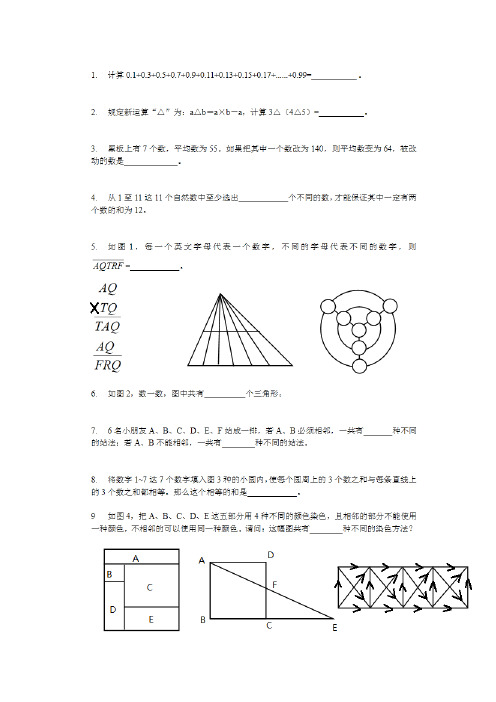
10. 已知平方差公式,a 2-b 2=(a+b )(a-b )计算:1002+992-982-972+962+952-942-932+......+42+32-22-12=____________。
11. 如图5,正方形ABCD 边长是5厘米,且三角形CEF 的面积比三角形ADF 的面积大5平方厘米,CE=_____________。
12. 有一片均匀生长的草地,可供18头牛吃40天,或者供12头牛与36只羊吃25天,如果一头牛每天的吃草量相当于3只羊每天的吃草量。
请问:这草地让17头牛与______只羊一起吃,刚好16天吃完。
13. 如图6,蚂蚁在线段上爬行,只能按照箭头方向走。
请问:从A 到B 不同路线有__________条。
14.李师傅要将甲乙两种零件加工成成品,开始时甲零件的数量是乙零件的2倍,每件产品需要5个甲零件和2个乙零件,加工30件成品后,剩下的甲乙零件数量相等,请问:李师傅还可以加工____________件成品。
15. AB 两辆汽车分别从甲乙两地同时相向出发,并且在两地不断往返行驶,两车在距离甲地40千米处第一次迎面相遇,两车继续行驶,在距离甲地10千米处第二次迎面相遇。
甲乙两地之间的距离___________。
16. 王经理打算申请电话号码,到电信营业厅发现目前只有“1234△6△8”的电话号可以申请,三角内的数字可以随意选择,其余不能改动,王经理准备申请一个同时能被8和11整除的号码。
请问:他申请的可能是____________。
17. 如图7,把从1开始的自然数按某种方式排列起来。
请问:200排在第________行第________列。
第18行第22列的数是__________。
18. 如图,在钝角三角形ABC 中,M 为AB 边的中点,MD 、EC 都垂直于BC 边,若三角形BDE 的面积是3平方厘米,则三角形ABC 的面积是_______平方厘米。
19. 小明跟爷爷聊天,爷爷对小明说:“当我的岁数是你爸现在的岁数时,你才5岁。
五年级陈省身杯模拟题(2)

五年级陈省身杯模拟题(2)1.两个自然数的和是15,要使两个整数的乘积最大,这两个整数分别是。
2.某镇街道分布如右图,一个居民要从A处前往B处。
如果规定只能走从左到右或从上到下的方向,那么该居民可选择的不同路线共有___条。
’3.某偶数N的各位数字的和是50。
N最小是。
4.我们把形如abba的四位数称为“对称数”,如1991,2002等。
在1000~10000之间有____个“对称数”。
5.下面的数表是按一定规律排列的,表中第8行第88个数是。
1 3 5 7 9 11 …2 6 10 14 18 22 …4 12 20 28 36 44 …8 24 40 56 72 88 …16 48 80 112 144 176 ……………………6.4名工人18分钟可加工零件30个。
如果要在2小时内加工零件900个,那么需要名工人。
7.一件工程,甲队独做12天可以完成任务。
如果甲队做3天后乙队做2天,则恰好完成工程的一半。
现在甲、乙两队合做若干天后,由乙队单独完成,已知两队合做时间与乙队独做时间相等。
完成任务共有天。
8.各位数字之和是奇数,并且是两个两位数的乘积的小于200的自然数共有个。
9.在下面的这些平方数中,有个是3的倍数。
1,4,9,16 (10000)10.用黑、白两种珠子按照一定规律摆成三角阵。
前四次摆的如下图,当摆到第个三角阵时,这个三角阵中的黑珠子第一次比白珠子多。
11.有一个两位数,把数码1加在它的前面可以得到一个三位数,加在它的后面也可以得到一个三位数,这两个三位数相差666。
则原来的两位数是。
12.用3根火柴棍可以摆成一个小三角形。
要摆成一个如右图所示的每条边有10根火柴棍的大三角形,共需要火柴棍根。
13.从写有1~9的九张卡片中抽出一张,其余的八张平分成四组,使第一组两张卡片上的两数之和等于7,第二组两张卡片上的两数之积等于6,使第三组两张卡片上的两数之差等于4,第四组两张卡片上的两数之商等于3。
五年级陈杯试题和答案

2015年陈省身杯五年级数学解析1.计算:150×13+1.3×50=_____。
【考点】计算【难度】2星【解析】150×13+13×5=(150+5)×13=20152.元旦那天,爸爸对小明说:“前天我30岁,但是今年我将满32岁。
”那么爸爸的生日在__月__日.【解析】12月31日3.一次考试,甲乙丙三人的平均分为88分,丁和戊的平均分为92分,则这次考试中他们五人的平均分为___分。
【考点】平均数【难度】2星【解析】88×3+92×2=448448÷5=89.64.将一个三角形的底变成了原来的3倍,高变成原来的一半,那么这个三角形的面积变成了原三角形面积的___倍。
【考点】三角形面积【难度】2星【解析】3÷2=1.55.小明每天从家到学校需要先步行10分钟到车站,然后再坐30分钟公交车到学校。
步行的速度是每秒2米,公交车行驶的速度是每秒10米,那么小明家距离学校__千米。
【考点】行程【难度】2星【解析】10分=600秒30分=1800秒2×600+1800×10=19200(米)=19.2(千米)6.冬至又称“冬节”,“贺冬”,是华夏二十四节气之一,与二十四节气中的“夏至”节气相对。
如果2014年12月22日是“冬至”,这一天恰好是星期一,那么2015年的“夏至”(6月22日)是星期___。
【考点】周期问题【难度】3星【解析】10+31+28+31+30+31+22=183183÷7=26余1所以为周一7.一个布袋子中装有9个小球,球上分别标有数字1至9,甲乙丙三人分别从布袋中拿走了4个,4个,1个小球,结果发现甲乙两个人摸出的球上数字之和相等,但都不是丙摸出小球上数字的倍数,则丙拿走的小球上所标的数字是___。
【考点】奇偶性【难度】2星【解析】1+2+3+4+5+6+7+8+9=45因为去掉一个数可以均分2份,所以去掉的是奇数。
2012年陈省身杯五年级模拟题一答案

参考答案一1.586000.2.22,23,24.提示:三个连续自然数之和等于中间数的3倍,所以中间数必是23的倍数.3.33.解:张老师比李老师大(17—15)×3=6(岁),今年张老师27+6=33(岁).4.21;8;22.解:由第一行得○=24÷4=6;由第二行得☆=(22—6×2)÷2=5.由第三行得△+口=18—6—5=7,由第四行得口+口+△=16—5=11,所以口=11—7=4,△=7—4=3.第一列:○+○+☆+口=6+6+5+4=21;第三列:○+☆+口+△=6+5+4+3=18;第四列:○+☆+○+☆=6+5+6+5=22.5.0.9.解:来回一趟上、下坡各走了2.4千米,共用2.4÷2+2.4÷3=2(时)所以回家要走2-1.1=0.9(时).6. 32.解:小明有书4+8=12(本),有光碟12×2+8=32(盘).7.23.提示:按右图拼8.答案不唯一.解:1.7共有3个偶数4个奇数,要满足每个圆圈内的四个数字之和是15(奇数),只有下面两种情况:三个圆内的数之和等于“祖”,“之”,“赛”各加一遍,“冲”,“邀”,“请”各加了两遍,“杯”加了三遍,所以有冲+邀+请+2杯=15×3-(1+2+…+7)=17.对于满足上式的数,可以试探寻找答案.例如对于左上图,杯=1,冲=3,邀=5,请=7,可得祖=6,之=4,赛=2(见下页左上图).又如对于右上图,杯=3,冲=1,邀=4,请=6,可得祖=7,之=5,赛=2(见下页右上图).注:除旋转,翻转外,本题只有上面两组本质不同的解.9.400.解:回赠现金后,相当于65元买100元的物品,所以最多可买260÷65×100=400(元). 实际操作:买200元物品,回赠70元,还有60+70=S130(元);再买100元物品,又回赠35元,还有30+35=65(元);向别人借35元,再买100元物品,又回赠35元,将回赠的35元还给别人.10.z.解:因为z选手认识所有的人,所以z选手不是C和B的搭档,只能是A选手的搭档.11.12.解:如右图割补,可得正方形DE’BE.正方形DE’BE的面积是16平方厘米,所以边长是4厘米.四边形BCDE的面积是 16-2×4÷2=12(平方厘米).12.280.解:因为第一堆中2元和5元的张数相同,所以第一堆的钱数是(2+5=)7的倍数.因为第二堆中2元和5元的钱数相同,所以第二堆的钱数既是2的倍数也是5的倍数.第二堆的总钱数是其中2元钱数的2倍,第一、二两堆的总钱数是第二堆中2元钱数的4倍,所以是8的倍数.【8,7,5】=280,这叠钱至少有280元.13.6.8元.解:3+0.5×(12.2-5)÷0.6=9(千米).8.5+0.3<甲、乙两地距离≤9,8.8<甲、乙两地距离≤9,4.4<12甲、乙两地距离≤4.6.到甲、乙两地中点需支付5+0.6×(4.5-3)4-0.5=6.8(元).14.17朵.解:由图看出,红与黄、蓝、白、紫相邻,所以红与绿相对;由两端的立方体看出黄与白相邻,所以蓝的对面是白,推知紫与黄相对.长方体下面共有花5+2+6+4=17(朵).15.9713。
2012年陈省身杯五年级模拟题三答案

参考答案 三1.【解析】 原式19=⨯+19.98372341998=⨯++=()【答案】1998 2.【解析】 把数列列出来:83,89,95,101,107,113,119,125,131,137,143,149,155,161,167,173,179,185,191【答案】191 3.【解析】 同学们观察会发现,两个乘数都非常大,不便直接相乘,可以引导学生按照两种思路给学生展开方法一:是学生喜欢的从简单情况找规律 9×9=81;99×99=9801 ;999×999=998001;9999×9999=99980001;…… 所以:2008920089999999⨯ 个个20079200799980001=个个0原式2007920072008999980001+1999= 个个0个401601000=个 方法二:观察一下你会发现,两个乘数都非常大,不便直接相乘,其中 999 很接近 1 000 ,于是我们采用添项凑整,简化运算。
原式210-⨯个个个个=()29=个个个个个200892008209990001000=⋅⋅⋅⋅⋅⋅+⋅⋅⋅个个个4016100=⋅⋅⋅ 个 所以末尾有4016个0【答案】4016个0 4.【解析】 包子的速度:90303÷=(米/秒),菠萝的速度:90156÷=(米/秒),相遇的时间:90(36)10÷+=(秒),包子距B 地的距离:9031060-⨯=(米).【答案】包子距B 地的距离是60米 5.【解析】 因为相遇前后甲,乙的速度和没有改变,如果相遇后两人和跑一圈用 24 秒,则相遇前两人和跑一圈也用 24 秒。
以甲为研究对象,甲以原速V 跑了 24 秒的路程与以(V +2 )跑了 24 秒的路程之和等于 400米,24V +24(V +2 )=400 易得V = 173米/秒【答案】173米/秒6.【解析】 1140524⨯⨯=(平方厘米)【答案】5平方厘米 7.【解析】 从上往下看,分别如左下图和右下图所示(图中数字为每一格的木块数)。
2012年陈省身杯五年级模拟题一

2012年陈省身杯模拟题(一)1.计算:586×124+29×586-586×53=_______.2.有三个连续的两位自然数,它们的和也是两位自然数,并且和是23的倍数,这三个自然数分别是_____,______,______.3.张老师与王鸿和金明的平均年龄是17岁;李老师与王鸿和金明的平均年龄是15岁.李老师今年27岁,张老师今年_______岁.4.观察下列图表的规律,然后填空:5.小华家到学校有上坡路和下坡路,没有平路,共2.4千米.小华每天上学要走1.1小时.已知小华上坡时每小时走2千米,下坡时每小时走3千米.那么小华放学回家要走_____小时.6.小明有书和光碟若干,光碟的数量比书的数量的3倍少4盘,比书的2倍多8盘,那么小明有光碟______盘.7.有10张长2厘米、宽1.5厘米的长方形硬纸片,用它们拼成一个大的长方形纸片,这个大长方形的周长最小是_____厘米.8.右图中“祖冲之杯邀请赛”恰恰代表了1,2,3,4,5,6,7这七个不同的数字,而且每个圆圈内的四个数字之和为15,那么祖=______,冲=______,之:_____,杯=_____,邀=______,请=_______,赛=______.9.一家商场开展优惠酬宾活动,凡购物满100元回赠35元现金(购物不足100元的,不参加优惠活动).现在某人有260元,他经过计算,买回了最多的物品,那么他最多买了______元的物品.10.世界乒乓球锦标赛期间,在一次各国运动员聚会时,有三对男女混合双打运动员恰好坐在一起.他们分别是X,Y,Z三个男选手和A,B,C三个女选手.其中X选手的搭档和C选手的搭档、B选手的搭档和A选手都是第一次见面,z选手认识所有的人,则A选手的搭档是_____.11.如右图,四边形ABCD的面积是16平方厘米,其中AD=CD,DE=BE,AE=2厘米,那么四边形BCDE的面积是_______平方厘米.12.现有一叠2元和5元的纸币若干,把它们分成钱数相同的两堆.第一堆中2元和5元的张数相同,第二堆中2元和5元的钱数相等,那么这一叠钱至少有_______元.13.西安市出租车车费的起步价是3千米以内都是5元,往后每增加0.5千米,计价器就增加0.6元.现在有一人从甲地到乙地乘出租车共支付车费12.20元.如果这个人从甲地到乙地先步行300米,然后再乘出租车,也要支付车费12.20元,那么坐出租车从甲地到甲、乙两地的中点需支付出租车费元。
2019鹏程杯5年级语文试卷

②国学大师季羡林学识渊.博.,德高望重。
解说:两个“渊博”意思相同,都有“深而且广”的意思。
B. ①这个人有三十岁模.样.。
②看你打扮成这模.样., 我几乎认不出来了。
解说:两个“模样”意思不同。①句中的“模样”指人的长相或装束打扮的样子,②
句中的“模样”表示约略的情况。
C. ①无钥.匙.启动系统能够通过车主随身携带的智能卡来开关车门和启动车辆。
B. 去逝
糟塌
魏格纳 按部就班
C. 慑服
松驰
很飘亮 目不暇接
D. 臆测
游弋
大自然 戎马倥偬
5.下列词语中都是反义词的一组是( A.严寒──酷暑 安谧──嘈杂 B.轻蔑──敬重 开心──苦闷 C.尊重──敬重 开心──苦闷 D.伟大──渺小 清晰──清楚
) 唇枪舌剑──心平气和 全神贯注──聚精会神 安居乐业──颠沛流离 一丝不苟──精益求精
25.短文告诉我们一个什么道理?(2 分)
答:
。
(三)阅读下文,回答后面问题。(10 分)
①暮春,中午,踩着畦垅间.苗或者锄草中耕,煦暖的阳光照得人浑身舒畅。②新鲜的
泥土气息,素淡的(shū)菜清香,一阵阵沁人心脾。③一会儿站起来,伸伸腰,用手背
育 擦擦额头的汗,看看苗间得稀还是稠,中耕得深还是浅,草锄得是不是干净,那时候人是
四年级全体同学:
请于今日下午到礼堂开会。会议内容:总结本月我年级各方面的情
况。请带笔和笔记本。
光明小学四年级组 2019 年 1 月 28 日
A.应写明开会时的注意事项。应删去标题“通知”二字。 B.应写明 开会的具体时间。正文的第一行应空两格。 C.应写明开会时参会的领导。发出通知单位的名称应写在日期的下一行。 D.应写明开会时讲话、发言的人。通知对象的名称不能顶格写,应空两格。
河南省郑州市新郑市实验小学五年级杯数学竞赛试题

河南省郑州市新郑市实验小学五年级杯数学竞赛试题一、拓展提优试题1.(15分)如图,正六边形ABCDEF的面积为1222,K、M、N分别AB,CD,EF的中点,那么三角形PQR的边长是.2.(15分)一个自然数恰有9个互不相同的约数,其中3个约数A,B,C满足:①A+B+C=79②A×A=B×C那么,这个自然数是.3.甲乙两人分别从AB两地同时出发相向而行,当甲走到一半时,乙将速度提高一倍,结果两人在距离B地1200米处相遇,并且最后同时到达,那么两地相距米4.(7分)棱长都是1厘米的63个白色小正方体和1个黑色小正方体,可以拼成一个大正方体,问:一共可以拼成种不同的含有64个小正方体的大正方体.5.幼儿园给小朋友派礼物,如果有2人各派4个,其余各派3个,则还剩余11个,如果4人各派3个,其余各派6个,则剩余10个,问一共有多少件礼物?6.甲、乙两车从A城市出发驶向距离300千米远的B城市.已知甲车比乙车晚出发1小时,但提前1小时到达B城市.那么,甲车在距离B城市千米处追上乙车.7.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有个细胞.8.如图,若长方形S长方形ABCD=60平方米,S长方形XYZR=4平方米,则四边形S四边=平方米.形EFGH9.如图,将一个等腰三角形ABC沿EF对折,顶点A与底边的中点D重合,若△ABC的周长是16厘米,四边形BCEF的周长是10厘米,则BC=厘米.10.对于自然数N,如果1﹣9这九个自然数中至少有六个数可以整除N,则称N是一个“六合数”,则在大于2000的自然数中,最小的“六合数”是.11.某长方体的长、宽、高(长、宽、高均大于1)是三个彼此互质的自然数,若这个长方体的体积是665,则它的表面积是.12.用一根34米长的绳子围成一个矩形,且矩形边长都是整数米,共有种不同的围法(边长相同的矩形算同一种围法).13.(8分)一个大于1的正整数加1能被2整除,加2能被3整除,加3能被4整除,加4能被5整除,这个正整数最小是.14.定义新运算:θa=,则(θ3)+(θ5)+(θ7)(+θ9)+(θ11)的计算结果化成最简真分数后,分子与分母的和是.15.松鼠A、B、C共有松果若干,松鼠A原有松果26颗,从中拿出10颗平分给B、C,然后松鼠B拿出自己的18颗松果平均分给A、C,最后松鼠C把自己现有松果的一半平分给A、B,此时3只松鼠的松果数量相同,则松鼠C原有松果颗.【参考答案】一、拓展提优试题1.解:如图延长BA和EF交于点O,并连接AE,由正六边形的性质,我们可知S ABCM=S CDEN=S EF AK=六边形面积,根据容斥原理,重叠部分三个三角形面积和等于阴影部分面积,且因为对称,△AKP,△CMQ,△ENR三个三角形是一样的,有KP=RN,AP=ER,RP=PQ,=,则=,=,由鸟头定理可知道3×KP ×AP =RP ×PQ , 综上可得:PR =2KP =RE ,那么由三角形AEK 是六边形面积的,且S △APK =S △AKE ,S △APK =S ABCDEF =47,所以阴影面积为47×3=141故答案为141.2.解:一个自然数N 恰有9个互不相同的约数,则可得N =x 2y 2,或者N =x 8,(1)当N =x 8,则九个约数分别是:1,x ,x 2,x 3,x 4,x 5,x 6,x 7,x 8,其中有3个约数A 、B 、C 且满足A ×A =B ×C ,不可能.(2)当N =x 2y 2,则九个约数分别是:1,x ,y ,x 2,xy ,y 2,x 2y ,xy 2,x 2y 2,其中有3个约数A 、B 、C 且满足A ×A =B ×C ,①A =x ,B =1,C =x 2,则x +1+x 2=79,无解.②A =xy ,B =1,C =x 2y 2,则xy +1+x 2y 2=79,无解.③A =xy ,B =x ,C =xy 2,则xy +x +xy 2=79,无解.④A =xy ,B =x 2,C =y 2,则xy +x 2+y 2=79,解得:,则N =32×72=441.⑤A =x 2y ,B =x 2y 2,C =x 2,则x 2y +x 2y 2+x 2=79,无解.故答案为441.3.2800[解答] 设两地之间距离为S 。
新5年级陈杯诊断学生版

限时60分钟完成1.1008+88+888++888个8的和的个位上的数字是_________。
2.有四个连续奇数的和是2008,则其中最小的一个奇数是_________。
3.在下边的数阵中,如果按照从上往下,从左往右的顺序数数,可以知道第1个数是1,第3个数是2,第6个数是3……,那么第99个数是_________。
4.在下图中,已知正方形ABCD 的面积是正方形EFGH 面积的4倍,正方形AMEN 的周长是4厘米,且四个角上的小正方形面积相等,那么正方形ABCD 的周长是_________厘米。
5.对自然数作如下操作:如果是偶数就除以2,如果是奇数就减去1,如此操作直到结果变成0为止。
那么经过6次操作后使结果变成0的数有_________个,分别是_________。
新五年级陈省身杯考点诊断试题6.下图中ABCD是平行四边形,图中的线段分别与AB,AD或船平行,则包含阴影三角形的平行四边形共有个。
7.商店里卖的电池有3节一盒和5节一盒两种包装,请找出一个数,凡购买的节数超过这个数时,售货员就不必拆盒。
这个数最小是。
8. 在下面的乘法竖式中,乘积是 .9.有一台数码照相机,成像质量分“最好”、“好”、“一般”三种.这台相机配的存储卡最多可存储“最好”的像片120张,或存储“好”的像片160张,或存储“一般”的像片280张.现在这张存储卡中已存有“最好的”像片30张.“好”的像片60张,那么,还能存“一般”的像片张.10.能被2007整除且后四位是2006的最小的自然数是 .11. 把一根线绳对折、对折、再对折,然后从对折后线绳的中间剪开,这根线绳被剪成了_______小段.12.培英学校和电视机厂之间有一条公路,原计划下午2点时培英学校派车去电视机厂接劳模来校作报告,往返需用1小时。
实际上这位劳模在下午1点便提前离厂步行向学校走来,途中遇到接他的汽车,劳模便立刻上车去往学校,并在下午2点40分到达。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级陈杯模拟题第一套
1.72×108+108×46-(118×142-118×134)= 。
2.修路队修一条路,如果每天修48米,需15天修完。
现在每天多修12米,需要______
天修完。
3.婷婷到游乐园游玩,游乐园有一张价目表:“骑木马,每10分钟1元;蹦床,每10分
钟2元;电动车,每10分钟5元;碰碰车,每10分钟8元。
”爸爸只让婷婷玩20分钟,那么买票的钱共有_______种可能。
4.在1—9中最多能排出______个数,使得这些数中没有一个数是另一个数的整数倍。
5.有三张卡片,正、反面各写有1个数字,第一张写有0和1。
第二张写有2和3,第三
张写有4和5。
从这三张卡片中取出两张,放成一排,那么一共可以组成_____个不同的两位数。
6.在下边的乘法算式中,被乘数是。
口口口口×口=8888口
7.若干个球分别放在甲、乙、丙、丁4个盒子中。
甲盒中的球最多,甲盒比乙盒多4个
球,乙盒与丙盒相差3个球,丙盒与丁盒相差2个球。
甲盒比放球最少的盒最少多放个球。
8.一列由三个数组成的数组,依次是
(1,2,4),(2,4,8),(3,6,12)……
第100组中的三个数之和是。
9.有一个自然数,若从中连续减去1,3,5……若干个相邻奇数后剩10,若从中连续减去
2,4,6……同样多个相邻偶数后剩3,这个自然数是。
10.下图中,等腰直角三角形ABC的面积是8,AE=CF,四边形BEOF的面积比三角形AOC
的面积大4,AE= 。
11.有一个怪钟,一圈共有20个格,每过7分钟指针跳一次,每跳一次要跳过3个格。
上
午10点整时指针刚从0跳到3,昨天晚上10点整时指针指向第格。
12.小明和小红只有1分和2分的硬币。
小明的1分硬币是小红1分硬币的2倍,小红的2
分硬币比小明的2分硬币多26枚。
小明有134枚硬币,比小红多13枚。
小明和小红的硬币的币值共分。
13.某裁缝做1件上衣的时间能做3条短裤或5个背心,他一天能做1件上衣、2条短裤、
3个背心。
那么他做上衣、短裤、背心各102件,需天?
14.在下列算式中,不同的汉字代表不同的数字,则“巧学英语”代表。
15.如右图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,
要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是平方米?
16.一项工程,甲单独做要12小时完成,乙单独做要18小时完成.若甲先做1小时,然
后乙接替甲做1小时,再由甲接替乙做1小时,……,两人如此交替工作,请问:完成任务时,共用了小时?
17.32003+2003除以7所得的余数是。
18.一个回文数是从前后两头读去都相同的整数(例如:28482)。
请问在100和10000之间
有个回文数。
19.有一个圆形跑道,甲、乙二人同时从同一点沿同一方向出发,当甲跑完三圈到达出发
点时恰好第一次追上乙。
如果两人骑上自行车,每秒都快了6米,那么甲骑完7圈到达出发点时恰好第一次追上乙。
乙每秒跑米?
20.小娟喜欢收集布偶动物,她将红、蓝、黄色的小熊、小猫、小狗布偶各1只
(共9只)排成三行三列的方阵,然后请她的弟弟来猜。
小娟提示说:
(a)有一只红色动物右边相连的格子上是小熊;
(b)蓝色小熊的左下方的格子上也是小熊;
(c)小狗的正上方相连的格子上不可以是小猫;
(d)有一只黄色动物的下面一行且不是正下方有黄色的小猫;
(e)红色小狗的左上方的格子上也是小狗;
(f)第一列第一行和第一列第二行的位置上只有一只黄色动物;
(g)在第一列上小熊的右边那一列最下方的格子上也是小熊;
(h)黄色动物同一列的右方的格子上(不一定是相连的格子)不可以有黄色的小狗。
请问在第二行第一列的格子上放的动物布偶的颜色是。
