高中数学人教版必修5课件:第二章 数列前n项和的求法(2课时) (共16+11张PPT)
合集下载
高中数学人教A版必修5数列数列求和(二)PPT课件

解得
,
或
,
舍 解得 ,即数列 的通项公式
;
,
数列 的前 n 项和
高中数学 人教A版 必修5 数列数 列求和 (二)P PT课件
.Hale Waihona Puke 高中数学 人教A版 必修5 数列数 列求和 (二)P PT课件
练习:已知数列 的前 n 项和 Ⅰ 求 的通项公式;
.
Ⅱ记
,求数列 的前 n 项和.
解: Ⅰ 数列 的前 n 项和
通项是什么?
=2(1-n+1 1)=n2+n1.
高中数学人教A版必修5数列数列求和 (二)P PT课件
高中数学 人教A版 必修5 数列数 列求和 (二)P PT课件
练习:在各项均为正数的等比数列
中,
求等比数列 的通项公式;
,且 ,
成等差数列.
若数列 满足
,求数列 的前 n 项和 .
解: 设数列列
的公比为 q,
,可得
;
时,
上式对
也成立,则
,
Ⅱ
则数列 的前 n 项和为
.
高中数学 人教A版 必修5 数列数 列求和 (二)P PT课件
,
;
高中数学人教A版必修5数列数列求和 (二)P PT课件
裂项相消法求和法(拆项法):
适用于分式的形式把一项拆成两个分式差的形式,然后再求和.
也就是将数列的每一项拆成二项或多项使数列中的项出现有规律的 抵消项,进而达到求和的目的。
归纳小结
(1)公式法.
(2)分组化归法.将该数列的通项变形后,每一项拆成两项或多项,重新分组,将一般数列
求和化为特殊数列求和.
(3)并项求和法.(4)错位相减法.(5)倒序相加法.
高中数学人教A版必修5第二章2.5等比数列前n项的求和公式课件

意思意思,第一天给我1元,第二天给我2元,第三天给我4
元,...以后就每天给我的钱是前一天的两倍,一直给我30天,
我们就算两清了,你看100万元,..哇,发财了!猪八戒:猴哥,你可别反悔呀!
孙悟空:那我们可以签一个合同嘛!说着就起草了一份合同.猪八戒
230 = 2 + 22 + ⋯ + 229 + 230
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
②
•
•
•
•
•
猪八戒应还孙悟空的钱:
等比数列
2
3
29
1, 2,2 ,2 , ⋯ ,2
30 = 1 +2+22 +⋯ + 228 + 229 ①
①×2得到:
230 = 2 + 22 + ⋯ + 229 +230
②
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
等比数列的前 n 项和公式
当 q≠1 时, Sn =
a1 ( 1- q n )
.
1-q
正想签字,可转念一想,发现不对劲了,这猴哥本来就精明,做了
生意之后更精了,他会不会又在耍我?
孙悟空借给猪八戒的钱:100×10000×30=3× (元)
就是 3千万元
猪八戒应还孙悟空的钱:
1, 2,22 ,23 , ⋯ ,229
30 = 1 +2+22 ⋯ + 228 + 229
元,...以后就每天给我的钱是前一天的两倍,一直给我30天,
我们就算两清了,你看100万元,..哇,发财了!猪八戒:猴哥,你可别反悔呀!
孙悟空:那我们可以签一个合同嘛!说着就起草了一份合同.猪八戒
230 = 2 + 22 + ⋯ + 229 + 230
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
②
•
•
•
•
•
猪八戒应还孙悟空的钱:
等比数列
2
3
29
1, 2,2 ,2 , ⋯ ,2
30 = 1 +2+22 +⋯ + 228 + 229 ①
①×2得到:
230 = 2 + 22 + ⋯ + 229 +230
②
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
等比数列的前 n 项和公式
当 q≠1 时, Sn =
a1 ( 1- q n )
.
1-q
正想签字,可转念一想,发现不对劲了,这猴哥本来就精明,做了
生意之后更精了,他会不会又在耍我?
孙悟空借给猪八戒的钱:100×10000×30=3× (元)
就是 3千万元
猪八戒应还孙悟空的钱:
1, 2,22 ,23 , ⋯ ,229
30 = 1 +2+22 ⋯ + 228 + 229
人教A版高中数学必修5课件:2.5等比数列的前n项和(共16张PPT)

求a 9 .
解: S6 63 9 2, q 1.
S3 7
7 63
a1 (1 q 3 ) , 1 q
a1 (1 q 6 ) ,
1 q
① ②
② 得 9 1 q3,
①
则 q2,a11.
a9a1q828256.
课堂练习
练习3:
已 知 在 等 比 数 列 a n 中 , S 3 3 ,a 3 1 ,
和
知三求二
课后思考
已 知 在 等 比 数 列 a n 中 , S 3 0 1 3 S 1 0 ,
S 1 0 S 3 0 1 4 0 ,则 S 2 0 _ _ _ _ _ _ .
当一个人用工作去迎接光明,光明很快就会来照耀着他。人在身处逆境时,适应环境的能力实在惊人。人可以忍受不幸,也可以战胜不幸,因为人有着惊人的 挥它,就一定能渡过难关。倘若你想达成目标,便得在心中描绘出目标达成后的景象;那么,梦想必会成真。心等待,就可以每一个人都具有特殊能力的电路, 知道,所以无法充分利用,就好像怀重宝而不知其在;只要能发掘出这项秘藏的能力,人类的能力将会完全大改观,也能展现出超乎常人的能力我这一生不曾 和伟大的著作都来自于求助潜意识心智无穷尽的宝藏。那些最能干的人,往往是那些即使在最绝望的环境里,仍不断传送成功意念的人。他们不但鼓舞自己, 成功,誓不休止。灵感并不是在逻辑思考的延长线上产生,而是在破除逻辑或常识的地方才有灵感。真正的强者,善于从顺境中找到阴影,从逆境中找到光亮 进的目标。每一种挫折或不利的突变,是带着同样或较大的有利的种子。什么叫做失败?失败是到达较佳境地的第一步。失败是坚忍的最后考验。对于不屈不 失败这回事。一次失败,只是证明我们成功的决心还够坚强。失败也是我需要的,它和成功对我一样有价值。我们关心的,不是你是否失败了,而是你对失败 失败?失败是到达较佳境地的第一步。没有人事先了解自己到底有多大的力量,直到他试过以后才知道。对于不屈不挠的人来说,没有失败这回事。要成功不 能,只要把你能做的小事做得好就行了。成功的唯一秘诀——坚持最后一分钟。只有胜利才能生存,只有成功才有代价,只有耕耘才有收获。只有把抱怨环境 的力量,才是成功的保证。不要为已消尽之年华叹息,必须正视匆匆溜走的时光。 当许多人在一条路上徘徊不前时,他们不得不让开一条大路,让那珍惜时间 面去。 敢于浪费哪怕一个钟头时间的人,说明他还不懂得珍惜生命的全部价值。成功=艰苦劳动+正确的方法+少说空话。合理安排时间,就等于节约时间。
高中数学人教A版必修5第二章:等比数列的前n项和ppt课件

P58 第1、2题
1 P61 A组 第1、2、3题
已知等比数列 ,
4
4
P58 第1、2题
2、已知等比数列{an}的前n项和
国王赏麦的故事
如2何求、等比数列已的Sn: 知等比数列{an}的前n项和
Sn 3n 1 2a,求实数a的值.
1 a 2 ,S 1 4 .则 q a 2、已知等比数列{an}的前n项和
1 例1:求等比数列
例1:求等比数列
3 的前8项的和。
的前8项的和。
3
等差数列求和方法回顾:(倒序相加) 等差数列求和方法回顾:(倒序相加) 国王赏麦的故事
已知等比数列 ,
2或-3 8或18
2 a 1 , a 2 1 6 则 q -6 ,S 185 已知等比数列 ,
Sn
a1(1na1qn 1q
(q )
1) (q 1)
q 1时:
Sn
a1a1qn 1q
a1anq 1q
注意:
1、使用公式求和时,需注意对 q 1 和 q 1 的情
况加以讨论;
2、推导公式的方法: 错位相减法
a1、 q、 n、 an、 sn 知三求二
公式应用:
例1:求等比数列
1 , 1 , 1 , 248
国王赏麦的故事
1 2 2 2 2 3 2 6 3
S 6 41 2 4 8 2 6 22 63 ①
2 S 6 42 4 8 2 6 2 2 6 3 2 6②4
②—64
中间各 数均为0
国王能兑现自己的承诺吗?
如何求等比数列的Sn:
的前8项的和。
解:由 a11 2,q1 41 21 2,n8,得
Sn
1 [1 (1)8] 22
1 P61 A组 第1、2、3题
已知等比数列 ,
4
4
P58 第1、2题
2、已知等比数列{an}的前n项和
国王赏麦的故事
如2何求、等比数列已的Sn: 知等比数列{an}的前n项和
Sn 3n 1 2a,求实数a的值.
1 a 2 ,S 1 4 .则 q a 2、已知等比数列{an}的前n项和
1 例1:求等比数列
例1:求等比数列
3 的前8项的和。
的前8项的和。
3
等差数列求和方法回顾:(倒序相加) 等差数列求和方法回顾:(倒序相加) 国王赏麦的故事
已知等比数列 ,
2或-3 8或18
2 a 1 , a 2 1 6 则 q -6 ,S 185 已知等比数列 ,
Sn
a1(1na1qn 1q
(q )
1) (q 1)
q 1时:
Sn
a1a1qn 1q
a1anq 1q
注意:
1、使用公式求和时,需注意对 q 1 和 q 1 的情
况加以讨论;
2、推导公式的方法: 错位相减法
a1、 q、 n、 an、 sn 知三求二
公式应用:
例1:求等比数列
1 , 1 , 1 , 248
国王赏麦的故事
1 2 2 2 2 3 2 6 3
S 6 41 2 4 8 2 6 22 63 ①
2 S 6 42 4 8 2 6 2 2 6 3 2 6②4
②—64
中间各 数均为0
国王能兑现自己的承诺吗?
如何求等比数列的Sn:
的前8项的和。
解:由 a11 2,q1 41 21 2,n8,得
Sn
1 [1 (1)8] 22
高中数学 第二章 数列 2.5 等比数列的前n项和 第2课时 数列求和课件 新人教A版必修5

(2)由(1)可得 bn=2n+n, 所以 b1+b2+b3+…+b10 =(2+1)+(22+2)+(23+3)+…+(210+10) =(2+22+23+…+210)+(1+2+3+…+10) =2(11--2210)+(1+120)×10 =(211-2)+55 =211+53=2 101.
第二章 数列
第 2 课时 数列求和
第二章 数列
1. 能 由 简 单 的 递 推 公 式 求 出 数 列 的 通 项 公 式. 2.掌握数列求和的几种基本方法.
1.基本求和公式 (1)等差数列的前 n 项和公式 Sn=n(a12+an)=na1+n(n2-1)d. (2)等比数列的前 n 项和公式 当 q=1 时,Sn=_n_a_1_; 当 q≠1 时,Sn=a1(11--qqn)=a11--aqnq.
求和时易忽视两边同 除以-3
(1)一般地,如果数列{an}是等差数列,{bn}是等比数列,求数 列{an·bn}的前 n 项和时,可采用错位相减法. (2)用错位相减法求和时,应注意 ①要善于识别题目类型,特别是等比数列公比为负数的情形更 值得注意; ②在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对 齐”,以便于下一步准确写出“Sn-qSn”的表达式; ③应用等比数列求和公式必须注意公比 q≠1 这一前提条件,如 果不能确定公比 q 是否为 1,应分两种情况讨论.
探究点二 裂项相消法求和
(2015·高考全国卷Ⅰ改编)数列{an}满足 a1=3,an+1=an +2. (1)求{an}的通项公式; (2)设 bn=ana1n+1,求数列{bn}的前 n 项和. [解] (1)由 a1=3,an+1=an+2, 所以{an}是首项为 3,公差为 2 的等差数列,通项公式为 an =2n+1.
高中数学人教版必修5课件:第二章 数列前n项和的求法(2课时) (共16+11张PPT)1

Sn
a1(1 qn ) 1q
(2)当q=1时, Sn = na1
5、错项相减法:
• 若在数列{an·bn}中,{an}成等差数列,{bn}成等比 数列,求和时一般在已知和式的两边都乘以组成 这个数列的等比数列的公比;然后再将得到的新 和式和原和式相减,转化为同倍数的等比数列求 和,这种方法就是错位相减法。
当 a=1时,S=1+2+3+…+n n(n 1)
2
当 a≠1时,(1-a)S= 1 an -naSn
1 a
n(n 1)
S
1
(1
2
an a)2
na n 1 a
a 1 a 1
1 an (1 a )2
na n 1 a
知识盘点
• 4、倒序相加法:
• 5、错项相减法:
课后作业
播下一个行动,收获一种习惯;播下一种习惯,收获一种性格;播下一种性格,收获一种命运。思想会变成语言,语言会变成行动,行动会变成习惯,习惯会变成性格。性 制,会变成生活的必需品,不良的习惯随时改变人生走向。人往往难以改变习惯,因为造习惯的就是自己,结果人又成为习惯的奴隶!人生重要的不是你从哪里来,而是你 时侯,一定要抬头看看你去的方向。方向不对,努力白费!你来自何处并不重要,重要的是你要去往何方,人生最重要的不是所站的位置,而是所去的方向。人只要不失去 这个世界唯一不变的真理就是变化,任何优势都是暂时的。当你在占有这个优势时,必须争取主动,再占据下一个优势,这需要前瞻的决断力,需要的是智慧!世上本无移 是:山不过来,我就过去。人生最聪明的态度就是:改变可以改变的一切,适应不能改变的一切!亿万财富不是存在银行里,而是产生在人的思想里。你没找到路,不等于 什么,你必须知道现在应该先放弃什么!命运把人抛入最低谷时,往往是人生转折的最佳期。谁能积累能量,谁就能获得回报;谁若自怨自艾,必会坐失良机人人都有两个 一个是心门,成功的地方。能赶走门中的小人,就会唤醒心中的巨人!要想事情改变,首先自己改变,只有自己改变,才可改变世界。人最大的敌人不是别人,而是自己, 1、烦恼的时候,想一想到底为什么烦恼,你会发现其实都不是很大的事,计较了,就烦恼。我们要知道,所有发生的一切都是该发生的,都是因缘。顺利的就感恩,不顺 寒潭,雁过而潭不留影;风吹疏竹,风过而竹不留声。”修行者的心境,就是“过而不留”。忍得住孤独;耐得住寂寞;挺得住痛苦;顶得住压力;挡得住诱惑;经得起折腾 得起责任;1提得起精神。闲时多读书,博览凝才气;众前慎言行,低调养清气;交友重情义,慷慨有人气;困中善负重,忍辱蓄志气;处事宜平易,不争添和气;对已讲 远,修身立正气;居低少卑怯,坦然见骨气;卓而能合群,品高养浩气淡然于心,自在于世间。云淡得悠闲,水淡育万物。世间之事,纷纷扰扰,对错得失,难求完美。若 陷于计较的泥潭,不能自拔。若凡事但求无愧于心,得失荣辱不介怀,自然落得清闲自在。人活一世,心态比什么都重要。财富名利毕竟如云烟,心情快乐才是人生的至宝 在脚踏实地的道路上;我们的期待在哪里?在路上,在勤劳勇敢的心路上;我们的快乐在哪里?在路上,在健康阳光的大道上;我们的朋友在哪里?在心里,在真诚友谊的 己负责;善于发现看问题的角度;不满足于现状,别自我设限;勇于承认错误;不断反省自己,向周围的成功者学习;不轻言放弃。做事要有恒心;珍惜你所拥有的,不要 美;不找任何借口。与贤人相近,则可重用;与小人为伍,则要当心;只满足私欲,贪图享乐者,则不可用;处显赫之位,任人唯贤,秉公办事者,是有为之人;身处困境 任;贫困潦倒时,不取不义之财者,品行高洁;见钱眼开者,则不可用。人最大的魅力,是有一颗阳光的心态。韶华易逝,容颜易老,浮华终是云烟。拥抱一颗阳光的心态 心无所求,便不受万象牵绊;心无牵绊,坐也从容,行也从容,故生优雅。一个优雅的人,养眼又养心,才是魅力十足的人。容貌乃天成,浮华在身外,心里满是阳光,才 随流水宁。心无牵挂起,开阔空净明。幸福并不复杂,饿时,饭是幸福,够饱即可;渴时,水是幸福,够饮即可;裸时,衣是幸福,够穿即可;穷时,钱是幸福,够用即可 困时,眠是幸福,够时即可。爱时,牵挂是幸福,离时,回忆是幸福。人生,由我不由天,幸福,由心不由境。心是一个人的翅膀,心有多大,世界就有多大。很多时候限 也不是他人的言行,而是我们自己。人心如江河,窄处水花四溅,宽时水波不兴。世间太大,一颗心承载不起。生活的最高境界,一是痛而不言,二是笑而不语。无论有多 幸福在于祥和,生命的祥和在于宁静,宁静的心境在于少欲。无意于得,就无所谓失去,无所谓失去,得失皆安谧。闹市间虽见繁华,却有名利争抢;田园间无争,却有柴 最终不过梦一场。心静,则万象皆静。知足者常在静中邂逅幸福。顺利人生,善于处理关系;普通人生,只会使用关系;不顺人生,只会弄僵关系。为人要心底坦荡,不为 不为假象所惑。智者,以别人惨痛的教训警示自己;愚者,用自己沉重的代价唤醒别人。对人多一份宽容,多一份爱心;对事多一份认真,多一份责任;对己多一点要求, 可满,乐不可极,警醒自己。静能生慧。让心静下来,你才能看淡一切。静中,你才会反观自己,知道哪些行为还需要修正,哪些地方还需要精进,在静中让生命得到升华 心静下来,你才能学会放下。你放下了,你的心也就静了。心不静,是你没有放下。静,通一切境界。人与人的差距,表面上看是财富的差距,实际上是福报的差距;表面 人品的差距;表面上看是气质的差距,实际上是涵养的差距;表面上看是容貌的差距,实际上是心地的差距;表面上看是人与人都差不多,内心境界却大不相同,心态决定 一件事。因为当一个人具有感恩的心,心会常常欢喜,总是觉得很满足,一个不感恩不满足的人,总是会觉得欠缺、饥渴。一个常感恩的人,会觉得自己很幸运,有时候其 一感恩,就变得很快乐。这种感恩的心,对自己其实是有很大利益。压力最大的时候,效率可能最高;最忙碌的时候,学的东西可能最多;最惬意的时候,往往是失败的开 光临。成长不是靠时间,而是靠勤奋;时间不是靠虚度,而是靠利用;感情不是靠缘分,而是靠珍惜;金钱不是靠积攒,而是靠投资;事业不是靠满足,而是靠踏实。知恩 为当一个人具有感恩的心,心会常常欢喜,总是觉得很满足,一个不感恩不满足的人,总是会觉得欠缺、饥渴。一个常感恩的人,会觉得自己很幸运,有时候其实没什么道 就变得很快乐。这种感恩的心,对自己其实是有很大利益。压力最大的时候,效率可能最高;最忙碌的时候,学的东西可能最多;最惬意的时候,往往是失败的开始;寒冷 长不是靠时间,而是靠勤奋;时间不是靠虚度,而是靠利用;感情不是靠缘分,而是靠珍惜;金钱不是靠积攒,而是靠投资;事业不是靠满足,而是靠踏实。以平常心观不 面前,平常心就是勇敢;在利诱面前,平常心就是纯洁;在复杂的环境面前,平常心就是保持清醒智慧。平常心不是消极遁世,而是一种境界,一种积极的人生。不仅要为 价值的人而努力。命运不是机遇,而是选择;命运不靠等待,全靠争取。成熟就是学会在逆境中保持坚强,在顺境时保持清醒。时间告诉你什么叫衰老,回忆告诉你什么叫 的赞许时,心灵才会真的自由。你没那么多观众,别那么累。温和对人对事。不要随意发脾气,谁都不欠你的。现在很痛苦,等过阵子回头看看,会发现其实那都不算事。 有绝交,才有至交学会宽容伤害自己的人,因为他们很可怜,各人都有自己的难处,大家都不容易。学会放弃,拽的越紧,痛苦的是自己。低调,取舍间,必有得失。不要 面前没人爱听那些借口。慎言,独立,学会妥协的同时,也要坚持自己最基本的原则。付出并不一定有结果。坚持可能会导致失去更多过去的事情可以不忘记,但一定要放 个最好的打算和最坏的打算。做一个简单的人,踏实而务实。不沉溺幻想。不庸人自扰。不说谎话,因为总有被拆穿的一天。别人光鲜的背后或者有着太多不为人知的痛苦 不管学习什么,语言,厨艺,各种技能。注意自己的修养,你就是孩子的第一位老师。孝顺父母。不只是嘴上说说,即使多打几个电话也是很好的。爱父母,因为他们给了 无私的人。
高中数学人教版必修五《2.5等比数列的前n项和2》课件

题型三 错位相减法求和
【例3】 (12分) 已知{an}是等差数列,其前n项和为Sn,{bn}是等比数列,且 a1=b1=2,a4+b4=27,S4-b4=10. (1)求数列{an}与{bn}的通项公式; (2)记Tn=a1b1+a2b2+…+anbn,n∈N*,证明Tn-8=an-1bn+1(n∈N*,n≥2). 名师导引: (1)如何求an、bn?(由条件列方程组求出公差d、公比q即可) (2)和式Tn有何特点?如何求Tn?(和式中的每一项均是由一等差数列和一等比 数列对应项的积构成,故运用错位相减法求Tn)
n1个2相加 2
= 2× n 1 -(2n-1)=-n. 2 n, n为偶数,
即 Sn= n, n为奇数.
(2)由(1)知 Tn=S1+S2+S3+…+Sn=-1+2-3+4-5+…+(-1)nn
=
n 2 n
, n为偶数时,
1 n n 1,
2
2
n为奇数时.
即 Tn=
n 2
,
n为偶数,
∵Tn=
1 31
+
3 32
+
5 33
+…+
2n 1 3n
,
①
∴
1 3
Tn=
1 32
+
3 33
+
5 34
+…+
2n 3 3n
+
2n 1 3n 1
.②
①-②,得
2 3
Tn= 1 3
+
2 32
+
2 33
人教A版高中数学必修5课件:2.5等比数列的前n项和(共16张PPT)

等比数列 {an},公比为 q ,它的前 n 项和 Sn a1 a2 a3 an1 an,
a2 a1q, a3 a2q, a4 a3q, an an1q,
a 2 a 3 a n q ( a 1 a 2 a 3 a n 1 )
S na 1q (S na n). (1 q )S na 1 a n q .
求a 9 .
解: S6 63 9 2, q 1.
S3 7
7 63
a1 (1 q 3 ) , 1 q
a1 (1 q 6 ) ,
1 q
① ②
② 得 9 1 q3,
①
则 q2,a11.
a9a1q828256.
课堂练习
练习3:
已 知 在 等 比 数 列 a n 中 , S 3 3 ,a 3 1 ,
方法拓展2
提取公比法
等比数列 {an},公比为 q ,它的前 n 项和
Sn a1 a2 a3 an1 an
Sn a1 a1q a21q 2 ana12qqn2 ana11qqn1
a1a 1 q(aq 1( a 1 a1 q a 2 a1q na 3 n a2 1q na 2n ) 1 )
qqS(Sn1(n1qq)a)SS1naqn2aa1aq1a123aan1qqa.n1q ann21a1q nan1a1aqnnq,
当当qq11时时, sSnnnna1a1,
当当qq11时时, sSnna1a(1111qqaqnn)q .
你还有其他方法去推导等比 数列前n项和公式吗
方法拓展1
累加法
和
知三求二
课后思考
已 知 在 等 比 数 列 a n 中 , S 3 0 1 3 S 1 0 ,
S 1 0 S 3 0 1 4 0 ,则 S 2 0 _ _ _ _ _ _ .
高中数学第二章数列2.5等比数列的前n项和(2)课件新人教A版必修5

an=SS1n,-Sn-1,nn≥=21, =12, n-1,nn≥=21,, n∈N*是等比数列;
当 Sn=2n+1-1 时,
an=SS1n,-Sn-1,nn≥=21,
=32, n,
n=1, n≥2,
n∈N*,不是等比数列.
第五页,共37页。
梳理 当 (sh公ū比lǐ)q≠1时,设A= q-a11,等比数列的前n项和公式是Sn=A(qn-1).
第二十三页,共37页。
答案 解析 (dá ( jiě xī) àn)
反思与感悟
注意观察(guānchá)序号之间的联系,发现解题契机;整体思想能使 问题解决过程变得简洁明快.
第二十四页,共37页。
跟踪训练3 设数列{an}是以2为首(wéishǒu)项,1为公差的等差数列;数列{bn}是
以1为首(wéishǒu)项,2为公比的等比数列b,a1+则 ba2+ba3+…+ba6
项和,则:①在其前2n项中, SS偶 奇=q; ②在其前 2n+1 项中,S 奇-S 偶=a1-a2+a3-a4+…-a2n+a2n+1=
a11+-a(-2n+q1)q=a1+1+a2qn+2(q≠-1).
第九页,共37页。
知识点三 错位(cuò wèi)相减法
思考(sīkǎo)
在上一节,我们是如何求公比不为1的等比数列{an}的前n项和 Sn=a1+a2+…+an的?
∴Sn=2-2n1-1-2nn=2-n+2n 2.
第二十六页,共37页。
反思与感悟
一般地,如果(rúguǒ)数列{an}是等差数列,{bn}是等比数列,求数列 {anbn}的前n项和时,可采用错位相减法.
第二十七页,共37页。
跟踪(gēnzōng)训练4 求和:Sn=x+2x2+3x3+…+nxn (解x≠答0).
人教版高中数学必修5第二章数列-《2.5等比数列的前n项和》课件(2)
变式训练:如果是前n项和呢?
1 1 1 2 3 2 2 2
1 2
1 1 n 1 n 2 2
1 2
1
1 1 2 2 2
1 1 1 2 3 2 2 2
1 1 1 1 2 3 4 2 2 2 2
1 2 2 1 3 2
1 4 2
吴敬所著的《九章算法比类大全》中 载有如下这样一首“数学诗”:
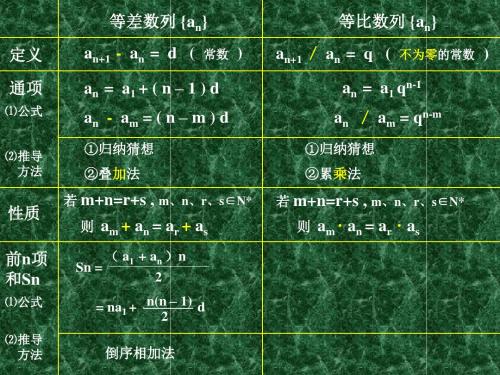
an - am = ( n – m ) d
①归纳猜想 ②叠加法 若 m+n=r+s , m、n、r、s∈N* 则 am + an = ar + as ( a1 + a n ) n Sn = 2 = na1 + n(n – 1) d 2 倒序相加法
⑵推导 方法
性质
前n项 和Sn
⑴公式 ⑵推导 方法
等比数列的前n项和
数学就像人类的一部特制的精密的大型望 远镜或显微镜一样,它大大延伸了人们洞察自 然地能力,看到了不掌握数学的人无法看到的 那个世界,能使人看到那些不懂数学的人无法 看到的东西。 ---张楚廷《数学文化》
五.小结
1.从知识方面来小结 na1 sn a1 (1 q n ) a1 an q 1 q 或 1 q
q 1
q 1
结论:若数列an 是等比数列,
则sm , s2m sm , s3m s2m,
也是等比数列
2.从数学思想方法方面来小结
1 2 2 2 2 =18446744073709551615
①归纳猜想 ②叠加法 若 m+n=r+s , m、n、r、s∈N* 则 am + an = ar + as ( a1 + a n ) n Sn = 2 = na1 + n(n – 1) d 2 倒序相加法
高中数学人教A版必修5第二章:求数列前n项和的几种常见方法课件

例3、求和(2 3 51) (4 3 52 )
(2n 3 5n )
解:(2 3 51) (4 3 52 ) (2n 3 5n )
(2 4 2n) (3 51 3 52 3 5n )
2(1 2 n) 3(51 52 5n )
2
n(n 1) 2
例4、求和1 2x 3x2 nxn1
解:设Sn 1 2x 3x2 4x3 nxn1①
当x
1时,Sn
1
2
3
n
n(n 1) 2
当x 1时,则xSn x 2x2 3x3 (n 1)xn1 nxn② ①-②得:(1 x)Sn 1 x x2 xn1 nxn
即(1
1 3
1 ...... 2 2 3
1 n 1
. n
Sn
1 22
2 23
n 2n
1
n 2n1
相减得 :
1 2
Sn
1 (
2
1 22
1 23
1 2n
)
n 2n1
1 2
(1
1 2n
)
1
1
n 2n1
1
1 2n
n 2n1
.
所以,
2 n2 Sn 2 2n1 (n N*).
常见的数列求和方法
(5)裂项求和法:有时把一个数列的通项公式分成两项差的形式, 相加过程消去中间项,只剩有限项再求和。
2(12n ) 12
n
2n1
n2
常见的数列求和方法
(3)分组求和法:把一个数列分成几个可以直接求和的数列
例2、求和: (a 1) (a2 2) (an n)
解:(a 1) (a2 2) (an n)
(人教新课标)高二数学必修5第二章 数列2-5《等比数列的前n项和》课件(共21张PPT)

解: Sn=1+a+a2+…+an-1, 当 a=1 时,Sn=1+1+…+1=n; 当 a≠1,且 a≠0 时,Sn=11--aan=aan--11. 当 a=0 时满足上式.
n a=1 ∴Sn=aan--11a≠1 .
乘公比
q≠1,q=1
错位相减 等比数列的 分类讨论
前n项和公式
等比数列的前n项和
设等比数列 a1, a2 , a3,, an ,
它的前n项和是 Sn a1 a2 a3 an
即 Sn a1 a1q a1q2 a1qn2 a1qn1. ⑴
⑴×q, 得
qSn
a1q a1q2 a1qn2 a1qn1 a1qn. ⑵
⑴-⑵,得 1 q Sn a1 a1qn ,
说明:这种求和方法称为错位相减法
当q≠1时, 当q=1时,
Sn
a1
1qn 1 q
Sn na1
于是
Sn
naa1(11, (qqn 1 q
1), ) ,(q
1).
注:(1)公式中涉及a1, q, n, an , Sn 五个量
于是得到5000(1 1.1n ) 30000 1 1.1
整理后,得1.1n 1.6 两边取对数,得n lg1.1 lg1.6
n lg1.6 0.20 5(年) lg1.1 0.041
变式 4:在等比数列{an}中,公比 q=-2,S5=22,则 a1 的值
整理,得 1+q3=9,解得 q=2. 将 q=2 代入a111--qq3=72,得 a1=12, 故 an=a1qn-1=2n-2.
例3:某商场第1年销售计算机5000台,如果平均每年的销售量比 上一年增加10%,那么从第1年起,约几年内可使总销售量达到 30000台(保留到个位)?
n a=1 ∴Sn=aan--11a≠1 .
乘公比
q≠1,q=1
错位相减 等比数列的 分类讨论
前n项和公式
等比数列的前n项和
设等比数列 a1, a2 , a3,, an ,
它的前n项和是 Sn a1 a2 a3 an
即 Sn a1 a1q a1q2 a1qn2 a1qn1. ⑴
⑴×q, 得
qSn
a1q a1q2 a1qn2 a1qn1 a1qn. ⑵
⑴-⑵,得 1 q Sn a1 a1qn ,
说明:这种求和方法称为错位相减法
当q≠1时, 当q=1时,
Sn
a1
1qn 1 q
Sn na1
于是
Sn
naa1(11, (qqn 1 q
1), ) ,(q
1).
注:(1)公式中涉及a1, q, n, an , Sn 五个量
于是得到5000(1 1.1n ) 30000 1 1.1
整理后,得1.1n 1.6 两边取对数,得n lg1.1 lg1.6
n lg1.6 0.20 5(年) lg1.1 0.041
变式 4:在等比数列{an}中,公比 q=-2,S5=22,则 a1 的值
整理,得 1+q3=9,解得 q=2. 将 q=2 代入a111--qq3=72,得 a1=12, 故 an=a1qn-1=2n-2.
例3:某商场第1年销售计算机5000台,如果平均每年的销售量比 上一年增加10%,那么从第1年起,约几年内可使总销售量达到 30000台(保留到个位)?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 4
)
L
(1
n
n
1
) 1
1
n
1
1
n
n
1
3、裂项相消法:
•
如果一个数列{an}的通项公式为
an
bn
1 cn
,
{bn}和{cn}均为等差数列,且∣bn-cn∣=d(d
为常数),则我们往往采用裂项相消法。
追踪练习
1、数列{an}的通项公式
an
n
1 (n
,
2)
求它的前n项和Sn。
? an
1
n (n 2)
1、公式法:
• 若问题可以转化为等差、等比数列, 则可以直接利用求和公式即可。
几个常用的数列求和:
12 22 32 n2 1 n(n 1)(2n 1) 6
13 23 33 n3 1 n2 (n 1)2 4
抛 砖
【2】求数列1 1 , 2 1 , 3 1, 4 1 ,
2 4 8 16
1
n
n
1 2
1(1
2n
n
1
) 2
合作交流
【例】求和:
1 (1 2) (1 2 22 ) ··· (1 2 22 ··· 2n1)
解:由题知
an 1 2 ··· 2n1
1 2n
2n
1
1 2
sn a1 a2 ··· an
2 22 ···2n n
2(1 2n ) n 1 2
追踪练习
(1)(a-1)+(a2-2)+ …+(an-n);
(2)(2-3×5-1)+(4-3×5-2)+…+ (2n-3×5-n)
抛砖引玉
【3】求和: 1 1 1 1
1 2 23 3 4
n (n 1)
? 解:an
1
n(n 1)
1
n
1
n 1
sn
(1
1) 2
(
如果题中的第n项本身就 是一个和式,那么可先将通 项公式化简再求和。
知识盘点
• 1、公式法: • 2、分组求和法: • 3、裂项相消法:
课后作业
不知道自己缺点的人,一辈子都不会想要改善。成功的花,人们只惊慕她现时的明艳!然而当初她的芽儿,浸透了奋斗的泪泉,洒遍了牺牲的血雨。成功的条件在于勇气和 信乃是由健全的思想和健康的体魄而来。成功了自己笑一辈子,不成功被人笑一辈子。成功只有一个理由,失败却有一千种理由。从胜利学得少,从失败学得多。你生而有 前进,形如蝼蚁。你一天的爱心可能带来别人一生的感谢。逆风的方向,更适合飞翔。只有承担起旅途风雨,才能最终守得住彩虹满天只有创造,才是真正的享受,只有拚 活。知识玩转财富。志不立,天下无可成之事。竹笋虽然柔嫩,但它不怕重压,敢于奋斗、敢于冒尖。阻止你前行的,不是人生道路上的一百块石头,而是你鞋子里的那一 爱,不必呼天抢地,只是相顾无言。最值得欣赏的风景,是自己奋斗的足迹。爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。生活不可能像你想 不会像你想的那么糟。时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵,昨天的太阳,晒不干今天的衣裳。实现梦想往往是一个艰苦的坚持的 到位,立竿见影。那些成就卓越的人,几乎都在追求梦想的过程中表现出一种顽强的毅力。世界上唯一不变的字就是“变”字。事实胜于雄辩,百闻不如一见。思路决定出路 细节决定成败,性格决定命运虽然你的思维相对于宇宙智慧来说只不过是汪洋中的一滴水,但这滴水却凝聚着海洋的全部财富;是质量上的一而非数量上的一;你的思维拥 所有过不去的都会过去,要对时间有耐心。人总会遇到挫折,总会有低潮,会有不被人理解的时候。如果你希望成功,以恒心为良友,以经验为参谋,以小心为兄弟,以希 个人不知道他要驶向哪个码头,那么任何风都不会是顺风。沙漠里的脚印很快就消逝了。一支支奋进歌却在跋涉者的心中长久激荡。上天完全是为了坚强你的意志,才在道 碍。拥有资源不能成功,善用资源才能成功。小成功靠自己,大成功靠团队。炫耀什么,缺少什么;掩饰什么,自卑什么。所谓正常人,只是自我防御比较好的人。真正的 防而又不受害。学习必须如蜜蜂一样,采过许多花,这才能酿出蜜来态度决定高度。外在压力增加时,就应增强内在的动力。我不是富二代,不能拼爹,但为了成功,我可 站在万人中央成为别人的光。人一辈子不长不短,走着走着,就进了坟墓,你是要轰轰烈烈地风光下葬,还是一把骨灰撒向河流山川。严于自律:不能成为自己本身之主人 他周围任何事物的主人。自律是完全拥有自己的内心并将其导向他所希望的目标的惟一正确的途径。生活对于智者永远是一首昂扬的歌,它的主旋律永远是奋斗。眼泪的存 伤不是一场幻觉。要不断提高自身的能力,才能益己及他。有能力办实事才不会毕竟空谈何益。故事的结束总是满载而归,就是金榜题名。一个人失败的最大原因,是对自 的信心,甚至以为自己必将失败无疑。一个人炫耀什么,说明内心缺少什么。一个人只有在全力以赴的时候才能发挥最大的潜能。我们的能力是有限的,有很多东西飘然于 之外。过去再优美,我们不能住进去;现在再艰险,我们也要走过去!即使行动导致错误,却也带来了学习与成长;不行动则是停滞与萎缩。你的所有不甘和怨气来源于你 你可以平凡,但不能平庸。懦弱的人只会裹足不前,莽撞的人只能引为烧身,只有真正勇敢的人才能所向披靡。平凡的脚步也可以走完伟大的行程。平静的湖面锻炼不出精 生活打造不出生活的强者。人的生命似洪水在奔流,不遇着岛屿、暗礁,难以激起美丽的浪花人生不怕重来,就怕没有将来。人生的成败往往就在于一念之差。人生就像一 为你在看别人耍猴的时候,却不知自己也是猴子中的一员!人生如天气,可预料,但往往出乎意料。人生最大的改变就是去做自己害怕的事情。如果不想被打倒,只有增加 你向神求助,说明你相信神的能力;如果神没有帮助你,说明神相信你的能力。善待自己,不被别人左右,也不去左右别人,自信优雅。活是欺骗不了的,一个人要生活得 象这杯浓酒,不经三番五次的提炼呵,就不会这样一来可口!生命不止需要长度,更需要宽度。时间就像一张网,你撒在哪里,你的收获就在哪里。世上最累人的事,莫过于 你感到痛苦时,就去学习点什么吧,学习可以使我们减缓痛苦。当世界都在说放弃的时候,轻轻的告诉自己:再试一次。过错是暂时的遗憾,而错过则是永远的遗憾!很多 结果,但是不努力却什么改变也没有。后悔是一种耗费精神的情绪后悔是比损失更大的损失,比错误更大的错误所以不要后悔。环境不会改变,解决之道在于改变自己。积 成功者的最基本要素。激情,这是鼓满船帆的风。风有时会把船帆吹断;但没有风,帆船就不能航行。即使道路坎坷不平,车轮也要前进;即使江河波涛汹涌,船只也航行 粹取出来的。浪费时间等于浪费生命。老要靠别人的鼓励才去奋斗的人不算强者;有别人的鼓励还不去奋斗的人简直就是懦夫。不要问别人为你做了什么,而要问你为别人 遥远的梦想和最朴素的生活,即使明天天寒地冻,金钱没有高贵,低贱之分。金钱在高尚人的手中,就会变得高尚;金钱在庸俗人手中,就会变得低级庸俗。涓涓细流一旦 大海也就终止了呼吸。漫无目的的生活就像出海航行而没有指南针。如果我没有,我就一定要,我一定要,就一定能。上一秒已成过去,曾经的辉煌,仅仅是是曾经。其实 在昨天,而是失败在没有很好利用今天。千万人的失败,都有是失败在做事不彻底,往往做到离成功只差一步就终止不做了。强者征服今天,懦夫哀叹昨天,懒汉坐等明天 只是不来的人,要来,千军万马也是挡不住的。求人不如求己;贫穷志不移;吃得苦中苦;方为人上人;失意不灰心;得意莫忘形。人们总是在努力珍惜未得到的,而遗忘 告诉我,无理取闹的年龄过了,该懂事了。时间是个常数,但也是个变数。勤奋的人无穷多,懒惰的人无穷少。手莫伸,伸手必被捉。党与人民在监督,万目睽睽难逃脱。汝 不伸能自觉,其实想伸不敢伸,人民咫尺手自缩。思考是一件最辛苦的工作,这可能是为什么很少人愿意思考的原因。我们不能成为贵族的后代,但我们可以成为贵族的祖先 年后的自己。自信!开朗!豁达!无论现在的你处于什么状态,是时候对自己说:不为模糊不清的未来担忧,只为清清楚楚的现在努力。无人理睬时,坚定执着。万人羡慕 志者常立志,
数列前n项和的求法(1)
Yesterday once more
• 等差数列前n项和公式:
Sn
n(a1 2
an )
Sn
na1
n(n 1) 2
d
• 等比数列前n项和公式:
Sn
na1 a1 (1
q
n
)
1 q
a1 anq 1 q
(q 1) (q 1)
学习目标
1、理解掌握数列的通项公式和数列的前n项 和公式;
2、熟练掌握等差、等比数列的求和方法; 3、培养学生的数学应用意识,加强分析问题、
解决问题的能力训练。 • 重点:数列求和的常用思想方法。 • 难点:运用数学知识和方法分析、解决数学
应用问题的能力。
抛 砖 【1】设数列{an}的通项为an=2n-7(n∈N*), 引 玉 则∣a1∣+ ∣a2∣+ …+∣a15∣=___。
引 的前n项和。
玉 解:因为an
n
1
2n
所以,sn
(1
1) 2
(2
1) 4
(3
1 8
)
L
(n
1 2n
)
=(1+2+3+ L
n(n 1)
2
n)+(
1 (1 2
1
1 2
+1+ 21n4)
1
2
1 8
+
L
+1 2n
)
n2 n
2
1 2n
1
2、分组求和法:
• 若 数 列 {an} 的 通 项 公 式 为 an=bn+cn , 其 中 {bn}、{cn}中一个是等差数列,另一个是等 比数列,求和时一般用分组求和法。
