南昌大学极值应用题
专题03 极值与最值问题(文理通用)(含详细答案)
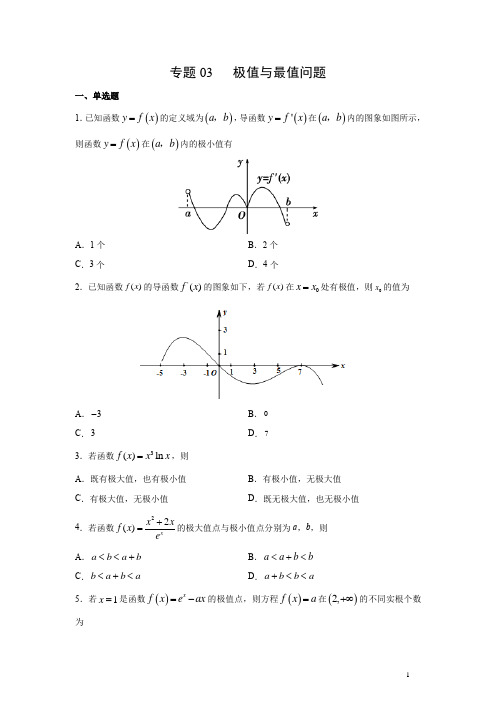
专题03 极值与最值问题一、单选题1.已知函数()y f x =的定义域为()a b ,,导函数()'y f x =在()a b ,内的图象如图所示,则函数()y f x =在()a b ,内的极小值有A .1个B .2个C .3个D .4个2.已知函数()f x 的导函数()'f x 的图象如下,若()f x 在0x x =处有极值,则0x 的值为A .3-B .0C .3D .73.若函数3()ln f x x x =,则 A .既有极大值,也有极小值 B .有极小值,无极大值 C .有极大值,无极小值D .既无极大值,也无极小值4.若函数22()xx x f x e+=的极大值点与极小值点分别为a ,b ,则 A .a b a b <<+ B .a a b b <+< C .b a b a <+<D .a b b a +<<5.若1x =是函数()xf x e ax =-的极值点,则方程()f x a =在()2,+∞的不同实根个数为A .1B .2C .3D .06.已知函数()y f x =的导函数()y f x ='的图象如图所示,则下列结论正确的是A .函数()y f x =在(),1-∞-上是增函数B .3x =是函数()y f x =的极小值点C .()()35f f ''<D .()()13f f -<7.已知32()f x x px qx =++的图象与x 轴相切于非原点的一点,且f (x )极小值=-4,那么p ,q 值分别为 A .8,6 B .9,6 C .4,2D .6,98.已知函数1ln ()e +=-x xf x x,则()f x 的最大值是 A .1- B .2- C .0D .1e -9.已知1x =是函数32()3f x ax x =-的极小值点,则函数()f x 的极小值为 A .0 B .1- C .2D .410.已知函数()2ln f x x a x =+的图象在(1,f (1))处的切线经过坐标原点,则函数y =f (x )的最小值为 A .11ln 222- B .1ln 24+ C .11ln 222+ D .111.已知函数()sin xf x e a x =-在区间0,3π⎛⎫ ⎪⎝⎭上有极值,则实数a 的取值范围是A .()0,1B .()1,eC .()1,2eD .31,2e π⎛⎫ ⎪⎝⎭12.若函数()221xf x e ax =-+有两个不同的极值点,则实数a 的取值范围是 A .4ea <- B .04ea -<< C .4e a >D .04ea <<13.已知函数()22ln 3f x x ax x =+-在2x =处取得极小值,则()f x 在1,32⎡⎤⎢⎥⎣⎦的最大值为 A .52-B .92ln 32-C .1-D .2ln 24-14.设函数,(),x xx af x e x x a⎧≥⎪=⎨⎪<⎩,若函数存在最大值,则实数a 的取值范围是A .1a ≤B .1a <C .1a e ≤D .1a e<15.已知函数()33f x x x =-,则下列说法正确的是 A .()f x 是偶函数 B .1是()f x 的极小值点 C .3是()f x 的极大值点 D .()f x 在区间()0,1内单调递增16.已知函数1()cos 1f x x x =-+,()'f x 为()f x 的导函数,则下列结论正确的个数是 ①当(1,0)x ∈-时,()0f x <;②函数()'f x 在1,2π⎛⎫- ⎪⎝⎭上只有一个零点;③函数()f x 在1,2π⎛⎫- ⎪⎝⎭上存在极小值点A .0B .1C .2D .317.函数()ln f x x x =-与()ln x g x xe x x =--的最小值分别为,a b ,则 A .a b = B .a b >C .a b <D .,a b 的大小不能确定18.若函数32()312(0)f x x ax x a =-+>存在两个极值点1x ,2x ,则()()12f x f x +的取值范围是 A .(,16]-∞ B .(,16)-∞ C .(16,)+∞D .[16,)+∞19.已知0a >,函数()()21sin cos 2f x a x x x x a =+-+++-,R x ∈.记函数()f x 的最小值为M ,函数()()f f x 的最小值为N ,当M N ≥时,a 的最大值是A .4B .3C .2D .1二、多选题1.函数()f x 的定义域为R ,它的导函数()y f x '=的部分图象如图所示,则下面结论正确的是A .在()1,2上函数()f x 为增函数B .在()3,5上函数()f x 为增函数C .在()1,3上函数()f x 有极大值D .3x =是函数()f x 在区间[]1,5上的极小值点 2.已知()1xe x x R ≥+∈,当且仅当0x =时取等号,则A .()1()x f x x x R e=+∈的最小值为1B .()()0xe f x x x=>的最小值为1C .()()ln 0f x x x x =->的最小值为1D .()1()0xf x xex =>的最小值13.下列函数最小值是2的是A .2210()y x x x=+≠ B .()1xx y e x R e =+∈C .)y x R =∈D .()210y x x x=+> 4.已知函数()3sin f x x x ax =+-,则下列结论正确的是 A .()f x 是奇函数B .当3a=-时,函数()f x 恰有两个零点C .若()f x 为增函数,则1a ≤D .当3a =时,函数()f x 恰有两个极值点三、填空题1.函数3()3f x x x =-在区间[]1,3-上的最小值为__________.2.函数21()ln 2f x x x =-的最小值为__________. 3.已知函数()32133f x x x =++在区间(),3+m m 上存在极大值与极小值,则实数m 的取值范围是__________.4.若函数32()f x x x =-在区间(,3)a a +内存在最大值,则实数a 的取值范围是__________. 5.若函数2()2(0)x f x m e x x m =⋅-+<在(0,1)上有极值点,则m 的取值范围为__________.6.函数()322f x x ax bx a =+++在1x =处取得极值10,则a b +=__________.四、双空题1.已知函数()4(0,0)af x x x a x=+>>在3x =时取得最小值,则a =__________;()f x 的最小值为__________.2.设函数32()(3)f x x a x ax =+++,若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为__________;函数()f x 的极大值点为__________. 3.曲线22y x x =+在点()1,3处的切线方程为__________,函数22y x x=+的极小值为__________.4.已知函数()ln xf x x=. (1)函数的最大值等于________;(2)若对任意[)12,,x x a ∈+∞,都有()()121f x f x e-≤成立,则实数a 的最小值是________.5.已知l ()1n f x x a x =--,若()f x 有最值,则a 的取值范围为__________;若当2(,)x e e ∈时,()0f x ≥,则a 的取值范围为__________.五、解答题1.已知函数32()2f x x ax bx =+++在1x =-处取得极值7. (1)求,a b 的值;(2)求函数()f x 在区间[2,2]-上的最大值2.已知函数3211()ln 332af x x x x x ⎛⎫=--+ ⎪⎝⎭. (1)若1a =,求()f x 在1x =处的切线方程; (2)若()f x 有2个极值点,求实数a 的取值范围. 3.已知函数()ln ()f x x ax a R =-∈. (1)求函数()f x 的单调区间;(2)当1a =时,()()(2)x g x f x x e =+-,记函数()y g x =在1,14⎡⎤⎢⎥⎣⎦上的最大值为m ,证明:3m <-.4.已知函数()()()()1ln ,1f x f x x ax x ag x x =--∈=+R .(1)当12a =-时,求()f x 的最小值; (2)当01a <≤时,()g x m ≤恒成立,求整数m 的最小值. 5.已知函数()ln bf x x a x x=-+,a ,b ∈R . (1)若a >0,b >0,且1是函数()f x 的极值点,求12a b+的最小值;(2)若b =a +1,且存在0x ∈[1e,1],使0()0f x <成立,求实数a 的取值范围. 6.设函数()22ln 2f x a x x =-(a R ∈).(1)若[1,1]a ∈-,()f x 在1x =处的切线在坐标轴上的截距之和为()g a ,求()g a 的范围;(2)讨论函数()f x 的极值情况,并求出当函数()f x 的极大值为0时实数a 的值. 7.已知函数()3xxf x xe e =-.(1)求() f x 的极值;(2)若()()ln g x f x x x '=-+在1,14⎡⎤⎢⎥⎣⎦上的最大值为λ,求证:()3467e fe λ---<<-.专题03 极值与最值问题一、单选题1.已知函数()y f x =的定义域为()a b ,,导函数()'y f x =在()a b ,内的图象如图所示,则函数()y f x =在()a b ,内的极小值有A .1个B .2个C .3个D .4个【试题来源】安徽省滁州市定远县重点中学2020-2021学年高二上学期期末(文) 【答案】A【分析】根据极小值点两侧函数的单调性是先减后增,对应导函数值是先负后正,结合图象即可求得结论.【解析】因为极小值点两侧函数的单调性是先减后增,对应导函数值是先负后正, 由图得导函数值先负后正的点有1个.所以函数()f x 在区间(,)a b 内极小值点的个数是1.故选A .2.已知函数()f x 的导函数()'f x 的图象如下,若()f x 在0x x =处有极值,则0x 的值为A .3-B .0C .3D .7【试题来源】江苏省盐城市一中、大丰高级中学等四校2020-2021学年高二上学期期末联考 【答案】B【分析】根据极值与导数的关系判断.【解析】由()'f x 知,0x =时,(0)0f '=,30x -<<时,()0f x '>,03x <<时,()0f x '<,0是极值点.虽然有(7)0f '=,但在7的两侧,()0f x '<,7不是极值点.故选B .3.若函数3()ln f x x x =,则 A .既有极大值,也有极小值 B .有极小值,无极大值 C .有极大值,无极小值D .既无极大值,也无极小值【试题来源】安徽省池州市2020-2021学年高二上学期期末(文) 【答案】B【分析】利用导数判断单调性,再判定极值即可. 【解析】依题意,222()3ln (3ln 1)f x x x x x x '=+=+;令()0f x '=,解得13x e -=,故当130,x e -⎛⎫∈ ⎪⎝⎭时,()0f x '<,当13,x e -⎛⎫∈+∞ ⎪⎝⎭时,()0f x '>,故当13x e -=时,函数()f x 有极小值,且函数无极大值,故选B .4.若函数22()xx x f x e+=的极大值点与极小值点分别为a ,b ,则 A .a b a b <<+ B .a a b b <+< C .b a b a <+<D .a b b a +<<【试题来源】安徽省皖西南联盟2020-2021学年高三上学期期末(文) 【答案】C【分析】利用导数求函数的极值点,再比较选项.【解析】22()xx f x e-'=,当x <<()0f x '>;当x <x >()0f x '<.故22()xx xf x e +=则a =b =,所以b a b a <+<.故选C5.若1x =是函数()xf x e ax =-的极值点,则方程()f x a =在()2,+∞的不同实根个数为 A .1 B .2 C .3D .0【试题来源】河南省豫南九校2020-2021学年高二上学期期末联考(文) 【答案】A【分析】首先根据极值点为1,求得a e =,再结合函数的单调性,判断实根个数. 【解析】由()'xf x e a =-,得()10'=-=f e a ,则a e =,()xf x e ex =-,函数()f x 在()2,+∞,()()'0,f x f x >单调递增,()222f e e e =-<,函数()y f x =与y a =的交点个数为1个.故选A.6.已知函数()y f x =的导函数()y f x ='的图象如图所示,则下列结论正确的是A .函数()y f x =在(),1-∞-上是增函数B .3x =是函数()y f x =的极小值点C .()()35f f ''<D .()()13f f -<【试题来源】河南省郑州市2020-2021学年高二上学期期末(文) 【答案】D【分析】由图得出函数()y f x =的单调性判断ABD ,根据(3)(5)0f f ''==判断C . 【解析】当(,1)x ∈-∞-时,()0f x '<,则函数()y f x =在(),1-∞-上是减函数,故A 错误;函数()y f x =在(1,3)-上单调递增,在(3,5)上单调递减,则3x =是函数()y f x =的极大值点,故B 错误;由图可知,(3)(5)0f f ''==,故C 错误; 函数()y f x =在[]1,3-上单调递增,则()()13f f -<,故D 正确;故选D.7.已知32()f x x px qx =++的图象与x 轴相切于非原点的一点,且f (x )极小值=-4,那么p ,q 值分别为 A .8,6 B .9,6 C .4,2D .6,9【试题来源】陕西省咸阳市武功县2021届高三下学期第二次质量检测(文) 【答案】D【分析】设切点为()(),00a a ≠,根据题意得到()2223()2f x x x a x ax a x =--+=,然后求导,再由f (x )极小值=-4求解.【解析】设切点为()(),00a a ≠,()2()f x x x px q =++,由题意得20x px q ++=有两个相等实根,所以()2223()2f x x x a x ax a x =--+=,()()2233()4f x x ax a x a x a '-+-=-=,令()0f x '=,得3ax =或x a =, 因为f (x )极小值=-4,而()04f a =≠-,所以()43a f =-,即2433a a a ⎛⎫-- ⎪⎝⎭, 解得3a=-,所以32()69f x x x x =++,所以6,9p q ==.故选D.8.已知函数1ln ()e +=-x xf x x,则()f x 的最大值是 A .1- B .2- C .0D .1e -【试题来源】河南省驻马店市2020-2021学年高三上学期期末考试(文) 【答案】A【解析】ln 1ln e e (ln )1()1(0)x x x x x x x f x x x x++--+-==-->,设()e 1=--x g x x ,()e 1x g x '=-,当0x >时,()0g x '>,()g x 是单调递增函数, 当0x <时,()0g x '<,()g x 是单调递减函数,所以min ()(0)0g x g ==,因为ln 0x x +=时有解,所以()()ln maxe ln 11101x x x x f x x+-+-=--=--=-.故选A . 9.已知1x =是函数32()3f x ax x =-的极小值点,则函数()f x 的极小值为 A .0 B .1- C .2D .4【试题来源】福建省南平市2020-2021学年高二上学期期末考试 【答案】B【分析】由1x =是函数32()3f x ax x =-的极小值点,根据()01f '=,求得2a =,进而利用导数,即可求解函数的极小值,得到答案.【解析】由题意,函数32()3f x ax x =-,可得2()363(2)f x ax x x ax '=-=-, 因为1x =是函数32()3f x ax x =-的极小值点,则()01f '=,即31(2)0a ⨯⨯-=,解得2a =,可得()6(1)f x x x '=-, 当0x <或1x >时,()0f x '>,()f x 单调递增; 当01x <<时,()0f x '<,()f x 单调递减, 所以当1x =是函数32()3f x ax x =-的极小值点, 所以函数的极小值为32(1)21311f =⨯-=-⨯.故选B .10.已知函数()2ln f x x a x =+的图象在(1,f (1))处的切线经过坐标原点,则函数y =f (x )的最小值为 A .11ln 222- B .1ln 24+ C .11ln 222+ D .1【试题来源】安徽省马鞍山市2020-2021学年高三上学期第一次教学质量监测(文) 【答案】C【分析】利用导数的几何意义求出1a =-,从而可得()2ln f x x x =-,求出导函数,利用导数判断出函数的单调性,由单调性即可求出最值.【解析】函数()2ln f x x a x =+,则()2n 11l 11f a =+=且()2af x x x'=+,所以()12f a '=+, 所以()()1011210f f a -'===+-,解得1a =-,所以()2ln f x x x =-,(0x >),()12f x x x'=-, 令()0f x '≥,即120x x -≥,解得x ≥, 令()0f x '<,即120x x -<,解得0x <<,所以函数在区间⎛ ⎝⎭上单调递减,在区间⎫+∞⎪⎪⎣⎭上单调递增. 所以()2min111ln 2222f x f ==-=-=+⎝⎭⎝⎭.故选C.11.已知函数()sin xf x e a x =-在区间0,3π⎛⎫ ⎪⎝⎭上有极值,则实数a 的取值范围是A .()0,1B .()1,eC .()1,2eD .31,2e π⎛⎫ ⎪⎝⎭【试题来源】安徽省蚌埠市2020-2021学年高三上学期第二次教学质量检查(理) 【答案】D【分析】求出导数()'f x ,由()0f x '=在0,3π⎛⎫⎪⎝⎭上有变号的解即得.【解析】()cos '=-xf x e a x ,由题意cos 0xe a x -=在0,3π⎛⎫ ⎪⎝⎭上有解,即cos xea x=在0,3π⎛⎫ ⎪⎝⎭上有解,记()cos x e g x x =,2(cos sin )()cos xe x x g x x +'=,当0,3x π⎛⎫∈ ⎪⎝⎭时,()0g x '>,()g x 单调递增,(0)1g =,3323cos 3e g e ππππ⎛⎫== ⎪⎝⎭,所以312e e π<<.故选D . 【名师点睛】本题考查导数与极值.函数在某个区间上有极值,则()'f x 在这个区间上有的零点,()0f x '=有解,又可转化为函数图象与直线有交点,从而再次转化为利用导数判断函数的单调性,求函数的值域.解题关键在于转化.12.若函数()221xf x e ax =-+有两个不同的极值点,则实数a 的取值范围是A .4e a <- B .04ea -<< C .4e a >D .04ea <<【试题来源】河南省驻马店市2020-2021学年高二上学期期末(文) 【答案】C【分析】由题意可知()4xf x e ax '=-有2个变号零点即4x e ax =有两个不等的实根,可转化为y a =与()4xeg x x=图象有两个不同的交点,对()g x 求导判断单调性,作出其图象,数形结合即可求解.【解析】因为函数()221x f x e ax =-+有两个不同的极值点,所以()4xf x e ax '=-有2个变号零点,即4x e ax =有两个不等的实根,因为0x =时显然不成立,所以0x ≠,可得4x e a x =,令()4x e g x x =,则y a =与()4xe g x x =图象有两个不同的交点即可.则()()22144164xx x x exe e g x x x--'==,所以()4x e g x x =在(),0-∞和()0,1单调递减,在()1,+∞单调递增,故()4x eg x x=的图象如图所示:当1x =时,()14e g =,由图知当4ea >时两个函数图象有2个不同的交点,可得原函数有两个极值点.所以实数a 的取值范围是4ea >,故选C 【名师点睛】本题解题的关键点是原函数有两个极值点等价于导函数有两个零点,令导函数等于0,该方程有2个不等的实根即可.13.已知函数()22ln 3f x x ax x =+-在2x =处取得极小值,则()f x 在1,32⎡⎤⎢⎥⎣⎦的最大值为 A .52-B .92ln 32-C .1-D .2ln 24-【试题来源】江西省南昌市新建区第一中学2020-2021学年高二上学期期末考试(理) 【答案】B【分析】由()20f '=求出a 的值,然后利用导数可求得函数()f x 在1,32⎡⎤⎢⎥⎣⎦的最大值. 【解析】()22ln 3f x x ax x =+-,则()223f x ax x=+-', 由题意可得()2420f a '=-=,解得12a =,则()212ln 32f x x x x =+-, ()22323x x f x x x x-+'=+-=,令()0f x '=,可得1x =或2x =,列表如下:所以,函数()f x 的极大值为()12f =-,极小值为()22ln24f =-, 又1112ln 228f ⎛⎫=-- ⎪⎝⎭,()932ln 32f =-,()()()95312ln 32ln 322ln 31022f f -=-+=-=->,则()()13f f <,所以,()()max 932ln 32f x f ==-.故选B .【名师点睛】利用导数求函数()y f x =在[],a b 上的最大值和最小值的步骤如下: (1)求函数()y f x =在(),a b 内的极值;(2)将函数()y f x =的各极值与端点处的函数值()f a 、f b 比较,其中最大的一个是最大值,最小的一个是最小值.14.设函数,(),x xx af x e x x a⎧≥⎪=⎨⎪<⎩,若函数存在最大值,则实数a 的取值范围是A .1a ≤B .1a <C .1a e ≤D .1a e<【试题来源】江西省新八校2020-2021学年高三上学期第一次联考(理) 【答案】C【分析】x a <时,()f x a <无最大值,因此x a ≥时,()xxf x e =有最大值,利用导数求解. 【解析】显然x a <时,()f x a <无最大值,x a ≥时,()x x f x e =存在最大值,1()xx f x e -'=, 当1x <时,()0f x '>,()f x 递增,当1x >时,()0f x '<,()f x 递减, 所以1x =时,()f x 取得极大值也是最大值.1(1)f e=, 因此()f x 要有最大值,必须满足11a a e ≤⎧⎪⎨≤⎪⎩,所以1a e ≤.故选C .【名师点睛】本题考查分段函数的最大值问题.解题时要注意()f x 的最大值是在定义域内的最大值,对分段函数来讲,每一段的函数值都不能比最大值大.因此本题在x a ≥时求得最大值1(1)f e =,除这个最大值取得到,即1a ≥以外还有必须满足1a e≤,否则函数无最大值.15.已知函数()33f x x x =-,则下列说法正确的是A .()f x 是偶函数B .1是()f x 的极小值点C .3是()f x 的极大值点D .()f x 在区间()0,1内单调递增【试题来源】贵州新高考联盟2021届高三下学期入学质量监测(文) 【答案】B【分析】利用函数解析式判断函数的奇偶性,得到A 项错误;对函数求导,研究函数的单调性,得到函数的极值点,可以判断B 、C 、D 的正确性. 【解析】因为()33f x x x =-,其定义域为R ,33()()3()(3)()f x x x x x f x -=---=--=-,所以()f x 是奇函数,所以A 项错; 2'()333(1)(1)f x x x x =-=+-,可以得到当1x <-或1x >时,'()0f x >,当11x -<<时,'()0f x <, 所以()f x 在(,1),(1,)-∞-+∞上单调增,在(1,1)-上单调减, 所以1是()f x 的极小值点,1-是()f x 的极大值点, 所以B 项正确,C 、D 两项都是错误的,故选B .【名师点睛】该题考查的是有关函数与导数的问题,解题思路如下: (1)根据函数的解析式,结合奇函数的定义,判断函数的奇偶性;(2)对函数求导,研究函数的单调性,进而求得函数的极值点以及函数在相应区间上的单调性,可判断选项的正误. 16.已知函数1()cos 1f x x x =-+,()'f x 为()f x 的导函数,则下列结论正确的个数是 ①当(1,0)x ∈-时,()0f x <;②函数()'f x 在1,2π⎛⎫- ⎪⎝⎭上只有一个零点;③函数()f x 在1,2π⎛⎫- ⎪⎝⎭上存在极小值点A .0B .1C .2D .3【试题来源】广西南宁市第三中学2021届高三下学期开学考试(理)【答案】C【分析】先求导可证得()21()sin 01f x x x '=-+>+, (1,0)x ∈-上恒成立,则函数()f x 在(1,0)x ∈-上递增,然后根据()00f =可知所以()0f x <在(1,0)x ∈-上恒成立;当0,2x π⎡⎫∈⎪⎢⎣⎭时,令()()21sin 1g x x x =-++,利用导数可证明得函数()g x 在0,2x π⎡⎫∈⎪⎢⎣⎭上递减,然后判断端点的函数值,根据零点的存在性定理判断函数()'f x 在1,2π⎛⎫- ⎪⎝⎭上只有一个零点;再根据②的结果,得出函数()f x 的单调性并判断极值点问题. 【解析】对于①,因为函数1()cos 1f x x x =-+,则()21()sin 1f x x x '=-++,当(1,0)x ∈-时,()()211,1x ∈+∞+,故()()21sin 01f x x x '=-+>+在(1,0)x ∈-上恒成立,所以函数()f x 在(1,0)x ∈-上递增,又()0cos010f =-=,所以()0f x <在(1,0)x ∈-上恒成立,故①正确;对于②,由①可知,当(1,0)x ∈-时,()()21sin 01f x x x '=-+>+,当0,2x π⎡⎫∈⎪⎢⎣⎭时,令函数()()21sin 1g x x x =-++, 则()()32cos 01g x x x '=--<+在0,2x π⎡⎫∈⎪⎢⎣⎭恒成立,故()g x 在0,2x π⎡⎫∈⎪⎢⎣⎭上递减, 又()010g =>,21sin 02212g πππ⎛⎫=-+< ⎪⎝⎭⎛⎫+ ⎪⎝⎭, 所以函数()g x 在0,2x π⎡⎫∈⎪⎢⎣⎭上有一个零点,故()'f x 在1,2π⎛⎫- ⎪⎝⎭上有一个零点,故②正确; 对于③,由②可知函数()0f x '=在1,2π⎛⎫- ⎪⎝⎭上有一根,设()00f x '=,则函数()f x 在()01,x -上递增,在0,2x π⎛⎫ ⎪⎝⎭上递减,故函数()f x 在0x x =处取得极大值,故③错. 故选C .【名师点睛】本题考查利用导数判断函数的单调性、极值点、零点等问题. 利用导数判断函数的极值问题,分析清楚函数的单调性是关键;判断函数零点个数问题时,先求导判断函数的单调性,然后计算区间端点的函数值,通过零点的存在性定理判断即可. 17.函数()ln f x x x =-与()ln x g x xe x x =--的最小值分别为,a b ,则 A .a b = B .a b >C .a b <D .,a b 的大小不能确定【试题来源】湖南省岳阳市平江县第一中学2020-2021学年高二上学期1月阶段性检测 【答案】A【分析】根据函数的单调性分别求出函数()f x ,()g x 的最小值,比较a ,b 即可.【解析】()f x 的定义域是()0,∞+,11()1x f x x x'-=-=, 令()0f x '<,解得01x <<,令()0f x '>,解得1x >,()f x 在(0,1)递减,在(1,)+∞递增,()f x 的最小值是()1f 1=,故1a =,()x g x xe lnx x =--,定义域(0,)+∞,()()()11111xx x g x x e xe x x+=+--=-', 令()1x h x xe =-,则()()10xh x x e '=+>,(0,)x ∈+∞则可得()h x 在(0,)+∞上单调递增,且()010h =-<,()110h e =->,故存在0(0,1)x ∈使得()0h x =即001xx e =,即000x lnx +=,当0(0,)x x ∈时,()0h x <,()0g x '<,函数()g x 单调递减,当()0x x ∈+∞,时,()0g x '>,函数()g x 单调递增, 故当0x x =时,函数取得最小值0000000()11xg x x e lnx x lnx x =--=--=,即1b =, 所以a b =,故选A .【名师点睛】题考查了函数的单调性,最值问题,考查导数的应用以及转化思想,解答本题的关键是由()()()11111xx x g x x e xe x x+=+--=-',得出当0(0,)x x ∈时,函数()g x 单调递减,当()0x x ∈+∞,时,函数()g x 单调递增,根据000x lnx +=,求出最小值,属于中档题.18.若函数32()312(0)f x x ax x a =-+>存在两个极值点1x ,2x ,则()()12f x f x +的取值范围是 A .(,16]-∞ B .(,16)-∞ C .(16,)+∞D .[16,)+∞【试题来源】内蒙古赤峰市2021届高三模拟考试(文) 【答案】B【分析】由条件可得2()3612f x x ax '=-+,则所以23643120a ∆=-⨯⨯>,即2a >,12122,4x x a x x +=⋅=,故()()12f x f x +3424a a =-+,设()3g 424a a a =-+,求出()g a 的单调性,得出其范围,得到答案.【解析】由32()312(0)f x x ax x a =-+>,则2()3612f x x ax '=-+因为函数()f x 存在两个极值点1x ,2x ,所以23643120a ∆=-⨯⨯>,即2a > ,12122,4x x a x x +=⋅=,()()()123232111222312312f x f x x ax x x ax x +-+-++=()()()()221211*********3212x x x x x x x a x x x x x ⎡⎤=--+-⋅++⎣⋅++⎦()()()()1212121212221233212a x x x x x x x x x x x x ⎡⎤⎡⎤=---+⎣⎦⎣⎦++⋅+⋅+()()22241234824a a a a a =---+3424a a =-+ ,设()3g 424a a a =-+,则()g a '()221224122a a =-+=--,当2a >时,()g a '0<,则()g a 在()2,+∞上单调递减.所以()()g g 216a <=,所以()()12f x f x +的取值范围是(,16)-∞,故选B.【名师点睛】本题考查函数的极值相关问题,解答本题的关键是由条件得出12122,4x x a x x +=⋅=,将条件代入得到()()12f x f x +3424a a =-+,属于中档题.19.已知0a >,函数()()21sin cos 2f x a x x x x a =+-+++-,R x ∈.记函数()f x 的最小值为M ,函数()()f f x 的最小值为N ,当M N ≥时,a 的最大值是A .4B .3C .2D .1【试题来源】成都市蓉城名校联盟2020-202学年高三上学期(2018级)第二次联考(文) 【答案】D【分析】利用导数分析函数()f x 的单调性,可得出M ,然后分10a -≤和10a ->两种情况讨论,利用函数()f x 的单调性可求得N ,验证M N ≥是否成立,由此可求得实数a 的最大值.【解析】因为0a >,()()21sin cos 2f x a x x x x a =+-+++-,所以()()211cos sin f x a x x x '=+-+-,记()()211cos sin g x a x x x =+-+-,所以()22sin cos 20g x a x x a '=+--≥>,所以,函数()g x 在R 上单调递增, 因为()00g =,当0x <时,()0g x <;当0x >时,()0g x >, 所以,函数()f x 在(),0-∞上单调递减,在()0,∞+上单调递增. 所以()()min 0121f x f a a ==+-=-,即1M a =-.①当10a -≤,即当1a ≤时,由上可知,函数()()ff x 的最小值为()01N f a ==-,满足M N ≥; ②当10a ->,即当1a >时,由上可知,函数()()ff x 的最小值为()1N f a =-,且()()101N f a f a M =->=-=,不合题意,综上所述,实数a 的最大值为1.故选D .【名师点睛】本题考查含有参数的复合函数的值域问题,利用导数分析函数()f x 的单调性,并求出函数()f x 的值域M 是解题的关键,其次就是要分10a -≤和10a ->两种情况讨论,结合函数()f x 的单调性求出复合函数()()f f x 的值域,这次解决此类问题的常用方法. 二、多选题1.函数()f x 的定义域为R ,它的导函数()y f x '=的部分图象如图所示,则下面结论正确的是A .在()1,2上函数()f x 为增函数B .在()3,5上函数()f x 为增函数C .在()1,3上函数()f x 有极大值D .3x =是函数()f x 在区间[]1,5上的极小值点【试题来源】河北省高碑店市高碑店一中2020-2021学年高二(励志班)上学期期末 【答案】AC【分析】根据图象判断出()f x 的单调区间、极值(点). 【解析】由图象可知()f x 在区间()1,2和()4,5上()'0fx >,()f x 递增;在区间()2,4上()'0f x <,()f x 递减.所以A 选项正确,B 选项错误.在区间()1,3上,()f x 有极大值为()2f ,C 选项正确.在区间[]1,5上,4x =是()f x 的极小值点,D 选项错误.故选AC. 2.已知()1xe x x R ≥+∈,当且仅当0x =时取等号,则A .()1()x f x x x R e=+∈的最小值为1B .()()0xe f x x x=>的最小值为1C .()()ln 0f x x x x =->的最小值为1D .()1()0xf x xex =>的最小值1【试题来源】浙江省丽水市2020-2021学年高一上学期期末 【答案】AC【分析】分别求导,判断函数单调性并求最值,判断正误.【解析】A :()1()x f x x x R e =+∈,11()1x x xe f x e e-'=-=,函数()f x 在,0上单调递减,在0,上单调递增,故函数()f x 的最小值为(0)1f =,A 选项正确;B :()()0xe f x x x =>,()21()x e x f x x-'=,函数()f x 在0,1上单调递减,在1,上单调递增,故函数()f x 的最小值为(1)f e =,B 选项错误;C :()()ln 0f x x x x =->,11()1x f x x x'-=-=,函数()f x 在0,1上单调递减,在1,上单调递增,故函数()f x 的最小值为(1)1f =,C 选项正确;D :()1()0xf x xe x =>,()1211211()xxxx e f x xex e x x-'=+⋅⋅=,函数()f x 在0,1上单调递减,在1,上单调递增,故函数()f x 的最小值为(1)f e =,D 选项错误;故选AC .【名师点睛】在解决类似的问题时,首先要注意区分函数最值与极值的区别.求解函数的最值时,要先求函数y =f (x )在[a ,b ]内所有使f ′(x )=0的点,再计算函数y =f (x )在区间内所有使f ′(x )=0的点和区间端点处的函数值,最后比较即得. 3.下列函数最小值是2的是A .2210()y x x x =+≠ B .()1xxy e x R e =+∈C .)y x R =∈D .()210y x x x=+> 【试题来源】辽宁省大连市2020-2021学年高三上学期期末 【答案】AB【分析】根据均值不等式等号成立的条件判断ABC ,利用导数的极值判断D 即可求解.【解析】2210()2y x x x =+≥=≠,当且仅当221x x =,即1x =±时等号成立,故A 正确;1()2x x y e x R e ∈≥+==,当且仅当1x x e e =,即0x =时等号成立,故B 正确;)2y x R =∈≥,当且仅当=时,即241x +=,显然等号不成立,故C 不正确;()210y x xx =+>,3221212x y x x x-'∴=-=,令0y '=可得x =,所以当x =时,y 而335464288=<=⎝⎭,故D 不正确.故选AB. 4.已知函数()3sin f x x x ax =+-,则下列结论正确的是A .()f x 是奇函数B .当3a=-时,函数()f x 恰有两个零点C .若()f x 为增函数,则1a ≤D .当3a =时,函数()f x 恰有两个极值点【试题来源】湖南省岳阳市平江县第一中学2020-2021学年高二上学期1月阶段性检测 【答案】ACD【分析】利用函数奇偶性的定义可判断A 选项的正误;利用导数分析函数()f x 的单调性,可判断B 选项的正误;利用导数与函数单调性的关系可判断C 选项的正误;利用导数以及零点存在定理可判断D 选项的正误.【解析】对于A 选项,函数()3sin f x x x ax =+-的定义域为R ,()()()()33sin sin f x x x ax x x ax f x -=-+-+=--+=-,函数()f x 为奇函数,A 选项正确;对于B 选项,当3a=-时,()3sin 3f x x x x =++,则()2cos 330f x x x '=++>,所以,函数()f x 在R 上为增函数,又()00f =,所以,函数()f x 有且只有一个零点,B选项错误;对于C 选项,()2cos 3f x x x a '=+-,由于函数()f x 为增函数,则()0f x '≥对任意的x ∈R 恒成立,即23cos a x x ≤+. 令()23cos g x x x =+,则()6sin g x x x '=-,则()6cos 0g x x ''=->,所以,函数()g x '在R 上为增函数,当0x <时,()()00g x g ''<=,此时,函数()g x 为减函数;当0x >时,()()00g x g ''>=,此时,函数()g x 为增函数. 所以,()()min 01g x g ==,1a ∴≤,C 选项正确;对于D 选项,当3a =时,()3sin 3f x x x x =+-,则()2cos 33f x x x '=+-.由B 选项可知,函数()f x '在(),0-∞上单调递减,在()0,∞+上单调递增,()()11cos10f f ''-==>,()020f '=-<,由零点存在定理可知,函数()f x '在()1,0-和()0,1上都存在一个零点, 因此,当3a =时,函数()f x 有两个极值点,D 选项正确.故选ACD . 【名师点睛】利用函数的单调性求参数,可按照以下原则进行: (1)函数()f x 在区间D 上单调递增()0f x '⇔≥在区间D 上恒成立; (2)函数()f x 在区间D 上单调递减()0f x '⇔≤在区间D 上恒成立; (3)函数()f x 在区间D 上不单调()f x '⇔在区间D 上存在极值点;(4)函数()f x 在区间D 上存在单调递增区间x D ⇔∃∈,使得()0f x '>成立; (5)函数()f x 在区间D 上存在单调递减区间x D ⇔∃∈,使得()0f x '<成立. 三、填空题1.函数3()3f x x x =-在区间[]1,3-上的最小值为__________. 【试题来源】陕西省宝鸡市金台区2020-2021学年高二上学期期末(文) 【答案】2-【分析】根据函数求导判断函数单调性,进而求得最值. 【解析】由3()3f x x x =-,得2()33f x x '=-.令0fx,解得11x =-,21x =.()f x 在区间[]1,1-上单调递减,在区间[]1,3上单调递增,所以最小值为(1)2f =-.【名师点睛】在解决类似的问题时,首先要注意区分函数最值与极值的区别.求解函数的最值时,要先求函数y =f (x )在[a ,b ]内所有使f ′(x )=0的点,再计算函数y =f (x )在区间内所有使f ′(x )=0的点和区间端点处的函数值,最后比较即得. 2.函数21()ln 2f x x x =-的最小值为__________. 【试题来源】陕西省西安市第八十三中学2020-2021学年高二上学期期末(理) 【答案】12【分析】求导,判断函数的单调性,根据单调性即可求解.【解析】21()ln 2f x x x =-,0x >,()211x f x x x x='-=-,令()0f x '>,解得1x >,令()0f x '≤,解得01x <≤,所以函数在(]0,1上单调递减;在()1,+∞上单调递增,所以()()min 112f x f ==. 3.已知函数()32133f x x x =++在区间(),3+m m 上存在极大值与极小值,则实数m 的取值范围是__________.【试题来源】浙江省金华十校2020-2021学年高二上学期期末 【答案】()3,2-- 【解析】()32133f x x x =++,则()()222f x x x x x '=+=+, 令()0f x '=,可得12x =-,20x =,列表如下:所以,函数()f x 的极大值点为2x =-,极小值点为0x =, 由于函数()32133f x x x =++在区间(),3+m m 上存在极大值与极小值, 所以,230m m <-⎧⎨+>⎩,解得32m -<<-.因此,实数m 的取值范围是()3,2--.【名师点睛】已知极值点求参数的值,先计算()0f x '=,求得x 的值,再验证极值点.由于导数为0的点不一定是极值点,因此解题时要防止遗漏验证导致错误.4.若函数32()f x x x =-在区间(,3)a a +内存在最大值,则实数a 的取值范围是__________. 【试题来源】江西省江西师范大学附属中学2020-2021学年高二上学期期末考试(理) 【答案】(3,2]--【分析】首先利用导数判断函数的单调性,再根据函数在开区间(),3a a +内存在最大值,可判断极大值点就是最大值点,列式求解. 【解析】由题可知 2()32(32)f x x x x x '=-=-所以函数()f x 在20,3⎛⎫ ⎪⎝⎭单调递减,在2(,0),,3⎛⎫-∞+∞ ⎪⎝⎭单调递增,故函数的极大值为(0)0f =.所以在开区间(,3)a a +内的最大值一定是(0)0,f =又(1)(0)0f f ==,所以 03,31a a a <<+⎧⎨+≤⎩ 得实数a 的取值范围是(3,2].--故答案为(]3,2-- 【名师点睛】由函数在开区间内若存在最大值,即极大值点在区间内,同时还得满足极大值点是最大值,还需列不等式31a +≤,不要忽略这个不等式. 5.若函数2()2(0)x f x m e x x m =⋅-+<在(0,1)上有极值点,则m 的取值范围为__________.【试题来源】河南省新乡市2020-2021学年高二上学期期末(文) 【答案】(2,0)-【分析】由函数2()2(0)x f x m e x x m =⋅-+<在(0,1)上有极值点,可得()22(0)x f x m e x m '=⋅-+<在(0,1)上有零点,再利用零点存在性定理列不等式求解即可. 【解析】因为2()2(0)x f x m e x x m =⋅-+<,所以()22(0)x f x m e x m '=⋅-+<, 因为函数2()2(0)x f x m e x x m =⋅-+<在(0,1)上有极值点, 所以()22(0)x f x m e x m '=⋅-+<在(0,1)上有零点,因为(0),22x y m e m x y =⋅-=<+在(0,1)上都递减,所以()'f x 在(0,1)上为减函数,所以(0)20(1)0f m f me =+>⎧⎨=<''⎩,解得20m -<<.故答案为(2,0)-.6.函数()322f x x ax bx a =+++在1x =处取得极值10,则a b +=__________.【试题来源】江苏省泰州中学2020-2021学年高二下学期期初检测 【答案】7-【分析】由()f x 在1x =处取得极值10,求得解得4 11a b =⎧⎨=-⎩或33a b =-⎧⎨=⎩,再结合函数的极值的概念进行检验,即可求解.【解析】由题意,函数()322f x x ax bx a =+++,可得()232f x x ax b '=++,因为()f x 在1x =处取得极值10,可得2(1)320(1)110f a b f a b a =++=⎧⎨=+++='⎩, 解得4 11a b =⎧⎨=-⎩或33a b =-⎧⎨=⎩, 检验知,当3,3a b =-=时,可得()223633(1)0f x x x x '=+=-≥-,此时函数()f x 单调递增,函数为极值点,不符合题意,(舍去); 当4,11a b ==-时,可得()23811(311)(1)f x x x x x '=+-=+-,当113x <-或1x >时,()0f x '>,()f x 单调递增; 当1113x -<<时,()0f x '<,()f x 单调递减, 当1x =时,函数()f x 取得极小值,符合题意.所以7a b +=-.故答案为7-. 【名师点睛】解决函数极值、最值综合问题的策略:(1)求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小;(2)求函数最值时,不可想当然地认为极值点就是最值点,要通过比较才能下结论; (3)函数在给定闭区间上存在极值,一般要将极值与端点值进行比较才能确定最值. 四、双空题1.已知函数()4(0,0)af x x x a x=+>>在3x =时取得最小值,则a =__________;()f x 的最小值为__________.【试题来源】2020-2021学年高一数学十分钟同步课堂专练(苏教版2019必修第一册) 【答案】36 24【分析】利用导数研究函数()f x 的单调性、极值与最值,结合已知列方程即可得出. 【解析】因为函数()4(0,0)af x x x a x=+>>,2224()4a x a f x x x -'=-==,(0,0)x a >>.由()0f x '>可得()f x 在⎫+∞⎪⎪⎝⎭上递增;由()0f x '<可得()f x 在⎛ ⎝⎭上递减;所以x =时,函数()f x 取得极小值也是最小值,因为函数()4(0,0)af x x x a x=+>>在3x =时取得最小值,3∴=,解得36a =.()f x 的最小值为f (3)3612243=+=.故答案为36,24. 2.设函数32()(3)f x x a x ax =+++,若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为__________;函数()f x 的极大值点为__________. 【试题来源】浙江省台州市五校2019-2020学年高二下学期期中联考 【答案】30x y += 1-【分析】根据奇函数的定义,得到30a +=,即3a =-,确定函数解析式,函数求导得切线的斜率,利用函数的单调性求得极值点.【解析】因为函数32()(3)f x x a x ax =+++是奇函数, 所以()()f x f x -=-,从而得到30a +=,即3a =-,所以3()3f x x x =-,因为2'()33f x x =-,所以'(0)3f =-,所以曲线()y f x =在点(0,0)处的切线方程为3y x =-,2'()330f x x =-<,则11x -<< ,所以函数在(1,1)-上是减函数,在(,1),(1,)-∞-+∞是增函数,所以函数的极大值点是1-,故答案为30x y +=;1-. 3.曲线22y x x =+在点()1,3处的切线方程为__________,函数22y x x=+的极小值为__________.【试题来源】浙江省温州市十校联合体2020-2021学年高二上学期期末联考 【答案】3y = 3【分析】根据导数的应用,求导可得222y x x'=-+,直接求切线方程和极小值点即可. 【解析】222y x x'=-+,所以斜率220k =-+=,所以直线方程为3y =, 令32222220x y x x x-'=-+==可得1x =, 当(0,1)x ∈和(,0)x ∈-∞时0y '<,22y x x=+为减函数;。
南昌大学高数试题及答案

南昌大学 2006~2007学年第一学期期末考试试卷一、填空题 (每空 3 分,共 15 分) : 1.函数1()lg(5)3f x x x =++--的定义域为_______________.2. 设函数 ,0,()ln(),0,x e x f x a x x -⎧<=⎨+≥⎩ 则a 为_____值时,()f x 在x =0处 连续.(a >0) 3. 若函数()f x 在x =0可导, 且f (0)=0,则0()limx f x x→=__________. 4.设()f x =在[1, 4]上使Lagrange(拉格朗日)中值定理成立的ξ=_____.5. 设220()sin ,xF x t dt =⎰则()dF x =_______________. 二、单项选择题 (每题 3 分,共15分):1. 0x =是函数1()sin f x x x=的( ).(A) 跳跃间断点. (B) 可去间断点. (C) 无穷间断点. (D) 振荡间断点. 2. 设曲线21x y e-=与直线1x =-相交于点P,曲线过点P 处的切线方程为( ).(A) 210.x y ++= (B) 230.x y +-= (C) 230.x y -+= (D) 220.x y --=3. 若函数()f x 在区间(,)a b 内可导,1x 和2x 是区间(,)a b 内任意两点, 且12x x <, 则至少存在一点ξ使( ). (A) ()()'()(),f b f a f b a ξ-=- 其中.a b ξ<< (B) 11()()'()(),f b f x f b x ξ-=- 其中1.x b ξ<< (C) 2121()()'()(),f x f x f x x ξ-=- 其中12.x x ξ<< (D) 22()()'()(),f x f a f x a ξ-=- 其中2.a x ξ<<4. 设函数()f x 在(,)-∞+∞上连续,则()d f x dx ⎡⎤⎣⎦⎰等于( ).(A) ().f x (B) ().f x dx (C) ().f x C + (D) '().f x dx5. 设43()()'()d d I f x dx f x dx f x dx dx dx=++⎰⎰⎰存在, 则I =( ).(A) 0. (B) ().f x(C) 2().f x (D) 2().f x C +三、计算下列极限 (共2小题, 每小题7分, 共14分) :1. 0lim.1cos x x→-2. tan 2(sin ).lim x x x π→四. 解下列各题 (共3小题, 每小题7分, 共21分):1.设ln y =求''(0).y2. 设函数()y y x =由方程23ln()sin x y x y x +=+确定,求'(0).y3. 设2022(),(),t x f u du y f t ⎧=⎪⎨⎡⎤⎪=⎣⎦⎩⎰ 其中()f u 具有二阶导数, 且()0,f u ≠ 求22.d y dx五.求下列不定积分 (共2小题,每小题7分,共14分): 1、81.(1)dx x x +⎰2. 2sin .x xdx ⎰六.已知1(2),'(2)0,2f f ==及20()1,f x dx =⎰求120''(2).x f x dx ⎰(7分)七.已知函数222,(1)x y x =-试求其单增、单减区间, 并求该函数的极值和拐点. (9分)八.设()f x 在[,)a +∞上连续,''()f x 在(,)a +∞内存在且大于零,记()()()().f x f a F x x a x a-=>- 证明:()F x 在(,)a +∞内单调增加. (5分)南昌大学 2006~2007学年第一学期期末考试试卷及答案一、填空题 (每空 3 分,共 15 分) : 1.函数1()lg(5)3f x x x =++--的定义域为 ( 2335;x x ≤<<<与 )2. 设函数 ,0,()ln(),0,x e x f x a x x -⎧<=⎨+≥⎩ 则a 为( e )值时,()f x 在x =0处 连续.(a >0) 3. 若函数()f x 在x =0可导, 且f (0)=0,则0()limx f x x→=( '(0)f ) 4.设()f x =在[1, 4]上使Lagrange(拉格朗日)中值定理成立的ξ=( 9/4 )一、 5. 设220()sin ,xF x t dt =⎰则()dF x =(22sin(4)x dx )二、单项选择题 (每题 3 分,共15分):1. 0x =是函数1()sin f x x x=的( B ).(A) 跳跃间断点. (B) 可去间断点. (C) 无穷间断点. (D) 振荡间断点. 2. 设曲线21x y e-=与直线1x =-相交于点P,曲线过点P 处的切线方程为( C ).(A) 210.x y ++= (B) 230.x y +-= (C) 230.x y -+= (D) 220.x y --=3. 若函数()f x 在区间(,)a b 内可导,1x 和2x 是区间(,)a b 内任意两点, 且12x x <, 则至少存在一点ξ使( C ). (A) ()()'()(),f b f a f b a ξ-=- 其中.a b ξ<< (B) 11()()'()(),f b f x f b x ξ-=- 其中1.x b ξ<< (C) 2121()()'()(),f x f x f x x ξ-=- 其中12.x x ξ<< (D) 22()()'()(),f x f a f x a ξ-=- 其中2.a x ξ<<4. 设函数()f x 在(,)-∞+∞上连续,则()d f x dx ⎡⎤⎣⎦⎰等于( B ). (A) ().f x (B) ().f x dx (C) ().f x C + (D) '().f x dx5. 设43()()'()d d I f x dx f x dx f x dx dx dx=++⎰⎰⎰存在, 则I =( D ).(A) 0. (B) ().f x(C) 2().f x (D) 2().f x C +三、计算下列极限 (共2小题, 每小题7分, 共14分) :1. 0lim.1cos x x→- 解:0x →时,211cos 2xx -,()2224111cos 22x x x -= ∴0lim1cos xx →=-022x x →=2. tan 2(sin ).lim x x x π→解:(1) 令()tan sin xy x = ln tan lnsin y x x =(2)2ln lim x y π→=2tan lnsin lim x x x π→= 2lnsin cot lim x xx π→==221cos sin 0csc lim x xx x π→=- (3) tan 2(sin )lim x x x π→=2lim x y π→ln 021lim y x e e π→===四. 解下列各题 (共3小题, 每小题7分, 共21分):1. 设ln y=求''(0).y 解:21[ln(1)ln(1).2y x x ==--+22112112'. 3212111x x y x x x x -⎡⎤⎛⎫∴=-=-+ ⎪⎢⎥--++⎣⎦⎝⎭分222222222112(1)411''.2(1)(1)2(1)(1) x x x y x x x x ⎡⎤+--=-+=--⎢⎥-+-+⎣⎦ 13''(0)1.722y =--=-于是分2. 设函数()y y x =由方程23ln()sin x y x y x +=+确定,求'(0).y解:方程两边对x 求导,得()23212'3'cos . 4x y x y x y x x y+=+++分0,1,'(0) 1. 7x y y ===当时由原方程得代入上式得分3. 设2022(),(),t x f u du y f t ⎧=⎪⎨⎡⎤⎪=⎣⎦⎩⎰ 其中()f u 具有二阶导数, 且()0,f u ≠ 求22.d y dx 解: 222 4()'(),().dy dx tf t f t f t dt dt==22222222224()'()4'(). ()4'()8''(). ()dydy tf t f t dt tf t dx dx f t dtdy d dy dx d d y f t t f t dx dt dx dx dx f t dt∴===⎛⎫⎪⎛⎫⎝⎭ ⎪+⎝⎭∴=== 五.求下列不定积分 (共2小题,每小题7分,共14分): 1、81.(1)dx x x +⎰解: 原式 =()78888888811111dx =dx 88(1)11x dx x x x x x x ⎛⎫=- ⎪++⎝⎭+⎰⎰⎰ 81ln ||ln |1|.8x x C =-++2. 2sin .x xdx ⎰解: 原式1cos211cos2224x xdx xdx x xdx -==-⎰⎰⎰ 211sin 2cos 2.448x x x x C =--+六.已知1(2),'(2)0,2f f ==及20()1,f x dx =⎰求120''(2).x f x dx ⎰(7分)解: 设2,t x = 则2122001''()''()24t x f x dx f t dt =⎰⎰222200011'()2'()2()88t f t tf t dt tdf t ⎡⎤⎡⎤=-=-⎣⎦⎣⎦⎰⎰ 220011()()(11)0.44t f t f t dt ⎡⎤=--=--=⎣⎦⎰ 七.已知函数222,(1)x y x =-试求其单增、单减区间, 并求该函数的极值和拐点. (9分)解: 34484',''.(1)(1)xx y y x x +==-- 1'0,0;''0,.y x y x ====-令得令得故(0,1)为单增区间,(,0)(1,);-∞+∞和为单减区间函数在0x =处取得极小值,极小值为0;点(1/2,2/9)-为拐点.八.设()f x 在[,)a +∞上连续,''()f x 在(,)a +∞内存在且大于零,记()()()().f x f a F x x a x a-=>- 证明:()F x 在(,)a +∞内单调增加. (5分)证明: 1()()'()'().f x f a F x f x x a x a -⎡⎤=-⎢⎥--⎣⎦由拉格朗日中值定理知存在(,),a x ξ∈使()()'().f x f a f x aξ-=- []1'()'()'().F x f x f x aξ∴=--由''()0f x >可知'()f x 在(,)a +∞内单调增加,因此对任意x 和(),a x ξξ<<有'()'(),f x f ξ>从而'()0,F x >故()F x 在(,)a +∞内单调增加.南昌大学 2009~2010学年第一学期期末考试试卷一、 填空题(每空 3 分,共 15 分)1. 设函数()arcsin ln 13xy x =+-,则它的定义域为。
2019年南昌大学-高数(下)试题及答案.doc

南昌大学2008〜2009学年第二学期期末考试试卷一、填空题(每空3分,共15分)彳彳一1. 已知向量a 二1,-1,4 ,b= 3,4,0 ,则以a,b为边的平行四边形的面积等于______ .二二1 ,,2. 曲面z^sinxcosy在点一,一,处14 4 2 丿的切平面方程是_____ .、 2 23. 交换积分次序J0 dx J x f ( x, y )dy = _.°°i4. 对于级数瓦—(a> 0),当a满足条件时收敛.n勻a15. 函数y二——展开成x的幕级数为2- x ------二、单项选择题(每小题3分,共15分)1.平面x - 2z二0的位置是( )(A)通过y轴(B)通过x轴(C)垂直于y轴(D)平行于xoz平面2. 函数z= f x, y在点x0, y0处具有偏导数f x x0, y0, f y x0, y0,是函数在该点可微分的( )(A )充要条件(B)充分但非必要条件(C)必要但非充分条件(D)既非充分又非必要条件3. 设z = e x cosy xsin y ,贝U dz|xw =( )y=0(B) e(dx dy)(A) e(C ) e'(dx dy ) (D ) e x (dxdy )4.若级数二a n x -1 n 在x …1处收敛,n =1则此级数在x = 2处( )(A )敛散性不确定 (B )发散 (C )条件收敛(D )绝对收敛5.微分方程y - xy = x 的通解是( )1 2x(B) y 二 e 2- 1设平面通过点 3,1, - 2,而且通过直线 求该平面方程. 四、(本题满分8分)设z= f xy,x • y ,其中f u,v 具有二阶连续偏导数,q- 2试求一Z和Z .x x y五、(本题满分8分) 计算三重积分 I, zdxdydzQ 其中 1( x,y,z )O 兰 xE1,1w y 兰 1,1乞 z 兰 2〉. 六、(本题满分8分)计算对弧长的曲线积分 L e x2 y2ds ,其中L 是圆周x 2 y 2 = R 2在第一象限的部分.(A )丄X 2(C ) y = Ce 2三、(本题满分8(D )y = Ce 2】X 2七、(本题满分9分)计算曲面积分他xdydz* zdzdx+ 3dxdy,其中无是柱面y x2 y2 = 1与平面z = 0和z = 1所围成的边界曲面外侧.八、(本题满分9分)求幕级数7 nx n"的收敛域及和函数.n 二1九、(本题满分9分)求微分方程y - 4y = e x的通解.十、(本题满分11分)设L是上半平面y •0内的有向分段光滑曲线,其起点为1,2,终点为2,3 ,r 『21『2 x '记I =人I xy2+—dx+ x2y-— Idyy丿i y丿1.证明曲线积分I与路径L无关;2 .求I的值.南昌大学2008〜2009学年第二学期期末考试试卷及答案一、填空题(每空3分,共15分)1. 已知向量a= 1,-1,4 ,b= 3,4,0 ,则以a,b为边的平行四边形的面积等于449 .(H 兀1 )2. 曲面z = sinxcosy在点一,一,—丨处<4 4 2)的切平面方程是x-y-2z1 = 0 .2 2 2 y3.交换积分次序 0dx x f x ,y d ^o dy o f x,ydx .14.对于级数送-n (a > 0),当a 满足条件a = 1 时收敛.n =1 a15. 函数y 二——展开成x 的幕级数2 — x□0 In =0二、单项选择题(每小题3分,共15分)1.平面x - 2z 二0的位置是 ( A )(A )通过y 轴 (B )通过x 轴(C )垂直于y 轴(D )平行于xoz 平面2.函数z 二f x, y 在点x 0, y 0处具有偏导数f x x 0, y 0 , f y x 0, y 0 ,是函数在该点可微分的(C )(A )充要条件 (B )充分但非必要条件3. 设z 二 e xcosy xsin y ,则 dz|xw 二( B )y=0(A ) e( B ) e (dx dy ) (C ) e*(dx dy )(D ) e x (dx dy )x n 2“ 1(C )必要但非充分条件(D )既非充分又非必要条件则此级数在x = 2处( D(A )敛散性不确定 (B )发散 4. 若级数£ a n (xT )n 在x=-1处收敛,n=1(C )条件收敛(D )绝对收敛5.微分方程y - xy 二x 的通解是(D )1x 2-1x 2(A) y = e 2 -1(B ) y = e 2- 1--x 2】X 2 (C ) y = Ce 2 (D ) y = Ce 2- 1三、(本题满分8分)设平面通过点 3,1, - 2,而且通过直线 x - 4 y ' 3 z x -二 ------ -,求该平面方程. 5 2 1解:由于平面通过点 A 3,1, - 2及直线上的点B 4,-3,0 , 因而向量 AB 二1,-4,2平行于该平面 该平面的法向量为:4n = (5,2,1) (1, 4,2) =(8, - 9, 22).则平面方程为:8(x - 4) - 9(y 3) - 22(-- 0) = 0. 或: 8(x 3)-9(y - 1)- 22(- 2“ 0.即:8x 9y 22- 59 二 0.四、(本题满分8分)设-=f x,y枚)y其中f( u V具有二阶连续偏导数,试求——和 -■x2, :z=—(f i y + f 2)=xy y=fi i x f i 2 y f i五、(本题满分8分)计算三重积分 111 zdxdydzQ其中X x, y,z )O 兰x 兰i, — i 兰y 兰i,i 兰z 兰2〉. i i 2z 2 解:」I zdxdydz dx dy zdz= i[2 一 0-ii 2Q 2六、(本题满分8分)计算对弧长的曲线积分 [jEds ,—DTlD二 2e RRd Re R0 2解法二:… R R R R Rx 兀 R=f e / ---------------- dx= Re arcsin = ReJ R 2-X2RO2f Lds = … …兀 f其中L 是圆周x 2 • y 2二R 2在第一象限的部分. 解法一:芒宀心$ =解法三:令x = Rcos ,2 1X f 2 2二 xyf ix y i f.if f 2y = Rsi n , 0乞 2 0 -i ■ i 2ds=七、 (本题满分9分)计算曲面积分他xdydz* zdzdx+ 3dxdy ,其中送是柱面x 2 y 2 = 1与平面z = 0和z = 1所围成的边界曲面外侧.解:P 二 x,Q 二 z , R = 3,由高斯公式:怵xdydz zdz3x dxdyy(已P cQ dR=H i ——+——— d v = J J d v 哙八、 (本题满分9分)求幕级数nx n "的收敛域及和函数.于是收敛域为九、(本题满分9分)求微分方程y - 4y 二e x 的通解.解:收敛半径:R= limn 匚 ana n 1易判断当-1时,原级数发散。
极限与连续的应用于极值问题练习题及解析

极限与连续的应用于极值问题练习题及解析在微积分中,极限和连续是两个核心概念。
它们不仅在理论上有重要的意义,而且在实际问题的求解过程中也发挥着重要的作用。
本文将针对极限和连续的应用于极值问题进行一些练习题的讨论和解析。
题目一:求函数f(x) = x^3 - 3x^2 - 9x的单调区间。
解析:首先,我们需要求出函数的一阶导数f'(x)和二阶导数f''(x)。
对函数f(x)进行求导得到f'(x) = 3x^2 - 6x - 9,再对f'(x)进行求导得到f''(x) = 6x - 6。
接下来,我们需要找出函数f(x)的临界点。
临界点即为函数f(x)的导数f'(x)为零的点。
令f'(x) = 0,解得x = -1和x = 3。
所以函数f(x)的临界点为x = -1和x = 3。
根据一阶导数的符号可以确定函数的单调性。
当x < -1时,f'(x) < 0;当-1 < x < 3时,f'(x) > 0;当x > 3时,f'(x) < 0。
由此可得函数f(x)的单调区间为(-∞,-1)和(3,+∞)。
题目二:确定函数f(x) = x^3 - 3x^2 - 9x的极值点及极值。
解析:根据题目一的解析,我们已经知道函数f(x)的临界点为x = -1和x = 3。
现在我们需要进一步确定这些点是否为极值点,并求出极值。
首先,我们需要求出函数f(x)的二阶导数f''(x)。
根据题目一的解析,f''(x) = 6x - 6。
接下来,我们可以对临界点进行二阶导数的带入计算。
当x = -1时,f''(-1) = 6(-1) - 6 = -12;当x = 3时,f''(3) = 6(3) - 6 = 12。
根据极值点的判定条件,当f''(x) > 0时,函数在该点处有极小值;当f''(x) < 0时,函数在该点处有极大值;当f''(x) = 0时,判定条件不成立。
DOC-南昌大学高数试题及答案

DOC-南昌大学高数试题及答案南昌大学高数试题及答案南昌大学 2010,20011学年第一学期期末考试试卷一、填空题(每空 3 分,共 15 分)1. 设y ex2,f ,x, 1,x且 ,x, 0,则 ,x,2. 2。
, ,x2011,sinx,dx 23. 反常积分 , 12x,lnx,2dx 。
4. 极限nlim n ln,n,1,,lnn 。
5. 设y x3,2x,xx,则dy 。
二、单项选择题 (每小题3分,共15分)1. 若f,x,和g,x,都为可导函数,则ddx xaf,x,g,t,dt ( ).(A)f,x,g,x, (B)f ,x,g ,x,(C)f ,x,g,x,,f,x,g ,x,(D)f,x,g,x,,f ,x, xag,t,dt2(设f,x, ex,3x,2,当x 0时,f,x,是比x的((A)高阶无穷小 (B)低阶无穷小(C)等价无穷小 (D)非等价的同阶无穷小3(设f,x,在 a,b 上连续,则在 a,b 上至少有一点,使得( )(A)f , , 0 (B)f, , 0 。
1 )f,x,dxf,b,,f,a, a(C)f, , (D)f , , b,abb,a 1 2,lnx x 1 1 e4(设函数f,x, ,在 ,3 内( ) 1x,11 x 3 e(A)不满足拉格朗日定理条件;(B)满足拉格朗日定理条件且(C)满足拉格朗日定理条件,但无法求出;(D)不满足拉格朗日定理条件,但有sinx x,x 05(设函数f,x, x0x 0,则x 0是f,x,的(1xsinxx 0(A)连续点 (B)可去间断点(C)跳跃间断点 (D)振荡间断点三、计算题(一)(每小题 8分,共 24分)1(求极限limex,sinx,1.x 0sin3x2(计算不定积分dx3(计算定积分 10ln,x,dx) 2四、计算题(二)(每小题 8分,共 16 分)1(求由方程y 1,x2,xey所确定的隐函数y y,x, dy的导数. dxx ln1,t2dyd2y 2(设求:. 2. tu2dxdxdu y 201,u ,, 五、解答题(每小题 8分,共 16 分)1(确定a,b的值,使点,1,3,是曲线y ax3,bx2,x的拐点,并求该曲线在点,1,3,处的切线方程(x3,42(设函数y ,求该函数的单调区间和极值( 2x六、应用题(本题满分8分)某房地产公司有50套公寓要出租(当租金定为每月1800 元时,公寓会全部租出去(当租金每月增加100元时,就有一套公寓租不出去,而租出去的房子每月需花费200元整的维修费用(试问房租定为多少可获得最大收入?七、证明题(本题满分8分)设f,x,可导,证明:f,x,的两个零点之间一定有f,x,,f ,x,的零点(南昌大学 2010,2011学年第一学期期末考试试卷及答案一、填空题(每空 3 分,共 15 分)1. 设y e,f ,x, 1,x且 ,x, 0, x23则 ,x,2. , 2,x2011,sinxdx常积分 21x,lnx,2dx 1 , ,2。
专科高数极值练习题

专科高数极值练习题专科高数极值练习题在专科高数学习中,极值是一个非常重要的概念。
它可以帮助我们找到函数图像上的最高点和最低点,从而解决实际问题中的最优化问题。
在这篇文章中,我们将通过一些极值练习题来深入理解和应用这个概念。
1. 求函数 f(x) = x^3 - 3x^2 + 4 的极值点。
首先,我们需要求出函数的导数 f'(x)。
对于这个函数,我们有 f'(x) = 3x^2 - 6x。
然后,我们令导数 f'(x) 等于零,即 3x^2 - 6x = 0。
通过解这个方程,我们可以得到 x = 0 或 x = 2。
接下来,我们可以求出这两个点对应的函数值,即 f(0) = 4 和 f(2) = 0。
因此,函数 f(x) 的极小值为 0,极大值为 4。
2. 求函数 g(x) = x^3 - 6x 的极值点。
同样地,我们需要计算函数的导数 g'(x)。
对于这个函数,我们有 g'(x) = 3x^2 - 6。
然后,我们令导数 g'(x) 等于零,即 3x^2 - 6 = 0。
通过解这个方程,我们可以得到x = ±√2。
接下来,我们可以求出这两个点对应的函数值,即g(√2)≈ -1.17 和 g(-√2) ≈ 1.17。
因此,函数 g(x) 的极小值为 -1.17,极大值为 1.17。
3. 求函数 h(x) = e^x - x 的极值点。
对于这个函数,我们可以直接计算它的导数 h'(x)。
通过求导,我们得到 h'(x) =e^x - 1。
然后,我们令导数 h'(x) 等于零,即 e^x - 1 = 0。
解这个方程,我们可以得到 x = ln(1) = 0。
接下来,我们可以求出这个点对应的函数值,即 h(0) = 1。
因此,函数 h(x) 的极小值为 1。
通过以上几个极值练习题,我们可以看到极值点在函数图像上具有重要的意义。
它们代表了函数的最高点和最低点,可以帮助我们解决实际问题中的最优化问题。
原题:大学数学最值—赵六问题(解析+例题)

原题:大学数学最值—赵六问题(解析+例题)赵六问题是一个在大学数学中经常出现的求解最值问题的经典例题。
在这道问题中,我们需要找到一个函数的最值点,并分析其特性和求解方法。
问题描述设函数$f(x)$满足条件:$f(1) = f(2) = 0$,且对于$x>2$,存在正数$k$,使得$f'(x) = k^x$成立。
求函数$f(x)$在$x>2$的最值。
解析为了求解$f(x)$在$x>2$的最值,我们需要先找到函数的导数$f'(x)$,并根据导数的特性来分析函数的变化趋势。
根据已知条件,对于$x>2$,有$f'(x) = k^x$。
因此,我们可以通过求解导数$f'(x)$来解决最值问题。
由于$k$是正数,那么$k^x$也是正数。
根据指数函数的特性,指数函数的值随着自变量的增大而增大。
因此,我们可以得出结论:函数$f(x)$在$x>2$的区间内是单调递增的。
单调递增的函数在$x>2$的区间内,其最小值应该出现在$x=2$的点。
因此,我们可以推断出函数$f(x)$在$x>2$的最小值为$0$,对应于$x=2$的点。
例题让我们通过一个例题来加深对赵六问题的理解:已知函数$f(x)$在$x>2$的区间内满足$f'(x) = 2^x$,且$f(1) =f(2) = 0$。
求函数$f(x)$在$x>2$的最大值及对应的$x$值。
解答根据已知条件,我们知道函数$f(x)$在$x>2$的区间内是单调递增的。
由于$f(1) = f(2) = 0$,我们可以推断出函数$f(x)$在$x=1$和$x=2$的点都是极小值点。
因此,我们可以初步判断函数$f(x)$在$x>2$的最大值应该出现在$x=2$之后的某个点。
由于函数$f(x)$是单调递增的,我们可以确定$x=2$是其最小值点。
根据指数函数的特性,我们可以发现$2^x$在$x>2$的区间内是不断增大的。
高考物理极值法解题例题解析

2019高考物理极值法解题例题解析俗话说,“习惯成自然”,良好的学习习惯对学习有着重要的促进作用,查字典物理网小编编辑整理了高考物理极值法解题例题解析,希望考生们通过对复习资料的娴熟来为考试复习锦上添花。
一、方法简介
通常状况下,由于物理问题涉及的因素众多、过程困难,很难干脆把握其改变规律进而对其做出精确的推断.但我们若将问题推到极端状态、极端条件或特别状态下进行分析,却可以很快得出结论.像这样将问题从一般状态推到特别状态进行分析处理的解题方法就是极端法.极端法在进行某些物理过程的分析时,具有独特作用,恰当应用极端法能提高解题效率,使问题化难为易,化繁为简,思路敏捷,推断精确.
用极端法分析问题,关键在于是将问题推向什么极端,采纳什么方法处理.详细来说,首先要求待分析的问题有“极端”的存在,然后从极端状态动身,回过头来再去分析待分析问题的改变规律.其实质是将物理过程的改变推到极端,使其改变关系变得明显,以实现对问题的快速推断.通常可采纳极端值、极端过程、特别值、函数求极值等方法.
二、典例分析
1.极端值法
对于所考虑的物理问题,从它所能取的最大值或最小值方面进行分析,将最大值或最小值代入相应的表达式,从而得到所需的结
论.
【例1】如图所示,电源内阻不能忽视,R1=10Ω,R2=8Ω,当开关扳到位置1时,电流表的示数为0.2A;当开关扳到位置2时,电流表的示数可能是。
几何定值与极值问题的例题与练习精品文档5页

几何定值和极值1. 几何定值问题(1)定量问题:解决定量问题的关键在探求定值,一旦定值被找出,就转化为熟悉的几何证明题了。
探求定值的方法一般有运动法、特殊值法及计算法。
(2)定形问题:定形问题是指定直线、定角、定向等问题。
在直角坐标平面上,定点可对应于有序数对,定向直线可以看作斜率一定的直线,实质上这些问题是轨迹问题。
2. 几何极值问题:最常见的几何极值问题大体包括:有关线段的最大最小问题;三角形面积的最大最小问题;角的最大最小问题等。
【例题分析】例1. 已知的两边的中点分别为M、N,P为MN上的任一点,BP、CP的延长线分别交AC、AB于D、E,求证:为定值。
分析:用运动法探求定值,先考虑特殊情况,令P在MN上向M运动,此时D点向A 运动,P点运动到M时,D点将与A点重合,而AM=MB,于是,于是转入一般证明。
证明:连结AP例2. 两圆相交于P、Q两点,过点P任作两直线与交一圆于A、B,交另一圆于、,AB 与交于点C,求证:为定值。
分析:设两圆为⊙O、⊙,现从运动极端分析,因为直线与都是以P为固定点运动的。
当与重合时,便成了左图的情况,而AC和分别成了两圆的切线。
且,QA、分别为直径。
容易求得这就是所求的定值。
证明:如右图,连结PQ、BQ、则有例3. 在定角XOY的角平分线上,任取一点P,以P为圆心,任作一圆与OX相交,靠近O点的交点为A,与OY相交,远离O点的交点为B,则为定角。
分析:先探求定值,根据特殊化求定值,一般证明的原则,先看图(2),如果以角平分线上任意一点P为圆心,以OP为半径作圆,此时,A点与O点重合,证明:如图(1),作例4. 已知E、F分别是四边形ABCD的AB、CD边上的中点求证:分析:本题即证EF的最大值为,因此可先考虑特殊情况,以找出等号成立的条件,再证一般情况。
证明:(1)当四边形中AD//BC时,如左图EF是梯形ABCD的中位线(2)当AD不平行BC时,如右图连结AC,取AC的中点G,再连结EG、FG在中,在中,又中,综合(1) (2),得【考点解析】例1. 如图,AD是⊙O的直径,B是AD延长线上一点,BE切⊙O于点E,交BE延长线于点C,若,弦EG交AD于点F。
函数的极值含最值经典题.doc

《函数的极值与最值》经典题例 1.已知函数 f x x 3 3x 2 ,求 f ( x) 的极值。
解:由题意得 f x3x 2 6x 3x x2令 f x0 ,解得 x 1 0 , x 2 2x 变化时, f ¢(x) 、 f ( x) 的变化情况如下表:x,00,22 2,f x +-0 +f x极大值极小值所以 f ( x) 的极大值为 f (0) = 0 ,极小值为 f (2) = - 4变式 .已知函数f x x 33ax 2( a > 0) ,求 f (x) 的极值。
1解:由题意得f x3x 2 6ax3x x 2a令 fx 0 ,解得 x 1 0 , x 2 2a (a > 0)x 变化时, f ¢ 、 f ( x) 的变化情况如下表:( x)x,00,2a2a2a,f x +-0 +f x极大值极小值所以 f ( x) 的极大值为 f (0) = 0 ,极小值为 f (2 a) = - 4a 3。
变式 2 .已知函数 f x x 3 3ax 2 ,求 f ( x) 的极值。
解:由题意得f x3x 2 6ax 3x x 2a令 fx0 ,解得 x 1 0 , x 2 2a①若 a < 0 ,当 x < 2a 或 x > 0 时, f (x) 0 , f ( x) 单调递增;当 2a < x < 0 f ( x)0 , f ( x) 单调递减。
所以极大值为 f (2 a) = - 4a 3 ,极小值为f (0) = 0 。
②若 a = 0 , f ¢(x) = 3x 2 ? 0 , f ( x) 在 (- ? ,? ) 单调递增,所以 f ( x) 既无极大值,也无极小值。
③若 a > 0 ,当 x > 2a 或 x < 0 时, f (x)0 , f ( x) 单调递增;当 2a < x < 0 f ( x)0 , f ( x) 单调递减。
求极值练习题

求极值练习题极值问题是数学中的一类重要题型,它经常出现在高等数学和应用数学的课程中。
求极值涉及到函数的最大值和最小值,是数学中的一种重要求解方法。
本文将通过解答几个极值练习题,来深入了解和掌握求极值的方法和技巧。
题目一:已知函数f(x) = 2x^3 - 3x^2 - 12x + 5,请求函数f(x)的极大值和极小值点及极值。
解答一:首先,我们需要求解函数的导数,然后找到导数为零的点,即可得到函数的极值点。
f'(x) = 6x^2 - 6x - 12令f'(x) = 0,我们可以得到方程6x^2 - 6x - 12 = 0。
化简后得到x^2 - x - 2 = 0,再因式分解可得(x-2)(x+1) = 0。
解得x=2或x=-1。
接下来,我们需要判断这两个解对应的点是极大值点还是极小值点。
可以通过二阶导数来判断,当二阶导数大于零时,对应的点为极小值点;当二阶导数小于零时,对应的点为极大值点。
f''(x) = 12x - 6将x=2和x=-1分别代入二阶导数,我们可以得到f''(2) = 18和f''(-1) = -18。
由此可知,x=2对应的点为极小值点,x=-1对应的点为极大值点。
代入函数f(x),我们可以计算出极小值为f(2) = -11,极大值为f(-1) = 18。
题目二:已知函数g(x) = e^x - 2x,请求函数g(x)的极值点及极值。
解答二:首先,我们需要求解函数的导数,然后找到导数为零的点,即可得到函数的极值点。
g'(x) = e^x - 2令g'(x) = 0,我们可以得到方程e^x - 2 = 0。
解这个方程可以得到x = ln(2)。
接下来,我们需要判断这个解对应的点是极大值点还是极小值点。
同样地,可以通过二阶导数来判断。
g''(x) = e^x将x=ln(2)代入二阶导数,我们得到g''(ln(2)) = e^ln(2) = 2。
10极值问题

极值问题一、绳子的极值问题1.如图所示,用细绳OA、OB、OC共同悬挂一重物,OA、OB、OC所能承受的最大拉力均为100 N。
已知OB水平,∠AOB=120°,为保证细绳都不断,所挂重物最多不能超过多重?答案:5032.如图所示,一物体重30N,用OC绳悬挂在O点,OC绳能承受的最大拉力为203N,再用一绳系OC绳的A点,AB绳能承受的最大拉力为30 N,现用水平力拉AB,可以把OA绳拉到与竖直方向成多大角度?答案:300解析:当OA绳与竖直方向的夹角θ逐渐增大时,OA绳和BA绳中的拉力都逐渐增大,其中某一根绳的拉力达到它本身能承受的最大拉力时,就不能再增大角度了,假设OA绳中的拉力先达到这一要求所以有此时F BA=故所求的最大角度为30°二、动态平衡相关的极值问题3.如图所示,用等长的细绳OA、OB悬挂着一个重力为G的重物,保持重物的位置不变,且保持OA与水平面的夹角为θ,使OB端沿半径等于绳长的圆周轨道向C点运动,在这个过程中,OB绳中的张力T B的最小值是多少?答案:Gcos θ4. (2018·山东师大附中一模)如图所示,三根长度均为L 的轻绳分别连接于C 、D 两点,A 、B 两端被悬挂在水平天花板上,相距2L ,现在C 点上悬挂一个质量为m 的重物,为使CD 绳保持水平,在D 点上可施加力的最小值为( )A .mg B.33mg C.12mg D.14mg 答案:C解析:由题图可知,要使CD 水平,各绳均应绷紧,则AC 与水平方向的夹角为60°;结点C 受力平衡,受力分析如图所示,则CD 绳的拉力F T =mg tan 30°=33mg ;D 点受绳子拉力大小等于F T ,方向向左;要使CD 水平,D 点两绳的拉力与外界的力的合力为零,则绳子对D 点的拉力可分解为沿BD 绳的F 1,及另一分力F 2,由几何关系可知,当力F 2与BD 垂直时,F 2最小,而F 2的大小即为拉力的大小;故最小力F =F T sin 60°=12mg 。
函数的极值和最值(习题).docx

【巩固练习】1. 设函数/(兀)在/?上可导,其导函数/©),且函数/(X )在x = -2处取得极小值,则函数y = xf(x)的图象可能是4•函数冷宀」的单调递减区间为5.已知 f (x) =x 3-6x 2 +9x-abc, a<b<c,且 f (a) =f (b) =f (c) =0.现给出如下结论: ®f (0) f (1) >0;②f (0) f (1)<0;③f (0) f (3) >0; @f (0) f (3) <0. 其中正确结论的序号是A.①③B.①④C.②③D.②④6•函数f(x)=xlnx(x>0)的单调递增区间是 ___________ o 7. 函数y=l+3x-x 3的极大值是 _______ ,极小值是 _________ o 8. 函数f(x)=12x-x 3在区间卜3,3]上的最小值是 __ - 9. 函数f (x)=ln(l+x)-x 的最大值为 __________ 。
(1) 求集合D (用区间表示)(2) 求函数/(x) = 2x 3-3(l + a)x 2 + 6股在D 内的极值点. 15. 设 /(x) = ae x + -^―+b(a > 0)ae x⑴求于(兀)在[0,+oo)上的最小值;3(II)设曲线y = /(x)在点(2 J ⑵)的切线方程为y =—无;求的值.2【参考答案与解析】2. 设a>0, b>0, c 是自然对数的底数A. 若 e 10 il 12+2a=e b +3b,贝!j a>bB. 若 e a +2a=e b +3b,则 a<bC. 若 e a -2a=e b -3b,贝!| a>bD. 若 e a -2a=e b -3b,贝0 a<b23.设函数 f (x) = —+lnx 贝9 ( )xA. x 二丄为f(x)的极大值点 B冷为3的极小值点C. x=2为f(x)的极大值点D. x=2为f(x)的极小值点A (-1, 1]B (0, 1] C[l,十8)D (0, +«)D = AC\B.1・ C 2. A 3. D 4. B 5. C6. ( — ,+oo)7. 3, -1:e11.【解析】若a>0,则8. -16;9. 0;10. — +6当x=-a时,f(x)的极大值为5a3o当x=3a时,f(x)的极小值为・27a\若a<0,则当x=3a时,f(x)的极大值为Qa?,当x=-a时,f(x)的极小值为5a312.aW—313.【解析】(I) a二-3, b二4(II)当x W [0, 3]时,f (x)的最大值为f (3) =9+8c因为对于任意的xE [0, 3],有f (x)<c2恒成立,所以9+8c<c2,解得c〈-1 或c>9,因此c的取值范围为(-8, -1) U (9, +8)14.【解析】(1)令g(兀)=2兀$-3(l + d)兀+6d ,△ = 9(1 + a)2 - 48a = 9a2 - 30a + 9 = 3(3d - l)(a - 3)。
极值、最值与导数习题(附答案)(可编辑修改word版)

极值、最值与导数
1.若函数f(x)=2x3-3x2+c 的极大值为6,那么c 的值为( )
A.0
B.5
C.6
D.1
f (x) =2
+ ln x
2.设函数x ,则( )
x =1
x =
1
A . 2 为f(x)的极大值点
B . 2 为f(x)的极小值点
C .x=2 为f(x)的极大值点
D .x=2 为f(x)的极小值点
3.函数f(x)=(x-3)e x 的单调递增区间是.
4.如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
①-2 是函数y=f(x)的极值点; ②1是函数y=f(x)的极值点;
③y=f(x)在x=0 处切线的斜率小于零; ④y=f(x)在区间(-2,2)上单调递增. 则正确命题的序号是.(写出所有正确命题的序号)
5.已知函数f(x)=-x3+3x2+9x-2.
(Ⅰ)求f(x)的单调递减区间; (Ⅱ)求f(x)在区间[-2,2]上的最大值与最小值.
答案:
1.C
2.D
3.(2,+∞)
4.①④
5. (Ⅰ)函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(Ⅱ)函数f(x)在闭区间[-2,2]上的最大值为f(2)=20,最小值为f(-1)=-7.。
高三数学利用导数求最值和极值试题

高三数学利用导数求最值和极值试题1. 设函数在处取极值,则= . 【答案】2. 【解析】因为,又函数在处取极值,所以,从而.【考点】1.函数导数的求法;2.三角恒等变形公式.2. 函数y =x 4-4x +3在区间[-2,3]上的最小值为( ) A .72 B .36 C .12D .0【答案】D【解析】因为y′=4x 3-4,令y′=0即4x 3-4=0,解得x =1.当x<1时,y′<0,当x>1时,y′>0,所以函数的极小值为y|x =1=0,而在端点处的函数值y|x =-2=27,y|x =3=72,所以y min =0.3. 函数的极小值是 . 【答案】. 【解析】,令,解得,列表如下:极大值极小值故函数在处取得极小值,即.【考点】函数的极值4. 函数f(x)=x 3-x 2-3x -1的图象与x 轴的交点个数是________.【答案】3【解析】f′(x)=x 2-2x -3=(x +1)(x -3),函数在(-∞,-1)和(3,+∞)上是增函数,在(-1,3)上是减函数,由f(x)极小值=f(3)=-10<0,f(x)极大值=f(-1)=>0知函数f(x)的图象与x 轴的交点个数为3.5. 已知a≤+lnx 对任意的x ∈[,2]恒成立,则a 的最大值为________.【解析】令f(x)=+lnx ,f′(x)=,当x ∈[,1)时,f′(x)<0,当x ∈(1,2]时,f′(x)>0,∴f(x)min =f(1)=0,∴a≤0,故a 最大值为0.6. [2014·长沙模拟]已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y =-x 3+81x -234,则使该生产厂家获取最大年利润的年产量为( ) A .13万件B .11万件C .9万件D .7万件【答案】C【解析】∵y=-x3+81x-234,∴y′=-x2+81.令y′=0,得x=9,x=-9(舍去).当0<x<9时,y′>0,函数f(x)单调递增;当x>9时,y′<0,函数f(x)单调递减.故当x=9时,y取最大值.7.函数已知时取得极值,则的值等于()A.2B.3C.4D.5【答案】D【解析】因为,所以,解得.故选D.8.已知常数a,b,c都是实数,f(x)=ax3+bx2+cx-34的导函数为f′ (x),f′(x)≤0的解集为{x|-2≤x≤3},若f(x)的极小值等于-115,则a的值是()A.-B.C.2D.5【答案】C【解析】依题意得f′(x)=3ax2+2bx+c≤0的解集是[-2,3],于是有3a>0,-2+3=-,-2×3=,解得b=-,c=-18a,函数f(x)在x=3处取得极小值,于是有f(3)=27a+9b+3c-34=-115,-a=-81,a=2,故选C.9.设函数f(x)=x e x,则().A.x=1为f(x)的极大值点B.x=1为f(x)的极小值点C.x=-1为f(x)的极大值点D.x=-1为f(x)的极小值点【答案】D【解析】∵f(x)=x e x,∴f′(x)=e x+x e x=e x(1+x).∴当f′(x)>0时,则x>-1,函数y=f(x)是增函数,同理可求,x<-1时函数f(x)为减函数.∴x=-1时,函数f(x)取得极小值.10.设函数.若是函数的极值点,1和是函数的两个不同零点,且,求.若对任意,都存在(为自然对数的底数),使得成立,求实数的取值范围.【答案】(1);(2).【解析】(1)对零点存在性定理的考查,借助是极值及1是零点建立两个方程解出和,然后对函数进行求导定出其单调性,再利用零点存在性定理尝试算出和,发现异号,得出零点所在的区间;(2)首先需要我们将两个变量的不等式恒成立问题转化成常见的一个变量的不等式有解问题,然后再构造这个不等式为函数,为了找的最小值并且让其小于0,我们利用试根法试出,然后只要让右零点在端点1右边即可,解出范围.试题解析:(1),∵是函数的极值点,∴.∵1是函数的零点,得,由解得. ∴,,令,,得;令得,所以在上单调递减;在上单调递增.故函数至多有两个零点,其中,因为,,,所以,故.(2)令,,则为关于的一次函数且为增函数,根据题意,对任意,都存在,使得成立,则在有解,令,只需存在使得即可,=,令,∵的两个零点分布在左右,又∵,∴的右零点必须大于1,∴,解得.综上所述,当时,对任意,都存在,使得成立.【考点】1.零点存在性定理;2.根的分布.11.若函数在处有极值,则函数的图象在处的切线的斜率为 .【答案】-5【解析】∵函数f(x)=(x-2)(x2+c)在x=1处有极值,∴f′(x)=(x2+c)+(x-2)×2x,∵f′(2)=0,∴(c+4)+(2-2)×2=0,∴c=-4,∴f′(x)=(x2-4)+(x-2)×2x,∴函数f(x)的图象x=1处的切线的斜率为f′(1)=(1-4)+(1-2)×2=-5.【考点】1.函数在某点取得极值的条件;2.利用导数研究曲线上某点切线方程12.设函数,.(1)记为的导函数,若不等式在上有解,求实数的取值范围;(2)若,对任意的,不等式恒成立,求m(m∈Z,m1)的值.【答案】(1);(2).【解析】(1)首先由已知条件将不等式转化为它在上有解等价于,再利用导数求函数的最小值;(2)由已知时,对任意的,不等式恒成立,等价变形为在上恒成立,为此只需构造函数,只要证明函数在上单调递增即可.试题解析:(1)不等式即为化简得由知,因而设由当时在上恒成立.由不等式有解,可得知即实数的取值范围是(2)当.由恒成立,得恒成立.设,由题意知,故当时函数单调递增,恒成立,即恒成立,因此,记,得,∵函数在上单调递增,在上单调递减,∴函数在时取得极大值,并且这个极大值就是函数的最大值.由此可得,故,结合已知条件,,可得.【考点】1.导数的应用;2.恒成立问题中的参数取值范围问题.13.某商场销售某种商品的经验表明,该商品每日的销售量(单位:千克)与销售价格(单位:元/千克)满足关系式其中为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.(1)求的值;(2)若该商品的成本为3元/千克,试确定销售价格的值,使商场每日销售该商品所获得利润最大.【答案】(1);(2)【解析】(1)商品每日的销售量与销售价格满足的关系中,只含有一个参数,所以只需一个条件即可,已知,代入解析式,可求;(2)利用函数思想,列利润关于销售价格的函数解析式,再求其最大值,利润=(每千克商品的利润)(每日销售量). 试题解析:(1)∵时,,,∴;(2)销售利润=2+∴于是,当变化时,,的变化情况如下表,由表知,是函数在区间内的极大值点,亦是最大值点,所以当时,函教取得最大值,且最大值为42.【考点】1、函数的应用;2、利用导数求函数的最值.14.设.(Ⅰ)若,求的单调区间;(Ⅱ) 若对一切恒成立,求的取值范围.【答案】(Ⅰ)的单调递增区间为,的单调递减区间为;(Ⅱ)【解析】(Ⅰ)将代入得:求的导数,由;便可得的单调区间.(Ⅱ)∴对一切恒成立等价于恒成立.这只要求出函数的最小值即可.试题解析:(Ⅰ)时,,故由得:;由得:;∴的单调递增区间为, 的单调递减区间为(II)令,则由得.所以在上单调递增, 在单调递减.所以由此得:又时,即为此时取任意值都成立综上得:【考点】1、函数的导数及其应用;2、不等关系.15.已知(a是常数)在[-2,2]上有最大值3,那么在[-2,2]上f(x)的最小值是____________.【答案】-37.【解析】,令得或.当变化时,随的变化如下表+_极大值.【考点】利用导数求函数的最值.16.若函数f(x)=x3-3bx+b在区间(0,1)内有极小值,则b应满足的条件是 _【答案】(0,1)【解析】解:由题意得f′(x)=3x2-3b,令f′(x)=0,则x=±又∵函数f(x)=x3-3bx+b在区间(0,1)内有极小值,∴0<<1,∴b∈(0,1),故答案为(0,1).17.已知有两个极值点、,且在区间(0,1)上有极大值,无极小值,则的取值范围是【答案】【解析】,且在区间(0,1)上有极大值,所以,.18.(本题满分15分)设函数.(Ⅰ)求函数的单调区间;(Ⅱ)已知对任意成立,求实数的取值范围;(Ⅲ)试讨论方程的零点个数.【答案】(1)极大值(2)(3)b=-e或b>0时有一个零点;-e<b<=0时,有无零点;b<-e时,有两个零点.【解析】本试题主要是考查了导数在研究函数中的运用。
电磁场中的极值问题

1 . (2018·四川省乐山市第二次调研)如图5所示,在平面直角坐标系xOy 平面内,直角三角形abc 的直角边ab 长为6d ,与y 轴重合,∠bac =30°,中位线OM 与x 轴重合,三角形内有垂直纸面向里的匀强磁场.在笫一象限内,有方向沿y 轴正向的匀强电场,场强大小E 与匀强磁场磁感应强度B 的大小满足E =v 0B .在x =3d 的N 点处,垂直于x 轴放置一平面荧光屏.电子束以相同的初速度v 0从y 轴上-3d ≤y ≤0的范围内垂直于y 轴向左射入磁场,其中从y 轴上y =-2d 处射入的电子,经磁场偏转后,恰好经过O 点.电子质量为m ,电荷量为e ,电子间的相互作用及重力不计.求图5(1)匀强磁杨的磁感应强度B ;(2)电子束从y 轴正半轴上射入电场时的纵坐标y 的范围;(3)荧光屏上发光点距N 点的最远距离L .答案 (1)m v 0ed (2)0≤y ≤2d (3)94d 解析 (1)设电子在磁场中做圆周运动的半径为r ;由几何关系可得r =d电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:e v 0B =m v 02r解得:B =m v 0ed(2)当电子在磁场中运动的圆轨迹与ac 边相切时,电子从+y 轴射入电场的位置距O 点最远,如图甲所示.设此时的圆心位置为O ′,有:O ′a =r sin 30°OO ′=3d -O ′a解得OO ′=d即从O 点进入磁场的电子射出磁场时的位置距O 点最远所以y m =2r =2d电子束从y 轴正半轴上射入电场时的纵坐标y 的范围为0≤y ≤2d(3)设电子从0≤y ≤2d 范围内某一位置射入电场时的纵坐标为y ,从ON 间射出电场时的位置横坐标为x ,速度方向与x 轴间夹角为θ,在电场中运动的时间为t ,电子打到荧光屏上产生的发光点距N 点的距离为L ,如图乙所示:根据运动学公式有:x =v 0ty =12·eE mt 2 v y =eE mt tan θ=v y v 0,tan θ=L 3d -x由题意知E =v 0B =m v 02ed解得:L =(3d -2y )·2y当3d -2y =2y即y =98d 时,L 有最大值 解得:L =94d2 .如图所示为研究电子枪中电子在电场中运动的简化模型示意图。
南昌大学-高数(上)试题及答案

南昌大学 2012~20013学年第一学期期末考试试卷一、 填空题(每空 3 分,共 15 分) 1. 函数)4(log )(22x x f -=在区间是连续的.。
2. 设()(1)(2)(2012)f x x x x x =+++,则=')0(f 。
3. 函数7186223+--=x x x y 的极大值点为。
4. 设2()()xt f x x t e dt -=-⎰,则()df x =。
5. 曲线231x ty t⎧=+⎪⎨=⎪⎩在2t =处的切线方程为。
二、 单项选择题 (每小题3分,共15分)1、设0lim ()x xf x a -→=,0lim ()x x f x b +→=,下列命题正确的是 ( ) A 、若b a =,则)(x f 一定连续;B 、若b a =,则2)(lim 0ba x f x x +=→; C 、若b a ≠,则2)(lim 0b a x f x x +=→; D 、若b a≠,则)()(lim 00x f x f xx =→. 2、已知()(),(1)2xf x dx F x C f dx =++=⎰⎰则( )A 、2()F x C +B 、()2xF C +C 、(1)2xF C ++ D 、2(1)2x F C ++.3、⎪⎩⎪⎨⎧=≠=0,00,1sin )(x x x x x f 在0=x 处( )A 、不连续;B 、连续但不可导;C 、可导,但导函数在该点不连续;D 、导函数在该点连续. 4、若反常积分kx e dx -∞⎰收敛, 则( )A 、0>k; B 、0≥k ;C 、0<k ;D 、0≤k .5、若 0sin ()xtx dt tα=⎰, 10()(1)x tx t dt β=+⎰, 则当0x +→时()x α与()x β是 ( )A 、高阶无穷小B 、低阶无穷小C 、等价无穷小D 、非等价的同阶无穷小.三、计算题(每小题 7分,共35分) 1、求下列极限()0111lim[]ln(1)x x x→-+ ()012lim x +→- 2、求下列不定积分或定积分()1cot xdx⎰() /22sin cos x x dx π-⎰()43⎰四、解答题(每小题 7分,共 14 分)1、设xx t x t x t t f ⎪⎭⎫ ⎝⎛-+=∞→lim )(,求. )(t f '2、由方程)sin(y x y +=可确定函数()y y x =,求22d y dx .五、应用题(每小题 7分,共 14分) 1、求曲线21x y e-=-的拐点和凹、凸的区间.2、求抛物线23y x=-与直线2y x =所围成的平面图形的面积.六、证明题(本题满分7分) 设()f x 在[0,1]上连续且满足 10()0f x dx =⎰,证明存在ξ∈(0,1)使得()(1)0f f ξξ+-=.南昌大学 2012~2013学年第一学期期末考试试卷及答案一、 填空题(每空 3 分,共 15 分)1. 函数)4(log )(22x x f -=在区间()2,2-是连续的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3.由直线y=0,x=8及抛物线y=x2围城一个曲边三角形,在曲边y=x2上求一点,使曲线在该点处的切线与直线y=0及x=8所围成的三角形面积最大。
例4.某人正处在森林地带中距公路2公里的A处,在公路右方8公里处有一个车站B,假定此人在森林地带中步行的速度为6公里∕小时,沿公路行走的速度为8公里∕小时,为了尽快赶到车站,他选择A-C-B,问C应在公路右方多少?他最快能在多少时间内到达B?
例1.某工厂生产某型号车床,年产量a台,分若干批进行生产,每批生产准备费为b元。设产品均匀投入市场,且上一批用完后立刻生产下一批,即平均库存量为批量的一半。设每年每台库存费为c元,求出一年中库存费与生产费的和与批量的函数关系。
例2.欲围一个面积为150平方米的矩形场地,所用材料的造价其正面是每平方米6元,其余三面是每平方米3元。问场地的长﹑宽为多米时,才能使所用材料费最少?
例5.
