2007年沈阳市中等学校招生统一考试数学试卷及答案(word版)
2007年全国各地高考数学试卷及答案(37套)word--完整版

2007年普通高等学校招生全国统一考试数学卷(四川.文)含答案
2007年普通高等学校招生全国统一考试数学卷(天津.理)含答案
2007年普通高等学校招生全国统一考试数学卷(天津.文)含答案
2007年普通高等学校招生全国统一考试数学卷(浙江.理)含答案
2007年普通高等学校招生全国统一考试数学卷(湖南.理)含答案
2007年普通高等学校招生全国统一考试数学卷(湖南.文)含答案
2007年普通高等学校招生全国统一考试数学卷(江西.理)含答案
2007年普通高等学校招生全国统一考试数学卷(江西.文)含答案
2007年普通高等学校招生全国统一考试数学卷(山东.理)含答案
2007年全国各地高考数学试卷及答案(37套)--完整版
2007年普通高等学校招生全国统一考试数学卷(全国卷Ⅰ.理)含答案
2007年普通高等学校招生全国统一考试数学卷(全国卷Ⅰ.文)含答案
2007年普通高等学校招生全国统一考试数学卷(全国卷Ⅱ.理)含答案
2007年普通高等学校招生全国统一考试数学卷(全国卷Ⅱ.文)含答案
宁夏和海南都是新课标教材,使用的是同一套数学题。
பைடு நூலகம் 四川省蓬安中学校 张万建 整理 zwjozwj@
2007年普通高等学校招生全国统一考试数学卷 (宁夏.海南.理) 含答案
2007年普通高等学校招生全国统一考试数学卷 (宁夏.海南.文) 含答案
2007年普通高等学校招生全国统一考试数学卷(江苏卷不分文理)含答案
注:使用全国卷Ⅰ的省份:河北 河南 山西 广西 ;
使用全国卷Ⅱ的省份:吉林 黑龙江 云南 贵州 新疆 青海 甘肃 内蒙 西藏
2007年全国各地中考试题130多份标题汇总

2007年全国各地中考试题130多份标题汇总2007年安徽省初中毕业学业考试数学试卷及答案2007年安徽省芜湖市初中毕业学业考试数学试卷及参考答案2007年北京市高级中等学校招生统一考试数学试卷及参考答案2007年福建省福州市毕业会考、高级中等学校招生考试卷及答案(扫描)2007年福建省福州市初中毕业会考、高级中等学校招生考试数学试卷及答案2007年福建省龙岩市初中毕业、升学考试数学试题及参考答案2007年福建省宁德市初中毕业、升学考试数学试题及参考答案2007年福建省泉州市初中毕业、升学考试数学试题2007年福建省三明市初中毕业生学业考试数学试题及参考答案2007年福建省厦门市初中毕业和高中阶段各类学校招生数学试题及答案2007年甘肃省白银等3市旧课程数学试题2007年甘肃省白银等7市新课程中考数学试题及参考答案2007年甘肃省兰州市初中毕业生学业考试数学试卷A卷及参考答案2007年甘肃省陇南市中考数学试题及参考答案2007年广东省初中毕业生学业考试数学试题2007年广东省佛山市高中阶段学校招生考试数学试卷2007年广东省广州市初中毕业生学业考试数学试卷2007年广东省茂名市初中学业与高中阶段学校招生考试试题及答案2007年广东省梅州市初中毕业生学业考试数学试题及参考答案2007年广东省韶关市初中毕业生学业考试数学试题及参考答案2007年广东省深圳市初中毕业生学业考试数学试卷及参考答案2007年广东省中山市初中毕业生学业考试数学试卷及参考答案2007年广西省河池市中等学校招生统一考试数学试题及参考答案(课改区)2007年广西省柳州市、北海市中考数学试卷(课改实验区用)2007年广西省南宁市中等学校招生考试(课改实验区)数学试题及参考答案2007年广西省玉林市、防城港市初中毕业升学考试数学试题及参考答案2007年广西省中等学校招生河池市统一考试数学试题及答案(非课改区)2007年贵州省安顺市初中毕业生学业课改实验区数学科试题2007年贵州省毕节地区高中、中专、中师招生统一考试2007年贵州省贵阳市初中毕业生学业考试数学试卷及参考答案2007年贵州省黔东南高中、中专、中师招生统一考试数学试题2007年贵州省遵义市初中学业统一考试数学试卷2007年海南省初中毕业升学考试数学试题2007年河北省初中毕业生升学考试数学试卷及参考答案2007年河北省课程改革实验区初中毕业生学业考试试题及参考答案2007年河南省高级中等学校招生学业考试试卷2007年河南省开封市高中阶段各类学校招生考试题2007年黑龙江省哈尔滨市初中升学考试数学试卷2007年黑龙江省牡丹江市课程改革实验区初中毕业学业考试数学试题2007年湖北省恩施自治州初中毕业、升学考试数学及答案2007年湖北省黄冈市普通高中和中等职业学校招生考试数学试题2007年湖北省荆门市初中毕业生学业考试数学试卷(含答案)(扫描版)2007年湖北省荆门市初中毕业生学业考试数学试题及参考答案2007年湖北省荆州市中考数学试题2007年湖北省潜江市、仙桃市、江汉油田初中毕业生学业考试试题及答案2007年湖北省十堰市初中毕业生学业考试数学试卷2007年湖北省武汉市新课程初中毕业生学业考试数学试卷2007年湖北省咸宁市初中毕业生学业考试数学试卷2007年湖北省襄樊市初中毕业、升学统一考试非课改区数学试题及参考答案2007年湖北省孝感市初中毕业生学业考试数学及答案2007年湖北省宜昌市初中毕业生学业考试数学试题及参考答案2007年湖南省长沙市初中毕业学业考试试卷及答案2007年湖南省常德市初中毕业学业考试数学试卷2007年湖南省郴州市基教试验区初中毕业学业考试数学试卷及答案2007年湖南省怀化市初中毕业学业考试数学试卷及参考答案2007年湖南省邵阳市初中毕业学业考试试题卷2007年湖南省湘潭市初中毕业学业考试数学试卷2007年湖南省永州市初中毕业学业考试数学试卷2007年湖南省岳阳市初中毕业学业考试试卷及参考答案2007年湖南省株洲市初中毕业学业考试数学试卷2007年吉林省长春市初中毕业生学业考试数学试题及答案2007年吉林省初中毕业生学业考试数学试题及参考答案2007年江苏省常州市初中毕业、升学统一考试数学试卷及参考答案2007年江苏省淮安市初中毕业暨中等学校招生文化统一考试数学试题2007年江苏省连云港市中考数学试题与参考答案2007年江苏省南京市初中毕业学业考试数学试题及参考答案2007年江苏省南通市初中毕业、升学考试数学试题2007年江苏省苏州市初中毕业暨升学考试试卷及参考答案2007年江苏省宿迁市中考数学试卷及参考答案2007年江苏省泰州市初中毕业、升学统一考试数学试题及答案2007年江苏省无锡市初中毕业高级中等学校招生考试数学试卷及参考答案2007年江苏省徐州市初中毕业、升学考试数学试题2007年江苏省盐城高中阶段招生统一考试数学试题(扫描版)2007年江苏省扬州市初中毕业、升学考试数学及参考答案(扫描版)2007年江苏省扬州市初中毕业、升学统一考试数学试题及参考答案2007年江苏省中考数学试卷及参考答案2007年江西省南昌市初中毕业暨中等学校招生考试数学试卷及参考答案2007年江西省中等学校招生考试数学试题及参考答案2007年辽宁省大连市初中毕业升学统一考试数学试题2007年辽宁省沈阳市中等学校招生统一考试数学试题及参考答案2007年辽宁省十二市初中毕业生学业考试数学试卷及参考答案2007年内蒙古自治区赤峰市初中毕业、升学统一考试数学试卷及参考答案2007年内蒙古自治区鄂尔多斯市初中毕业升学考试数学试题及参考答案2007年内蒙古自治区呼和浩特市中考数学试卷及参考答案2007年内蒙古自治区乌兰察布市初中升学考试数学试题及参考答案2007年宁夏回族自治区课改实验区初中毕业暨高中招生考试试题及答案2007年山东省滨州市中等学校招生统一考试数学试卷及参考答案2007年山东省德州市中等学校招生考试数学试题及参考答案2007年山东省东营市初中毕业暨高中阶段教育学校招生考试数学试题及答案2007年山东省济南市高中阶段学校招生考试数学试题及答案2007年山东省济宁市中等学校招生考试数学试题及参考答案2007年山东省聊城市普通高中招生统一考试数学试卷及参考答案2007年山东省临沂市初中毕业与高中招生考试考数学试卷及答案(扫描版)2007年山东省临沂市初中毕业与高中招生考试数学试题(Word版含答案)2007年山东省青岛市中考数学试卷(含答案)2007年山东省日照市中等学校统一招生考试数学试题及参考答案2007年山东省泰安市年中等学校招生考试数学试卷(课改实验区用)2007年山东省泰安市中等学校招生考试数学试卷及参考答案(非课改区)2007年山东省威海市初中升学考试数学试题及参考答案2007年山东省潍坊市初中学业水平考试数学试卷及参考答案2007年山东省烟台市初中毕业、升学统一考试数学试卷2007年山东省枣庄市中等学校招生考试数学试题及答案2007年山东省中等学校招生考试数学试题2007年山东省淄博市中等学校招生考试数学试题2007年山西省临汾市初中毕业生学业数学考试试题及参考答案2007年陕西省基础教育课程改革实验区初中毕业学业考试数学试题2007年上海市初中毕业生统一学业考试试卷及答案2007年四川省巴中市高中阶段教育招生考试2007年四川省成都市高中阶段教育学校统一招生考试试卷及参考答案2007年四川省德阳市初中毕业生学业考试数学试卷及答案2007年四川省乐山市高中阶段教育学校招生统一考试数学试题及参考答案2007年四川省泸州市初中毕业暨高中阶段学校招生统一考试数学试题及答案2007年四川省眉山市高中阶段教育学校招生考试数学试卷及参考答案2007年四川省绵阳市高级中等教育学校招生统一考试数学试题(含答案)2007年四川省内江初中毕业会考暨高中阶段招生考试试卷2007年四川省内江市初中毕业会考暨高中阶段招生考试数学试卷及参考答案2007年四川省南充市高中阶段学校招生统一考试数学试卷及参考答案2007年四川省宜宾市高中阶段学校招生考试数学试卷2007年四川省资阳市高中阶段学校招生统一考试数学试题及参考答案2007年四川省自贡市初中毕业暨升学考试数学试题及参考答案2007年台湾地区中考数学第一次测验试题及参考答案2007年天津市中考数学试卷及答案2007年云南省高中(中专)招生统一考试(课改实验区)数学试题及答案2007年云南省昆明市高中(中专)招生统一考试数学试卷2007年云南省双柏县初中毕业考试数学试卷(含答案)2007年浙江省初中毕业生学业考试数学试题及参考答案2007年浙江省杭州市数学中考试题及参考答案2007年浙江省湖州市初中毕业生学业考试数学试卷及参考答案2007年浙江省嘉兴市初中毕业生学业考试数学参考答案2007年浙江省嘉兴市初中毕业生学业考试数学试卷2007年浙江省金华中考数学试题及参考答案2007年浙江省丽水市初中毕业生学业考试数学试卷及参考答案2007年浙江省宁波市中考数学试题及参考答案2007年浙江省衢州市初中毕业生学业水平考试数学试题及参考答案2007年浙江省绍兴市初中毕业生学业考试数学试卷2007年浙江省台州市初中毕业生学业考试数学试卷及参考答案2007年浙江省温州市初中毕业学业考试数学试卷2007年浙江省义乌市初中毕业生学业考试数学试题及参考答案2007年浙江省舟山市初中毕业生学业考试数学试题及参考答案2007年重庆市初中毕业生学业暨高中招生考试试卷及参考答案。
辽宁省2007年中职生升高招生考试(1)

辽宁省2007年中职生升高职招生考试电器专业综合课试卷一、单选(每小题4分:共60分)1、为了保证工厂供电生产和生活用电的需要,必须达到的四项基本要求是()A、安全、可靠、快速、经济B、安全、可靠、节能、经济C、安全、可靠、优质、经济D、安全、节能、优质、经济2、将电气设备正常情况下不带电的金属外壳接地,称为()A、工作接地B、保护接地C、重复接地D、临时接地3、变压器瓦斯继电保护中,瓦斯继电器上油杯上触点接通时,起作用是()A、接通继电器B、接通控制回路C、是断路器跳闸D、接通报警回路4、PE线所用材质与相线相同时,按热稳定要求选择截面,当相线线芯面积小于16mm时,PE线最小截面为()A、与相线线芯截面相同B、为相线线芯截面的1/2C、为相线线芯的截面的1/3D、为相线线芯截面的1/45、按《供配电系统设计规范》规定,正常运行情况下,电动机电压偏差允许值(以U N的百分数表示为)()A.%5± B%8± C%10± D%15±6、一台三相变压器额定电压为220/110V,Y,yo接法,低压侧额定电流为1000A,高压侧额定电流为()A.500AB.1000AC.1732AD.2000A7、一台单相变压器额定电压为220V/110V,在低压侧作短路实验,测得的短路阻抗值为6Ω,若在高压侧作短路实验测得短路阻抗值为()A.3ΩB.6ΩC.12ΩD.24Ω8.当他励直流电动机外电压和励磁电流不变时,增加其负载,则电动机的()A.电枢电流IM增大,转速n降低 B.电枢电流IM减少,转速n升高C.电枢电流IM减少,转速n降低 D.电枢电流IM增大,转速n升高9.关于直流电动机下列说法正确的是()A.直流电动机的额定功率指输入的电功率B.直流电动机无电刷一样可以工作C.直流电动机的转子转向不可改变D.同一台直流电动机既可作发电机运行,也可作电动机运行10.关于三相感应电动机下列说法正确的是()A三相感应电动机的起动电流很大,所以其起动转矩也很大B三相感应电动机的起动电流和起动转矩都与电机所加的电源电压成正比C在机械和工艺允许的条件下,感应电机的气隙越小越好D感应电动机空载运行时的功率因数很高11.三相异步电动机主回路装配的熔丝所起的作用是()A过载保护 B短路保护 C失压保护 D欠压保护12.交流接触器铁心上短路环的作用是()A消除铁心振动 B增大铁芯磁通 C减缓铁心冲击 D压紧铁心叠片13.PLC运行时CPU的工作方式为()A隔行扫描 B定时扫描 C循环扫描 D中断扫描14.FX2系列PLC中,定时器编号为T10,K200所表示的含义为()A 定时时间为0.2s B定时时间为2sC 定时时间为20S D定时时间为200S15 、某控制系统中,有8个输入信号和24个输出信号,应选用PLC的编号是()A FX2-16M B FX2--24MC FX2--32MD FX2--48M二、填空题(每空4分,共60分)16、电弧是一种强烈的()现象,它的特点是温度高,光亮很强。
2007年普通高等学校招生全国统一考试(辽宁卷)数 学(供文科考生使用)

2007年普通高等学校招生全国统一考试(辽宁卷)数 学(供文科考生使用)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共60分)参考公式:如果事件A B ,互斥,那么 球的表面积公式()()()P A B P A P B +=+ 24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ,那么34π3V R =n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径()(1)k kn k n n P k C p p -=-一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合{13}A =,,{234}B =,,,则A B =( )A .{1}B .{2}C .{3}D .{1234},,, 2.若函数()y f x =的反函数...图象过点(15),,则函数()y f x =的图象必过点( )A .(51),B .(15),C .(11),D .(55),3.双曲线221169x y -=的焦点坐标为( )A .(,B .(0,,(0 C .(50)-,,(50), D .(05)-,,(05),4.若向量a 与b 不共线,0≠a b ,且⎛⎫-⎪⎝⎭a a c =ab a b ,则向量a 与c 的夹角为( )A .0B .π6C .π3D .π25.设等差数列{}n a 的前n 项和为n S ,若39S =,636S =,则789a a a ++=( )A .63B .45C .36D .276.若m n ,是两条不同的直线,αβγ,,是三个不同的平面,则下列命题中的真命题...是( )A .若m βαβ⊂⊥,,则m α⊥B .若m β⊥,m α∥,则αβ⊥C .若αγ⊥,αβ⊥,则βγ⊥D .若m αγ=,n βγ=,m n ∥,则αβ∥7.若函数()y f x =的图象按向量a 平移后,得到函数(1)2y f x =--的图象,则向量a =( )A .(12)-,B .(12),C .(12)-,D .(12)-,8.已知变量x y ,满足约束条件20170x y x x y -+⎧⎪⎨⎪+-⎩≤,≥,≤,则y x 的取值范围是( )A .965⎡⎤⎢⎥⎣⎦,B .[)965⎛⎤-∞+∞ ⎥⎝⎦,,C .(][)36-∞+∞,,D .[36],9.函数212log (56)y x x =-+的单调增区间为( )A .52⎛⎫+∞ ⎪⎝⎭,B .(3)+∞,C .52⎛⎫-∞ ⎪⎝⎭, D .(2)-∞,10.一个坛子里有编号为1,2,…,12的12个大小相同的球,其中1到6号球是红球,其余的是黑球.若从中任取两个球,则取到的都是红球,且至少有1个球的号码是偶数的概率为( )A .122B .111C .322D .21111.设p q ,是两个命题:251:||30:066p x q x x ->-+>,,则p 是q 的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件12.将数字1,2,3,4,5,6拼成一列,记第i 个数为i (i 126)a =,,,,若11a ≠,33a ≠,55a ≠,135a a a <<,则不同的排列方法种数为( )A .18B .30C .36D .48第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.13.已知函数()y f x =为奇函数,若(3)(2)1f f -=,则(2)(3)f f ---= 。
2007年沈阳市数学中考题

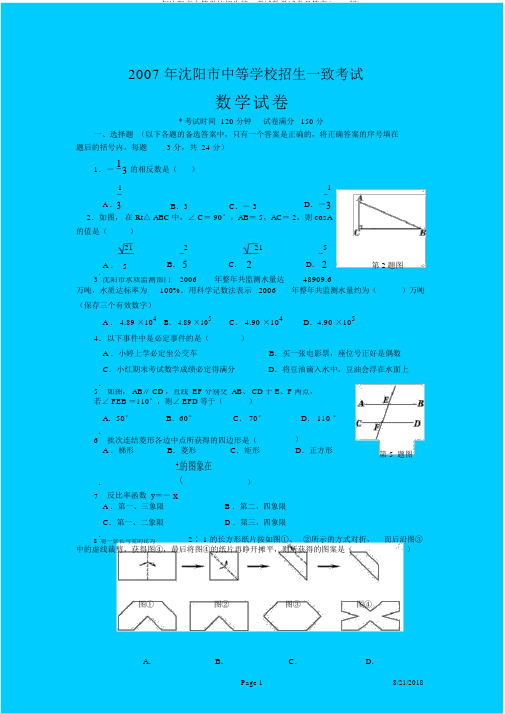
1.(07年沈阳市中考题) -13的相反数是 ( ) A .13 B .3 C .-3 D .-132.(07年沈阳市中考题)如图,在Rt△ABC 中∠C=90°,AB=5,AC=2,则cosA 的值是 ( )A B .25 C D .523.(07年沈阳市中考题)沈阳市水质监测部门2006年全年共监测水量达48909.6万吨,水质达标率为100%.用科学记数法表示2006年全年共监测水量约为( )万吨(保留三个有效数字) ( )A .4.89×104B .4.89×105C .4.90 ×104D .4.90×1054.(07年沈阳市中考题)下列事件中是必然事件的是 ( )A .小婷上学一定坐公交车B .买一张电影票,座位号正好是偶数C .小红期末考试数学成绩一定得满分D .将豆油滴入水中,豆油会浮在水面上 5.(07年沈阳市中考题)如图,AB∥CD,直线EF 分别交AB 、CD 于E 、F 两点,若 ∠FEB=110°,则∠EFD 等于 ( ) A .50° B .60° C .70° D .110°6.(07年沈阳市中考题)依次连结菱形各边中点所得到的四边形是 ( ) A .梯形 B .菱形 C .矩形 D .正方形 7.(07年沈阳市中考题)反比例函数y=-4x的图象在 ( ) A.第一、三象限 B .第二、四象限 C .第一、二象限 D .第三、四象限 8.(07年沈阳市中考题)将一张长与宽的比为2:1的长方形纸片按如图1、2所示的方式对折,然后沿图3中的虚线裁剪,得到图4,最后将图4的纸片再展开铺平,则所得到的图案是 ( )9.(07年沈阳市中考题)分解因式:x 3-25x= . 10.(07年沈阳市中考题)已知一组数据1,a ,4,4,9,它的平均数是4,则a 等于 ,这组数据的众数是 . 11.(07年沈阳市中考题)如图,AC 、BD 相交于点0,∠A=∠D,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是 .12.(07年沈阳市中考题)如图,小鸣将测倾器安放在与旗杆AB 底部相距6m 的C 处,量出测倾器的高度CD=1m ,测得旗杆顶端B 的仰角α=60°,则旗杆AB 的高度为 (计算结果保留根号)13.(07年沈阳市中考题)有一组数:1,2,5,10,17,26,…,请观察这组数的构成规律,用你发现的规律确定第8个数为 . 14.(07年沈阳市中考题)如图,在正方形网格中,以点A 为旋转中心,将△ABC 按逆时针方向旋转90°,画出旋转后的△AB 1C 1.15.(07年沈阳市中考题)将抛物线y=2(x+1)2-3向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为 . 16.(07年沈阳市中考题)如图,△ABC 是边长为3的等边三角形,△BDC 是等腰三角形,且∠BDC=120°.以D 为顶点作一个60°角,使其两边分别交AB 于点M ,交AC 于点N ,连结MN ,则△AMN 的周长为 .17.(07年沈阳市中考题)计算:18.(07年沈阳市中考题)解不等式组,并把它的解集在数轴上表示出来.19.(07年沈阳市中考题)如图,已知在口ABCD 中,E 、F 是对角线BD 上的两点,BE=DF ,点G 、H 分别在BA 和DC 的延长线上,且AG=CH ,连结GE 、EH 、HF 、FG . 求证:四边形GEHF 是平行四边形.20.(07年沈阳市中考题)甲、乙两个施工队共同完成某居民小区绿化改造工程,乙队先单独做2天后,再由两队合作10天就能完成全部工程.已知乙队单独完成此项工程所需天数是甲队单独完成此项工程所需天数的45,求甲、乙两个施工队单独完成此项工程各需多少天? 21.(07年沈阳市中考题)2006年沈阳市城市环境空气质量达到了有记录以来的最高水平,优良天气的天数在全国副省级以上城市排名第9,排名在北京、天津、重庆等城市之前.空气质量分为优良天气、轻度污染、中度污染、重度污染四种类型,有关部门将我市2001年~2006年前三类空气质量的天数制成条形统计图,请根据统计图解答下列问题:(1)根据统计图可知,和前一年比, 年优良天气的天数增加最多,这一年优良天气的天数比前一年优良天气的天数的增长率约为 ;(精确到1%)(2)在图中给出了我市2001~2006年优良天气天数的扇形统计图中的部分数据,请你补全此统计图,并写出计算过程;(精确到1%)(3)根据这6年沈阳市城市空气质量的变化,谈谈你对我市环保的建议.22. (07年沈阳市中考题)如图,已知A 、B 、C 、D 是⊙0上的四个点,AB=BC,BD 交 AC 于点E ,连结CD 、AD . (1)求证:DB 平分∠ADC;(2)若BE=3,ED=6,求AB 的长.23. (07年沈阳市中考题)如图所给的A 、B 、C 三个几何体中,按箭头所示的方向为它们的正面,设A 、B 、C 三个几何体的主视图分别是A 1、B 1、C 1;左视图分别是A 2、B 2、C 2;俯视图分别是 A 3、B 3、C 3. (1)请你分别写出A 1、A 2、A 3、B 1、B 2、B 3、C 1、C 2、C 3图形的名称;(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A 1、A 2、A 3的三张卡片放在甲口袋中,画有B 1、B 2、B 3的三张卡片放在乙口袋中,画有C 1、C 2、C 3的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.①通过补全下面的树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率;②小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜.这个游戏对双方公平吗?为什么?24.(07年沈阳市中考题)已知在矩形ABCD 中,AB=4,BC=252,0为BC 上一点,BO=72,如图所示,以BC 所在直线为x 轴,0为坐标原点建立平面直角坐标系,M 为线段OC 上的一点.(1)若点M 的坐标为(1,0),如图①,以OM 为一边作等腰△OMP,使点P 在矩形ABCD 的一边上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P 的坐标;(2)若将(1)中的点M 的坐标改为(4,0),其他条件不变,如图②,那么符合条件的等腰三角形有几个?求出所有符合条件的点P 的坐标;(3)若将(1)中的点M 的坐标改为(5,0),其他条件不变,如图③,请直接写出符合条件的等腰三角形有几个.(不必求出点P 的坐标)25.(07年沈阳市中考题)化工商店销售某种新型化工原料,其市场指导价是每千克160元(化工商店的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.(1)为了扩大销售量,化工商店决定适当调整价格,调整后的价格按八折销售,仍可获得实际售价的20%的利润.求化工商店调整价格后的标价是多少元?打折后的实际售价是多少元?(2)化工商店为了解这种原料的月销售量y(千克)与实际售价x(元/千克)之间的关系,每个月调整一次实际售价,试销一段时间后,部门负责人把试销情况列成下表:①请你在所给的平面直角坐标系中,以实际售价x(元/千克)为横坐标,月销售量y(千克)为纵坐标描出各点,观察这些点的发展趋势,猜想y与x之间可能存在怎样的函数关系;②请你用所学过的函数知识确定一个满足这些数据的y与x之间的函数表达式,并验证你在①中的猜想;③若化工商店某月按同一实际售价共卖出这种原料450千克,请你求出化工商店这个月销售这种原料的利润是多少元?26.(07年沈阳市中考题)已知抛物线y=ax2+kx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-1Ox+16=0的两个根,且抛物线的对称轴是直线x=-2.(1)求A、B、C三点的坐标;(2)求此抛物线的表达式;(3)连结AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.2007年沈阳市中等学校招生统一考试数学试题参考答案及评分标准一、选择题(每小题3分,共24分)1.A 2.B 3.A 4.D 5.C 6.C 7.B 8.A二、填空题(每小题3分,共24分)9.x (x +5)(x -5) 10.2,4 11.AO =DO 或AB =DC 或BO =CO 12.(63+1)m 13.50 14.如图15.y =2x 216.6三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分)17.解:原式=1-3+5+9-5 …………………………………………………4分=7 ……………………………………………………………………6分18.解:解不等式2x -5≤3(x -1)得x ≥-2 ……………………………………2分 解不等式x +72>4x 得x <1 ……………………………………………………………4分∴不等式组的解集为-2≤x <1 ……………………………………………………6分 在数轴上表示为:………………………………………………8分19.证明:∵四边形ABCD 是平行四边形 ∴AB =CD ,AB ∥CD∴∠GBE =∠HDF …………………………………………………………………2分 又∵AG =CH ∴BG =DH 又∵BE =DF∴△GBE ≌△HDF …………………………………………………………………5分 ∴GE =HF ,∠GEB =∠HFD ∴∠GEF =∠HFE ∴GE ∥HF∴四边形GEHF 是平行四边形. ……………………………………………………8分 20.解:设甲施工队单独完成此项工程需x 天,则乙施工队单独完成此项工程需45x 天, …………………………………………1分根据题意,得10x +1245x =1 …………………………………………………………4分 解这个方程,得x =25 ………………………………………………………………6分 经检验,x =25是所列方程的根 ……………………………………………………7分 当x =25时,45x =20 …………………………………………………………………9分答:甲、乙两个施工队单独完成此项工程分别需25天和20天. ……………10分 四.(每小题10分,共20分)第14题图21.解:(1)2003,45% ……………………………………………………………4分 (2)由图①,得162+204+295+301+317+321=1600 301÷1600≈0.19=19%321÷1600≈0.20=20% …………………7分 ∴2004年19%,2006年20%正确补全统计图. ………………………8分 (3)建议积极向上即可. ………………10分 22.(1)证明:∵ AB =BCAB BC ∴= ………………………………2分∴∠BDC =∠ADB ,∴DB平分∠ADC ……………………………………………4分(2)解:由(1)可知AB BC =,∴∠BAC =∠ADB ∵∠ABE =∠ABD∴△ABE ∽△DBA ……………………………………………………………………6分 ∴AB BE =BDAB∵BE =3,ED =6∴BD =9 ……………………………………………………………………………8分 ∴AB 2=BE ·BD =3×9=27∴AB =33 …………………………………………………………………………10分 五、(本题12分)23.解:(1)由已知可得A 1、A 2是矩形,A 3是圆;B 1、B 2、B 3都是矩形;C 1是三角形,C 2、C 3是矩形. ………………………………………………………3分 (2)①补全树状图如下:……………………………………………………………………………………………7分 由树状图可知,共有27种等可能结果,其中三张卡片上的图形名称都相同的结果有12种,∴三张卡片上的图形名称都相同的概率是1227=49 …………9分②游戏对双方不公平.由①可知,三张卡片中只有两张卡片上的图形 名称相同的概率是1227=49,即P (小刚获胜)=49三张卡片上的图形名称完全不同的概率是327=19,即P (小亮获胜)=19∵49>19 ∴这个游戏对双方不公平. ……………………………………………12分 六、(本题12分)第21题(2)图24.解:(1)符合条件的等腰△OMP 只有1个.点P 的坐标为(12,4) ……2分(2)符合条件的等腰△OMP 有4个. …………………………………………3分 如图①,在△OP 1M 中,OP 1=OM =4, 在Rt △OBP 1中,BO =72,BP 1=OP 21-OB 2=42-(72)2=152∴P 1(-72,152) ……………………………………………………………………5分在Rt △OMP 2中,OP 2=OM =4,∴P 2(0,4) 在△OMP 3中,MP 3=OP 3,∴点P 3在OM 的垂直平分线上,∵OM =4,∴P 3(2,4)在Rt △OMP 4中,OM =MP 4=4,∴P 4(4,4) …………………………………9分 (3)若M (5,0),则符合条件的等腰三角形有7个. …………………………12分 点P 的位置如图②所示七、(本题12分)25.解:(1)依题意,每千克原料的进货价为160×75%=120(元) ……………2分 设化工商店调整价格后的标价为x 元, 则 0.8x -120=0.8x ×20% 解得 x =187.5187.5×0.8=150(元) ………………………………………………………………4分 ∴调整价格后的标价是187.5元,打折后的实际售价是150元 .…………………5分 (2)①描点画图,观察图象,可知这些点的发展趋势近似是一条直线, 所以猜想y 与x 之间存在着一次函数关系.………………………………………………………………………………………7分 ②根据①中的猜想,设y 与x 之间的函数表达式为y =kx +b , 将点(150,500)和(160,480)代入表达式,得⎩⎪⎨⎪⎧ 500=150k +b 480=160k +b 解得⎩⎪⎨⎪⎧k =-2b =800∴y 与x 的函数表达式为y =-2x +800 ……………………………………………9分 将点(168,464)和(180,440)代入y =-2x +800均成立,第26题图(批卷教师用图)即这些点都符合y =-2x +800的发展趋势.∴①中猜想y 与x 之间存在着一次函数关系是正确的. …………………………10分 ③设化工商店这个月销售这种原料的利润为w 元, 当y =450时,x =175∴w =(175-120)×450=24750(元)答:化工商店这个月销售这种原料的利润为24750元. …………………………12分 八、(本题14分)26.解:(1)解方程x 2-10x +16=0得x 1=2,x 2=8 ………………………………1分 ∵点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,且OB <OC ∴点B 的坐标为(2,0),点C 的坐标为(0,8) 又∵抛物线y =ax 2+bx +c 的对称轴是直线x =-2∴由抛物线的对称性可得点A 的坐标为(-6,0) …………………………………4分 (2)∵点C (0,8)在抛物线y =ax 2+bx +c 的图象上 ∴c =8,将A (-6,0)、B (2,0)代入表达式,得⎩⎪⎨⎪⎧0=36a -6b +80=4a +2b +8 解得⎩⎨⎧a =-23b =-83∴所求抛物线的表达式为y =-23x 2-83x +8 ………………………………………7分(3)依题意,AE =m ,则BE =8-m , ∵OA =6,OC =8,∴AC =10 ∵EF ∥AC ∴△BEF ∽△BAC ∴EF AC =BE AB 即EF 10=8-m8∴EF =40-5m 4过点F 作FG ⊥AB ,垂足为G ,则sin ∠FEG =sin ∠CAB =45∴FG EF =45 ∴FG =45·40-5m 4=8-m ∴S =S △BCE -S △BFE =12(8-m )×8-12(8-m )(8-m )=12(8-m )(8-8+m )=12(8-m )m =-12m 2+4m ……………………………10分 自变量m 的取值范围是0<m <8 …………………………………………………11分 (4)存在.理由:∵S =-12m 2+4m =-12(m -4)2+8 且-12<0,∴当m =4时,S 有最大值,S 最大值=8 ……………………………………………12分∵m =4,∴点E 的坐标为(-2,0)∴△BCE 为等腰三角形. …………………………………………………………14分(以上答案仅供参考,如有其它做法,可参照给分)。
2007沈阳英语中考真题(非样题)

2007年沈阳市中等学校招生统一考试英语试卷(考试时间120分钟试卷满分150分)一.英语知识与运用(共20小题,每小题1分;满分20分)A) 单项填空从A.B.C.D中选出可以填入空白处的最佳选项,并将其字母序号填入题前的括号内。
( )1.-Hi,Mike!Our class has just won the basketball match against Class Two.-That’s great._______A.You are welcome.B.Never mind.C.Congratulations!D.It’s a pleasure. ( )2.-Look! What’s the postman giving Mrs.Chen?-He’s giving_____a letter.A.itB.himC.meD.her( )3._________you go to bed earlier,you won’t feel tired in the mornings.A.UnlessB.BecauseC.IfD.When( )4.-I think Shanghainese food is__________Sichuan food.-I don’t agre e.I like Sichuan food better.A.better thanB.so good asC.more thanD.as well as( )5.You must always be careful____electricity.It’s dangerous.A.toB.atC.forD.with( )6.In the art show, a lot of enjoyment_____to foreign friends by the Chinese paintings.A.is givingB.is givenC.will givenD.has given( )7.All the students in my class decided to have the next meeting in one____time.A.weekB.weeksC.week’sD.weeks’( )8.After they passed their exams.they____by having a party.A.succeededB.celebratedC.preparedD.received( )9.The suitcase(手提箱)was____heavy for me to carry, so I pulled it up the stairs and into my flat.A.quiteB.soC.veryD.too( )10.The food in that restaurant____delicious, but it tastes bad.A.looksB.feelsC.becomesD.gets( )11.Jack has never been to Disneyland before, but he____there this summer.A.has beenB.is goingC.wentD.goes( )12.Excuse me, could you tell me when____the new Olympic Center?A.are we visitedB.will we visitC.we are visitedD.we will visit( )13.People____breathe when they are under water.A.can’tB.mustn’tC.shouldn’tD.needn’t( )14.Everyone knows that___Great Wall of China is very famous.A.aB.anC.theD.(不填)( )15.We need some more coffee. There is only___left.A.littleB.a littleC.fewD.a fewB) 完成对话从方框A-G中选出可以填入对话空白处(16-20)的最佳选项,并将其字母序号填入题前的括号内。
沈阳市2007年中考数学模拟试卷(2)

2007年中考数学模拟试卷(2)姓名 班级 座号一、选择题:(每小题4分,共40分)1.下列各组数中,互为相反数的是( ) A .2与21B .21)(-与1C .-1与2)1(-D .2与|-2| 2.下列计算,正确的是( )A .22(a 54232)b a b =B .222)(ba b a -=-C .y x yx y x +=++22 D .y x y x -+()()=y x -3.已知⊙O1的半径为5cm ,⊙O2的半径为3cm ,且圆心距O1O2=7cm , 则⊙O1与⊙O2的位置关系是 ( )A .外离B .外切C .相交D .内含 4.某青年排球队12名队员的年龄情况如下:则这个队队员年龄的众数和中位数是 ( )A .19,20B .19,19C .19,20.5D .20,19 5.抛物线y = 2x 2-3x +l 的顶点坐标为 ( ) A .(-34,18) B .(34,-18) C .(34,18) D .(-34,-18)6.六张完全相同的卡片上,分别画有等边三角形、正六边形、矩形、平行四边形、等腰梯形、菱形,现从中随机抽取一张,卡片上画的恰好既是轴对称图形又是中心对称图形的概率为 ( ) A .21 B .65 C .31 D .327.已知点(2,152 )是反比例函数y=21m x-图象上一点,则此函数图象必经过点( ) A 、(3,-5) B 、(5,-3) C 、(-3,5) D 、(3,5) 8.如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是 ( )9. 下列图形中,不可能围成立方体的是( )A. B. C. D.10.下面是一天中四个不同时刻两个建筑物的影子:将它们按时间先后顺序进行排列,正确的是 ( ) A 、③④②① B 、②④③① C 、③④①② D 、③①②④ 二、填空题:(每小题5分,共30分)11.请写出一个顶点在x 轴上,且开口方向向下的二次函数解析式 。
2007年辽宁省沈阳市初中毕业生学业考试语文试卷(word版含答案)

2007年沈阳市中等学校招生统一考试语文试卷★考试时间1 50分钟,试卷满分150分。
卷面的文字书写要求规范、工整、清楚,标点正确。
一、积累与运用(满分25分)1.阅读下面一段文字,按要求回答问题。
(4分)敦煌莫高窟,它的第249号窟复制品正在沈阳世界遗产博览会上展出。
这组艺术珍宝包括一尊弥勒佛、两尊菩萨和分为11个部分的敦蝗壁壁画组成。
虽是复制品,但论近观还是远看,都与实物相差无几,令人叹为观止。
(1)请在后面的横线上写出加点字“复”的读音:(1分)(2)按照部首检字法,加点字“煌”应查部。
(1分)(3)填人选段横线处的成语,最恰当的一项是( ) (1分)A.横空出世B.举世闻名C.得天独厚D.高山仰止(4)选段画浪线句子有一处语病,请将改正后的句子写在下面的空白处。
(1分)2.下列各项中表述有误的一项是( ) (2分)A. 王维,字摩诘,唐代诗人、画家。
B.茅盾是现代著名作家,我们学过他创作的《白杨礼赞》。
C.《日出》中的人物有小职员黄省三和银行襄理王利发。
D.《曹刿论战》选自《左传》。
《左传》相传是春秋时鲁国史官左丘明所写。
3.走进名著。
(4分)(1)阅读下面文字,按要求回答问题。
(3分)祥子的泪要落下来。
他不会和别人谈心,因为他的话都是血作的,窝在心的深处。
①本段文字选自小说《》。
(1分)②请用简洁的语言概括发生在祥子身上的一件事。
(2分)(2)这个人物生性狷介而总是落落寡合。
恩师被杀,他却违逆众人,反对发电报。
他与作者在回国后结成好朋友,由于苦闷困顿.最终悲惨地死去。
这个人物出自散文集《朝花夕抬》,他的名字是。
(1分)4.诗文默写填空。
(8分)(1)(I)山舞银蛇,,欲与天公试比高。
(2) 浩荡离愁白日斜,。
(3),夜吟应觉月光寒。
(4)塞下秋来风景异,。
(5)默而识之,学而不厌,,何有于我哉?(6)今天下三分,益州疲弊,。
(7)《观沧海》中写大海水波动荡、山岛高耸突兀的句子是,。
5.对《春望》赏析有误的一项是( )(2分)国破山河在.城春草木深。
(word完整版)九年级数学总复习试卷及参考答案

九年级数学总复习练习卷一.选择题(共10小题)1.在Rt△ABC中,∠C=90°,cosA=,则tanB等于()A.B.C.D.2.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果3a=4b,则cosB的值是()A.B.C.D.3.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列关系中错误的是()A.b=c•cosB B.b=a•tanB C.b=c•sinB D.a=b•tanA 4.一斜坡的坡度是1:,则此斜坡的坡角是()A.15°B.30°C.45°D.60°5.∠A为锐角,若cosA=,则∠A的度数为()A.75°B.60°C.45°D.30°6.如图,在△ABC中,∠C=90°,AB=10,BC=8,则sin∠A=()A.B.C.D.7.在Rt△ABC中∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,c=3a,tanA 的值为()A.B.C.D.38.已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AB等于()A.6B.C.10D.129.在Rt△ABC中,∠C=90°,∠B=25°,AB=5,则BC的长为()A.5sin25°B.5tan65°C.5cos25°D.5tan25°10.南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A 和C之间的距离为()A.10海里B.20海里C.20海里D.10海里二.填空题(共6小题)11.已知α为锐角,且sinα=cosα,则α=.12.如果α是锐角,且cotα=tan25°,那么α=度.13.小明同学沿坡度为i=1:的山路向上行走了100米,则小明上升的高度是米.14.若tanα=5,则=.15.如图是某幼儿园的滑滑梯的简易图,已知滑坡AB的坡度是1:3,滑坡的水平宽度是6m,则高BC为m.16.小明沿着坡度为1:的坡面向上走了300米,此时小明上升的垂直高度为米.三.解答题(共11小题)17.如图,某渔船向正东方向航行,在B处测得A岛在北偏东的45°方向,岛C在B处的正东方向且相距30海里,从岛C测得A岛在北偏西的60°方向,已知A岛周围8海里内有暗礁.如果渔船继续向东航行,有无触礁危险?(≈1.4,≈1.7)18.计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)19.如图,在Rt△ABC中,∠C=90°,BC=6,tan∠A=.求AB的长和sin∠B 的值.20.计算:﹣sin30°(cos45°﹣sin60°)21.计算:(1)sin260°﹣tan30°•cos30°+tan45°(2)cos245°+sin245°+sin254°+cos25422.如图,学校的实验楼对面是一幢教工宿舍楼,小敏在实验楼的窗口C测得教工宿台楼顶部D仰角为15°,教学楼底部B的俯角为22°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教工宿舍楼的高BD.(结果精确到0.1m,参考数据:tanl5°≈0.268,tan22°=0.404)23.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.25.阅读理解:我们已经学习的直角三角形知识包括:勾股定理,30°、45°特殊角的直角三角形的边之间的关系等,在解决初中数学问题上起到重要作用,锐角三角函数是另一个研究直角三角形中边角间关系的知识,通过锐角三角函数也可以帮助解决数学问题.阅读下列材料,完成习题:如图1,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A 的正弦(sine),记作sinA,即sinA==例如:a=3,c=7,则sinA=问题:在Rt△ABC中,∠C=90°(1)如图2,BC=5,AB=8,求sinA的值.(2)如图3,当∠A=45°时,求sinB的值.(3)AC=2,sinB=,求BC的长度.26.济南市纬十二路的一座过街天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.(1)求新坡面的坡角a;(2)原天桥底部正前方7米处(PB的长)有一文化墙PM,若新坡面下A 处与文化墙之间需留下至少3米宽的人行道,问文化墙是否需要拆除?请说明理由.(约为1.732)27.阅读下列材料,并完成相应的任务.初中阶段,我们所学的锐角三角函数反映了直角三角形中的边角关系:sinα=cosα=tanα=一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinαcosβ+cosαsinβsin(α﹣β)=sinαcosβ﹣cosαsinβ例如sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=根据上述材料内容,解决下列问题:(1)计算:sin75°=;(2)在Rt△ABC中,∠A=75°,∠C=90°,AB=4,请你求出AC和BC的长.九年级数学总复习练习卷一.选择题(共10小题)1.在Rt△ABC中,∠C=90°,cosA=,则tanB等于()A.B.C.D.【分析】根据题意画出图形,进而表示出AC,BC,AB的长,进而求出答案.【解答】解:如图所示:∵cosA=,∴设AC=7x,AB=25x,则BC=24x,则tanB=.故选:C.【点评】此题主要考查了互余两角三角函数关系,正确表示出三角形各边长是解题关键.2.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果3a=4b,则cosB的值是()A.B.C.D.【分析】根据锐角三角函数的定义可得cosB=,然后根据题目所给3a=4b 可求解.【解答】解:因为在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C 对边,如果3a=4b,令b=3x,则a=4x,所以c=5x,所以cosB=故选:D.【点评】本题考查了锐角三角函数的定义,解答本题的关键是掌握cosB=,3.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列关系中错误的是()A.b=c•cos B B.b=a•tanB C.b=c•sinB D.a=b•tanA 【分析】本题可以利用锐角三角函数的定义求解即可.【解答】解:在Rt△ABC中,∠C=90°,则tanA=,tanB=,cosB=,stnB=;因而b=c•sinB=a•tanB,a=b•tanA,错误的是b=c•cosB.故选:A.【点评】利用锐角三角函数的定义,正确理解直角三角形边角之间的关系.在直角三角形中,如果已知一边及其中的一个锐角,就可以表示出另外的边.4.一斜坡的坡度是1:,则此斜坡的坡角是()A.15°B.30°C.45°D.60°【分析】坡度=坡角的正切值,依此求出坡角的度数.【解答】解:设坡角为α,由题意知:tanα==,∴∠α=30°.即斜坡的坡角为30°.故选:B.【点评】此题考查的是解直角三角形的应用﹣坡度坡角问题,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h:l=tanα.5.∠A为锐角,若cosA=,则∠A的度数为()A.75°B.60°C.45°D.30°【分析】根据特殊角的三角函数值求解.【解答】解:∵∠A为锐角,cosA=,∴∠A=60°.故选:B.【点评】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.6.如图,在△ABC中,∠C=90°,AB=10,BC=8,则sin∠A=()A.B.C.D.【分析】根据锐角的正弦等于对边比斜边列式计算即可得解.【解答】解:∵∠C=90°,AB=10,BC=8,∴在Rt△ABC中,sinA===,故选:A.【点评】本题考查的是锐角三角函数的定义,掌握锐角A的对边a与斜边c 的比叫做∠A的正弦是解题的关键.7.在Rt△ABC中∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,c=3a,tanA 的值为()A.B.C.D.3【分析】根据锐角三角函数的定义即可求出答案.【解答】解:由题意可知:sinA===,∴tanA==,故选:B.【点评】本题考查锐角三角函数,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.8.已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AB等于()A.6B.C.10D.12【分析】根据锐角三角函数的定义即可求出答案.【解答】解:∵tanA=,∴sinA=,∴=,∴AB=10,故选:C.【点评】本题考查锐角三角函数,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.9.在Rt△ABC中,∠C=90°,∠B=25°,AB=5,则BC的长为()A.5sin25°B.5tan65°C.5cos25°D.5tan25°【分析】在Rt△ABC中,由AB及∠B的值,可求出BC的长.【解答】解:在Rt△ABC中,∠C=90°,∠B=25°,AB=5,∴BC=AB•cos∠B=5cos25°.故选:C.【点评】本题考查了解直角三角形,牢记直角三角形中边角之间的关系是解题的关键.10.南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A 和C之间的距离为()A.10海里B.20海里C.20海里D.10海里【分析】过点A作AD⊥BC于点D,设AD=x,则CD=x,AC=x,BD=x,结合BC=10(1+)即可求出x的值,进而即可得出A和C之间的距离.【解答】解:过点A作AD⊥BC于点D,如图所示.设AD=x,则CD=x,AC=x,BD=x.∵BC=BD+CD=(+1)x=10(1+),∴x=10,∴AC=10.故选:A.【点评】本题考查了解直角三角形的应用﹣方向角问题,通过解一元一次方程求出AD的长度是解题的关键.二.填空题(共6小题)11.已知α为锐角,且sinα=cosα,则α=45°.【分析】根据一个角的正弦等于这个角的余角的余弦解答.【解答】解:∵sinα=cos(90°﹣α),∴α=90°﹣α,解得,α=45°,故答案为:45°.【点评】本题考查的是同角三角函数的关系,掌握一个角的正弦等于这个角的余角的余弦是解题的关键,12.如果α是锐角,且cotα=tan25°,那么α=65度.【分析】依据α是锐角,且cotα=tan25°,即可得出α=65°.【解答】解:∵α是锐角,且cotα=tan25°,∴α=65°,故答案为:65.【点评】本题主要考查了互余两角三角函数的关系,若∠A+∠B=90°,那么sinA=cosB或sinB=cosA.13.小明同学沿坡度为i=1:的山路向上行走了100米,则小明上升的高度是50米.【分析】由斜坡的坡度i=1:=,可得坡角α的度数,再求得斜坡的正弦值sinα,那么它垂直上升的高度可利用正弦函数求得.【解答】解:∵斜坡的坡度i=1:=,∴坡角α=60°,∴斜坡的正弦值sinα=,∴小明上升的高度是100×sinα=50(米).故答案为50.【点评】本题考查了解直角三角形的应用﹣﹣﹣坡度坡角问题,根据坡度求出坡角是解题的关键.坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h:l=tanα.14.若tanα=5,则=.【分析】根据同角的三角函数的关系即可求出答案.【解答】解:原式=∵tanα=5,∴原式=故答案为:【点评】本题考查同角三角函数的关系,解题的关键熟练运用同角三角函数的关系,本题属于基础题型.15.如图是某幼儿园的滑滑梯的简易图,已知滑坡AB的坡度是1:3,滑坡的水平宽度是6m,则高BC为2m.【分析】根据滑坡的坡度及水平宽,可求出坡面的铅直高度,此题得解.【解答】解:∵滑坡AB的坡度是1:3,滑坡的水平宽度是6m,∴AC=6m,∴BC=×6=2m.故答案为:2.【点评】本题考查了解直角三角形的应用中的坡度坡角问题,牢记坡度的定义是解题的关键.16.小明沿着坡度为1:的坡面向上走了300米,此时小明上升的垂直高度为150米.【分析】根据坡度算出坡角的度数,利用坡角的正弦值即可求解.【解答】解:∵坡度tanα==1:=,∴α=30°.∴上升的垂直高度=坡长×sin30°=300×=150(米).故答案为150.【点评】此题考查了解直角三角形的应用﹣坡度坡角问题,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h:l=tanα.掌握坡度、坡角的定义是解答本题的关键.三.解答题(共11小题)17.如图,某渔船向正东方向航行,在B处测得A岛在北偏东的45°方向,岛C在B处的正东方向且相距30海里,从岛C测得A岛在北偏西的60°方向,已知A岛周围8海里内有暗礁.如果渔船继续向东航行,有无触礁危险?(≈1.4,≈1.7)【分析】判断渔船有无危险只要求出点A到BC的距离,与8海里比较大小就可以.【解答】解:若渔船继续向东航行,无触礁的危险.理由如下:如图,过点A作AD⊥BC于点D.由题意得:∠ABD=45°,∠ACD=30°.设AD=x海里.在Rt△ABD中,∵∠ABD=45°,∴BD=AD=x海里.在Rt△ACD中,∵∠ACD=30°,∴CD=AD=x海里.∵BD+DC=30,∴x+x=30,解得x=15(﹣1),17(﹣1)≈10.5>8,即:若渔船继续向东航行,无触礁危险.【点评】本题考查了解直角三角形的应用﹣方向角问题,特殊角的三角函数等知识,解题的关键是添加辅助线构造直角三角形,把实际问题转化为解直角三角形问题,属于中考常考题型.18.计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)【分析】先分析图形,根据题意构造直角三角形.本题涉及到两个直角三角形△CEF、△CGE,利用其公共边CE构造等量关系,借助FG=EF﹣GE=100,构造关系式求解.【解答】解:由题意知CD⊥AD,EF∥AD.∴∠CEF=90°.设CE=x米,∵在Rt△CEF中,tan∠CFE=,∴EF===x,∵在Rt△CEG中,tan∠CGE=,∴GE===x.∵FG=EF﹣GE=100,∴x﹣x=100,解得x=50.∴CD=CE+ED=50+1.5(米).答:古塔CD的高度是(50+1.5)米.【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,此类题目要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.19.如图,在Rt△ABC中,∠C=90°,BC=6,tan∠A=.求AB的长和sin∠B 的值.【分析】根据∠A的正切值用BC表示出AC,再利用勾股定理列式求解即可得到BC的长,然后求出AB的长,再根据锐角的正弦等于对边比斜边列式计算即可得解.【解答】解:∵在Rt△ABC中,∠C=90°,BC=6,tan∠A==,∴AC=12,∴AB===6,∴sin∠B===.【点评】本题考查了锐角三角函数的定义,勾股定理,用BC表示出AC是解题的关键.20.计算:﹣sin30°(cos45°﹣sin60°)【分析】依据30°、45°、60°角的各种三角函数值,即可得到计算结果.【解答】解:原式=﹣(﹣)=﹣==【点评】本题主要考查了特殊角的三角函数值,其应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.21.计算:(1)sin260°﹣tan30°•cos30°+tan45°(2)cos245°+sin245°+sin254°+cos254°【分析】根据特殊角的锐角三角函数的值即可求出答案.【解答】解:(1)原式=()2﹣×+1=﹣+1=,(2)原式=(cos245°+sin245°)+(sin254°+cos254°)=1+1=2【点评】本题考查锐角三角函数的定义,解题的关键是熟练运用特殊角的锐角三角函数的定义,本题属于基础题型.22.如图,学校的实验楼对面是一幢教工宿舍楼,小敏在实验楼的窗口C测得教工宿台楼顶部D仰角为15°,教学楼底部B的俯角为22°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教工宿舍楼的高BD.(结果精确到0.1m,参考数据:tanl5°≈0.268,tan22°=0.404)【分析】(1)作CH⊥BD于H,如图,利用仰角和俯角定义得到∠DCH=15°,∠BCH=22°,然后计算它们的和即可得到∠BCD的度数;(2)利用正切定义,在Rt△DCH中计算出DH=30tan15°=8.04,在Rt△BCH 中计算出BH=30tan22°=12.12,然后计算BH+DH即可得到教工宿舍楼的高BD.【解答】解:(1)作CH⊥BD于H,如图,根据题意得∠DCH=15°,∠BCH=22°,∴∠BCD=∠DCH+∠BCH=15°+22°=37°;(2)易得四边形ABHC为矩形,则CH=AB=30,在Rt△DCH中,tan∠DCH=,∴DH=30tan15°=30×0.268=8.04,在Rt△BCH中,tan∠BCH=,∴BH=30tan22°=30×0.404=12.12,∴BD=12.12+8.04=20.16≈20.1(m).答:教工宿舍楼的高BD为20.1m.【点评】本题考查了解直角三角形的应用﹣仰角俯角问题:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.23.计算:sin45°+cos45°.【分析】直接利用特殊角的三角函数值代入求出答案.【解答】解:原式=+=.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.24.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.【分析】在Rt△BCD中由勾股定理求得BC=4,在Rt△ABC中求得AB=4,再根据三角函数的定义求解可得.【解答】解:在Rt△BCD中,∵CD=3、BD=5,∴BC===4,又AC=AD+CD=8,∴AB===4,则sinA===,cosA===,tanA===.【点评】本题主要考查锐角的三角函数的定义,解题的关键是掌握勾股定理及三角函数的定义.25.阅读理解:我们已经学习的直角三角形知识包括:勾股定理,30°、45°特殊角的直角三角形的边之间的关系等,在解决初中数学问题上起到重要作用,锐角三角函数是另一个研究直角三角形中边角间关系的知识,通过锐角三角函数也可以帮助解决数学问题.阅读下列材料,完成习题:如图1,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A 的正弦(sine),记作sinA,即sinA==例如:a=3,c=7,则sinA=问题:在Rt△ABC中,∠C=90°(1)如图2,BC=5,AB=8,求sinA的值.(2)如图3,当∠A=45°时,求sinB的值.(3)AC=2,sinB=,求BC的长度.【分析】(1)根据正弦函数的定义解答;(2)设AC=x,则BC=x,利用方程解答;(3)由锐角三角函数定义求得AB=4,然后由勾股定理解答.【解答】解:(1)sinA=;(2)在Rt△ABC中,∠A=45°,设AC=x,则BC=x,AB=,则sinB=;(3)sinB=,则AB=4,由勾股定理得:BC2=AB2﹣AC2=16﹣12=4,∴BC=2.【点评】考查了锐角三角函数定义,勾股定理,直角三角形的性质以及特殊角的三角函数值.注意:勾股定理应用的前提条件是在直角三角形中.26.济南市纬十二路的一座过街天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.(1)求新坡面的坡角a;(2)原天桥底部正前方7米处(PB的长)有一文化墙PM,若新坡面下A 处与文化墙之间需留下至少3米宽的人行道,问文化墙是否需要拆除?请说明理由.(约为1.732)【分析】(1)作CH⊥AB于H,如图,利用坡度的定义得到tan∠CAH===,然后根据特殊角的三角函数值求出∠CAH即;(2)另一条坡度定义得到tan∠CBH==,所以BH=CH=6,再利用=得到AH=6,接着计算出AB≈4.392,然后根据3+4.392>7可判断文化墙需要拆除.【解答】解:(1)作CH⊥AB于H,如图,在Rt△ACH中,∵tan∠CAH===,∴∠CAH=30°,即新坡面的坡角a为30°;(2)文化墙需要拆除.理由如下:∵tan∠CBH==,∴BH=CH=6,∵=,∴AH=CH=6≈10.392,∴AB=AH﹣BH=6﹣6=4.392,∵3+4.392>7,∴文化墙需要拆除.【点评】本题考查了解直角三角形的应用﹣坡度坡角问题:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.27.阅读下列材料,并完成相应的任务.初中阶段,我们所学的锐角三角函数反映了直角三角形中的边角关系:sinα=cosα=tanα=一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinαcosβ+cosαsinβsin(α﹣β)=sinαcosβ﹣cosαsinβ例如sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=根据上述材料内容,解决下列问题:(1)计算:sin75°=;(2)在Rt△ABC中,∠A=75°,∠C=90°,AB=4,请你求出AC和BC的长.【分析】(1)根据公式可求.(2)根据锐角的三角函数值,求AC和BC的值.【解答】解:(1)sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°=×+×=,故答案为:.(2)Rt△ABC中,∵sin∠A=sin75°==∴BC=AB×=4×=∵∠B=90﹣∠A∴∠B=15°∵sin∠B=sin15°==∴AC=AB×=【点评】本题考查了同角三角函数关系,利用特殊的三角函数值求线段的长度是本题的关键.。
2007年辽宁省大连市初中毕业升学统一考试数学试题(含答案)-

2007年辽宁省大连市初中毕业升学统一考试数学试题一.选择题(本题共8小题,每小题3分,共24分)说明:将下列各题唯一正确的答案代号填到题后的括号内。
1.-8的相反数是( )。
A 、8B 、-8C 、18 D 、18- 2.在平面直角坐标系中,点P(-2,3)在( )。
A 、第一象限B 、第二象限C 、第三象限D 、第四象限 3.在一条东西向的跑道上,小亮先向东走了8米,记作“+8米”,又向西走了10米,此时他的位置可记作( )。
A 、+2米B 、-2米C 、+18米D 、-18米4.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,若OA =2,则BD 的长为( )。
A 、4B 、3C 、2D 、15.下列图形能折成正方体的是( )。
6.如图,AB 、AC 是⊙O 的两条切线,B 、C 是切点,若∠A =70°,则∠BOC 的度数为( )。
A 、130°B 、120°C 、110°D 、100°7.五箱苹果的质量分别为(单位:千克):18、20、21、22、19,则这五箱苹果质量的平均数和中位数分别为( )。
A 、19和20B 、20和19C 、20和20D 、20和21 8.如图,直线y =kx +b 经过点A 、B ,则k 的值为( )。
A 、3B 、32 C 、23 D 、32- 二.填空题(本题共7小题,每小题3分,共21分)说明:将答案直接填在题后的横线上。
9.把780000用科学记数法表示为__________________。
10.方程x 2-2=0的解为_________________。
11.如图,在△ABC 中,∠C =90°,AB =10cm ,sinA =45,则BC 的长为___cm 。
12.计算:211x xxx-⋅-=________________。
13.如图,为了测量学校旗杆的高度,小东用长为3.2的竹竿做测量工具。
沈阳市中等学校招生统一考试数学试题和答案

七、(本题12分)
25.已知:如图①所示,在 和 中, , , ,且点 在一条直线上,连接 分别为 的中点.
边上的高为211分
依题意设点 的坐标为
点 在抛物线 上
解得, ,
,
以 为顶点的四边形是平行四边形,
, ,
当点 的坐标为 时,
点 的坐标分别为 , ;
当点 的坐标为 时,
点 的坐标分别为 , .14分
(以上答案仅供参考,如有其它做法,可参照给分)
长13米,且 ,则河堤的高 为米.
15.观察下列图形的构成规律,根据此规律,第8个图形中有个圆.
第15题图
16.在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,点 到直线 的距离为 ,且 是直角三角形,则满足条件的点 有个.
三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)
(2)直接写出这两个格点四边形的周长.
四、(每小题10分,共20分)
21.如图所示, 是 的一条弦, ,垂足为 ,交 于点 ,点 在 上.
(1)若 ,求 的度数;
(2)若 , ,求 的长.
22.小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局.
所以 是原方程的根8分
(将 代入最简公分母检验同样给分)
七年级数学下册期末试卷测试卷 (word版,含解析)

七年级数学下册期末试卷测试卷 (word 版,含解析)一、选择题1.如图,下列结论中错误的是( )A .∠1与∠2是同旁内角B .∠1与∠4是内错角C .∠5与∠6是内错角D .∠3与∠5是同位角2.下列图中的“笑脸”,是由上面教师寄语中的图像平移得到的是( )A .B .C .D . 3.若点P 在第四象限内,则点P 的坐标可能是( )A .()4,3B .()3,4-C .()3,4--D .()3,4- 4.下列四个命题:①两条直线相交,若对顶角互补,则这两条直线互相垂直;②两条直线被第三条直线所截,内错角相等;③如果两条直线都与第三条直线平行,那么这两条直线也互相平行;④经过直线外一点,有且只有一条直线与已知直线平行.其中是真命题的个数是( )A .1B .2C .3D .45.如图,//AB CD ,P 为平行线之间的一点,若AP CP ⊥,CP 平分∠ACD ,68ACD ∠=︒,则∠BAP 的度数为( )A .56︒B .58︒C .66︒D .68︒6.下列说法:①两个无理数的和可能是有理数:②任意一个有理数都可以用数轴上的点表示;③33mn π-+是三次二项式;④立方根是本身的数有0和1;其中正确的是( ) A .①② B .①③ C .①②③ D .①②④ 7.如图,//AB CD ,//BC DE ,若140CDE ∠=︒,则B 的度数是( )A .40°B .60°C .140°D .160° 8.在平面直角坐标系中,对于点P (x ,y ),我们把点P ′(y ﹣1,﹣x ﹣1)叫做点P 的友好点,已知点A 1的友好点为点A 2,点A 2的友好点为点A 3,点A 3的友好点为点A 4,⋯⋯以此类推,当点A 1的坐标为(2,1)时,点A 2021的坐为( )A .(2,1)B .(0,﹣3)C .(﹣4,﹣1)D .(﹣2,3)二、填空题9.已知223130x x y -+--=,则x +y=___________10.点(m ,1)和点(2,n)关于x 轴对称,则mn 等于_______.11.如图,直线AB 与直线CD 交于点O ,OE 、OC 是AOC ∠与∠BOE 的角平分线,则AOD ∠=______度.12.如图,点D 、E 分别在AB 、BC 上,DE ∥AC ,AF ∥BC ,∠1=70°,则∠2=_____°.13.如图,将一张长方形纸片沿EF 折叠后,点A ,B 分别落在A ′,B ′的位置.如果∠1=59°,那么∠2的度数是_____.14.对于三个数a ,b ,c ,用M{a ,b ,c}表示这三个数的平均数,用min{a ,b ,c}表示这三个数中最小的数.例如:M{-1,2,3}=123433-++=,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=_______.15.如图,点A(1,0),B(2,0),C是y轴上一点,且三角形ABC的面积为2,则点C的坐标为_____.16.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).动点P从点A处出发,并按A﹣B﹣C﹣D﹣A﹣B…的规律在四边形ABCD的边上以每秒1个单位长的速度运动,运动时间为t秒.若t=2021秒,则点P所在位置的点的坐标是_____.三、解答题17.计算下列各题:2213-123181632163125()2-318.求下列各式中的x.(1)x2-81=0(2)(x﹣1)3=819.如图所示,已知∠1+∠2=180°,∠B=∠3,请你判断DE和BC平行吗?说明理由.(请根据下面的解答过程,在横线上补全过程和理由)解:DE∥BC.理由如下:∵∠1+∠4=180°(平角的定义),∠1+∠2=180°(),∴∠2=∠4().∴∥().∴∠3=().∵∠3=∠B(),∴=().∴DE∥BC().20.如图,在平面直角坐标系中,三角形OBC 的顶点都在网格格点上,一个格是一个单位长度.(1)将三角形OBC 先向下平移3个单位长度,再向左平移2个单位长度(点1C 与点C 是对应点),得到三角形111O B C ,在图中画出三角形111O B C ;(2)直接写出三角形111O B C 的面积为____________.21.阅读下面的文字,解答问题 22的小数部分我们不可能全部212 21,将这个数减去其整数部分,差就是小数部分. 479273, ∴7272)请解答:(157整数部分是 ,小数部分是 .(211a 7b ,求|a ﹣b 11(3)已知:5x +y ,其中x 是整数,且0<y <1,求x ﹣y 的相反数.二十二、解答题22.(1)如图1,分别把两个边长为1cm 的小正方形沿一条对角线裁成4个小三角形拼成一个大正方形,则大正方形的边长为______cm ;(2)若一个圆的面积与一个正方形的面积都是22πcm ,设圆的周长为C 圆.正方形的周长为C 正,则C 圆______C 正(填“=”,或“<”,或“>”)(3)如图2,若正方形的面积为2900cm ,李明同学想沿这块正方形边的方向裁出一块面积为2740cm 的长方形纸片,使它的长和宽之比为5:4,他能裁出吗?请说明理由?二十三、解答题23.如图,//MN PQ ,直线AD 与MN 、PQ 分别交于点A 、D ,点B 在直线PQ 上,过点B 作BG AD ⊥,垂足为点G .(1)如图1,求证:90MAG PBG ∠+∠=︒;(2)若点C 在线段AD 上(不与A 、D 、G 重合),连接BC ,MAG ∠和PBC ∠的平分线交于点H 请在图2中补全图形,猜想并证明CBG ∠与AHB ∠的数量关系;24.已知//PQ MN ,将一副三角板中的两块直角三角板如图1放置,90ACB EDF ∠=∠=︒,45ABC BAC ∠=∠=︒,30DFE ∠=︒,60DEF ∠=︒.(1)若三角板如图1摆放时,则α∠=______,β∠=______.(2)现固定ABC 的位置不变,将DEF 沿AC 方向平移至点E 正好落在PQ 上,如图2所示,DF 与PQ 交于点G ,作FGQ ∠和GFA ∠的角平分线交于点H ,求GHF ∠的度数; (3)现固定DEF ,将ABC 绕点A 顺时针旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF 的一条边平行时,请直接写出BAM ∠的度数.25.解读基础:(1)图1形似燕尾,我们称之为“燕尾形”,请写出A ∠、B 、C ∠、D ∠之间的关系,并说明理由;(2)图2形似8字,我们称之为“八字形”,请写出A ∠、B 、C ∠、D ∠之间的关系,并说明理由:应用乐园:直接运用上述两个结论解答下列各题(3)①如图3,在ABC ∆中,BD 、CD 分别平分ABC ∠和ACB ∠,请直接写出A ∠和D ∠的关系 ;②如图4,A B C D E F ∠+∠+∠+∠+∠+∠= .(4)如图5,BAC ∠与BDC ∠的角平分线相交于点F ,GDC ∠与CAF ∠的角平分线相交于点E ,已知26B ∠=︒,54C ∠=︒,求F ∠和E ∠的度数.26.如果三角形的两个内角α与β满足290αβ+=︒,那么我们称这样的三角形是“准互余三角形”.(1)如图1,在Rt ABC 中,90ACB ∠=︒,BD 是ABC 的角平分线,求证:ABD △是“准互余三角形”;(2)关于“准互余三角形”,有下列说法:①在ABC 中,若100A ∠=︒,70B ∠=︒,10C ∠=︒,则ABC 是“准互余三角形”; ②若ABC 是“准互余三角形”,90C ∠>︒,60A ∠=︒,则20B ∠=︒;③“准互余三角形”一定是钝角三角形.其中正确的结论是___________(填写所有正确说法的序号);(3)如图2,B ,C 为直线l 上两点,点A 在直线l 外,且50ABC ∠=︒.若P 是直线l 上一点,且ABP △是“准互余三角形”,请直接写出APB ∠的度数.【参考答案】一、选择题1.B解析:B【分析】根据同位角、内错角、同旁内角的定义结合图形进行判断即可.【详解】解:如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;∠1与∠6是直线a与直线b被直线c所截的内错角,而∠6与∠4是邻补角,所以∠1与∠4不是内错角,因此选项B符合题意;∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;故选:B.【点睛】本题主要考查同位角、内错角、同旁内角,掌握同位角、内错角、同旁内角的定义是关键.2.D【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.【详解】解:A、B、C都不是由平移得到的,D是由平移得到的.故选:D.【点睛】解析:D【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.【详解】解:A、B、C都不是由平移得到的,D是由平移得到的.故选:D.【点睛】本题考查平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.3.B【分析】根据第四象限内点坐标的特点:横坐标为正,纵坐标为负即可得出答案.【详解】根据第四象限内点坐标的特点:横坐标为正,纵坐标为负,只有()3,4-满足要求, 故选:B .【点睛】本题主要考查平面直角坐标系中点的坐标的特点,掌握各个象限内点的坐标的特点是解题的关键.4.C【分析】根据对顶角的性质和垂直的定义判断①;根据内错角相等的判定方法判定②;根据平行线的判定对③进行判断;根据经过直线外一点,有且只有一条直线与已知直线平行判断④即可【详解】解:两条直线相交,若对顶角互补,则这两条直线互相垂直,所以①正确;两条互相平行的直线被第三条直线所截,内错角相等;,所以②错误;如果两条直线都与第三条直线平行,那么这两条直线也互相平行,所以③正确; 经过直线外一点,有且只有一条直线与已知直线平行,所以④正确.故选:C .【点睛】本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,熟练掌握相关性质是解题的关键.5.A【分析】过P 点作PM //AB 交AC 于点M ,直接利用平行线的性质以及平行公理分别分析即可得出答案.【详解】解:如图,过P 点作PM //AB 交AC 于点M .∵CP 平分∠ACD ,∠ACD =68°,∴∠4=12∠ACD =34°.∵AB //CD ,PM //AB ,∴PM //CD ,∴∠3=∠4=34°,∵AP ⊥CP ,∴∠APC =90°,∴∠2=∠APC -∠3=56°,∵PM //AB ,∴∠1=∠2=56°,即:∠BAP 的度数为56°,故选:A .【点睛】此题主要考查了平行线的性质以及平行公理等知识,正确利用平行线的性质分析是解题关键.6.A【分析】根据无理数的运算、数轴的定义、多项式的定义、立方根的运算逐个判断即可.【详解】①两个无理数的和可能是有理数,说法正确(0=,0是有理数②有理数属于实数,实数与数轴上的点是一一对应关系,则任意一个有理数都可以用数轴上的点表示,说法正确③3327mn mn ππ=-+-+是二次二项式,说法错误④立方根是本身的数有0和±1,说法错误综上,说法正确的是①②故选:A .【点睛】本题考查了无理数的运算、数轴的定义、多项式的定义、立方根的运算,熟记各运算法则和定义是解题关键.7.A【分析】根据平行线的性质求出∠C ,再根据平行线的性质求出∠B 即可.【详解】解:∵BC ∥DE ,∠CDE =140°,∴∠C =180°-140°=40°,∵AB ∥CD ,∴∠B =40°,故选:A .【点睛】本题考查了平行线的性质的应用,注意:平行线的性质有①两直线平行,内错角相等,②两直线平行,同位角相等,③两直线平行,同旁内角互补.8.A【分析】根据友好点的定义及点A1的坐标为(2,1),顺次写出几个友好点的坐标,可发现循环规律,据此可解.【详解】解:观察,发现规律:A1(2,1),A2(0,-3),A3(-4,-1),A解析:A【分析】根据友好点的定义及点A1的坐标为(2,1),顺次写出几个友好点的坐标,可发现循环规律,据此可解.【详解】解:观察,发现规律:A1(2,1),A2(0,-3),A3(-4,-1),A4(-2,3),A5(2,1),…,∴A4n+1(2,1),A4n+2(0,-3),A4n+3(-4,-1),A4n+4(-2,3)(n为自然数).∵2021=505×4+1,∴点A2021的坐标为(2,1).故选:A.【点睛】本题考查了规律型的点的坐标,从已知条件得出循环规律:每4个点为一个循环是解题的关键.二、填空题9.-1【解析】【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【详解】解:由题意得,x-2=0,x2-3y-13=0,解得x=2,y=-3,所以,x+y=2+解析:-1【解析】【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【详解】解:由题意得,x-2=0,x2-3y-13=0,解得x=2,y=-3,所以,x+y=2+(-3)=-1.故答案为:-1.【点睛】本题考查非负数的性质:几个非负数的和为0时,这几个非负数都为0.10.-2【分析】直接利用关于x轴对称点的性质得出m,n的值进而得出答案.【详解】∵点A(m,1)和点B(2,n)关于x轴对称,∴m=2,n=-1,故mn=−2.故填:-2.【点睛】此题解析:-2【分析】直接利用关于x轴对称点的性质得出m,n的值进而得出答案.【详解】∵点A(m,1)和点B(2,n)关于x轴对称,∴m=2,n=-1,故mn=−2.故填:-2.【点睛】此题主要考查了关于x轴对称点的性质,正确掌握关于x轴对称点的性质是解题关键.11.60【分析】由角平分线的定义可求出∠AOE=∠EOC=∠COB=60°,再根据对顶角相等即可求出∠AOD的度数.【详解】∵OE平分∠AOC,∴∠AOE=∠EOC,∵OC平分∠BOE,∴解析:60【分析】由角平分线的定义可求出∠AOE=∠EOC=∠COB=60°,再根据对顶角相等即可求出∠AOD的度数.【详解】∵OE平分∠AOC,∴∠AOE=∠EOC,∵OC平分∠BOE,∴∠EOC=∠COB∴∠AOE=∠EOC=∠COB,∵∠AOE+∠EOC+∠COB=180︒∴∠COB=60°,∴∠AOD=∠COB=60°,故答案为:60【点睛】本题主要考查了角平分线的应用以及对顶角相等的性质,熟练运用角平分线的定义是解题的关键.12.70【分析】根据两直线平行,同位角相等可得∠C=∠1,再根据两直线平行,内错角相等可得∠2=∠C.【详解】∵DE∥AC,∴∠C=∠1=70°,∵AF∥BC,∴∠2=∠C=70°.故答解析:70【分析】根据两直线平行,同位角相等可得∠C=∠1,再根据两直线平行,内错角相等可得∠2=∠C.【详解】∵DE∥AC,∴∠C=∠1=70°,∵AF∥BC,∴∠2=∠C=70°.故答案为70.【点睛】本题考查了平行线的性质,熟记性质并准确识图是解题的关键.13.62°【分析】根据折叠的性质求出∠EFB′=∠1=59°,∠B′FC=180°−∠1−∠EFB′=62°,根据平行线的性质:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁解析:62°【分析】根据折叠的性质求出∠EFB′=∠1=59°,∠B′FC=180°−∠1−∠EFB′=62°,根据平行线的性质:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.:求出即可.【详解】解:∵将一张长方形纸片沿EF折叠后,点A、B分别落在A′、B′的位置,∠1=59°,∴∠EFB′=∠1=59°,∴∠B′FC=180°−∠1−∠EFB′=62°,∵四边形ABCD是矩形,∴AD∥BC,∴∠2=∠B′FC=62°,故答案为:62°.【点睛】本题考查了对平行线的性质和折叠的性质的应用,解此题的关键是求出∠B′FC的度数,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.14.或【详解】【分析】根据题中的运算规则得到M{3,2x+1,4x-1}=1+2x,然后再根据min{2,-x+3,5x}的规则分情况讨论即可得.【详解】M{3,2x+1,4x-1}==2x+1解析:12或13【详解】【分析】根据题中的运算规则得到M{3,2x+1,4x-1}=1+2x,然后再根据min{2,-x+3,5x}的规则分情况讨论即可得.【详解】M{3,2x+1,4x-1}=321413x x+++-=2x+1,∵M{3,2x+1,4x-1}=min{2,-x+3,5x},∴有如下三种情况:①2x+1=2,x=12,此时min{2,-x+3,5x}= min{2,52,52}=2,成立;②2x+1=-x+3,x=23,此时min{2,-x+3,5x}= min{2,73,103}=2,不成立;③2x+1=5x,x=13,此时min{2,-x+3,5x}= min{2,83,53}=53,成立,∴x=12或13,故答案为12或13.【点睛】本题考查了阅读理解题,一元一次方程的应用,分类讨论思想的运用等,解决问题的关键是读懂题意,依题意分情况列出一元一次方程进行求解.15.(0,4)或(0,-4).【分析】设△ABC边AB上的高为h,利用三角形的面积列式求出h,再分点C在y轴正半轴与负半轴两种情况解答.【详解】解:设△ABC边AB上的高为h,∵A(1,0),解析:(0,4)或(0,-4).【分析】设△ABC边AB上的高为h,利用三角形的面积列式求出h,再分点C在y轴正半轴与负半轴两种情况解答.【详解】解:设△ABC边AB上的高为h,∵A(1,0),B(2,0),∴AB=2-1=1,∴△ABC的面积=12×1•h=2,解得h=4,点C在y轴正半轴时,点C为(0,4),点C在y轴负半轴时,点C为(0,-4),所以,点C的坐标为(0,4)或(0,-4).故答案为:(0,4)或(0,-4).【点睛】本题考查了三角形的面积,坐标与图形性质,求出AB边上的高的长度是解题的关键.16.(0,1)【分析】根据点A、B、C、D的坐标可得出AB、AD及矩形ABCD的周长,由题意可知P 点的运动是绕矩形ABCD的周长的循环运动,然后进行计算求解即可.【详解】解:∵A(1,1), B解析:(0,1)【分析】根据点A、B、C、D的坐标可得出AB、AD及矩形ABCD的周长,由题意可知P点的运动是绕矩形ABCD的周长的循环运动,然后进行计算求解即可.【详解】解:∵A(1,1),B(-1,1),C(-1,-2), D(1,-2)∴AB= CD= 2,AD= BC= 3,∴四边形ABCD 的周长= AB+ AD+BC+CD= 10∵P点的运动是绕矩形ABCD的周长的循环运动,且速度为每秒一个单位长度∴P点运动一周需要的时间为10秒∵2021=202×10+1∴当t=2021秒时P的位置相当于t=1秒时P的位置∵t=1秒时P的位置是从A点向B移动一个单位∴此时P点的坐标为(0,1)∴t=2021秒时P点的坐标为(0,1)故答案为:(0,1).【点睛】本题主要考查了点的坐标与运动方式的关系,解题的关键在于找出P点一个循环运动需要花费的时间.三、解答题17.(1)5;(2)-2;(3)2【解析】【分析】根据实数的性质进行化简,再求值.【详解】解:(1)==5;(2)-× =-×4=-2;(3)-++=-6+5+3=2.【点睛】此题主要解析:(1)5;(2)-2;(3)2【解析】【分析】根据实数的性质进行化简,再求值.【详解】解12×4=-2;【点睛】此题主要考查实数的计算,解题的关键是熟知实数的性质.18.(1)x=±9;(2)x=3【分析】(1)方程整理后,利用平方根定义开方即可求出解;(2)利用立方根定义开立方即可求出解.【详解】解:(1)方程整理得:x2=81,开方得:x=±9;(解析:(1)x=±9;(2)x=3【分析】(1)方程整理后,利用平方根定义开方即可求出解;(2)利用立方根定义开立方即可求出解.【详解】解:(1)方程整理得:x2=81,开方得:x=±9;(2)方程整理得:(x-1)3=8,开立方得:x-1=2,解得:x=3.【点睛】本题考查了平方根、立方根,熟练掌握各自的定义是解本题的关键.19.已知;同角的补角相等;AB;EF;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;已知;∠B;∠ADE;等量代换;同位角相等,两直线平行【分析】求出∠2=∠4,根据平行线的判定得出AB解析:已知;同角的补角相等;AB;EF;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;已知;∠B;∠ADE;等量代换;同位角相等,两直线平行【分析】求出∠2=∠4,根据平行线的判定得出AB∥EF,根据平行线的性质得出∠3=∠ADE,求出∠B=∠ADE,再根据平行线的判定推出即可.【详解】解:DE∥BC,理由如下:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知),∴∠2=∠4(同角的补角相等),∴AB∥EF(内错角相等,两直线平行),∴∠3=∠ADE (两直线平行,内错角相等),∵∠3=∠B (已知),∴∠B =∠ADE (等量代换),∴DE ∥BC (同位角相等,两直线平行),【点睛】此题考查了平行线的判定与性质,熟练掌握平行线的性质定理及判定定理是解题的关键. 20.(1)见解析;(2)5【分析】(1)根据平移的性质先确定O 、B 、C 的对应点O1、B1、C1的坐标,然后顺次连接O1、B1、C1即可;(2)根据的面积=其所在的长方形面积减去周围三个三角形的面积解析:(1)见解析;(2)5【分析】(1)根据平移的性质先确定O 、B 、C 的对应点O 1、B 1、C 1的坐标,然后顺次连接O 1、B 1、C 1即可;(2)根据111O B C 的面积=其所在的长方形面积减去周围三个三角形的面积进行求解即可.【详解】解:(1)如图所示,111O B C 即为所求;(2)由题意得:11111143421313=5222O B C S =⨯-⨯⨯-⨯⨯-⨯⨯△. 【点睛】本题主要考查了平移作图,三角形面积,解题的关键在于能够熟练掌握平移作图的方法. 21.(1)7;-7;(2)5;(3)13-.【分析】(1)估算出的范围,即可得出答案;(2)分别确定出a 、b 的值,代入原式计算即可求出值;(3)根据题意确定出等式左边的整数部分得出y 的值,进而求解析:(1)7;(2)5;(3)【分析】(1(2)分别确定出a、b的值,代入原式计算即可求出值;(3)根据题意确定出等式左边的整数部分得出y的值,进而求出y的值,即可求出所求.【详解】解:(1)∵78,∴7.故答案为:7.(2)∵34,∴a,3∵23,∴b=2∴=5(3)∵23∴11<12,∵,其中x是整数,且0﹤y<1,∴x=11,y=,∴x-y==【点睛】本题考查的是无理数的小数部分和整数部分及其运算.估算无理数的整数部分是解题关键.二十二、解答题22.(1);(2)<;(3)不能,理由见解析【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的解析:(12)<;(3)不能,理由见解析【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的周长,利用作商法比较这两数大小即可;(3)利用方程思想求出长方形的长边,与正方形边长比较大小即可;【详解】解:(1)∵小正方形的边长为1cm ,∴小正方形的面积为1cm 2,∴两个小正方形的面积之和为2cm 2,即所拼成的大正方形的面积为2 cm 2,设大正方形的边长为x cm ,∴22x = , ∴x∴;(2)设圆的半径为r ,∴由题意得22r ππ=, ∴r = ∴=22C r π=圆设正方形的边长为a∵22a π=, ∴a∴=4C a =正∴1C C ===<圆正 故答案为:<;(3)解:不能裁剪出,理由如下:∵正方形的面积为900cm 2,∴正方形的边长为30cm∵长方形纸片的长和宽之比为5:4,∴设长方形纸片的长为5x ,宽为4x ,则54740x x ⋅=,整理得:237x =,∴22(5)252537925900x x ==⨯=>,∴22(5)30x >,∴530x >,∴长方形纸片的长大于正方形的边长,∴不能裁出这样的长方形纸片.【点睛】本题通过圆和正方形的面积考查了对算术平方根的应用,主要是对学生无理数运算及比较大小进行了考查.二十三、解答题23.(1)证明见解析;(2)补图见解析;当点在上时,;当点在上时,.【分析】(1)过点作,根据平行线的性质即可求解;(2)分两种情况:当点在上,当点在上,再过点作即可求解.【详解】(1)证明:解析:(1)证明见解析;(2)补图见解析;当点C 在AG 上时,290AHB CBG ∠-∠=︒;当点C 在DG 上时,290AHB CBG ∠+∠=︒.【分析】(1)过点G 作//GE MN ,根据平行线的性质即可求解;(2)分两种情况:当点C 在AG 上,当点C 在DG 上,再过点H 作//HF MN 即可求解.【详解】(1)证明:如图,过点G 作//GE MN ,∴MAG AGE ∠=∠,∵//MN PQ ,∴//GE PQ .∴PBG BGE ∠=∠.∵BG AD ⊥,∴90AGB ∠=︒,∴90MAG PBG AGE BGE AGB ∠+∠=∠+∠=∠=︒.(2)补全图形如图2、图3,猜想:290AHB CBG ∠-∠=︒或290AHB CBG ∠+∠=︒.证明:过点H 作//HF MN .∴1AHF ∠=∠.∵//MN PQ ,∴//HF PQ∴2BHF ∠=∠,∴12AHB AHF BHF ∠=∠+∠=∠+∠.∵AH 平分MAG ∠,∴21MAG ∠=∠.如图3,当点C 在AG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠+∠=∠,∵//MN PQ ,∴MAG GDB ∠=∠,2212290AHB MAG PBG CBGGDB PBG CBG CBG∴∠=∠+∠=∠+∠+∠=∠+∠+∠=︒+∠即290AHB CBG ∠-∠=︒.如图2,当点C 在DG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠-∠=∠.∴2212290AHB MAG PBG CBG CBG ∠=∠+∠=∠+∠-∠=︒-∠.即290AHB CBG ∠+∠=︒.【点睛】本题考查了平行线的基本性质、角平分线的基本性质及角的运算,解题的关键是准确作出平行线,找出角与角之间的数量关系.24.(1)15°;150°;(2)67.5°;(3)30°或90°或120°【分析】(1)根据平行线的性质和三角板的角的度数解答即可;(2)根据平行线的性质和角平分线的定义解答即可;(3)分当B解析:(1)15°;150°;(2)67.5°;(3)30°或90°或120°【分析】(1)根据平行线的性质和三角板的角的度数解答即可;(2)根据平行线的性质和角平分线的定义解答即可;(3)分当BC ∥DE 时,当BC ∥EF 时,当BC ∥DF 时,三种情况进行解答即可.【详解】解:(1)作EI ∥PQ ,如图,∵PQ∥MN,则PQ∥EI∥MN,∴∠α=∠DEI,∠IEA=∠BAC,∴∠DEA=∠α+∠BAC,∴α= DEA -∠BAC=60°-45°=15°,∵E、C、A三点共线,∴∠β=180°-∠DFE=180°-30°=150°;故答案为:15°;150°;(2)∵PQ∥MN,∴∠GEF=∠CAB=45°,∴∠FGQ=45°+30°=75°,∵GH,FH分别平分∠FGQ和∠GFA,∴∠FGH=37.5°,∠GFH=75°,∴∠FHG=180°-37.5°-75°=67.5°;(3)当BC∥DE时,如图1,∵∠D=∠C=90 ,∴AC∥DF,∴∠CAE=∠DFE=30°,∴∠BAM+∠BAC=∠MAE+∠CAE,∠BAM=∠MAE+∠CAE-∠BAC=45°+30°-45°=30°;当BC∥EF时,如图2,此时∠BAE=∠ABC=45°,∴∠BAM=∠BAE+∠EAM=45°+45°=90°;当BC∥DF时,如图3,此时,AC ∥DE ,∠CAN =∠DEG =15°,∴∠BAM =∠MAN -∠CAN -∠BAC =180°-15°-45°=120°.综上所述,∠BAM 的度数为30°或90°或120°.【点睛】本题考查了角平分线的定义,平行线性质和判定:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用,理清各角度之间的关系是解题的关键,也是本题的难点.25.(1),理由详见解析;(2),理由详见解析:(3)①;②360°;(4); .【分析】(1)根据三角形外角等于不相邻的两个内角之和即可得出结论;(2)根据三角形内角和定理及对顶角相等即可得出结解析:(1)D A B C ∠=∠+∠+∠,理由详见解析;(2)A D B C ∠+∠=∠+∠,理由详见解析:(3)①1902D A ∠=︒+∠;②360°;(4)124E ∠=︒; =14F ∠︒.【分析】(1)根据三角形外角等于不相邻的两个内角之和即可得出结论;(2)根据三角形内角和定理及对顶角相等即可得出结论;(3)①根据角平分线的定义及三角形内角和定理即可得出结论;②连结BE ,由(2)的结论及四边形内角和为360°即可得出结论;(4)根据(1)的结论、角平分线的性质以及三角形内角和定理即可得出结论.【详解】(1)D A B C ∠=∠+∠+∠.理由如下:如图1,BDE B BAD ∠=∠+∠,CDE C CAD ∠=∠+∠,BDC B BAD C CAD B BAC C ∴∠=∠+∠+∠+∠=∠+∠+∠,D A B C ∴∠=∠+∠+∠; (2)A D B C ∠+∠=∠+∠.理由如下:在ADE ∆中,180AED A D ∠=︒-∠-∠,在BCE ∆中,180BEC B C ∠=︒-∠-∠,AED BEC ∠=∠,A D B C ∴∠+∠=∠+∠;(3)①180A ABC ACB ∠=︒-∠-∠,180D DBC DCB ∠=︒-∠-∠,BD 、CD 分别平分ABC∠和ACB ∠,∴1122ABC ACB DBC DCB ∠+∠=∠+∠,1111180()180(180)902222D ABC ACB A A ∴∠=︒-∠+∠=︒-︒-∠=︒+∠. 故答案为:1902D A ∠=︒+∠.②连结BE .∵C D CBE DEB ∠+∠=∠+∠,360A B C D E F A ABE F BEF ∴∠+∠+∠+∠+∠+∠=∠+∠+∠+∠=︒. 故答案为:360︒;(4)由(1)知,BDC B C BAC ∠=∠+∠+∠,26B ∠=︒,54C ∠=︒,80BDC BAC ∴∠=︒+∠,402CDF CAE ∴∠=︒+∠,4BAC CAE ∠=∠,2BDC CDF ∠=∠,1902GDE CDF ∴∠=︒-∠,26180AGD B GDB CDF ∠=∠+∠=︒+︒-∠,3GAE CAE ∠=∠,3336064(2)644012422E GAE AGD GDE CAE CDF ∴∠=︒-∠-∠-∠=︒-∠-∠=︒+⨯︒=︒; 180180(206)2262264014F AGF GAF CDF CAE CDF CAE ∠=︒-∠-∠=︒-︒-∠-∠=-︒+∠-∠=-︒+︒=︒.【点睛】本题考查了角平分线的性质,三角形内角和;熟练掌握角平分线的性质,进行合理的等量代换是解题的关键.26.(1)见解析;(2)①③;(3)∠APB 的度数是10°或20°或40°或110°【分析】(1)由和是的角平分线,证明即可;(2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角解析:(1)见解析;(2)①③;(3)∠APB 的度数是10°或20°或40°或110°【分析】(1)由90ABC A ∠+∠=︒和BD 是ABC 的角平分线,证明290ABD A ∠+∠=︒即可; (2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角形”的定义,分类讨论:①2∠A +∠ABC =90°;②∠A +2∠APB =90°;③2∠APB +∠ABC =90°;④2∠A +∠APB =90°,由三角形内角和定理和外角的性质结合“准互余三角形”的定义,即可求出答案.【详解】(1)证明:∵在Rt ABC 中,90ACB ∠=︒,∴90ABC A ∠+∠=︒,∵BD 是ABC ∠的角平分线,∴2ABC ABD ∠=∠,∴290ABD A ∠+∠=︒,∴ABD △是“准互余三角形”;(2)①∵70,10B C ∠=︒∠=︒,∴290B C ∠+∠=︒,∴ABC 是“准互余三角形”,故①正确;②∵60A ∠=︒, 20B ∠=︒,∴210090A B ∠+∠=︒≠︒,∴ABC 不是“准互余三角形”,故②错误;③设三角形的三个内角分别为,,αβγ,且αβγ<<,∵三角形是“准互余三角形”,∴290αβ+=︒或290αβ+=︒,∴90αβ+<︒,∴180()90γαβ=︒-+>︒,∴“准互余三角形”一定是钝角三角形,故③正确;综上所述,①③正确,故答案为:①③;(3)∠APB 的度数是10°或20°或40°或110°;如图①,当2∠A +∠ABC =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A =20°,∴∠APB =110°;如图②,当∠A +2∠APB =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A+∠APB=50°,∴∠APB=40°;如图③,当2∠APB+∠ABC=90°时,△ABP是“准直角三角形”,∵∠ABC=50°,∴∠APB=20°;如图④,当2∠A+∠APB=90°时,△ABP是“准直角三角形”,∵∠ABC=50°,∴∠A+∠APB=50°,所以∠A=40°,所以∠APB=10°;综上,∠APB的度数是10°或20°或40°或110°时,ABP△是“准互余三角形”.【点睛】本题是三角形综合题,考查了三角形内角和定理,三角形的外角的性质,解题关键是理解题意,根据三角形内角和定理和三角形的外角的性质,结合新定义进行求解.。
2007年沈阳课改区数学模拟试卷

沈阳课改区2007年中考模拟考试北师大版数学试卷一、选择题:(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填入题后的括号内,每小题3分,共24分)1、若每人每天浪费水0.32升,那么100万人每天浪费的水,用科学记数法表示为()A、3.2×107升B、3.2×106升C、 3.2×105升D、3.2×104升2、计算5)3()2(02⨯+-所得的结果是()A、4B、 9C、 -1D、 13、下面是一天中四个不同时刻两个建筑物的影子:将它们按时间先后顺序进行排列,正确的是( )A、③④②①B、②④③①C、③④①②D、③①②④4、下列图形中,不可能围成正方体的是()A. B. C. D.5、六张完全相同的卡片上,分别画有等边三角形、正六边形、矩形、平行四边形、等腰梯形、菱形,现从中随机抽取一张,卡片上画的恰好既是轴对称图形又是中心对称图形的概率为()A.21B.65C.31D.326、已知点(2,152 )是反比例函数y=21m x -图象上一点,则此函数图象必经过点 ( ) A 、(3,-5) B 、(5,-3) C 、(-3,5) D 、(3,5)7、已知⊙O 1和⊙O 2的半径分别为3crn 和5 cm ,两圆的圆心距是6 cm ,则这两圆的位置关系是 ( ) A 、外离 B 、相交 C 、内切 D 、内含8、现往一塑料圆柱形杯子(重量注水,已知10秒钟能注满杯子,之后注入的水会溢出,下列四个图象中,能反映从注水开始,15秒内注水时间t 与杯底压强P 的图象是 ( )二、填空题(每小题3分,共24分)9、已知1x =时,分式2x bx a+-无意义,4x =时分式的值为零,则b a +=__________.10、若不等式(2k+3)x <2k+3的解集是x >1,则k 的范围是_____________. 11、如图,粮仓顶部是圆锥形,这个圆锥的底面圆的周长为36m ,母线长为8m .为防雨需在粮仓顶部铺上油毡,需要铺油毡的面积是_________.12、为了了解中央电视台春节联欢晚会的收视率,应采用适合的调查方式为 ____(选填“普查”或“抽样调查”).13、请你添加一个条件,使矩形ABCD 成为一个正方形,你添加的条件是________________. 14、如下图是小明用火柴搭的1条、2条、3条“金鱼”……,则搭n 条“金鱼”需要火柴 根. ……1条 2条 3条15、对于多项式nn y x -,因式分解的结果是))()((22y x y x y x ++-;一个多边形的外角都等于600,这个多边形的边数为m ,则点P (n m ,)关于x 轴对称点的坐标为_______.16、如图,小王使一长为4cm ,宽为3cm 的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A 位置变化为12A A A →→,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A 翻滚到A 2位置时共走过的路径长为________.三、(第17小题6分,第18、19小题各8分,第20小 题10分,共32分)17、先化简,后求值:)11(122aa a a +⨯+-, 其中m =260tan 0+.18、今年十一五规划中提出建设社会主义新农村,推进农村城市化的进程,继续减轻农民负担。
2007年沈阳市中考数学试题答案

2007年沈阳市中等学校招生统一考试数学试题参考答案及评分标准一、选择题(每小题3分,共24分)1.A 2.B 3.A 4.D 5.C 6.C 7.B 8.A二、填空题(每小题3分,共24分)9.x (x +5)(x -5) 10.2,4 11.AO =DO 或AB =DC 或BO =CO 12.(63+1)m 13.5014.如图15.y =2x 2 16.6三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分)17.解:原式=1-3+5+9-5 …………………………………………………4分=7 ……………………………………………………………………6分18.解:解不等式2x -5≤3(x -1)得x ≥-2 ……………………………………2分解不等式x +72>4x 得x <1 ……………………………………………………………4分 ∴不等式组的解集为-2≤x <1 ……………………………………………………6分 在数轴上表示为:………………………………………………8分 19.证明:∵四边形ABCD 是平行四边形∴AB =CD ,AB ∥CD∴∠GBE =∠HDF …………………………………………………………………2分 又∵AG =CH∴BG =DH又∵BE =DF∴△GBE ≌△HDF …………………………………………………………………5分 ∴GE =HF ,∠GEB =∠HFD∴∠GEF =∠HFE∴GE ∥HF∴四边形GEHF 是平行四边形. ……………………………………………………8分 第14题图20.解:设甲施工队单独完成此项工程需x 天,则乙施工队单独完成此项工程需45x 天, …………………………………………1分 根据题意,得 10x +1245x =1 …………………………………………………………4分 解这个方程,得x =25 ………………………………………………………………6分 经检验,x =25是所列方程的根 ……………………………………………………7分当x =25时,45x =20 …………………………………………………………………9分 答:甲、乙两个施工队单独完成此项工程分别需25天和20天. ……………10分 四.(每小题10分,共20分)21.解:(1)2003,45% ……………………………………………………………4分(2)由图①,得162+204+295+301+317+321=1600301÷1600≈0.19=19%321÷1600≈0.20=20% …………………7分∴2004年19%,2006年20%正确补全统计图. ………………………8分(3)建议积极向上即可. ………………10分22.(1)证明:∵ AB =BC AB BC∴= ………………………………2分 ∴∠BDC =∠ADB ,∴DB 平分∠ADC ……………………………………………4分(2)解:由(1)可知 AB BC=,∴∠BAC =∠ADB ∵∠ABE =∠ABD∴△ABE ∽△DBA ……………………………………………………………………6分 ∴AB BE =BD AB∵BE =3,ED =6∴BD =9 ……………………………………………………………………………8分 ∴AB 2=BE ·BD =3×9=27∴AB =33 …………………………………………………………………………10分五、(本题12分)23.解:(1)由已知可得A 1、A 2是矩形,A 3是圆;B 1、B 2、B 3都是矩形;C 1是三角形,C 2、C 3是矩形. ………………………………………………………3分(2)①补全树状图如下:第21题(2)图……………………………………………………………………………………………7分 由树状图可知,共有27种等可能结果,其中三张卡片上的图形名称都相同的结果有12种,∴三张卡片上的图形名称都相同的概率是1227=49…………9分 ②游戏对双方不公平.由①可知,三张卡片中只有两张卡片上的图形名称相同的概率是1227=49,即P (小刚获胜)=49三张卡片上的图形名称完全不同的概率是327=19,即P (小亮获胜)=19∵49>19∴这个游戏对双方不公平. ……………………………………………12分 六、(本题12分)24.解:(1)符合条件的等腰△OMP 只有1个.点P 的坐标为(12,4) ……2分 (2)符合条件的等腰△OMP 有4个. …………………………………………3分 如图①,在△OP 1M 中,OP 1=OM =4,在Rt △OBP 1中,BO =72, BP 1=OP 21-OB 2=42-(72)2=152 ∴P 1(-72,152) ……………………………………………………………………5分 在Rt △OMP 2中,OP 2=OM =4,∴P 2(0,4)在△OMP 3中,MP 3=OP 3,∴点P 3在OM 的垂直平分线上,∵OM =4,∴P 3(2,4)在Rt △OMP 4中,OM =MP 4=4,∴P 4(4,4) …………………………………9分(3)若M (5,0),则符合条件的等腰三角形有7个. …………………………12分 点P 的位置如图②所示七、(本题12分)25.解:(1)依题意,每千克原料的进货价为160×75%=120(元) ……………2分设化工商店调整价格后的标价为x 元,则 0.8x -120=0.8x ×20% 解得 x =187.5 187.5×0.8=150(元) ………………………………………………………………4分 ∴调整价格后的标价是187.5元,打折后的实际售价是150元 .…………………5分(2)①描点画图,观察图象,可知这些点的发展趋势近似是一条直线,所以猜想y 与x 之间存在着一次函数关系.………………………………………………………………………………………7分 ②根据①中的猜想,设y 与x 之间的函数表达式为y =kx +b ,将点(150,500)和(160,480)代入表达式,得⎩⎪⎨⎪⎧ 500=150k +b 480=160k +b 解得⎩⎪⎨⎪⎧k =-2b =800 ∴y 与x 的函数表达式为y =-2x +800 ……………………………………………9分 将点(168,464)和(180,440)代入y =-2x +800均成立,即这些点都符合y =-2x +800的发展趋势.∴①中猜想y 与x 之间存在着一次函数关系是正确的. …………………………10分 ③设化工商店这个月销售这种原料的利润为w 元,当y =450时,x =175∴w =(175-120)×450=24750(元)答:化工商店这个月销售这种原料的利润为24750元. …………………………12分八、(本题14分)26.解:(1)解方程x 2-10x +16=0得x 1=2,x 2=8 ………………………………1分 ∵点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,且OB <OC∴点B 的坐标为(2,0),点C 的坐标为(0,8)又∵抛物线y =ax 2+bx +c 的对称轴是直线x =-2∴由抛物线的对称性可得点A 的坐标为(-6,0) …………………………………4分(2)∵点C (0,8)在抛物线y =ax 2+bx +c 的图象上∴c =8,将A (-6,0)、B (2,0)代入表达式,得⎩⎪⎨⎪⎧ 0=36a -6b +80=4a +2b +8 解得⎩⎨⎧ a =-23b =-83∴所求抛物线的表达式为y =-23x 2-83x +8 ………………………………………7分 (3)依题意,AE =m ,则BE =8-m ,∵OA =6,OC =8,∴AC =10∵EF ∥AC ∴△BEF ∽△BAC∴EF AC =BE AB 即EF 10=8-m 8∴EF =40-5m 4过点F 作FG ⊥AB ,垂足为G ,则sin ∠FEG =sin ∠CAB =45∴FG EF =45 ∴FG =45·40-5m 4=8-m ∴S =S △BCE -S △BFE =12(8-m )×8-12(8-m )(8-m ) =12(8-m )(8-8+m )=12(8-m )m =-12m 2+4m ……………………………10分 自变量m 的取值范围是0<m <8 …………………………………………………11分(4)存在.理由:∵S =-12m 2+4m =-12(m -4)2+8 且-12<0, ∴当m =4时,S 有最大值,S 最大值=8 ……………………………………………12分 ∵m =4,∴点E 的坐标为(-2,0)∴△BCE 为等腰三角形. …………………………………………………………14分(以上答案仅供参考,如有其它做法,可参照给分)第26题图(批卷教师用图)。
2007年沈阳市中等学校招生统一考试数学试卷及答案(word版)
2007 年沈阳市中等学校招生一致考试数学试卷* 考试时间120 分钟试卷满分150 分一、选择题(以下各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每题 3 分,共 24 分)1.-13的相反数是()11A .3B.3C.- 3D.-32.如图,在 Rt△ ABC 中,∠ C= 90°,AB= 5,AC= 2,则 cosA的值是()212215A .5B.5C.2D.2第2题图.年整年共监测水量达48909.63 沈阳市水质监测部门 2006万吨,水质达标率为100%.用科学记数法表示 2006年整年共监测水量约为()万吨(保存三个有效数字)A . 4.89 ×104B. 4.89 ×105C. 4.90 ×104D.4.90 ×1054.以下事件中是必定事件的是()A .小婷上学必定坐公交车B.买一张电影票,座位号正好是偶数C.小红期末考试数学成绩必定得满分D.将豆油滴入水中,豆油会浮在水面上.5如图, AB∥ CD ,直线 EF 分别交 AB、 CD 于 E、F 两点,若∠ FEB =110°,则∠ EFD 等于()A.50°B.60°C. 70°D. 110 °.)6挨次连结菱形各边中点所获得的四边形是(A .梯形B.菱形C.矩形D.正方形第 5题图.4的图象在()7反比率函数 y=-xA .第一、三象限B .第二、四象限C.第一、二象限 D .第三、四象限.2∶ 1 的长方形纸片按如图①、②所示的方式对折,而后沿图③8 将一张长与宽的比为中的虚线裁剪,获得图④,最后将图④的纸片再睁开摊平,则所获得的图案是()图①图②图③图④二、填空(每小 3 分,共 24 分).分解因式: x 325x.910.已知一数据1, a, 4, 4, 9,它的均匀数是4, a 等于,数据的众数是..如, AC、 BD 订交于点 O,∠ A=∠ D,你再充一个条件,使得△AOB≌11△DOC ,你充的条件是.第 11第 1212.如,小将器安置在与旗杆AB 底部相距 6m 的 C ,量出器的高度CD= 1m,得旗杆端 B 的仰角= 60°,旗杆 AB 的高度.(算果保存根号)13.有一数: 1,2, 5, 10, 17, 26,⋯⋯,察数的组成律,用你的律确立第 8 个数.14.如,在正方形网格中,以点 A 旋中心,将△ ABC 按逆方向旋90°,画出旋后的△ AB1C1.第 1415.将抛物y2(x 1)2 3 向右平移1个位,再向上平移3个位,所得抛物的表达式..3 的等三角形,△ BDC 是等腰三角形,且∠ BDC = 120 °.以16 如,△ ABC 是D 点作一个 60°角,使其两分交AB 于点 M,交 AC 于点 N,接 MN ,△ AMN的周.第 16三、(第 17 小题 6 分,第 18、 19 小题各 8 分,第 20 小题 10 分,共 32 分)17.计算:(π- 3)0- | 5- 3|+(-1)-2-5.32x-5≤ 3(x-1)18.解不等式组 x+ 7,并把它的解集在数轴上表示出来.2> 4x19.如图,已知在□ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在 BA 和 DC 的延伸线上,且 AG= CH,连结 GE、 EH、 HF 、FG .求证:四边形 GEHF 是平行四边形.第 19题图.2 天后,再由20甲、乙两个施工队共同达成某居民小区绿化改造工程,乙队先独自做两队合作10 天就能达成所有工程.已知乙队独自达成此项工程所需天数是甲队独自达成此项工程所需天数的45,求甲、乙两个施工队独自达成此项工程各需多少天?四、(每题10 分,共 20 分)21.2006 年沈阳市城市环境空气质量达到了有记录以来的最好水平,优秀天气的天数在全国副省级以上城市排名第9,排名在北京、天津、重庆等城市以前.空气质量分为优秀天气、轻度污染、中度污染、重度污染四种种类,相关部门将我市2001 年—— 2006 年前三类空气质量的天数制成条形统计图,请依据统计图解答以下问题:2001 年—— 2006 年沈阳市优秀天气、轻度污染、中度污染天数统计图第 21 题图①( 1)依据图①中的统计图可知,和前一年比,年优秀天气的天数增添最多,这一年优秀天气的天数比前一年优秀天气的天数的增添率约为;(精准到1%)(2)在图②中给出了我市 2001 年—— 2006 年优秀天气天数的扇形统计图中的部分数据,请你补全此统计图,并写出计算过程;(精准到 1%)( 3)依据这 6 年沈阳市城市空气质量的变化,说说你对我市环保的建议.2001 年—— 2006 年沈阳市优秀天气天数统计图第 21 题图②22.如图,已知 A、B、 C、 D 是⊙ O 上的四个点, AB= BC, BD 交 AC 于点 E,连结CD、AD .(1)求证: DB 均分∠ ADC ;(2)若 BE=3, ED = 6,求 AB 的长.第 22题图五、(此题 12 分)23.如图所给的 A、 B、 C 三个几何体中,按箭头所示的方向为它们的正面,设A、B、C 三个几何体的主视图分别是A1、 B1、 C1;左视图分别是A2、 B2、C2;俯视图分别是A3、B3、 C3.( 1)请你分别写出 A1、 A2、 A3、 B1、 B2、 B3、 C1、 C2、 C3图形的名称;( 2)小刚先将这9 个视图分别画在大小、形状完整同样的9 张卡片上,并将画有A1、A2、A3的三张卡片放在甲口袋中,画有B1、B2、B3的三张卡片放在乙口袋中,画有C1、C2、C3的三张卡片放在丙口袋中,而后由小亮随机从这三个口袋中分别抽取一张卡片.① 经过补全下边的树状图,求出小亮随机抽取的三张卡片上的图形名称都同样的概率;② 小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称同样时,小刚获胜;三张卡片上的图形名称完整不一样时,小亮获胜.这个游戏对两方公正吗?为何?解:( 1)ABC( 2)①树状图:第 23题图六、(此题 12 分)25, O 为 BC 上一点, BO=7,以下图,以24.已知在矩形 ABCD 中, AB =4, BC=22BC 所在直线为 x 轴, O 为坐标原点成立平面直角坐标系,M 为线段 OC 上的一点.( 1)若点 M 的坐标为( 1,0),如图①,以 OM 为一边作等腰△ OMP ,使点 P 在矩形ABCD 的一边上,则切合条件的等腰三角形有几个?请直接写出所有切合条件的点P 的坐标;(2)若将( 1)中的点 M 的坐标改为( 4,0),其余条件不变,如图②,那么切合条件的等腰三角形有几个?求出所有切合条件的点P 的坐标;(3)若将( 1)中的点 M 的坐标改为( 5,0),其余条件不变,如图③,请直接写出符合条件的等腰三角形有几个.(不用求出点P 的坐标)第 24题图七、(本 12 分)25.化工商铺售某种新式化工原料,其市指价是每千克160 元(化工商铺的售价能够在市指价的基上行浮),种原料的价是市指价的75%.(1)了大售量,化工商铺决定适合整价钱,整后的价钱按八折售,仍可得售价的20%的利.求化工商铺整价钱后的价是多少元?打折后的售价是多少元?( 2)化工商铺认识种原料的月售量y(千克)与售价x(元 /千克)之的关系,每个月整一次售价,一段后,部人把状况列成下表:售价x(元 /千克)⋯150160168180⋯月售量y(千克)⋯500480464440⋯①你在所的平面直角坐系中,以售价x(元 /千克)横坐,月售量y (千克)坐描出各点,察些点的展,猜想y 与 x 之可能存在怎的函数关系;②你用所学的函数知确立一个足些数据的y 与 x 之的函数表达式,并你在①中的猜想;③若化工商铺某月按同一售价共出种原料450 千克,你求出化工商铺个月售种原料的利是多少元?第 25八、(此题 14 分)26.已知抛物线 y = ax 2+bx + c 与 x 轴交于 A 、B 两点,与 y 轴交于点 C ,此中点 B 在 x 轴的正半轴上,点 C 在 y 轴的正半轴上,线段 OB 、 OC 的长( OB<OC )是方程 x 2- 10x + 16= 0 的两个根,且抛物线的对称轴是直线x =- 2.( 1)求 A 、 B 、 C 三点的坐标;( 2)求此抛物线的表达式;( 3)连结 AC 、 BC ,若点 E 是线段 AB 上的一个动点(与点 A 、点 B 不重合),过点 E作 EF ∥AC 交 BC 于点 F ,连结 CE ,设 AE 的长为 m ,△ CEF 的面积为 S ,求 S 与 m 之间的函数关系式,并写出自变量 m 的取值范围;( 4)在( 3)的基础上试说明 S 能否存在最大值,若存在,恳求出S 的最大值,并求出此时点 E 的坐标,判断此时△ BCE 的形状;若不存在,请说明原因.第26题图2007 年沈阳市中等学校招生一致考试数学试题参照答案及评分标准一、选择题(每题 3 分,共 24 分)1.A 2.B 3.A 4.D 5.C 6.C 7.B 8.A二、填空题(每题3 分,共 24 分).x (x + 5)( x - 5)10 .2, 4.9 11 AO =DO 或 AB = DC 或 BO = CO12 . 13.50( 6 3+ 1) m 14 .如图第14题图15.y = 2x 216. 6三、(第 17 小 6 分,第 18、19小 各 8 分,第 20 小 10 分,共 32 分)17.解:原式= 1- 3+ 5+ 9- 5⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分 =7⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分 18.解:解不等式 2x - 5≤3( x - 1)得 x ≥- 2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分 解不等式x + 7> 4x 得 x<1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分2∴不等式 的解集 - 2≤ x < 1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分在数 上表示 :⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分19. 明:∵四 形ABCD 是平行四 形∴ AB = CD ,AB ∥ CD∴∠ GBE =∠ HDF ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分又∵ AG = CH∴ BG = DH又∵ BE = DF∴△ GBE ≌△ HDF ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分∴ GE = HF ,∠ GEB =∠ HFD∴∠ GEF =∠ HFE∴ GE ∥ HF∴四 形 GEHF 是平行四 形 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分20 .解: 甲施工 独达成此 工程需 x 天,乙施工 独达成此 工程需45x天,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分10 12依据 意,得x +4 = 1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分5x解 个方程,得 x = 25⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分, x = 25 是所列方程的根⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分当 x = 25 ,4x = 20 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分5答:甲、乙两个施工 独达成此 工程分 需25 天和 20 天.⋯⋯⋯⋯⋯ 10 分四.(每小10 分,共 20 分)21.解 : ( 1 )2003 ,45% ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分( 2)由 ①,得162+ 204+ 295+ 301+ 317+ 321=1600301 ÷ 1600 ≈0.19= 19%321 ÷ 1600 ≈0.20= 20% ⋯⋯⋯⋯⋯⋯⋯7 分∴ 2004 年 19%, 2006 年 20%正确 全 .⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8 分( 3)建 极向上即可 . ⋯⋯⋯⋯⋯⋯10 分.AB = BC22 ( 1) 明:∵AB BC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分∴∠ BDC =∠ ADB ,∴ DB 均分∠ ADC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分( 2)解:由( 1)可知 AB BC ,∴∠ BAC =∠ ADB∵∠ ABE =∠ ABD∴△ ABE ∽△ DBA⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分AB BD∴BE=AB∵ BE = 3, ED = 6∴BD =9⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8 分∴ AB 2= BE ·BD =3×9= 27∴AB =3 3⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分五、(本 12分)23.解:( 1)由已知可得 A 1、 A 2 是矩形, A 3 是 ; B 1、 B 2、B 3 都是矩形;C 1 是三角形, C 2、 C 3 是矩形 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分( 2)① 全 状 以下:⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分由 状 可知,共有27 种等可能 果,此中三 卡片上的 形名称都同样的 果有 12 种,∴三 卡片上的 形名称都同样的概率是124 ⋯⋯⋯⋯ 9 分27=9②游 两方不公正 .由①可知,三 卡片中只有两 卡片上的 形名称同样的概率是12= 4,即 P (小刚获胜) = 42799三 卡片上的 形名称完整不一样的概率是3= 1,即 P (小亮获胜) =12799∵ 4>1∴ 个游 两方不公正 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分99六、(本12 分)24.解:( 1)切合条件的等腰△OMP 只有 1 个 .点 P 的坐 ( 1, 4)⋯⋯2分2( 2)切合条件的等腰△OMP 有 4 个 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分如 ①,在△ OP 1M 中, OP 1=OM = 4,7在 Rt △OBP 1 中, BO =2,BP 1=2 2 27 215OP 1- OB =4-( )= 22∴P (- 7,15) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分12 2在 Rt △OMP 2 中, OP 2= OM = 4,∴ P 2( 0, 4) 在△ OMP 3 中, MP 3= OP 3,∴点 P 3 在 OM 的垂直均分 上,∵ OM =4,∴ P 3(2, 4)在 Rt △OMP 4 中, OM = MP 4= 4,∴ P 4( 4, 4) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 9 分( 3)若 M ( 5, 0), 切合条件的等腰三角形有 7 个 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分点 P 的地点如 ②所示七、(本 12 分)25.解:( 1)依 意,每千克原料的 价 160 ×75%= 120(元) ⋯⋯⋯⋯⋯ 2 分化工商铺 整价钱后的 价x 元,0.8x - 120=0.8x ×20%解得 x =187.5187.5 ×0.8= 150(元) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分 ∴ 整价钱后的 价是187.5 元,打折后的 售价是150 元 .⋯⋯⋯⋯⋯⋯⋯5 分( 2)①描点画 , 察 象,可知 些点的 展 近似是一条直 ,因此猜想 y 与 x 之 存在着一次函数关系 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分②依据①中的猜想,y 与 x 之 的函数表达式y = kx +b ,将点( 150, 500)和( 160, 480)代入表达式,得500= 150k+ b k=- 2解得b= 800480= 160k+ b∴ y 与 x 的函数表达式y=- 2x+ 800⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分将点( 168, 464)和( 180, 440)代入 y=- 2x+ 800 均成立,即些点都切合 y=- 2x+800 的展.∴①中猜想 y 与 x 之存在着一次函数关系是正确的.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分③ 化工商铺个月售种原料的利w 元,当 y= 450 , x=175∴w=( 175-120)×450= 24750(元)答:化工商铺个月售种原料的利24750 元.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分八、(本 14 分)26.解:( 1)解方程 x2- 10x+ 16= 0 得 x1= 2,x2=8⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∵点 B 在 x 的正半上,点 C 在 y 的正半上,且OB<OC∴点 B 的坐( 2, 0),点 C 的坐( 0, 8)又∵抛物 y= ax2+ bx+ c 的称是直x=- 2∴由抛物的称性可得点 A 的坐(- 6,0)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分(2)∵点 C(0, 8)在抛物 y= ax2+ bx+ c 的象上∴ c=8,将 A(- 6, 0)、 B( 2, 0)代入表达式,得20=36a- 6b+8a=-3解得80= 4a+ 2b+ 8b=-3∴所求抛物的表达式y=-2x2-8x+8⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分33(3)依意, AE= m, BE= 8- m,∵ OA= 6,OC= 8,∴ AC= 10∵EF∥ AC ∴△ BEF ∽△ BAC∴E F = BE即EF=8-mACAB108∴E F= 40- 5m4点 F 作 FG⊥ AB,垂足G, sin∠ FEG = sin∠ CAB=4 5∴FG=4∴ FG =4·40-5m= 8- m EF 554∴S= S△BCE- S△BFE=1( 8- m)×8-1( 8- m)( 8-m)221 1 1 2+ 4m ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 10 分= ( 8- m )( 8- 8+m )=2( 8- m ) m =- m22自 量 m 的取 范 是 0< m < 8⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11 分( 4)存在.原因:∵ S =- 1m 2+ 4m =- 1( m -4) 2+ 8且- 1< 0,222∴当 m = 4 , S 有最大 , S 最大值 = 8 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分∵ m = 4,∴点 E 的坐 (- 2, 0)∴△ BCE 等腰三角形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 14 分第 26(批卷教 用 )(以上答案 供参照,若有其余做法,可参照 分)。
中等学校招生统一考试数学试题和答案

中等学校招生统一考试数 学 试 题一选择题1. 2013年第一季度,沈阳市公共财政预算收入完成196亿元(数据来源:4月16日《沈阳日报》),将196亿用科学记数法表示为 (A )81.9610⨯ (B )819.610⨯ (C )101.9610⨯ (D )1019.610⨯2. 右图是一个几何体的三视图,这个几何体的名称是 (A )圆柱体 (B )三棱锥 (C )球体 (D )圆锥体3. 下面的计算一定正确的是(A )3362b b b += (B )222(3)9pq p q -=-(C )3585315y y y = (D )933b b b ÷=4. 如果1m =,那么m 的取值范围是(A )0<m <1 (B )1<m <2 (C )2<m <3 (D )3<m <4 5. 下列事件中,是不可能事件的是(A )买一张电影票,座位号是奇数 (B )射击运动员射击一次,命中9环 (C )明天会下雨 (D )度量三角形的内角和,结果是360°6. 计算2311x x +--的结果是 (A )11x - (B )11x - (C )51x - (D )51x-7. 在同一平面直角坐标系中,函数1y x =-与函数1y x=的图象可能是8. 如图,ABC △中,AE 交BC 于点D ,∠C =∠E ,AD =4,BC =8,BD ∶DC =5∶3,则DE 的长等于(A )203 (B )154 (C )163 (D )174二填空题9. 分解因式:2363a a ++=_________.10. 一组数据2,4,x ,1-的平均数为3,则x 的值是_________.11. 在平面直角坐标系中,点M (-3,2)关于原点的对称点的坐标是_________. 12. 若关于x 的一元二次方程240x x a ++=有两个不相等的实数根,则a 的取值范围是__________.13. 如果x =1时,代数式2234ax bx ++的值是5,那么x =-1时,代数式3234ax bx ++的值是__________.14. 如图,点A 、B 、C 、D 都在O ⊙上,90ABC ∠=°,AD =3,CD =2,则O ⊙的直径的长是__________.15. 有一组等式:22221223++=,22222367++=,2222341213++=,2245++220=221……请观察它们的构成规律,用你发现的规律写出第8个等式为_________.16. 已知等边三角形ABC 的高为4,在这个三角形所在的平面内有一点P ,若点P 到AB 的距离是1,点P 到AC 的距离是2,则点P 到BC 的最小距离和最大距离分别是________. 三解答题17. 计算:2016sin 30(2)22-⎛⎫-+-+ ⎪⎝⎭°.18. 一家食品公司将一种新研发的食品免费送给一些人品偿,并让每个人按A (不喜欢)、B (一般)、C (比较喜欢)、D (非常喜欢)四个等级对该食品进行评价,图1和图2是该公司采集数据后,绘制的两幅不完整的统计图.请你根据以上统计图提供的信息,回答下列问题: (1)本次调查的人数为________人;(2)图1中,a =________,C 等级所占的圆心角的度数为_______度; (3)请直接在答题卡中补全条形统计图.19. 如图,ABC △中,AB =BC ,BE AC ⊥于点E ,AD BC ⊥于点D ,45BAD ∠=°,AD 与BE 交于点F ,连接CF . (1)求证:BF =2AE ;(2)若CD =AD 的长.20. 在一个不透明的盒子中放有三张卡片,每张卡片上写有一个实数,分别为3+6.(卡片除了实数不同外,其余均相同)(1)从盒子中随机抽取一张卡片,请直接..写出卡片上的实数是3的概率.(2)先从盒子中随机抽取一张卡片,将卡片上的实数作为被减数,卡片不放回,再随机抽取一张卡片,将卡片上的实数作为减数.请你用列表法或树状图(树形图)法,求出两次抽取的卡片上的实数之差为有理数的概率.21. 身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G 处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角37°.(1)求风筝距地面的高度GF;(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根5米长的竹竿能否触到挂在树上的风筝?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)22. 如图,OC 平分∠MON ,点A 在射线OC 上,以点A 为圆心,半径为2的A ⊙与OM 相切于点B ,连接BA 并延长交A ⊙于点D ,交ON 于点E . (1)求证:ON 是A ⊙的切线;(2)若60MON ∠=°,求图中阴影部分的面积.(结果保留π)23. 某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.某日,从早8点开始到上午11点,每个普通售票窗口售出的车票数1y (张)与售票时间x (小时)的正比例函数关系满足图1中的图象,每个无人售票窗口售出的车票数2y (张)与售票时间x (小时)的函数关系满足图2中的图象.(1)图2中图象的前半段(含端点)是以原点为顶点的抛物线的一部分,根据图中所给数据确定抛物线的表达式为_______,其中自变量x 的取值范围是________. (2)若当天共开放5个无人售票窗口,截至上午9点,两种窗口共售出的车票数不少于1 450张,则至少需要开放多少个普通售票窗口?(3)上午10点时,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同,试确定图2中图象的后半段一次函数的表达式.24. 定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”. 性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.理解:如图1,在ABC △中,CD 是AB 边上的中线,那么ACD △和BCD △是“友好三角形”,并且ACD BCD S S =△△.应用:如图2,在矩形ABCD 中,AB =4,BC =6,点E 在AD 上,点F 在BC 上,AE =BF ,AF 与BE 交于点O .(1)求证:AOB △和AOE △是“友好三角形”;(2)连接OD ,若AOE △和DOE △是“友好三角形”,求四边形CDOF 的面积. 探究:在ABC △中,30A ∠=°,AB =4,点D 在线段AB 上,连接CD ,ACD △和BCD△是“友好三角形”,将ACD △沿CD 所在直线翻折,得到A CD '△,若AC D '△与ABC △重合部分的面积等于ABC △面积的14,请直接..写出ABC △的面积.25.如图,在平面直角坐标系中,抛物线25y x bx c =++经过点A (32,0)和点B (1,),与x 轴的另一个交点为C .(1)求抛物线的函数表达式;(2)点D 在对称轴的右侧,x 轴上方的抛物线上,且BDA DAC ∠=∠,求点D 的坐标; (3)在(2)的条件下,连接BD ,交抛物线对称轴于点E ,连接AE . ①判断四边形OAEB 的形状,并说明理由;②点F 是OB 的中点,点M 是直线BD 上的一个动点,且点M 与点B 不重合,当BMF ∠=13MFO ∠时,请直接..写出线段BM 的长.参考答案 选择题 1.C 2.A 3.C 4.B 5.D 6.B 7.C 8.B 填空题 9. 23(1)a + 10.711.(3,-2) 12. a <4 13.314.15. 2222897273++= 16. 1,7 解答题17. 解:原式=2126122-⨯++= 18. (1)200;(2)a =35,126;(3)19. (1)证明:∵45AD BC BAD ∠=⊥,°, ∴45ABD BAD ∠=∠=°, ∴AD =BD.∵AD BC BE AC ⊥,⊥,∴90CAD ACD ∠+∠=°,90CBE ACD ∠+∠=°, ∴CAD CBE ∠=∠.又∵90CDA BDF ∠=∠=°, ∴ADC BDF △≌△, ∴AC =BF .∵AB =BC ,BE AC ⊥, ∴AE =EC ,即AC =2AE . ∴BF =2AE .(2)解:∵ADC BDF △≌△,∴DF =CD .∴在Rt CDF △中,CF ∵BE AC AE EC =⊥,, ∴AF =FC =2.∴AD =AF +DF 20. (1)13; (2)画树状(形)图得:由树状(形)图(或表格)可知,共有6种可能出现的结果,每种结果出现的可能性相同,其中两次抽取的卡片上的实数之差为有理数的结果有2种,分别为+6)和+6,),因此,两次抽取的卡片上的实数之差为有理数的概率为2163=. 21. 解:(1)过点A 作AP GF ⊥于P ,由题意得AP =BF =12,AB =PF =1.4,37GAP ∠=°. 在Rt PAG △中,tan GPPAG AP∠=,∴GP =AP ·tan37°≈12×0.75=9. ∴GF =GP +PF =9+1.4=10.4.答:风筝距地面的高度为10.4米. (2)由题意可知MN =5,MF =3,∴在Rt MNF △中,4NF =.∵10.4-5-1.65=3.75<4, ∴能触到挂在树上的风筝.22. (1)证明:过点A 作AF ON ⊥于F . ∵OM 是A ⊙的切线, ∴AB OM ⊥. ∵OC 平分∠MON , ∴AF =AB =2.∴ON 是A ⊙的切线.(2)解:∵60MON AB OM ∠=°,⊥, ∴30OEB ∠=°. ∵AF ON ⊥, ∴60FAE ∠=°.∴在Rt AEF △中,tan FEFAE AF∠=,∴tan 60EF AF ==°.∴21602ππ23603AEF ACF S S S AF EF AF =-=-=△阴影扇形. 23. 解:(1)260y x =,302x ≤≤;(2)上午9点180y =,260y =. 设需要开放x 个普通售票口.依题意得806051450x +⨯≥,解得3148x ≥. ∵x 为整数, ∴15x =.答:至少需要开放15个普通售票窗口.(3)解:设11y k x =,把(1,80)代入得80=1k ,∴180y x =,当2x =时,1160y =,上午10点21160y y ==.由(1)得当32x =时,2135y =. ∴图2中一次函数过点(32,135)、(2,160).设一次函数表达式为22y k x b =+,可得22313522160.k b k b ⎧+=⎪⎨⎪+=⎩,解得25060.k b =⎧⎨=⎩,∴一次函数的表达式为25060y x =+. 24. (1)证明:∵四边形ABCD 是矩形,∴AD BC ∥, ∴EAO BFO ∠=∠.又∵AOE FOB AE BF ∠=∠=,, ∴AOE FOB △≌△,∴EO =BO .∴AOE △与AOB △是“友好三角形”.(2)∵AOE △与DOE △是“友好三角形”, ∴AOE DOE S S =△△,132AE ED AD ===. ∵AOB △与AOE △是“友好三角形”, ∴AOB AOE S S =△△.∵AOE FOB △≌△,∴AOE FOB S S =△△.∴AOD ABF S S =△△. ∴1246243122ABF ABCD CDCF S S S =-=⨯-⨯⨯⨯=△矩形四边形. 探究:2或25. 解:(1)将3(0)2A ,、B (1,)代入25y x bx c =++得,9305425b c b c ⎧⨯++=⎪⎪⎨⎪++=⎪⎩,∴5b c ⎧=-⎪⎨=⎪⎩∴255y x =-+. (2)当BDA DAC ∠=∠时,BD x ∥轴.∵(1B ,∴当y =25x =-+, 解得1214x x ==,.∴(4D(3)①四边形OAEB是平行四边形.理由如下:抛物线的对称轴是52 x=.∴53122 BE=-=.∵3 (0) 2 A,,∴32 OA BE==.又∵BE OA∥,∴四边形OAEB是平行四边形.②12或52.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年沈阳市中等学校招生统一考试数 学 试 卷*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分)1.-13的相反数是( )A .13B .3C .-3D .-132.如图,在Rt △ABC 中,∠C =90°,AB =5,AC =2,则cos A 的值是( )A .215 B .25 C .212 D .523.沈阳市水质监测部门2006年全年共监测水量达48909.6万吨,水质达标率为100%.用科学记数法表示2006年全年共监测水量约为( )万吨(保留三个有效数字)A .4.89×104B .4.89×105C .4.90×104D .4.90×105 4.下列事件中是必然事件的是( )A .小婷上学一定坐公交车B .买一张电影票,座位号正好是偶数C .小红期末考试数学成绩一定得满分D .将豆油滴入水中,豆油会浮在水面上 5.如图,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F 两点, 若∠FEB =110°,则∠EFD 等于( )A .50°B .60°C .70°D .110° 6.依次连接菱形各边中点所得到的四边形是( ) A .梯形 B .菱形 C .矩形 D .正方形 7.反比例函数y =-4x的图象在( )A .第一、三象限B .第二、四象限C .第一、二象限D .第三、四象限8.将一张长与宽的比为2∶1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( )图① 图② 图③ 图④A .B .C .D .第2题图第5题图二、填空题(每小题3分,共24分)9.分解因式:325x x -= .10.已知一组数据1,a ,4,4,9,它的平均数是4,则a 等于 ,这组数据的众数是 .11.如图,AC 、BD 相交于点O ,∠A =∠D ,请你再补充一个条件,使得△AOB ≌ △DOC ,你补充的条件是 .12.如图,小鸣将测倾器安放在与旗杆AB 底部相距6m 的C 处,量出测倾器的高度CD =1m ,测得旗杆顶端B 的仰角α=60°,则旗杆AB 的高度为 .(计算结果保留根号)13.有一组数:1,2,5,10,17,26,……,请观察这组数的构成规律,用你发现的规律确定第8个数为 .14.如图,在正方形网格中,以点A 为旋转中心,将△ABC 按逆时针方向旋转90°,画出旋转后的△AB 1C 1.15.将抛物线22(1)3y x =+-向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为 .16.如图,△ABC 是边长为3的等边三角形,△BDC 是等腰三角形,且∠BDC =120°.以D 为顶点作一个60°角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,则△AMN 的周长为 .第14题图第16题图第11题图第12题图三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分) 17.计算:(π-3)0-|5-3|+(-13)-2-5.18.解不等式组⎩⎪⎨⎪⎧2x -5≤3(x -1)x +72>4x ,并把它的解集在数轴上表示出来.19.如图,已知在□ABCD 中,E 、F 是对角线BD 上的两点,BE =DF ,点G 、H 分别在BA 和DC 的延长线上,且AG =CH ,连接GE 、EH 、HF 、FG .求证:四边形GEHF 是平行四边形.20.甲、乙两个施工队共同完成某居民小区绿化改造工程,乙队先单独做2天后,再由两队合作10天就能完成全部工程.已知乙队单独完成此项工程所需天数是甲队单独完成此项工程所需天数的45,求甲、乙两个施工队单独完成此项工程各需多少天?第19题图四、(每小题10分,共20分)21.2006年沈阳市城市环境空气质量达到了有记录以来的最好水平,优良天气的天数在全国副省级以上城市排名第9,排名在北京、天津、重庆等城市之前.空气质量分为优良天气、轻度污染、中度污染、重度污染四种类型,有关部门将我市2001年——2006年前三类空气质量的天数制成条形统计图,请根据统计图解答下列问题:2001年——2006年沈阳市优良天气、轻度污染、中度污染天数统计图(1)根据图①中的统计图可知,和前一年比,年优良天气的天数增加最多,这一年优良天气的天数比前一年优良天气的天数的增长率约为;(精确到1%)(2)在图②中给出了我市2001年——2006年优良天气天数的扇形统计图中的部分数据,请你补全此统计图,并写出计算过程;(精确到1%)(3)根据这6年沈阳市城市空气质量的变化,谈谈你对我市环保的建议.2001年——2006年沈阳市优良天气天数统计图第21题图①第21题图②22.如图,已知A 、B 、C 、D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD 、AD .(1)求证:DB 平分∠ADC ;(2)若BE =3,ED =6,求AB 的长.五、(本题12分)23.如图所给的A 、B 、C 三个几何体中,按箭头所示的方向为它们的正面,设A 、B 、C 三个几何体的主视图分别是A 1、B 1、C 1;左视图分别是A 2、B 2、C 2;俯视图分别是A 3、B 3、C 3.(1)请你分别写出A 1、A 2、A 3、B 1、B 2、B 3、C 1、C 2、C 3图形的名称;(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A 1、A 2、A 3的三张卡片放在甲口袋中,画有B 1、B 2、B 3的三张卡片放在乙口袋中,画有C 1、C 2、C 3的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.① 通过补全下面的树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率; ② 小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜.这个游戏对双方公平吗?为什么?解:(1) A B C(2)①树状图:第22题图第23题图24.已知在矩形ABCD 中,AB =4,BC =252,O 为BC 上一点,BO =72,如图所示,以BC 所在直线为x 轴,O 为坐标原点建立平面直角坐标系,M 为线段OC 上的一点.(1)若点M 的坐标为(1,0),如图①,以OM 为一边作等腰△OMP ,使点P 在矩形ABCD 的一边上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P 的坐标;(2)若将(1)中的点M 的坐标改为(4,0),其它条件不变,如图②,那么符合条件的等腰三角形有几个?求出所有符合条件的点P 的坐标;(3)若将(1)中的点M 的坐标改为(5,0),其它条件不变,如图③,请直接写出符合条件的等腰三角形有几个.(不必求出点P 的坐标)第24题图25.化工商店销售某种新型化工原料,其市场指导价是每千克160元(化工商店的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.(1)为了扩大销售量,化工商店决定适当调整价格,调整后的价格按八折销售,仍可获得实际售价的20%的利润.求化工商店调整价格后的标价是多少元?打折后的实际售价是多少元?(2)化工商店为了解这种原料的月销售量y(千克)与实际售价x(元/千克)之间的关系,每个月调整一次实际售价,试销一段时间后,部门负责人把试销情况列成下表:实际售价x(元/千克)…150 160 168 180 …月销售量y(千克)…500 480 464 440 …①请你在所给的平面直角坐标系中,以实际售价x(元/千克)为横坐标,月销售量y (千克)为纵坐标描出各点,观察这些点的发展趋势,猜想y与x之间可能存在怎样的函数关系;②请你用所学过的函数知识确定一个满足这些数据的y与x之间的函数表达式,并验证你在①中的猜想;③若化工商店某月按同一实际售价共卖出这种原料450千克,请你求出化工商店这个月销售这种原料的利润是多少元?第25题图26.已知抛物线y =ax 2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C ,其中点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,线段OB 、OC 的长(OB <OC )是方程x 2-10x +16=0的两个根,且抛物线的对称轴是直线x =-2.(1)求A 、B 、C 三点的坐标; (2)求此抛物线的表达式;(3)连接AC 、BC ,若点E 是线段AB 上的一个动点(与点A 、点B 不重合),过点E 作EF ∥AC 交BC 于点F ,连接CE ,设AE 的长为m ,△CEF 的面积为S ,求S 与m 之间的函数关系式,并写出自变量m 的取值范围;(4)在(3)的基础上试说明S 是否存在最大值,若存在,请求出S 的最大值,并求出此时点E 的坐标,判断此时△BCE 的形状;若不存在,请说明理由.2007年沈阳市中等学校招生统一考试数学试题参考答案及评分标准一、选择题(每小题3分,共24分)1.A 2.B 3.A 4.D 5.C 6.C 7.B 8.A 二、填空题(每小题3分,共24分)9.x (x +5)(x -5) 10.2,4 11.AO =DO 或AB =DC 或BO =CO 12.(63+1)m 13.50 14.如图15.y =2x 2 16.6第14题图第26题图三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分)17.解:原式=1-3+5+9-5 …………………………………………………4分=7 ……………………………………………………………………6分18.解:解不等式2x -5≤3(x -1)得x ≥-2 ……………………………………2分 解不等式x +72>4x 得x <1 ……………………………………………………………4分∴不等式组的解集为-2≤x <1 ……………………………………………………6分 在数轴上表示为:………………………………………………8分19.证明:∵四边形ABCD 是平行四边形 ∴AB =CD ,AB ∥CD∴∠GBE =∠HDF …………………………………………………………………2分 又∵AG =CH ∴BG =DH 又∵BE =DF∴△GBE ≌△HDF …………………………………………………………………5分 ∴GE =HF ,∠GEB =∠HFD ∴∠GEF =∠HFE ∴GE ∥HF∴四边形GEHF 是平行四边形. ……………………………………………………8分 20.解:设甲施工队单独完成此项工程需x 天,则乙施工队单独完成此项工程需45x 天, …………………………………………1分根据题意,得10x +1245x =1 …………………………………………………………4分 解这个方程,得x =25 ………………………………………………………………6分 经检验,x =25是所列方程的根 ……………………………………………………7分 当x =25时,45x =20 …………………………………………………………………9分答:甲、乙两个施工队单独完成此项工程分别需25天和20天. ……………10分 四.(每小题10分,共20分)21.解:(1)2003,45% ……………………………………………………………4分(2)由图①,得162+204+295+301+317+321=1600301÷1600≈0.19=19%321÷1600≈0.20=20% …………………7分 ∴2004年19%,2006年20%正确补全统计图. ………………………8分 (3)建议积极向上即可. ………………10分 22.(1)证明:∵ AB =BCAB BC ∴= ………………………………2分∴∠BDC =∠ADB ,∴DB 平分∠ADC ……………………………………………4分 (2)解:由(1)可知AB BC =,∴∠BAC =∠ADB ∵∠ABE =∠ABD∴△ABE ∽△DBA ……………………………………………………………………6分 ∴AB BE =BDAB∵BE =3,ED =6∴BD =9 ……………………………………………………………………………8分 ∴AB 2=BE ·BD =3×9=27∴AB =33 …………………………………………………………………………10分 五、(本题12分)23.解:(1)由已知可得A 1、A 2是矩形,A 3是圆;B 1、B 2、B 3都是矩形;C 1是三角形,C 2、C 3是矩形. ………………………………………………………3分 (2)①补全树状图如下:……………………………………………………………………………………………7分 由树状图可知,共有27种等可能结果,其中三张卡片上的图形名称都相同的结果有12种,∴三张卡片上的图形名称都相同的概率是1227=49 …………9分②游戏对双方不公平.由①可知,三张卡片中只有两张卡片上的图形 名称相同的概率是1227=49,即P (小刚获胜)=49三张卡片上的图形名称完全不同的概率是327=19,即P (小亮获胜)=19∵49>19 ∴这个游戏对双方不公平. ……………………………………………12分 六、(本题12分)24.解:(1)符合条件的等腰△OMP 只有1个.点P 的坐标为(12,4) ……2分 (2)符合条件的等腰△OMP 有4个. …………………………………………3分 如图①,在△OP 1M 中,OP 1=OM =4,在Rt △OBP 1中,BO =72, BP 1=OP 21-OB 2=42-(72)2=152 ∴P 1(-72,152) ……………………………………………………………………5分 在Rt △OMP 2中,OP 2=OM =4,∴P 2(0,4)在△OMP 3中,MP 3=OP 3,∴点P 3在OM 的垂直平分线上,∵OM =4,∴P 3(2,4)在Rt △OMP 4中,OM =MP 4=4,∴P 4(4,4) …………………………………9分(3)若M (5,0),则符合条件的等腰三角形有7个. …………………………12分 点P 的位置如图②所示七、(本题12分)25.解:(1)依题意,每千克原料的进货价为160×75%=120(元) ……………2分 设化工商店调整价格后的标价为x 元,则 0.8x -120=0.8x ×20% 解得 x =187.5187.5×0.8=150(元) ………………………………………………………………4分 ∴调整价格后的标价是187.5元,打折后的实际售价是150元 .…………………5分(2)①描点画图,观察图象,可知这些点的发展趋势近似是一条直线, 所以猜想y 与x 之间存在着一次函数关系.………………………………………………………………………………………7分 ②根据①中的猜想,设y 与x 之间的函数表达式为y =kx +b ,将点(150,500)和(160,480)代入表达式,得⎩⎪⎨⎪⎧ 500=150k +b 480=160k +b 解得⎩⎪⎨⎪⎧k =-2b =800 ∴y 与x 的函数表达式为y =-2x +800 ……………………………………………9分 将点(168,464)和(180,440)代入y =-2x +800均成立,即这些点都符合y =-2x +800的发展趋势.∴①中猜想y 与x 之间存在着一次函数关系是正确的. …………………………10分 ③设化工商店这个月销售这种原料的利润为w 元,当y =450时,x =175∴w =(175-120)×450=24750(元)答:化工商店这个月销售这种原料的利润为24750元. …………………………12分八、(本题14分)26.解:(1)解方程x 2-10x +16=0得x 1=2,x 2=8 ………………………………1分 ∵点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,且OB <OC∴点B 的坐标为(2,0),点C 的坐标为(0,8)又∵抛物线y =ax 2+bx +c 的对称轴是直线x =-2∴由抛物线的对称性可得点A 的坐标为(-6,0) …………………………………4分(2)∵点C (0,8)在抛物线y =ax 2+bx +c 的图象上∴c =8,将A (-6,0)、B (2,0)代入表达式,得⎩⎪⎨⎪⎧ 0=36a -6b +80=4a +2b +8 解得⎩⎨⎧ a =-23b =-83∴所求抛物线的表达式为y =-23x 2-83x +8 ………………………………………7分 (3)依题意,AE =m ,则BE =8-m ,∵OA =6,OC =8,∴AC =10∵EF ∥AC ∴△BEF ∽△BAC∴EF AC =BE AB 即EF 10=8-m 8∴EF =40-5m 4过点F 作FG ⊥AB ,垂足为G ,则sin ∠FEG =sin ∠CAB =45∴FG EF =45 ∴FG =45·40-5m 4=8-m ∴S =S △BCE -S △BFE =12(8-m )×8-12(8-m )(8-m )=12(8-m )(8-8+m )=12(8-m )m =-12m 2+4m ……………………………10分 自变量m 的取值范围是0<m <8 …………………………………………………11分(4)存在.理由:∵S =-12m 2+4m =-12(m -4)2+8 且-12<0, ∴当m =4时,S 有最大值,S 最大值=8 ……………………………………………12分 ∵m =4,∴点E 的坐标为(-2,0)∴△BCE 为等腰三角形. …………………………………………………………14分(以上答案仅供参考,如有其它做法,可参照给分)第26题图(批卷教师用图)。
