高一第一学期必修2第一章单元卷1
天天练 人教版(2019)高一必修1 第1、2章 单元测试卷

天天练 人教版(2019)高一必修1 第1、2章 单元测试卷一、单选题1. 下列哪一项不是细胞学说的主要内容A.细胞是生物体结构和功能的基本单位B.一切动物和植物都是由细胞构成的C.病毒没有细胞结构,但也属于生物D.细胞只能来自细胞分裂2. 下列有关生命形式的叙述,正确的是A.细胞学说阐明了一切动植物以细胞为基本单位B.真核生物细胞和原核细胞都具有细胞膜、细胞质和细胞核这说明了细胞结构具有统一性C.乳酸菌细胞的染色体主要由DNA和蛋白质组成D.噬菌体能合成自身的蛋白质3. 从生命系统的结构层次角度分析,下列哪项与其它三项存在明显不同( )A.变形虫B.一池塘C.一片森林D.生物圈4.下图是用显微镜观察植物细胞的叶绿体实验中的两个视野,要把视野中的物像从甲图转为乙图,下列操作步骤正确的排序是①转动细准焦螺旋②转动粗准焦螺旋③移动装片④调节光圈(或转换反光镜)⑤转动转换器A.③一⑤一②一①B.①一③一②一⑤C.③一⑤-④一①D.③一①一④一③5. 下列生物中属于原核生物的一组是A.黑藻B.草履虫C.发菜D.蘑菇6. 下列有关组成细胞的化学元素的叙述,正确的是A.组成细胞最基本的元素是氮B.活细胞内含量最多的元素是氧C.Mg、Zn、Ca等大量元素是生物体必不可少的D.微量元素对于生物体来说可有可无7. 下列关于有机物的鉴定实验中,易导致实验失败的操作是①蛋白质鉴定时,将NaOH溶液和CuSO4溶液混合后再加入样液②还原糖鉴定时,需要进行水浴加热③脂肪鉴定时,实验材料选用花生油,染色剂选用苏丹Ⅳ ④脂肪鉴定过程中,对装片染色后需用清水漂洗后放在显微镜下镜检A.①④B.①③C.②③D.③④8.下列有关细胞中元素和化合物的叙述,正确的是()A.用苏丹Ⅲ染液对脂肪组织进行染色时,可用无水酒精冲洗浮色B.脂肪分子中含H比糖类多,是主要的能源物质C.氨基酸脱水缩合产生水,水中的氧来自氨基酸的羧基D.DNA和RNA主要组成元素的种类不同,碱基种类不完全相同9. 下列能与斐林试剂反应生成砖红色沉淀的是①果糖②乳糖③蔗糖④纤维素⑤淀粉⑥脂肪A.①②B.②③④C.①⑤⑥D.①②④10. 某一物质分子式为C55 H70 O19 N10 S2,这种物质最有可能是 ( )A.糖类B.脂质C.核酸D.蛋白质11. 下列关于脂质的叙述,正确的是()A.脂质中的磷脂是细胞膜的组成成分B.维生素D和性激素不属于固醇类物质C.脂肪比相同质量的多糖彻底氧化产能少D.脂质在核糖体、内质网和高尔基体上合成12. 下列哪组糖类物质能与①~③中的叙述依次对应①存在于RNA中而不存在于DNA中的糖类②存在于植物细胞中而不存在于动物细胞中的二糖③存在于动物细胞中而不存在于植物细胞中的多糖A.核糖、麦芽糖、乳糖B.脱氧核糖、乳糖、乳糖C.核糖、蔗糖、糖原D.脱氧核糖、麦芽糖、糖原13.水是生命之源,下列有关水的叙述,正确的是()A.结合水一般不参与代谢,它使各种组织器官有一定形状、硬度B.水在细胞内的存在状态有自由水和结合水两种,生命活动越旺盛,结合水的含量就越高C.夏季,人在高温作业或剧烈活动后要喝淡盐水是为了补充水分及降温D.冬天针叶树体内结合水的含量会减少14. 蚕丝和棉花都是纺织业的重要原料,它们的成分分别属于A.糖类、糖类B.蛋白质、蛋白质C.蛋白质、糖类D.糖类、蛋白质15. 下列有关蛋白质结构和功能的叙述中,正确的是A.催产素和血管舒张素均为九肽,但它们的功能差异很大,完全取决于构成两者的氨基酸种类B.由三个不同种类的氨基酸构成的三肽最多有27种C.鸡蛋煮熟后,蛋白质变性失活,但并未引起蛋白质分子中肽键的断裂D.肽键中元素组成的不同也是影响蛋白质结构多样性的原因16. 下列叙述中,错误的是A.多聚体水解后的产物是它的单体B.脂肪彻底氧化分解后的产物是CO2和H2O,所以CO2和H2O是脂肪的单体C.淀粉和纤维素的单体都是单糖D.DNA和RNA单体的分子组成不同17. 下列叙述中,是淀粉、纤维素和糖原的共同特征的是()A.都是细胞内储存能量的主要物质B.都含有C、H、O、N C.都是还原糖D.基本组成单位都是葡萄糖18. 核酸是细胞内携带遗传信息的物质,以下关于DNA与RNA特点的比较,正确的是()A.在细胞内存在的主要部位相同B.构成的五碳糖不同C.核苷酸之间的连接方式不同D.构成的碱基相同19. 下列各项对组成细胞有机物的描述,正确的是()A.细胞质中不含有脱氧核糖核酸B.组成淀粉、糖原、纤维素的单体都是葡萄糖C.多肽链在核糖体上一旦形成便具有生物活性D.质量相同的糖、脂肪氧化分解所释放的能量是相同的20. 下列关于胆固醇的叙述,错误的是A.胆固醇在动物内脏、蛋黄等食物中含量丰富B.只要不摄入胆固醇,体内就不会有胆固醇C.胆固醇是构成动物细胞膜的重要成分D.老年人的血管内壁上容易沉积胆固醇21. 下列关于淀粉、脂肪、蛋白质和核酸4 种生物分子的叙述,正确的是()A.都能被相应的酶水解B.都是水溶性物质C.都含 C、H、O、N 这4 种元素D.都是人体细胞中的能源物质22. 下列有关DNA和RNA的叙述,正确的是A.真核细胞中的DNA全部存在于细胞核中,RNA全部存在于细胞质中B.DNA与RNA的碱基完全不同C.DNA通常由两条链构成,RNA通常由一条链构成D.DNA和RNA都可以为生命活动提供能量23. 2008年8月底,在市场上出售的某些品牌的婴幼儿配方奶粉及液态奶中被检测出三聚氰胺,这是一些不法商家为了提高奶粉及液态奶中的含氮量而添加的。
高一北师大版数学必修2第一章 立体几何初步单元测试题试卷含答案解析

第二章测试时间120分钟 满分150分一、选择题(本大题共10小题,每小题5分,共50分.在下列四个选项中,只有一项是符合题意的)1.已知点P (-3,1),点Q 在y 轴上,且直线PQ 的倾斜角为120° ,则Q 点的坐标为( )A .(0,2)B .(0,-2)C .(2,0)D .(-2,0)解析 设Q (0,y ),由k =y -13=-3,得y =-2.答案 B2.已知两条直线y =ax -2和y =(a +2)x +1互相垂直,则a 等于( )A .2B .1C .0D .-1解析 由题意,得a (a +2)=-1,得a =-1. 答案 D3.已知过点A (-2,m )和B (m,4)的直线与直线2x +y -1=0平行,则m 的值为( )A .0B .-8C .2D .10解析 由4-mm +2=-2,得m =-8.答案 B4.若点A 是点B (1,2,3)关于x 轴对称的点,点C 是点D (2,-2,5)关于y 轴对称的点,则|AC |=( )A .5 B.13 C .10D.10解析 A (1,-2,-3),C (-2,-2,-5)代两点间距离公式即可.答案 B5.直线y +4=0与圆x 2+y 2-4x +2y -4=0的位置关系是( ) A .相切B .相交,但直线不经过圆心C .相离D .相交且直线经过圆心 答案 A6.已知M (-2,0),N (2,0),则以MN 为斜边的直角三角形直角顶点P 的轨迹方程是( )A .x 2+y 2=4(x ≠±2)B .x 2+y 2=4C .x 2+y 2=2(x ≠±2)D .x 2+y 2=2解析 由题可知,点P 的轨迹是以MN 为直径的圆(除去M 、N 两点),∴点P 的轨迹方程是x 2+y 2=4(x ≠±2).答案 A7.若直线3x +2y -2m -1=0与直线2x +4y -m =0的交点在第四象限,则实数m 的取值范围是( )A .(-∞,-2)B .(-2,+∞)C.⎝⎛⎭⎪⎫-∞,-23D.⎝⎛⎭⎪⎫-23,+∞解析 由⎩⎪⎨⎪⎧3x +2y -2m -1=0,2x +4y -m =0,得⎩⎨⎧x =3m +24,y =-m -28.由题意,得⎩⎨⎧3m +24>0,-m +28<0,得m >-23.答案 D8.已知圆C 的方程为x 2+y 2-4x =0,若圆C 被直线l :x +y +a =0截得的弦长为23,则a =( )A .2+ 2 B.2 C .2± 2D .-2±2解析 由弦长公式,得3=4-⎝ ⎛⎭⎪⎪⎫2+a 12+122, 得a =-2± 2. 答案 D9.将直线2x -y +λ=0沿x 轴向左平移1个单位,所得直线与x 2+y 2+2x -4y =0相切,则实数λ的值为( )A .-3或7B .-2或8C .0或10D .1或11解析 将直线平移后得到y =2(x +1)+λ=2x +2+λ, 由题可知,|-2-2+2+λ|22+(-1)2=5, 得λ=-3,或λ=7,故选A. 答案 A10.若圆x 2+y 2-2x -4y =0的圆心到直线x -y +a =0的距离为22,则a 的值为( )A .-2或2 B.12或32 C .2或0D .-2或0解析 圆的圆心(1,2),∴d =|1-2+a |2=22,得a =0,或a =2.答案 C二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中横线上)11.当a 为任意实数时,直线ax -y +1-3a =0恒过定点________. 解析 原方程可化为a (x -3)-(y -1)=0,∴直线l 过(3,1). 答案 (3,1)12.直线x -2y +5=0与圆x 2+y 2=8相交于A ,B 两点,则|AB |=________.解析 圆心到该直线的距离d =55=5,∴弦长=2(22)2-(5)2=2 3. 答案 2313.两圆相交于两点(1,3)和(m ,-1),两圆圆心都在直线x -y +c =0上,且m 、c 均为实数,则m +c =________.解析 根据两圆相交的性质可知,两点(1,3)和(m ,-1)的中点⎝ ⎛⎭⎪⎫1+m 2,1在直线x -y +c =0上,并且过两点的直线与x -y +c =0垂直,故有⎩⎨⎧1+m2-1+c =0,3-(-1)1-m ×1=-1,∴m =5,c =-2,∴m +c =3. 答案 314.若不同两点P ,Q 的坐标分别为(a ,b ),(3-b,3-a ),则线段PQ 的垂直平分线l 的斜率为________;圆(x -2)2+(y -3)2=1关于直线l 对称的圆的方程为________.解析 ∵k PQ =3-a -b3-b -a =1,又k l ·k PQ =-1∴k l =-1,又(2,3)关于l 的对称点为(0,1), 故所求的圆的方程为x 2+(y -1)2=1. 答案 -1 x 2+(y -1)2=115.过圆x 2+y 2-x +y -2=0与x 2+y 2=5的交点,且圆心在直线3x -4y -1=0上的圆的方程为________.解析 设所求的圆的方程为x 2+y 2-x +y -2+ λ(x 2+y 2-5)=0,即(1+λ)x 2+(1+λ)y 2-x +y -2-5λ=0.∴圆心为⎝ ⎛⎭⎪⎫12(1+λ),-12(1+λ). 由32(1+λ)-42(1+λ)-1=0,得λ=-32 故所求的圆的方程为(x +1)2+(y -1)2=13. 答案 (x +1)2+(y -1)2=13三、解答题(本大题共有6小题,共75分.解答时应写出必要的文字说明,证明过程或演算步骤)16.(12分)已知两条直线l 1:mx +8y +n =0和l 2:2x +my -1=0.试确定m ,n 的值,使(1)l 1和l 2相交于点(m ,-1);(2)l 1∥l 2;(3)l 1⊥l 2,且l 1在y 轴上的截距为-1. 解 (1)∵m 2-8+n =0,且2m -m -1=0, ∴m =1,n =7.(2)由m ·m -8×2=0,得m =±4, 由8×(-1)-n ·m ≠0,得n ≠±2,即m =4,n ≠-2时,或m =-4,n ≠2时,l 1∥l 2. (3)当且仅当m ·2+8·m =0,即m =0时,l 1⊥l 2,又-n8=-1,∴n =8. 即m =0,n =8时,l 1⊥l 2,且l 1在y 轴上的截距为-1.17.(12分)△ABC 中,顶点A 的坐标为(1,2),高BE ,CF 所在直线的方程分别为2x -3y +1=0,x +y =0,求这个三角形三条边所在直线的方程.解 由已知,直线AC 的斜率为-32, 直线AB 的斜率为1.∴直线AC 的方程为3x +2y -7=0, 直线AB 的方程为x -y +1=0.再由⎩⎪⎨⎪⎧x +y =0,3x +2y -7=0,可解得C 点坐标为(7,-7).由⎩⎪⎨⎪⎧2x -3y +1=0,x -y +1=0,可解得B 点坐标为(-2,-1) . 于是直线BC 的方程为2x +3y +7=0.18.(12分)已知圆x 2+y 2-12x =0的圆心为Q ,过点P (0,2)且斜率为k 的直线与圆Q 相交于不同两点A ,B ,求实数k 的取值范围.解 x 2+y 2-12x =0可化为(x -6)2+y 2=36,又直线过点P (0,2),斜率为k ,故l 的方程为y =kx +2,即kx -y +2=0,由题意,得|6k +2|k 2+1<6,得k <43.∴k 的取值范围是⎝⎛⎭⎪⎫-∞,43.19.(13分)已知P (1,2)为圆x 2+y 2=9内一定点,过P 点任作直线,与圆相交,求弦的中点的轨迹方程.解 设过P 点的直线与圆相交于A ,B 两点,C 为AB 的中点,设C (x ,y ),由题意,得当P 与C 不重合时,△OPC 为直角三角形,∴C 点在以OP 为直径的圆上,又OP 的中点⎝ ⎛⎭⎪⎫12,1,|OP |=12+22=5,∴点C 的轨迹方程为⎝ ⎛⎭⎪⎫x -122+(y -1)2=54(除去P 点).又当x =1,y =2时上式仍成立,∴点C 的轨迹方程为⎝ ⎛⎭⎪⎫x -122+(y -1)2=54.20.(13分)已知方程x 2+y 2-2x -4y +m =0. (1)若此方程表示圆,求m 的取值范围;(2)若(1)中的圆与直线x +2y -4=0相交于M ,N 两点,且OM ⊥ON (O 为坐标原点),求m ;(3)在(2)的条件下,求以MN 为直径的圆的方程. 解 (1)原方程化为(x -1)2+(y -2)2=5-m . ∵此方程表示圆, ∴5-m >0. ∴m <5.(2)设M (x 1,y 1),N (x 2,y 2), 则x 1=4-2y 1,x 2=4-2y 2, 得x 1x 2=16-8(y 1+y 2)+4y 1y 2. ∵OM ⊥ON , ∴x 1x 2+y 1y 2=0.∴16-8(y 1+y 2)+5y 1y 2=0.①由⎩⎪⎨⎪⎧x =4-2y ,x 2+y 2-2x -4y +m =0,得 5y 2-16y +m +8=0. ∴y 1+y 2=165,y 1y 2=8+m 5. 代入①得m =85.(3)以MN 为直径的圆的方程为 (x -x 1)(x -x 2)+(y -y 1)(y -y 2)=0, 即x 2+y 2-(x 1+x 2)x -(y 1+y 2)y =0.∴所求圆的方程为x 2+y 2-85x -165y =0.21.(13分)已知圆C :x 2+y 2+2x -4y +1=0,O 为坐标原点,动点P 在圆外,过点P 作圆C 的切线,设切点为M .(1)若点P 运动到(1,3)处,求此时切线l 的方程; (2)求满足|PM |=|PO |的点P 的轨迹方程.解 (1)把圆C 的方程化为标准方程为(x +1)2+(y -2)2=4,∴圆心为(-1,2),半径为2.①当l 的斜率不存在时,l 的方程为x =1满足条件.②当l 的斜率存在时,设斜率为k ,则l :y -3=k (x -1),即kx -y +3-k =0.由题意,得|-k -2+3-k |1+k 2=2,得k =-34. ∴l 的方程为3x +4y -15=0.综上得,满足条件的切线l 的方程为x =1,或3x +4y -15=0. (2)设P (x ,y ),∵|PM |=|PO |, ∴(x +1)2+(y -2)2-4=x 2+y 2. 整理得2x -4y +1=0.即点P 的轨迹方程为2x -4y +1=0.。
人教版生物必修一第一二章单元测试题及答案

高一生物必修一第一、二章单元测试题第一部分选择题(共30小题每小题2分共60分)(每小题只有一个正确答案,多答、不答、不在答题页作答均不给分,请在答题页作答)1、生物体结构和功能的基本单位是()A、组织B、细胞C、器官D、生命2、下列具细胞结构的生物是()A、大肠杆菌B、酵母菌C、噬菌体D、烟草花叶病毒3、艾滋病(AIDS )是由下列哪个系统的细胞被感染引起的()A、中枢神经系统B、淋巴系统C、呼吸系统D、运动系统4、下列生物属于单细胞个体的是()A、小白菜B、草履虫C、人D、SARS病毒5、下列对生命系统结构层次的研究的正确顺序是()A、细胞-组织-器官-系统-生物体-种群-群落-生物圈-生态系统B、细胞-组织-器官-生物体-系统-种群-群落-生物圈-生态系统C、细胞-组织-器官-系统-生物体-种群-群落-生态系统-生物圈D、细胞-组织-器官-系统-种群-生物体-群落-生态系统-生物圈6、下列是活细胞的是()A、口腔上皮细胞B、角质化的指甲C、性激素D、抗体7、在低倍显微镜下看到的物像不在视野中央,而在左上角,该怎样移动装片()A、向左上角移B、向右上角移C、向左下角移D、向右下角移8、由低倍转为高倍后,只可调节的是()A、细准焦螺旋B、粗准焦螺旋C、临时装片D、上升镜筒9、真核细胞与原核细胞的根本区别是()A、有无核膜B、有无细胞壁C、大小D、新陈代谢类型10、下列生物属于原核生物的是()A、乙肝病毒B、酵母菌C、疟原虫D、放线菌11、下列每组生物都属于真核生物的一组是()A、沙眼衣原体、大肠杆菌B、蓝藻和酵母菌C、草履虫和变形虫D、支原体、放线菌12、属于自养生物的是()A、蘑菇B、大肠杆菌噬菌体C、发菜D、猪肉涤虫13、细胞学说的建立者主要是()A、达尔文与孟德尔B、爱因斯坦C、施莱登和施旺D、摩尔根14、不属于细胞学说的主要内容的是()A、一切动植物都由细胞发育而来,并由细胞及其代谢产物所构成B、细胞是一个相对独立的单位,是具有生命体的有机体C、细胞是一切生物结构和功能的基本单位D、新细胞可以从老细胞中产生15、下列属于大量元素的一组是()A、Ca、C、O、MnB、H、O、K、ClC、P、N、C、MoD、N、S、O、Mg16、组成人体细胞的主要元素中占细胞鲜重重百分比最多的是()A、氧兀素B、氢兀素C、碳兀素D、硅兀素17、检测细胞中蛋白质所试剂是()A、苏丹IVB、斐林试剂C、碘液D、双缩月尿试剂18、斐林试剂鉴定还原性糖时最终出现的现象是()A、紫色B、红色C、蓝色D、醇红色沉淀19、组成胰岛素的单体是()A、葡萄糖B、核甘酸C、磷脂D、氨基酸20、以下不是氨基酸的是()COOH|A、NH2—CH2—COOHB、H2N—CH—C—OH||OOH H NH 2| | |C、HOOC—CH—N—HD、H—C—O—OH|CH321 、判断以下结构式里没有肽键的是()A、NH2—CH2—CO—NH—CH2—COOHB、HOOC—CH2—C—O—NH—COOHO H C6H5 H O|| | | | ||C、NH2—CH2—C—N—C(CH3)2—COOHD、NH2—CH—C—N—CH2—C—OH||O22、在人体细胞中除了细胞核外,以下哪些结构里还含有DNA ()A、线粒体B、叶绿体C、细胞质D、液泡23、脱氧核苷酸单体缩合成的多聚体是()A、DNAB、RNAC、核酸D、碱基24、细胞内组成RNA 的五碳糖是()A、核糖B、葡萄糖C、脱氧核糖D、麦芽糖25、斐林试剂与下列糖类水浴加热出现砖红色沉淀的是()A、果糖B、蔗糖C、淀粉D、纤维素26、构成膜系结构的重要成分的一组是()A、脂肪和固醇B、V D和磷脂C、蛋白质和胆固醇D、磷脂和胆固醇27、下列属于固醇类的物质是()A、淀粉酶B、性激素C、木纤维D、生长素28、“朴雪”乳酸亚铁口服液可以有效地治疗人类缺铁性贫血症,这是因为其中的Fe2+进入人体后能()A、调节血液的酸碱平衡B、构成红细胞中的血红蛋白C、调节血液渗透压D、促进更多红细胞的产生29、菜农种植青菜的土地里缺了Ca2+,会造成青菜()A、变黄B、烂心C、没反应D、干枯了30、夏季酷暑时分,在室外作业的人们应多饮()A、纯净水B、盐汽水C、牛奶D、果汁第二部分 非选择题(共12小题 每空1分 (请把正确答案答在答题页,不在答题页作答不给分)31、一片森林中的校树苗、小校树、大楼树组成了一个 ; 一定区域内的动物、植物和 微生物等全部生物构成了 32、要水解一个由3条肽链构成,100个氨基酸组成的蛋白质大分子,需有 个水分子参加 反应,被打断了 个肽键;如果氨基酸的平均相对分子质量为 128,那么,此蛋白质分子的相对分子质量为33、写出以下符号或结构所代表的名称:34、下图为某生物的细胞结构模式图,据图回答: (1)下图为 类细胞,判断的理由是 (2)该细胞与植物细胞共有的结构有 ;(3)该细胞的遗传物质储存于 中,和该生物的运动有关的结构是 。
高中政治同步练习 必修2 第1单元检测卷1含答案

第一单元检测卷(A)一、选择题(每小题3分,共60分)1.生产资料的所有制形式即劳动资料和劳动对象归谁所有。
生产资料所有制()①是生产关系的核心②是由社会的基本性质决定的③是经济制度的基础④决定生产力发展A.①④B.②④C.①③D.②③2.(2021·安徽池州期末检测)进入新时代,我们要进一步巩固和发展公有制经济,充分发挥其经济社会发展“压舱石”和“稳定器”作用。
公有制经济之所以能成为经济社会发展的“压舱石”和“稳定器”,是因为公有制是()①社会主义经济制度的基础②中国特色社会主义制度的重要支柱③中国共产党执政兴国的重要支柱和依靠力量④国家对社会生产和经济发展进行宏观调控的制度基础A.①②B.②③C.①④D.③④3.目前中央企业超八成集中在石油石化、电力、国防、通信、运输、矿业、冶金、机械行业,承担着我国几乎全部的原油、天然气和乙烯生产,提供了全部的基础电信服务和大部分增值服务。
中央企业这样做的目的是()A.提高国有经济在社会总资产中的比重B.增强公有制经济对国民经济命脉的控制作用C.发挥国有经济在国民经济中的主导作用D.坚持公有制为主体、多种所有制经济共同发展4.(2021·山东德州期末检测)在社会实践活动中,德州市某高级中学(5)班同学们分组调研了学校附近的中国建设银行、德百集团、中国电信、陕西面馆、刘氏眼镜的生产经营情况。
同学们的调研对象() ①都关系民生,是国民经济命脉部门②都应当守法经营,讲求社会效益③都以营利为目的,向社会提供商品或服务④都属于企业,在所有制中处于主体地位A.①③B.①④C.②③D.②④5.(2021·山东德州期末检测)作为积极稳妥推进混改的重要抓手和渠道,中国诚通国有企业混改基金聚焦核心领域和关键技术的混合所有制改革,重点布局国家战略领域、竞争性领域、科技创新领域和产业链关键领域。
这一做法()①致力于国有经济布局优化,持续提升国有资本运营效率②是为了调动国内外各种资本的积极性、主动性和创造性③将导致国有资产的总量减少,非公有资产的总量增加④有利于增强国有经济竞争力、创新力、控制力、影响力、抗风险能力A.①②B.①④C.②③D.③④6.(2021·山东枣庄期末检测)为了探索与现代生产力水平相适应的农村集体经济经营方式,枣庄市某村不断推进经营方式改革。
高一化学必修2第一章单元测试试卷 (含答案)

高一化学必修2第一章单元测试试卷2009 年3月3日可能用到的相对原子质量:H:1 Mg:24 C:12 O:16 S:32 Cl:35.5 Br:80 Na:23 Al:27 K:39 Fe:56 Cu:64 Ag:108一、单选题(本题包括12小题,每小题2分,24分)1、19世纪中叶,门捷列夫的突出贡献是()A.提出原子学说 B.发现元素周期律C.提出分子学说 D.发现氧气2、下列各微粒中,核外电子总数相等的是()A.K+和Na+ B.CO2和NO2C.CO和CO2D.N2和CO3、下列递变规律不正确的是()A.Na、Mg、Al还原性依次减弱 B.I2、Br2、Cl2氧化性依次增强C.C、N、O原子半径依次增大 D.P、S、Cl最高正价依次升高4、核外电子层结构相同的一组微粒是()A.Mg2+、Al3+、Cl-、NeB.Na+、F-、S2-、ArC.K+、Ca2+、S2-、ArD.Mg2+、Na+、Cl-、S2-5、下列粒子的结构示意图正确的是()6、能说明A元素非金属性比B元素非金属性强的是()A.A原子得到电子的数目比B原子少B .A 元素的最高正价比B 元素的最高正价要高C .气态氢化物溶于水后的酸性:A 比B 强 D . A 单质能与B 的氢化物水溶液反应,生成B 单质7 、 A 、B 、C 、D 、E 是同一周期的五种主族元素,A 和B 的最高价氧化物对应的水化物均呈碱性,且碱性B >A ,C 和D 的气态氢化物的稳定性C >D ;E 是这五种元素中原子半径最小的元素,则它们的原子序数由小到大的顺序是( )A.A 、B 、C 、D 、EB.E 、C 、D 、B 、AC.B 、A 、D 、C 、ED.C 、D 、A 、B 、E8、已知短周期元素的离子+2A a 、+B b 、-3C c 、-D d 都具有相同的电子层结构,则下列叙述正确的是( )A .原子半径A >B >D >C B .原子序数d >c >b >aC .离子半径C >D >B >A D .单质的还原性A >B >D >C9、钛(Ti )金属常被称为未来钢铁。
高中生物必修2第一章遗传因子的发现单元测试

高中生物必修2第一章遗传因子的发现单元测试第I卷(选择题)一、单选题1.(2020秋·云南保山·高一校考期中)下列属于相对性状的是()A.狗的短毛和狗的卷毛B.羊的黑毛和兔的白毛C.牛的棕毛和牛的黑毛D.豌豆子叶的黄色和种子的圆滑2.(2022春·陕西宝鸡·高一统考期末)两种纯合豌豆杂交,F1全部为黄色圆粒,那么F2中重组类型所占比例为5/8,则亲本的表现型组合为()A.黄皱×绿圆B.黄圆×绿皱C.黄圆×绿圆D.黄皱×黄圆3.(2021春·重庆·高二西南大学附中校考开学考试)豌豆高茎对矮茎为显性,黄色籽粒对绿色籽粒为显性,圆粒对皱粒为显性,三对相对性状独立遗传。
现有高茎黄色皱粒和矮茎绿色圆粒两个纯合品系,将其杂交种植得到F1,F1自由交配得到F2,则在F2中高茎绿色圆粒的比例,以及高茎绿色圆粒中纯合子的比例为()A.3/641/64B.9/641/64C.9/641/9D.3/641/34.(2021春·河南驻马店·高一校联考期中)下列有关遗传概念的说法,正确的是()A.杂合子自交,后代可能会出现纯合子B.A和A、A和a、a和a都是等位基因C.兔子的长毛和白毛属于相对性状D.隐性性状指生物体不能表现出来的性状5.(2022春·山东济南·高一济南市章丘区第四中学校联考期中)显性上位指两对独立遗传的基因中,一种显性基因对另一种显性基因的表现有遮盖作用,起遮盖作用的基因称为显性上位基因。
只有当显性上位基因不存在时,被遮盖的基因才得以表达。
猫的毛色由B/b和D/d两对独立遗传的等位基因控制,基因B控制黑色的形成,基因D控制白色的形成。
基因B和基因D同时存在时,基因D为显性上位基因;基因B和基因D都不存时,猫的毛色为灰色。
现有纯合白色猫和纯合黑色猫交配得到F1,F1雌雄个体随机交配得到F2,F2的表型及比例为白色﹔黑色:灰色=12:3:1。
高一化学必修2第一章测试题及答案

可能用到的相对原子质量:H-1 O-16 Cl-35.5 Na-23 Li-7 K-39 Rb-85 Cs-133 Ag-108第 I 卷 (选择题共 55 分)一.选择题(每小题只有一个选项符合题意。
每小题2 分,共 10 分)1.19 世纪门捷列夫的突出贡献是( )A.提出了原子学说B.提出了分子学说C.发现了稀有气体D.发现了元素周期律2.在元素周期表中,第三、四、五、六周期元素的数目分别是 ( ) A.8、8、18、32 B.8、18、18、32C.8、18、18、18 D.8、8、18、183.某些建筑材料含有放射性元素氡( ),会对人体产生一定危害。
该原子中中子数和质子数之差是( )A.136 B.50 C.86 D.2224.下列表达方式错误的是 ( )..A.H ∶Cl B. C.18 O D.O=C=O85.下列物质中,既含离子键又含共价键的是( )A.Na O B.NH C.Ca(OH) D.CaBr2 3 2 2二.选择题(每小题只有一个选项符合题意。
每小题2 分,共 45 分)6.我国的“神舟五号”载人飞船已发射成功,“嫦娥”探月工程也已正式启动。
据科学家预测,月球的土壤中吸附着数百万吨的 3 He ,每百吨 3 He 核聚变所释放出的能量相当于目2 2前人类一年消耗的能量。
在地球上,氮元素主要以 4 He 的形式存在。
下列说法正确的是2( )A. 4 He 原子核内含有 4 个质子2B. 3 He 和 4 He 互为同位素2 2C. 3 He 原子核内含有 3 个中子2D. 4 He 的最外层电子数为 2,所以 4 He 具有较强的金属性2 27.元素性质呈周期性变化的决定因素是 ( )A.元素相对原子质量依次递增B.元素的最高正化合价呈周期性变化C.元素原子最外层电子排布呈周期性变化D.元素金属性或非金属性呈周期性变化8.下列说法正确的是( )A.元素的种类由核外电子数决定B.原子的种类由原子核内质子数与中子数共同决定C.核外电子排布相同的两个原子一定是同种原子D.某元素的原子核内有m 个质子, n 个中子,则该元素的相对原子质量为m + n 9.下列说法中,正确的是 ( )A.周期表中的主族都有非金属元素B.周期表中的主族都有金属元素C.周期表中的非金属元素都位于短周期D.周期表中的非金属元素都位于主族和 0 族10.下列各组中前者的碱性比后者强的是( )A. KOH和Al(OH)B. Mg(OH) 和NaOH3 2C. Al(OH) 和Mg(OH)D. Mg(OH) 和Ca(OH)3 2 2 211.某元素的原子的最外层电子数是次外层的a 倍(a>1),则该原子核内质子数是( ) A.2a B.a+2 C.2a+10 D.2a+212.某元素X 最高价含氧酸的化学式为H XO ,则在其气态氢化物中X 元素的化合价为( )n 2n-2A.5n-2 B.3n-12 C.3n-6 D.n-1013.下列氢化物中稳定性由强到弱的顺序正确的是( )A.CH >NH >H O>HF B.SiH >NH >H S>HCl4 3 2 4 3 2C.HF>H O>NH >PH D.NH >PH >H S>HBr2 3 3 3 3 214.下列叙述中能肯定说明金属A 比金属 B 的活泼性强的是( )A.A 原子最外层电子数比 B 原子的最外层电子数少B.A 原子电子层数比 B 原子的电子层数多C.1molA 从酸中置换生成的H 比 1mol B 从酸中置换生成的H 多2 2D.常温时, A 能从酸中置换出氢,而 B 不能15.下列关于化学键的说法正确的是 ( )A.构成单质分子的微粒一定含有共价键B.全部由非金属元素组成的化合物不一定是共价化合物C.非极性键只存在于双原子单质分子中D.不同元素组成的多原子分子里的化学键一定都是极性键16.1993 年 8 月,国际原子量委员会确认我国张青莲教授测定的锑原子量(121.760)为标准原子量,已知锑有两种以上天然同位素,则 121.760 是( )A.锑元素的质量与12C 原子质量 1/12 的比值B.一个锑原子的质量与12C 原子质量 1/12 的比值C.按各种锑的天然同位素的相对原子质量与这些同位素所占的一定百分比计算出的平均值D.按各种锑的天然同位素质量数与这些同位素所占的一定百分比计算出的平均值已知17.下列关于元素化合价的叙述错误的是( )A.IIIA 族的 B 和Al 都能形成+3 价的化合物B.IVA 族的 C 和 Si 都能形成+4 价的化合物C.VA 族的 N 和 P 都能形成+5 价的化合物D.VIA 族的O 和 S 都能形成+6 价的化合物18.无机化学命名委员会(国际组织)在 1999 年作出决定,把长式周期表原先的主副族序号取消,由左到右按原顺序编为18 列,稀有气体为第18 列,按这个规定,下列说法正确的是 ( )A.第三列所含元素最多B .从上到下第一列元素单质熔点逐渐升高,而第 17 列元素单质熔点逐渐降低C .从上到下第一列元素单质密度逐渐升高,而第 17 列元素单质密度逐渐降低D .第 18 列最外层电子数均为 8,化学性质十分稳定19.若短周期中的两种元素可以形成原子个数比为 2 ∶3 的化合物,则这两种元素的原子序 数之差不可能是( )A . 1B . 3C .5D .620.钾与另一种碱金属组成的合金 18.0g 和水完全反应,产生氢气 0.2g ,合金中的另一种 金属是 ( )A .LiB .NaC .RbD .Cs第 II 卷(非选择题 共 45 分)三.填空题(30 分)21. (6 分) (1)写出表示含有 8 个质子、 10 个中子、 10 个电子的离子的符号 (2)周期表中位于第 8 纵行的铁元素属于第 族。
必修二第一章单元测试卷详解

第一单元测试卷第一章(60分钟100分)一、选择题(本题包括15小题,每小题4分,共60分)1.(2013·江苏高考改编)下列有关化学用语表示正确的是( )A.CO2的比例模型:B.氢氧根离子的电子式:H]-C.氯原子的结构示意图:D.中子数为146、质子数为92的铀(U)原子U【解析】选B。
CO2分子中,碳原子半径大于氧原子半径,所以CO2的比例模型中球应该是一大二小,A错误;OH-为阴离子,故其电子式应加“[ ]”带上电荷,B正确;氯原子最外层有7个电子,即,C错误;铀原子的质量数为146+92=238,故原子符号为U,D错误。
2.(2014·济南高一检测)短周期主族元素的原子,前者一定大于后者的是( )A.中子数、质子数B.质量数、核电荷数C.最高正化合价数、负化合价数D.核外电子数、其阳离子核外电子数【解析】选D。
H没有中子,则中子数小于质子数,故A错误;质量数=质子数+中子数,质子数等于核电荷数,若为普通氢原子,质量数等于核电荷数,故B错误;O、F没有正化合价,则没有最高正化合价,且第ⅣA族元素的最高正价与最低负价的绝对值相等,故C错误;原子失去电子变成阳离子,故阳离子的核外电子数一定小于原子的核外电子数,故D正确。
3.(2014·山东高考)根据原子结构及元素周期律的知识,下列推断正确的是( )A.同主族元素含氧酸的酸性随核电荷数的增加而减弱B.核外电子排布相同的微粒化学性质也相同C.Cl-、S2-、Ca2+、K+半径逐渐减小D Cl与Cl得电子能力相同【解析】选D。
同主族元素的最高价含氧酸的酸性随核电荷数的增加而减弱,A 错误;核外电子排布相同的微粒,性质不一定相同,如S2-与Cl-,B错误;当核外电子排布相同时,核电荷数越大,微粒半径越小,半径大小顺序应为S2->Cl->K+>Ca2+,C错误;同种元素的原子得电子能力相同,D正确。
【变式训练】(2014·苏州高一检测)下列排列顺序不正确的是( )A.原子半径:钠>硫>氯B.最高价氧化物对应的水化物的酸性:HClO4>H2SO4>H3PO4C.最高正化合价:氯>硫>磷D.热稳定性:碘化氢>溴化氢>氯化氢【解析】选D。
(完整版)高一化学必修二第一章习题含答案

高一化学必修2第一章单元测试题一、选择题1.下列元素中,最高正化合价数值最大的是( )。
A .CB .FC .SD .Ne2.已知某粒子,则元素R 的原子序数是( )。
n A Z RA .ZB .A-ZC .Z-nD .Z+n3.元素的性质随着元素原子序数的递增而呈周期性变化的原因是( )。
A .元素原子的核外电子排布呈周期性变化 B .元素的原子半径呈周期性变化C .元素的化合价呈周期性变化D .元素的金属性、非金属性呈周期性变化4.下列粒子半径之比小于1的是( )。
A .r (Na +)/ r (Na) B .r (Cl -)/ r (Cl) C .r (Na)/ r (Mg)D .r (Ca)/ r (Mg)5.有A 、B 、C 、D 四种金属,投入水中只有D 反应放出氢气,将A 投入C 的盐溶液中可置换出金属C ,B 的最高价氧化物的水化物碱性比A 的最高价氧化物的水化物碱性强,则四种金属的金属性强弱顺序正确的是( )。
A .A >B >C >D B .D >B >A >C C .B >A >C >DD .C >A >B >D6.下列事实不能说明非金属性Cl >I 的是( )。
A .Cl 2+2I -==2Cl -+I 2 B .稳定性:HCl >HI C .酸性:HClO 4>HIO 4 D .酸性:HClO 3>HIO 37.下列说法错误的是( )。
A .原子半径:F <Mg <K B .稳定性:PH 3>H 2S >NH 3 C .酸性:H 3PO 4<H 2SO 4<HClO 4D .碱性:Al(OH)3<Mg(OH)2<KOH 8.运用元素周期律分析下面的推断,其中不正确的是( )。
A .锂(Li )与水反应比钠与水反应剧烈B .砹(At )为有色固体,AgAt 难溶于水也不溶于稀硝酸C .在氧气中,铷(Rb )的燃烧产物比钠的燃烧产物更复杂D.HBrO4的酸性比HIO4的酸性强9.X元素的阳离子和Y元素的阴离子都具有与Ar原子相同的电子层结构,下列叙述正确的是()。
必修2 第一章单元测试卷

第一章单元测试卷第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每题5分,共60分)1.下列说法不正确的是()A.圆柱的侧面展开图是一个矩形B.圆锥的过轴的截面是一个等腰三角形C.直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥D.圆台平行于底面的截面是圆面答案C2.如图所示的直观图的原平面图形是()A.任意三角形C.任意四边形B.直角梯形D.平行四边形答案B3.三视图如图所示的几何体是()A.三棱锥C.四棱台B.四棱锥D.三棱台答案B4.下图中的图形经过折叠不能围成棱柱的是()3 32 3 2 3 3答案 D5.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图所示,是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是()A .1C .快B .6D .乐答案 B解析 如图所示,将题图折成正方体,可得 2 的下面是 6.32π6.已知正方体外接球的体积是 ,那么正方体的棱长等于()A .2 24 2 C.B.D.2 3 34 3 3答案 D解析 过正方体的相对侧棱作球的截面,可得正方体的对角线是球的直径.设正方体的棱长为 a ,球的半径为 R ,则有 2R = 3a ,所以 R3a 4π 3a 32π 4 3= ,则 ( )3= ,解得 a = .故选 D.7.一个圆锥的侧面展开图的圆心角为 90°,它的表面积为 a ,则它的底面积为( )522C.6D.34aA.a C.B. D.a3a4答案Aπ解析设圆锥的母线长为l,底面圆半径为r,则2πr=l·,故la=4r,由题意知πrl+πr2=a,所以πr2=.58.在正方体的八个顶点中,有四个顶点恰好是正四面体的顶点,则正方体的表面积与此正四面体的表面积之比为()A.32B.23答案A解析如图,设正方体的棱长为a,则正四面体A-B D C的11所有棱长均为2a.正方体的表面积S=6a2,13正四面体的表面积S=4××(2a)2=23a2.2∴S∶S=6a2∶23a2=3∶1.129.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为()3 3 33 3 3 3 3答案 C解析 由正(主)视图可知去掉的长方体在正对视线的方向,从侧(左)视图可以看出去掉的长方体在原长方体的左侧,由以上各视图的描述可知 C 选项的俯视图符合,C 正确.10.两个半径为 1 的铁球,熔化成一个大球,则大球的表面积为()A .6π3C .4 4πB .8πD .8 3 2π答案 C4π 8π 4π解析大球的体积是 2× ×13= ,设大球的半径为 R ,则有8π 3 3 3R 3= ,解得 R = 2,所以大球的表面积为 4π( 2)2=4 4π.故选 C.11.一平面截一球得到直径是 6 cm 的圆面,球心到这个平面的距离是 4 cm ,则该球的体积是()100π A. cm 3500π C. cm 3208πB. cm 3416 13πD. cm 33332C.3π2333 33222答案C解析设球的半径为R,则32+42=R2,故R=5.44500π所以球的体积为V=πR3=π×125=(cm3).12.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的体积为()πA.2B.πD.3π答案C6262解析解法一:如下图,AD=,AO=AD=,SO=SA2-AO2=3.2233∴R2=(3-R)2+.∴R=.球的体积为π.解法二:构造棱长为1的正方体如上图,则C A BD为棱长为2的正11四面体,正方体的外接球也为正四面体的外接球.此时球的直径为33,因此球的体积为π.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.设某几何体的三视图如下(尺寸的长度单位为m)6 2 23则该几何体的体积为________ m 3.答案 4解析 这是一个三棱锥,高为 2,底面三角形一边为 4,这边上的高1为 3,体积等于 ×2×4×3=4.614.若一个底面边长为 ,侧棱长为 6的正六棱柱的所有顶点都在一个球的面上,则此球的体积为________.答案 4 3π解析 2R =6( ×2)2+( 6)2=2 3,4∴R= 3,V = πR 3=4 3π. 球15.若干毫升水倒入底面半径为 2 cm 的圆柱形器皿中,量得水面的高度为 6 cm ,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是________ cm.答案 616.如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现:3 V4 2πR 3S 4πR 2 23 圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为________,________.答案3 3 2 2解析 设球的半径为 R ,则圆柱的底面半径为 R ,高为 2R ,∴V 圆柱 =πR 2×2R=2πR 3,4π V 2πR 3 3 V = R 3,∴ 圆柱= = .球 球 3∵S圆柱 =2πR×2R +2×πR 2=6πR 2,S =4πR 2,球S 6πR 2 3 ∴ 圆柱= = .球三、解答题(本大题共 6 小题,共 70 分)17.(10 分)一个几何体的三视图及其尺寸如下(单位:cm),求该几何体的表面积和体积.解析 由三视图知道该几何体是圆锥,且母线长为 5 cm ,底面半径是 3 cm ,圆锥的高是 4 cm ,所以其表面积是 S =π×3×(3+5)= 表124π cm 2,其体积 V = π×32×4=12π cm 3.18.(12 分)正方体的每条棱长都增加 1 cm ,它的体积扩大为原来的8 倍,求此正方体的棱长.3 2 3 答案 1 cm分析 利用待定系数法求解.设出正方体的棱长,根据体积扩大为原来的 8 倍列方程,解方程得正方体的棱长.设正方体的棱长为 a cm ,由题意,得(a +1)3=8a 3,解得 a =1,即此正方体的棱长为 1 cm.19.(12 分)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;解析 (1)如下图所示,(2)所求多面体体积V =V-V 长方体正三棱锥1 1 284=4×4×6- ×( ×2×2)×2= (cm 3).20.(12 分)根据三视图想象物体原形,并画出物体的实物草图:(1)三视图甲; (2)三视图乙.2223 3答案21.(12 分)已知六棱锥 P -ABCDEF ,其中底面 ABCDEF 是正六边形,点 P 在底面的投影是正六边形的中心,底面边长为 2 cm ,侧棱长为 3 cm ,求六棱锥 P -ABCDEF 的表面积和体积.解析 先求底面正六边形的面积,S六边形 ABCDEF=△6S OBC 1=6× ×2×2sin60°=6 3(cm 2),S 侧面=6S 1=6× ×2×△PCD CDPC 2-( )2=6 32-12=12 2(cm 2),∴S P -ABCDEF =S 六边形 ABCDEF +S 侧面=(6 3+12 2)(cm 2).在 △R t POC 中,PO = PC 2-OC 2= PC 2-BC 2= 9-4= 5(cm),∴V六棱锥 P -ABCDEF 1 1= Sh = ×6 3× 5=2 15(cm 3).22.(12 分)如图,是从上下底面处在水平状态下的棱长为 a 的正方体 ABCD -A B C D 中分离出来的.1 1 1 13 2 66(1)∠DC D 在图中的度数和它表示的角的真实度数都是 45°,对吗? 1 1(2)∠A C D 的真实度数是 60°,对吗?1 1(3)设 BC =1 cm ,如果用图示中这样一个装置来盛水,那么最多能盛多少体积的水?解析 (1)对;(2)对;(3)由题意知,以平面 B CD 为水平面,可盛最多体积的水,此时 V 1 11 1 1=VC -B D C =VC -B C D = × ×1×1×1= (cm 3). 1 1 1 1 1 11∴最多能盛 cm 3 的水.水。
高一物理必修2第1章《功与功率》单元测试

高一物理必修2第1章《功与功率》单元测试 班级 姓名 座号注:本试卷中,210/g m s =一、不定项选择(共50分。
每题5分。
漏选得2分,不选、错选均不得分)1、一学生用F=100N 的力将质量为0.5kg 的足球迅速踢出。
球在水平地面上滚动的距离S=20m ,则该生对足球做的功应是(g 取10m /s 2) ( ) A 、2000J ; B 、1000J ; C 、100J ; D 、无法计算。
2、下列有关功的说法,正确的是 ( )A 、只要物体发生了位移,就一定有力对它做功;B 、凡是受力的物体,一定有力对它做功;C 、只要物体在力的方向上发生了位移,则力一定对它做了功;D 、物体既受了力又发生了位移,一定有力对它做功。
3、如图1所示,A 、B 叠放着,A 用绳系在固定的墙上,用力F 拉着B 右移,用F '、ABF 和BA F 分别表示绳对A 的拉力、A 对B 的摩擦力和B 对A 的摩擦力,则( ) A 、F 做正功,AB F 做负功,BA F 做正功,F '不做功B 、F 和BA F 做正功,AB F 和F '做负功C 、F 做正功,其他力都不做功D 、F 做正功,AB F 做负功,BA F 和F '不做功4、一个水平力F 作用在物体上,使它在力的方向上移动了一段距离S 。
第一次在动摩擦因数为μ1的水平面上,做的功为W 1,功率为P 1;第二次是在动摩擦因数为μ2的水平面上,做的功为W 2,做功的功率为P 2。
已知μ1>μ2,则以下结论正确的是( ) A 、W 1=W 2,P 1<P 2 B 、W 1=W 2,P 1=P 2 C 、W 1>W 2,P 1=P 2 D 、W 1<W 2,P 1>P 25、一个质量为m 的小球做自由落体运动,那么,在前t 秒内重力对它做功的平均功率p 及在t 秒末重力做功的瞬时功率P 分别为 ( ) A 、22p mg t = 2212p mg t = B 、22p mg t = 22p mg t = C 、2212p mg t =22p mg t = D 、22p mg t = 222p mg t = 6、如图2所示,物体A 和物体B 与地面的动摩擦因数相同,A 和B 的质量相等,在力F 的图1F命题:陈家钰作用下,一起沿水平地面向右移动s ,则( ) A 、摩擦力对A 、B 做功相等 B 、A 、B 的支持力均不做功C 、F 对A 做的功与A 对B 做的功相等D 、合外力对A 做的功与合外力对B 做的功相等7、如图3所示,木块A 放在木块B 的左上端,用恒力F 拉至B 的右端,第一次让B 可以在光滑地面上自由滑动,F 做的功为W 2;,第二次将B 固定在地面上,F 做的功为W 1;比较两次做功,可能是( ) A 、W 1<W 2 B 、W 1>W 2C 、W 1=W 2D 、无法比较8、一个质量为m 的木块以一定的初速度从坡底滑上一个足够长的倾角为α的斜面,它沿斜面向上滑行s 的距离后,又回头滑回底端。
高一化学必修二第一章综合检测试题

必修2第一章考生留意:1.测验时间:60分钟,满分100分。
2.可能用到的原子量:H:1 O:16 :23第Ⅰ卷(共40分)一.选择题(每小题只有一个正确选项,每小题2分,共22分)1.据报道,月球上有大量3存在,以下关于3的说法正确的是A.是4的同素异形体 B.比4多一个中子C.是4的同位素 D.比4少一个质子2.下列叙述正确的是A.40 K和40 原子中的质子数和中子数都相等B.某元素最外层只有一个电子,则它肯定是ⅠA族元素C.任何原子或离子的组成中都含有质子D.同位素的不同核素物理、化学性质完全相同3.下列化合物中既有离子键又有共价键的是A. B.C.D.N24.在元素周期表中金属元素与非金属元素的分界线旁边的一些元素能用于制A.合金B.半导体C.催化剂D.农药5.下列说法错误的是A.含有共价键的化合物肯定是共价化合物B.在共价化合物中肯定含有共价键C.含有离子键的化合物肯定是离子化合物D.双原子单质分子中的共价健肯定是非极性键6.下列各组中属于同位素关系的是A .K 4019与Ca 4020B .T 2O 与H 2OC .K 4019与K 3919 D .金刚石与石墨7.元素性质呈周期性改变的确定因素是A .元素原子半径大小呈周期性改变B .元素原子量依次递增C .元素原子最外层电子排布呈周期性改变D .元素的最高正化合价呈周期性改变8.某元素原子的最外层电子数是次外层电子数的3倍,且最外层电子数与次外层电子数之和小于10。
该元素为A .锂B .铍C .氧D .钙9.下列各组中化合物的性质比较,不正确的是A .酸性:4>4>4B .碱性:>()2>()3C .稳定性:3>H 2S >D .非金属性:F >O >S10.某主族元素R 的最高正价与最低负化合价的代数和为4,由此可以推断A .R 肯定是第四周期元素B .R 肯定是ⅣA 族元素C .R 的气态氢化物比同周期其他元素气态氢化物稳定D .R 气态氢化物化学式为H 2R 11.下列电子式或结构式错误的是二.选择题(本题包括6小题,每小题3分,共18分。
人教A版高一数学必修2第一章单元测试题含详细答案
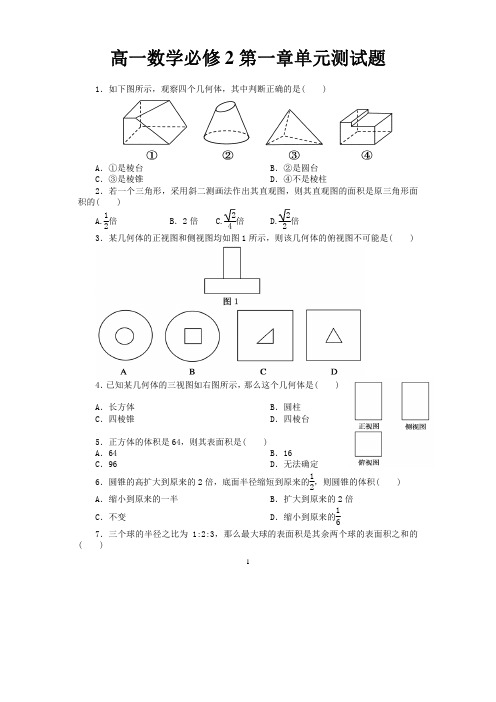
1高一数学必修2第一章单元测试题1.如下图所示,观察四个几何体,其中判断正确的是( )A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱2.若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的( )A.12倍 B.2倍 C.24倍 D.22倍 3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是()4.已知某几何体的三视图如右图所示,那么这个几何体是( )A.长方体 B.圆柱 C.四棱锥 D.四棱台5.正方体的体积是64,则其表面积是( ) A.64 B.16 C.96 D.无法确定6.圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积( )A.缩小到原来的一半 B.扩大到原来的2倍C.不变 D.缩小到原来的167.三个球的半径之比为1:2:3,那么最大球的表面积是其余两个球的表面积之和的( )2A.1倍 B.2倍 C.95倍 D.74倍 8.有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A.12πcm 2B.15πcm 2C.24πcm 2 D.36πcm 29.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A.7 B.6 C.5 D.310.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )A.32,1B.23,1C.32,32D.23,3211.某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为5的等腰三角形.则该几何体的体积为( )3A.24 B.80C.64D.24012.如果用表示1个立方体,用表示两个立方体叠加,用表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是()4姓名:座位号:一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.圆台的底半径为1和2,母线长为3,则此圆台的体积为________.14.一个几何体的三视图如图所示,则这个几何体的体积为___________________。
高中数学必修一第一、二章单元测试卷及答案2套

高中数学必修一第一、二章单元测试卷及答案2套测试卷一(时间:120分钟 满分:150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(-2)2] 12 等于( ) A .- 2 B. 2 C .-22 D.222.已知函数f (x )=11-x的定义域为M ,g (x )=ln(1+x )的定义域为N ,则M ∩N =( )A .{x |x >-1}B .{x |x <1}C .{x |-1<x <1}D .∅3.若0<m <n ,则下列结论正确的是( ) A .2m>2nB.⎝ ⎛⎭⎪⎫12m <⎝ ⎛⎭⎪⎫12nC .log 2m >log 2nD .log 12 m >log 12n4.已知函数f (x )=⎩⎪⎨⎪⎧2x+1,x <1,x 2+ax ,x ≥1,若f (f (0))=4a ,则实数a 等于( )A.12B.45C .2D .9 5.函数f (x )=|log 2x |的图象是( )6.函数y =x +43-2x的定义域是( )A.⎝⎛⎦⎥⎤-∞,32B.⎝⎛⎭⎪⎫-∞,32 C.⎣⎢⎡⎭⎪⎫32,+∞D.⎝ ⎛⎭⎪⎫32,+∞7.已知U =R ,A ={x |x >0},B ={x |x ≤-1},则(A ∩∁U B )∪(B ∩∁U A )=( ) A .∅ B .{x |x ≤0} C .{x |x >-1}D .{x |x >0或x ≤-1}8.下列函数f (x )中,满足“对任意x 1,x 2∈(0,+∞)当x 1<x 2时,都有f (x 1)>f (x 2)”的是( )A .f (x )=1xB .f (x )=(x -1)2C .f (x )=e xD .f (x )=ln(x +1)9.函数y =1-x 2+91+|x |( ) A .是奇函数B .是偶函数C .既是奇函数又是偶函数D .是非奇非偶函数10.下列函数中,既是奇函数又是增函数的是( ) A .y =x +1 B .y =-x 2C .y =1xD .y =x |x |11.已知函数y =f (x )的图象与函数y =log 21x +1的图象关于y =x 对称,则f (1)的值为( )A .1B .-1 C.12 D .-1212.若函数f (x )=log a (x +1)(a >0,a ≠1)的定义域和值域都是0,1],则a 等于( ) A.13 B. 2 C.22D .2 第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上) 13.函数f (x )=lg(x -1)+5-x 的定义域为________. 14.若函数f (x )=ax -1-2(a >0,a ≠1),则此函数必过定点________.15.计算81- 14 +lg 0.01-ln e +3log 32=________.16.函数f (x )=ex 2+2x的增区间为________.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知a >0,且a ≠1,若函数f (x )=2a x-5在区间-1,2]的最大值为10,求a 的值.18.(本小题满分12分)设A ={x |-2≤x ≤5},B ={x |m -1≤x ≤2m +1}. (1)当x ∈N *时,求A 的子集的个数; (2)当x ∈R 且A ∩B =∅时,求m 的取值范围.19.(本小题满分12分)已知函数f (x )=m -22x +1是R 上的奇函数,(1)求m 的值;(2)先判断f (x )的单调性,再证明.20.(本小题满分12分)已知函数f (x )=log a (x -1),g (x )=log a (3-x )(a >0且a ≠1). (1)求函数h (x )=f (x )-g (x )的定义域;(2)利用对数函数的单调性,讨论不等式f (x )≥g (x )中x 的取值范围.21.(本小题满分12分) 设函数f (x )=ax -1x +1,其中a ∈R . (1)若a =1,f (x )的定义域为区间0,3],求f (x )的最大值和最小值;(2)若f (x )的定义域为区间(0,+∞),求a 的取值范围,使f (x )在定义域内是单调减函数.22.(本小题满分12分)已知13≤a ≤1,若函数f (x )=ax 2-2x +1在区间1,3]上的最大值为M (a ),最小值为N (a ),令g (a )=M (a )-N (a ).(1)求g (a )的函数表达式;(2)判断函数g (a )在区间⎣⎢⎡⎦⎥⎤13,1上的单调性,并求出g (a )的最小值.答案1.B 解析:(-2)2] 12 =(2)2] 12 = 2.2.C 解析:由1-x >0得x <1,∴M ={x |x <1}.∵1+x >0,∴x >-1.∴N ={x |x >-1}.∴M ∩N ={x |-1<x <1}.3.D 解析:∵y =2x 是增函数,又0<m <n ,∴2m <2n;∵y =⎝ ⎛⎭⎪⎫12x 是减函数,又0<m <n ,∴⎝ ⎛⎭⎪⎫12m >⎝ ⎛⎭⎪⎫12n; ∵y =log 2x 在(0,+∞)上是增函数,又0<m <n , ∴log 2m <log 2n .4.C 解析:∵f (0)=20+1=2,∴f (f (0))=f (2)=22+2a =4a , ∴2a =4,∴a =2.5.A 解析:结合y =log 2x 可知,f (x )=|log 2x |的图象可由函数y =log 2x 的图象上不动下翻得到,故A 正确.解题技巧:函数图象的对称变换规律: 函数y =f x 的图象―――――――――――――――――→y 轴左侧图象去掉,右侧保留并“复制”一份翻到y 轴左侧函数y =f |x |的图象函数y =f x 的图象――――――――――――――――――→x 轴上方图象不变,下方图象翻到上方函数y =|f x |的图象6.B 解析:由3-2x >0得x <32.7.D 解析:∁U B ={x |x >-1},∁U A ={x |x ≤0},∴A ∩∁U B ={x |x >0},B ∩∁U A ={x |x ≤-1},∴(A ∩∁U B )∪(B ∩∁U A )={x |x >0或x ≤-1}.8.A 解析:由题意知需f (x )在(0,+∞)上为减函数. 9.B 解析:f (-x )=1--x 2+91+|x |=1-x 2+91+|x |=f (x ),故f (x )是偶函数,故选B.10.D 解析:函数y =x +1为非奇非偶函数,函数y =-x 2为偶函数,y =1x和y =x |x |是奇函数,但y =1x不是增函数,故选D.11.D 解析:(m ,n )关于y =x 的对称点(n ,m ),要求f (1),即求满足1=log 21x +1的x 的值,解得x =-12.12.D 解析:∵x ∈0,1],∴x +1∈1,2].当a >1时,log a 1≤log a (x +1)≤log a 2=1,∴a =2;当0<a <1时,log a 2≤log a (x +1)≤log a 1=0与值域0,1]矛盾.13.(1,5] 解析:由⎩⎪⎨⎪⎧x -1>0,5-x ≤0,解得1<x ≤5.14.(1,-1) 解:当x =1时,f (1)=a 1-1-2=a 0-2=-1,∴过定点(1,-1).解题技巧:运用整体思想和方程思想求解. 15.-16 解析:原式=13-2-12+2=-16.16.-1,+∞) 解析:设f (x )=e t ,t =x 2+2x ,由复合函数性质得,f (x )=e x 2+2x的增区间就是t =x 2+2x 的增区间-1,+∞).17.解:当0<a <1时,f (x )在-1,2]上是减函数,当x =-1时,函数f (x )取得最大值,则由2a -1-5=10,得a =215,当a >1时,f (x )在-1,2]上是增函数,当x =2时,函数取得最大值,则由2a 2-5=10,得a =302或a =-302(舍). 综上所述,a =215或302.18.解:(1)由题意知A 中元素为{1,2,3,4,5}, ∴A 的子集的个数为25=32.(2)∵x ∈R 且A ∩B =∅,∴B 可分为两个情况. ①当B =∅时,即m -1>2m +1,解得m <-2;②当B ≠∅时,可得⎩⎪⎨⎪⎧2m +1<-2,m -1≤2m +1或⎩⎪⎨⎪⎧m -1>5,m -1≤2m +1,解得-2≤m <-32或m >6.综上知,m 的取值范围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫m ⎪⎪⎪m <-32或m >6.19.解:(1)据题意有f (0)=0,则m =1. (2)f (x )在R 上单调递增,以下给出证明: 任取x 1,x 2∈R ,且x 1<x 2,f (x 2)-f (x 1)=-22x 2+1+22x 1+1=22x 2-2x 12x 2+12x 1+1. ∵x 2>x 1,∴2x 2>2x 1,∴f (x 2)-f (x 1)>0,则f (x 2)>f (x 1), 故f (x )在R 上单调递增.解题技巧:若函数f (x )的定义域内含有0且为奇函数时,则必有f (0)=0.20.解:(1)由⎩⎪⎨⎪⎧x -1>0,3-x >0,得1<x <3.∴函数h (x )的定义域为(1,3). (2)不等式f (x )≥g (x ),即为log a (x -1)≥log a (3-x ).(*)①当0<a <1时,不等式(*)等价于⎩⎪⎨⎪⎧1<x <3,x -1≤3-x ,解得1<x ≤2;②当a >1时,不等式(*)等价于⎩⎪⎨⎪⎧1<x <3,x -1≥3-x ,解得2≤x <3.综上,当0<a <1时,原不等式的解集为(1,2]; 当a >1时,原不等式的解集为2,3). 21.解:f (x )=ax -1x +1=a x +1-a -1x +1=a -a +1x +1, 设x 1,x 2∈R ,则f (x 1)-f (x 2)=a +1x 2+1-a +1x 1+1=a +1x 1-x 2x 1+1x 2+1.(1)当a =1时,f (x )=1-2x +1,设0≤x 1<x 2≤3, 则f (x 1)-f (x 2)=2x 1-x 2x 1+1x 2+1,又x 1-x 2<0,x 1+1>0,x 2+1>0, ∴f (x 1)-f (x 2)<0,∴f (x 1)<f (x 2). ∴f (x )在0,3]上是增函数,∴f (x )max =f (3)=1-24=12,f (x )min =f (0)=1-21=-1.(2)设x 1>x 2>0,则x 1-x 2>0,x 1+1>0,x 2+1>0.若使f (x )在(0,+∞)上是减函数,只要f (x 1)-f (x 2)<0,而f (x 1)-f (x 2)=a +1x 1-x 2x 1+1x 2+1,∴当a +1<0,即a <-1时,有f (x 1)-f (x 2)<0, ∴f (x 1)<f (x 2).∴当a ∈(-∞,-1)时,f (x )在定义域(0,+∞)内是单调减函数.22.解:(1)∵13≤a ≤1,∴f (x )的图象为开口向上的抛物线,且对称轴为x =1a ∈1,3].∴f (x )有最小值N (a )=1-1a.当2≤1a ≤3,a ∈⎣⎢⎡⎦⎥⎤13,12时, f (x )有最大值M (a )=f (1)=a -1;当1≤1a <2,a ∈⎝ ⎛⎦⎥⎤12,1时, f (x )有最大值M (a )=f (3)=9a -5;∴g (a )=⎩⎪⎨⎪⎧a -2+1a ⎝ ⎛⎭⎪⎫13≤a ≤12,9a -6+1a ⎝ ⎛⎭⎪⎫12<a ≤1.(2)设13≤a 1<a 2≤12,则g (a 1)-g (a 2)=(a 1-a 2)⎝⎛⎭⎪⎫1-1a 1a 2>0,∴g (a 1)>g (a 2),∴g (a )在⎣⎢⎡⎦⎥⎤13,12上是减函数. 设12<a 1<a 2≤1,则g (a 1)-g (a 2)=(a 1-a 2)⎝ ⎛⎭⎪⎫9-1a 1a 2<0,∴g (a 1)<g (a 2),∴g (a )在⎝ ⎛⎦⎥⎤12,1上是增函数.∴当a =12时,g (a )有最小值12.测试卷二(时间:120分钟 满分:150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.80-lg 100的值为( )A .2B .-2C .-1 D.122.已知f (x )=x 12,若0<a <b <1,则下列各式中正确的是( )A .f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1bB .f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1b <f (b )<f (a )C .f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1b <f ⎝ ⎛⎭⎪⎫1aD .f ⎝ ⎛⎭⎪⎫1a <f (a )<f ⎝ ⎛⎭⎪⎫1b<f (b )3.下列不等式成立的是(其中a >0且a ≠1)( ) A .log a 5.1<log a 5.9 B .a 0.8<a 0.9C .1.70.3>0.93.1D .log 32.9<log 0.52.24.函数f (x )=log a (4x -3)过定点( )A .(1,0) B.⎝ ⎛⎭⎪⎫34,0 C .(1,1) D.⎝ ⎛⎭⎪⎫34,15.在同一坐标系中,当0<a <1时,函数y =a -x与y =log a x 的图象是( )6.已知函数f (x )=⎩⎪⎨⎪⎧3x,x ≤0,log 2x ,x >0,则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫12的值是( )A .-3B .3 C.13 D .-137.用固定的速度向如图形状的瓶子中注水,则水面的高度h 和时间t 之间的关系可用图象大致表示为( )8.已知f (x 6)=log 2x ,那么f (8)等于( ) A.43 B .8 C .18 D.12 9.函数y =xlg 2-x的定义域是( )A .0,2)B .0,1)∪(1,2)C .(1,2)D .0,1)10.函数f (x )=ln x 的图象与函数g (x )=x 2-4x +4的图象的交点个数为( ) A .0 B .1 C .2 D .311.已知函数f (x )在0,+∞)上是增函数,g (x )=-f (|x |),若g (lg x )>g (1),则x 的取值范围是( )A.⎝ ⎛⎭⎪⎫110,10 B .(0,10) C .(10,+∞)D.⎝⎛⎭⎪⎫110,10∪(10,+∞)12.设f (x )为定义在R 上的奇函数,当x ≥0时,f (x )=2x+2x +b (b 为常数),则f (-1)=( )A .-3B .-1C .1D .3第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上) 13.若x log 23=1,则3x=________.14.若点(2,2)在幂函数y =f (x )的图象上,则f (x )=________.15.已知函数y =log a ⎝ ⎛⎭⎪⎫14x +b (a ,b 为常数,其中a >0,a ≠1)的图象如图所示,则a+b 的值为__________.16.下列说法中,正确的是________.(填序号)①任取x>0,均有3x>2x;②当a>0且a≠1时,有a3>a2;③y=(3)-x是增函数;④y=2|x|的最小值为1;⑤在同一坐标系中,y=2x与y=2-x的图象关于y轴对称.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分12分)计算下列各式的值:(1)(32×3)6+(2×2)43-(-2 012)0;(2)lg 5×lg 20+(lg 2)2. 18.(本小题满分12分)设f(x)=a-22x+1,x∈R.(其中a为常数)(1)若f(x)为奇函数,求a的值;(2)若不等式f(x)+a>0恒成立,求实数a的取值范围.19.(本小题满分12分)已知函数f(x)=lg(2+x),g(x)=lg(2-x),设h(x)=f(x)+g(x).(1)求函数h(x)的定义域;(2)判断函数h(x)的奇偶性,并说明理由.20.(本小题满分14分)已知函数f(x)=log2|x|.(1)求函数f(x)的定义域及f(-2)的值;(2)判断函数f(x)的奇偶性;(3)判断f (x )在(0,+∞)上的单调性,并给予证明.21.某种产品的成本f 1(x )与年产量x 之间的函数关系的图象是顶点在原点的抛物线的一部分(如图1),该产品的销售单价f 2(x )与年销售量之间的函数关系图象(如图2),若生产出的产品都能在当年销售完.(1)求f 1(x ),f 2(x )的解析式;(2)当年产量多少吨时,所获利润最大,并求出最大值.22.(本小题满分12分) 设f (x )=-2x+m2x +1+n(m >0,n >0).(1)当m =n =1时,证明:f (x )不是奇函数; (2)设f (x )是奇函数,求m 与n 的值;(3)在(2)的条件下,求不等式f (f (x ))+f ⎝ ⎛⎭⎪⎫14<0的解集.答案 创优单元测评 (第一章 第二章) 名校好题·能力卷]1.C 解析:80-lg 100=1-2=-1.2.C 解析:∵0<a <b <1,∴1<1b <1a .∴0<a <b <1b <1a.又∵f (x )=x 12在(0,+∞)单调递增,∴f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1b <f ⎝ ⎛⎭⎪⎫1a. 3.C 解析:选项A ,B 均与0<a <1还是a >1有关,排除;选项C 既不同底数又不同指数,故取“1”比较,1.70.3>1.70=1,0.93.1<0.90=1,所以1.70.3>0.93.1正确.选项D 中,log 32.9>0,log 0.52.2<0,D 不正确.解题技巧:比较几个数的大小问题是指数函数、对数函数和幂函数的重要应用,其基本方法是:将需要比较大小的几个数视为某类函数的函数值,其主要方法可分以下三种:(1)根据函数的单调性(如根据一次函数、二次函数、指数函数、对数函数、幂函数的单调性),利用单调性的定义求解;(2)采用中间量的方法(实际上也要用到函数的单调性),常用的中间量如0,1,-1等; (3)采用数形结合的方法,通过函数的图象解决.4.A 解析:令4x -3=1可得x =1,故函数f (x )=log a (4x -3)过定点(1,0).5.C 解析:当0<a <1时,y =a -x=⎝ ⎛⎭⎪⎫1a x 是过(0,1)点的增函数,y =log a x 是过(1,0)点的减函数.故选C.6.C 解析:f ⎝ ⎛⎭⎪⎫12=log 212=-1,f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫12=f (-1)=3-1=13.7.B 解析:由题图可知,当t 越来越大时,h 的增长速度越来越快,而A ,D 是匀速增长的,瓶子应为直筒状,C 表示的瓶子应是口大于底,故选B.8.D 解析:令x 6=8可知x =± 2.又∵x >0,∴x =2,∴f (8)=log 22=log 2212 =12.9.B 解析:由题意可知,要使函数有意义,只需⎩⎪⎨⎪⎧x ≥0,2-x >0且2-x ≠1,解得0≤x <2且x ≠1.∴函数y =xlg2-x的定义域为0,1)∪(1,2).10.C 解析:g (x )=x 2-4x +4=(x -2)2,在同一平面直角坐标系内画出函数f (x )=lnx 与g (x )=(x -2)2的图象(如图).由图可得两个函数的图象有2个交点.11.A 解析:因为g (lg x )>g (1),所以f (|lg x |)<f (1),又f (x )在0,+∞)单调递增,所以0≤|lg x |<1,解得110<x <10.12.A 解析:∵f (x )是R 上的奇函数,∴f (0)=0. 又x ≥0时,f (x )=2x +2x +b ,∴20+b =0,b =-1. ∴当x ≥0时,f (x )=2x+2x -1. ∴f (1)=21+2×1-1=3.∵f (x )是R 上的奇函数,∴f (-1)=-f (1)=-3. 13.2 解析:∵x log 23=1,∴x =log 32, ∴3x=3log 32=2.解题技巧:注意换底公式与对数恒等式的应用.14.x 12 解析:设f (x )=x α(α为常数),由题意可知f (2)=2α=2, ∴α=12,∴f (x )=x 12 .15.34 解析:将图象和两坐标轴的交点代入得log a b =2,log a ⎝ ⎛⎭⎪⎫34+b =0,34+b =1,a 2=b ,从图象看出,0<a <1,b >0,解得a =12,b =14,a +b =34.16.①④⑤ 解析:对于①,可知任取x >0,3x >2x一定成立. 对于②,当0<a <1时,a 3<a 2,故②不一定正确. 对于③,y =(3)-x=⎝⎛⎭⎪⎫33x ,因为0<33<1,故y =(3)-x是减函数,故③不正确. 对于④,因为|x |≥0,∴y =2|x |的最小值为1,正确. 对于⑤,y =2x与y =2-x的图象关于y 轴对称,是正确的.(2)原式=lg 5×lg(5×4)+(lg 2)2=lg 5×(lg 5+lg 4)+(lg 2)2=(lg 5)2+lg 5lg 4+(lg 2)2 =(lg 5)2+2lg 5lg 2+(lg 2)2=(lg 5+lg 2)2=1.18.解:(1)因为x ∈R ,所以f (0)=0得a =1. (2)f (x )=a -22x +1,因为f (x )+a >0恒成立, 即2a >22x +1恒成立.因为2x+1>1,所以0<22x +1<2,所以2a ≥2,即a ≥1. 故a 的取值范围是1,+∞).19.解:(1)∵h (x )=f (x )+g (x )=lg(x +2)+lg(2-x ),要使函数h (x )有意义,则有⎩⎪⎨⎪⎧x +2>0,2-x >0,解得-2<x <2.所以,h (x )的定义域是(-2,2).(2)由(1)知,h (x )的定义域是(-2,2),定义域关于原点对称, 又∵ h (-x )=f (-x )+g (-x )=lg(2-x )+lg(2+x ) =g (x )+f (x )=h (x ),∴ h (-x )=h (x ),∴ h (x )为偶函数. 20.解:(1)依题意得|x |>0,解得x ≠0, 所以函数f (x )的定义域为(-∞,0)∪(0,+∞). f (-2)=log 2|-2|=log 2212 =12.(2)设x ∈(-∞,0)∪(0,+∞),则-x ∈(-∞,0)∪(0,+∞).f (-x )=log 2|-x |=log 2|x |=f (x ),所以f (-x )=f (x ),所以函数f (x )是偶函数.(3)f (x )在(0,+∞)上是单调增函数.证明如下: 设x 1,x 2∈(0,+∞),且x 1<x 2,则f (x 1)-f (x 2)=log 2|x 1|-log 2|x 2|=log 2x 1x 2. 因为0<x 1<x 2,所以x 1x 2<1,所以log 2x 1x 2<0,即f (x 1)<f (x 2),所以f (x )在(0,+∞)上是单调增函数. 21.解:(1)设f 1(x )=ax 2,将(1 000,1 000)代入可得1 000=a ×1 0002, 所以a =0.001,所以f 1(x )=0.001x 2.设f 2(x )=kx +b ,将(0,3),(1 000,2)代入可得k =-0.001,b =3, 所以f 2(x )=-0.001x +3. (2)设利润为f (x ),则f (x )=xf 2(x )-f 1(x )=(-0.001x +3)x -0.001x 2=-0.002x 2+3x =-0.002(x 2-1500x +7502)+1 125,所以当x =750时,f (x )max =1 125.解题技巧:解应用题的一般思路可表示如下:22.(1)证明:当m =n =1时,f (x )=-2x+12x +1+1.由于f (1)=-2+122+1=-15,f (-1)=-12+12=14,所以f (-1)≠-f (1),f (x )不是奇函数. (2)解:f (x )是奇函数时,f (-x )=-f (x ), 即-2-x+m 2-x +1+n =--2x+m2x +1+n对定义域内任意实数x 成立. 化简整理得(2m -n )·22x+(2mn -4)·2x+(2m -n )=0,这是关于x 的恒等式,所以⎩⎪⎨⎪⎧2m -n =0,2mn -4=0,解得⎩⎪⎨⎪⎧m =-1,n =-2或⎩⎪⎨⎪⎧m =1,n =2.经检验⎩⎪⎨⎪⎧m =1,n =2符合题意.(3)解:由(2)可知,f (x )=-2x+12x +1+2=12⎝⎛⎭⎪⎫-1+22x +1,易判断f (x )是R 上单调减函数.由f (f (x ))+f ⎝ ⎛⎭⎪⎫14<0,得f (f (x ))<f ⎝ ⎛⎭⎪⎫-14,f (x )>-14,2x <3,得x <log 23,即f (x )>0的解集为(-∞,log 23).。
高一数学必修第一二章测试题及答案

高一数学必修第一二章测试题及答案The Standardization Office was revised on the afternoon of December 13, 2020第一.二章《三角函数》单元检测试卷一、选择题:(本答题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.在平行四边形ABCD 中,BD CD AB +-等于()A .B .C .D .2.若|a |=2,|b |=5,|a +b |=4,则|a -b |的值()A .13B .3C .42D .73.函数sin(2)3y x π=+图像的对称轴方程可能是()A .6x π=-B .12x π=-C .6x π=D .12x π=5.点A(x,y)是300°角终边上异于原点的一点,则xy值为() 333333函数)32sin(π-=x y 的单调递增区间是()A .⎥⎦⎤⎢⎣⎡+-125,12ππππk k Z k ∈ B .⎥⎦⎤⎢⎣⎡+-1252,122ππππk k Z k ∈C .⎥⎦⎤⎢⎣⎡+-65,6ππππk k Z k ∈ D .⎥⎦⎤⎢⎣⎡+-652,62ππππk k Z k ∈ 7.sin(-310π)的值等于() A .21B .-21C .23D .-238.在△ABC 中,若)sin()sin(C B A C B A +-=-+,则△ABC 必是() A .等腰三角形B .直角三角形C .等腰或直角三角形D .等腰直角三角9.函数x x y sin sin -=的值域是()A .0B .[]1,1-C .[]1,0D .[]0,2-10.函数x x y sin sin -=的值域是()A .[]1,1-B .[]2,0C .[]2,2-D .[]0,2-11.函数x x y tan sin +=的奇偶性是()A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数 12.比较大小,正确的是() A .5sin 3sin )5sin(<<- B .5sin 3sin )5sin(>>-C .5sin )5sin(3sin <-<D .5sin )5sin(3sin >->二、填空题(每小题5分,共20分)13.终边在坐标轴上的角的集合为_________.14.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是________________. 15.已知角α的终边经过点P(-5,12),则sin α+2cos α的值为______.16.一个扇形的周长是6厘米,该扇形的中心角是1弧度,该扇形的面积是________________. 三、解答题:(本大题共6小题,共70分。
高中物理 必修一 第1~2章单元测试试卷(含答案解析)

高中物理必修一第1~2章单元测试试卷(含答案解析)(时间 45分钟满分 100分)一、选择题(每小题4分,共80分,只有一个正确答案)1.下列物体中,不能看作质点的是()A.计算从北京开往上海的途中,与上海距离时的火车B.研究航天飞机相对地球的飞行周期时,绕地球飞行的航天飞机C.沿地面翻滚前进的体操运动员D. 比较两辆行驶中的车的快慢2.下列关于参考系的描述中,正确的是()A.参考系必须是和地面连在一起的物体B.被研究的物体必须沿与参考系的连线运动C.参考系必须是正在做匀速直线运动的物体或是相对于地面静止的物体D.参考系是为了研究物体的运动而假定为不动的那个物体3.若汽车的加速度方向与速度方向一致,当加速度减小时,则A.汽车的速度也减小B.汽车的速度先增大后减小C.当加速度减小到零时,汽车静止D.当加速度减小到零时,汽车的速度达到最大4.下列关于速度的说法正确的是A.速度是描述物体位置变化的物理量B.速度方向就是物体运动的方向C.位移方向和速度方向一定相同D.匀速直线运动的速度方向是可以改变的5.如图所示是做直线运动的甲、乙两物体的s-t图象,下列说法中不正确的是()A.甲启动的时刻比乙早t1 s.B.当t = t2 s时,两物体相遇C.当t = t2 s时,两物体相距最远D. 当t = t3 s时,两物体相距s1 m6.下面关于加速度的描述中正确的有()A.加速度描述了物体速度变化的多少B.加速度在数值上等于单位时间里速度的变化C.当加速度与位移方向相反时,物体做减速运动D.当加速度与速度方向相同且又减小时,物体做减速运动7.下列关于平均速度和瞬时速度的说法中正确的是 ( )A.做变速运动的物体在相同时间间隔里的平均速度是相同的B.瞬时速度就是运动的物体在一段较短的时间内的平均速度C.平均速度就是初末时刻瞬时速度的平均值D.某物体在某段时间里的瞬时速度都为零,则该物体在这段时间内静止8. 对做减速运动的物体(无往返),下列说法中正确的是 ( )A.速度和位移都随时间减小B.速度和位移都随时间增大C.速度随时间增大,位移随时间减小D.速度随时间减小,位移随时间增大9.如图所示为一物体做直线运动的v-t 图象,根据图象做出的以下判断中,正确的是( )A.物体始终沿正方向运动B.物体先沿正方向运动,在t =2 s 后开始沿负方向运动C.在t = 2 s 前物体位于出发点负方向上,在t = 2 s 后位于出发点正方向上D.在t = 2 s 时,物体距出发点最远10. 物体M 从A 运动到B ,前半程平均速度为v 1,后半程平均速度为v 2,那么全程的平均速度是:( )A.(v 1+v 2)/2B.21v v ⋅C.212221v v v v ++D.21212v v v v + 11.做匀加速直线运动的物体的加速度为3 m/s 2,对任意1 s 来说,下列说法中不正确的是A.某1 s 末的速度比该1 s 初的速度总是大3 m/sB.某1 s 末的速度比该1 s 初的速度总是大3倍C.某1 s 末的速度比前1 s 末的速度大3 m/sD.某1 s 末的速度比前1 s 初的速度大6 m/s12.a 、b 两个物体从同一地点同时出发,沿同一方向做匀变速直线运动,若初速度不同,加速度相同,则在运动过程中①a 、b 的速度之差保持不变②a 、b 的速度之差与时间成正比③a 、b 的位移之差与时间成正比④a 、b 的位移之差与时间的平方成正比A.①③B.①④C.②③D.13.自由落体第5个0.5 s 经过的位移是第1个0.5 s 经过的位移的倍数为A.5B.9C.10D.2514.一小球从A 点由静止开始做匀变速直线运动,若到达B 点时速度为v ,到达C 点时速度为2v ,则AB ∶BC 等于A.1∶1B.1∶2C.1∶3D.1∶415.物体从某一高度自由下落,第1 s 内就通过了全程的一半,物体还要下落多少时间才会落地A.1 sB.1.5 sC.2 sD.(2-1)s16.物体的初速度为v 0,以加速度a 做匀加速直线运动,如果要它的速度增加到初速度的n 倍,则物体的位移是A.av n 2)1(202- B.a v n 2202 C.a v n 2)1(20- D.a v n 2)1(202- 17.做匀加速运动的列车出站时,车头经过站台某点O 时速度是1 m/s ,车尾经过O 点时的速度是7 m/s ,则这列列车的中点经过O 点时的速度为A.5 m/sB.5.5 m/sC.4 m/sD.3.5 m/s18.甲乙两个质点同时同地向同一方向做直线运动,它们的v —t 图象如图所示,则A.乙比甲运动的快B.2 s 乙追上甲C.甲的平均速度大于乙的平均速度D.乙追上甲时距出发点40 m 远19.一个石子从高处释放,做自由落体运动,已知它在第1 s 内的位移大小是s ,则它在第3 s 内的位移大小是A.5sB.7sC.9sD.3s20..从某高处释放一粒小石子,经过1 s 从同一地点释放另一小石子,则它们落地之前,两石子之间的距离将A.保持不变B.不断变大C.不断减小D.有时增大有时减小二、填空题(每题4分,共20分)21. 甲、乙两物体都以5 m/s 的初速度向东做变速直线运动,经5 s 后,甲的速度变为零,乙的速度变为10 m/s ,则物体甲的平均加速度大小为___________、方向___________;物体乙的加速度大小为___________、方向___________22. 如图所示为甲、乙、丙三个物体在同一直线上运动的 s-t图象,比较前5 s 内三个物体的平均速度大小为甲v ______乙v ______丙v ;比较前 10 s 内三个物体的平均速度大小有甲v ′____乙v ′____丙v ′(填“>”“=’“<”)23.做匀加速直线运动的物体,速度从v 增加到2v 时经过的位移是s ,则它的速度从v 增加到3v 时发生的位移是__________.24.一质点从静止开始以1 m/s 2的加速度做匀加速运动,经过5 s 后做匀速运动,最后2 s 的时间使质点匀减速到静止,则质点匀速运动时的速度为 减速运动时的加速度为25.一物体从离地H 高处自由下落h 时,物体的速度恰好是着地时速度的一半,则它落下的位移h 等于______.参考答案1.C2.D3.BD4.B5.C6. B7. D8.D9. D10.D 解析:本题考查平均速度的概念。
高一必修第一、二单元英语试卷及答案

精心整理高一必修第一、二单元英语试卷及答案Ⅰ.单词拼写(每个1分,共10分)1.Theywantedtofindthe________(源头)oftheYellowRiver.信仰哭泣 平衡 体力)again.8.It’simportanttoknowyourown________(弱点).9.Thesupermarketisfullof________(顾客)atweekends.10.Beinganhonestmanyoushouldn’ttell________(谎言). Ⅱ.用所给短语的正确形式填空(每个1分,共10分)7.I________toheraboutwhatIwasdoing.8.Herunsthreemileseverymorningto________.9.WatchFrank—hewillcheatifhethinkshecan________it.10.Just________,sheopenedtheletterofherbrother’s.Ⅲ.单句填空(每个1分,共20分)1.Weallknowtheweatherinthesouthismuchwarmerthan________inth5.—party.—I________.Seeyoulater.6.—________Isendyouthebookthisevening?7.WhenHarrywasatcollege,he________gotothereadingroomaftersu ppereveryday.8.Travelers________(remind)thattheyshouldbringtheirIDcardsw.1113.Hewas______(lie)intheshadeofthetree.14.Ijusthadtosatisfymy________(curious),soIopenedtheparcel.15.Tomakemembersofateamperformbetter,thetrainerfirstofallhastoknowtheir________(strong)andweaknesses.16.DoIgeta________(count)ifIbuyawholecaseofwine? 17.Itmakessensetoeatareasonablybalanceddietwhen___________r).他四处张望,好像在寻找什么。
牛津译林版英语必修2 Unit1单元检测卷(一)含答案

单元检测 (一)第一部分听力(共两节,满分20分)第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.How much does she have to pay if she buys one now?A.$5.00. B.$4.50. C.$3.50.2.Where does the conversation most probably take place?A.In a library.B.At a restaurant.C.In a bookstore.3.What do you think is the woman?A.A cook. B.A student. C.A manager.4.Where does the man prefer to live?A.In the city.B.In the country.C.Near the town.5.What conclusion can be drawn from the man’s answer?A.He likes the brown wool.B.He doesn’t like either.C.He likes the black and white silk.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6至8题。
6.Where was the man from?A.India. B.Austria. C.Australia.7.What’s the weather like in Australia during June and July?A.It’s hot and dry.B.It’s cold and rainy.C.It’s warm and rainy.8.Which month is the best time for visitors there?A.June. B.July. C.December.听第7段材料,回答第9至11题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章测试卷第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每题5分,共60分)1.下列说法不正确的是()A.圆柱的侧面展开图是一个矩形B.圆锥的过轴的截面是一个等腰三角形C.直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥D.圆台平行于底面的截面是圆面答案 C2.如图所示的直观图的原平面图形是()A.任意三角形B.直角梯形C.任意四边形D.平行四边形答案 B3.三视图如图所示的几何体是()A.三棱锥B.四棱锥C.四棱台D.三棱台答案 B4.下图中的图形经过折叠不能围成棱柱的是()答案 D5.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图所示,是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是()A.1B.6C .快D .乐答案 B解析 如图所示,将题图折成正方体,可得2的下面是6.6.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的体积为( ) A.π2 B .π C.32π D.3π答案 C解析 解法一:如下图,AD =62,AO =23AD =63,SO =SA 2-AO 2=233. ∴R 2=(233-R)2+23.∴R =32.球的体积为32π.解法二:构造棱长为1的正方体如上图,则C 1A 1BD 为棱长为2的正四面体,正方体的外接球也为正四面体的外接球.此时球的直径为3,因此球的体积为32π. 7.一个圆锥的侧面展开图的圆心角为90°,它的表面积为a ,则它的底面积为( ) A.a 5 B.a 3 C.a 2 D.a 4答案 A解析 设圆锥的母线长为l ,底面圆半径为r ,则2πr =l·π2,故l =4r ,由题意知πrl+πr 2=a ,所以πr 2=a5.8.若某空间几何体的三视图如图所示,则该几何体的体积是( )A.13B.23 C .1 D .2答案 C解析 空间几何体的直观图为平放的直三棱柱,且直三棱柱底面为直角三角形,两直角边边长分别为1和2,侧棱长为2,直接利用公式可知V =2×12×1×2=1.9.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如图所示,则该几何体的俯视图为( )答案 C解析 由正(主)视图可知去掉的长方体在正对视线的方向,从侧(左)视图可以看出去掉的长方体在原长方体的左侧,由以上各视图的描述可知C 选项的俯视图符合,C 正确. 10.两个半径为1的铁球,熔化成一个大球,则大球的表面积为( ) A .6π B .8π C .434π D .832π答案 C解析 大球的体积是2×4π3×13=8π3,设大球的半径为R ,则有4π3R 3=8π3,解得R =32,所以大球的表面积为4π(32)2=434π.故选C. 11.某几何体的三视图如图所示,则它的体积是( )A .8-2π3B .8-π3C .8-2π D.2π3答案 A解析 圆锥的底面半径为1,高为2,该几何体体积为正方体体积减去圆锥体积,即V =22×2-13×π×12×2=8-23π,正确选项为A.12.某几何体的三视图如图所示,其体积为( )A.103B.83 C.43 D.23答案 A解析 由已知中的三视图,可知该几何体是一个以边长为2的等腰直角三角形为底面的三棱柱,其高为2,切去了一个以边长为2的等腰直角三角形为底面的三棱锥,其高为1, ∴V 三棱柱=12×2×2×2=4,V 三棱锥=13×2×2×12×1=23.故得该几何体的体积为V =V 三棱柱-V 三棱锥=4-23=103,故选A.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.某几何体的三视图如图所示,则该几何体的体积是________.答案 16π-16解析 由三视图可知该几何体是一个底面半径为2,高为4的圆柱中间挖去一个底面边长为2,高为4的正四棱柱后剩下的部分,所以其体积为π×22×4-22×4=16π-16.14.若一个底面边长为62,侧棱长为6的正六棱柱的所有顶点都在一个球的面上,则此球的体积为________. 答案 43π解析 2R =(62×2)2+(6)2=23, ∴R =3,V 球=43πR 3=43π.15.若干毫升水倒入底面半径为2 cm 的圆柱形器皿中,量得水面的高度为6 cm ,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是________ cm. 答案 616.如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现:圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为________,________.答案32 32解析 设球的半径为R ,则圆柱的底面半径为R ,高为2R , ∴V 圆柱=πR 2×2R =2πR 3, V 球=4π3R 3,∴V 圆柱V 球=2πR 343πR3=32.∵S 圆柱=2πR ×2R +2×πR 2=6πR 2,S 球=4πR 2, ∴S 圆柱S 球=6πR 24πR 2=32. 三、解答题(本大题共6小题,共70分)17.(10分)一个几何体的三视图及其尺寸如下(单位:cm),求该几何体的表面积和体积.解析 由三视图知道该几何体是圆锥,且母线长为5 cm ,底面半径是3 cm ,圆锥的高是4 cm ,所以其表面积是S 表=π×3×(3+5)=24π cm 2, 其体积V =13π×32×4=12π cm 3.18.(12分)正方体的每条棱长都增加1 cm ,它的体积扩大为原来的8倍,求此正方体的棱长.答案 1 cm分析 利用待定系数法求解.设出正方体的棱长,根据体积扩大为原来的8倍列方程,解方程得正方体的棱长.设正方体的棱长为a cm ,由题意,得(a +1)3=8a 3,解得a =1,即此正方体的棱长为1 cm. 19.(12分)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积;解析 (1)如下图所示,(2)所求多面体体积V =V 长方体-V 正三棱锥 =4×4×6-13×(12×2×2)×2=2843(cm 3).20.(12分)已知六棱锥P -ABCDEF ,其中底面ABCDEF 是正六边形,点P 在底面的投影是正六边形的中心,底面边长为2 cm ,侧棱长为3 cm ,求六棱锥P -ABCDEF 的表面积和体积. 解析 先求底面正六边形的面积,S 六边形ABCDEF =6S △OBC =6×12×2×2sin60°=63(cm 2),S 侧面=6S △PCD =6×12×2×PC 2-(CD2)2=632-12=122(cm 2), ∴S P -ABCDEF =S 六边形ABCDEF +S 侧面 =(63+122)(cm 2). 在Rt △POC 中,PO =PC 2-OC 2=PC 2-BC 2=9-4=5(cm), ∴V 六棱锥P -ABCDEF =13Sh =13×63×5=215(cm 3).21.(12分)已知几何体A -BCED 如图(1)所示,其三视图如图(2)所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A -BCED 的体积为16.(1)求实数a 的值;(2)将直角三角形ABD 绕斜边AD 所在直线旋转一周,求该旋转体的表面积.解析 (1)由该几何体的三视图知AC 可视为几何体A -BCED 的高,且体积V =13×4×(a +4)×42=16,∴a =2. (2)在Rt △ABD 中,AB =42,BD =2,AD =6. 过点B 作AD 的垂线BH ,垂足为H ,易得BH =423.该旋转体由两个同底的圆锥构成,圆锥底面半径BH =423, 所以圆锥底面周长C =2π·423=823π,两个圆锥的母线长分别为42和2,故该旋转体的表面积S =12×82π3(2+42)=(32+82)π3.22.(12分)如图,是从上下底面处在水平状态下的棱长为a 的正方体ABCD -A 1B 1C 1D 1中分离出来的.(1)∠DC 1D 1在图中的度数和它表示的角的真实度数都是45°,对吗? (2)∠A 1C 1D 的真实度数是60°,对吗?(3)设BC =1 cm ,如果用图示中这样一个装置来盛水,那么最多能盛多少体积的水? 解析 (1)对; (2)对;(3)由题意知,以平面B 1CD 1为水平面,可盛最多体积的水,此时V 水=VC 1-B 1D 1C =VC -B 1C 1D 1=13×12×1×1×1=16(cm 3).∴最多能盛16cm 3的水.1.在正方体的八个顶点中,有四个顶点恰好是正四面体的顶点,则正方体的表面积与此正四面体的表面积之比为( ) A. 3 B. 2 C.62D.33答案 A解析 如图,设正方体的棱长为a ,则正四面体A -B 1D 1C 的所有棱长均为2a.正方体的表面积S 1=6a 2, 正四面体的表面积S 2=4×34×(2a)2=23a 2. ∴S 1∶S 2=6a 2∶23a 2=3∶1.2.一平面截一球得到直径是6 cm 的圆面,球心到这个平面的距离是4 cm ,则该球的体积是( ) A.100π3 cm 3B.208π3 cm 3C.500π3 cm 3D.41613π3cm 3答案 C解析 设球的半径为R ,则32+42=R 2,故R =5.所以球的体积为V =43πR 3=43π×125=500π3(cm 3).3.设某几何体的三视图如下(尺寸的长度单位为m)则该几何体的体积为________ m 3. 答案 4解析 这是一个三棱锥,高为2,底面三角形一边为4,这边上的高为3,体积等于16×2×4×3=4.4.画出下列两物体的三视图:答案 (1)三视图甲; (2)三视图乙.。
