第5章 推理与证明技术
推理与证明

推理与证明Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】第3讲推理与证明【知识要点】1.归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或由个别事实概括出一般结论的推理2.类比推理是从特殊到特殊的推理,是寻找事物之间的共同或相似性质。
类比的性质相似性越多,相似的性质与推测的性质之间的关系就越相关,从而类比得出的结论就越可靠。
3.类比推理的一般步骤:①找出两类事物之间的相似性或者一致性。
②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想)【典型例题】1、(2011江西)观察下列各式:72=49,73=343,74=2401,…,则72011的末两位数字为()A、01B、43C、07D、492、(2011江西)观察下列各式:55=3125,56=15625,57=78125,…,则52011的末四位数字为()A、3125B、5625C、0625D、81253、(2010临颍县)平面内平行于同一条直线的两条直线平行,由此类比思维,我们可以得到()A、空间中平行于同一平面的两个平面平行B、空间中平行于同一条直线的两条直线平行C、空间中平行于同一条平面的两条直线平行D、空间中平行于同一条直线的两个平面平行4、(2007广东)设S是至少含有两个元素的集合,在S上定义了一个二元运算“*”(即对任意的a,b∈S,对于有序元素对(a,b),在S中有唯一确定的元素与之对应)有a*(b*a)=b,则对任意的a,b∈S,下列等式中不恒成立的是()A、(a*b)*a=aB、[a*(b*a)]*(a*b)=aC、b*(b*b)=bD、(a*b)*[b*(a*b)]=b5、(2007广东)如图是某汽车维修公司的维修点环形分布图.公司在年初分配给A,B,C,D四个维修点某种配件各50件.在使用前发现需将A,B,C,D四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为()A、15B、16C、17D、186、(2006陕西)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3, 4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为()A、4,6,1,7B、7,6,1,4C、6,4,1,7D、1,6,4,77、(2006山东)定义集合运算:A⊙B={z︳z=xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为()A、0B、6C、12D、188、(2006辽宁)设⊕是R上的一个运算,A是V的非空子集,若对任意a,b∈A,有a⊕b∈A,则称A对运算⊕封闭.下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是()A、自然数集B、整数集C、有理数集D、无理数集9、(2006广东)对于任意的两个实数对(a,b)和(c,d),规定:(a,b)=(c,d),当且仅当a=c,b=d;运算“”为:(a,b)(c,d)=(ac-bd,bc+ad);运算“⊕”为:(a,b)⊕(c,d)=(a+c,b+d),设p,q∈R,若(1,2)(p,q)=(5,0),则(1,2)⊕(p,q)=()A、(4,0)B、(2,0)C、(0,2)D、(0,-4)10、(2005湖南)设f0(x)=sinx,f1(x)=f′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2005(x)=()A、sinxB、-sinxC、cosxD、-cosx11、(2004安徽)已知数列{an}满足a0=1,an=a+a1+…+an-1 ,n≥1、,则当n≥1时,an=()A、2nB、C、2n-1D、2n-112、若数列{an}满足a1=1,a2=2,an=(n≥3且n∈N*),则a17=()A、1B、2C、D、2-98713、如图所示的三角形数阵叫“莱布尼兹调和三角形”,有,则运用归纳推理得到第11行第2个数(从左往右数)为()A、 B、 C、 D、14、根据给出的数塔猜测1 234 567×9+8=()1×9+2=1112×9+3=111123×9+4=1 1111 234×9+5=11 11112 345×9+6=111 111.15、将n个连续自然数按规律排成右表,根据规律,从2008到2010,箭头方向依次是()A、 B、 C、 D、16、下列推理过程利用的推理方法分别是()(1)通过大量试验得出抛硬币出现正面的概率为;(2)函数f(x)=x2-|x|为偶函数;(3)科学家通过研究老鹰的眼睛发明了电子鹰眼.A、演绎推理,归纳推理,类比推理B、类比推理,演绎推理,类比推理C、归纳推理,合情推理,类比推理D、归纳推理,演绎推理,类比推理17、下列表述正确的是()①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.A、①②③B、②③④C、②④⑤D、①③⑤18、在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形,则第n个三角形数为()A、nB、C、n2-1D、1、(2011陕西)观察下列等式1=12+3+4=93+4+5+6+7=254+5+6+7+8+9+10=49照此规律,第五个等式应为 5+6+7+8+9+10+11+12+13=81.2、(2011陕西)观察下列等式1=12+3+4=93+4+5+6+7=254+5+6+7+8+9+10=49…照此规律,第n个等式为 n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2 .。
推理与证明复习课HW上课课件

01
02
03
04
掌握推理与证明的基本概念和 原则
熟悉各种推理和证明的方法和 技巧
能够运用所学知识解决实际问 题
培养逻辑思维能力,提高分析 问题和解决问题的能力
02 推理部分复习
直接推理
01
02
03
定义
直接推理是从已知事实出 发,通过逻辑演绎得出结 论的过程。
例子
如果A(事实)发生,则B (结论)一定发生。
构造法
总结词
构造法是一种通过构造具体的实例或反例来证明或反驳命题的方法,常常用于 解决一些难以用常规方法证明的数学问题。
详细描述
构造法需要找到与问题相关的具体实例或反例,通过这些实例或反例的性质和 特点来证明或反驳命题。这种方法需要一定的创造性和想象力,但有时可以解 决一些非常棘手的问题。
反证法在证明中的应用
05 练习题与答案
练习题一
总结词
基础推理练习
详细描述
此练习题主要考察学生的基础推理能力,涉及逻辑推理的基本规则和概念,适合初学者练习。
练习题二
总结词
复杂逻辑推理
详细描述
此练习题难度较大,需要学生综 合运用逻辑推理规则和技巧,解 决复杂的逻辑推理问题。
练习题三
总结词
证明题练习
详细描述
此练习题重点考察学生的证明能力,需要学生根据已知条件,运用逻辑推理规则,完成 数学命题的证明。
推理与证明复习课hw上课课件
目录
• 引言 • 推理部分复习 • 证明部分复习 • 经典例题解析 • 练习题与答案 • 总结与展望
01 引言
课程简介
课程名称
推理与证明复习课
适用对象
对推理和证明感兴趣的学生,具备一定数学基础
推理证明与证明方法

推理证明与证明方法推理是指通过一系列逻辑性的推导和推论,从已有的前提得出结论的过程。
在数学、哲学、逻辑学和科学研究等领域中,推理是一种重要的思维方式和证明方法。
本文将探讨推理证明的基本概念、推理的类型以及常见的证明方法。
一、推理证明的基本概念推理证明是指基于已知事实和前提,通过逻辑推导和推论的方式,得出一个结论或者证明一个命题的过程。
其目的是通过合理和严密的推理,使得结论具有说服力,能够被他人接受。
推理证明的过程通常分为两个步骤:前提和推导。
前提是指已知的事实、定理或假设,推导是在前提的基础上通过逻辑关系进行推演,从而得到新的结论。
推演的过程中,可以使用各种推理方法和推理规则。
二、推理的类型根据推理的方式和形式,推理可以分为直接推理和间接推理两种类型。
1. 直接推理:直接推理是通过已知的前提和一系列逻辑推理规则,直接得出结论的推理方式。
例如,对于一个条件命题“A蕴含B”,如果已知“A为真”,那么可以直接推导出“B为真”。
2. 间接推理:间接推理是通过否定前提的逻辑关系,从而得到结论的推理方式。
例如,通过反证法可以证明一个命题的真伪。
假设目标命题为真,然后通过逻辑推理推导到一个矛盾的结论,从而推断目标命题为假。
三、常见的证明方法为了实现证明的目的,推理过程中常采用多种证明方法。
以下介绍几种常见的证明方法。
1. 直接证明法:直接证明法是通过直接推理的方式,从已知的前提出发,逐步推导证明目标命题的真伪。
例如,对于证明一个数是偶数的命题,可以通过直接证明“该数能被2整除”来得到结论。
2. 归谬法:归谬法是一种间接证明法,通过假设目标命题为假,然后逐步推导到一个矛盾的结论,从而证明目标命题为真。
这种方法常用于证明一个命题的唯一性或者不存在性。
3. 数学归纳法:数学归纳法是一种证明数学命题的常用方法。
它分为基础步和归纳步两个阶段。
首先证明基础步,即证明当n取某个特定值时,命题成立;然后证明归纳步,假设当n=m时命题成立,再证明当n=m+1时命题也成立。
(整理版)回顾《推理与证明》
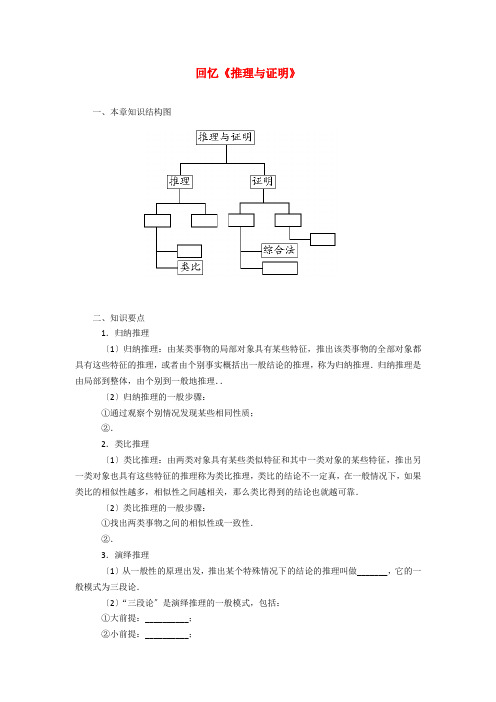
回忆《推理与证明》一、本章知识结构图二、知识要点1.归纳推理〔1〕归纳推理:由某类事物的局部对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理.归纳推理是由局部到整体,由个别到一般地推理..〔2〕归纳推理的一般步骤:①通过观察个别情况发现某些相同性质;②.2.类比推理〔1〕类比推理:由两类对象具有某些类似特征和其中一类对象的某些特征,推出另一类对象也具有这些特征的推理称为类比推理,类比的结论不一定真,在一般情况下,如果类比的相似性越多,相似性之间越相关,那么类比得到的结论也就越可靠.〔2〕类比推理的一般步骤:①找出两类事物之间的相似性或一致性.②.3.演绎推理〔1〕从一般性的原理出发,推出某个特殊情况下的结论的推理叫做_______,它的一般模式为三段论.〔2〕“三段论〞是演绎推理的一般模式,包括:①大前提:__________;②小前提:__________;③结论:根据一般原理,对特殊情况做出的判断.4.综合法一般地,利用条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.5.分析法一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归纳为判定一个明显成立的条件〔条件、定理、定义、公理等〕,这种证明的方法叫做分析法.6.反证法.三、考前须知1.归纳和类比都是____________.前者是由特殊到一般,局部到整体的推理,后者是由___________到特殊的推理,但二者都能由推测未知,都能用于猜测,推理的结论不一定为真,有待进一步证明.2.演绎推理与合情推理不同,是由______到特殊的推理,是数学证明的根本推理形式,也是公理化体系所采用的推理形式.另一方面,合情推理与演绎推理又是相辅相成的,前者是后者的前提,后者论证前者的可靠性.3.______和_______是数学证明的两类根本证明方法.直接证明的两类根本方法是_______和_______,_________是从条件推导出结论的证明方法;_________是由结论追溯到条件的证明方法,在解决数学问题时,常把它们结合起来使用.间接证法的一种根本方法是__________,它是从结论反面成立出发,推出矛盾的证明方法.。
推理与证明精品课件

*对应演练*
如图是三个拼在一起的正方形,求证:α+β=
π . 4
证明:根据题意,0<α<
1 ∴0<α+β<π,又tanα= , 3 1 1 + tanα + tanβ 2 3 = 1. ∴tan(α+β)= = 1 1 1 - tanα ·tan β 1- • 2 3 π ∵0<α+β<π,∴α+β= . 4
判定一个明显成立的条件(已知条件、定理、定义、公理等)为
止,这种证明方法叫做分析法.
四、间接证明 反证法是间接证明的一种基本方法. 一般地,假设 原命题 不成立(即在原命题的条件 下,结论不成立),经过正确的推理,最后得出 矛盾 ,
因此说明假设错误,从而证明了原命题成立,这样的证 明方法叫做反证法.
【证明】要证
2
2 )2 .
即 a2 +
1 1 2 2 +4 a + 2 +4 a a 1 1 2 ≥ + 2 + 2 + 2 2 (a + ) + 2 a a a
2
1 1 从而只要证 2 a + 2 ≥ 2 (a + ) a a 1 1 2 2 只要证 4(a + 2 ) ≥ (a + 2 + 2 ) 2 a a 1 2 2 即 a + 2 ≥ ,而上述不等式显然成立, a
在△ABD中,AD⊥BC,即∠ADB=90°—— 小前提 所以△ABD是直角三角形
(2)因为直角三角形斜边上的中线等于斜边的一半
——大前提
而M是Rt△ABD斜边AB的中点,DM是斜边上的中线 ——小前提
第五章 复合命题及其推理

“只有努力学习,才能取得好成绩。”可转换为 “只有没有取得好成绩,才没有努力学习。”
要领 否定式:调换否定前后件,不换联结词。
四、充分条件、必要条件假言命题和选言命题 间的转换
联言命题一般用并列、递进、转折、顺承 关系的复句表达,有时也用单句。 郭沫若是历史学家和文学家。 苏步青和华罗庚都是数学家。 和平和发展是中印两国人民的共同愿望。
2、构成
①联言支:即构成联言命题的支命题。 ②联言联项:即联结联言肢的联结词 二肢联言命题的逻辑形式:p并且q或 p∧q 联项有时可以省略
2、构成 ①选言支:即构成选言命题的支命题。 ②选言联项:即联结选言支并确定选言支之 间关系的联结词。 一个人的死,或重于泰山,或轻于鸿毛。 不是鱼死,就是网破。 他也许是数学家,也许是哲学家。
(二)选言命题的种类
1、相容选言命题 ①什么是相容选言命题 是反映若干可能的对象情况中至少有一种 存在的复合命题。 这场球赛失败的原因或者是队员技术水 平不高,或者是队员之间配合不好。 这场战争的失败或因兵力弱,或因指挥 失误。
二、假言命题的种类
(一)充分条件假言命题 1、什么是充分条件和充分条件假言命题 ①什么是充分条件 在情况p和q之间,有p必有q;无p未 必无q,这时p是q的充分条件。 A、p:摩擦 q:生热 B、p:x等于2 q:x的平方等于4 ◆“有之必然,无之未必不然”的条 件。
②什么是充分条件假言命题
就是反映一事物情况存在是另一事物 情况存在的充分条件的假言命题。
(二)复合命题推理的种类 联言推理、选言推理、假言推理和负 命题等值关系推理四种基本类型。
第二节
联言命题和选言命题
一、联言命题 (一)联言命题及其构成 1、什么是联言命题 是反映若干事物情况同时存在的复合 命题。
推理与证明

学案:推理与证明一、基础知识讲解1.推理一般包括合情推理和演绎推理.2.合情推理:根据已有的事实和正确的结论(包括定义、公理、定理等)、实验和实践的结果,以及个人的经验和直觉等推测某些结果的推理过程.归纳、类比是合情推理常用的思维方法.3.归纳推理:根据一类事物的部分对象具有某种性质,推出这类事物的所有对象都具有这种性质的推理.4.归纳推理的一般步骤:⑴通过观察个别情况发现某些相同性质;⑵从已知的相同性质中推出一个明确表达的一般性命题(猜想).5.类比推理:根据两类不同事物之间具有某些类似性,推出其中一类事物具有另一类事物类似的性质的推理.6.类比推理的一般步骤:⑴找出两类事物之间的相似性或一致性;⑵从一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).7.演绎推理:根据一般性的真命题导出特殊性命题为真的推理.8.直接证明的两种基本方法:分析法和综合法;间接证明的一种基本方法──反证法.9.分析法:从原因推导到结果的思维方法.10.综合法:从结果追溯到产生这一结果的原因的思维方法.11.反证法:判定非q为假,推出q为真的方法.12.应用反证法证明命题的一般步骤:⑴分清命题的条件和结论;⑵做出与命题结论相矛盾的假定;⑶由假定出发,应用正确的推理方法,推出矛盾的结果;⑷间接证明命题为真.13.数学归纳法:设{p n}是一个与自然数相关的命题集合,如果⑴证明起始命题p1成立;⑵在假设p k成立的前提上,推出p k+1也成立,那么可以断定,{p n}对一切正整数成立.14.数学归纳法的步骤:(1)证明当(如或2等)时,结论正确;(2)假设时结论正确,证明时结论也正确.二、疑难知识导分析讲解1.归纳推理是根据一类事物的部分对象具有某种性质,推出这类事物的所有对象都具有这种性质的推理. 而类比推理是根据两类不同事物之间具有某些类似性,推出其中一类事物具有另一类事物类似的性质的推理.2.应用反证法证明命题的逻辑依据:做出与命题结论相矛盾的假定,由假定出发,应用正确的推理方法,推出矛盾的结果3. 数学归纳法是一种证明方法,归纳推理是一种推理方法.三、经典例题讲解a}是正数组成的数列,其前n项和为n s,并且对于所有的自然数n,n a与2的等差中项等于[例1] {ns与2的等比中项.na}的前3项;(1)写出数列{na}的通项公式(写出推证过程);(2)求数列{n[例2] 用数学归纳法证明对于任意自然数,[例3]是否存在自然数m,使得对任意自然数,都能被整除,若存在,求出的最大值,并证明你的结论;若不存在,说明理由.[例4] 设点1A 是曲线C :)0,0(1>>=y x xy 与直线x y =的交点,过1A 点作直线x y =的垂线交轴于1B ,过1B 点作直线x y =的平行线交曲线C 于2A ,再过2A 点作1B 2A 的垂线作交X 轴于2B ,如此继续下去可得到一系列的点,,…,,…如图,试求的横坐标的通项公式.[例5] 有n 个圆,其中每两个圆都相交于两点,并且每三个圆都不相交于同一点,求证:这n 个圆把平面分成f(n)=n 2-n +2个部分.[例6] 已知n ≥2,n ∈N ,求证:1221)1211()711)(511)(311(+>-++++n n四、巩固练习1.用数学归纳法证明等式“1+2+3+…+(n +3)=2)4)(3(++n n (n N )”,当n =1时,左边应为____________.2.已知数列{n a }的前n 项和n n a n s -=2,则{n a }的前四项依次为_______,猜想n a =__________.3.已知数列:,}{且满足的各项都是正数n a .),4(,21,110N n a a a a n n n ∈-==+证明N n a a n n ∈<<+,21.4.已知不等式n n n 其中],[log 21131212>+++ 为大于2的整数,][log 2n 表示不超过n 2log 的最大整数. 设数列}{n a 的各项为正,且满足 ,4,3,2,),0(111=+≤>=--n a n na a b b a n n n 证明,5,4,3,][l o g 222=+<n n b ba n .5. 自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用x n 表示某鱼群在第n 年年初的总量,n ∈N *,且x 1>0.不考虑其它因素,设在第n 年内鱼群的繁殖量及捕捞量都与x n 成正比,死亡量与x n 2成正比, 这些比例系数依次为正常数a ,b ,c. (1)求x n+1与x n 的关系式;(2)猜测:当且仅当x 1,a ,b ,c 满足什么条件时,每年年初鱼群的总量保持不变?(3)设a =2,c =1,为保证对任意x 1∈(0,2),都有x n >0,n ∈N *,则捕捞强度b 的 最大允许值是多少?证明你的结论.。
推理与证明的基本方法

推理与证明的基本方法推理和证明是逻辑学和数学中的两个重要概念。
它们在我们日常思考和解决问题的过程中发挥着至关重要的作用。
本文将介绍推理和证明的基本方法,包括归纳法、演绎法和逆证法等。
一、归纳法归纳法是一种从特殊到一般的推理方法。
它基于观察和实验的结果,通过总结和概括个别事实或情况的规律性,得出普遍规律性的结论。
归纳法常被应用于科学研究和实证研究中。
例如,根据对大量数据的观察,我们可以归纳出某种事物的一般特征或规律。
二、演绎法演绎法是一种从一般到特殊的推理方法。
它基于一系列前提条件和逻辑关系,通过严密的推理推导,得出特殊情况下的结论。
演绎法常被应用于数学和逻辑推理中。
例如,根据一定的数学定理和公理,我们可以通过演绎法推导出具体的数学问题的解决方法。
三、逆证法逆证法是证明方法中的一种。
它常用于证明数学命题的正确性。
逆证法的基本思想是通过假设命题为假,然后推导出与已知事实矛盾的结论,从而证明命题实际为真。
逆证法常用于解决一些较为复杂的数学问题,尤其是涉及到数学定理的证明中。
四、数学归纳法数学归纳法是一种证明自然数性质的方法。
它分为一阶数学归纳法和二阶数学归纳法,其中一阶数学归纳法最为常用。
一阶数学归纳法的证明过程包括两个步骤:首先证明当n为某个特定值时命题成立,然后假设当n=k时命题成立,再用此假设来证明当n=k+1时命题也成立。
通过这种逐个推理的方式,我们可以证明自然数性质适用于所有自然数。
总结:推理与证明是思考和解决问题的基本方法。
归纳法通过总结和概括观察结果,得出普遍规律性的结论;演绎法通过严密的推理推导,得出特殊情况下的结论;逆证法通过假设命题为假,推导出与已知事实矛盾的结论,从而证明命题实际为真;数学归纳法用于证明自然数性质的正确性。
在实际问题的解决中,我们可以根据具体情况选择适当的推理和证明方法,从而得出准确和可靠的结论。
侦探学园Q 挑战究极诡计【攻略】

17.警卫室
a.询问的闪光点
.上岛康之——资料室的钥匙
18.教师室
a.询问的闪光点
.宫本秀久——和成濑分别之后
关于管理楼
b.调查的闪光点
.红书旁边的桌子
19.资料室
a.调查的闪光点
.门口的残渣(好像是点心的渣子)
.门
20.紧急楼梯
a.调查的闪光点
.门边的盒子(是空的点心袋子)
19.本州的毒蛇——赤栋蛇
20.氧化物非金属元素单体——黄磷
21.石蕊试纸从哪里提炼——青苔
二、铠武者杀人事件
1.摩天轮升降场
a.调查的闪光点
.地上的脚印(留下的不是脚印吗)
.画面右边的地面(拖过什么的痕迹)
.花丛(花丛里的花枯萎了)
2.公园内道路
a.询问的闪光点
.成濑俊则——关于久武圭吾(董事长的继承人应该就是)
关于录像记录室(跑出了一小群人)
11.公园内道路
a.询问的闪光点
.成濑俊则——关于圭吾的铠甲(谋反武将的铠甲)
关于录像记录室
关于董事长(有个私生子)
12.录像记录室
a.调查的闪光点
.顶上的显示器
.桌上的电脑边(这个装置真棒)
.电脑桌上的白布条(居然有根布条)
.画面右侧抽屉处(有条数据线连着)
13.公园内道路
17.检测指纹使用的金属粉——铝
18.由暗适应亮——1分钟
19.由亮适应暗——1小时
20.游戏汉化作者——NAILGO
二、不在场证据之壁
1.运动公园
a.询问闪光点:
.若杉纪美——刚才说了些什么
事件的关系人
认识犯人吗
人工智能中的自动化推理与证明技术

人工智能中的自动化推理与证明技术人工智能(Artificial Intelligence,AI)是当今科技领域的热门话题,其不断发展和普及正在深刻地改变着人类社会的方方面面。
在人工智能的众多分支领域中,自动化推理与证明技术(Automated Reasoning and Proof Technology)作为其中的重要组成部分,其在推理和证明过程中的应用正在逐渐受到重视和应用。
自动化推理与证明技术是指利用计算机技术,通过对逻辑规则和知识库的深度分析和推理,自动化地生成推论和证明结果的过程。
这种技术不仅在人工智能领域中具有重要意义,同时也在数学、计算机科学、哲学等领域中有着广泛的应用和价值。
在人工智能领域,自动化推理与证明技术主要通过逻辑推理、规则推理、知识表示等方式,帮助计算机系统模拟人类的推理和决策过程,实现智能化的功能。
通过对大量已知的事实和规则进行深度学习和分析,计算机系统可以自动化地生成推论和结论,从而为人类在决策、问题解决、智能控制等方面提供强大的支持和帮助。
自动化推理与证明技术的应用范围非常广泛,涵盖了人类社会生活中的各个领域。
在工业生产中,自动化推理技术可以帮助企业优化生产流程,提高效率和质量;在医疗健康领域,这种技术可以辅助医生进行诊断和治疗决策,提高医疗水平和效率;在交通运输领域,自动化推理技术可以帮助交通管理部门实现智能交通管控,缓解交通拥堵问题。
除了在应用领域中的重要作用外,自动化推理与证明技术在学术研究领域也具有重要意义。
通过对逻辑规则和知识库的深度分析和推理,研究人员可以深入探讨数学、哲学等领域中的一些复杂问题,推动学科的发展和进步。
例如,在人工智能领域中,研究人员通过对博弈论、逻辑推理等问题的深入研究,推动了智能算法和智能系统的发展和应用。
自动化推理与证明技术的发展壮大离不开相关领域的学术研究和产业实践的支持。
在学术界,研究人员们通过对不同领域中的逻辑规则和知识库的深入挖掘和分析,推动了自动化推理技术的不断创新和进步。
逻辑推理与证明方法总结

逻辑推理与证明方法总结逻辑推理和证明方法是逻辑学领域中非常重要的概念和方法。
在这篇文章中,我们将讨论逻辑推理和证明方法的基本概念、常见的形式以及它们在解决问题和判断正确性方面的作用。
一、逻辑推理的基本概念逻辑推理是基于形式逻辑的方法,通过推断来得出结论。
它不依赖于实际情况,而只关注逻辑关系的合理性。
逻辑推理可以分为两种类型:演绎推理和归纳推理。
1. 演绎推理:演绎推理是从一般规则或前提中推导出特定结论的过程。
它基于“如果…那么…”的逻辑形式,又称为条件推理。
演绎推理可分为三种形式:假言推理、拒取推理和三段论。
2. 归纳推理:归纳推理是从特殊案例中推导出一般规律的过程。
它基于观察和经验,并通过类比和概率来得出结论。
归纳推理常用于科学实验、统计分析和常识判断等领域。
二、常见的证明方法证明方法是通过推理和逻辑推导来证明某个命题或结论的有效方法。
下面是几种常见的证明方法:1. 直接证明法:直接证明法通过逻辑推理和前提的已知条件,直接得出结论的正确性。
它通常使用“假设-推导-结论”的结构,逐步推导出最终的结论。
2. 反证法:反证法通过假设反面命题为真,然后通过推理推导出矛盾的结论,从而证明原命题为假。
反证法常用于证明数学定理和逻辑命题。
3. 归谬法:归谬法是通过证明某个命题的反面导致自相矛盾的结论,从而推翻该反命题,进而证明原命题的正确性。
4. 数学归纳法:数学归纳法是通过证明命题对某个基础情况成立,然后证明对于任意情况都成立的方法。
它将问题分解为基础情况和递推情况两部分,通过归纳法证明了所有情况都满足命题。
三、逻辑推理和证明方法的应用逻辑推理和证明方法广泛应用于数学、哲学、计算机科学等领域,具有重要的理论和实践意义。
1. 在数学中,逻辑推理和证明方法是数学证明的基础。
数学家通过逻辑推理和证明方法建立了数学定理和公理体系,为数学研究提供了强大的工具。
2. 在哲学中,逻辑推理和证明方法是研究思维、知识和真理的重要工具。
《推理与证明二》PPT课件

A
A.充分条件 C.充要条件
B.必要条件 D.等价条件
分析法是执果索因,允许原因能推出结论 即可,并不一定需要充要条件,故必须为充分条件.
2.若a,b∈R,且a≠b,有下列四个式子
①a2+ab>2b2;
②a5+b5>a3b2+a2b3;
③a2+b2≥2(a-b-1); ④ + >2.
其中一定成立的有( )
典例精讲
题型一 用综合法证明 例1已知点P是直角三角形ABC所在平面外的一点,O
是斜边AB的中点,并且PA=PB=PC,求证:PO⊥平面 ABC.
分析要证明PO⊥平面ABC,也就是要证明PO
垂直于平面ABC内的两条相交直线.
连接OC,OP,如图所示, 因为AB是Rt△ABC的斜边,O是AB的中点, 所以OA=OB=OC. 又因为PA=PB=PC, 所以△POA≌△POB≌△POC, 所以∠POA=∠POB=∠POC. 因为∠POA+∠POB=180°,所以∠POA=∠POB=90°,所以∠P
又因为a+b+c>0,所以b+c>-a>0, 所以ab+bc+ac=a(b+c)+bc<0. 这与已知ab+bc+ac>0矛盾,所以a<0也不可能. 综上述,a>0成立. 同理可知b>0,c>0成立.
所以原命题得证.
点评 反证法证明问题的一般步骤是:(1)反设:
假设所要证明的结论不成立,也就是假设在已知条 件下,存在与要证明的结论相反的情形;(2)归谬: 由反设出发,结合已知条件,通过正确的逻辑推理, 推得矛盾;(3)存真:由所得的矛盾断言反设不真, 从而肯定原命题的正确性.
第5章推理与证明技术

7/1故5/2:020G1∧G2∧…∧Gn→H是永真公式。
8
电子科技大学离散数学课程组——国家精品课程
判定定理(续)
“”若G1∧G2∧…∧Gn→H是永真式,但G1, G2, …,Gn H不是有效的推理形式,
故存在G1, G2, …,Gn, H的一个解释I,使 得G1, G2, …,Gn都为真,而H为假,故 G1∧G2∧…∧Gn为真,而H为假,即是说 G1∧G2∧…∧Gn →H为假,这 就与 G1∧G2∧…∧Gn→H是永真式相矛盾,
公式。
7/15/2020
10
电子科技大学离散数学课程组——国家精品课程
5.2.2 判断有效结论的常用方法
要求
Г={G1, G2, …,Gn} Г H
也就是 G1∧G2∧…∧Gn→H 为永真公式
因而 真值表技术、演绎法和 间接证明方法
7/15/2020
11
电子科技大学离散数学课程组——国家精品课程
引入事实
事实库
规则匹配
新事实
事实=结论?
触发规则
N
公理库
将事实加入到事实库中
Y 结束
7/15/2020
19
电子科技大学离散数学课程组——国家精品课程
引入推理规则
在数理逻辑中,主要的推理规则有: ① P规则(称为前提引用规则):在推导的过程中, 可随时引入前提集合中的任意一个前提; ② 规则T(逻辑结果引用规则):在推导的过程 中,可以随时引入公式S,该公式S是由其前的一个 或多个公式推导出来的逻辑结果。 ③ 规则CP(附加前提规则):如果能从给定的 前提集合Г与公式P推导出S,则能从此前提集合Г 推导出P→S。
结论:陈某是凶手。
则可描述为:P→R,┐R ┐P
推理与证明方法PPT共40页

•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起之苗,不见其增,日 有所长 。
பைடு நூலகம்
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
推理与证明方法
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
第五章 论证与推理

[思考] 以下的推理有效吗?
[推理6] 真理都经得起实践检验 法轮功不是真理
---------------------------------------所以,法轮功经不起实践检验
[推理7] 只有社会主义能够救中国 我们坚持社会主义
-------------------------------所以我们能够救中国
(推理6和推理6#的结构)
同样,推理7和推理7#具有如下相同的推理形式: 只有p,才q p -------------------所以,q 推理7#无效说明该推理形式无效,即该形式不能保证
从真前提一定得出真结论,该推理形式无效说明具有该形 式的任一推理都无效,因而推理7无效,尽管推理7的前提 和结论都是真的。
[例4] 所有的人都有思想。狗不是人。所以,狗没有思想。
通过以下哪个推理,能最有力地说明上述推理不成立?
A.所有商品都是劳动产品。太阳光不是商品。因此,太阳光 不是劳动产品。
推理6#无效足以说明推理6无效;推理7#无效足以说明推理 7无效。为什么呢?
事实上,推理6和推理6#具有如下相同的推理形式: 所有M都是P S不是M ---------------------
所以,S不是M 推理5#无效说明该推理形式无效,即该形式不能保证从真 前提一定得出真结论;该推理形式无效说明具有该形式的任 一推理都无效,因而推理5无效,尽管推理5的前提和结论都 是真的。
证据支持度为0证据支持度小于100但是很高证据支持度小于100但是较高证据支持度无值推理1所有的金属都是导电的铁是金属所以铁是导电的推理2铁是导电的铜是导电的银是导电的锡是导电的金是导电的金银铜铁锡都是金属所以金属都是导电推理32005北京有人的寿命是399岁所以2006北京有人可能活到400岁推理4实践是检验真理的唯一标准所以马克思主义理论是检验真理的标准推理5北京2005年元霄下大雪所以2004年中国载人飞船发射成功推理1的证据支持度是100
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.2
命题逻辑的推理理论
推理 判断
概念 描述问题 的句子;
对概念的肯 Add Your Text 定与否定的 判断;
从一个或多 个前提推出 结论的思维 过程。
2016/2/4
4
电子科技大学离散数学课程组——国家精品课程
推理的有效性和结论的真实性
有效的推理不一定产生真实的结论; 而产生真实结论的推理过程未必是有效的。
推理定律(续)
(选言/析取三段论)
I11:┐G, G H H
6)I10:┐G, G∨H H
7)I12:G, G→H H
(分离规则)
8)I13:┐H, G→H ┐G (否定后件式) 9)I14:G→H, H→I G→I (假言三段论) 10)I15:G∨H, G→I, H→I I (二难推论)
3.王某案发之晚并未外出。 结论:陈某是凶手。 则可描述为:P→R,┐R ┐P P∨Q,┐P Q
2016/2/4
┐R
Q (否定后件式) (选言三段论)
17
电子科技大学离散数学课程组——国家精品课程
例子(续2)
4)、前提: 1.如果某同学为省二级以上运动员,则他 将被大学录取。 P→R 2.如果某同学高考总分在560分以上,则 将被大学录取。 Q→R 3.某同学高考总分在560分以上或者是省 二级运动员。 P∨Q 结论:该同学被大学录取。 R 则上述例子可描述为: P∨Q,P→R,Q→R R
2016/2/4
16
电子科技大学离散数学课程组——国家精品课程
例子(续1)
3)、某人在某日晚归家途中被杀害,据多方调查确 证,凶手必为王某或陈某,但后又查证,作案之晚 王某在工厂值夜班,没有外出,根据上述案情可得: 前提:1.凶手为王某或陈某。 P∨Q
2.如果王某是凶手,则他在作案当晚必外 出 P→R
2016/2/4
25
电子科技大学离散数学课程组——国家精品课程
例5.2.4
设n是一个整数,证明:如果n2是奇数,那么n 是奇数。
证明 设n是偶数,则n=2k,这里k是一个整数。 于是有: n2=(2k)2=4k2=2(2k2) 所以n2是偶数。 因而证明了若n是偶数,则n2是偶数,它是已知 命题的逆否式。因此,证明了所给的命题。
推导出P→S。
2016/2/4
20
电子科技大学离散数学课程组——国家精品课程
演绎的定义
定义5.2.2 从前提集合Г 推出结论H的一个演绎是指构造 命题公式的一个有限序列:
H1,H2,„„,Hn
其中,Hi或者是Г 中的某个前提,或者是前面
的某些Hj(j<i)的有效结论,并且Hn就是H,则
称公式H为该演绎的有效结论,或者称从前提Г 能 够演绎出结论H来。
G1∧G2∧„∧Gn为真,而H为假,即是说
G1∧G2∧„∧Gn →H为假,这
就与
G1∧G2∧„∧Gn→H是永真式相矛盾, 所以G1, G2, „,Gn H是有效的推理形式。
2016/2/4
9
电子科技大学离散数学课程组——国家精品课程
“”与“→”的不同
1.“→”仅是一般的蕴涵联结词,G→H的结果仍是一个公
2016/2/4
故:G1∧G2∧„∧Gn→H是永真公式。
8
电子科技大学离散数学课程组——国家精品课程
判定定理(续)
“”若G1∧G2∧„∧Gn→H是永真式,但G1,
G2, „,Gn H不是有效的推理形式,
故存在G1, G2, „,Gn, H的一个解释I,使
得G1, G2, „,Gn都为真,而H为假,故
有效的推理中可能包含为“假”的前提,
而无效的推理却可能得到为“真”的结论 。
2016/2/4
5
电子科技大学离散数学课程组——国家精品课程
推理的有效性和结论的真实性
所谓推理有效,
指的是它的结论是它的前提的合乎逻辑的结果。
即,如果它的前提都为真,那么所得的结论也
必然为真,而并不是要求前提或结论一定为真或为 假; 如果推理是有效的话,那么不可能它的前提都为 真时,而它的结论为假。
2016/2/4
(二难推论)
18
电子科技大学离散数学课程组——国家精品课程
3
演绎法
演绎法是从前提(假设)出发,依据公认的推理 规则和推理定律,推导出一个结论来。
引入事实 事实库 规则匹配 新事实
事实=结论?
触发规则
公理库
NY结束来自将事实加入到事实库中2016/2/4
19
电子科技大学离散数学课程组——国家精品课程
P Q G1 1 G2 H 1 1 P 0 1 1 Q G1 G2 H 0 0 1 1 0 0 (3)
13
P Q G1 G2 H
1 0 1
0 0 1
0 1 0
1 1
0 1
1 0 1 1
1
0 1 (2)
0
1 0
1
0 0
0 1 1
1 1
电子科技大学离散数学课程组——国家精品课程
2
推理定律
(简化规则) (添加规则) I2:G∧H H I4:H G∨H
电子科技大学离散数学课程组——国家精品课程
离散数学
电子科技大学
计算机科学与工程学院
示 范 性 软 件 学 院
2016年2月4日星期四
电子科技大学离散数学课程组——国家精品课程
第5章
推理与证明技术
1 2 3 4
命题逻辑的推理理论 谓词逻辑的推理理论 数学归纳法的使用
CP规则相关证明
2016/2/4
2
电子科技大学离散数学课程组——国家精品课程
5.1 本章学习要求
重点掌握
一般掌握
了解
1 掌握各种不同 类型的规则和 公理,特别是 命题逻辑和谓 词逻辑的推理 规则和公理
2016/2/4
2 熟练掌握不同 证明方法的证 明原理、不同
3 理解谓词逻辑 的精髓,将其 思想贯穿于所
的应用场景
有的证明之中
3
电子科技大学离散数学课程组——国家精品课程
P T(1) P T⑵⑶ T⑷ P T⑹ T⑺ T⑸⑻ T(9)
22
电子科技大学离散数学课程组——国家精品课程
设前提Г={P∨Q,PR,Q→S},G=S∨R。证明 Г G 。
证明2⑴ ┐S ⑵ Q→S ⑶ ┐Q ⑷ P∨Q ⑸ P ⑹ PR ⑺ (P→R)(R→P) ⑻ P→R ⑼ R ⑽ ┐S→R ⑾ S∨R P(附加前提) P T,⑴,⑵,I P T,⑶,⑷,I P T,⑹,E T,⑺,I T,⑸,⑻,I CP,⑴, ⑼ T, ⑽,E
引入推理规则
在数理逻辑中,主要的推理规则有:
① P规则(称为前提引用规则):在推导的过程中,
可随时引入前提集合中的任意一个前提;
② 规则T(逻辑结果引用规则):在推导的过程
中,可以随时引入公式S,该公式S是由其前的一个 或多个公式推导出来的逻辑结果。 ③ 规则CP(附加前提规则):如果能从给定的 前提集合Г 与公式P推导出S,则能从此前提集合Г
记G1, G2, „,Gn H,此时称G1, G2, „,Gn H为有
效的(efficacious),否则称为无效的(inefficacious)。 G1, G2, „,Gn称为一组前提(Premise),有时用集合Г 来表示,记Г = {G1, G2, „,Gn}。H称为结论(conclusion)。 又称H是前提集合的逻辑结果。记为Г H。
1) I1:G∧H G 2) I3:G G∨H
设G,H,I,J是任意的命题公式,则有:
3) I5:┐G G→H
I6:H G→H
4) I7:┐(G→H) G
I8:┐(G→H) ┐H 5) I9:G,H G∧H
2016/2/4
14
电子科技大学离散数学课程组——国家精品课程
2
2016/2/4
12
电子科技大学离散数学课程组——国家精品课程
例5.2.1
判断下列H是否是前提G1,G2的逻辑结果
(1)
(2) (3)
解 0 0 1 0 1 1
2016/2/4
H:Q;
H: ┐P; H: Q;
0 1 1 (1) 1 0 1 0 0 1 0 0
G1:P;G2:P→Q;
G1:P→Q;G2:┐Q; G1:┐P;G2:P→Q。
2016/2/4
27
电子科技大学离散数学课程组——国家精品课程
定义5.2.3
G1∧G2∧„∧Gn是矛盾式当且仅当
也就是 G1∧G2∧…∧Gn→H
为永真公式
因而
2016/2/4
真值表技术、演绎法和 间接证明方法
11
电子科技大学离散数学课程组——国家精品课程
1、真值表技术
设P1,P2,„,Pn是出现在前提G1,G2,„,Gn和结 论H中的一切命题变元, 如果将P1,P2,„,Pn中所有可能的解释及 G1,G2,„,Gn,H的对应真值结果都列在一个表中, 根据“→”的定义,则有判断方法如下:
2016/2/4
26
电子科技大学离散数学课程组——国家精品课程
定义5.2.3
假设G1,G2,„,Gn是一组命题公式,P1,P2,„,Pn
是出现在中的一切命题变元,I是它的任意解释,
若有解释I使G1∧G2∧„∧Gn取值为“真”,则称
公式G1,G2,„,Gn是一致的,或者说是相容的。
如对任意的解释I,都有G1∧G2∧„∧Gn取值为 “假”,则称公式G1,G2,„,Gn是不一致的。或者说 G1∧G2∧„∧Gn是一个矛盾式。
式,
而“”却描述了两个公式G,H之间的一种逻辑蕴涵 关系,G H的“结果”,是非命题公式;
