2018年高考数学一轮复习感知高考刺金四百题:第86—90题(含答案解析)
2018年高考数学一轮复习感知高考刺金四百题:第376—380题(含答案解析)

感知高考刺金376题设函数()3,f x x a a a x=--+∈R ,若关于x 的方程()2f x =有且仅有三个不同的实数根,且它们成等差数列,则实数a 的取值构成的集合是 . 解:3322x a a x a a x x--+=⇒-+=+ 方程的根有且仅有三个,即左右两个函数的交点有且仅有三个, 故考查函数1,2,x x a y x a a a x x a≥⎧=-+=⎨-<⎩与232y x =+的图象 这里要注意1y x a a =-+的图象虽然随着a 的变化在移动,但是有规律的移动,“V ”型图的尖底(),a a 是沿着y x =移动的,而232y x =+的图象是确定不变的。
由322a x x+=-解得()11x a =-()21x a =- 由32x x+=解得31x =-,43x = 故画出图象只有两种情况(两个交点在第三象限,一个在第一象限(此时0a <)或三个交点都在第一象限(此时0a >))即1312x +=-⋅(如左图)或1232x x +=(如右图)即()9155a a -=-⇒=-或()()1321a a -=-+24810340a a a a ⇒-⇒--=⇒=又因为此时0a >,故a =综上,95a ⎧⎪∈-⎨⎪⎪⎩⎭感知高考刺金377题已知锐角ABC ∆的内角3A π=,点O 为三角形外接圆的圆心,若OA xOB yOC =+ ,则2x y -的取值范围是 .解法一:这是典型的求平面向量基本定理系数和问题,常用“作三点共线”的办法来解决。
由3A π=,得23BOC π∠=,不妨如图固定,,O B C 三点,因为ABC ∆是锐角三角形,所以点A 在 'DC上运动,取OB 的中点为'B ()2''OA xOB yOC xOB y OC =+=+-这样就构造出了系数和2x y -作直线OA 与直线''B C 交于E ,于是作出了',',B C E 三点共线。
2018年高考数学一轮复习感知高考刺金四百题:第186190题 含解析 精品

感知高考刺金186数列模块2.已知函数()(2318,3133x tx x f x t x ⎧-+≤⎪=⎨->⎪⎩,记()()*n a f n n =∈N .若{}n a 是递减数列,则实数t 的取值范围是 .解:{}n a 是递减数列,从4a 开始,必须满足130t -< 又对1,2,3n =,根据二次函数的性质,需要满足对称轴3522t > 注意还要满足34a a >,即991813t t -+>-, 综上得543t <<感知高考刺金187数列模块3.已知集合21|,*2n n A n n λ-⎧⎫=≥∈⎨⎬⎩⎭N ,若A 中有且仅有3个元素,则实数λ的取值范围是 .解:令212n n n b n a -=,考查n n b a ⎧⎫⎨⎬⎩⎭的单调性,111212352222n n n n n n n b b n n na a -------=-= 当2n =时,110n n n n b b a a --->,即2121b ba a > 当3n ≥时,110n n n n b b a a ---<,此时n n b a ⎧⎫⎨⎬⎩⎭单调递减 1112b a =,2234b a =,3358b a =,44716b a = 由题意知,A 中有且仅有3个元素,只需大于第四项即可,所以71162λ<≤ 点评:数列作为一种特殊的函数,特殊性在于自变量n 取正整数,函数图象是不连续的点。
因此在涉及数列单调性问题时,既可以从函数单调性的角度去理解,也可以有数列判断单调性特有的方法,后项减前项与0比较大小解决。
这个题目最经典的题根就是“递增数列{}n a 的通项公式为2n a n n λ=+,则λ的取值范围是 。
”这里就既可以从二次函数单调递增的角度,也可以用10n n a a -->的角度来求解。
感知高考刺金188数列模块4.在各项均为正整数的单调递增数列{}n a 中,121,2a a ==且132112,*k k k k a a k N a a +++⎛⎫⎛⎫++=∈ ⎪⎪⎝⎭⎝⎭,则9a = . 解:当1k =时,由132112k k k k a a a a +++⎛⎫⎛⎫++= ⎪⎪⎝⎭⎝⎭及121,2a a ==得4312112a a ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭ 又数列{}n a 是各项均为正整数的单调递增数列,所以3312112a a ⎛⎫⎛⎫++> ⎪⎪⎝⎭⎝⎭所以233320a a --<3a <<,又3*a N ∈,所以33a =,所以45a = 当2k =时,由5231125a ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭,所以58a = 当3k =时,由6251128a ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭,所以613a = 当4k =时,由72811213a ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭,所以721a = 继续下去,可得955a =本题可以发现数列其实是斐波那契数列,故由132112,*k k k k a a k N a a +++⎛⎫⎛⎫++=∈ ⎪⎪⎝⎭⎝⎭得 ()()12321k k k k k k a a a a a a ++++++=-可以发现12321,k k k k k k a a a a a a ++++++==+,即斐波那契数列.感知高考刺金189数列模块5.设n S 是等差数列{}n a 的前n 项和,若数列{}n a 满足2n n a S An Bn C +=++且0A >,则1B C A+-的最小值是 . 解:设n a pn q =+,则()232222n n p q pn q np p q a S pn q n n q +++++=++=++ 故2322p A p q B q C ⎧=⎪⎪+⎪=⎨⎪=⎪⎪⎩,解得3B CA -=故13B C B C A B C+-=+-≥-感知高考刺金190数列模块6.已知函数()()[)()[)()11sin 2,2,2121sin 22,21,222n n x n x n n f x n N x n x n n ππ+⎧-+∈+⎪⎪=∈⎨⎪-++∈++⎪⎩,若数列{}m a 满足()*2m m a f m ⎛⎫=∈ ⎪⎝⎭N ,且{}m a 的前m 项和为m S ,则20142006S S -= .解:()[)()[)()11sin 2,4,422,,*21sin 22,42,442n m n m n m n n m a f n m x n x n n ππ+⎧-+∈+⎪⎪⎛⎫==∈∈⎨ ⎪⎝⎭⎪-++∈++⎪⎩N N所以42n a n =,412n a n +=+,4221n a n +=+,4322n a n +=++ 故201420062007200820148042S S a a a -=+++=。
2018年高考数学一轮复习感知高考刺金四百题:第86—90题(含答案解析)

感知高考刺金861.若对任意的[]0,5x ∈,不等式1145m n x x +≤+恒成立,则m 的最大值为 ,n 的最小值为 。
解:当0x =时,1145m nx x +≤≤+恒成立,此时,m n ∈R 当(]0,5x ∈时,1114545m n m nx x x +≤≤+⇔≤-≤45m n ⇔≤≤45m n⇔≤ 令()f x =,则()f x 在(]0,5x ∈时单调递增,所以()11,815f x ⎛⎤∈-- ⎥⎝⎦所以11,48515m n ≤-≥-,即11,23m n ≤-≥- 2.某商场开展促销抽奖活动,摇出的中奖号码是8,2,5,3,7,1,参加抽奖的每位顾 客从0~9这10个号码中任意抽出六个组成一组,若顾客抽出的六个号码中至少有5 个与摇出的号码相同(不计顺序)即可得奖,则中奖的概率是 。
解:542感知高考刺金871.若I 是椭圆()222210x y a b a b+=>>焦点三角形12PF F ∆的内心,12PF F ∆的角平分线交12F F 于M ,则PI IM= 。
解法一:设12,PF m PF n ==,则2m n a += 又12PF F ∆的角平分线交12F F 于M ,所以1212PF PF F MF M=所以11211222PF PF PF a aF MF M F Mc c+===+ 因为1F I 也是12PF F ∠的角平分线,所以11PI PF a IMF Mc== 解法二:特殊情况法:因为题干里没有说是哪个焦点三角形,但却要求求定值,所以选取上顶点作为P ,则内心在y 轴上,设()0,I r ,则由()1122222S c b a c r ∆=⋅⋅=+ 得bcr a c=+,所以1PI b r a c a IM r c c -+==-=2.某中学的一个研究性学习小组共有10名同学,其中男生x 名(3≤x ≤9),现从中选出 3人参加一项调查活动,若至少有一名女生去参加的概率为()f x ,则()max f x = 。
2018年高考数学一轮复习感知高考刺金四百题:第76—80题(含答案解析)

感知高考刺金761.已知ABC ∆的外接圆的圆心为O ,满足:CO mCA nCB =+u u u r u u u r u u u r ,432m n +=,且CA =u u u r 6CB =u u u r ,则CA CB =u u u r u u u r g。
解法一:2CO mCA CO nCB CO =+u u u r u u u r u u u r u u u r u u u r gg ,所以()2241864312R m n m n =+=+=,即R = 所以外接圆的圆心就在边CA 的中点,所以2B π= 所以236CA CB CB ==u u u r u u u r u u u r g解法二:2CO CA mCA nCB CA =+u u u r u u u r u u u r u u u r u u u r g g ,2CO CB mCA CB nCB =+u u u r u u u r u u u r u u u r u u u r g g所以2448m nCA CB =+u u u r u u u r g ,1836n mCA CB =+u u u r u u u r g又432m n +=,所以36CA CB =u u u r u u u r g 解法三:322223CA n CB CO mCA nCB m ⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r取CA 的中点D ,取CB 的三等分点E ,则322n CO mCD CE =+u u u r u u u r u u u r 又3212n m +=,所以,,O D E 三点共线 所以2CDE π∠=,所以2323362CA CB CD CE CD ===u u u r u u u r u u u r u u u r u u u r g g 点评:本题是三角形外心与向量融合的典范,常规套路要熟悉。
2018年高考数学一轮复习感知高考刺金四百题:第361—365题(含答案解析)

感知高考刺金361题设x ∈R ,[]x 表示不超过x 的最大整数. 若存在实数t ,使得[]1t =,22t ⎡⎤=⎣⎦,…,n t n ⎡⎤=⎣⎦同时..成立..,则正整数n 的最大值是 . 解:由[]1t =得12t ≤<由22t ⎡⎤=⎣⎦得223t ≤< 由44t ⎡⎤=⎣⎦得445t ≤<,所以22t ≤由33t ⎡⎤=⎣⎦得334t ≤<,所以56t ≤<由55t ⎡⎤=⎣⎦得556t ≤<与56t ≤<,故正整数n 的最大值是4感知高考刺金362题过点()1,1M -的直线l 交圆()22:11C x y -+=于点,A B ,O 为坐标原点,若在线段AB 上的Q 满足112MA MB MQ+=,则min OQ = . 解:设()11,A x y ,()22,B x y ,(),Q m n ,直线():11l y k x =++则11MA +,21MB +,1MQ =+ 由112MA MB MQ+=得12112111x x m +=+++ 由()()221111x y y k x ⎧-+=⎪⎨=++⎪⎩得()()()2222122210k x k k x k +++-++= 所以21222221k k x x k +-+=-+,()212211k x x k +=-+ 所以421k m =-+ 所以()42111n m m ⎛⎫=-++ ⎪+⎝⎭整理得点(),Q m n 满足的轨迹方程为210m n --=所以min OQ感知高考刺金363题如图,已知点D 为ABC ∆的边BC 上一点,3BD DC =,()*n E n ∈N 为AC 边上一列点,满足()11324n n n n n E A a E B a E D +=-+,其中数列{}n a 满足0n a >,11a =,则{}n a 的通项公式为 .解:由3BD DC =可得1344n n n E D E B E C =+ 又()11324n n n n n E A a E B a E D +=-+,且n n E C E A λ= 故()113132444n n n n n n E D E B a E B a E D λ+⎡⎤=+-+⎢⎥⎣⎦即()13131324164n n n n a E B a E D λλ+⎛⎫⎡⎤+=++ ⎪⎢⎥⎣⎦⎝⎭ 因为,n n E B E D 不共线,故()1310416313204n n a a λλ+⎧+=⎪⎪⎨⎪++=⎪⎩,两式相除消去λ得132n n a a +=+,又11a =,所以1231n n a -=⋅-感知高考刺金364题若点A 在圆C :22(1)(2)4x y -++=上运动,点B 在y 轴上运动,则对定点(3,2)P 而言,||PA PB +的最小值为 .解法1:设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-.若设||r PA PB =+,则由题意可得222112(6)(4)x y y r -++-=.即,点A 在以2(6,4)D y -为圆心,以r 为半径的圆D :2222(6)(4)x y y r -++-=上. 由圆C 与圆D 有公共点A可得2||5r CD +≥=≥,从而3r ≥.解法2:设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-.从而,1||(63PA PB x x +=≥=-≥.解法3:由点A 在圆C 上可设(12cos ,22sin )A θθ+-+,(0,)B t ,则(2cos 5,2sin 6)PA PB t θθ+=-+-.故||(2cos 52cos 3PA PB θ+=≥=-≥. 解法4:设Q 为AB 的中点,则2PA PB PQ +=,过,,P Q A 作y 轴的垂线,垂足分别为',','P Q A .由于13|'||||'||||'|||22PP PQ QQ PQ AA PQ ≤+=+≤+, 因此33|||'|22PQ PP ≥-=,即||2||3PA PB PQ +=≥. 解法5:设'B 为点B 关于点P 的对称点,则|||'||'|PA PB PA PB B A +=-=.由于点'B 在直线6x =上,点A 在圆C :22(1)(2)4x y -++=上可得|'|523B A ≥-=.解法6:同解法5,设'A 为点A 关于点P 的对称点,则|||'||'|PA PB PB PA A B +=-=.由于点'A 在圆'C :22(5)(6)4x y -+-=上,点B 在y 轴上可得|'|523A B ≥-=感知高考刺金365题设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,则112u x y =+的取值范围为 . 解:可行域如图所示,()1,2A ,()4,2B ,()3,1C ,所以14,12x y ≤≤≤≤设点(),P x y 是可行域内一动点, 目标函数112u x y=+既是关于x 的减函数,又是关于y 的减函数 所以当点P 与点C 重合时,此时x 取得最大值4,同时y 取得最大值2,此时u 取得最小值为1114222+=⋅ 对于每一个固定的y 的值,要使u 取得最大值,应使x 取得最小值,即点P 应位于线段AB 上,此时()5212x y y =-≤≤()()111152522252u y x y y y y y =+=+=--()12y ≤≤ 所以()max 54u y =,此时()1,2P 与点A 重合 综上所述,1524u ≤≤。
2018年高考数学一轮复习感知高考刺金四百题含答案解析)

感知高考刺金361题设x ∈R ,[]x 表示不超过x 的最大整数. 若存在实数t ,使得[]1t =,22t ⎡⎤=⎣⎦,…,n t n⎡⎤=⎣⎦同时成立....,则正整数n 的最大值是 . 解:由[]1t =得12t ≤<由22t ⎡⎤=⎣⎦得223t ≤< 由44t ⎡⎤=⎣⎦得445t ≤<,所以22t ≤<由33t ⎡⎤=⎣⎦得334t ≤<,所以56t ≤<由55t ⎡⎤=⎣⎦得556t ≤<与56t ≤<n 的最大值是4感知高考刺金362题过点()1,1M -的直线l 交圆()22:11C x y -+=于点,A B ,O 为坐标原点,若在线段AB 上的Q 满足112MA MB MQ+=,则min OQ = . 解:设()11,A x y ,()22,B x y ,(),Q m n ,直线():11l y k x =++则11MA +,21MB =+,1MQ + 由112MA MB MQ +=得12112111x x m +=+++ 由()()221111x y y k x ⎧-+=⎪⎨=++⎪⎩得()()()2222122210k x k k x k +++-++= 所以21222221k k x x k +-+=-+,()212211k x x k +=-+ 所以421k m =-+所以()42111n m m ⎛⎫=-++ ⎪+⎝⎭整理得点(),Q m n 满足的轨迹方程为210m n --=所以min OQ ==感知高考刺金363题如图,已知点D 为ABC ∆的边BC 上一点,3BD DC =u u u r u u u r,()*n E n ∈N 为AC 边上一列点,满足()11324n n n n n E A a E B a E D +=-+u u u u r u u u u r u u u u r,其中数列{}n a 满足0n a >,11a =,则{}n a 的通项公式为 .解:由3BD DC =u u u r u u u r可得1344n n n E D E B E C =+u u u u r u u u u r u u u u r又()11324n n n n n E A a E B a E D +=-+u u u u r u u u u r u u u u r,且n n E C E A λ=u u u u r u u u u r故()113132444n n n n n n E D E B a E B a E D λ+⎡⎤=+-+⎢⎥⎣⎦u u u u r u u u u r u u u u r u u u u r即()131********n n n n a E B a E D λλ+⎛⎫⎡⎤+=++ ⎪⎢⎥⎣⎦⎝⎭u u u u r u u u u r 因为,n n E B E D u u u u r u u u u r 不共线,故()1310416313204n na a λλ+⎧+=⎪⎪⎨⎪++=⎪⎩, 两式相除消去λ得132n n a a +=+,又11a =,所以1231n n a -=⋅-感知高考刺金364题若点A 在圆C :22(1)(2)4x y -++=上运动,点B 在y 轴上运动,则对定点(3,2)P 而言,||PA PB +u u u r u u u r的最小值为 .解法1:设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-u u u r u u u r.若设||r PA PB =+u u u r u u u r ,则由题意可得222112(6)(4)x y y r -++-=.即,点A 在以2(6,4)D y -为圆心,以r 为半径的圆D :2222(6)(4)x y y r -++-=上.由圆C与圆D 有公共点A 可得2222||(61)(6)5r CD y +≥=-+-≥,从而3r ≥.解法2:设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-u u u r u u u r.从而,22211211||(6)(4)(6)63PA PB x y y x x +=-++-≥-=-≥u u u r u u u r.解法3:由点A 在圆C 上可设(12cos ,22sin )A θθ+-+,(0,)B t ,则(2cos 5,2sin 6)PA PB t θθ+=-+-u u u r u u u r.故222||(2cos 5)(2sin 6)(2cos 5)52cos 3PA PB t θθθθ+=-++-≥-=-≥u u u r u u u r. 解法4:设Q 为AB 的中点,则2PA PB PQ +=u u u r u u u r u u u r,过,,P Q A 作y 轴的垂线,垂足分别为',','P Q A .由于13|'||||'||||'|||22PP PQ QQ PQ AA PQ ≤+=+≤+, 因此33|||'|22PQ PP ≥-=,即||2||3PA PB PQ +=≥u u u r u u u r u u u r .解法5:设'B 为点B 关于点P 的对称点,则|||'||'|PA PB PA PB B A +=-=u u u r u u u r u u u r u u u r u u u u r .由于点'B 在直线6x =上,点A 在圆C :22(1)(2)4x y -++=上可得|'|523B A ≥-=u u u u r.解法6:同解法5,设'A 为点A 关于点P 的对称点,则|||'||'|PA PB PB PA A B +=-=u u u r u u u r u u u r u u u r u u u u r .由于点'A 在圆'C :22(5)(6)4x y -+-=上,点B 在y 轴上可得|'|523A B ≥-=u u u u ryxB'PCOA B感知高考刺金365题设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,则112u x y =+的取值范围为 .解:可行域如图所示,()1,2A ,()4,2B ,()3,1C , 所以14,12x y ≤≤≤≤设点(),P x y 是可行域内一动点, 目标函数112u x y=+既是关于x 的减函数,又是关于y 的减函数 所以当点P 与点C 重合时,此时x 取得最大值4, 同时y 取得最大值2,此时u 取得最小值为1114222+=⋅ 对于每一个固定的y 的值,要使u 取得最大值,应使x 取得最小值,即点P 应位于线段AB 上,此时()5212x y y =-≤≤()()111152522252u y x y y y y y =+=+=--()12y ≤≤ 所以()max 54u y =,此时()1,2P 与点A 重合 综上所述,1524u ≤≤感知高考刺金366题已知点,A B 是双曲线22122x y -=右支上两个不同的动点,O为坐标原点,则OA OB u u u r u u u rg的最小值为 .解法一:韦达定理当AB k 存在时,设:AB l y kx b =+()222221122022x y k x kbx b y kx b⎧-=⎪⇒----=⎨⎪=+⎩212122222,11kb b x x x x k k ++==-- ()()()()221212*********OA OB x x y y x x kx b kx b k x x kb x x b =+=+++=++++u u u r u u u r g()2222222222222241221111b k b k k b k k k k ++=+++==+>----当AB k 不存在是,222x y x m⎧-=⎨=⎩,则22121222OA OB x x y y m m =+=+-=u u u r u u u r g综上,2OA OB ≥u u u r u u u rg解法二:由于,A B 两点运动,故采取“一定一动”的原则,不妨先在B 点确定的情况下,让A 点运动到最小值,然后再让B 点运动,即取最小值的最小值。
2018年高考数学一轮复习感知高考刺金四百题第356—360题(含答案解析)

感知高考刺金题
已知实数满足关系式,则的最小值是.
解法一:题干中出现的全是两数的和、平方和与乘积,所以考虑用均值不等式链条。
由或
所以
点评:这里注意因为题干中没有告诉我们的正负性,所以不能直接用来
求的取值范围,所以改为用重要不等式来来做。
虽然答案正好一样,但做法要注意。
解法二:遇到结构,所以用代数的极化恒等式变形。
令,则问题转变为已知,求的最小值。
因为
所以还需要计算定义域,即
所以
解法三:设,则视为的两根
所以
所以或
当且仅当时取得最小值。
感知高考刺金题
已知点为圆与圆的公共点,圆,圆,若,,则点与直线上任意一点之间的距离的最小值为.
解:设,,则,
所以,即
同理
所以是方程的两个实根
所以
所以点的轨迹方程为
所以点到直线的最短距离为
感知高考刺金题
已知向量满足,,则的取值范围是.
解:(一)几何角度
由和可以画图,找到向量模长的几何意义。
解法一:基底法
因为
因为三者都未知,属于一问三不知问题,所以考虑转基底做。
那么题目中哪些向量适合做基底呢?显然两个
向量长度已知,适合做基底。
(这里夹角未知是应该的,不然整个图就确定下来,就
不会是求最小值了。
)
所以由三点共线,且,可知
所以
解法二:解三角形
设,
则在与中运用余弦定理得
解得
又在中,利用三角形两边之和大于等于第三边得,即
所以
(二)代数角度
解法三:换元思想。
2018年高考数学一轮复习感知高考刺金四百题:第96—100题(含答案解析)

感知高考刺金961.在ABC ∆中,内角,,A B C 所对应的边分别为,,a b c ,且BC,则c b b c+的最大值为 ,此时内角A 的值为 。
解法一:由21sin 2ABC S bc A ∆==所以2222cos 2cos 4sin 6c b c b a bc A A A A b c bc bc π++⎛⎫+===+=+ ⎪⎝⎭ 所以当3A π=时,max4c b b c ⎛⎫+= ⎪⎝⎭ 解法二:以BC 为x 轴,BC 中点为原点建系,则,0,,022a a B C ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,A x ⎛⎫ ⎪ ⎪⎝⎭ABAC =所以b c ==当0x =时,1b c= 当0x >时,b c =,当且仅当x =时取等号所以令2b t⎡⎤=∈⎣⎦,1y t=+单调递减,所以当2t =时,即x =时,max 4y = 此时AB =,AC =,则2221cos 22b c a A bc +-==,所以3A π= 由对称性可知,0x <时也一样。
2.某人抛掷一枚硬币,出现正反的概率都是12,构造数列{}n a ,使11n n a n ⎧=⎨-⎩(当第次出现正面时)(当第次出现反面时),记()12*n n S a a a n =+++∈ N ,则42S =时的概率为 。
解:42S =,需四次中有3次正面,1次反面,故344124C P ==感知高考刺金971.点P 为椭圆()222210x y a b a b+=>>在第一象限的弧上的任意一点,过P 引x 轴,y 轴的平行线,分别交直线b y x a=-于,Q R 两点,交y 轴,x 轴于,M N 两点,记OMQ ∆与ONR ∆的面积为12,S S ,当2ab =时,2212S S +的最小值为 。
解:设()cos ,sin ,0,2P a b πααα⎛⎫∈ ⎪⎝⎭, 则()()0,sin ,cos ,0M b N a αα,()()sin ,sin ,cos ,cos Q a b R a b αααα-- 所以()()()()1211sin sin ,cos cos 22S a b S a b αααα== ()()22224444122222221sin cos sin cos 411sin cos 2sin cos 1sin 222S S a b ααααααααα+=+=+=+-=-≥ 当且仅当4πα=时取得最小值。
2018年高考数学一轮复习感知高考刺金四百题:第96—100题含解析

感知高考刺金961.在ABC ∆中,内角,,A B C 所对应的边分别为,,a b c ,且BC,则c b b c+的最大值为 ,此时内角A 的值为 。
解法一:由21sin 2ABCS bc A ∆==所以2222cos 2cos 4sin 6c b c b a bc A A A A b c bc bc π++⎛⎫+===+=+ ⎪⎝⎭ 所以当3A π=时,max4c b b c⎛⎫+= ⎪⎝⎭解法二:以BC 为x 轴,BC 中点为原点建系,则,0,,022a a B C ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,A x ⎛⎫⎪ ⎪⎝⎭ABAC =所以b c=当0x =时,1b c=当0x >时,bc=,当且仅当x =时取等号所以令2b t⎡⎤=∈⎣⎦,1y t=+单调递减,所以当2t =时,即x =时,max 4y = 此时AB =,AC =,则2221cos 22b c a A bc +-==,所以3A π= 由对称性可知,0x <时也一样。
2.某人抛掷一枚硬币,出现正反的概率都是12,构造数列{}na ,使11n n a n ⎧=⎨-⎩(当第次出现正面时)(当第次出现反面时),记()12*n n S a a a n =+++∈N ,则42S =时的概率为 。
解:42S=,需四次中有3次正面,1次反面,故344124C P ==感知高考刺金971.点P 为椭圆()222210x y a b a b +=>>在第一象限的弧上的任意一点,过P 引x 轴,y 轴的平行线,分别交直线by x a =-于,Q R 两点,交y 轴,x 轴于,M N 两点,记OMQ∆与ONR∆的面积为12,S S ,当2ab =时,2212S S +的最小值为 。
解:设()cos ,sin ,0,2P a b πααα⎛⎫∈ ⎪⎝⎭, 则()()0,sin ,cos ,0M b N a αα,()()sin ,sin ,cos ,cos Q a b R a b αααα-- 所以()()()()1211sin sin ,cos cos 22Sa b S a b αααα== ()()22224444122222221sin cos sin cos 411sin cos 2sin cos 1sin 222S S a b ααααααααα+=+=+=+-=-≥当且仅当4πα=时取得最小值。
2018年高考数学一轮复习感知高考刺金四百题:第216—220题(含答案解析)

感知高考刺金216题已知实数a b c <<,设函数()111f x x a x b x c=++---的两个零点分别为()1212,x x x x <,则下列关系中恒成立的是( )(A )12a x x b c <<<< (B )12x a b x c <<<<(C )12a x b x c <<<< (D )12a x b c x <<<<解:()111f x x a x b x c=++---的两个零点, 即()()()()()()()g x x a x b x a x c x c x b =--+--+--的两个零点因为()g x 开口向上,()()()g b b a b c =--,又a b c <<,所以()0g b <即函数()g x 的零点一个大于b ,一个小于b ,且()0g a >,()0g c >所以根据“一上一下,中间一点”的原则,可知12a x b x c <<<<,选C感知高考刺金217题已知点()1,2A 在抛物线2:2y px Γ=上,若ABC ∆的三个顶点都在抛物线Γ上,记三边,,AB BC CA 所在直线的斜率分别为123,,k k k ,则123111k k k -+= . 解:2:4y x Γ=,设211,4y B y ⎛⎫ ⎪ ⎪⎝⎭,222,4y C y ⎛⎫ ⎪ ⎪⎝⎭ 所以222212121122123121211221114444122444y y y y y y y y k k k y y y y ---+++-+=-+=-+=--- 点评:抛物线题目的计算量相对于椭圆、双曲线要小一些,主要是基于抛物线上的点的设法2,2y y p ⎛⎫ ⎪ ⎪⎝⎭,在化简过程中利用好平方差公式,可以使得计算简便。
2018年高考数学一轮复习感知高考刺金四百题:第136—140题(含答案解析)

感知高考刺金136设函数()()2,f x x ax b a b =++∈R ,记(),M a b 为()y f x =在[]1,1-上的最大值(1)设2a ≥,求证:(),2M a b ≥(2)若(),2M a b ≤,请求出a b +的最值。
证明:(1)因为对称轴012a x =-≤-或012ax =-≥ ()()(){}{}maxmax 1,1max 1,1f x f f a b a b =-=++-+证法一:规划视角()()()()()22221112112110a b a b b a b a b a b a a b ++≤-+⇔++++≤+-++⇔+≤故(){}()()max1,410max 1,11,410b a a b f x a b a b b a a b ⎧+++>⎪=++-+=⎨+-+≤⎪⎩,又结合2a ≥, 可以从规划视角来解题,以a 为横坐标,b 为横坐标建系,画出可行域()4102a b a +>⎧⎪⎨≥⎪⎩如图1所示,目标函数1122b ab a ++++=视为可行域内的点(),a b 到直线10x y ++=的距离的2倍,显然当(),a b 取点()2,1--时min 1222b a ++=⋅=同理,可行域()4102a b a +≤⎧⎪⎨≥⎪⎩如图2所示,目标函数1a b -+=视为可行域内的点(),a b 到直线10x y -++=的距离(),a b 取点()2,1-时min 12b a +-= 综上,(),2M a b ≥ 证法二:绝对值不等式()()(){}{}()()max max 1,1max 1,11111222f x f f a b a b a b a b a b a ba =-=++-+++--++++-+≥≥=≥解法三:(){},max 1,1M a b a b a b =++-+ 令1b t +=,则()(){},max ,M a b g t t a t a ==+-在同一个坐标系中画出1y t a =+和2y t a =-的图象,两者取其大,则显然当0t =时,()min 2g t a =≥故(),2M a b ≥ (2)解法一:规划视角()()()222211221231,211221231848122424424f a b a b a b a M a b f a b a b a b a a b a a a b f a b ⎧⎧⎪=++≤⎪⎧-≤++≤--≤≤-+⎪⎪⎪⎪≤⇔-=-++≤⇔-≤-++≤⇔-≤≤+⎨⎨⎨⎪⎪⎪-≤-≤⎩⎛⎫⎪⎪-≤≤+-=-≤ ⎪⎩⎪⎝⎭⎩显然又是一个规划问题了。
2018年高考数学一轮复习感知高考刺金四百题:第201—205题含解析

感知高考刺金201题解析几何模块4.已知曲线C 的方程221x y +=,()2,0A -,存在一定点()(),02B b b ≠-和常数λ,对曲线C 上的任意一点(),M x y ,都有MA MB λ=成立,则点(),P b λ到直线()220m n x ny n m ++++=的最大距离为 .解法一:由MA MB λ=得()()222222x y x b y λ⎡⎤++=-+⎣⎦即()()()222222211244x y b x b λλλλ-+--+=- 故2222240411b b λλλ⎧+=⎪⎨-=⎪-⎩,将22b λ=-代入22241b λλ-=-得22520b b ++=,得12b =-,2λ= 又直线()220m n x ny n m ++++=恒过定点()2,0-,所以由几何性质知点1,22P ⎛⎫- ⎪⎝⎭到直线()220m n x ny n m ++++=的最大距离为点()2,0-与1,22P ⎛⎫- ⎪⎝⎭的距离为52 解法二:作为小题,由MA MB λ=知是阿氏圆轨迹,故取圆22:1C x y +=直径上的两个点()()1,0,1,0-,即可得1311b b λ==+-,解得12b =-,2λ= 感知高考刺金202题解析几何模块5.已知M 是28x y =的对称轴和准线的交点,点N 是其焦点,点P 在该抛物线上,且满足PM m PN =,当m 取得最大值时,点P 恰在以M 、N 为焦点的双曲线上,则该双曲线的离心率为 .解:作''PP M P ⊥,由抛物线定义'PP PN ='1cos PN PP PM m PN m PM PMθ=⇒===,其中'MPP NMP θ=∠=∠要使m 取得最小值,即cos θ最小,即NMP θ=∠最大值,即''2PMP MPP π∠=-∠最小,此时MP 是抛物线的切线. 设MP 的方程为2y kx =-,与28x y =联立得()2820x kx --=因为相切,故264640k ∆=-=,解得1k =故()4,2P ,2424a PM PN =-=-由24c =,得1e感知高考刺金203题解析几何模块6. 已知斜率为1的直线l 过双曲线()222210,0x y a b a b -=>>的左焦点F ,且与双曲线左、右支分别交于,A B 两点,若A 是线段BF 的中点,则双曲线的离心率为 . 解:由题意知122y y =()222222422120x y b a y b cy b a b x y c ⎧-=⎪⇒--+=⎨⎪=-⎩ 2121224212122232b c y y y b a b y y y b a ⎧+==⎪⎪-⎨⎪==⎪-⎩所以222492c b a =-,所以2218c a e =⇒=感知高考刺金204题解析几何模块7. 已知点P 是双曲线()222210,0x y a b a b -=>>上的动点,12,F F 是其左、右焦点,O 坐标原点,若12PF PF OP +则此双曲线的离心率是 . 解:设12,PF m PF n ==,则()22222222122422m n OP F F m n OP c +=+⇒+=+ 又2m n a -=,所以22224m mn n a -+= 所以2222224mn OP c a =+- ()222222222222444m n OP c OP c a OP b +=+++-=+ 所以22244m n b OP OP +⎛⎫=+ ⎪⎝⎭所以m n OP +的最大值在OP a =时取到,所以22446b a += 所以222b a =,即e =感知高考刺金205题解析几何模块8.在平面直角坐标系xOy 中,圆C 的方程为()()22119x y -+-=,直线:3l y kx =+与圆C 相交于,A B 两点,M 为弦AB 上一动点,以M 为圆心,2为半径的圆与圆C 总有公共点,则实数k 的取值范围是 . 解:两圆有公共点的充要条件是15CM ≤≤,而5CM ≤恒成立,故只要min 1CM ≥时两圆必有公共点.由平面几何知识可知,min CM 为点C 到直线l 的距离d ,所以1d =≥,解得34k ≥-。
2018年高考数学一轮复习感知高考刺金四百题:第136—140题(含答案解析)

感知高考刺金136设函数()()2,f x x ax b a b =++∈R ,记(),M a b 为()y f x =在[]1,1-上的最大值(1)设2a ≥,求证:(),2M a b ≥(2)若(),2M a b ≤,请求出a b +的最值。
证明:(1)因为对称轴012a x =-≤-或012ax =-≥ ()()(){}{}max max 1,1max 1,1f x f f a b a b =-=++-+证法一:规划视角()()()()()22221112112110a b a b b a b a b a b a a b ++≤-+⇔++++≤+-++⇔+≤故(){}()()max1,410max 1,11,410b a a b f x a b a b b a a b ⎧+++>⎪=++-+=⎨+-+≤⎪⎩,又结合2a ≥, 可以从规划视角来解题,以a 为横坐标,b 为横坐标建系,画出可行域()4102a b a +>⎧⎪⎨≥⎪⎩如图1所示,目标函数1122b ab a ++++=视为可行域内的点(),a b 到直线10x y ++=的距离的2倍,显然当(),a b 取点()2,1--时min 1222b a ++=⋅=同理,可行域()4102a b a +≤⎧⎪⎨≥⎪⎩如图2所示,目标函数1a b -+=视为可行域内的点(),a b 到直线10x y -++=的距离(),a b 取点()2,1-时min 12b a +-=综上,(),2M a b ≥ 证法二:绝对值不等式()()(){}{}()()max max 1,1max 1,11111222f x f f a b a b a b a b a b a b a =-=++-+++--++++-+≥≥=≥解法三:(){},max 1,1M a b a b a b =++-+令1b t +=,则()(){},max ,M a b g t t a t a ==+-在同一个坐标系中画出1y t a =+和2y t a =-的图象,两者取其大,则显然当0t =时,()min 2g t a =≥故(),2M a b ≥ (2)解法一:规划视角()()()222211221231,211221231848122424424f a b a b a b a M a b f a b a b a b a a b a a a b f a b ⎧⎧⎪=++≤⎪⎧-≤++≤--≤≤-+⎪⎪⎪⎪≤⇔-=-++≤⇔-≤-++≤⇔-≤≤+⎨⎨⎨⎪⎪⎪-≤-≤⎩⎛⎫⎪⎪-≤≤+-=-≤ ⎪⎩⎪⎝⎭⎩显然又是一个规划问题了。
【配套K12】2018数学高考一轮复习刺金四百题:第86—90题(含答案解析)

感知高考刺金861.若对任意的[]0,5x ∈,不等式1145m n x x +≤+恒成立,则m 的最大值为 ,n 的最小值为 。
解:当0x =时,1145m nx x +≤≤+恒成立,此时,m n ∈R 当(]0,5x ∈时,1114545m n m nx x x +≤≤+⇔≤≤45m n ⇔≤≤45m n⇔≤ 令()f x =,则()f x 在(]0,5x ∈时单调递增,所以()11,815f x ⎛⎤∈-- ⎥⎝⎦所以11,48515m n ≤-≥-,即11,23m n ≤-≥- 2.某商场开展促销抽奖活动,摇出的中奖号码是8,2,5,3,7,1,参加抽奖的每位顾 客从0~9这10个号码中任意抽出六个组成一组,若顾客抽出的六个号码中至少有5 个与摇出的号码相同(不计顺序)即可得奖,则中奖的概率是 。
解:542感知高考刺金871.若I 是椭圆()222210x y a b a b+=>>焦点三角形12PF F ∆的内心,12PF F ∆的角平分线交12F F 于M ,则PI IM= 。
解法一:设12,PF m PF n ==,则2m n a += 又12PF F ∆的角平分线交12F F 于M ,所以1212PF PF F MF M=所以11211222PF PF PF a aF MF M F Mc c+===+因为1F I 也是12PF F ∠的角平分线,所以11PI PF a IMF Mc==解法二:特殊情况法:因为题干里没有说是哪个焦点三角形,但却要求求定值,所以选取上顶点作为P ,则内心在y 轴上,设()0,I r ,则由()1122222S c b a c r ∆=⋅⋅=+ 得bcr a c=+,所以1PI b r a c a IM r c c -+==-=2.某中学的一个研究性学习小组共有10名同学,其中男生x 名(3≤x ≤9),现从中选出 3人参加一项调查活动,若至少有一名女生去参加的概率为()f x ,则()max f x = 。
2018年高考数学一轮复习感知高考刺金四百题:第201—205题(含答案解析)
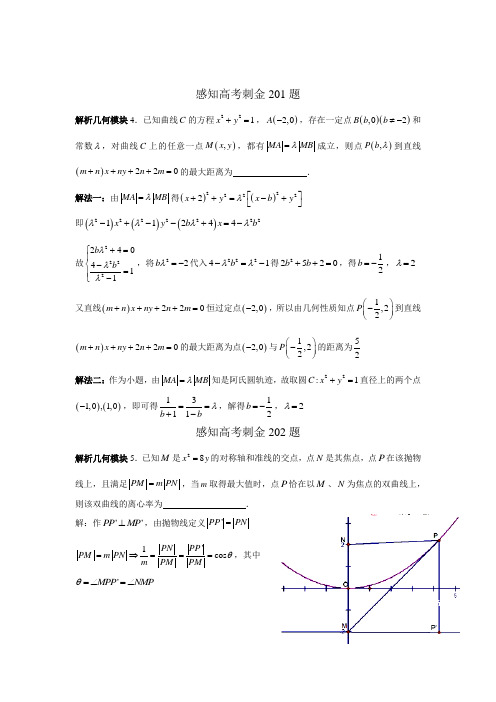
感知高考刺金201题解析几何模块4.已知曲线C 的方程221x y +=,()2,0A -,存在一定点()(),02B b b ≠-和常数λ,对曲线C 上的任意一点(),M x y ,都有MA MB λ=成立,则点(),P b λ到直线()220m n x ny n m ++++=的最大距离为 .解法一:由MA MB λ=得()()222222x y x b y λ⎡⎤++=-+⎣⎦即()()()222222211244x y b x b λλλλ-+--+=- 故2222240411b b λλλ⎧+=⎪⎨-=⎪-⎩,将22b λ=-代入22241b λλ-=-得22520b b ++=,得12b =-,2λ= 又直线()220m n x ny n m ++++=恒过定点()2,0-,所以由几何性质知点1,22P ⎛⎫- ⎪⎝⎭到直线()220m n x ny n m ++++=的最大距离为点()2,0-与1,22P ⎛⎫- ⎪⎝⎭的距离为52 解法二:作为小题,由MA MB λ=知是阿氏圆轨迹,故取圆22:1C x y +=直径上的两个点()()1,0,1,0-,即可得1311b b λ==+-,解得12b =-,2λ= 感知高考刺金202题解析几何模块5.已知M 是28x y =的对称轴和准线的交点,点N 是其焦点,点P 在该抛物线上,且满足PM m PN =,当m 取得最大值时,点P 恰在以M 、N 为焦点的双曲线上,则该双曲线的离心率为 .解:作''PP MP ⊥,由抛物线定义'PP PN ='1cos PN PP PM m PN m PM PMθ=⇒===,其中'MPP NMP θ=∠=∠要使m 取得最小值,即cos θ最小,即NMP θ=∠最大值,即''2PMP MPP π∠=-∠最小,此时MP 是抛物线的切线.设MP 的方程为2y kx =-,与28x y =联立得()2820x kx --=因为相切,故264640k ∆=-=,解得1k = 故()4,2P,24a PM PN =-= 由24c =,得1e =感知高考刺金203题解析几何模块6. 已知斜率为1的直线l 过双曲线()222210,0x y a b a b -=>>的左焦点F ,且与双曲线左、右支分别交于,A B 两点,若A 是线段BF 的中点,则双曲线的离心率为 .解:由题意知122y y =()222222422120x y b a y b cy b a b x y c ⎧-=⎪⇒--+=⎨⎪=-⎩ 2121224212122232b c y y y b a b y y y b a ⎧+==⎪⎪-⎨⎪==⎪-⎩所以222492c b a =-,所以2218c a e =⇒=感知高考刺金204题解析几何模块7. 已知点P 是双曲线()222210,0x y a b a b -=>>上的动点,12,F F 是其左、右焦点,O 坐标原点,若12PF PF OP +,则此双曲线的离心率是 .解:设12,PF m PF n ==,则()22222222122422m n OP F F m n OP c +=+⇒+=+ 又2m n a -=,所以22224m mn n a -+= 所以2222224mn OP c a =+- ()222222222222444m n OP c OP c a OP b +=+++-=+ 所以22244m n b OP OP +⎛⎫=+ ⎪⎝⎭ 所以m n OP +的最大值在OP a =时取到,所以22446b a+=所以222b a =,即e =感知高考刺金205题解析几何模块8.在平面直角坐标系xOy 中,圆C 的方程为()()22119x y -+-=,直线:3l y kx =+与圆C 相交于,A B 两点,M 为弦AB 上一动点,以M 为圆心,2为半径的圆与圆C 总有公共点,则实数k 的取值范围是 . 解:两圆有公共点的充要条件是15CM ≤≤,而5CM ≤恒成立,故只要min 1CM ≥时两圆必有公共点.由平面几何知识可知,min CM 为点C 到直线l 的距离d ,所以1d =≥,解得34k ≥-。
2018年高考数学一轮复习感知高考刺金四百题:第396—400题(含答案解析)

感知高考刺金396题 已知椭圆22221x y a b +=,12,F F 是椭圆的左、右焦点,,A C 是椭圆上关于x 轴对称的两点,B 为短轴的端点,线段AB 恰好过右焦点,若1AB CF ⊥,则椭圆的离心率e = . 解:设()0,B b ,()2,0F c ,()2,BF c b =- ,()22,F A BF c b λλλ==- ,()(),,A A x c y c b λλ-=-即,A A x c c y b λλ=+=-,则(),C c c b λλ+ 所以12F C bk c c λλ=+,2F B bk c =-1212F C F B bb k kc c c λλ⎛⎫⋅=⋅-=- ⎪+⎝⎭2222cb c λ⇒=- 点A 在椭圆上,所以2222222222222211c c c b b c b c a b ⎛⎫⎛⎫+ ⎪ ⎪--⎝⎭⎝⎭+=化简得2245a c a e =⇒=感知高考刺金397题【2017新课标卷II,理14】若x,y 满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩,,则z x y =+的最大值为____________。
解:第一步:由约束条件,画出可行域 ,如图 先确定满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩,的可行域,作出3条直线,围成一个三角形区域;第二步:把目标函数()0z ax by b =+≠化为a z y xb b =-+,作直线a y x b =-将目标函数z x y =+变形为y x z =-+,作直线y x =-; 第三步:平移直线a y x b =-,确定目标函数最值把直线y x =-进行平行,确定平移到什么位置截距最大,然后把该点坐标代入z x y =+求最大值.当z 取最大值时,直线y x z =-+的纵截距最大,故将直线尽可能地向上平移到D (1,12),则z x y =+的最大值为23感知高考刺金398题【2017新课标卷II,理14】函数23()sin 4f x x x =-([0,])2x π∈的最大值是____________. 解:()22311cos cos 44f x x x x x =--=-+=2(cos 1x -+,由[0,]2x π∈可得cos [0,1]x ∈,当cos x =时,函数()f x 取得最大值1. 点评:本题经三角函数式的化简将三角函数的问题转化为二次函数的问题,二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,有关二次函数的问题,数形结合、密切联系图象是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面进行分析.感知高考刺金399题【2017全国Ⅱ,文8】函数2()ln(28)f x x x =--的单调递增区间是____________。
2018年高考数学一轮复习感知高考刺金四百题:第91—95题(含答案解析)

感知高考刺金911.若,x y 满足()()22221log 4cos 434cos xy y y xy ⎡⎤+=-+-⎢⎥⎢⎥⎣⎦,则c o s y x = 。
解:()()()222221log 4cos 432114cos xy y y y xy ⎡⎤+=-+-=--+≤⎢⎥⎢⎥⎣⎦又()()22221log 4cos log 214cos xy xy ⎡⎤+≥=⎢⎥⎢⎥⎣⎦所以()()2221log 4cos 14cos xy xy ⎡⎤+=⎢⎥⎢⎥⎣⎦即()()2214cos 24cos 2xy xy y ⎧+=⎪⎨⎪=⎩解得()1cos 22xy y ⎧=⎪⎨⎪=⎩或()1cos 22xy y ⎧=-⎪⎨⎪=⎩所以()2cos422cos 211y x x =-=-评注:本题是夹逼原理的应用。
2.已知10个产品中有3个次品,现从其中抽出若干个产品,要使这3个次品全部被抽出的概率不小于0.6,则至少应抽出产品 个。
解:33371035n n C C C -≥,即()()12310985n n n --≥⋅⋅,解得9n ≥感知高考刺金921.已知ABC ∆是边长为的正三角形,EF 为ABC ∆的外接圆O 的一条直径,M 为ABC ∆的边上的动点,则ME MF 的取值范围是 。
解:ABC ∆的外接圆O 的半径为2 由极化恒等式可得22244EF ME MF MO MO =-=- 由图易得[]1,2OM ∈,所以[]3,0ME MF ∈-2.已知P 箱中有红球1个,白球9个,Q 箱中有白球7个,(P 、Q 箱中所有的球除颜色外完全相同).现随意从P 箱中取出3个球放入Q 箱,将Q 箱中的球充分搅匀后,再 从Q 箱中随意取出3个球放入P 箱,则红球从P 箱移到Q 箱,再从Q 箱返回P 箱中的概率等于 。
解:121219************C C C C P C C =⋅=感知高考刺金931.在ABC ∆中,6AC =,7BC =,1cos 5A =,O 是ABC ∆的内心,若OP xOA yOB =+,其中01,01x y ≤≤≤≤,则动点P 的轨迹所覆盖的面积为 。
2018年高考数学一轮复习感知高考刺金四百题:第1—5题(含答案解析)

感知高考刺金11.已知P 是ABC ∆内任一点,且满足AP xAB y AC =+,x 、y R ∈,则2y x +的取值范围是 ___ . 解法一:令1x y AQ AP AB AC x y x y x y ==++++,由系数和1x y x y x y+=++,知点Q 在线段BC 上.从而1APx y AQ +=<.由x 、y 满足条件0,0,1,x y x y >>⎧⎨+<⎩易知2(0,2)y x +∈. 解法二:因为题目没有特别说明ABC ∆是什么三角形,所以不妨设为等腰直角三角形,则立刻变为线性规划问题了.2.在平面直角坐标系中,x 轴正半轴上有5个点, y 轴正半轴有3个点,将x 轴上这5个点和y 轴上这3个点连成15条线段,这15条线段在第一象限内的交点最多有 个.答案:30个感知高考刺金21.定义函数()[[]]f x x x =,其中[]x 表示不超过x 的最大整数,如:[1.5]1[ 1.3]2=-=-,,当*[0)()x n n N ∈∈,时,设函数()f x 的值域为A ,记集合A 中的元素个数为n a ,则式子90n a n+的最小值为 . 【答案】13.【解析】当[)0,1n ∈时,[]0x x ⎡⎤=⎣⎦,其间有1个整数; 当[),1n i i ∈+,1,2,,1i n =-时,[]2(1)i x x i i ⎡⎤≤<+⎣⎦,其间有i 个正整数,故 (1)112(1)12n n n a n -=++++-=+,9091122na n n n +=+-, 由912n n=得,当13n =或14时,取得最小值13. 2. 有七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙、丙两倍同学要站在一起,则不同的站法有 种.答案:192种感知高考刺金31.已知直线l ⊥平面α,垂足为O .在矩形ABCD 中,1AD =,2AB =,若点A 在l 上移动,点B 在平面α上移动,则O ,D 两点间的最大距离为 .解:设AB 的中点为E ,则E 点的轨迹是球面的一部分,1OE =,DE所以1OD OE ED ≤+=当且仅当,,O E D 三点共线时等号成立.2. 将A、B、C、D四个球放入编号为1,2,3的三个盒子中,每个盒子中至少放一个球且A、B两个球不能放在同一盒子中,则不同的放法有 种.答案:30种感知高考刺金41. 在平面直角坐标系xOy 中,设定点(),A a a ,P 是函数()10y x x=>图象上一动点.若点,P A之间的最短距离为则满足条件的实数a 的所有值为 . 解:函数解析式(含参数)求最值问题()222222211112222AP x a a x a x a x a a x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-=+-++-=+-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 因为0x >,则12x x+≥,分两种情况: (1)当2a ≥时,min AP =,则a(2)当2a <时,min AP =则1a =-2. 将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有 种.答案:90种感知高考刺金51.已知,x y ∈R ,则()222x y x y ⎛⎫++- ⎪⎝⎭的最小值为 .解: 构造函数1y x =,22y x=-,则(),x x 与2,y y ⎛⎫- ⎪⎝⎭两点分别在两个函数图象上,故所求看成两点(),x x 与2,y y ⎛⎫- ⎪⎝⎭之间的距离平方, 令222080222y x m x mx m m y x =+⎧⎪⇒++=⇒∆=-=⇒=⎨=-⎪⎩,所以y x =+1y x =平行的22y x =-的切线,故最小距离为2d =所以()222x y x y ⎛⎫++- ⎪⎝⎭的最小值为4 2. 某单位要邀请10位教师中的6人参加一个研讨会,其中甲、乙两位教师不能同时参加,则邀请的不同方法有 种.答案:140种。
2018年高考数学一轮复习感知高考刺金四百题:第96—100题(含答案解析)

感知高考刺金961.在ABC ∆中,内角,,A B C 所对应的边分别为,,a b c ,且BC,则c b b c+的最大值为 ,此时内角A 的值为 。
解法一:由21sin 212ABC S bc A ∆==所以2222cos 2cos 4sin 6c b c b a bc A A A A b c bc bc π++⎛⎫+===+=+ ⎪⎝⎭ 所以当3A π=时,max4c b b c ⎛⎫+= ⎪⎝⎭ 解法二:以BC 为x 轴,BC 中点为原点建系,则,0,,022a a B C ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,6A x a ⎛⎫ ⎪ ⎪⎝⎭AB =AC所以b c == 当0x =时,1b c= 当0x >时,b c =,当且仅当x =时取等号所以令2b t c ⎡⎤=∈⎣⎦,1y t t=+单调递减,所以当2t =-时,即3x =时,max 4y =此时AB =,AC =,则2221cos 22b c a A bc +-==,所以3A π= 由对称性可知,0x <时也一样。
2.某人抛掷一枚硬币,出现正反的概率都是12,构造数列{}n a ,使11n n a n ⎧=⎨-⎩(当第次出现正面时)(当第次出现反面时),记()12*n n S a a a n =+++∈L N ,则42S =时的概率为 。
解:42S =,需四次中有3次正面,1次反面,故344124C P ==感知高考刺金971.点P 为椭圆()222210x y a b a b+=>>在第一象限的弧上的任意一点,过P 引x 轴,y 轴的平行线,分别交直线b y x a=-于,Q R 两点,交y 轴,x 轴于,M N 两点,记OMQ ∆与ONR ∆的面积为12,S S ,当2ab =时,2212S S +的最小值为 。
解:设()cos ,sin ,0,2P a b πααα⎛⎫∈ ⎪⎝⎭, 则()()0,sin ,cos ,0M b N a αα,()()sin ,sin ,cos ,cos Q a b R a b αααα-- 所以()()()()1211sin sin ,cos cos 22S a b S a b αααα== ()()22224444122222221sin cos sin cos 411sin cos 2sin cos 1sin 222S S a b ααααααααα+=+=+=+-=-≥ 当且仅当4πα=时取得最小值。
2018年高考数学一轮复习感知高考刺金四百题:第81—85题(含答案解析)

感知高考刺金811.在平面直角坐标系xoy 中,直线2y x =-+与圆()2220x y r r +=>交于,A B 两点,O 为坐标原点,若圆上有一个C 满足5344OC OA OB =+,则r = 。
解法一:将5344OC OA OB =+两边平方,得222225915cos 16168r r r r AOB =++∠, 3cos 5AOB ∠=-又圆心到直线2y x =-+的距离为d所以cos2AOB ∠ 所以223215r ⋅-=-,所以r =解法二:由5344OC OA OB =+得53288OC OA OB =+设OC 与AB 交于点M ,则,,A M B 三点共线。
,22CO r AO BO r OM ====,且35AM BM = 所以利用cos cos AMO BMO ∠=-∠得,AM BM ==所以AB =过O 作AB 的垂线交AB 于D,根据圆心到直线的距离为OD =2225r ⎛⎫+= ⎪ ⎪⎝⎭解得r =2.从1,2,3,4,5五个数中随机地依次选取三个不同的数,则所取的三个数按照挑选的顺序排列恰能构成等差数列的概率是 . 解:358215A =感知高考刺金821.已知()y f x =是定义在[]2,2-上的奇函数,当(]0,2x ∈时,()21x f x =-,函数()22g x x x m =-+,如果对于[][]122,2,2,2x x ∀∈-∃∈-,使得()()21g x f x =,则实数m 的取值范围是 。
解:()[]3,3f x ∈-,()[]1,8g x m m ∈-+若对于[][]122,2,2,2x x ∀∈-∃∈-,使得()()21g x f x =,只需()f x 的值域包含于()g x 的值域即可。
即8313m m +≥⎧⎨-≤-⎩,解得52m -≤≤-2.在同一层楼有一排8间会议室,现要安排4个不同学科的研讨会在这8间研讨室,要求任意两个研讨会不相邻的安排方法有 种.解:45120A =感知高考刺金831.在平行四边形ABCD 中,BH CD ⊥于H ,BH 交AC 于点E ,若3BE =,215AB AC AE AC BE CB AE -+-=,则AE EC= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
感知高考刺金86
1.若对任意的[]0,5x ∈,不等
式1145m n x x +
≤+恒成立,则m 的最大值为 ,n 的最小值为 。
解:当0x =
时,1145m n
x x +≤
≤+恒成立,此时,m n ∈R 当(]0,5x ∈
时,1114545m n m n
x x x +≤
≤+⇔≤-≤
45m n ⇔
≤≤
45m n
⇔≤ 令()
f x =
,则()f x 在(]0,5x ∈时单调递增,所以()11,815f x ⎛⎤
∈-- ⎥⎝⎦
所以
11,48515m n ≤-≥-,即11
,23
m n ≤-≥- 2.某商场开展促销抽奖活动,摇出的中奖号码是8,2,5,3,7,1,参加抽奖的每位顾 客从0~9这10个号码中任意抽出六个组成一组,若顾客抽出的六个号码中至少有5 个与摇出的号码相同(不计顺序)即可得奖,则中奖的概率是 。
解:542
感知高考刺金87
1.若I 是椭圆()22
2210x y a b a b
+=>>焦点三角形12PF F ∆的内心,12PF F ∆的角平分线交12
F F 于M ,则
PI IM
= 。
解法一:设12,PF m PF n ==,则2m n a += 又12PF F ∆的角平分线交12F F 于M ,所以
1212PF PF F M
F M
=
所以
11211222PF PF PF a a
F M
F M F M
c c
+=
=
=+
因为1F I 也是12PF F ∠的角平分线,所以
11PI PF a IM
F M
c
=
=
解法二:特殊情况法:因为题干里没有说是哪个焦点三角形,但却要求求定值,所以选取上顶点作为P ,则内心在y 轴上,设()0,I r ,则由()11
22222
S c b a c r ∆=⋅⋅=+ 得bc
r a c
=
+,所以1PI b r a c a IM r c c -+==-=
2.某中学的一个研究性学习小组共有10名同学,其中男生x 名(3≤x ≤9),现从中选出 3人参加一项调查活动,若至少有一名女生去参加的概率为()f x ,则()max f x = 。
解:()()()3
31012111098
x
x x x C f x C --=-=-⋅⋅,单调递减
故()max 119
120
f x =
感知高考刺金88
1.已知12,F F 是椭圆()22
2210x y a b a b
+=>>的两个焦点,直线l 过
焦点1F 与椭圆交于,A B 两点,2ABF ∆是以2BAF ∠为直角的等腰直角三角形,则椭圆离心率e = 。
解:设2AF m =,1AF n =,1BF p =
,2BF =
则222224n p m
m n a
p a
m n c +=⎧⎪+=⎪
+=⎪+=⎩
可求得m n ==
所以2
2
2
4c +=
所以(
)
22
3
1
e =
,所以e =
变式:已知12,F F 是椭圆()22
2210x y a b a b
+=>>的两个焦点,直线l 过焦点1F 与椭圆交于,A B
两点,2ABF ∆是直角三角形,则椭圆离心率e 的取值范围是 。
解:(1)当22
BF A π
∠=
时,
若直线AB 的斜率不存在,则2
2b c a
=,即2210e e +-=
,解得1e = 若直线AB 的斜率存在,设直线AB 的方程为()()0y k x c k =+≠,代入椭圆方程22
221
x y a b
+=得()()
2222222222220a k b x k a cx a c k a b +++-=
则2222222
1212222222
2,k a c a c k a b x x x x a k b a k b --+==++
由22
BF A π∠=得220AF BF =
所以()()12120c x c x y y --+=
即()()()()212120c x c x k x c x c --+++=
所以()
224244a c b k b -=,所以22440a c b ->,即2222ac b a c >=-
,所以1e >
(2)当22BAF π∠=时,22
22222
1x y a b
x y c ⎧+=⎪⎨⎪+=⎩
有解,即()22
2220a x c b c =-≥ 所以c b ≥
,即e ≥
综上可得,1e
2.已知集合A={12,14,16,18,20},B={11,13,15,17,19},在A 中任取一个元素用()1,2,3,4,5i a i =表示,在B 中任取一个元素用()1,2,3,4,5j b j =表示,则所取两数满足
i j a b >的概率为 。
解:123453
555
++++=⋅
感知高考刺金89
1.若等差数列
{}n a 满足22
11010a a +=,则1011
S a a a
=+++ 的最大值为 。
解法一:由2211010a a +=得()2
2
1010910a d a -+=
而101119101045S a a a a d =+++=+ ,所以10925
S
d a =
- 所以2
2
10103105S a a ⎛⎫-+= ⎪⎝⎭整理得关于10a 的方程221010610100525S S a a ⎛⎫-+-= ⎪⎝⎭有实根
所以2
236401002525S S ⎛⎫--≥ ⎪⎝⎭
,解得5050S -≤≤
解法二:
由题可设110,a a θθ
,公差1019a a d -=
=
所以()
()101119101045550sin S a a a a d θθθϕ=+++=+==- 当且仅当()sin 1θϕ-=时,max 50S =
2.在圆周上有10个等分点,以这些点为顶点,每3个点可以构成一个三角形,如果随机选
择3个点,刚好构成直角三角形的概率是 。
解:直径有5条,故直角三角形有1
8
540C ⋅= 31040401
1203
P C =
==
感知高考刺金90
1.已知在数列{}n a 中,11a =,23a =,对任意*n N ∈,都有232n n n a a +≤+⋅,121n n a a +≥+成立,则数列{}n a 的通项公式为 。
解:
2222131112424242n n n n n n n n
a a a a ++++⎛⎫
≤⋅+⇒-≤⋅- ⎪⎝⎭
若n 是偶数时,12
2
222211111112424242n
n
n n n n n
a a a ---⎛⎫⎛⎫⎛⎫⎛⎫
-≤⋅-≤≤-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭
, 所以21n n a ≤-
若n 是奇数时,1
2
212
1111111242422n n
n n n n a a a ---⎛⎫⎛⎫⎛⎫
⎛⎫-≤⋅-≤≤-=- ⎪ ⎪ ⎪
⎪⎝⎭⎝⎭⎝⎭
⎝⎭
所以21n n a ≤-
综上,对任意*n N ∈,21n n a ≤-
又()()111121121212n n n n n n a a a a a +++≥+⇒+≥+≥≥+= 所以对任意*n N ∈,21n n a ≥- 综上可得21n n a =-,*n N ∈
评注:这是夹逼原理在数列中的应用。
2.为了支持拆迁工作,某镇决定接受一批移民,其中有3户互为亲戚关系,将这3户移民随机安置到5个村民组,则这3户中恰好有2户安置到同一村民组的概率为 。
解:2235335412
512525
C A P ⨯⨯===。
