局解复习笔记(L5)
白中英《计算机组成原理》(第5版)笔记和课后习题详解复习答案

白中英《计算机组成原理》(第5版)笔记和课后习题详解完整版>精研学习网>无偿试用20%资料
全国547所院校视频及题库全收集
考研全套>视频资料>课后答案>往年真题>职称考试
第1章计算机系统概论
1.1复习笔记
1.2课后习题详解
第2章运算方法和运算器
2.1复习笔记
2.2课后习题详解
第3章多层次的存储器
3.1复习笔记
3.2课后习题详解
第4章指令系统
4.1复习笔记
4.2课后习题详解
第5章中央处理器
5.1复习笔记
5.2课后习题详解
第6章总线系统
6.1复习笔记
6.2课后习题详解
第7章外存与I/O设备
7.1复习笔记
7.2课后习题详解
第8章输入输出系统
8.1复习笔记
8.2课后习题详解
第9章并行组织与结构
9.1复习笔记
9.2课后习题详解
第10章课程教学实验设计
第11章课程综合设计。
图形推理-学习笔记
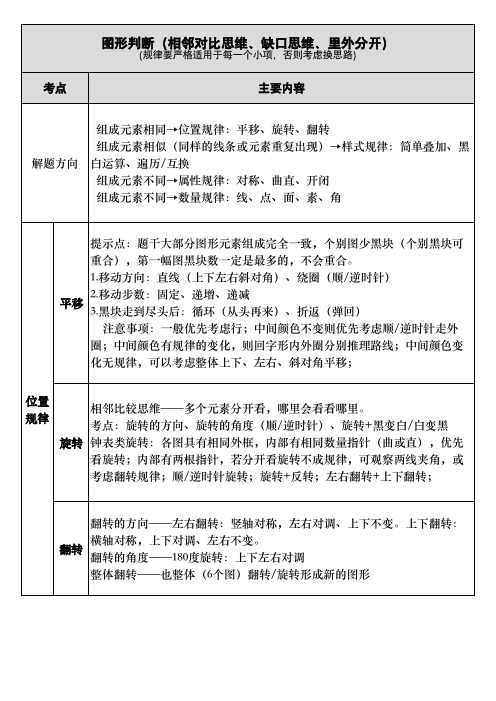
翻转的方向——左右翻转:竖轴对称,左右对调、上下不变。上下翻转: 横轴对称,上下对调、左右不变。 翻转 翻转的角度——180度旋转:上下左右对调 整体翻转——也整体(6个图)翻转/旋转形成新的图形
1
1.简单叠加,叠加后求同/求异(抓住1-2条线突破);
叠加
2.位置变化(旋转/翻转)+求同/求异;行和列分别用不同的叠加规律。 ⚠要注意辨析:谁叠在谁的上面、谁被覆盖;区分部分叠加VS完全叠加、
优先考虑——切不出来的图形,用排除法。 六面体:六面体只能切出锐角三角形,切不出直角三角形、钝角三角形。 截面 圆柱:圆柱斜切得到弧线,不可能切出梯形。 图 ⚠️注意:空心没有实线;不同角度的截面无法共存,即刀不能拐弯切(eg. 不能外部横切矩形、同时内部斜切椭圆);刀切过圆柱的弧面得到的是曲 线;关注切面的角(直角/锐角);辨析实心和空心的颜色。
2
数量 规律
交点特征——有出头色彩,如十字形、T字型、L字型 曲直交点特征——图形均为类圆曲线,圆和弧线多且曲直相交 切点特征——类圆曲线+点连接 圆内交点——每幅图都仅有一个圆,线条贯穿圆内外 点 其他考点——曲曲/直直交点数(和/差),内外交点(图形均有外框,内 外分开看:内部交点、外部交点、内外交点的和/差),黑点/白点连接形 成的部分数,线条经过或覆盖的点的数量,点在四个角的位置移动,相连 黑圆圈的数量变化(eg.各行分别有1、2、3个黑圆相连)
3
属性 规律
对称的考点主要有:对称方式,对称轴数量/方向,对称轴两侧空间的形 状,对称轴经过的点/线/面的数量。 1.轴对称——提示点:等腰三角形/梯形、箭头及其变形、五角星、一边一 个相同元素(如Y)。 具体考点——对称轴的方向/数量,对称轴与图形中某点/某线的关系(对 称轴经过交点/直线/与线重合),对称轴的自身的角度,对称轴旋转的角 度,字母和汉字要注意书写笔画长短/大小是否严格符合对称性,对称轴是 对称 否经过所有面,最大/最小面的对称性,两个对称图形要考虑对称轴之间的 关系。 2.中心对称——旋转180度后完全重合;两个相同图形反着放。提示点:平 行四边形,S、N、Z字型,风车及其变形。 3.轴+中心对称——存在两条互相垂直的对称轴。 4.整体对称:图形米字型整体对称,五个图以第三个图为轴成轴对称,白块 /黑块的整体对称性,对称轴的数量对称(如对称轴数量分别为 4/1/2/2/1/4)。
武汉大学《分析化学》(第5版)(上册)笔记和课后习题(含考研真题)详解

武汉大学《分析化学》(第5版)(上册)笔记和课后习题(含考研真题)详解目录内容简介目录第1章概论1复习笔记2课后习题详解1.3名校考研真题详解第2章分析试样的采集与制备1复习笔记2课后习题详解2.3名校考研真题详解第3章分析化学中的误差与数据处理1复习笔记2课后习题详解3.3名校考研真题详解第4章分析化学中的质量保证与质量控制1复习笔记2课后习题详解4.3名校考研真题详解第5章酸碱滴定法1复习笔记2课后习题详解5.3名校考研真题详解第6章络合滴定法1复习笔记2课后习题详解6.3名校考研真题详解第7章氧化复原滴定法1复习笔记2课后习题详解7.3名校考研真题详解第8章沉淀滴定法和滴定分析小结1复习笔记2课后习题详解8.3名校考研真题详解第9章重量分析法1复习笔记2课后习题详解9.3名校考研真题详解第10章吸光光度法1复习笔记2课后习题详解10.3名校考研真题详解第11章分析化学中常用的别离和富集方法1复习笔记2课后习题详解11.3名校考研真题详解第第1章概论1.1复习笔记一、分析化学的定义分析化学是开展和应用各种理论、方法、仪器和策略以获取有关物质在相对时空内的组成和性质的信息的一门科学,又被称为分析科学。
二、分析方法的分类与选择1.分类〔1〕按分析要求定性鉴由哪些元素、原子团或化合物所组成。
定量测定中有关成分的含量。
结构分析:研究物质的分子结构、晶体结构或综合形态。
〔2〕按分析对象无机分析、有机分析。
〔3〕按测定原理化学分析:以物质的化学反响及其计量关系为根底,如重量分析法和滴定分析法等。
仪器分析:通过测量物质的物理或物理化学参数进行分析,如光谱分析、电化学分析等。
〔4〕按试样用量常量分析、半微量分析、微量分析、超微量分析。
〔5〕按工作性质例行分析、仲裁分析。
2.分析方法的选择对分析方法的选择通常应考虑以下几方面:〔1〕测定的具体要求,待测组分及其含量范围,欲测组分的性质;〔2〕获取共存组分的信息并考虑共存组分对测定的影响,拟定适宜的别离富集方法,以提高分析方法的选择性;〔3〕对测定准确度、灵敏度的要求与对策;〔4〕现有条件、测定本钱及完成测定的时间要求等。
局解考试重点整理.docx

(―)名词解释神经点:颈从皮支从胸锁乳突肌后缘中点浅出时,位置农浅且相対集中,常为颈部手术阻滞麻醉的穿针点。
胸膜腔::脏胸膜与壁胸膜之间形成的潜在性间隙.纵膈:是左右纵隔胸膜Z间所有器官,结构和组织的总称.心包腔:浆膜性心观肌、壁两层在出入心的大血管根部相移行,两层之间的间隙称心包腔°斜角肌间隙:前、中斜角肌与第一肋z间形成-呈三角形的间隙,称为斜处肌间隙颈动脉稍:颈总动脉,颈内动脉,颈内静脉和迷走神经等形成的筋膜鞘.心包斜窦:在左心房后壁,左右肺静脉,下腔静脉与心包后壁之间的间隙。
肘后三角:肘关节屈曲呈直角时,胧骨内、外上擁和尺骨鷹嘴3点构成等腰三角形。
胆建三角:肝总管、胆粪管其上方的川:下而之间共同围成一三角区,称为胆•囊三角心包横窦:位于左肺静脉,右肺静脉,下腔静脉,左心房后壁和心包后壁Z间的间隙。
椎动脉三角:内侧界为颈长肌,外侧界为前斜角肌, 下界为锁骨下动脉第1段,尖为第6颈椎横突前结节.锁胸筋膜:为胸部筋膜深层,张于喙突、锁骨下川1、胸小肌上缘之间,有头静脉、肩峰动脉、胸外侧神经及淋巴管穿过肺根:出入肺门的结构(主支气管、肺动脉、肺静脉、支气管动静脉、神经、淋巴管)被结缔组织包绕连于纵隔称肺根,肺根对肺起固定、支持作用。
肾区:即脊肋角,在竖脊肌外侧缘与第12肋的夹角区域称肾区。
肝门:肝脏而正中有略呈“H”形的三条沟,长约5cm,其中横行的沟位于肝脏面正中,有肝左、右管居前,肝固有动脉左、右支届中,肝门静脉左、右支,肝的神经和淋巴管等由此出入,故称为肝门。
动脉导管三角:位于主动脉弓的左前方,前界为左膈神经,后界为左迷走神经,下界为左肺动脉。
三角内有动脉韧帶、左喉返神经和心浅从。
该三角是手术寻找动脉导管的标志。
股鞘,股管:股鞘为腹横筋膜与儁筋膜向下延续包绕于股动、静脉上部形成的筋膜鞘呈漏斗形,长约3-4CM。
股鞘内有两条纵行的纤维隔,将鞘腔分为三部分:外侧部容纳股动脉,中间部分窝纳股静脉,内侧部称股管(二)简答题1、颈动脉三角的境界和内容:境界颈动脉三角位于胸锁乳突肌上份前缘、肩胛舌骨肌上腹和二腹肌后腹Z间。
解析几何问题中常见的技巧专题课件高三数学一轮复习

解:直线 AM 的斜率为1时,直线 AM 的方程为 y = x +2,
代入椭圆方程并化简得5 x 2+16 x +12=0.
6
解得 x 1=-2, x 2=- ,所以 M
5
6
4
− ,
5
5
.
高中总复习·数学(提升版)
(2)当直线 AM 的斜率变化时,直线 MN 是否过 x 轴上的一定
解析:
2
由双曲线方程 x 2- =1知 a =1, b =3,则其渐近线方程
9
为 y =±3 x .观察选项知,四个点均在双曲线外,∴点 A , B 分别在双
曲线的两支上,∴-3< kAB <3.设 A ( x 1, y 1), B ( x 2, y 2),则
12 −
22 −
12
9
22
9
= 1,
4
点, A , B 分别是 C 1, C 2在第二、四象限的公共点.若四边形 AF 1 BF 2
为矩形,则 C 2的离心率是(
A. 2
3
C.
2
B. 3
D.
6
2
)
高中总复习·数学(提升版)
解析:
由已知,得 F 1(- 3 ,0), F 2( 3 ,0),设双曲线 C 2
的实半轴长为 a ,由椭圆及双曲线的定义和已知,可得
,
2
−
,
2
3
2
,=
− ,
3 2
1 2
3 2
1
3 2
2
2
2
2
= c - a + b = c - a + ( a - c )= c -
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第4章静定拱【圣才出品】

李廉锟《结构⼒学》笔记和课后习题(含考研真题)详解-第4章静定拱【圣才出品】第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】⼀、拱的基本概念及特点 ★★表4-1-1 拱的基本概念及特点表4-1-2 有拉杆和⽆拉杆三铰拱的区别与联系⼆、三铰拱的计算 ★★★★★1.⽀座反⼒的计算(见表4-1-3)表4-1-3 ⽀座反⼒的计算2.内⼒的计算(见表4-1-4)表4-1-4 三铰拱的内⼒计算三、三铰拱的合理拱轴线(见表4-1-5) ★★★表4-1-5 三铰拱的合理拱轴线4.2 课后习题详解复习思考题1.拱的受⼒情况和内⼒计算与梁和刚架有何异同?答:(1)拱与梁的受⼒情况和内⼒计算的区别①约束反⼒⽅⾯,拱在竖向荷载作⽤下会产⽣⽔平反⼒(推⼒),⽽梁在竖向荷载作⽤下不会产⽣⽔平反⼒(推⼒);②内⼒分布⽅⾯,由于⽔平推⼒的存在,拱的弯矩常⽐跨度、荷载相同的梁的弯矩⼩得多,使得拱截⾯上的应⼒分布较为均匀;③内⼒分析⽅法⽅⾯,若只有竖向荷载时,梁只需进⾏简单的整体分析即可求解,⽽拱由于⽔平⼒的存在,需要整体分析与局部分析相结合。
(2)拱与刚架的受⼒情况和内⼒计算的异同①内⼒分析⽅法⽅⾯,拱与刚架的受⼒情况和内⼒计算的特点和所应⽤⽅法基本⼀致,例如三铰刚架也属于拱式结构;②拱的轴线是曲线,刚架杆的轴线是直线,在应⽤平衡条件计算内⼒时,拱仍然取投2.在⾮竖向荷载作⽤下怎样计算三铰拱的反⼒和内⼒?能否使⽤式(4-1)和(4-2)?答:(1)对于三铰拱承受⾮竖向荷载的情况,可将⾮竖向荷载分解为⽔平荷载和竖向荷载。
(2)仍然可以应⽤式(4-1)和(4-2),将⽔平反⼒加上⾮竖向荷载⽔平⽅向上的分量⼀起代⼊公式中进⾏求解。
(4-1)o AV AV o BV BV o c H F F F F M F f ??=??=?=cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F =-??=-?=+3.什么是合理拱轴线?试绘出图4-2-1各荷载作⽤下三铰拱的合理拱轴线形状。
尹定邦《设计学概论》复习笔记及课后习题详解第5章

第5章设计的类型复习笔记一、视觉传达设计(一)什么是视觉传达设计1.符号(1)含义广义的符号,是利用一定媒介来代表或指称某一事物的东西。
(2)作用①符号是实现信息贮存和记忆的工具。
②符号是表达思想情感的物质手段。
③符号是信息的载体,具有形式表现、信息叙述和传达的功能。
(3)分类①视觉符号系统。
所谓视觉符号,是指人类的视知觉器官眼睛所能看到的,表现事物一定性质(质地或现象)的符号。
②听觉符号系统。
③触觉符号系统④味觉和嗅觉符号系统。
2.传递(1)含义所谓传达,是指信息发送者利用符号向接受者传递信息的过程。
(2)程序一般可以归纳为“谁”、“把什么”、“向谁传达”、“效果、影响如何”这四个程序。
3.视觉传达设计(1)概念视觉传达设计是利用视觉符号来进行信息传达的设计。
(2)传达实现的条件信息的发送者和接收者必须具备部分相同的信息知识背景,即信息传达所用的符号至少有一部分既存在于发送者的符号贮备系统中,也存在于接收者的符号贮备系统中。
(3)传达设计的基本原则信息传达设计中作为发送者的设计师必须针对接收者,根据接收者的知识背景与传达内容来选择符号媒介。
(4)主要功能视觉传达设计的主要功能是传达信息。
(5)过程视觉传达设计的过程是设计者将思想和概念转变为视觉符号形式的过程。
(6)视觉设计师与视觉艺术家的不同视觉设计师的工作受到更多的限制。
①必须使用他的特定对象易于认知和理解的视觉符号。
②必须考虑他的设计的复制或制作计划的问题。
(7)视觉传达设计的发展历程①文字的发明是人类信息传达文明史上的第一次革命。
②中国造纸术的发明是第二次革命。
③印刷术的发明,使视觉传达设计迈向大众传播信息。
④现代的视觉传达设计是从以招贴画为中心的印刷品设计发展起来的。
⑤20世纪20~30年代,摄影图版开始被用于招贴等视觉设计中。
⑥20世纪40~50年代影像技术的革命,大大拓展了视觉设计的领域。
⑦20世纪80年代,电脑辅助设计技术开创了视觉传达设计的新纪元。
古扎拉蒂《计量经济学基础》复习笔记和课后习题详解(定性响应回归模型)【圣才出品】

第15章定性响应回归模型15.1 复习笔记考点一:定性响应模型的性质★★定性响应模型是指模型中的回归子是一个二值或二分变量的模型,通常被称为概率模型。
回归子也可以是多分响应变量或多类型响应变量。
将二值响应变量建立成概率模型的方法包括线性概率模型(LPM)、logit模型、probit模型和tobit模型。
考点二:线性概率模型(LPM)★★★★1.LPM的定义以下述回归模型为例说明:Y i=β1+β2X i+u i。
其中X表示家庭收入;Y=1,则表示该家庭拥有住房;Y=0,则该家庭不拥有住房。
该模型被称为线性概率模型,因为Y i在给定X i下的条件期望E(Y i|X i)可解释为在给定X i下事件(家庭拥有住房)发生的条件概率,即Pr(Y i=1|X i)。
2.LPM的特征令P i表示“Y i=1”(即事件发生)的概率,而1-P i表示“Y i=0”(即事件不发生)的概率,则变量Y i服从贝努利概率分布。
根据期望的定义,有:E(Y i)=0(1-P i)+1P i=P i。
此外有:E(Y i|X i)=β1+β2X i =P i,即模型的条件期望事实上可以解释为Y i的条件概率。
该模型的约束条件为:0≤E(Y i|X i)≤1。
3.LPM的问题(1)干扰项u i的非正态性若把方程写成:u i=Y i-β1-β2X i,u i的概率分布见表15-1。
表15-1 u i的概率分布可见u i服从贝努利分布而不是正态分布。
虽然干扰项不满足正态性假定,但OLS的点估计值仍具有无偏性。
此外在大样本下,OLS估计量一般都趋于正态分布,因此LPM的统计推断仍可用正态性假定下的OLS程序。
(2)干扰项的异方差性即使LPM中的干扰项满足零均值和无序列相关性假定,但也不能说它具有同方差性。
对于贝努利分布,理论上的均值和方差分别为P和P(1-P),可见方差是均值的函数,而均值的取值依赖于X的值,因此LPM中的干扰项具有异方差性。
计量经济学复习笔记(注释)

计量经济学复习笔记CH1导论1、计量经济学:以经济理论和经济数据的事实为依据,运用数学、统计学的方法,通过建立数学模型来研究经济数量关系和规律的一门经济学科。
研究主体是经济现象及其发展变化的规律。
2、运用计量分析研究步骤:模型设定——确定变量和数学关系式估计参数——分析变量间具体的数量关系模型检验——检验所得结论的可靠性模型应用——做经济分析和经济预测3、模型变量:解释变量:表示被解释变量变动原因的变量,也称自变量,回归元。
被解释变量:表示分析研究的对象,变动结果的变量,也成应变量。
内生变量:其数值由模型所决定的变量,是模型求解的结果。
外生变量:其数值由模型意外决定的变量。
外生变量数值的变化能够影响内生变量的变化,而内生变量却不能反过来影响外生变量。
前定内生变量:过去时期的、滞后的或更大范围的内生变量,不受本模型研究范围的内生变量的影响,但能够影响我们所研究的本期的内生变量。
前定变量:前定内生变量和外生变量的总称。
数据:时间序列数据:按照时间先后排列的统计数据。
截面数据:发生在同一时间截面上的调查数据。
面板数据:虚拟变量数据:表征政策,条件等,一般取0或1.4、估计评价统计性质的标准无偏:E(^β)=β 随机变量,变量的函数?有效:最小方差性一致:N趋近无穷时,β估计越来越接近真实值5、检验经济意义检验:所估计的模型与经济理论是否相等统计推断检验:检验参数估计值是否抽样的偶然结果,是否显著计量经济检验:是否符合计量经济方法的基本假定预测检验:将模型预测的结果与经济运行的实际对比CH2 CH3 线性回归模型模型(假设)——估计参数——检验——拟合优度——预测1、模型(线性)(1)关于参数的线性 模型就变量而言是线性的;模型就参数而言是线性的。
Y i =β1+β2lnX i +u i线性影响 随机影响Y i =E (Y i |X i )+u i E (Y i |X i )=f(X i )=β1+β2lnX i引入随机扰动项,(3)古典假设A 零均值假定 E (u i |X i )=0B 同方差假定 Var(u i |X i )=E(u i 2)=σ2C 无自相关假定 Cov(u i ,u j )=0D 随机扰动项与解释变量不相关假定 Cov(u i ,X i )=0E 正态性假定u i ~N(0,σ2)F 无多重共线性假定Rank(X)=k2、估计在古典假设下,经典框架,可以使用OLS方法:OLS 寻找min ∑e i2 ^β1ols = (Y 均值)-^β2(X 均值)^β2ols = ∑x i y i /∑x i 23、性质OLS 回归线性质(数值性质)(1)回归线通过样本均值 (X 均值,Y 均值)(2)估计值^Y i 的均值等于实际值Y i 的均值(3)剩余项e i 的均值为0(4)被解释变量估计值^Y i 与剩余项e i 不相关 Cov(^Y i ,e i )=0(5)解释变量X i 与剩余项e i 不相关 Cov(e i ,X i )=0在古典假设下,OLS 的统计性质是BLUE 统计 最佳线性无偏估计4、检验(1)Z 检验Ho:β2=0 原假设 验证β2是否显著不为0标准化: Z=(^β2-β2)/SE (^β2)~N (0,1) 在方差已知,样本充分大用Z 检验拒绝域在两侧,跟临界值判断,是否β2显著不为0(2)t 检验——回归系数的假设性检验方差未知,用方差估计量代替 ^σ2=∑e i 2/(n-k) 重点记忆t =(^β2-β2)/^SE (^β2)~t (n-2)拒绝域:|t|>=t 2/a (n-2)拒绝,认为对应解释变量对被解释变量有显著影响。
白中英《计算机组成原理》(第5版)笔记和课后习题详解

读书笔记模板
01 思维导图
03 目录分析 05 读书笔记
目录
02 内容摘要 04 作者介绍 06 精彩摘录
思维导图
关键字分析思维导图
原理
课程
第版
笔记
重难点
教学实验
设计
原理
教材
计算机 习题
运算器
笔记
笔记
概论
复习
运算
系统
第章
内容摘要
白中英所著的《计算机组成原理》(第5版,科学出版社)是我国高校采用较多的计算机专业优秀教材,也被 众多高校指定为计算机专业考研参考书目。作为该教材的辅导书,本书具有以下几个方面的特点:1.整理名校笔 记,浓缩内容精华。在参考了国内外名校名师讲授白中英《计算机组成原理》的课堂笔记基础上,本书每章的复 习笔记部分对该章的重难点进行了整理,同时对重要知识点进行点拨,因此,本书的内容几乎浓缩了配套教材的 知识精华。2.解析课后习题,提供详尽答案。本书参考大量计算机组成原理相关资料对该教材的重难点课(章) 后习题进行了详细的分析和解答,并对相关重要知识点进行了延伸和归纳。
9.2课后习题 详解
作者介绍
读书笔记
这是《白中英《计算机组成原理》(第5版)笔记和课后习题详解》的读书笔记模板,可以替换为自己的心得。
精彩摘录
这是《白中英《计算机组成原理》(第5版)笔记和课后习题详解》的读书笔记模板,可以替换为自己的精彩 内容摘录。
谢谢观看
目录分析
1.1复习笔记
1.2课后习题 详解
2.1复习笔记
2.2课后习题 详解
3.1复习笔记
3.2课后习题 详解
4.1复习笔记
贾俊平《统计学》复习笔记课后习题详解及典型题详解(时间序列分析和预测)【圣才出品】

第13章时间序列分析和预测13.1 复习笔记一、时间序列及其分解1.时间序列(1)概念:时间序列是同一现象在不同时间上的相继观察值排列而成的序列,也称动态数列或时间数列。
(2)时间序列的两要素任何一个时间序列都具有两个基本要素:一是统计指标所属的时间,也称为时间变量;二是统计指标在特定时间的具体指标值。
(3)研究时间序列的目的①在编制时间序列的基础上,可以计算平均发展水平,进行动态水平分析;②可以计算各种速度指标,进行速度分析;③利用相关的数学模型,对现象的变动进行趋势分析。
2.时间序列的类型(1)平稳序列它是基本上不存在趋势的序列。
这类序列中的各观察值基本上都在某个固定的水平上波动,虽然在不同的时间段波动的程度不同,但并不存在某种规律,其波动可以看成是随机的。
(2)非平稳序列它是包含趋势、季节性或周期性的序列,它可能只含有其中的一种成分,也可能含有几种成分,因此非平稳序列可以分为有趋势的序列、有趋势和季节性的序列、几种成分混合而成的复合型序列。
3.时间序列的4种成分(1)趋势(T)也称长期趋势,它是时间序列在长时期内呈现出来的某种持续上升或持续下降的变动。
时间序列中的趋势可以是线性的,也可以是非线性的。
(2)季节性(S)也称季节变动,它是时间序列在一年内重复出现的周期性波动。
季节性中的“季节”一词是广义的,它不仅仅是指一年中的四季,其实是指任何一种周期性的变化。
(3)周期性(C)也称循环波动,它是时间序列中呈现出来的围绕长期趋势的一种波浪形或振荡式变动。
(4)随机性(I)也称不规则波动,它是时间序列中除去趋势、周期性和季节性之后的偶然性波动。
4.时间序列的分解模型将时间序列分解成长期趋势、季节变动、周期变动和随机变动四个因素后,可以认为时间序列Y t是这四个因素的函数,即Y t=f(T t,S t,C t,I t),其中较常用的是加法模型和乘法模型,其表现形式为:加法模型:Y t=T t+S t+C t+I t乘法模型:Y t=T t×S t×C t×I t注意:时间序列组合模型中包含了四种因素,这是时间序列的完备模式,但是并不是在每个时间序列中这四种因素都同时存在。
高中数学解析几何总结(非常全)

高中数学解析几何总结(非常全)高中数学解析几何第一部分:直线一、直线的倾斜角与斜率1.倾斜角α直线l向上的方向与x轴正向所成的角叫做直线的倾斜角α,其范围为0≤α<180度。
2.斜率直线倾斜角α的正切值叫做这条直线的斜率,表示为k=tanα。
1)倾斜角为90度的直线没有斜率。
2)每一条直线都有唯一的倾斜角,但并不是每一条直线都存在斜率。
当直线垂直于x轴时,其斜率不存在,因此在研究直线的有关问题时,应考虑到斜率的存在与不存在这两种情况,否则会产生漏解。
3)设经过A(x1,y1)和B(x2,y2)两点的直线的斜率为k,则当x1≠x2时,k=(y1-y2)/(x1-x2);当x1=x2时,斜率不存在。
二、直线的方程1.点斜式已知直线上一点P(x,y)及直线的斜率k(倾斜角α),求直线的方程,可以用点斜式表示为y-y1=k(x-x1)。
需要注意的是,当直线斜率不存在时,不能用点斜式表示,此时方程为x=x1.2.斜截式若已知直线在y轴上的截距(直线与y轴焦点的纵坐标)为b,斜率为k,则直线方程为y=kx+b。
特别地,斜率存在且经过坐标原点的直线方程为y=kx。
需要正确理解“截距”这一概念,它具有方向性,有正负之分,与“距离”有区别。
3.两点式若已知直线经过(x1,y1)和(x2,y2)两点,且(x1≠x2,y1≠y2),则直线的方程为(y-y1)/(x-x1)=(y2-y1)/(x2-x1)。
需要注意的是,不能表示与x轴和y轴垂直的直线。
4.截距式若已知直线在x轴,y轴上的截距分别是a,b(a≠0,b≠0),则直线方程为xy/a + y/b = 1.需要注意的是,截距式方程不能表示经过原点的直线,也不能表示垂直于坐标轴的直线。
5.一般式任何一条直线方程均可写成一般式:Ax+By+C=0(A、B不同时为零)。
反之,任何一个二元一次方程都表示一条直线。
首先,我们需要指出直线方程的特殊形式可以化为直线方程的一般式,但一般式不一定能化为特殊形式,这取决于系数A、B、C是否为零。
(完整)局解复习

局部解剖学复习思考题第一部分头颈部及脊柱区一、名词解释1、颈A鞘-—颈筋膜向两侧扩展,包绕颈总A,颈内A,颈内V及迷走N所形成的筋膜鞘。
2、腱膜下间隙——腱膜下间隙又称腱膜下疏松CT,是帽状腱膜与颅骨外膜之间一层疏松CT,头皮借此层与颅骨外膜疏松结合,头皮撕脱伤多自此层分离.3、神经点——在胸锁乳突肌后缘中点处,颈丛皮支浅出颈筋膜的集中点,是临床颈部皮N阻滞麻醉的部位。
4、腮腺床-—腮腺深面的茎突诸肌,颈内A、V和后4对脑N,共同形成“腮腺床”.5、枕下三角——位于枕下,项区上部深层,由头后大直肌、头上斜肌,头下斜肌围成的三角,内有枕下N和椎A通过。
6、椎十字韧带—寰椎横韧带中部向上、向下各发出一纵行纤维束,分别附着于枕骨大孔的前缘和枢椎体后面,纵横纤维共同构成寰椎十字韧带,有限制突齿后移的作用。
7、钩椎关节——又称Luschka关节,3~7颈椎体上面外侧缘的椎体钩与下面外侧缘的唇缘所构成的关节,称钩椎关节。
8、甲状腺悬韧带——甲状腺假被膜增厚,连于甲状腺侧叶内侧面和峡部后面称甲状腺悬韧带,对甲状腺有固定作用.9、椎A三角——是指颈长肌、前斜角肌、锁骨下A第一段及第6颈椎前结节围成的锥形区,称椎A三角,内有椎A、V,甲状腺下A,颈交感干及颈胸N节等。
10、头皮—头部软组织由浅入深依次为肤、浅筋膜,帽状腱膜与枕额肌,腱膜下疏松CT和颅骨外膜。
其中浅部三层结合紧密,不易分离,人们常将此3层合称“头皮"。
11。
颈A三角—--位于胸锁乳突肌、二腹肌后腹和肩胛舌骨肌上腹之间的三角区域,内有舌骨大角,颈总A及分支。
12。
颈袢—-由上根和下根在环状软骨平面合成。
C1前支先和舌下N联合再于二腹肌后腹下方离开舌下N下行,即为颈袢上根。
颈袢下根源自C2、C3的前支,他们离开颈丛后于颈内V浅面联合下行,在颈A鞘的前外侧面与上根汇合而成颈袢。
颈袢发出的分支支配大部分舌骨下肌。
13斜角肌间隙:指前、中斜角肌与第1肋之间的间隙,有锁骨下A和臂丛通过。
罗宾斯《组织行为学》(第14版)笔记和课后习题(含考研真题)详解
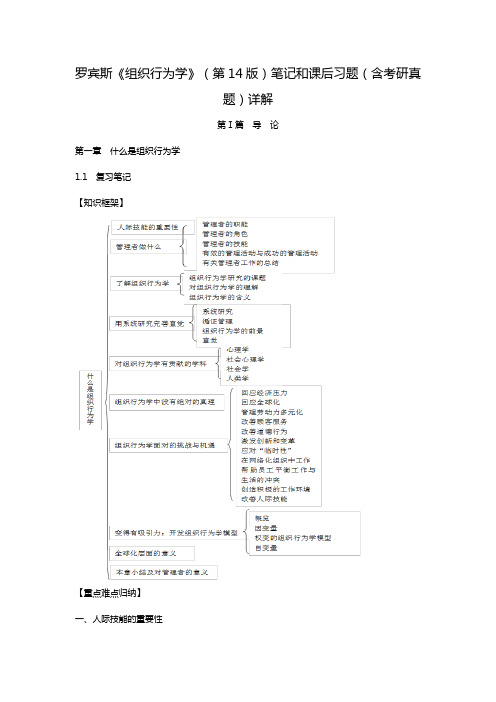
罗宾斯《组织行为学》(第14版)笔记和课后习题(含考研真题)详解第Ⅰ篇导论第一章什么是组织行为学1.1 复习笔记【知识框架】【重点难点归纳】一、人际技能的重要性人际技能的重要性表现在以下几个方面:(1)在决定管理者的职业生涯能否真正飞黄腾达上,领导和沟通技能很重要;(2)管理者人际技能的开发有助于组织吸引和留住高绩效的员工;(3)在当今竞争日益激烈、要求日趋提高的工作环境中,管理者需要具备良好的人际技能。
二、管理者做什么管理者通过他人来完成工作。
在工作中做出决策、分配资源和指导他人的活动,从而实现工作目标。
管理者在组织当中完成他们的工作。
组织是一种人们有目的地组合起来的社会单元,它由两个或多个个体组成,在一个相对连续的基础上运作,以实现一个或一系列共同目标。
1.管理者的职能亨利·法约尔提出,所有的管理者都发挥五种职能:计划、组织、指挥、协调和控制。
把这些职能可简化为四种:计划、组织、领导和控制。
(1)计划计划职能包括:①确定组织的目标;②制定达成这些目标的总体战略;③把计划划分出各种层级,以便对不同的活动进行整合和协调。
(2)组织组织职能包括:①决定要完成什么样的任务;②谁来承担这些任务;③如何把任务进行分类;④谁向谁报告工作以及在什么地方做出决策。
(3)领导领导是指导和协调他人工作。
当管理者激励下属,指导别人的活动,选择最有效的沟通渠道以及解决成员之间的冲突时,他们就是在进行领导。
(4)控制为了保证各项事情按部就班地发展,管理者必须对组织的绩效进行监控。
他们要对实际的绩效与预定的目标进行比较,如果出现重大偏离,管理者的工作就是要使组织回到正确的轨道上来。
这种监控、比较以及对可能的错误进行纠正的活动,就是控制职能。
2.管理者的角色明茨伯格指出,管理者扮演着10种不同但高度相关的角色,或者说表现出10种不同的工作相关行为。
如表1-1所示,这10种角色可以归纳为:人际角色、信息传递者角色以及决策角色。
《解析几何》知识点复习1

《解析几何》知识点复习1解析几何是数学中一个非常重要的分支,它将代数与几何巧妙地结合在一起,通过建立坐标系,用代数方法来研究几何图形的性质和相互关系。
接下来,让我们一起对解析几何的一些关键知识点进行复习。
一、坐标系坐标系是解析几何的基础,最常见的是直角坐标系(也称为笛卡尔坐标系)。
在直角坐标系中,我们通过两条互相垂直的数轴,即 x 轴和 y 轴,来确定平面上点的位置。
一个点的坐标就是它在 x 轴和 y 轴上的投影所对应的数值,通常表示为(x, y)。
此外,还有极坐标系。
在极坐标系中,一个点的位置由极径和极角来确定。
极径是该点到极点的距离,极角是极轴(通常为 x 轴的正半轴)到该点的连线与极轴所成的角。
二、直线1、直线的方程点斜式:若已知直线上一点(x₁, y₁) 以及直线的斜率 k,则直线方程为 y y₁= k(x x₁)。
斜截式:若直线的斜率为 k,且在 y 轴上的截距为 b,则直线方程为 y = kx + b。
两点式:若已知直线上两点(x₁, y₁) 和(x₂, y₂),则直线方程为(y y₁)/(y₂ y₁) =(x x₁)/(x₂ x₁)。
一般式:Ax + By + C = 0 (A、B 不同时为 0)。
2、直线的位置关系平行:两条直线斜率相等。
垂直:两条直线斜率之积为-1。
3、距离公式点到直线的距离:d =|Ax₁+ By₁+ C| /√(A²+ B²) ,其中(x₁, y₁) 是点的坐标,Ax + By + C = 0 是直线方程。
三、圆1、圆的方程标准方程:(x a)²+(y b)²= r²,其中(a, b) 是圆心坐标,r 是半径。
一般方程:x²+ y²+ Dx + Ey + F = 0 (D²+ E² 4F > 0),圆心坐标为(D/2, E/2) ,半径为√(D²+ E² 4F) / 2 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
局部解剖学复习笔记Q1:大隐静脉起止、行程、属支:大隐静脉起于足背静脉弓内侧缘,经内踝前方,沿小腿内侧缘伴隐神经上行,经股骨内侧髁后方约2cm进入大腿内侧部与股内侧皮神经伴行,在耻骨结节外下方穿隐静脉裂孔汇入股静脉,汇入处称隐股点。
大隐静脉的五个属支:旋髂浅静脉、腹壁浅静脉、阴部外静脉、股内侧浅静脉、股外侧浅静脉。
Q2:股前群肌的名称、位置、起止和作用股前群肌肉包括:缝匠肌和股四头肌(股直肌、股中间肌、股内/外侧肌)。
缝匠饥起于髂前上棘,止于胫骨上端内侧面,用于屈髋、屈膝;股四头肌汇成髌韧带,止于胫骨粗隆,用于伸膝。
Q3:股三角位置、境界和内容物股三角的上界是腹股沟韧带,外侧界为缝匠肌内侧缘,内侧界为长收肌内侧缘。
表面覆以阔筋膜,底凹陷,由外向内依次为髂腰肌、耻骨肌、和长收肌。
补充:阔筋膜在耻骨结节外下方3—4cm处形成一个卵圆形的薄弱区,成为隐静脉裂孔(卵圆窝),其表面覆盖一层多孔的疏松结缔组织膜,称为筛筋膜或外筛板。
腹横筋膜与髂筋膜向下延伸并包绕股A、股V上段的筋膜成为股鞘,由外向内依次为股A、股V和股管。
股疝即是因小肠进入股管盲端透过隐静脉裂孔突出而发生嵌顿。
Q4:小腿前群肌和外侧群肌的名称、排列和作用(P189)Q5:臀大肌、梨状肌的位置、起止和作用臀大肌起于髂骨翼外面、骶骨背侧、骶结节韧带,止于臀肌粗隆和髂胫束,用于伸髋。
梨状肌起于2—4骶前孔外侧,止于股骨大转子,用于外展、外旋髋关节。
Q6:梨状肌上下孔的神经血管及其排列顺序:(由外向内)坐骨N,股后皮N,臀下N,臀下A、V,阴部内V、A、和阴部N。
Q7:坐骨神经与梨状肌的关系及其在股后部的行程坐骨神经与梨状肌的关系因人而异,可分为3种情况7种类型:常见型:坐骨神经以一总干从梨状肌下孔出盆;典型高分支型:坐骨神经在盆内即分为胫神经和腓总神经,前者出梨状肌下孔,后者从梨状肌纤维中穿出;其他类型:包括:坐骨神经总干下哦那个梨状肌中间或梨状肌上孔出盆;坐骨神经在盆内分支,但分支出盆位置不典型;骶丛根穿梨状肌后吻合成坐骨神经等。
出盆后,至臀大肌深面,经坐骨结节与大转子之间中点稍内侧处下降入股后区,临床上常用此处为坐骨神经压痛点的检查位置。
Q8:小隐静脉的起止、行程和注入部位起于足背静脉弓的外侧端,经外踝后下方延伸至小腿后面,伴腓肠神经沿正中线上行,至腘窝下角穿腘筋膜进入腘窝,上升一段后注入腘静脉.Q9:腘窝的境界、内容物及毗邻关系境界:上外侧界:股二头肌腱上内侧界:半腱肌、半膜肌下外侧界:腓肠肌外侧头下内侧界:腓肠肌内侧头内容物及毗邻关系:(由浅至深)胫神经、腘静脉、腘动脉、腓总神经、腘深淋巴结等Q10:小腿后群浅层肌的名称起止和作用Q11:踝管的组成内容及排列踝管内容物由前向后依次为:胫骨后肌腱,趾长屈肌腱,胫后A、V和胫N,趾长屈肌腱。
踝管便狭窄时,压迫其内容物,形成“踝管综合征”Q12:胸大肌的位置起止及作用胸大肌起于锁骨内侧端、胸骨及上6肋软骨,止于肱骨大结节嵴。
用于上臂内收内旋和前屈。
Q13:腋窝的境界、内容及毗邻关系(P133、134)腋窝由1顶(锁骨、1肋、肩胛骨上缘)、1底(皮肤和浅深筋膜)和前壁(皮肤、浅深筋膜、胸大小肌、胸锁筋膜)、后(皮肤、浅深腋腔内有腋动脉、腋静脉、臂丛及其分支、腋淋巴结和丰富的疏松结缔组织。
Q14:腋A的分段及分支(P136、137)腋A在第一肋外缘处接锁骨下A,经腋窝至背阔肌下缘续于肱A。
按胸小肌的位置将腋A分为3段:(1)从第一肋外侧缘至胸小肌上缘,发出胸肩峰A。
(2)在胸小肌的后方发出胸外侧A。
(3)从胸小肌下缘至背阔肌下缘,发出肩胛下A和旋肱前、后A。
Q15:头静脉、肘正中静脉和贵要静脉的起止行程和注入部位(P141)头静脉:起于手背静脉网桡侧,转至前臂前面,沿前臂桡侧、臂外侧上行,经三角肌和胸大肌之间的浅沟注入腋静脉或锁骨下静脉。
肘正中静脉:贵要静脉:起于手背静脉网尺侧,转至前臂前面,沿前臂尺侧、臂内侧上行,在臂下1/3处穿过深筋膜,注入肱静脉或腋静脉。
Q16:肱二头肌的起止和作用(P146)肱二头肌的起点:(长头:肩胛骨关节盂上方,短头:肩胛骨喙突),止点:(桡骨粗隆),作用:(屈肘、前臂旋后)。
Q17:前臂前群肌各肌层的层次排列和作用(P150)前臂前群肌共9块,位于尺、桡骨与前臂骨间膜前面,可分为浅深两层。
浅层:从桡侧到尺侧为肱桡肌(屈肘、前臂旋转)、旋前园肌(屈肘、前臂旋转)、桡侧腕屈肌(屈肘、屈腕、手外展)、掌长肌(屈腕、紧张掌腱膜)和尺侧腕屈肌(屈腕、手内收),其深面为指浅屈肌(屈近侧指关节、掌指关节、腕)。
深面:桡侧为拇长屈肌(屈拇指),尺侧为指深屈肌(屈远侧指关节、掌指关节、腕),两肌远侧深面为旋前方肌(前臂旋前)。
Q18:尺神经和正中神经的分支分布(P143)尺神经:自臂丛的内侧束发出,行于腋动脉和腋静脉之间,在臂上部与肱动脉伴行,约于臂部中点行向臂后方,在肱骨内上髁后方经尺神经沟进入前臂和手部。
正中神经:自臂丛的外侧束和内侧束分别发出外侧根和内侧根。
两根共同夹持腋动脉向下合成正中神经的干。
在臂上部行于肱动脉的外侧,约至臂中部越过肱动脉行于其内侧之前臂和手部。
Q19:腕管组成和通过结构(P154)腕管:由屈肌支持带和腕骨沟共同围成。
管内有指浅、深屈肌腱和拇长屈肌腱等9条肌腱通过,分别是屈肌总腱鞘(尺侧囊)和拇长屈肌腱鞘(桡侧囊)包绕,两鞘均超过屈肌支持带近侧和远侧2.5cm,两鞘之间有正中神经通过,当腕骨骨折是可压迫正中神经引起腕管综合征。
Q20:正中神经、尺神经在手部的分支和分布(P158)正中神经:紧贴腕横韧带深面入手掌,通过先发一个返支,绕屈肌支持带远侧缘行向近侧,多有桡动脉伴行,该支支配除拇收肌以外的鱼际诸肌。
然后发出3支指掌侧总神经与同名动脉伴行至掌骨头处,各分为两支指掌侧固有动脉,分布于桡侧3个半指掌侧及中、远节背侧的皮肤,并有分支支配第1、2蚓状肌。
尺神经浅支:由尺神经通过屈肌支持带浅面后立即分出。
浅支有分为两支:其中一支为至小指内侧缘的小指掌侧固有神经;另一支为指掌侧神经。
后者有分为两支指掌侧固有神经,行于第4、5指的相对缘,分布于尺侧一个半指的掌侧皮肤。
Q21:肱三头肌的起止和作用(P144)肱三头肌位于彼得后面,有三个头,即长头、内侧头和外侧头。
长头起于肩胛骨关节盂的下方,外侧头起于肱骨后面桡神经沟的外上方,内侧头起于桡神经沟的内下方;止于尺骨鹰嘴。
主要作用是伸肘关节,长头尚可伸肩关节。
Q22:前臂后群肌各肌的层次排列和作用(P153)前臂肌后群共有10块,分为浅、深两层。
浅层肌:自桡侧向尺侧有桡侧腕长伸肌(伸、外展桡腕关节)、桡侧腕短伸肌(伸桡腕关节)、指伸肌(伸指、伸腕)、小指伸肌(伸小指、伸腕)和尺侧腕伸肌(伸、内收桡腕关节)。
深层肌:旋后肌(前臂后旋)位于上外侧部,其余从桡侧向尺侧为拇长展肌(外展拇指及桡腕关节)、拇短伸肌(伸拇掌指关节)、拇长伸肌(伸拇指)和示指伸肌(伸示指)。
Q23:桡神经的行程和分支分布(P137) 医学笔记起自臂丛后束,行向外下,在肱三头肌深面紧贴肱骨体中部后面沿桡神经沟向下外行,肌支支配肱三头肌、肱桡肌及前臂所有的伸肌,皮支分布于手背桡侧半背面的皮肤。
Q24:斜方肌、背阔肌和竖脊肌的位置起止和作用斜方肌:(起于枕骨上项线、枕外隆凸、项韧带、第7颈椎和全部胸椎棘突,止于锁骨、肩峰、肩胛冈,用于上提、下降、内收肩胛骨)背阔肌:(起于下部胸椎和全部腰椎棘突、骶正中嵴和髂嵴,止于肱骨小结节,用于肩关节后伸、旋内和内收)竖脊肌:(起于骶骨背面、骶结节韧带、腰椎棘突、髂嵴后部、熊腰筋膜,止于肋骨、椎骨的横突和棘突以及颞骨乳突等,用于一侧收缩,使脊柱向同侧屈;两侧同时收缩,是脊柱后伸,竖直去干)Q25:三边孔和四边孔的组成和通过内容三边孔(三边隙)的上下外侧界分别是:肩胛下肌和小圆肌,大圆肌,肱三头肌长头,通过三边孔的结构是旋肩胛动、静脉。
Q26:听诊三角和腰上三角境界(P118、P120)听诊三角:又称肩胛旁三角,位于肩胛骨下角的内侧,。
下界为背阔肌的上缘,内侧界为斜方肌的外下缘,上外侧界为肩胛骨内侧缘的下部。
Q27:颈丛皮支的穿出点和分支分布(P22)颈丛皮支由胸锁乳突肌后缘中点浅出,位置表浅且相对集中,常为颈丛皮支阻滞麻醉的穿刺点。
分支分布:A.枕小神经:它勾饶副神经,沿胸锁乳突肌后缘上升,分布至枕部及耳廓背面上部的皮肤。
B.耳大神经:为颈丛皮支中最大的分支,绕胸锁乳突肌后院浅出,沿胸锁乳突肌表面上行,分布至耳郭及腮腺区皮肤。
C.颈横神经:横过胸锁乳突肌中份,穿颈阔肌浅面向前,分布至颈前区皮肤。
D.锁骨上神经:分为三支行向外下方,在胸骨上缘出浅出,分布至颈前外侧部/胸前臂上部和肩部等处皮肤。
Q28:颈动脉三角和肌三角的境界和内容(P28、P30)颈动脉三角:境界:由胸锁乳突肌上份前缘,肩胛舌骨肌上腹和二腹肌后腹围成。
内容:1、动脉:颈总动脉、颈外动脉、颈内动脉。
2、静脉:面静脉、舌静脉和甲状腺上、中静脉。
3、神经:舌下神经、副神经、迷走神经。
4、二腹肌后腹:表面有耳大神经、下颌后静脉及面神经颈支;深面有颈内动、静脉,颈外动脉和末3对脑神经及颈交感干;上缘有耳后动脉、面神经及舌咽神经等;下缘有枕动脉和舌下神经。
肌三角:境界:位于颈前正中线、胸锁乳突肌前缘和肩胛舌骨肌上腹之间。
内容:浅层有胸骨舌骨肌和肩胛舌骨肌上腹,深层有胸骨甲状肌和甲状舌骨肌,在气管前筋膜深部有甲状腺、甲状旁腺、气管颈部和食管颈部等器官。
Q29:胸锁乳突肌的位置起止和作用(P20)胸锁乳突肌的胸骨头、锁骨头与锁骨上缘之间为锁骨上小窝。
胸锁乳突肌后缘中点有颈丛皮支穿出,为颈部皮肤浸润麻醉的阻滞点Q30:颈动脉鞘的组成及内容物的排列(P34)颈动脉鞘上起颅底,下续纵隔。
在鞘内全长有颈内静脉和迷走神经,鞘内上部有颈内动脉,颈总动脉行于其下部。
在鞘的上部,颈内动脉居前内侧,颈内静脉在其后外方,迷走神经行于二者之间的后内方;在鞘的下部,颈内静脉位于前外侧,颈总动脉位于后内侧,二者之间的后外方有迷走神经。
颈动脉鞘浅面有胸锁乳突肌、胸骨舌骨肌、胸骨甲状肌和肩胛舌骨肌下腹、颈袢及甲状腺上、中静脉;鞘的后方有甲状腺下动脉通过,隔椎前筋膜有颈交感干、椎前肌和颈椎横突等;鞘的内侧有咽和食管颈部、喉和气管颈部、喉返神经和甲状腺侧叶等。
Q31:颈总动脉、颈外动脉的起止行程和颈外动脉的主要分支(P20)有乳突尖与下颌角连线的中点,右侧至右胸锁关节、左侧至左锁骨上小窝作一连线。
该线以甲状软骨上缘为界,上端颈外动脉的投影,下段为颈总动脉的投影。
Q32:迷走神经的颈部行程、毗邻及分支(P37)右迷走神经下行于右颈总动脉和右颈内静脉之间,经右锁骨下动脉第一段前面时发出右喉返神经绕经右锁骨下动脉的下方和后方返回颈部;左迷走神经在左颈总动脉和左颈内静脉之间下行入胸腔。
