基于BP神经网络算法的正余弦函数逼近
基于 BP神经网络曲线曲面函数逼近方法

基于BP神经网络曲线曲面函数逼近方法周丰,闫光荣北京航空航天大学机械工程及自动化学院,北京(1000191)E-mail:zhoua188a@摘要:人工神经网络是近年来智能控制与智能自动化领域的热点,其结构简单,可操作性强,具有很强的自适应、自学习等优点,因而在函数逼近、模式识别、故障诊断、智能控制、信号处理等领域都有广泛的应用。
BP神经网络由于它的学习能力和非线性特性,使其能够对非线性函数进行很好的逼近。
本文通对BP神经网络结构和MATLAB软件及其BP神经网络工具箱的应用研究,利用BP神经网络工具箱设计BP神经网络,用于对非线性函数的逼近,通过网络的训练、测试达到了预期的效果,并对逼近函数曲线进行误差分析,从而为进一步建立更好的神经网络模型,以及对进一步曲线曲面方面神经网络应用研究提出了方向。
关键词:曲线曲面;BP神经网络;函数逼近;MATLAB软件1.引言人工神经网络是一种宏观意义下的仿生算法,它模仿的机制是一切生命与智能的产生与进化过程[1]。
作为仿生结构算法的人工神经网络,是一类由结点相互联接所组成的计算模型,每一个结点通过简单的运算完成从输入到输出的计算,然后这一输出结果通过连接传到其他结点(理论上亦可传到自身)。
本文运用了这种学习算法原理的方法完成了曲线函数逼近的训练过程。
在数值分析领域,用一个简单的函数y(x)近似替代某个复杂的函数f(x)被称作函数逼近,其中被称作被逼近函数,被成为逼近函数,所谓简单函数,在数值计算中主要指可以用四则运算进行的函数,一般为有理函数,最常用的是多项式或分段多项式,数值计算中通常由经典的数值计算方法来实现,本文尝试通过BP神经网络仿真来实现函数的逼近,通过输入矢量和相应的输出矢量训练一个网络以逼近一个函数。
函数逼近在曲线曲面基函数未知的情况下对函数形状的逼近有很大的实际应用价值,一般情况下对曲线曲面的构建都是采用函数插值和逼近两种方法,要求构造一条曲线顺序通过这些数据点,称为对这些数据点进行插值(interpolation),所构造的曲线称为插值曲线。
BP神经网络——逼近应用
BP网络在函数逼近中的应用BP网络由很强的映射能力,主要用于模式识别分类、函数逼近、函数压缩等。
下面将通过实例来说明BP网络在函数逼近方面的应用。
要求设计一个BP网络,逼近以下函数:g(x)=1+sin(k*pi/4*x),实现对该非线性函数的逼近。
其中,分别令k=1,2,4进行仿真,通过调节参数(如隐藏层节点个数等)得出信号的频率与隐层节点之间,隐层节点与函数逼近能力之间的关系。
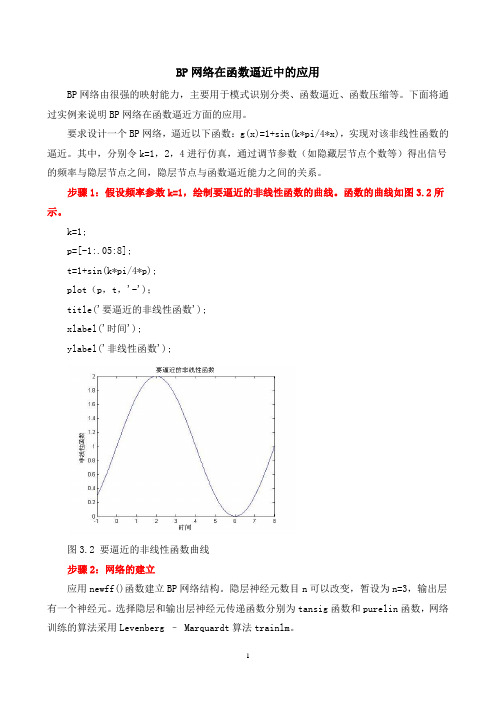
步骤1:假设频率参数k=1,绘制要逼近的非线性函数的曲线。
函数的曲线如图3.2所示。
k=1;p=[-1:.05:8];t=1+sin(k*pi/4*p);plot(p,t,'-');title('要逼近的非线性函数');xlabel('时间');ylabel('非线性函数');图3.2 要逼近的非线性函数曲线步骤2:网络的建立应用newff()函数建立BP网络结构。
隐层神经元数目n可以改变,暂设为n=3,输出层有一个神经元。
选择隐层和输出层神经元传递函数分别为tansig函数和purelin函数,网络训练的算法采用Levenberg – Marquardt算法trainlm。
n=3;net = newff(minmax(p),[n,1],{'tansig' 'purelin'},'trainlm');对于初始网络,可以应用sim()函数观察网络输出。
y1=sim(net,p);figure;plot(p,t,'-',p,y1,':')title('未训练网络的输出结果');xlabel('时间');ylabel('仿真输出--原函数-');同时绘制网络输出曲线,并与原函数相比较,结果如图3.3所示。
图3.3 未训练网络的输出结果因为使用newff( )函数建立函数网络时,权值和阈值的初始化是随机的,所以网络输出结构很差,根本达不到函数逼近的目的,每次运行的结果也有时不同。
基于BP神经网络的函数逼近方法及其MATLAB实现.doc

基于BP神经网络的函数逼近方法及其MATLAB实现作者:李超群落k孝摘要:MATLAB软件及其BP神经网络工具箱函数的应用,结合一个实际的例子详细阐述了基于BP神经网络的函数逼近过程及其MATLAB实现方法。
数值计算方法已经在各个学科领域得到了广泛应用,并且促使新的有效数值方法不断出现。
计算工具的使用为科学计算带来了很大的方便,但山于计算机字长的限制,许多夏杂的、大规模的计算问题需简化。
神经网络是对生物神经系统的模拟,其信息处理功能是山网络单元(神经元)的输入输出特性(激活特性)、网络的拓扑结构(神经元的连接方式)、连接权的大小(突触联系强度)和神经元的阂值(视作特殊的连接权)所决定的。
在神经网络的实际应用中,绝大部分的神经网络模型使用的是BP神经网络或其变化形式,它也是前馈神经网络的核心部分。
BP神经网络的主要特点是非线性映射能力,这种能力使其能够对任意非线性函数进行很好的逼近。
鉴于函数逼近及BP神经网络的这些特点,本文提出了基于BP神经网络的函数逼近方法。
此外,本文开创性地遗弃了C、C++、VC等传统的高级编程语言,采用功能强大的MATLAB语言编程,直接调用MATLAB软件包中的BP神经网络工具箱函数,使程序简捷明了,达到了事半功倍的效果。
1BP神经网络及其函数垣近能力BP神经网络是一•种单向传播的多层前馈网络,网络除了有输入输出节点外,还有一层或多层的隐含层节点,同层节点中没有任何连接,层间节点中实行全连接。
输入信号从输入层节点依次传过各隐含层节点,最后传到输出层节点。
每层节点的输出只影响下一层节点的输出。
各层节点的传递函数通常为双曲1E切S型(sigmoN)函数,但输出层节点的传递函数有时为线性函数。
BP神经网络可以看作是一个从输入到输出的高度非线性映射,即严:及”i及”,/(J)=y。
对于样本集合:输入xi(E及”)和输出yj于及”),可认为存在某一映射好使得8(Xj)=y6(i = l, 2, An)成立。
BP神经网络在Matlab函数逼近中的应用

燕山大学模式识别与智能系统导论题目: BP网络在函数逼近中的应用专业:控制工程姓名: X X X 学号:一BP神经网络及其原理............................................................ - 1 -1.1 BP神经网络定义............................................................. - 1 -1.2 BP神经网络模型及其基本原理..................................... - 1 -1.3 BP神经网络的主要功能................................................. - 3 -1.4 BP网络的优点以及局限性............................................. - 3 - 二基于MATLAB的BP神经网络工具箱函数 ........................ - 6 -2.1 BP网络创建函数............................................................. - 7 -2.2 神经元上的传递函数...................................................... - 7 -2.3 BP网络学习函数............................................................. - 8 -2.4 BP网络训练函数............................................................. - 9 - 三BP网络在函数逼近中的应用.............................................. - 10 -3.1 问题的提出.................................................................... - 10 -3.2 基于BP神经网络逼近函数......................................... - 10 -3.3 不同频率下的逼近效果................................................ - 14 -3.4 讨论................................................................................ - 17 -一BP神经网络及其原理1.1 BP神经网络定义BP (Back Propagation)神经网络是一种神经网络学习算法。
基于BP神经网络工具箱实现函数逼近

VoI . 38 No 9
湖
南
农
¥t J、
2 01 1年 9 月
Sep. 2011
HUNAN AG刚CUUr URAL 数逼近
王 丽 萍
( 安大 学 , 长 陕西 西安 70 5 ) 1 0 4
摘 要 : 用计算机 高级语 言编程对神 经 网络 B 模 型进行仿真和辅助设计是件 十分麻烦的事情, 了解决这个 运 P 为 矛盾, aa 神 经网络工具箱 中专 门编制 了大量有 关设计 B 网络模型的工具 函 。 M tb l P 数 文章分析 了 M fb aa 软件 包中人工 l 神 经网络 工具箱 的有 关 B P网络的工具函数,结合一个 实际的例 子详细阐述 了基 于 B P神 经网络 的函数逼近过程及其
l ⅣG - i g Li p n
(h n " nvri, ' hn i7 05 ,hn) C aga U i sy Xin S ax 1 0 4 i n e t a C a
Ab t a t T e h - e e o u e a g a e p o r mmi g o h P n u a ewo k smu ai n a d mo e - i e sr c h ih l v l c mp tr ln u g r g a g n n t e B e rl n t r i l t n d l a d d o
p c a e o ri ca e r l n t r o l o ft e B ew r t i u c in , o i e t ea ld p a t a x m— a k g fa t i ln u a ewo k to b x o h P n t o k u i t f n t s c mb n d wi a d ti r c i le a i f ly o h e c p e b s d o P n u a ewo k f n t n a p o i t n p c s n l a e n B e r l n t r u c i p r x mai r e s a d MAT AB i lme t t n o o o L mp e n ai . o Ke wo d : t b y r s Ma l ;BP n u a ew r ; o l o a e r ln t o k t ob x
基于BP神经网络的函数逼近实验及MATLAB实现_曹旭帆

! ( 3) 由 ymj = F
W y m m- 1 ij i
计算从第一层直至输
i
出层各节点 j的输出 ymj , 其中上标 m 为 BP 网络的层
标号, F 为神经元的激励函数 ymi - 1为 BP网络 m - 1层
的 i节点的输出, Wmij为 m - 1层的 i节点到 m 层的 j节
点的连接权值, M = M, M - 1, ∀, 1。
!mj = !mj +
m j
( 9) 返回 2, 输入下一组数据前重复 ( 2) ∃ ( 8)的
过程。由此可见, BP 算法的主要思路是从后向前逐层
传播输出层的误差, 并用此误差修正前层权值。
对于 BP 神经网络, 有一个重要定理, 对于任何闭
区间内的连续函数, 都可以用一个三层的 BP 网络逼
近, 本文要研究的问题就是 BP 网络的 隐层神经元个
根据上述一系列实验以及各种算法的训练速度计算量及内存需求量我们设计的bp网络net隐层神经元数目定为16输入输出层神经元数目为1隐层输出层传递函数均为tansig训练函数为traingdx用样本训练网络net训练步数为10000步目标误差0000001bp网络net经过训练达到误差精度要求逼近误差e为00044959netiw11表示隐层16个神经元和输入层1神经元之间的连接权值netlw21表示输出层1个神经元和隐层16个神经元之间的连接权值netb1表示隐层16个神经元的阈值netb2表示输出个神经元的阈值bp网络net的各项权值和阈值如下
关键词: BP 神经网络; MATLAB; 函数逼近; 多项式拟合
中图分类号: TP183
文献标识码: A
文章编号: 1006- 7167( 2008) 05- 0034- 05
Matlab的BP神经网络工具箱及其在函数逼近中的应用

Matlab的BP神经⽹络⼯具箱及其在函数逼近中的应⽤1.神经⽹络⼯具箱概述Matlab神经⽹络⼯具箱⼏乎包含了现有神经⽹络的最新成果,神经⽹络⼯具箱模型包括感知器、线性⽹络、BP⽹络、径向基函数⽹络、竞争型神经⽹络、⾃组织⽹络和学习向量量化⽹络、反馈⽹络。
本⽂只介绍BP神经⽹络⼯具箱。
2.BP神经⽹络⼯具箱介绍BP神经⽹络学习规则是不断地调整神经⽹络的权值和偏值,使得⽹络输出的均⽅误差和最⼩。
下⾯是关于⼀些BP神经⽹络的创建和训练的名称:(1)newff:创建⼀前馈BP⽹络(隐含层只有⼀层)(2)newcf:创建⼀多层前馈BP⽹络(隐含层有多层)(3)train:训练⼀个神经⽹络(4)sim:仿真⼀个神经⽹络以上⼏个是最主要的语句,在后⾯的实例应⽤中会详细说明⽤法。
3.BP神经⽹络⼯具箱在函数逼近中的应⽤BP神经⽹络具有很强的映射能⼒,主要⽤于模式识别分类、函数逼近、函数压缩等。
下⾯通过实例来说明BP⽹络在函数逼近⽅⾯的应⽤。
本⽂需要逼近的函数是f(x)=1+sin(k*pi/2*x),其中,选择k=2进⾏仿真,设置隐藏层神经元数⽬为n,n可以改变,便于后⾯观察隐藏层节点与函数逼近能⼒的关系。
3.1 k=2,n=5时的仿真实验先作出⽬标曲线的图形,以下为matlab代码:clear allclc%%%%%%%%%%设置⽹络输⼊值和⽬标值%%%%%%%%%%k=2;%f(x)中的k值x=[-1:.05:8];f=1+sin(k*pi/2*x);plot(x,f,'-');title('要逼近的⾮线性函数');xlabel('时间');ylabel('⾮线性函数');接着⽤newff函数建⽴BP神经⽹络结构,以下为matlab代码:%%%%%%%%%%建⽴⽹络%%%%%%%%%%n=5;%隐藏层节点数net = newff(minmax(x),[n,1],{'tansig' 'purelin'},'trainlm');%对于初始⽹络,可以应⽤sim()函数观察⽹络输出。
神经网络激活函数[BP神经网络实现函数逼近的应用分析]
![神经网络激活函数[BP神经网络实现函数逼近的应用分析]](https://img.taocdn.com/s3/m/6f4ac08759f5f61fb7360b4c2e3f5727a5e924b1.png)
神经网络激活函数[BP神经网络实现函数逼近的应用分析]神经网络激活函数是神经网络中非常重要的组成部分,它决定了神经网络的非线性特性,并且对于神经网络的求解效果和性能有着重要的影响。
本文将对神经网络激活函数进行详细的分析和探讨,并以BP神经网络实现函数逼近的应用为例进行具体分析。
1.神经网络激活函数的作用(1)引入非线性:神经网络通过激活函数引入非线性,使其具备处理非线性问题的能力,能够更好的逼近任意非线性函数。
(2)映射特征空间:激活函数可以将输入映射到另一个空间中,从而更好地刻画特征,提高神经网络的表达能力,并且可以保留原始数据的一些特性。
(3)增强模型的灵活性:不同的激活函数具有不同的形状和性质,选择合适的激活函数可以增加模型的灵活性,适应不同问题和数据的特点。
(4)解决梯度消失问题:神经网络中经常会遇到梯度消失的问题,通过使用合适的激活函数,可以有效地缓解梯度消失问题,提高神经网络的收敛速度。
2.常用的神经网络激活函数(1)Sigmoid函数:Sigmoid函数是一种常用的激活函数,它的输出值范围在(0,1)之间,具有平滑性,但是存在梯度消失问题。
(2)Tanh函数:Tanh函数是Sigmoid函数的对称形式,它的输出值范围在(-1,1)之间,相对于Sigmoid函数来说,均值为0,更符合中心化的要求。
(3)ReLU函数:ReLU函数在输入为负数时输出为0,在输入为正数时输出为其本身,ReLU函数简单快速,但是容易出现神经元死亡问题,即一些神经元永远不被激活。
(4)Leaky ReLU函数:Leaky ReLU函数是对ReLU函数的改进,当输入为负数时,输出为其本身乘以一个小的正数,可以解决神经元死亡问题。
(5)ELU函数:ELU函数在输入为负数时输出为一个负有指数衰减的值,可以在一定程度上缓解ReLU函数带来的神经元死亡问题,并且能够拟合更多的函数。
3.BP神经网络实现函数逼近的应用BP神经网络是一种常用的用于函数逼近的模型,它通过不断调整权重和偏置来实现对目标函数的拟合。
实验二基于BP神经网络算法的函数逼近

实验二基于BP神经网络算法的函数逼近一、引言函数逼近是神经网络应用的重要领域之一、在实际问题中,我们常常需要使用一个适当的数学函数来近似描述现象与问题之间的关系。
BP神经网络作为一种常用的函数逼近方法,具有良好的逼近性能和普适性,能够对非线性函数进行逼近,并且在实际应用中已经得到了广泛的应用。
本实验将通过BP神经网络算法对给定的函数进行逼近,验证其逼近效果和性能。
二、实验目标1.理解和掌握BP神经网络算法的基本原理和步骤;2.掌握使用BP神经网络进行函数逼近的方法;3.通过实验验证BP神经网络在函数逼近中的性能。
三、实验步骤1.准备数据集选择一个待逼近的非线性函数,生成一组训练数据和测试数据。
训练数据用于训练神经网络模型,测试数据用于评估逼近效果。
2.构建神经网络模型根据待逼近的函数的输入和输出维度,确定神经网络的输入层和输出层的神经元个数,并选择适当的激活函数和损失函数。
可以根据实际情况调整隐藏层的神经元个数,并添加正则化、dropout等技术来提高模型的泛化能力。
3.初始化网络参数对于神经网络的参数(权重和偏置)进行随机初始化,通常可以采用均匀分布或高斯分布来初始化。
4.前向传播和激活函数通过输入数据,进行前向传播计算,得到网络的输出值,并通过激活函数将输出值映射到合适的范围内。
5.计算损失函数根据网络的输出值和真实值,计算损失函数的值,用于评估模型的训练效果。
6.反向传播和权重更新通过反向传播算法,计算各个参数的梯度,根据学习率和梯度下降算法更新网络的参数。
7.循环迭代训练重复以上步骤,直至达到预设的训练停止条件(如达到最大迭代次数或损失函数满足收敛条件)。
8.模型测试和评估使用测试数据评估训练好的模型的逼近效果,可以计算出逼近误差和准确度等指标来评估模型的性能。
四、实验结果通过对比逼近函数的真实值和模型的预测值,可以得到模型的逼近效果。
同时,通过计算逼近误差和准确度等指标来评估模型的性能。
基于BP神经网络工具箱实现函数逼近

基于BP神经网络工具箱实现函数逼近
王丽萍
【期刊名称】《湖南农机》
【年(卷),期】2011(038)009
【摘要】运用计算机高级语言编程对神经网络BP模型进行仿真和辅助设计是件十分麻烦的事情,为了解决这个矛盾,Matlab神经网络工具箱中专门编制了大量有关设计BP网络模型的工具函数.文章分析了Matlab软件包中人工神经网络工具箱的有关BP网络的工具函数,结合一个实际的例子详细阐述了基于BP神经网络的函数逼近过程及其MATLAB实现方法.
【总页数】3页(P29-31)
【作者】王丽萍
【作者单位】长安大学,陕西西安710054
【正文语种】中文
【中图分类】TP393.02
【相关文献】
1.基于BP神经网络的函数逼近实验及MATLAB实现 [J], 曹旭帆;叶舟;万俊;李晶
2.基于BP神经网络的函数逼近的MATLAB实现 [J], 冯蓉;杨建华
3.基于BP神经网络的非线性函数逼近及SAS实现 [J], 李君艺;张宇华
4.基于BP神经网络的函数逼近方法及其MATLAB实现 [J], 蒋良孝;李超群
5.BP神经网络实现函数逼近的应用分析 [J], 李浩;王婷
因版权原因,仅展示原文概要,查看原文内容请购买。
基于BP神经网络算法的函数逼近

基于BP神经网络算法的函数逼近神经网络是一种基于生物神经元工作原理构建的计算模型,可以通过学习和调整权重来逼近非线性函数。
其中,基于误差反向传播算法(BP)的神经网络是最常见和广泛应用的一种,其能够通过反向传播来调整网络的权重,从而实现对函数的近似。
BP神经网络的算法包括了前馈和反向传播两个过程。
前馈过程是指输入信号从输入层经过隐藏层传递到输出层的过程,反向传播过程是指将网络输出与实际值进行比较,并根据误差来调整网络权重的过程。
在函数逼近问题中,我们通常将训练集中的输入值作为网络的输入,将对应的目标值作为网络的输出。
然后通过反复调整网络的权重,使得网络的输出逼近目标值。
首先,我们需要设计一个合适的神经网络结构。
对于函数逼近问题,通常使用的是多层前馈神经网络,其中包括了输入层、隐藏层和输出层。
隐藏层的神经元个数和层数可以根据具体问题进行调整,一般情况下,通过试验和调整来确定最优结构。
然后,我们需要确定误差函数。
对于函数逼近问题,最常用的误差函数是均方误差(Mean Squared Error)。
均方误差是输出值与目标值之间差值的平方和的均值。
接下来,我们进行前馈过程,将输入值通过网络传递到输出层,并计算出网络的输出值。
然后,我们计算出网络的输出与目标值之间的误差,并根据误差来调整网络的权重。
反向传播的过程中,我们使用梯度下降法来最小化误差函数,不断地调整权重以优化网络的性能。
最后,我们通过不断训练网络来达到函数逼近的目标。
训练过程中,我们将训练集中的所有样本都输入到网络中,并根据误差调整网络的权重。
通过反复训练,网络逐渐优化,输出值逼近目标值。
需要注意的是,在进行函数逼近时,我们需要将训练集和测试集分开。
训练集用于训练网络,测试集用于评估网络的性能。
如果训练集和测试集中的样本有重叠,网络可能会出现过拟合现象,导致在测试集上的性能下降。
在神经网络的函数逼近中,还有一些注意事项。
首先是选择适当的激活函数,激活函数能够在网络中引入非线性,使网络能够逼近任意函数。
基于BP网络的函数逼近研究

134 •电子技术与软件工程 Electronic Technology & Software Engineering计算机技术应用• the Application of Computer Technology表小区平均载波频率,B N 为NB-IoT 和FDD-LTE 的可用带宽,B 是现有GSM 总带宽所需带宽。
在不影响GSM 网络容量的前提下,充分利用低频20M 频段,尽量选择频率点,避免干扰,以满足FDD-LTE 演进的需要。
根据上述带宽计算方法,计算了当前网络GSM 网络负载情况,得到了NB-IoT 和FDD-LTE 的可用带宽,并进行了网络重划分。
900M 网络re-tilling 模式如图2所示。
当GSM 网络负载较重时,网络清频功能可配置5M 的FDD-LTE 和600K NB-IoT 网络;当GSM 网络负载较低时,可以将FDD-LTE 中心频率恒定带宽扩展到10M ;当GSM 网络的负载可以进一步降低时,新增5M FDD-LTE ,直至GSM 网络完全退网。
3.3 组网规划组网规划即网络部署规划,根据规划,确定网络规划方案、站点规模输出。
基于FDD-LTE 部署的NB-IoT ,可以快速构建蜂窝物联网。
基于NB-IoT 的FDD-LTE 有三种部署模式。
分别为单独部署、保护带部署和带内部署。
虽然保护带不占用FDD-LTE 频段资源,但设备复杂,技术要求高,目前仅有少数厂商支持此种终端设备。
采用带内方式部署时LTE 与LTE 之间的干扰比较严重,而为避免干扰,则需要消耗容量,技术难度大。
所以考虑到容量和覆盖容量,应采用单独部署的方式。
NB-IoT 网络应以满足业务需求为导向,充分考虑物联网的业务分布。
部分现有LTE 设备可以通过软件升级来支持NB-IoT ,但仍有60%的老设备不能同时支持NB-IoT 和LTE ,所以需要根据本地业务需求,逐步升级更替。
4 结束语本文重点研究了基于FDD-LTE 的NB-IoT 联合规划业务部署方案。
BP网络逼近sin函数

alpha = 0.4;%学习速率
error = 0.0001;%误差阈值
M = 200;
%%训练数据200
for m = 1:M
y = sin(0.01*pi*m);%实际样本输出
for k = 1:50
%%对每个数据训练50次
for i = 1:hideLayer %隐层
hold on
plot (x,y1,'r-');
legend('标准sin图像','BP逼近的sin图像')
figure;
plot(e1);
title('错误率')
p(i) = logsig(w1(i) * x(m) + b1(i));
end
a = 0; %输出层
for j = 1:hideLayer
q(j) = p(j) * w2(j);
a = a + q(j);
end
a = a + b2;
if m <= 100
A = logsig(a);
elseif m > 100
bp网络函数逼近神经网络函数逼近函数逼近函数逼近论matlab函数逼近函数逼近理论函数逼近论方法样条函数逼近样条函数及其逼近复变函数逼近
%%网络结构1-2-1,学习率alpha=0.4
clear all;
close all;
clc;
input = 1; %输入层像两个数
hideLayer = 2;%隐藏层神经元个数
outputLayer = 1;%输出层神经元个数
x = [0.01*pi:0.01*pi:2*pi];%输入向量(1*200)
基于BP神经网络算法的正余弦函数逼近

实验二 基于BP 神经网络算法的正余弦函数逼近班级:学号:姓名:1. 实验目的(1) 掌握MATLAB 子函数编写与调用。
(2) 理解BP 神经元网络算法的原理,并利用程序实现通过BP 算法逼近任意非线性函数。
2. 实验内容与实验要求(1) 掌握BP 神经网络算法的原理。
(2) 掌握MATLAB 子函数的编写方法及调用方法。
(3) 根据BP 神经网络算法的原理,编写MA TLAB 程序,逼近非线性函数。
3. 实验原理一个2×3×1的神经网络即输入层有两个节点,隐层含三个节点,输出层有一个节点,图1 神经网络结构图图中ij w )5,4,3;2,1(==j i 为输入层与隐层的权值,jk w )6;5,4,3(==k j 为隐层与输出层的权值,1x 、2x 是神经网络的输入值,y 是网络的输出值,p y 为教师信号,e 为神经网络的实际输出与期望输出的误差。
在这个神经网络中,节点1,2是输入层, 节点3,4,5是隐层,节点6是输出层;输入层和隐层之间的权值依次252423151413,,,,,w w w w w w ,隐层和输出层间的权值为564636,,w w w ,下角标为节点的编号;隐层和输出层节点的阈值依次为3θ,4θ,5θ,6θ。
①前馈计算设隐层的第j 个节点的输入和输出分别为:∑=⋅=N i i ij j O wI 1)(j j I f O =其中)(j I f 为激励函数 j I j e I f -+=11)(由于隐层的输出就是输出层的输入,则输出层第k 个节点的总输入和输出分别为: ∑=⋅=H j j jk k O wI 1)(k k k I f O y ==若网络输出与实际输出存在误差,则将误差信号反向传播,并不断地修正权值,直至误差达到要求为止。
②权值调整设误差函数定义为: ∑=-=M k k k p y d E 12)(21 为了简便,以下计算都是针对每个节点而言,误差函数p E 记作E 。
BP神经网络实现函数逼近python实现

机器学习作业一BP神经网络实现函数逼近一.算法描述BP(Back Propagation)神经网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。
它的学习规则是使用梯度下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP神经网络模型拓扑结构包括输入层(input)、隐层(hidden layer)和输出层(output layer)。
二.数据描述逼近函数y = sin(x)三.算法参数输入学习率,迭代次数,逼近函数,神经网络规模输出逼近的函数四.实验流程反向传播算法(Back Propagation)分二步进行,即正向传播和反向传播。
这两个过程简述如下:1.正向传播输入的样本从输入层经过隐单元一层一层进行处理,传向输出层;在逐层处理的过程中。
在输出层把当前输出和期望输出进行比较,如果现行输出不等于期望输出,则进入反向传播过程。
2.反向传播反向传播时,把误差信号按原来正向传播的通路反向传回,逐层修改连接权值,以望代价函数趋向最小。
输入层输入向量(n维):X=(x1,x2,…,xi,…,xn)T隐层输出向量(隐层有m个结点):Y=(y1,y2,…,yj,…,ym)T输出层输出向量(l维):O=(o1,o2,…,ok,…,ol)T期望输出向量:d=(d1, d2,…,dk,…,dl)T输入层到隐层之间的权值矩阵:V=(V1,V2,…,Vj,…,Vm)隐层到输出层之间的权值矩阵用:W=(W1,W2,…,Wk,…,Wl)对输出层第k个结点和隐含层的第j个结点有如下关系:激活函数f(x)常用sigmoid函数(一个在生物学中常见的S型的函数,也称为S 形生长曲线)或者tanh(双曲正切)函数。
BP神经网络函数逼近

X2
Ym Xn
输入层
隐含层
输出层
图 1 BP 神经网络拓扑结构图 图 1 中, X1, X2, …, Xn 是 BP 神经网络的输入值, Y1, Y2, …, Ym 是 BP 神 经网络的预测值,ωij 和ωjk 为 BP 神经网络权值。从图 2 可以看出, BP 神经网络 可以看成一个非线性函数, 网络输入值和预测值分别为该函数的自变量和因变 量。当输入节点数为 n, 输出节点数为 m 时, BP 神经网络就表达了从 n 个自变量 到 m 个因变量的函数映射关系。
3 学习训练
BP 神经网络预测前首先要训练网络, 通过训练使网络具有联想记忆和预测 能力。BP 神经网络的训练过程包括以下几个步骤。 步骤 1:网络初始化。 根据系统输入输出序列(X, Y)确定网络输入层节点数 n、 隐含层节点数 l,输出层节点数 m,初始化输入层、隐含层和输出层神经元之间的 连接权值ωij,ωjk,初始化隐含层阈值 a,输出层阈值 b,给定学习速率和神经元激 励函数。 步骤 2:隐含层输出计算。根据输入向量 X, 输入层和隐含层间连接权值ωij 以及隐含层阈值 a,计算隐含层输出 H。
2
院系:理学院
专业:光学工程
学号:s111201003
姓名:李润
2 主要用途
BP 网络主要用于: (1)函数逼近:用输入矢量和相应的输出矢量训练网络逼近某个函数; (2)模式识别:用一个特定的输出矢量将它与输入矢量联系起来; (3)分类:把输入矢量以所定义的合适的方法进行分类; (4)数据压缩:减少输出矢量维数以便于传输或存储。 在人工神经网络的实际工程应用中,特别在自动控制领域中,大多数神经网 络模型是采用 BP 网络或它的变化形式,它也是前向网络的核心部分,体现了人 工神经网络最精华的部分。
bp神经网络进行多项式函数的逼近 吐血推荐1

神经网络及应用实验报告院系:电气工程学院班级:adf3班姓名:adsf学号:20sdf实验二、基于BP网络的多层感知器一:实验目的:1. 理解多层感知器的工作原理2. 通过调节算法参数了解参数的变化对于感知器训练的影响3. 了解多层感知器局限性二:实验原理:BP的基本思想:信号的正向传播误差的反向传播–信号的正向传播:输入样本从输入层传入,经各隐层逐层处理后,传向输出层。
–误差的反向传播:将输入误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号来作为修正各单元权值的依据。
1.基本BP算法的多层感知器模型:2.BP学习算法的推导:当网络输出与期望输出不等时,存在输出误差E将上面的误差定义式展开至隐层,有进一步展开至输入层,有调整权值的原则是使误差不断地减小,因此应使权值的调整量与误差的梯度下降成正比,即η∈(0,1)表示比例系数,在训练中反应学习速率BP算法属于δ学习规则类,这类算法被称为误差的梯度下降(Gradient Descent)算法。
三:实验内容:Hermit多项式如下式所示:f(x)=1.1(1-x+2x^2)exp(-x^2/2)采用BP算法设计一个单输入单输出的多层感知器对该函数进行逼近。
训练样本按以下方法产生:样本数P=100,其中输入样本xi服从区间[-4,4]内的均匀分布,样本输出为F(xi)+ei ,ei为添加的噪声,服从均值为0,标准差为0.1的正态分布。
隐层采用Sigmoid激活函数f(x)=1/(1+1/e^x),输出层采用线性激活函数f(x)=x。
注意:输出层采用的线性激活函数,不是Sigmoid激活函数,所以迭代公式需要根据前面的推导过程重新推导。
四:实验步骤:1. 用Matlab编程,实现解决该问题的单样本训练BP网络,设置一个停止迭代的误差Emin和最大迭代次数。
在调试过程中,通过不断调整隐层节点数,学习率η,找到收敛速度快且误差小的一组参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 基于BP 神经网络算法的正余弦函数逼近1. 实验目的(1) 掌握MATLAB 子函数编写与调用。
(2) 理解BP 神经元网络算法的原理,并利用程序实现通过BP 算法逼近任意非线性函数。
2. 实验内容与实验要求(1) 掌握BP 神经网络算法的原理。
(2) 掌握MATLAB 子函数的编写方法及调用方法。
(3) 根据BP 神经网络算法的原理,编写MA TLAB 程序,逼近非线性函数。
3. 实验原理一个2×3×1的神经网络即输入层有两个节点,隐层含三个节点,输出层有一个节点,图1 神经网络结构图图中ij w )5,4,3;2,1(==j i 为输入层与隐层的权值,jk w )6;5,4,3(==k j 为隐层与输出层的权值,1x 、2x 是神经网络的输入值,y 是网络的输出值,p y 为教师信号,e 为神经网络的实际输出与期望输出的误差。
在这个神经网络中,节点1,2是输入层, 节点3,4,5是隐层,节点6是输出层;输入层和隐层之间的权值依次252423151413,,,,,w w w w w w ,隐层和输出层间的权值为564636,,w w w ,下角标为节点的编号;隐层和输出层节点的阈值依次为3θ,4θ,5θ,6θ。
①前馈计算设隐层的第j 个节点的输入和输出分别为:∑=⋅=N i i ij j O wI 1)(j j I f O =其中)(j I f 为激励函数 j I j e I f -+=11)(由于隐层的输出就是输出层的输入,则输出层第k 个节点的总输入和输出分别为: ∑=⋅=H j j jk k O wI 1)(k k k I f O y ==若网络输出与实际输出存在误差,则将误差信号反向传播,并不断地修正权值,直至误差达到要求为止。
②权值调整设误差函数定义为: ∑=-=M k k k p y d E 12)(21 为了简便,以下计算都是针对每个节点而言,误差函数p E 记作E 。
输出层权值的调整权值修正公式为: jkjk w E w ∂∂-=∆η jkk k w I I E ∂∂∂∂-=η 定义反传误差信号k δ为:k k k k k I O O E I E ∂∂∂∂-=∂∂-=δ 式中 )(k k kO d O E --=∂∂ )()(k kk k k I f I I f I O '=∂∂=∂∂ )1()](1)[()(k k k k k O O I f I f I f -=-=' 所以 )(k k k O d -=δ)1(k k O O -又 j H j j jk jk jk k O O w w w I =∂∂=∂∂∑=)(1由此可得输出层的任意神经元权值的修正公式:j k jk O w ηδ=∆或 j k k k k jk O O d O O w ))(1(--=∆η ( 隐层权值的调整 ijij w E w ∂∂-=∆η ijj j w I I E ∂∂∂∂-=η i jO I E ∂∂-=η 式中 i Ni i ij ij ij O O w w w E =⋅∂∂=∂∂∑=)(1由于误差函数E 与隐层输入j I 不存在直接的函数关系,因此不能直接求得,所以 jj j j I O O E I E ∂∂∂∂-=∂∂- jj M k j k k I I f O I I E ∂∂⋅∂∂∂∂-=∑=)()(1 )()()(11j Hj j jk j M k k I f O w O I E '⋅⋅∂∂∂∂-=∑∑== )()(1j M k jk k I f w '⋅=∑=δ 隐层的反传误差信号为∑=⋅'=M k jk k j i w I f 1)(δδ由此可得,隐层权值的修正公式为;i M k jk k j ij O w I f w ⋅⋅'=∆∑=)()(1δη或 i Mk jk k j j ij O w O O w ⋅⋅-=∆∑=)()1(1δη4.实验设备(1)计算机(2)MATLAB软件5.实验流程(1)初始化w ij=0,w jk=0,e0=0,e1=0,e2=0,q0=0,x j=0,q1= 0,q0=0,k1=5,k=100。
(2)循环1开始,计算三角函数y=sin(4*3.14*k1*s/360)的值(3)循环2开始,进行前馈的计算,x(k+1)=x(k)+q(k),out1(k+1)=(1-exp(-x(k+1))) / (1+exp(-x(k+1)));out2(k+1)=1/(1-exp(-x(k+1)));n1(k+1)=w ij(k)∗out1(k+1);n2(k+1)=n1(k+1)+p(k)。
y1(k+1)=1/(1+exp(-n2(k+1))),y2(k+1)=(1-exp(-n2(k+1)))/(1+exp(-n2(k+1)))(4)计算偏差e2(k+1)=(y(k+1)-y2(k+1))^2/2;修正项xj1(k+1)=e2(k+1)-e2(k);xj2(k+1)=e2(k+1)-2*e2(k)+e1(k);反传信号的偏差为δ(k+1)=y1(k+1)*(1-y2(k+1))*(y(k+1)-y2(k+1)) (5)调整隐层权值Δw(k+1)=δ(k+1)∗w ij(k)∗(1−out1(k+1))∗out2(k+1)Δq=q1-q0;q2(k+1)=q1(k)+0.8*Δw(k+1)+0.4*Δq;Δw ij(k+1)=w ij(k+1)−w ij(k);w ij(k+1)=w ij(k)+0.8∗δ(k+1)∗xj(k+1)+0.6∗Δw ij(k+1)q0(k+1)=q1(k);q1(k+1)=q2(k+1).(6)调整输出层权值Δh=w jk(k+1)−w jk(k);w jk(k+1)=w jk(k)+0.4∗δ(k+1)∗out1(k+1)+0.75∗Δh w20(k+1)=w21(k);w21(k+1)=w jk(k+1)Δp=p(k+1)-p(k);p(k+1)=p(k)+0.9*δ(k+1)+0.6∗Δpp1(k+1)=p1(k);p1(k+1)=p(k+1).(7)判断偏差e,若小于0.0000001,则循环2结束;否则,跳转执行步骤(2)直到循环1结束。
(8) 得出实验结果为三角函数y=sin(4*3.14*k1*s/360)与逼近曲线的图形。
6. 实验结果7. 实验结果分析利用BP 神经网络算法基本能实现非线性函数的逼近,但只能对正余弦进行逼近。
在函数y 取得最大值时,误差比其他区域要大,说明在峰值时刻的点越难逼近。
而且逼近的程度与权值的加权系数有很大关系。
8. 实验代码%BP Algorithms Program%Giving initial value;%初始化w10=[0 0;0 0;0 0];w11=[0 0;0 0;0 0];w20=[0;0;0];w21=[0;0;0];q0=[0 0 0];q1=[0 0 0];p0=0;p1=0;xj=[0;0];e0=0;e1=0;e2=0;k1=5;k2=100;01020304050607080-1-0.8-0.6-0.4-0.20.20.40.60.81BP Algorithmfor s=1:72yp1=sin(4*3.14*k1*s/360);for k=1:k2;%前馈计算%得到m1,o1两个数组(3 * 1 )for i=1:3x=w11(i,1)*xj(1,:)+w11(i,2)*xj(2,:); %xj(1,:)表示取行q1(:,i)表示取列z=x+q1(:,i); %相当于加一个初始化时的值o=(1-exp(-z))./(1+exp(-z)); % 算的是Oi 激励函数1为f1(z)=(1-e^(-z))/(1+e^(-z))m=1./(1+exp(-z)); % 算的是Oi1 激励函数2为f2(z)=1./(1+e^(-z))m1(i,:)=m; %把m的值赋给m1数组相对应的行o1(i,:)=o; %把o的值赋给o1数组相对应的行endyb=0;for i=1:3yb=yb+w21(i,:)*o1(i,:); % yb=Ikendyi=yb+p1; % yi为修正后的值n=1./(1+exp(-yi)); % 在函数2下的输出函数值n->Oky=(1-exp(-yi))./(1+exp(-yi)); % 在函数1下的输出函数值y->y%calculation error between aim and practice output;e0=e1;e1=e2;e2=((yp1-y).^2)./2; % y的权值误差函数的计算,放入e2xj1=e2-e1; % 对修正项的修正,放入xj1xj2=e2-2*e1+e0;xj=[xj1;xj2]; %总的修正数组xj( 2 * 1 )d2=n*(1-y)*(yp1-y); %d2:输出的反传误差信号%隐层的权值调整%revising weighted value and threshold value in hidden layer;for i=1:3u=w21(i,:)*d2; % u->dartak*wjkd1=(1-o1(i,:)).*u; %d1->(1-oj)*ud0=m1(i,:)*d1; % d0->m1*d1; d0=Λwijqw=q1(:,i)-q0(:,i);q2=q1(:,i)+0.8*d0+0.4*qw; %设定的阈值与计算出的阈值之间的偏差q3(:,i)=q2;for j=1:2dw=w11(i,j)-w10(i,j);w12=w11(i,j)+0.8*d0*xj(j,:)+0.6*dw;%设定的阈值与计算出的阈值之间的偏差w13(i,j)=w12;endendw10=w11;w11=w13;q0=q1;q1=q3;%输出层的权值调整%revising weighted value and threshold value in output layer;for i=1:3h=w21(i,:)-w20(i,:);w22=w21(i,:)+0.4*d2*o1(i,:)+0.75*h;w23(i,:)=w22;endw20=w21;w21=w23;ph=p1-p0;p2=p1+0.9*d2+0.6*ph;p0=p1;p1=p2;%writing error value and output value;if e2<0.0000001,break;else k=k+1;endende(s)=e2;ya(s)=yp1;yo(s)=y;s=s+1;endw11=w13;w21=w23;%graphicss1=s-1;s=1:s1;plot(s,ya,s,yo,s,yo,'g.',s,e,s,e,'rx')title('BP Algorithm');clear all。
