郑承沛材料力学各章作业(第2学期24学时)
材料力学第五版课后题答案

[习题2-2]一打入基地内的木桩如图所示,杆轴单位长度的摩擦力f=kx**2,试做木桩的后力图。
解:由题意可得:33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=,其横截面面尺寸如图所示。
荷载kN F 1000=,材料的密度3/35.2m kg =ρ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:g Al F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积:)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:)()(x EA Fdx l d =∆ ,⎰⎰==∆l l x A dxE F dx x EA F l 00)()(l xr r r r =--121,22112112d x l d d r x l r r r +-=+⋅-=,2211222)(u d x l d d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ,dx l d d du d x l d d d 2)22(12112-==+-du d d l dx 122-=,)()(22)(221212udud d l du u d d lx A dx -⋅-=⋅-=ππ因此, )()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆πlld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。
长沙理工大学材料力学练习册答案详解

第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
20(MPa )20d(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B )AC AC /2,/2ττσ==;(C )AC AC /2,/2ττσ==;(D )AC AC /2,/2ττσ=-=。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(b)(a)(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的;(C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c)之间的关系,有下列四种答案,正确答案是( D )。
τ(a)(b)(c)(A )三种应力状态均相同;(B )三种应力状态均不同;(C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
(A)(B)(D)(C)解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料;8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。
福州大学至诚学院材料力学历年试卷
,
.
二
承受
O a
•B
* .
@ Fn
::
L
=k = '
:
rip .
K
平偞
与刚 度 毒 件
中 傄
戮敦 喊 朱阑
奸
四
•y·
e
射
芦 B5 国廿 丅
O
疝 如 图所示
ÁB 梁
瓦
2 oa
试校食A B
•t
是否
237c m
s
,
·
足 正 座 力 强度
.
丽
j
-
·
条件儅 Ot z 和 1ºñ
q-
15k N T m
+p
融
砂
1
卷 学至诚学院期末试 福 州大
2 00 8
(B)
卷
2 009 年
翔 二2 009 学年棠! 学期 课程名称 乻 材料 学乼 寿 白
与
磊
月
日
主考教 I
犷 毒 拓林 位看儉
班级
m
讨
•B
µ
孬 孝钲 时间Ï 20 夯
;
专业
考生学号
解答错误毒打
考生姓名
解答不完全正 时 婚正分
二 瓦 试题解答正确辅
二龆 刃
u
íi t F
+o
:L
为
5
偟
P- 1
=
翎
居· 2 杓 G P a
( 入
僇 亡些
8 3 c 旒4. Á
-
6 93 c m
2
已 知 材料
CD
如 砥定安全 系数为 予汇 偟 试 校核
材料力学(64学时)教学大纲

北京工业大学“材料力学III(64学时)”课程教学大纲英文名称:Mechanics of Materials (64)课程编号:0000163课程类型:技术基础课学时:64 学分:4适用对象:机类、土建类、近机类各相关专业先修课程:高等数学、理论力学使用教材及参考书:教材:《材料力学》,郑承沛编著,北京工业大学出版社,1999年8月再版;参考书:《材料力学(I)、(II)》,单辉祖编著,高等教育出版社,1999年9月第1版,2002年2月第4次印刷;《Mechanics of Materials (Fifth Edition)》,James M. Gere, Brooks/Cole, 2001.一、 课程性质、目的和任务材料力学是变形体力学入门的技术基础课。
教学任务是:构筑作为工程制造技术根基的知识结构;通过揭示杆件强度、刚度、稳定性等知识发生过程,培养学生分析解决问题的能力;以理论分析为基础,培养学生的实验动手能力;发挥其它课程不可替代的综合素质教育作用。
二、 课程教学内容及要求(符号说明:[1] :掌握、[2] :理解、[3] :了解、△:自学或粗讲标记、[!]:重点、[*]:难点)(1) 绪论:材料力学的任务及研究对象,变形固体的基本假设[1],外力、内力、应力、应变的基本概念[1,*],杆件变形的基本形式[3]。
(2) 轴向拉压:截面法、轴力与轴力图[1];直杆横截面及斜截面的应力[1],强度条件[!],安全因数概念[1],许用应力的确定方法[2];拉压杆变形,纵向变形、线应变,横向变形、泊松比,虎克定律,弹性模量,节点位移计算[1];材料拉伸及压缩时的力学性能,应力-应变曲线,材料在卸载及再加载时的力学性能,材料的塑性[2]。
应力集中的概念,圣维南原理[3];拉压超静定问题[!,*],温度及装配应力简介[△];连接件的强度计算,剪切及挤压的实用计算[1]。
(3) 扭转:扭转概念,纯剪切,切应力互等定理,剪切虎克定律[1];扭矩及扭矩图,圆轴扭转时的应力与应变[1,!],扭转强度及刚度条件[1];简单扭转超静定问题[3];简介矩形截面杆和开口、闭口薄壁杆件扭转时应力及变形特征[3]。
完整版材料力学各章重点内容总结

完整版材料力学各章重点内容总结材料力学各章重点内容总结第一章绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章轴向拉压、轴力图:注意要标明轴力的大小、单位和正负号。
、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
、轴向拉压时横截面上正应力的计算公式: F N注意正应力有正负号,A拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:注意角度是指斜截面与横截面的夹角七、线应变一-没有量纲、泊松比一没有量纲且只与材料有关、l胡克定律的两种表达形式: E , I 出注意当杆件伸长时I 为正,EA缩短时I 为负。
八、低碳钢的轴向拉伸实验:会画过程的应力一应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p,弹性极限e )、屈服阶段(屈服极限s )、强化阶段(强度极限 b )和局部变形阶段会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力一应变曲线cos 2 ,sin2五、轴向拉压时横截面上正应力的强度条件F N,maxmaxA六、利用正应力强度条件可解决的三种问题: 1?强度校核maxF N ,maxA定要有结论 2.设计截面A F N,max3.确定许可荷载F^max A180八、圆轴在扭转时的刚度条件maxT maxGI p(注意单位:给出的许用单九、衡量材料塑性的两个指标:伸长率耳100 及断面收缩率 A-A 1100,工程上把 5 的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。
对没有明显屈服极限的塑性材料,如何来确定其屈服指标?见课本第24页。
材料力学习题集[有答案]
![材料力学习题集[有答案]](https://img.taocdn.com/s3/m/e757450587c24028905fc317.png)
习题2-1图习题2-2图习题2-3图习题2-4图材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪习题2-5图习题2-6图习题2-1图习题2-2图一种答案是正确的。
正确答案是 C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F xM=; (B ))(d d Q x q x F -=,Q d d F xM-=; (C ))(d d Q x q x F -=,Q d d F xM=; (D ))(d d Q x q xF =,Q d d F xM-=。
材料力学习题答案
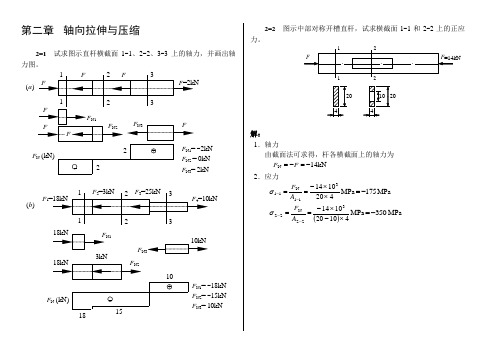
第二章轴向拉伸与压缩2-1 试求图示直杆横截面1-1、2-2、3-3上的轴力,并画出轴((b)2-2图示中部对称开槽直杆,试求横截面1-1和2-2上的正应力。
解:1.轴力由截面法可求得,杆各横截面上的轴力为kN14N-=-=FF2.应力4201014311N11⨯⨯-==--AFσMPa175-=MPa()410201014322N22⨯-⨯-==--AFσMPa350-=MPa2-3 图示桅杆起重机,起重杆AB 的横截面是外径为mm 20、内径为mm 18的圆环,钢丝绳BC 的横截面面积为2mm 10。
试求起重杆AB 和钢丝绳=2kN解:1.轴力取节点B 为研究对象,受力如图所示,0=∑x F : 045cos 30cos N N =++οοF F F AB BC0=∑y F : 045sin 30sin N =--οοF F AB由此解得: 83.2N -=AB F kN , 04.1N =BC F kN 2.应力起重杆横截面上的应力为()223N 182041083.2-⨯⨯-==πσABAB AB A F MPa 4.47-=MPa 钢丝绳横截面上的应力为101004.13N ⨯==BC BC BC A F σMPa 104=MPa2-4 图示由铜和钢两种材料组成的等直杆,铜和钢的弹性模量分别为GPa 1001=E 和GPa 2102=E 。
若杆的总伸长为mm 126.0Δ=l ,试求载荷F 和杆横截面上的应力。
解:1.横截面上的应力 由题意有 ⎪⎪⎭⎫⎝⎛+=+=∆+∆=∆2211221121E l E l A E Fl A E Fl l l l σ 由此得到杆横截面上的应力为3322111021040010100600126.0⨯+⨯=+∆=E l E l l σMPa 9.15=MPa 2.载荷24049.15⨯⨯==πσA F N 20=kN2-5 图示阶梯形钢杆,材料的弹性模量GPa 200=E ,试求杆横截面上的最大正应力和杆的总伸长。
材料力学全部习题解答 ppt课件

得泊松比
' 0.33
22
解:1.轴力分析 由 F E
A
得
2.确定 F 及 值
根据节点A的平衡方程
FEA
得
23
A
l1 解:1.计算杆件的轴向变形
l2
由(2-15)可知: FN1 F50KN(拉力)
由胡克定理得
FN2 2F502KN (压力)
杆1的伸长为 l1F E N 1A 1l1 1200 50 10 9 1 03 4 00 1. 5 10 60.936m m
则,根据 Iz=Iz0+Aa2
得: Iz= I'zA y c2= 1 .7 3 1 0 -3m 4
30
(b) 沿截面顶端建立坐标轴z’,y轴不变
Z
A = 0 .8 0 .5 0 .5 5 0 .4 = 0 .1 8 m 2
ydA
yc=
A
A
0.15
0.7
0.8
0.5 ydy20.05 ydy0.5 ydy
此值虽然超过 ,但超过的百分数在5%以内,故仍符合强
度要求。
21
2-21 图示硬铝试样,厚度δ=2mm,试验段板宽b=20mm,标距l=70mm。在 轴向拉F=6kN的作用下,测得试验段伸长Δl=0.15mm,板宽缩短Δb=0.014mm。 试计算硬铝的弹性模量E与泊松比μ。
解:轴向正应变 l0.0m 15 m 1% 0 0 0.2% 14
解:1.问题分析 由于横截面上仅存在沿截面高度线性分布
的 正 应 力 , 因 此 , 横 截 面 上 只 存 在 轴 力 FN 及弯矩Mz,而不可能存在剪力和扭矩。
7
2.内力计算
根据题意,设 kya.代入数据得:
2019-2019学年第2学期《材料力学》复习要点_参考简答题答案共8页文档

2019-2019学年第2学期《材料力学》复习要点——参考简答题答案1、什么是变形固体?材料力学中关于变形固体的基本假设是什么?【解答】:在外力作用下,一切固体都将发生变形,故称为变形固体。
材料力学中对变形固体所作的基本假设:连续性假设:认为整个物体体积内毫无空隙地充满物质。
均匀性假设:认为物体内的任何部分,其力学性能相同。
各向同性假设:认为在物体内各个不同方向的力学性能相同。
小变形假设:认为固体在外力作用下发生的变形比原始尺寸小得很多,因此在列平衡方程求约束力或者求截面内力时,一般按构件原始尺寸计算。
2、什么是截面法?简要说明截面法的四个基本步骤。
【解答】:用一个假想截面,将受力构件分开为两个部分,取其中一部分为研究对象,将被截截面上的内力以外力的形式显示出来,根据保留部分的平衡条件,确定该截面内力大小、内力性质(轴力、剪力、扭转还是弯矩,符号的正负)的一种方法。
截面法贯穿于材料力学的始终,一定要反复练习,熟练掌握。
截面法的四个基本步骤:(1)截:在需要确定内力处用一个假想截面将杆件截为两段。
(2)取:取其中任何一段为研究对象(舍弃另一段)。
(3)代:用被截截面的内力代替舍弃部分对保留部分所产生的作用。
(4)平:根据保留部分的平衡条件,确定被截截面的内力数值大小和内力性质。
3、什么是材料的力学性能?低碳钢拉伸试验要经历哪四个阶段?该试验主要测定低碳钢的哪些力学性能指标?【解答】:材料的力学性能是指:在外力作用下材料在变形和破坏方面所表现出的各种力学指标。
如强度高低、刚度大小、塑性或脆性性能等。
低碳钢拉伸试验要经历的四个阶段是:弹性阶段、屈服阶段、强化阶段、颈缩断裂阶段。
低碳钢拉伸试验主要测定低碳钢的力学性能指标有:屈服极限、强度极限、延伸率、断面收缩率等。
4、什么是极限应力?什么是许用应力?轴向拉伸和压缩的强度条件是什么(内容、表达式)?利用这个强度条件可以解决哪三类强度问题?【解答】:材料失效时所达到的应力,称为极限应力。
材料力学第二,三章

四、 能量法
F
l
Δl
2 1 FN l W = F Δl = Vε = 2 2 EA
利用应变能的概念来求解构件变形、节点位移等问 题——能量法
例
设横梁ABCD为刚梁,横截面面积为 76.36mm² 的钢索绕过
无摩擦的定滑轮。设 P=20kN,试求刚索的应力和 C点的垂 直位移。设刚索的 E =177GPa。
O
A PA
FN 2P +
20kN规律:某 截面上轴 D 力等于截 面一侧所 有轴向外 力的代数 和,其中 D 指向截面 的轴向外 PD 力为正, 否则为负。
请判断下列两组情形是否等价?
F A C B
力的可传性不 可用!
A
00
C
F B
F
A
C
B
力的平移定理 不可用!
不可用:加减平衡 系公理,二力平衡 件
{
σs或σ0.2 σb
塑性材料 脆性材料
⎛ FN ⎞ ⎟ ≤ [σ ] 2.拉压杆强度条件: σ max = ⎜ ⎝ A ⎠ max FN l 3. 胡克定律的两种形式: Δl = EA 当 σ ≤ σp σ = Eε 2 1 FN l 4.拉压杆的变形能: V = vε = σ ε ε 2 EA 2
解(1)以ABD为对象求钢
A 800 B 60° 60° C P 400 400
索内力
mA = T sin60o × 0.8 − 1.2P ∑ + 1.6T sin60o = 0
XA A YA
B
T C
T P
D
∴T = P / 3 = 11 . 55 kN
A 800
B
60° 60° C 400 P400
《材料力学》习题册附答案

F12312练习 1 绪论及基本概念1-1 是非题(1) 材料力学是研究构件承载能力的一门学科。
( 是 )(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
(是)(3) 构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
( 是 ) (4) 应力是内力分布集度。
(是 )(5) 材料力学主要研究构件弹性范围内的小变形问题。
(是 ) (6) 若物体产生位移,则必定同时产生变形。
(非 ) (7) 各向同性假设认为,材料沿各个方向具有相同的变形。
(F ) (8) 均匀性假设认为,材料内部各点的力学性质是相同的。
(是)(9) 根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(非) (10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(非 )1-2 填空题(1) 根据材料的主要性质对材料作如下三个基本假设:连续性假设、均匀性假设 、各向同性假设 。
(2) 工程中的强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。
(3) 保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性三个方面。
3(4) 图示构件中,杆 1 发生 拉伸 变形,杆 2 发生 压缩 变形,杆 3 发生 弯曲 变形。
(5) 认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设。
根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6) 图示结构中,杆 1 发生 弯曲变形,构件 2发生 剪切 变形,杆件 3 发生 弯曲与轴向压缩组合。
变形。
(7) 解除外力后,能完全消失的变形称为 弹性变形,不能消失而残余的的那部分变形称为 塑性变形 。
(8) 根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。
1-3选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
材料力学(I)第四章(配孙训方版)

M (x)
距右端为x的任意横截面上的剪力FS(x)和弯矩M(x),根 据截面右侧梁段上的荷载有
FS ( x ) = qx
(0 ≤ x < l ) (0 ≤ x < l )
x qx 2 M ( x ) = − qx ⋅ = − 2 2
29
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
2. 作剪力图和弯矩图 根据剪力方程和弯矩方程作出剪力图和弯矩图分别如 图b和图c。按照习惯,剪力图中正值的剪力值绘于x轴上方, 弯矩图中正值的弯矩值则绘于x轴的下方(即弯矩值绘于梁 弯曲时其受拉的边缘一侧)。 (b) FS ( x ) = qx
)(
)
M A = 96.5 kN ⋅ m
15
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
2. 此梁的约束力亦可将梁在中间铰C处拆开,先利用 CB段梁作为分离体求约束力FBy和AC段梁在中间铰C处作用 在CB段梁上的FCx和FCy,然后利用AC段梁作为分离体求约 束力FAx,FAy和MA。
16
37
Fb (0 < x < a ) FS ( x ) = FA = l Fb M ( x ) = FA x = x (0 ≤ x ≤ a ) l
13
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
于是可求得约束力如下:
∑M
− 20 × 103 N
(
C
=0 m
× 3 m × 2.5 m + 5 ×103 N ⋅ m + FBy × 5 m = 0
FBy = 29 kN
)
14
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
材料力学第二章3

3)绘制变形图 切线代圆弧法,由法国的工 程师,Willot在1877年提出 的,又叫Willot作图法。
湖北汽车工业学院 马迅制作
4)确定节点的位移 水平位移:
垂直位移:
在小变形条件下,可按结构原几何尺寸计算约束 反力和内力。可采用上述切线代圆弧的方法确定简 单桁架节点位移,使分析问题大为简化。
湖北汽车工业学院 马迅制作
A 1.18(mm)
湖北汽车工业学院 马迅制作
5
2-9 CASTIGLIANO 定理
卡氏定理:在载荷系作用下,处于平衡状态的,服从叠 加原理的任意线弹性体系,它的总应变能对于任一载荷 的一次偏微分,等于此载荷的作用点沿其作用线方向的 位移,即
i
U Fi
1.定理中的载荷和位移,是广义(Generalized)的。当载荷是 力时,便是线位移;当载荷是力偶矩时,便是角位移。 2. 注意求得的位移是载荷作用点沿其作用线方向的位移。
2. 计算杆系的应变能
FN1 45 FN2 P
10 103 A
F2 L F2 L U U AB U AC N1 AB N 2 AC 2 AAB E1 2 AAC E2
3. 利用功能原理
2 2 P A FN 1L1 FN 2 L2 2 2 A1E1 2 A2 E2
200 106 1 100 106 1 6 9 100 10 200 10 2 4000 10 6 10 109
应变能 : 弹性体因变形而储存的能量,strain energy
湖北汽车工业学院 马迅制作
4
2.拉压杆的应变能
P
外力功为:
1 W PL 2
单元体应变能:
dU= ( σx σx
《材料力学》附录I截面的几何性质习题解
附录I 截里的几许本量 习题解之阳早格格创做[习题I-1]试供图示各截里的阳影线里积对付x 轴的静积.(a )解:)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅= (b ) 解:)(42250265)6520(3mm y A S c x =⨯⨯=⋅=(c )解:)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅= (d )解:)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅= [习题I-2]x 轴的静矩,并决定其形心的坐标.解:用二条半径线战二个共心圆截出一微分里积如图所示.dx xd dA ⋅=)(θ;微分里积的纵坐标:θsin x y =;微分里积对付x 轴的静矩为:半圆对付x 轴的静矩为:[习题I-3]试决定图示各图形的形心位子. (a ) 解:(b) 解:(c) 解:[习题I-4]解:用二条半径线战二个共心圆截出一微分里积如图所示.为:[习题I-5].解:圆的圆程为:里积,微分里积为:[习题I-6] 试供图示正圆形对付其对付角线的惯性矩.解:正圆形四条边的曲线圆程如图所示(设火仄坐标轴为.[习题I-7] 试分别供图示环形战箱形截里对付其对付称轴x 的惯性矩. (a) 解:)(21177368])175150(1[17514.3641)1(64144424mm D I x =-⨯⨯=-=απ(b)[习题I-8]试供图示三角形截里对付通过顶面A 并仄止于底边BC 的轴的惯性矩.解:已知三角形截里对付以BC 边为轴的惯性矩是,利用仄止轴定理,可供得截里对付形心轴的惯性矩 所以再次应用仄止轴定理,得[习题I-9]试供图示的半圆形截里对付于轴的惯性矩,其中轴取半圆形的底边仄止,相距1 m. 解:已知半圆形截里对付其底边的惯性矩是,用仄止轴定理得截里对付形心轴的惯性矩 再用仄止轴定理,得截里对付轴的惯性矩[习题I-10] 试供图示拉拢截里对付于形心轴x 的惯性矩. 解:由于三圆曲径相等,并二二相切.它们的圆心形成一个边少为的等边三角形.该等边三角形的形心便是拉拢截里的形心,果此底下二个圆的圆心,到形心轴的距离是上头一个圆的圆心到轴的距离是d 632.利用仄止轴定理,得拉拢截里对付轴的惯性矩如下: [习题I-11]试供图示各拉拢截里对付其对付称轴的惯性矩. 解:(a )22a 号工字钢对付其对付称轴的惯性矩是.利用仄止轴定理得拉拢截里对付轴的惯性矩(b )等边角钢的截里积是,其形心距中边沿的距离是28.4 mm ,供得拉拢截里对付轴的惯性矩如下:习题I-11(b )图图形 b h Ixc a A Ix中间矩形 10 600 180000000 0 6000 180000000 上矩形 250 10 20833 305 2500 232583333 下矩形 250 10 20833 305 2500 232583333 左上L 形 1795100 1926 143869495 左上L 形 1795100 1926 143869495 左下L 形 1795100 1926 143869495 左下L 形17951001926143869495 A a I I xc x 2+=1220644645[习题I-12]试供习题I-3a 图所示截里对付其火仄形心轴的惯性矩.闭于形心位子,可利 用该题的截止.解:形心轴位子及几许尺寸如图所示.惯性矩估计如下:试供图示各截里对付其形心轴x的惯性矩.习题I-13(a)图形bi hi Ai Yci AiYci Yc ai Ixc Ix(mm4)上矩形1000 100 100000 650 65000000 225 83333333 5145833333 下矩形300 600 180000 300 54000000 125 5400000000 8212500000 齐图280000 119000000 425习题I-13(c)图形bi hi r Ai Yci AiYci Yc Ixc(mm4) ai Ix(mm4)矩形2140 1150 2461000 575 1415075000 271222708333 159 333213698275 半圆790 -980333 335 -328692667 42750202791 399齐图1480667 1086382333 734半圆:π3/4ryc=半圆:ππ9/88/44rrIxc-=习题I-13(d)图形bi hi Ai Yci AiYci Yc ai Ixci Ix(mm4)从下往上2216 3520 8 28160 37475093 4924386131814 2520 23 57960 35941160 324821280 16 674 10784 367 3957728 0 408242699 408242699 2214 3080 711 2189880 32950307 333432587 449 4005 2893613 3427034 464367735习题I-13( b)图形bi hi Ai Yci AiYci Yc ai Ixc Ix(mm4)上图(3) 25 150 3750 275 1031250 148 7031250 89601489 中图(2) 200 150 30000 125 3750000 2 56250000 56328044 下图(1) 100 50 5000 25 125000 102 1041667 52667577 齐图38750 4906250 127 1985971105 123909 9127341 382 202330291 4[习题I-14] 正在曲径aD8=圆截里中,启了一个aa42⨯的矩形孔,如图所示.试供截里对付其火仄形心轴战横曲轴形心的惯性矩xI战y I.解:先供形心主轴的位子截里图形对付形心轴的静矩(里积矩)等于整:(y轴背下为正)(拉拢图形对付过圆心轴x1的惯性矩)(拉拢图形对付形心轴x的惯性矩)习题I-14b(a) h(a) r(a) Ai(a2) Yci(a) AiYci Yc(a) Ixc ai Ix(a4) 矩形4 2 -8.00 1 -8 2.667 1.1893 14.0圆 4 50.27 0 0 201.062 -0.1893 202.942.27 -8 -0.1893 188.9 [习题I-15]正圆形截里中启了一个曲径为mmd100=的半圆形孔,如图所示.试决定截里的形心位子,并估计对付火仄形心轴战横曲形心轴的惯性矩.解:习题I-15图形 bi hi rAiYci AiYciYcIxci ai Ix正圆形 200 20040000 100 4000000 133333333 2 133546801 半圆 50 -3927 79 -30936568597724 2860346 齐图360733690635 102130686455π34100r y c -=ππ98844r r I xc -⋅=A a I I xc x 2+=形心位子:X (0,102).对付火仄形心轴的惯性矩:4130686455m m I x =.对付横曲形心轴的惯性矩:习题I-15图形 a r Iy (mm 4) 正圆形 200半圆 50 2454367齐图13087896681244r a I y ⋅-=π[习题I-16] 图示由二个a 20号槽钢组成的拉拢截里,若欲使截里对付二对付称轴的惯性矩x I 战y I 相等,则二槽钢的间距a 应为几?解:20a 号槽钢截里对付其自己的形心轴、的惯性矩是,;横截里积为;槽钢背到其形心轴的距离是.根据惯性矩定义战仄止轴定理,拉拢截里对付,轴的惯性矩分别是 ;若即等式二边共除以2,而后代进数据,得 于是所以,二槽钢相距[习题I-17] 试供图示截里的惯性积xy I解:设矩形的宽为b 下为h ,形心主惯性轴为c c y x 0,则由仄止移轴公式得:故,矩形截里对付其底边取左边所形成的坐标系的惯性积为:2241h b I xy =[习题I-18] 图示截里由二个mm mm mm 10125125⨯⨯的等边角钢及缀板(图中实线)拉拢而成.试供该截里的最大惯性矩max I 战最小惯性矩习题I-17 图形 b h Ixy 左矩形 10 100 250000 下矩形: 100 10 250000 沉复加的矩形 10102500齐图上图+下图-沉复图= 497500解:从图中可知,该截里的形心C位于二缀板共共的形心上.过C C.C后所得到的坐标系是截里的的二条对付称轴,也便是该截查型钢表得:12.5号等边角钢的参数如下:,,,角钢形心主惯性轴取截里形心主惯性轴之间的距离:(注:缀板用实线绘出,表示其里积可忽略没有计)[习题I-19].论断:1、过正圆形形心的一对付相互笔曲的轴,它们的惯性矩相等,它们的惯性积为整;2、过正圆形形心的一对付相互笔曲的轴,绕形心转化之后,惯性矩、惯性积脆持没有变.[习题I-20]决定图示截里的形心主惯性轴的位子,并供形心主惯性矩.(a )解:截里的形心主惯性轴取横曲矩形的形心主惯性轴沉合.Ix Iy Ixy-259200000 Ix0= 704109187-259200000Iy0=54184146224)(2120xy y x yx y x I I I I I I I +-±+=(b)解:以20号槽钢(图I )的下边沿为x 轴,左边沿为y 轴,修坐坐标系.8号槽钢编号为图II.则拉拢截里的形心估计如下:习题I-20(b) 少度单位:cm图形 Ai Xci Yci AiXci AiYci Xc Yc I 10 64 II 16 -15 齐图习题I-20(b )图形 Ai iabiIxci' Iyci' Ixci Iyci Ixciyci' Ixciyci tan2a0a0Ix0Iy0I 1981 165 0 II齐2296249[习题21]试用近似法供习题I-4出的透彻值相比较.解:圆的圆程为:把y轴的半径10过仄分面,做x轴的仄止线.从下往上,每个分块的中面的y坐标取x坐标如下表所示.[习题I-22](提示:最简朴的证法是利用惯性积的仄止移轴公式,并利用一对付相互笔曲的坐标轴中有一为截里的对付称轴时,其惯性积为整的特性.)解。
本科课程教案

与
教学难点
1、教学重点:
(1)塑性材料和脆性材料的不同力学性能;
(2)杆件拉伸、压缩的内力、应力、应变,及构件的强度和刚度计算;
(3)扭转的内力、应力、应变,及构件的强度和刚度计算;
(4)梁的弯曲内力、应力、应变,及构件的强度和刚度计算;
(5)二向应力状态分析;
(6)强度理论的应用;
(7)组合变形的解题技巧;
作业:
习题练习:3.1
上课时间:第四周星期一第1~2小节
上课地点::
教学内容:
1、推导圆轴扭转时横截面正应力公式;2、圆截面极惯性矩和截面抗扭系数;3圆轴相对扭转角计算公式。
讲授重点:
推导圆轴扭转时横截面正应力公式的过程,并运用公式计算实心、空心轴应力。
教学方法:讲授法(提问质疑)
考试考核方式
(含期中考试、
测验、作业)
1、平时成绩占30%
2、期末考试成绩占70%
其他内容
《材料力学A》课程授课教案
上课时间:第一周星期一第1~2小节
上课地点:线上
学生出勤:
教学内容、教学重点、讲授方法:
教学内容:
课程特点、课程要求
绪论:1、材料力学的任务;2、变形固体的基本假设;3、内力、应力和截面法;4、位移、变形与应变;5、杆件变形的基本形式。
讲授重点:
拉压构件强度条件及应用;轴向拉伸或压缩时的变形计算。
教学方法:讲授法
通过练习引导学生首先要会运用变形计算公式,正确计算等直杆变形量,然而变形并非位移。这里就可以提示学生各变形之间要满足协调关系,这是材料力学所有变形都要满足的条件,不仅是拉压变形。
此处,应该指出考虑各变形之间的协调时,小变形条件是求解的关键,杆件伸长量(压缩量)是小变形,杆件转角也是小位移,所以通过杆变形后位置作垂线可找到最终位置。
