2003年07月试卷

合集下载

2003 年全国高考化学试题及答案

2003 年普通高等学校招生全国统一考试理科综合能力测试本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至5页，第Ⅱ卷6至11页。

满分300分。

考试用时150分钟。

第Ⅰ卷（选择题共22题每题6分，共132分）在下列各题的四个选项中，只有一个选项是最符合题目要求的。

以下数据可供解题时参考：原子量：H 1 Li7 Be 9 C 12 O 16 Na 23 Mg 24 P 31 Cl 35.5 K 39 Ca 401 取适量干重相等的4份种子进行不同处理：（甲）风干，（乙）消毒后浸水萌发，（丙）浸水后萌发，（丁）浸水萌发后煮熟冷却、消毒。

然后分别放入4个保温瓶中。

一段时间后，种子堆内温度最高的是A 甲B 乙C 丙D 丁2 植物叶片从幼到老的整个生命活动过程中A 有机物输出也输入，矿质元素只输入B 有机物只输出，矿质元素只输入C 有机物只输出，矿质元素输入也输出D 有机物与矿质元素都既输入，又输出3 下列关于叶绿素合成与功能的叙述，错误的是A 光是叶绿素合成的必要条件B 低温抑制叶绿素的合成C 矿质元素影响叶绿素的合成D提取的叶绿素溶液，给予适宜的温度、光照和CO2，可进行光合作用4 一只成年雄狗仍然保持幼年的体态，且精神委靡、反应迟钝、行动呆笨，无求偶行为，其原因是A 睾丸发育不全B 甲状腺功能低下C 生长激素分泌不足D生长激素分泌不足、睾丸发育不全※5据图判断，下列叙述不符合生态学原理的是A 物质经过多级利用，实现了良性循环B 每一级生产环节都获得产品，提高了生态经济效益C 由于食物链延长，能量逐级损耗，系统总能量利用效率降低D 由于各级产物都可以利用，减少了废物和污染6 人类探测月球发现，在月球的土壤中含有较丰富的质量数为3的氦，它可以作为未来核聚变的重要原料之一。

氦的该种同位素应表示为※A 43He B 32He C 42He D 33He◎7 在两个容积相同的容器中，一个盛有HCl气体，另一个盛有H2和Cl l2的混合气体。

人力资源管理师二级理论知识历年真题试卷汇编12_真题-无答案

人力资源管理师（二级）理论知识历年真题试卷汇编12(总分100,考试时间90分钟)1. 单选题单项选择题以下备选答案中只有一项最符合题目要求，不选、错选均不得分。

1. 人力资源规划在整个人力资源管理活动中占有( )。

(2003年7月二级真题)A. 一般地位B. 特殊地位C. 重要地位D. 必要地位E. 突出位置2. 在工作分析的基本流程中，用书面形式表达分析结果的阶段是( )。

(2006年5月二级真题)A. 准备阶段B. 实施阶段C. 结果形成阶段D. 应用与反馈阶段3. 岗位设置的数目应符合( )数量原则。

(2003年7月二级真题)A. 最多B. 最低C. 最高D. 适中E. 最大4. 制度化管理的( )在于以科学确定的制度规范为组织协作行为的基本约束机制。

(2003年7月二级真题)A. 内容B. 方法C. 手段D. 实质E. 形式5. 相对于内部招聘而言，外部招聘有利于( )。

(2003年11月二级真题)A. 培养员工的忠诚度B. 促进团结、消除矛盾C. 招聘到高质量人才D. 激励员工、鼓舞士气6. 在招聘时，当企业要招募的人员集中在某个专业领域，时间、地点限制不太重要时，企业发布招聘信息的媒体是( )。

(2005年11月二级真题)A. 电视B. 杂志C. 报纸D. 户外广告7. 笔试不具备的优点是( )。

(2004年6月二级真题)A. 可以大规模地进行评价B. 成绩评定较为客观C. 评价成本较低D. 适用于各类能力的考评8. 下列对情境模拟方法理解错误的是( )。

(2004年11月二级真题)A. 它将应聘者置于某种模拟环境中B. 评价者事先必须接受专门的培训C. 它无法测查应聘者在语言表达能力方面的素质D. 评价者通过对应聘者的观察来了解应聘者的综合素质9. 在招聘评估中，录用比和应聘比在一定程度上反映录用人员的( )。

(2004年11月二级真题)A. 数量B. 成本C. 质量D. 规模10. ( )不是培训前期的准备工作。

2003年全国统一高考数学试卷(理科)

2003年全国统一高考数学试卷（理科）一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2003•全国）已知x∈（﹣，0），cosx=，则tan2x等于（）A．B．﹣C．D．﹣2．（5分）（2003•全国）圆锥曲线的准线方程是（）A．ρcosθ=﹣2 B．ρcosθ=2 C．ρsinθ=﹣2 D．ρsinθ=23．（5分）（2003•全国）设函数若f（x0）＞1，则x0的取值范围是（）A．（﹣1，1）B．（﹣1，+∞）C．（﹣∞，﹣2）∪（0，+∞）D．（﹣∞，﹣1）∪（1，+∞）4．（5分）（2003•全国）函数y=2sinx（sinx+cosx）的最大值为（）A．B．C．D．25．（5分）（2003•全国）已知圆C：（x﹣a）2+（y﹣2）2=4及直线l：x﹣y+3=0，当直线l被C截得的弦长为时，则a等于（）A．B．C． D．6．（5分）（2003•全国）已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是（）A．2πR2B．C．D．7．（5分）（2003•全国）已知方程（x2﹣2x+m）（x2﹣2x+n）=0的四个根组成一个首项为的等差数列，则|m﹣n|等于（）A．1 B．C．D．8．（5分）（2003•全国）已知双曲线中心在原点且一个焦点为F（，0），直线y=x﹣1与其相交于M、N两点，MN中点的横坐标为﹣，则此双曲线的方程是（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=19．（5分）（2003•全国）函数f（x）=sinx，x∈的反函数f﹣1（x）=（）A．﹣arcsinx，x∈[﹣1，1]B．﹣π﹣arcsinx，x∈[﹣1，1]C．﹣π+arcsinx，x∈[﹣1，1]D．π﹣arcsinx，x∈[﹣1，1]10．（5分）（2003•全国）已知长方形的四个项点A（0，0），B（2，0），C（2，1）和D（0，1），一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后，依次反射到CD．DA和AB上的点P2．P3和P4（入射角等于反射角），设P4坐标为（x4，0），若1＜x4＜2，则tanθ的取值范围是（）A．（，1）B．（，）C．（，）D．（，）11．（5分）（2003•全国）等于（）A．3 B．C．D．612．（5分）（2003•全国）棱长都为的四面体的四个顶点在同一球面上，则此球的表面积为（）A．3πB．4πC．3D．6π二、填空题（共4小题，每小题4分，满16分）13．（4分）（2003•全国）在的展开式中，x3的系数是（用数字作答）14．（4分）（2003•全国）使log2（﹣x）＜x+1成立的x的取值范围是．15．（4分）（2003•全国）如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色．现有4种颜色可供选择，则不同的着色方法共有种．（以数字作答）16．（4分）（2003•全国）下列五个正方体图形中，l是正方形的一条对角线，点M、N、P分别为其所在棱的中点，能得出l⊥面MNP的图形的序号是（写出所有符合要求的图形序号）．三、解答题（共6小题，满分74分）17．（12分）（2003•全国）已知复数z的辐角为60°，且|z﹣1|是|z|和|z﹣2|的等比中项．求|z|．18．（12分）（2003•全国）如图，直三棱柱ABC﹣A1B1C1中，底面是等腰直角三角形，∠ACB=90°，侧棱AA1=2，D、E分别是CC1与A1B的中点，点E在平面ABD 上的射影是△ABD的重心G．（Ⅰ）求A1B与平面ABD所成角的大小（结果用反三角函数值表示）；（Ⅱ）求点A1到平面AED的距离．19．（12分）（2003•全国）已知c＞0，设P：函数y=c x在R上单调递减，Q：不等式x+|x﹣2c|＞1的解集为R．如果P和Q有且仅有一个正确，求c的取值范围．20．（12分）（2003•全国）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南方向300km的海面P处，并以20km/h的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？21．（12分）（2003•全国）已知常数a＞0，在矩形ABCD中，AB=4，BC=4a，O 为AB的中点，点E、F、G分别在BC、CD、DA上移动，且，P为GE 与OF的交点（如图），问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由．22．（14分）（2003•全国）（1）设{a n}是集合{2s+2t|0≤s＜t且s，t∈Z}中所有的数从小到大排列成的数列，即a1=3，a2=5，a3=6，a4=9，a5=10，a6=12，…将数列{a n}各项按照上小下大，左小右大的原则写成如下的三角形数表：35 69 10 12﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣…①写出这个三角形数表的第四行、第五行各数；②求a100（2）设{b n}是集合{2r+2s+2t|0≤r＜s＜t，且r，s，t∈Z}中所有的数从小到大排列成的数列，已知b k=1160，求k．2003年全国统一高考数学试卷（理科）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2003•全国）已知x∈（﹣，0），cosx=，则tan2x等于（）A．B．﹣C．D．﹣【考点】GS：二倍角的三角函数；GF：三角函数的恒等变换及化简求值．【专题】11 ：计算题．【分析】先根据cosx，求得sinx，进而得到tanx的值，最后根据二倍角公式求得tan2x．【解答】解：∵cosx=，x∈（﹣，0），∴sinx=﹣．∴tanx=﹣．∴tan2x===﹣×=﹣．故选：D．【点评】本题主要考查了三角函数中的二倍角公式．属基础题．2．（5分）（2003•全国）圆锥曲线的准线方程是（）A．ρcosθ=﹣2 B．ρcosθ=2 C．ρsinθ=﹣2 D．ρsinθ=2【考点】Q8：点的极坐标和直角坐标的互化．【专题】11 ：计算题．【分析】首先把圆锥曲线方程转化为直角坐标系的方程，然后根据抛物线的准线方程的公式求出准线方程，再转化为极坐标方程即得到答案．【解答】解：圆锥曲线由极坐标与直角坐标系的关系，可转化为直角坐标系上的方程，即为抛物线x2=8y，则准线方程为y=﹣2，再转化为极坐标方程为ρsinθ=﹣2．故选：C．【点评】此题主要考查极坐标与直角坐标系的转化，以及抛物线的准线方程的求解问题，属于综合性的问题有一定的难度．3．（5分）（2003•全国）设函数若f（x0）＞1，则x0的取值范围是（）A．（﹣1，1）B．（﹣1，+∞）C．（﹣∞，﹣2）∪（0，+∞）D．（﹣∞，﹣1）∪（1，+∞）【考点】3B：分段函数的解析式求法及其图象的作法．【专题】11 ：计算题．【分析】将变量x0按分段函数的范围分成两种情形，在此条件下分别进行求解，最后将满足的条件进行合并．【解答】解：当x0≤0时，，则x0＜﹣1，当x0＞0时，则x0＞1，故x0的取值范围是（﹣∞，﹣1）∪（1，+∞），故选：D．【点评】本题考查了分段函数已知函数值求自变量的范围问题，以及指数不等式与对数不等式的解法，属于常规题．4．（5分）（2003•全国）函数y=2sinx（sinx+cosx）的最大值为（）A．B．C．D．2【考点】GS：二倍角的三角函数；H4：正弦函数的定义域和值域．【分析】把函数式展开，可以看出要逆用正弦和余弦的二倍角公式，变为y=Asin（ωx+φ）的形式，在定义域是全体实数的条件下，根据正弦的值域求本题的最值．【解答】解：∵y=2sinx（sinx+cosx）∴y=2sin2x+2sinxcosx∴y=1﹣cos2x+sin2x=sin（2x﹣）+1∵当x∈R时，sin（2x﹣）∈[﹣1，1]∴y的最大值为+1，故选：A．【点评】三角函数是高中一年级数学教学中的一个重要内容，公式繁多应用灵活给学生的学习带来了一定的困难．为了学生掌握这一单元的知识，必须使学生熟练的掌握所有公式，在此基础上并能灵活的运用公式．5．（5分）（2003•全国）已知圆C：（x﹣a）2+（y﹣2）2=4及直线l：x﹣y+3=0，当直线l被C截得的弦长为时，则a等于（）A．B．C． D．【考点】J9：直线与圆的位置关系．【分析】弦心距、半径、半弦长满足勾股定理，半径是2，半弦长是，则弦心距是1，用点到直线的距离可以求解a．【解答】解：圆C：（x﹣a）2+（y﹣2）2=4的圆心（a，2），半径是2，半弦长是，则弦心距是1，圆心到直线的距离：1=∴故选：C．【点评】本题考查直线与圆的位置关系，弦心距、半径、半弦长满足勾股定理，是基础题．6．（5分）（2003•全国）已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是（）A．2πR2B．C．D．【考点】7F：基本不等式及其应用．【分析】将全面积表示成底面半径的函数，用配方法求二次函数的最大值【解答】解：设内接圆柱的底面半径为r，高为h，全面积为S，则有∴h=3R﹣3r∴S=2πrh+2πr2=﹣4πr2+6πRr=﹣4π（r2﹣Rr）=﹣4π（r﹣）2+πR2∴当r=时，S取的最大值πR2．故选：B．【点评】考查实际问题的最值问题，常转化成函数的最值7．（5分）（2003•全国）已知方程（x2﹣2x+m）（x2﹣2x+n）=0的四个根组成一个首项为的等差数列，则|m﹣n|等于（）A．1 B．C．D．【考点】83：等差数列的性质；73：一元二次不等式及其应用．【专题】11 ：计算题．【分析】设4个根分别为x1、x2、x3、x4，进而可知x1+x2和x3+x4的值，进而根据等差数列的性质，当m+n=p+q时，a m+a n=a p+a q．设x1为第一项，x2必为第4项，可得数列，进而求得m和n，则答案可得．【解答】解：设4个根分别为x1、x2、x3、x4，则x1+x2=2，x3+x4=2，由等差数列的性质，当m+n=p+q时，a m+a n=a p+a q．设x1为第一项，x2必为第4项，可得数列为，，，，∴m=，n=．∴|m﹣n|=．故选：C．【点评】本题主要考查了等差数列的性质．解题的关键是运用了等差数列当m+n=p+q时，a m+a n=a p+a q的性质．8．（5分）（2003•全国）已知双曲线中心在原点且一个焦点为F（，0），直线y=x﹣1与其相交于M、N两点，MN中点的横坐标为﹣，则此双曲线的方程是（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1【考点】KB：双曲线的标准方程．【分析】先设出双曲线的方程，然后与直线方程联立方程组，经消元得二元一次方程，再根据韦达定理及MN中点的横坐标可得a、b的一个方程，又双曲线中有c2=a2+b2，则另得a、b的一个方程，最后解a、b的方程组即得双曲线方程．【解答】解：设双曲线方程为﹣=1．将y=x﹣1代入﹣=1，整理得（b2﹣a2）x2+2a2x﹣a2﹣a2b2=0．由韦达定理得x1+x2=，则==﹣．又c2=a2+b2=7，解得a2=2，b2=5，所以双曲线的方程是．故选：D．【点评】本题主要考查代数方法解决几何问题，同时考查双曲线的标准方程与性质等．9．（5分）（2003•全国）函数f（x）=sinx，x∈的反函数f﹣1（x）=（）A．﹣arcsinx，x∈[﹣1，1]B．﹣π﹣arcsinx，x∈[﹣1，1]C．﹣π+arcsinx，x∈[﹣1，1]D．π﹣arcsinx，x∈[﹣1，1]【考点】HV：反三角函数；4R：反函数．【专题】11 ：计算题．【分析】先用诱导公式求出f（x）=sin（π﹣x），x∈，然后可以反函数的定义求解即可．【解答】解：函数f（x）=sinx，x∈所以：函数f（x）=sin（π﹣x），x∈可得π﹣x=arcsiny y∈[﹣1，1]∴f﹣1（x）=π﹣arcsinx，x∈[﹣1，1]故选：D．【点评】本题考查反函数的求法，是基础题．10．（5分）（2003•全国）已知长方形的四个项点A（0，0），B（2，0），C（2，1）和D（0，1），一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后，依次反射到CD．DA和AB上的点P2．P3和P4（入射角等于反射角），设P4坐标为（x4，0），若1＜x4＜2，则tanθ的取值范围是（）A．（，1）B．（，）C．（，）D．（，）【考点】IQ：与直线关于点、直线对称的直线方程．【专题】16 ：压轴题．【分析】先画草图，帮助理解，取BC上的点P1为中点，则P4和中点P0重合，tanθ=，用排除法解答．【解答】解：考虑由P0射到BC的中点上，这样依次反射最终回到P0，此时容易求出tanθ=，由题设条件知，1＜x4＜2，则tanθ≠，排除A．B．D，故选：C．【点评】由于是选择题，因而可以特殊值方法解答：排除验证法，也可以用动态观点判定答案．11．（5分）（2003•全国）等于（）A．3 B．C．D．6【考点】6F：极限及其运算；D5：组合及组合数公式．【专题】11 ：计算题；16 ：压轴题．【分析】利用组合数的性质对原式进行等价转化，得到．【解答】解：∵C22+C32+C42+…+C n2=C33+C32+C42++C n2=C43+C42+…+C n2═C n+13，，∴．故选：B．【点评】本题考查数列的极限，解题时要注意组合数的计算和应用．12．（5分）（2003•全国）棱长都为的四面体的四个顶点在同一球面上，则此球的表面积为（）A．3πB．4πC．3D．6π【考点】LG：球的体积和表面积．【专题】11 ：计算题；16 ：压轴题．【分析】本题考查的知识点是球的体积和表面积公式，由棱长都为的四面体的四个顶点在同一球面上，可求出内接该四面体的正方体棱长为1，又因为正方=4πR2，体的对角线即为球的直径，即球的半径R=，代入球的表面积公式，S球即可得到答案．【解答】解：借助立体几何的两个熟知的结论：（1）一个正方体可以内接一个正四面体；（2）若正方体的顶点都在一个球面上，则正方体的体对角线就是球的直径．则球的半径R=，∴球的表面积为3π，故选：A．【点评】棱长为a的正方体，内接正四面体的棱长为a，外接球直径等于长方体的对角线长a．二、填空题（共4小题，每小题4分，满16分）13．（4分）（2003•全国）在的展开式中，x3的系数是﹣（用数字作答）【考点】DA：二项式定理．【专题】11 ：计算题．【分析】首先根据题意，写出的二项展开式，可得9﹣2r=3，解可得r=3，将其代入二项展开式，计算可得答案．【解答】解：根据题意，对于，=C99﹣r•x9﹣r•（﹣）r=（﹣）r•C99﹣r•x9﹣2r，有T r+1令9﹣2r=3，可得r=3，当r=3时，有T4=﹣x3，故答案﹣．【点评】本题考查二项式定理的应用，注意系数与二项式系数的区别．14．（4分）（2003•全国）使log2（﹣x）＜x+1成立的x的取值范围是（﹣1，0）．【考点】4H：对数的运算性质；7E：其他不等式的解法．【专题】13 ：作图题；44 ：数形结合法．【分析】在坐标系中画出函数f（x）=log2（﹣x）和g（x）=x+1，图象，结合图象判定即可．【解答】解：利用作图法可以判断f（x）=log2（﹣x）和g（x）=x+1，相交于（﹣1，0）前者是单调递减，后者是单调递增．所以只有﹣1＜x＜0时，log2（﹣x）＜x+1成立故答案为：（﹣1，0）．【点评】本题考查对数函数的图象，数形结合法解不等式，是中档题．15．（4分）（2003•全国）如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色．现有4种颜色可供选择，则不同的着色方法共有72种．（以数字作答）【考点】D5：组合及组合数公式．【专题】11 ：计算题；16 ：压轴题；32 ：分类讨论．【分析】分类型，选3种颜色时，就是②④同色，③⑤同色；4种颜色全用，只能②④或③⑤用一种颜色，其它不相同，求解即可．【解答】解：由题意，选用3种颜色时：涂色方法C43•A33=24种4色全用时涂色方法：C21•A44=48种所以不同的着色方法共有72种．故答案为：72【点评】本题考查组合及组合数公式，考查分类讨论思想，避免重复和遗漏情况，是中档题．16．（4分）（2003•全国）下列五个正方体图形中，l是正方形的一条对角线，点M、N、P分别为其所在棱的中点，能得出l⊥面MNP的图形的序号是①④⑤（写出所有符合要求的图形序号）．【考点】LS：直线与平面平行．【专题】15 ：综合题；16 ：压轴题．【分析】能得出l⊥面MNP，关键是看平面MNP中有没有与1垂直的直线，逐一判断即可．【解答】解：如图，设正方体为ABCD﹣A1B1C1D1．在题图①中，连结AB1，则AB1⊥MN，又AB1是l在面ABB1A1内的射影，∴l⊥MN．同理，l⊥MP．∴l⊥平面MNP．故①符合．在题图②中，延长MP交C1D1的延长线于E，连结NE，若l⊥面MNP，则l ⊥NE．又C1D是l在平面CDD1C内的射影，CD1⊥C1D，∴l⊥CD1．∴l⊥平面CDD1C1，矛盾．∴②不符合．在题图③中，平面MNP与题图①中的平面MNP不是同一平面，它们又过同一点，∴题图③不符合．在题图④中，l⊥MP，l⊥MN，∴l⊥平面MNP．延长PM交AB于F，取CD的中点G，则GN∥MP，∴G∈平面MNP．连结FG交BC于H，则H∈平面MNP，可证H是BC的中点．∴题图④与题图⑤中的平面MNP实为同一平面．∴⑤也符合．答案：①④⑤【点评】点评：本题要先想象直观判断哪些图形符合，再加以推理，考查了空间想象能力、反证法、线面的位置关系等知识，通过这个试题可看出试题在向增加思维量、综合考查同学们的各种能力转化．三、解答题（共6小题，满分74分）17．（12分）（2003•全国）已知复数z的辐角为60°，且|z﹣1|是|z|和|z﹣2|的等比中项．求|z|．【考点】A1：虚数单位i、复数；87：等比数列的性质；A8：复数的模．【专题】11 ：计算题．【分析】本题考查的复数的基本概念及等比数列的性质，由复数z的辐角为60°，我们可以使用待定系数法设出复数Z，然后根据|z﹣1|是|z|和|z﹣2|的等比中项，结合等比数列的性质构造方程，解方程求出待定的系数，即可得到Z值，进而求出复数的模．【解答】解：设z=（rcos60°+rsin60°i），则复数z的实部为．由题设|z﹣1|2=|z|•|z﹣2|，即：（z﹣1）（﹣1）=|z|∴r2﹣r+1=r，整理得r2+2r﹣1=0．解得r=﹣1，r=﹣﹣1（舍去）．即|z|=﹣1．【点评】解决复数问题时，我们多使用待定系数法，即设出复数的值，然后根据题目中的其它条件，列出方程，解方程求出系数，即可得到未知复数的值．18．（12分）（2003•全国）如图，直三棱柱ABC﹣A1B1C1中，底面是等腰直角三角形，∠ACB=90°，侧棱AA1=2，D、E分别是CC1与A1B的中点，点E在平面ABD 上的射影是△ABD的重心G．（Ⅰ）求A1B与平面ABD所成角的大小（结果用反三角函数值表示）；（Ⅱ）求点A1到平面AED的距离．【考点】MI：直线与平面所成的角；L2：棱柱的结构特征；MK：点、线、面间的距离计算．【专题】11 ：计算题．【分析】（1）连接BG，则BG是BE在面ABD的射影，易证∠EBG是A1B与平面ABD所成的角，设F为AB中点，连接EF、FC，在三角形EBG中求出此角；（2）连接A1D，有，建立等量关系，求出点A1到平面AED的距离即可．【解答】解：（Ⅰ）连接BG，则BG是BE在面ABD的射影，即∠EBG是A1B与平面ABD所成的角．设F为AB中点，连接EF、FC，∵D，E分别是CC1，A1B的中点，又DC⊥平面ABC，∴CDEF为矩形，连接DE，G是△ADB的重心，∴G∈DF，在直角三角形EFD中，EF2=FG•FD=FD2，∵EF=1，∴FD=．于是ED=，EG=∵FC=，CD=1∴AB=2，A1B=2，EB=，∴A1B与平面ABD所成的角是arcsin；（Ⅱ）连接A1D，有∵ED⊥AB，ED⊥EF，又EF∩AB=F，∴ED⊥平面A1AB，设A1到平面AED的距离为h，则，，．∴，即A1到平面AED的距离为．【点评】本小题主要考查线面关系和直棱柱等基础知识，同时考查空间想象能力和推理运算能力．19．（12分）（2003•全国）已知c＞0，设P：函数y=c x在R上单调递减，Q：不等式x+|x﹣2c|＞1的解集为R．如果P和Q有且仅有一个正确，求c的取值范围．【考点】4B：指数函数的单调性与特殊点；R5：绝对值不等式的解法．【专题】11 ：计算题；15 ：综合题．【分析】函数y=c x在R上单调递减，推出c的范围，不等式x+|x﹣2c|＞1的解集为R，推出x+|x﹣2c|的最小值大于1，P和Q有且仅有一个正确，然后求出c 的取值范围．【解答】解：函数y=c x在R上单调递减⇔0＜c＜1．不等式x+|x﹣2c|＞1的解集为R⇔函数y=x+|x﹣2c|在R上恒大于1．∵x+|x﹣2c|=∴函数y=x+|x﹣2c|在R上的最小值为2c．∴不等式x+|x﹣2c|＞1的解集为R⇔2c＞1⇔c＞．如果P正确，且Q不正确，则0＜c≤．如果P不正确，且Q正确，则c＞1．∴c的取值范围为（0，]∪（1，+∞）．【点评】本题考查绝对值不等式的解法，指数函数单调性的应用，是中档题．20．（12分）（2003•全国）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南方向300km的海面P处，并以20km/h的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？【考点】JF：圆方程的综合应用．【专题】12 ：应用题；16 ：压轴题．【分析】建立坐标系：以O为原点，正东方向为x轴正向．设在时刻：t（h）台风中心P（x，y）的坐标进而可知此时台风侵袭的区域，根据题意可知其中r（t）=10t+60，若在t时，该城市O受到台风的侵袭，则有（0﹣x）2+（0﹣y）2≤（10t+60）2，进而可得关于t的一元二次不等式，求得t的范围，答案可得．【解答】解：如图建立坐标系：以O为原点，正东方向为x轴正向．在时刻：t（h）台风中心P（x，y）的坐标为令（x′，y′）是台风边缘线上一点，则此时台风侵袭的区域是（x′﹣x）2+（y′﹣y）2≤[r（t）]2，其中r（t）=10t+60，若在t时，该城市受到台风的侵袭，则有（0﹣x）2+（0﹣y）2≤（10t+60）2，即，即t2﹣36t+288≤0，解得12≤t≤24．答：12小时后该城市开始受到台风侵袭．【点评】本题主要考查了圆的方程的综合运用．考查了学生运用所学知识解决实际问题的能力．21．（12分）（2003•全国）已知常数a＞0，在矩形ABCD中，AB=4，BC=4a，O 为AB的中点，点E、F、G分别在BC、CD、DA上移动，且，P为GE 与OF的交点（如图），问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由．【考点】J3：轨迹方程；K4：椭圆的性质．【专题】11 ：计算题；16 ：压轴题．【分析】建立坐标系，按题意写出A，B，C，D四点的坐标，进而根据解出E，F，G三点的坐标参数表示，求出OF与GE两条直线的方程，两者联立即可求出点P的坐标满足的参数方程，消去参数，得到点P的轨迹方程．由于参数a的取值范围影响曲线的形状故按参数a的范围来对曲线进行分类．【解答】解：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到定点距离的和为定值．按题意有A（﹣2，0），B（2，0），C（2，4a），D（﹣2，4a）设=k（0≤k≤1），由此有E（2，4ak），F（2﹣4k，4a），G（﹣2，4a﹣4ak）．直线OF的方程为：2ax+（2k﹣1）y=0，①直线GE的方程为：﹣a（2k﹣1）x+y﹣2a=0．②从①，②消去参数k，得点P（x，y）坐标满足方程2a2x2+y2﹣2ay=0，整理得．当时，点P的轨迹为圆弧，所以不存在符合题意的两点；当时，点P轨迹为椭圆的一部分，点P到该椭圆焦点的距离的和为定长；当时，点P到椭圆两个焦点的距离之和为定值；当时，点P到椭圆两个焦点的距离之和为定值2a．【点评】考查解析法求点的轨迹方程，本题在做题时引入了参数k，故得到的轨迹方程为参数方程，需要消去参数得到轨迹方程，又当字母的取值范围对曲线的形状有影响时，要对其范围进行讨论以确定轨迹的具体性状．考查分类讨论的数学思想．22．（14分）（2003•全国）（1）设{a n}是集合{2s+2t|0≤s＜t且s，t∈Z}中所有的数从小到大排列成的数列，即a1=3，a2=5，a3=6，a4=9，a5=10，a6=12，…将数列{a n}各项按照上小下大，左小右大的原则写成如下的三角形数表：35 69 10 12﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣…①写出这个三角形数表的第四行、第五行各数；②求a100（2）设{b n}是集合{2r+2s+2t|0≤r＜s＜t，且r，s，t∈Z}中所有的数从小到大排列成的数列，已知b k=1160，求k．【考点】8B：数列的应用．【专题】11 ：计算题；15 ：综合题；16 ：压轴题．【分析】（1）①用（t，s）表示2t+2s，先利用前几个数找到其规律，是每一个的横坐标从0增加到对应的行数，而纵坐标为行数，就可求出第四行、第五行各数；②解法一：因为100=（1+2+3+4++13）+9，所以可以知道a100位于第14行第8列，即可求出a100．解法二：直接把设a100=2s0+2t0，再利用条件确定对应的正整数s0，t0即可．（2）利用上面的结论可以快速找到{b n}的规律，再结合组合数对其求解即可．【解答】（1）解：用（t，s）表示2t+2s，下表的规律为3（0，1）5（0，2）6（1，2）9（0，3）10（1，3）12（2，3）①第四行17（0，4）18（1，4）20（2，4）24（3，4）第五行33（0，5）34（1，5）36（2，5）40（3，5）48（4，5）②解法一：因为100=（1+2+3+4+…+13）+9，所以a100=（8，14）=28+214=16640解法二：设a100=2s0+2t0，只须确定正整数s0，t0．数列{a n}中小于2t0的项构成的子集为{2t+2s|0≤s＜t＜t0}，其元素个数为，依题意．满足等式的最大整数t0为14，所以取t0=14．因为100﹣C142=s0+1，由此解得s0=8，∴a100=214+28=16640．（2）解：b k=1160=210+27+23，令M={c∈B|C＜1160}（其中，B={2r+2s+2t|0≤r＜s＜t}）因M={c∈B|c＜210}∪{c∈B|210＜c＜210+27}∪{c∈B|210+27＜c＜210+27+23}．现在求M的元素个数：{c∈B|c＜210}={2r&+2s+2t|0≤r＜s＜t＜10}，其元素个数为C103：{c∈B|210＜c＜210+27}={210&+2s+2r|0≤r＜s＜7}．某元素个数为C72：{c∈B|210+27＜c＜210+27+23}={210+27+2r|0≤r＜3}某元素个数为C107：k=C103+C72+C32+1=145．另法：规定2r+2t+2s=（r，t，s），b k=1160=210+27+23=（3，7，10）则b1=20+21+22=（0，1，2）C22依次为（0，1，3）（0，2，3）（1，2，3）C32（0，1，4）（0，2，4）（1，2，4）（0，3，4）（1，3，4）（2，3，4）C42（0，1，9）（0，2，9）（6，8，9）（7，8，9）C92（0，1，10）（0，2，10）（0，7，10）（1，7，10）（2，7，10）（3，7，10）C72+4k=（C22+C32++C92）+C72+4=145．【点评】本题考查数列的应用是数列这一块的难题，适合做压轴题．考点卡片1．分段函数的解析式求法及其图象的作法【知识点的认识】分段函数是定义在不同区间上解析式也不相同的函数．若函数在定义域的不同子集上的对应法则不同，可用几个式子来表示函数，这种形式的函数叫分段函数．已知一个分段函数在某一区间上的解析式，求此函数在另一区间上的解析式，这是分段函数中最常见的问题．【解题方法点拨】求解函数解析式的几种常用方法主要有1、待定系数法，如果已知函数解析式的构造时，用待定系数法；2、换元法或配凑法，已知复合函数f[g（x）]的表达式可用换元法，当表达式较简单时也可用配凑法；3、消参法，若已知抽象的函数表达式，则用解方程组消参的方法求解f（x）；另外，在解题过程中经常用到分类讨论、等价转化等数学思想方法．分段函数是一类重要的函数模型．解决分段函数问题，关键抓住在不同的段内研究问题．【命题方向】分段函数是今后高考的热点题型．常考题型为函数值的求解，不等式有关问题，函数的图形相联系的简单问题．2．指数函数的单调性与特殊点【知识点归纳】1、指数函数单调性的讨论，一般会以复合函数的形式出现，所以要分开讨论，首先讨论a的取值范围即a＞1，0＜a＜1的情况．再讨论g（x）的增减，然后遵循同增、同减即为增，一减一增即为减的原则进行判断．2、同增同减的规律：（1）y=a x如果a＞1，则函数单调递增；（2）如果0＜a＜1，则函数单调递减．3、复合函数的单调性：（1）复合函数为两个增函数复合：那么随着自变量X的增大，Y值也在不断的增大；（2）复合函数为两个减函数的复合：那么随着内层函数自变量X的增大，内层函数的Y值就在不断的减小，而内层函数的Y值就是整个复合函数的自变量X．因此，即当内层函数自变量X的增大时，内层函数的Y值就在不断的减小，即整个复合函数的自变量X不断减小，又因为外层函数也为减函数，所以整个复合函数的Y值就在增大．因此可得“同增”若复合函数为一增一减两个函数复合：内层函数为增函数，则若随着内层函数自变量X的增大，内层函数的Y值也在不断的增大，即整个复合函数的自变量X不断增大，又因为外层函数为减函数，所以整个复合函数的Y值就在减小．反之亦然，因此可得“异减”．3．对数的运算性质【知识点的认识】对数的性质：①=N；②log a a N=N（a＞0且a≠1）．log a（MN）=log a M+log a N；log a=log a M﹣log a N；log a M n=nlog a M；log a=log a M．4．反函数【知识点归纳】【定义】一般地，设函数y=f（x）（x∈A）的值域是C，根据这个函数中x，y 的关系，用y把x表示出，得到x=g（y）．若对于y在中的任何一个值，通过x=g （y），x在A中都有唯一的值和它对应，那么，x=g（y）就表示y是自变量，x 是因变量是y的函数，这样的函数y=g（x）（x∈C）叫做函数y=f（x）（x∈A）的反函数，记作y=f（﹣1）（x）反函数y=f（﹣1）（x）的定义域、值域分别是函数y=f （x）的值域、定义域．【性质】反函数其实就是y=f（x）中，x和y互换了角色（1）函数f（x）与他的反函数f﹣1（x）图象关于直线y=x对称；函数及其反函数的图形关于直线y=x对称（2）函数存在反函数的重要条件是，函数的定义域与值域是一一映射；（3）一个函数与它的反函数在相应区间上单调性一致；（4）大部分偶函数不存在反函数（当函数y=f（x），定义域是{0}且f（x）=C （其中C是常数），则函数f（x）是偶函数且有反函数，其反函数的定义域是{C}，值域为{0}）．奇函数不一定存在反函数，被与y轴垂直的直线截时能过2个及以上点即没有反函数．若一个奇函数存在反函数，则它的反函数也是奇函数．（5）一切隐函数具有反函数；（6）一段连续的函数的单调性在对应区间内具有一致性；（7）严格增（减）的函数一定有严格增（减）的反函数【反函数存在定理】；（8）反函数是相互的且具有唯一性；（9）定义域、值域相反对应法则互逆（三反）；（10）原函数一旦确定，反函数即确定（三定）（在有反函数的情况下，即满足（2））．5．极限及其运算【知识点的知识】1．数列极限（1）数列极限的表示方法：（2）几个常用极限：③对于任意实常数，当|a|＜1时，a n=0，当|a|=1时，若a=1，则a n=1；若a=﹣1，则a n=（﹣1）n不存在当|a|＞1时，a n=不存在．（3）数列极限的四则运算法则：如果，那么特别地，如果C是常数，那么．（4）数列极限的应用：求无穷数列的各项和，特别地，当|q|＜1时，无穷等比数列的各项和为S=（|q|＜1）．（化循环小数为分数方法同上式）注：并不是每一个无穷数列都有极限．=a2．函数极限；（1）当自变量x无限趋近于常数x0（但不等于x0）时，如果函数f（x）无限趋进于一个常数a，就是说当x趋近于x0时，函数f（x）的极限为a．记作=a或当x→x0时，f（x）→a．注：当x→x0时，f（x）是否存在极限与f（x）在x0处是否定义无关，因为x→x0并不要求x=x0．（当然，f（x）在x0是否有定义也与f（x）在x0处是否存在极限无关．函数f（x）在x0有定义是存在的既不充分又不必要条件．）如P（x）=在x=1处无定义，但存在，因为在x=1处左右极限均等于零．（2）函数极限的四则运算法则：如果，那么。

2003高考语文试卷

2003年高考语文试题分析余闻2003年高考语文试卷在考试内容和结构上与2002年大体相当。

在内容方面，有变化的是：①文言虚词由20个减少为18个。

②在阅读方面，将文言文和现代文阅读要求的“概括中心思想”改为“概括中心意思”，并且首次在现代文阅读中提出了信息“整合”的概念。

在试卷结构方面，2003年考题与2002年完全相同，相信考生拿到这份试卷不会感到陌生。

2003年试卷中的语言知识题继续体现出对语言基础知识以及基本能力的考查。

其中部分试题在考后引起了一些争议，主要涉及到现代汉语文字、词语使用的规范问题和现代汉语语法知识和应用的一些问题。

不过这些争议恰恰给中学老师和学生这样一些提示：使用现代汉语的文字和词语一定要注意规范的写法和用法，有些字的写法虽然在古代存在，或者在有关古代汉语的字典、词典中可以查到，而现在再这么写、这么用就不规范了。

比如在现代汉语中，“伶俐”就不能写做“伶利”，这就像“海湾”的“湾”不能再写作“弯”，“暮色”的“暮”不能再写作“莫”一样，所以“伶牙利齿”或“灵牙利齿”就应该看做是不规范的或者说是错误的写法。

这一点试题分析中做了说明，就是提醒大家今后碰到类似的问题也同样如此。

而对于现代汉语的语法问题，也应该明确，在中学阶段只需要让学生掌握一些最简单最基础的语法知识，或者说只需要让学生做到凭借正常的语感能判断出几种常见的语病就可以了（这一点在“教学大钢”和“考试说明”中都有明确提示）。

而一些更复杂的语法分析内容是没有必要都教给学生的，甚至老师也不一定都能讲清楚。

因此无论是考试还是教学，如果过多纠缠在一些似是而非的细节问题上，不但可能事倍功半，甚至可能误人子弟，对中学生正确和灵活地使用语法反而是一种消极的引导。

对有些人关心的语法分析问题，试题分析中虽然做了详细说明，但目的其实不在于让大家去搞懂这些问题，而更多的是提醒大家没有必要去无谓地争论这样一些问题。

2003年的作文题仍然是话题作文，并且继续体现了高考作文的开放性原则。

山东省2003年中考试卷

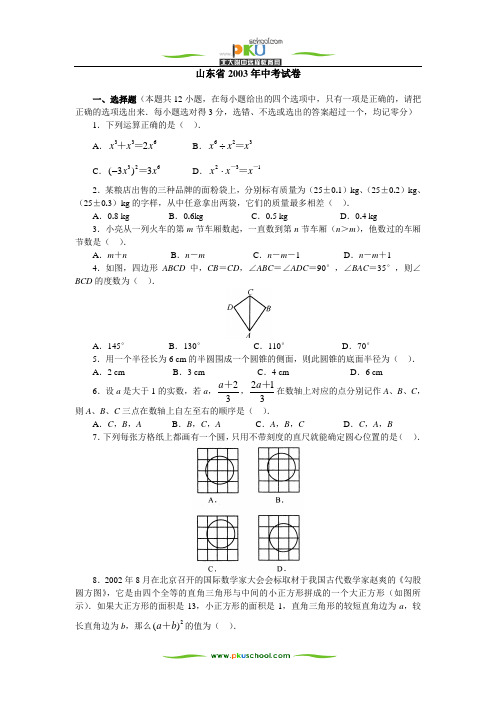
山东省2003年中考试卷一、选择题（本题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个，均记零分） 1．下列运算正确的是（）． A ．6332x x x ＝＋ B ．326x x x ＝÷ C ．6233)3(x x ＝- D ．132－－＝x x x⋅2．某粮店出售的三种品牌的面粉袋上，分别标有质量为（25±0.1）kg 、（25±0.2）kg 、（25±0.3）kg 的字样，从中任意拿出两袋，它们的质量最多相差（）．A ．0.8 kgB ．0.6kgC ．0.5 kgD ．0.4 kg 3．小亮从一列火车的第m 节车厢数起，一直数到第n 节车厢（n ＞m ），他数过的车厢节数是（）．A ．m ＋nB ．n －mC ．n －m －1D ．n －m ＋14．如图，四边形ABCD 中，CB ＝CD ，∠ABC ＝∠ADC ＝90°，∠BAC ＝35°，则∠BCD 的度数为（）．A ．145°B ．130°C ．110°D ．70°5．用一个半径长为6 cm 的半圆围成一个圆锥的侧面，则此圆锥的底面半径为（）． A ．2 cm B ．3 cm C ．4 cm D ．6 cm 6．设a 是大于1的实数，若a ，32＋a ，312＋a 在数轴上对应的点分别记作A 、B 、C ，则A 、B 、C 三点在数轴上自左至右的顺序是（）．A ．C ，B ，A B ．B ，C ，A C ．A ，B ，CD ．C ，A ，B 7．下列每张方格纸上都画有一个圆，只用不带刻度的直尺就能确定圆心位置的是（）．8．2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图所示）．如果大正方形的面积是13，小正方形的面积是1，直角三角形的较短直角边为a ，较长直角边为b ，那么2)(b a ＋的值为（）．A．13 B．19 C．25 D．1699．如图是某蓄水池的横断面示意图，分深水区和浅水区．如果这个蓄水池以固定的流量注水，下面哪个图象能大致表示水的最大深度h和时间t之间的关系?（）．10．若A（a，6），B（2，a），C（0，2）三点在同一条直线上，则a的值为（）．A．4或－2 B．4或－1 C．－4或1 D．－4或211．工人师傅在一个长为25 cm，宽为18 cm的矩形铁皮上，剪去一个和三边都相切的圆A后，在剩余部分的废料上再剪出一个最大的圆B，则圆B的直径是（）．7cm B．8 cm C．7 cm D．4 cm A．212．在一列数1，2，3，4，…，1000中，数字“0”出现的次数一共是（）．A．182 B．189 C．192 D．194二、填空题（本题共4小题，每小题填对得4分，共16分．只要求填写最后结果）13．某市召集20名特级教师参加教改研讨会，与会的特级教师每两人之间都握手一次，那么他们之间一共握手________次．14．赵刚利用科学计算器计算0.15＋0.27时，虽然按键正确，但结果总是0，其原因是________．15．某工厂2002年的年产值为26948万元，比2001年增长8.2％．若年增长率保持不变，预计2005年该厂的年产值为________万元（结果精确到万元）．16．如图所示的曲边三角形可按下述方法作出：分别以正三角形的一个顶点为圆心，边长为半径，画弧使其经过另外两个顶点，然后擦去正三角形，三段圆弧所围成的图形就是一个曲边三角形．如果一个曲边三角形的周长为π，那么它的面积为________．三、解答题（本题共7小题，共68分．解答应写出文字说明、证明过程或演算步骤） 17．计算（本题满分8分，可用计算器计算）：＝＋＋1212222⨯________，＝＋＋12321333333++⨯________，＝＋＋123432144444444++++⨯________．由此你可以猜想出哪些类似的等式________________________________________． 18．（本题满分9分）给出两块相同的正三角形纸片（如图（1），图（2）），要求用其中一块剪拼成一个底面为正三角形的三棱锥模型，另一块剪拼成一个上下底面为正三角形的直三棱柱模型，使它们的表面面积都与原三角形的面积相等．请设计一种剪拼方法，分别用虚线标示在图（1）、图（2）中，并作简要说明：19．（本题满分9分）已知抛物线1C 的解析式是5422＋－＝x x y ，抛物线2C 与抛物线1C 关于x 轴对称，求抛物线2C 的解析式．20．（本题满分10分）我省某城镇邮政局对甲、乙两个支局的报刊发行部2002年度报纸的发行量进行了统计，并绘成统计图如下：请根据上面统计图反映的信息，回答问题：（1）哪个支局发行《齐鲁晚报》的份数多?多多少?（2）分别写出上面两个统计图中提供的6个统计数据的中位数；（3）已知甲、乙两个支局所服务的居民区住户分别是11280户、8600户，哪个居民区平均每户订阅报纸的份数多?试说明理由．21．（本题满分10分）如图，割线ABC 与⊙O 相交于B 、C 两点，D 为⊙O 上一点，E 为弧BC 的中点，OE 交BC 于F ，DE 交AC 于G ，∠ADG ＝∠AGD ．（1）求证：AD 是⊙O 的切线；（2）如果AB ＝2，AD ＝4，EG ＝2．求⊙O 的半径．22．（本题满分10分）已知方程组⎩⎨⎧=ax y x y ＋＝2,42有两个实数解为⎩⎨⎧=11,y y x x ＝和⎩⎨⎧=,,22y y x x ＝且021≠⋅x x ，21x x ≠，设2111x x b ＋＝．（1）求a 的取值范围；（2）试用关于a 的代数式表示出b ；（3）是否存在使b ＝3的a 的值?若存在就求出所有这样的a 的值；若不存在，请说明理由．23．（本题满分12分）如图，正三角形ABC 的中心O 恰好为扇形ODE 的圆心，且点B 在扇形内．要使扇形ODE 绕点O 无论怎样转动，△ABC 与扇形重叠部分的面积总等于△ABC 的面积的31，扇形的圆心角应为多少度?说明你的理由．参考答案一、选择题（每小题选对得3分，选错、不选或选出的答案超过一个，均记零分） 1．D 2．B 3．D 4．C 5．B 6．B 7．A 8．C 9．C 10．A 11．B 12．C 二、填空题（只要求填写最后结果，每小题填对得4分）13．190 14．将小数点的位数设为0（或设定计算结果取整数） 15．34136 16．23π- 三、解答题 17．（本题满分8分）121，12321，1234321（每空1分）1234543211234543215555555555=++++++++⨯， 1123456543212345654321666666666666=++++++++++⨯， 3211234567654123456765432177777777777777=++++++++++++⨯ 5432112345678761234567876543218888888888888888=++++++++++++++⨯，7654321123456789812345678987654321999999999999999999=++++++++++++++++⨯．每写对一个式子得1分，满分8分． 18．（本题满分9分）解：（1）如图，沿正三角形三边中点连结折起，可拼得一个底面为正三角形的三棱锥．………………………………………………………………………………………………4分如图，在正三角形三个角上剪出三个相同的四边形，其较长的一组邻边边长为三角形边长的41，有一组对角为直角，余下部分按虚线折起，可成为一个缺上底而下底为正三角形的直三棱柱，而剪出的三个相同的四边形恰好拼成这个三棱柱的上底．…………………9分 19．（本题满分9分）解：经检验，点A （0，5）、B （1，3）、C （－1，11）都在抛物线1C 上，点A 、B 、C 关于x 轴的对称点分别为1A （0，－5）、1B （1，－3）、1C （－1，－11），它们都在抛物线2C 上．抛物线2C 的解析式为c bx ax y ++=2，则⎪⎩⎪⎨⎧-=+--=++-=.1135c b a c b a c ，，，解得⎪⎩⎪⎨⎧-==-=.542c b a ，，所以抛物线解析式是5422-+-=x x y ．评分要点：（1）选定抛物线1C 上的三点，得1分．（2）确定所求的抛物线2C 上的三点的坐标，得3分．（3）正确列出方程组并求出解，得4分．（4）写出解析式得1分．满分得9分． 20．（本题满分10分）解：（1）甲支局发行《齐鲁晚报》840份，乙支局发行《齐鲁晚报》880份，乙支局比甲支局多发行40份．…………………………………………………………………………4分（2）甲图中6个统计数据的中位数是4.5，乙图中6个统计数据的中位数是3.6． …………………………………………………………………………………………………7分（3）由统计图知，甲支局订阅报纸共2820份，平均每户订阅报纸的份数是2820÷11280＝0.25．乙支局订阅报纸2580份，平均每户订阅报纸的份数是2580÷8600＝0.3．所以乙支局所服务的居民区住户比甲支局服务的居民区住户平均每户多订阅报纸0.05份．……………………………………………………………………………………………10分 21．（本题满分10分）（1）证明：∵ E 为弧BC 的中点， ∴ BC OE ⊥于F ．∴ ∠AGD ＋∠ODE ＝∠EGF ＋∠OED ＝90° 连结OD ，则OD ＝OE ． ∴ ∠ODE ＝∠OED ． ∵ ∠AGD ＝∠ADG ，∴ ∠ADG ＋∠ODG ＝90°，即OD ⊥AD ． ∴ AD 是⊙O 的切线．……………………………………………………………………5分（2）由AD ＝4，AB ＝2，AC AB AD ⋅=2，得AC ＝8．∵ AD ＝AG ，∴ BG ＝2，CG ＝4．由EG ＝2，CG BG GD EG ⋅⋅=，得DG ＝4． ∴ AD ＝DG ＝GD ，∴∠ADG ＝60°，作OH ⊥ED 于H ，则∠EOH ＝60°，…………………………………………………8分在Rt △OEH 中，EH ＝21（EG ＋GD ）＝3， ∴ 23360sin =︒=EH OE ．即⊙O 的半径为233．…………………………………………………………………10分 22．（本题满分10分）（1）由原方程组可得关于x 的二次方程：0)1(4422=+-+a x a x ．………………………………………………………………1分 ∵ 原方程组有两个不同的实数解，即上述二次方程有两个不等实根，∴ △016)]1(4[22>--=a a ，解得：21＜a ．………………………………………3分（2）由根与系数的关系得：a x x -=+121，4221a x x =⋅……………………………………………………………5分∴ 22121)1(4aa x x x xb -=+=⋅………………………………………………………………6分（3）当3=b 时，3)1(42=-aa ，解得： 21-=a ，21322>=a （舍去）．………………………………………………………9分 ∴ 所求a 的值为－2．…………………………………………………………………10分 23．（本题满分12分）解：当扇形圆心角为120°时，△ABC 与扇形重叠部分的面积，总等于△ABC 的面积的31．……………………………………………………………………………………………2分证明如下：（1）当扇形的圆心角与正三角形的中心角重合时，显然，△ABC 与扇形重叠部分的面积等△ABC 的面积的31．…………………………………………………………………4分（2）当扇形的圆心角与正三角形的中心角不重合时，如图，连结OA 、OB ，设OD 交AB 于F ，OE 交BC 于G ． ∵ O 是正三角形的中心，∴ OA ＝OB ，∠OAF ＝∠OBG ，∠AOB ＝120° ∴ ∠AOF ＝120°－∠BOF ， ∠BOG ＝120°－∠BOF ， ∠AOF ＝∠BOG ．∠AOF ≌△BOG ．…………………………………………………………………………8分即ABC AOB OFBG S S S ∆∆==31四边形，即△ABC 与扇形重叠部分的面积，总等于△ABC 的面积的31．…………………………………………………………………………………10分同理可证，当扇形ODE 旋转至其他位置时，结论仍成立．…………………………11分由（1）、（2）可知，当扇形的圆心角为120°时，△ABC 与扇形重叠部分的面积，总等于△ABC 的面积的31．……………………………………………………………………12分。

2003年全国统一高考理综真题试题及答案

2003年江苏省高考综合考试理科综合试卷本试卷分第I卷(选择题)和第11卷(非选择题)两部分，第1卷1至6页，第Ⅱ卷7至14页。

满分150分。

考试用时120分钟。

第1卷(选择题共75分)注意事项：1．答第1卷前，考生务必将自己的姓名、考试号、考试科目涂写在答题卡上。

考试结束，将试题卷和答题卡一并交回。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试题卷上。

一、本卷共25题，每题3分，共75分．在下列各题的四个选项中，只有一个选项是符合题目要求的．1．生物的生命活动都要消耗能量，这些能量由呼吸作用提供．活细胞内进行有氧呼吸的主要场所是A.高尔基体 B．线粒体C.叶绿体D.核糖体2．如果—个人多食少动，即摄人的食物过多，消耗的物质过少，容易导致身体的肥胖，其主要原因是体内的A.有机物氧化分解成C02和H20 B．葡萄糖合成肝糖元C.非脂肪类有机物转变脂肪D.葡萄糖合成肌糖元3.用0.3g/mL的蔗糖溶液可以使洋葱表皮细胞发生质壁分离，在发生质壁分离的原生质层和细胞壁之间充满的物质是A.蔗糖溶液B.水C.细胞液D.空气4.某园艺场经过长期精心选育，培养出一株形态优美的兰花.如果要保持每本的优良性状，并尽快大规模繁殖，最适合的繁殖方式是A.分裂生殖B.有性生殖C.孢子生殖D.组织培养5.下面是—个草原生态系统食物网的模式图，该食物网中共有食物链A.3条B.4条C.5条D.6条6.2002年诺贝尔化学奖授予利用“质谱分析法”和“核磁共振技术”等对生物大分子进行研究并作出重大贡献的科学家.下列物质中属于生物大分子的是 A.乙醇 B.葡萄糖 C.氨基酸 D.蛋白质7．136C N M R - (核磁共振)可以用于含碳化合物的结构分析．有关136C N M R -的说法正确的是A ．质子数为6B ．电子数为13C ．中子数为6D ．质量数为68．环境污染已成为人类社会面临的重大威胁之—．下列气体的排放不会造成大气污染的是 A ．S02 B ．N 2 C ．N02 D ．CO9．下列物质不属于有机物的是 A.CH 4 B ．CH 3CHO C ．NaCl D ．C 6H 610．不属于碱金属元素的是 A ．Li B ．Na C ．K D ．A111．下列说法正确的是A ．绿色食品是指不含任何化学物质的食品B ．纳米材料是一种称为“纳米”的新物质制成的材料C ．光导纤维是以二氧化硅为主要原料制成的高性能通讯材料D ．废旧干电池必须集中回收，目的是调剂给贫困地区使用 12．下列物质中既能跟盐酸反应，又能跟氢氧化钠溶液反应的是 A.Al(OH)3 B ．NaCl 溶液 C. K 2S04溶液 D ．稀H 2S0413.下列化合物中，不能由单质直接化合而得到的是 A.NH 3 B.Na 202C.FeCl 2D.FeCl 314.a g 的铜丝灼烧变黑，立即放人下列的某种物质中发生反应，铜丝变红且反应后铜丝质量仍为a g.则该物质是 A.稀H 2S04 B.C 2H 5OHC.CuS04溶液D.NaOH 溶液15.在O.1mol ／L 的CH 3COOH 溶液中存在如下电离平衡： CH 3COOH CH3COO -+H +对于该平衡，下列叙述正确的是A.加入少量NaOH 固体，平衡向正反应方向移动B.加水，反应速率增大，平衡向逆反应方向移动 C 滴加少量0.1mol ／LHCl 溶液，溶液中C(H +)减少 D.加入少量CH 3COONa 固体，平衡向正反应方向移动16.已知C 4H 10的同分异构体有两种:CH 3-CH 2-CH 2—CH 3、CH 3-CH(CH 3)-CH 3则C 4H 9OH 属于醇类的同分异构体共有A.1种B.2种C.3种D.4种 17.以下关于力的几种说法中，错误的是 A.力是物体间的相互作用 C.力是维持物体运动的原因 B.力能使物体发生形变 D.力是物体产生加速度的原因18.已知C 4H 10的同分异构体有两种:CH 3-CH 2-CH 2—CH 3、CH 3-CH(CH 3)-CH 318．如图所示，某质点沿半径为厂的半圆弧由口点运动到凸点，则它通过的位移和路程分别是 A ．0；0B ．2r ，向东； πrC ．r ，向东； πrD ．2r ，向东 2r19．下列涉及分子动理论的表述中，正确的是 A ．物质是由大量分子组成的B ．物体内分子的无规则运动，在通常条件下也可能停止C ．物体内分子之间的作用力一定表现为引力D ．物体内分子之间的作用力一定表现为斥力20．相隔—段距离的两个点电荷，它们之间的静电力为F ，现使其中—个点电荷的电量变为原来的2倍，同时将它们间的距离也变为原来的2倍，则它们之间的静电力变为 A ．2F B ．4F C ．2F D ．4F21．光导纤维在信息传递方面有很多应用．利用光导纤维进行光纤通信所依据的原理是 A.光的折射 B ．光的全反射 C 光的干涉 D ．光的色散 22．下列衰变中，属于。

2003年上海高考数学真题试卷及答案解析(理科)

绝密★启用前 2003年普通高等学校招生全国统一考试（上海卷）数学试卷（理工农医类）（满分150分，考试时间120分钟）考生注意1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题.第Ⅰ卷（共110分）一、填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分1．函数)4sin(cos )4cos(sin ππ+++=x x x x y 的最小正周期T= . 2．若=∈=+=απααπ则其中的解是方程),2,0(,1)cos(23x x .3．在等差数列}{n a 中，a 5=3, a 6=－2,则a 4+a 5+…+a 10= 4．在极坐标系中，定点A ),2,1(π点B 在直线0sin cos =+θρθρ上运动，当线段AB 最短时，点B 的极坐标是5．在正四棱锥P —ABCD 中，若侧面与底面所成二面角的大小为60°，则异面直线PA 与BC所成角的大小等于 .（结果用反三角函数值表示） 6．设集合A={x ||x |<4},B={x |x 2－4x +3>0}, 则集合{x |x ∈A 且}B A x ∉= . 7．在△ABC 中，sinA;sinB:sinC=2:3:4,则∠ABC= .（结果用反三角函数值表示） 8．若首项为a 1，公比为q 的等比数列}{n a 的前n 项和总小于这个数列的各项和，则首项a 1，公比q 的一组取值可以是（a 1，q ）= .9．某国际科研合作项目成员由11个美国人、4个法国人和5个中国人组成.现从中随机选出两位作为成果发布人，则此两人不属于同一个国家的概率为 .（结果用分数表示）10．方程x 3+lg x =18的根x ≈ .（结果精确到0.1） 11．已知点),0,24(),2,0(),2,0(nC n B n A +-其中n 的为正整数.设S n 表示△ABC 外接圆的面积，则n n S ∞→lim = .12．给出问题：F 1、F 2是双曲线201622y x -=1的焦点，点P 在双曲线上.若点P 到焦点F 1的距离等于9，求点P 到焦点F 2的距离.某学生的解答如下：双曲线的实轴长为8，由 ||PF 1|－|PF 2||=8，即|9－|PF 2||=8，得|PF 2|=1或17.该学生的解答是否正确？若正确，请将他的解题依据填在下面空格内，若不正确，将正确的结果填在下面空格内.二、选择题（本大题满分16分）本大题共4题，每题都给出代号为A 、B 、C 、D 的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分. 13．下列函数中，既为偶函数又在（0，π）上单调递增的是（） A ．y=tg|x |. B ．y=cos(－x ).C ．).2sin(π-=x y D ．|2|xctgy =. 14．在下列条件中，可判断平面α与β平行的是（）A ．α、β都垂直于平面r .B ．α内存在不共线的三点到β的距离相等.C ．l ，m 是α内两条直线，且l ∥β，m ∥β.D ．l ，m 是两条异面直线，且l ∥α，m ∥α, l ∥β，m ∥β.15．a 1、b 1、c 1、a 2、b 2、c 2均为非零实数，不等式a 1x 2+b 1x +c 1>0和a 2x 2+b 2x +c 2>0的解集分别为集合M 和N ，那么“212121c c b b a a ==”是“M=N ”的（）A ．充分非必要条件.B ．必要非充分条件.C ．充要条件D ．既非充分又非必要条件.16．f (x )是定义在区间[－c,c]上的奇函数，其图象如图所示：令g （x ）=af （x ）+b ，则下列关于函数g （x ）的叙述正确的是（）A ．若a <0,则函数g （x ）的图象关于原点对称.B ．若a =－1，－2<b<0,则方程g （x ）=0有大于2的实根.C ．若a ≠0,b=2,则方程g （x ）=0有两个实根.D ．若a ≥1,b<2,则方程g （x ）=0有三个实根.三、解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤. 17．（本题满分12分）已知复数z1=cosθ－i，z2=sinθ+i，求| z1·z2|的最大值和最小值.18．（本题满分12分）已知平行六面体ABCD—A1B1C1D1中，A1A⊥平面ABCD，AB=4，AD=2.若B1D⊥BC，直线B1D 与平面ABCD所成的角等于30°，求平行六面体ABCD—A1B1C1D1的体积.19．（本题满分14分）本题共有2个小题，第1小题满分5分，第2小题满分9分. 已知数列}{n a （n 为正整数）是首项是a 1，公比为q 的等比数列.（1）求和：;,334233132031223122021C a C a C a C a C a C a C a -+-+-（2）由（1）的结果归纳概括出关于正整数n 的一个结论，并加以证明.20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.如图，某隧道设计为双向四车道，车道总宽22米，要求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状. （1）若最大拱高h 为6米，则隧道设计的拱宽l 是多少？（2）若最大拱高h 不小于6米，则应如何设计拱高h 和拱宽l ，才能使半个椭圆形隧道的土方工程量最最小？（半个椭圆的面积公式为lh S 4π=，柱体体积为：底面积乘以高.本题结果精确到0.1米）21．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分7分.在以O 为原点的直角坐标系中，点A （4，－3）为△OAB 的直角顶点.已知|AB|=2|OA|，且点B 的纵坐标大于零.（1）求向量AB 的坐标；（2）求圆02622=++-y y x x 关于直线OB 对称的圆的方程；（3）是否存在实数a ，使抛物线12-=ax y 上总有关于直线OB 对称的两个点？若不存在，说明理由：若存在，求a 的取值范围.22．（本题满分18分）本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分7分.已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x+T)=T f(x)成立.（1）函数f(x)= x是否属于集合M？说明理由；（2）设函数f(x)=a x（a>0,且a≠1）的图象与y=x的图象有公共点，证明：f(x)=a x∈M；（3）若函数f(x)=sin kx∈M ,求实数k的取值范围.2003年普通高等学校招生全国统一考试（上海卷）数学（理工农医类）答案一、（第1题至第12题）1．π. 2．π34. 3．－49 . 4．)43,22(π. 5．arctg2. 6．[1,3]. 7．.611arccos8．10,0)(21,1(1<<>q a 的一组数）. 9．19011910．2.6 . 11．4π 12．|PF 2|=17.二、（第13题至第16题）题号 13 14 15 16 代号CDDB三、（第17题至第22题） 17．[解].2sin 412cos sin 2)sin (cos )cos sin 1(|)sin (cos cos sin 1|||2222221θθθθθθθθθθθ+=+=-++=-++=⋅i z z故||21z z ⋅的最大值为,23最小值为2.18．[解]连结BD ，因为B 1B ⊥平面ABCD ，B 1D ⊥BC ，所以BC ⊥BD.在△BCD 中，BC=2，CD=4，所以BD=32.又因为直线B 1D 与平面ABCD 所成的角等于30°，所以 ∠B 1DB=30°，于是BB 1=31BD=2.故平行六面体ABCD —A 1B 1C 1D 1的体积为S ABCD ·BB 1=38. 19．[解]（1）.)1(33,)1(231312111334233132031212111223122021q a q a q a q a a C a C a C a C a q a q a q a a C a C a C a -=-+-=-+--=+-=+-（2）归纳概括的结论为：若数列}{n a 是首项为a 1，公比为q 的等比数列，则nnn n n n n n n n nnn nnnn n nn n n n n n n n n n n n n n n q a C q C q C q qC C a C q a C q a C q a qC a C a C a C a C a C a C a n q a C a C a C a C a C a )1(])1([)1()1(:.,)1()1(133********122111011342312011134231201-=-++-+-=-++-+-=-++-+--=-++-+-++ 证明为正整数20．[解]（1）如图建立直角坐标系，则点P （11，4.5），椭圆方程为12222=+by a x .将b=h =6与点P 坐标代入椭圆方程，得3.3377882,7744≈===a l a 此时.因此隧道的拱宽约为33.3米.（2）[解一]由椭圆方程12222=+by a x ，得.15.4112222=+b a4.6,1.312222229,211,215.411,.29924,,2,995.41125.41122222222≈=≈======≥====≥⨯⨯≥+b h a l b a b a S ab lh S b h a l ab ab b a 此时得有取最小值时当所以且即因为πππ故当拱高约为6.4米、拱宽约为31.1米时，土方工程量最小.[解二]由椭圆方程12222=+b y a x ，得.15.4112222=+b a 于是,121481222-⋅=a a b ,121121121,,99,12181)2421212(481)242121121121(481222222222-=-≥⨯=+≥+-+-=a a S ab a a b a 有取最小值时当即得.229,211==b a 以下同解一.21．[解]（1）设⎩⎨⎧=-=+⎪⎩⎪⎨⎧=⋅==,034100,0||||||2||},,{22v u v u v u AB 即则由得},3,4{.86,86-+=+=⎩⎨⎧-=-=⎩⎨⎧==v u v u v u 因为或所以v －3>0,得v =8,故={6，8}.（2）由OB ={10，5}，得B （10，5），于是直线OB 方程：.21x y =由条件可知圆的标准方程为：(x －3)2+y(y+1)2=10, 得圆心（3，－1），半径为10.设圆心（3，－1）关于直线OB 的对称点为（x ,y ）则,31,231021223⎩⎨⎧==⎪⎪⎩⎪⎪⎨⎧-=-+=-⋅-+y x x y y x 得故所求圆的方程为(x －1)2+(y －3)2=10. （3）设P (x 1,y 1), Q (x 2,y 2) 为抛物线上关于直线OB 对称两点，则.23,022544,02252,,2252,202222222212212121212121>>-⋅-=∆=-++⎪⎪⎩⎪⎪⎨⎧-=-=+⎪⎪⎩⎪⎪⎨⎧-=--=+-+a a a a aa x a x x x a a x x a x x x x y y y y x x 得于是由的两个相异实根为方程即得故当23>a 时，抛物线y=ax 2－1上总有关于直线OB 对称的两点. 22．[解]（1）对于非零常数T ，f (x +T)=x +T, T f (x )=T x . 因为对任意x ∈R ，x +T= T x 不能恒成立，所以f (x )=.M x ∉（2）因为函数f (x )=a x （a >0且a ≠1）的图象与函数y=x 的图象有公共点，所以方程组：⎩⎨⎧==xy a y x有解，消去y 得a x =x ,显然x =0不是方程a x =x 的解，所以存在非零常数T ，使a T =T.于是对于f (x )=a x 有)()(x Tf a T a a a T x f x x T T x =⋅=⋅==++ 故f (x )=a x ∈M.（3）当k=0时，f (x )=0，显然f (x )=0∈M.当k ≠0时，因为f (x )=sin kx ∈M ，所以存在非零常数T ，对任意x ∈R ，有f (x +T)=T f (x )成立，即sin(kx +k T)=Tsin kx .因为k ≠0，且x ∈R ，所以kx ∈R ，kx +k T ∈R ，于是sin kx ∈[－1，1]，sin(kx +k T) ∈[－1，1]，故要使sin(kx +k T)=Tsin kx .成立，只有T=1±，当T=1时，sin(kx +k )=sin kx 成立，则k =2m π, m ∈Z .当T=－1时，sin(kx－k)=－sin kx成立，即sin(kx－k+π)= sin kx成立，则－k+π=2mπ, m∈Z ，即k=－2(m－1)π, m∈Z . 综合得，实数k的取值范围是{k|k= mπ, m∈Z}。

贵州省贵阳市2003年中考化学试卷

贵州省贵阳市2003年中考试卷可能用到的相对原子质量：H —l C —12 O —16 Cl 一35.5 Ca —40 Cu —64一、选择题（本大题共30分，每小题2分。

每小题只有一个正确答案，请将正确答案的序号填写在括号里）1．生活中的下列现象属于化学变化的是（）A ．纸张燃烧B ．酒精挥发C ．石蜡熔化D ．瓷器破碎 2．我们呼吸的空气中，体积分数约占78％的气体是（）A ．氧气B ．氮气C ．二氧化碳D ．稀有气体 3．水的相对分子质量为（）A ．16B ．17C ．18D ．32 4．下列气体中，能使带火星的木条复燃的是（）A ．氧气B ．氢气C ．空气D ．二氧化碳 5．下列仪器中，不能在酒精灯火焰上直接加热的是（）A ．试管B ．烧杯C ．蒸发D ．燃烧匙 6．下列物质属于纯净物的是（）A ．硝酸钾B ．空气C ．稀硫酸D ．石灰石 7．在医院里常用乙醇作消毒剂，乙醇的俗称为（）A ．蒸馏水B ．食盐水C ．酒精D ．高锰酸钾溶液 8．下列物质中为白色固体的是（）A ．木炭B ．氧化铜C ．氯酸钾D ．二氧化锰 9．若将亚硝酸钠（2NaNO ）误作食盐食用，会使人中毒，甚至死亡。

2NaNO中N元素的化合价为（）A ．＋2B ．＋3C ．＋4D ．＋5 10．下列物质中，难溶于水的是（）A ．42SO HB ．NaOHC ．3AgNO D ．2Cu(OH)11．与元素化学性质关系最密切的是原子的（）A ．质子数B ．中子数C ．电子数D ．最外层电子数 12．下列物质中，能使紫色石蕊试液变红的是（）A ．水B ．盐酸C ．氯化钠溶液D ．氢氧化钙溶液 13．下列各类反应中，反应物和生成物均无单质的是（）A ．化合反应B ．分解反应C ．置换反应D ．复分解反应 14．下列各物质的溶液既能跟酸反应又能跟某些碱溶液反应的是（） A ．3KNOB ．3FeClC ．NaOHD ．32CO K15．下列关于溶液的说法正确的是（） A ．溶液都是无色的 B ．溶液都是混合物C ．饱和溶液都是浓溶液D ．均一、稳定的液体都是溶液二、填空题（本大题共28分，每空1分，每个化学方程式2分）16．请在下列表格内填写有关物质的名称或化学式，并写出它们的所属类别（单质、氧17．请写出下列各符号的意义：（1）2H________ （2）23N________（3）2S－________ （4）＋4Na________18．现有下列物质：①熟石灰②活性炭③一氧化碳④二氧化碳⑤纯碱⑥盐酸⑦氢气，请按以下要求填空。

2003年高考数学试卷(全国理)

页脚内容1绝密★启用前2003年普通高等学校招生全国统一考试数学(理工农医类)一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知==-∈x tg x x 2,54cos ),0,2(则π（）A ．247 B ．247-C ．724 D ．724-2．圆锥曲线的准线方程是θθρ2cos sin 8= （）A ．2cos -=θρB ．2cos =θρC ．2sin -=θρD ．2sin =θρ3．设函数的取值范围是则若0021,1)(,.0,,0,12)(x x f x x x x f x >⎪⎩⎪⎨⎧>≤-=- （）A ．（－1，1）B ．（－1，+∞）C ．),0()2,(+∞⋃--∞D ．),1()1,(+∞⋃--∞4．函数)cos (sin sin 2x x x y +=的最大值为（）A ．21+B ．12-C ．2D ．2页脚内容25．已知圆截得被当直线及直线C l y x l a x a x C .03:)0(4)2()(:22=+->=-+-的弦长为32时，则a =（）A ．2B ．22-C ．12-D ．12+6．已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（）A ．22R πB ．249R πC ．238R πD ．223r π7．已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成的一个首项为41的等差数列，则 =-||n m（）A ．1B ．43 C ．21 D ．838．已知双曲线中心在原点且一个焦点为与其相交于直线1),0,7(-=x y F M 、N 两点，MN 中点的横坐标为,32-则此双曲线的方程是（）A ．14322=-y xB ．13422=-y xC ．12522=-y xD ．15222=-y x 9．函数=∈=-)(]23,2[,sin )(1x f x x x f 的反函数ππ（）A ．]1,1[,arcsin -∈-x xB ．]1,1[,arcsin -∈--x x π页脚内容3C ．]1,1[,arcsin -∈+-x x πD ．]1,1[,arcsin -∈-x x π10．已知长方形的四个项点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB 的中点P 0沿与AB 夹角为θ的方向射到BC 上的点P 1后，依次反射到CD 、DA 和AB 上的点P 2、P 3和P 4（入射解等于反射角），设P 4坐标为（θtg ,2x 1),0,44则若<<x 的取值范围是（）A ．)1,31(B ．)32,31(C ．)21,52(D ．)32,52(11．=++++++++∞→)(lim 11413122242322nnn C C C C n C C C C ΛΛ（）A ．3B ．31C ．61 D ．612．一个四面体的所有棱长都为2，四个项点在同一球面上，则此球的表面积为（）A ．3πB ．4πC ．3π3D ．6π二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上. 13．92)21(xx -展开式中9x 的系数是 . 14．使1)(log 2+<-x x 成立的x 的取值范围是 . 15．如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种.（以数字作答）16．下列五个正方体图形中，l是正方体的一条对角线，点M、N、P分别为具所在棱的中点，能得出l⊥面MNP的图形的序号是 .（写出所有符合要求的图形序号）三、解答题：本大题共6小题，共74分. 解答应写出文字的说明，证明过程或演算步骤.17．（本小题满分12分）已知复数z的辐角为60°，且|1|-z是||z和|2|-z的等比中项. 求||z.页脚内容418．(本小题满分12分)如图，在直三棱柱ABC—A1B1C1中，底面是等腰直角三形，∠ACB=90°，侧棱AA1=2，D、E分别是CC1与A1B的中点，点E在平面ABD上的射影是△ABD的重心G.（Ⅰ）求A1B与平面ABD所成角的大小（结果用反三角函数值表示）；（Ⅱ）求点A1到平面AED的距离.页脚内容519．（本小题满分12分）已知.0c设>P：函数x cy=在R上单调递减.Q：不等式1x+cx的解集为R，如果P和Q有且仅有一个正确，求c的取值范围.|2|>-页脚内容6页脚内容720．（本小题满分12分）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O （如图）的东偏南)102arccos(=θθ方向300km 的海面P 处，并以20km/h 的速度向西偏北45°方向移动. 台风侵袭的范围为圆形区域，当前半径为60km,并以10km/h 的速度不断增大. 问几小时后该城市开始受到台风的侵袭？页脚内容821．（本小题满分14分）已知常数,0>a 在矩形ABCD 中，AB=4，BC=4a ，O 为AB 的中点，点E 、F 、G 分别在BC 、CD 、DA 上移动，且DADGCD CF BC BE ==，P 为GE 与OF 的交点（如图），问是否存在两个定点，使P 到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由.页脚内容922．（本小题满分12分，附加题4分）（Ⅰ）设Z}t s,,0|2{2}{t ∈<≤+且是集合t s a s n 中所有的数从小到大排列成的数列，即.,12,10,9,6,5,3654321Λ======a a a a a a将数列}{n a 各项按照上小下大，左小右大的原则写成如下的三角形数表： 3 5 6 9 10 12 — — — —— — — — — （i ）写出这个三角形数表的第四行、第五行各数；（i i ）求100a .（Ⅱ）（本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分）页脚内容10设Z}t s,r,,0|22{2}{r ∈<<≤++且是集合t s r b s t n 中所有的数都是从小到大排列成的数列，已知k.,1160求=k b绝密★启用前2003年普通高等学校招生全国统一考试数学(理工农医类)答案一、选择题1．D 2．C 3．D 4．A 5．C 6．B 7．C 8．D 9．D 10．C 11．B 12．A页脚内容11二、填空题13．221- 14．（-1，0） 15．72 16．①④⑤ 三、解答题： 17．解：设)60sin 60cos οοr r z +=，则复数.2rz 的实部为2,r z z r z z ==-由题设 .12||).(12,12:.012,421,)2)(2(||)1)(1(:|2||||1|2222-=--=-==-++-=+-∴--=---⋅=-z r r r r r r r r r z z z z z z z z 即舍去解得整理得即18．（Ⅰ）解：连结BG ，则BG 是BE 在ABD 的射影，即∠EBG 是A 1B 与平面ABD 所成的角. 设F 为AB 中点，连结EF 、FC ，.32arcsin .323136sin .3,32,22,2.36321,2)4(.3,1,31.,,,,,,112211所成的角是与平面于是分中在直角三角形的重心是连结为矩形平面又的中点分别是ABD B A EB EG EBG EB B A AB CD FC EG ED FD EF FD FD FG EF EFD DF G ADB G DE CDEF ABC DC B A CC E D ∴=⋅==∠∴===∴===⨯===∴==⋅=∈∴∆∴⊥ΘΛΛΘΘ（Ⅱ）解：,,,F AB EF EF ED AB ED =⋂⊥⊥又Θ.36236232222,.,.,.,.,111111*********的距离为到平面中在的距离到平面是即平面垂足为作面且面平面平面面又面AED A AB B A A A K A AB A AED A K A AED K A K AE K A AE AB A AED AB A AED AED ED AB A ED ∴=⨯=⋅=∆⊥∴⊥=⋂⊥∴⊂⊥∴19．页脚内容12解：函数x c y =在R 上单调递减.10<<⇔c不等式.1|2|1|2|上恒大于在函数的解集为R c x x y R c x x -+=⇔>-+).,1[]21,0(.1,,.210,,.21121|2|.2|2|,2,2,2,22|2|+∞⋃≥≤<>⇔>⇔>-+∴-+=∴⎩⎨⎧<≥-=-+的取值范围为所以则正确且不正确如果则不正确且正确如果的解集为不等式上的最小值为在函数c c Q P c Q P c c R c x x c R c x x y c x c c x c x c x x Θ20．解：如图建立坐标系以O 为原点，正东方向为x 轴正向.在时刻：（1）台风中心P （y x ,）的坐标为⎪⎪⎩⎪⎪⎨⎧⨯+⨯-=⨯-⨯=.22201027300,2220102300t y t x 此时台风侵袭的区域是,)]([)()(22t r y y x x ≤-+-其中,6010)(+=t t r 若在t 时刻城市O 受到台风的侵袭，则有 .)6010()0()0(222+≤-+-t y x 即22)22201027300()2220102300(t t ⨯+⨯-+⨯-⨯2412,028836,)6010(22≤≤≤+-+≤t t t t 解得即答：12小时后该城市开始受到台风的侵袭.21．根据题设条件，首先求出点P 坐标满足的方程，据此再判断是否存在的两定点，使得点P 到两点距离的和为定值.按题意有A （－2，0），B （2，0），C （2，4a ），D （－2，4a ）设)10(≤≤==k DADC CD CF BC BE 由此有E （2，4a k ），F （2－4k ，4a ），G （－2，4a －4ak ）直线OF 的方程为：0)12(2=-+y k ax ①页脚内容13直线GE 的方程为：02)12(=-+--a y x k a ②从①，②消去参数k ，得点P （x,y ）坐标满足方程022222=-+ay y x a 整理得1)(21222=-+aa y x 当212=a 时，点P 的轨迹为圆弧，所以不存在符合题意的两点. 当212≠a 时，点P 轨迹为椭圆的一部分，点P 到该椭圆焦点的距离的和为定长。

2003年普通高等学校招生全国统一考试文理综合试卷及答案

绝密★启用前2003年普通高等学校招生全国统一考试文理综合本试卷分第Ⅰ卷和第Ⅱ卷（非选择题）两部分。

共150分。

考试时间120分。

第Ⅰ卷（共216分）考生注意：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上。

一、本大题共36道选择题，每题6分，共216分。

每题有一个最符合题目要求的答案。

影响工业区位的因素很多，不同工业部门具有不同的区位指向。

回答1-2题。

1．区位宜接近原料产地的是（）A．葡萄酒厂、羊毛加工厂、水果罐头厂B．服装加工厂、羊毛加工厂、水果罐头厂C．造船厂、飞机制造厂、电子装配厂D．钢铁厂、时装加工厂、家具厂2．啤酒厂、家具厂、面包加工厂的区位属于（）A．原材料指向型B．技术指向型C．劳动力指向型D．市场指向型图1表示重庆附近长江某水文站的气温降水状况及该江段补给类型，读图回答3-4题。

3．图1中①所示的补给类型为A．地下水补给B．降雨补给C．冰雪融水补给D．湖水补给4．导致②类型补给春多夏少的主要因素是A．春季增温快，冬季积雪多B．夏季气温高，蒸发旺盛图1C．春季多风，流域内多地形雨D．夏季单一暖气流控制，少锋面雨图2是1999年我国高速公路分布图。

读图回答5-6题。

5．1999年，我国各地区高速公路发展程度存在着很大差异，其中（）A．西南三省高速公路网已基本形成B．华北平原高速公路网已基本形成C．非季风区没有高速公路D．沿海岛屿没有高速公路6．与我国高速公路分布明显相关的是图2A．经济发展水平B．气温高低C．降水量多少D．气象灾害频率东北地区是近代以来列强极力争夺的战略要地。

为捍卫国家统一和民族尊严，中华儿女进行了不屈不挠的抗争。

回答7-9题。

7．甲午战后，经三国干涉，日本被迫交还辽东半岛。

这反映①列强在华争夺趋于白热化②清政府的外交政策取得成效③清政府国际地位极端低下④日本无力对付三国的联合威慑A．①②③B．②③④C．①②④D．①③④8．1904-1905年以中国东北为主战场的日俄战争，出现了“日胜俄败”的结局，使中国的志士仁人受到了强烈的刺激。

2003年全国高考数学试卷

{c ∈ B | 210 < c < 210 + 27}= {210 + 2s + 2r | 0 ≤ r < s < 7}.
C
2 7
:{c ∈ B
|
210
+
27
<
c
<
210
+
27
+
23} = {210
+
27
+
2r
|
0
≤
r
<
3}
C170 : k = C130 + C72 + C32 + 1 = 145.
2
| z −1 |2 =| z | ⋅ | z − 2 | : (z −1)(z −1) =| z | (z − 2)(z − 2),∴ r 2 − r + 1 = r r 2 − 2r + 4, r 2 + 2r −1 = 0. : r = 2 −1, r = − 2 −1(). | z |= 2 −1.
10
2 10
−
20
×
2 2
t,
⎪ ⎪⎩
y
=
−300 ×
72 10
+
20
×
2 2
t.
°
(x − x)2 + ( y − y) ≤ [r(t)]2 ,
r(t) = 10t + 60, t
O°
2
(0 − x)2 + (0 − y)2 ≤ (10t + 60)2. (300 × 2 − 20 × 2 t)2 + (−300 × 7 2 + 20 × 2 t)2

2003年全国统一高考数学试卷(河南卷)

2003年全国统一高考数学试卷(河南卷)一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 设函数f(x) = x^2 4x + 3，则f(x) = 0的解集是（）A. {1, 3}B. {1, 3}C. {1, 3}D. {1, 3}2. 已知向量a = (2, 3)，b = (1, 4)，则向量a与向量b的点积是（）A. 8B. 2C. 2D. 83. 在等差数列{an}中，a1 = 2，d = 3，则数列的前5项之和是（）A. 45B. 40C. 35D. 304. 已知圆的方程为x^2 + y^2 = 16，则圆的半径是（）A. 2B. 4C. 3D. 65. 设直线L的斜率为1/2，且经过点(2, 3)，则直线L的方程是（）A. y = 1/2x + 4B. y = 1/2x + 3C. y = 1/2x + 4D. y =1/2x + 36. 已知三角形ABC的三个内角A、B、C的对边分别为a、b、c，且a = 3，b = 4，C = 90°，则三角形ABC的面积是（）A. 6B. 8C. 10D. 127. 设函数f(x) = 2x 1，则函数f(x)在区间(0, +∞)上是（）A. 递增的B. 递减的C. 常数函数D. 无单调性8. 已知等比数列{an}中，a1 = 2，q = 3，则数列的第5项是（）A. 162B. 81C. 54D. 279. 设函数f(x) = |x 1|，则函数f(x)的图像在x轴上的截距是（）A. 1B. 0C. 1D. 无法确定10. 已知直线L1：x + 2y 3 = 0，L2：2x y + 1 = 0，则这两条直线的交点坐标是（）A. (1, 1)B. (1, 1)C. (1, 1)D. (1, 1)11. 在等差数列{an}中，a1 = 5，d = 2，则数列的前10项之和是（）A. 50B. 45C. 40D. 3512. 已知圆的方程为x^2 + y^2 4x 6y + 9 = 0，则圆心的坐标是（）A. (2, 3)B. (2, 3)C. (2, 3)D. (2, 3)二、填空题（本大题共4小题，每小题5分，共20分。

2003年普通高等学校招生全国统一考试语文试题及答案(全国卷)

绝密★启用前2003年普通高等学校招生全国统一考试语文(全国卷)本试卷分第I卷（选择题），和第Ⅱ卷两部分，第I卷1—5页，第Ⅱ卷5—8页。

共150分。

考试时间150分钟第Ⅰ卷（45分）注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂在答题卡上。

2．每小题选取出答案后，用铅笔把答题卡上对应题的答案标号涂黑。

如要改动，用橡皮擦干净后，再选取涂其它答案。

不能答在试题卷上。

3．考试结束,将本试卷和答题卡一并交回。

一、（18分，每小题3分）1．下列词语中加点字的读音完全相同的一组是A．宦．官豢．养盥．洗患．得患失风云变幻．B．莅．临乖戾．官吏．呕心沥．血不寒而栗．C．翌．日对弈．肄．业苦心孤诣．雄关险隘．D．羡．慕汗腺．霰．弹诌．媚阿谀借花献．佛2．下列各组词语中没有错别字的一组是A．部署备受青睐恰如其分可望而不可即B．报道伶牙利齿群贤毕至一年之计在于春C．揣度共商国是唾手可得冒天下之大不违D．通谍猝不及防大相径庭盛名之下其实难副3．依次填入下列各句横线处的词语，恰当的一组是①报载孙中山的孙女孙穗芳女士近年多次________北京大学，为推动孙中山研究做出了贡献。

②北京市政府对城市建设布局做出了________，在2008年前将每年增加800万平方米的绿地。

③邓亚萍现在留给大家的印象，________日渐成熟的仪表风度，________依然保留的拼搏精神。

A．莅临计划不仅是／而且是B．莅临规划不是／而是C．亲临规划不仅是／而且是D．亲临计划不是／而是4．下列各句中加点的成语使用不恰当的一项是A．滥挖天山雪莲现象日益猖獗的原因之一是，违法者众多且分布广泛，而管理部门人手不足，因此执法时往往捉襟见肘．．．．。

B．今年头场雪后城市主干道上都没有发生车辆拥堵现象，在这种秩序井然的背后，包含着交通部门未雨绸缪．．．．的辛劳。

C．一项社会调查显示，如果丈夫的收入低于妻子，一部分男性难免会感到自惭形秽．．．．，甚至无端地对自己进行心理折磨。

2003年高考试卷

2003年普通高等学校招生全国统一考试
生物试卷（全真模拟四SYZX）
一、单选题（本大题包括26小题，每小题2分，共52分。每小题只有一个选项符合题意）
1、蓝藻是一种古老的微生物，下列能说明蓝藻对其他众多生物的进化上起重要作用的叙述是
A、有的蓝藻能固氮，因而能生长于极其贫瘠的环境中，适应性强
B、蓝藻光合作用释放O2，一部分O2又可进一步形成臭氧
A．2M B．3M C．4M D．6M
29．螳螂在生殖季节，雌螳螂将与自己交配的雄螳螂吃掉，以补充孕育后代所需要的营养物质，螳螂的这种行为对于种群来说具有（）
A．竞争B．捕食C．种内互助D．种内斗争
30．在一个有性体间的随机交配外，还需要下列那些条件，才能说明此种群的基因库是稳定.
A、1号管可以去除，应将1号管中BTB液体换成澄清石灰水
B、该装置无法检验酒精的生成，仍需再补充其他装置
C、温度偏高，导致发酵管内O2少，酵母菌繁殖速度减慢，不利于发酵
D、为使发酵管中尽量少的含有O2，应先将葡萄糖液煮沸，待冷却后加入鲜酵母，再加少许石蜡油，使之浮于混合液表面。
3、污水处理厂利用微生物净化污水，你认为合适的微生物代谢类型应与下列哪种生物相同A、乳酸菌B、蘑菇。C、硝化细菌D、金鱼藻
下列有关叙述中正确的是a狭披针叶性状属于显性性状b亲本与f中的披针形叶植株的基因型不同c子二代的基因型共有3d让子二代中的植株随机传粉理论上讲产生狭披针叶雄株的概率为3169有丝分裂能保持亲子代遗传物质的稳定性下列实例中与此无关的是a花药离体培养获得单倍体植株b杂合体豌豆自花传粉产生种子c杂合体亲本通过组织培养保持杂种优势d三倍体无籽西瓜通过组织培养扩大种植面积10当血液流过人体某器官后氧气含量尿素含量均下降和氧气含量和尿素含量均上升的器官分别是a肝脏和肾脏b心脏和肝脏d肾脏和肺

人大统计学专业课初试题

2003年人大统计学专业课初试题一、（15分）考虑两个国家之间按GDP进行经济比较。

假定在既定汇率水平上，甲国GDP与乙国GDP之间的比例为1：20。

一场金融危机放生之后，如果甲国货币相对乙国货币贬值了50%，那么，在新的汇率水平上，两国GDP之间的比例将变化为1：40。

请问：我们能否根据比较结果说甲国的经济发展水平下降了50%？这种比较所包含的统计方法问题是什么？二、（15分）假定一时期国际收支平衡表上“储备资产变动”一项为正差额100亿元，据此，应用国际收支平衡表原理判断当期国际收支的顺、逆差状况。

三、（30分）以下是某经济总体1985和2001两年份城镇居民住户部门的调查资料。

要求：（1）列表计算各年城镇住户部门的原始收入、可支配收入和最终消费支出；（15分）（2）计算有关指标，比较说明城镇居民住户部门经济活动特征的变化。

（15分）四、（30分）一家种业开发股份公司研究出三个新的小麦品种：品种一、品种二、品种三。

公司为研究不同品种对产量的影响，选择了四个面积相同的地块进行试验，分别为：地块一、地块二、地块三、地块四。

经过试验获得产量数据，经分析得到下面的方差分析表（α=0.05）：（1）将方差分析表中划线部分的数值补齐；（6）（2）分析小麦品种对产量的影响是否显著；（4）（3）分析不同地块对产量的影响是否显著；（4）（4）在产量变动的差异中，被品种所解释的百分比是多少？（3）（5）在产量变动的差异中，被地块所解释的百分比是多少？（3）（6）上面的分析包含哪些假定？（10）五、（30分）统计资料表明，某地区职工年人均病假天数为5.1天。

某公司从本公司职工中随机抽取了46名职工作为样本，测得其平均病假天数为7天，样本标准差为2.5天。

公司领导想知道本公司职工是否比其他单位的职工更容易生病。

（1）公司领导感兴趣的原假设和替换假设是什么？（3）（2）若令α=0.05，请用假设检验的方法帮助公司领导作出判断（写清检验步骤，并作示意图）。

广东省03年7月—05年1月工作岗位研究原理与应用试卷参考答案及评分标准

2003年7月广东省高等教育自学考试工作岗位研究原理与应用（考试时间：150分钟）（课程代号：8410）一、单项选择题（在每小题的备选答案中选出一个正确的答案，并将正确答案的号码填在题干的括号内。

每小题1分，共24分）1、个人在社会中所从事的作为主要生活来源的工作叫做（）。

A、岗位B、职务C、职业D、职级2、岗位培训的前提是（）。

A、定编B、定员C、定岗D、岗位规范化3、方法研究和时间研究的总称叫做（）。

A、工作研究B、工作分析C、工作评价D、程序分析4、在一个组织中，功能大的岗位，其能级就（）。

A、复杂B、简单C、高D、低5、在岗位调查表中，若采用封闭式答题则适用于（）方式。

A、面谈B、现场观测C、书面调查D、电话调查6、（）是对操作者整个工作日的工时利用情况，按时间消耗的顺序，进行观察、记录和分析的一种方法。

A、工作日写实B、测时C、时间研究D、时间分析7、岗位描述是对有关岗位工作的（）。

A、详细描述B、一般性说明C、特征描述D、重点描述8、从内容和范围来看，工作说明书和岗位规范的关系是（）。

A前者包含后者 B、后者包含前者 C、两者含义相同 D、两者互不相干9、采用序列法进行岗位评价时，为了让岗位的序数差更好地反映出岗位的相对价值差，可采用（）。

A、个案分析法B、函数变换法C、系统分析法D、结构变换法10、在岗位测评中，信度是指（）。

A、收集资料的可信程度B、测评方法的可靠程度C、测评过程的准确程度D、测评结果的前后一致性程度11、岗位分类适用于（）。

A、国家机关职能部门B、军队C、社会团体D、各种企业、事业单位12、岗位分类总的原则是（）。

A、以人为中心B、以事为中心C、以物为中心D、以岗位为中心13、对劳动强度的测定主要是用测定（）。

A、能量代谢法B、心率法C、体温法D、排汗量法14、劳动紧张程度应该包括（）。

的紧张程度。

A、心理B、生理C、生理和心理D、肌肉15、广州地区的企业，工作地点的温度达到（），则属于高温作用。

2003年数学试卷

选择题
下列哪个数字是偶数？
A. 3
B. 5
C. 8 （正确答案）
D. 7
一个直角三角形的直角边分别为3cm和4cm，那么它的斜边长度最接近哪个值？
A. 5cm （正确答案）
B. 6cm
C. 7cm
D. 8cm
小明有10块糖，他给了小红3块后，自己还剩下几块？
A. 5块
B. 6块
C. 7块（正确答案）
D. 8块
下列哪个分数等于0.5？
A. 1/3
B. 2/5
C. 1/2 （正确答案）
D. 3/4
一个正方形的边长是4cm，它的面积是多少平方厘米？
A. 8cm²
B. 12cm²
C. 16cm² （正确答案）
D. 20cm²
下列哪个数能被3整除？
A. 14
B. 17
C. 18 （正确答案）
D. 21
小华的生日在第三季度，那么他的生日可能在几月？
A. 1月
B. 4月
C. 7月（正确答案）
D. 10月
下列哪个图形有4条对称轴？
A. 等边三角形
B. 正方形（正确答案）
C. 长方形
D. 圆形
5+7×2的运算结果是多少？
A. 9
B. 14
C. 19 （正确答案）
D. 24。

2003年山东高考数学试卷

2003年山东高考数学试卷一、选择题（每题3分，共30分）下列说法正确的是( )A. 0是集合{x | x^2 - 4 = 0} 的子集B. 直线l经过点P(1,2)和Q(-1,4)，则l的斜率为-1C. 已知函数f(x) = x^3 - 3x^2 + 2，则f'(x) = 3x^2 - 6xD. 若随机变量X服从正态分布N(μ, σ^2)，则P(μ - σ < X < μ + σ) = 0.6826已知函数f(x) = 2sin(2x + π/3)，则下列说法错误的是( )A. 函数f(x)的最小正周期为πB. 函数f(x)的图象关于点(π/12, 0)对称C. 函数f(x)在区间(-π/12, 5π/12)内单调递增D. 函数f(x)的图象关于直线x = π/6对称二、填空题（每题5分，共20分）若复数z满足(1 + i)z = 2 - i，则z = _______。

已知函数f(x) = ln x - ax (a ∈ℝ) 的图象在点(1, f(1))处的切线斜率为-2，则a =_______。

在△ABC中，角A, B, C所对的边分别为a, b, c，若a = 2, b = 3, cos C = 1/3，则sin A = _______。

在平面直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ^2 - 4ρcosθ - 3 = 0，则曲线C的普通方程为_______。

三、解答题（共70分）（12分）已知函数f(x) = x^3 - 3x^2 + ax + 1 有两个不同的极值点，求实数a的取值范围，并讨论f(x)的单调性。

（12分）设F₁, F₂分别为双曲线C：(x^2/a^2) - (y^2/b^2) = 1 (a > 0, b > 0) 的左、右焦点，P为y轴正半轴上一点，以OP为直径的圆在第一象限与双曲线的渐近线交于点M，若点P, M, F₂三点共线，且△MF₁F₂的面积为△OPF₂面积的4倍，求双曲线C的离心率。