复旦中学2011-2012学年度第二学期期末教学质量检测试题
2011-2012学年初中毕业班质量检测数学试卷含答案

新世纪教育网 精品资料版权所有@新世纪教育网2011-2012学年初中毕业班质量检测试卷数学(满分:150分;考试时间:120分钟)题号一二三总分1-8 9-16 17 1819 20 21 22 23 24 25得分一、精心选一选。
(本小题共8小题,每小题4分,共32分,每小题给出的选项有且只有一个是正确的,请把正确选项的代号写在题后的括号内,答对得4分,不答、答错或答案超过一个一律0分)1.下列图形中属于中心对称的是()。
A.B.C.D.2.一组数据:2、1、5、4的方差和中位数依次是()。
A.2.5;2 B.1.5;3 C.2.5;3 D.1.5;23.若△ABC∽△DEF,△ABC与△DEF的相似比是2:3,那么S△DEF:S△ABC=()。
A.9:4 B.3:2 C.4:9 D.2:34.64的立方根是()。
A.8 B.2 C.±8 D.±25.如图,底面半径为2,母线长为8的圆锥,一直蚂蚁若从A出发,绕侧面一周回到A点,它爬行最短路线长()。
A.4 B.83C.10 D.826.如图,菱形ABCD中,DE⊥AB,cosA=53,BE=2,则tan∠DBE值为()。
A.21B.2 C.25D.55得分评卷人学校__________________________班级_______________姓名________________考场座位号_____________第5题图 第6题图 第7题图 7.如图,直线2+=x y 与双曲线xm y 3-=在第二象限有两个交点,那么m 的取值范围在数轴上表示正确的是( )。
A. B.C .D .8.如图,MN 是⊙O 直径,MN=2,A 是半圆的三等分点,B 是弧AN 的中点,P 是直线MN 上一动点,那么PA+PB 最小值是( )。
A .2B .2C .1D .22二、细心填一填。
(本大题共8小题,每小题4分,共32分,直接把答案写在题中的横线上。
2011~2012学年度第二学期七年级期末质量检测数学试题及参考答案评分标准

ADECB图1图2乒乓球30%排球 20%足球25%篮球 20% 其它5% 图3第二学期七年级期末质量检测数学试题试题总量:共4页22小题 命题人:Kevin 考试时间:120分钟 试卷分值:120分第Ⅰ卷 (基础题;满分100分)一、选择题(本题满分18分,共有6道小题,每小题3分)1.如图1,AD ∥BC ,点E 在BD 的延长线上,若∠ADE =155°,则∠DBC 的度数为 A .155° B .50° C .45° D .25°2.如图2是测量一颗玻璃球体积的过程:(1)将300ml 的水倒进一个容量为500ml 的杯子中;(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出. 根据以上过程,推测这样一颗玻璃球的体积在A .20cm 3以上,30cm 3以下B .30cm 3以上,40cm 3以下C .40cm 3以上,50cm 3以下D .50cm 3以上,60cm 3以下 3.在直角坐标系中,第四象限的点M 到横轴的距离为28,到纵轴的距离为6,则M 点的坐标为A.)28,6(--B.)6,28(-C.)28,6(-或)28,6(-D.)28,6(- 4. 若一个多边形的内角和为外角和的3倍,则这个多边形为 A.八边形 B.九边形 C.十边形 D.十二边形 5. 图3是某班学生最喜欢的球类活动人数统计图,则下列说法不正确...的是 A.该班喜欢乒乓球的学生最多; B.该班喜欢排球与篮球的学生一样多;C.该班喜欢足球的人数是喜欢排球人数的1.25倍; D.该班喜欢其它球类活动的人数为5人.6.不等式组⎩⎨⎧<<+<<-5321x a x a 的解集为23+<<a x ,则a 的取值范围是A 、1>aB 、3≤aC 、1<a 或3>aD 、31≤<a()()6304342-÷+⎪⎭⎫ ⎝⎛-⨯-)6()2(422-+--xy x xy x 二、填空题(本题满分18分,共有6道小题,每小题3分)7、在平面直角坐标系中,点P 在x 轴上,且点P 到y 轴的距离为4,则点P 的坐标是_________.8、某校去年有学生1000名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名?设去年有寄宿学生x 名,走读学生y 名,则可列出方程组为 .9、某工厂从10万个灯泡中随意抽取100个灯泡作寿命测试,以便确定这批灯泡的质量.在这里,总体是_______________,样本是_______________ 10、如图:一长方形纸片剪去一个角后,得到一个五边形ABCFE ,则图中∠1+∠2= 度.11、若不等式组2 < x < a 的整数解有3个,则a 的取值范围是 .12、用火柴棒按如图的方式搭一行三角形,搭一个三 角形需3支火柴棒,搭2个三角形需5支火柴棒,搭 3个三角形需7支火柴棒,照这样的规律下去,搭n 个三角形需要S 支火柴棒,那么用n 的代数式表示S 的式子是________________(n 为正整数).三、解答题(本题满分64分,共有5道小题) 13.(本题满分24分) (一)(本题满分8分)解方程组和解不等式组(1)⎩⎨⎧=+=-.732,423y x y x (2)⎪⎩⎪⎨⎧=++-=-2322)1(3)(4yx y y x(二)(本题满分8分)(1)、计算: (2)、化简: (三)(本题满分8分)(1)3(x+1)-1=x-2 (2)2546+=--x x x 14.(本题满分10分)如图,EF//AD ,1∠=2∠.说明:∠DGA+∠BAC=180°.请将说明过程填写完成. 解:∵EF//AD ,(已知)∴2∠=_____.(_____________________________).又∵1∠=2∠,(______)∴1∠=_____,(________________________). ∴AB//______,(____________________________) ∴∠DGA+_______=_____°.(_____________________________)FE D CBA(第14题)21321CB AEDFG15.(本题满分10分)小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图. 根据以上提供的信息,解答下列问题: (1)补全频数分布表. (2)补全频数分布直方图. (3)绘制相应的频数分布折线图.(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?16.(本题满分10分)如图:已知AB ∥DE ∥CF ,若∠ABC=70°,∠CDE=130°,求∠BCD 的度数。
2011—2012学年下学期期末考试

第1页,共4页第2页,共4页2011—2012学年下学期期末考试高二物理试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共100分,考试时间为90分钟。
注意事项:1.在答题卷上填写考号和座位序号,姓名,并将考号涂黑;2.将答案写在答题卷对应题号上面,交卷时只交答题卷。
第Ⅰ卷(选择题,共48分)一、选择题(本题共有12个小题,在每小题给出的四个答案中,有的只有一个选项正确,有的有多个选项正确,全部选对的得分4分,选对但没选全的得2分,有选错的得0分)1、在物理学史上,奥斯特首先发现电流周围存在磁场。
随后,物理学家提出“磁生电”的闪光思想。
很多科学家为证实这种思想进行了十多年的艰苦研究,首先成功发现“磁生电”的物理学家是( ) A .牛顿 B .爱因斯坦 C .法拉第 D .霍金2.小萌家楼道灯的控制电路中接入了光传感器。
在天黑时,灯就亮;在天亮时,灯就熄灭。
这样天黑时,不管是否有人经过楼道,灯都是亮着的,白白浪费了宝贵的电能。
学了传感器后,小萌同学就试着改进楼道灯,以节约能源。
她设想在楼道灯控制电路中接入另一个传感器,在天黑时,出现声音灯才开启,这样便可节约大量电能。
你认为小萌应接入的传感器是( ) A .温度传感器 B .力传感器 C .声传感器 D.以上说法都不对 3.如图所示,长直导线旁边同一平面内有一矩形线圈abcd ,导线中通有竖直向上的电流。
下列操作瞬间,能在线圈中产生沿adcba 方向电流的是( )A .线圈向右平动B .线圈竖直向下平动C .线圈以ab 边为轴转动D .线圈向左平动4.某交流发电机正常工作时,电动势e=E m sin ωt ,若将线框转速提高一倍,匝数提高一倍,其他条件不变,则电动势的变化规律是:( ) e ’=E m sin ωt ; B .e ’=4E m sin2ωt ; C .e ’=2E m sin ωt ; D .e ’=2E m sin2ωt 5.阻值为10Ω的电阻接到电压波形如图所示的交流电源上.以下说法中正确的是( ) A .电压的有效值为10V B .通过电阻的电流有效值为22AC .电阻消耗电功率为5WD .电阻每秒种产生的热量为10J6、如图所示电路中,L 为电感线圈,电阻不计,A 、B 为两灯泡,则( ) A .合上S 时,A 先亮,B 后亮B .合上S 时,A 、B 同时亮C .合上S 后,A 变亮,B 熄灭D .断开S 时,A 熄灭,B 重新亮后再熄灭 7.关于光电效应,下列说法正确的是( )A .极限频率越大的金属材料逸出功越大B .只要光照射的时间足够长,任何金属都能产生光电效应C .从金属表面出来的光电子的最大初动能越大,这种金属的逸出功越小D .入射光的光强一定时,频率越高,单位时间内逸出的光电子数就越多 8.如图所示是玻尔理论中氢原子的能级图,现让一束单色光 照射一群处于基态的氢原子,受激发的氢原子能自发地辐射出三种不同频率的光,则照射氢原子的单色光的光子能量为( )A .13.6 eVB .12.09 eVC .10.2 eVD .3.4 eV9.远距离输送一定功率的交变电流,若输电电压提高到原来的k 倍,则下列正确的是( )A .输电导线的电功率损失不变;B .输电导线的电压损失不变;C .输电导线的电功率损失是原来的1/k 2;D .输电导线的电压损失是原来的1/k 2; 10.关于天然放射现象,叙述正确的是( )A .若使放射性物质的温度升高,其半衰期将减少B .β衰变所释放的电子是原子核外的电子电离形成的C .在α、β、γ这三种射线中,γ射线的穿透能力最强,α射线的电离能力最强D .铀核(235 92U )衰变为铅核(20682Pb)的过程中,要经过8次α衰变和10次β衰变11.如图,是一交流电压随时间变化的图象,此交流电压的有效值等于( )V A 、B 、50C 、75D 、50第6题图第3页,共4页第4页,共4页12、图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20 Ω,L1、L 2为规格相同的两只小灯泡,S1为单刀双掷开关。
上海中学、复旦附中等八校2011届高三联合调研数学理

上海八校2011届高三联合调研考试数学试题(理科)考生注意: 1.答卷前,考生务必在答题纸上将姓名、准考证号填写清楚.2.本试卷共有23道试题,满分150分.考试时间120分钟.一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分. 1. 函数21x y =+的反函数为 . 2. 平面上的点(3,4)A 绕原点顺时针旋转π2后, 所得点B 的坐标为 .3. 设m 是实数.若复数1i im +-的实部为0(i 表示虚数单位), 则m = .4. 若复数z 是方程2240x x -+=的一个根, 则||z = . 5. 在右边所示流程图中, 若输入的x 值是3, 则最后输出的n 的值为 . 6. 设m 是正实数.若椭圆2221691xym ++=的焦距为8, 则m = .7. 设k 是实数.若方程22144xyk k -=-+表示的曲线是双曲线,则k 的取值范围为 .8. 已知命题“a A ∈”是命题“132110111aa =”的充分非必要条件, 请写出一个满足条件的非空集合A , 你写的非空集合A 是 .9. 设全集U R =.若集合11A xx ⎧⎫=≥⎨⎬⎩⎭, 则U A =ð . 10.设A 是三角形的内角.若1sin cos 5A A -=, 则tan 2A = .11.设a 是实数.若函数()|||1|f x x a x =+--是定义在R 上的奇函数, 但不是偶函数, 则函数()f x 的递增区间为 .12.在数列{}n a 中, 10a ≠, 当*n N ∈时, 111n n a a n +⎛⎫=+⎪⎝⎭.数列{}n a 的前n 项和为n S , 则2limn n nS S →∞= . 13.若平面向量,a b满足||2a = , (2)12a b b +⋅=, 则||b的取值范围为 . 14.设1,,,,a b S a b c d b c cd R ⎧⎫⎛⎫⎪⎪=∈=⎨⎬⎪⎝⎭⎪⎪⎩⎭, 2,,,,0a b S a b c d a d b c c d R ⎧⎫⎛⎫⎪⎪=∈==+=⎨⎬ ⎪⎝⎭⎪⎪⎩⎭.已知矩阵2468A B ⎛⎫=+⎪⎝⎭, 其中1A S ∈, 2B S ∈.那么A B -= . 二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得 5分,否则一律得零分. 15.根据以下各组条件解三角形, 解不唯一...的是 ( ) A .60A ︒=, 75B ︒=, 1c = B .5a =, 10b =, 15A ︒=.C .5a =, 10b =, 30A ︒=.D .15a =, 10b =, 30A ︒=.16.对于数列{}n a , 如果存在正实数M , 使得数列中每一项的绝对值均不大于M , 那么称该数列为有界的, 否则称它为无界的.在以下各数列中, 无界的数列为 ( )A .12a =, 123n n a a +=-+.B .12a =, 112n n a a +=+.C .12a =, 1arctan 1n n a a +=+.D .12a =, 11n a +=.17.设,,a b k 是实数, 二次函数2()f x x ax b =++满足: (1)f k -与()f k 异号, (1)f k +与()f k 同号.在以下关于()f x 的零点的命题中, 假命题的序号为 ( )① 该二次函数的两个零点之差一定大于2; ② 该二次函数的零点都小于k ; ③ 该二次函数的零点都大于1k -.A .①②.B .②③.C .①③.D .①②③.18.将图中的正方体标上字母, 使其成为正方体1111ABC D A B C D -, 不同的标字母方式共有( )A .24种B .48种C.72种D .144种三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤. 19.(本题满分12分)已知a 是实数, 三条直线250x y -+=, 40x y a -++=, 0x a +=中任意两条的交点均不在椭圆22211x y +=上, 求a 的取值范围. 20.(本题满分12分)某学生解下面的题目时, 出现了错误.指出该学生从哪一个步骤开始犯了第一个错误, 并从该步骤开始改正他的解答.【题目】有一块铁皮零件, 它的形状是由边长为40cm 的正方形C D E F 截去一个三角形ABF 所得的五边形A B C D E , 其中A F 长等于12cm, B F 长等于10cm, 如图所示.现在需要截取矩形铁皮, 使得矩形相邻两边在,CD DE 上.请问如何截取, 可以使得到的矩形面积最大? (图中单位: cm )21.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.已知函数1π()sincossin 2222x x f x x ⎛⎫=++ ⎪⎝⎭. (1) 写出()f x 的最小正周期以及单调区间;(2) 若函数5π()cos 4h x x ⎛⎫=+⎪⎝⎭, 求函数22log ()log ()y f x h x =+的最大值, 以及使其取得最大值的x 的集合.22.(本题满分18分) 本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.可以证明, 对任意的*n N ∈, 有2333(12)12n n +++=+++ 成立.下面尝试推广该命题:(1) 设由三项组成的数列123,,a a a 每项均非零, 且对任意的{1,2,3}n ∈有23331212()n n a a a a a a +++=+++ 成立, 求所有满足条件的数列;(2)设数列{}n a 每项均非零,且对任意的*n N∈有23331212()n n a a a a a a +++=+++ 成立, 数列{}n a 的前n 项和为n S .求证:2112n n n a a S ++-=, *n N ∈;(3) 是否存在满足(2)中条件的无穷数列{}n a , 使得20122011a =-? 若存在, 写出一个这样的无穷数列(不需要证明它满足条件); 若不存在, 说明理由.23.(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.已知函数()2f x x x m =-, 常数m R ∈. (1) 设0m =.求证: 函数()f x 递增;(2) 设0m >.若函数()f x 在区间[0,1]上的最大值为2m , 求正实数m 的取值范围; (3) 设20m -<<.记1()()f x f x =, 1()(())k k f x f f x +=, *k N ∈.设n 是正整数, 求关于x 的方程()0n f x =的解的个数.。
2012学年第二学期期末试卷答案

附加题译文
• 皇上与群臣议论怎样禁止盗贼。有人请求使用 严厉的刑法来禁止他们。皇上微笑着说:“老百 姓之所以去做盗贼,是由于赋税太多,劳役、兵役 太重,官吏们又贪得无厌,老百姓吃不饱,穿不 暖,这是切身的问题,所以也就顾不得廉耻了。 我应当去掉奢侈的花费,节省开支,减轻徭役, 少收赋税,选拔和任用廉洁的官吏,让老百姓穿 的吃的都有富余,那么他们自然就不会去做盗贼 了,怎么能用严厉的刑法呢!” 从这以后,过了 几年,天下太平,没有人把别人掉在路上的东西 拾起来据为己有,大门可以不关,商人和旅客可 以露宿。
• 15、答: 我给老师吃糖,使老师感受到非 人日子里人世间爱的温暖;老师面对坎坷 的积极的人生态度,给了我生活的勇气。
• 16、D
• 17、暴雨的折磨;坐车人的冷漠 • 18、1)用柳表现风用风表现云起了层 层加深的作用。2)越写暴雨的猛烈越显 得祥子可怜。3)用恶劣的暴雨环境衬托 祥子痛苦的境遇铺陈故事情节的发展深化 小说的思想意义。 • 19、语言描写;性格特点:冷漠、缺乏 同情心、自私。社会现实:世态炎凉、人 情冷漠。
• 12、我们要为人民的利益坚持好的,为 人民的利益改正错的。 • 举例论证。
• 13、无比快乐——万分难过——羞愧难当 ——解脱轻松——鼓起勇气
14、 • 1)答: 我并不是恶作剧,真心想给老师吃颗糖, 却不知道里面是块肥皂泥。 2)答: 我以为在老师受伤的心里,又插上了一 刀,为此内心一直有“痛”(难过、愧疚)。
• 4、示例:校运会的百米短跑比赛即将开始 了。看台上,观众们将巴掌大的地方挤得 水泄不通。大家群情激昂、人声鼎沸。所 有的人都在焦急地等待枪响的一刻。
• 5、 • (1)中国烟民队伍庞大;吸烟导致死亡的 人数很多;吸烟减短人的寿命。 (2)示例:吸烟导致致命肺部疾病;吸烟 致癌;孕期吸烟危害胎儿健康;吸烟会要 你的命。 (意对即可)
2024届上海市复旦中学物理高一第二学期期末质量检测试题含解析

2024届上海市复旦中学物理高一第二学期期末质量检测试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,有的只有一项符合题目要求,有的有多项符合题目要求。
全部选对的得5分,选对但不全的得3分,有选错的得0分。
1、(本题9分)一架飞机以200 m/s的速度在高空沿水平方向做匀速直线运动,每隔1 s 先后从飞机上自由释放A、B、C三个物体,若不计空气阻力,则A.在运动过程中A在B前200 mB.在运动过程中B在C前200 mC.A、B、C在空中排列成一条竖直线D.A、B、C在空中排列成一条抛物线2、(本题9分)如图所示,绷紧的水平传送带始终以恒定速率1v运行。
初速度大小为2v 的小物块从与传送带等高的光滑水平地面上的A处滑上传送带。
若从小物块滑上传送带开始计时,小物块在传送带上运动的v t 图像(以地面为参考系)如图乙所示。
已知2v>1v,则()A.2t时刻,小物块离A处的距离达到最大B.2t时刻,小物块相对传送带滑动的距离达到最大C.0~2t时间内,小物块受到的摩擦力方向先向右后向左D.0~3t时间内,小物块始终受到大小不变的摩擦力作用3、如图所示,A、B为某小区门口自动升降杆上的两点,A在杆的顶端,B在杆的中点处. 杆从水平位置匀速转至竖直位置的过程中,A、B两点A .角速度大小之比2:lB .角速度大小之比1:2C .线速度大小之比2:lD .线速度大小之比1:24、 (本题9分)图中接地金属球A 的半径为R ,球外点电荷的电荷量为Q ,到球心的距离为r.该点电荷的电场在球心的场强大小等于( )A .B .C .0D .5、一个质量为m 的足球,以v 0速度由地面踢起,当它到达离地面高为h 的B 点处(取B 点为重力势能零参考平面,重力加速为g ),下列说法中正确的是A .在B 点重力势能为mghB .在B 点的动能为2012mv mgh + C .在B 点的机械能为2012mv mgh +D .在B 点的机械能为2012mv mgh -6、 (本题9分)如图所示,某同学用绳子拉动木箱,使它从静止开始沿粗糙水平路面运动至具有某一速度(木箱对路面的压力不为0),木箱获得的动能一定( )A .小于拉力所做的功B .等于拉力所做的功C .等于克服摩擦力所做的功D .等于合力所做的功7、质量相等的A 、B 两球在光滑水平面上沿同一直线、同一方向运动,A 球的动量是7 kg·m/s ,B 球的动量是5 kg·m/s ,当A 球追上B 球发生碰撞,则碰撞后A 、B 两球的动量可能值是( )A .p A =6 kg·m/s ,pB =6 kg·m/s B .p A =3 kg·m/s ,p B =9 kg·m/sC .p A =-2 kg·m/s ,p B =14 kg·m/sD .p A =-4 kg·m/s ,p B =17 kg·m/s8、 (本题9分)一重球从高h 处下落,如图所示,到A 点时接触弹簧,压缩弹簧至最低点位置B 。
2011~2012学年下期期末考试

2011~2012学年下期期末考试七年级语文参考答案一、(23分)1.B (2分) 2.C (2分) 3.B (2分) 4.D (2分)5.(1)去掉“一个班级”。
(2)将“是否”去掉或在“事业”后加“能否”。
6.(1)双袖龙钟泪不干此夜曲中闻折柳(2)夸父与日逐走(3)朔气传金柝,寒光照铁衣(4)宾客意少舒,稍稍正坐(5)快乐的日子将会来临。
(默写一空1分,共8分。
若出现错字、漏字、添字,该空不得分)7.(1)随着年龄的递减,喜欢戏剧的人越来越少,不喜欢戏剧的人越来越多。
(两个画线句写出一个即可得1分)(2)因为喜欢戏剧的人越来越少,如不加以保护,戏剧就会走向灭亡。
或戏剧文化是我国优秀传统文化的一个重要组成部分,保护戏剧就是保护传统文化,传承戏剧就是弘扬传统文化。
(2分,四个画线句,任答一句的意思即可给2分。
)(3)培养兴趣,让传统戏剧走进校园,开设戏剧课;经常组织孩子观看戏剧,进行戏剧表演;多组织一些义务送戏剧下乡进社区活动,扩大戏剧的影响;政府加大投入,开办戏剧学校,培养戏剧传承人等。
(只要建议合理可行,写出一条即可给2分)二、(13分)8.文章写了几个小男孩..”,“傻子”的父亲...,..通过做工作..了一个“傻子...在社区玩耍时,耍弄使孩子们改正了错误,也使“傻子”恢复..的故事。
(主要人物1分,事件..了对小朋友的信赖经过1分,事件结果“恢复信赖”1分,共3分)9.激动伤心或害怕(一空1分,共2分)10.示例一:父亲是一个聪明智慧....(或明白事理....)的人,儿子被人耍弄,他不急不躁,只是请求孩子们再陪儿子玩一次摔背,还孩子以信赖。
示例二:一个懂得用正确的方法教育引导....)的父亲。
当孩子被耍弄非常害....孩子(或懂得尊重孩子怕时,他蹲下来,耐心劝慰孩子。
(概括出父亲特点1分,加点词只答出一个即可;结合文章内容1分。
共2分,以上两个示例答出一个即可)11.(1)形象地描写了孩子们闯祸后一哄而散的情景..。
2011-2012学年第二学期初中学生学习水平综合评价参考答案

2011-2012学年第二学期初中学生学习水平综合评价九年级语文1.(3分) D A 蓬蒿. (hāo) B 颓.唐(tuí) C荣膺.(yīng)2.(3分) C A.顶礼膜拜 B.无缘无故 D.无精打采3(3分)C(随机应变:跟着情况的变化,掌握时机,灵活应付,中性词;见风转舵:比喻顺着情势改变态度,含贬义)4(3分)B(A.搭配不当,把“目光”改为“焦点”; C .语序不当,“不但”与“我区市民”对调;D. 成分残缺,应删去“通过”或“让”)5(3分)B(A.句中“人们引起了无限遐思”偷换了主语,与前文句子“作者寥寥数笔”这个主语不一致;C、D项“把四月的万种风情写尽”和“万种风情的四月被写尽”与上句的“写尽四月的百般娇媚”的句式不统一和谐。
)6(4分)(1)我区市民对垃圾分类情况认识不足。
(2分)(2)加大宣传力度,普及垃圾分类的知识。
(共2分,前后句共两点意思,答出一点得1分,意同即可)7.(10分)(1)(4分)B E(A顺序颠倒; C“俩”——“两”,缺“者”字; D“做”——“作”,“身前生后——生前身后”; F“游来”——“来游”,“苍”——“沧”)(2)(4分)(任选4题,多选则按前4题计分)①得之心而寓之酒也;②野渡无人舟自横;③江山代有才人出;④千树万树梨花开。
⑤无可奈何花落去;⑥山河破碎风飘絮。
(3)(2分)(本题有2分为附加分,加分后第7题分数累加不能超过10分。
)①长风破浪会有时,直挂云帆济沧海。
②沉舟侧畔千帆过,病树前头万木春。
评分标准:每空1分,凡错、漏、多一字,该空不得分8.(5分)(1)通“弼”辅佐(2)这种(3)您(4)做宰相(5)将近9.(3分)B即使(A:参与;时候; C:国家;国都; D:原因,缘故;旧知识)10.(3分)看出曹刿是一个小心谨慎、当机立断的谋士(1分);曹刿说“未可”的时候,是因为没掌握敌情,还不能追赶齐军(1分);说“可矣”是在掌握了敌军情况的基础上作出的判断(1分)。
2011-2012学年度第二学期期末考试试卷九年级语文

2011-2012学年度第二学期期末考试九年级语文一、基础部分(23分)弘謇中学“共此一轮明月”的语文综合性学习活动正在进行,请你参与。
(15分)〖仰望苍穹〗我喜欢夜,因为夜是深邃的眼睛,好像有着shén mì而又深奥的哲理。
无论是繁星镶嵌的夜,还是伴有圆月的夜,都会给我无限的xiá xiǎng,而窗前那一片苍穹便是我的夜的全部。
无须仰视,苍穹尽在眼前,因我正处于guān shǎng最佳之处。
1.根据拼音用正楷写出相应的汉字。
(3分)(▲▲)(▲▲)(▲▲)〖解读明月〗2.请写出下面句中加点的“月亮”的含义。
(4分)”的局面。
①张謇纪念馆的落成,改变了海门旅游景点“满天星星独缺月亮..▲。
②新时代男人应该努力像太阳一样,但女人却不一定要当月亮..▲〖登月梦近〗3.阅读下面的新闻,完成题目。
(5分)昨日,记者从国防科工局获悉,嫦娥三号预计2013年发射。
探月工程副总指挥刘东奎介绍,嫦娥三号目前处于初样研制阶段,正在进行大量试验验证工作,预计在2013年发射。
刘东奎表示,我国的探月工程分“绕、落、回”三步走。
嫦娥三号达到的主要任务是“落”,将首次实现我国探测器在地外天体着陆。
二期工程之后,将进入三期工程,实现中国探月工程“回”的任务,主要是发射无人月球探测器到月球并采样返回,现在已经论证了实施方案,并得到批准,目前正在组织实施,计划大致在2020年之前完成这项工程。
①请为上面的新闻拟写一个标题。
(2分)▲②文中的划线部分有语病,请提出修改意见。
(2分)嫦娥三号主要达到的任务是“落”,将首次实现我国探测器在地外天体着陆。
修改意见:▲③根据上面材料的信息,中国人最早什么时候可以登上月球?(1分)▲〖望月抒怀〗4.活动节目单中,诗朗诵《水调歌头明月几时有》之后是舞蹈《荷塘月色》,请你写一段简短的串词(30字左右)。
(3分)▲5.用课文原句填空。
(8分)①居高声自远,▲。
(虞世南《蝉》)②▲,病树前头万木春。
上海重点中学20112012学年下学期高二年级期

上海重点中学2011-2012学年下学期高二年级期末考试数学试卷(理科)本试卷共有23道试题,满分150分,考试时间120分钟。
一、填空题(本大题满分56分)本大题共有14题,每个空格填对得4分,否则一律得零分. 1. 抛物线2x y =的准线方程是 .2. 方程222424x xC C =的解为 . 3. 在5(31)x -的展开式中,设各项的系数和为a ,各项的二项式系数和为b ,则ab= . 4. 若圆锥的侧面展开图是半径为2、圆心角为90︒的扇形,则这个圆锥的全面积是 .5. 某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋友1本,则不同的赠送方法共有 种.6. 将4个不同的球任意放入3个不同的盒子中,则每个盒子中至少有1个球的概率为 .(结果用最简分数表示)7. 已知123F i j k =+- ,223F i j k =-+- ,3345F i j k =-+ ,若1F 、2F 、3F共同作用于一个物体上,使物体从点1M (1,-2,1)移到点2M (3,1,-2),则合力所做的功为 .8. 抛物线24y x =的准线与x 轴的交点为K ,抛物线的焦点为F ,M 是抛物线上的一点,且||2||FM FK =,则△MFK 的面积为 .9. 在圆周上有10个等分点,以这些点为顶点,每3个点可以构成一个三角形,如果随机选择了3个点,刚好构成直角三角形的概率是 .10. 如图,在由二项式系数所构成的杨辉三角形中,第_____行中从左至右第14与第15个数的比为3:2.11. 边长分别为a 、b 的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则ba的取值范围是 .12. 已知平面α截一球O 得圆M ,圆M 的半径为r ,圆M 上两点A 、B 间的弧长为2rπ,又球心O 到平面α的距离为r ,则A 、B 两点间的球面距离为 .13. 若对于任意实数x ,都有()()()()2344012342222x a a x a x a x a x =++++++++,则3a 的值为 . 14. 给n 个自上而下相连的正方形着黑色或白色. 当4n ≤时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示:由此推断,当6n =时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,选对得5分,否则一律得零分. 15. 经过原点且与抛物线23(1)4y x =+-只有一个公共点的直线有多少条? ( ) A. 0 B. 1 C. 2 D. 316. 正四面体ABCD 的表面积为S ,其中四个面的中心分别是E 、F 、G 、H .设四面体EFGH 的表面积为T ,则TS等于 ( ) A.49 B. 19 C. 14 D. 1317. 甲乙两人一起去游园,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是 ( ) A.136 B. 19 C. 536D. 1618. 给出下列四个命题:(1) 若平面α上有不共线的三点到平面β的距离相等,则//αβ; (2) 两条异面直线在同一平面内的射影可能是两条平行直线;(3) 两条异面直线中的一条平行于平面α,则另一条必定不平行于平面α; (4) a 、b 为异面直线,则过a 且与b 平行的平面有且仅有一个.其中正确命题的个数是 ( ) A. 0个 B. 1个 C. 2个 D. 3个三、解答题(本大题满分74分)本大题共5题,解答下列各题必须写出必要的步骤 . 19.(本题满分12分)已知矩形ABCD 内接于圆柱下底面的圆O ,PA 是圆柱的母线,若6AB =,8AD =,异面直线PB 与CD 所成的角为arctan 2,求此圆柱的体积.20.(本题满分14分)本题共有4个小题,第1小题满分3分,第2小题满分3分,第3小题满分4分,第4小题满分4分.m 个元素环绕在一条封闭曲线上的排列,称为环状排列.已知m 个不同元素的环状排列的所有种数为(1)!m -.请利用此结论来解决下列问题,要求列式并给出计算结果.(1)从10个不同的元素中选出8个元素的环状排列的所有种数为多少?(2)某班8个班干部中有1个班长,2个副班长,现在8个干部围坐一张圆桌讨论班级事务,则分别满足下列条件的此8人的坐法有多少种? (i )班长坐在两个副班长中间; (ii )两个副班长不能相邻而坐; (iii )班长有自己的固定座位.21.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分 .如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,2AP AB ==,4AD =,E F 、依次是PB PC 、的中点.(1)求直线EC 与平面PAD 所成的角(结果用反三角函数值表示); (2)求三棱锥P AFD -的体积.22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.如图,点P 为斜三棱柱111C B A ABC -的侧棱1BB 上一点,1BB PM ⊥交1AA 于点M ,1BB PN ⊥交1CC 于点N .(1)求证:MN CC ⊥1;(2)在任意DEF ∆中有余弦定理:DFE EF DF EF DF DE ∠⋅-+=cos 2222.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.(3)在(2)中,我们看到了平面图形中的性质类比到空间图形的例子,这样的例子还有不少.下面请观察平面勾股定理的条件和结论特征,试着将勾股定理推广到空间去.勾股定理的类比三角形ABC四面体O -ABC条件 AB ⊥AC OA 、OB 、OC 两两垂直 结论AB 2+AC 2=BC 2?请完成上表中的类比结论,并给出证明.23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.在平面直角坐标系中,O 为坐标原点. 已知曲线C 上任意一点(,)P x y (其中0x ≥)到定点(1,0)F 的距离比它到y 轴的距离大1. (1)求曲线C 的轨迹方程;(2)若过点(1,0)F 的直线l 与曲线C 相交于A 、B 不同的两点,求OA OB ⋅的值;(3)若曲线C 上不同的两点M 、N 满足0OM MN ⋅= ,求ON的取值范围.上海重点中学2011-2012学年下学期高二年级期末考试数学试卷(理科)参考答案一、填空题(本大题满分56分)1. 14y =-2. 0,2,43. 14.54π5. 106.23434439C P =7. 48. 9.1310. 3411. 1(,)2+∞12.13. -814. 21;43二、选择题(本大题满分20分) 15. D 16. B 17. D 18. C三、解答题(本大题满分74分) 19.(本题满分12分)解:设圆柱下底面圆O 的半径为r ,连AC ,由矩形ABCD 内接于圆O ,可知AC 是圆O 的直径,……2分于是210r AC =,得5r =,……………4分由AB ∥CD ,可知PBA ∠就是异面直线PB 与CD 所成的角, 即arctan 2PBA ∠=,故tan 2PBA ∠=.………………7分 在直角三角形PAB 中,tan 12PA AB PBA =∠=,…………9分 故圆柱的体积22512300V r PA =π⋅=π⨯⨯=π.……………12分 20.(本题满分14分)解:(1) 8107!226800C ⋅=----------------------3分(2-i ) 225!240P ⋅= ----------------------6分(2-ii ) 间接法:227!6!3600P -⋅=;插空法:265!3600P ⋅=----------------------10分 (2-iii ) 7!5040= ----------------------14分 21.(本题满分14分)(1)解法一:分别以AB AD AP 、、为x 轴、y 轴、z 轴建立空间直角坐标系,各点坐标分别是(0 0 0)A ,,,(2 0 0)B ,,,(2 4 0)C ,,,(0 4 0)D ,,,(0 0 2)P ,,,∴(1 0 1)E ,,,(1 2 1)F ,,, (1 4 1)EC =-,,, (2分)又∵AB ⊥平面PAD ,∴平面PAD 的法向量为(2,0,0)n AB ==, (4分)设直线EC 与平面PAD 所成的角为α,则sin ||||EC n EC n α⋅===⋅(6分) ∴直线EC 与平面PAD所成的角为. (7分)解法二:∵PA ⊥平面ABCD ,∴CD PA ⊥,又CD AD ⊥,∴CD ⊥平面PAD ,取PA 中点G ,CD 中点H ,联结EG GH GD 、、,则EG AB CD ////且1=12EG AB =,EGHC ∴是平行四边形,∴HGD ∠即为直线EC 与平面PAD 所成的角. (3分) 在Rt GAD ∆中,GD = 在Rt GHD ∆中,tan HD HGD GD ∠===, (6分)∴直线EC 与平面PAD 所成的角为. (7分) (2)解法一:由(1)解法一的建系得,(1 2 1)AF = ,,,(0 4 0)AD =,,,设平面AFD 的法向量为(,,)n x y z = ,点P 到平面AFD 的距离为d ,由0AF n ⋅= ,0AD n ⋅=得20x y z ++=且40y =,取1x =得(1,0,1)n =- ,(9分)∴AP n d n⋅=== , (11分)又AF FD ==2AFD S ==△ (13分)∴1433P AFD V -=⨯=. (14分)解法二:易证PE 即为三棱锥P AFD -底面上的高,且PE = (11分)底面AFD △边AD 上的高等于AE ,且AE =AFD S =△(13分)1144323P AFD V -=⨯⨯=. (14分)解法三:依题意,//EF 平面PAD ,∴P AFD F PAD E PAD D PAE V V V V ----=== (11分)11114224322123D PAE V PA AB AD -=⨯⨯⨯⨯⨯=⨯⨯⨯=. (14分) 22.(本题满分16分)(1)证:MN CC PMN CC PN CC PM CC BB CC ⊥⇒⊥∴⊥⊥⇒111111,,//平面 ;(4分)(2)解:在斜三棱柱111C B A ABC -中,有αcos 21111111111222A ACC B BCC A ACC B BCC A ABB S S S S S ⋅-+=,其中α为平面B B CC 11与平面A A CC 11所组成的二面角.(7分)∴⊥,1PMN CC 平面 上述的二面角为MN P ∠,在PMN ∆中,2222cos PM PN MN PN MN MNP =+-⋅∠⇒MNP CC MN CC PN CC MN CC PN CC PM ∠⋅⋅⋅-+=cos )()(211111222222,由于111111111,,BB PM S CC MN S CC PN S A ABB A ACC B BCC ⋅=⋅=⋅=,∴有αcos 21111111111222A ACC B BCC A ACC B BCC A ABB S S S S S ⋅-+=. (10分) (3)空间勾股定理的猜想:已知四面体O -ABC 的三条侧棱OA 、OB 、OC 两两垂直,则有2222OAB OAC OBC ABC S S S S ∆∆∆∆++=.(13分) 证法一:作OD ⊥AB ,垂足为D ,连结CD22222222221111()4444ABCS AB CD AB OC OD AB OC AB OD ∆=⋅⋅=⋅⋅+=⋅⋅+⋅⋅ 222222222222111()444AOB AOB AOC COB AOB OA OB OC S OA OC OB OC S S S S ∆∆∆∆∆=⋅+⋅+=⋅⋅+⋅⋅+=++ (16分) 证法二:作OH ⊥平面ABC ,垂足为H ,易得H 为△ABC 的垂心。
2012年七年级(下)期末教学质量监测数学试题(含答案)

2011-2012学年度下学期期终教学质量监测七年级数学试题.1. 下列运算正确的是()A.22aaa=⋅B.33)(abab=C.632)(aa=D.5210aaa=÷2.下列事件属于必然事件的是()A.投出铅球后,经过一段时间铅球会落地B.明天我市最高气温为56℃C.中秋节晚上能看到月亮D.下雨后有彩虹出现3.在平面直角坐标系中,点P(-2,2x+1)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限4.方程组⎩⎨⎧=+=-422yxyx的解是( )A.⎩⎨⎧==21yxB.⎩⎨⎧==13yxC.⎩⎨⎧-==2yxD.⎩⎨⎧==2yx5. 若一个三角形三个内角度数的比为2︰7︰4,那么这个三角形是()A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等边三角形6.如图,已知AB∥CD, 则图中与∠1互补的角有()A.2个B.3 个C.4 个D.5个7. 已知三角形的两边分别为4和9,则此三角形的第三边可能是()A. 4B. 5C.9D.138.下列说法正确的是()A.在一次抽奖活动中,“中奖的概率是1100”表示抽奖100次就一定会中奖B.随机抛一枚硬币,落地后正面一定朝上C.同时掷两枚均匀的骰子,朝上一面的点数和为6D.在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是1139.在平面直角坐标系中,点A (2,3)与点B 关于x 轴对称,则点B 的坐标为( ). A.(3,2) B.(-2,-3) C.(-2,3) D.(2,-3) 10.)104.0()103.0()10(52⨯⋅⨯-⋅-等于( ) A .8102.1⨯ B .71012.0⨯-C .7102.1⨯D .81012.0⨯-11.一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( ) A.5个 B.6个 C.7个 D.8个 12.下列说法正确的是( )A.三角形中最小的锐角一定小于600 ;B.直角三角形的高线只有一条;C.在同圆中任意两条直径都相互平分;D. 长度相等的两条弧叫做等弧 13. 如图,直线AB ∥CD ,∠A =70︒,∠C =40︒,则∠E 等于( ) A .30°B .40°C .60°D .70°14. 下列说法正确的是( )A.一个角的补角一定大于它本身,B. 一个角的余角一定小于它本身C. 一个钝角减去一个锐角的差一定是一个锐角,D.同角的补角相等15.计算()201220110221-(-⨯--)π的结果是( ).A .-2B .-1C . 2D .3二、填空题:将结果直接填写在每题的横线上.16. 一个角的补角比这个角的余角的2倍还大180,则这个角的度数为 .17. 如果从多边形的一个顶点出发可以引5条对角线,那么这个多边形的内角和为 .18. 如图,已知CD 平分∠ACD ,DE ∥AC ,∠1=30°,则∠2= 度.19. 方程4320x y +=的所有非负整数解为: .20. 如果点Q (m +2,m -1)在直角坐标系的x 轴上,则点Q 的坐标为 . 21.如图,用代数式表示阴影部分面积为 .A C BDE三、解答题(本大题共7个小题)22.计算1.3222)()(ab b a2. )21)(43)(32(222z xy z yz x --3. )4.03.0)(2.01.0(n m n m +-4.2)2(b a -23. 从-2,-1,2这三个数中任取两个不同的数作为点的坐标,求该点在第四象限的概率是多少?24.尺规作图(保留作图痕迹,不写作法)已知:线段a 、b (a >b ),求作△ABC ,使AB =AC =a ,BC =2b25. 先化简,再求值.(3a +1)(2a -3)-(6a -5)(a -4),其中a =-2.ab26. 某工程队在“村村通”工程中,用8天的时间修筑了一条爱心路,如图是修筑的公路长度y(米)与时间x(天)之间的关系图象.根据图象提供的信息,求爱心路的长度.27. 小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?28. 把地球的赤道近似地看做一个圆,如果环绕地球赤道有一个同心圆,它的周长比赤道仅多出10米,小博士(身高:157厘米)告诉同学们,她可以绕着赤道转一圈,而头却碰不到外面的圆,你相信吗?试用学过的知识加以说明.(π取3.14)参考答案一、选择题: 每小题3分,满分45分二、填空题:每小题3分,满分18分 16.18° 17.1080° 18. 60° 19.⎩⎨⎧==42y x ,⎩⎨⎧==05y x 20. (3,0)21. 2c bc ac -+三、解答题(本大题共7个小题,满分57分)22.(每小题3分,本题满分12分,缺少必要的步骤酌情减分)1. 87b a 2.43341z y x 3. 2208.002.003.0n mn m -- 4. 2)2(b a -=222244)2(22)2)(2(b ab a b ab ab a b a b a +-=-+--=--23.(本题满分6分)解:从-2,-1,2这三个数中任取两个不同的数作为点的坐标,所有可能的结果数为6,即(-2,-1),(-2,2),(-1,-2),(-1,2),(2,-2),(2,-1)……2分这些点中在第四象限的有两个,即(2,-2),(2,-1),………………………4分所以P (点在第四象限)3162==………………………………………………6分 24(本题满分6分,每做出一条边得2分).略 25.(本题满分6分)原式=205246329622-++--+-a a a a a a =2322-a ………………4分 当2-=a 时,6723)2(222322-=--=-a ………………………………6分 26(本题满分9分)解:设两点(2,180)(4,288)所在直线为b kx y +=,…………1分则可得方程组⎩⎨⎧=+=+28841802b k b k ,…………………………………………4分解这个方程组得⎩⎨⎧==7254b k ,………………………………………………6分所以7254+=x y ,………………………………………………………7分 当8=x 时,50472854=+⨯=y ,……………………………………8分答:这条爱心路长504米……………………………………………………9分. 注;其它做法,只要合理均得分,如以下方法:,54)24()180288(=-÷- 324)28(54=-⨯,504180324=+27(本题满分10分)解:设平路有x 米,坡路有y 米,………………………………………………2分 根据题意得10,608015.6040x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩…………………………………………………………………6分 解这个方程组,得300,400.x y =⎧⎨=⎩所以x +y =700.…………………………9分所以小华家离学校700米.………………………………………………………10分28(本题满分8分) 解:相信.设地球赤道的周长C ,因为赤道与环绕赤道的圆是同心圆, 所以两个圆的半径之差为59.12102210≈=-+πππC C (米), 因为59.1米>57.1米,所以我相信小博士的话. (也可参考教材164页例2解答)。
【3套打包】上海复旦实验中学最新七年级下册数学期末考试试题(含答案)

新人教版七年级第二学期下册期末模拟数学试卷(含答案)一.选择题:每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题意的,把所选项前的字母代号填在答题栏内.相信你一定能选对!1.(3分)在下列方程中3x﹣1=5,xy=1,x﹣=6,(x+y)=7,x﹣y2=0,二元一次方程的个数是()A.1个B.2个C.3个D.4个2.(3分)在式子:3x﹣y=6中,把它改写成用含x的代数式表示y,正确的是()A.y=3x﹣6B.y=3x+6C.x=y+2D.x=﹣y+2 3.(3分)下列调查:①调查某批次汽车的抗撞击能力;②了解某班学生的体重情况;③调查春节联欢晚会的收视率;④选出某校短跑最快的学生参加全市比赛.其中适宜抽样调查的是()A.①②B.①③C.②③D.②④4.(3分)我们可以用图示所示方法过直线a外的一点P折出直线a的平行线b,下列判定不能作为这种方法依据的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.同旁内角互补,两直线平行D.平行于同一条直线的两条直线互相平行5.(3分)若2x|k|+(k﹣1)y=3是关于x,y的二元一次方程,则k的值为()A.﹣1B.1C.1或﹣1D.06.(3分)(教材变式题)用加减法解方程组解题步骤如下:(1)①﹣②,得12y=﹣36,y=﹣3(2)①×5+②×7,得96x=12,x=,下列说法正确的是()A.步骤(1),(2)都不对B.步骤(1),(2)都对C.此题不适宜用加减法D.加减法不能用两次7.(3分)“黑发不知勤学早,白首方悔读书迟.”2018年扬州市教育局正式发布《关于大力倡导实施“五个一百工程”的指导意见》,为了了解某校八年级500名学生对“五个一百工程”的知晓情况,从中随机抽取了50名学生进行调查,在这次调查中,样本是()A.500名学生B.所抽取的50名学生对“五个一百工程”的知晓情况C.50名学生D.每一名学生对“五个一百工程”的知晓情况8.(3分)若m>n,则下列各式中一定成立的是()A.m﹣2>n﹣2B.m﹣5<n﹣5C.﹣2m>﹣2n D.4m<4n9.(3分)不等式组的解集在数轴上表示正确的是()A.B.C.D.10.(3分)如图,在一个单位面积为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,点A2019的横坐标为()A.1010B.﹣1010C.1008D.﹣1008二.填空题:共5小题,每小题3分,共15分.11.(3分)已知3x2m﹣2y n=1是关于x、y的二元一次方程,则mn=.12.(3分)在平面直角坐标系中,第四象限内的点P到x轴的距离是3,到y轴的距离是4,则点P坐标为.13.(3分)若点P(1﹣m,m)在第一象限,则(m﹣1)x>1﹣m的解集为.14.(3分)样本的50个数据分别落在4个组内,第1、2、4组数据的个数分别是6、12、22,则落在第3组的频数是.15.(3分)某商场店庆活动中,商家准备对某种进价为600元、标价为1100元的商品进行打折销售,但要保证利润率不低于10%,则最低折扣是.三.解答题:本题有7小题,共55分,只要你认真审题,细心运算,一定能解答正确!解答应写出文字说明、证明过程或推演过程.16.(7分)计算:(1)+﹣22(2)﹣23﹣(﹣2)×(﹣)+(﹣+)×(﹣24)17.(8分)解方程组(1)(用代入消元法)(2)(用加减消元法)18.(7分)已知:如图,线段AC和BD相交于点G,连接AB,CD,E是CD上一点,F 是DG上一点,FE∥CG,且∠1=∠A.(1)求证:AB∥DC;(2)若∠B=30°,∠1=65°,求∠EFG的度数.19.(7分)已知2a﹣3x+1=0,3b﹣2x﹣16=0(1)用含x的代数式分别表示a,b;(2)当a≤4<b时,求x的取值范围.20.(8分)贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:(1)本次接受调查的观众共有人;(2)扇形统计图中,扇形C的圆心角度数是.(3)请补全条形统计图;(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.21.(9分)为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.(1)求A、B两种车型各有多少个座位?(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B 型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.22.(9分)阅读材料:基本不等式≤(a>0,b>0),当且仅当a=b时,等号成立.其中我们把叫做正数a、b的算术平均数,叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.例如:在x>0的条件下,当x为何值时,x+有最小值,最小值是多少?解:∵x>0,>0∴≥即是x+≥2∴x+≥2当且仅当x=即x=1时,x+有最小值,最小值为2.请根据阅读材料解答下列问题(1)若x>0,函数y=2x+,当x为何值时,函数有最值,并求出其最值.(2)当x>0时,式子x2+1+≥2成立吗?请说明理由.2018-2019学年山东省济宁市金乡县七年级(下)期末数学试卷参考答案与试题解析一.选择题:每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题意的,把所选项前的字母代号填在答题栏内.相信你一定能选对!1.【解答】解:在下列方程中3x﹣1=5(否),xy=1(否),x﹣=6(否),(x+y)=7(是),x﹣y2=0(否),二元一次方程的个数是1个,故选:A.2.【解答】解:3x﹣y=6,﹣y=6﹣3x,y=3x﹣6,故选:A.3.【解答】解:①调查某批次汽车的抗撞击能力,适合抽样调查,符合题意;②了解某班学生的体重情况,适合全面调查,不符合题意;③调查春节联欢晚会的收视率,适合抽样调查,符合题意;④选出某校短跑最快的学生参加全市比赛,适合全面调查,不符合题意;故选:B.4.【解答】解:如图,由折叠可得,∵∠BPC=∠ADP=90°,∴a∥b,故A选项能作为这种方法依据;∵∠EPD=∠ADP=90°,∴a∥b,故B选项能作为这种方法依据;∵∠BPD+∠ADP=180°,∴a∥b,故C选项能作为这种方法依据;∵a⊥CD,b⊥CD,∴a∥b(同一平面内,垂直于同一条直线的两条直线互相平行),故D选项不能作为这种方法依据;故选:D.5.【解答】解:由题意知:|k|=1,k﹣1≠0,解得k=﹣1.故选:A.6.【解答】解:因为在解方程组时并不限制加减消元法使用的次数,所以D显然错误;由于两方程中x的系数相等,故适合用加减法,故C错误;①﹣②,得12y=﹣36,y=﹣3,正确,故A错误;故选:B.7.【解答】解:样本是所抽取的500名学生对“五个一百工程”的知晓情况,.故选:B.8.【解答】解:∵m>n,∴m﹣2>n﹣2,m﹣5>n﹣5,﹣2m<﹣2n,4m>4n,故选:A.9.【解答】解:由2x>3x﹣1,解得x<1,x≤1,解得x≤4,∴不等式组的解集为x<1,故选:A.10.【解答】解:观察图形可以看出A1﹣﹣A4;A5﹣﹣﹣A8;...每4个为一组,∵2019÷4=504 (3)∴A2019在x轴负半轴上,纵坐标为0,∵A3、A7、A11的横坐标分别为0,﹣2,﹣4,∴A2019的横坐标为﹣(2019﹣3)×=﹣1008.∴A2019的横坐标为﹣1008.故选:D.二.填空题:共5小题,每小题3分,共15分.11.【解答】解:∵3x2m﹣2y n=1是关于x、y的二元一次方程,∴2m=1,n=1,∴m=0.5,∴mn=0.5×1=0.5,故答案为:0.5.12.【解答】解:∵点P在第四象限且到x轴的距离是3,到y轴的距离是4,∴点P的横坐标为4,纵坐标为﹣3,∴点P的坐标是(4,﹣3).故答案为:(4,﹣3).13.【解答】解:∵点P(1﹣m,m)在第一象限,∴1﹣m>0,即m﹣1<0;∴不等式(m﹣1)x>1﹣m,∴(m﹣1)x>﹣(m﹣1),不等式两边同时除以m﹣1,得:x<﹣1,故答案为:x<﹣1.14.【解答】解:第3组数据的频数:50﹣6﹣12﹣22=10,故答案为:10.15.【解答】解:设可以打x折1100x﹣600≥600×10%解得x≥60%,即最低折扣是6折.故答案为:6折.三.解答题:本题有7小题,共55分,只要你认真审题,细心运算,一定能解答正确!解答应写出文字说明、证明过程或推演过程.16.【解答】解:(1)原式=﹣5+9﹣4=0;(2)原式=﹣8﹣+20﹣9=2.17.【解答】解:(1),由①得:x=4+y,③,把③代入②得:4(4+y)+2y=﹣1,解得:y=;把y=代入①得:x=,∴二元一次方程组的解为;(2)由①×2﹣②得:15x=30,解得:x=2,把x=2代入②得:3×2+4y=10,解得:y=1,∴二元一次方程组的解为,18.【解答】解:(1)∵FE∥CG,∴∠1=∠C,又∵∠1=∠A,∴∠C=∠A,∴AB∥DC;(2)∵AB∥DC,∴∠D=∠B=30°,∵∠1=65°,∴∠EFG=∠D+∠1=30°+65°=95°.19.【解答】解:(1)由2a﹣3x+1=0,得a=,由3b﹣2x﹣16=0,得b=;(2)∵a≤4<b,∴a=≤4,b=>4,解得:﹣2<x≤3.20.【解答】解:(1)由条形统计图可知,A类人数是60人,由扇形统计图可知,A类人数所占的百分比为60%,则本次接受调查的观众人数为:60÷60%=100(人),故答案为:100;(2)扇形C的圆心角度数为:360°××100%=54°,故答案为:54°;(3)C类人数为:100﹣60﹣20﹣5=15(人),补全条形统计图如图所示;(4)观众中对该电影满意的人数为:3000×=2850(人).21.【解答】解:(1)设每辆A型车有x个座位,每辆B型车有y个座位,依题意,得:,解得:.答:每辆A型车有45个座位,每辆B型车有60个座位.(2)设租m辆A型车,n辆B型车,依题意,得:45m+60n=480,解得:n=8﹣m.∵m,n为整数,∴(舍去),,,∴有两种租车方案,方案1:租4辆A型车、5辆B型车;方案2:租8辆A型车、2辆B型车.当租4辆A型车、5辆B型车时,所需费用为350×4+400×5=3400(元),当租8辆A型车、2辆B型车时,所需费用为350×8+400×2=3600(元).∵3400<3600,∴租4辆A 型车、5辆B 型车所需租金最少,最少租金为3400元. 22.【解答】解:(1)∵x >0, ∴2x >0, ∴2x +≥2=2,当且仅当2x =即x =时,2x +有最小值,最小值为2.(2)式子不成立. 理由:∵x >0, ∴x 2+1>0,>0,∴x 2+1+≥2=2,当且仅当x 2+1=即x =0时,不等式成立,∵x >0,∴不等式不能取等号,即不成立.最新七年级(下)数学期末考试题【答案】一、选择题(共10小题,每小题3分,满分30分) 1.下列实数中,属于无理数的是( )A 、227B 、3.14CD 、0 答案:C2.下面调查中,适宜采用全面调查方式的是( ) A 、调查某批次汽车的抗撞击能力 B 、调查市场上某种食品的色素含量是否符合国家标准C 、了解某班学生的视力情况D 、调查春节联欢晚会的收视率 答案:C3.如图,直线a ∥b ,直角三角形的直角顶点在直线b 上,已知∠1=48°,则∠2的度数是( )A 、42°B 、52°C 、48°D 、58° 答案:A4.若m >n ,则下列不等式变形错误的是( ) A 、m ﹣5>n ﹣5 B 、6m >6n C 、﹣3m >﹣3n D 、21m x +>21nx + 答案:C 5.方程组3759y x x y =+⎧⎨+=⎩的解是( )A 、1272x y ⎧=⎪⎪⎨⎪=⎪⎩B 、1252x y ⎧=-⎪⎪⎨⎪=⎪⎩ C 、41x y =-⎧⎨=-⎩ D 、21x y =⎧⎨=-⎩ 答案:B6.点A 在第二象限,且距离x 轴2个单位长度,距离y 轴4个单位长度,则点A 的坐标是( )A 、(﹣4,2)B 、(﹣2,4)C 、(4,﹣2)D 、(2,﹣4) 答案:A7.如图所示,下列条件中,不能判断AD ∥BC 的是( )A 、∠1=∠4B 、∠3=∠4C 、∠2+∠3=180°D 、∠1+∠D =180° 答案:A8.将正整数依次按下表规律排列,则数2009应排的位置是第__行第__列A 、第669行第2列B 、第669行第3列C 、第670行第2列D 、第670行第3列 答案:D9.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?设合伙人数为x 人,羊价为y 钱,根据题意,可列方程组为( ) A 、54573y x y x =+⎧⎨=+⎩ B 、54573y x y x =-⎧⎨=+⎩ C 、54573y x y x =+⎧⎨=-⎩ D 、54573y x y x =-⎧⎨=-⎩答案:A10.若关于x 的不等式6234x xa x x +<+⎧⎪⎨+>⎪⎩有且只有四个整数解,则实数a 的取值范围是( )A 、6<a ≤7B 、18<a ≤21C 、18≤a <21D 、18≤a ≤21 答案:B ;二、填空题(共6小题,每小题3分,共18分) 11的值是 . 答案:312.如图,已知直线AB ,CD 相交于点O ,OA 平分∠EOC ,∠EOC =70°,则∠BOD 的度数等于 度.答案:3513.将点P(a+1,﹣2a)向上平移2个单位得到的点在第一象限,则a的取值范围是.答案:﹣1<a<114.来自某综合市场财务部的报告表明,商场2014年1﹣4月份的投资总额一共是2017万元,商场2014年第一季度每月利润统计图和2014年1﹣4月份利润率统计图如下(利润率=利润÷投资金额).则商场2014年4月份利润是万元.答案:12315.在关于x,y的方程组:①841ax ybx y+=⎧⎨+=-⎩:②(1)8(1)41a x yb x y--=⎧⎨--=-⎩中,若方程组①的解是31xy=⎧⎨=-⎩,则方程组②的解是.答案:41 xy=⎧⎨=⎩16.已知:a、b、c是三个非负数,并且满足3a+2b+c=5,2a+b﹣3c=1,设m=3a+b﹣7c,设s为m的最大值,则s的值为.答案:-1 11三.(解答题,共8小题,共72分)17.(8分)解方程组:4421 x yx y-=⎧⎨+=-⎩.解:化为:228421x y x y -=⎧⎨+=-⎩,解得:76176x y ⎧=⎪⎪⎨⎪=-⎪⎩18.(8分)解不等式组,并把解集在数轴上表示出来:3(2)41213x x xx --≥⎧⎪+⎨>-⎪⎩ 解:由(1)得:x ≤1,由(2)得:x <4, 解集为:x ≤1,数轴上表示如下:19.(8分)某校有1000名学生,小明想了解全校学生每月课外阅读书籍的数量情况,随机抽取了部分学生,得到如统计图(1)一共抽查了多少人?(2)每月课外阅读书籍数量是1本的学生对应的圆心角度数是? (3)估计该校全体学生每月课外阅读书籍的总量大约是多少本? 解:(1)一共抽查了:2222%=100(人); (2)每月课外阅读书籍数量是1本的学生比例:30100=30%, 对应的圆心角为30360100⨯︒=108° (3)每月课外阅读书籍数量是2本的学生比例:1-0.22-0.30=48%, 总量:30%×1000×1+48%×1000×2+22%×1000×3=1920(本) 20.(8分)完成下面证明如图,AB 和CD 相交于点O ,∠A =∠D ,OE ∥AC 且OE 平分∠BOC求证:AC∥BD证明:∵OE∥AC∠A=()OE平分∠BOC∠1=∠2()∠A=∠D()∠D=()OE∥()AC∥BD()解:∠1;两直线平行同位角相等;角平分线的定义;已知;∠2;等量代换;BD;同位角相等两直线平行;平行于同一直线的两条直线平行;21.(8分)如图,在边长为1的正方形网格中,A(2,4),B(4,1),C(﹣3,4)(1)平移线段AB到线段CD,使点A与点C重合,写出点D的坐标.(2)直接写出线段AB平移至线段CD处所扫过的面积.(3)平移线段AB,使其两端点都在坐标轴上,则点A的坐标为.解:(1)D(-1,1)(2)15(3)(0,3)或(﹣2,0);22.(10分)某木板加工厂将购进的A 型、B 型两种木板加工成C 型,D 型两种木板出售,已知一块A 型木板的进价比一块B 型木板的进价多10元,且购买2块A 型木板和3块B 型木板共花费220元.(1)A 型木板与B 型木板的进价各是多少元?(2)根据市场需求,该木板加工厂决定用不超过8780元购进A 型木板、B 型木板共200块,若一块A 型木板可制成2块C 型木板、1块D 型木板;一块B 型木板可制成1块C 型木板、2块D 型木板,且生产出来的C 型木板数量不少于D 型木板的数量的1113. ①该木板加工厂有几种进货方案?②若C 型木板每块售价30元,D 型木板每块售价25元,且生产出来的C 型木板、D 型木板全部售出,哪一种方案获得的利润最大,求出最大利润是多少? 解:(1)设A 型木板与B 型木板的进价各是x ,y 元,则有1023220x y x y ⎧⎨+=⎩-=,解得:5040x y =⎧⎨=⎩, 所以,A 型木板的进价是50元, B 型木板的进价是40元。
复旦大学2011~2012学年《高等数学A下》第二学期期末考试试卷及答案

复旦大学数学科学学院2011~2012学年第二学期期末考试试卷A 卷数学科学学院1.(本题满分42分,每小题7分)计算下列各题: (1)设4yx yx z -+=,求dz 。
(2)求曲线1)32()12(22=+++++y x y x 所围有界区域的面积。
(装 订 线 内 不 要 答 题 )(3)计算三重积分⎰⎰⎰Ω+dxdydz y x )(22,其中Ω为抛物面22y x z +=与平面hz =(0>h )所围的有界闭区域。
(4)计算第一类曲面积分⎰⎰∑dS y 2,其中∑是球面2222a z y x =++(0>a )。
(5)求幂级数∑∞=+1!1n nx n n 的和函数。
(6)求微分方程y x y xdx dy =-4(0>x ,0>y )的通解。
2.(本题满分8分)求函数222),,(z y x z y x f ++=在条件1=++cz by ax 下的最小值,其中a ,b ,c 为常数。
3.(本题满分10分)确定常数λ,使得右半平面}0|),({>x y x 上的向量值函数i r λ)(2),(24y x xy y x +=j λ)(242y x x +-为某二元函数),(y x u 的梯度,并求),(y x u 。
4.(本题满分10分)计算第二类曲面积分⎰⎰∑-+-zxdxdy xydzdx dydz x 48)1(22,其中∑是由Oxy 平面上的曲线2y e x =(10≤≤y )绕x 轴旋转一周而成的旋转曲面,且该曲面的法向量与x 轴正向的夹角不小于2π。
5.(本题满分10分)设)(x y n 是定解问题⎪⎩⎪⎨⎧='==--0)1(,0)1(,122y y x dxdyndx y d x n 的解( ,3,2=n )。
(1)求)(x y n ( ,3,2=n );(2)问级数∑∞=2ln )0(n n n y 是否收敛?请说明理由。
6.(本题满分12分)设πϕ<<0。
上海复旦初级中学人教版七年级下学期期末数学试题

下海复旦初级中学人教版七年级下学期期末数学试题一、选择题1.12-等于()A.2-B.12C.1 D.12-2.如图,P1是一块半径为1的半圆形纸板,在P1的右上端剪去一个直径为1的半圆后得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪去的半圆的半径)得到图形P3、P4…P n…,记纸板P n的面积为S n,则S n-S n+1的值为( )A.12nπ⎛⎫⎪⎝⎭B.14nπ⎛⎫⎪⎝⎭C.2112nπ+⎛⎫⎪⎝⎭D.2112nπ-⎛⎫⎪⎝⎭3.已知方程组5430x yx y k-=⎧⎨-+=⎩的解也是方程3x-2y=0的解,则k的值是()A.k=-5 B.k=5 C.k=-10 D.k=10 4.下列各组数中,是二元一次方程5x﹣y=4的一个解的是()A.31xy=⎧⎨=⎩B.11xy=⎧⎨=⎩C.4xy=⎧⎨=⎩D.13xy=⎧⎨=⎩5.足球比赛中,每场比赛都要分出胜负每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为x负的场数为y,则可列方程组为()A.8312x yx y+=⎧⎨-=⎩B.8312x yx y-=⎧⎨-=⎩C.18312x yx y+=⎧⎨+=⎩D.8312x yx y-=⎧⎨+=⎩6.下列图形中,能将其中一个三角形平移得到另一个三角形的是()A.B.C.D.7.下列运算正确的是()A.a2+a2=a4B.(﹣b2)3=﹣b6C.2x•2x2=2x3D.(m﹣n)2=m2﹣n28.下列图形中,∠1和∠2是同位角的是()A.B.C.D.9.若一个多边形的每个内角都等于与它相邻外角的2倍,则它的边数为()A .4B .5C .6D .810.已知x ay b=⎧⎨=⎩是方程组24213x y x y -=⎧⎨+=⎩的解,则32a b -的算术平方根为( )A .4±B .4C .2D .2±二、填空题11.若a m =5,a n =3,则a m +n =_____________. 12.已知:()521x x ++=,则x =______________.13.若x +3y -4=0,则2x •8y =_________.14.已知()4432234464a b a a b a b ab b +=++++,则()4a b -=__________.15.一个多边形的内角和与外角和之差为720︒,则这个多边形的边数为______. 16.已知某种植物花粉的直径为0.00033cm ,将数据0.00033用科学记数法表示为 ________________.17.PM2.5是指大气中直径小于或等于0.0000025m 的颗粒物,将0.0000025用科学计数法表示为________________.18.已知x 2+2kx +9是完全平方式,则常数k 的值是____________.19.某校七年级社会实践小组去商场调查商品的销售情况,了解到该商场以每件80元的价格购进某品牌衬衫500件,并以每件120元的价格销售400件.该商场准备采取促销措施,将剩下的衬衫降价销售,每件衬衫至多降价______元,销售完这批衬衫才能达到盈利45%的预期目标.20.已知点m (3a -9,1-a ),将m 点向左平移3个单位长度后落在y 轴上,则a= __________ .三、解答题21.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC 的三个顶点的位置如图所示.现将△ABC 平移,使点C 变换为点D ,点A 、B 的对应点分别是点E 、F . (1)在图中请画出△ABC 平移后得到的△EFD ; (2)在图中画出△ABC 的AB 边上的高CH ; (3)△ABC 的面积为_______.22.先化简,再求值:(3x +2)(3x -2)-5x (x +1)-(x -1)2,其中x 2-x -10=0.23.如图,直线MN ∥GH ,直线l 1分别交直线MN 、GH 于A 、B 两点,直线l 2分别交直线MN 、GH 于C 、D 两点,且直线l 1、l 2交于点E ,点P 是直线l 2上不同于C 、D 、E 点的动点.(1)如图①,当点P 在线段CE 上时,请直写出∠NAP 、∠HBP 、∠APB 之间的数量关系: ;(2)如图②,当点P 在线段DE 上时,(1)中的∠NAP 、∠HBP 、∠APB 之间的数量关系还成立吗?如果成立,请说明成立的理由;如果不成立,请写出这三个角之间的数量关系,并说明理由.(3)如果点P 在直线l 2上且在C 、D 两点外侧运动时,其他条件不变,请直接写出∠NAP 、∠HBP 、∠APB 之间的数量关系 .24.己知关于,x y 的方程组4325x y a x y a -=-⎧⎨+=-⎩,(1)请用a 的代数式表示y ;(2)若,x y 互为相反数,求a 的值.25.如图1,在△ABC 的AB 边的异侧作△ABD ,并使∠C =∠D ,点E 在射线CA 上. (1)如图,若AC ∥BD ,求证:AD ∥BC ; (2)若BD ⊥BC ,试解决下面两个问题: ①如图2,∠DAE =20°,求∠C 的度数;②如图3,若∠BAC =∠BAD ,过点B 作BF ∥AD 交射线CA 于点F ,当∠EFB =7∠DBF 时,求∠BAD 的度数.26.已知a +a 1-=3, 求(1)a 2+21a(2)a 4+41a 27.计算: (1)022019()32020-- (2)4655x x x x ⋅+⋅28.先化简,再求值:(1)()()()462a a a a --+-,其中12a =-; (2)2(x 2)(2x 1)(2x 1)4x(x 1)+++--+,其中13x =.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】由题意直接根据负指数幂的运算法则进行分析计算即可. 【详解】 解: 12-=12. 故选:B. 【点睛】本题考查负指数幂的运算,熟练掌握负指数幂的运算法则是解题的关键.2.C解析:C 【分析】首先分析题意,找到规律,并进行推导得出答案. 【详解】 根据题意得,n ≥2, S 1=12π×12=12π, S 2=12π﹣12π×(12)2, … S n =12π﹣12π×(12)2﹣12π×[(12)2]2﹣…﹣12π×[(12)n ﹣1]2, S n +1=12π﹣12π×(12)2﹣12π×[(12)2]2﹣…﹣12π×[(12)n ﹣1]2﹣12π×[(12)n ]2, ∴S n ﹣S n +1=12π×(12)2n =(12)2n +1π. 故选C .【点睛】考查学生通过观察、归纳、抽象出数列的规律的能力.3.A解析:A【分析】根据方程组5430x yx y k-=⎧⎨-+=⎩的解也是方程3x-2y=0的解,可得方程组5320x yx y-=⎧⎨-=⎩,解方程组求得x、y的值,再代入4x-3y+k=0即可求得k的值.【详解】∵方程组5430x yx y k-=⎧⎨-+=⎩的解也是方程3x-2y=0的解,∴5320x yx y-=⎧⎨-=⎩,解得,1015xy=-⎧⎨=-⎩;把1015xy=-⎧⎨=-⎩代入4x-3y+k=0得,-40+45+k=0,∴k=-5.故选A.【点睛】本题考查了解一元二次方程,根据题意得出方程组5320x yx y-=⎧⎨-=⎩,解方程组求得x、y的值是解决问题的关键.4.B解析:B【分析】把x与y的值代入方程检验即可.【详解】解:A、把31xy=⎧⎨=⎩代入得:左边=15﹣1=14,右边=4,∵左边≠右边,∴31xy=⎧⎨=⎩不是方程的解;B、把11xy=⎧⎨=⎩代入得:左边=5﹣1=4,右边=4,∵左边=右边,∴11xy=⎧⎨=⎩是方程的解;C、把4xy=⎧⎨=⎩代入得:左边=0﹣4=﹣4,右边=4,∵左边≠右边,∴4xy=⎧⎨=⎩不是方程的解;D、把13xy=⎧⎨=⎩代入得:左边=5﹣3=2,右边=4,∵左边≠右边,∴13xy=⎧⎨=⎩不是方程的解,故选:B.【点睛】本题主要考查了二元一次方程的解的知识点,准确代入求职是解题的关键.5.A解析:A【分析】设这个队胜x场,负y场,根据在8场比赛中得到12分,列方程组即可.【详解】解:设这个队胜x场,负y场,根据题意,得8 312 x yx y+=⎧⎨-=⎩.故选:A.【点睛】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.6.A解析:A【解析】【分析】利用平移的性质,结合轴对称、旋转变换和位似图形的定义判断得出即可.【详解】A、可以通过平移得到,故此选项正确;B、可以通过旋转得到,故此选项错误;C、是位似图形,故此选项错误;D、可以通过轴对称得到,故此选项错误;故选A.【点睛】本题考查了平移的性质以及轴对称、旋转变换和位似图形,正确把握定义是解题的关键.7.B解析:B 【分析】根据合并同类项法则、幂的乘方法则、单项式乘单项式法则和完全平方公式法则解答即可. 【详解】A 、a 2+a 2=2a 2,故本选项错误;B 、(﹣b 2)3=﹣b 6,故本选项正确;C 、2x •2x 2=4x 3,故本选项错误;D 、(m ﹣n )2=m 2﹣2mn +n 2,故本选项错误. 故选:B . 【点睛】本题考查了整式的运算,合并同类项、幂的乘方、单项式乘单项式和完全平方公式,熟练掌握运算法则是解题的关键.8.D解析:D 【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角进行分析即可. 【详解】解:根据同位角定义观察图形可知A 、B 、C 选项中的均不符合同位角的定义,只有选项D 中的图形符合, 故选D . 【点睛】本题考查同位角,关键是掌握同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.9.C解析:C 【分析】设出外角的度数,表示出内角的度数,根据一个内角与它相邻的外角互补列出方程,解方程得到答案. 【详解】解:设外角为x ,则相邻的内角为2x , 由题意得,2180x x +=︒, 解得,60x =︒,多边形的边数为:360606÷︒=, 故选:C . 【点睛】本题考查的是多边形内、外角的知识,理解一个多边形的一个内角与它相邻外角互补是解题的关键.10.B解析:B 【分析】把方程组24213x y x y -=⎧⎨+=⎩的解求解出来即可得到a 、b 的值,再计算32a b -的算术平方根即可得到答案; 【详解】解:24213x y x y -=⎧⎨+=⎩①②把①式×5得:248x y -= ③, 用②式-③式得:55y = , 解得:y=1,把1y = 代入①式得到:24x -= ,即:6x = ,又x a y b =⎧⎨=⎩是方程组24213x y x y -=⎧⎨+=⎩的解,所以61a b =⎧⎨=⎩,故3216a b -=,所以32a b -的算术平方根=16的算术平方根,4== , 故答案为:4; 【点睛】本题主要考查了二元一次方程组的求解以及算术平方根的定义,掌握用消元法求解二元一次方程组的解是解题的关键;二、填空题 11.15 【分析】根据幂的运算公式即可求解. 【详解】 ∵am=5,an=3,∴am+n= am×an=5×3=15 故答案为:15. 【点睛】此题主要考查幂的运算,解题的关键是熟知同底数幂的逆运解析:15【分析】根据幂的运算公式即可求解.【详解】∵a m=5,a n=3,∴a m+n= a m×a n=5×3=15故答案为:15.【点睛】此题主要考查幂的运算,解题的关键是熟知同底数幂的逆运算.12.-5或-1或-3【分析】根据零指数幂和1的任何次幂都等于1分情况讨论求解.【详解】解:根据0指数的意义,得:当x+2≠0时,x+5=0,解得:x=﹣5.当x+2=1时,x=﹣1,当x+2解析:-5或-1或-3【分析】根据零指数幂和1的任何次幂都等于1分情况讨论求解.【详解】解:根据0指数的意义,得:当x+2≠0时,x+5=0,解得:x=﹣5.当x+2=1时,x=﹣1,当x+2=﹣1时,x=﹣3,x+5=2,指数为偶数,符合题意.故答案为:﹣5或﹣1或﹣3.【点睛】本题考查零指数幂和有理数的乘方,掌握零指数幂和1的任何次幂都是1是本题的解题关键.13.16【分析】根据幂的运算公式变形,再代入x+3y=4即可求解.【详解】∵x+3y-4=0∴x+3y=4∴2x•8y=2x•(23)y=2x+3y=24=16.故答案为:16.【点睛】解析:16【分析】根据幂的运算公式变形,再代入x+3y=4即可求解.【详解】∵x+3y-4=0∴x+3y=4∴2x•8y=2x•(23)y=2x+3y=24=16.故答案为:16.【点睛】此题主要考查幂的运算,解题的关键是熟知幂的运算公式.14.a4-4a3b+6a2b2-4ab3+b4【分析】原式变形后,利用(a+b)4=a4+4a3b+6a2b2+4ab3+b4,即可得到(a-b)4的结果.【详解】解:根据题意得:(a-b)4=解析:a4-4a3b+6a2b2-4ab3+b4【分析】原式变形后,利用(a+b)4=a4+4a3b+6a2b2+4ab3+b4,即可得到(a-b)4的结果.【详解】解:根据题意得:(a-b)4=[a+(-b)]4=a4-4a3b+6a2b2-4ab3+b4,故答案为:a4-4a3b+6a2b2-4ab3+b4【点睛】此题考查了完全平方公式,熟练掌握公式是解本题的关键.15.8【解析】【分析】根据多边形的内角和公式(n-2)•180°与外角和定理列式求解即可.【详解】设这个多边形的边数是n,则(n-2)•180°-360°=720°,解得n=8.故答案为解析:8【解析】【分析】根据多边形的内角和公式(n-2)•180°与外角和定理列式求解即可.【详解】设这个多边形的边数是n ,则(n-2)•180°-360°=720°,解得n=8.故答案为8.【点睛】本题考查了多边形的内角和与外角和定理,任意多边形的外角和都是360°,与边数无关.16.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解析:43.310-⨯【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:将数据0.00033用科学记数法表示为43.310-⨯,故答案为:43.310-⨯.【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.17.5×10-6【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解析:5×10-6【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.0000025=2.5×10-6,故答案为2.5×10-6.【点睛】本题考查了用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.18. 3【分析】利用完全平方公式的结构特征判断即可求出k的值.【详解】∵关于字母x的二次三项式x2+2kx+9是完全平方式,∴k=±3,故答案为:3.【点睛】此题考查了完全平方式,熟练解析:±3【分析】利用完全平方公式的结构特征判断即可求出k的值.【详解】∵关于字母x的二次三项式x2+2kx+9是完全平方式,∴k=±3,故答案为:±3.【点睛】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.19.【分析】设每件衬衫降价x元,正好达到预期目标,根据销售收入-成本=利润,即可得出关于x的一元一次方程,解之即可得出结论.【详解】解:设每件衬衫降价x元,正好达到预期目标,根据题意得:120解析:20【分析】设每件衬衫降价x元,正好达到预期目标,根据销售收入-成本=利润,即可得出关于x的一元一次方程,解之即可得出结论.【详解】解:设每件衬衫降价x元,正好达到预期目标,根据题意得:120×400+(120-x)×(500-400)-80×500=80×500×45%,解得:x=20.答:每件衬衫降价10元,正好达到预期目标.【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.20.4【分析】向左平移3个单位则横坐标减去3纵坐标不变,再根据y轴上点的横坐标为0即可得出答案.【详解】解:由题意得:3a-9-3=0,解得:a=4.故答案为4.【点睛】本题考查了坐标与解析:4【分析】向左平移3个单位则横坐标减去3纵坐标不变,再根据y轴上点的横坐标为0即可得出答案.【详解】解:由题意得:3a-9-3=0,解得:a=4.故答案为4.【点睛】本题考查了坐标与图形变化-平移.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.同时考查了y轴上的点的坐标特征.三、解答题21.(1)见详解;(2)见详解;(3)152.【分析】(1)按要求作图即可;(2)按要求作图即可;(3)根据勾股定理求出AB和CH的长即可得出面积.【详解】(1)△EFD如图所示,;(2)CH 如图所示,;(3)根据勾股定理可得:223+635221+25∴S △ABC =12×AB ×CH=12×355152. 【点睛】 本题考查了平移作图,勾股定理,掌握知识点是解题关键.22.3x 2-3x -5,25【分析】原式第一项利用平方差公式化简,第二项利用单项式乘以多项式法则计算,最后一项利用完全平方公式展开,去括号合并得到最简结果,将已知的方程变形后代入即可求值.【详解】原式=()222945521x x x x x -----+=222945521x x x x x ----+-=2335x x --,当2100x x =--,即210x x =-时,原式=()235310525x x -=⨯-=-【点睛】本题考查整式的混合运算-化简求值,涉及的知识点有:完全平方公式、平方差公式、去括号法则及合并同类项法则,熟练掌握以上公式及法则是解题的关键.23.(1)∠APB =∠NAP +∠HBP ;(2)见解析;(3)∠HBP =∠NAP +∠APB(1)过P 点作PQ ∥GH ,根据平行线的性质即可求解;(2)过P 点作PQ ∥GH ,根据平行线的性质即可求解;(3)根据平行线的性质和三角形外角的性质即可求解.【详解】解:(1)如图①,过P 点作PQ ∥GH ,∵MN ∥GH ,∴MN ∥PQ ∥GH ,∴∠APQ =∠NAP ,∠BPQ =∠HBP ,∵∠APB =∠APQ +∠BPQ ,∴∠APB =∠NAP +∠HBP ,故答案为:∠APB =∠NAP+∠HBP ;(2)如图②,过P 点作PQ ∥GH ,∵MN ∥GH ,∴MN ∥PQ ∥GH ,∴∠APQ +∠NAP =180°,∠BPQ +∠HBP =180°,∵∠APB =∠APQ +∠BPQ ,∴∠APB =(180°﹣∠NAP )+(180°﹣∠HBP )=360°﹣(∠NAP +∠HBP ); (3)如备用图,∵MN ∥GH ,∴∠PEN =∠HBP ,∵∠PEN =∠NAP +∠APB ,∴∠HBP =∠NAP +∠APB.故答案为:∠HBP =∠NAP +∠APB.【点睛】此题考查了平行公理的推论:平行于同一条直线的两直线平行,以及平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,熟记定理是解题的关键.24.(1)31y a =-+;(2)12a =-.(1)通过消元的方法,消去x ,即可用a 的代数式表示y ;(2)令y x =-,再将x 、x -代入方程组,即可求解.【详解】解:(1)由43x y a -=-得:43x a y =-+,将其代入25x y a +=-得:4325a y y a -++=-,整理得:393y a =-+,即31y a =-+.故答案为31y a =-+.(2)若x 、y 互为相反数,则y x =-再将x 、y 代入方程组:4325x x a x x a +=-⎧⎨-=-⎩, 解得12a =-. 故答案为12a =-. 【点睛】 本题考查次二元一次方程组的运用,难度一般,熟练掌握消元法是顺利解题的关键.25.(1)见解析;(2)35°;(3)117°【分析】(1)由AC ∥BD 得∠D =∠DAE ,角的等量关系证明∠DAE 与∠C 相等,根据同位角得AD ∥BC ;(2)由BD ⊥BC 得∠HBC =90°,余角的性质和三角形外角性质解得∠C 的度数为35°; (3)由BF ∥AD 得∠D =∠DBF ,垂直的定义得∠DBC =90°,三角形的内角和定理,角的和差求得∠DBA =∠CBA =45°,由已知条件∠EFB =7∠DBF ,角的和差得出∠BAD 的度数为117°.【详解】解:(1)如图1所示:∵AC ∥BD ,∴∠D =∠DAE ,又∵∠C =∠D ,∴∠DAE =∠C ,∴AD∥BC;(2)①如图2所示:∵BD⊥BC,∴∠HBC=90°,∴∠C+∠BHC=90°,又∵∠BHC=∠DAE+∠D,∠C=∠D,∠DAE=20°,∴20°+2∠C=90°,∴∠C=35°;②如图3所示:∵BF∥AD,∴∠D=∠DBF,又∵∠C=∠D,∴∠C=∠D=∠DBF,又∵BD⊥BC,∴∠DBC=90°,又∵∠D+∠DBA+∠BAD=180°,∠C+∠CBA+∠BAC=180°.∠BAC=∠BAD,∴∠DBA=∠CBA=45°,又∵∠EFB=7∠DBF,∠EFB=∠FBC+∠C,∴7∠DBF=2∠DBF+∠DBC,解得:∠DBF=18°,∴∠BAD=180°﹣45°﹣18°=117°.【点睛】本题考查了平行线的判定与性质,余角的性质,三角形的内角和性质,三角形的外角性质,角的和差等相关知识点,掌握平行线的判定与性质,三角形内角和和外角的性质是解题的关键.26.(1)7;(2)47.【分析】(1)根据13a a -+=得出13a a +=,进而得出219a a ⎛⎫+= ⎪⎝⎭,从而可得出结论; (2)根据(1)中的结论可知2217a a +=,故2221()49a a +=,从而得出441a a +的值. 【详解】解:(1)∵13a a -+=, ∴13a a+=, ∴21()9a a +=,即:22129a a++=, ∴2217a a+=; (2)由(1)知:2217a a +=, ∴2221()49a a +=,即:441249a a ++=, ∴44147a a+=. 【点睛】本题主要考查的是负整数指数幂和分式的运算,解题的关键是熟练掌握完全平方公式的灵活应用.27.(1)89;(2)102x ; 【分析】 (1)根据零指数幂和负整数指数幂的运算法则即可计算;(2)根据同底数幂的乘法法则和合并同类项即可计算.【详解】(1)原式=1-19=89; (2)原式=x 10+x 10=2x 10.【点睛】本题考查整式的混合运算,负整数指数幂,零指数幂,解答本题的关键是明确各法则的计算方法.28.(1)-8a+12,16;(2)x 2+3,139【分析】(1)直接利用多项式乘法去括号,进而合并同类项,再将已知数据代入求出答案;(2)直接利用多项式乘法去括号,进而合并同类项,再将已知数据代入求出答案.【详解】解:(1)原式=a2-4a-(a2-2a+6a-12)=a2-4a-(a2+4a-12)=a2-4a-a2-4a+12=-8a+12把12a=-代入得:原式=-8×(1-2)+12=16;(2)原式=x2+4x+4+4x2-1-4x2-4x =x2+3把13x=代入得:原式=(13)2+3=139.【点睛】本题考查了多项式乘法,合并同类项,平方差公式和完全平方公式.细心运算是解题关键.。
上海复旦实验中学人教版七年级下册期末生物期末试卷及答案-全册

上海复旦实验中学人教版七年级下册期末生物期末试卷及答案-全册一、选择题1.现代类人猿和人类的共同祖先是()A.森林古猿B.黑猩猩C.长臂猿D.大猩猩2.有关人类生殖和发育的叙述,错误的是()A.睾丸和卵巢是产生生殖细胞的器官B.受精卵形成的场所是输卵管C.女性输卵管结扎后不能产生月经D.胚胎发育的场所是子宫3.一类比较简单的有机物,种类很多,大多数是人体自身不能制造的,只能从食物中摄取,该类物质是()A.脂肪B.糖类C.蛋白质D.维生素4.将花生种子在白纸上挤压,可以看到纸上留下油迹,这说明花生中含有()A.蛋白质B.糖类C.维生素D.脂肪5.如图,表示淀粉、脂肪和蛋白质在消化道中各部份被消化的程度。
请据图判断:淀粉开始被消化的部位是()A.口腔B.食道C.小肠D.大肠6.下图是某同学探究唾液淀粉酶对淀粉消化的实验操作过程,下列各项关于实验结果的描述中,正确的是()A.1变蓝,2变蓝B.1变蓝,2不变蓝C.1不变蓝,2变蓝D.1不变蓝,2不变蓝7.小明在吃葡萄时将核咽了下去,葡萄核在体内的“旅程”是()A.口腔→咽→胃→食道→大肠→小肠→肛门B.口腔→咽→胃→食道→小肠→肛门→大肠C.口腔→咽→食道→胃→小肠→大肠→肛门D.口腔→咽→胃→食道→小肠→大肠→肛门8.如图表示某人在两种状态下的呼吸情况,据图分析正确的是A.曲线Ⅰ可能为运动状态B.曲线Ⅱ可能为平静状态C.曲线Ⅰ状态时,呼吸频率较慢D.曲线Ⅱ状态时,呼吸深度较小9.对“痰”和“口水”的有关叙述中,正确的是()A.“痰”和“口水”产生的部位相同B.“痰”和“口水”所含的成分相同C.“痰”是消化器官分泌的,而“口水”是呼吸器官产生的D.“痰”内有灰尘和部分病菌,而“口水”中一般含有消化酶10.某些新冠肺炎重症患者需要气管插管来辅助呼吸,如下图所示。
为了保证双肺都能获得氧气,气管插管从患者口腔进入后,依次经过和最终到达的位置是()A.咽、食管、气管B.咽、食管、气管、支气管C.咽、喉、气管D.咽、喉、气管、支气管、肺泡11.下列人体器官中没有排泄功能的是A.肛门B.肺C.皮肤D.肾脏12.图是尿液形成过程示意图,据图分析,下列叙述正确的是()A.①是入球小动脉,②是出球小静脉B.③是肾小管C.④是肾小囊D.⑤是毛细血管13.下列有关肾小球的叙述中,不正确的是()A.入球小血管和出球小血管均为小动脉B.肾小球若发生病变,可能导致血尿C.肾小球中的液体是原尿D.肾小球是由毛细血管缠绕而成的血管球14.如图是人体泌尿系统的组成图,下列叙述错误的...是()A.尿液排出体外的途径依次①②③④B.尿的生成连续的,尿的排出是间歇的C.尿液在③内形成D.④是尿液排出体外的通道15.如图是人体内三种血管关系的示意图,图中箭头表示血流方向,则血管P和血管Q分别是()A.动脉,静脉B.静脉,动脉C.静脉,静脉D.动脉,毛细血管16.某 A 型血的人因意外受伤需大量输血,应该给他输A.O 型血B.AB 型血C.A 型血D.B 型血17.如图是血液流经某器官的示意图,下列表述正确的是()A.b表示心脏,则c血管里流的是静脉血B.b表示肺,则c血管里流的是静脉血C.b表示小肠,则c血管里流的是动脉血D.b表示肾小球,则c血管里流的是动脉血18.图是肺泡的结构示意图,下列关于肺泡的叙述不正确的是A.肺泡壁由一层上皮细胞构成B.肺泡壁被丰富的毛细血管包围C.肺泡数目很多D.肺动脉里流动的是动脉血19.某人因车祸大腿受伤(如图所示),鲜红的血液喷射而出。
上海复旦实验中学七年级下册数学期末试卷测试卷附答案
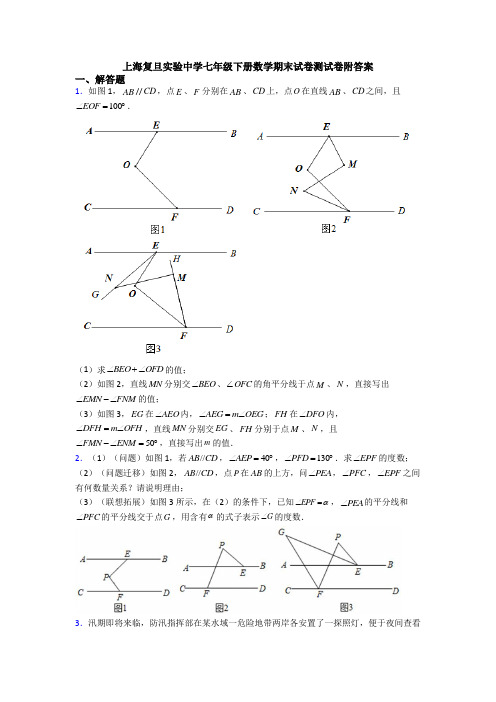
上海复旦实验中学七年级下册数学期末试卷测试卷附答案一、解答题1.如图1,AB //CD ,点E 、F 分别在AB 、CD 上,点O 在直线AB 、CD 之间,且100EOF ∠=︒.(1)求BEO OFD ∠+∠的值;(2)如图2,直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ,直接写出EMN FNM ∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG m OEG ∠=∠;FH 在DFO ∠内,DFH m OFH ∠=∠,直线MN 分别交EG 、FH 分别于点M 、N ,且50FMN ENM ∠-∠=︒,直接写出m 的值.2.(1)(问题)如图1,若//AB CD ,40AEP ∠=︒,130PFD ∠=︒.求EPF ∠的度数; (2)(问题迁移)如图2,//AB CD ,点P 在AB 的上方,问PEA ∠,PFC ∠,EPF ∠之间有何数量关系?请说明理由;(3)(联想拓展)如图3所示,在(2)的条件下,已知EPF α∠=,PEA ∠的平分线和PFC ∠的平分线交于点G ,用含有α的式子表示G ∠的度数.3.汛期即将来临,防汛指挥部在某水域一危险地带两岸各安置了一探照灯,便于夜间查看河水及两岸河堤的情况.如图1,灯A 射出的光束自AM 顺时针旋转至AN 便立即回转,灯B 射出的光束自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯A 射出的光束转动的速度是a ︒/秒,灯B 射出的光束转动的速度是b ︒/秒,且a 、b 满足20)34(a b a b -++-=.假定这一带水域两岸河堤是平行的,即//PQ MN ,且45BAN ∠=︒.(1)求a 、b 的值;(2)如图2,两灯同时转动,在灯A 射出的光束到达AN 之前,若两灯射出的光束交于点C ,过C 作CD AC ⊥交PQ 于点D ,若20BCD ∠=︒,求BAC ∠的度数;(3)若灯B 射线先转动30秒,灯A 射出的光束才开始转动,在灯B 射出的光束到达BQ 之前,A 灯转动几秒,两灯的光束互相平行? 4.已知,//AB CD .点M 在AB 上,点N 在CD 上.(1)如图1中,BME ∠、E ∠、END ∠的数量关系为: ;(不需要证明);如图2中,BMF ∠、F ∠、FND ∠的数量关系为: ;(不需要证明)(2)如图 3中,NE 平分FND ∠,MB 平分FME ∠,且2180E F ∠+∠=,求FME ∠的度数;(3)如图4中,60BME ∠=,EF 平分MEN ∠,NP 平分END ∠,且//EQ NP ,则FEQ ∠的大小是否发生变化,若变化,请说明理由,若不变化,求出么FEQ ∠的度数. 5.已知AB ∥CD ,线段EF 分别与AB ,CD 相交于点E ,F .(1)请在横线上填上合适的内容,完成下面的解答:如图1,当点P 在线段EF 上时,已知∠A =35°,∠C =62°,求∠APC 的度数; 解:过点P 作直线PH ∥AB , 所以∠A =∠APH ,依据是 ;因为AB ∥CD ,PH ∥AB , 所以PH ∥CD ,依据是 ; 所以∠C =( ),所以∠APC =( )+( )=∠A +∠C =97°. (2)当点P ,Q 在线段EF 上移动时(不包括E ,F 两点): ①如图2,∠APQ +∠PQC =∠A +∠C +180°成立吗?请说明理由;②如图3,∠APM =2∠MPQ ,∠CQM =2∠MQP ,∠M +∠MPQ +∠PQM =180°,请直接写出∠M ,∠A 与∠C 的数量关系.二、解答题6.问题情境(1)如图1,已知//, 125155AB CD PBA PCD ︒︒∠=∠=,,求BPC ∠的度数.佩佩同学的思路:过点P 作//PN AB ,进而//PN CD ,由平行线的性质来求BPC ∠,求得BPC ∠︒;问题迁移(2)图2,图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合90,//,ACB DF CG AB ︒∠=与FD 相交于点E ,有一动点P 在边BC 上运动,连接, PE PA ,记,PED PAC αβ∠=∠∠=∠.①如图2,当点P 在,C D 两点之间运动时,请直接写出APE ∠与,αβ∠∠之间的数量关系;②如图3,当点P 在,B D 两点之间运动时,APE ∠与,αβ∠∠之间有何数量关系?请判断并说明理由.7.阅读下面材料:小颖遇到这样一个问题:已知:如图甲,//,AB CD E 为,AB CD 之间一点,连接,,35,37BE DE B D ∠=︒∠=︒,求BED ∠的度数.她是这样做的: 过点E 作//,EF AB 则有,BEF B ∠=∠因为//,AB CD 所以//.EF CD ① 所以,FED D ∠=∠所以,BEF FED B D ∠+∠=∠+∠ 即BED ∠=_ ; 1.小颖求得BED ∠的度数为__ ; 2.上述思路中的①的理由是__ ; 3.请你参考她的思考问题的方法,解决问题:已知:直线//,a b 点,A B 在直线a 上,点,C D 在直线b 上,连接,,AD BC BE 平分,ABC DE ∠平分,ADC ∠且,BE DE 所在的直线交于点E .(1)如图1,当点B 在点A 的左侧时,若,ABC ADC αβ∠=∠=,则BED ∠的度数为 ;(用含有,αβ的式子表示).(2)如图2,当点B 在点A 的右侧时,设,ABC ADC αβ∠=∠=,直接写出BED ∠的度数(用含有,αβ的式子表示).8.已知,如图①,∠BAD =50°,点C 为射线AD 上一点(不与A 重合),连接BC . (1)[问题提出]如图②,AB ∥CE ,∠BCD =73 °,则:∠B = .(2)[类比探究]在图①中,探究∠BAD 、∠B 和∠BCD 之间有怎样的数量关系?并用平行....线的性质....说明理由. (3)[拓展延伸]如图③,在射线BC 上取一点O ,过O 点作直线MN 使MN ∥AD ,BE 平分∠ABC 交AD 于E 点,OF 平分∠BON 交AD 于F 点,//OG BE 交AD 于G 点,当C 点沿着射线AD 方向运动时,∠FOG 的度数是否会变化?若变化,请说明理由;若不变,请求出这个不变的值.9.已知直线//EF MN ,点,A B 分别为EF , MN 上的点.(1)如图1,若120FAC ACB ∠=∠=︒,12CAD FAC ∠=∠, 12CBD CBN ∠=∠,求CBN∠与ADB ∠的度数;(2)如图2,若120FAC ACB ∠=∠=︒,13CAD FAC ∠=∠, 13CBD CBN ∠=∠,则ADB =∠_________︒;(3)若把(2)中“120FAC ACB ∠=∠=︒,13CAD FAC ∠=∠, 13CBD CBN ∠=∠”改为“FAC ACB m ∠=∠=︒,1CAD FAC n∠=∠, 1CBD CBN n ∠=∠”,则ADB =∠_________︒.(用含,m n 的式子表示)10.综合与探究综合与实践课上,同学们以“一个含30角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a ,b ,且//a b ,三角形ABC 是直角三角形,90BCA ∠=︒,30BAC ∠=︒,60ABC ∠=︒操作发现:(1)如图1.148∠=︒,求2∠的度数;(2)如图2.创新小组的同学把直线a 向上平移,并把2∠的位置改变,发现21120∠-∠=︒,请说明理由. 实践探究:(3)填密小组在创新小组发现的结论的基础上,将图2中的图形继续变化得到图3,AC 平分BAM ∠,此时发现1∠与2∠又存在新的数量关系,请写出1∠与2∠的数量关系并说明理由.三、解答题11.解读基础:(1)图1形似燕尾,我们称之为“燕尾形”,请写出A ∠、B 、C ∠、D ∠之间的关系,并说明理由;(2)图2形似8字,我们称之为“八字形”,请写出A ∠、B 、C ∠、D ∠之间的关系,并说明理由:应用乐园:直接运用上述两个结论解答下列各题(3)①如图3,在ABC ∆中,BD 、CD 分别平分ABC ∠和ACB ∠,请直接写出A ∠和D ∠的关系 ;②如图4,A B C D E F ∠+∠+∠+∠+∠+∠= .(4)如图5,BAC ∠与BDC ∠的角平分线相交于点F ,GDC ∠与CAF ∠的角平分线相交于点E ,已知26B ∠=︒,54C ∠=︒,求F ∠和E ∠的度数.12.如图①,AD 平分BAC ∠,AE ⊥BC ,∠B=450,∠C=730. (1) 求DAE ∠的度数;(2) 如图②,若把“AE ⊥BC ”变成“点F 在DA 的延长线上,FE BC ⊥”,其它条件不变,求DFE ∠ 的度数;(3) 如图③,若把“AE ⊥BC ”变成“AE 平分BEC ∠”,其它条件不变,DAE ∠的大小是否变化,并请说明理由.13.操作示例:如图1,在△ABC 中,AD 为BC 边上的中线,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1=S 2.解决问题:在图2中,点D 、E 分别是边AB 、BC 的中点,若△BDE 的面积为2,则四边形ADEC 的面积为 . 拓展延伸:(1)如图3,在△ABC 中,点D 在边BC 上,且BD =2CD ,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1与S 2之间的数量关系为 .(2)如图4,在△ABC 中,点D 、E 分别在边AB 、AC 上,连接BE 、CD 交于点O ,且BO =2EO ,CO =DO ,若△BOC 的面积为3,则四边形ADOE 的面积为 . 14.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.15.如图①所示,在三角形纸片ABC 中,70C ∠=︒,65B ∠=︒,将纸片的一角折叠,使点A 落在ABC 内的点A '处. (1)若140∠=︒,2∠=________.(2)如图①,若各个角度不确定,试猜想1∠,2∠,A ∠之间的数量关系,直接写出结论. ②当点A 落在四边形BCDE 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,A ∠,1∠,2∠之间又存在什么关系?请说明.(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的123456∠+∠+∠+∠+∠+∠和是________.【参考答案】一、解答题1.(1) ;(2)的值为40°;(3). 【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解; (2)过点M 作MK ∥AB ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM 解析:(1)260BEO DFO ∠+∠=︒ ;(2)EMN FNM ∠-∠的值为40°;(3)53.【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解;(2)过点M 作MK ∥A B ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM =∠OEM =x ,∠CFN =∠OFN =y ,由∠BEO +∠DFO =260°可求x -y =40°,进而求解;(3)设直线FK 与EG 交于点H ,FK 与AB 交于点K ,根据平行线的性质即三角形外角的性质及50FMN ENM ∠-∠=︒,可得50KFD AEG ∠-∠=︒,结合260AEG n OEG DFK n OFK BEO DFO ∠=∠=∠∠+∠=︒,,,可得11180100AEG AEG KFD KFD n n ∠+∠+︒-∠-∠=︒,即可得关于n 的方程,计算可求解n 值. 【详解】证明:过点O 作OG ∥AB ,∵AB ∥CD , ∴AB ∥OG ∥CD ,∴180180BEO EOG DFO FOG ∠+∠=︒∠+∠=︒,, ∴360BEO EOG DFO FOG ∠+∠+∠+∠=︒, 即360BEO EOF DFO ∠+∠+∠=︒, ∵∠EOF =100°,∴∠260BEO DFO +∠=︒;(2)解:过点M 作MK ∥AB ,过点N 作NH ∥CD ,∵EM 平分∠BEO ,FN 平分∠CFO , 设BEM OEM x CFN OFN y ∠=∠=∠=∠=,, ∵260BEO DFO ∠+∠=︒∴21802260BEO DFO x y ∠+∠=+︒-=︒, ∴x -y =40°,∵MK ∥AB ,NH ∥CD ,AB ∥CD , ∴AB ∥MK ∥NH ∥CD ,∴EMK BEM x HNF CFN y KMN HNM ∠=∠=∠=∠=∠=∠,,, ∴EMN FNM EMK KMN HNM HNF ∠+∠=∠+∠-∠+∠() x KMN HNM y =+∠-∠-=x -y =40°,故EMN FNM ∠-∠的值为40°;(3)如图,设直线FK 与EG 交于点H ,FK 与AB 交于点K ,∵AB ∥CD , ∴AKF KFD ∠=∠,∵AKF EHK HEK EHK AEG ∠=∠+∠=∠+∠, ∴KFD EHK AEG ∠=∠+∠, ∵50EHK NMF ENM ∠=∠-∠=︒, ∴50KFD AEG ∠=︒+∠, 即50KFD AEG ∠-∠=︒,∵AEG n OEG ∠=∠,FK 在∠DFO 内,DFK n OFK ∠=∠.∴1180180CFO DFK OFK KFD KFD n ∠=︒-∠-∠=︒-∠-∠ ,1AEO AEG OEG AEG AEG n ∠=∠+∠=∠+∠,∵260BEO DFO ∠+∠=︒, ∴100AEO CFO ∠+∠=︒,∴11180100AEG AEG KFD KFD n n ∠+∠+︒-∠-∠=︒,即(180)1KFD AEG n ⎛⎫⎪⎝∠⎭+-∠︒=, ∴115080n ⎛⎫⎪⨯⎭︒︒⎝+=, 解得53n = . 经检验,符合题意, 故答案为:53.【点睛】本题主要考查平行线的性质,角平分线的定义,灵活运用平行线的性质是解题的关键.2.(1)90°;(2)∠PFC=∠PEA+∠P ;(3)∠G=α 【分析】(1)根据平行线的性质与判定可求解;(2)过P 点作PN ∥AB ,则PN ∥CD ,可得∠FPN=∠PEA+∠FPE ,进而可得∠PF解析:(1)90°;(2)∠PFC =∠PEA +∠P ;(3)∠G =12α 【分析】(1)根据平行线的性质与判定可求解;(2)过P 点作PN ∥AB ,则PN ∥CD ,可得∠FPN =∠PEA +∠FPE ,进而可得∠PFC =∠PEA +∠FPE ,即可求解;(3)令AB 与PF 交点为O ,连接EF ,根据三角形的内角和定理可得∠GEF +∠GFE =12∠PEA +12∠PFC +∠OEF +∠OFE ,由(2)得∠PEA =∠PFC -α,由∠OFE +∠OEF =180°-∠FOE =180°-∠PFC 可求解. 【详解】解:(1)如图1,过点P 作PM ∥AB , ∴∠1=∠AEP . 又∠AEP =40°, ∴∠1=40°. ∵AB ∥CD , ∴PM ∥CD ,∴∠2+∠PFD=180°.∵∠PFD=130°,∴∠2=180°-130°=50°.∴∠1+∠2=40°+50°=90°.即∠EPF=90°.(2)∠PFC=∠PEA+∠P.理由:过P点作PN∥AB,则PN∥CD,∴∠PEA=∠NPE,∵∠FPN=∠NPE+∠FPE,∴∠FPN=∠PEA+∠FPE,∵PN∥CD,∴∠FPN=∠PFC,∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;(3)令AB与PF交点为O,连接EF,如图3.在△GFE中,∠G=180°-(∠GFE+∠GEF),∵∠GEF=12∠PEA+∠OEF,∠GFE=12∠PFC+∠OFE,∴∠GEF+∠GFE=12∠PEA+12∠PFC+∠OEF+∠OFE,∵由(2)知∠PFC=∠PEA+∠P,∴∠PEA=∠PFC-α,∵∠OFE+∠OEF=180°-∠FOE=180°-∠PFC,∴∠GEF+∠GFE=12(∠PFC−α)+12∠PFC+180°−∠PFC=180°−12α,∴∠G=180°−(∠GEF+∠GFE)=180°−180°+12α=12α.【点睛】本题主要考查平行线的性质与判定,灵活运用平行线的性质与判定是解题的关键.3.(1),;(2)30°;(3)15秒或82.5秒【分析】(1)解出式子即可;(2)根据,用含t 的式子表示出,根据(2)中给出的条件得出方程式 ,求出 t 的值,进而求出的度数; (3)根据灯B 的解析:(1)3a =,1b =;(2)30°;(3)15秒或82.5秒 【分析】(1)解出式子()2340a b a b -++-=即可;(2)根据//PQ MN ,用含t 的式子表示出BCA ∠,根据(2)中给出的条件得出方程式()()9090180229020⎡⎤∠=︒-∠=︒-︒-︒=︒-︒=︒⎣⎦BCD BCA t t ,求出 t 的值,进而求出BAC∠的度数;(3)根据灯B 的要求,t <150,在这个时间段内A 可以转3次,分情况讨论. 【详解】解:(1)2|3|(4)0a b a b -++-=. 又|3|0a b -≥,2(4)0a b +-≥.3a ∴=,1b =;(2)设A 灯转动时间为t 秒,如图,作//CE PQ ,而//,PQ MN ////,PQ CE MN ∴1803ACE CAN t ∴∠=∠=︒-︒,BCE CBD t ∠=∠=︒,()()18031802∴∠=∠+∠=︒+︒-︒=︒-︒BCA CBD CAN t t t ,90ACD ∠=︒,[]9090180(2)(2)9020∴∠=︒-∠=︒-︒-︒=︒-︒=︒BCD BCA t t ,55∴=t()1803∠=︒-︒CAN t ,()()451803313516513530∴∠=︒-︒-︒=︒-︒=︒-︒=︒⎡⎤⎣⎦BAC t t(3)设A 灯转动t 秒,两灯的光束互相平行. 依题意得0150t << ①当060t <<时,两河岸平行,所以()233t ∠=∠=︒ 两光线平行,所以2130t ∠=∠=+︒ 所以,13∠=∠ 即:330=+t t , 解得15t =; ②当60120t <<时,两光束平行,所以()2330t ∠=∠=+︒ 两河岸平行,所以12180∠+∠=︒13180t ∠=-︒所以,318030180-++=t t , 解得82.5t =;③当120150t <<时,图大概如①所示 336030t t -=+,解得195150t =>(不合题意)综上所述,当15t =秒或82.5秒时,两灯的光束互相平行. 【点睛】这道题考察的是平行线的性质和一元一次方程的应用.根据平行线的性质找到对应角列出方程是解题的关键.4.(1)∠BME =∠MEN−∠END ;∠BMF =∠MFN +∠FND .(2)120°(3)∠FEQ 的大小没发生变化,∠FEQ =30°. 【分析】(1)过E 作EHAB ,易得EHABCD ,根据平行线的性质解析:(1)∠BME =∠MEN −∠END ;∠BMF =∠MFN +∠FND .(2)120°(3)∠FEQ 的大小没发生变化,∠FEQ =30°. 【分析】(1)过E 作EH //AB ,易得EH //AB //CD ,根据平行线的性质可求解;过F 作FH //AB ,易得FH //AB //CD ,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME+∠END)+∠BMF−∠FND=180°,可求解∠BMF=60°,进而可求解;∠BME,进而可求解.(3)根据平行线的性质及角平分线的定义可推知∠FEQ=12【详解】解:(1)过E作EH//AB,如图1,∴∠BME=∠MEH,∵AB//CD,∴HE//CD,∴∠END=∠HEN,∴∠MEN=∠MEH+∠HEN=∠BME+∠END,即∠BME=∠MEN−∠END.如图2,过F作FH//AB,∴∠BMF=∠MFK,∵AB//CD,∴FH//CD,∴∠FND=∠KFN,∴∠MFN=∠MFK−∠KFN=∠BMF−∠FND,即:∠BMF=∠MFN+∠FND.故答案为∠BME=∠MEN−∠END;∠BMF=∠MFN+∠FND.(2)由(1)得∠BME=∠MEN−∠END;∠BMF=∠MFN+∠FND.∵NE平分∠FND,MB平分∠FME,∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,∵2∠MEN+∠MFN=180°,∴2(∠BME+∠END)+∠BMF−∠FND=180°,∴2∠BME+2∠END+∠BMF−∠FND=180°,即2∠BMF+∠FND+∠BMF−∠FND=180°,解得∠BMF=60°,∴∠FME=2∠BMF=120°;(3)∠FEQ的大小没发生变化,∠FEQ=30°.由(1)知:∠MEN=∠BME+∠END,∵EF平分∠MEN,NP平分∠END,∴∠FEN=12∠MEN=12(∠BME+∠END),∠ENP=12∠END,∵EQ//NP,∴∠NEQ=∠ENP,∴∠FEQ=∠FEN−∠NEQ=12(∠BME+∠END)−12∠END=12∠BME,∵∠BME=60°,∴∠FEQ=12×60°=30°.【点睛】本题主要考查平行线的性质及角平分线的定义,作辅助线是解题的关键.5.(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①∠APQ+∠PQC=∠A+∠C+180°成立,理由见解答过程;②3∠PMQ+∠A+∠C=360°.解析:(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①∠APQ+∠PQC=∠A+∠C+180°成立,理由见解答过程;②3∠PMQ+∠A+∠C=360°.【分析】(1)根据平行线的判定与性质即可完成填空;(2)结合(1)的辅助线方法即可完成证明;(3)结合(1)(2)的方法,根据∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,即可证明∠PMQ,∠A与∠C的数量关系.【详解】解:过点P作直线PH∥AB,所以∠A=∠APH,依据是两直线平行,内错角相等;因为AB∥CD,PH∥AB,所以PH∥CD,依据是平行于同一条直线的两条直线平行;所以∠C=(∠CPH),所以∠APC=(∠APH)+(∠CPH)=∠A+∠C=97°.故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①如图2,∠APQ+∠PQC=∠A+∠C+180°成立,理由如下:过点P 作直线PH ∥AB ,QG ∥AB , ∵AB ∥CD , ∴AB ∥CD ∥PH ∥QG ,∴∠A =∠APH ,∠C =∠CQG ,∠HPQ +∠GQP =180°,∴∠APQ +∠PQC =∠APH +∠HPQ +∠GQP +∠CQG =∠A +∠C +180°. ∴∠APQ +∠PQC =∠A +∠C +180°成立; ②如图3,过点P 作直线PH ∥AB ,QG ∥AB ,MN ∥AB , ∵AB ∥CD ,∴AB ∥CD ∥PH ∥QG ∥MN ,∴∠A =∠APH ,∠C =∠CQG ,∠HPQ +∠GQP =180°,∠HPM =∠PMN ,∠GQM =∠QMN ,∴∠PMQ =∠HPM +∠GQM ,∵∠APM =2∠MPQ ,∠CQM =2∠MQP ,∠PMQ +∠MPQ +∠PQM =180°, ∴∠APM +∠CQM =∠A +∠C +∠PMQ =2∠MPQ +2∠MQP =2(180°﹣∠PMQ ), ∴3∠PMQ +∠A +∠C =360°. 【点睛】考核知识点:平行线的判定和性质.熟练运用平行线性质和判定,添加适当辅助线是关键.二、解答题6.(1)80;(2)①;② 【分析】(1)过点P 作PG ∥AB ,则PG ∥CD ,由平行线的性质可得∠BPC 的度数; (2)①过点P 作FD 的平行线,依据平行线的性质可得∠APE 与∠α,∠β之间的数量关系;解析:(1)80;(2)①APE αβ∠=∠+∠;②APE βα∠=∠-∠ 【分析】(1)过点P 作PG ∥AB ,则PG ∥CD ,由平行线的性质可得∠BPC 的度数;(2)①过点P 作FD 的平行线,依据平行线的性质可得∠APE 与∠α,∠β之间的数量关系;②过P 作PQ ∥DF ,依据平行线的性质可得∠β=∠QPA ,∠α=∠QPE ,即可得到∠APE =∠APQ -∠EPQ =∠β-∠α.解:(1)过点P作PG∥AB,则PG∥CD,由平行线的性质可得∠B+∠BPG=180°,∠C+∠CPG=180°,又∵∠PBA=125°,∠PCD=155°,∴∠BPC=360°-125°-155°=80°,故答案为:80;(2)①如图2,过点P作FD的平行线PQ,则DF∥PQ∥AC,∴∠α=∠EPQ,∠β=∠APQ,∴∠APE=∠EPQ+∠APQ=∠α+∠β,∠APE与∠α,∠β之间的数量关系为∠APE=∠α+∠β;②如图3,∠APE与∠α,∠β之间的数量关系为∠APE=∠β-∠α;理由:过P作PQ∥DF,∵DF∥CG,∴PQ∥CG,∴∠β=∠QPA,∠α=∠QPE,∴∠APE=∠APQ-∠EPQ=∠β-∠α.【点睛】本题主要考查了平行线的性质,解决问题的关键是过拐点作平行线,利用平行线的性质得出结论.7.;2.平行于同一条直线的两条直线平行;3.(1);(2).1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案; (2)根据B解析:1.72;2.平行于同一条直线的两条直线平行;3.(1)1122αβ+;(2)1118022αβ-+.【分析】1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案;(2)根据BE 平分,ABC DE ∠平分,ADC ∠求出11,22ABE CDE αβ∠=∠=,过点E 作EF ∥AB ,根据平行线的性质求出∠BEF =12α,11801802DEF CDE β∠=︒-∠=︒-,再利用周角求出答案. 【详解】1、过点E 作//,EF AB 则有,BEF B ∠=∠ 因为//,AB CD 所以//.EF CD ① 所以,FED D ∠=∠所以,BEF FED B D ∠+∠=∠+∠ 即BED ∠=72; 故答案为:72; 2、过点E 作//,EF AB 则有,BEF B ∠=∠ 因为//,AB CD所以EF ∥CD (平行于同一条直线的两条直线平行), 故答案为:平行于同一条直线的两条直线平行; 3、(1)∵BE 平分,ABC DE ∠平分,ADC ∠ ∴1111,2222ABE ABC CDE ADC αβ∠=∠=∠=∠=,过点E 作EF ∥AB ,由1可得∠BED =BEF FED ABE CDE ∠+∠=∠+∠,∴∠BED =1122αβ+,故答案为:1122αβ+;(2)∵BE 平分,ABC DE ∠平分,ADC ∠∴1111,2222ABE ABC CDE ADC αβ∠=∠=∠=∠=,过点E 作EF ∥AB ,则∠ABE =∠BEF =12α,∵//,AB CD ∴EF ∥CD ,∴180CDE DEF ∠+∠=︒,∴11801802DEF CDE β∠=︒-∠=︒-,∴11360360(180)22BED DEF BEF βα∠=︒-∠-∠=︒-︒--=1118022αβ-+.【点睛】此题考查平行线的性质:两直线平行内错角相等,两直线平行同旁内角互补,平行线的推论,正确引出辅助线是解题的关键.8.(1);(2),见解析;(3)不变, 【分析】(1)根据平行线的性质求出,再求出的度数,利用内错角相等可求出角的度数;(2)过点作∥,类似(1)利用平行线的性质,得出三个角的关系; (3)运用解析:(1)23︒;(2)BCD A B ∠=∠+∠,见解析;(3)不变, 25FOG ∠=︒ 【分析】(1)根据平行线的性质求出50A DCE ∠=∠=︒,再求出BCE ∠的度数,利用内错角相等可求出角的度数;(2)过点C 作CE ∥AB ,类似(1)利用平行线的性质,得出三个角的关系;(3)运用(2)的结论和平行线的性质、角平分线的性质,可求出FOG ∠的度数,可得结论.【详解】(1)因为CE ∥AB ,所以50A DCE ∠=∠=︒,B BCE ∠=∠因为∠BCD =73 °,所以23BCE BCD DCE ∠=∠-∠=︒,故答案为:23︒(2)BCD A B ∠=∠+∠,如图②,过点C 作CE ∥AB ,则A DCE ∠=∠,B BCE ∠=∠.因为BCD DCE BCE ∠=∠+∠,所以BCD BAD B ∠=∠+∠,(3)不变,设ABE x ∠=,因为BE 平分ABC ∠,所以CBE ABE x ∠=∠=.由(2)的结论可知BCD BAD ABC ∠=∠+∠,且50BAD ︒∠=,则:502BCD x ∠=︒+.因为MN ∥AD ,所以502BON BCD x ∠=∠=︒+,因为OF 平分BON ∠, 所以1252COF NOF BON x ∠=∠=∠=︒+. 因为OG ∥BE ,所以COG CBE x ∠=∠=,所以2525FOG COF COG x x ∠=∠-∠=+-=︒︒.【点睛】本题考查了平行线的性质和角平分线的定义,解题关键是熟练运用平行线的性质证明角相等,通过等量代换等方法得出角之间的关系.9.(1)120º,120º;(2)160;(3)【分析】(1)过点作,,根据 ,平行线的性质和周角可求出,则 ,再根据 , ,可得 , ,可求出 ,,根据 即可得到结果;(2)同理(1)的求法,解析:(1)120º,120º;(2)160;(3)()1360n m n -⋅- 【分析】(1)过点,C D 作CG EF ,DH EF ,根据 120FAC ACB ∠=∠=︒,平行线的性质和周角可求出120GCB ∠=︒,则 120CBN GCB ∠=∠=︒,再根据 12CAD FAC ∠=∠, 12CBD CBN ∠=∠,可得 1602CBD CBN ∠=∠=︒, 1602CAD FAC ∠=∠=︒,可求出 60ADH FAD ∠=∠=︒,60BDH DBN ∠=∠=︒,根据 ADB ADH BDH ∠=∠+∠即可得到结果;(2)同理(1)的求法,根据120FAC ACB ∠=∠=︒,13CAD FAC ∠=∠, 13CBD CBN ∠=∠求解即可;(3)同理(1)的求法,根据FAC ACB m ∠=∠=︒,1CAD FAC n ∠=∠,1CBD CBN n ∠=∠求解即可;【详解】解:(1)如图示,分别过点,C D 作CG EF ,DH EF ,∵EF MN ,∴EF MN CG DH ,∴120ACG FAC ∠=∠=︒,∴360120GCB ACG ACB ∠=︒-∠-∠=︒,∴120CBN GCB ∠=∠=︒,∵1602CBD CBN ∠=∠=︒, 1602CAD FAC ∠=∠=︒∴60DBN CBN CBD ∠=∠-∠=︒,又∵60FAD FAC CAD ∠=∠-∠=︒,∴60ADH FAD ∠=∠=︒,60BDH DBN ∠=∠=︒,∴120ADB ADH BDH ∠=∠+∠=︒.(2)如图示,分别过点,C D 作CG EF ,DH EF ,∵EF MN ,∴EF MN CG DH ,∴120ACG FAC ∠=∠=︒,∴360120GCB ACG ACB ∠=︒-∠-∠=︒,∴120CBN GCB ∠=∠=︒, ∵1403CBD CBN ∠=∠=︒, 1403CAD FAC ∠=∠=︒∴80DBN CBN CBD ∠=∠-∠=︒,又∵80FAD FAC CAD ∠=∠-∠=︒,∴80ADH FAD ∠=∠=︒,80BDH DBN ∠=∠=︒,∴160ADB ADH BDH ∠=∠+∠=︒.故答案为:160;(3)同理(1)的求法∵EF MN ,∴EF MN CG DH , ∴ACG FAC m ∠=∠=︒,∴3603602GCB ACG ACB m ∠=︒-∠-∠=︒-︒,∴3602CBN GCB m ∠=∠=︒-︒, ∵13602m CBD CBN n n ︒-︒∠=∠=, 1m CAD FAC n n︒∠=∠= ∴()()360213602=3602m n m DBN CB D m n N n CB ︒-︒-︒-︒-︒∠-∠=-=∠︒, 又∵()1n m FAD FAC CAD m m n n -︒∠=∠-∠=︒-=︒, ∴()1n ADH FAD m n -∠=∠=︒, ()13602n BDH DBN m n-∠=∠=︒-︒, ∴()()()1113602=360n n n ADB ADH BDH m m m n n n --∠=∠+∠=-︒︒-︒︒-+︒. 故答案为:()1360n m n-⋅-. 【点睛】 本题主要考查了平行线的性质和角度的运算,熟悉相关性质是解题的关键.10.(1);(2)理由见解析;(3),理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠ 解析:(1)242∠=︒;(2)理由见解析;(3)12∠=∠,理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠DBC ,则∠ABD =∠ABC−∠DBC =60°−∠1,进而得出结论;(3)过点C 作CP ∥a ,由角平分线定义得∠CAM =∠BAC =30°,∠BAM =2∠BAC =60°,由平行线的性质得∠1=∠BAM =60°,∠PCA =∠CAM =30°,∠2=∠BCP =60°,即可得出结论.【详解】解:(1)如图1 148∠=︒,90BCA ∠=︒,3180142BCA ∴∠=︒-∠-∠=︒,//a b ,2342∴∠=∠=︒;图1(2)理由如下:如图2. 过点B 作//BD a ,图22180ABD ∴∠+∠=︒,//a b ,//b BD ∴,1∴∠=∠DBC ,601ABD ABC DBC ∴∠=∠-∠=︒-∠,2601180∴∠+︒-∠=︒,21120∴∠-∠=︒;(3)12∠=∠,图3理由如下:如图3,过点C 作//CP a , AC 平分BAM ∠,30CAM BAC ∴∠=∠=︒,260BAM BAC ∠=∠=︒,又//a b ,//CP b ∴,160BAM ∠=∠=︒,30PCA CAM ∴∠=∠=︒,903060BCP BCA PCA ∴∠=∠-∠=︒-︒=︒,又//CP a ,260BCP ∴∠=∠=︒,12∠∠∴=.【点睛】本题是三角形综合题目,考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识;本题综合性强,熟练掌握平移的性质和平行线的性质是解题的关键.三、解答题11.(1),理由详见解析;(2),理由详见解析:(3)①;②360°;(4); .【分析】(1)根据三角形外角等于不相邻的两个内角之和即可得出结论;(2)根据三角形内角和定理及对顶角相等即可得出结解析:(1)D A B C ∠=∠+∠+∠,理由详见解析;(2)A D B C ∠+∠=∠+∠,理由详见解析:(3)①1902D A ∠=︒+∠;②360°;(4)124E ∠=︒; =14F ∠︒.【分析】(1)根据三角形外角等于不相邻的两个内角之和即可得出结论;(2)根据三角形内角和定理及对顶角相等即可得出结论;(3)①根据角平分线的定义及三角形内角和定理即可得出结论;②连结BE ,由(2)的结论及四边形内角和为360°即可得出结论;(4)根据(1)的结论、角平分线的性质以及三角形内角和定理即可得出结论.【详解】(1)D A B C ∠=∠+∠+∠.理由如下:如图1,BDE B BAD ∠=∠+∠,CDE C CAD ∠=∠+∠,BDC B BAD C CAD B BAC C ∴∠=∠+∠+∠+∠=∠+∠+∠,D A B C ∴∠=∠+∠+∠; (2)A D B C ∠+∠=∠+∠.理由如下:在ADE ∆中,180AED A D ∠=︒-∠-∠,在BCE ∆中,180BEC B C ∠=︒-∠-∠,AED BEC ∠=∠,A D B C ∴∠+∠=∠+∠;(3)①180A ABC ACB ∠=︒-∠-∠,180D DBC DCB ∠=︒-∠-∠,BD 、CD 分别平分ABC∠和ACB ∠,∴1122ABC ACB DBC DCB ∠+∠=∠+∠,1111180()180(180)902222D ABC ACB A A ∴∠=︒-∠+∠=︒-︒-∠=︒+∠.故答案为:1902D A ∠=︒+∠.②连结BE .∵C D CBE DEB ∠+∠=∠+∠,360A B C D E F A ABE F BEF ∴∠+∠+∠+∠+∠+∠=∠+∠+∠+∠=︒. 故答案为:360︒;(4)由(1)知,BDC B C BAC ∠=∠+∠+∠,26B ∠=︒,54C ∠=︒,80BDC BAC ∴∠=︒+∠,402CDF CAE ∴∠=︒+∠,4BAC CAE ∠=∠,2BDC CDF ∠=∠,1902GDE CDF ∴∠=︒-∠,26180AGD B GDB CDF ∠=∠+∠=︒+︒-∠,3GAE CAE ∠=∠,3336064(2)644012422E GAE AGD GDE CAE CDF ∴∠=︒-∠-∠-∠=︒-∠-∠=︒+⨯︒=︒; 180180(206)2262264014F AGF GAF CDF CAE CDF CAE ∠=︒-∠-∠=︒-︒-∠-∠=-︒+∠-∠=-︒+︒=︒.【点睛】本题考查了角平分线的性质,三角形内角和;熟练掌握角平分线的性质,进行合理的等量代换是解题的关键.12.(1)∠DAE =14°;(2)∠DFE =14°;(3)∠DAE 的大小不变,∠DAE =14°,证明详见解析.【分析】(1)求出∠ADE 的度数,利用∠DAE=90°-∠ADE 即可求出∠DAE解析:(1)∠DAE =14°;(2)∠DFE =14°;(3)∠DAE 的大小不变,∠DAE =14°,证明详见解析.【分析】(1)求出∠ADE 的度数,利用∠DAE=90°-∠ADE 即可求出∠DAE 的度数.(2)求出∠ADE 的度数,利用∠DFE=90°-∠ADE 即可求出∠DAE 的度数.(3)利用AE 平分∠BEC ,AD 平分∠BAC ,求出∠DFE=15°即是最好的证明.【详解】(1)∵∠B=45°,∠C=73°,∴∠BAC=62°,∵AD 平分∠BAC ,∴∠BAD=∠CAD=31°,∴∠ADE=∠B+∠BAD=45°+31°=76°,∵AE ⊥BC ,∴∠AEB=90°,∴∠DAE=90°-∠ADE=14°.(2)同(1),可得,∠ADE=76°,∵FE⊥BC,∴∠FEB=90°,∴∠DFE=90°-∠ADE=14°.(3)DAE∠=14°∠的大小不变.DAE理由:∵ AD平分∠ BAC,AE平分∠BEC∴∠BAC=2∠BAD,∠BEC=2∠AEB∵∠BAC+∠B+∠BEC+∠C =360°∴2∠BAD+2∠AEB=360°-∠B-∠C=242°∴∠BAD+∠AEB=121°∵∠ADE=∠B+∠BAD∴∠ADE=45°+∠BAD∴∠DAE=180°-∠AEB-∠ADE=180°-∠AEB-45°-∠BAD=135°-(∠AEB+∠BAD)=135°-121°=14°【点睛】本题考查了三角形内角和定理和三角形外角的性质,熟练掌握性质是解题的关键. 13.解决问题:6;拓展延伸:(1)S1=2S2 (2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)解析:解决问题:6;拓展延伸:(1)S1=2S2(2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)作△ABD的中线AE,则有BE=ED=DC,从而得到△ABE的面积=△AED的面积=△ADC的面积,由此即可得到结论;(2)连接AO.则可得到△BOD的面积=△BOC的面积,△AOC的面积=△AOD的面积,△EOC的面积=△BOC的面积的一半,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,求出a、b的值,即可得到结论.试题解析:解:解决问题连接AE.∵点D、E分别是边AB、BC的中点,∴S△ADE=S△BDE,S△ABE=S△AEC.∵S△BDE =2,∴S△ADE =2,∴S△ABE=S△AEC=4,∴四边形ADEC的面积=2+4=6.拓展延伸:解:(1)作△ABD的中线AE,则有BE=ED=DC,∴△ABE的面积=△AED的面积=△ADC的面积= S2,∴S1=2S2.(2)连接AO.∵CO=DO,∴△BOD的面积=△BOC的面积=3,△AOC的面积=△AOD的面积.∵BO=2EO,∴△EOC的面积=△BOC的面积的一半=1.5,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,解得:a=6,b=4.5,∴四边形ADOE的面积为=a+b=6+4.5=10.5.14.(1)见详解;(2)15°;(3)67.5°;(4)45cm;(5)10s或30s或40s 【分析】(1)运用角平分线定义及平行线性质即可证得结论;(2)如图2,过点E作EK∥MN,利用平行线性解析:(1)见详解;(2)15°;(3)67.5°;(4)45cm;(5)10s或30s或40s【分析】(1)运用角平分线定义及平行线性质即可证得结论;(2)如图2,过点E作EK∥MN,利用平行线性质即可求得答案;(3)如图3,分别过点F、H作FL∥MN,HR∥PQ,运用平行线性质和角平分线定义即可得出答案;(4)根据平移性质可得D′A=DF,DD′=EE′=AF=5cm,再结合DE+EF+DF=35cm,可得出答案;(5)设旋转时间为t秒,由题意旋转速度为1分钟转半圈,即每秒转3°,分三种情况:①当BC∥DE时,②当BC∥EF时,③当BC∥DF时,分别求出旋转角度后,列方程求解即可.【详解】(1)如图1,在△DEF中,∠EDF=90°,∠DFE=30°,∠DEF=60°,∵ED平分∠PEF,∴∠PEF=2∠PED=2∠DEF=2×60°=120°,∵PQ∥MN,∴∠MFE=180°−∠PEF=180°−120°=60°,∴∠MFD=∠MFE−∠DFE=60°−30°=30°,∴∠MFD=∠DFE,∴FD平分∠EFM;(2)如图2,过点E作EK∥MN,∵∠BAC=45°,∴∠KEA=∠BAC=45°,∵PQ∥MN,EK∥MN,∴PQ∥EK,∴∠PDE=∠DEK=∠DEF−∠KEA,又∵∠DEF=60°.∴∠PDE=60°−45°=15°,故答案为:15°;(3)如图3,分别过点F、H作FL∥MN,HR∥PQ,∴∠LFA=∠BAC=45°,∠RHG=∠QGH,∵FL∥MN,HR∥PQ,PQ∥MN,∴FL∥PQ∥HR,∴∠QGF+∠GFL=180°,∠RHF=∠HFL=∠HFA−∠LFA,∵∠FGQ和∠GFA的角平分线GH、FH相交于点H,∴∠QGH=12∠FGQ,∠HFA=12∠GFA,∵∠DFE=30°,∴∠GFA=180°−∠DFE=150°,∴∠HFA=12∠GFA=75°,∴∠RHF=∠HFL=∠HFA−∠LFA=75°−45°=30°,∴∠GFL=∠GFA−∠LFA=150°−45°=105°,∴∠RHG=∠QGH=12∠FGQ=12(180°−105°)=37.5°,∴∠GHF=∠RHG+∠RHF=37.5°+30°=67.5°;(4)如图4,∵将△DEF沿着CA方向平移至点F与A重合,平移后的得到△D′E′A,∴D′A=DF,DD′=EE′=AF=5cm,∵DE+EF+DF=35cm,∴DE+EF+D′A+AF+DD′=35+10=45(cm),即四边形DEAD′的周长为45cm;(5)设旋转时间为t秒,由题意旋转速度为1分钟转半圈,即每秒转3°,分三种情况:BC∥DE时,如图5,此时AC∥DF,∴∠CAE=∠DFE=30°,∴3t=30,解得:t=10;BC∥EF时,如图6,∵BC∥EF,∴∠BAE=∠B=45°,∴∠BAM=∠BAE+∠EAM=45°+45°=90°,∴3t=90,解得:t=30;BC∥DF时,如图7,延长BC交MN于K,延长DF交MN于R,∵∠DRM=∠EAM+∠DFE=45°+30°=75°,∴∠BKA=∠DRM=75°,∵∠ACK=180°−∠ACB=90°,∴∠CAK=90°−∠BKA=15°,∴∠CAE=180°−∠EAM−∠CAK=180°−45°−15°=120°,∴3t=120,解得:t =40,综上所述,△ABC 绕点A 顺时针旋转的时间为10s 或30s 或40s 时,线段BC 与△DEF 的一条边平行.【点睛】本题主要考查了平行线性质及判定,角平分线定义,平移的性质等,添加辅助线,利用平行线性质是解题关键.15.(1)50°;(2)①见解析;②见解析;(3)360°.【分析】(1)根据题意,已知,,可结合三角形内角和定理和折叠变换的性质求解; (2)①先根据折叠得:∠ADE=∠A′DE ,∠AED=∠A′解析:(1)50°;(2)①见解析;②见解析;(3)360°.【分析】(1)根据题意,已知70C ∠=︒,65B ∠=︒,可结合三角形内角和定理和折叠变换的性质求解;(2)①先根据折叠得:∠ADE=∠A′DE ,∠AED=∠A′ED ,由两个平角∠AEB 和∠ADC 得:∠1+∠2等于360°与四个折叠角的差,化简得结果;②利用两次外角定理得出结论;(3)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'GF+∠B'FG )以及(∠C'DE+∠C'ED )和(∠A'HL+∠A'LH ),再利用三角形的内角和定理即可求解.【详解】解:(1)∵70C ∠=︒,65B ∠=︒,∴∠A′=∠A=180°-(65°+70°)=45°,∴∠A′ED+∠A′DE =180°-∠A′=135°,∴∠2=360°-(∠C+∠B+∠1+∠A′ED+∠A′DE )=360°-310°=50°;(2)①122A ∠+∠=∠,理由如下由折叠得:∠ADE=∠A′DE ,∠AED=∠A′ED ,∵∠AEB+∠ADC=360°,∴∠1+∠2=360°-∠ADE-∠A′DE -∠AED-∠A′ED=360°-2∠ADE-2∠AED ,∴∠1+∠2=2(180°-∠ADE-∠AED )=2∠A ;②221A ∠=∠+∠,理由如下:∵2∠是ADF 的一个外角∴2A AFD ∠=∠+∠.∵AFD ∠是A EF '△的一个外角∴1∠=∠+∠AFD A'又∵A A'∠=∠∴221∠=∠+∠A(3)如图由题意知,∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠B'GF+∠B'FG)-(∠C'DE+∠C'ED)-(∠A'HL+∠A'LH)=720°-(180°-∠B')-(180°-C')-(180°-A')=180°+(∠B'+∠C'+∠A')又∵∠B=∠B',∠C=∠C',∠A=∠A',∠A+∠B+∠C=180°,∴∠1+∠2+∠3+∠4+∠5+∠6=360°.【点睛】题主要考查了折叠变换、三角形、四边形内角和定理.注意折叠前后图形全等;三角形内角和为180°;四边形内角和等于360度.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复旦中学2011-2012学年度第二学期期末教学质量检测试题(卷1)八 年 级 数 学一﹑精心选一选,你一定很棒(每题4分,共40分)1.下列运算中,正确的是A .326a a a =÷ B .2222x y x y =⎪⎭⎫ ⎝⎛ C .1=+++b a b b a a D .y x x xy x x +=+22 2.下列说法中,不正确...的是 A .为了解一种灯泡的使用寿命,宜采用普查的方法 B .众数在一组数据中若存在,可以不唯一 C .方差反映了一组数据与其平均数的偏离程度D .对于简单随机样本,可以用样本的方差去估计总体的方差 3.能判定四边形是平行四边形的条件是A .一组对边平行,另一组对边相等B .一组对边相等,一组邻角相等C .一组对边平行,一组邻角相等D .一组对边平行,一组对角相等4.反比例函数k y x=在第一象限的图象如图所示,则k 的值可能是A .1B .2C .3D .45.在平面直角坐标系中,已知点A (0,2),B (32-,0), C (0,2-),D (32,0),则以这四个点为顶点的四边形ABCD 是A .矩形B .菱形C .正方形D .梯形6.某校八年级(2)班的10名团员在“情系灾区献爱心”捐款活动中,捐款情况如下(单位:元):10 8 12 15 10 12 11 910 13.则这组数据的A .平均数是11B .中位数是10C .众数是10.5D .方差是3.97.一个三角形三边的长分别为15cm ,20cm 和25cm ,则这个三角形最长边上的高为 A.15cm B.20cm C.25cm D.12cm 8.已知,反比例函数的图像经过点M (k+2,1)和N(-2,2k ),则这个反比例函数是A.xy 1=B.xy 1-= C.xy 2=D.xy 2-=9.如图所示,有一张一个角为600的直角三角形纸片,沿其一 条中位线剪开后,不能拼成的四边形是A.邻边不等的矩形B.等腰梯形C.有一角是锐角的菱形D.正方形10填入下表:某同学根据上表分析得出如下结论:①甲、乙两班学生跳绳成绩的平均水平相同,②乙班优秀的人数多于甲班优秀的人数(每分钟跳绳次数≥170为优秀),③甲班的成绩的波动情况比乙班的成绩的波动大。
上述结论正确的是 A. ①②③B. ①②C. ②③D. ①③二﹑细心填一填,你一定能行(每题4分,共24分) 11.当x = 时,分式211x x -+的值为0,某种感冒病毒的直径为0.0000000031米,用科学记数法表示为 . 12.请写出命题:“等腰三角形的两个底角相等”的逆命题 . 13.如图,□ABCD 中,AE,CF 分别是∠BAD,∠BCD 的角平分线,请添加一个条件 使四边形AECF 为菱形.14.已知梯形ABCD 中,AD ∥BC ,∠ABC=60°,AE 为梯形的高,且BE=1,则AD=______. 15.如图,矩形ABCD 的对角线BD 过O 点,BC ∥x 轴,且A (2,-1),则经过C 点的反比例函数的解析式为 .16.如图,是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm ),计算两圆孔中心A 和B 的距离为______mm .三、解答题(每题6分,共30分)16题图A BE C DF 13题图17.(本题6分)计算:230120.125200412-⎛⎫-⨯++- ⎪⎝⎭18.(本题6分)先化简,再求值:412)211(22-++÷+-x x x x ,其中3-=x19.(本题6分)解方程:482222-=-+-+x x x x x20.(本题6分)如图,在等腰梯形ABCD 中,AB ∥DC ,AC 、BD 是对角线, △ABD ≌△ABE 。
求证:四边形AEBC 是平行四边形。
21. (本题6分)已知反比例函数5m y x-=,(1)若在此反比例函数图象的每一条曲线上,y 都随着x 的增大而减小,求m 的取值范围值;(2)若点A (2,3)在此反比例函数图象上,求其解析式.四、解答题(每题12分,共36分) 22.(本题12分)在学校组织的“喜迎世博,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ; (2(3①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩;第23题图一班竞赛成绩统计图二班竞赛成绩统计图③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩.23.(本题12分) 如图,在矩形ABCD 中,对角线AC,BD 相交于O ,DE 垂直平分OC ,若AD=4,求AB,AC,DE 的长.24. (本题l2分)北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率100%=⨯利润成本)五、解答题(每题10分,共20分)25. (本题l0分)已知:如图,等腰梯形ABCD 中,AD ∥BC ,AB =DC ,点P 是腰DC 上的一个动点(P 与D 、C 不重合),点E 、F 、G 分别是线段BC 、PC 、BP 的中点.(1)试探索四边形EFP G 的形状,并说明理由;(2)若∠A =120°,AD =2,DC =4,当PC 为何值时,四边形EFPG 是矩形?并加以证明.26.(本题l0分)如图,在平面直角坐标系中,直线AB 与y 轴和x 轴分别交于点A 、点B ,与反比例函数m y x=在第一象限的图象交于点C(1,6)、点D(3,n).过点C 作CE ⊥y 轴于E ,过点D 作DF ⊥x 轴于F . (1)求m ,n 的值;(2)求直线AB 的函数解析式;(3)求:△OCD 的面积。
A DPF CE GB复旦中学2009-2010学年度第二学期期末教学质量检测试题(卷2)八年级数学答题卷二﹑填空题(每题4分,共24分)11.________,________;12.______________________________;13.___________________;14.________;15._________;16.________.三、解答题(每题6分,共30分)17.(本题6分)计算:230120.125200412-⎛⎫-⨯++- ⎪⎝⎭18.(本题6分)先化简,再求值:412)211(22-++÷+-x x x x ,其中3-=x19.(本题6分)解方程:482222-=-+-+x x x x x20. (本题6分)已知反比例函数5m y x-=,(1)若在此反比例函数图象的每一条曲线上,y 都随着x 的增大而减小,求m 的取值范围值;(2)若点A (2,3)在此反比例函数图象上,求其解析式.21.(本题6分)如图,在等腰梯形ABCD 中,AB ∥DC ,AC 、BD 是对角线, △ABD ≌△ABE 。
求证:四边形AEBC 是平行四边形。
四、解答题(每题12分,共36分) 22.(本题12分)在学校组织的“喜迎世博,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ;第23题图一班竞赛成绩统计图二班竞赛成绩统计图(2)请你将表格补充完整:(3①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩; ③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩.23.(本题12分) 如图,在矩形ABCD 中,对角线AC,BD 相交于O ,DE 垂直平分OC ,若AD=4,求AB,AC,DE 的长.24. (本题l2分)北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元. (1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率100%=⨯利润成本)五、解答题(每题10分,共20分)25. (本题l0分)已知:如图,等腰梯形ABCD中,AD∥BC,AB=DC,点P是腰DC上的一个动点(P与D、C不重合),点E、F、G分别是线段BC、PC、BP的中点.(1)试探索四边形EFP G的形状,并说明理由;(2)若∠A=120°,AD=2,DC=4,当PC为何值时,四边形EFPG是矩形?并加以证明.26.(本题l0分)如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数myx在第一象限的图象交于点C(1,6)、点D(3,n).过点C作CE⊥y轴于E,过点D作DF⊥x轴于F.(1)求m,n的值;(2)求直线AB的函数解析式;(3)求:△OCD的面积。
A DPFCEGB。
