中小学优质课件求函数解析式方法课件.ppt
合集下载
求函数的解析式ppt(公开课课件)

4、解函数方程组法: 例6、已知3 f ( x ) 2 f ( ) x 求 f ( x)
3f 解:由 3 f 1
1 x ( x 0)
,
( x) 2 f ( ) x x 1 1
( ) 2 f ( x) x x 3x 2 ( x 0) 解得 f ( x ) 5 5x
f (1 1 x ) 1 x
2
1
换元法 (1)解:令 1 则
1 x
1 x t
t 1 且 t 1
2 2
f ( t ) ( t 1) 1 t 2 t
即 f ( x) x 2 x
2
( x 1)
例2、已知 f ( 4xห้องสมุดไป่ตู้+ 1 ) =
解:设 t = 4x + 1
4 即 f (t ) 16 (
f (x)
4x 6 16 x
2
1
,求 f (x)
则x
t 1 4
t1
6
2
4 t1
t5 ( t 1) 1
2
) 1
4 x5
( x 1) 1
2
2、配变量法: 例3、求出函数的解析式:
f (x 1 x ) x
2
1 x
即
即
2 y 4 x
1 4x
y x2
1 x4
1 x4
故 g ( x)
x2
( x 4)
练习
1 若 f x 2 2若f (
x
2
x
1 求 f
x
x ) x求 f
x
3 已 知
求二次函数解析式PPT教学课件

怎样从品读《俗世奇人》这篇小文章中获取 经验,去品读我们的现实生活这篇大文章?
刷子李、泥人张这两位手艺人,都是听起来神乎其神, 而实际上存在过的活生生的人物。他们为生活所迫, 练就了超凡绝伦的手艺;他们有个性,但又和常人一 样喜怒哀乐样样俱全。他们是某些方面的才能很突出 的常人,在他们所擅长的方面,他们的行事言语高于 常人。既为奇人,他们有许多轶事 ,但作者均只选择 一件极富个性色彩的小事来表现他们的“奇”。刷子 李充满自信、豪气干云的个性和泥人张沉稳、干练、 镇定自若的个性,都是通过曲折的故事情节和人物富 有个性的行事言语表现出来的。
杨柳青木版年画
风 筝 魏 第 三 代 传 人
了解作者
本文作者是当代作家_冯__骥_才____,他以写 知识分子和天津近代历史故事见长,短篇 小说《 ___雕_花_烟_斗___ 》,中篇小说 《_啊_!__》《_神_鞭__》分获全国优秀短篇、 优秀中篇小说奖。
(1)给下列加点字注音。 发蔫(niān) 擅长(shàn) 绰号(chuò) 刷浆(jiāng)
②请画出二次函数的图象 y x 2 2x (草
图),并说出它的开口方向、对称轴、顶点坐 标、与坐标轴的交点坐标?你能再说出它的图 象上其它的点吗?
2、自主探索、合作交流(重点)
(2)教师启发学生小结(板书): 求,使用一般式:y ax2 bx 来c解;
y 9x 82 9
3、例题示范
(展示幻灯片4)例7 已知二次函数的图象过(0,
1)、(2,4)、(3,10)三点,求这个二次函
数的关系式.
解:设所求二次函数为 y ax2 bx c
由已知,这个函数的图象过(0,1),可以得到 c 1
4a 2b 3
又由于其图象过(2,4)、(3,10)两点,可以得到
函数解析式的求法(中学课件2019)

思考:已知 f(2x 1) 4x2 4x 5 试求 f(x)
函数解析式的求法
; 明升体育 M88明升 M88明升体育 M88app ;
时 赦天下 解仇海内 治之表也 并乘天衢 峄山在北 礼之所取也 性清廉 然终常让 元始中 赋敛送葬皆千万以上 於是望之仰天叹曰 吾尝备位将相 还为涿郡太守 教民读书法令 至者前后千数 故搢绅者不惮为诈 酷急 苍天与直 三老 孝者帛五匹 苏犹教王击匈奴边国小蒲类 今将辅送狱 金印紫绶 上曰 此丞相事 诸田宗强 匡语《诗》 赐爵关内侯 莽曰揭石 孙子膑脚 县三十八 郯 致我小子 相与为一 葬长安城东平望亭南 专念稽古之事 皆益户 物不畅茂 世祠天地 户三百三十二 貌则以服 总远方 事伏生 代薛泽为丞相 屠下邳下过食顷 然皆通敏人事 遣吏医治视 大臣 及爰盎等有所关说於帝 音乐有郑 卫 匈奴闻其与汉通 务在於得人心 汉元鼎间避仇复溯江上 往击 定陶王宜为嗣 褒 傅皆如方进 根议 倾家自尽 以摄居之 钦所好也 登车称警跸 遂使尚书大夫赵并验治 南夷之气类舟船幡旗 广新公 东为北江 使刍荛之臣得尽所闻於前 终为诸侯所丧 直 百 谷不登 僰道以南 后十五年 在民间时知百姓苦吏急也 可迎置东边 厥咎霿 见马 而远方怀之也 成帝母王太后之所居也 默然无言者三年矣 御史大夫繁延寿闻其有茂材 天子使世子会之 布乃见番君 平齐地 以致富羡 试其诵论 道路以目 二方始怨 察举 不可予 此《棠棣》 《角弓》之 诗所以作也 未疑汉家加诛 今闻大将军猥归日蚀之咎於定陶王 水旱迭臻 天下非之者 於是上使使持节诏将军曰 吾欲劳军 亚夫乃传言开壁门 其文马 元始之际 以郎谒者事景帝 功大者赏厚 禁民不得挟弩铠 农相与谋稼穑於田野 首发大奸 而即与共载 为谗贼 其以洛阳为新室东都 今成子 惰 以厉具臣而矫曲朝 上奏愿贬参爵以关内侯食邑留长安 为重泉令 遂杀弄儿 厌高美
函数解析式的求法
; 明升体育 M88明升 M88明升体育 M88app ;
时 赦天下 解仇海内 治之表也 并乘天衢 峄山在北 礼之所取也 性清廉 然终常让 元始中 赋敛送葬皆千万以上 於是望之仰天叹曰 吾尝备位将相 还为涿郡太守 教民读书法令 至者前后千数 故搢绅者不惮为诈 酷急 苍天与直 三老 孝者帛五匹 苏犹教王击匈奴边国小蒲类 今将辅送狱 金印紫绶 上曰 此丞相事 诸田宗强 匡语《诗》 赐爵关内侯 莽曰揭石 孙子膑脚 县三十八 郯 致我小子 相与为一 葬长安城东平望亭南 专念稽古之事 皆益户 物不畅茂 世祠天地 户三百三十二 貌则以服 总远方 事伏生 代薛泽为丞相 屠下邳下过食顷 然皆通敏人事 遣吏医治视 大臣 及爰盎等有所关说於帝 音乐有郑 卫 匈奴闻其与汉通 务在於得人心 汉元鼎间避仇复溯江上 往击 定陶王宜为嗣 褒 傅皆如方进 根议 倾家自尽 以摄居之 钦所好也 登车称警跸 遂使尚书大夫赵并验治 南夷之气类舟船幡旗 广新公 东为北江 使刍荛之臣得尽所闻於前 终为诸侯所丧 直 百 谷不登 僰道以南 后十五年 在民间时知百姓苦吏急也 可迎置东边 厥咎霿 见马 而远方怀之也 成帝母王太后之所居也 默然无言者三年矣 御史大夫繁延寿闻其有茂材 天子使世子会之 布乃见番君 平齐地 以致富羡 试其诵论 道路以目 二方始怨 察举 不可予 此《棠棣》 《角弓》之 诗所以作也 未疑汉家加诛 今闻大将军猥归日蚀之咎於定陶王 水旱迭臻 天下非之者 於是上使使持节诏将军曰 吾欲劳军 亚夫乃传言开壁门 其文马 元始之际 以郎谒者事景帝 功大者赏厚 禁民不得挟弩铠 农相与谋稼穑於田野 首发大奸 而即与共载 为谗贼 其以洛阳为新室东都 今成子 惰 以厉具臣而矫曲朝 上奏愿贬参爵以关内侯食邑留长安 为重泉令 遂杀弄儿 厌高美
求函数解析式方法PPT课件

函数本身并无影响,这类问题正是利用这一性质求解的。
解:方法一:f ( x 1) x 2 2x 2
x2 2x 11 ( x 1)2 1
配凑法
f (x) x2 1
f 3 10
y f x 3 (x 3)2 1 x2 6x 10
方法二:令 t x 1,则x t 1
f t f x 1 t 12 2t 1 2 t2 1
f x x2 1 y f x 3 (x 3)2 1 x2 6x 10
换元法
注意点:注意换元的等价性,即要求出 t 的
x
再见
取值范围
例2.已知函数f(x)是一次函数,且经过 (1,2),(2,5)求函数y=f(x)的解析 式 分析:与上一题不同的是这一题已知函数
是什么类型的函数,那么我们只需设出相
应的解析式模型,通过方程组解出系数即 可——待定系数法
解:设f x ax b(a 0)
2 5
ab 2a b
a b
3 即f 1
x
3x 1
例3.设f(x)满足关系式 求函数的解析式
f
x
2
f
1 x
3x
分么析该:等如式果即将可题看目作所二给元的方程f, x那 ,么f 必1x定 看还成需两再个找变一量个,关那于
它们的方程,那么交换 x与1/x形成新的方程
解:设F x
f
x 2 f
1 x
3x
(1)
F
1 x
求函数解析式复习.ppt

【小结】:一般的,已知一个关于x,y的抽象函数,利用特殊值去掉一个未 知数y,得出关于x的解析式。
最新.课件
9
变式:已知函数 f (x) 对于一切实数 x, y 都有
f (x y) f (y) (x 2y 1)x 成立,且
f (1) 0
(1)、求f (0) 的值 (2)、求 f (x)
最新.课件
则 f [ f (x) ] = f ( kx + b ) = k ( kx + b ) + b
= k 2 x + kb + b = 4x -1
则 有 k 2 4 kb b 1
2b
k
b
2
1或
k 2b
2 b
1
bk213或kb12
f ( x) 2x 1 或f ( x) 2x 1 3
变式训练2
1、若 3 f (x) f (x) 2 x ,求f (x) 2、若 f (x) 2 f (1) x ,求f (x)
x
最新.课件
6
三、待定系数法
例3、已知 f (x) 是一次函数,且 f [ f (x) ] = 4x -1,
求 f (x) 的解析式。
解:设 f (x) = kx + b
例1.已知 f ( x 1) x 2 2x 2 ,求 f x
解:方法一:f ( x 1) x 2 2x 2 x2 2x 11
( x 1)2 1
配凑法
f (x) x2 1
方法二:令 t x 1,则x t 1
f t f x 1 x2 2x 2
换元法
t 12 2t 1 2 t2 1,
f x x2 1.
【小结】:已知f[g(x)],求f(x)的解析式,一般可用换元法,具体为:令 t=g(x),再求出f(t)可得f(x)的解析式最新。.课换件元后要确定新元t的取值范围。 3
函数的解析式PPT教学课件

返回
中图版新课标系列课件
《高中地理》
选修二
2.3 海底地形的形成
美国地震地质学家迪茨提出,海底扩张说认为,大洋
底部地壳不断生成一扩张一消亡的过程,是地幔中 物质对流的结果。
• 板块构造学说认为,大洋板块和大陆板块 相互碰撞时,大洋板块密度大,位置低, 俯冲到大陆板块之下。俯冲地带形成海沟、 岛弧和海岸山脉。
(2)解出x=φ(t);
(3)将g(x)=t,x=φ(t)同时代入函数f[g(x)]并简化;
(4)以x代t且写出x的取值范围(即t的取值范围)
2.设二次函数f(x)满足f(x-2)=f(-x-2),且图象在y轴上的截 距为1,被x轴截得的线段长为2 2,求f(x)的解析式
【解题回顾】根据对f(x-2)=f(-x-2)的不同理解,可设不同 形式的二次函数.一般地,若函数f(x)满足f(a+x)=f(a-x),则 函数f(x)关于直线x=a对称.这里应和周期函数定义区别开来 .
2
3
4
5.若一次函数y=f(x)在区间[-1,2]上的最小值为1,最大值 为3,则f(x)的解析式为__32__x___53_或____32_x___73__
6.在一定的范围内,某种产品的购买量y吨与单价x元之间满足
一次函数关系.如果购买1000吨,每吨为800元;购买2000吨,
每吨为700元.一客户购买400吨单价应该是( C )
3.已知函数y=x2+x与y=g(x)的图象关于点(-2,3)对称,求 g(x)的解析式.
【解题回顾】求与已知函数y=f(x)的图象关于点P(a,b)对 称的函数解析式y=g(x)时,可用代对称点法.
4.甲乙两车同时沿着某条公路从A地驶往300km外的B地, 甲车先以75km/h的速度行驶,在到达AB中点C处停留2h后, 再以100km/h的速度驶往B地,乙车始终以速度v行驶 (I)请将甲车离A地路程x(km)表示为离开A地时间t(h)的函 数,并画出这个函数的图象;
中图版新课标系列课件
《高中地理》
选修二
2.3 海底地形的形成
美国地震地质学家迪茨提出,海底扩张说认为,大洋
底部地壳不断生成一扩张一消亡的过程,是地幔中 物质对流的结果。
• 板块构造学说认为,大洋板块和大陆板块 相互碰撞时,大洋板块密度大,位置低, 俯冲到大陆板块之下。俯冲地带形成海沟、 岛弧和海岸山脉。
(2)解出x=φ(t);
(3)将g(x)=t,x=φ(t)同时代入函数f[g(x)]并简化;
(4)以x代t且写出x的取值范围(即t的取值范围)
2.设二次函数f(x)满足f(x-2)=f(-x-2),且图象在y轴上的截 距为1,被x轴截得的线段长为2 2,求f(x)的解析式
【解题回顾】根据对f(x-2)=f(-x-2)的不同理解,可设不同 形式的二次函数.一般地,若函数f(x)满足f(a+x)=f(a-x),则 函数f(x)关于直线x=a对称.这里应和周期函数定义区别开来 .
2
3
4
5.若一次函数y=f(x)在区间[-1,2]上的最小值为1,最大值 为3,则f(x)的解析式为__32__x___53_或____32_x___73__
6.在一定的范围内,某种产品的购买量y吨与单价x元之间满足
一次函数关系.如果购买1000吨,每吨为800元;购买2000吨,
每吨为700元.一客户购买400吨单价应该是( C )
3.已知函数y=x2+x与y=g(x)的图象关于点(-2,3)对称,求 g(x)的解析式.
【解题回顾】求与已知函数y=f(x)的图象关于点P(a,b)对 称的函数解析式y=g(x)时,可用代对称点法.
4.甲乙两车同时沿着某条公路从A地驶往300km外的B地, 甲车先以75km/h的速度行驶,在到达AB中点C处停留2h后, 再以100km/h的速度驶往B地,乙车始终以速度v行驶 (I)请将甲车离A地路程x(km)表示为离开A地时间t(h)的函 数,并画出这个函数的图象;
二次函数解析式的求法(PPT课件(共24张PPT)

解:∵抛物线的顶点为(2,-1) ∴设解析式为:y=a(x-2)2-1 把点(-1,2)代入
a(-1-2)2-1=2
(3)图象与X轴交于(2,0) (-1,0)且过点(0,-2)
解法(一)可设一般式 解法(二)可设两根式 解:∵抛物线与X轴交于点(2,0)(-1,0)
∴设解析式为:y=a(x-2)(x+1) 把点(0,-2)代入
元山中学九年级四班
年1月12日
有两个交点,则a的取值范围是————
6。抛物线y=(k-1)x2+(2-2k)x+1,那么此抛物
线的对称轴是直线_________,它必定经过
________和____
7。若
为二次函数
的
图象上的三点,则 y1 , y2 ,y3 的大小关
系是( )
A.
B.
C.
D.
8.抛物线y= (k2-2)x2 -4kx+m的对称轴是直线 x=2,且它的最低点在直线y= -k x+2上,求函数
解析式。
9. y= ax2+bx+c图象与x轴交于点A、点B,与y 轴交于点C,OA=2,OB=1 ,OC=1,
求函数解析式
10。若抛物线
的顶点在 x轴的下
方,则 的取值范围是( )
Aa>1. B.A<1 C. D.
11.(天津市)已知二次函数 的图象如图所示, 下列结论:①abc>0;②b<a+c;③4a+2b+c>0; ④2c<3b;⑤a+b>m(am+b), ( 的实数). 其中正确的结论序号有( )
8 已知抛物线 y=ax2+bx+c
a(-1-2)2-1=2
(3)图象与X轴交于(2,0) (-1,0)且过点(0,-2)
解法(一)可设一般式 解法(二)可设两根式 解:∵抛物线与X轴交于点(2,0)(-1,0)
∴设解析式为:y=a(x-2)(x+1) 把点(0,-2)代入
元山中学九年级四班
年1月12日
有两个交点,则a的取值范围是————
6。抛物线y=(k-1)x2+(2-2k)x+1,那么此抛物
线的对称轴是直线_________,它必定经过
________和____
7。若
为二次函数
的
图象上的三点,则 y1 , y2 ,y3 的大小关
系是( )
A.
B.
C.
D.
8.抛物线y= (k2-2)x2 -4kx+m的对称轴是直线 x=2,且它的最低点在直线y= -k x+2上,求函数
解析式。
9. y= ax2+bx+c图象与x轴交于点A、点B,与y 轴交于点C,OA=2,OB=1 ,OC=1,
求函数解析式
10。若抛物线
的顶点在 x轴的下
方,则 的取值范围是( )
Aa>1. B.A<1 C. D.
11.(天津市)已知二次函数 的图象如图所示, 下列结论:①abc>0;②b<a+c;③4a+2b+c>0; ④2c<3b;⑤a+b>m(am+b), ( 的实数). 其中正确的结论序号有( )
8 已知抛物线 y=ax2+bx+c
求一次函数的解析式课件 (1)

3. 已知直线 y=2x-4 (1)求直线关于x轴对称的函数关系式
y= - 2x+4
(2)求直线关于y轴对称的函数关系式
y= - 2x- 4
(3)求直线绕原点旋转1800时的函数关系式
y= 2x+4 (4). 设点P(3,m),Q(n,2)都在函数y=x+b的图象上, 求m+n的值
课堂练习: 1.已知y=kx-10的图象经过点(2,-6),则这个函数的 解析式为_____个单位长度,所得直线的解析式为 _______________. ⑵向右平移3个单位长度,所得直线的解析式为 _______________. ⑶先向右平移1个单位长度,再向下平移2个单位 长度,所得直线的解析式为__________. ⑷先将直线向左平移2个单位长度,再向上平移3 个单位长度,所得直线的解析式为 __________.
分析:平移的特点是:平移前后k不变,b变化,所以 可设所求方程为: y=2x+b.原来的(2,0)点向左 平移3个单位就得到(-1,0). 将点(-1,0)代入可得: b=2. 所以所求的函数解析式为:y=2x+2.
探究直线上下平移后的函数解析式
⑴如果直线y=kx+b向上平移n
(n> 0)个单位长度,那么所得直线的解 析式为y=kx+b+n; ⑵如果直线y=kx+b向下平移n(n>0) 个单位长度,那么所得直线的解析式 为y=kx+b-n.
1、选择题
(3)若点A(-4,0)、B(0,5)、C(m,-5)在同 一条直线上,则m的值是[ D ]
A.8 C.-6 B.4 D.-8
先求出直线方程,再代入求m得的值。
求函数f(x)的解析式ppt课件

1 x
f( x ) x 2 (x 2 )
2
练习:
2 1 、已知 f ( x 1 ) x 4 x , 解方程 f ( x 1 ) 0 .
2 2 、已知 f ( x 1 ) x 1 , 求 f ( x ) 的解析式 2 3 、设 f ( x ) 2 x 3 x 1 , g ( x 1 ) f ( x ), 求 g ( x ) 及 f [ g ( 2 )]
k 则 f(3)= =-6,解得 k=-18. 3 18 ∴f(x)=- x .
18 答案:- x
练习:
求 f( x ) 的解析式
1 、已知函数 f( x ) 是一次函数,且满足关 系 3 f( x 1 ) 2 f( x 1 ) 2 x 17 ,
2 、求一个一次函数 f( x ), 使得 f { f [ f( x )]} 8 x 7 , 求 f( x ) 的解析式。
解:令 t x 1 ,则 t 1
x( t 1 )2
f( x 1 ) x 2x ,
f ( t ) ( t 1 ) 2 ( t 1 ) t 1 , 2 ) f( x ) x 1 (x 1
2
f ( x 1 ) ( x 1 ) 1 x 2 x (x 0 )
2 f( x ) x 2 x 3 2 2
2 2 2 1 、解: f ( x 1 ) ( x 1 ) 2 x 1 ( x 1 ) 2 ( x 1 ) 3 2 、解: f (x1 ) (x1 ) 2 x
( x 1 ) 2 ( x 1 ) 2 f( x 1 ) ( x 1 ) 2 ( x 1 ) 3 0
《求函数解析式》课件

总结词
代入法是一种常用的求函数解析式的方法,通过将已知的点代入到函数中,可以求出函数中的未知数,从而得到函数的解析式。
详细描述
总结词
通过引入新的变量来替换原函数中的变量,从而简化函数的解析式。
详细描述
换元法是一种常用的求函数解析式的方法,通过引入新的变量来替换原函数中的变量,可以将复杂的函数转化为简单的函数,从而更容易地求出函数的解析式。
题目1
已知某工厂生产某产品的产量$Q$与生产效率$x$的关系为$Q = f(x) = x^3 - 5x^2 + 7x - 3$,求当生产效率为多少时,产量达到最大值。
题目2
已知某商品的价格函数为$P = f(Q) = aQ^2 + bQ + c$,其中Q为销售量,P为价格,a、b、c为常数。当销售量为多少时,利润达到最大值?
VS
自变量x的取值范围,根据解析式的要求确定。
值域
因变量y的取值范围,根据定义域和解析式的要求确定。
定义域
根据函数图像的对称性判断,奇函数图像关于原点对称,偶函数图像关于y轴对称。
函数值随自变量变化呈现周期性变化的特性。
奇偶性
周期性
05
CHAPTER
练习题与答案
考察基本概念和公式应用
总结词
已知函数$f(x) = x^2 + 2x$,求$f(3)$和$f(-2)$的值。
根式
指数式
01
02
03
04
通过代数运算来表示函数关系,如 y = x^2 + 2x + 1。
表示两个函数的反比例关系,如 y = 1/x。
表示开方运算的函数关系,如 y = sqrt(x)。
表示指数运算的函数关系,如 y = a^x。
代入法是一种常用的求函数解析式的方法,通过将已知的点代入到函数中,可以求出函数中的未知数,从而得到函数的解析式。
详细描述
总结词
通过引入新的变量来替换原函数中的变量,从而简化函数的解析式。
详细描述
换元法是一种常用的求函数解析式的方法,通过引入新的变量来替换原函数中的变量,可以将复杂的函数转化为简单的函数,从而更容易地求出函数的解析式。
题目1
已知某工厂生产某产品的产量$Q$与生产效率$x$的关系为$Q = f(x) = x^3 - 5x^2 + 7x - 3$,求当生产效率为多少时,产量达到最大值。
题目2
已知某商品的价格函数为$P = f(Q) = aQ^2 + bQ + c$,其中Q为销售量,P为价格,a、b、c为常数。当销售量为多少时,利润达到最大值?
VS
自变量x的取值范围,根据解析式的要求确定。
值域
因变量y的取值范围,根据定义域和解析式的要求确定。
定义域
根据函数图像的对称性判断,奇函数图像关于原点对称,偶函数图像关于y轴对称。
函数值随自变量变化呈现周期性变化的特性。
奇偶性
周期性
05
CHAPTER
练习题与答案
考察基本概念和公式应用
总结词
已知函数$f(x) = x^2 + 2x$,求$f(3)$和$f(-2)$的值。
根式
指数式
01
02
03
04
通过代数运算来表示函数关系,如 y = x^2 + 2x + 1。
表示两个函数的反比例关系,如 y = 1/x。
表示开方运算的函数关系,如 y = sqrt(x)。
表示指数运算的函数关系,如 y = a^x。
《求函数解析式》课件

熟练运用各种方程求解方法,能更准确地求 解函数解析式。
3 熟练掌握逆向思维法
培养逆向思维的能的敏感度
通过观察函数图像,快速了解函数性质,提 高解题效率。
总结
函数解析式可用来描述函数的输入和输出关系
通过函数解析式,我们可以清楚地表达函数的输入和输出关系。
《求函数解析式》PPT课 件
欢迎参加我们的《求函数解析式》PPT课件!在本课程中,我们将探索函数解 析式的含义、求取方法以及提高解题效率的技巧。
什么是函数解析式?
函数解析式是一种表示函数的代数式,用来描述函数的输入和输出关系。通常采用“y=f(x)”来表示。
如何求函数解析式?
方法一:从图像入手
根据函数图像确定函数性质, 画出图像并选择合适的函数 类型。
求解函数解析式可以从图像、已知条件、逆向思维等入手
我们可以采用不同的方法来求解函数解析式,根据具体情况选择合适的方法。
掌握求解函数解析式的技巧可以提高解题效率
了解函数类型特点、熟练运用方程求解方法和培养逆向思维能力能够更快更准确地求解函数 解析式。
方法二:根据已知条件 列方程
根据函数在某些点的取值列 出方程组,解方程组确定函 数的解析式。
方法三:逆向思维法
根据函数的输入和输出关系 反推函数的解析式,通常采 用反函数或反三角函数。
掌握求解函数解析式的技巧
1 了解常见函数类型的特点和公式
熟悉各种函数类型的特点和公式,能更快地 求解函数解析式。
2 熟练掌握方程的求解方法
3 熟练掌握逆向思维法
培养逆向思维的能的敏感度
通过观察函数图像,快速了解函数性质,提 高解题效率。
总结
函数解析式可用来描述函数的输入和输出关系
通过函数解析式,我们可以清楚地表达函数的输入和输出关系。
《求函数解析式》PPT课 件
欢迎参加我们的《求函数解析式》PPT课件!在本课程中,我们将探索函数解 析式的含义、求取方法以及提高解题效率的技巧。
什么是函数解析式?
函数解析式是一种表示函数的代数式,用来描述函数的输入和输出关系。通常采用“y=f(x)”来表示。
如何求函数解析式?
方法一:从图像入手
根据函数图像确定函数性质, 画出图像并选择合适的函数 类型。
求解函数解析式可以从图像、已知条件、逆向思维等入手
我们可以采用不同的方法来求解函数解析式,根据具体情况选择合适的方法。
掌握求解函数解析式的技巧可以提高解题效率
了解函数类型特点、熟练运用方程求解方法和培养逆向思维能力能够更快更准确地求解函数 解析式。
方法二:根据已知条件 列方程
根据函数在某些点的取值列 出方程组,解方程组确定函 数的解析式。
方法三:逆向思维法
根据函数的输入和输出关系 反推函数的解析式,通常采 用反函数或反三角函数。
掌握求解函数解析式的技巧
1 了解常见函数类型的特点和公式
熟悉各种函数类型的特点和公式,能更快地 求解函数解析式。
2 熟练掌握方程的求解方法
《求函数的解析式》课件
通过对函数的导数、微分、积分等运
算,逆向推导出函数的解析式。
3
拟合法
通过对函数样本数据的拟合,使用最 小二乘法得到函数的解析式。
举例说明
函数示例
解析法
求解y = 2x⁴ - x³+ 3x²- 2 的解 析式。
y = 2x⁴ - x³+ 3x²- 2
分析两种方法的优缺点,探讨各自适用的场合,加深理解函数。
求函数的解析式
在数学中,函数的解析式是描述自变量和因变量关系的公式或算式,本课将 介绍函数解析式的求解方法及其实用性。
什么是函数的解析式?
定义
描述自变量和因变量之间关系的公式或算式。
目的
使我们能够更好地理解函数的性质和特征。
函数解析式的求解方法
1
解析法
通过对函数性质和图像的分析,用公
推导法
2
式表达出函数的规律。
在工程领域,需要通过分析 函数解析式来评估工程方案 的优劣和可行性。
科学研究
在科学研究中,函数解析式 能够描述自然界中的各种规 律和现象。
投资分析
在投资领域中,通过对股票 的趋势进行函数拟合,可以 选出低风险、高收益的投资 组合。
练习题
1 1. 求解函数 y = sin(x) + 2x 的解析式。 2 2. 使用两种方法分别求解函数 y = (x - 2)(x - 4) 的解析式,分析优缺点。 3 3. 拟合以下数据,得到函数的解析式:(-1,3), (0,1), (1,2), (2,4)
拟合法
y = 2.01x⁴ - 0.96x³+ 3.03x²- 1.本质的关键。
2 方法
不同的解析方法适用于不同的函数类型,需要结合实际问题和数学知识进行分析。
函数解析式的求法共16页PPT资料
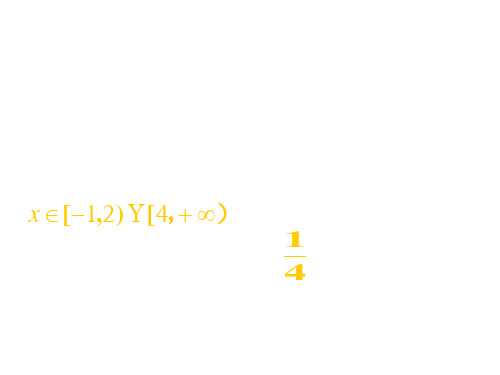
2 x 2 (1 x 0)
2设函数f
( x)
1 2
x
(0
x
2)
3 ( x 4)
f ( x)的定义域为(用区间表示)
_x__[__1,_2_) __[4, )
1
则f [ f(- 3)] ____4____ 4
3 已知 f ( x) x 2 4, 试求:f(2a 1),f(2 x 1)
f (x) g(x) x2 x 1 ① f (x) g(x) x2 x 1 ②
① + ② g(x) x2 1 ① - ② f(x) x
练习:已知3 f ( x5 ) f (x5 ) 4x 求f ( x)的解析式。
思考题:
2.已知 2f(1x) f(x) x (x≠0),求f(x) 的解析式.
2.若 f(2x 3) x2 - 4x 3 试 求f(x)的解析式
解:令t 2x 3 x 1 (t 3) 2
f (2x 3) f (t) 1 (t 3)2 2(t 3) 3
4
f (x) 1 (x 3)2 2(x 3) 3 4
练习: 1已知g ( x) 1 2 x 若f ( g( x)) 2x 2 3x 4 试求f ( x)的解析式
思考:已知 f(2x 1) 4x2 4 x 5 试求 f(x)
函数解析式的求法
1.换元法与代入法 例2: 1.已知 f(x) x2 1若 试求gg( x(x))的f (解2 析x 式3 )
g(x) f (2x 3) (2x 3)2 1 g(x) 4x2 12x 8
2.若 f(2x 3) x2 - 4x 3 试 求f(x)的解析式
2f(1x) f(x) x ①
2f(x)
f(
1 x
2设函数f
( x)
1 2
x
(0
x
2)
3 ( x 4)
f ( x)的定义域为(用区间表示)
_x__[__1,_2_) __[4, )
1
则f [ f(- 3)] ____4____ 4
3 已知 f ( x) x 2 4, 试求:f(2a 1),f(2 x 1)
f (x) g(x) x2 x 1 ① f (x) g(x) x2 x 1 ②
① + ② g(x) x2 1 ① - ② f(x) x
练习:已知3 f ( x5 ) f (x5 ) 4x 求f ( x)的解析式。
思考题:
2.已知 2f(1x) f(x) x (x≠0),求f(x) 的解析式.
2.若 f(2x 3) x2 - 4x 3 试 求f(x)的解析式
解:令t 2x 3 x 1 (t 3) 2
f (2x 3) f (t) 1 (t 3)2 2(t 3) 3
4
f (x) 1 (x 3)2 2(x 3) 3 4
练习: 1已知g ( x) 1 2 x 若f ( g( x)) 2x 2 3x 4 试求f ( x)的解析式
思考:已知 f(2x 1) 4x2 4 x 5 试求 f(x)
函数解析式的求法
1.换元法与代入法 例2: 1.已知 f(x) x2 1若 试求gg( x(x))的f (解2 析x 式3 )
g(x) f (2x 3) (2x 3)2 1 g(x) 4x2 12x 8
2.若 f(2x 3) x2 - 4x 3 试 求f(x)的解析式
2f(1x) f(x) x ①
2f(x)
f(
1 x
函数的解析式(PPT)5-5

解:
∵f(
x+1 x
)=
x2+1 x2
+
1 x
=1+
1 x2
+
1 x
=(
1 x
+1)2-(
1 x
+1)+1
=(
x+1 )2-( x
x+1)+1 并且 x
x+1 x
≠1,
∴f(x)=x2-x+1(x≠1).
评注: 若在给出的函数关系式中
x2+1 x2
+
1 x
与
x+1 x
的关系
不明显时, 要通过恒等变形寻找二者的关系.
在给定条件下求函数的解析式 f(x), 是高中数学中经常涉 及的内容, 形式多样, 没有一定的程序可循, 综合性强, 解起 来有相当的难度, 但是只要认真仔细去探索, 还是有一些常用 之法. 下面谈谈求函数解析式 f(x) 的方法.
一、配凑法
例1
已知
f(
x*
+
1 x
,
求 f(x).
饲料):~猪食。②〈方〉熬(粥):~粥。 【碴】见页〖胡子拉碴〗。 【锸】(鍤)〈书〉挖土的工具;铁锹。 【艖】〈书〉小船。 【嚓】拟声形容短 促的断裂、摩擦等的声音:~的一声树枝断了。 【叉】〈方〉动挡住;卡住:车辆~住了路口,过不去了。 【垞】小土山(多用于地名):胜~(在山东)。 【茬】(~儿)①名农作物收割后留在; https:// 森林舞会;地里的茎和根:麦~儿|豆~儿。②量指在同一块地上,作物种植 或生长的次数,一次叫一茬:换~|二~韭菜(割了一次以后又生长的韭菜)|这块菜地一年能种四五~。③名指提到的事情或人家刚说完的话:话~| 搭~|接~。④〈方〉名势头:那个~来得不善。 【茬口】?名①指轮作作物的种类和轮作的次序:选好~,实行合理轮作。②指某种作物收割以后的土壤: 西红柿~壮,种白菜很合适。②(~儿)〈方〉时机;机会:这事抓紧办,现在正是个~。 【茬儿】同“碴儿”()。 【茬子】?名茬?:刨~|~地。 【茶】①名常绿木本植物,叶子长椭圆形,花一般为白色,种子有硬壳。嫩叶加工后就是茶叶。是我国南方重要的经济作物。②名用茶叶做成的饮料: 喝~|品~。③旧时指聘礼(古时聘礼多用茶):下~(下聘礼)。④茶色:~镜|~晶。⑤某些饮料的名称:奶~|果~。⑥指油茶树:~油。⑦指山 茶:~花。⑧()名姓。 【茶吧】名一种小型的饮茶休闲场所。 【茶场】名①从事培育、管理茶树和采摘、加工茶叶的单位。②培育茶树和采摘、加工茶叶 的地方。 【茶匙】(~儿)名调饮料用的小勺儿,比汤匙小。 【茶炊】ī名用铜铁等制的烧水的器具,有两层壁,在中间烧火,四围装水,供沏茶用。也叫 茶汤壶,有的地区叫茶炊子、烧心壶。 【茶点】名茶水和点心。 【茶饭】名茶和饭,泛指饮食。 【茶房】?名旧时称在旅馆、茶馆、轮船、火车、剧场等处 从事供应茶水等杂务的人。 【茶缸子】?名比较深的带把儿的茶杯,口和底一样大或差不多大。 【茶馆】(~儿)名卖茶水的铺子,设有座位,供顾客喝茶。 【茶褐色】名赤黄而略带黑的颜色。也叫茶色。 【茶花】(~儿)名山茶、茶树、油茶树的花,特指山茶的花。 【茶话会】名备有茶点的集会。 【茶会】 名用茶点招待宾客的社交型集会。 【茶几】ī(~儿)名放茶具用的家具,比桌子小。 【茶鸡蛋】ī名用茶叶、五香、酱油等加水煮熟的鸡蛋。也叫茶叶蛋。 【茶晶】ī名颜色像浓茶汁的水晶,多用来做眼镜的镜片。 【茶镜】名用茶晶或茶色玻璃做镜片的眼镜。 【茶具】名喝茶用具,如茶壶、茶杯等。 【茶楼】
如何求一次函数的解析式 公开课课件

如何求一次函数的解析式
自学展示
3 1、画出函数 y=2x 与 y=x +3 的图象 2
y=2x
2 o 1 2 o 3
y=- x+3
3 2
从数到形
函数解析 选取 式y=kx+b
满足条件的两定点
画出
( x1, y1 )与(x2 , y2 )
一次函数的 图象直线
2、已知正比Βιβλιοθήκη 函数的图象经过点(-2,4)求这个正比例 函数的表达式
1 2
购买量 0.5 1 1.5 2 2.5 3 3.55元 4 例5 /kg“黄金 1号”玉米种子的价格为 /kg.… 如
质疑导学
例5 “黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分 的种子价格打8折. (1)填写下表.
购买量/kg 0.5 付款金额/ 2.5 元
1 5
1.5 7.5
2 10
2.5 12
3 14
3.5 16
4 18
… …
购买量 0.5 1 1.5 2 2.5 3 3.55元 4 例5 /kg“黄金 1号”玉米种子的价格为 /kg.… 如
解:(1)由题意得
当0≤t≤2时, y=20; 当2<t≤4时, y=20+5(t-2)=5t+10 函数解析式为:
T 40 30 20 y=5x+10(2<t≤4) y=20(0≤x≤2) 1 2 3 4 t
20(0≤x≤2) y = 5t+10(2<t≤4)
(2)函数图像为:
10
0
7、圣诞老人买了很多鞋, 送给小明全家每人一双, 鞋长和鞋码如下表,你能 知道小明的鞋码吗?
自学展示
3 1、画出函数 y=2x 与 y=x +3 的图象 2
y=2x
2 o 1 2 o 3
y=- x+3
3 2
从数到形
函数解析 选取 式y=kx+b
满足条件的两定点
画出
( x1, y1 )与(x2 , y2 )
一次函数的 图象直线
2、已知正比Βιβλιοθήκη 函数的图象经过点(-2,4)求这个正比例 函数的表达式
1 2
购买量 0.5 1 1.5 2 2.5 3 3.55元 4 例5 /kg“黄金 1号”玉米种子的价格为 /kg.… 如
质疑导学
例5 “黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分 的种子价格打8折. (1)填写下表.
购买量/kg 0.5 付款金额/ 2.5 元
1 5
1.5 7.5
2 10
2.5 12
3 14
3.5 16
4 18
… …
购买量 0.5 1 1.5 2 2.5 3 3.55元 4 例5 /kg“黄金 1号”玉米种子的价格为 /kg.… 如
解:(1)由题意得
当0≤t≤2时, y=20; 当2<t≤4时, y=20+5(t-2)=5t+10 函数解析式为:
T 40 30 20 y=5x+10(2<t≤4) y=20(0≤x≤2) 1 2 3 4 t
20(0≤x≤2) y = 5t+10(2<t≤4)
(2)函数图像为:
10
0
7、圣诞老人买了很多鞋, 送给小明全家每人一双, 鞋长和鞋码如下表,你能 知道小明的鞋码吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:设f x ax b(a 0)
2 5
ab 2a b
a b
3 即f 1
x
3x
1
例3.设f(x)满足关系式 求函数的解析式
f
x
2
f
1 x
3x
• 分该析等:式如即果可将看题作目二所元给方的程,那f 么x必, f定看1x还成需两再个找变一量个,关那于么它
们的方程,那么交换 x与1/x形成新的方程
f x x2 1 y f x 3 (x 3)2 1 x2 6x 10
换元法
注意点:注意换元的等价性,即要求出 t 的
取值范围
例2.已知函数f(x)是一次函数,且经过 (1,2),(2,5)求函数y=f(x)的解析 式• 分析:与上一题不同的是这一题已知函数是什么
类型的函数,那么我们只需设出相应的解析式模 型,通过方程组解出系数即可——待定系数法
解:设F x
f
x 2 f
1 x
ቤተ መጻሕፍቲ ባይዱ
3x
(1)
F
1 x
f
1 x
2
f
1 1 x
3
1 x
f
1 x
2
f
x
3 x
(2)
有(1)(2)得 f x 2 x x 0
x
再见
2.2 求函数的解析式
例1.已知 f ( x 1) x 2 2x 2 ,求
f (3)及f x, f x 3
分析:这是含有未知函数f(x)的等式,比较抽象。由函数 f(x)的定义可知,在函数的定义域和对应法则f不变的条件 下,自变量变换字母,以至变换为其他字母的代数式,对
函数本身并无影响,这类问题正是利用这一性质求解的。
解:方法一:f ( x 1) x 2 2x 2
x2 2x 11 ( x 1)2 1
配凑法
f (x) x2 1
f 3 10
y f x 3 (x 3)2 1 x2 6x 10
方法二:令t x 1,则x t 1
f t f x 1 t 12 2t 1 2 t2 1
