浙江省诸暨市牌头中学2018年浙江省数学竞赛模拟练习四
浙江省诸暨市牌头中学2018届高三学考物理模拟试题2 含

2018年4月学考模拟测试(二)班级_____________姓名________________注意:可能用到的参数:重力加速度g均取10m/s2。
一、选择题I(本题共13小题,每小题3分,共39分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分。
)1.下列物理量中属于标量的是A.路程B.位移C.速度D.加速度2.下列均属于国际制基本单位的是A.m、N、J B.m、kg、J C.m、kg、s D.kg、m/s、N3.中国女排在2016年奥运会比赛中再度夺冠。
图为比赛中精彩瞬间的照片,此时排球受到的力有A.推力B.重力、推力C.重力、空气对球的作用力D.重力、推力、空气对球的作用力4.如图所示,无人机在空中匀速上升时,不断增加的能量是A.动能B.动能、重力势能C.重力势能、机械能D.动能、重力势能、机械能5.在G20峰会“最忆是杭州”的文艺演出中,芭蕾舞演员保持如图所示姿式原地旋转,此时手臂上A、B两点角速度大小分别为ωA、ωB,线速度大小分别为v A、v B,则A.ωA<ωB B.ωA>ωBC.v A<v B D.v A>v B6.某探险者在野外攀岩时,踩落一小石块,约5s后听到石块直接落到崖底的声音,探险者离崖底的高度最接近的是A.25m B.50m C.110m D.150m7.一水平固定的水管,水从管口以不变的速度源源不断地喷出。
水管距地面高h=1.8m,水落地的位置到管口的水平距离x =1.2m 。
不计空气阻力和摩擦阻力,水从管口喷出的初速度大小为A .1.2m/sB .2.0m/sC .3.0m/sD .4.0m/s8.如图为某一电场的电场线,M 、N 、P 为电场线上的三个点,M 、N 是同一电场线上两点。
下列判断正确的是A .M 、N 、P 三点中N 点的场强最大B .M 、N 、P 三点中N 点的电势最高C .负电荷在M 点的电势能大于在N 点的电势能D .正电荷从M 点自由释放,电荷将沿电场线运动到N 点9.一根细橡胶管中灌满盐水,两端用短粗铜丝塞住管口。
最新-2018年全国初中数学竞赛(浙江赛区)复赛试题及参考答案02018 精品

2018年全国初中数学竞赛(浙江赛区)复赛试题(2018年4月1月 下午1∶00-3∶00)班级__________学号__________姓名______________得分______________一、选择题(共6小题,每小题5分,满分30分) 1.若x 3+x 2+x +1=0,则x -27+x-26+…+x -1+1+x +…+x 26+x 27的值是( )(A )1(B )0 (C )-1(D )22.定义:定点A 与⊙O 上的任意一点之间的距离的最小值称为点A 与⊙O 之间的距离.现有一矩形ABCD 如图,AB =14cm ,BC =12cm ,⊙K 与矩形的边AB 、BC 、CD 分别相切于点E 、F 、G ,则点A 与⊙K 的距离为 ( )(A )4cm(B )8cm(C )10cm(D )12cm3.某班选举班干部,全班有50名同学都有选举权和被选举权,他们的编号分别为1,2,…,50.老师规定:同意某同学当选的记“1”,不同意(含弃权)的记“0”.如果令a i ,j =⎩⎨⎧1,第i 号同学同意第j 号同学当选,2,第i 号同学不同意第j 号同学当选.其中i =1,2,…,50;j =1,2,…,50.则同时同意第1号和第50号同学当选的人数可表示为 ( )(A )a 1,1+a 1,2+…+a 1,50+a 50,1+a 50,2+…+a 50,50 (B )a 1,1+a 2,1+…+a 50,1+a 1,50+a 2,50+…+a 50,50 (C )a 1,1a 1,50+a 2,1a 2,50+…+a 50,1a 50,50 (D )a 1,1a 50,1+a 1,2a 50,2+…+a 1,50a 50,504.若a b +c =b c +a =ca +b =t ,则一次函数y =tx +t 2的图象必定经过的象限是( )(A )第一、二象限 (B )第一、二、三象限 (C )第二、三、四象限(D )第三、四象限5.满足两条直角边长均为整数,且周长恰好等于面积的整数倍的直角三角形的个数有( )(A )1个 (B )2个 (C )3个 (D )无穷多个 6.如图,以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ,设正方形的中心为O ,连结AO ,如果AB =4,AO =62,那么AC 的长等于( )(A )12 (B )16 (C )43 (D )8 2 二、填空题(共6小题,每小题6分,共满分36分)7.函数y =|x +1|+|x +2|+|x +3|,当x =___________时,y 有最小值,最小值等于___________.AFA8.以立方体的8个顶点中的任意3个顶点为顶点的三角形中,正三角形的个数为__________.9.如图,△ABC中,∠A的平分线交BC于D,若AB=6cm,AC=4cm,∠A=60º,则AD 的长为___________cm.10.设x1,x2,x3,...,x2018为实数,且满足x1x2x3...x2018=x1-x2x3...x2018=x1x2-x3 (x2018)=…=x1x2x3…x2018-x2018=1,则x2000的值是__________.11.正六边形轨道ABCDEF的周长为7.2米,甲、乙两只机器鼠分别从A,C两点同时出发,均按A→B→C→D→E→F→A→…方向沿轨道奔跑,甲的速度为9.2厘米/秒,乙的速度为8厘米/秒,那么出发后经过___________秒钟时,甲、乙两只机器鼠第一次出现在同一条边上.12.正整数M的个位上的数字与数20132015的个位上的数字相同,把M的个位上的数字移到它的左边第一位数字之前就形成一个新的数N.若N是M的4倍,T是M的最小值,则T的各位数字之和等于___________.三、解答题(共4小题,满分54分)13.(本题满分12分)已知二次函数y=ax2+bx+c的图象G和x轴有且只有一个交点A,与y轴的交点为B(0,4),且ac=b.(1)求该二次函数的解析表达式;(2)将一次函数y=-3x的图象作适当平移,使它经过点A,记所得的图象为L,图象L与G的另一个交点为C,求△ABC的面积.14.(本题满分12分)如图,AB ∥CD 、AD ∥CE ,F 、G 分别是AC 和FD 的中点,过G 的直线依次交AB 、AD 、CD 、CE 于点M 、N 、P 、Q ,求证:MN +PQ =2PN .15.(本题满分14分)2018个质点均匀分布在半径为R 的圆周上,依次记为P 1,P 2,P 3,…,P 2018.小明用红色按如下规则去涂这些点:设某次涂第i 个质点,则下次就涂第i 个质点后面的第i 个质点.按此规则,小明能否将所有的质点均涂成红色?若能,请给出一种涂点方案;若不能,请说明理由.A B CD E F G P Q M N16.(本题满分16分)从连续自然数1,2,3,…,2018中任意取n个不同的数.(1)求证:当n=1018时,无论怎样选取这n个数,总存在其中的4个数的和等于4017;(2)当n≤1018(n是正整数)时,上述结论成立否?请说明理由.2018年全国初中数学竞赛(浙江赛区)复赛试题参考答案一、选择题(共6小题,每小题5分,满分30分) 1.答案:C解:由3210x x x +++=,得1x =-,所以2627--+x x + … +x x ++-11+ … +2726x x +=-1.2.答案:A解:连结AK 、EK ,设AK 与⊙O 的交点为H ,则AH 即为所求, 因为AK =22AE EK +=10,所以AH = 4. 3.答案:C解:由题意得C 正确. 4.答案:A解:由已知可得t c b a c b a )(2++=++,当0a b c ++≠时,12t =,1124y x =+,直线过第一、二、三象限; 当0a b c ++=时,1t =-,1y x =-+,直线过第一、二、四象限.综合上可得,直线必定经过的象限是第一、二象限.5.答案:C解:设直角三角形的两条直角边长为,a b (a b ≤),则12a b k ab ++=⋅(a ,b ,k 均为正整数),化简,得(4)(4)8ka kb --=,所以4148ka kb -=⎧⎨-=⎩或4244ka kb -=⎧⎨-=⎩.解得1512k a b =⎧⎪=⎨⎪=⎩或234k a b =⎧⎪=⎨⎪=⎩或⎪⎩⎪⎨⎧===.8,6,1b a k 即有3组解.6.答案:B解:在AC 上取一点G ,使CG =AB =4,连接OG ,则△OG C ≌△OAB ,所以OG =OA =26, ∠AOG =90°,所以△AOG 是等腰直角三角形,AG =12,所以AC =16.二、填空题(共6小题,每小题6分,满分36分)7.答案:-2,2解:当x ≤-3时,y = -3x -6;当-3<x ≤-2时,y = -x ; 当-2<x ≤-1时,y =x +4;AD(第2题)AB CEFO G(第6题)当x >-1时,y =3x +6.;所以当x =-2时,y 的值最小,最小值为2. 8.答案:8个解:正三角形的各边必为立方体各面的对角线,共有8个正三角形. 9.答案:5312 解:由S △ABC =S △ABD + S △ADC ,得︒⋅⋅60sin 21AC AB =︒⋅⋅+︒⋅⋅30sin 2130sin 21AC AD AD AB . 解得AD =5312.10.答案:1,或253±-解:由已知,321x x x ...200032120001x x x x x -=1,321x x x (1999)32119991x x x x x -=1,解得123200012319991515,22x x x x x x x x±±==. 所以12000=x ,或200032x ±=-. 11.答案:238104解:设甲跑完x 条边时,甲、乙两老鼠第一次出现在同一条边上,此时甲走了120x 厘米,乙走了2.91208x ⨯厘米,于是⎪⎪⎩⎪⎪⎨⎧≤-+⨯>--+-⨯.,1201202402.91208120)1(1202402.9)1(1208x x x x解得328327<≤x .因x 是整数,所以x =8,即经过2.98120⨯=232400=238104秒时,甲、乙两只机器鼠第一次出现在同一条边上.12.答案:36 解:20152013的个位数字是7,所以可设710+=k M ,其中k 是m 位正整数,则k N m+⨯=107.由条件N =4M ,得k m+⨯107=)710(4+k ,即39)410(7-=m k .当m =5时,k 取得最小值17948.所以T =179487,它的各位数字之和为36. 三、解答题(共4题,满分54分) 13.(12分)解:(1)由B (0,4)得,c =4.G 与x 轴的交点A (2ba-,0),由条件ac b =,得b c a =,所以2b a -=22c -=-,即A (2-,0).所以4,4240.b a a b =⎧⎨-+=⎩解得1,4.a b =⎧⎨=⎩所求二次函数的解析式为244y x x =++.(2)设图象L 的函数解析式为y =3-x +b ,因图象L 过点A (2-,0),所以6b =-,即平移后所得一次函数的解析式为y =36x --.令36x --=244x x ++, 解得12x =-,25x =-.将它们分别代入y =36x --, 得10y =,29y =.所以图象L 与G 的另一个交点为C (5-,9). 如图,过C 作CD ⊥x 轴于D ,则 S △ABC =S 梯形BCDO -S △ACD -S △ABO =111(49)53924222+⨯-⨯⨯-⨯⨯=15.(第13题)14.(12分)证明:延长BA 、EC ,设交点为O ,则四边形OADC 为平行四边形. ∵ F 是AC 的中点, ∴ DF 的延长线必过O 点,且31=OG DG . ∵ AB ∥CD , ∴DNANPN MN =. ∵ AD ∥CE ,∴DNCQPN PQ =. ∴ +PN MN =PN PQ DN AN DNCQ+ =DNCQ AN +.又=OQ DN 31=OG DG , ∴ OQ =3DN .∴ CQ =OQ -OC =3DN -OC =3DN -AD ,AN =AD -DN , 于是,AN +CQ =2DN , ∴+PN MN =PNPQ DN CQAN +=2,即 MN +PQ =2PN .15.(14分)解:不能.理由:设继i P 点涂成红色后被涂到的点是第j 号,则j =2,22007,22007,22007.i i i i ≤⎧⎨->⎩若i =2018,则j =2018,即除2007P 点涂成红色外,其余均没有涂到. 若i ≠2018,则2i ≠2018,且2i ≠4014,即2i -2018≠2018, 表明2007P 点永远涂不到红色.16.(16分)解:(1)设123x x x ,,,…,1007x 是1,2,3,…,2018中任意取出的1018个数.首先,将1,2,3,…,2018分成1004对,每对数的和为2018,BACMN P E FQDG O每对数记作(m ,2018-m ) ,其中m =1,2,3, (1004)因为2018个数取出1018个数后还余1001个数,所以至少有一个数是1001个数之一的数对至多为1001对,因此至少有3对数,不妨记为112233(2009)(2009)(2009)m m m m m m ---,,,,, (123m m m ,,互不相等)均为123x x x ,,,…,1007x 中的6个数.其次,将这2018个数中的2018个数(除1004、2018 外)分成1003对,每对数的和为2018,每对数记作(k ,2018-k ) ,其中k =1,2, (1003)2018个数中至少有1018个数被取出,因此2018个数中除去取出的数以外最多有1001个数,这1003对数中,至少有2对数是123x x x ,,,…,1007x 中的4个数,不妨记其中的一对为11(2008)k k -,.又在三对数112233(2009)(2009)(2009)m m m m m m ---,,,,,,(123m m m ,,互不相等)中至少存在1对数中的两个数与11(2008)k k -,中的两个数互不相同,不妨设该对数为11(2009)m m -,,于是1111200920084017m m k k +-++-=. (2)不成立.当1006n =时,不妨从1,2,…,2018中取出后面的1018个数:1003 ,1004, (2018)则其中任何四个不同的数之和不小于1003+1004+1018+1018=4018>4017; 当1006n <时,同样从1,2,…,2018中取出后面的n 个数,其中任何4数之和大于1003+1004+1018+1018=4018>4017. 所以1006n ≤时都不成立.。
浙江省诸暨市牌头中学2017-2018学年高二数学周练卷3

2017-2018下牌头中学高二数学周练卷一、选择题1.复数z=1﹣i ,则对应的点所在象限为( )A .第一象限B .第二象限C .第三象限D .第四象限2.设,则a ,b ,c 的大小关系是( )A .a >b >cB .a >c >bC .b >a >cD .b >c >a3.已知函数f (x )=﹣x 2+2,g (x )=log 2|x|,则函数F (x )=f (x )•g(x )的大致图象为( )A .B .C .D .4.已知βα,是两个不同的平面,n m ,是两条不同的直线,则下列命题不正确...的是( ) A .若α⊥m n m ,//,则α⊥n B .若n m =⋂βαα,//,则n m //C .若αβ⊥⊥m m ,,则βα//D .若βα⊂⊥m m ,,则βα⊥5.已知函数f (x )=﹣2sin (2x+φ)(|φ|<π),若,则f (x )的一个单调递增区间可以是( )A .B .C .D .6.已知点F 是双曲线=1(a >0,b >0)的右焦点,点E 是左顶点,过F 且垂直于x 轴的直线与 双曲线交于点A ,若tan ∠AEF <1,则双曲线的离心率e 的取值范围是( )A .(1,+∞)B .(1,2)C .(1,1+)D .(2,2+)7.若函数y=f (x )的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f (x )具有 T 性质.下列函数中具有T 性质的是( )A .y=sinxB .y=lnxC .y=e xD .y=x 3 8.已知函数f (x )(x∈R)是以4为周期的奇函数,当x∈(0,2)时,f (x )=ln (x 2﹣x+b ).若函数f (x ) 在区间[﹣2,2]上有5个零点,则实数b 的取值范围是( )A .﹣1<b ≤1B .≤b ≤C .﹣1<b <1或b=D .<b ≤1或b=二、填空题:9.已知数列{}n a 满足递推关系式1221-+=+n n n a a (n ∈N *),且⎭⎬⎫⎩⎨⎧+n n a 2λ为等差数列,则λ的值是 __10.若抛物线C :y 2=2px 的焦点在直线x+y ﹣3=0上,则实数p= ;抛物线C 的准线方程为 .11.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且a=2,b=,B=60°,则△ABC 的面积为 .12.如果一个几何体的三视图如图所示,其中正视图中△ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为______.13.在平面上,过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影.若点P (﹣1,0)在直线ax ﹣y ﹣a ﹣2=0上的投影是Q ,则Q 的轨迹方程是 .14.已知f (x )=,则 fx∈R 时,如果函数f (x )>g (x )恒成立,那么称函数f (x )是函数g (x )的“优越函数”.若函数f (x )=2x 2+x+2﹣|2x+1|是函数g (x )=|x ﹣m|的“优越函数”,则实数m 的取值范围是 .三、解答题:15.设△ABC 的三内角A ,B ,C 所对的边分别为a ,b ,c ,已知(2b ﹣c )cosA=acosC .(1)求A ;(2)若a=1,求b+c 的取值范围.16.在如图所示的空间几何体中,平面⊥ACD 平面ABC ,ACD ∆与ACB ∆均是边长为2的等边三角形,2=BE ,直线BE 和平面ABC 所成的角为︒60,且点E 在平面ABC 上的射影落在ABC ∠的平分线上.(I )求证://DE 平面ABC ;(II )求二面角A BC E --的余弦值.17.已知椭圆E : +=1(a >b >0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P (,)在椭圆E 上.(Ⅰ)求椭圆E 的方程;(Ⅱ)设不过原点O 且斜率为的直线l 与椭圆E 交于不同的两点A ,B ,线段AB 的中点为M ,直线OM 与椭圆E 交于C ,D ,证明:︳MA ︳•︳MB ︳=︳MC ︳•︳MD ︳18.已知函数f(x)=lnx﹣x2,g(x)=x2+x,m∈R,令F(x)=f(x)+g(x).(Ⅰ)求函数f(x)的单调递增区间;(Ⅱ)若关于x的不等式F(x)≤mx﹣1恒成立,求整数m的最小值;,x2满足F(x1)=﹣F(x2),求证:x1+x2﹣1.(Ⅲ)若m=﹣1,且正实数x19.已知二次函数f(x)=ax2+bx的图象过点(-4n,0),且f′(0)=2n(n∈N*).(1)求f(x)的解析式;(2)若数列{a n }满足1a n +1=f ′⎝ ⎛⎭⎪⎫1a n ,且a 1=4,求数列{a n }的通项公式; (3)对于(2)中的数列{a n },求证:①∑n k =1a k <5;②43≤∑nk =1 a k a k +1<2.。
浙江省诸暨市牌头中学全国高中数学联赛模拟试题(七)新人教A版

浙江省诸暨市牌头中学全国高中数学联赛模拟试题(七)新人教A 版 第一试一、选择题:(每小题6分,共36分)a 、b 是异面直线,直线c 与a 所成的角等于c 与b 所成的角,则这样的直线c 有(A )1条 (B )2条 (C )3条 (D )无数条已知f(x)是R 上的奇函数,g(x)是R 上的偶函数,若f(x)-g(x)=x2+2x+3,则f(x)+g(x)=(A )-x2+2x-3 (B )x2+2x-3 (C )-x2-2x+3 (D )x2-2x+3已知△ABC ,O 为△ABC 内一点,∠AOB=∠BOC=∠COA=32π,则使AB+BC+CA ≥m(AO+BO+CO) 成立的m 的最大值是(A )2 (B )35 (C )3 (D )23设x=0.820.5,y=sin1,z=log37则x 、y 、z 的大小关系是(A )x <y <z (B )y <z <x (C )z <x <y (D )z <y <x 整数⎥⎦⎤⎢⎣⎡+31010951995的末尾两位数字是 (A )10 (B )01 (C )00 (D )20设(a,b)表示两自然数a 、b 的最大公约数.设(a,b)=1,则(a2+b2,a3+b3)为(A )1 (B )2 (C )1或2 (D )可能大于2二、填空题:(每小题9分,共54分)若f(x)=x10+2x9-2x8-2x7+x6+3x2+6x+1,则f(2-1)= .设F1、F2是双曲线x2-y2=4的两个焦点,P 是双曲线上任意一点,从F1引∠F1PF2平分线的垂线,垂足为M ,则点M 的轨迹方程是 .给定数列{xn},x1=1,且n n n x x x -+=+3131,则x1999-x601= .正方体ABCD-A1B1C1D1的棱长为1,E 是CD 中点,F 是BB1中点,则四面体AD1EF 的体积是 . 在坐标平面上,由条件⎪⎩⎪⎨⎧+-≤--≥321x y x y 所限定的平面区域的面积是 .12个朋友每周聚餐一次,每周他们分成三组,每组4人,不同组坐不同的桌子.若要求这些朋友中任意两个人至少有一次同坐一张桌子,则至少需要 周.三、(20分) 已知椭圆12222=+b y a x 过定点A(1,0),且焦点在x 轴上,椭圆与曲线|y|=x 的交点为B 、C .现有以A 为焦点,过B 、C 且开口向左的抛物线,抛物线的顶点坐标M(m,0).当椭圆的离心率e 满足1322<<e ,求实数m 的取值范围.四、(20分)a 、b 、c 均为实数,a ≠b ,b ≠c ,c ≠a . 证明:23≤a c c b b a b a c a c b c b a -+-+--++-++-+222<2.五、(20分)已知f(x)=ax4+bx3+cx2+dx ,满足(i )a 、b 、c 、d 均大于0;(ii )对于任一个x ∈{-2, -1,0,1,2},f(x)为整数;(iii )f(1)=1,f(5)=70.试说明,对于每个整数x ,f(x)是否为整数.第二试一、(50分)设K 为△ABC 的内心,点C1、B1分别为边AB 、AC 的中点,直线AC 与C1K 交于点B2,直线AB 于B1K 交于点C2.若△AB2C2于△ABC 的面积相等,试求∠CAB .二、(50分)设5sin i 5cosππ+=w ,f(x)=(x-w)(x-w3)(x-w7)(x-w9).求证:f(x)为一整系数多项式,且f(x)不能分解为两个至少为一次的整系数多项式之积.三、(50分)在圆上有21个点.求在以这些点为端点组成的所有的弧中,不超过120°的弧的条数的最小值.参考答案第一试一、选择题: 题号1 2 3 4 5 6 答案 D A C B C C二、填空题:1、4;2、x2+y2=4;3、0;4、245;5、16;6、5.三、⎪⎪⎭⎫ ⎝⎛+423,1.四、证略.五、是.第二试一、60°;二、证略.三、100.。
2016-2017学年浙江省诸暨市牌头中学高二下学期数学竞赛训练题(一)

提示:用3X 3的数表证明,再在数表中取出一个 3X 3子表。
高二数学竞赛训练题(一) 2017.51、已知 A={xx 2 —4x+3c0} , B = {x21」+a 兰 0,x 2 — 2(a +7 X+5 兰 0},若 A 匸 B ,则实数a 的取值范围是 ___________ 。
.2过点P 作斜率为的直线与双曲线交于 A B 两点,与y 轴交于点M 若PM 是 PA 与PB 的等2 比中项,则双曲线的半焦距为 —J3 _____3、在棱长为1的正方体 ABCD-ABQD 中,已知 O 是底面ABQD 的中心,M 是棱BB 上的点, 且S DBM : S O 1B 1 M - 2 :3,则四面体OADM 的体积是4、已知 f (x )满足 f (x ) + f -------------- i = 1 + x(x 式 0,1),则 g(x)=x —2f(x)的值域是I X 丿_ (-叫 V (0,址) ___ 。
5、 正数 a 、b 、c 满足 a E b +c E3a ,3b 2 兰 a (a + c )兰 5b 2,则-―2c 的最小值是 _-18a 5 — 6、 已知D 是边长为1的正△ ABC 边BC 上的点,△ ABD △ ACD 的内切圆半径分别为 r 1、r 2,;3■- 6若满足r 1 + r 2 = —— 的点D 有两个(设为 D 、D 2),贝U DC 2=_—— __ 。
5 — 57、 在任何n 个连续的正整数中,使得必有一数其各位数字之和是7的倍数成立的最小的正整 数n 是 ___ 13 ____ 。
8、 已知正整数数列首项为2013,末项为1,且对任意的k 一2均有a^ a k ,则满足条件的数列共有 _________ 201 ____ 个。
9、 在(2n+1)X ( 2n+1)数表中,每行均是等差数列,每列各数平方后为等差数列。
证明:左上X 2、已知双曲线的中心在原点,焦点在坐标轴上,点P ( -2,0)到其渐近线的距离为 2 6 3112右下=左下X右上。
浙江省诸暨市牌头中学2018-2019学年上学期高三期中数学模拟题

浙江省诸暨市牌头中学2018-2019学年上学期高三期中数学模拟题班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1.设a,b为正实数,1122 ab+≤,23()4()a b ab-=,则logab=()A.0B.1-C.1D.1-或0【命题意图】本题考查基本不等式与对数的运算性质等基础知识,意在考查代数变形能与运算求解能力. 2.在ABC∆中,,,a b c分别为角,,A B C所对的边,若2cosa b C=,则此三角形一定是()A.等腰直角三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形3.已知iz311-=,iz+=32,其中i是虚数单位,则21zz的虚部为()A.1-B.54C.i-D.i54【命题意图】本题考查复数及共轭复数的概念,复数除法的运算法则,主要突出对知识的基础性考查,属于容易题.4.某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m n+的值是()A.10B.11C.12D.13【命题意图】本题考查样本平均数、中位数、茎叶图等基础知识,意在考查识图能力和计算能力.5.已知实数[]4,0x∈-,[]0,3y∈,则点(,)P x y落在区域240xyy xy x≤⎧⎪≥⎪⎨+≤⎪⎪--≤⎩内的概率为()A.56B.12C.512D.712【命题意图】本题考查线性规划、几何概型等基础知识,意在考查基本运算能力.6. 函数()2cos()f x x ωϕ=+(0ω>,0ϕ-π<<)的部分图象如右图所示,则 f (0)的值为( )A.32-B.1-C.D.【命题意图】本题考查诱导公式,三角函数的图象和性质,数形结合思想的灵活应用. 7. 对于复数,若集合具有性质“对任意,必有”,则当时,等于 ( )A1 B-1 C0 D8. 函数f (x )=sin (ωx +φ)(ω>0,-π2≤φ≤π2)的部分图象如图所示,则φω的值为( )A.18 B .14C.12D .19. 函数()f x 在定义域R 上的导函数是'()f x ,若()(2)f x f x =-,且当(,1)x ∈-∞时,'(1)()0x f x -<,设(0)a f =,b f =,2(log 8)c f =,则( )A .a b c <<B .a b c >>C .c a b <<D .a c b << 10.在复平面内,复数1zi+所对应的点为(2,1)-,i 是虚数单位,则z =( ) A .3i --B .3i -+C .3i -D .3i +11.已知点P 是双曲线C :22221(0,0)x y a b a b-=>>左支上一点,1F ,2F 是双曲线的左、右两个焦点,且12PF PF ⊥,2PF 与两条渐近线相交于M ,N 两点(如图),点N 恰好平分线段2PF ,则双曲线的离心率是( )A.5B.2 D.2【命题意图】本题考查双曲线的标准方程及其性质等基础知识知识,意在考查运算求解能力. 12.在ABC ∆中,10a =,60B =,45C =,则等于( )A .10B .1)C 1D .二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.当0,1x ∈()时,函数()e 1x f x =-的图象不在函数2()g x x ax =-的下方,则实数a 的取值范围是___________.【命题意图】本题考查函数图象间的关系、利用导数研究函数的单调性,意在考查等价转化能力、逻辑思维能力、运算求解能力.14.某工厂产生的废气经过过虑后排放,过虑过程中废气的污染物数量P (单位:毫克/升)与时间t (单位:小时)间的关系为0e ktP P -=(0P ,k 均为正常数).如果前5个小时消除了10%的污染物,为了 消除27.1%的污染物,则需要___________小时.【命题意图】本题考指数函数的简单应用,考查函数思想,方程思想的灵活运用. 15.已知函数21()sin cos sin 2f x a x x x =-+的一条对称轴方程为6x π=,则函数()f x 的最大值为___________.【命题意图】本题考查三角变换、三角函数的对称性与最值,意在考查逻辑思维能力、运算求解能力、转化思想与方程思想.16.已知圆22240C x y x y m +-++=:,则其圆心坐标是_________,m 的取值范围是________. 【命题意图】本题考查圆的方程等基础知识,意在考查运算求解能力.三、解答题(本大共6小题,共70分。
浙江省诸暨市牌头中学浙江省数学竞赛模拟练习二及答案

浙江省数学竞赛模拟练习二1、记[]x 表示不超过实数x 的最大整数,则集合[][][]{}{}100*32≤∈⋂∈++x N x R x x x x 共有_________个元素。
2、若关于x 的方程x ae x =2有三个不同的实根,则实数a 的取值范围是________。
若关于x 的方程x k k x =-2在区间[]1,1+-k k 上有两个不相等的实根,则实数k 的取值范围是________。
3、计算=︒2016cos ______。
若函数()x b xx a x f tan cos 2sin +++=的最大值与最小值之和为4,则=+b a ______。
4、已知平面向量a 、b 、c ()222=-+⋅=⋅==c b a c b a -的最大值、最小值分别为M 、m ,则=mM ______。
5、在△ABC 中,若c a b C B +-=2cos cos ,则=∠B ______。
6、设数列{}n a 满足21=a ,且()()8421=+-+n n a a ,则=+++na a a 11121 ______。
7、已知0,>y x ,且22=+y x ,则xy y x 2242+的最小值为______。
8、已知抛物线C 以椭圆E 的中心为焦点,抛物线C 经过椭圆E 的两个焦点,且与椭圆E 恰有三个交点,则椭圆E 的离心率为______。
9.已知曲线E :9102-+-=x x y 及点A (1,0),若曲线E 上存在相异的两点B 、C ,其到直线013:=+x l 的距离分别为|AB|、|AC|,则|AB|+|AC|=______。
10、已知边长为a 的正方形ABCD 的顶点A 在平面β内,其余顶点均在平面β的同侧,且B 、D 两点到平面β的距离分别为1、2,若平面ABCD 与平面β的夹角为30°,则a =______。
11.在单位正方体ABCD-A 1B 1C 1D 1中,O 为正方形ABCD 的中心,点M 、N 分别在棱A 1D 1、CC 1上,A 1M=21,CN=32,则四面体OMNB 1的体积为______。
浙江省诸暨市牌头中学高二下学期数学竞赛训练题(二)

高二数学竞赛训练题(二)2017.51、已知()3x x f y +=为偶函数,且()1010=f ,函数()()4+=x f x g ,则()=-10g _____。
2、已知向量满足a 、b 1=3=,(3a -2b )⊥a ,则a 、b 的夹角为____。
3、在正四棱锥P-ABCD 中,已知A 1、C 1为PA 、PC 的中点,则=-ABCDP D BC A V V 11________。
4、已知0,0>>y x ,y x a +=,22y xy x b +-=,xy c λ=,若a 、b 、c 能作为三角形的三边长,则正实数λ的范围是________。
5、对于每个正整数n ,设曲线1+=n xy 在点(1,1)处的切线与x 轴的交点的横坐标为n x ,令n n x a lg =,则=+++9921a a a ________。
6、在实数范围内,方程()111892223=----+x x x x x 的解集为________。
7、方程[][]x x xx 1313+=+的所有非整数解为________。
8、平面直角坐标系中,直线L 过双曲线122=-y x 的一个焦点,且与双曲线交于A 、B 两点,若以AB 为直径的圆与y 轴相切,则|AB|=________。
9、已知△ABC 三个顶点均在抛物线()022>=p px y 上,且△ABC 的重心恰为抛物线的焦点,若边BC 所在直线方程为204=-y x ,则=p ___________。
10、已知实数y x ,满足yx y x 4422+=+,则yx88+的取值范围是________。
11、给定平面上四点O 、A 、B 、C ,满足OA=4,OB=3,OC=2,3=⋅OC OB ,则△ABC 的面积的最大值为________。
12、若对任意的[]1,0∈x ,都有()()011442≥--+-x x x x k 成立,则k 的最小值为_____。
浙江省诸暨市牌头中学2018届高三9月月考数学试题

牌头中学2017-2018学年第一学期9月考试卷高三数学一、选择题(共8题,每题5分,共40分)(请把选择题答案涂在答题卡上.............) 1、已知函数()()()()()()()323121--+--+--=x x x x x x x f 有两个零点,这两个零点所在的区间为()(A )(-∞,1)∪(2,3) (B )(1,2)∪(3,+∞) (C )(-∞,1)∪(3,+∞)(D )(1,2)∪(2,3)2、定义非空集合P 、Q 之间的运算为:P-Q={x|x ∈P 且x ∉Q},P ·Q={x|x ∈P 且x ∈Q},若非空集合P ≠Q ,M=(P-Q )·R ,N=P ·R-Q ·R ,则下列关系一定成立的是 ( ) (A )M=N(B )M ⊆N(C )M ⊇N(D )M ≠N 3、设函数()x f 是一次函数,()[]34-=x x f f ,则()=1f()(A )3或1 (B )1(C )1或-1(D )-3或14、如图所示,将正方形纸片三次对折后,沿图中AB 线剪掉一个等腰直角三角形,展开铺平得到的图形是 ( A)5、如图,在平面直角坐标系中,直线33+-=x y 与x 轴、y 轴分别交于A 、B 两点,以AB 为边在第一象限作正方形ABCD ,点D 在双曲线)0(≠=k xky 上。
将正方形沿x 轴负方向平移a 个单位长度后,点C 恰好落在该双曲线上,则a 的值是 ( B) A 、1 B 、2 C 、3 D 、46、已知函数|1|1)(-=x e x f ,1312)(+=x ex f ,2|)()(|2)()()(2121x f x f x f x f x g -++=,若]5,1[,-∈b a ,且当],[,21b a x x ∈时,0)()(2121>--x x x g x g 恒成立,则a b -的最大值为( D )A 、2B 、3C 、4D 、57、已知函数()f x 的定义域为(32,1)a a -+,且(1)f x +为偶函数,则实数a 的值可以是 ( B )A.23B.2C.4D.6二、填空题(共7题,共36分)(请把填空题答案写在答题卷上.............) 7、直线1=y 与曲线a x x y +-=||2有四个交点,则a 的取值范围是 。
浙江省诸暨市牌头中学2017-2018学年高中数学竞赛训练题Word版答案不全 (3)

2017-2018学年数学竞赛训练题1、函数()2411x x x x f -+-++=的值域为__________。
2、方程()20132013sin x x =π的实根个数为_______。
3、设数列{}n a 满足121==a a ,()3321≥-=--n a a a n n n ,则=2013a _______。
3*、已知互不相等的三个实数a 、b 、c 成等比数列,且a c log 、c b log 、b a log 构成公差为d 的等差数列,则d =_______。
4、设△ABC 的外心P 满足()AC AB AP +=52,则=∠BAC cos _______。
5、设()∑==++300015021k kk x c x x ,则∑==10003k k c _______。
6、在直线3+=x y 上任取一点P ,若过点P 且以双曲线341222=-y x 的焦点为椭圆的焦点,则具有最短长轴的椭圆方程为_______。
6*、设F 为椭圆C :13422=+y x 的右焦点,过椭圆C 外一点P 作椭圆的切线,切点为M 。
若∠PFM=90°,则点P 的轨迹方程为_______。
7、在四棱锥P-ABCD 中,已知四边形ABCD 为矩形,且AB=4,BC=3,PA=PB=PC=PD=5,AC 与BD 交于点O ,M 为边PC 的中点,则OM 与平面PBC 所成的角为_______。
7*、已知四面体P-ABC 的体积为1,G 、K 分别是△ABC 、△PBC 的重心,过G 作直线分别与AB 、AC 交于点M 、N ,则四棱锥K-MNCB 的体积的最大值为_______。
8、已知正实数x 、y 、z 满足xyz+xy+yz+zx+x+y+z=3,则u=xyz (x+y+z )的最大值为_______。
8*、已知a 、b 、c 、d [)+∞-∈,1,且a +b +c +d =0,则a b +b c +c d 的最大值为_______。
浙江省诸暨市牌头中学高三数学 期末综合练习四

高三第一学期期末综合练习(四)1.设不等式组4,010x y y x x +≤⎧⎪-≥⎨⎪-≥⎩表示的平面区域为D .若圆C :222(1)(1)(0)x y r r +++=>经过区域D 上的点,则r 的取值范围是 ( )(A) 22,32⎡⎤⎣⎦(B) 22,25⎡⎤⎣⎦ (C) (0,25⎤⎦ (D) (0,32⎤⎦2.已知各项均不为零的数列{}n a ,定义向量()1,n n n c a a +=u u r *,(,1),n b n n n N =+∈u u r,则下列命题中是真命题的是 ( )(A)若对任意的*n N ∈,都有n c u u r ∥n b u u r 成立,则数列{}n a 是等差数列(B)若对任意的*n N ∈,都有n c u u r ∥n b u u r 成立,则数列{}n a 是等比数列(C)若对任意的*n N ∈,都有n c u u r ⊥n b u u r 成立,则数列{}n a 是等差数列(D)若对任意的*n N ∈,都有n c u u r ⊥n b u u r 成立,则数列{}n a 是等比数列3.若关于x 的方程x x a a -=有三个不相同的实数根,则实数a 的取值范围是( )(A) ()4,4- (B) (),4-∞- (C) ()4,+∞ (D) ()(),44,-∞-+∞U4.已知双曲线22221(0,0)x y a b a b-=>>,12A A 、是实轴顶点,F 是右焦点,()0,B b 是虚轴端点,若在线段BF 上(不含端点)存在不同的两点(1,2)i p i =,使得12(1,2)i P A A i ∆=构成以12A A 为斜边的直角三角形,则双曲线离心率e 的取值范围是 ( )(A )(2,)+∞ (B )51(,)2++∞ (C )51(1,)2+ (D )51(2,)2+ 5.已知正四面体A BCD -中,P 为AD 的中点,则过点P 与侧面ABC 和底面BCD 所在平面都成ο60的平面共有(注:若二面角l αβ--的大小为ο120,则平面α与平面β所成的角也为ο60)( ) (A )2个 (B )4个 (C )6个 (D )无数个6.已知{a n }是首项为1的等比数列,若S n 是{a n }的前n 项和,且28S 3=S 6,则数列⎩⎨⎧⎭⎬⎫1a n 的前4项和为______.7.经过点P (2,-3)作圆x 2+2x +y 2=24的弦AB ,使得点P 平分弦AB ,则弦AB 所在直线的方程为_______。
2017-2018学年浙江省诸暨市牌头中学高三数学(理)周练十(理)

2017-2018 学年上牌头中学高三数学周练十(理)班级姓名参照公式:假如事件 A , B 互斥,那么柱体的体积公式P(A+B)=P(A)+P(B)V Sh此中 S 表示柱体的底面积, h 表示柱体的高假如事件 A , B 互相独立,那么锥体的体积公式P(A · B)=P(A)·P( B)1V假如事件 A 在一次试验中发生的概率是p,那么 nSh3次独立重复试验中事件A 恰巧发生 k 次的概率此中 S 表示锥体的底面积, h 表示锥体的高k kn-k球的表面积公式P n (k)= C n p (1- p) (k=0,1,2,, , n) 台体的体积公式S=4πR 2 1S 1S 2S 2 )球的体积公式V= h(S 14 3VπR 3此中 S 1,S 2 分别表示台体的上、下底面积,3h 表示台体的高此中 R 表示球的半径一、选择题:本大题共 10 小题,每题5 分,共 50 分。
1. 设会合 S ={x| 3< x ≤6}, T = {x| x 2- 4x - 5≤0},则=()R (S ∩T)A .(-≦ ,3] ∪ (6,+≦ )B .(-≦ ,3] ∪(5,+≦ )3C .(-≦ ,- 1)∪ (6,+≦ )4D . (-≦ , - 1)∪(5,+≦ )2. 已知 i 是虚数单位,则 3 i =2 i A .- 1+ i B .-1 -i3.设函数 f(x)=x 2- ax + b (a ,b ∈R ),则“有两个不一样的实根”是“( )5C .1+ iD . 1- if( x)= 0 在区间 [ 1,2] 正视图侧视图2 < a < 4 ” 的()3A .充足不用要条件B .必需不充足条件俯视图C .充足必需条件D .既不充足也不用要条件4.若某几何体的三视图(单位: cm)以下图,则该几何体的体积(第 4题图)等于( )A .10 cm 3B .20 cm 3C . 30 cm 3D . 40 cm 35 .已知 α, β, γ 是三个不一样的平面,α∩ γ= m , β∩ γ=n . ( )A .若 m ⊥ n ,则 α⊥ βB .若 α⊥ β,则 m ⊥ nC .若 m ∥n ,则 α∥ βD .若 α∥β,则 m ∥ n6.已知箱中共有 6 个球,此中红球、黄球、蓝球各 2 个.每次从该箱中取 1 个球 (有放回,每球取到的时机均等 ),共取三次.设事件A :“第一次取到的球和第二次取到的球颜色 同样”,事件B :“三次取到的球颜色都同样”,则 P(B| A)=( )1 12 D . 1A .B .C .6337.设 a ,b 为单位向量,若向量 c 知足 | c - (a + b )| =| a - b | ,则| c | 的最大值是( y)A .2 2B . 2C . 2D .1lQFAO xP8.如图, A , F 分别是双曲线x 2y 21 ( a ,b >0) 的左顶C : 22a b点、右焦点,过 F 的直线 l 与 C 的一条渐近线垂直且与 另一条渐近线和 y 轴分别交于 P , Q 两点.若 AP ⊥AQ ,则 C 的离心率是 ( )A . 2B . 31 13 1 17 C . 4 D . 49.若 0< x , y < π,且 sin x =x cos y ,则2B . x < y <xPA .y <xC . x<y < xD . x < yF44 2 2D10.如图,正三棱锥 P - ABC 的全部棱长都为 4.点 D ,E ,F 分别E在棱 PA , PB , PC 上,知足 DE = EF = 3, DF =2 的△ DEF 个数 C是AA . 1B . 2C . 3D . 4B二、填空题:本大题共 7 小题,每题 4 分,共 28 分。
浙江省诸暨市牌头中学2019届高三上学期周练数学试题(四)
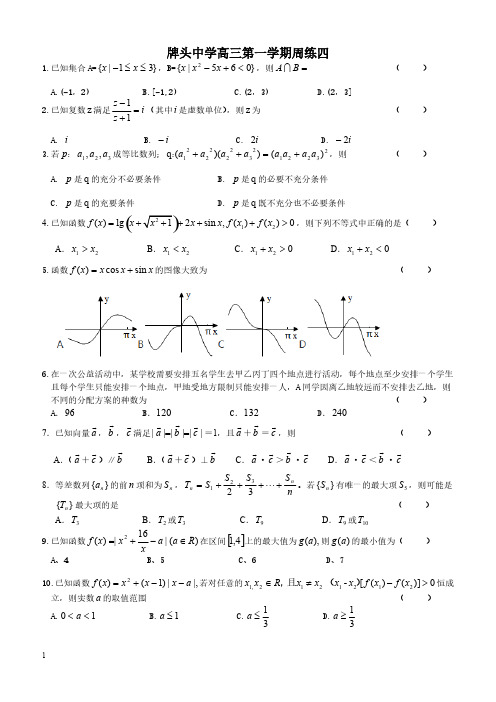
牌头中学高三第一学期周练四1.已知集合A=,B=,则( )}31|{≤≤-x x }065|{2<+-x x x =B A A.(-1,2) B.[-1,2) C.(2,3) D.(2,3]2.已知复数满足(其中是虚数单位),则为( )z i z z =+-11i z A. B. C. D. i i -i 2i 2-3.若成等比数列;,则( )321,,a a a p :2322123222221)())((q a a a a a a a a +=++:A. 是的充分不必要条件 B. 是的必要不充分条件p q p q C. 是的充要条件 D. 是既不充分也不必要条件p q p q 4.已知函数,则下列不等式中正确的是()(212()lg 12sin ,()()0f x x x x x f x f x =+++++>A .12x x >B .12x x <C .120x x +>D .120x x +<5.函数的图像大致为( )x x x x f sin cos )(+=6.在一次公益活动中,某学校需要安排五名学生去甲乙丙丁四个地点进行活动,每个地点至少安排一个学生且每个学生只能安排一个地点,甲地受地方限制只能安排一人,A 同学因离乙地较远而不安排去乙地,则不同的分配方案的种数为( )A .B .C .D .961201322407.已知向量,,满足=1,且+=,则( )a b c ||||||c b a ==a b c A .(+)∥ B .(+)⊥ C .·>· D .·<·a cb ac b a c b c a c b c8.等差数列的前项和为,。
若有唯一的最大项,则可能是}{n a n n S nS S S S T n n ++++= 32321}{n S 5S 最大项的是()}{n T A . B .或C .D .或3T 2T 3T 9T 9T 10T 9.已知函数在区间上的最大值为则的最小值为( ))(|16|)(2R a a xx x f ∈-+=[]4,1),(a g )(a g A 、4B 、5C 、6D 、710.已知函数若对任意的 恒成|,|)1()(2a x x x x f --+=,R x x ∈2,121x x ≠且0)]()([-2121>-x f x f x x )(立,则实数的取值范围( )a A. B. C. D.10<<a 1≤a 31≤a 31≥a12.已知,那么_________,____________tan =2α=-)4tan(α=-αααcos sin sin 213.设,则= ;()()()()55221051112+++++++=-x a x a x a a x 0a =_ ___ .543215432a a a a a ++++14.已知函数,则 ;若 =)(x f ⎩⎨⎧≥<--0,30),(log 13x x x x =-)1(f ==a a f 则,3)(15.已知等差数列{a n }的前n 项和,若,则 ,n S ,5,131==a a 362=-+k k S S =d =k 16.已知定点满足=2,动点与动点满足=4,,且B A ,|AB |→P M |PB |→R ∈-+=→→→λλλ,AP )1(AB AM =,则的取值范围是 ,若动点也满足,则的取|MP |→|MA |→→→⋅AP AM C 4|CB |=→→→⋅AC AM 值范围是 .17.对正整数n ,设曲线)1(x x y n -=在2x =处的切线与y 轴交点的纵坐标为n a ,则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和的公式是 .18.已知向量,.函数的图像相邻两条对称轴的距离(sin ,sin )a x x ωω= (sin ,cos )(0)b x x ωωω=> ()f x a b =⋅为.4π(Ⅰ)求的值;ω(Ⅱ)当时,求函数的值域.[0,]4x π∈()f x19.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c 已知2222a c ac b +=5cos 0A B +=.(1)求cos C ;(2)若ABC ∆的面积52S =,求b .20.已知,数列的各项均为正数,前项和为,且,,设,*N n ∈}{n a n nS 11=a 22=a nn n a a b 212+=-(1)若数列是公比为3的等比数列,求;}{n b nS 2(2)若对任意,恒成立,求数列的通项公式;*N n ∈22na S n n +=}{n a (3)若,数列也为等比数列,求数列的通项公式.)12(32-=n n S }{1+n n a a }{n a21.已知函数2431()()2-==-+x f x g x x ax (I )若在处的切线与也相切,求的值;()y f x =1x =()y g x =a (II )若,求函数的最大值.1a =()()y f x g x =+22.已知函数()b x a ax x x f +-+-=2233231, ),(R b a ∈(1)当3=a 时, 若()x f 有3个零点, 求b 的取值范围;(2)对任意]1,54[∈a , 当[]m a a x ++∈,1时恒有()a x f a ≤'≤-, 求m 的最大值,并求此时()x f 的最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7、若平面上四点 A、 B、 C、D,满足任意三点不共线,且
4AC 2AB AD ,则 S ABD ___。 S ABC
8、设 f x 是定义在 R 上 的函数,满足 f x
cos2 x
ห้องสมุดไป่ตู้
3,f x
sin 2 x
1 ,则函数 f x =______。
4
4
9、ABCD-A1B1C1D1 为正四棱柱,已知 AB1 与底面 A1B1C1D1 所成角的 正切值为 a ,则二面 角 A-B1D1-A1
的正切值为 ______。 10、如图,椭圆 C : x2 y2 1(0 m 1) 的左顶点为 A ,
m
M 是椭圆 C 上异于点 A 的任意一点,点 P 与点 A 关于点 M 对称.若椭圆 C 上存在点 M ,使得 OP OM ,则 m的取值范围是 _________.
11、已知 b, c R ,二次函数 f x
1
a1 a2
,
an 1
求所有实数 a ,使得 0 an 1 , n 2 。
答案: 3 ; -1259
; 3; 2;
2
; 0, ; 4;
1
sin 2 x ;
2a ;
2 0,
3
。
2
4
4
4
11、令 f x
x x1 x x2 ,可知 c2 c bc f 0 f 1
1 0, 。
16
12、 k 0 ,弦长为 3 。
4、若 a R , b R ,且 max min 2x 4, ax2 xR
5、已知函数 f ( x ) |1 3 sin 2x | ,若 f (2 x a)
b,5 3x 2 ,则 a b ______。
f (2 x a ) 恒成 立,则实数 a 的最小正
值为
.
6、已 知函数 f x cos a sin x sin bcosx 无零 点,则 a2 b2的取值范围为 ______。
2
x
bx
c 在( 0,1)上与 x 轴有两个不同的交点, 求 c 2
c
bc
的取值范围。
12、已知 A 为抛物线 y2 2x 上的动点,定点 B 的坐标为( 2, 0),以 AB 为直径作圆 C,若圆 C 截
直线 x
ky
3 2
0 所得的弦长为定值;求此弦长和实数
k 的值。
13、设数列 an 定义 为 a1 a , an 1 1
2018 年浙江省数学竞赛模拟卷四
1、已知复数 z1 、 z2 ,且 z1 2 z2 2 , z1 z2
7 ,则 z1 z2 的值为 ______ 。
2、若 x R ,则 展开式 x3 1 x 4 9 中常数项为 ______。
3、设 [x] 表示不超过 x 的最大整数,则方程 3x2-10[x]+3=0 的所有实数根的个数为 ______。
1 13、 an 1 1
a1 a2
,可化为 Sn 1
1
。
an 1
an 1 1
由 Sn 与 an 的关系得: an
1 an 1 1
1 ,可化为 an 1
an 1
an 2 an 2 an
n 1
2。
由递推可知,当 0 an 1时,一定有 0 an 1 1。
所以只要 0
a2
1
1 a1
1 ,得 a
0。
