机组组合问题的优化方法综述
航空发动机效率提升研究及优化措施分析

航空发动机效率提升研究及优化措施分析航空发动机效率的提升是航空产业发展的重要课题之一。
随着对环境保护和能源效率的需求不断增加,航空发动机的效率优化成为了关键的研究领域。
本文将讨论航空发动机效率的相关概念、研究方法以及现有的优化措施,并对未来的发展进行前瞻性展望。
首先,我们需要明确航空发动机效率的概念。
航空发动机效率是指在单位时间内产生的动力输出与所消耗的燃料能量之间的比值。
通过提高航空发动机的效率,可以减少燃料的消耗量,降低航空运输对能源的依赖,同时也能减少对环境的污染。
目前,航空发动机效率提升的研究主要集中在以下几个方面:1. 燃料燃烧效率的提高:通过改进燃烧室的设计和燃料注入系统,优化燃料与空气的混合过程,可以提高燃料的燃烧效率。
此外,采用燃料增压系统和高效的压缩机,可以提高整个燃烧过程中的压缩比,进一步提高燃烧效率。
2. 减少内部损失:航空发动机内部存在着多种损失,如摩擦损失、冷却损失、机械损失等。
通过改进涡轮机的结构和材料,减少叶轮和导叶之间的摩擦损失;优化冷却系统,提高冷却效率,减少冷却损失;采用先进的机械设计和材料,降低机械损失。
这些措施可以显著减少内部损失,提高航空发动机的效率。
3. 废气再利用:航空发动机在燃烧过程中会产生大量废气。
通过在废气排放中回收能量,如采用废气涡轮增压、废气余热回收等技术,可以提高发动机的能量利用率,进一步提高效率。
除了以上的研究领域,航空发动机效率提升还面临着一些挑战。
首先,高效率往往伴随着高温和高压,在设计和制造方面会面临更高的要求;其次,航空发动机的能效提升需要综合考虑安全性、可靠性和经济性等方面的因素,需要协调各种技术和指标的平衡。
未来,航空发动机效率提升的发展方向是多方面的。
一方面,随着新材料、新工艺的出现,航空发动机的设计和制造将更加先进和精细化,进一步提高效率;另一方面,航空发动机将更加智能化,通过数据分析和预测,实现优化运行和维护,进一步提升效率。
组合优化问题简介

组合优化问题简介在我们的日常生活和工作中,经常会遇到各种各样需要做出最优选择的情况。
比如,在旅行时规划最佳路线,以使花费的时间和费用最少;在生产线上安排工序,以提高生产效率和降低成本;在物流运输中选择最优的配送方案,以减少运输时间和成本等等。
这些问题都属于组合优化问题。
组合优化问题是一类在离散的、有限的可行解集合中,寻找最优解的问题。
这里的“组合”意味着解决方案是由多个元素的组合而成,而“优化”则表示我们要找到其中最好的那个组合。
让我们以一个简单的例子来理解组合优化问题。
假设你要从城市 A 前往城市 C,中间需要经过城市 B。
从 A 到 B 有三条路线可选择,分别需要花费 2 小时、3 小时和 4 小时;从 B 到 C 也有三条路线可选择,分别需要花费 1 小时、2 小时和 3 小时。
那么,要找到从 A 到 C 的最短时间路线,就需要考虑所有可能的组合,即 3×3=9 种组合,然后从中挑选出总时间最短的那一种。
组合优化问题具有一些显著的特点。
首先,可行解的数量通常是有限的,但可能非常庞大。
就像上面的例子,仅仅是两个阶段的选择就有 9 种可能,如果涉及更多的阶段和更多的选择,可行解的数量会呈指数级增长,这使得直接枚举所有可能的解变得非常困难,甚至在计算上是不可行的。
其次,组合优化问题的目标函数通常是明确的。
在上述例子中,目标就是找到从 A 到 C 的总时间最短的路线,这个目标是清晰可度量的。
再者,很多组合优化问题具有实际的应用背景和重要的经济价值。
例如,在资源分配问题中,如何将有限的资源分配给不同的项目或任务,以实现最大的效益;在网络设计中,如何规划网络拓扑结构,以最小化建设成本和提高网络性能;在排班问题中,如何安排员工的工作时间表,以满足业务需求并减少人力成本等。
常见的组合优化问题包括旅行商问题(TSP)、背包问题、装箱问题、指派问题等。
旅行商问题是一个经典的组合优化问题。
假设有一个旅行商要访问n 个城市,每个城市只能访问一次,最后回到出发城市。
电力系统机组组合问题的研究

电力系统机组组合问题的研究1. 本文概述电力系统机组组合问题是电力系统运行和规划中的一个重要议题。
在这篇文章中,我们将深入探讨如何通过优化算法和决策支持系统来提高电力系统的经济性、可靠性和可持续性。
本文首先介绍了电力系统机组组合问题的研究背景和意义,阐述了在当前能源转型和电力市场改革的大背景下,如何通过科学合理的机组组合来实现电力系统的高效运行。
接着,文章将回顾相关领域的研究进展,包括传统的优化方法和近年来兴起的智能优化算法,以及它们在电力系统机组组合问题中的应用情况。
本文还将讨论电力系统机组组合问题面临的挑战和未来的研究方向,特别是在考虑环境保护和可再生能源融入的情况下,如何实现电力系统的绿色、低碳转型。
文章将介绍本文的研究方法和主要内容安排,为读者提供一个清晰的研究框架和阅读指南。
通过本文的研究,我们期望能够为电力系统的运行和规划提供有价值的参考和指导,为实现能源的可持续发展贡献力量。
2. 电力系统机组组合问题的理论基础电力系统机组组合问题(Unit Commitment Problem, UCP)是电力系统运行中的一个核心优化问题,旨在确定在未来某个时间段内,哪些发电机组应该开启或关闭,以及它们的出力水平应该是多少,从而满足预期的电力需求,同时优化运行成本和其他相关指标。
UCP是一个复杂的组合优化问题,涉及到大量的决策变量和约束条件,其理论基础涉及多个学科领域的知识。
UCP的理论基础包括电力系统的基本运行原理。
电力系统由多个发电机组、输电网和配电网组成,这些组成部分之间的相互作用和相互影响构成了电力系统运行的基础。
发电机组的出力、电网的传输容量以及负荷的变化等因素都会影响到电力系统的稳定运行。
在解决UCP时,必须充分考虑这些因素,确保电力系统的安全、稳定和经济运行。
UCP的理论基础还包括优化理论和算法。
由于UCP是一个复杂的组合优化问题,传统的数学方法往往难以直接求解。
需要借助优化理论和算法来寻找问题的最优解。
发电机机组最优组合数学模型
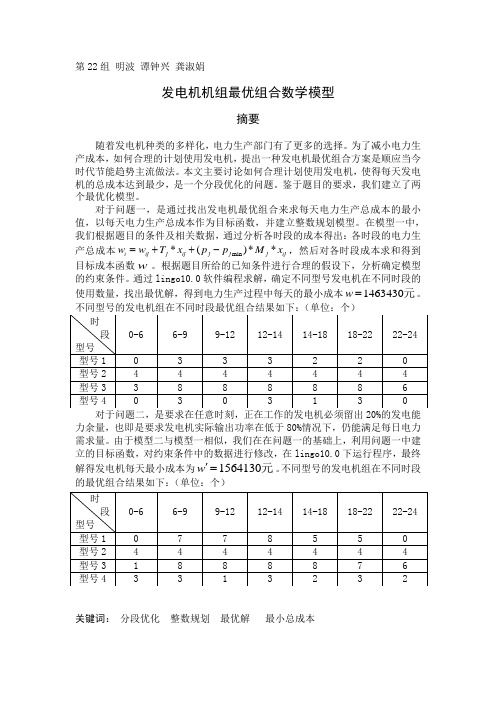
第22组 明波 谭钟兴 龚淑娟发电机机组最优组合数学模型摘要随着发电机种类的多样化,电力生产部门有了更多的选择。
为了减小电力生产成本,如何合理的计划使用发电机,提出一种发电机最优组合方案是顺应当今时代节能趋势主流做法。
本文主要讨论如何合理计划使用发电机,使得每天发电机的总成本达到最少,是一个分段优化的问题。
鉴于题目的要求,我们建立了两个最优化模型。
对于问题一,是通过找出发电机最优组合来求每天电力生产总成本的最小值,以每天电力生产总成本作为目标函数,并建立整数规划模型。
在模型一中,我们根据题目的条件及相关数据,通过分析各时段的成本得出:各时段的电力生产总成本min *()**i ij j ij j j j ij w w T x p p M x =++-,然后对各时段成本求和得到目标成本函数w 。
根据题目所给的已知条件进行合理的假设下,分析确定模型的约束条件。
通过lingo10.0软件编程求解,确定不同型号发电机在不同时段的使用数量,找出最优解,得到电力生产过程中每天的最小成本1463430w =元。
力余量,也即是要求发电机实际输出功率在低于80%情况下,仍能满足每日电力需求量。
由于模型二与模型一相似,我们在在问题一的基础上,利用问题一中建 立的目标函数,对约束条件中的数据进行修改,在lingo10.0下运行程序,最终解得发电机每天最小成本为1564130w '=元。
不同型号的发电机组在不同时段的最优组合结果如下:(单位:个)关键词: 分段优化 整数规划 最优解 最小总成本1. 问题重述为满足每日电力需求(单位为兆瓦(MW)),可以选用四种不同类型的发电机。
每日电力需求如下表1。
每种发电机都有一个最大发电能力,当接入电网时,其输出功率不应低于某一最小输出功率。
所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。
机组组合问题的优化方法综述

机组组合问题的优化方法综述一、引言机组组合问题是一个经典的优化问题,广泛应用于电力系统、制造业、物流运输等领域。
该问题主要关注如何在满足一定约束条件下,合理选择一组设备或机组,以实现某种特定的目标,如总成本最低、总产量最大等。
随着科技的发展和实际需求的不断变化,机组组合问题的规模和复杂性也在不断增加,因此,研究和发展新的优化方法以解决这类问题具有重要的理论和实践意义。
二、机组组合问题的定义和特性机组组合问题是指在给定一组设备或机组,每个设备或机组都有各自的运行成本、运行时间、可用性等属性,如何在这些设备或机组中选择一部分,使得满足某种特定目标(如总成本最低、总产量最大等)的同时,满足一系列约束条件(如设备数量限制、总运行时间限制等)。
这类问题具有以下特性:组合性:问题的解是一组设备的组合,而非单一设备或机组。
约束性:问题的解必须满足一系列的约束条件。
复杂性:问题的规模和复杂性往往随着设备或机组的数量的增加而增加。
动态性:设备的状态和环境可能会随时间变化,需要动态调整机组组合。
三、经典优化方法线性规划:线性规划是一种常用的数学优化方法,可以通过构建和解决线性方程组来找到最优解。
在机组组合问题中,可以通过构建成本、产量等与设备选择和运行时间之间的线性方程组,求解最优解。
动态规划:动态规划是一种通过将问题分解为子问题,并逐一求解子问题的最优解以得到原问题的最优解的方法。
在机组组合问题中,可以通过构建状态转移方程,求解每个状态下的最优解。
遗传算法:遗传算法是一种模拟生物进化过程的优化方法,通过选择、交叉、变异等操作来产生新的解,并逐步逼近最优解。
在机组组合问题中,可以通过编码设备选择和运行时间的组合作为染色体,进行选择、交叉、变异等操作,以找到最优解。
模拟退火:模拟退火是一种以一定概率接受非最优解的优化方法,通过模拟金属退火的过程来寻找最优解。
在机组组合问题中,可以通过对每个解进行评估,并以一定概率接受非最优解,以避免陷入局部最优解。
组合优化问题的分析与求解

组合优化问题的分析与求解在我们的日常生活和工作中,经常会遇到各种各样需要做出最优决策的情况。
比如,物流运输中如何规划路线以最小化成本,生产线上如何安排工序以最大化效率,资源分配中如何分配有限的资源以满足最大的需求等等。
这些问题都属于组合优化问题,它们的共同特点是在有限的可行解集合中,寻找一个最优的解。
组合优化问题是一个具有广泛应用和重要意义的研究领域。
它不仅在数学、计算机科学、运筹学等学科中有着深厚的理论基础,还在工程、管理、经济等实际领域中发挥着重要的作用。
解决组合优化问题,可以帮助我们提高生产效率、降低成本、优化资源配置,从而实现更好的经济效益和社会效益。
那么,什么是组合优化问题呢?简单来说,组合优化问题就是在给定的约束条件下,从有限个可行解中找出一个最优解的问题。
这些可行解通常是由一些离散的元素组成,比如整数、集合、排列等。
而最优解则是指在满足约束条件的前提下,使得某个目标函数达到最大值或最小值的解。
组合优化问题的一个典型例子是旅行商问题(Travelling Salesman Problem,TSP)。
假设有一个旅行商要访问 n 个城市,每个城市只能访问一次,最后要回到出发城市。
已知城市之间的距离,那么如何规划旅行路线,使得旅行的总距离最短?这个问题看似简单,但实际上是一个非常复杂的组合优化问题,因为可能的路线数量随着城市数量的增加呈指数增长。
再比如背包问题(Knapsack Problem)。
有一个背包,其容量有限,同时有一系列物品,每个物品有一定的价值和重量。
如何选择物品放入背包,使得背包中物品的总价值最大,同时不超过背包的容量限制?这也是一个常见的组合优化问题。
为了求解组合优化问题,人们提出了许多方法。
其中,精确算法是一种能够保证找到最优解的方法,但它们通常只适用于规模较小的问题。
例如,分支定界法就是一种常见的精确算法。
它通过不断地将问题分解为子问题,并对每个子问题进行评估和剪枝,逐步缩小搜索范围,最终找到最优解。
风电火电抽水蓄能联合优化机组组合模型

风电火电抽水蓄能联合优化机组组合模型一、概述随着全球能源结构的转变和可再生能源的大力发展,风电作为一种清洁、可再生的能源形式,在全球范围内得到了广泛的关注和快速的发展。
风电的随机性、间歇性和波动性给电网的稳定运行带来了挑战。
为了克服风电的这些缺点,提高其并网量和稳定性,风电、火电与抽水蓄能电站的联合运行成为了研究的热点。
风电因其发电过程中CO2排放低,近年来在全球范围内得到了大力发展。
风电的不稳定性、不可预测性以及电网接纳风电的能力限制等问题,使得风电的大规模并网变得困难。
为了克服这些问题,研究者们提出了风电与火电、抽水蓄能电站的联合运行方式。
这种方式不仅能够利用抽水蓄能电站的调峰填谷能力,提高电网消纳风电的能力,还能够实现能源的互补和优化配置,提高整个系统的经济效益和环保效益。
本文旨在研究风电、火电与抽水蓄能电站的联合优化机组组合模型。
我们分析了风电的不确定性及其对电网的影响,然后建立了考虑风电不确定性影响及抽蓄水头变化影响的联合优化机组组合模型。
通过该模型,我们可以实现对风电、火电和抽水蓄能电站的协调优化,提高风电的并网量和稳定性,同时降低整个系统的发电成本。
本文的研究对于提高电网运行的安全性和经济性,促进风电的大规模开发和利用具有重要意义。
同时,也为其他间歇式能源的接入和消纳提供了有益的参考和借鉴。
在接下来的章节中,我们将详细介绍风电、火电与抽水蓄能电站的联合优化机组组合模型的建立过程、求解方法以及实际应用效果。
通过具体的算例分析和比较,我们将展示该模型的有效性和优越性,为相关领域的研究和实践提供有力的支持和指导。
1. 介绍风电、火电和抽水蓄能的基本概念及其在能源系统中的作用。
风电,即风力发电,是一种利用风力驱动风力发电机组的可再生能源发电方式。
风力发电以其清洁、可再生的特性,在全球范围内得到了广泛的关注和应用。
风力发电的随机性和波动性是其显著的特点,这使得风电并网需要其他能源发电作为备用服务,以保证电力供给的稳定性。
机组组合问题的优化方法综述

机组组合问题的优化方法综述陈皓勇 王锡凡(西安交通大学电力工程系 710049 西安)摘 要 机组组合问题是编制短期发电计划首先要解决的问题,合理的开停机方案将带来很大的经济效益,由于问题十分复杂,很难找出理论上的最优解,文中介绍了机组组合问题的数学模型,分类综述了从60年代起该问题的主要解法,比较了各种方法的优缺点,并提出了尚待研究的问题。
关键词 发电计划 机组组合 优化方法分类号 TM 7321998205215收稿。
国家教委博士点基金资助项目。
0 引言电力系统经济调度的目的是在满足系统安全约束、电能质量要求的条件下尽可能提高运行的经济性。
经济调度的效益很大,根据国外资料和华北、东北等电网的实际测算,节省能源可达总耗量的015%~115%[1]。
经济调度是一个十分复杂的系统优化问题,从总体上解决,难度非常大,常分解为一系列的子问题分别处理。
从短期发电计划来看,可分为机组组合、火电计划、水电计划、交换计划、燃料计划等子问题。
其中机组的优化组合是编制短期发电计划首先要解决的问题,它的经济效益一般大于负荷经济分配的效益。
文献[2,3]中介绍了电力系统经济调度和机组组合问题的数学模型和基本方法。
机组组合问题是一个高维数、非凸的、离散的、非线性的优化问题,很难找出理论上的最优解,但由于它能够带来显著的经济效益,人们一直在积极研究,提出各种方法来解决这个问题,如启发式方法、优先顺序法、动态规划法、整数规划和混合整数规划法、分支定界法、拉格朗日松弛法、专家系统法、人工神经网络法、模拟退火算法、遗传算法等,文献[4,5]介绍了历年来机组组合问题的各种解法和相关参考文献。
本文对机组组合问题的主要解法进行了更深入的探讨,并加以分类综述,比较了各种方法的优缺点,提出了尚待研究的问题。
1 机组组合问题的数学模型根据实际系统不同的要求,对于机组组合问题可以建立不同的模型。
在一般情况下,应以系统各发电机组的开停机状态和出力为控制变量,在满足系统负荷和备用要求、线路潮流限制及机组爬坡速率(ram p rate ,即功率变化速率)、最小开停机时间、燃料总量等约束条件下,使开停机费用和运行费用之和最小。
鲁棒优化在电力系统机组组合中的应用综述

鲁棒优化在电力系统机组组合中的应用综述
宫成;宋靓云;王卫;王腾飞;夏世威;张东英
【期刊名称】《科学技术与工程》
【年(卷),期】2022(22)12
【摘要】随着高比例可再生能源并网,电力系统运行的不确定性进一步增强,加剧了电力系统调度运行的决策难度。
鲁棒优化(robust optimization,RO)方法处理该类问题具有一定优势,综述了鲁棒优化在电力系统机组组合决策中的应用。
首先分析了经典鲁棒优化不确定性集的构造、单阶段及二阶段经典鲁棒优化一般模型,并对二阶段经典鲁棒优化机组组合(robust optimization unit commitment,RO-UC)模型及求解方法进行归纳;其次,阐述了基于随机向量矩和随机变量概率分布的模糊集构建,并总结分布鲁棒优化机组组合(distribution robust optimization unit commitment,DRO-UC)在电力系统问题中的应用;最后对比分析了经典鲁棒优化和分布鲁棒优化方法特点和适应场景,并对鲁棒优化机组组合研究方向进行展望。
【总页数】9页(P4687-4695)
【作者】宫成;宋靓云;王卫;王腾飞;夏世威;张东英
【作者单位】国网北京市电力公司;华北电力大学电气与电子工程学院
【正文语种】中文
【中图分类】TM732
【相关文献】
1.进化优化算法在电力系统机组优化组合中的应用研究
2.机组组合问题的仿射可调整鲁棒优化模型与算法
3.电力系统中机组组合的现代智能优化方法综述
4.机组组合问题的仿射可调整鲁棒优化模型与算法
5.风电不确定下机组组合的鲁棒优化研究
因版权原因,仅展示原文概要,查看原文内容请购买。
航空发动机多学科综合优化设计

目 录
• 引言 • 航空发动机多学科优化设计理论 • 航空发动机多学科综合优化设计方法 • 航空发动机多学科综合优化设计案例分析 • 航空发动机多学科综合优化设计展望
01
CATALOGUE
引言
研究背景
航空发动机是飞机的心脏,其性能直接影响到飞机的安全和效率。随着科技的发 展,对航空发动机的性能要求也越来越高,因此需要不断进行优化设计。
总结词
涡轮叶片优化设计
详细描述
涡轮叶片是航空发动机中承受高温和高应力的关键部件,其性能对发动机的可靠性、寿命和性能具有 重要影响。通过对涡轮叶片进行优化设计,可以提高其耐热性能、抗疲劳性能和冷却效果,从而延长 发动机的寿命。具体包括改进叶片材料、优化叶片形状和冷却系统等措施。
案例三:某型航空发动机控制系统优化设计
多目标优化算法研究 研究适用于航空发动机多学科优 化设计的高效多目标优化算法, 解决多目标、多约束优化问题。
智能优化与决策支持 结合人工智能、大数据等技术, 开发智能优化与决策支持系统, 实现多学科优化设计的智能化和 自动化。
THANKS
感谢观看
分解协调法
分解协调法是一种将复杂的多学科问题分解为若干个相对简单的子问题,并分别对子问题进行优化的 方法。
该方法通过合理地分解多学科问题,将不同学科的约束和目标分别进行优化,再通过协调子问题的解, 达到整体性能最优。
分解协调法能够降低多学科问题的复杂度,提高计算效率和可操作性,适用于大规模的多学科优化问题 。
航空发动机多学科优化设计特点
高度复杂性
航空发动机多学科优化设计涉及多个学科领域,如热力学 、流体力学、结构力学、控制理论等,需要综合考虑各种 因素之间的相互作用和影响。
机组组合问题的模型与优化方法综述

机组组合问题的模型与优化方法综述机组组合(UnitCommitment,简称UC)是指在满足用户负荷需求、负荷平衡和发电成本最低的条件下,将可用机组分段投运,选择合适的机组组合投运方式。
UC问题具有实用性,是系统优化调度和可靠性分析的基础,在电力系统运行中具有重要的实际意义。
UC问题包括多个约束条件和目标函数,故是一个典型的约束多目标优化问题。
由于它具有约束多目标、非线性和非凸性等特点,因而具有极大的挑战性和复杂性,有可能存在多个局部最优解,使得UC问题很难得到全局最优解。
为此,多年来学者们开展了大量的理论研究和应用研究,提出了大量的UC模型和算法,其中给出的模型和算法具有较高的准确性和可靠性,为提高系统运行效率提供了有效的支持。
一、数学模型UC问题的数学模型由一般的线性规划问题和约束最优化问题构成,其具体形式为:最小化发电成本:Minz =cj*ΣPj使得:1.系统负荷平衡:ΣPj-Pd = 02.机组投运约束:Rmin≤Rj≤Rmax3.机组运行时间约束:Tu≤Σtj≤Td4.机组上下网约束:Σ(tj-tj-1)≥Tu5.发电量约束:Pmaxj≥Pj≥Pminj6.连续发电约束:Σ(Tj-Tj-1)≥TD7.发电机最大负荷变化量约束:|Pj+1-Pj|≤PmaxΔP上式中,cj为单位发电量的发电成本,Pd为负荷需求,Pj为单位机组的发电量,Rmin、Rmax分别为机组的最小、最大运行比例,Tu、Td分别为机组的最小、最大运行时间,tj为机组的实际运行时间,TD为机组的连发约束,PmaxΔP为机组的最大负荷变化量,Pmaxj、Pminj分别为机组的最大、最小发电量。
二、优化方法UC问题大多使用多目标优化方法进行求解。
传统的多目标优化方法主要有改进拓扑搜索、“缩放因子-改进拓扑搜索”模型、双线性规划模型等,这些方法的优化结果受到随机初始状态的影响,且很容易陷入局部最优解。
而近年来,随着智能计算、数据挖掘和大数据技术的发展,新一代优化算法如混合优化、支持向量机、遗传算法、蚁群算法、人工神经网络等已被用于UC问题的求解。
基于优先级排序和内点法的机组优化组合

基于优先级排序和内点法的机组优化组合王剑;刘天琪;刘学平【摘要】机组优化组合的目标是确定电力系统煤耗量和网损最小的发电调度方式.优化模型中考虑了机组爬坡率的限制、输电网络断面安全约束,针对寻优效率提出了一种优先级排序和内点法相结合的机组组合优化方法.按能耗指标形成机组优先级排序表,以获得尽可能好的开机方式初始值;用局部寻优法在初始值附近的可行域内寻求最优组合状态;对负荷分配的连续性子问题用内点法求解.通过对IEEE-39节点10机系统进行仿真计算,验证了所提方法收敛速度快、耗时少,对处理机组组合问题具有有效性和适用性.【期刊名称】《电力系统保护与控制》【年(卷),期】2010(038)013【总页数】6页(P55-60)【关键词】机组组合;优先级表;内点法;负荷分配【作者】王剑;刘天琪;刘学平【作者单位】四川大学电气信息学院,四川,成都,610065;四川大学电气信息学院,四川,成都,610065;四川大学电气信息学院,四川,成都,610065【正文语种】中文【中图分类】TM760 引言动态经济调度是考虑系统负荷各个时段之间的联系,计入机组出力的一些技术约束的一种优化调度方法,是一个动态机组组合问题,对提高系统经济性和安全性有着重要的意义。
近年来,国家实施节能调度政策[1],对于火电机组,煤耗低的多发、满发,煤耗高的机组少发、不发,这可能会导致断面潮流越限[2],网络安全制约是必须考虑的问题。
传统经济调度涉及机组启停决策和负荷优化分配,目前研究工作正在朝着考虑多种约束条件、大规模电网、快速收敛的算法和更好的优化结果方向发展。
文献[3-5]分别考虑了机组爬坡速率约束、旋转备用约束、网络断面潮流约束。
在算法方面,文献[6]提出具有状态约束的动态系统优化调度方法,但计及网络的动态优化调度问题尚需进一步研究。
文献[7]中提出了一种动态经济调度的快速解耦算法。
近年来,智能优化算法引入到电力系统中,如遗传算法、模拟退火算法、禁忌搜索算法、粒子群算法、蚁群算法、人工神经网络等[8],这类算法不要求严格的数学模型,寻优过程本质是随机的,迭代次数较多,计算速度慢,并且优化结果受初值及寻优规则的影响,算法本质是启发式的,缺乏刚性[9-10]。
机组组合问题的优化方法综述

机组组合问题的优化方法综述一、本文概述随着能源行业的快速发展,电力系统的稳定性和经济性越来越受到关注。
机组组合问题,即在满足电力系统负荷需求的优化发电机组的运行组合,以提高电力系统的整体运行效率和经济性,成为当前研究的热点。
本文旨在综述机组组合问题的优化方法,对现有的各类优化算法进行全面分析和比较,为相关领域的研究者和实践者提供有益的参考。
本文将简要介绍机组组合问题的基本概念和数学模型,为后续的优化方法分析奠定基础。
将重点介绍并分析传统优化方法,如线性规划、动态规划、整数规划等,以及现代启发式优化算法,如遗传算法、粒子群优化算法、模拟退火算法等。
这些算法在机组组合问题中的应用将被详细阐述,包括其优点、缺点以及适用范围。
本文将总结机组组合问题优化方法的发展趋势,并对未来的研究方向进行展望。
通过本文的综述,读者可以全面了解机组组合问题的优化方法,为进一步提高电力系统的稳定性和经济性提供理论支持和实践指导。
二、机组组合问题的数学模型机组组合问题(Unit Commitment Problem, UCP)是电力系统运行中的一个核心问题,其目标是在满足系统负荷需求、系统安全约束以及机组运行约束的前提下,通过优化决策各机组的启停状态以及出力分配,来实现某种运行成本的最小化。
为了有效地解决UCP,首先需要建立其相应的数学模型。
机组组合问题的数学模型通常由目标函数和约束条件两部分组成。
目标函数通常与系统的运行成本相关,例如总燃料成本、排放成本或综合成本等。
约束条件则涵盖了电力系统的各种物理和运行限制,如功率平衡约束、机组出力上下限约束、爬坡率约束、旋转备用约束等。
在数学形式上,机组组合问题可以表示为一个混合整数线性规划(Mixed Integer Linear Programming, MILP)问题。
其中,整数变量用于表示机组的启停状态(0表示停机,1表示运行),而连续变量则用于表示机组的出力。
由于机组组合问题是一个NP难问题,其求解复杂度随着机组数量和系统规模的增加而迅速增长,因此在实际应用中,通常需要采用启发式算法、智能优化算法或近似求解方法来求得满意解。
不确定机组组合处理方法评述

不可 靠 般 而言 . 以把机组 组 合 问题 中的不确 定 一 可 性 隐式 表达 为 一个 固定备 用 需 求 的不 等 式 约束 . 加
入 上 述模 型 中 。 如下 式 :
, v
t f t
划 、 糊优 化 和 机会 约 束 规 划 3种 显 式 处理 不 确 定 模
t =l i =1
() 1 () 2
的系 统 负 荷 ( 1% 功率 计及 备 用之 后 , 组组 合 问题 变 为 系统 负荷 P 机 和 系统 固定 备用 R 共 同 的函数 . 解 可表 示 为如 下 ‘ 其
形式 :
步、 网络 安 全性 、 环境 保 护 和节 约 能 源要 求 提 高 、 电
力 市 场化 改 革 以及 多 种 可再 生 能 源发 电 的接 人 . 机 组 组 合 问题 不断 发 展 . 终 吸 引着 电力 _ 始 T业界 和学
者 的 目光 电力 系统机 组 组合 问题 本质 上 是一个 不 确 定性 优 化 问题 传 统机 组 组 合 问题 [2把 这种 不 1 ,
(
— ) T ≥ i
j一『 =7 t
( 1… , i , Ⅳ) =
() 5
式 中 : 为 总 时 段 数 :, 机 组 总 数 : ,为 、 F为 总 发 电
成本; 为机组i 时段的 y : 在t 状态; 为机组 在t p 时
段 的 出力 ; 为 预 测 的第 t p 时段 系统 总负 荷 ;式 ( ) 3 为机 组 出力约 束 , , 分别 为 机组 的最 大和 最 p p 小 出力 限值 ; ( ) 式 ( ) 式 4 、 5 为机 组 最 小启 停 时 间 约
性 的技术 进 行 了分析 、 比较和评 述
考虑风电的电力系统机组组合两阶段优化方法

考虑风电的电力系统机组组合两阶段优化方法*孟安波,马留洋,殷豪(广东工业大学自动化学院,广州510006)摘要:电的随机性和波动性给电力系统的安全经济运行带来了严峻的挑战,合理的风电不确定性模型及机组组 合优化方法是保证电力系统日前调度安全性和经济性的关键。
为此,提出一种考虑风电的电力系统机组组合 两阶段随机优化方法。
根据风电出力历史数据的非参数经验分布,生成符合风电随机性和波动性的风电动态 场景。
考虑到场景削减过程中容易忽略的一些极端边界场景会增加系统的弃风或切负荷风险,提出以削减后 的场景和极端边界场景为输人的机组组合两阶段优化模型。
同时,为求解机组组合这一非线性混合整数优化 问题,提出一种混合遗传纵横交叉算法的优化方法。
通过实验仿真结果证明了所提模型和方法用于求解考虑 风电的电力系统机组组合问题时的合理性和有效性。
关键词:风电;机组组合;动态场景;两阶段优化;混合遗传纵横交叉算法中图分类号:TM731 文献标识码:B 文章编号:1001-1390(2018)07>0008"08 Two-stage optimization method for unit commitment of powersystem considering wind powerMeng Anbo, Ma Liuyang, Yin Hao{School of A utomation, Guangdong University of Technology, Guangzhou 510006, China) Abstract :The randomness and volatility of wind power bring serious challenges to the safe and economical operation of power system. Reasonable wind power uncertainty model and unit commitment optimization method are the key to ensure the safety and economy of dispatching in power system. A two-stage stochastic optimization method for unit commitment of power system considering wind power is proposed in this paper. According to the nonparametric empirical distribution of wind power output history data, wind power dynamic scenarios are produced accorded with wind power randomness and volatility. Considering that some extreme boundary scenarios that are easily overlooked in the process of scenarios reduction will increase the risk of wind or load shedding, a two-stage optimization model of unit commitment with reduced scenarios and extreme boundary scenarios is proposed. Meanwhile, in order to solve the nonlinear mixed integer optimization problem of unit commitment,a hybrid genetic and crisscross optimization algo- rithm is proposed. The simulation results show that the proposed model and method are effective when solving the problem of unit commitment with wind power system.Keywords:wind power, unit commitment, dynamic scenarios, two-stage optimization, hybrid genetic and crisscross optimization algorithm〇引言随着电力需求的不断扩大以及新能源的不断发 展,电力工业发生了巨大的变化。
机组组合基于Benders分解与割平面的方法及约束优化SQP算法研究

1、构建机组组合问题的数学模型,包括机组功率、运行成本、排放约束等。
2、利用Benders分解将原问题分解为多个子问题,每个子问题只包含部分约 束条件。
3、对于每个子问题,利用割平面方法进行求解。具体步骤包括: (1)根据子问题的约束条件,利用线性规划方法求解初始最优解;
(2)根据最优解的情况,生成新的割平面,并添加到约束条件中; (3)重复执行步骤(1)和步骤(2),直到满足终止条件。
4、将所有子问题的最优解进行 组合,得到原问题的可行解。
41、利用约束优化策略的SQP算法对可行解进行优化,得到最终的最优解。 具体步骤包括:
(1)根据可行解的情况,构造一个初始SQP问题; (2)利用SQP算法对SQP问题进行求解,得到最优解;
(3)根据最优解的情况,对原始问题的可行解进行更新; (4)重复执行步骤(2)和步骤(3),直到满足终止条件。
(2)启发式算法。启发式算法是一类基于经验或规则的近似求解方法,在 机组组合问题中也得到了广泛应用。例如,遗传算法、模拟退火算法、蚁群算法 等在机组组合问题求解中均有成功应用的案例。这些算法通常将机组组合问题转 化为一个多目标优化问题,并利用启发式信息进行迭代搜索,最终找到一组近似 最优解。
4、机组组合问题的未来研究方 向
引言
机组组合问题是指在一定约束条件下,将若干个不同类型或型号的机器或设 备组合在一起,使其满足特定的生产需求或性能指标。这类问题在能源、制造、 交通等诸多领域都具有广泛的应用,对于提高生产效率和降低成本具有重要意义。 然而,机组组合问题同时也是一类典型的NP难问题,求解难度较大。因此,研究 机组组合问题的优化方法一直是学术界和工业界的焦点。
机组组合基于Benders分解与割平 面的方法及约束优化SQP算法研究
电力系统调度中的优化算法

电力系统调度中的优化算法电力系统调度是指在一定时段内,根据供电负荷和电源出力的变化情况,合理安排电力生成和配送,以保证电力系统稳定运行的过程。
在电力系统调度中,优化算法的应用可以提高调度效率和降低调度成本,是电力系统调度的重要组成部分。
一、常用的优化算法1.遗传算法遗传算法是一种模拟自然选择和遗传机制的优化算法。
遗传算法通过对包含可能解决方案的种群进行操作,不断进行自然选择、交叉、变异和适应度评价等过程,最终找到符合要求的最优解。
在电力系统调度中,遗传算法可以用于发电机出力调度、线路输电功率调度、电能质量控制等方面。
2.粒子群算法粒子群算法是一种基于群体智慧的优化算法。
该算法通过模拟粒子在多维状态空间中搜索最优解,实现优化问题的求解。
在电力系统调度中,粒子群算法可以用于电力市场竞标、电力负荷预测、风电光伏发电预测等方面。
3.模拟退火算法模拟退火算法是一种利用物理退火原理寻找最优解的随机优化算法。
该算法通过在解空间中随机搜索,以一定概率接受劣解,以避免陷入局部最优解。
在电力系统调度中,模拟退火算法可以用于输电线路容量分配、配电变压器负载分配等方面。
二、应用实例1.电力市场竞标电力市场竞标是指发电厂根据市场需要,以市场价格向电力市场提供电力供给,完成电力交易的过程。
优化算法在电力市场竞标中的应用,可以通过计算合理的发电计划和交易价格,实现发电厂效益最大化和市场货源最优化。
遗传算法、粒子群算法等优化算法的应用,可以帮助发电厂制定最优的发电计划和交易策略,提高其市场竞争力。
2.电力负荷预测电力负荷预测是指通过对历史数据和相关因素的分析,预测未来一段时间的负荷变化情况。
优化算法在电力负荷预测中的应用,可以通过建立预测模型,预测未来负荷变化趋势和幅度,进而制定合理的供电计划和调度策略,提高电力系统调度的效率和精度。
粒子群算法、遗传算法等优化算法的应用,可以帮助电力系统制定最优的供电计划和调度策略,确保系统的稳定运行。
航空公司机组排班的优化模型研究与算法实现

航空公司机组排班的优化模型研究与算法实现航空公司机组排班问题是指根据航班需求和机组的人力资源限制,合理安排机组的工作时间和休息时间,以满足航班运行的需要。
机组排班的合理性直接影响航空公司的运行效率和服务质量。
因此,研究机组排班的优化模型和算法实现具有重要的实际意义。
在机组排班问题中,需要考虑许多限制条件,例如机组成员的工作时间限制、休息时间要求、航班需求以及机组成员之间的配对要求等。
同时,还需要考虑到机组成员的技能匹配和航班的特殊需求,如国际航班、长途航班等。
因此,机组排班问题是一个复杂的组合优化问题。
针对机组排班问题的优化模型研究可以采用多种方法,其中一种常见的方法是使用整数线性规划模型。
整数线性规划模型可以将机组排班问题转化为一个数学规划问题,通过定义决策变量、目标函数和约束条件,寻找最优的机组排班方案。
同时,还可以引入一些启发式算法和元启发式算法来求解机组排班问题,如遗传算法、模拟退火算法、禁忌搜索算法等。
除了整数线性规划模型和启发式算法,还可以通过建立机组排班问题的图模型来求解。
图模型可以将机组成员、航班和机组成员之间的关系表示为节点和边,通过图论的方法来求解机组排班问题。
例如,可以使用最小费用最大流算法来求解机组排班问题。
在算法实现方面,可以使用多种编程语言和工具来实现机组排班的优化算法。
例如,可以使用Python编程语言来实现整数线性规划模型和启发式算法,通过调用相关的数学规划库和启发式算法库来求解机组排班问题。
同时,还可以使用MATLAB等工具来进行模型建立和求解。
航空公司机组排班问题的优化模型研究和算法实现是一个复杂而重要的课题。
通过合理的模型设计和算法选择,可以有效地解决机组排班问题,提高航空公司的运行效率和服务质量。
希望本文的介绍对读者在理解和研究机组排班问题方面有所帮助。
火电机组优化运行关键技术分析论文[大全5篇]
![火电机组优化运行关键技术分析论文[大全5篇]](https://img.taocdn.com/s3/m/595519b96aec0975f46527d3240c844769eaa015.png)
火电机组优化运行关键技术分析论文[大全5篇]第一篇:火电机组优化运行关键技术分析论文摘要:火电厂作为我国电厂的主要组成部分,为社会发展提供电能支持,推进社会现代化建设。
但火电厂运行中需要消耗大量能源,同时还会造成严重的环境污染,不符合可持续发展战略,火电厂实行节能减排已成为必然。
有鉴于此,文章中以火电厂火电机组为切入点,分析火电机组节能降耗的原理,并给出火电机组优化运行的主要技术,分析节能运行的方法,以供参考。
关键词:火电机组;节能降耗;运行措施近些年我国社会经济快速发展,市场对电能的需求量持续增加,火电厂的规模与数量也在快速增加,做好节能减排工作已成为火电厂工作的主要内容。
火电厂运行中发电机组作为主要设备,其能耗直接决定火电厂的能耗。
通过优化火电机组运行模式,可以提高机组运行效率并降低能耗,增加火电厂经济效益,提高市场竞争力,本研究就此展开论述。
1火电机组优化运行分析能源供应日趋紧张化的背景下,火电厂更应该提高节能意识,强化能源管理工作,在保证正常运行的基础上降低能源消耗,提高火电厂的经济效益。
如何有效运行火电机组,达成节能降耗目的已成为火电厂行业研究的重要课题。
火电厂优化运行,指的是不增加新投入的基础上,通过调整运行参数并改变运行方式的方法,提高能源利用率。
火电厂的优化分成两类,即单设备优化与全厂优化。
前者通过优化单机的热经济性指标,后者则对全厂机组设备进行优化[1]。
火电机组运行优化及节能研究,有助于降低火电厂运行成本。
火电机组优化运行试验内容,主要包括:调整锅炉、调整汽轮机组与辅机、优化热控系统等。
此外,大型火电机组的热力系统构成较为复杂,很多因素都会对机组性能产生影响,单纯的理论研究需要附加较多的假设条件,还需要进行简化处理,难以获得准确的经济化的运行方案。
因此实际优化时,通过试验的方法获得各个机组在不同条件的运行数据,并通过全面分析、综合计算,获得最优运行方式,给火电厂运行提供指导与参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机组组合问题的优化方法综述陈皓勇 王锡凡(西安交通大学电力工程系 710049 西安)摘 要 机组组合问题是编制短期发电计划首先要解决的问题,合理的开停机方案将带来很大的经济效益,由于问题十分复杂,很难找出理论上的最优解,文中介绍了机组组合问题的数学模型,分类综述了从60年代起该问题的主要解法,比较了各种方法的优缺点,并提出了尚待研究的问题。
关键词 发电计划 机组组合 优化方法分类号 TM 7321998205215收稿。
国家教委博士点基金资助项目。
0 引言电力系统经济调度的目的是在满足系统安全约束、电能质量要求的条件下尽可能提高运行的经济性。
经济调度的效益很大,根据国外资料和华北、东北等电网的实际测算,节省能源可达总耗量的015%~115%[1]。
经济调度是一个十分复杂的系统优化问题,从总体上解决,难度非常大,常分解为一系列的子问题分别处理。
从短期发电计划来看,可分为机组组合、火电计划、水电计划、交换计划、燃料计划等子问题。
其中机组的优化组合是编制短期发电计划首先要解决的问题,它的经济效益一般大于负荷经济分配的效益。
文献[2,3]中介绍了电力系统经济调度和机组组合问题的数学模型和基本方法。
机组组合问题是一个高维数、非凸的、离散的、非线性的优化问题,很难找出理论上的最优解,但由于它能够带来显著的经济效益,人们一直在积极研究,提出各种方法来解决这个问题,如启发式方法、优先顺序法、动态规划法、整数规划和混合整数规划法、分支定界法、拉格朗日松弛法、专家系统法、人工神经网络法、模拟退火算法、遗传算法等,文献[4,5]介绍了历年来机组组合问题的各种解法和相关参考文献。
本文对机组组合问题的主要解法进行了更深入的探讨,并加以分类综述,比较了各种方法的优缺点,提出了尚待研究的问题。
1 机组组合问题的数学模型根据实际系统不同的要求,对于机组组合问题可以建立不同的模型。
在一般情况下,应以系统各发电机组的开停机状态和出力为控制变量,在满足系统负荷和备用要求、线路潮流限制及机组爬坡速率(ram p rate ,即功率变化速率)、最小开停机时间、燃料总量等约束条件下,使开停机费用和运行费用之和最小。
有的模型为了简化,忽略了某些约束,如线路潮流约束;有的模型考虑了水火电协调问题;另外一些模型考虑了负荷的随机性和发电机的可靠性。
设I 为可供调度的发电机集合;T ={1,2,…, T },为调度期间内的时段集合。
对每台发电机i ∈I 和每个时段t ∈T ,定义一个向量变量x it ,其分量为发电机i 在t 时段的所有连续变量。
例如,x it =[p it ,r it ]T ,p it 表示发电机i 在t 时段的有功;r it 表示该发电机提供的备用。
另外定义一个标量(或向量)变量z it 来表示发电机i 在t 时段的所有离散变量。
例如,z it =1如果发电机i 在t 时段开机0如果发电机i 在t 时段停机 把所有的x it 和z it 写成矩阵X 和Z ,即X =(x it )i ∈I ,t ∈T ,Z =(z it )i ∈I ,t ∈T 。
另外用x iT 表示(x it )t ∈T ,用x I t 表示(x it )i ∈I ,用z iT 表示(z it )t ∈T ,则机组组合问题可以写成下面的混合整数规划问题:m in X ,Z{c (X )+s (Z ):P (X )≤0,R (X ,Z )≤0,M (X ,Z )≤0,U (Z )≤0} c (X )=∑itc it(x it)是各机组各时段燃料费用的总和;s (Z )=∑is i(z iT)是各机组的开停机费用之和;P (X )=(P t (x I t ))t ∈T 是系统的负荷和备用约束;在忽略网损的情况下,可写为Πt ,∑ipit=d t ;Πt ,∑irit≥r t ,d t 和r t 分别是系统t 时段的负荷和备用;P (X )中也可包括线路潮流、节点电压等约束(将约束条件写成P (X )≤0的形式是为了简化,实际上也包括等式约束);R (X ,Z )=(R i (x iT ,z iT ))i ∈I 表示机151999年2月 电 力 系 统 自 动 化A utom ati on of E lectric Pow er System s 第23卷 第4期组爬坡速率限制、燃料总量限制等;机组i的爬坡速率限制可写为Πt,p it-∃p i≤p i,t+1≤p it+∃p i,其中∃p i为机组i在相邻两个时段内的最大允许功率变化量;机组能量限制则可写为∑tp it≤e i;e i为发电机可利用的最大能量;M(X,Z)=(M it(x it, z it))i∈I,t∈T是耦合离散变量z it和连续变量x it的约束,例如对于机组功率,有Πi,t,z it p it m in≤p it≤z it p it m ax,其中p it m in和p it m ax分别为机组最小、最大输出功率;U(Z)=(U i(z iT))i∈I是机组最短开停机时间限制,对一台典型的热力机组,不允许在关机后T dow n小时内重新开机或在开机后T up小时内关机。
2 启发式方法启发式方法(heu ristic m ethod)是最早使用的一类优化方法,这种方法没有严格的理论依据,依靠直观的判断或实际调度的经验寻找最优解。
启发式方法在机组组合问题中的应用有以下两种情况。
211 局部寻优法其基本的思路是从一个尽可能好的初始解出发,在其邻域内寻优,通过迭代求得最优解或次优解。
文献[6~8]是有关机组组合的早期文献。
文献[6]寻找和利用运行费用变化与开停机时间改变量之间的近似关系;文献[7]考虑了负荷经济分配的等微增率准则、负荷的随机性和机组的停运率;文献[8]则把优化过程分为一个次优化过程和一个优化过程,次优化过程使用一些调度的逻辑规则寻找可行的次优解,而优化过程则在次优化过程所得解的基础上再优化。
局部寻优法计算速度快,所需内存少,但往往找不到最优解。
局部寻优法可同后面将提到的较新的专家系统方法结合使用。
212 优先顺序法优先顺序法(p ri o rity list)将系统可调度的机组按某种经济特性指标事先排出顺序,根据系统负荷大小按这种顺序依次投切机组。
优先顺序法提出较早,现在仍在研究和应用之中。
文献[9]采用优先顺序法和等煤耗微增率准则考虑一个多区域电网的经济调度问题。
经典的优先顺序法在排序过程中不考虑负荷变化,是一种静态排序策略。
文献[10]提出了一种考虑负荷变化的优先顺序法,称为顺序投入法(sequen tial un it comm itm en t),在调度过程中动态地考虑机组排列。
文献[11]将传统的经济指标即平均满负荷费用(average fu ll load co st)和投入利用因子(comm itm en t u tilizati on facto r)结合使用,作为排序的指标,取得了更好的效果。
文献[12]在顺序投入法中引入了一个全局决策过程,以克服这种方法有时找不到最优解或次优解的缺陷。
优先顺序法计算速度快,占用内存少,常常找不到最优解,但能满足一般的应用要求,优先顺序法既可单独使用,也可与动态规划法等方法结合使用。
3 动态规划法动态规划法(dynam ic p rogramm ing)是解决多阶段决策过程最优化的一种数学方法,在枚举各种可能的状态组合的过程中,这种方法巧妙地摒弃了那些不需要考虑的解。
动态规划法要求所求解的问题具有明确的阶段性。
此方法的细节可参阅文献[13,14]。
用动态规划法求解机组组合问题时,整个调度期间T被分成若干个时段,通常每个时段为1h,每个时段即动态规划过程中的一个阶段。
各阶段的状态即为该时段所有可能的机组开停状态组合。
从初始阶段开始,从前向后计算到达各阶段各状态的累计费用(包括开停机费用和运行时的燃料费),再从最后阶段累计费用最小的状态开始,由后向前回溯,依次记录各阶段使总的累计费用最小的状态,这样就可得到最优的开停机方案,在计算运行所需的燃料费用时,需使用负荷经济分配算法。
若使用完全状态的动态规划法,对于N台机组的系统,若要考虑T个时段的机组组合问题,则总的状态数为2N×T,当N和T增大时,计算量将急剧增加,形成所谓“维数灾”。
为克服这个困难,常采取一定的措施来限制状态的数目。
首先可立即排除那些明显不可行的组合,剩下的状态数仍然是大量的,可采用多种方法进行处理。
D P—SC(dynam ic p rogramm ing sequen tial com b inati on)法将动态规划法和优先顺序法相结合,机组只能按优先顺序开停,大大减少了状态数,但可能丢失最优解或次优解。
D P—TC(dynam ic p rogramm ing truncated com b inati on)法选取优先顺序表前面一定数目的机组的开停状态组合作为各阶段的状态,状态数增加,计算量增大,但优化效果较好。
D P—STC(dynam ic p rogramm ing sequen tial truncated com b inati on)法则先使用优先顺序法或D P—SC法产生一个“额定机组组合”,以此额定组合为中心在优先顺序表中选取一定数目的机组,再使用D P—TC法求最优解,该法计算量最大,但优化效果最好。
还有其它近似方法,多是将动态规划法和优先顺序法结合使用,总的目标是在计算量与优化效果之间寻求折衷。
25动态规划法可以处理作为时间函数的开机费用和最小开停机时间约束,但必须在各阶段的状态中包括机组的累计开机和停机时间,这样状态数会大大增加,即使使用上述限制状态数目的办法,计算量仍然很大,必须采取简化方法。
在动态规划法由前向后计算的过程中,计算出对应于每个状态的累计开停机时间,这个累计开停机时间对应于到达该状态的最优路径,动态规划法只允许那些满足最小开停机时间约束的状态转移。
累计开停机时间也用于计算开机费用。
应该注意的是,这只是一种近似计算方法,可能丢失最优解。
动态规划法另一个难于处理的问题是机组爬坡速率限制,即机组功率变化速率限制。
对于某个给定的状态来说,爬坡速率限制是前一阶段与其相连的状态的函数,对于这个状态,相关于每个前一阶段状态都要进行一次经济负荷分配计算,使占用内存量和计算时间增加,因此只能通过近似方法解决。
在停机的过程中,考虑爬坡速率约束也会丢失最优解。
动态规划法在机组组合问题中得到了广泛的应用,被结合到经济调度软件包中,已有许多实用的成果。
最早的动态规划法的应用不同于上述过程,文献[15,16]中,动态规划法以有功功率为状态,求达到各功率值的机组最优组合,并结合了优先顺序法。
