几何证明(1)
2023年数学中考试题精选:几何综合证明(一)

1.(2023.营口24题)在平行四边形ABCD中,∠ADB=90°,点E在CD 上,点G在AB上,点F在BD的延长线上,连接EF,DG, ∠FED=∠ADG,ADBD =DG EF=k.(1)如图1,当k=1时,请用等式表示线段AG与线段DF的数量关系________;(2)如图2,当k=√(3)时,写出线段AD,DE和DF之间的数量关系,并说明理由;(3)在(2)的条件下,当点G是AB的中点时,连接BE,求tan∠EBF的值2.(2023.本溪铁岭辽阳25题)在Rt△ABC中,∠ACB=90°,CA=CB,点O为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.(1)如图1,当点D与点O重合时,请直接写出线段AD与线段EF 的数量关系;(2)如图2,当点D在线段AB上时,求证:CG+BD=√2BC;(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出S1S2的值.3.(2023.大连25题)综合与实践问题情境:数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质。
已知AB=AC,∠A>90°,点E为AC上一动点,将△ABE以BE为对称轴翻折,同学们经过思考后进行如下探究:独立思考:小明:“当点D落在BC上时,∠EDC=2∠ACB.”小红:“若点E为AC中点,给出AC与DC的长,就可求出BE的长.”补足探究:奋进小组的同学们经过探究后提出问题1,请你回答:问题1:在等腰△ABC中,AB=AC,∠A>90°,△BDE由△ABE翻折得到.(1)如图1,当点D落在BC上时,求证:∠EDC=2∠ACB;(2)如图2,若点E为AC中点,AC=4,CD=3,求BE的长.问题解决:小明经过探究发现:若将问题1中的等腰三角形换成∠A<90°的等腰三角形,可以问题进一步拓展.问题2:如图3,在等腰△ABC中,∠A<90°,AB=AC=BD=4,2∠D=∠ABD.若CD=1,则求BC的长.4.(2023.牡丹江26题)平行四边形ABCD中,AE⊥BC,垂足为E,连接DE,将ED绕点E逆时针旋转90°,得到EF,连接BF.(1)当点E在线段BC上,∠ABC=45°时,如图1,求证:AE+EC=BF;(2)当点E在线段BC延长线上,∠ABC=45°时,如图2,当点E在线段CB延长线上,∠ABC=135°时,如图3,请猜想并直接写出线段AE,EC,BF的数量关系;(3)在(1)、(2)的条件下,若BE=3,DE=5,则CE=______.5.(2023.贵州省25题)如图1,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.(1)【动手操作】如图2,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为______度;(2)【问题探究】根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;(3)【拓展延伸】如图3,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD将于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.6.(2023.沈阳24题)如图1.在平行四边形纸片中,AB=10,AD=6,∠DAB=60°,点E为BC边上的一点(点E不与点C重合),连接AE,将平行四边形ABCD纸片沿AE所在直线折叠,点C,D的对应点分别为C`,D`,射线C`E与射线AD将于点F.(1)求证:AF=EF;(2)如图2,当EF⊥AF时,DF的长为______;(3)如图3,当CE=2时,过点F作FM⊥AE,垂足为点M,延长FM 交C`D`于点N,连接AN,EN,求△ANE的面积。
重庆中考2017-2018学年上期几何证明习题一 (1)

重庆中考2017-2018学年上期几何证明习题一1、如图,在Rt △ABC 中,∠A=30°,点D 是AB 边上的中点,斜边AB 的中点,DM ⊥DN ;连接DM,DN 分别交BC,CA 于点E,F ; (1)如图1,若CD =4,求△ABC 的周长;(2)如图2,若点E 为AC 的中点,将线段CE 绕点C 旋转60°,使点E 至点F 处,连接BF 交CD 于点M ,取DF 的中点N ,连接MN ,求证:MN=2CM(3)如图3,以点C 为旋转中心将线段CD 绕点C 顺时针旋转90°,使点D 至点E 处,连接BE 交CD 于点M ,连接DE ,取DE 的中点N ,连接MN ,试猜想线段BD 、MN 、MC 之间的关系并证明;2.如图,∠BAC =60°,∠CDE =120°,AB =AC ,DC =DE ,连接BE ,P 为BE 的中点 (1) 如图1,若A 、C 、D 三点共线,求∠PAC 的度数 (2) 如图2,若A 、C 、D 三点不共线,求证:AP ⊥DP(3) 如图3,若点C 线段BE 上,AB =1,CD =2,请直接写出PD 的长度EDABCMNFE DABCMN图1图3图2CBAD3、如图,△ABC 中,以AC 为斜边向下作等腰Rt △ADC ,直角边AD 交BC 于点E ,(1) 如图1,若∠ACB=30°, ∠B=45°, , 求线段DC 的长; (2) 如图2,若等腰Rt △ADC 的直角顶点D 恰好落在线段BC 的垂直平分线上,过点A 作AF ⊥BC 于点F ,连接DF ,求证:4.如图,Rt △ABC 中,∠C=90°,点D 是AC 上的一点,过D 作DE ⊥AB ,垂足为点E ,连接BD ,∠ADE=∠BDE.(1)如图1,若BC=2 ,AC=4,求AE 的长;(2)如图2,AG //BD ,且AG=CD ,点F 是线段BC 的中点.求证:∠FDC=∠DGA.图2图1ABCDCB图2B CD24题图224题图15、在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AMN,设旋转角为,记直线BN与CM的交点为P.(1)求证:BD1=CE1(2)若∠C PD1=2∠CAD1,求CE1的长;(3)连接PA,求△ABP面积的最大值;6、在Rt △ABC 中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△,设旋转角为,记直线与的交点为P.(1)如图1,当时,线段的长等于,线段的长等于;(直接填写结果)(2)如图2,当时,求证:,且;(3)①设BC的中点为M,则线段PM的长为;②点P到AB所在直线的距离的最大值为.(直接填写结果)ABCDEMABCDEMN PNEDCB A图1图2图37、已知:△ACB 与△DCE 为两个有公共顶点C 的等腰直角三角形,且∠ACB=∠DCE=90°,AC=BC ,DC=EC .把△DCE 绕点C 旋转,在整个旋转过程中,设BD 的中点为N ,连接CN . (1)如图①,当点D 在BA 的延长线上时,连接AE ,求证:AE=2CN ;(2)如图②,当DE 经过点A 时,过点C 作CH ⊥BD ,垂足为H ,设AC 、BD 相交于F ,若NH=4,BH=16,求CF 的长.8、.如图,△ABC 中, ∠AB C =45°,CD ⊥AB 于点D ,G 为DC 上一点,且AD=DG ,连接BG 延长交AC 于点E ,连接ED ,过点B 作BF ⊥ED ,交ED 延长线于点F (1) 若∠GB C =30°,DB= ,求△GBC 的面积; (2) 求证:AC+GE=9、如图,等边△ABC 的边长为4,BD 为AC 边上的中线,E 为BC 边上一点(不与B 、C 重合).(1)如图1,若DE ⊥BC ,连接AE ,求AE 的长; (2)如图2,若DE 平分∠BDC ,求BE 的长;(3)如图3,连接AE ,交BD 于点M .以AM 为边作等边△AMN ,连接BN .请猜想∠CAE 、∠CBD 、∠BMN 之间的数量关系,并证明你的结论.BCDA图1BC DA 图2图3BCDEM NA10、如图,在△ABCAC=BC ,点D 是AB 边上一点,连接DC ,满足DA=DC , (1)如图1,点G 在AB 边上且BG=BC 连接CG ,若∠A CB=80°求∠GCD 的度数; (2)如图2,点E 是BC 边上一点且DE=DB ,点F 和点H 分别是AB 和EC 的中点,连接CD 交FH 于点G ,求证:CD=FH+DF11、等腰Rt △ABC 中,∠BAC=90°,CD ⊥AC ,点M 是AC 上一点,且AM=CD ,AH ⊥BC 于 点H ,当点E 是AD 的中点时,连接BE 交AH 、AC 于点N 、M , 求证:AD= BN12、菱形ABCD 中,一射线BE 分∠ABC 为∠ABE 与∠CBE ,且∠ABE :∠CBE=7:3.BE 交对角线AC 于F ,交CD 于E .过B 作BK ⊥AD 于K 点,交AC 于M ,且∠DAC=15°. (1)求∠DEB 的度数; (2)求证:2CF=CM+2FB .图2图1GDBCFECAABDGH图2HDHD13、 如图,在△ABC 中,AB=AC=10,∠BAC=90°,D 为△ABC 下方一点,且AD 平分 ∠BDC ,(1)求证:∠ADC=45°;(2)如图2,作CE 平分∠BCD 交AD 于点E , ①、若5DE=2AE ,求CD 的长;②、如图3,分别作∠ABC 、∠ACB 的平分线BF 、CF ,连接EF ,求EF 的最小值;14、如图,四边形ABCD 中,AD=DB=BC ,∠ADB=∠DBC=90°,点E 是边CD 上任意一点,连接AE 交BD 于点G ,过点B 作AE 的垂线,垂足为点M ,交边CD 于点F ,连接FG 、DM , (1)若DE=AD ,求证:∠DBM=∠DEM (2)求证:AG=BF+FG (3)求∠DOG 的度数;图1图3图2ABCEFAB CDED CBAABCEF GMD2问ABCEF H GMD3问15、如图1,在△AOB 中,∠AOB=90°AO=BO , 点C 在边AB 上,连接CO ,过点O 作CO 的垂线,在垂线上取一点D ,使DO=CO ,连接BD 、CD , (1)求证:BD ⊥AB(2)如图2,取线段BC 的中点E ,连接OE ,AD ,求证:OE ⊥AD ,且AD=2OE△BEG ≌△COE △AOD ≌△BOG16、如图1,在△ABC 中,∠BAC=90°AB=AC ,将AB 绕点A 按顺时针旋转60°,连接CD ,与∠BAC 的角平分线AE 交于点E ,连接BE ; (1)若BE=2,求∠BEC 的度数及AE 的长度;(2)如图2,以BC 为边在△ABC 外作△BCF ,且∠BCF=60°,连接EF ,求证:CF+BF= EF图1图2图2图2图1DDEABCEFCBA17、如图,在△ABC中, AB=AC,D为线段BC的延长线上一点,DB=DA,BE⊥AD于点E,取BE的中点F,连接AF;(1)若BE=2, ,求AF的长;(2)若∠BAC=∠DAF 求证:2AF=AD;(3)请直接写出线段AD、BE、AE的数量关系;18、等腰Rt△ABC和等腰Rt△ADE中,∠BAC=∠DAE=90°,其中B、E、D三点共线且DE交AC于点F,(1)如图1,若点E 是BD的中点, AD=1,求∠BDC 的度数和BC的长;(2)如图2,在AB上取一点G,使BG+AB=BC ,连接EG,若点E 是BF的中点,求证:EG//AD;CDA FAEB FBDE CG图1图2D图219、如图,△ABC 中,∠ACB=90°,AC=BC ,点E 是BC 上一点,连接AE , (1)如图1,若∠BAE=15°, 时,求AB 的长;(2)如图2,延长BC 至点D ,使DC=BC ,将线段AE 绕点A 按顺时针旋转90°得到线段AF ,连接DF ,过点B 作BGBC 交FC 的延长线于点G , 求证:BG=BE ;图1图2GCEDBFE BAAC。
5.6几何证明举例(1)

,
• 则能使△ABD≌△ACD(任加一条件)
• (4)如图AB=CD,DE=AF,CF=BE,∠AFB=60°,
• ∠CDE=80°,那么∠ABC
。
D
(第3题)
小结
判定三角形全等的方法有:
“ASA”, “ AAS”,“SAS” “SSS”.
利用三角形全等可以得到线段相等或角相等.
再见
2021/6/20
证明:∵∠B=∠B′, ∠C=∠C′
(已知)
∴∠A=∠A′ (三角形内角和定理)
在△ABC与△ABC中, ∠A=∠A′ (已证) AB=A′B′ (已知) ∠B=∠B′ (已知)
∴△ABC≌△ABC (ASA)
已知:如图,AB=CB, AD=CD. 求知:∠A=∠C
2021/6/20
5
全全等全等三等三角三角形角形对形对应对应边应边上角上的的的高平中相分线等线相相等等
B(E)
F A
C
O Dபைடு நூலகம்
达标测评:
• 1、选择题:
• (1)(2011江西南昌)如图
• 下列条件中,不能证明△ABD≌△ACD的是( )
.
• A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=DC
• C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
• (2)下列各组条件中,可保证ΔABC与ΔA′B′C′全等的是( )
.
情境导入
• 如图,某同学把一把三角形的玻璃打碎成了三块, • 现在要到玻璃店去配一块大小形状完全一样的玻璃, • 那么最省事的办法是( ) • (A)带①和②去 (B)带①去 • (C)带②去 (D)带③去 •
你还记得有关全等三角形的 几个公理吗?
几何定理证明范文

几何定理证明范文要证明几何定理,通常需要使用几何性质和已知条件,以及运用几何推理和数学推断等方法。
本文选取了三个较为经典的几何定理进行证明,分别是直角三角形的勾股定理、垂线定理和相交弦定理。
下面分别对这三个定理进行证明。
一、直角三角形的勾股定理直角三角形的勾股定理是指在一个直角三角形中,直角边的平方等于两个直角边分别平方之和。
即若有一个直角三角形ABC,其中∠C=90°,则有AB²=AC²+BC²。
证明过程如下:设直角三角形ABC,其中∠C=90°。
连接AC和BC,延长AC到点D,使得CD=BC。
由于∠C=90°,则四边形ABCD是一个矩形。
根据矩形的性质,对角线互相平分。
即AC=BD,BC=AD。
根据勾股定理的推广形式,有AC²=AB²+BC²,以及BD²=AB²+AD²。
由于AC=BD,所以AB²+BC²=AB²+AD²。
消去AB²,得BC²=AD²。
因此,直角三角形的勾股定理得证。
二、垂线定理垂线定理是指在平面上,如果一直线段垂直于另一直线段,那么这两条直线段互相垂直。
即若有一直线段AB垂直于另一直线段CD,则有∠ABC=90°。
证明过程如下:设直线段AB垂直于CD,交于点M。
连接AM和BM。
根据垂线的性质,AM和BM分别垂直于CD,即∠CAM=90°和∠CBM=90°。
根据平行线的性质,互相平行的直线切割同一条直线时,所得的对应角相等。
因此,∠CAB=∠ACM=90°,即∠ABC=90°。
这样,垂线定理得证。
三、相交弦定理相交弦定理是指在一个圆内,两条相交弦的互补弦乘积相等。
即若有一圆内的两条弦AB和CD相交于点E,则有AE×EB=CE×ED。
11[1].5__几何证明举例(1)
![11[1].5__几何证明举例(1)](https://img.taocdn.com/s3/m/3c4960d349649b6648d747d5.png)
11.5《几何证明举例》导学案(1)课本内容:P130—131 例1 例2课前准备:直尺学习目标:1. 会证明下列定理:SAS ASA2. 能根据上述定理证明有关的命题3、养成善于思考,善于探究,善于推理,言必有据的好习惯一. 自主预习课本P130——131的内容,独立完成课后练习1、2后,与小组同学交流(课前完成)二. 回顾课本P28-31 P120—121思考下列问题:1、SAS 定理的内容2、ASA 定理的内容3、几何证明的过程的步骤三、巩固练习1、在ΔABC 和ΔDEF 中,按照下列给出的条件,能用“SAS ”公理判断ΔABC ≌ΔDEF 的是()A 、AB=DE ∠A=∠D BC=EFB 、AB=EF ∠A=∠D AC=DFC 、AB=BC ∠B=∠E DE=EFD 、BC=EF ∠C=∠F AC=DF2、.如图5—47,△ABC≌△CDA,并且BC =DA ,那么下列结论错误的是 ()A .∠1=∠2B .AC =CA C .AB =AD D .∠B=∠D3. :如图,点B 在AE 上,∠CAB=∠DAB,要使ΔABC ≌ΔABD,可补充的一个条件是ED CB A4. :如图,AE=AD,要使ΔABD ≌ΔACE,请你增加一个条件是5、:如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC ≌ΔAED 的条件有( )个.A. 4B. 3C. 2D. 16:已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD四、学习小结回顾这一节所学的,看看你学会了吗?五、达标检测1、如图,已知△ABC 的六个元素,则下面甲、乙、丙三个三角形中和△ABC 全等的图形是 ( )A .甲和乙 B.乙和丙 C.只有乙 D.只有丙2.如图,已知MB =ND,∠MBA =∠NDC,下列不能判定△ABM ≌△CDN 的条件是( )A .∠M =∠NB .AB =CDC .AM =CND .AM ∥CN3.某同学把一块三角形的玻璃打碎也成了三块,现在要到玻璃店去配一块完EDC AB 21ED CBA EC BA全一样的玻璃,那么最省事的办法是()A.带①去B.带②去C.带③去D.带①和②去5.如图5—54,已知△ABC≌△DEF,AF=5cm,(1)求CD的长,(2)AB与DE平行吗?为什么?解:(1)∵ △ABC≌DEF(已知),∴ AC=DF( ).∴ AC-FC=DF-FC(等式性质).即_________=_________.∵ AF=5cm∴ _________=5cm.(2)∵ △ABC≌△DEF(已知),∴ ∠A=__________( ).∴ AB∥_________( ).6:如图,AC和BD相交于点O,OA=OC,OB=OD 求证:DC∥ABAODBC六、布置作业。
几何证明题及其答案1

例1:如图2-4-27,四边形ABCD 是正方形,△ECF 是等 腰直角三角形,其中CE=CF ,G 是CD 与EF 的交点. (1)求证:△BCF ≌△DCE .(2)若BC=5,CF=3,∠BFC=900,求DG :GC 的值.例2:已知如图2-4-28,BE 是⊙O 的走私过圆上一点作⊙O 的切线交EB 的延长线于P .过E 点作ED ∥AP 交⊙O 于D ,连结DB 并延长交PA 于C ,连结AB 、AD .(1)求证:2AB PB BD = .(2)若PA=10,PB=5,求AB 和CD 的长.例3:如图2-4-29,⊙1O 和⊙2O 相交于A 、B 两点,圆心1O 在⊙2O 上,连心线1O 2O 与⊙1O 交于点C 、D ,与⊙2O 交于点E ,与AB 交于点H ,连结AE .(1)求证:AE 为⊙1O 的切线.(2)若⊙1O 的半径r=1,⊙2O 的半径32R =,求公共弦AB 的长. (3)取HB 的中点F ,连结1O F ,并延长与⊙2O 相交于点G ,连结EG ,求EG 的长.例4 如图2-4-30,A 为⊙O 的弦EF 上的一点,OB 是和这条弦垂直的半径,垂足为H,BA 的延长线交⊙O 于点C ,过点C 作⊙O 的切线与EF 的延长线交于点D . (1)求证:DA=DC图2-4-27GFED CB A 图2-4-28C 321OEPB A O 2O 1H G F ED B CA 图2-4-28(2)当DF :EF=1:8且DF=2时,求AB AC 的值.(3)将图2-4-30中的EF 所在的直线往上平移到⊙O 外,如图2-4-31,使EF 与OB 的延长线交⊙O 于点C ,过点C 作⊙O 的切线交EF 于点D .试猜想DA=DC 是否仍然成立,并证明你的结论.【提高训练】1.如图2-4-32,已知在△ABC 中,AB=AC ,D 、E 分别是AB 和BC 上的点,连结DE 并延长与AC 的延长线相交于点F .若DE=EF ,求证:BD=CF .2.点O 是△ABC 所在平面内一动点,连结OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连结,如果DEFG 能构成四边形.(1)如图2-4-33,当O 点在△ABC 内时,求证四边形DEFG 是平行四边形.(2)当点O 移动到△ABC 外时,(1)中的结论是否成立?画出图形,并说明理由.(3)若四边形DEFG 为矩形,O 点所在位置应满足什么条件?试说明理由.图2-4-30H FE D O C B A K 图2-4-30HF E DO CBA 图2-4-32F EDC B A 图2-4-33O GF E D CB A3.如图2-4-35,等腰梯形ABCD中,AD∥BC,∠DBC=450.翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E.若AD=2,BC=8,求:(1)BE的长.(2)∠CDE的正切值.4.如图2-4-35,四边形ABCD内接于⊙O,已知直径AD=2,∠ABC=1200,∠ACB=450,连结OB交AC于点E.(1)求AC的长.(2)求CE:AE的值.(3)在CB的延长上取一点P,使PB=2BC,试判断直线PA和⊙O的位置关系,并加以证明你的结论.5.如图2-4-36,已知AB是⊙O的直径,BC、CD分别是⊙O的切线,切点分别为B、D,E 是BA和CD的延长线的交点.(1)猜想AD与OC的位置关系,并另以证明.(2)设A DO C的值为S,⊙O的半径为r,试探究S与r的关系.(3)当r=2,1sin3E∠=时,求AD和OC的长.图2-4-34FEDC BAO图2-4-35PEDCBA图2-4-36OEDCBA答案例1.分析与解答 (1)∵四边形 ABCD 是正方形,∴∠BCF+∠FCD=900,BC=CD .∵△ECF 是等腰直角三角形,CF=CE .∴∠ECD+∠FCD=900.∴∠BCF=∠ECD .∴△BCF ≌△DCE(2)在△BFC 中,BC=5,CF=3,∠BFC=900. ∴BF=2222534BC CF -=-=.∵△BCF ≌△DCE ,∴DE=BF=4,∠BFC=∠DEC=∠FCE=900. ∴DE ∥FC .∴△DGE ∽△CGF .∴DG :GC=DE :CF=4:3.例2.分析与解答 (1)证明:∵PA 是⊙O 的切线,∴∠1=∠2. ∵ED ∥AP ,∴∠P=∠PED .而∠3=∠BED ,∴∠3=∠P .∴△ABD ∽△PBA .∴2AB PB BD =. (2)连结OA 、AE .由切割线定理得,2PA PB BD = .即2105(5)BE =⨯+, ∴BE=15.又∴△PAE ∽△PBA ,∴2AE PAAB PB==,即AE=2AB . 在Rt △EBA 中,22215(2)AB AB =+,∴35AB =.将AB 、PB 代入2AB PB BD = ,得BD=9. 又∵∠BDE=900,ED ∥AP , ∴DC ⊥PA .∴BC ∥OA .∴BC PBOA PO=. ∴515315252BC =⨯=+.∴CD=12 例3.分析与解答 (1)连结A 1O .∵1O E 为⊙2O 的直径,∴∠1O AE=900. 又∵1O A 为⊙1O 的半径,∴AE 为⊙1O 的切线.(2)∵1O A=r=1,1O E=2R=3,△A 1O E 为Rt △,AB ⊥1O E , ∴△A 1O E ∽△H 1O A .∴2111O A O H O E = . ∴113O H =.2242223AB AH OA OH ==-=. (3)∵F 为HB 的中点,∴HF=1243HF AB ==, ∴221133O F O H HF =+=.∵11HO F GO E ∠=∠. ∴Rt △1O HF ∽Rt △1OGE .∴11O F HFO E EG=. ∴11HF O EEG O F = ,即233623EG ⨯==. 例4.分析与解答 (1)连结OC ,则OC ⊥DC ,∴∠DCA=900-∠ACO=900-∠B .又∠DAC=∠BAE=900-∠B ,∴∠DAC=∠DCA .∴DA=DC .(2)∵DF :EF=1:8,2DF =,∴EF=8DF=82, 又DC 为⊙O 的切线,∴229218DC DF DE ==⨯= . ∴1832DC ==.∴32AD DC ==,32222AF AD DF =-=-=, 822262AE EF AF =-=-=. ∴622224AB AC AE AF ==⨯= .(3)结论DA=DC 仍然成立.理由如下:如图2-4-31,延长BO 交⊙O 于K ,连结CK ,则∠KCB=900.又DC 是⊙O 的切线,∴∠DCA=∠CKB=900-∠CBK .又∠CBK=∠HBA ,∴∠BAH=900-∠HBA=900-∠CBK . ∴∠DCA=∠BAH .∴DA=DC . 提高部分:【答案】 1.过D 作DG ∥AC 交BC 于G ,证明△DGE ≌△FCE 2.(1)证明DG ∥EF 即可(2)结论仍然成立,证明略(3)O 点应在过A 点且垂直于BC 的直线上(A 点除外),说理略. 3.(1)BE=5 (2)3tan 5CDE ∠=4.(1)3AC = (2)1:2CE AE =(3)∵1:2CE AE =,PB=2BC ,∴CE :AE=CB :PB . ∴BE ∥AP .∴AO ⊥AP .∴PA 为⊙O 的切线5.(1)AD ∥OC ,证明略(2)连结BD ,在△ABD 和△OCB 中,∵AB 是直径,∴∠ADB=∠OBC=900. 又∵∠OCB=∠BAD ,∴Rt △ABD ∽Rt △OCB .∴AD ABOB OC=.222S AD OC AB OB r r r ==== , ∴22S r = (3)433AD =,23OC =.。
几何证明举例(1)

在ABD和ABD中
ADB ADB B B
A
AB AB
ABD ABD
AD AD
B D C B
A D C
已知:如图, ABC ABC, AD, AD分别是边 BC, BC上的中线。 求证:AD AD.
证明:ABC ABC
AB AB, BC BC,B B
求证:BH=AC
A
HE
B
C D
Hale Waihona Puke 选做题• 已知:如图,在△ABC中,D为BC上的一点, AD平分∠EDC,且∠E=∠B,DE=DC
• 求证:AB=AC
作业
课后练习2
谢谢聆听,再见!
3、利用三角形全等可以得到线段相等或角相等.
4、证明两条线段(或角)相等的方法:(1)先观察 要证明的线段(或角)在那两个可能全等的三角形中, 再证明这两个三角形全等;(2)若图中没有全等三角 形,可以把要证明的线段(或角)用和它相等的线段 (或角)代换,再证明它们所在的三角形全等;(3) 如果没有相等的线段(或角)代换,可设法作辅助线 构造全等三角形。
例 已知:如图,AB=AC,DB=DC. 求证:∠B=∠C.
A
B
C
D
例 已知:如图,AB=AC,DB=DC. 求证:∠B=∠C.
A
1
B
3
2C
4
D
变式1、 已知:如图,AB=AC,∠B=∠C. 求证: DB=DC.
A
1
B
3 ?
2C
4
?
D
练习
已知:如图,PB=PC,CE、BD相交于
点P,∠BDA=∠CEA. 求证:AB=AC. A
3.某同学把一块三角形的玻璃打碎也成了三块, 现在要到玻璃店去配一块完全一样的玻璃,那么
全国通用版中考数学:勾股定理有关的几何证明(一)—详解版

【例1】如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N,求证:AN2-BN2=AC2.证明:∵MN⊥AB于N,∴BN2=BM2-MN2,AN2=AM2-MN2,∴BN2-AN2=BM2-AM2,又∵∠C=90°,∴AM2=AC2+CM2 ,∴BN2-AN2=BM2-AC2-CM2,又∵BM=CM,∴BN2-AN2=-AC2,即AN2-BN2=AC2.【例2】四边形ABCD,AC⊥BD ,探究AB2,CD2,BC2,AD2之间的数量关系.【解析】AD2+BC2=AB2+CD2,设AC与BD的交点为E∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;故答案为:AD2+BC2=AB2+CD2,1.我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,∠DCB=30°.求证:四边形ABCD是以DC、BC为勾股边的勾股四边形.证明:连接CE,∵△DBE是由△ABC的顶点B按顺时针方向旋转60°而得,∴AC=DE,BC=BE,∠CBE=60°,∴△BCE是等边三角形,∴∠BCE=60°,EC=BC,又∵∠DCB=30°,∴∠DCE=90°,∴在Rt△DCE中,DE2=DC2+CE2∴AC2=DC2+BC2即四边形ABCD是以DC,BC为勾股边的勾股四边形.2.在△ABC中,AD⊥BC于D,求证:AB2+CD2=AC2+BD2.证明:在Rt△ABD中,根据勾股定理得:AB2-BD2=AD2;在Rt△ACD中,根据勾股定理得:AC2-CD2=AD2,∴AB2-BD2=AC2-CD2=AD2,则AB2+CD2=AC2+BD2.3.如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD2+CD2=2AD2.证明:作AE⊥BC于E,如图所示:∵在△ABC中,∠BAC=90°,AB=AC,1BC,∴BE=CE=AE=2∴BD2+CD2=(BE+DE)2+(CE-DE)2=2AE2+2DE2=2AD2.4.如图,在△ABC中,∠C=90°,点P、Q分别在BC、AC上,求证:AP2+BQ2=AB2+PQ2.证明:∵在RT△APC中,AP2=AC2+CP2,在RT△BCQ中,BQ2=BC2+CQ2,∴AP2+BQ2=AC2+CP2+BC2+CQ2,∵在RT△ABC中,AC2+BC2=AB2,在RT△APC中,PC2+CQ2=PQ2,∴AP2+BQ2=AC2+CP2+BC2+CQ2=AB2+PQ2.5.如图,在△ABC中,∠C=90°,D是AC的中点,DE⊥AB于点E.求证:BC2=BE2-AE2.证明:连接BD,∵D是AC的中点,∴CD=AD.∵∠C=90°,DE⊥AB,∴BE2-AE2=(BD2-DE2)-(AD2-DE2)=BD2-AD2=(BC2+CD2)-AD2=BC2.【例1】在△ABC中,以AB为斜边,作Rt△ABD,使点D落在△ABC内,∠ADB=90°,AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).证明:BF2+FC2=2AD2,理由:如图3,连接AF、CD.∵EF⊥AC,且AE=EC,∴FA=FC,∠FAC=∠FCA,∵EF⊥AC,且AE=EC,∴∠DAC=∠DCA,DA=DC,∵AD=BD,∴BD=DC,∴∠DBC=∠DCB,∵∠FAC=∠FCA,∠DAC=∠DCA,∴∠DAF=∠DCB,∴∠DAF=∠DBC,∴∠AFB=∠ADB=90°,在Rt△ADB中,DA=DB,∴AB2=2AD2,在Rt△ABF中,BF2+FA2=AB2=2AD2,∵FA=FC∴BF2+FC2=2AD2.【例2】如图,∠C=90°,AM=CM,MP⊥AB于点P,求证:BP2=AP2+BC2.证明:∵△ABC是直角三角形,∠C=90°,∴AB2=BC2+AC2,则AB2-AC2=BC2.又∵在直角△AMP中,AP2=AM2-MP2,∴AB2-AC2+(AM2-MP2)=BC2+(AM2-MP2).又∵AM=CM,∴AB2-AC2+(AM2-MP2)=BC2+(MC2-MP2),①∵△APM是直角三角形,∴AM2=AP2+MP2,则AM2-MP2=AP2,②∵△BPM与△BCM都是直角三角形,∴BM2=BP2+MP2=MC2+BC2,MC2+BC2-MP2=BM2-MP2=BP2,③把②③代入①,得AB2-AC2+AP2=BP2,即BP2=AP2+BC2.1.如图,已知AM是△ABC的BC边上的中线,证明:AB2+AC2=2(AM2+MC2).证明:过点A作AD⊥BC于点D,在Rt△ABD中,AB2=AD2+BD2①,在Rt△ACD中,AC2=AD2+CD2②,由①+②得:AB2+AC2=2AD2+BD2+CD2,在Rt△ADM中,AD2=AM2-DM2,则AB2+AC2=2AM2-2DM2+BD2+CD2,∵AM是△ABC的BC边上的中线,∴BM=MC,∴BD2=(BM+DM)2=(MC+DM)2=MC2+2MC•DM+DM2,CD2=(MC-DM)2=MC2-2MC•DM+DM2,∴AB2+AC2=2AM2-2DM2+MC2+2MC•DM+DM2+MC2-2MC•DM+DM2,∴AB2+AC2=2AM2+2MC2=2(AM2+MC2).2.在△ABC中,AB=AC.(1)如图,若点P是BC边上的中点,连接AP.求证:BP•CP=AB2-AP2;(2)如图,若点P是BC边上任意一点,上面(1)的结论还成立吗?若成立,请证明、若不成立,请说明理由;(3)如图,若点P是BC边延长线上一点,线段AB,AP,BP,CP之间有什么样的数量关系?画出图形,写出你的结论.(不必证明)(1)证明:∵AB=AC,P是BC的中点,∴AP⊥BC,∴AB2-AP2=BP2=BP•CP;(2)成立,理由如下:如图所示,过点A作AD⊥BC于D,∵AB=AC,∴BD=CD在Rt△ABD中,AB2=AD2+BD2①在Rt△APD中,AP2=AD2+PD2②①-②得:AB2-AP2=BD2-PD2=(BD+PD)(BD-PD)=PC•BP;(3)结论:AP2-AB2=BP•CP.如图所示,理由如下:P是BC延长线任一点,连接AP,并做AD⊥BC,交BC于D,∵AB=AC,AD⊥BC,∴BD=CD,在Rt△ABD中,AB2=AD2+BD2,在Rt△ADP中,AP2=AD2+DP2,∴AP2-AB2=(AD2+BD2)-(AD2+DP2)=PD2-BD2,又∵BP=BD+DP,CP=DP-CD=DP-BD,∴BP•CP=(BD+DP)(DP-BD)=DP2-BD2,∴AP2-AB2=BP•CP.3.已知AM是△ABC的中线.(1)求证:AB2+AC2=2(AM2+BM2);(2)若AD是高,求证:AB2-AC2=2BC•MD.证明:(1)在Rt△ABD中,AB2=AD2+BD2①,在Rt△ACD中,AC2=AD2+CD2②,由①+②得:AB2+AC2=2AD2+BD2+CD2,在Rt△ADM中,AD2=AM2-DM2,则AB2+AC2=2AM2-2DM2+BD2+CD2,∵AM是△ABC的BC边上的中线,∴BM=MC,∴BD2=(BM+DM)2=(MC+DM)2=MC2+2MC•DM+DM2,CD2=(MC-DM)2=MC2-2MC•DM+DM2,∴AB2+AC2=2AM2-2DM2+MC2+2MC•DM+DM2+MC2-2MC•DM+DM2,∴AB2+AC2=2AM2+2BM2=2(AM2+BM2).(2)∵AD是高,∴△ABD和△ACD是直角三角形,∴AB2=BD2+AD2,AC2=AD2+DC2,∴AB2-AC2=BD2-DC2=(BD+CD)(BD-CD)=BC(BM+MD-CD),∵AM是中线,∴AB2-AC2=BC(CM+MD-CD)=BC(MD+MD)=2BC•MD.。
1几何证明选讲 - 简单难度 - 讲义

几何证明选讲知识讲解一、相似三角形的判定及有关性质1.平行线等分线段定理定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.2.平行线分线段成比例定理定理:三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.3.相似三角形的判定及性质1)相似三角形的判定定义:对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数).预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.判定定理1:对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.判定定理2:对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应_成比例且夹角相等,两三角形相似.判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.2)两个直角三角形相似的判定定理:①如果两个直角三角形的一个锐角对应相等,那么它们相似.②如果两个直角三角形的两条直角边对应成比例,那么它们相似.③如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.3)相似三角形的性质性质定理:①相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方;④相似三角形外接圆(或内切圆)的直径比、周长比等于相似比,外接圆(或内切圆)的面积比等于相似比的平方4.直角三角形的射影定理定理:直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.二、直线与圆的位置关系1.圆周角定理圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.圆心角定理:圆心角的度数等于它所对弧的度数.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.2.圆内接四边形的性质与判定定理1)性质定理1:圆的内接四边形的对角互补.定理2:圆内接四边形的外角等于它的内角的对角. 2)判定判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.推论:如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.3.三角形的内切圆1)三角形的内切圆:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2)多边形的内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.3)直角三角形内切圆的半径与三边的关系设、、分别为中、、的对边,面积为,则内切圆半径为,.若,则. 4.圆的切线的性质及判定定理1)性质性质定理:圆的切线垂直于经过切点的半径. 推论1:经过圆心且垂直于切线的直线必过切点. 推论2:经过切点且垂直于切线的直线必过圆心.2)判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.cb cbaO F ED CBACBAC B A a b c ABC △A ∠B ∠C ∠S sr p=()12p a b c =++90C ∠=︒()12r a b c =+-5.弦切角的性质定理:弦切角等于它所夹的弧所对的圆周角.6.与圆有关的比例线段1)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积 相等. 如图,弦和交于内一点,则.2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的 积相等.3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段 长的比例中项.如图,在中,是的切线,是的割线,则题意中满足4)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.AB CD O ⊙P PA PB PC PD ⋅=⋅O e AB O e AD O e 2AB AC AD =⋅BA经典例题一.选择题(共12小题)1.(2017秋•天心区校级期末)如图,△ABC被一边平行于BC的矩形所截,AB 被截成三等份,则图中阴影部分的面积是△ABC的面积的()A.13B.19C.29D.492.(2017秋•江北区校级月考)如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为()A.12B.4√3C.8√3D.63.(2016春•海南校级期末)如图,已知圆的直径AB=13,C为圆上一点,过C 作CD⊥AB于点D(AD>BD),若CD=6,则AD的长为()A.8B.9C.10D.114.(2016秋•武邑县校级月考)如图所示,在▱ABCD中,E为CD上一点,DE:CE=2:3,连接AE,BE,BD,且AE,BD交与点F,则S△DEF:S△EBF:S△ABF等于()A.4:10:25B.4:9:25C.2:3:5D.2:5:255.(2016春•淇滨区校级月考)如图所示,AB∥CD∥EF,且AO=OD=DF,BC=6,则BE等于()A.9B.10C.11D.126.(2015•朝阳区二模)如图,将一张边长为1的正方形纸ABCD折叠,使得点B 始终落在边AD上,则折起部分面积的最小值为()A.14B.38C.25D.127.(2014春•红桥区期末)如图,在梯形ABCD中,AB∥CD∥EF,若AB=5,CD=2,EF=4,则梯形ABFE与梯形EFDC的面积比是()A.23B.12C.92D.348.(2012春•红旗区校级期中)如图,E是平行四边形ABCD的边AB延长线上一点,且DC:BE=3:2,则AD:BF=()A.32B.23C.52D.259.(2017秋•天心区校级期末)如图,从▱O外一点A引圆的切线AD和割线ABC,已知AD=4√2,AC=8,▱O的半径为4,则圆心O到AC的距离为()A.3√2B.2√3C.4√3D.4√210.(2017秋•天心区校级期末)如图,▱O是△ABC的外接圆,AD是▱O的直径,连接CD,AC=2,AD=3,则cosB的值为()A.32B.√53C.52D.2311.(2017春•无极县校级期中)两条相交直线的平行投影是()A.两条相交直线B.一条直线C.一条折线D.两条相交直线或一条直线12.(2015•安徽模拟)如图,一个底面半径为R的圆柱被与其底面所成角是30°的平面所截,截面是一个椭圆,则该椭圆的离心率是()A.12B.√32C.√33D.23二.填空题(共13小题)13.(2016春•河南期中)若两个相似三角形的周长比为3:4,则它们的三角形面积比是.14.(2017秋•天宁区校级月考)如图D是△ABC的边AB上的一点,过D点作DE∥BC交AC于E.已知AD:DB=3:4,则S△ADE:S四边形BCDE为.15.(2015•汕头模拟)如图,在△ABC中,DE∥BC,DF∥AC,AE=2,EC=1,BC=4,则BF=.16.(2015•揭阳校级三模)在梯形ABCD中,AD∥BC,AD=2,BC=5,点E、F分别在AB、CD上,且EF∥AD,若AEEB =34,则EF的长为.17.(2015•汕尾模拟)如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于.18.(2015春•周口校级月考)如图在Rt△ABC中∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BD=.19.(2014•郴州二模)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为.20.(2014春•天津期末)如图,在△ABC中,M,N是AB的三等分点,E,F是AC的三等分点,若BC=1,则ME+NF=.21.(2017•张家口模拟)在直角△ABC中,斜边BC=6,以BC中点O为圆心,作半径为2的圆,分别交BC于两点,若|AP|=m,|AQ|=n,则m2+n2=.22.(2014春•清远期末)如图,⊙O上一点C在直径AB上的射影为D,AC=4,AD=2,则⊙O的面积是.23.(2013春•天心区校级期末)在如图所示的锐角三角形空地中,欲建一个面积不小于300m2的内接矩形花园(阴影部分),则其边长x(单位m)的取值范围是.24.(2016•丰台区一模)如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=.25.(2016•天津校级模拟)如图,PA是圆O的切线,切点为A,PO交圆O于B、C两点,PA=√3,PB=1,则AC=.。
青岛版数学八年级上册 5.6几何证明举例第1课时课件(共12张PPT)

第1课时
一、预习诊断
1.具备下列条件的两个三角形中,不一定全等的是( ) (A)有两边一角对应相等 (B) 三边对应相等 (C)两角一边对应相等 (D)有两直角边对应相等的两个直角 三角形 2.下列命题中:(1)形状相同的两个三角形是全等形; (2)在两个三角形中,相等的角是对应角,相等的边是对应边; (3)全等三角形对应边上的高、中线及对应角平分线分别相等。 其中正确命题的个数有( ) A.3个 B.2个 C.1个 D.0个
(根据图形结合题意写出已直和求证,给出证明)
这样,全等三角形的判定就有了基本事实SAS, ASA,SSS以及定理AAS,利用它们和全等三角形的 对应边、对应角相等就可以进一步推证全等三角形的 有关线段或角相等。
例1:已知:如图,AB=CB,AD=CD。
求证:∠A=∠C。
分析:要证∠A=∠C,只要证明它们所在的两个三角形 全等即可,但是图中没有两个全等三角形时,应通过尝 试添加辅助线构造全等三角形,使待证的角或线段是这 两个全等三角形的对应角或对应边。
A
A
A
B D C B D C
A
B D C B D C A
B D C B D C
三、系统总结
1.判定两个三角形全等的基本事实有: SAS,ASA,SSS,判定定理是AAS。 2.证明两个角或两条线段相等时,可以 考察它们是否在给出的两个全等三角形 中。如果没有,应尝试通过添加辅助线 构造两个全等三角形,使待证的角或线 段分别是两个全等三角形的对应角或对 应边。
你学会了吗?
1.已知,如图AB=CD,AD=BC,求证: ∠A=∠C
思考:怎样添加辅 助线才能使∠A与∠C 存在于两个全等三角形 中而且是两个三角形的 对应角呢?
初二几何证明一(线段垂直平分线、角平分线和等腰三角形的性质)

线段垂直平分线、角平分线和等腰三角形的性质知识点梳理1、 线段垂直平分线性质定理及其逆定理:定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等. 逆定理:和一条线段两个端点距离相等的点,在这条线段的直平分线上.2、 角平分线的性质定理及其逆定理:定理:在角的平分线上的点到这个角两边的距离相等.逆定理:在一个角的内部(包括顶点)且到这个角两边距离相等的点,在这个角的平分线上.D21P CABEO1、 等腰三角形的性质等边对等角:等腰三角形的两个底角相等。
三线合一:等腰三角形的顶角的平分线,底边上的中线,底边上的高的重合 证明以下推论:等腰三角形的两底角的平分线相等; 两条腰上的中线相等; 两条腰上的高相等。
等腰三角形的一腰上的高与底边的夹角等于顶角的一半4、 等腰三角形的判定:等角对等边:有两个角相等的三角形是等腰三角形 ◆ 命题、公理、定理命题:判断性的语句 陈述句,一般由题设和结论组成,写成“如果……,那么……”的形式 几个重要的公理(不需证明): (1) 两点之间线段最短;(2) 过直线外一点有且只有一条直线与已知直线平行 (3) 过一点有且只有一条直线与已知直线垂直;(4) 同位角相等,两直线平行; (5)两直线平行,同位角相等。
1、已知:如图,∠ABC ,∠ACB 的平分线交于F ,过F 作DE ∥BC ,交AB 于D ,交AC 于E 。
求证:BD +EC =DE 。
2、已知:如图所示△ABC ,∠ACB=90°,D 为BC 延长线上一点,E 是AB 上一点,EM 垂直平分BD ,M 为垂足,DE 交AC 于F ,求证:E 在AF 的垂直平分线上.3、如图,已知:CD 、CE 分别是AB 边上的高和中线,且ACE ECD DCB ∠=∠=∠。
求证:90o ACB ∠=CA4、如图,已知:在,90,30ooABC C A ∆∠=∠=中,DE 垂直平分AB ,FM 垂直平分AD ,GN 垂直平分BD 。
博雅几何证明(一)------对角互补四边形

可编辑几何证明(一)---- 对角互补方法点拨:已知中有公共端点的两条线段相等,利用互补及平角可得另一对角相等,再通过添加辅助线得到全等的的三个条件解决问题。
补例(2013聊城)如图,四边形ABCD 中,∠A=∠BCD=90°,BC=CD ,CE⊥AD,垂足为E , 求证:AE=CE .例:如图,△ABC 是等腰直角三角形,AB=AC ,P 是△ABC 外一点,且PB ⊥PC试判断PA 、PB 、PC 的关系,并加以证明变式一:如图,△ABC 是等腰三角形,AB=AC ,∠BAC=120°,P 是△ABC 外一点,且∠BPC=60°,试判断PA 、PB 、PC 的关系,并加以证明变式二:如图,△ABC 是等腰三角形,AB=AC ,∠BAC=α,P 是△ABC 外一点,且∠BAC +∠BPC=180°,试判断PA 、PB 、PC 的关系,并加以证明(用含α的式子 表示变式三如图,△ABC 是等腰直角三角形,AB=BC ,P 是△ABC 外一点,且∠BPC=135°, 试判断PA 、PB 、PC 的关系,并加以证明A B PCABPCAB CPABPC可编辑变式四如图,△ABC 是直角三角形,∠ABC=90°,∠BAC=α,P 是△ABC 外一点,且∠BAC +∠BPC=180°,试判断PA 、PB 、PC 的关系,并加以证明(用含α的式子 链接中考1.已知:如图13,在ABC △中,,AB AC BAC α=∠=( 不大于90o),点P 为ABC △外一点,且o1902APC α∠=+,连接BP .(1)当o60α=时,APC ∠= o;,,PA PB PC 这三条线段满足的数量关系是 ;(2)如图14,当o60α=时,探究,,PA PB PC 三条线段之间的数量关系,并证明; (3)用含α的式子表示,,PA PB PC 三条线段之间的数量关系,并证明.图13 图14 2、链接中考:2013甘井子一模25题。
中考几何证明题 (1)

第1页 共5页几何证明1.如图1,在正方形ABCD 中,点P 为AD 延长线上一点,连接AC 、CP ,过点C 作CF ⊥CP 于点C ,交AB 于点F ,过点B 作BM ⊥CF 于点N ,交AC 于点M . (1)若78AP AC =,4BC =,求ACP S ∆; (2)若2CP BM FN -=,求证:BC MC =;(3)如图2,在其他条件不变的情况下,将“正方形ABCD ”改为“矩形ABCD ”,且 AB ≠BC ,AC =AP ,取CP 中点E ,连接EB ,交AC 于点O ,猜想:∠AOB 与∠ABM 之间有何数量关系?请说明理由.2、如图,点E 为正方形ABCD 的边BC 所在直线上的一点,连接AE ,过点C 作CF AE F ⊥于,连接BF 。
(1)如图1,当点E 在CB 的延长线上,且AC EC =时,求证:12BF AE =; (2)如图2,当点E 在线段BC 上,且AE 平分BAC ∠时,求证:AB BE AC +=; (3)如图3,当点继续往右运动到BC 中点时,过点D 作DH AE H ⊥于,连接BH ,求证:45BHF ∠= 。
3、如图1,正方形ABCD中,点E为AD上任意一点,连接BE,以BE为边向BE 右侧作正方形BEFG,EF交CD于点M,连接BM,N为BM的中点,连接GN,FN。
(1)若AB=4,AE:DE=3:1,求EM的长;(2)求证:GN=FN(3)如图2,移动点E,使得FN⊥CD于点Q时,请探究CM与DE的数量关系并说明理由。
图1 图2 4、已知:在□ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD 于F,过点D作DG⊥AE于G,延长DG交BC于H(1)如图1,若点E与点C重合,且AF,求AD的长(2)如图2,连接FH,求证:∠AFB=∠HFB(3)如图3,连接AH交BF于M,当M为BF的中点时,请直接写出AF与FH 的数量关系。
沪科版几何证明题重点题型(一)

沪科版几何证明题重点题型(一)安徽实验中学 教授一证线段相等1. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB2 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC3如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .: BA CDF2 1 EF E DC BA4如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
MFECBA5AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CFFDCBA6如图:AB=CD ,AE=DF ,CE=FB 。
求证:AF=DE 。
FE DCBA7.已知:如图所示,AB =AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证: AE =AF 。
8.已知:如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F,求证:BE=CD.9如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F。
求证:DE=DF.10.如图:AB=AC,ME⊥AB,MF⊥AC,垂足分别为E、F,ME=MF。
求证:MB=MCC11.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。
求证:(1)EC=BF;(2)EC⊥BFAEB MCFACD EF12 如图:BE ⊥AC ,CF ⊥AB ,BM=AC ,CN=AB 。
求证:(1)AM=AN ;(2)AM ⊥AN 。
13 如图,已知AC ⊥AB ,DB ⊥AB ,AC =BE ,AE =BD ,试猜想线段CE 与DE 的大小与位置关系,并证明你的结论.14如图,已知AB =DC ,AC =DB ,BE =CE ,求证:AE =DE.15、如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF . 求证:AC=EF .16、已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在BD 上,PM ⊥AD 于M ,•PN ⊥CD 于N ,判断PM 与PN 的关系.A CEDB ABECDFGEDCBAP D ACBM N17、如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE . 、18如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .i. 求证:MB =MD ,ME =MFii. 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.19已知,如图,AB=CD ,DF ⊥AC 于F ,BE ⊥AC 于E ,DF=BE 。
中考几何证明与计算(1)
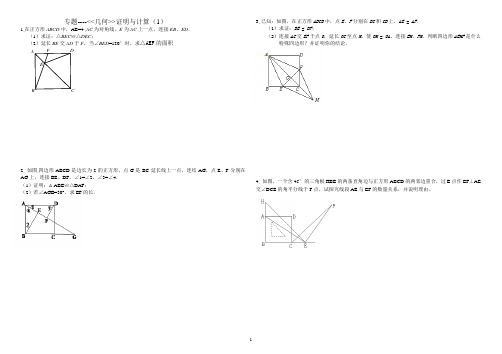
专题----<<几何>>证明与计算(1)1,在正方形ABCD中,AB=4 ,AC为对角线,E为AC上一点,连接EB、ED.(1)求证:△BEC≌△DEC;F,当∠BED=120°时,求△AEF的面积2, 如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.(1)证明:△ABE≌△DAF;(2)若∠AGB=30°,求EF的长.3,已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.(1)求证:BE = DF;(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.4, 如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。
125. 在正方形ABCD 中,点E 、F 分别在BC 、CD 上,且∠BAE=30º,∠DAF=15 º.(1)求证: EF=BE+DF ; (2)若AB=3,求△AEF 的面积。
6,如图,已知在正方形ABCD 中,AB=2,P 是边BC 上的任意一点,E 是边BC 延长线上一点,E 是边BC 延长线上一点,连接AP ,过点P 作PF 垂直于AP ,与角DCE 的平分线CF 相交于点F ,连接AF ,于边CD 相交于点G ,连接PG 。
(1)求证:AP=FP(2)当BP 取何值时,PG//CFE7,如图,在ABC ∆中,点D 为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .如果,90,AB AC BAC =∠=//点D 在线段BC 上运动.且45BCA ∠= 时,①请你判断线段CF BD 、之间的位置..关系,并说明理由(要求写出证明过程).②若,3,24==CF AC 求正方形ADEF 的边长(要求写出计算过程).8,如图,已知正方形ABCD 的边长是2,E 是AB 的中点,延长BC 到点F 使CF =AE . (1)若把ADE △绕点D 旋转一定的角度时,能否与CDF △重合?请说明理由. (2)现把DCF △向左平移,使DC 与AB 重合,得ABH △,AH 交ED 于点G .求证:AH ED ⊥,并求AG 的长FE D C B AF H E B C。
几何证明1

[课堂练通考点]1.如图,AB ∥EM ∥DC ,AE =ED ,EF ∥BC ,EF =12 cm ,则BC 的长为______ cm.解析:⎭⎪⎬⎪⎫AB ∥EM ∥DC AE =ED ⇒E 为AD 中点, M 为BC 的中点.又EF ∥BC ⇒EF =MC =12 cm ,∴BC =2MC =24 cm.答案:242.如图,在四边形ABCD 中,E 是AB 上一点,EC ∥AD ,DE ∥BC ,若S △BEC =1,S △ADE =3,则S △CDE =________.解析:∵EC ∥AD ,∴S △DCE ∶S △ADE =EC ∶AD ,∵DE ∥BC ,∴S △BCE ∶S △CDE =BC ∶ED ,又因为∠ECB =∠DEC =∠ADE ,∠BEC =∠EAD ,∴△BEC ∽△EAD ,∴EC ∶AD =BC ∶ED .∴S △DCE ∶S △ADE =S △BCE ∶S △CDE ,于是S △CDE = 3. 答案: 33.(2013·广东高考)如图,在矩形ABCD 中,AB =3,BC =3,BE ⊥AC ,垂足为E ,则ED =________.解析:∵tan ∠BCA =BA BC =33,所以∠BCA =30°,∠ECD =90°-∠BCA =60°.在Rt △BCE 中,CE =BC ·cos ∠BCA =3cos 30°=332.在△ECD 中,由余弦定理得 ED =CE 2+CD 2-2CE ·CD ·cos ∠ECD =⎝⎛⎭⎫3322+(3)2-2×332×3×12=212. 答案:2124.如图,在△ABC 中,F 为边AB 上的一点,BF AF =m n(m ,n >0),取CF 的中点D ,连接AD 并延长交BC 于点E .则BE EC=________.解析:如图,作FG ∥BC 交AE 于点G ,则FG CE =FD DC =1,BE FG =AB AF =m +n n.两式相乘即得BE EC =m +n n. 答案:m +n n5.在平行四边形ABCD 中,点E 在边AB 上,且AE ∶EB =1∶2,DE 与AC 交于点F ,若△AEF 的面积为6 cm 2,则△ABC 的面积为________ cm 2.解析:令E =a ,EF =b ,则12ab =6. 由题意知EB =2a .DF =3b .∴S △ABC =12·AB ·DE =12×3a ×4b =12×12ab =12×6=72. 答案:72[课下提升考能]1.如图,在△ABC 中,DE ∥BC ,BE 与CD 相交于点O ,直线AO与DE 交于N ,AO 的延长线与BC 交于M ,若DN ∶MC =1∶4,则NE ∶BM =________,AE ∶EC =________.解析:∵OD OC =DN MC =14, OE OB =OD OC =14, ∴NE BM =OE OB =14,又DE BC =OD OC =14, ∴AE AC =DE BC =14, ∴AE ∶EC =1∶3.答案:1∶4 1∶32.如图,在△ABC 中,点D ,E 分别在AB ,AC 上,下列条件能判定△ADE 与△ABC 相似的所有序号为________.①∠ADE =∠C ;②∠AED =∠B ;③AD AC =AE AB ;④DE BC =AE AB;⑤DE ∥BC .解析:由题图可知∠A 为公共角,由判定定理可知,①②正确;由∠A 为夹角可知,③正确;由平行线分线段成比例的定理的推论知⑤正确;④不符合两边及其夹角法.答案:①②③⑤3.在△ABC 中,EF ∥CD ,∠AFE =∠B ,AE =6,ED =3,AF =8,则AC =________,CD 2BC 2=________. 解析:由EF ∥CD 可知,△AEF ∽△ADC .于是有AE AD =AF AC, 由已知条件代入得,66+3=8AC,所以AC =12. 又由∠AFE =∠B ,得△AFE ∽△ABC ,从而△ACD ∽△ABC .所以CD BC =AD AC =6+312=34,即CD 2BC 2=916. 答案:12 9164.在△ABC 中,∠ACB =90°,CD ⊥AB 于D ,AD ∶BD =2∶3.则△ACD 与△CBD 的相似比为________.解析:如图所示,在Rt △ACB 中,CD ⊥AB ,由射影定理得:CD 2=AD ·BD ,又∵AD ∶BD =2∶3,令AD =2x ,BD =3x (x >0),∴CD 2=6x 2,∴CD =6x .又∵∠ADC =∠BDC =90°,∴△ACD ∽△CBD .易知△ACD 与△CBD 的相似比为AD CD =2x 6x =63. 答案:6∶35.如图,CD 是Rt △ABC 斜边AB 上的高,将△BCD 沿CD 折叠,B点恰好落在AB 的中点E 处,则∠A 等于________.解析:由题意知:BC =EC ,又∵E 为AB 的中点,∠ACB =90°,∴EC =12AB . 即BC =12AB .∴∠A =30°.答案:30°6.将三角形纸片ABC 按如图所示的方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .已知AB =AC =3,BC =4,若以点B ′、F 、C 为顶点的三角形与△ABC 相似,则BF =________.解析:设BF =x .若△CFB ′∽△CBA ,则CF CB =B ′F AB ,即4-x 4=x 3. ∴12-3x =4x ,∴x =127. 若△CFB ′∽△CAB ,则CF CA =B ′F AB, 即4-x 3=x 3,得x =2. 即BF =2或127. 答案:2或1277.如图,在▱ABCD 中,E 是DC 边的中点,AE 交BD 于O ,S △DOE =9cm 2,S △AOB =________.解析:∵在▱ABCD 中 ,AB ∥DE ,∴△AOB ∽△EOD ,∴S △AOB S △DOE =⎝⎛⎭⎫AB DE 2. ∵E 是CD 的中点,∴DE =12CD =12AB , 则AB DE =2,∴S △AOB S △DOE=22=4, ∴S △AOB =4S △DOE =4×9=36(cm)2.答案:36 cm 28.已知如图,在梯形ABCD 中,AD ∥BC ∥EF ,E 是AB 的中点,EF交BD 于G ,交AC 于H .若AD =5,BC =7,则GH =________.解析:令BD 交AC 于M ,由AD ∥EF ∥BC 且AE =EB 知BG =GD ,AH =HC .又AD =5,BC =7.AD ∥BC 知BM MD =CM MA =BC AD =75. 又GM MD =HM MA =15.∴GH AD =15∴GH =1.答案:19.如图,M 是平行四边形ABCD 的边AB 的中点,直线l 过点M分别交AD ,AC 于点E ,F .若AD =3AE ,则AF ∶FC =________.解析:延长ME 交CD 的延长线于点G ,则△AME ∽△DGE ,所以AE ED =AM DG =12,所以DG =2AM =DC .又△AMF ∽△CGF ,所以AF FC =AM CG =14. 答案:1410.如图,在△ABC 中,∠A =60°,∠ACB =70°,CF 是△ABC 的边AB 上的高,FP ⊥BC 于点P ,FQ ⊥AC 于点Q ,则∠CQP 的大小为________.解析:由FP ⊥BC ,FQ ⊥AC ,得C ,Q ,F ,P 四点共圆,所以∠CQP =∠CFP =∠B =180°-(∠A +∠C )=180°-(60°+70°)=50°.答案:50°11.两个相似三角形面积的比为3∶5,已知较大的三角形大边上的高为3,则较小的三角形大边上的高为________.解析:相似三角形的面积比等于对应边上高的比的平方,易得所求的高为355. 答案:35512.如图所示,在△ABC 中,DE ∥BC ,EF ∥CD ,若BC =3,DE =2,DF =1,则AB 的长为________.解析:∵DE ∥BC ,∴AD AB =AE AC =DE BC =23, EC AC =13. 又∵EF ∥CD ,∴DF AD =13. ∴AD =3.∴AB =32·AD =92. 答案:9213.如图所示,在梯形ABCD 中,AB ∥CD ,AB =4,CD =2,E ,F 分别为AD ,BC 上的点,且EF =3,EF ∥AB ,则梯形ABFE 与梯形EFCD 的面积比为________.解析:将线段AD 与BC 延长交于点H (如图所示).根据相似三角形面积之比等于相似比的平方,可得S △HCD S △HEF =49,S △HCD S △HAB =416, 故梯形ABFE 与梯形EFCD 的面积比为7∶5.答案:7∶514.在△ABC 中,∠ACB =90°,AC =2,点D 在BC 边上,且CD =1.若∠CAD =∠B ,则BD =________.解析:作出草图,依据题意tan ∠CAD =tan ∠B ,即12=21+BD,∴BD =3. 答案:315.如图,在△ABC 中,D 是AC 的中点,E 是BC 延长线上一点,过A 作AH ∥BE .连接ED 并延长交AB 于F ,交AH 于H .如果AB =4AF ,EH =8,则DF 的长为________.解析:∵AH ∥BE ,∴HF HE =AF AB. ∵AB =4AF ,∴HF HE =14, ∵HE =8,∴HF =2.∵AH ∥BE ,∴HD DE =AD DC. ∵D 是AC 的中点,∴HD DE=1. ∵HE =HD +DE =8,∴HD =4,∴DF =HD -HF =4-2=2.答案:216.如图,在△ABC 中,D 是AC 的中点,E 是BD 的三等分点,AE的延长线交BC 于F ,则S △BEF S 四边形DEFC的值为________. 解析:过D 点作DM ∥AF 交BC 于M ,因为DM ∥AF ,所以BF BM =BE BD =13,因为EF ∥DM ,所以S △BEFS △BDM =19,即S△BDM =9S △BEF ,又S △DMCS △BDM =23,即S △DMC =23S △BDM =6S △BEF ,所以S 四边形DEFC =14S △BEF ,因此S △BEFS 四边形DEFC =114.答案:11417.如图,在△ABC 中,D 为BC 边的中点,E 为AD 上的一点,延长BE 交AC 于点F .若AE AD =14,则AF AC 的值为________.解析:如图,过点A 作AG ∥BC ,交BF 的延长线于点G .∵AE AD =14,∴AE ED =13.又∵△AGE ∽△DBE ,∴AG BD =AE ED =13.∵D 为BC 中点,BC =2BD ,∴AG BC =16.∵△AGF ∽△CBF ,∴AF FC =AG BC =16,∴AF AC =17.答案:17。
§5.6 几何证明举例(1)

年级八年级 学科 数学 第 五 单元第 7 课时 总计 课时 2013年 10月 31日1§5.6 几何证明举例(1)课程标准:掌握三角形全等的判定定理,并会运用此定理证明相关的命题。
学习目标:1、 证明并掌握定理:两角及其中一组等角的对边分别相等的两个三角形全等。
并会运用此定理证明相关的命题。
2、 在证明过程中,体验数学的转化思想,提升学生综合运用知识的能力。
3、 养成善于思考,善于探究,善于推理,言必有据的好习惯。
学习重点:证明“角角边”定理。
学习难点:会灵活运用全等三角形的基本事实、性质和定理证明相关命题。
我的目标以及突破重难点的设想:学前准备:学情分析:学案使用说明以及学法指导:预习案一、忆一忆1、你还记得有关全等三角形的判定方法有哪些吗?全等三角形的性质是什么? 其中哪些作为基本事实?2、几何证明的步骤是什么?(简写)二、做一做已知:如图,AB 和CD 相交于点O ,OA=OD ,OC=OB求证:△OAC ≌ △ODB课型: 新授 执笔: 马海丽 审核: 滕广福 韩增美2 探究案探究一:全等三角形的判定AAS求证:如果一个三角形的两角及其中一角的对边与另一个三角形的两角及其中的一角的 对边对应相等,那么这两个三角形全等。
点拨:1、判定三角形全等的根据:基本事实: 定理:2、利用全等三角形的对应边和对应角的定义,可以进一步推证有关的线段或角相等。
小试牛刀:已知:如图,AB=AC ,DB=DC.求证:∠B=∠C.探究二:全等三角形的三线(小组合作交流)已知:如图,△ABC ≌△A'B'C',AD 和A'D'分别是对应角的平分线。
求证:AD=A'D'。
思考:全等三角形对应边上的中线以及高有什么性质?证明你的结论。
课堂小结:训练案课本177页 练习1,2题我的反思:A CBD。
)什么是几何证明[1]
![)什么是几何证明[1]](https://img.taocdn.com/s3/m/f28a9702ba1aa8114431d96b.png)
下面两个命题的题设和结论分别是什么?
(1)内错角相等,两直线平行。
题设 题设 结论 结论
(2)两直线平行,内错角相等。
观察上面的两个命题的题设和结论,你有什么发现?
互逆命题: 在两个命题中,
如果第一个命题的题设是第二个命题的结论, 而第一个命题的结论是第二个命题的题设, 那么这两个命题叫做互逆命题。 如果把其中一个命题叫做原命题, 那么另一个命题叫做它的逆命题。 说出下列命题的逆命题,并判断真假。 小试牛刀: (1)同角的补角相等 (2)全等三角形的对应边相等
汶上集镇初级中学 徐龙召
复习回顾:
1.我们学习了哪八大公理?
①直线公理 : _ _ _ __ _ _ ____ 2. 文字命题证明的一般步骤有哪些? ②平行公理: _ _ _ __ _ _ ____ ①分清命题的题设和结论,画出图形。 3. 求证:两直线平行,内错角相等。 ③等式的基本性质公理 : _______ ②根据命题的题设和结论,结合图形, 3 ④不等式的基本性质公理 : _______ 已知:如图,a∥b. 写出已知和求证。 2 1 __ 求证:∠ 1=∠2 ⑤平行线的性质公理 : _______ ③证明。 ⑥平行线的判定公理 : _______ __ 证明:∵ a∥b (已知)
1.平行线的判定定理
2.互逆命题 3.互逆定理 作业布置: P124习题11.3
必做题:A组 选做题:B组 4 1 5 题 2 题
再
见
∴ ∠1=∠3 (两直线平行,同位角相等) ⑦全等三角形的判定公理 :______ ∵ ∠2=∠3 (对顶角相等) ⑧全等三角形的性质公理 : _ ______ ∴ ∠1=∠2 (等量代换) 平行线的性质定理: 两直线平行,内错角相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(08河北)(本小题满分10分)
如图14-1,A B C △的边B C 在直线l 上,A C B C ⊥,且AC BC =;E F P △的边F P 也在直线l 上,边E F 与边A C 重合,且EF FP =.
(1)在图14-1中,请你通过观察、测量,猜想并写出A B 与A P 所满足的数量关系和位置关系;
(2)将E F P △沿直线l 向左平移到图14-2的位置时,E P 交A C 于点Q ,连结A P ,BQ .猜想并写出BQ 与A P 所满足的数量关系和位置关系,请证明你的猜想;
(3)将E F P △沿直线l 向左平移到图14-3的位置时,E P 的延长线交A C 的延长线于点Q ,连结A P ,
BQ .你认为(2)中所猜想的BQ 与A P 的数量关系和位置关系还成立吗?若成立,给出证明;若不成
立,请说明理由.
2.如图10-1,点E 是边长为1的正方形ABCD 的对角线BD 上的一个动点(不与B 、D 两点重合),过点E 作直线MN ∥DC ,交AD 于M ,交BC 于N ,连接AE ,作EF ⊥AE 于E ,交直线CB 于F . ⑴ 如图10-1,当点F 在线段CB 上时,通过观察或测量,猜想△AEF 的形状,并证明你的猜想; ⑵ 如图10-2,当点F 在线段CB 的延长线上时,其它条件不变,⑴中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由;
⑶ 在点E 从点D 向点B 的运动过程中,四边形AFNM 的面积是否会发生变化?若发生了变化,请说明理由;若没有发生变化,请求出其面积的值.
2.如图1,已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上,连接AE 、GC . (1)试猜想AE 与GC 有怎样的位置关系,并证明你的结论.
(2)将正方形DEFG 绕点D 按顺时针方向旋转,使点E 落在BC 边上,如图2,连接AE 和CG 。
你认为
(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
图10-1
A
B
C
D
图10-2
C
D
A
(E ) B C
(F ) P l
l
l
B F
C 图14-1
图14-2
图14-3
1.有边长为4的正方
形ABCD ,将一把三角尺的直角顶点P 放在正方形的对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q 。
(1)当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的数量关系?试证明你的结论;
(2)当点Q 在边DC 的延长线上时,线段PQ 与线段PB 之间是否有(1)中的数量关系?试证明你的结论;
(3)当点Q 在边DC 的延长线上时,△PCQ 是否可能成为等腰三角形,如果可能,求出相应的AP 的长。
2.如图(1),△ABC 和△ADE 是两个大小不同的等腰直角三角形,点C 在AE 上,∠BAC=∠DAE=90
(1)
(2) (3) 如果将图(2)中的△ABC 绕点A DC,BE 是怎样的数量关系和位置关系?直接写出结论不证明。
1.在图12-1到图12-3中,点O 是正方形ABCD 对角线AC 的中点,M P N △为直角三角形,∠MPN=90°
.正
方形ABCD 保持不动,M P N △沿射线AC 向右平移,平移过程中P 点始终在射线AC 上,且保持
PM
(1) (2)
B D (3) (4)
B G E
(第4题)
F
(图1)
(图2)
垂直于直线AB 于点E, PN 垂直于直线BC 于点F .
(1)如图12-1,当点P 与点O 重合时,OE 与OF 的数量关系为 ;
(2)如图12-2,当P 在线段OC 上时,猜想OE 与OF 有怎样的数量关系与位置关系?并对你的猜想
结果给予证明;
(3)如图12-3,当点P 在AC 的延长线上时,OE 与OF 的数量关系为 ;位置关系
为 .
2.角的直角三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DE ,长直角边为DF),将直角三角板DEF 绕D 点按逆时针方向旋转。
(1)在图1中,DE 交AB 于M ,DF 交BC 于N 。
①证明DM =DN ;
②在这一旋转过程中,直角三角板DEF 与△ABC 的重叠部分为四边形DMBN ,请说明四边形DMBN 的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积; (2)继续旋转至如图2的位置,延长AB 交DE 于M ,延长BC 交DF 于N ,DM =DN 是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)继续旋转至如图3的位置,延长FD 交BC 于N ,延长ED 交AB 于M ,DM =DN 是否仍然成立?请写出结论,不用证明。
3.(2010沈阳市)(12分)如图1,在△ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转,若B 、P 在直线a 的异侧,
BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接PM 、PN ;
(1) 延长MP 交CN 于点E(如图2)。
求证:△BPM ≅△CPE ; 求证:PM = PN ;
(2) 若直线a 绕点A 旋转到图3的位置时,点B 、P 在直线a 的同侧,其它条件不变。
此时 PM=PN 还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a 绕点A 旋转到与BC 边平行的位置时,其它条件不变。
请直接判断四边形MBCN 的形状及此时PM=PN 还成立吗?不必说明理由。
a A B
C
P
M
N A B
C
M N a
P
A B
C P
N M
a
A
A
A
B
B B C
C C
D D D
N
N N
E
E F
E
F
F
M M
M
图1 图2 图3 (第25题图)
C 图12-1
图12-2
N
图12-3。
