几何证明题简单题
七年级数学典型几何证明50题
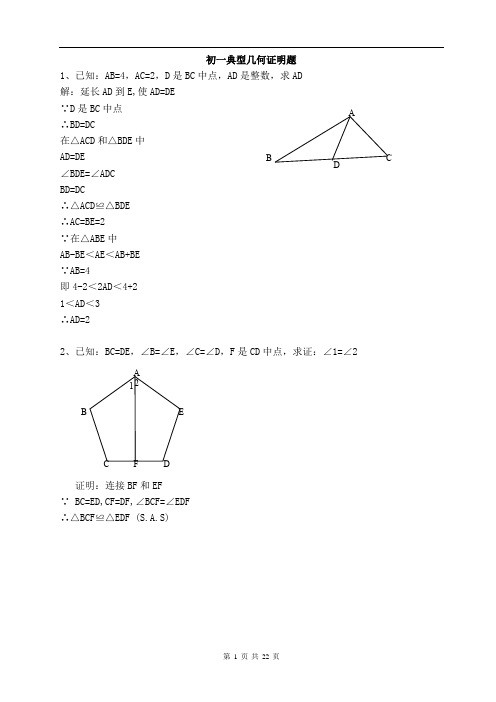
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
小学数学几何证明练习题

小学数学几何证明练习题题目一:平行线的证明题1. 请证明过直线l上的一点P,存在且唯一一条与直线l平行的直线。
2. 证明平行线具有传递性,即如果直线a // 直线b,直线b // 直线c,那么直线a // 直线c。
题目二:三角形和四边形的证明题1. 已知三角形ABC,通过顶点A作BC边的垂线,垂足为D。
请证明:∠ABD = ∠ACD。
2. 已知四边形ABCD,AB // CD,通过顶点A、D分别作BC、AD的垂线,垂足分别为E、F。
请证明∆ABE ≌ ∆CDF。
题目三:平行四边形的证明题1. 已知ABCD是平行四边形,E是AD边的中点,F是BC边的中点。
请证明:EF || AB。
2. 已知ABCD是平行四边形,对角线AC和BD交于点O。
请证明:AO ≌ CO。
题目四:圆的证明题1. 已知AB是圆的直径,C是圆上任意一点,AC交圆于点D。
请证明:∠ABC = 90°。
2. 已知O是ΔABC外接圆的圆心,交BC边于点D。
请证明:∠BAC = ∠BDO。
题目五:相似三角形的证明题1. 已知∆ABC和∆DEF相似,且∠A = ∠D,∠B = ∠E。
请证明:∠C = ∠F。
2. 已知∆ABC和∆EFD相似,且∠B = ∠E,∠F = ∠C。
请证明:∠A = ∠D。
题目六:角平分线的证明题1. 已知∠A和∠B是一个点P的相邻角,角APB的边PC是∠APB 的角平分线。
请证明∠APC = ∠BPC。
2. 已知∠A和∠B是一个点P的相邻角,角APB的边PC是∠APB 的角平分线。
请证明AP = BP。
注意:以上题目仅为示例题目,实际出题时可根据需要和学生水平进行调整。
(完整版)初中几何证明题五大经典(含答案)
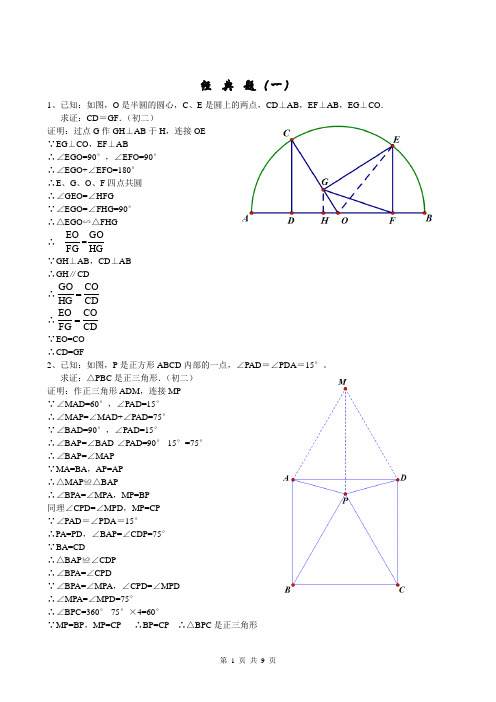
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
几何证明练习题带答案

几何证明练习题带答案一、选择题1. 已知三角形ABC中,AB=AC,点D在BC上,且BD=DC。
求证:∠BAD=∠CAD。
A. 利用等腰三角形性质B. 利用角平分线定理C. 利用等边三角形性质D. 利用相似三角形性质答案:B2. 已知线段AB和CD平行,且M是线段AB上的一点,N是线段CD上的一点,MN与AB、CD不平行。
求证:∠AMN≠∠CNM。
A. 利用平行线性质B. 利用内错角定理C. 利用同位角定理D. 利用补角定理答案:A二、填空题1. 在三角形ABC中,若∠A=90°,AB=AC,那么∠B=∠C=______。
答案:45°2. 已知三角形ABC中,AB=5,AC=7,BC=6,根据勾股定理可知这是一个______三角形。
答案:直角三、简答题1. 如何证明三角形内角和定理?答案:在三角形ABC中,延长BC至点D,根据外角定理,∠ACD=∠A+∠B。
又因为∠ACD+∠C=180°,所以∠A+∠B+∠C=180°,证明了三角形内角和为180°。
2. 如何证明圆内接四边形的对角互补?答案:设圆内接四边形ABCD,连接对角线AC和BD,由于AC和BD 都是圆的直径,根据圆周角定理,∠A+∠C=90°,∠B+∠D=90°。
因此,对角互补。
四、证明题1. 已知三角形ABC中,AB=AC,点D在BC上,且BD=DC。
证明∠BAD=∠CAD。
证明:由于AB=AC,根据等腰三角形性质,∠ABC=∠ACB。
又因为BD=DC,根据等边三角形性质,∠ABD=∠ACD。
因此,∠BAD=∠ABC-∠ABD=∠ACB-∠ACD=∠CAD。
2. 已知圆O中,弦AB和CD相交于点P,PA=PB,PC=PD。
证明:OP垂直于AB和CD。
证明:由于PA=PB,根据圆周角定理,∠APB=∠PBA。
同理,∠CPD=∠PDC。
因为∠APB+∠CPD=180°,所以∠OPB+∠OPD=90°。
几何证明练习题带答案

几何证明练习题带答案几何证明是数学中的一个重要部分,它要求学生运用逻辑推理和几何知识来证明几何命题的正确性。
以下是一些几何证明的练习题,以及相应的答案。
# 练习题1题目:证明在一个三角形中,大边对大角。
答案:设三角形ABC中,AB > AC。
我们需要证明∠B > ∠C。
证明:1. 延长BA和AC,使它们相交于点D。
2. 根据三角形的外角性质,我们知道∠BAC = ∠BAD + ∠DAC。
3. 由于AB > AC,根据三角形的边角关系,我们知道BD > CD。
4. 根据边角边(SAS)相似准则,三角形ABD ∽ 三角形ACD。
5. 相似三角形对应角相等,所以∠BAD = ∠CAD。
6. 因此,∠BAC = ∠BAD + ∠DAC > ∠DAC,即∠B > ∠C。
# 练习题2题目:证明在一个圆中,等弦所对的圆心角相等。
答案:设圆O中有两弦AB和CD,且AB = CD。
我们需要证明∠AOB = ∠COD。
证明:1. 根据圆的性质,我们知道OA = OB = OC = OD。
2. 由于AB = CD,根据SSS(边边边)相似准则,三角形OAB ∽ 三角形OCD。
3. 相似三角形对应角相等,所以∠AOB = ∠COD。
# 练习题3题目:证明直角三角形斜边上的中线等于斜边的一半。
答案:设直角三角形ABC中,∠C = 90°,D为斜边AB的中点。
我们需要证明CD = 1/2 AB。
证明:1. 连接CD。
2. 由于D为AB的中点,根据中点定理,我们知道CD = 1/2 AB。
3. 根据直角三角形斜边上的中线性质,我们知道CD垂直于AB,并且CD是AB的一半。
# 练习题4题目:证明平行四边形的对角线互相平分。
答案:设平行四边形ABCD,对角线AC和BD相交于点E。
我们需要证明E是AC和BD的中点。
证明:1. 由于ABCD是平行四边形,我们知道AB || CD且AB = CD。
初二数学 几何证明初步经典练习题 含答案

几何证明初步练习题1、三角形的内角和定理:三角形的内角和等于180°.推理过程:○1 作CM ∥AB ,则∠A= ,∠B= ,∵∠ACB +∠1+∠2=1800( ,∴∠A+∠B+∠ACB=1800. ○2 作MN ∥BC ,则∠2= ,∠3= ,∵∠1+∠2+∠3=1800,∴∠BAC+∠B+∠C=1800. 2.求证:在一个三角形中,至少有一个内角大于或者等于60°。
3、.如图,在△ABC 中,∠C >∠B,求证:AB >AC 。
4. 已知,如图,AE5. 已知:如图,EF ∥AD ,∠1 =∠2. 求证:∠AGD +∠BAC = 180°.反证法经典例题6.求证:两条直线相交有且只有一个交点.7.如图,在平面内,AB 是L 的斜线,CD 是L 的垂线。
求证:AB 与CD 必定相交。
8.2一.角平分线--轴对称9、已知在ΔABC 中,E为BC的中点,AD 平分BAC ∠,BD ⊥AD 于D .AB =9,AC=13求DE的长第9题图 第10题图 第11题图分析:延长BD交AC于F.可得ΔABD ≌ΔAFD .则BD =DF .又BE =EC ,即D E为ΔBCF 的中位线.∴DE=12FC=12(AC-AB)=2. 10、已知在ΔABC 中,108A ∠=,AB =AC ,BD 平分ABC ∠.求证:BC =AB +CD . 分析:在BC上截取BE=BA,连接DE.可得ΔBAD ≌ΔBED .由已知可得:18ABD DBE ∠=∠=,108A BED ∠=∠=,36C ABC ∠=∠=.∴72DEC EDC ∠=∠=,∴CD=CE ,∴BC =AB +CD .11、如图,ΔABC 中,E是BC 边上的中点,DE ⊥BC 于E ,交BAC ∠的平分线AD 于D ,过D 作DM ⊥AB 于M,作DN ⊥AC 于N .求证:BM =CN .分析:连接DB 与DC .∵DE 垂直平分BC ,∴DB =DC .易证ΔAMD ≌ΔAND .∴有DM =DN .∴ΔBMD ≌ΔCND (HL).∴BM =CN .二、旋转12、如图,已知在正方形ABCD 中,E在BC 上,F在DC 上,BE +DF=EF .求证:45EAF ∠=. C B ADE F D A B C B A E D NM B D A C分析:将ΔADF 绕A顺时针旋转90得ABG .∴GAB FAD ∠=∠.易证ΔAGE ≌ΔAFE .∴ 1452FAE GAE FAG ∠=∠=∠= 13、如图,点E 在ΔABC 外部,D 在边BC 上,DE 交AC 于F .若123∠=∠=∠,AC=AE.求证:ΔABC ≌ΔADE .分析:若ΔABC ≌ΔADE ,则ΔADE 可视为ΔABC 绕A逆时针旋转1∠所得.则有B ADE ∠=∠.∵12B ADE ∠+∠=∠+∠,且12∠=∠.∴B ADE ∠=∠.又∵13∠=∠.∴BAC DAE ∠=∠.再∵AC=AE.∴ΔABC ≌ΔADE .14、如图,点E为正方形ABCD的边CD上一点,点F为CB的延长线上的一点,且EA⊥AF.求证:DE=BF.分析:将ΔABF 视为ΔADE 绕A顺时针旋转90即可.∵90FAB BAE EAD BAE ∠+∠=∠+∠=.∴FBA EDA ∠=∠. 又∵90FBA EDA ∠=∠=,AB=AD.∴ΔABF ≌ΔADE .(ASA)∴DE=DF. 平移第14题图 第15题图 第16题图 第17题图三、平移15、如图,在梯形ABCD 中,BD ⊥AC ,AC =8,BD =15.求梯形ABCD 的中位线长. 分析:延长DC到E使得CE=AB.连接BE.可得ACEB .可视为将AC平移到BE.AB平移到CE.由勾股定理可得DE=17.∴梯形ABCD中位线长为8.5.16、已知在ΔABC 中,AB =AC ,D 为AB 上一点,E为AC 延长线一点,且BD =CE .求证:DM =EM 分析:作DF∥AC交BC于F.易证DF=BD=CE.则DF可视为CE平移所得.∴四边形DCEF为DCEF .∴DM=EM.线段中点的常见技巧 --倍长四、倍长17、已知,AD为ABC 的中线.求证:AB+AC>2AD.分析:延长AD到E使得AE=2AD.连接BE易证ΔBDE ≌ΔCDA .∴BE=AC.∴AB+AC>2AD.18、如图,AD 为ΔABC 的角平分线且BD =CD .求证:AB =AC . 分析:延长AD到E使得AD=ED.易证ΔABD ≌ΔECD .∴EC=AB. ∵BAD CAD ∠=∠.∴E CAD ∠=∠.∴AC=EC=AB. 19、已知在等边三角形ABC中,D和E分别为BC与AC上的点,且AE=CD.连接AD与BE交于点P,作BQ⊥AD于Q.求证:BP=2PQ.分析:延长PD到F使得FQ=PQ.在等边三角形ABC中AB=BC=AC,60ABD C ∠=∠=.又∵AE=CD,∴BD=CE.∴ΔABD ≌ΔBCE .∴CBE BAD ∠=∠.∴60BPQ PBA PAB PBA DBP ∠=∠+∠=∠+∠=.易证ΔBPQ ≌ΔBFQ .得BP=BF,又60BPD ∠=.∴ΔBPF 为等边三角形.∴BP=2PQ.中位线五、中位线、中线:20、已知在梯形ABCD 中,AD ∥BC ,E和F分别为BD 与AC 的中点, 求证:1()2EF BC AD =-. 分析:取DC中点G,连接EG与FG.则EG为ΔBCD 中位线,FG为ΔACD 的中位线. ∴EG∥=12BC ,FG ∥=12AD .∵AD ∥BC .∴过一点G有且只有一条直线平行于已知直线BC,即E、F、G共线.∴1()2EF BC AD =-. 直角三角形斜边上的中线等于斜边的一半21、已知,在ABCD 中BD AB 21=.E为OA的中点,F为OD中点,G为BC中点. 求证:EF=EG.分析:连接BE .∵BD AB 21=,AE=O E.∴BE⊥CE,∵BG=CG. ∴BD EG 21=.又EF为ΔAOD 的中位线.∴AD EF 21=.∴EF=EG. 22、在ΔABC 中,AD是高,CE是中线,DC=BE,DG⊥CE于G.求证:(1)CG=EG.(2)2B BCE ∠=∠.分析:(1)连接DE.则有DE=BE=DC.∴Rt ΔCDG ≌Rt ΔEDG (HL).∴EG=CG.∵DE=BE.∴B BDE DEC BCE ∠=∠=∠+∠.∵DE=CD.∴DEC BCE ∠=∠.∴2B BCE ∠=∠.几何证明初步测验题(1)一、选择题(每空3 分,共36 分)1、使两个直角三角形全等的条件是( )A 、一组锐角对应相等B 、两组锐角分别对应相等C 、一组直角边对应相等D 、两组直角边分别对应相等2、如图,已知AB ∥CD ,∠A =50°,∠C =∠E .则∠C =( )A .20°B .25°C .30°D .40°第2题图 第4题图 第6题图 第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中( )A .有两个角是直角B .有两个角是钝角C .有两个角是锐角D .一个角是钝角,一个角是直角4、如图,直线AB 、CD 相交于点O ,∠BOE=90°,OF 平分∠AOE ,∠1=15°30’,则下列结论不正确的是( ) A D B E F OC B E F ED G AA.∠2=45° B.∠1=∠3 C.∠AOD+∠1=180° D.∠EOD=75°30’5、下列说法中,正确的个数为()①三角形的三条高都在三角形内,且都相交于一点②三角形的中线都是过三角形的某一个顶点,且平分对边的直线③在△ABC中,若∠A=12∠B=13∠C,则△ABC是直角三角形④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18A.1个 B.2个 C.3个 D.4个6、如图,在AB=AC的△ABC中,D是BC边上任意一点,DF⊥AC于F,E在AB边上,使ED⊥BC于D,∠AED=155°,则∠EDF等于()A、50°B、65°C、70°D、75°7、如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A. B.9、如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为()A.仅小明对 B.仅小亮对 C.两人都对 D.两人都对第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,•则四个结论正确的是().①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确; B.仅①和②正确; C.仅②③正确; D.仅①和③正确11、如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是()①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A.1 B.2 C.3 D.412、如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.13B.12C.23D.不能确定二、填空题(每空3 分,共15 分)13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
初二数学几何证明题(5篇可选)

初二数学几何证明题(5篇可选)第一篇:初二数学几何证明题1.在△ABC中,AB=AC,D在AB上,E在AC的延长线上,且BD=CE,线段DE交BC于点F,说明:DF=EF。
2.已知:在正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN垂直DM于点M,且交∠CBE的平分线于点N.(1)求证:MD=MN.(2)若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变,则(1)的结论还成立吗?如果成立,请证明,如果不成立,请说明理由。
3.。
如图,点E,F分别是菱形ABCD的边CD和CB延长线上的点,且DE=BF,求证∠E=∠F。
4,如图,在△ABC中,D,E,F,分别为边AB,BC,CA,的中点,求证四边形DECF为平行四边形。
5.如图,在菱形ABCD中,∠DAB=60度,过点C作CE垂直AC 且与AB的延长线交与点E,求证四边形AECD是等腰梯形?6.如图,已知平行四边形ABCD中,对角线AC,BD,相交与点0,E是BD延长线上的点,且三角形ACE是等边三角形。
1.求证四边形ABCD是菱形。
2.若∠AED=2∠EAD,求证四边形ABCD是正方形。
7.已知正方形ABCD中,角EAF=45度,F点在CD边上,E点在BC边上。
求证:EF=BE+DF第二篇:初二几何证明题1如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DCCF.(1)求证:D是BC的中点;(2)如果AB=ACADCF的形状,并证明你的结论AEB第三篇:初二几何证明题初二几何证明题1.已知:如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E。
M为AB中点,联结ME,MD、ED求证:角EMD=2角DAC证明:∵M为AB边的中点,AD⊥BC,BE⊥AC,∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图,已知四边形ABCD中,AD=BC,E、F分别是AB、CD中点,AD、BC的延长线与EF的延长线交于点H、D求证:∠AHE=∠BGE证明:连接AC,作EM‖AD交AC于M,连接MF.如下图:∵E是CD的中点,且EM‖AD,∴EM=1/2AD,M是AC的中点,又因为F是AB的中点∴MF‖BC,且MF=1/2BC.∵AD=BC,∴EM=MF,三角形MEF为等腰三角形,即∠MEF=∠MFE.∵EM‖AH,∴∠MEF=∠AHF ∵FM‖BG,∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题,并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。
数学几何证明题

数学几何证明题一、在三角形ABC中,若AB = AC,且D为BC的中点,则AD与BC的关系是?A. AD垂直于BCB. AD平行于BCC. AD是BC的一半D. AD与BC相交于一点非中点(答案)A二、在平行四边形ABCD中,若AB = BC,则该平行四边形是?A. 矩形B. 菱形C. 正方形D. 梯形(答案)B三、在圆O中,弦AB与弦CD相交于点P,若AP = PB,且CP = PD,则OP与AB、CD的关系是?A. OP垂直于AB且垂直于CDB. OP平行于AB且平行于CDC. OP是AB、CD的角平分线D. OP与AB、CD无特定关系(答案)A四、在三角形ABC中,若角A = 60度,且角B的平分线与角C的外角平分线相交于点D,则角D的度数是?A. 30度B. 60度C. 90度D. 120度(答案)C五、在矩形ABCD中,对角线AC与BD相交于点O,若AC = 2AB,则角AOB的度数是?A. 30度B. 45度C. 60度D. 90度(答案)C六、在三角形ABC中,若D、E分别是AB、AC的中点,且DE = 1/3BC,则三角形ABC的形状是?A. 等边三角形B. 等腰三角形C. 直角三角形D. 一般三角形(答案)C七、在圆O中,若弦AB的长度等于半径OA,则角AOB的度数是?A. 30度B. 45度C. 60度D. 90度(答案)C(注:此题假设弦AB不是直径)八、在平行四边形ABCD中,若M、N分别是AB、CD的中点,且MN = 1/2AD,则平行四边形ABCD是?A. 矩形B. 菱形C. 正方形D. 梯形(但此选项不可能,因为已给出是平行四边形)(答案)A九、在三角形ABC中,若角A = 角B + 角C,则三角形ABC是?A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形(答案)C十、在圆O中,若弦AB与弦CD平行,且AB = 2CD,则弦AB与弦CD之间的距离与半径的关系是?A. 等于半径B. 小于半径C. 大于半径D. 与半径无关(答案)B(注:此题假设弦AB与弦CD不是同一个圆上的直径)。
中考数学经典几何证明题60例附试题分析和参考答案
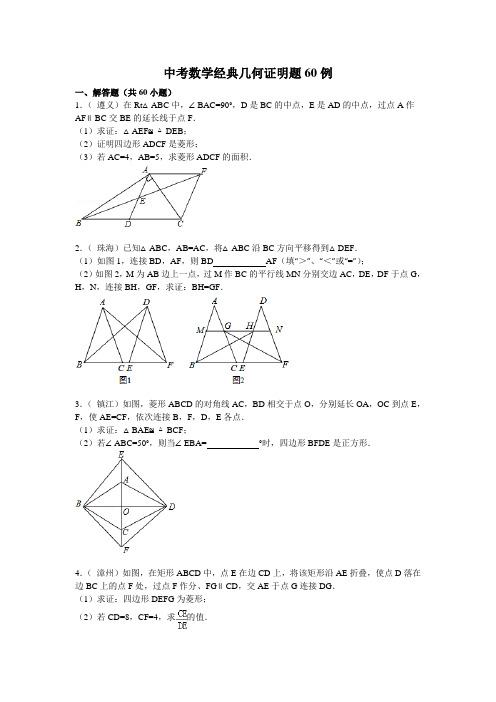
中考数学经典几何证明题60例一、解答题(共60小题)1.(遵义)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)证明四边形ADCF是菱形;(3)若AC=4,AB=5,求菱形ADCF的面积.2.(珠海)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.(1)如图1,连接BD,AF,则BD AF(填“>”、“<”或“=”);(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.3.(镇江)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.(1)求证:△BAE≌△BCF;(2)若∠ABC=50°,则当∠EBA=°时,四边形BFDE是正方形.4.(漳州)如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求的值.5.(玉林)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O 的切线CD交AB的延长线于点C,E为的中点,连接DE,EB.(1)求证:四边形BCDE是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O的半径r.6.(永州)如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.(1)求证:∠ABC=∠EDC;(2)求证:△ABC≌△EDC.7.(营口)如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.(1)求证:PC是⊙O的切线;(2)若PD=,AC=8,求图中阴影部分的面积;(3)在(2)的条件下,若点E是的中点,连接CE,求CE的长.8.(徐州)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:四边形BFCE是平行四边形;(2)若AD=10,DC=3,∠EBD=60°,则BE=时,四边形BFCE是菱形.9.(宿迁)如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.(1)求证:四边形BDFC是平行四边形;(2)若△BCD是等腰三角形,求四边形BDFC的面积.10.(湘西州)如图,在▱ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.(1)求证:△ADE≌△CBF;(2)求证:四边形BFDE为矩形.11.(咸宁)已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)证明:不论m为何值时,方程总有实数根;(2)m为何整数时,方程有两个不相等的正整数根.12.(咸宁)如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.13.(梧州)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.(1)求证:HF=AP;(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.14.(威海)如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE=3,求AC的长.15.(铜仁市)已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.16.(通辽)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.17.(铁岭)如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.(1)若DE=BF,求证:四边形AFCE是平行四边形;(2)若四边形AFCE是菱形,求菱形AFCE的周长.18.(天水)如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证:(1)AC•PD=AP•BC;(2)PE=PD.19.(泰安)如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E 为AC中点,BD平分∠ABC,点F在AB上,且BF=BC.求证:(1)DF=AE;(2)DF⊥AC.20.(随州)如图,射线PA切⊙O于点A,连接PO.(1)在PO的上方作射线PC,使∠OPC=∠OPA(用尺规在原图中作,保留痕迹,不写作法),并证明:PC是⊙O的切线;(2)在(1)的条件下,若PC切⊙O于点B,AB=AP=4,求的长.21.(绥化)如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.(1)求证:BD+2DE=BM.(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG=.22.(苏州)如图,在△ABC中,AB=AC,分别以B、C为圆心,BC长为半径在BC下方画弧.设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD(1)求证:AD平分∠BAC;(2)若BC=6,∠BAC=50°,求DE、DF的长度之和(结果保留π).23.(上海)已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.(1)求证:DE⊥BE;(2)如果OE⊥CD,求证:BD•CE=CD•DE.24.(厦门)如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.求证:四边形ABCD是矩形.25.(庆阳)如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.(1)当AB=2时,求△GEC的面积;(2)求证:AE=EF.26.(青海)如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.27.(钦州)如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.(1)求证:BC是⊙O的切线;(2)连接OC,如果OC恰好经过弦BD的中点E,且tanC=,AD=3,求直径AB的长.28.(黔东南州)如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.(1)求证:PN与⊙O相切;(2)如果∠MPC=30°,PE=2,求劣弧的长.29.(潜江)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.(1)求证:PB是⊙O的切线;(2)当OB=3,PA=6时,求MB,MC的长.30.(盘锦)如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.(1)若CD=2,BP=4,求⊙O的半径;(2)求证:直线BF是⊙O的切线;(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.31.(内江)如图,将▱ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC 于点O.(1)求证:△ABD≌△BEC;(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.32.(南通)如图,在▱ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.(1)求证:△AED≌△CFB;(2)若∠A=30°,∠DEB=45°,求证:DA=DF.33.(南平)如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.(1)求证:∠BAD=∠BDC;(2)若∠BDC=28°,BD=2,求⊙O的半径.(精确到0.01)34.(南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.35.(南充)如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB;(2)AF=2CD.36.(南昌)(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D 的形状为A.平行四边形B.菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.37.(梅州)如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连接BD,与AC交于点E,连接AD,CD.(1)求证:△ABC≌△ADC;(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.38.(龙岩)如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.(1)求证:AE=DC;(2)已知DC=,求BE的长.39.(柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.(1)求证:AB=AC;(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.40.(辽阳)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.(1)求证:直线FG是⊙O的切线;(2)若AC=10,cosA=,求CG的长.41.(连云港)如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F 处,DF交AB于点E.(1)求证;∠EDB=∠EBD;(2)判断AF与DB是否平行,并说明理由.42.(莱芜)如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD 交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.43.(酒泉)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.(1)求证:四边形CEDF是平行四边形;(2)①当AE=cm时,四边形CEDF是矩形;②当AE=cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)44.(荆门)已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O 于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sinA=,求BH的长.45.(吉林)如图①,半径为R,圆心角为n°的扇形面积是S扇形=,由弧长l=,得S扇形==••R=lR.通过观察,我们发现S扇形=lR类似于S三角形=×底×高.类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分交作扇环)的面积公式及其应用.(1)设扇环的面积为S扇环,的长为l1,的长为l2,线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=×(上底+下底)×高,用含l1,l2,h的代数式表示S扇环,并证明;(2)用一段长为40m的篱笆围成一个如图②所示的扇环形花园,线段AD的长h为多少时,花园的面积最大,最大面积是多少?46.(黄石)在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.47.(黄冈)已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.(1)求证:∠BCP=∠BAN(2)求证:=.48.(湖北)如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.49.(葫芦岛)如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.(1)求证:AB与⊙O相切;(2)若等边三角形ABC的边长是4,求线段BF的长?50.(呼伦贝尔)如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.(1)求证:△ADE≌△CBF;(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.51.(呼伦贝尔)如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.(1)求证:AB=AC;(2)若PC=2,求⊙O的半径.52.(贺州)如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.(1)求证:DC是⊙O的切线;(2)若OE=cm,AC=2cm,求DC的长(结果保留根号).53.(贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.(1)求证:AF=EF;(2)求证:BF平分∠ABD.54.(河南)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.(1)求证:△CDP≌△POB;(2)填空:①若AB=4,则四边形AOPD的最大面积为;②连接OD,当∠PBA的度数为时,四边形BPDO是菱形.55.(桂林)如图,在▱ABCD中,E、F分别是AB、CD的中点.(1)求证:四边形EBFD为平行四边形;(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.56.(贵港)如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E 是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.(1)若AB=4,求的长;(结果保留π)(2)求证:四边形ABMC是菱形.57.(甘南州)如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.(1)求证:CF=CH;(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM 是什么四边形?并证明你的结论.58.(东莞)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求BG的长.59.(大庆)如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.(1)证明:AB=CD;(2)证明:DP•BD=AD•BC;(2)证明:BD2=AB2+AD•BC.60.(赤峰)如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO 交PO延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是的切线.(2)若PB=6,DB=8,求⊙O的半径.中考数学经典几何证明题60例参考答案与试题解析一、解答题(共60小题)1.(遵义)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)证明四边形ADCF是菱形;(3)若AC=4,AB=5,求菱形ADCF的面积.考点:菱形的判定与性质;全等三角形的判定与性质;直角三角形斜边上的中线;三角形中位线定理.专题:证明题.分析:(1)根据AAS证△AFE≌△DBE;(2)利用①中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.解答:(1)证明:①∵AF∥BC,∴∠AFE=∠DBE,∵E是AD的中点,AD是BC边上的中线,∴AE=DE,BD=CD,在△AFE和△DBE中,,∴△AFE≌△DBE(AAS);(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.∵DB=DC,∴AF=CD.∵AF∥BC,∴四边形ADCF是平行四边形,∵,∠BAC=90°,D是BC的中点,E是AD的中点,∴AD=DC=BC,∴四边形ADCF是菱形;(3)解:设菱形DC边上的高为h,∴RT△ABC斜边BC边上的高也为h,∵BC==,∴DC=BC=,∴h==,菱形ADCF的面积为:DC•h=×=10.点评:本题考查了全等三角形的性质和判定,平行四边形的判定,菱形的判定的应用,菱形的面积计算,主要考查学生的推理能力.2.(珠海)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.(1)如图1,连接BD,AF,则BD=AF(填“>”、“<”或“=”);(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.考点:全等三角形的判定与性质;等腰三角形的性质;平移的性质.专题:证明题.分析:(1)根据等腰三角形的性质,可得∠ABC与∠ACB的关系,根据平移的性质,可得AC与DF的关系,根据全等三角形的判定与性质,可得答案;(2)根据相似三角形的判定与性质,可得GM与HN的关系,BM与FN的关系,根据全等三角形的判定与性质,可得答案.解答:(1)解:由AB=AC,得∠ABC=ACB.由△ABC沿BC方向平移得到△DEF,得DF=AC,∠DFE=∠ACB.在△ABF和△DFB中,,△ABF≌△DFB(SAS),BD=AF,故答案为:BD=AF;(2)证明:如图:MN∥BF,△AMG∽△ABC,△DHN∽△DEF,=,=,∴MG=HN,MB=NF.在△BMH和△FNG中,,△BMH≌△FNG(SAS),∴BH=FG.点评:本题考查了全等三角形的判定与性质,利用了平移的性质,相似三角形的判定与性质,全等三角形的判定与性质.3.(镇江)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.(1)求证:△BAE≌△BCF;(2)若∠ABC=50°,则当∠EBA=20°时,四边形BFDE是正方形.考点:菱形的性质;全等三角形的判定与性质;正方形的判定.专题:证明题.分析:(1)由题意易证∠BAE=∠BCF,又因为BA=BC,AE=CF,于是可证△BAE≌△BCF;(2)由已知可得四边形BFDE对角线互相垂直平分,只要∠EBF=90°即得四边形BFDE 是正方形,由△BAE≌△BCF可知∠EBA=∠FBC,又由∠ABC=50°,可得∠EBA+∠FBC=40°,于是∠EBA=×40°=20°.解答:(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,∴AB=BC,∠BAC=∠BCA,∴∠BAE=∠BCF,在△BAE与△BCF中,∴△BAE≌△BCF(SAS);(2)∵四边形BFDE对角线互相垂直平分,∴只要∠EBF=90°即得四边形BFDE是正方形,∵△BAE≌△BCF,∴∠EBA=∠FBC,又∵∠ABC=50°,∴∠EBA+∠FBC=40°,∴∠EBA=×40°=20°.故答案为:20.点评:本题考查了菱形的性质,全等三角形的判定与性质以及正方形的判定.本题关键是根据SAS证明△BAE≌△BCF.4.(漳州)如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求的值.考点:翻折变换(折叠问题);勾股定理;菱形的判定与性质;矩形的性质.专题:证明题.分析:(1)根据折叠的性质,易知DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,易证FG=FE,故由四边相等证明四边形DEFG为菱形;(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出的值.解答:(1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,∵FG∥CD,∴∠2=∠3,∴FG=FE,∴DG=GF=EF=DE,∴四边形DEFG为菱形;(2)解:设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,在Rt△EFC中,FC2+EC2=EF2,即42+(8﹣x)2=x2,解得:x=5,CE=8﹣x=3,∴=.点评:本题主要考查了折叠的性质、菱形的判定以及勾股定理,熟知折叠的性质和菱形的判定方法是解答此题的关键.5.(玉林)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O 的切线CD交AB的延长线于点C,E为的中点,连接DE,EB.(1)求证:四边形BCDE是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O的半径r.考点:切线的性质;平行四边形的判定;扇形面积的计算.专题:证明题.分析:(1)由∠BOD=60°E为的中点,得到,于是得到DE∥BC,根据CD 是⊙O的切线,得到OD⊥CD,于是得到BE∥CD,即可证得四边形BCDE是平行四边形;(2)连接OE,由(1)知,,得到∠BOE=120°,根据扇形的面积公式列方程即可得到结论.解答:解:(1)∵∠BOD=60°,∴∠AOD=120°,∴=,∵E为的中点,∴,∴DE∥AB,OD⊥BE,即DE∥BC,∵CD是⊙O的切线,∴OD⊥CD,∴BE∥CD,∴四边形BCDE是平行四边形;(2)连接OE,由(1)知,,∴∠BOE=120°,∵阴影部分面积为6π,∴=6π,∴r=6.点评:本题考查了切线的性质,平行四边形的判定,扇形的面积公式,垂径定理,证明是解题的关键.6.(永州)如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.(1)求证:∠ABC=∠EDC;(2)求证:△ABC≌△EDC.考点:全等三角形的判定与性质.专题:证明题.分析:(1)根据四边形的内角和等于360°求出∠B+∠ADC=180°,再根据邻补角的和等于180°可得∠CDE+∠ADE=180°,从而求出∠B=∠CDE;(2)根据“边角边”证明即可.解答:(1)证明:在四边形ABCD中,∵∠BAD=∠BCD=90°,∴90°+∠B+90°+∠ADC=360°,∴∠B+∠ADC=180°,又∵∠CDE+∠ADC=180°,∴∠ABC=∠CDE,(2)连接AC,由(1)证得∠ABC=∠CDE,在△ABC和△EDC中,,∴△ABC≌△EDC(SAS).点评:本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,根据四边形的内角和定理以及邻补角的定义,利用同角的补角相等求出夹角相等是证明三角形全等的关键,也是本题的难点.7.(营口)如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.(1)求证:PC是⊙O的切线;(2)若PD=,AC=8,求图中阴影部分的面积;(3)在(2)的条件下,若点E是的中点,连接CE,求CE的长.考点:切线的判定;扇形面积的计算.专题:证明题.分析:(1)连接OC,证明△PAO≌△PCO,得到∠PCO=∠PAO=90°,证明结论;(2)证明△ADP∽△PDA,得到成比例线段求出BC的长,根据S阴=S⊙O﹣S△ABC 求出答案;(3)连接AE、BE,作BM⊥CE于M,分别求出CM和EM的长,求和得到答案.解答:(1)证明:如图1,连接OC,∵PA切⊙O于点A,∴∠PAO=90°,∵BC∥OP,∴∠AOP=∠OBC,∠COP=∠OCB,∵OC=OB,∴∠OBC=∠OCB,∴∠AOP=∠COP,在△PAO和△PCO中,,∴△PAO≌△PCO,∴∠PCO=∠PAO=90°,∴PC是⊙O的切线;(2)解:由(1)得PA,PC都为圆的切线,∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90°,∴∠PAD+∠DAO=∠DAO+∠AOD,∴∠PAD=∠AOD,∴△ADP∽△ODA,∴,∴AD2=PD•DO,∵AC=8,PD=,∴AD=AC=4,OD=3,AO=5,由题意知OD为△的中位线,∴BC=6,OD=6,AB=10.∴S阴=S⊙O﹣S△ABC=﹣24;(3)解:如图2,连接AE、BE,作BM⊥CE于M,∴∠CMB=∠EMB=∠AEB=90°,∵点E是的中点,∴∠ECB=∠CBM=∠ABE=45°,CM=MB=3,BE=AB•cos45°=5,∴EM==4,则CE=CM+EM=7.点评:本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质,灵活运用切线的性质:圆的切线垂直于过切点的半径和切线的判定是解题的关键.8.(徐州)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:四边形BFCE是平行四边形;(2)若AD=10,DC=3,∠EBD=60°,则BE=4时,四边形BFCE是菱形.考点:平行四边形的判定;菱形的判定.专题:证明题.分析:(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.解答:(1)证明:∵AB=DC,∴AC=DF,在△AEC和△DFB中,∴△AEC≌△DFB(SAS),∴BF=EC,∠ACE=∠DBF∴EC∥BF,∴四边形BFCE是平行四边形;(2)当四边形BFCE是菱形时,BE=CE,∵AD=10,DC=3,AB=CD=3,∴BC=10﹣3﹣3=4,∵∠EBD=60°,∴BE=BC=4,∴当BE=4 时,四边形BFCE是菱形,故答案为:4.点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及勾股定理等知识.此题综合性较强,难度适中,注意数形结合思想的应用,注意掌握辅助线的作法.9.(宿迁)如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.(1)求证:四边形BDFC是平行四边形;(2)若△BCD是等腰三角形,求四边形BDFC的面积.考点:平行四边形的判定与性质;等腰三角形的性质.专题:证明题.分析:(1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;(2)分①BC=BD时,利用勾股定理列式求出AB,然后利用平行四边形的面积公式列式计算即可得解;②BC=CD时,过点C作CG⊥AF于G,判断出四边形AGCB 是矩形,再根据矩形的对边相等可得AG=BC=3,然后求出DG=2,利用勾股定理列式求出CG,然后利用平行四边形的面积列式计算即可得解;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾.解答:(1)证明:∵∠A=∠ABC=90°,∴BC∥AD,∴∠CBE=∠DFE,在△BEC与△FED中,,∴△BEC≌△FED,∴BE=FE,又∵E是边CD的中点,∴CE=DE,∴四边形BDFC是平行四边形;(2)①BC=BD=3时,由勾股定理得,AB===2,所以,四边形BDFC的面积=3×2=6;②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,所以,AG=BC=3,所以,DG=AG﹣AD=3﹣1=2,由勾股定理得,CG===,所以,四边形BDFC的面积=3×=3;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;综上所述,四边形BDFC的面积是6或3.点评:本题考查了平行四边形的判定与性质,等腰三角形的性质,全等三角形的判定与性质,(1)确定出全等三角形是解题的关键,(2)难点在于分情况讨论.10.(湘西州)如图,在▱ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.(1)求证:△ADE≌△CBF;(2)求证:四边形BFDE为矩形.考点:矩形的判定;全等三角形的判定与性质;平行四边形的性质.专题:证明题.分析:(1)由DE与AB垂直,BF与CD垂直,得到一对直角相等,再由ABCD为平行四边形得到AD=BC,对角相等,利用AAS即可的值;(2)由平行四边形的对边平行得到DC与AB平行,得到∠CDE为直角,利用三个角为直角的四边形为矩形即可的值.解答:证明:(1)∵DE⊥AB,BF⊥CD,∴∠AED=∠CFB=90°,∵四边形ABCD为平行四边形,∴AD=BC,∠A=∠C,在△ADE和△CBF中,,∴△ADE≌△CBF(AAS);(2)∵四边形ABCD为平行四边形,∴CD∥AB,∴∠CDE+∠DEB=180°,∵∠DEB=90°,∴∠CDE=90°,∴∠CDE=∠DEB=∠BFD=90°,则四边形BFDE为矩形.点评:此题考查了矩形的判定,全等三角形的判定与性质,以及平行四边形的性质,熟练掌握矩形的判定方法是解本题的关键.11.(咸宁)已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)证明:不论m为何值时,方程总有实数根;(2)m为何整数时,方程有两个不相等的正整数根.考点:根的判别式;解一元二次方程-公式法.专题:证明题.分析:(1)求出方程根的判别式,利用配方法进行变形,根据平方的非负性证明即可;(2)利用一元二次方程求根公式求出方程的两个根,根据题意求出m的值.解答:(1)证明:△=(m+2)2﹣8m=m2﹣4m+4=(m﹣2)2,∵不论m为何值时,(m﹣2)2≥0,∴△≥0,∴方程总有实数根;(2)解:解方程得,x=,x1=,x2=1,∵方程有两个不相等的正整数根,∴m=1或2,m=2不合题意,∴m=1.点评:本题考查的是一元二次方程根的判别式和求根公式的应用,掌握一元二次方程根的情况与判别式△的关系:△>0⇔方程有两个不相等的实数根;△=0⇔方程有两个相等的实数根;△<0⇔方程没有实数根是解题的关键.12.(咸宁)如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.考点:切线的性质;菱形的判定与性质;相似三角形的判定与性质.专题:证明题.分析:(1)连接OD、OE、ED.先证明△AOE是等边三角形,得到AE=AO=0D,则四边形AODE是平行四边形,然后由OA=OD证明四边形AODE是菱形;(2)连接OD、DF.先由△OBD∽△ABC,求出⊙O的半径,然后证明△ADC∽△AFD,得出AD2=AC•AF,进而求出AD.解答:(1)证明:如图1,连接OD、OE、ED.∵BC与⊙O相切于一点D,∴OD⊥BC,∴∠ODB=90°=∠C,∴OD∥AC,∵∠B=30°,∴∠A=60°,∵OA=OE,∴△AOE是等边三角形,∴AE=AO=0D,∴四边形AODE是平行四边形,∵OA=OD,∴四边形AODE是菱形.(2)解:设⊙O的半径为r.∵OD∥AC,∴△OBD∽△ABC.∴,即10r=6(10﹣r).解得r=,∴⊙O的半径为.如图2,连接OD、DF.∵OD∥AC,∴∠DAC=∠ADO,∵OA=OD,∴∠ADO=∠DAO,∴∠DAC=∠DAO,∵AF是⊙O的直径,∴∠ADF=90°=∠C,∴△ADC∽△AFD,∴,∴AD2=AC•AF,∵AC=6,AF=,∴AD2=×6=45,∴AD==3.点评:本题考查了切线的性质、圆周角定理、等边三角形的判定与性质、菱形的判定和性质以及相似三角形的判定和性质,是一个综合题,难度中等.熟练掌握相关图形的性质及判定是解本题的关键.13.(梧州)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.(1)求证:HF=AP;(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.考点:正方形的性质;全等三角形的判定与性质;勾股定理.专题:证明题.分析:(1)先根据EQ⊥BO,EH⊥AB得出∠EQN=∠BHM=90°.根据∠EMQ=∠BMH得出△EMQ∽△BMH,故∠QEM=∠HBM.由ASA定理得出△APB≌△HFE,故可得出结论;(2)由勾股定理求出BP的长,根据EF是BP的垂直平分线可知BQ=BP,再根据锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=4,再根据EQ=EF﹣QF即可得出结论.解答:(1)证明:∵EQ⊥BO,EH⊥AB,∴∠EQN=∠BHM=90°.∵∠EMQ=∠BMH,∴△EMQ∽△BMH,∴∠QEM=∠HBM.在Rt△APB与Rt△HFE中,,∴△APB≌△HFE,∴HF=AP;(2)解:由勾股定理得,BP===4.∵EF是BP的垂直平分线,∴BQ=BP=2,∴QF=BQ•tan∠FBQ=BQ•tan∠ABP=2×=.由(1)知,△APB≌△HFE,∴EF=BP=4,∴EQ=EF﹣QF=4﹣=.点评:本题考查的是正方形的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.14.(威海)如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE=3,求AC的长.考点:相似三角形的判定与性质;等腰三角形的性质;圆周角定理.专题:证明题.分析:(1)连结AE,如图,根据圆周角定理,由AC为⊙O的直径得到∠AEC=90°,然后利用等腰三角形的性质即可得到BE=CE;(2)连结DE,如图,证明△BED∽△BAC,然后利用相似比可计算出AB的长,从而得到AC的长.解答:(1)证明:连结AE,如图,∵AC为⊙O的直径,∴∠AEC=90°,∴AE⊥BC,而AB=AC,∴BE=CE;(2)连结DE,如图,∵BE=CE=3,∴BC=6,∵∠BED=∠BAC,而∠DBE=∠CBA,∴△BED∽△BAC,∴=,即=,∴BA=9,∴AC=BA=9.点评:本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了角平分线的性质和圆周角定理.15.(铜仁市)已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.考点:全等三角形的判定与性质;等边三角形的判定与性质.专题:证明题.分析:作DG∥BC交AC于G,先证明△DFG≌△EFC,得出GD=CE,再证明△ADG是等边三角形,得出AD=GD,即可得出结论.解答:证明:作DG∥BC交AC于G,如图所示:则∠DGF=∠ECF,在△DFG和△EFC中,,∴△DFG≌△EFC(AAS),∴GD=CE,。
几何证明练习题及答案

几何证明练习题及答案题目1:已知三角形ABC中,AB=AC,点D在BC上,且AD垂直于BC。
证明:三角形ABD与三角形ACD全等。
答案:由于AB=AC,所以三角形ABC是等腰三角形。
根据等腰三角形的性质,角BAD等于角CAD。
又因为AD垂直于BC,所以角ADB和角ADC都是直角。
因此,我们有:- AD=AD(公共边)- ∠BAD=∠CAD(等腰三角形的性质)- ∠ADB=∠ADC=90°(直角)根据SAS(边角边)全等条件,三角形ABD与三角形ACD全等。
题目2:已知三角形ABC中,AB=AC,点E在AB上,点F在AC上,且BE=CF。
证明:三角形AEF是等腰三角形。
答案:由于AB=AC,三角形ABC是等腰三角形。
根据等腰三角形的性质,角ABC等于角ACB。
又因为BE=CF,我们可以得出:- AB=AC(已知)- BE=CF(已知)- ∠ABC=∠ACB(等腰三角形的性质)根据SSS(边边边)全等条件,三角形BEC与三角形CFB全等。
因此,角BEC等于角CFB。
由于角AEF是三角形AEF的外角,根据外角定理,角AEF等于角BEC加角CFB。
因此:- ∠AEF=∠BEC+∠CFB- ∠AEF=2∠BEC(因为∠BEC=∠CFB)由于角AEF是三角形AEF的两个相等的角,所以三角形AEF是等腰三角形。
题目3:已知四边形ABCD中,AB平行于CD,BC平行于AD,且AB=CD。
证明:四边形ABCD是平行四边形。
答案:由于AB平行于CD且BC平行于AD,根据平行四边形的定义,我们可以推断出AD也平行于BC。
因此,四边形ABCD的对边都是平行的。
又因为AB=CD,根据平行四边形的判定条件,我们可以得出四边形ABCD是平行四边形。
题目4:已知三角形ABC中,角A等于角C,点D在BC上,且AD垂直于BC。
证明:三角形ABD与三角形CBD是等腰三角形。
答案:由于角A等于角C,根据三角形内角和定理,我们可以得出角A+角C+角B=180°。
圆几何证明题

圆几何证明题1、〔6分〕在三角形ABC 中,∠ACB=90°,AC=6,BC=8,以C 为圆心,以AC 为半径作圆C ,交AB 于点D ,求BD 的长2、〔6分〕等边三角形ABC 的边长为2,尺规作图,作三角形ABC 的外接圆O , 求圆O 的半径3、〔6分〕在圆O 中,点A 、B 、C 、D 在圆O 上,假设∠ADB=∠ADC=60°,判断三角形ABC 的形状4、〔7分〕如图,Rt △ABC 中,BC=9, AB=12.过点A 作AE ⊥AB ,且AE=16,连接BE 交AC 于点P .⑴求PA 的长; ⑵以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由;5、〔8分〕如图,⊙O 的直径34,30,4=︒=∠=BC ABC AB ,D 时线段BC 的中点,〔1〕试判断点D 与⊙O 的位置关系,并说明理由;〔2〕过点D 作AC DE ⊥,垂足为点E ,求证直线DE是⊙O 的切线。
6、〔7分〕如下图,AB 是⊙O 的弦,半径OC 、OD 分别交AB 于点E 、F ,且AE=BF ,请你找出线段OE 与OF 的数量关系,并给予证明.7、〔8分〕如图的两个圆是以O 为圆心的同心圆,大圆的弦AC OB D 21题图 第23题图DO B CA E FAB 是小圆的切线,C 为切点,且AB=10cm,求圆环的面积.8、〔9分〕如图,以等腰△ABC 的腰AB 为⊙O 的直径交底边BC 于D ,DE ⊥AC 于E 。
求证:〔1〕DB=DC〔2〕DE 为⊙O 的切线 9、如图,M 在△ABC 的AC 边上,且MB = MA = MC ,AB 是⊙O 的直径, 求证:BC 是⊙O 的切线10、:如图,在Rt △ABC 中,∠ABC = 90°,半圆O 切BC 于点B ,切AC 于点D ,交AB 于点E ,BC= BE =2,求AE 和AD 的长11、如图,两个同心圆,大圆的弦AB 与小圆相切于点P ,大圆的弦CD 经过点P ,且CD = 13,PD = 4,求两圆组成的圆环的面积12、如图,AB 是⊙O 的直径,BC 是弦,延长BC 到D ,使CD = BC ,CE 切⊙O 于点C ,交AD 于E ,求证:CE ⊥AD13、:如图,△ABC 接于⊙O ,∠BAC 的平分线交⊙O 于点D ,交⊙O 的切 线BF 于点F ,B 为切点,求证:〔1〕BD 平分∠CBF ;〔2〕AB · BF = AF · CD14、:如图,O 是线段AB 上一点,以OB 为半径的⊙O 交线段AB 于点C ,以线段AO 为直径的半圆交⊙O 于点D ,过点B 作AB 的垂线与AD 的延长线交于点E ,连结CD ,假设AC = 2,且AC 、AD 是关于* 的方程*2 -k*+4 =0 的两个根〔1〕证明:AE 切⊙O 于点D ;〔2〕求线段EB 的长;〔3〕求tan ∠ADC 的值AD BE CO15、如图80309,点A在⊙O外,射线AO与⊙O交于F,G两点,点H在⊙O上,弧FH=弧GH,点D是弧FH上一个动点〔不运动至F〕,BD是⊙O的直径,连结AB,交⊙O于点C,连结CD,交AO于点E,且OA=5,OF=1,设AC=*,AB=y。
第19章几何证明(基础、常考、易错、压轴)分类专项训练(原卷版)

第19章几何证明(基础、常考、易错、压轴)分类专项训练【基础】一、单选题1.(2022·上海·八年级专题练习)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在()V的三条中线的交点A.ABCV三边的垂直平分线的交点B.ABCV三条角平分线的交点C.ABCV三条高所在直线的交点D.ABC2.(2022·上海·八年级单元测试)三角形的外心是三角形的()A.三条中线的交点B.三条角平分线的交点C.三边垂直平分线的交点D.三条高所在直线的交点3.(2022·上海·八年级专题练习)下列命题中,真命题是()A.三角形的一个外角大于这个三角形的内角B.如果两个角的两边分别平行,那么这两个角相等C.一对邻补角的角平分线互相垂直D.面积相等的两个三角形全等4.(2022·上海·八年级专题练习)如图,将线段OA绕点O逆时针旋转45°,得到线段OB.若OA=8,则点A经过的路径长度为()A.4p B.3p C.2p D.p5.(2022·上海·同济大学附属七一中学八年级期中)下列语句不是命题的是()A.两条直线相交有且只有一个交点B.两点之间线段最短C.延长AB到D,使2BD AB=D.等角的补角相等6.(2022·上海浦东新·八年级期中)在下列各命题中,是假命题的是( )A.在一个三角形中,等边对等角B.全等三角形的对应边相等C.同旁内角相等,两直线平行D.等角的补角相等7.(2022·上海·八年级单元测试)如图,已知钓鱼竿AC的长为6m,露在水面上的鱼线BC长为,某钓者想看看鱼钩上的情况,把鱼竿AC转动到AC¢的位置,此时露在水面上的鱼线B C¢¢,则BB¢的长为()A B.C D.8.(2022·上海·八年级专题练习)下列命题中,其逆命题是真命题的命题个数()(1)全等三角形的对应角相等; (2) 对顶角相等; (3) 等角对等边;(4)两直线平行,同位角相等; (5)全等三角形的面积相等;A.1个B.2个C.3个D.4个9.(2022·上海·八年级单元测试)如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB于点R,PS⊥AC于点S,若PR=PS,则下列结论正确的个数是( )(1)PQ=PB;(2)AS=AR;(3)△BRP≌△PSC (4)∠C=∠SPCA.1个B.2个C.3个D.4个二、填空题10.(2022·上海·八年级专题练习)命题:“对顶角相等”的逆命题是_____________________________.11.(2022·上海市市西初级中学八年级期中)命题“等腰三角形的两个底角相等”的逆命题是_________.12.(2022·上海·八年级专题练习)请写出“两直线平行,同位角相等”的结论:_____.13.(2022·上海·八年级专题练习)平面内在角的内部(包括顶点)且到角的两边距离相等的点的轨迹是这个角的 _____.14.(2022·上海·八年级专题练习)命题“如果a b =,那么22a b =”的逆命题是_______,逆命题是______命题(填“真”或“假”)15.(2022·上海市南洋模范初级中学八年级期中)底边为已知线段BC 的等腰三角形ABC 的顶点A 的轨迹是_____.16.(2022·上海浦东新·八年级期中)“若0ab >,则0a >,0b >”_____命题(选填“是”或“不是”).17.(2022·上海·八年级专题练习)命题“等腰三角形两底角的平分线相等”的逆命题是________________.18.(2022·上海·八年级专题练习)把“同角的余角相等”改成“如果…,那么…”:_____________.19.(2022·上海·同济大学附属七一中学八年级期中)把命题“同角的余角相等”写成“如果……,那么……”的形式为______.20.(2022·上海·八年级专题练习)平面上经过A 、B 两点的圆的圆心的轨迹是_____.21.(2022·上海·八年级专题练习)命题“直角三角形的两个锐角互余”的逆命题为_____.22.(2022·上海·八年级专题练习)到点A 的距离等于6cm 的点的轨迹是________________.23.(2022·上海·八年级专题练习)“全等三角形的对应角相等”的逆命题是_______________________________.24.(2022·上海·八年级期末)已知两点A 、B ,到这两点距离相等的点的轨迹是____________.25.(2022·上海·八年级专题练习)如图,在Rt △ABC 中,∠C =90°,AD 平分∠CAB ,BC =12cm ,AC =9cm ,那么BD 的长是_____.26.(2022·上海·八年级单元测试)已知直角坐标平面内的两点分别为A (﹣3,1)、B (1,﹣2),那么A 、B 两点间的距离等于_____.27.(2022·上海·八年级专题练习)“,则=a b ”的逆命题为___________________.三、解答题28.(2022·上海·八年级单元测试)如图,在正方形ABCD中,点E、F分别在AD、CD边上,且AE DF=,联结BE、AF.求证:AF BE=.【常考】一.选择题(共5小题)1.(2020秋•闵行区期中)下列命题是真命题的是( )A.两个锐角的和还是锐角B.全等三角形的对应边相等C.同旁内角相等,两直线平行D.等腰三角形既是轴对称图形,又是中心对称图形2.(2019秋•虹口区校级月考)如图,BD,CE分别是△ABC的高线和角平分线,且相交于点O,若∠BCA =70°,则∠BOE的度数是( )A.60°B.55°C.50°D.40°3.(2022秋•杨浦区期中)若两条平行线被第三条直线所截,则下列说法错误的是( )A.一对同位角的平分线互相平行B.一对内错角的平分线互相平行C.一对同旁内角的平分线互相平行D.一对同旁内角的平分线互相垂直4.(2019秋•浦东新区校级月考)在Rt△ABC中,∠C=90°,有一点D同时满足以下三个条件:①在直角边BC上;②在∠CAB的角平分线上;③在斜边AB的垂直平分线上,那么∠B为( )A.15°B.30°C.45°D.60°5.(2022秋•徐汇区校级期中)在△ABC中,AB=4,AC=6,AD是BC边上的中线,则AD的取值范围是( )A.0<AD<10B.1<AD<5C.2<AD<10D.0<AD<5二.填空题(共11小题)6.(2021秋•奉贤区校级期中)将命题“同角的补角相等”改写成“如果…那么…”形式为 .7.(2022秋•闵行区校级期中)将一副三角板如图所示放置(其中含30°角的三角板的一条较短直角边与另一块三角板的斜边放置在一直线上),那么图中∠1= 度.8.(2021秋•静安区校级期末)命题“等腰三角形两底角的平分线相等”的逆命题是 .9.(2022秋•徐汇区校级期中)命题“同旁内角相等,两直线平行”是 (填“真“或“假”)命题10.(2022秋•闵行区校级期中)将命题“对顶角相等”改为“如果…那么…”的形式为: .11.(2022秋•虹口区校级期中)已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.其中正确的是 .(填写序号)12.(2021秋•徐汇区校级期末)如图,在△ABC中,∠ACB=90°,∠A=20°,CD与CE分别是斜边AB 上的高和中线,那么∠DCE= 度.13.(2022秋•徐汇区校级期中)如图,在△ABC和△DEF中,∠ACB=∠EFD=90°,点B、F、C、D在同一直线上,已知AB⊥DE,且AB=DE,AC=6,EF=8,DB=10,则CF的长度为 .14.(2020秋•徐汇区校级期中)“等腰三角形两腰上的中线相等.”的逆命题是 .15.(2022秋•徐汇区校级期中)在△ABC中,∠BAC=α,边AB的垂直平分线交边BC于点D,边AC的垂直平分线交边BC于点E,连接AD,AE,则∠DAE的度数为 .(用含α的代数式表示)16.(2022秋•虹口区校级期中)如图,已知:△ABC中,∠C=90°,AC=40,BD平分∠ABC交AC于D,AD:DC=5:3,则D点到AB的距离是 .三.解答题(共2小题)17.(2022秋•静安区校级期中)如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.(1)求证:△AMB≌△ENB;(2)若AM+BM+CM的值最小,则称点M为△ABC的费马点.若点M为△ABC的费马点,试求此时∠AMB、∠BMC、∠CMA的度数;(3)小翔受以上启发,得到一个作锐角三角形费马点的简便方法:如图②,分别以△ABC的AB、AC 为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费马点.试说明这种作法的依据.18.(2021秋•崇明区校级期末)如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M、N分别是边BD、AC的中点.(1)求证:MN⊥AC;(2)当AC=8cm,BD=10cm时,求MN的长.【易错】一.选择题(共4小题)1.(2022秋•黄浦区校级月考)下列命题中,是真命题的是( )A.从直线外一点向直线引垂线,这条垂线段就是这个点到这条直线的距离B.过一点,有且只有一条直线与已知直线平行C.两条直线被第三条直线所截,同旁内角互补D.两点之间,线段最短2.(2021秋•浦东新区期末)下列三个数为边长的三角形不是直角三角形的是( )A.3,3,3B.4,8,4C.6,8,10D.5,5,53.(2021秋•浦东新区期中)在下列各原命题中,逆命题是假命题的是( )A.两直线平行,同旁内角互补B.如果两个三角形全等,那么这两个三角形的对应边相等C.如果两个三角形全等,那么这两个三角形的对应角相等D.两个相等的角是对顶角4.(2019秋•浦东新区校级月考)BP和CP是△ABC两个外角的平分线,则∠BPC为( )A .B .90°+C .90°﹣D .∠A二.填空题(共2小题)5.(2020秋•浦东新区校级期末)以线段MN 为底边的等腰三角形的顶角顶点的轨迹是 .6.(2020秋•浦东新区校级月考)在△ABC 中,AB =13cm ,AC =15cm ,高AD =12cm ,则BC = .三.解答题(共1小题)7.(2019秋•浦东新区期末)如图(1),已知锐角△ABC 中,CD 、BE 分别是AB 、AC 边上的高,M 、N 分别是线段BC 、DE 的中点.(1)求证:MN ⊥DE .(2)连接DM ,ME ,猜想∠A 与∠DME 之间的关系,并证明猜想.(3)当∠A 变为钝角时,如图(2),上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.【压轴】一、单选题1.(2020·上海市曹杨第二中学附属学校八年级期中)如图,D 为BAC Ð的外角平分线上一点,过D 作DE AC ^于E ,DF AB ^交BA 的延长线于F ,且满足FDE BDC Ð=Ð,则下列结论:①CDE V ≌BDF V ;②CE AB AE =+;③BDC BAC Ð=Ð;④DAF CBD Ð=Ð.其中正确的结论有( ).A .1个B .2个C .3个D .4个二、填空题2.(2022·上海市民办文绮中学八年级阶段练习)在ABC V 中,12AB AC ==,30A Ð=°,点E 是AB 中点,点D 在AC 上,DE =ADE V 沿着DE 翻折,点A 的对应点是点F ,直线EF 与AC 交于点G ,那么DGF △的面积=__________.三、解答题3.(2022·上海·测试·编辑教研五八年级期末)梯形ABCD 中,AD BC ∥,90B Ð=°,4AB =,5BC =,点G 是CD 中点,过点G 作CD 的垂线交射线BC 于点F ,DCF Ð的角平分线交射线BA 于点E ,交直线GF 于点P .(1)当点F 与点B 重合时,求CD 的长;(2)若点F 在线段BC 上,AD x =,CF y =,求y 关于x 的函数关系式,并写出函数定义域;(3)联结DP、DE,当DPEV是以DP为腰的等腰三角形时,求AD的长.4.(2022·上海·八年级专题练习)已知△ABC和△ADE都是等腰直角三角形,其中∠ABC=∠ADE=90°,连接BD、EC,点M为EC的中点,连接BM、DM.(1)如图1,当点D、E分别在AC、AB上时,求证:△BMD为等腰直角三角形;(2)如图2,将图1中的△ADE绕点A逆时针旋转45°,使点D落在AB上,此时(1)中的结论“△BMD为等腰直角三角形”还成立吗?请对你的结论加以证明;(3)如图3,将图2中的△ADE绕点A逆时针旋转90°时,△BMD为等腰直角三角形的结论是否仍成立?若成立,请证明;若不成立,请说明理由.5.(2022·上海·八年级专题练习)如图,在直角坐标平面内,正比例函数y=的图像与一个反比例函数图像在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.(1)求反比例函数的解析式;(2)在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;(3)已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.6.(2022·上海松江·八年级期末)如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1,点D是边AC上一点(不与点A、C重合),EF垂直平分BD,分别交边AB、BC于点E、F,联结DE、DF.(1)如图1,当BD⊥AC时,求证:EF=AB;(2)如图2,设CD=x,CF=y,求y与x的函数解析式,并写出函数的定义域;(3)当BE=BF时,求线段CD的长.7.(2022·上海·八年级专题练习)已知:如图,在△ABC纸片中,AC=3,BC=4,AB=5,按图所示的方法将△ACD 沿AD 折叠,使点C 恰好落在边AB 上的点C ′处,点P 是射线AB 上的一个动点.(1)求折痕AD 长.(2)点P 在线段AB 上运动时,设AP =x ,DP =y .求y 关于x 的函数解析式,并写出此函数的定义域.(3)当△APD 是等腰三角形时,求AP 的长.8.(2021·上海·八年级专题练习)在直角梯形ABCD 中,//AB CD ,BC AB ^,AB AD =,联结BD ,如图(a ).点P 沿梯形的边,按照点A B C D A ®®®®移动,设点P 移动的距离为x ,BP y =.(1)当点P 从点A 移动到点C 时,y 与x 的函数关系如图(b )中折线MNQ 所示.则AB =______,BC =_____,CD =_____.(2)在(1)的情况下,点P 按照点A B C D A ®®®®移动(点P 与点A 不重合),BDP △是否能为等腰三角形?若能,请求出所有能使BDP △为等腰三角形的BP 的值;若不能,请说明理由.9.(2021·上海·八年级专题练习)如图,在四边形ABCD 中,∠ADC=∠ABC=90°,CB=CD ,点E 、F 分别在AB 、AD 上,AE=AF .连接CE 、CF .(1)求证:CE=CF ;(2)如果∠BAD=60°,CD=①当AF=x 时,设EFC S y D =,求y 与x 的函数关系式;(不需要写定义域)②当AF=2时,求△CEF 的边CE 上的高.10.(2020·上海市曹杨第二中学附属学校八年级期中)如图,在ABC V 中,2ACB B Ð=Ð,BAC Ð平分线AO 交BC 于点D ,点H 为AO 上一动点,过H 作直线l AO ^于H ,分别交直线AB 、AC 、BC 于点N 、E 、M .=;(1)当直线l经过点C时(如图2),求证:BN CD(2)当M是线段BC的中点时,写出线段CE和线段CD之间的数量关系,并证明;(3)请直接写出BN、CE和CD之间的数量关系.。
初中经典几何证明练习题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD ∴CD CO HG GO = ∴CD CO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG∴GN ∥AD ,GN=21AD∴∠DEN=∠GNM ∵AM=BM ,AG=CG∴GM ∥BC ,GM=21BC∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30°∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC∴DF BG FD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC 求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
几何证明练习题带答案

几何证明练习题带答案一、选择题1. 已知三角形ABC中,AB=AC,D是BC的中点,连接AD,若∠BAC=80°,则∠ADB的度数为______。
A. 80°B. 50°C. 60°D. 40°2. 在平行四边形ABCD中,E是AB的中点,F是CD的中点,连接EF,若AB=10,BC=6,则EF的长度为______。
A. 8B. 6C. 5D. 33. 已知在三角形ABC中,AB=AC,∠BAC=90°,若AB=6,则三角形ABC的面积为______。
A. 9B. 18C. 12D. 15二、填空题1. 在三角形ABC中,若∠A=60°,AB=AC,且BC=8,则三角形ABC的面积为______。
2. 已知在直角三角形ABC中,∠C=90°,AB=10,BC=8,则AC的长度为______。
三、证明题1. 证明:在等腰三角形ABC中,若AB=AC,点D在BC上,且BD=CD,则AD平分∠BAC。
2. 证明:若四边形ABCD为平行四边形,E是AB的中点,F是CD的中点,连接EF,则EF平分对角线AC。
四、解答题1. 在三角形ABC中,AB=AC,点D在BC上,且BD=CD,求证:三角形ABD与三角形ACD全等。
2. 在平行四边形ABCD中,E是AB的中点,F是CD的中点,连接EF,求证:EF是平行四边形ABCD的对角线AC的中位线。
答案:一、选择题1. C2. A3. A二、填空题1. 16√32. 6√3三、证明题1. 证明:在等腰三角形ABC中,AB=AC,根据等腰三角形的性质,我们知道∠ABD=∠ACD。
又因为BD=CD,根据SAS(边-角-边)相似准则,我们可以证明三角形ABD与三角形ACD全等。
由于全等三角形的对应角相等,因此AD平分∠BAC。
2. 证明:因为ABCD是平行四边形,所以AB∥CD。
根据平行线的性质,我们知道∠AEB=∠DFC。
初中经典几何证明练习题集(含答案解析)
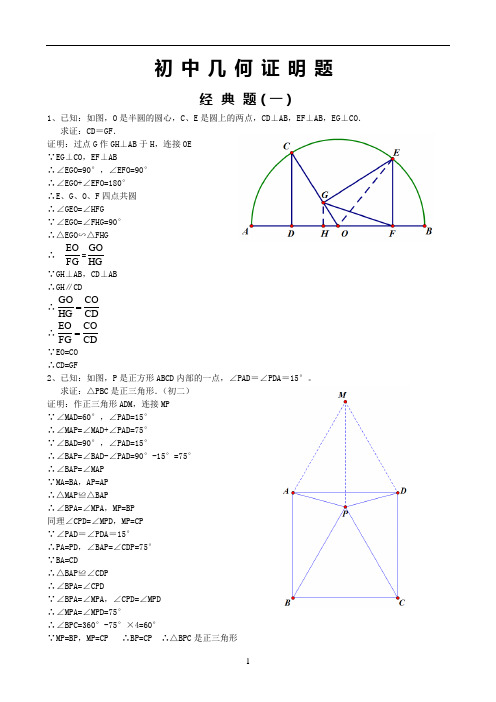
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
(完整)立体几何证明基础题

立体几何证明基础题一.解答题(共28小题)1.如图,在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点(1)求证:PB∥平面EFG;(2)求证:BC⊥EG.2.如图,在三棱锥P﹣ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.(1)求证DE∥PA(2)求证:DE∥平面PAC;(3)求证:AB⊥PB.3.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE且CE=AC=2BD,试在AE上确定一点M,使得DM∥平面ABC.4.如图:在四棱锥P﹣ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且PA=AB=2.(Ⅰ)证明:BC⊥平面AMN;(Ⅱ)求三棱锥N﹣AMC的体积;(Ⅲ)在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,求出PE的长;若不存在,说明理由.5.如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA上的动点.(1)求四棱锥P﹣ABCD的体积;(2)如果E是PA的中点,求证:PC∥平面BDE;(3)是否不论点E在侧棱PA的任何位置,都有BD⊥CE?证明你的结论.6.已知四棱锥A ﹣BCDE ,其中AB=BC=AC=BE=1,CD=2,CD ⊥面ABC,BE ∥CD,F 为AD 的中点. (Ⅰ)求证:EF ∥面ABC ; (Ⅱ)求证:平面ADE ⊥平面ACD ; (Ⅲ)求四棱锥A ﹣BCDE 的体积.7.如图,四棱柱ABCD ﹣A 1B 1C 1D 1中,平面A 1ABB 1⊥平面ABCD ,且∠ABC=.(1)求证:BC ∥平面AB 1C 1;(2)求证:平面A 1ABB 1⊥平面AB 1C 1.8.如图,三角形ABC中,AC=BC=,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.(Ⅰ)求证:GF∥底面ABC;(Ⅱ)求证:AC⊥平面EBC;(Ⅲ)求几何体ADEBC的体积V.9.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.(Ⅰ)证明:PA∥平面BMQ;(Ⅱ)已知PD=DC=AD=2,求点P到平面BMQ的距离.10.已知直三棱柱ABC ﹣A 1B 1C 1的底面△ABC 中,∠C=90°,BC=,BB 1=2,O 是AB 1的中点,D是AC 的中点,M 是CC 1的中点, (1)证明:OD ∥平面BB 1C 1C ; (2)试证:BM ⊥AB 1.11.如图,在四棱锥P ﹣ABCD 中,四边形ABCD 是平行四边形,E 、F 分别是AB 、PC 中点,求证:EF ∥面PAD .12.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 是AA 1的中点,求证: (Ⅰ)A 1C ∥平面BDE ; (Ⅱ)平面A 1AC ⊥平面BDE .13.如图,四棱锥P ﹣ABCD 中,底面ABCD 为矩形,E 为PD 的中点. (1)求证:PB ∥平面AEC ;(2)若PA ⊥平面ABCD ,PA=AD ,求证:平面AEC ⊥平面PCD .14.如图,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD ,E 是PC 的中点. 求证: (1)PA ∥平面BDE ; (2)BD ⊥平面PAC .15.如图,正四棱柱ABCD ﹣A 1B 1C 1D 1,底面边长AB=1,侧棱长AA 1=2. (Ⅰ)求正四棱柱ABCD ﹣A 1B 1C 1D 1的表面积; (Ⅱ)证明:AC ⊥平面BDD 1B 1.16.已知正方体ABCD ﹣A 1B 1C 1D 1,O 是底ABCD 对角线的交点.求证: (1)C 1O ∥面AB 1D 1; (2)A 1C ⊥面AB 1D 1.17.如图所示,在正方体ABCD ﹣A 1B 1C 1D 1中,M ,E,F,N 分别为A 1B 1,B 1C 1,C 1D 1,D 1A 1的中点,求证: (1)E ,F ,D ,B 四点共面; (2)面AMN ∥平面EFDB .18.如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 是DD 1的中点. 求证:(1)直线BD 1∥平面PAC(2)①求异面直线PC 与AA 1所成的角. ②平面PAC ⊥平面BDD 1.19.如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.(Ⅰ)求证:AB1⊥平面A1CE;(Ⅱ)求直线A1C1与平面A1CE所成角的正弦值.20.如图,在正方体ABCD﹣A1B1C1D1中,E、F、G分别是AB、AD、C1D1的中点.求证:平面D1EF∥平面BDG.21.(文科)如图,正方体ABCD﹣A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.22.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点,求证:(1)EN∥平面PDC;(2)BC⊥平面PEB;(3)平面PBC⊥平面ADMN.23.如图,在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点.(1)求证:DE∥平面PAC;(2)求证:AB⊥PC.24.如图所示,在四棱锥P﹣ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=.(1)求证:PD⊥平面ABCD;(2)求证:平面PAC⊥平面PBD.25.如图,在三棱柱ABC ﹣A 1B 1C 1中,侧棱AA 1⊥底面ABC ,AB ⊥BC,D 为AC 的中点,A 1A=AB=2. (1)求证:AB 1∥平面BC 1D ;(2)过点B 作BE ⊥AC 于点E,求证:直线BE ⊥平面AA 1C 1C (3)若四棱锥B ﹣AA 1C 1D 的体积为3,求BC 的长度.26.如图,已知四棱锥P ﹣ABCD 的底面ABCD 是菱形,PA ⊥平面ABCD ,点F 为PC 的中点. (1)求证:PA ∥平面BDF ; (2)求证:PC ⊥BD .27.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 是CC 1的中点. (1)求证:AC 1⊥BD . (2)求证:AC 1∥平面BDE .28.已知空间四边形ABCD (如图所示),E 、F 分别是AB 、AD 的中点,G 、H 分别是BC 、CD 上的(完整)立体几何证明基础题点,且CG=BC,CH=DC.求证:①E、F、G、H四点共面;②三直线FH、EG、AC共点.立体几何证明基础题参考答案与试题解析一.解答题(共28小题)1.如图,在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点(1)求证:PB∥平面EFG;(2)求证:BC⊥EG.【分析】(1)推导出GF∥PB,由此能证明PB∥平面EFG.(2)推导出EF⊥BC,GF⊥BC,从而BC⊥平面EFG,由此能证明BC⊥EG.【解答】证明:(1)∵点F,G分别为BC,PC,的中点,∴GF∥PB,∵PB⊄平面EFG,FG⊂平面EFG,∴PB∥平面EFG.(2)∵在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点,∴EF∥AC,GF∥PB,∴EF⊥BC,GF⊥BC,∵EF∩FG=F,∴BC⊥平面EFG,∵EG⊂平面EFG,∴BC⊥EG.【点评】本题考查线面平行、线线垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.2.如图,在三棱锥P﹣ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.(1)求证DE∥PA(2)求证:DE∥平面PAC;(3)求证:AB⊥PB.【分析】(1)由D,E分别是AB,PB的中点,能证明DE∥PA.(2)由PA⊂平面PAC,DE∥PA,且DE⊄平面PAC,能证明DE∥平面PAC.(3)推导出AB⊥PC,AB⊥BC,得AB⊥平面PBC,由此能证明AB⊥PB.【解答】证明:(1)因为D,E分别是AB,PB的中点,所以DE∥PA.(2)因为PA⊂平面PAC,DE∥PA,且DE⊄平面PAC,所以DE∥平面PAC.(3)因为PC⊥平面ABC,且AB⊂平面ABC,所以AB⊥PC.又因为AB⊥BC,且PC∩BC=C.所以AB⊥平面PBC.又因为PB⊂平面PBC,所以AB⊥PB.【点评】本题考查线线平行、线面平行、线线垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.3.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE且CE=AC=2BD,试在AE上确定一点M,使得DM∥平面ABC.【分析】AE中点为M,取AC中点为N,通过证明四边形MNBD是平行四边形得出DM∥BN,从而可得DM∥平面ABC.【解答】解:取AE中点为M,取AC中点为N,连结MD,MN,NB,在△ABC中,∵M,N分别是边AC,AE的中点,∴CE=2MN且MN∥CE,又∵CE=2BD且BD∥CE,∴MN∥BD且MN=BD,∴四边形BDMN是平行四边形.∴DM∥BN,又∵BN⊂平面ABC,DM⊄平面ABC,∴DM∥平面ABC.故M为AE的中点时,DM∥平面ABC.【点评】本题考查了线面平行的判定,属于基础题.4.如图:在四棱锥P﹣ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且PA=AB=2.(Ⅰ)证明:BC⊥平面AMN;(Ⅱ)求三棱锥N﹣AMC的体积;(Ⅲ)在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,求出PE的长;若不存在,说明理由.【分析】(I)要证线与面垂直,只要证明线与面上的两条相交线垂直,找面上的两条线,根据四边形是一个菱形,从菱形出发找到一条,再从PA⊥平面ABCD,得到结论.(II)要求三棱锥的体积,首先根据所给的体积确定用哪一个面做底面,会使得计算简单一些,选择三角形AMC,做出底面面积,利用体积公式得到结果.(III)对于这种是否存在的问题,首先要观察出结论,再进行证明,根据线面平行的判定定理,利用中位线确定线与线平行,得到结论.【解答】解:(Ⅰ)证明:∵ABCD为菱形,∴AB=BC又∠ABC=60°,∴AB=BC=AC,又M为BC中点,∴BC⊥AM而PA⊥平面ABCD,BC⊂平面ABCD,∴PA⊥BC 又PA∩AM=A,∴BC⊥平面AMN(II)∵又PA⊥底面ABCD,PA=2,∴AN=1•AN∴三棱锥N﹣AMC的体积S△AMC=(III)存在点E,取PD中点E,连接NE,EC,AE,∵N,E分别为PA,PD中点,∴又在菱形ABCD中,∴,即MCEN是平行四边形∴NM∥EC,又EC⊂平面ACE,NM⊄平面ACE∴MN∥平面ACE,即在PD上存在一点E,使得NM∥平面ACE,此时.【点评】本题考查空间中直线与平面之间的位置关系,是一个非常适合作为高考题目出现的问题,题目包含的知识点比较全面,重点突出,是一个好题.5.如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA上的动点.(1)求四棱锥P﹣ABCD的体积;(2)如果E是PA的中点,求证:PC∥平面BDE;(3)是否不论点E在侧棱PA的任何位置,都有BD⊥CE?证明你的结论.【分析】(1)利用四棱锥的体积计算公式即可;(2)利用三角形的中位线定理和线面平行的判定定理即可证明;(3)利用线面垂直的判定和性质即可证明.【解答】解:(1)∵PA⊥底面ABCD,∴PA为此四棱锥底面上的高.∴V==.四棱锥P﹣ABCD(2)连接AC交BD于O,连接OE.∵四边形ABCD是正方形,∴AO=OC,又∵AE=EP,∴OE∥PC.又∵PC⊄平面BDE,OE⊂平面BDE.∴PC∥平面BDE.(3)不论点E在侧棱PA的任何位置,都有BD⊥CE.证明:∵四边形ABCD是正方形,∴BD⊥AC.∵PA⊥底面ABCD,∴PA⊥BD.又∵PA∩AC=A,∴BD⊥平面PAC.∵CE⊂平面PAC.∴BD⊥CE.【点评】熟练掌握线面平行、垂直的判定和性质定理及四棱锥的体积计算公式是解题的关键.6.已知四棱锥A﹣BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.(Ⅰ)求证:EF∥面ABC;(Ⅱ)求证:平面ADE⊥平面ACD;(Ⅲ)求四棱锥A﹣BCDE的体积.【分析】(Ⅰ)取AC中点G,连接FG、BG,根据三角形中位线定理,得到四边形FGBE为平行四边形,进而得到EF∥BG,再结合线面平行的判定定理得到EF∥面ABC;(Ⅱ)根据已知中△ABC为等边三角形,G为AC的中点,DC⊥面ABC得到BG⊥AC,DC⊥BG,根据线面垂直的判定定理得到BG⊥面ADC,则EF⊥面ADC,再由面面垂直的判定定理,可得面ADE⊥面ACD;(Ⅲ)方法一:四棱锥四棱锥A﹣BCDE分为两个三棱锥E﹣ABC和E﹣ADC,分别求出三棱锥E﹣ABC和E﹣ADC的体积,即可得到四棱锥A﹣BCDE的体积.的高,求出底面面积和方法二:取BC的中点为O,连接AO,可证AO⊥平面BCDE,即AO为VA﹣BCDE高代入棱锥体积公式即可求出四棱锥A﹣BCDE的体积.【解答】证明:(Ⅰ)取AC中点G,连接FG、BG,∵F,G分别是AD,AC的中点∴FG∥CD,且FG=DC=1.∵BE∥CD∴FG与BE平行且相等∴EF∥BG.EF⊄面ABC,BG⊂面ABC∴EF∥面ABC…(4分)(Ⅱ)∵△ABC为等边三角形∴BG⊥AC又∵DC ⊥面ABC ,BG ⊂面ABC ∴DC ⊥BG ∴BG 垂直于面ADC 的两条相交直线AC,DC ,∴BG ⊥面ADC . …(6分) ∵EF ∥BG ∴EF ⊥面ADC∵EF ⊂面ADE ,∴面ADE ⊥面ADC . …(8分) 解:(Ⅲ)方法一:连接EC ,该四棱锥分为两个三棱锥E ﹣ABC 和E ﹣ADC ..…(12分)方法二:取BC 的中点为O ,连接AO,则AO ⊥BC ,又CD ⊥平面ABC , ∴CD ⊥AO ,BC ∩CD=C ,∴AO ⊥平面BCDE , ∴AO 为V A ﹣BCDE 的高,,∴.【点评】本题考查的知识点是直线与平面平行的判定,平面与平面垂直的判定,棱锥的体积,其中熟练掌握空间线面平行或垂直的判定、性质、定义、几何特征是解答此类问题的关键.7.如图,四棱柱ABCD ﹣A 1B 1C 1D 1中,平面A 1ABB 1⊥平面ABCD,且∠ABC=.(1)求证:BC ∥平面AB 1C 1;(2)求证:平面A 1ABB 1⊥平面AB 1C 1.【分析】(1)根据BC ∥B 1C 1,且B 1C 1⊂平面AB 1C 1,BC ⊄平面AB 1C 1,依据线面平行的判定定理推断出BC ∥平面AB 1C 1.(2)平面A 1ABB 1⊥平面ABCD ,平面ABCD ∥平面A 1B 1C 1D 1,推断出平面A 1ABB 1⊥平面A 1B 1C 1D 1,又平面A 1ABB 1∩平面A 1B 1C 1D 1=A 1B 1,A 1B 1⊥C 1B 1,C 1B 1⊂平面AB 1C 1,根据面面垂直的性质推断出平面A 1ABB 1⊥平面AB 1C 1.【解答】证明:(1)∵BC ∥B 1C 1,且B 1C 1⊂平面AB 1C 1,BC ⊄平面AB 1C 1, ∴BC ∥平面AB 1C 1.(2)∵平面A 1ABB 1⊥平面ABCD ,平面ABCD ∥平面A 1B 1C 1D 1, ∴平面A 1ABB 1⊥平面A 1B 1C 1D 1,∵平面A 1ABB 1∩平面A 1B 1C 1D 1=A 1B 1,A 1B 1⊥C 1B 1, ∴C 1B 1⊂平面AB 1C 1,∴平面A 1ABB 1⊥平面AB 1C 1.【点评】本题主要考查了线面平行和面面垂直的判定定理.注重了对基础知识的考查.8.如图,三角形ABC 中,AC=BC=,ABED 是边长为1的正方形,平面ABED ⊥底面ABC ,若G 、F 分别是EC 、BD 的中点. (Ⅰ)求证:GF ∥底面ABC ;(Ⅱ)求证:AC⊥平面EBC;(Ⅲ)求几何体ADEBC的体积V.【分析】(1)证法一:证明一条直线与一个平面平行,除了可以根据直线与平面平行的判定定理以外,通常还可以通过平面与平面平行进行转化,比如取BE的中点H,连接HF、GH,根据中位线定理易证得:平面HGF∥平面ABC,进一步可得:GF∥平面ABC.证法二:根据直线与平面平行的判定定理可知:如果不在一个平面内的一条直线和平面内的一条直线平行,那么直线和这个平面平行.故只需在平面ABC中找到与GF平行的直线即可.因为G、F分别是EC、BD的中点,故平移是可以通过构造特殊的四边形、三角形来实现.证法三:根据直线与平面平行的判定定理可知:如果不在一个平面内的一条直线和平面内的一条直线平行,那么直线和这个平面平行.故只需在平面ABC中找到与GF平行的直线即可.因为G、F分别是EC、BD的中点,所以构造中位线是常用的找到平行直线的方法.(2)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.有时候题目中没有现成的直线与直线垂直,需要我们先通过直线与平面垂直或者平面与平面垂直去转化一下.由第一问可知:GF∥平面ABC,而平面ABED⊥平面ABC,所以BE⊥平面ABC,所以BE⊥AC;又由勾股定理可以证明:AC⊥BC.(3)解决棱锥、棱柱求体积的问题,关键在于找到合适的高与对应的底面,切忌不审图形,盲目求解;根据平面与平面垂直的性质定理可知:CN⊥平面ABED,而ABED是边长为1的正方形,进一步即可以求得体积.【解答】解:(I)证法一:取BE的中点H,连接HF、GH,(如图)∵G、F分别是EC和BD的中点∴HG∥BC,HF∥DE,(2分)又∵ADEB为正方形∴DE∥AB,从而HF∥AB∴HF∥平面ABC,HG∥平面ABC,HF∩HG=H,∴平面HGF∥平面ABC∴GF∥平面ABC(5分)证法二:取BC的中点M,AB的中点N连接GM、FN、MN(如图)∵G、F分别是EC和BD的中点∴(2分)又∵ADEB为正方形∴BE∥AD,BE=AD∴GM∥NF且GM=NF∴MNFG为平行四边形∴GF∥MN,又MN⊂平面ABC,∴GF∥平面ABC(5分)证法三:连接AE,∵ADEB为正方形,∴AE∩BD=F,且F是AE中点,(2分)∴GF∥AC,又AC⊂平面ABC,∴GF∥平面ABC(5分)(Ⅱ)∵ADEB为正方形,∴EB⊥AB,∴GF∥平面ABC(5分)又∵平面ABED⊥平面ABC,∴BE⊥平面ABC(7分)∴BE⊥AC又∵CA2+CB2=AB2∴AC⊥BC,∵BC∩BE=B,∴AC⊥平面BCE(9分)(Ⅲ)连接CN,因为AC=BC,∴CN⊥AB,(10分)又平面ABED⊥平面ABC,CN⊂平面ABC,∴CN⊥平面ABED.(11分)∵三角形ABC是等腰直角三角形,∴,(12分)∵C﹣ABED是四棱锥,==(14分)∴VC﹣ABED【点评】本小题主要考查空间线面关系、面面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.9.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.(Ⅰ)证明:PA∥平面BMQ;(Ⅱ)已知PD=DC=AD=2,求点P到平面BMQ的距离.【分析】(1)连结AC交BQ于N,连结MN,只要证明MN∥PA,利用线面平行的判定定理可证;(2)由(1)可知,PA∥平面BMQ,所以点P到平面BMQ的距离等于点A到平面BMQ的距离.【解答】解:(1)连结AC交BQ于N,连结MN,因为∠ADC=90°,Q为AD的中点,所以N为AC的中点.…(2分)当M为PC的中点,即PM=MC时,MN为△PAC的中位线,故MN∥PA,又MN⊂平面BMQ,所以PA∥平面BMQ.…(5分)(2)由(1)可知,PA∥平面BMQ,所以点P到平面BMQ的距离等于点A到平面BMQ的距离,所以VP﹣BMQ =VA﹣BMQ=VM﹣ABQ,取CD的中点K,连结MK,所以MK∥PD,,…(7分)又PD⊥底面ABCD,所以MK⊥底面ABCD.又,PD=CD=2,所以AQ=1,BQ=2,,…(10分)所以VP﹣BMQ =VA﹣BMQ=VM﹣ABQ=.,…(11分)则点P到平面BMQ的距离d=…(12分)【点评】本题考查了线面平行的判定定理的运用以及利用三棱锥的体积求点到直线的距离.10.已知直三棱柱ABC ﹣A 1B 1C 1的底面△ABC 中,∠C=90°,BC=,BB 1=2,O 是AB 1的中点,D 是AC 的中点,M 是CC 1的中点, (1)证明:OD ∥平面BB 1C 1C ; (2)试证:BM ⊥AB 1.【分析】(1)连B 1C 利用中位线的性质推断出OD ∥B 1C ,进而根据线面平行的判定定理证明出OD ∥平面BB 1C 1C .(2)先利用线面垂直的性质判断出CC 1⊥AC ,进而根据线面垂直的判定定理证明出AC ⊥平面BB 1C 1C ,进而可知AC ⊥MB .利用证明△BCD ∽△B 1BC,推断出∠CBM=∠BB 1C ,推断出BM ⊥B 1C ,最后利用线面垂直的判定定理证明出BM ⊥平面AB 1C ,进而可知BM ⊥AB 1. 【解答】证明:(1)连B 1C ,∵O 为AB 1中点,D 为AC 中点, ∴OD ∥B 1C ,又B 1C ⊂平面BB 1C 1C,OD ⊄平面BB 1C 1C,∴OD ∥平面BB 1C 1C . (2)连接B 1C ,∵直三棱柱ABC ﹣A 1B 1C 1,∴CC 1⊥平面ABC AC ⊂平面ABC, ∴CC 1⊥AC,又AC ⊥BC ,CC 1,BC ⊂平面BB 1C 1C , ∴AC ⊥平面BB 1C 1C ,BM ⊂平面BB 1C 1C , ∴AC ⊥MB .在Rt △BCM 与Rt △B 1BC 中,==,∴△BMC ∽△B 1BC, ∴∠CBM=∠BB 1C,∴∠BB 1C+∠B 1BM=∠CBM+∠B 1BM=90°, ∴BM ⊥B 1C ,AC ,B 1C ⊂平面AB 1C , ∴BM ⊥AB 1C , ∵AB 1⊂平面AB 1C , ∴BM ⊥AB 1.【点评】本题主要考查了线面平行和线面垂直的判定定理的应用.证明线线平行和线线垂直是解题的关键.11.如图,在四棱锥P ﹣ABCD 中,四边形ABCD 是平行四边形,E 、F 分别是AB 、PC 中点,求证:EF ∥面PAD .【分析】取PD的中点G,连接FG、AG,由PF=CF,PG=DG,所以FG∥CD,且FG=CD.又因为四边形ABCD是平行四边形,且E是AB的中点.所以AE∥CD,且AE=CD.证得四边形EFGA是平行四边形,所以EF∥AG,由线面平行的判定定理即可得证.【解答】证明:取PD的中点G,连接FG、AG.因为PF=CF,PG=DG,所以FG∥CD,且FG=CD.又因为四边形ABCD是平行四边形,且E是AB的中点.所以AE∥CD,且AE=CD.所以FG∥AE,且FG=AE,所以四边形EFGA是平行四边形,所以EF∥AG.又因为EF⊄平面PAD,AG⊂平面PAD,所以EF∥平面PAD.【点评】本题考查直线与平面平行的证明,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.12.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 是AA 1的中点,求证: (Ⅰ)A 1C ∥平面BDE ; (Ⅱ)平面A 1AC ⊥平面BDE .【分析】(Ⅰ)连接AC 交BD 于O,连接EO ,△A 1AC 中利用中位线,得EO ∥A 1C .再结合线面平行的判定定理,可得A 1C ∥平面BDE;(II )根据正方体的侧棱垂直于底面,结合线面垂直的定义,得到AA 1⊥BD .再结合正方形的对角线互相垂直,得到AC ⊥BD ,从而得到BD ⊥平面A 1AC,最后利用面面垂直的判定定理,可以证出平面A 1AC ⊥平面BDE .【解答】证明:(Ⅰ)连接AC 交BD 于O ,连接EO , ∵E 为AA 1的中点,O 为AC 的中点 ∴EO 为△A 1AC 的中位线 ∴EO ∥A 1C又∵EO ⊂平面BDE ,A 1C ⊄平面BDE ∴A 1C ∥平面BDE ;…(6分)(Ⅱ)∵AA 1⊥平面ABCD,BD ⊂平面ABCD ∴AA 1⊥BD又∵四边形ABCD 是正方形 ∴AC ⊥BD ,∵AA1∩AC=A,AA1、AC⊂平面A1AC∴BD⊥平面A1AC又∵BD⊂平面BDE∴平面A1AC⊥平面BDE.…(12分)【点评】本题以正方体为例,要求我们证明线面平行和面面垂直,着重考查了空间直线与平面的位置关系和平面与平面位置关系等知识点,属于基础题.13.如图,四棱锥P﹣ABCD中,底面ABCD为矩形,E为PD的中点.(1)求证:PB∥平面AEC;(2)若PA⊥平面ABCD,PA=AD,求证:平面AEC⊥平面PCD.【分析】(1)连接BD交AC于O点,连接EO,只要证明EO∥PB,即可证明PB∥平面AEC;(2)要证平面PDC⊥平面AEC,需要证明CD⊥AE,AE⊥PD,即垂直平面AEC内的两条相交直线.【解答】证明:(1)连接BD交AC于O点,连接EO,∵O为BD中点,E为PD中点,∴EO∥PB,又EO⊂平面AEC,PB⊄平面AEC,∴PB∥平面AEC.(2)∵PA⊥平面ABCD,CD⊂平面ABCD,∴PA⊥CD,又AD⊥CD,且AD∩PA=A,∴CD⊥平面PAD,又AE⊂平面PAD,∴CD⊥AE.∵PA=AD,E为PD中点,∴AE⊥PD.又CD∩PD=D,∴AE⊥平面PDC,又AE⊂平面PAD,∴平面PDC⊥平面AEC.【点评】本题考查了线面平行,面面垂直的判定定理,属于基础题.14.如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:(1)PA∥平面BDE;(2)BD⊥平面PAC.【分析】(1)连接OE,根据三角形中位线定理,可得PA∥EO,进而根据线面平行的判定定理,得到PA∥平面BDE.(2)根据线面垂直的定义,可由PO⊥底面ABCD得到BD⊥PO,结合四边形ABCD是正方形及线面垂直的判定定理可得BD⊥平面PAC【解答】证明(1)连接OE,在△CAP中,CO=OA,CE=EP,∴PA∥EO,又∵PA⊄平面BDE,EO⊂平面BDE,∴PA∥平面BDE.(2)∵PO⊥底面ABCD,BD⊂平面ABCD,∴BD⊥PO又∵四边形ABCD是正方形,∴BD⊥AC∵AC∩PO=O,AC,PO⊂平面PAC∴BD⊥平面PAC【点评】本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,熟练掌握空间线面关系的判定定理是解答的关键.15.如图,正四棱柱ABCD ﹣A 1B 1C 1D 1,底面边长AB=1,侧棱长AA 1=2. (Ⅰ)求正四棱柱ABCD ﹣A 1B 1C 1D 1的表面积; (Ⅱ)证明:AC ⊥平面BDD 1B 1.【分析】(I)求出各面的面积即可得出表面积;(II )根据BB 1⊥平面ABCD 可得AC ⊥BB 1,根据正方形ABCD 的性质可得AC ⊥BD ,从而有AC ⊥平面BDD 1B 1.【解答】解:(I)正四棱柱的表面积为1×1×2+1×2×4=10. (II )连接AC,BD,B 1D 1,∵BB 1⊥平面ABCD ,AC ⊂平面ABCD , ∴AC ⊥BB 1,∵四边形ABCD 是正方形, ∴AC ⊥BD,又BD ⊂平面BDD 1B 1,BB 1⊂平面BDD 1B 1,BD ∩BB 1=B , ∴AC ⊥平面BDD 1B 1.【点评】本题考查了直棱柱的结构特征,线面垂直的判定,属于基础题.16.已知正方体ABCD ﹣A 1B 1C 1D 1,O 是底ABCD 对角线的交点.求证: (1)C 1O ∥面AB 1D 1; (2)A 1C ⊥面AB 1D 1.【分析】(1)欲证C 1O ∥面AB 1D 1,根据直线与平面平行的判定定理可知只需证C 1O 与面AB 1D 1内一直线平行,连接A 1C 1,设A 1C 1∩B 1D 1=O 1,连接AO 1,易得C 1O ∥AO 1,AO 1⊂面AB 1D 1,C 1O ⊄面AB 1D 1,满足定理所需条件;(2)欲证A 1C ⊥面AB 1D 1,根据直线与平面垂直的判定定理可知只需证A 1C 与面AB 1D 1内两相交直线垂直根据线面垂直的性质可知A 1C ⊥B 1D 1,同理可证A 1C ⊥AB 1,又D 1B 1∩AB 1=B 1,满足定理所需条件.【解答】证明:(1)连接A 1C 1,设A 1C 1∩B 1D 1=O 1,连接AO 1, ∵ABCD ﹣A 1B 1C 1D 1是正方体, ∴A 1ACC 1是平行四边形,∴A1C1∥AC且A1C1=AC,又O1,O分别是A1C1,AC的中点,∴O1C1∥AO且O1C1=AO,∴AOC1O1是平行四边形,∴C1O∥AO1,AO1⊂面AB1D1,C1O⊄面AB1D1,∴C1O∥面AB1D1;(2)∵CC1⊥面A1B1C1D1∴CC1⊥B1D!,又∵A1C1⊥B1D1,∴B1D1⊥面A1C1C,即A1C⊥B1D1,∵A1B⊥AB1,BC⊥AB1,又A1B∩BC=B,AB1⊥平面A1BC,又A1C⊂平面A1BC,∴A1C⊥AB1,又D1B1∩AB1=B1,∴A1C⊥面AB1D1【点评】本题主要考查了线面平行、线面垂直的判定定理,考查对基础知识的综合应用能力和基本定理的掌握能力.17.如图所示,在正方体ABCD﹣A1B1C1D1中,M,E,F,N分别为A1B1,B1C1,C1D1,D1A1的中点,求证:(1)E,F,D,B四点共面;(2)面AMN∥平面EFDB.【分析】(1)由E,E分别是B1C1,C1D1的中点,知EF∥B1D1,从而得到EF∥BD,由此能证明E,F,B,D,四点共面.(2)由题设条件推导出MN∥EF,AN∥CF,由此能够证明面MAN∥面EFDB.【解答】证明:(1)∵E,E分别是B1C1,C1D1的中点,∴EF∥B1D1 ,∵B1D1∥BD,∴EF∥BD,∴E,F,B,D,四点共面.(2)∵M,N分别是A1B1,D1A1的中点,∴MN∥B1D1,∵EF∥B1D1,∴MN∥EF,∵F,N分别是D1C1、A1B1的中点,∴NF A1D1,∵,∴NF AC,∴四边形NFCA是平行四边形,∴AN∥CF,∵MN∩AN=N,EF∩DF=F,∴面MAN∥面EFDB.【点评】本题考查四点共面的证明,考查两个平面平行的证明.解题时要认真审题,注意中位线定理和平行公理的合理运用.18.如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 是DD 1的中点. 求证:(1)直线BD 1∥平面PAC(2)①求异面直线PC 与AA 1所成的角. ②平面PAC ⊥平面BDD 1.【分析】(1)连接BD ,交AC 于O,连接PO ,由三角形的中位线定理和线面平行的判定定理,即可得证;(2)①连接PC 1,AA 1∥CC 1,∠C 1CP 即为异面直线PC 与AA 1所成的角,分别求出△C 1CP 的三边,由解三角形即可得到所求角;②运用正方形的对角线垂直和线面垂直的性质定理,可得AC ⊥平面BDD 1B 1,再由面面垂直的判定定理,即可得证.【解答】(1)证明:连接BD ,交AC 于O ,连接PO , 在△BDD1中,OP 为中位线,可得OP∥BD1,又OP⊂平面PAC,BD1⊄平面PAC,则直线BD1∥平面PAC;(2)①连接PC1,AA1∥CC1,∠C1CP即为异面直线PC与AA1所成的角,在△C1CP中,C1C=2,PC===,PC1===,由PC2+PC12=CC12,可得△C1CP为等腰直角三角形,则异面直线PC与AA1所成的角为45°;②证明:在底面ABCD中,AB=AD,即有四边形ABCD为正方形,可得AC⊥BD,D1D⊥平面ABCD,AC⊂平面ABCD,即有D1D⊥AC,D1D∩BD=D,可得AC⊥平面BDD1B1,AC⊂平面PAC,则平面PAC⊥平面BDD1.【点评】本题考查线面平行的判定,注意运用中位线定理和线面平行的判定定理,考查异面直线所成角的求法,注意运用平移法,考查面面垂直的判定,注意运用线面垂直的判定和性质,考查空间想象能力和推理能力,属于基础题.19.如图,在直三棱柱ABC ﹣A 1B 1C 1中,∠ACB=90°,AC=CB=CC 1=2,E 是AB 中点. (Ⅰ)求证:AB 1⊥平面A 1CE ;(Ⅱ)求直线A 1C 1与平面A 1CE 所成角的正弦值.【分析】(Ⅰ)由ABC ﹣A 1B 1C 1是直三棱柱,可知CC 1⊥AC ,CC 1⊥BC ,∠ACB=90°,AC⊥BC .建立空间直角坐标系C ﹣xyz .则A ,B 1,E ,A 1,可得,,,可知,根据,,推断出AB 1⊥CE ,AB 1⊥CA 1,根据线面垂直的判定定理可知AB 1⊥平面A 1CE . (Ⅱ)由(Ⅰ)知是平面A 1CE 的法向量,,进而利用向量数量积求得直线A 1C 1与平面A 1CE 所成角的正弦值【解答】(Ⅰ)证明:∵ABC ﹣A 1B 1C 1是直三棱柱, ∴CC 1⊥AC,CC 1⊥BC, 又∠ACB=90°, 即AC ⊥BC .如图所示,建立空间直角坐标系C ﹣xyz .A (2,0,0),B 1(0,2,2),E(1,1,0),A 1(2,0,2), ∴,,.又因为 ,,∴AB 1⊥CE ,AB 1⊥CA 1,AB 1⊥平面A 1CE . (Ⅱ)解:由(Ⅰ)知,是平面A 1CE 的法向量,,∴|cos <,>|==.设直线A 1C 1与平面A 1CE 所成的角为θ,则sinθ=|cos <,>|=.所以直线A 1C 1与平面A 1CE 所成角的正弦值为.【点评】本题主要考查了线面垂直的判定定理,向量的数量积的运用,法向量的运用.综合考查了学生所学知识的灵活运用.20.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 、F 、G 分别是AB 、AD 、C 1D 1的中点.求证:平面D 1EF ∥平面BDG .【分析】欲证平面D 1EF ∥平面BDG,根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行,EF ∥BD 又EF ⊄平面BDG ,BD ⊂平面BDG 根据线面平行的性质可知EF ∥平面BDG ,同理可证D 1E ∥平面BDG ,EF ∩D 1E=E ,满足定理条件. 【解答】证明:∵E 、F 分别是AB 、AD 的中点,∴EF ∥BD 又EF ⊄平面BDG ,BD ⊂平面BDG ∴EF ∥平面BDG ∵D 1G EB ∴四边形D 1GBE 为平行四边形,D 1E ∥GB 又D 1E ⊄平面BDG,GB ⊂平面BDG∴D 1E ∥平面BDG,EF ∩D 1E=E , ∴平面D 1EF ∥平面BDG【点评】本小题主要考查空间中的线面关系,考查线面平行的判定,考查识图能力和逻辑思维能力与推理论证能力,考查转化思想,属于基础题.21.(文科)如图,正方体ABCD ﹣A 1B 1C 1D 1中,M ,N,E ,F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点, 求证:平面AMN ∥平面EFDB .【分析】连接B 1D 1,NE ,分别在△A 1B 1D 1中和△B 1C 1D 1中利用中位线定理,得到MN ∥B 1D 1,EF ∥B 1D 1,从而MN ∥EF,然后用直线与平面平行的判定定理得到MN ∥面BDEF .接下来利用正方形的性质和平行线的传递性,得到四边形ABEN 是平行四边形,得到AN ∥BE ,直线与平面平行的判定定理得到AN ∥面BDEF,最后可用平面与平面平行的判定定理,得到平面AMN ∥平面EFDB ,问题得到解决.【解答】证明:如图所示,连接B 1D 1,NE∵M,N ,E ,F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点 ∴MN ∥B 1D 1,EF ∥B 1D 1 ∴MN ∥EF又∵MN ⊄面BDEF ,EF ⊂面BDEF ∴MN ∥面BDEF∵在正方形A 1B 1C 1D 1中,M ,E ,分别是棱 A 1B 1,B 1C 1的中点∴NE∥A1B1且NE=A1B1又∵A1B1∥AB且A1B1=AB∴NE∥AB且NE=AB∴四边形ABEN是平行四边形∴AN∥BE又∵AN⊄面BDEF,BE⊂面BDEF∴AN∥面BDEF∵AN⊂面AMN,MN⊂面AMN,且AN∩MN=N∴平面AMN∥平面EFDB【点评】本题借助于正方体模型中的一个面面平行位置关系的证明,着重考查了三角形的中位线定理、线面平行的判定定理和面面平行的判定定理等知识点,属于基础题.22.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点,求证:(1)EN∥平面PDC;(2)BC⊥平面PEB;(3)平面PBC⊥平面ADMN.【分析】(1)先证明AD∥MN由N是PB的中点,E为AD的中点,底面ABCD是边长为2的菱形得EN∥DM,DM⊂平面PDC,可得EN∥平面PDC;(2)由侧面PAD是正三角形,且与底面ABCD垂直,E为AD的中点,得PE⊥AD,PE⊥EB,PE⊥BC,由∠BAD=60°,AB=2,AE=1,由余弦定理可得BE=,由正弦定理可得:BE⊥AD,有由AD∥BC可得BE⊥BC,可得BC⊥平面PEB;(3)由(2)知BC⊥平面PEB,EN⊂平面PEB可得PB⊥MN,由AP=AB=2,N是PB的中点,得PB ⊥AN,有MN∩AN=N.PB⊥平面ADMN,可证平面PBC⊥平面ADMN.【解答】解:(1)∵AD∥BC,AD⊂平面ADMN,BC⊄平面ADMN,∴BC∥平面ADMN,∵MN=平面ADMN∩平面PBC,BC⊂平面PBC,∴BC∥MN.又∵AD∥BC,∴AD∥MN.∴ED∥MN∵N是PB的中点,E为AD的中点,底面ABCD是边长为2的菱形,∴ED=MN=1∴四边形ADMN是平行四边形.∴EN∥DM,DM⊂平面PDC,∴EN∥平面PDC;(2)∵侧面PAD是正三角形,且与底面ABCD垂直,E为AD的中点,∴PE⊥AD,PE⊥EB,PE⊥BC∵∠BAD=60°,AB=2,AE=1,由余弦定理可得BE=,由正弦定理可得:BE⊥AD∴由AD∥BC可得BE⊥BC,∵BE∩PE=E∴BC⊥平面PEB;(3)∵由(2)知BC⊥平面PEB,EN⊂平面PEB∴BC⊥EN∵PB⊥BC,PB⊥AD∴PB⊥MN∵AP=AB=2,N是PB的中点,∴PB⊥AN,∴MN∩AN=N.PB⊥平面ADMN,∵PB⊂平面PBC∴平面PBC⊥平面ADMN.【点评】本题主要考察了平面与平面垂直的判定,直线与平面平行的判定,直线与平面垂直的判定,属于基本知识的考查.23.如图,在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点.(1)求证:DE∥平面PAC;(2)求证:AB⊥PC.【分析】(1)推导出DE∥AC,由此能证明DE∥平面PAC.(2)连结PD,CD,则PD⊥AB,CD⊥AB,从而AB⊥平面PDC,由此能证明AB⊥PC.【解答】证明:(1)∵在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点.∴DE∥AC,∵DE⊄平面PAC,AC⊂平面PAC,∴DE∥平面PAC.(2)连结PD,CD,∵正三棱锥P﹣ABC中,D是AB的中点,∴PD⊥AB,CD⊥AB,∵PD∩CD=D,∴AB⊥平面PDC,∵PC⊂平面PDC,∴AB⊥PC.【点评】本题考查线面平行的证明,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.24.如图所示,在四棱锥P﹣ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=.(1)求证:PD⊥平面ABCD;(2)求证:平面PAC⊥平面PBD.【分析】(1)由勾股定理逆定理可证明AD⊥PD,PD⊥CD即可得出PD⊥平面ABCD;(2)由(1)可得PD⊥AC,结合AC⊥BD,得出AC⊥平面PBD,从而平面PAC⊥平面PBD.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明练习题
1、如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请完整说明为何△ABC与△DEC全等的理由.
2、如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.
3、如图,在三角形ABC中,角ACB=90度,AC=BC,E为AC边的中点,过点A作AD 垂直AB交BE的延长线于点D
如图,在△ABC中,∠ACB=90度,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE 的延长线于点D,CG平分角ACB交BD于点G,F为AB边上的一点,连接CF,且∠ACF=∠CBG,求证:(1)AF=CG (2)CF=2DE
4、在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,过点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A 重合),如图1,DE与AC交于点P,易证:BD=DP.(无需写证明过程)
(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由;
(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.
5、如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE与G点,交DF与F点,CE交DF于H点、交BE于E点.
求证:△EBC≌△FDA.
6、在平行四边形ABCD中,将△ABC沿AC对折,
使点B落在B′处,A B′和CD相交于点O.
求证:OA=OC.
7、如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.(1)求证:BE=DF;
(2)求证:AF∥CE.
8、如图,▱ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
9、如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE平行AB,EF
平行AC
(1)求证:BE=AF
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积。
