新北师大版九年级数学下册第一章《锐角三角函数2》公开课课件
合集下载
初中数学锐角三角函数公开课ppt课件

探究活动一
思考:梯子在上升变“陡”的 过程中,哪些量发生了变化?
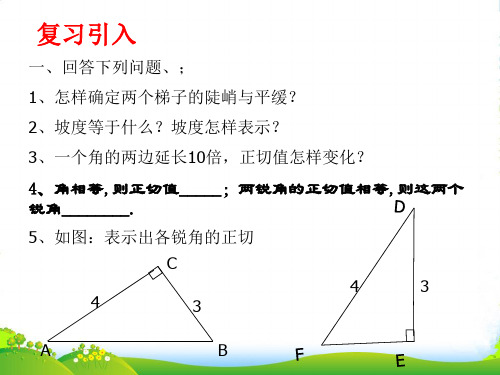
铅 直 高 度
B
倾斜角
A 水平宽度 C
探究活动一
如图,比较梯子AB和EF哪个更陡?
图1
探究活动一
如图,比较梯子AB和EF哪个更陡?
5m
1
2m
图2
3
M
2
2 .5m
5m
探究活动一
如图,比较梯子AB和EF哪个更陡?
6m
3m
图3
2.5 m
A
100米
C
即坡度等于坡角的正切
第四关:拓展创新
1.如下图,某人从山脚下的点A处走了200米爬 到了山顶的点B处,已知点B到山脚的垂直距离为 100米,该山的坡度为
3 3
.
200m
100m
100
3
第四关:拓展创新
2.某一建筑物的楼顶是“人”字型,并铺上红瓦装饰。现知 道楼顶的坡度超过0.5时,瓦片会滑落下来. 请你根据图中数据说明这一楼顶铺设的瓦片是否会滑落下来?
13m 13 24m B 12
A 5
┌
13
C
D 24
求锐角三角函数时,构造直角三角形是 很重要的.
第五关:挑战自我
直角三角形纸片的两直角边长分别为6,8,现
将△ABC如图那样折叠,使点A与点B重合,折
痕为DE,则tan∠CBE的值是多少?
C
C 6 B
8
A B
6
E
8
A
D
复习回顾
两边之和大于第三边,两边之差小于第三边
C
邻边
A
∠A=45°
……
B
BC 2 1 AC 2
北师大版九年级数学下册第1章第2节特殊角的三角函数值(共24张PPT)课件

特殊角三角函数值
一.复习巩固: 1.正弦、余弦、正切、的定义 在△ABC中,∠C为直角. A
sin A=
∠A的对边 斜边
=
a c
cos A=
∠A的邻边 斜边
=
b c
∠A的对边 tanA= ∠A的邻边
=
a
b
B
c
a
对 边
┓
b
邻边 C
0<sinA<1
0<cosA<1
tan A>0
2.Rt△ABC中,∠C=90°, a:b=5:12,
B
k
2k
C
45° A k
3.特殊角三角函数值表
三α角函数 sinα
cosα
tanα
30° 45°
1
2
2
2
3
2
2
2
3
1
3
60°
3 2
1 2
3
求下列各式的值:
(1) 2sin30°-cos45°= 2 1 -
2
2 2
=
2 2 2
(2) sin60°tan30°= 3 3 = 1 23 2
(3) sin230°+ cos230°= (1)2 ( 2
板,进行观察与推算sin30°,sin45°,sin60°,
cos30°,cos45° ,cos60°的值.
B
B
k 60° 2k
C
30°
3k
sin 30 1
2
cos 30 3 2
k
2k
A C k 45° A
sin 45 2 sin 60 3
2
2
cos 45 2 cos 60 1
一.复习巩固: 1.正弦、余弦、正切、的定义 在△ABC中,∠C为直角. A
sin A=
∠A的对边 斜边
=
a c
cos A=
∠A的邻边 斜边
=
b c
∠A的对边 tanA= ∠A的邻边
=
a
b
B
c
a
对 边
┓
b
邻边 C
0<sinA<1
0<cosA<1
tan A>0
2.Rt△ABC中,∠C=90°, a:b=5:12,
B
k
2k
C
45° A k
3.特殊角三角函数值表
三α角函数 sinα
cosα
tanα
30° 45°
1
2
2
2
3
2
2
2
3
1
3
60°
3 2
1 2
3
求下列各式的值:
(1) 2sin30°-cos45°= 2 1 -
2
2 2
=
2 2 2
(2) sin60°tan30°= 3 3 = 1 23 2
(3) sin230°+ cos230°= (1)2 ( 2
板,进行观察与推算sin30°,sin45°,sin60°,
cos30°,cos45° ,cos60°的值.
B
B
k 60° 2k
C
30°
3k
sin 30 1
2
cos 30 3 2
k
2k
A C k 45° A
sin 45 2 sin 60 3
2
2
cos 45 2 cos 60 1
北师大版九年级数学下册第一章《 锐角三角函数》课件
行家看“门道”
w例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
w求:BC的长.
C
w解:在Rt△ABC中,
sin ABC BC 0.6,
200
AC200
B C 20 0 .6 0 1.20
┌
A
B
w2.在Rt△ABC中,∠C=90°,
w(1)AC=3,AB=6,求sinA和cosB
求sin∠ACD,cos∠ACD和tan∠ACD.
4.在Rt△ABC中,∠C=90°,sinA和cosB 有什么关系?
驶向胜利 的彼岸
有古
一人
个云
在:
路“
上读
。万
”卷
从书
古,
至行
今万
,里
学路
习。
和”
旅今
行人
都说
是:
相“
辅要
相么
You made my day!
成读 的书
两,
件要
事么
。旅
。行
,
身
体
和
灵
请思考:在Rt△ABC中, sinA和cosB有什么关系?
独立
P9习题1.2 1,2,3,4题 作业
1. 如图,分别求∠α,∠β的正弦,余弦,和正切.
α
36
9
2.在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.5 求:CD,sinC.
┐
xβ
3.在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5.
魂
总
要
我们,还在路上……
(2)BC=3,sinA=
5 13
,求AC和AB.
北师大版九年级数学下册第一章1锐角三角函数第2课课件

3. 已知角A为梯子与地面所成的角,sin A的值越 大 ,梯子越 陡;cos A的值越 小 ,梯子越陡.
1. 如图,在Rt△ABC 中,∠C=90°,AC=3,BC=4,则sin A的值为( D ) 2. 如图,在平面直角坐标系中,点A的坐标为(4,3), 那么cos已知点A(2,1)和点B(3,0),则sin ∠AOB的 值为( A )
4. 如图,在下面的网格中,小正方形的边长均为1,点A,B,O都在格点上, 则∠AOB 的正弦值和余弦值分别是( D )
B 5
③若∠A为锐角,化简式子:
第一章 直角三角形的边角关系
1. 锐角三角函数 第2课时
1. 如 图 , 在 Rt△ABC 中 , ∠ C = 90° , ∠ A 的 对边 与
斜边 的比叫做∠A的正弦,记作 sin A ,即sin A=
;∠A的
邻边 与 斜边 的比叫做∠A的余弦,记作 cos A,即cos A=
.
2. 锐角A的 正弦 、 余弦 和 正切 都是∠A 的三角函数.
5. 如图,在Rt△ABC 中,∠C =90°,AB =10,BC =6,求sin A,cos A,tan A的值.
【基础训练】 1. 在△ABC 中,∠C=90°,3BC=4AC,则下列结论正确的是( C )
2. 在△ABC 中,∠C =90°,AB=15,sin A=13,则BC 等于( B )
北师大版九年级数学下册《直角三角形的边角关系——锐角三角函数》教学PPT课件(4篇)

同理, cos
A=
AC ,cos AB
A1
=
A1C A1 B1
.
B1 B
∵AB=A1B1,
AC AB
>
A1C ,即cos A1 B1
A > cos
A1,
A A1
C
∴梯子的倾斜程度与cos A也有关系, cos A的值越 小,梯子越陡.
如图:在Rt △ABC中,∠C=90°,
sin
A
A的对边 斜边
B1 B2 B3
A
C3 C2
C1
Rt△AB1C1∽Rt△AB2C2
新课学习
直角三角形的边与角的关系:
(2)BA1CC11
和B2C2
AC2
有什么关系?
B1
B2 B3
A
C3 C2
C1
B1C1 = B2C2 AC1 AC2
新课学习
直角三角形的边与角的关系: (3)如果改变B2在梯子上的位置(如B3)呢?
B2
斜边的比值、邻边与斜边的比值将怎
样变化?
C1 C2
A1
这是一个变化的过程.对边与斜边的比值、邻边与
斜边的比值都随着倾斜角的改变而改变.同时,如果给
定一个倾斜角的值,它的对边与斜边的比值、邻边与
斜边的比值是唯一确定的.
讲授新课
斜边
B ∠A的对边
A
C
∠A的邻边
定义:在Rt△ABC中,如果锐角A确定,那
∴ B1C1∥ B2C2,
C1 C2
A1
∴Rt△B1A1C1 ∽ Rt△B2A1C2.
讲授新课
想一想:如图.
(2)BA11CA11 和
A1C2 B2 A1
北师大版 九下第一章直角三角形的边角关系 锐角三角函数(正弦)优质课件

5
A
E
B
D
C
与斜边的比值是定值
2.探究问题:
(3)在Rt△ABC中,∠C=90°,
∠A=40°,则 ∠A的对边
B
斜边
=?
C
40° A
结论:直角三角形中,40°角的对边 与斜边的比值是定值
在Rt△ABC中, ∠ C=90°,∠A的 值确定后,∠A的对边与斜边的比值 是一个定值吗? 规律一: 当∠A的大小相等时,比值也相等
(4)SinB=0.8 (√ )
2)如图,sinA=
BC( ×)
AB
练一练
4.如图 A 300
B 3 C
7
则 sinA=___12___ .
5.△ABC中,AB=8,BC=6,△ABC 的面积是12,求sinB的值.
【变一变】
已知△ABC中, AB=8,BC=6,sinA
=
5
A
试求△ABC的面积. 6
C
A
sin A = = ,
AB 13
AC AB2 BC2 132 - 52 12,
sin B AC 12 . AB 13
练一练
2、在Rt△ABC中, ∠C=90°, 求sinA和sinB的值。
B
3
A4
C
3∠、C填=9空0°已,知s:in如A=图,23,在△ABC中,
(1)BC=2,则AB= 3 ;
规律二: 当∠A的大小变化时,比值也变化
2、在Rt△ABC中,∠C=90°,我们把
锐角A的对边与斜边的比叫做∠A的正弦 ,
记作 sinA 。
在Rt△ABC中,∠C=90°
sinA=
∠A的对边 斜边
B
a =c
《 锐角三角函数》 (第1课时)示范公开课教学PPT课件【北师大版九年级数学下册】

注意:坡度是坡角的正切.坡度越大,坡面越陡.
典例精析
《自动扶梯》
典例精析
例 下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
4m α
8m (甲)
13 m 5m
β
(乙)
解:甲梯中,tanα= 4 1 . 82
乙梯中,tanβ= 5 5 .
132 52 12
因为tanα>tanβ,所以甲梯更陡.
议一议 在下图中,梯子的倾斜程度与tan A有关系吗?
答:tan A的值越大,梯子越陡.
探究新知
正切也经常用来描述山坡的坡度(坡面的铅直高度与 水平宽度的比称为坡度(或坡比)).
60 m
例如,有一山坡在水平方向上
每前进100 m就升高60 m
α
那么山坡的坡度就是tan α= 60 3
100 m
100 5
探究新知
如图,在Rt△ABC中,如果锐角A确定,那么∠A的 对边与邻边的比便随之确定,这个比叫做∠A的正切 (tangent),记作tan A,即tan A= ∠A的对边.
∠A的邻边
B
∠A的对边
A ∠A的邻边 C 说明:tanA是一个完整的符号,它表示∠A的正切, 记号里习惯省去角的符号“∠”.
探究新知
北师大版·统编教材九年级数学下册
第一章 直角三角形的边角关系
1.1 锐角三角函数 第 1 课时
学习目标
1.经历探索直角三角形中边角关系的过程. 2.理解锐角三角函数(正切)的意义,并能够举例说明. 3.能够运用tan A表示直角三角形中两边的比. 4.能够根据直角三角形中边角关系,进行简单的计算.
解:在Rt△ABC中, AC= AB2 BC2 2002 552 5 1479 (m). 所以tan A= BC 55 ≈0.286
(北师大版)数学九年级下册:三角函数的计算课件

如图,在Rt△ABC中,∠C=90°,BC=ABsin160 .
你知道sin160等于多少吗? 我们可以借助科学计算器求锐角的三 角函数值.
怎样用科学计算器求锐角的三角函数值呢? 请与同伴交流你是怎么做的?
做一做P16 3
知识在于积累
驶向胜利 的彼岸
用科学计算器求锐角的三角函数值,要用到三个键:
例如,求sin160,cos420, tan850和 sin cos tan sin720 38′25″的按键盘顺序如下:
老师期望: 你能独立获得成功.
小结 拓展
回味无穷
由锐角的三角函数值反求锐角
驶向胜利 的彼岸
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
sin A 1 2
∠A= 300 sin A 3
2
∠A=
600 sin A 2
2
∠A= 450
cos A 1 2
∠A= 600 cos A
想一想P19 1
数学源于生活的需求
如图,为了方便行人,市政府在10m 高的天桥.两端修建了40m长的斜道. 这条斜道的倾斜角是多少? 如图,在Rt△ABC中,
sin A BC 10 1 . AC 40 4
那么∠A是多 少度呢? 要解决这问题,我们可以借助科学计算器.
请与同伴交流你是怎么做的?
怎 么解?
老师提示:上表的显示结果是以度为 单位的,再按 dms 键即可显示以 “度,分,秒”为单位的结果.
例题欣赏P240
洞察力与内秀
驶向胜利 的彼岸
例1 如图,工件上有一V型槽,测得它的上口宽20mm,深19. 2mm.求V型角(∠ACB)的大小(结果精确到10 ).
解 : tan ACD AD 10 0.5208, CD 19.2
你知道sin160等于多少吗? 我们可以借助科学计算器求锐角的三 角函数值.
怎样用科学计算器求锐角的三角函数值呢? 请与同伴交流你是怎么做的?
做一做P16 3
知识在于积累
驶向胜利 的彼岸
用科学计算器求锐角的三角函数值,要用到三个键:
例如,求sin160,cos420, tan850和 sin cos tan sin720 38′25″的按键盘顺序如下:
老师期望: 你能独立获得成功.
小结 拓展
回味无穷
由锐角的三角函数值反求锐角
驶向胜利 的彼岸
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
sin A 1 2
∠A= 300 sin A 3
2
∠A=
600 sin A 2
2
∠A= 450
cos A 1 2
∠A= 600 cos A
想一想P19 1
数学源于生活的需求
如图,为了方便行人,市政府在10m 高的天桥.两端修建了40m长的斜道. 这条斜道的倾斜角是多少? 如图,在Rt△ABC中,
sin A BC 10 1 . AC 40 4
那么∠A是多 少度呢? 要解决这问题,我们可以借助科学计算器.
请与同伴交流你是怎么做的?
怎 么解?
老师提示:上表的显示结果是以度为 单位的,再按 dms 键即可显示以 “度,分,秒”为单位的结果.
例题欣赏P240
洞察力与内秀
驶向胜利 的彼岸
例1 如图,工件上有一V型槽,测得它的上口宽20mm,深19. 2mm.求V型角(∠ACB)的大小(结果精确到10 ).
解 : tan ACD AD 10 0.5208, CD 19.2
【最新】北师大版九年级数学下册第一章《三角函数的有关计算(2)》公开课课件 (2).ppt

sin A 1 ∠A= 2
30 0 sin A 3 ∠A=
2
60 0 sin A 2 ∠A= 2
45 0
倍
cos A 1 ∠A= 2
60 0 cos A 2 ∠A=
2
45 0 cos A 3 ∠A= 30 0 2
速 课 时
tan A 3 ∠A= 3
30 0 tanA 3 ∠A= 60 0 tanA1∠A= 45 0
北师大版 九年级(下)
3 三角函数的计算(2)
倍 速 课 时 学 练
回顾与思考
直角三角的边角关系
w直角三角形三边的关系: 勾股定理 a2+b2=c2.
w直角三角形两锐角的关系:两锐角互余 A+B=900.
w直角三角形边与角之间的关系:锐角三角函数
sinAcoBs a,coAs sinBb,tanA1/tanBa.
c
c
b
倍 w互余两角之间的三角函数关系:
速 课
wsinA=cosB,tanA=1/tanB.
时 学 练
w同角之间的三角函数关系: wsin2A+cos2A=1. tanA sinA.
A
cosA
B c
┌
b
C
w特殊角300,450,600角的三角函数值.
想一想P
数学源于生活的需求
w如图,为了方便行人,市政府在10m 高的天桥.两端修建了40m长的斜道. 这条斜道的倾斜角是多少?
w例如,
按键的顺序
显示结果
SinA=0.9816
shift Sin-1 0 . 9 8 1 6 =
Sin-1=0.9816 =78.99184039
倍
CosA=0.8607
新北师大版数学九年级下册1.1锐角三角函数公开课

即tanα= BC
AC
锐角α 的正弦,余弦和统称∠ α 的三角函数 (trigonmetric function)
如果∠A是Rt△ABC的一个锐角(如图),则有
sinA=
A的对边 斜边
cosA=
A的邻边 斜边
tanA=
A的对边 A的邻边
那么∠B呢?
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字 构成的,原意是三角形的测量,也就是解三角 形.后来范围逐渐扩大,成为研究三角函数及其 应用的一个数学分支.
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
B
BC B1C1 AC AC1 BC
(2) AB 和 AB1 , AB 和AB1 , AC
和
B1C1 AC1
有什么关系?
A
(3)如果改变B在梯子上的位置
呢?
C C1
一般地,对于每一个确定的锐角α,在角的 一边上任取一点B,作BC⊥AC于点C,则比 值 BC , AC , BC 都是一个确定的值,与点B在角 B
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
和 BA1CC11有什么关系?
(3)如果改变B在梯子上的位置
呢?
C1
想一想
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
B
BC
(2) AB
AC
锐角α 的正弦,余弦和统称∠ α 的三角函数 (trigonmetric function)
如果∠A是Rt△ABC的一个锐角(如图),则有
sinA=
A的对边 斜边
cosA=
A的邻边 斜边
tanA=
A的对边 A的邻边
那么∠B呢?
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字 构成的,原意是三角形的测量,也就是解三角 形.后来范围逐渐扩大,成为研究三角函数及其 应用的一个数学分支.
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
B
BC B1C1 AC AC1 BC
(2) AB 和 AB1 , AB 和AB1 , AC
和
B1C1 AC1
有什么关系?
A
(3)如果改变B在梯子上的位置
呢?
C C1
一般地,对于每一个确定的锐角α,在角的 一边上任取一点B,作BC⊥AC于点C,则比 值 BC , AC , BC 都是一个确定的值,与点B在角 B
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
和 BA1CC11有什么关系?
(3)如果改变B在梯子上的位置
呢?
C1
想一想
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
B
BC
(2) AB
北师大版九年级数学下册第一章《锐角三角函数(第2课时)》公开课课件 (2)

B
tanA= A的对边 A的邻边
斜边
∠A的对边 ┌ A ∠A的邻边 C
想一想P1 2
本领大不大 悟心来当家
如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻 边的比便随之确定.此时,其它边之间的比值也确定吗?
结论: 在Rt△ABC中,如果锐角A确定 时,那么∠ A的对边与斜边的比, 邻边与斜边的比也随之确定.
A
B
斜边
∠A的对边 ┌ ∠A的邻边 C
想一想P2 3
正弦与余弦
驶向胜利 的彼岸
在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,
记作sinA,即 sinA= A的对边
A的斜边
在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,
记作cosA,即
cosA= A的邻边
B
A的斜边 斜边
锐角A的正弦,余弦,正切和都 是做∠A的三角函数.
相信自己
驶向胜利 的彼岸
12. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求sinA,cosA,tanA, 和
sinB,cosB,tanB,. (2)BC=3,sinA=0.6,求AC 和AB.
A
C
(3)AC=4,cosA=0.8,求BC.
13.在梯形ABCD中 ,AD//BC,AB=DC=13,AD=8,BC=18.
求:BC的长.
C
解:在Rt△ABC中,
s in AB C B C 0.6,
AC200
?怎样
解答
B C 2 0 0 .6 0 1.20
老师期望:
A
200
┌ B
请你求出cosA,tanA,sinC,cosC和tanC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)1-2 sin30°cos30°(2)3tan30°-tan45°+2sin60°
(3) cos 60 1 sin 60
1 tan 30
解: (1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
12 1 3 22
1 3 2
3
3
3 1 2
3
2
3 1 3 2 3 1
cos 45 sin 45
tan 45
解: (1) cos260°+sin260°
1 2
2
3 2
2
=1
(2)
cos 45 sin 45
tan
45
sin 2 60 表示 ( sin 60 )2,即
22 1
22
( sin60 )( sin60 )
=0
四、巩固练习
1. 求下列各式的值:
3、在Rt△ABC中,∠C=90°,化简
1-2sinAcosA
八、小 结
在Rt△ABC中
sinA= A的对边 = a A的斜边 c
cosA= A的邻边 = b A的斜边 c
tanA=
A的对边 A的邻边
=
a b
角度与数值之间的对应函数关系
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角函数
另一条直角边长= 2a2 a2 3a
a
30°
sin 30 a 1
cos 30 3a 3
3a
2a 2
2a 2
a3 tan 30
3a 3
sin 60 3a 3 cos 60 a 1
2a 2
2a 2
tan 60 3a 3 a
2a 3a
60°
a
设两条直角边长为a,则斜边长= a2 a2 2a
B
BC 7, AC 21
7
求∠A、∠B的度数. 解: 由勾股定理
A
21
C
2
2
AB AC2 BC 2 21 7 28 2 7
sin A BC 7 1 AB 2 7 2
∴ A=30°
∠B = 90°- ∠ A = 90°-30° = 60°
(3)如图,已知圆锥的高AO等于圆锥
1.1 锐角三角函数(3)
一、复习引入
在直角三角形中, 一直个角锐三角角形的A正BC弦中是,怎么定义的? 一一把 记个个∠ 作锐锐As的 i角 角n对 A的 的=边余 正与AA弦 切的 的 斜是 是边 对 斜 的 边 边怎怎比么么叫ac定定做义义∠A的的的??正弦,
把∠A 的邻边与斜边的ቤተ መጻሕፍቲ ባይዱ叫做∠A 的余弦,
sin 45 a
2
a cos 45
2
2a 2
2a 2
2a
a
a
tan 45 1 a
45°
a
30°、45°、60°角的正弦值、余弦值和正切值如 下表:
锐角a 三角函数
30°
45°
60°
sin a
1
2
3
2
2
2
cos a
3
2
1
2
2
2
tan a
3
1
3
3
三、典例分析
例1、求下列各式的值:
(1)cos260°+sin260°(2)
的底面半径OB的 3 倍,求 .
解: 在图中,
tan a AO 3OB 3 OB OB
a 60
A
O
B
六、巩固练习
1.求下列各式的值
(1)tan45°-sin30°·cos60°(2) 2.求满足下列条件的锐角α:
sin 600 1 tan 600 2 tan 450
(1) 2cosα- 2 =0 (2) tan(α+10°)= 3
斜边c
A的邻边 a 记作 cosA= 斜边 = c
A
b
把∠A 的对边与邻边的比叫做∠A 的正切,
A的对边 a 记作 tanA= A的邻边 = b
B
对边a C
二、探索新知
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值.
60°
30° 45°
45°
设30°所对的直角边长为a,那么斜边长为2a 2a
❖ 10、人的志向通常和他们的能力成正比例。2021/2/92021/2/92021/2/92/9/2021 1:53:44 AM ❖ 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/2/92021/2/92021/2/9Feb-219-Feb-21 ❖ 12、越是无能的人,越喜欢挑剔别人的错儿。2021/2/92021/2/92021/2/9Tuesday, February 09, 2021 ❖ 13、志不立,天下无可成之事。2021/2/92021/2/92021/2/92021/2/92/9/2021
sin a cos a tan a
30°
1 2 3 2
3 3
45°
2 2
2 2
1
60°
3 2
1 2
3
特殊角的三角函数值是由三角形的特殊性质得到的, 识记理解特殊角的三角函数值
九、作 业
作业: 1、识记特殊角的三角函数值 2、课本第82页第3题
同学们,再见!
❖ 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/2/92021/2/9Tuesday, February 09, 2021
1
cos 60
1
(3)
2 1 2 3 3 =2
1 sin 60 tan 30 1 3 3
23
五、典例分析
例2
(1)如图,在Rt△ABC中,∠C= 90°, AB 6 ,BC 3
求∠A的度数.
B
解: 在图中,
6
3
sin A BC 3 2
A
C
AB 6 2
A 45
(2)在Rt△ABC中,∠C=90°,
1
A
3.在 Rt△ABC 中,∠C=90°,若 sinA= 2 ,
则 BC∶AC∶AB 等于( )
A.1∶2∶5
B.1∶ 3 ∶ 5
C. 1∶ 3 ∶ 2
D.1∶2∶ 3
C
1、(1)3 (2)1 ;2、(1)45°(2)50°
4
2
B
3、C
七、应用拓展
如图,在△ABC中,∠A=30度, tanB 3 , AC 2 3,
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂
足为D,BC=2,BD= 3, 分别求出△ABC、△ACD、
△BCD中各锐角.
C
AD
B
1?scio n232s40+ 5+ta2 t4an5n + c3o s026 isn3 0 0
2、已知:α为锐角,且满足 ,求3 αt的a度n数2。-4t a+ n3 =0
2
求AB。
C
解:过点C作CD⊥AB于点D
∠A=30度, AC 2 3
sin A CD 1 CD 1 2 3
AC 2
2
3
A
cos A AD AC
3 2
AD
3 2
2
33
tan B CD 3 BD 2
BD
3 2 2 3
AB AD BD 3 2 5
D
B
构造直角三 角形,利用 锐角三角函 数,进行边 角转化
