2005年黄冈市中考数学试题与答案(非课改)
2005年湖北省黄冈中学期末考试卷

2005年湖北省黄冈中学期末考试卷一、 选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的,把正确答案的代号填在第三大题前面的表中相应位置上.1.0sin 2lim tan x x x→的值是( ) A .0B .1C .2D .4 2.222A lim A nn n n n →∞+的值是( ) A .0B .2C .12D .14 3.当z =2z 100+z 50+1的值等于( ) A .1 B .–1C .iD .–i 4.函数y =x sin x +cos x 的一个单调递增区间是( )A .(–2π,0)B .(0,2π)C .(2π,π)D .(π,32π) 5.无穷等比数列{a n }的首项为a 1=3,前n 项和为S n ,且8S 6=7S 3,则lim n n S →∞等于( ) A .2B .–2C .6D .–6 6.已知cos sin lim cos sin nn n n n θθθθ→∞-+=–1(0≤θ≤2π),则θ的取值范围是( ) A .4π B .0≤θ<4π C .4π<θ≤2π D .4π≤θ≤2π 7.0e 1lim x x x→-的值是( ) A .0 B .1 C .e D .1e8.数列{a n }中,a 1=13,2a n +a n +1=173n +,则12lim()n n a a a →∞+++L 的值是( ) A .23 B .12 C .2318 D .729.将1,2,3,…,9这9个数字填在如图中的9个空格中,要求每一行从左到右,每一列从上到下依次增大.当3,4固定在图中位置时,填写空格的方法种数是( )A .6B .12C .18D .2410.已知函数f (x )是R 上的可导函数,下列命题:(1)若f (x )是奇函数,则f ′(x )是偶函数;(2)若f (x )是偶函数,则f ′(x )是奇函数;(3) 若f (x )是周期函数,则f ′(x )也是周期函数.其中正确的命题的个数是( )A .0B .1C .2D .311.过点P(1,1)作y =x 3的两条切线l 1、l 2,设l 1、l 2的夹角为θ,则tan θ等于( )A 3B .913C .1513D .953 4A .f (13)B .f (1)C .f (2)D .f (3)二、 填空题:本大题共4小题,每小题4分,共16分,把正确答案填在第三大题前面的表中相应位置上.133i 对应的向量按顺时针方向旋转6π,所得向量对应的复数是 14.已知函数f (x )=110),x x x ⎧+-⎪>⎨⎪⎩是R 上的连续函数,则实数a 的值是 15.已知222lim 2x x ax b x x →++--=2,则a +b 的值是 16.已知a n 是f n (x )=(1+x )n +1的展开式中含x n 的项的系数,S n 为数列{a n }的前n 项和,则12111lim()n nS S S →∞+++L 的值是三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知O 是坐标原点,向量1OZ uuu u r ,2OZ u u u u r 分别对应复数z 1,z 2,且z 1=36a ++(19–a 2)i ,z 2=21a-+(2a –5)i (其中a ∈R ),若1z +z 2可以与实数比较大小,试求向量1OZ uuu u r ,2OZ u u u u r 的数量积.18.(本小题满分12分)一个电视节目要求参加者回答A 、B 两个问题,若没正确回答任何一个问题则赠送价值20元的纪念品;若正确回答一个问题则赠送价值100元的礼品;若两个问题都正确回答则赠送价值400元的礼品.某观众应邀参加这个节目,已知该观众正确回答A 问题的概率是0.75,正确回答B 问题的概率是0.2.(1)求该观众正确回答的问题的个数ξ的分布列;(2)求该观众参加这个节目获得物品的价值η的数学期望.19.(本小题满分12分)设函数f (x )=–13x 3+2ax 2–3a 2x +b ,其中0<a <1,b ∈R . (1)求函数f (x )的的单调区间和极值;(2)若当x ∈[a +1,a +2]时,恒有f ′(x )≥–a ,试确定a 的取值范围.20.(本小题满分12分)已知函数f (x 3x +y = f (x )上一点P (x 0,f (x 0))作曲线的切线l 分别交x 、y 轴于M 、N 两点,O 为坐标原点.(1)求x 0=1时,切线l 的的方程;(2)求S ΔMON 的最小值及此时点P 的坐标.21.(本小题满分12分)已知函数f(x)=ln(2–x)+ax在区间(0,1]上是增函数.(1)求实数a的取值范围;(2)若数列{a n}满足a1∈(0,1),a n+1=ln(2–a n)+a n(n∈N*),证明:0<a n<a n+1<1.22.(本小题满分14分)已知函数f(x)=x3+bx2+cx+d在(0,+ )上是增函数,在[–1,0]上是减函数,且方程f(x)=0有三个根,它们分别为α,–1,β.(1)求c的值;(2)求证:f(0)≤–12;(3)求|α–β|的取值范围.参考答案17.解:∵1z +z 2=36a +–(19–a 2)i +21a -+(2a –5)i=(36a ++21a -)+ (a 2+2 a –24)i ∈R ,∴a 2+2 a –24=0,解得a =4或a =–6(舍去).∴z 1=310+3i ,z 2=–23+3i ,∴向量1OZ uuu u r ,2OZ u u u u r 的数量积为 (310,3)· (–23,3)=445.18.解:(1)∵P(ξ=0)=(1–0.75)×(1–0.2)=0.2,P(ξ=1)= 0.75×(1–0.2) +(1–0.75)×0.2=0.65,P(ξ=2)=0.75×0.2=0.15, ξ 0 1 2P 0.2 0.65 0.1519.解:(1)∵f ′(x )=–x 2+4ax –3a 2=–(x –3a )( x –a ),∴当x <a 时,f ′(x )<0;当a <x <3a 时,f ′(x )>0;当x >3a 时,f ′(x )<0,∴(–∞,a )和(3a ,+∞)是f (x )的的单调递减区间,(a ,3a )是f (x )的的单调递增区间.当x =a 时,f (x )有极小值f (a )=–13a 3+2 a 3–3a 3+b =–43a 3+b ;当x =3a 时,f (x )有极大值f (3a )=–13(3a )3+2 a (3a )2–3a 2(3a )+b =b .(2)∵f ′(x )=–x 2+4ax –3a 2=–(x –2a )2+ a 2,其图象对称轴是直线x =2a , 而2a <a +1<a +2,∴在区间[a +1,a +2]上,单调递减,从而f ′(x )≥f ′(a +2),即 f ′(x )≥4a –4.又∵f ′(x )≥–a 恒成立,∴01,4 4.a a a <<⎧⎨-≤-⎩解得45≤a <1.20.解:(1)∵f ′(x 23x +⇒f ′(1)=14, f (1)=2,∴切线l 的的方程是y –2=14(x –1),即x –4y +7=0 (2)∵切线l 的方程是y 03x +0123x +(x –x 0),∴点M 、N 的坐标分别是M (–x 0–6,0),N 0023x +),∴S ΔMON =12|–(x 0+6)•023x +2043x +其中x 0>–3.题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C D D B A C B B A D B D 题号 13 14 15 16 答案 1–3i 0 –6 119S ′ΔMON 20000012(6)3(6)23x x x x ++-+⋅+2000008(3)3x x ++ 00008(3)3x x ++,∴当–3<x 0<–2时,S ′ΔMON <0;当x 0=–2时,S ′ΔMON =0;当x 0>–2时,S ′ΔMON >0. 故当x 0=–2时,S ΔMON 2423-+.此时点P 的坐标为(–2,1).21.解:(1)∵f ′(x )=12x -+a , ∴12x -+a ≥0在x ∈(0,1)上恒成立,即a ≥–12x -在x ∈(0,1)上恒成立.又∵x ∈(0,1)时,–12x -∈(12,1),∴a ≥1.(2)由(1)知,g (x )= ln(2–x )+x 是(0,1]上的增函数.∴当0<x <1时,g (x )<g (1)=1.下面用数学归纳法证明题中结论成立:当n =1时,一方面a 2=g (a 1) <g (1)=1;另一方面, a 1∈(0,1)⇒2–a 1∈(1,2)⇒ ln(2–a 1)>0⇒a 2>a 1,所以0<a 1<a 2<1.假设当n =k 时不等式成立,即0<a k <a k +1<1,则由0<a k +1<1,同上法可证0<a k +1<a k +2<1. 综上所述,0<a n <a n +1<1对任何正整数n 都成立.22.解:(1)f ′(x )=3x 2+2bx +c.由题意知函数f (x )在x =0处有极小值,所以c = f ′(0)=0.(2)∵f (x )在(0,+∞)上是增函数,在[–1,0]上是减函数,∴f ′(x )= 3x 2+2bx ≥0在(0,+∞)上恒成立,f ′(x )= 3x 2+2bx ≤0在(–1,0)上恒成立, 即b ≥–32x 在(0,+∞)上恒成立, 在(–1,0)上也恒成立,∴b ≥32.又∵f (–1)=–1+b –c +d =b +d –1=0⇒d =1–b ,∴f (0)=d =1–b ≤–12.(3)∵f (x )=x 3+bx 2+1–b =(x +1)[x 2+(b –1)x +1–b ],∴α,β是x 2+(b –1)x +1–b =0的两根,∴|α–β2(1)4(1)b b ---2(1)4b +-注意到b ≥32,所以|α–β|≥32.。
往年湖北省黄冈市中考数学真题及答案

往年年湖北省黄冈市中考数学真题及答案一、选择题(下列个题四个选项中,有且仅有一个是正确的.每小题3分,共24分)1.(3分)﹣8的立方根是()A.﹣2 B.±2 C.2 D.﹣2.(3分)如果α与β互为余角,则()A.α+β=180°B.α﹣β=180° C.α﹣β=90°D.α+β=90°3.(3分)下列运算正确的是()A.x2•x3=x6B.x6÷x5=x C.(﹣x2)4=x6D.x2+x3=x54.(3分)如图所示的几何体的主视图是()A.B.C.D.5.(3分)函数y=中,自变量x的取值范围是()A.x≠0 B.x≥2 C.x>2且x≠0 D.x≥2且x≠06.(3分)若α、β是一元二次方程x2+2x﹣6=0的两根,则α2+β2=()A.﹣8 B.32 C.16 D.407.(3分)如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为()cm2.A.4πB.8πC.12π D.(4+4)π8.(3分)已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为()A.B.C.D.二、填空题(共7小题,每小题3分,共21分)9.(3分)计算:|﹣|= .10.(3分)分解因式:(2a+1)2﹣a2= .11.(3分)计算:﹣= .12.(3分)如图,若AD∥BE,且∠ACB=90°,∠CBE=30°,则∠CAD= 度.13.(3分)当x=﹣1时,代数式÷+x的值是.14.(3分)如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD= .15.(3分)如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为cm2.三、解答题(本大题共10小题,满分共75分)16.(5分)解不等式组:,并在数轴上表示出不等式组的解集.17.(6分)浠州县为了改善全县中、小学办学条件,计划集中采购一批电子白板和投影机.已知购买2块电子白板比购买3台投影机多4000元,购买4块电子白板和3台投影机共需44000元.问购买一块电子白板和一台投影机各需要多少元?18.(6分)已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.19.(6分)红花中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛.(1)请用树状图或列表法列举出各种可能选派的结果;(2)求恰好选派一男一女两位同学参赛的概率.20.(7分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.(1)求证:EB=EC;(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.21.(7分)某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:(1)本次被调查的学生有名;(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?22.(9分)如图,已知双曲线y=﹣与两直线y=﹣x,y=﹣kx(k>0,且k≠)分别相交于A、B、C、D四点.(1)当点C的坐标为(﹣1,1)时,A、B、D三点坐标分别是A(, ),B(, ),D(, ).(2)证明:以点A、D、B、C为顶点的四边形是平行四边形.(3)当k为何值时,▱ADBC是矩形.23.(7分)如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).(2)已知距观测点D处100海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:≈1.41,≈1.73)24.(9分)某地实行医疗保险(以下简称“医保”)制度.医保机构规定:一:每位居民年初缴纳医保基金70元;二:居民每个人当年治病所花的医疗费(以定点医院的治疗发票为准),年底按下列方式(见表一)报销所治病的医疗费用:居民个人当年治病所花费的医疗费医疗费的报销方法不超过n元的部分全部由医保基金承担(即全部报销)超过n元但不超过6000元的部分个人承担k%,其余部分由医保基金承担超过6000元的部分个人承担20%,其余部分由医保基金承担如果设一位居民当年治病花费的医疗费为x元,他个人实际承担的医疗费用(包括医疗费中个人承担部分和年初缴纳的医保基金)记为y元.(1)当0≤x≤n时,y=70;当n<x≤6000时,y= (用含n、k、x的式子表示).(2)表二是该地A、B、C三位居民2013年治病所花费的医疗费和个人实际承担的医疗费用,根据表中的数据,求出n、k的值.表二:居民 A B C某次治病所花费的治疗费用x(元)400 800 1500个人实际承担的医疗费用y(元)70 190 470(3)该地居民周大爷2013年治病所花费的医疗费共32000元,那么这一年他个人实际承担的医疗费用是多少元?25.(13分)已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,﹣1),B(3,﹣1),动点P从点O 出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.(1)求经过O、A、B三点的抛物线的解析式,并确定顶点M的坐标;(2)用含t的代数式表示点P、点Q的坐标;(3)如果将△OPQ绕着点P按逆时针方向旋转90°,是否存在t,使得△OPQ的顶点O或顶点Q在抛物线上?若存在,请求出t的值;若不存在,请说明理由;(4)求出S与t的函数关系式.往年年湖北省黄冈市中考数学试卷参考答案与试题解析一、选择题(下列个题四个选项中,有且仅有一个是正确的.每小题3分,共24分)1.(3分)(往年•黄冈)﹣8的立方根是()A.﹣2 B.±2 C.2 D.﹣【分析】如果一个数x的立方等于a,那么x是a的立方根,根据此定义求解即可.【解答】解:∵﹣2的立方等于﹣8,∴﹣8的立方根等于﹣2.故选:A.【点评】此题主要考查了立方根的定义,求一个数的立方根,应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.注意一个数的立方根与原数的性质符号相同.2.(3分)(往年•黄冈)如果α与β互为余角,则()A.α+β=180°B.α﹣β=180° C.α﹣β=90°D.α+β=90°【分析】根据互为余角的定义,可以得到答案.【解答】解:如果α与β互为余角,则α+β=900.故选:D.【点评】此题主要考查了互为余角的性质,正确记忆互为余角的定义是解决问题的关键.3.(3分)(往年•黄冈)下列运算正确的是()A.x2•x3=x6B.x6÷x5=x C.(﹣x2)4=x6D.x2+x3=x5【分析】根据同底数幂的乘法和除法法则可以解答本题.【解答】解:A.x2•x3=x5,故A错误;B.x6÷x5=x,故B正确;C.(﹣x2)4=x8,故C错误;D.x2+x3不能合并,故D错误.故选:B.【点评】主要考查同底数幂相除底数不变指数相减,同底数幂相乘底数不变指数相加,熟记定义是解题的关键.4.(3分)(往年•黄冈)如图所示的几何体的主视图是()A.B.C.D.【分析】根据从正面看得到的图形是主视图,可得答案.【解答】解:从正面看,象一个大梯形减去一个小梯形,故选:D.【点评】本题考查了简单组合体的三视图,从正面看得到的图形是主视图.5.(3分)(往年•黄冈)函数y=中,自变量x的取值范围是()A.x≠0 B.x≥2 C.x>2且x≠0 D.x≥2且x≠0【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.【解答】解:由题意得,x﹣2≥0且x≠0,∴x≥2.故选:B.【点评】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.6.(3分)(往年•黄冈)若α、β是一元二次方程x2+2x﹣6=0的两根,则α2+β2=()A.﹣8 B.32 C.16 D.40【分析】根据根与系数的关系得到α+β=﹣2,αβ=﹣6,再利用完全平方公式得到α2+β2=(α+β)2﹣2αβ,然后利用整体代入的方法计算.【解答】解:根据题意得α+β=﹣2,αβ=﹣6,所以α2+β2=(α+β)2﹣2αβ=(﹣2)2﹣2×(﹣6)=16.故选:C.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=﹣,x1•x2=.7.(3分)(往年•黄冈)如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为()cm2.A.4πB.8πC.12π D.(4+4)π【分析】表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.【解答】解:底面圆的半径为2,则底面周长=4π,∵底面半径为2cm、高为2cm,∴圆锥的母线长为4cm,∴侧面面积=×4π×4=8π;底面积为=4π,全面积为:8π+4π=12πcm2.故选:C.【点评】本题利用了圆的周长公式和扇形面积公式求解,牢记公式是解答本题的关键.8.(3分)(往年•黄冈)已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC 边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为()A.B.C.D.【分析】判断出△AEF和△ABC相似,根据相似三角形对应边成比例列式求出EF,再根据三角形的面积列式表示出S与x的关系式,然后得到大致图象选择即可.【解答】解:∵EF∥BC,∴△AEF∽△ABC,∴=,∴EF=•10=10﹣2x,∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),纵观各选项,只有D选项图象符合.故选:D.【点评】本题考查了动点问题函数图象,主要利用了相似三角形的性质,求出S与x的函数关系式是解题的关键,也是本题的难点.二、填空题(共7小题,每小题3分,共21分)9.(3分)(往年•黄冈)计算:|﹣|= .【分析】根据负数的绝对值等于它的相反数,可得答案案.【解答】解:|﹣|=,故答案为:.【点评】本题考查了绝对值,负数的绝对值是它的相反数.10.(3分)(往年•黄冈)分解因式:(2a+1)2﹣a2= (3a+1)(a+1).【分析】直接利用平方差公式进行分解即可.【解答】解:原式=(2a+1+a)(2a+1﹣a)=(3a+1)(a+1),故答案为:(3a+1)(a+1).【点评】此题主要考查了公式法分解因式,关键是掌握平方差公式:a2﹣b2=(a+b)(a﹣b).11.(3分)(往年•黄冈)计算:﹣= .【分析】先进行二次根式的化简,然后合并同类二次根式求解.【解答】解:原式=2﹣=.故答案为:.【点评】本题考查了二次根式的加减法,关键是掌握二次根式的化简以及同类二次根式的合并.12.(3分)(往年•黄冈)如图,若AD∥BE,且∠ACB=90°,∠CBE=30°,则∠CAD= 60 度.【分析】延长AC交BE于F,根据直角三角形两锐角互余求出∠1,再根据两直线平行,内错角相等可得∠CAD=∠1.【解答】解:如图,延长AC交BE于F,∵∠ACB=90°,∠CBE=30°,∴∠1=90°﹣30°=60°,∵AD∥BE,∴∠CAD=∠1=60°.故答案为:60.【点评】本题考查了平行线的性质,直角三角形两锐角互余的性质,熟记性质是解题的关键.13.(3分)(往年•黄冈)当x=﹣1时,代数式÷+x的值是3﹣2.【分析】将除法转化为乘法,因式分解后约分,然后通分相加即可.【解答】解:原式=•+x=x(x﹣1)+x=x2﹣x+x=x2,当x=﹣1时,原式=(﹣1)2=2+1﹣2=3﹣2.故答案为:3﹣2.【点评】本题考查了分式的化简求值,熟悉除法法则和因式分解是解题的关键.14.(3分)(往年•黄冈)如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD= 4.【分析】连结OD,设⊙O的半径为R,先根据圆周角定理得到∠BOD=2∠BAD=60°,再根据垂径定理由CD⊥AB 得到DE=CE,在Rt△ODE中,OE=OB﹣BE=R﹣2,利用余弦的定义得cos∠EOD=cos60°=,即=,解得R=4,则OE=2,DE=OE=2,所以CD=2DE=4.【解答】解:连结OD,如图,设⊙O的半径为R,∵∠BAD=30°,∴∠BOD=2∠BAD=60°,∵CD⊥AB,∴DE=CE,在Rt△ODE中,OE=OB﹣BE=R﹣2,OD=R,∵cos∠EOD=cos60°=,∴=,解得R=4,∴OE=4﹣2=2,∴DE=OE=2,∴CD=2DE=4故答案为:4.【点评】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和解直角三角形.15.(3分)(往年•黄冈)如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为或5或10 cm2.【分析】因为等腰三角形腰的位置不明确,所以分(1)腰长在矩形相邻的两边上,(2)一腰在矩形的宽上,(3)一腰在矩形的长上,三种情况讨论.(1)△AEF为等腰直角三角形,直接利用面积公式求解即可;(2)先利用勾股定理求出AE边上的高BF,再代入面积公式求解;(3)先求出AE边上的高DF,再代入面积公式求解.【解答】解:分三种情况计算:(1)当AE=AF=5厘米时,∴S△AEF=AE•AF=×5×5=厘米2,(2)当AE=EF=5厘米时,如图BF===2厘米,∴S△AEF=•AE•BF=×5×2=5厘米2,(3)当AE=EF=5厘米时,如图DF===4厘米,∴S△AEF=AE•DF=×5×4=10厘米2.故答案为:,5,10.【点评】本题主要考查矩形的角是直角的性质和勾股定理的运用,要根据三角形的腰长的不确定分情况讨论.三、解答题(本大题共10小题,满分共75分)16.(5分)(往年•黄冈)解不等式组:,并在数轴上表示出不等式组的解集.【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.【解答】解:解①得:x>3,解②得:x≥1.,则不等式组的解集是:x>3.【点评】本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.17.(6分)(往年•黄冈)浠州县为了改善全县中、小学办学条件,计划集中采购一批电子白板和投影机.已知购买2块电子白板比购买3台投影机多4000元,购买4块电子白板和3台投影机共需44000元.问购买一块电子白板和一台投影机各需要多少元?【分析】设购买1块电子白板需要x元,一台投影机需要y元,根据①买2块电子白板的钱﹣买3台投影机的钱=4000元,②购买4块电子白板的费用+3台投影机的费用=44000元,列出方程组,求解即可.【解答】解:设购买1块电子白板需要x元,一台投影机需要y元,由题意得:,解得:.答:购买一块电子白板需要8000元,一台投影机需要4000元.【点评】此题主要考查了二元一次方程组的应用,解题关键是弄清题意,找出合适的等量关系,列出方程组.18.(6分)(往年•黄冈)已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.【分析】连接AD,利用SSS得到三角形ABD与三角形ACD全等,利用全等三角形对应角相等得到∠EAD=∠FAD,即AD为角平分线,再由DE⊥AB,DF⊥AC,利用角平分线定理即可得证.【解答】证明:连接AD,在△ACD和△ABD中,,∴△ACD≌△ABD(SSS),∴∠EAD=∠FAD,即AD平分∠EAF,∵DE⊥AE,DF⊥AF,∴DE=DF.【点评】此题考查了全等三角形的判定与性质,以及角平分线定理,熟练掌握全等三角形的判定与性质是解本题的关键.19.(6分)(往年•黄冈)红花中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛.(1)请用树状图或列表法列举出各种可能选派的结果;(2)求恰好选派一男一女两位同学参赛的概率.【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;(2)由(1)可求得恰好选派一男一女两位同学参赛的有8种情况,然后利用概率公式求解即可求得答案.【解答】解:(1)画树状图得:则共有12种等可能的结果;(2)∵恰好选派一男一女两位同学参赛的有8种情况,∴恰好选派一男一女两位同学参赛的概率为:=.【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.20.(7分)(往年•黄冈)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.(1)求证:EB=EC;(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.【分析】(1)连接OD,由BC是⊙O的切线得出∠BCA=90°,由DE是⊙O的切线,得出ED=EC,∠ODE=90°,故可得出∠EDB=∠EBD,由此可得出结论.(2)当以点O、D、E、C为顶点的四边形是正方形时,则△DEB是等腰直角三角形,据此即可判断.【解答】(1)证明:连接OD,∵AC是直径,∠ACB=90°,∴BC是⊙O的切线,∠BCA=90°.又∵DE是⊙O的切线,∴ED=EC,∠ODE=90°,∴∠ODA+∠EDB=90°,∵OA=OD,∴∠OAD=∠ODA,又∵∠OAD+∠DBE=90°,∴∠EDB=∠EBD,∴ED=EB,∴EB=EC.(2)解:当以点O、D、E、C为顶点的四边形是正方形时,则∠DEB=90°,又∵ED=EB,∴△DEB是等腰直角三角形,则∠B=45°,∴△ABC是等腰直角三角形.【点评】本题考查了切线的性质以及切线长定理、圆周角定理,解题的关键是连接OD得垂直,构造出等腰三角形,利用“等角的余角相等解答.21.(7分)(往年•黄冈)某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:(1)本次被调查的学生有200 名;(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?【分析】(1)喜好“核桃味”牛奶的学生人数除以它所占的百分比即可得本次被调查的学生人数;(2)用本次被调查的学生的总人数减去喜好原味、草莓味、菠萝味、核桃味的人数得出喜好香橙味的人数,补全条形统计图即可,用喜好“菠萝味”牛奶的学生人数除以总人数再乘以360°,即可得喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数;(3)用喜好草莓味的人数占的百分比减去喜好原味的人数占的百分比,再乘以该校的总人数即可.【解答】解:(1)10÷5%=200(名)答:本次被调查的学生有200名,故答案为:200;(2)200﹣38﹣62﹣50﹣10=40(名),条形统计图如下:=90°,答:喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数为90°;(3)1200×()=144(盒),答:草莓味要比原味多送144盒.【点评】本题考查的是条形统计图和扇形统计图的综合运用;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.22.(9分)(往年•黄冈)如图,已知双曲线y=﹣与两直线y=﹣x,y=﹣kx(k>0,且k≠)分别相交于A、B、C、D四点.(1)当点C的坐标为(﹣1,1)时,A、B、D三点坐标分别是A(﹣2 , ),B( 2 , ﹣),D ( 1 , ﹣1 ).(2)证明:以点A、D、B、C为顶点的四边形是平行四边形.(3)当k为何值时,▱ADBC是矩形.【分析】(1)由C坐标,利用反比例函数的中心对称性确定出D坐标,联立双曲线y=﹣与直线y=﹣x,求出A与B坐标即可;(2)由反比例函数为中心对称图形,利用中心对称性质得到OA=OB,OC=OD,利用对角线互相平分的四边形为平行四边形即可得证;(3)由A与B坐标,利用两点间的距离公式求出AB的长,联立双曲线y=﹣与直线y=﹣kx,表示出CD的长,根据对角线相等的平行四边形为矩形,得到AB=CD,即可求出此时k的值.【解答】解:(1)∵C(﹣1,1),C,D为双曲线y=﹣与直线y=﹣kx的两个交点,且双曲线y=﹣为中心对称图形,∴D(1,﹣1),联立得:,消去y得:﹣x=﹣,即x2=4,解得:x=2或x=﹣2,当x=2时,y=﹣;当x=﹣2时,y=,∴A(﹣2,),B(2,﹣);故答案为:﹣2,,2,﹣,1,﹣1;(2)∵双曲线y=﹣为中心对称图形,且双曲线y=﹣与两直线y=﹣x,y=﹣kx(k>0,且k≠)分别相交于A、B、C、D四点,∴OA=OB,OC=OD,则以点A、D、B、C为顶点的四边形是平行四边形;(3)若▱ADBC是矩形,可得AB=CD,联立得:,消去y得:﹣=﹣kx,即x2=,解得:x=或x=﹣,当x=时,y=﹣;当x=﹣时,y=,∴C(﹣,),D(,﹣),∴CD==AB==,整理得:(4k﹣1)(k﹣4)=0,k1=,k2=4,又∵k≠,∴k=4,则当k=4时,▱ADBC是矩形.【点评】此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,一次函数与反比例函数的交点,平行四边形,矩形的判定,两点间的距离公式,以及中心图形性质,熟练掌握性质是解本题的关键.23.(7分)(往年•黄冈)如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN 上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).(2)已知距观测点D处100海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:≈1.41,≈1.73)【分析】(1)作CE⊥AB,设AE=x海里,则BE=CE=x海里.根据AB=AE+BE=x+x=100(+1),求得x 的值后即可求得AC的长;过点D作DF⊥AC于点F,同理求出AD的长;(2)作DF⊥AC于点F,根据AD的长和∠DAF的度数求线段DF的长后与100比较即可得到答案.【解答】解:(1)如图,作CE⊥AB,由题意得:∠ABC=45°,∠BAC=60°,设AE=x海里,在Rt△AEC中,CE=AE•tan60°=x;在Rt△BCE中,BE=CE=x.∴AE+BE=x+x=100(+1),解得:x=100.AC=2x=200.在△ACD中,∠DAC=60°,∠ADC=75°,则∠ACD=45°.过点D作DF⊥AC于点F,设AF=y,则DF=CF=y,∴AC=y+y=200,解得:y=100(﹣1),∴AD=2y=200(﹣1).答:A与C之间的距离AC为200海里,A与D之间的距离AD为200(﹣1)海里.(2)由(1)可知,DF=AF=×100(﹣1)≈126.3海里,∵126.3>100,所以巡逻船A沿直线AC航线,在去营救的途中没有触暗礁危险.【点评】本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系解答.24.(9分)(往年•黄冈)某地实行医疗保险(以下简称“医保”)制度.医保机构规定:一:每位居民年初缴纳医保基金70元;二:居民每个人当年治病所花的医疗费(以定点医院的治疗发票为准),年底按下列方式(见表一)报销所治病的医疗费用:居民个人当年治病所花费的医疗费医疗费的报销方法不超过n元的部分全部由医保基金承担(即全部报销)超过n元但不超过6000元的部分个人承担k%,其余部分由医保基金承担超过6000元的部分个人承担20%,其余部分由医保基金承担如果设一位居民当年治病花费的医疗费为x元,他个人实际承担的医疗费用(包括医疗费中个人承担部分和年初缴纳的医保基金)记为y元.(1)当0≤x≤n时,y=70;当n<x≤6000时,y= 0.01k(x﹣n)+70(n<x≤6000)(用含n、k、x的式子表示).(2)表二是该地A、B、C三位居民2013年治病所花费的医疗费和个人实际承担的医疗费用,根据表中的数据,求出n、k的值.表二:居民 A B C某次治病所花费的治疗费用x(元)400 800 1500个人实际承担的医疗费用y(元)70 190 470(3)该地居民周大爷2013年治病所花费的医疗费共32000元,那么这一年他个人实际承担的医疗费用是多少元?【分析】(1)根据医疗报销的比例,可得答案;(2)根据医疗费用的报销费用,可得方程组,再解方程组,可得答案;(3)根据个人承担部分的费用,可得代数式,可得答案.【解答】解:(1)由题意得当0≤x≤n时,y=70;当n<x≤6000时,y=0.01k(x﹣n)+70(n<x≤6000);(2)由A、B、C三人的花销得,解得;(3)由题意得70+(6000﹣500)×40%+(32000﹣6000)×20%=70+2200+5200=7470(元).答:这一年他个人实际承担的医疗费用是7470元.【点评】本题考查了一次函数的应用,根据题意列函数解析式是解题关键.25.(13分)(往年•黄冈)已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,﹣1),B(3,﹣1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.(1)求经过O、A、B三点的抛物线的解析式,并确定顶点M的坐标;(2)用含t的代数式表示点P、点Q的坐标;(3)如果将△OPQ绕着点P按逆时针方向旋转90°,是否存在t,使得△OPQ的顶点O或顶点Q在抛物线上?若存在,请求出t的值;若不存在,请说明理由;(4)求出S与t的函数关系式.【分析】(1)设抛物线解析式为y=ax2+bx(a≠0),然后把点A、B的坐标代入求出a、b的值,即可得解,再把函数解析式整理成顶点式形式,然后写出顶点M的坐标;(2)根据点P的速度求出OP,即可得到点P的坐标,再根据点A的坐标求出∠AOC=45°,然后判断出△POQ 是等腰直角三角形,根据等腰直角三角形的性质求出点Q的坐标即可;(3)根据旋转的性质求出点O、Q的坐标,然后分别代入抛物线解析式,求解即可;(4)求出点Q与点A重合时的t=1,点P与点C重合时的t=1.5,t=2时PQ经过点B,然后分①0<t≤1时,重叠部分的面积等于△POQ的面积,②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积分别列式整理即可得解.【解答】解:(1)设抛物线解析式为y=ax2+bx(a≠0),把点A(1,﹣1),B(3,﹣1)代入得,,解得,∴抛物线解析式为y=x2﹣x,∵y=x2﹣x=(x﹣2)2﹣,∴顶点M的坐标为(2,﹣);(2)∵点P从点O出发速度是每秒2个单位长度,∴OP=2t,∴点P的坐标为(2t,0),∵A(1,﹣1),∴∠AOC=45°,∴点Q到x轴、y轴的距离都是OP=×2t=t,∴点Q的坐标为(t,﹣t);(3)∵△OPQ绕着点P按逆时针方向旋转90°,∴旋转后点O、Q的对应点的坐标分别为(2t,﹣2t),(3t,﹣t),若顶点O在抛物线上,则×(2t)2﹣×(2t)=﹣2t,解得t=(t=0舍去),∴t=时,点O(1,﹣1)在抛物线y=x2﹣x上,若顶点Q在抛物线上,则×(3t)2﹣×(3t)=﹣t,解得t=1(t=0舍去),∴t=1时,点Q(3,﹣1)在抛物线y=x2﹣x上.(4)点Q与点A重合时,OP=1×2=2,t=2÷2=1,点P与点C重合时,OP=3,t=3÷2=1.5,t=2时,OP=2×2=4,PC=4﹣3=1,此时PQ经过点B,所以,分三种情况讨论:①0<t≤1时,S=S△OPQ=×(2t)×=t2,②1<t≤1.5时,S=S△OP′Q′﹣S△AEQ′=×(2t)×﹣×(t﹣)2=2t﹣1;③1.5<t<2时,S=S梯形OABC﹣S△BGF=×(2+3)×1﹣×[1﹣(2t﹣3)]2=﹣2(t﹣2)2+=﹣2t2+8t﹣;所以,S与t的关系式为S=.。
湖北省黄冈市中考数学试题分类解析 专题09 三角形

【2013版中考12年】湖北省黄冈市2002-2013年中考数学试题分类解析 专题09 三角形一、选择题1. (湖北省黄冈市2002年3分)已知∠A 为锐角,且cosA≤21,那么【 】 (A ) 0°<A≤60° (B )60°≤A <90° (C )0°<A ≤30° (D )30°≤A<90°【答案】B 。
【考点】锐角三角函数的增减性,特殊角的三角函数值。
【分析】∵cos60°=12,余弦函数值随角增大而减小, ∴当cosA≤12时,∠A≥60°。
又∠A 是锐角,∴60°≤A<90°。
故选B 。
2. (湖北省黄冈市2003年3分)在△ABC 中,AB =AC =3,BC =2,则6 cosB 等于【 】.A .3B .2C . 33D .323. (湖北省黄冈市2004年3分)若直角三角形的三边长分别为2,4,x ,则x 的可能值有【 】A 、1个B 、2个C 、3个D 、4个【答案】B 。
【考点】勾股定理,分类思想的应用。
【分析】x 可为斜边也可为直角边,因此解本题时要对x 的取值进行讨论:当x 为斜边时,x 2=22+42=20,所以x=;当4为斜边时,x 2=16﹣4=12,x=。
故选B。
(2<4,不可能是斜边)4. (湖北省黄冈市大纲卷2005年4分)如图,△ABC中,AB = AC,D为BC中点,E为AD 上任意一点,过C作CF∥AB交BE的延长线于F,交AC于G,连结CE。
下列结论中正确的有【】5. (湖北省黄冈市课标卷2005年3分)中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD的长为【】6. (湖北省黄冈市课标卷2005年4分)如图,△ABC中,AB = AC,D为BC中点,E为AD 上任意一点,过C作CF∥AB交BE的延长线于F,交AC于G,连结CE。
湖北省黄冈市2005年中考化学试题(Word版有答案)

湖北省黄冈市2005年初中毕业生学业水平考试理科综合试题(课改区)考前须知:1.本试卷分为选择题和非选择题两大多数,选择题的答案必须用2B铅笔涂填在答案卡上,写在试卷上无效。
非客观性试题请用钢笔或圆珠笔直接在试卷上解答。
2.物理试题中g取10N/Kg3.相对原子质量:H:1 O:16 C:12 N:14 Cl:35.5 Zn:65 Cu:64第一局部选择题(1~29小题,共48分)一、选择题(此题包括29小题,共48分。
其中19~21小题有1~2个选项符合题意,其它的均只有一个选项符合题意。
)9.以下成语中,一定包含有化学变化的是(C)A.木已成舟 B.花香四溢 C.烛炬成灰 D.滴水成冰10.以下各图是初中化学常见的几个实验操作,其中错误的选项是(A )11.以下相关生活常识的说法中,准确的是(C)A.发现家里煤气泄露时,立即打开排气扇B.多喝“汽水”可治胃酸过多C.多吃蔬菜、水果,补充维生素C,增强人体抵抗力D.用工业酒精兑制白酒12.在生产和科学研究中,需要用到一些保护气。
当焊接金属时,为了隔绝空气,能作为保护气的一组是(D)A.H2、N2B.N2、O2 C.CO2、CO D.N2、Ar13.钛和钛的合金被认为是21世纪的重要材料,它们具有很多优良的性能,如熔点高、密度小、可塑性好、易于加工,钛合金与人体有很好的“相容性”。
根据它们的主要性能,以下用途不切合实际的是(A)A.用来做保险丝B.用于制造航天飞机C.用来制造人造骨D.用于制造船舶14.某星期天,小明同学回家发现自家田里的小麦出现大面积倒伏现象,就向其父母提出了一条合理化建议:明年应在小麦生长期增施抗倒伏的化肥,你认为增施的化肥是(D )A.NH4NO3 B.CO(NH2)2 C.Ca(H2PO4)2 D.KCl15.以下情况:①煤的燃烧;②工业废气的任意排放;③燃放鞭炮;④用汽油为燃料的汽车尾气的排放;⑤用氢气为燃料的新型燃气车排放的尾气。
2005年湖北黄冈市中考数学试题及答案(实验区)-推荐下载

D.16
500
200
E
Q(升)
O5 B
O5
Q(升)
120%
83%
D
9 D
F
50 t(分钟) 3
95 t(分钟)
100
95%
C
13、(本题满分 7 分)你喜欢玩游戏吗?现请你玩一个转盘游戏。如图所示的两个转盘中 指针落在每一个数字上的机会均等,现同时自由转动甲乙两个转盘,转盘停止后,指针各 指向一个数字,用所指的两个数字作乘积。
⑵
D.– 1
B. x3 x5 x8
1
你学习
1
D.( 2x – 3 y) (– 2x + 3y ) = 4x 2 – 9 y 2
,将 x – xy 2 分解因式
祝
进步
1
;
个空心圆;
9、不等式组 2x 1 3
3x 1 x 3 8
1 2
x
1
的解集应为( )
A、 x 2 B、 2 x 2 C、 2 x 1 D、 x 2 或 7
2.反比例函数 y = x的图象经过点(tan45°,cos60°),则 k =
3、水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表示。
如图是一个正方体的平面展开图,若图中的“进”表示正方体的前面,“步”表示右面,
“习”表示下面,则“祝”、“你”、“学”分别表示正方体的________。
3
12、某超市购进了一批不同价格的皮鞋,下表是该超市在近几年统计的平均数据。
皮鞋价(元) 160
销售百分率
60%
要使该超市销售皮鞋收入最大,该超市应多购( )的皮鞋。
140%
75%
A、160 元 B、140 元 C、120 元 D、100 元
近十年(2003-2012年)黄冈中考数学试题及答案

⑴ 由观察所得, 班的标准差较大; ⑵ 若两班合计共有 60 人及格,问参加者最少获 分才可以及格。 四、多项选择题(本大题共两道小题,每小题 4 分,共 8 分,在每小题给出的四个选项中, 至少有一项是符合题目要求的,请把所有符合题目要求的答案的序号填入题后的括号 内,全对得 4 分;对而不全的酌情扣分;有对有错、全错或不答的均得 0 分) 15. 下列各式经过化简后与 27x 3 是同类二次根式的是( (A) ) .
21. (11 分)在全国抗击“非典”的斗争中,黄城研究所的医学专家们经过日夜奋战,终于 研制出一种治疗非典型肺炎的抗生素.据临床观察:如果成人按规定的剂量注射这种抗 生素,注射药液后每毫升血液中的含药量 y(微克)与时间 t(小时)之间的关系近似地
满足图所示的折线. ⑴ 写出注射药液后每毫升血液中含药量 y 与时间 t 之间的函数关系式及自变量的取值范 围; ⑵ 据临床观察:每毫升血液中含药量不少于 4 微克时,控制“非典”病情是有效的.如 果病人按规定的剂量注射该药液后,那么这一次注射的药液经过多长时间后控制病情开 始有效?这个有效时间有多长? ⑶ 假若某病人一天中第一次注射药液是早晨 6 点钟,问怎样安排此人从 6:00~20:00 注射药液的时间,才能使病人的治疗效果最好?
n 5 0 ,则 m=
。
,n =
,此时将 mx2 ny2 分解因式得
mx2 ny2 =
4. 顺次连结菱形四条边的中点的四边形是 5. 当 x=sin60°时,代数式
形. 。
2x 2 4x x 2 2x 4x 2 的值等于 x2 x 4x 4 2 x
Байду номын сангаас
6. 如图,把直角三角形 ABC 的斜边 AB 放在定直线 l 上,按顺时针 A 向在 l 上转动两次, 使它转到△A’’B’’C’’的位置.设 BC=1,AC= 3 ,则顶点 A 运动到点 A’’的位置时, 点 A 经过的路线与直线 l 所围成的面积是 (计算结果不取近似
湖北省黄冈市2005年中考试卷
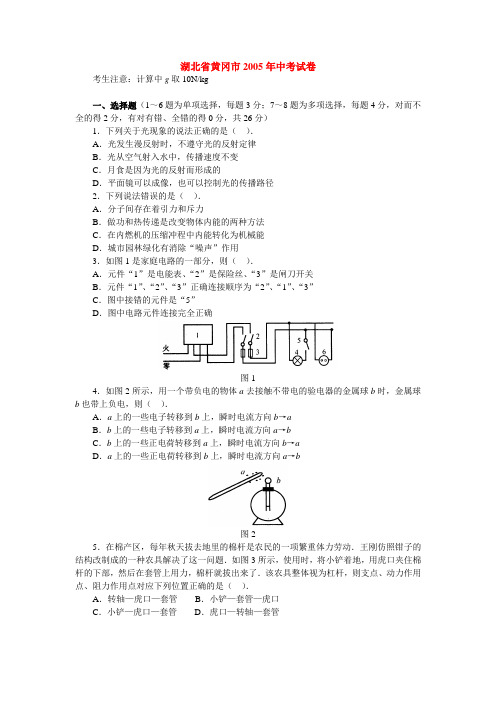
湖北省黄冈市2005年中考试卷考生注意:计算中g取10N/kg一、选择题(1~6题为单项选择,每题3分;7~8题为多项选择,每题4分,对而不全的得2分,有对有错、全错的得0分,共26分)1.下列关于光现象的说法正确的是().A.光发生漫反射时,不遵守光的反射定律B.光从空气射入水中,传播速度不变C.月食是因为光的反射而形成的D.平面镜可以成像,也可以控制光的传播路径2.下列说法错误的是().A.分子间存在着引力和斥力B.做功和热传递是改变物体内能的两种方法C.在内燃机的压缩冲程中内能转化为机械能D.城市园林绿化有消除“噪声”作用3.如图1是家庭电路的一部分,则().A.元件“1”是电能表、“2”是保险丝、“3”是闸刀开关B.元件“1”、“2”、“3”正确连接顺序为“2”、“1”、“3”C.图中接错的元件是“5”D.图中电路元件连接完全正确图14.如图2所示,用一个带负电的物体a去接触不带电的验电器的金属球b时,金属球b也带上负电,则().A.a上的一些电子转移到b上,瞬时电流方向b→aB.b上的一些电子转移到a上,瞬时电流方向a→bC.b上的一些正电荷转移到a上,瞬时电流方向b→aD.a上的一些正电荷转移到b上,瞬时电流方向a→b图25.在棉产区,每年秋天拔去地里的棉杆是农民的一项繁重体力劳动.王刚仿照钳子的结构改制成的一种农具解决了这一问题.如图3所示,使用时,将小铲着地,用虎口夹住棉杆的下部,然后在套管上用力,棉杆就拔出来了.该农具整体视为杠杆,则支点、动力作用点、阻力作用点对应下列位置正确的是().A.转轴—虎口—套管B.小铲—套管—虎口C.小铲—虎口—套管D.虎口—转轴—套管图36.如图4所示的电路,下列分析正确的是( ). A .1S 断开,2S 、3S 闭合,电路总电阻最大 B .3S 断开,1S 、2S 闭合,电路总电阻最小 C .3S 闭合,1S 、2S 断开,1L 、2L 并联 D .1S 闭合,2S 、3S 断开,1L 、2L 串联图47.火车减速进站的过程中,下列说法正确的是( ). A .火车的动能在不断减小B .火车在水平方向受到的合力为零C .火车在竖直方向上受到一对平衡力作用D .火车刹车是利用增大闸瓦对车轮的压力来增大摩擦的 8.关于电和磁,下列说法中正确的是( ). A .磁场是由无数磁感线组成的B .指南针能指南北是因为地球周围存在磁场C .只要导体在磁场中运动,就能产生感应电流D .电动机转动过程是电能转化为机械能的过程二、填空题(每题3分,共15分) 9.六月中旬,“非典”得到了有效的控制,但人们对其防范措施没有减弱.一天,小明早上照例测量体温后,用力甩了体温计,随即将体温计放到窗台上,上学去了.晚上回家发现体温计的示数为________℃(如图5所示).他以此判断今天的最高气温应________(选填“>”、“<”或“=”)这个示数,其理由是________.图510.上物理课复习时,老师写下一副热学对联,上联是“杯中冰水,水结冰冰温未降”;下联是“盘内水冰,冰化水水温不升”.对联中包含的状态变化是________和________,反映一个共性是____________________________________________________________.11.小华参观展览会,在一个小展室里可见一个女导游在介绍商品,如图6所示,试着与她握手,却发现是一个虚拟导游,可望不可及.后来他发现这个女导游只是在一个玻璃屏风后倒立的电视机屏幕上经过处理的一个形象而已.则这个玻璃屏风是________镜,这个虚拟导游是________像(选填“虚”或“实”),电视机屏幕与玻璃屏风的距离应满足的条件是___________________________________________________________.图612.一天,小明看到煤气公司价格牌上写着:冬季55元/瓶,夏季51元/瓶.他寻思着,为什么夏季价格低?他查找了煤气资料:煤气冬季密度33kg/m 100.88⨯,夏季33kg /m 100.8⨯,煤气瓶容积30.015m .通过计算发现夏季价格比冬季价格________(选填“高”或“低”).若两季价格一样,夏季应标价为________元/瓶.如果按质量计价,煤气价格应是________元/kg . 13.如图7是某同学利用一端封闭的玻璃管探究气体体积与压强关系的实验装置图.实验时,用水银在管内封入一定质量的气体,将管倒插在水银槽中,使管内外水银面相平,此时管内空气柱的长度4cm .每向上提起玻璃管时,管内水银面升高、空气柱增长,并作相应测量.下表是该同学在实验过程中记录的部分数据.(在实验过程中温度保持不变,外界压强始终为76cmHg 0=p ,玻璃管横截面积为22cm )(1)第3次遗漏的数据应为________3cm ,第4次遗漏的数据为________cm . (2)通过上面实验数据分析可得出一个结论:一定质量的气体,温度不变时,_______ ________________.图7三、作图题(每题2分,共6分)14.如图8是美国轰炸伊拉克的精确制导导弹,正在飞向巴格达.请在图中作出导弹的受力示意图.图815.图9中的两架敌机,一架是实际飞机,一架是从潜水艇上观察到的该飞机的像,请用光的作图法确定哪架是实际飞机.图916.为迎接体育中考,某同学自行设计了如图10所示的握力计.弹簧处于自然状态时,滑片P与滑动变阻器R断开,当手在A、B之间握压时,压缩弹簧,P在R上滑动,握力越大,电流表示数越大.请用笔画线完成电路连接.图10四、综合题(共23分,要求写出必要的文字说明、公式和过程,只有最后结果的不得分)17.(5分)今年6月1日三峡库区正式蓄水,6月2日文物工作者还在加紧库区的文物挖掘和搬迁工作,一位工作者发现了一古代的小酒杯.请你选用下列提供的器材测量小酒杯的密度(酒杯的密度大于水的密度,水作为辅助器材可以直接选用).器材:①量筒(内径大于酒杯的口径)②天平③弹簧测力计④刻度尺⑤密度计⑥细线(1)实验器材:___________________(只填序号)(2)实验步骤:(3)密度表达式:ρ=18.(5分)市场上有一种双能源太阳能热水器,晴天享用太阳能,阴天可用电加热.如图11是该热水器电路图.电热管R 标有“220V 1100W ”字样,0R 与R 构成保温电路.当S 连到2时,电热管正常工作,给水箱里的水加热;当S 连到3时,热水器处于保温状态,保温功率为100W . (1)求R 、0R 的值.(2)保温时R 实际功率是多少?图1119.(6分)如图12是某养鱼专业户设置在鱼池中央的增氧机,它由三个浮球和连杆把电动潜水泵固定在一起构成,整个设备总质量300kg ,潜水泵额定电功率3kW .增氧机不工作时,浮球有一半露出水面.增氧机工作时,即潜水泵抽水,每5min 可将kg 101.444⨯水送到5m 高的空中让其自由下落,从而达到增氧目的.(1)连杆和水泵的体积不计,每个浮球的体积是多少? (2)增氧机正常工作时,其效率为多少?(3)增氧机工作时,试分析浮球露出水面的体积有何变化?(不计算,只作答)图1220.(7分)如图13是HG2003家用蒸汽电熨斗示意图和铭牌.使用时水箱中的水滴入被加热的底板气室迅速汽化产生向下的蒸汽.图13(1)某师傅在用熨斗干烫衣服时,用了19N 向下的力压熨斗,在此过程中,衣服受到的压强是多大?(2)用熨斗汽烫时先预热,使金属底板的温度从20℃升高到220℃,温控开关自动断开.已知底板的质量为1kg ,铁的比热容为J 100.463/(kg ·℃).问蒸汽电熨斗预热时底板吸收多少热量?(3)汽烫时,水滴入汽室,由于水升温汽化带走热量.当底板温度降到190℃时,温控开关自动闭合,当加热到220℃时又断开,如此反复.若蒸汽电熨斗大体按图14所示程序工作,10min 烫一件衣服共消耗多少电能?图14参考答案一、选择题(1~6题为单项选择,每题3分;7~8题为多项选择,每题4分,对而不全的得2分,有对有错、全错的得0分;共26分)1.D 2.C 3.C 4.A 5.B 6.D 7.A 、C 、D 8.B 、D 二、填空题(每题3分,每空1分,共15分)9.35 = 体温计有小缩口,温度上升时,水银柱上升,温度降低时,水银柱不下降10.凝固 熔化 温度不变(或“晶体物质在熔化、凝固过程中温度保持不变”) 11.凸透镜 实 大于1倍焦距小于2倍焦距 12.高 50 4.17 13.16 57 体积与压强成反比(或“压强越大,体积越小”)三、作图题(每题2分,共6分)14.要求作出三个力,即重力、阻力、推力15.要求光路完整,光线行进方向、虚实线正确16.要求变阻器下端连入电路,注意电池、电流表正负接线柱,确保握力大,电流指示增大四、综合题(共23分,要求写出必要的文字说明、公式和过程,只有最后结果的不得分,下面给出的解答仅供参考,其他解法,只要正确合理,参照给分) 17.(5分)器材1分;步骤3分;表达式1分.任何方法合理即可,下面提供三种方法.方法一:(1)天平、量筒(2)a .用天平测出小酒杯的质量m b .让量筒装一定体积的水,记1Vc .将小酒杯浸没入量筒的水中,记下液面示数2V (3)12V V m-=ρ方法二:(1)弹簧测力计、量筒、细线 (2)a .让量筒装适量的水b .用细线系住小酒杯,然后用弹簧测力计测其重力Gc .再将小酒杯浸没入量筒的水中,读出弹簧测力计的示数F(3)水-=ρρFG G方法三:(1)量筒(2)a .让量筒装一定体积的水,记1Vb .将小酒杯漂浮在水面,记下液面示数2Vc .将小酒杯浸没入水中,记下液面示数3V (3)水--=ρρ1312V V V V18.(5分)(1)Ω44W1100)V 220(22===P U R (1分) S →2时,只有R 接入电路,R 正常工作,故电源电压U =220V S →3时,R 和0R 串联,W 100'=P∵ 02'R R U P +=∴ R P U R -'20= Ω=Ω-44044W100)V 220(2=(2分) (2)保温时,流过R 的电流'I ,有 A 115220V W 100''==U P I =R 消耗的实际功率W 1.944)A 115('22===Ω⨯R I P R (2分) 19.(6分) (1)m =300kg增氧机不工作时,它漂浮在水面上,有G F =浮 设每个浮球的体积为V ,则浮力浮F 有 Vg g V F ρρ23==排浮,mg G = (1分) ∴mg Vg =ρ23∴ 33k g /m100.13kg300232⨯⨯⨯=ρm V =3m 2.0= (2分)(2)P =3000W ,t =5min =300s ,kg 101.444⨯=水m h =5m ,则 有用功mgh W =有5m 10N/kg kg 101.444⨯⨯⨯=J 107.25⨯=总功J 109300s 3000W 5⨯⨯===总Pt W (1分)效率%====总有808.0J109J102.755⨯⨯W W η (1分) (3)增氧机工作时,对喷出水有向上的作用力,由于力的作用是相互的,故水对增氧机有向下的作用力,浮球要下沉一些,露出水面的体积要减小 (1分) 20.(7分) (1)m =1.3kg ,'F =19N ,222m 101.6160cm -==⨯S熨斗熨烫衣服时,对衣服的压力F =mg +'F =1.3kg ×10N/kg +19N =32N 2000P a m101.632N22===-⨯S F P (2分) (2)1kg '=m ,J 100.463⨯=c /(kg ·℃),0t =20℃,t =220℃,则 )('0t t cm Q -=吸3100.46⨯=J/(kg ·℃)×1kg ×(220℃-20℃)J 109.24⨯= (3分) (3)P =1000W ,450s 5s15s 15ss 600=+=⨯t ,则W =Pt =1000W ×450s =5104.5⨯J (2分)。
黄冈市中考数学试题与答案

2003黄冈市中考数学试卷与答案一、填空题(每小题 3分,共18分)1. 一 4的相反数是;一 8的立方根是;9的平方根是.2. 2003年6月1日9时,举世瞩目的三峡工程正式下闸蓄水,首批4台机组率先发电,预计年内可发电5 500 000 000度,这个数用科学记数法表示,记为度. 近似数0 . 30精确到位,有个有效数字.3. 若 m —1+(JF —5)= 0 ,贝U m =, n =,此时将 mx 2 - ny 2分解因式得 mx 2 - ny 2 =。
4•顺次连结菱形四条边的中点的四边形是形.使它转到厶A'B'C'的位置•设BC = 1, AC =3,则顶点 A 运动到点A'的位置时,点A 经过的路线与直线I 所围成的面积是(计算结果不取近似、单项选择题(每小题 3分,共15 分)).(A ) (a+bf=a 2+b 2(B ) a 3+a 2=2a 5(C ) (—2x 3 f = 4x 6(D ) (-1)4=18. 在直角坐标系中,点 P (2x — 6, x — 5)在第四象限,贝U x 的取值范围是().(A ) 3v x v 5( B ) 一■ 3v x v 5 ( C ) 一■ 5 v x v 3 ( D ) 一■ 5v x v — 39. 在厶 ABC 中,AB = AC = 3, BC = 2,贝 U 6cosB 等于().(A ) 3( B ) 2 (C ) 3 3 ( D ) 2.32 210. 关于x 的方程k x 2k -1 x 0有实数根,则下列结论正确的是().(A )1当k = 时方程两根互为相反数(B )当k = 0时方程的根是x =— 1 (C )当k =士 12一 1 一时方程两根互为倒数(D )当k < 时方程有实数根411. 某公司员工分别住在 A , B , C 三个住宅区, A 区有30人,B 区有15人区有10人.三 个区在同一条直线上,位置如图所示•该公司的接送车打算在此间只设一个停靠点, 为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在 ().(A ) A 区 (B ) B 区 (C ) C 区 (D ) A , B 两区之间5.当x = sin60°时,代数式 c 2 ‘2x —4x----------- x2x 2x出的值等于。
黄冈中考数学试题及答案2005
二00五年湖北省黄冈市初中升学统一考试数 学 试 题<课改区)<满分:120分 考试时间:120分钟)一、填空题<每空3分,共24分)1.错误!的相反数是 ,立方等于– 64的数是 ,将x – xy 2分解因式的结果是 ;iKzaInL3ic 2.反比例函数y = 错误!的图象经过点<tan45°,cos60°),则k = ;iKzaInL3ic 3、水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表示。
如图是一个正方体的平面展开图,若图中的“进”表示正方体的前面,“步”表示右面,“习”表示下面,则“祝”、“你”、“学”分别表示正方体的________。
iKzaInL3ic4某一时刻测得一棵小树的高为1.5M 这棵大树的影长为3M ,则这棵大树的实际高度为 M ;iKzaInL3ic5.某同学在电脑中打出如下排列的若干个圆<图中●表示实心圆,○表示空心圆):● ○●●○●●●○●●●●○●●●●●○●●●●●●○若将上面一组圆依此规律复制得到一系列圆,那么前2005个圆中有 个空心圆;6、图⑴中的梯形符合____条件时,可以经过旋转和翻折形成图案⑵。
号里,不填、错填或多填均不得分,每小题3分,共18分)iKzaInL3ic 7.已知y x ,为实数,且()02312=-+-y x ,则y x -的值为< )A .3B .– 3C .1D .– 18.下列运算中正确的是< ) A .10552x x x =+B .()()853x x x -=-∙--C .(– 2x 2y> 3·4x – 3 = – 24x 3y 3D .( 错误!x – 3 y> (– 错误!x + 3y > = 错误!x 2 – 9y 2iKzaInL3ic 9、不等式组()()⎪⎩⎪⎨⎧≤--+<--+-1213128313xx x x 的解集应为< ) ⑴ ⑵A 、2-<xB 、722≤<-x C 、12≤<-x D 、2-<x 或x ≥110、如图,在平行四边形ABCD 中,EF ∥AB ,DE ∶EA = 2∶3,EF = 4,则CD 的长为< )iKzaInL3icA .错误!B .8C .1011是一定的。
湖北省黄冈市2005年初中升学统一考试1

湖北省黄冈市2005年初中升学统一考试英语试题试卷类型:A(满分120分,考试用时120分钟)考生注意:本试题分为选择题和非选择题两大部分。
选择题的答案必须用2B铅笔填涂在答题卡上,写在试卷上无效;非选择题请用黑色墨水的钢笔或中性笔直接在试卷上解答。
第一部分选择题(共80分)一、听力(共二节,计25分)得分评卷人第一节(共9小题;每题1分,满分9分)听下面9段对话。
每段对话后面有一个小题,从题后所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. A. Good. B. Not bad. C. Very good.2. A. He likes to stay and play after school. B. He likes to do his homework after school.C. He likes school and does homework every day.3. A.2. B.3. C.1.4. A. Headmaster and students. B. Teacher and students. C. Parents and children.5. A. There’s something wrong with her throat. B. She doesn’t want to read that.C. She is modest.6. A. Raining heavily. B. Snowing, but not heavily. C. Snowing heavily.7. A.11:15. B.11:05. C. 10:11.8. A. He was cleaning the floor. B. He was drawing on the wall. C. He was playing football.9. A. The cinema. B. The office. C. The hospital.得分评卷人第二节(共16小题;每题1分,满分16分)听下面5段对话或独白。
湖北省黄石市2005年初中升学统一考试数学试卷(含解答)-
湖北省黄石市2005年初中升学统一考试数学试卷一、单项选择题(本大题共12小题,每小题3分,满分36分) 1.9的平方根是( )A .3B .±3C .-3D .±31 2.下列计算正确的是( )A .a 3-a 2=aB .(a 2)3=a 5C .a 6÷a 2=a 3 D .a 2·a 3=a 53.如图:D 是△ABC 的AB 边上的一点,过点D 作DE ∥BC 交AC 于E , 若AD :DB=1:2,则BC :DE 等于( ) A .B .C .D .A .1:3B .2:3C .3:1D .2:1 4.据2004年《黄石年鉴》记载,2003年全市财政收入1905000000元,用科学计数法表示为( )A .1.905×109元B .1.905×1010元C .1.905×1011元D .1.905×1012元 5.下列图案中既是中心对称图形,又是轴对称图形的是( )6.函数112-+=xx y 的自变量x 的取值范围是( ) A .21-≥x B .1≠x C .121-≠-≥x x 且 D .121≠-≥x x 且 7.解方程0322222=--+-x x x x ,如果设y x x =-22,那么原方程组可化为( ) A .0232=++y y B .0232=+-y y C .0232=-+y yDE B AD .0232=--y y8.已知0>k ,则函数xky kx y -==,r 的图象大致是下图中的()A .B .C .D .9.已知关于x 的不等式2x+m>-5的解集如图所示,则m 的值为( ) A .1 B .0 C .-1 D .-210.如图所示,把一个正方形三次对折后沿虚线剪下,则所得图形是( )11.下列四个命题(1)对角线互相垂直的平行四边形是正方形; (2)对角线相等的梯形是等腰梯形. (3)过弦的中点地直线必经过圆心; (4)圆的切线垂直于经过切点的半径. 其中正确的命题是( )A .(1)、(2)B .(2)、(3)C .(2)、(4) D.(1)、(4)12.小阳发现电线杆AB 的影子落在土坡的坡面CD 和地面BC上,量得CD=8米,BC=20米,CD 与地面成30º角,且此时测得1米杆的影长为2米,则电线杆的高度为( )A .9米B .28米C .()37+米 D.()3214+米 二、填空题(本大题共5小题,每小题3分,满分15分)13.最简根式b a a b a 23++与是同类二次根式,=ab ___________.14.已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为________. 15.分解因式:=--+22962y y x x ____________________________________. 16.民意商场对某种商品作调价,按原价8折出售,此时商品的利润是10%,此商品的进价为1000元,则商品的原价是____________.17.矩形ABCD 中,AB=8,BC=15,如果分别以A 、C 为圆心的两圆相切,点D 在⊙C 内,点B 在⊙C 外,那么⊙A 的半径r 的取值范围是___________________. 三、解答题(本大题有8个题,满分69分)18.(本题满分7分)计算:()()23217227215-----+⎪⎭⎫⎝⎛+--.19.(本题满分7分)先化简再求值.2222222323ba aba b ab a b a b a ab --÷+++-,其中115-=+=5b a ,.20.(本题满分7分)已知:如图,AD=BC ,∠D=∠C ,AC 交BD 于点E ,求证:AC=BD.DECBA21.(本题满分8分)一次函数b x y +=与反比例函数xk y 3+=图象的交点为A(m,n),且m,n(m<n)是关于x的一元二次方程()03722=++-+k x k kx 的两个不相等的实数根,其中k 为非负整数,m,n 为常数.(1) 求k 的值;(2) 求点坐标与一次函数的解析式.22.(本题满分8分)初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图A 、D 是人工湖边的两座雕塑,AB 、BC 是湖滨花园的小路,小东同学进行如下测量,B 点在A 点北偏东60º方向,C 点在B 点北偏东45º方向,C 点在D 点正东方向,且测得AB=20米,BC=40米,求AD 的长。
2005年数学中考模拟试题

ABC(B) D ABC(D)…(A)D lABCDE湖北省黄冈市2006年初中学业水平考试数学试题(课改实验区)(考试时间120分钟 满分120分)一.填空题(每空3分,满分24分)01.=02 ,4的算术平方根是 ,2cos60°+tan45°= 。
02.函数x y -=2中自变量x 的取值范围是 。
03.化简=32。
04.将a a -3分解因式,结果为 。
05.已知圆锥的侧面展开图是一个半园,则这个圆锥的母线长与底面半径长的比是 。
06.将边长为8cm 的正方形ABCD 的四边沿直线l 想右滚动(不滑动),当正方形滚动两周时,正方形的顶点A 所经过的路线的长是 cm 。
二.单项选择题(请将下列各题中唯一正确的答案序号填入题后的括号内,不填、填错或多填均不得分,每小题3分,共15分)07.下列运算正确的是( )A 、23532x x x -=- B 、52232=+C 、5)(x -²102)(x x -=-D 、5235363)3()93(a x ax ax x a -=-÷- 08.反比例函数22)12(--=m xm y ,当x >0时,y 随x 的增大而增大,则m 的值时( )A 、±1B 、小于21的实数 C 、-1 D 、1 09.计算:329632-÷--+m m m m 的结果为( ) A 、1 B 、33+-m m C 、33-+m m D 、33+m m10.一个无盖的正方体纸盒,将它展开成平面图形,可能的情形共有( )A 、11种B 、9种C 、3种D 、7种 11.如图,在光明中学学生耐力测试比赛中,甲、乙两学生测试的路程S(米)与时间t(秒)之间的函数关系图像分别为折线OABC和线段OD ,下列说法正确的是( ) A 、乙比甲先到达终点B 、乙测试的速度随时间增加而增大C 、比赛进行到29.4秒时,两人出发后第一次相遇D 、比赛全程甲的测试速度始终比乙的测试速度快三.解答下列各题12.(本题满分6分)如图,DB ∥AC ,且DB=21AC ,E 是AC 的中点,求证:BC=DE 。
2005年湖北省武汉中考非课改区数学卷-中考数学试题、初中数学中考试卷、模拟题-初中数学试卷

2005年湖北省武汉中考非课改区数学卷-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载2005年武汉市中考数学试题及答案A卷一、判断题(共10小题,每小题2分,共20分)下列各题请你判断正误,若是正确的,请在答题卡上将A涂黑,若是错误的,请在答题卡上将B涂黑。
1.方程的二次项系数为3,一次项系5。
2.函数中,自变量x的取值范围是。
3.直角坐标系中,点P(6,-7)在第四象限。
4.函数是反比例函数。
5.数据5,3,7,8,2的平均数是5。
6.。
7.在同圆或等圆中,相等的圆心角所对的弧相等。
8.长度相等的两弧是等弧。
9.三角形的外心到三角形各顶点的距离都相等。
10.两圆相外切,这两个圆的公切线共有三条。
二、选择题(共10小题,每小题4分,共40分)下列各题均有四个备选答案,其中且只有一个是正确的。
请在答题卡中将正确答案的代号涂黑。
11.一元二次方程的根为().(A)x=1(B)x=-1(C),(D)12.不解方程,判别方程5-7x+5=0的根的情况是().(A)有两个相等的实数根(B)有两个不相等的实数根(C)只有一个实数根(D)没有实数根13.函数中自变量x的取值范围是().(A)x≠-1 (B)x>-1(C)x≠1(D)x≠014.下列函数中,一次函数是().(A)(B)(C)(D)15.一次函数y=x+1的图象在().(A)第一、二、三象限(B)第一、三、四象限(C)第一、二、四象限(D)第二、三、四象限16.如图,已知圆心角∠BOC=,则圆周角∠BAC的度数为().(A)(B)(C)(D)17.已知圆的半径为6.5cm,如果一条直线和圆心的距离为9cm,那么这条直线和这个圆的位置关系是().(A)相交(B)相切(C)相离(D)相交或相离18.已知∠和∠的半径分别为3cm和4cm,圆心距=10cm,那么∠和∠的位置关系是().(A)内切(B)相交(C)外切(D)外离19.过∠内一点M的最长弦长为10cm,最短弦长为8cm,那么OM的长为().(A)3cm(B)6cm(C)cm(D)9cm20.若二次函数,当x取,(≠)时,函数值相等,则当x取+时,函数值为().(A)a+c(B)a-c(C)-c(D)cB卷三、选择题下列各题中均有四个备选答案,其中有且只有一个是正确的。
