画直线算法
直线算法的技巧

直线算法的技巧直线算法是计算机图形学中最基本的算法之一,用于在屏幕上绘制直线。
本文将就直线算法的一些技巧进行详细讲解。
直线算法通常需要一个起始点(x1, y1)和一个终止点(x2, y2),然后在这两个点之间绘制一条直线。
最基本的直线算法是数字微分分析法(DDA)和中点画线法(Bresenham算法)。
这两种算法的核心思想都是利用直线的斜率来进行像素点的逼近。
在使用DDA算法绘制直线时,可以通过增加步长来减少精度损失。
DDA算法的步骤如下:1. 计算斜率:计算直线的斜率m = (y2 - y1) / (x2 - x1)。
2. 判断斜率:判断斜率的绝对值是否在0和1之间。
如果是,我们可以选择在x上递增逼近y或在y上递增逼近x。
3. 增加步长:计算递增的步长,对于长度较大的直线,可以通过增加步长来减少计算数量。
4. 开始绘制:从起始点开始,根据斜率和步长计算下一个要绘制的像素点的坐标。
5. 终止条件:当当前的坐标达到终止点时,终止绘制。
中点画线法(Bresenham算法)是一种更高效的直线算法,它通过使用整数运算和位移来避免了浮点数运算,提高了绘制速度。
Bresenham算法的步骤如下:1. 初始化:初始化起始点(x1, y1)和终止点(x2, y2),并计算dx = x2 - x1 和dy = y2 - y1 。
2. 计算斜率:判断斜率m = dy / dx,以决定使用什么方式增加x和y的值(水平递增或垂直递增)。
3. 计算误差:计算误差项E = -0.5,并对dx和dy进行判断,确定每个点移动时误差项的变化。
若dx > dy,则E += dy;否则,E += dx。
4. 绘制像素点:从起始点开始,每次根据误差项判断,决定是在y上递增还是在x上递增,并根据计算出的新的坐标绘制像素点。
5. 更新误差项:在每次绘制完成后,根据dx和dy更新误差项的值。
6. 终止条件:当当前的坐标达到终止点时,终止绘制。
dda算法画直线例题

dda算法画直线例题dda算法是一种常用于计算机图形学中的算法,用于在计算机中绘制直线或其他几何形状。
本例题将通过dda算法绘制一条直线,帮助读者了解该算法的基本原理和应用。
一、算法概述dda算法是一种分治算法,它将原始的直线绘制问题分解为更小的子问题,逐个解决这些子问题,最终得到完整的绘制结果。
该算法的核心思想是通过逐点地更新像素位置,逐步逼近目标位置,从而实现直线的绘制。
二、实现步骤1.初始化:设置绘图窗口大小,确定要绘制的直线起点和终点。
2.循环迭代:对于每个像素点,按照dda算法的步骤进行更新。
具体步骤如下:a.计算当前像素点到直线起点的距离(dx),并将其与偏移量(delta)比较。
b.如果dx小于或等于delta,则当前像素点已经在直线上,无需进一步更新。
c.否则,根据dda算法的公式计算新的像素位置(new_x),并将其与当前像素位置进行比较。
d.如果new_x小于或等于当前像素位置,则将当前像素位置更新为new_x;否则,继续迭代下一个像素点。
3.重复步骤2直到绘制完整个窗口。
三、代码实现以下是一个简单的代码实现,使用c语言描述dda算法绘制直线的过程:```c#include<stdio.h>#include<stdlib.h>#include<math.h>#defineWIDTH800//绘图窗口宽度#defineHEIGHT600//绘图窗口高度voiddraw_line(intstart_x,intstart_y,intend_x,intend_y){inti,j,dx,dy,delta,new_x,new_y;for(i=0;i<HEIGHT;i++){for(j=0;j<WIDTH;j++){dx=end_x-start_x;dy=end_y-start_y;delta=sqrt(dx*dx+dy*dy);//计算偏移量if(dx<=delta||j==0){//如果当前像素点到直线起点的距离小于或等于偏移量,或者当前像素位置是第一帧,直接输出当前像素位置printf("%d,%d",j,i);}else{//否则,根据dda算法的公式计算新的像素位置并输出new_x=start_x+(j-WIDTH/2)*dx/delta;new_y=start_y+(i-HEIGHT/2)*dy/delta;printf("%d,%d",new_x,new_y);}}printf("\n");//换行}}intmain(){intstart_x=50,start_y=50;//直线起点坐标intend_x=200,end_y=150;//直线终点坐标draw_line(start_x,start_y,end_x,end_y);//绘制直线并输出结果return0;}```这段代码通过循环迭代的方式,逐点更新像素位置,从而实现直线的绘制。
直线生成算法DDA、Midpoint、Bresenham

1、直线生成算法1.算法分析1)DDA设直线两端点:P1(x1,y1)及 P0(x0,y0),dx=x1-x0,dy=y1-y0直线斜率:k=dy/dx直线方程: y=k*x+b有:y1=k*x1+b=k*x0+k*dx+b=y0+k*dx当dx=1时,有y1=y0+k算法复杂度:加法+取整优点:避免了y=k*x+b 方程中的浮点乘法,比直接用点斜式画线快 缺点:需浮点数加法及取整运算,不利于硬件实现.2)Midpoint当前像素点为P(xP,yP),下一个像素点有两种可选择点P1(xP+1,yP),P2(xP+1,yP+1)。
若M=(xP+1,yP+0.5)为P1与P2的中点,Q 为理想直线与x=xP+1垂线的交点。
x Pi=(xi, yi ) M Q P1 p2y当M 在Q 的上方时,应取P1为下一点;当M 在Q 的下方时,应取P2为下一点;直线段L (P0(x0,y0),P1(x1,y1)),用方程F (x,y )=ax+by+c=0表示 a=y0-y1,b=x1-x0,c=x0y1-x1y0有点与L 的关系:线上:F (x,y )=0上方:F (x,y )>0下方:F (x,y )<0判别式:d=F(M)=F(xP+1,yP+0.5)=a(xP+1)+b(yP+0.5)+cD 是xP,yP 的线性函数,可采用增量计算,提高运算效率:1)若d>=0,取P1,d1=d+a,增量为a2)若d<=,取P2,d2=d+a+b,增量为a+b可用2d 代替d 来摆脱浮点运算,写出仅含整数运算的算法3)Bresenhamy x F(x,y)=0 F(x,y)>0 F(x,y)<0 (x1,y1)(x0,y0)设直线方程为y=kx+b,有y1=y0+k(x-x0)=y0+k是否增1取决于误差项d的值,初始值d0=0X每增加1,有d=d+k令e=d-0.5,e0=-0.5,增量为k当e>=0时,取当前像素(xi,yi)的右上方像素(xi+1,yi+1),e 减小1;当e<0时,更接近于右方像素(xi+1,yi)。
简述画直线的几种操作方式

简述画直线的几种操作方式一、概述画直线是计算机图形学中的基本操作之一,通常用于绘制线条、边框等。
在计算机图形学中,有多种方式可以实现画直线的功能。
本文将介绍几种常见的画直线操作方式。
二、DDA算法DDA算法是一种基本的画直线算法,它采用逐点比较的方式来确定像素点的位置。
具体实现过程如下:1. 计算出两个端点之间的斜率k;2. 根据斜率k确定每个像素点在x轴和y轴上移动的距离;3. 从起始点开始,不断计算下一个像素点的位置,并在屏幕上绘制。
优点:实现简单,适用于硬件实现。
缺点:精度不高,容易出现锯齿状。
三、Bresenham算法Bresenham算法是另一种常见的画直线算法,它采用整数运算来确定像素点位置。
具体实现过程如下:1. 计算出两个端点之间的斜率k;2. 根据斜率k确定每个像素点在x轴和y轴上移动的距离;3. 从起始点开始,根据当前位置和误差值选择下一个像素点,并在屏幕上绘制。
优点:精度高,画出的直线平滑。
缺点:实现复杂,不适用于硬件实现。
四、中点画线算法中点画线算法是一种基于Bresenham算法的改进版,它通过引入中点来减少计算量。
具体实现过程如下:1. 计算出两个端点之间的斜率k;2. 根据斜率k确定每个像素点在x轴和y轴上移动的距离;3. 从起始点开始,根据当前位置和误差值选择下一个像素点,并在屏幕上绘制;4. 在误差值发生变化时,更新中点的位置。
优点:精度高,计算量较小。
缺点:实现复杂,不适用于硬件实现。
五、直线段裁剪直线段裁剪是指将一条直线段截取为位于窗口内部的一段直线。
常见的裁剪算法有Cohen-Sutherland算法和Liang-Barsky算法。
Cohen-Sutherland算法将窗口分为九个区域,并通过比较端点与窗口边界的关系来确定哪些部分需要保留。
Liang-Barsky算法则通过计算交点来确定截取后的直线段。
六、总结以上介绍了几种常见的画直线操作方式,包括DDA算法、Bresenham算法、中点画线算法以及直线段裁剪算法。
DDA算法

2.1.1 生成直线的DDA算法数值微分法即DDA法(Digital Differential Analyzer),是一种基于直线的微分方程来生成直线的方法。
一、直线DDA算法描述:设(x1,y1)和(x2,y2)分别为所求直线的起点和终点坐标,由直线的微分方程得= m =直线的斜率(2-1) 可通过计算由x方向的增量△x引起y的改变来生成直线:x i+1=x i+△x (2-2)y i+1=y i+△y=y i+△x·m (2-3) 也可通过计算由y方向的增量△y引起x的改变来生成直线:y i+1=y i+△y (2-4)x i+1=x i+△x=x i+△y/m (2-5) 式(2-2)至(2-5)是递推的。
二、直线DDA算法思想:选定x2-x1和y2-y1中较大者作为步进方向(假设x2-x1较大),取该方向上的增量为一个象素单位(△x=1),然后利用式(2-1)计算另一个方向的增量(△y=△x·m=m)。
通过递推公式(2-2)至(2-5),把每次计算出的(x i+1,y i+1)经取整后送到显示器输出,则得到扫描转换后的直线。
之所以取x2-x1和y2-y1中较大者作为步进方向,是考虑沿着线段分布的象素应均匀,这在下图中可看出。
另外,算法实现中还应注意直线的生成方向,以决定Δx及Δy是取正值还是负值。
三、直线DDA算法实现:1、已知直线的两端点坐标:(x1,y1),(x2,y2)2、已知画线的颜色:color3、计算两个方向的变化量:dx=x2-x1dy=y2-y14、求出两个方向最大变化量的绝对值:steps=max(|dx|,|dy|)5、计算两个方向的增量(考虑了生成方向):xin=dx/stepsyin=dy/steps6、设置初始象素坐标:x=x1,y=y17、用循环实现直线的绘制:for(i=1;i<=steps;i++){ putpixel(x,y,color);/*在(x,y)处,以color色画点*/ x=x+xin;y=y+yin;}四、直线DDA算法演示:五、直线DDA算法特点:该算法简单,实现容易,但由于在循环中涉及实型数的运算,因此生成直线的速度较慢。
bresenham算法画直线例题

Bresenham算法是计算机图形学中常用的一种画直线的算法。
它的原理是利用像素点在屏幕上的排列规律,从而高效地计算出直线上的像素点。
本文将以一个具体的例题来说明Bresenham算法的原理及应用。
1. 问题描述假设我们需要在一个分辨率为800x600的屏幕上,画一条直线,起点坐标为(100, 200),终点坐标为(400, 300)。
请使用Bresenham算法计算直线上的像素点,并用符号“*”表示出来。
2. Bresenham算法原理Bresenham算法的核心思想是利用像素点的整数坐标值与直线的斜率之间的关系,从而逐个确定直线上的像素点。
具体步骤如下:- 计算直线的斜率k,即k = (y2 - y1) / (x2 - x1),其中(x1, y1)为起点坐标,(x2, y2)为终点坐标。
- 以起点坐标作为初始值,从左至右依次求解直线上各点像素的坐标。
- 对于每一个x坐标,根据斜率k的大小确定y坐标的增长方向。
3. Bresenham算法应用根据上述原理,我们来解决具体的例题。
计算直线的斜率k:k = (300 - 200) / (400 - 100) = 1/3以起点坐标(100, 200)作为初始值,从左至右依次求解直线上各点像素的坐标。
当x坐标从100递增至400时,y坐标的增长方向由斜率k来确定。
具体计算如下:- 当x=100时,y=200- 当x=101时,y=200+1/3≈200- 当x=102时,y=200+2/3≈201- ...- 当x=400时,y=300现在,我们可以得到直线上的像素点坐标,并用符号“*”表示出来。
4. 结果展示根据上述计算,我们可以得到该直线上的像素点坐标,展示如下:(100, 200) *(101, 200) *(102, 201) *...(400, 300) *通过Bresenham算法,我们成功地计算出了直线上的像素点,并用符号“*”进行了展示。
Bresenham快速画3D直线算法

Bresenham快速画3D直线算法--------yangzhengyun一、简述前段时间一个学弟正在做一个LED立方,说想做了送给女友。
但他说在画直线,球,波浪等图案时,总是找不到一个很好的算法,导致显示刷屏很慢甚至出现闪屏的现象,问我有没有什么好的算法。
刚好前段时间我也在弄这个,刚开始的时候,我竟然也被“如何画一条3D直线”难倒了,有的人说——画直线还不简单啊,两个点确定一条直线,那是高中数学里面最简单不过的方程式了。
没错,如果是运用高中的方程式来编程,确实很简单,但是……我们先来看一下直线的方程式吧:如我们知道了两个坐标点:A(x1,y1,z1),B(x2,y2,z2)。
那么直线的方程是:K=(x-x1)/(x2-x1)=(y-y1)/(y2-y1)=(z-z1)/(z2-z1)这就不化简了,但是你们有木有发现一个问题。
对,那就是都是进行浮点运算。
我们试想想,如果是用8位的单片机来做的话,速度不知道将会慢到什么程度了。
且,画直线函数基本可以说是底层的驱动函数,如果一个驱动函数都占据了很多的运行时间的话,上层的代码写的再好也是无用的。
为此我们必须找到一个好的办法,避开浮点运算。
即把浮点数据转换成整形数据进行运算,这样速度可以得到很大的提升。
为此,我们首选的就是Bresenham算法了,它引入了一个误差常量e(即后面用到的ey,ez),e的值为-1/2;在这个运算思路中,我们还是要用到上面的直线方程做为基础。
所以,在看这个代码的时候,你必须先有这点数学的基本知识才行,不然你看的就云里雾里,两眼冒金星了。
下面帖出的是本人经过上网预览大量资料后,写出的三维基于Bresenham算法的画直线函数,二维的就不贴出了,因为二维的在网上有大把的源码,但是三维现成源码就不多了,当然资料还是有的。
里面的算法,和二维算法的思路是一样的,具体的各位学弟们自己去网上查吧,百度一下“Bresenham算法”够你看了,要有多详细有多详细。
Bresenham快速画直线算法

Bresenham快速画直线算法 现在的计算机的图像的都是⽤像素表⽰的,⽆论是点、直线、圆或其他图形最终都会以点的形式显⽰。
⼈们看到屏幕的直线只不过是模拟出来的,⼈眼不能分辨出来⽽已。
那么计算机是如何画直线的呢,其实有⽐较多的算法,这⾥讲的是Bresenham的算法,是光栅化的画直线算法。
直线光栅化是指⽤像素点来模拟直线,⽐如下图⽤蓝⾊的像素点来模拟红⾊的直线。
给定两个点起点P1(x1, y1), P2(x2, y2),如何画它们直连的直线呢,即是如何得到上图所⽰的蓝⾊的点。
假设直线的斜率0<k>0,直线在第⼀象限,Bresenham算法的过程如下:1.画起点(x1, y1).2.准备画下⼀个点,X坐标加1,判断如果达到终点,则完成。
否则找下⼀个点,由图可知要画的点要么为当前点的右邻接点,要么是当前点的右上邻接点。
2.1.如果线段ax+by+c=0与x=x1+1的交点y坐标⼤于(y+*y+1))/2则选右上那个点 2.2.否则选右下那个点。
3.画点4.跳回第2步5.结束 算法的具体过程是怎样的呢,其实就是在每次画点的时候选取与实现直线的交点y坐标的差最⼩的那个点,例如下图:关键是如何找最近的点,每次x都递增1,y则增1或者不增1,由上图,假设已经画了d1点,那么接下来x加1,但是选d2 还是u点呢,直观上可以知道d2与⽬标直线和x+1直线的交点⽐较近即纵坐标之差⼩也即与(x+1, y+1)点纵坐标差⼤于0.5,所当然是选d2,其他点了是这个道理。
⼀、算法原理简介:算法原理的详细描述及部分实现可参考:假设以(x, y)为绘制起点,⼀般情况下的直观想法是先求m = dy /dx(即x每增加1, y的增量),然后逐步递增x, 设新的点为x1 = x + j,则y1 = round(y + j * m)。
可以看到,这个过程涉及⼤量的浮点运算,效率上是⽐较低的(特别是在嵌⼊式应⽤中,DSP可以⼀周期内完成2次乘法,⼀次浮点却要上百个周期)。
Bresenham画直线算法

Bresenham画直线算法发表于:03-28 20:23 | 分类:代码阅读:(4) 评论:(0)给定两个点起点P1(x1, y1), P2(x2, y2),如何画它们直连的直线呢,即是如何得到上图所示的蓝色的点。
假设直线的斜率0<k>0,直线在第一象限,Bresenham算法的过程如下:1.画起点(x1, y1).2.准备画下一个点,X坐标加1,判断如果达到终点,则完成。
否则找下一个点,由图可知要画的点要么为当前点的右邻接点,要么是当前点的右上邻接点。
2.1.如果线段ax+by+c=0与x=x1+1的交点y坐标大于(y+*y+1))/2则选右上那个点2.2.否则选右下那个点。
3.画点4.跳回第2步5.结束具体的算法如下,原理就是比较目标直线与x+1直线交点的纵坐标,哪个离交点近就去哪个void Bresenhamline(int x0, int y0, int x1, int y1, int color){int x, y, dx, dy;float k, e;dx = x1 - x0;dy = y1 - y0;k = dy / dx;e = -0.5;x = x0;y = y0;for (x= x0;x < x1; x++){drawpixel(x, y, color);//这个是画点子函数e = e + k;if (e > 0){y++;e = e - 1;}}}上述Bresenham算法在计算直线斜率与误差项时用到小数与除法。
可以改用整数以避免除法。
等式两边同时乘以2*dx,得到2*e*dx = 2*e*dx + 2dy, 2*e*dx = 2*e*dx - 2*dx.由于算法中只用到误差项的符号,因此可作如下替换:2*e*dx.改进的Bresenham画线算法程序:将e统一乘以2*dx即变成了整数的Bresenhan算法了,^_^void InterBresenhamline (int x0, int y0, int x1, int y1, int color){int dx = x1 - x0;int dy = y1 - y0;int dx2 = dx << 1;//乘2int dy2 = dy << 1;//乘2int e = -dx;int x = x0;int y = y0;for (x = x0; x < x1; x++){drawpixel (x, y, color);e=e + dy2;if (e > 0){y++;e = e - dx2;}}}其他象限或斜率不同可以转换一下位置即可,这里不具体展开。
布雷森汉姆直线算法

布雷森汉姆直线算法布雷森汉姆直线算法(Bresenham's Line Algorithm)是一种计算机图形学中常用的直线绘制算法,其通过在离散的像素格上选择最接近实际直线路径的点来实现高效绘制直线的目的。
该算法由Jack Elton Bresenham在1962年首次提出,被广泛应用于图形显示、打印机及数码扫描仪等领域。
布雷森汉姆直线算法的核心思想是利用整数运算来代替浮点运算,从而提高计算效率。
该算法通过仅使用加法、减法和位移等基本运算,不需要乘法运算和浮点数运算,从而适用于资源有限的嵌入式系统和低成本的图形设备。
算法的基本步骤如下:1. 根据起点P1(x1,y1)和终点P2(x2,y2)确定直线斜率k。
2. 如果|k|≤1,则沿x轴方向递增遍历起点P1到终点P2,并在每个像素上绘制。
若k>1,则沿y轴方向递增遍历P1到P2,绘制每个像素。
3. 对于每一步,根据递增的方向选择相应的像素。
4. 根据斜率k来决定误差累积量,调整绘制位置,保证直线的连续性。
该算法的优势在于其简单而高效的原理,使得绘制直线的速度非常快。
与传统的基于浮点运算的算法相比,布雷森汉姆直线算法的计算开销较小,而且能够得到非常接近实际直线路径的结果,几乎没有明显的视觉差异。
这使得该算法在计算资源有限的场景下非常有用,例如在嵌入式系统中,可以利用该算法绘制图形界面的边界、线条等。
然而,布雷森汉姆直线算法也存在一些局限性。
由于只考虑了整数坐标,因此绘制出来的直线可能会有些锯齿状,这在一些高精度要求的场景下可能会表现出明显的视觉噪点。
此外,该算法仅适用于绘制直线,并不能直接应用于曲线、圆等其他形状的绘制。
总之,布雷森汉姆直线算法是一种非常经典和实用的绘制直线的算法。
它通过巧妙地利用整数计算来取代浮点计算,以提高效率和减少计算资源开销。
虽然存在一些局限性,但在大多数场景下,它仍然是一种高效且精确的绘制直线的选择,对于计算机图形学的发展和应用有着重要的指导意义。
三种直线段绘制方法:DDA算法、B算法和中点分割法

三种直线段绘制⽅法:DDA算法、B算法和中点分割法⼀、综述三种直线段绘制⽅法:DDA算法、B算法和中点分割法。
在MFC环境中测试上述三种算法并对⽐分析三种算法的误差及效率。
⼆、程序框架MFC程序:cgDrawLineView.h为视图层的头⽂件,负责声明各种成员变量和成员函数;cgDrawLineView.cpp为视图层的源⽂件,负责实现直线的三种绘制、误差分析及messageBox显⽰。
CSelectControl.h为窗⼝⾯板中的按键及⽂本定义成员变量及成员函数。
CSelectControl.cpp实现⾯板的功能,如点击按键绘制图像、分析误差等。
三、算法描述1. DDA算法原理:根据直线的微分⽅程计算dy=m*dx(1)将给定端点作为输⼊参数;(2)初始化,初值加上0.5确保精度;(3)⽐较起⽌点⽔平和垂直的差值⼤数作为计算步数steps;(4)每步计算dx,dy分别为差数除以steps;(5)从起始点开始确定相邻两点间的增量并进⾏递推计算。
2. B算法(1)设定interChange、Xsign、Ysign便于判断位置并计算误差初值e = 2 * min - max;(min和max分别为⽔平距离和垂直距离的最值)(2)设置点(Xi, Yi) 的颜⾊值,并求下⼀误差ei+1;如果 ei >= 0 则ei+1 =ei+m-1;否则ei+1 = ei + m;(3)根据不同象限,确定X和Y变化符号的正负,进⾏下⼀次(2)(3)循环直⾄结束;3. 中点分割法原理:递归⼆分法结束条件:|P1-P2|<=1(1)将直线段求中点坐标,若可以细分,则进⾏⼀次递归;(2)如果中点坐标⽆法继续递归,则设置坐标的颜⾊值;(3)执⾏⾄所有点都完成了颜⾊值的设置,程序结束。
四、处理流程主要处理流程为:1. 在DrawLineView.h中定义double ddaError, ddaSmooth, bError, bSmooth, mpError, mpSmooth;void MidPointline(CDC* pDC, float x1, float y1, float x2, float y2);2. 在DrawLineView.cpp中完成初始赋值、函数具体实现以及误差、时间、平滑度计算和messageBox的弹出3. 在IDD_SELECTCONTROL中新添加button(MidPoint Line)且添加类向导,完善void CCSelectControl::OnClickedMidpointline()函数4. 在DrawLineView.cpp中完成pDoc->m_opMode ==2的调⽤程序基本完成五、运⾏结果当点击DDA Line时调⽤DDA直线⽣成函数当点击B Line时调⽤B直线⽣成函数当点击MidPoint时调⽤中点分割直线⽣成函数点击Comparision时先后调⽤三种直线⽣成函数,并弹出调⽤时间(受限于电脑运⾏速度原因只运⾏单次,计算次数for循环注释掉了,如有需要可取消注释,重新⽣成结果)、误差和光滑其中,RunTime值越低表⽰效率越⾼,Error越⼩表⽰误差越⼩,Smooth越⼩表⽰直线越光滑。
计算机图形学第3章

第3章 基本图形生成算法
3.1 生成直线的常用算法
均假定所画直线的斜率k∈[0,1]。
3.1.1 DDA画线算法
DDA(Digital Differential Analyzer)画线 算法也称数值微分法,是一种增量算法。它的算 法实质是用数值方法解微分方程,通过同时对x和 y各增加一个小增量,计算下一步的x、y值。
边界表示的四连通区域种子填充算法 内点表示的四连通区域种子填充算法 边界表示的八连通区域种子填充算法 内点表示的八连通区域种子填充算法
第3章 基本图形生成算法
1.边界表示的四连通区域种子填充算法
基本思想:从多边形内部任一点(像素)出发,依“左 上右下”顺序判断相邻像素,若其不是边界像素且没有被填 充过,对其填充,并重复上述过程,直到所有像素填充完毕。 可以使用栈结构来实现该算法,算法的执行步骤如下: 种子像素入栈,当栈非空时,重复执行如下三步操作: (1)栈顶像素出栈; (2)将出栈像素置成多边形填充的颜色; (3)按左、上、右、下的顺序检查与出栈像素相邻的 四个像素,若其中某个像素不在边界上且未置成多边形色, 则把该像素入栈。
过各行各列像素中心构造一组虚拟网格线,按直 线从起点到终点的顺序计算直线与各垂直网格线的交 点,然后确定该列像素中与此交点最近的像素。 由图3-5不难看出:若s<t, 则Si比较靠近理想直线,应 选Si;若s≥t,则Ti比较靠近 理想直线,应选Ti。
第3章 基本图形生成算法
令dx=x2-x1,dy=y2-y1 递推公式 :di 1 di 2dy 2dx( yi yi 1 ) di的初值: d1 2dy dx 当di≥0时,选Ti,
第3章 基本图形生成算法
bresenham算法画直线例题

bresenham算法画直线例题摘要:1.介绍Bresenham算法2.Bresenham算法的原理3.使用Bresenham算法画直线的步骤4.Bresenham算法的应用示例5.总结Bresenham算法在计算机图形学中的重要性正文:Bresenham算法是一种计算几何中用于画直线的算法,由英国计算机科学家Jack Bresenham于1965年提出。
该算法广泛应用于计算机图形学、视频游戏和各种嵌入式系统。
Bresenham算法的核心思想是使用简单的加法和减法运算,以及位运算来计算直线上的每个点的坐标,从而实现画直线的目标。
Bresenham算法的原理基于对直线方程y = mx + b的观察。
当m为正数时,直线是从左下到右上的;当m为负数时,直线是从左上到右下的。
根据这个特点,Bresenham算法将画直线的过程分为两个阶段:第一阶段是向上扫描,第二阶段是向下扫描。
在每一阶段,算法仅使用简单的加法和减法运算来更新当前点的坐标。
使用Bresenham算法画直线的步骤如下:1.初始化x和y坐标,以及直线的斜率m和截距b。
2.判断m的正负性。
如果m为正,进入第一阶段;如果m为负,进入第二阶段。
3.在第一阶段,每次将y坐标加b,然后将x坐标加m,直到x坐标达到最大值或y坐标达到最小值。
4.在第二阶段,每次将y坐标加b,然后将x坐标减m,直到x坐标达到最小值或y坐标达到最大值。
5.如果需要,可以将画直线的过程进行迭代,以获得更高的精度。
Bresenham算法在计算机图形学中具有重要应用价值。
它不仅计算简单、速度快,而且可以在各种不同的硬件平台上实现。
下面给出一个使用Bresenham算法画直线的示例:```pythondef bresenham_line(x0, y0, x1, y1):m = (y1 - y0) / (x1 - x0)b = y0 - m * x0x = x0y = y0e = 0if m < 0:y = y0while x < x1:put_pixel(x, y)e = e + abs(m)if e > abs(b):x = x + 1e = e - abs(m)y = y + 1else:x = x0while y < y1:put_pixel(x, y)e = e + abs(m)if e > abs(b):y = y + 1e = e - abs(m)x = x + 1bresenham_line(0, 0, 10, 5)```总之,Bresenham算法是一种简单而有效的计算几何画直线方法。
实验报告(Bresenham画线算法)

实验报告(Bresenham画线算法)一、实验目得根据Bresenham画线算法,掌握绘制直线得程序设计方法。
二、实验原理为了说明算法原理,我们首先考虑斜率非负且不超过 1 得直线得光栅化过程。
设直线得起点坐标为 (x s , ys),终点坐标为(x e ,ye),则直线得方程为:因此,其隐函数表示为:其中:显然,对于直线上得点,F(x , y)等于零;对于直线下方得点,F(x , y)大于零;而对直线上方得点,F(x,y) 小于零。
假设当前选择得像素点就是 (xi , yi),那么下一步要选择得像素点可能就是 NE (xi+1,yi+1),也可能就是 E (xi+1 , yi)。
选择得原则就是瞧哪一个离直线与x= xi+1得交点最近。
运用中点法则,我们只需考察中点 M 在直线得哪一侧,即计算:F(M) = F(xi + 1, yi + 1/2) = a(xi + 1) + b( yi + 0、5) + c并确定其正负号.由于根据函数值F(xi+1, yi + 1/2) 进行判定,所以我们定义一个判定函数如下:di= 2F(xi + 1, yi +1/2)根据定义:di = 2a(xi + 1) + 2byi + b + 2c当 d i 〈0 时,M 在直线得上方,取 E 为下一个像素点;当 d 〉0时, M 在直线得下方,取NE 为下一个像素点;当 d = 0时,两者都可以选,我们约定选 E。
di 得计算需要做4次加法与两次乘法。
因此,为了有效地计算判定函数,我们需要建立关于 di得递推公式。
显然,di 得变化依赖于下一个像素点选得就是 NE 还就是 E。
当 di 〈 0 时,下一个像素点就是 E,那么:di+1=2F(xi + 2, yi + 1/2)= 2a(xi + 2) +2byi + b +2c = di + 2a当 di > 0 时,下一个像素点就是NE,则:di+1= 2F(xi+2, yi+ 1 +1/2)=2a(xi+ 2) + 2b(yi+1)+b+2c= d i + 2a + 2b由此,得到计算判定函数 di 得递推公式:因为直线上得第一个像素点就就是直线得起点(xs, ys),所以判定函数di 得初值为:d0 = 2a(xs + 1) + 2bys + b + 2c = 2dy -dx故满足条件得直线得Bresnham 算法得步骤如下:Step 1、初始化dx = xe-xs ,dy = ye - ys , x = xs , y = ys , d = 2dy -dx;Step 2、当x〈xe 时,执行下述操作:(1)画像素点(x,y);(2)求下一个像素点:x = x + 1;if (d > 0)then y= y + 1;(3)计算判定函数 d:if (d 〉 0) then d =d+ 2dy -2dx;else d = d + 2dy;Step 3、算法结束。
中点画线算法例题及解题思路

中点画线算法例题及解题思路
中点画线算法是一种用于在计算机图形中绘制直线的算法。
它的基本思想是通过计算直线上的两个端点,然后使用中点坐标来逐步逼近直线。
下面是一个中点画线算法的例题及解题思路:
题目:使用中点画线算法绘制直线y=2x+1,其中x的范围是[0,10]。
解题思路:
1.确定直线的起点和终点:根据题目,直线的起点为(0,1),终点为(10,21)。
2.初始化当前点为起点:将起点(0,1)作为当前点。
3.循环计算中点坐标:根据中点画线算法,每次计算当前点和终点之间的中点坐标。
4.判断中点是否在直线上:使用线性插值判断中点是否在直线上。
如果中点在直线上,则将当前点更新为中点,否则将当前点更新为终点。
5.重复步骤3和4,直到当前点与终点重合。
6.将当前点的坐标绘制到图形上。
下面是使用Python实现中点画线算法的代码:
总结:中点画线算法是一种通过计算直线上的中点坐标来逐步逼近直线的算法。
通过循环计算中点坐标并判断中点是否在直线上,可以逐步逼近直线并绘制出直线的近似轨迹。
计算机图形学实验—中点算法画直线

计算机图形学实验报告班级:软件1102姓名:***学号:************中点算法的线段光栅化一、设计思想和算法流程1.假定直线斜率0<K<1假定直线斜率0<K<1,且已确定点亮象素点P (X p ,Y p ),则下一个与直线最接近的像素只能是P1点或P2点。
设M 为中点,Q 为交点,现需确定下一个点亮的象素。
当M 在Q 的下方-> P 2离直线更近更近->取P 2 。
M 在Q 的上方-> P 1离直线更近更近->取P 1M 与Q 重合, P 1、P 2任取一点。
问题:如何判断M 与Q 点的关系?由常识知:若y=kx+b;F(x,y)=y-kx-b;则有 ()()()⎪⎩⎪⎨⎧<>=点在直线下方0,点在直线上方0,点在直线上面0,y x F y x F y x F假设直线方程为:ax +by +c=0 (y=(-a/b)x-c/b)通过两点不能唯一确定a,b,c,取 a=y 0-y 1, b=x 1-x 0, c=x 0y 1-x 1y 0F(x,y)=ax +by +c=b(y-(-a/b)x-c/b); ()()()⎪⎩⎪⎨⎧<>=点在直线下方0,点在直线上方0,点在直线上面0,y x F y x F y x F则有∴欲判断M 点是在Q 点上方还是在Q 点下方,只需把M 代入F (x ,y ),并检查它的符号。
构造判别式:d=F(M)=F(x p +1,y p +0.5)=a(x p +1)+b(y p +0.5)+c当d<0,M 在直线(Q 点)下方,取右上方P 2;当d>0,M 在直线(Q 点)上方,取右方P 1;当d=0,选P 1或P 2均可,约定取P 1;能否采用增量算法呢?若d ≥0 ---->M 在直线上方->取P1;此时再下一个象素的判别式为 d 1=F(x p +2, y p +0.5)=a(x p +2)+b(y p +0.5)+c= a(x p +1)+b(y p +0.5)+c +a=d+a ;增量为a若d<0 ------>M 在直线下方->取P2;此时再下一个象素的判别式为 d 2= F(x p +2, y p +1.5)=a(x p +2)+b(y p +1.5)+c= a(x p +1)+b(y p +0.5)+c +a +b=d+a+b ;增量为a+b画线从(x0, y0)开始,d的初值d0=F(x0+1, y0+0.5)= a(x0 +1)+b(y0 +0.5)+c= F(x0, y0)+a+0.5b = a+0.5b由于只用d 的符号作判断,为了d来摆脱小数,提高效率。
VisualStudio实现任意情况bresenham画直线算法

VisualStudio实现任意情况bresenham画直线算法bresenham算法在计算机绘图时⼗分常⽤,其原理在⽹上都能找到,这⾥就不做赘述啦,很多⼩伙伴在⽹上找能在Visual Sudio MFC环境下实现的代码,总是遇到各种问题,不能正常运⾏,这⾥直接上能在VS上实现代码(亲测有效)。
CDC * pDC = this->GetDC();int dx, dy, x, y;int increment;bool if_xy_swap = false;if (abs(x1 - x0) < abs(y1 - y0)){if_xy_swap = true;swap(&x0, &y0);swap(&x1, &y1);}if (x0 > x1) {swap(&x0, &x1);swap(&y0, &y1);}increment = y0 < y1 ? 1 : -1;dx = x1 - x0;dy = y1 - y0;int h = abs(2 * dy) - dx;if (if_xy_swap)pDC->SetPixel(y0, x0, RGB(255, 0, 0));elsepDC->SetPixel(x0, y0, RGB(255, 0, 0));x = x0;y = y0;while (x < x1){if (h > 0) {h += abs(2 * dy) - 2 * dx;y += increment;if_xy_swap ? pDC->SetPixel(y, x, RGB(255, 0, 0)) : pDC->SetPixel(x, y, RGB(255, 0, 0));}else {h += abs(2 * dy);if_xy_swap ? pDC->SetPixel(y, x, RGB(255, 0, 0)) : pDC->SetPixel(x, y, RGB(255, 0, 0));}x++;}⼤家可以去执⾏下,应该是能成功实现(除了垂直的直线——代码较简单,没写在⾥⾯了)。
带宽度的直线绘制算法c++
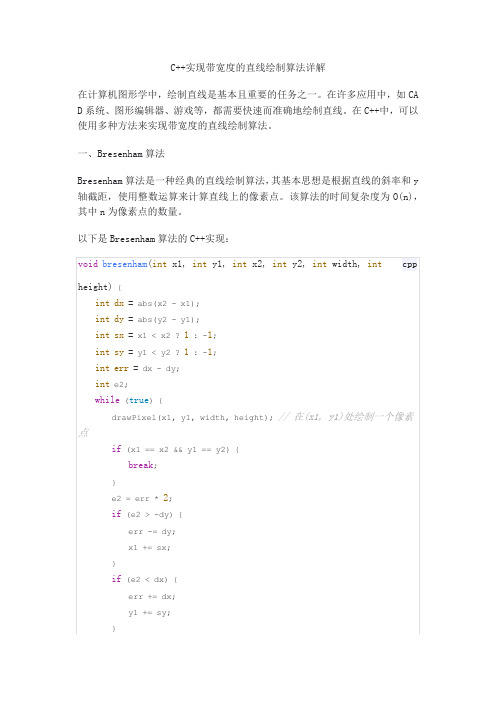
C++实现带宽度的直线绘制算法详解
在计算机图形学中,绘制直线是基本且重要的任务之一。
在许多应用中,如CA D系统、图形编辑器、游戏等,都需要快速而准确地绘制直线。
在C++中,可以使用多种方法来实现带宽度的直线绘制算法。
一、Bresenham算法
Bresenham算法是一种经典的直线绘制算法,其基本思想是根据直线的斜率和y 轴截距,使用整数运算来计算直线上的像素点。
该算法的时间复杂度为O(n),其中n为像素点的数量。
以下是Bresenham算法的C++实现:
其中,drawPixel(x, y, width, height)函数用于在坐标(x, y)处绘制一个像素点,width和height分别为画布的宽度和高度。
该函数的具体实现取决于所使用的图形库或API。
二、中点圆算法
中点圆算法是一种改进的Bresenham算法,用于绘制圆形。
该算法的基本思想是使用中点公式来计算圆上的像素点,从而避免了Bresenham算法中的整数运算。
该算法的时间复杂度为O(n),其中n为像素点的数量。
以下是中点圆算法的C++实现:
其中,drawPixel(x, y, width, height)函数用于在坐标(x, y)处绘制一个像素点,width和height分别为画布的宽度和高度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值微分(DDA)法
• 增量算法:在一个迭代算法中,如果每一 步的x、y值是用前一步的值加上一个增量 来获得,则称为增量算法。 • DDA算法就是一个增量算法。
数值微分(DDA)法
void DDALine(int x0,int y0,int x1,int y1,int color) { int x; float dx, dy, y, k; dx, = x1-x0, dy=y1-y0; k=dy/dx, y=y0; for (x=x0; x≤x1, x++) { drawpixel (x, int(y+0.5), color); y=y+k; } }
F ( x, y ) = 0 F ( x, y ) > 0 F ( x, y ) < 0 点在直线上面 点在直线上方 点在直线下方
P2 Q
P=(xp,yp) P1
∴欲判断M点是在Q点上方还是在Q点下方, 只需把M代入F(x,y),并检查它的符号。
中点画线法
构造判别式: d=F(M)=F(xp+1,yp+0.5) =a(xp+1)+b(yp+0.5)+c 当d<0,M在直线(Q点)下 P=(xp,yp) 方,取右上方P2; 当d>0,M在直线(Q点)上 方,取右方P1; 当d=0,选P1或P2均可, 约定取P1; 能否采用增量算法呢?
中点画线法
– 当M在Q的下方-> P2离直线更近更近->取P2 。 – M在Q的上方-> P1离直线更近更近->取P1 – M与Q重合, P1、P2任取一点。
P2 Q
P=(xp,yp) P1 – 问题:如何判断M与Q点的关系?
中点画线法
由常识知:若y=kx+b; F(x,y)=y-kx-b;则有
。 。
(X i , Yi)
。
(X i+1 ,Yi + k)
。
(X i , Int(Yi +0.5))
数值微分(DDA)法
•基本思想
已知过端点P0 (x0, y0), P1(x1, y1)的直线段L y=kx+b 直线斜率为
y − y0 1 k = x − x0 1
考虑当x从xi xi+1时y的变化规律: 设∆x=xi+1- xi xi+1= xi+ ∆x
数值微分(DDA)法
•
x 0 1 2 3 4 5
例:画直线段P0(0,0)--P1(5,2) k=0.4
int(y+0.5) 0 0 0.4 0 0.8 1 1.2 1 1.6 2 2.0 2 y
Line: P0(0, 0)-- P1(5, 2) 3 2 1 0 1 2 3 4 5
数值微分(DDA)法
斜率不在[0,1]的直线的处理
• 若k<-1 • 对(-y0,x0)和(-y1,x1)所确定的 直线进行扫描转换, 每确定一组(x,y), 输出(y,-x)。
(-y0,x0)
(x1,(x1,-y1)
(x0,y0)
(-y1,x1)
(x1,y1) (x,(x,-y0)
3 Bresenham算法 教材上介绍的) 算法( 算法
算法步骤为: 算法步骤 1.输入直线的两端点P0(x0,y0)和P1(x1,y1)。 2.计算初始值△x、△y、e=-0.5、x=x0、y=y0。 3.绘制点(x,y)。 4.e更新为e+k,判断e的符号。若e>0,则(x,y)更新 为(x+1,y+1),同时将e更新为e-1;否则(x,y)更新 为(x+1,y)。 5.当直线没有画完时,重复步骤3和4。否则结束。
• 缺点: 在此算法中,y、k必须是float,且每一 步都必须对y进行舍入取整,不利于硬件实现。
2 中点画线法
• 原理:
P2 Q
P=(xp,yp) P1
假定直线斜率0<K<1,且已 确定点亮象素点P(X ,Y ), 则下一个与直线最接近的像 素只能是P1点或P2点。设M 为中点,Q为交点
p p
现需确定下一个点亮的象素。
第二讲 直线的生成
图形的扫描转换(光栅化):确定一个像素集合, 用于显示一个图形的过程。步骤如下: 1、确定有关像素 2、用图形的颜色或其它属性,对像素进行写操作。 对一维图形,若不考虑线宽,则用一个像素宽的 直线来显示图形。二维图形的光栅化,即区域的填充: 确定像素集,填色或图案。 任何图形的光栅化,必须显示在一个窗口内,否 则不予显示。即确定一个图形的哪些部分在窗口内, 哪些在窗口外,即裁剪。
P2 Q P1
中点画线法
若d≥0 ---->M在直线上方->取P1; 此时再下一个象素的判别式为 d1=F(xp+2, yp+0.5) =a(xp+2)+b(yp+0.5)+c = a(xp +1)+b(yp +0.5)+c +a =d+a; 增量为a
P2 Q
P=(xp,yp) P1
中点画线法
• 若d<0 ------>M在直线下方->取P2; • 此时再下一个象素的判别式为 d2= F(xp+2, yp+1.5) =a(xp+2)+b(yp+1.5)+c = a(xp +1)+b(yp +0.5)+c +a +b =d+a+b ; P2 增量为a+b
e=e+k e=e+△y/△x △x e= △x e+ △y
改进2:用2e△x来替换e 改进
e=-0.5
• e初=-△x, • 每走一步有e=e+2△y。 • if (e>0) then e=e-2△x
2e=-1
算法步骤: 算法步骤 1.输入直线的两端点P0(x0,y0)和P1(x1,y1)。 2.计算初始值△x、△y、e=-△x、x=x0、y=y0。 △ 3.绘制点(x,y)。 4.e更新为e+2△y,判断e的符号。若e>0,则(x,y) △ 更新为(x+1,y+1),同时将e更新为e-2△x;否则 △ (x,y)更新为(x+1,y)。 5.当直线没有画完时,重复步骤3和4。否则结束。
。 。
(X i , Yi)
。
(X i+1, kX i+1+b)
。
(X i , Yi)
这种方法直观,但效率太低, 这种方法直观,但效率太低,因为每一步需要 一次浮点乘法、一次浮点加法和一次舍入运算。 一次浮点乘法、一次浮点加法和一次舍入运算。
1 数值微分法(DDA) 数值微分法(DDA)
假定直线的起点、终点分别为:(x0,y0), (x1,y1), 且都为整数。
0 直接计算法
假定直线的起点、终点分别为:(x0,y0), (x1,y1), 且都为整数。 计算出斜率k=(y1-y0)/(x1-x0) , 在Y轴的截距b=y0-k*x0
。 。
(X i , Yi)
。
栅格交点表示象素点位置
(X i+1, kX i+1+b)
。
(X i , Yi)
直接计算法
这样一来, 的值, 这样一来,只要给定 x的值,根据解析式立即 的值 可以计算出对应的y值 然后输出(x,round(y)). 可以计算出对应的 值,然后输出
改进1:令e=d-0.5 改进
xi +1 = xi + 1 y = yi + 1 (e > 0) i +1 yi (e ≤ 0)
• e初=-0.5, • 每走一步有e=e+k。 • if (e>0) then e=e-1
xi +1 = xi + 1 y = yi + 1 (d > 0.5) i +1 yi (d ≤ 0.5)
Q
P=(xp,yp) P1
中点画线法
• 画线从 0, y0)开始,d的初值 画线从(x 开始, 的初值 开始 d0=F(x0+1, y0+0.5)= a(x0 +1)+b(y0 +0.5)+c = F(x0, y0)+a+0.5b = a+0.5b 由于只用d 的符号作判断,为了只包含整数运算, 由于只用 的符号作判断,为了只包含整数运算 可以用2d代替 来摆脱小数,提高效率。 代替d来摆脱小数 可以用 代替 来摆脱小数,提高效率。
中点画线法
• 例:用中点画线法P0(0,0) P1(5,2) 用中点画线法
a=y0-y1=-2 b=x1-x0=5 d0=2a+b=1 d1=2a=-4 d2=2(a+b)=6
i 1 2 3 4
xi yi 0 0 1 0 2 1 3 1
d 1 -3 3 -1 5
3 2 1 0 1 2 3 4 5
5 4 2
斜率不在[0,1]的直线的处理
• 设起点和终点分别为(x0,y0)和(x1,y1) • 若k>1 • 则(y0,x0)和(y1,x1)所确定的 直线斜率k€ [0,1], 适用于前面讨论的情形。 • 对(y0,x0)和(y1,x1)所确定的 直线进行扫描转换, 每确定一组(x,y),输出(y,x)。
(y0,x0) (x0,y0)
(x1,y1)
(y1,x1)
斜率不在[0,1]的直ຫໍສະໝຸດ 的处理• 若-1<k<0 • 先对(x0,-y0)和(x1,-y1)所确定的 • 直线进行扫描转换, • 每确定一组(x,y),输出(x,-y)。
