如三节点三角形单元
算例分析

一、平面3节点三角形单元分析的算例如图所示为一矩形薄平板,在右端部受集中力F =10000N 作用,材料常数为:弹性模量7110E Pa =⨯、泊松比13μ=,板的厚度为0.1t m =,试按平面应力问题计算各个节点位移及支座反力。
解:(1) 结构的离散化与编号对该结构进行离散,单元编号及节点编号如图4-20(b)所示,即有二个3节点三角形单元。
载荷F 按静力等效原则向节点1、节点2移置等效。
节点位移列阵:[]11223344Tq u v u v u v u v =节点外载列阵:00000022TF F F ⎡⎤=--⎢⎥⎣⎦约束的支反力列阵:33440000Tx y x y R R R R R ⎡⎤=⎣⎦其中33(,)x y R R 和44(,)x y R R 分别为节点3和节点4的两个方向的支反力。
(2) 各个单元的描述当两个单元取图示中的局部编码(i ,j ,m )时,其单元刚度矩阵完全相同,即(1),(2)ii ij im ji jj jm mi mjmm k k k k k k k k k k ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦=(3) 建立整体刚度方程按单元的位移自由度所对应的位置进行组装可以得到整体刚度矩阵,该组装过程可以写成(1)(2)k k k =+具体写出单元刚度矩阵的各个子块在总刚度矩阵中的对应位置如下代入整体刚度方程Kq =P 中,有(4) 边界条件的处理及刚度方程求解该问题的位移边界条件为33440,0,0,0u v u v ====,将其代入上式中,划去已知节点位移对应的第5行至第8行(列),有由上式可求出节点位移如下[]1122[] 1.888.99 1.508.42TT F u v u v Et=--- (5) 支反力的计算将所求得的节点位移式代入总刚度方程中,可求得支反力如下3112924()23233x Et R u v v F =--+=- 31129214()0.0732333y Et R u v u F =--+=-42292()2323x Et R u v F =--=422921() 1.073233y Et R u v F =--=二、MATLAB —平面3节点三角形单元分析的算例(Triangle2D3Node)解:(1) 结构的离散化与编号将结构离散为二个3节点三角形单元,单元编号及节点编号如图4-20(b)所示。
有限元基础知识归纳

有限元知识点归纳1.、有限元解的特点、原因?答:有限元解一般偏小,即位移解下限性原因:单元原是连续体的一局部,具有无限多个自由度。
在假定了单元的位移函数后,自由度限制为只有以节点位移表示的有限自由度,即位移函数对单元的变形进行了约束和限制,使单元的刚度较实际连续体加强了,因此,连续体的整体刚度随之增加,离散后的刚度较实际的刚度K为大,因此求得的位移近似解总体上将小于精确解。
2、形函数收敛准那么〔写出某种单元的形函数,并讨论收敛性〕P49(1)在节点i处N i=1,其它节点N i=0;(2)在单元之间,必须使由其定义的未知量连续;(3)应包含完全一次多项式;(4)应满足∑Ni=1以上条件是使单元满足收敛条件所必须得。
可以推证,由满足以上条件的形函数所建单元是完备协调的单元,所以一定是收敛的。
4、等参元的概念、特点、用时注意什么?〔王勖成P131〕答:等参元—为了将局部坐标中几何形状规那么的单元转换成总体〔笛卡尔〕坐标中的几何形状扭曲的单元,以满足对一般形状求解域进行离散化的需要,必须建立一个坐标变换。
即:为建立上述的变换,最方便的方法是将上式表示成插值函数的形式,即:其中m是用以进行坐标变换的单元节点数,xi,yi,zi是这些结点在总体〔笛卡尔〕坐标内的坐标值,Ni’称为形状函数,实际上它也是局部坐标表示的插值函数。
称前者为母单元,后者为子单元。
还可以看到坐标变换关系式和函数插值表示式:在形式上是相同的。
如果坐标变换和函数插值采用相同的结点,并且采用相同的插值函数,即m=n,Ni’=Ni,那么称这种变换为等参变换。
5、单元离散?P42答:离散化既是将连续体用假想的线或面分割成有限个局部,各局部之间用有限个点相连。
每个局部称为一个单元,连接点称为结点。
对于平面问题,最简单、最常用的离散方式是将其分解成有限个三角形单元,单元之间在三角形顶点上相连。
这种单元称为常应变三角形单元。
常用的单元离散有三节点三角形单元、六节点三角形单元、四节点四边形单元、八节点四边形单元以及等参元。
一用三结点三角形平面单元计算平面结构的应力和位移讲解
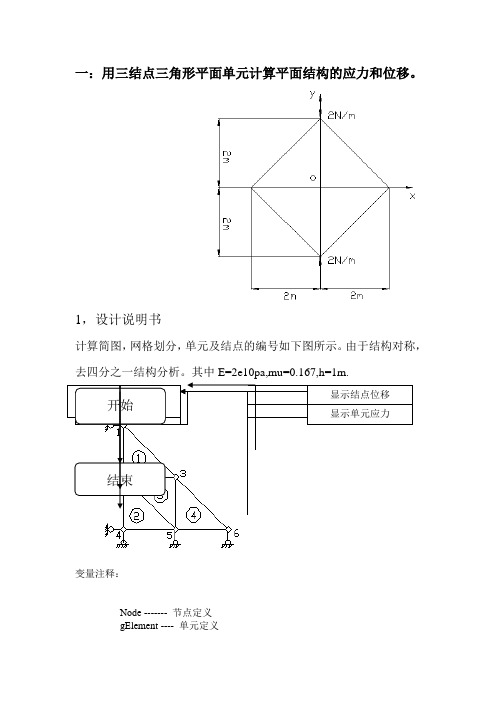
一:用三结点三角形平面单元计算平面结构的应力和位移。
1,设计说明书计算简图,网格划分,单元及结点的编号如下图所示。
由于结构对称,去四分之一结构分析。
其中E=2e10pa,mu=0.167,h=1m.变量注释:Node ------- 节点定义gElement ---- 单元定义gMaterial --- 材料定义,包括弹性模量,泊松比和厚度gBC1 -------- 约束条件gNF --------- 集中力gk------------总刚gDelta-------结点位移子程序注释:PlaneStructualModel ———定义有限元模型SolveModel ———————求解有限元模型DisplayResults ——————显示计算结果k = StiffnessMatrix( ie )———计算单元刚度AssembleStiffnessMatrix( ie, k )—形成总刚es = ElementStress( ie )————计算单元应力function exam1% 输入参数:无% 输出结果:节点位移和单元应力PlaneStructualModel ; % 定义有限元模型SolveModel ; % 求解有限元模型DisplayResults ; % 显示计算结果return ;function PlaneStructualModel% 定义平面结构的有限元模型% 输入参数:无% 说明:% 该函数定义平面结构的有限元模型数据:% gNode ------- 节点定义% gElement ---- 单元定义% gMaterial --- 材料定义,包括弹性模量,泊松比和厚度% gBC1 -------- 约束条件% gNF --------- 集中力global gNode gElement gMaterial gBC1 gNF% 节点坐标% x ygNode = [0.0, 2.0 % 节点10.0, 1.0 % 节点21.0, 1.0 % 节点30.0, 0.0 % 节点41.0, 0.0 % 节点52.0, 0.0] ; % 节点6% 单元定义% 节点1 节点2 节点3 材料号gElement = [3, 1, 2, 1 % 单元15, 2, 4, 1 % 单元22, 5, 3, 1 % 单元36, 3, 5, 1]; % 单元4 % 材料性质% 弹性模量泊松比厚度gMaterial = [1e0, 0, 1] ; % 材料1% 第一类约束条件% 节点号自由度号约束值gBC1 = [ 1, 1, 0.02, 1, 0.04, 1, 0.04, 2, 0.05, 2, 0.06, 2, 0.0] ;% 集中力% 节点号自由度号集中力值gNF = [ 1, 2, -1] ;returnfunction SolveModel% 求解有限元模型% 输入参数:无% 说明:% 该函数求解有限元模型,过程如下% 1. 计算单元刚度矩阵,集成整体刚度矩阵% 2. 计算单元的等效节点力,集成整体节点力向量% 3. 处理约束条件,修改整体刚度矩阵和节点力向量% 4. 求解方程组,得到整体节点位移向量global gNode gElement gMaterial gBC1 gNF gK gDelta% step1. 定义整体刚度矩阵和节点力向量[node_number,dummy] = size( gNode ) ;gK = sparse( node_number * 2, node_number * 2 ) ;f = sparse( node_number * 2, 1 ) ;% step2. 计算单元刚度矩阵,并集成到整体刚度矩阵中[element_number,dummy] = size( gElement ) ;for ie=1:1:element_numberk = StiffnessMatrix( ie ) ;AssembleStiffnessMatrix( ie, k ) ;end% step3. 把集中力直接集成到整体节点力向量中[nf_number, dummy] = size( gNF ) ;for inf=1:1:nf_numbern = gNF( inf, 1 ) ;d = gNF( inf, 2 ) ;f( (n-1)*2 + d ) = gNF( inf, 3 ) ;end% step4. 处理约束条件,修改刚度矩阵和节点力向量。
第七章 平面问题的有限单元法(Q4)

8
4节点四边形单元
y, v
u1 v 1 u2 u de 2 u3 u3 u4 u 4 displacements at node 1 displacements at node 2 displacements at node 3 displacements at node 4
x 1 2 3 4 N1 x1 N 2 x2 N 3 x3 N 4 x4 y 1 2 3 4 N1 y1 N 2 y2 N 3 y3 N 4 y4
1 N (1 )(1 ) 1 4 N 1 (1 )(1 ) 2 4 1 N (1 )(1 ) 3 4 N 1 (1 )(1 ) 4 4
1 4
Nj 1 4 (1 j )(1 j )
4 ( 1, +1) ( u4, v4)
1
N3 1 4 (1 )(1 ) N4 1 4 (1 )(1 )
N 3 at node 1 1 4 (1 )(1 ) 1 0 N 3 at node 2 1 4 (1 )(1 ) 1 0
同理:
1 1 1 1 1 y1 2 1 1 1 1 1 y2 1 1 1 1 4 3 y3 1 1 1 1 y4 4
K e B DBtd
e
T
11
等参单元
对于一般的四边形单元,在总体坐标系下构造 位移插值函数,则计算形状函数矩阵、单元刚 度矩阵及等效节点载荷列阵时十分冗繁;而对 于矩形单元,相应的计算要简单的多。 矩形单元明显的缺点是不能很好的符合曲线边 界,因此可以采用矩形单元和三角形单元混合 使用(网格划分困难)。更为一般的方法是通 过等参变换将局部自然坐标系内的规格化矩形 单元变换为总体坐标系内的任意四边形单元( 包括高次曲边四边形单元)。 等参单元的提出为有限元法成为现代工程实
简支梁的有限单元法分析-三角形三节点单元

三角形三节点平面单元
王 峰
有限元分析的基本步骤:
结构离散化
单元分析
整体分析
1 结构离散化
图示为简支梁,梁的厚度为t,泊松比m =0.3,弹性 模量为E=2e+5Mpa,用三节点三角形单元进行离散, 直角三角形边长为2。
2 单元分析
单元分析的主要内容:由节点位移求内部任一点的
物理方程
{s }=[D]{} 而 { }=[B]{}e (求应力的表达式) {s }=[D][B]{ }e
记 [S]=[D][B]
[S]应力矩阵: [S]=[Si Sj Sm]
2.5节点力与节点位移的关系
令实际受力状态在虚位移状态上做虚功,虚功方程:
({ *}e )T {F}e { *}T tdxdy s
位移,由节点位移求单元应变、应力和节点力。
单元分析的步骤:
节点 (1) 位移
单元内部 各点位移
(2)
单元 (3) 应变
单元 应力
(4)
节点 力
单元分析
2.1 形函数
形函数反映了单元的位移形态,是坐标的函数。 三节点三角形单元的形函数为:
1 Ni ( x, y ) (ai bi x ci y )(i , j , m) 2A ai x j ym xm y j (i , j , m) bi y j ym ci xm x j
Ni 1 Ni 1 bi , ci x 2 A y 2 A
因此,三角形单元的应变矩阵[B]是常量,
(i , j , m)
代入数据得到:
1 0 0 0 1 0 1 B 0 0 0 1 0 1 2 0 1 1 0 1 1
汽车结构有限元分析试题及答案(精华)

一、20分)(×) 1. 节点的位置依赖于形态,而并不依赖于载荷的位置( √ ) 2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元(×) 3. 不能把梁单元、壳单元和实体单元混合在一起作成模型( √ ) 4. 四边形的平面单元尽可能作成接近正方形形状的单元(×) 5. 平面应变单元也好,平面应力单元也好,如果以单位厚来作模型化处理的话会得到一样的答案(×) 6. 用有限元法不可以对运动的物体的结构进行静力分析( √ ) 7. 一般应力变化大的地方单元尺寸要划的小才好(×) 8. 所谓全约束只要将位移自由度约束住,而不必约束转动自由度( √ ) 9. 同一载荷作用下的结构,所给材料的弹性模量越大则变形值越小( √ ) 10 一维变带宽存储通常比二维等带宽存储更节省存储量。
二、填空(20 分)1.平面应力问题与薄板弯曲问题的弹性体几何形状都是薄板,但前者受力特点是:平行于板面且沿厚度均布载荷作用,变形发生在板面内;后者受力特点是:垂直于板面的力的作用,板将变成有弯有扭的曲面。
2 .平面应力问题与平面应变问题都具有三个独立的应力分量:σx,σy,τxy ,三个独立的应变分量:εx,εy,γxy,但对应的弹性体几何形状前者为薄板,后者为长柱体。
3.位移模式需反映刚体位移,反映常变形,满足单元边界上位移连续。
4 .单元刚度矩阵的特点有:对称性,奇异性,还可按节点分块。
5.轴对称问题单元形状为:三角形或四边形截面的空间环形单元,由于轴对称的特性,任意一点变形只发生在子午面上,因此可以作为二维问题处理。
6.等参数单元指的是:描述位移和描述坐标采用相同的形函数形式。
等参数单元优点是:可以采用高阶次位移模式,能够模拟复杂几何边界,方便单元刚度矩阵和等效节点载荷的积分运算。
7.有限单元法首先求出的解是节点位移,单元应力可由它求得,其计算公式为} = [D][B]6}e 。
(完整版)计算力学复习题答案

计算力学试题答案1. 有限单元法和经典Ritz 法的主要区别是什么?答:经典Ritz 法是在整个区域内假设未知函数,适用于边界几何形状简单的情形;有限单元法是将整个区域离散,分散成若干个单元,在单元上假设未知函数。
有限单元法是单元一级的Ritz 法。
2、单元刚度矩阵和整体刚度矩阵各有什么特征?刚度矩阵[K ]奇异有何物理意义?在求解问题时如何消除奇异性?答:单元刚度矩阵的特征:⑴对称性⑵奇异性⑶主元恒正⑷平面图形相似、弹性矩阵D 、厚度t 相同的单元,相同⑸的分块子矩阵按结点号排列,每一子矩阵代表一个结点,占两行两列,eK eK 其位置与结点位置对应。
整体刚度矩阵的特征:⑴对称性⑵奇异性⑶主元恒正⑷稀疏性⑸非零元素呈带状分布。
的物理意义是任意给定结构的结点位移所得到的结构结点力总体上满足力和力矩的平衡。
[]K 为消除的奇异性,需要引入边界条件,至少需给出能限制刚体位移的约束条件。
[]K 3. 列式说明乘大数法引入给定位移边界条件的原理?答:设:,则将 j j a a =jj jjk k α=j jj jP k a α=即:修改后的第个方程为j 112222j j jj j j n n jj jk a k a k a k a k a αα+++++= 由于得 jj j jj j k a k a αα≈所以 j ja a ≈对于多个给定位移时,则按序将每个给定位移都作上述修正,得到全部进行修正()12,,,l j c c c = 后的K 和P ,然后解方程即可得到包括给定位移在内的全部结点位移值。
4. 何为等参数单元?为什么要引入等参数单元?答:等参变换是对单元的几何形状和单元内的场函数采用相同数目的结点参数及相同的插值函数进行变换,采用等参变换的单元称之为等参数单元。
借助于等参数单元可以对于一般的任意几何形状的工程问题和物理问题方便地进行有限元离散,其优点有:对单元形状的适应性强;单元特性矩阵的积分求解方便(积分限标准化);便于编制通用化程序。
数值模拟:第五讲 平面问题(二)——三角形单元分析

2) 单元刚度方程和单元刚度矩阵的建立是单元分析的核心内容。
3) 一般情况下,单元应变矩阵是坐标的函数矩阵,所以单元刚度矩 阵的计算需要进行积分运算。
4) 所建立的单元刚度矩阵反映了一般弹性体小单元近似的弹性性质, 是单元特性的核心。
.
• 单元刚度矩阵的计算
➢ 弹性力学平面问题的单元刚度矩阵通式:Fra bibliotekllm
s2llm
3)形函数在单元上的积分:
Ni(x,y)dxdy
A 3
(i l,m,n)
.
5.2.4 单元应变和应力
• 已知节点位移插值形式的单元位移模式:
u v
N
e
• 代入平面问题几何方程(应变~位移关系)得到单元应变:
xxyy 0x
0
y uv 0x
0 yN 0l
0 Nl
(简单三角形单元的形函数只有2个独立)
.
➢ 性质3(推论):简单三角形单元的形函数在边界上的性质。 某节点的形函数在该点邻边上呈线性分布,取值在0~1之间, 在该点对边上值为零。
简单三角形单元形函数的几何意义
❖ 由形函数表达式和性质1可画出下列形函数几何图形。
.
❖ 根据位移模式表达式及其形函数的性质,可以推断出两个相邻 三角形单元上位移分布形状和公共边界上位移的情况:
.
• 针对三节点三角形单元,可以导出单元形函数 的下列性质。
➢ 性质1:单元上某节点的形函数在该节点的值为1,在其它节点 的值为零。
N l ( xl , yl ) 1 N l (xm , ym ) 0 N l (xn, yn ) 0
(l,m,n)
➢ 性质2:单元上所有形函数之和等于1。
Nl NmNn1
三节点三角形单元算例

三节点三角形单元算例1.引言1.1 概述概述部分(1.1)概述部分旨在介绍本篇文章的主题和背景信息。
本文将重点讨论三节点三角形单元算例,并对其进行详细的分析和结果总结。
三节点三角形单元是有限元分析中常用的一个基本单元,用于建模和模拟复杂的结构系统。
它由三个节点和三条连接这些节点的边组成。
通过这些节点和边的组合,我们可以将结构系统离散成数学模型,进而进行计算和分析。
本文将首先介绍节点的定义和作用。
节点是结构系统中的一个关键概念,它代表了结构的局部特点和重要信息。
在有限元分析中,节点不仅仅是一个几何点,更是一个存储了与该节点相关信息的数据点。
节点的定义和位置决定了单元的布局以及整个结构系统的建模精度。
接着,本文将详细讨论三角形单元的定义和特征。
三角形单元是由三个节点和三条连接这些节点的边组成的简单形状。
这种单元具有较好的适应性和计算效率,广泛应用于各类结构系统的模拟和分析。
通过对三角形单元的了解,我们可以更好地理解和应用有限元方法进行结构分析。
在本文的结论部分,将以一个具体的算例为例,展示三节点三角形单元的应用和分析过程。
通过该算例的分析,我们将得出一些结论和总结,并对三节点三角形单元的适用性和精度进行评估。
在本文的后续章节中,将对节点定义、三角形单元定义、算例分析以及结果总结等内容进行详细阐述,并对相关问题进行讨论和分析。
通过全面的介绍和讨论,我们旨在提供一个全面、准确和有用的指南,帮助读者更好地理解和应用三节点三角形单元算例。
文章结构部分的内容可以按如下方式编写:1.2 文章结构本文共分为引言、正文和结论三个部分。
引言部分首先概述了本文的背景和意义。
随后,介绍了文章的结构,包括本文主要从节点定义和三角形单元定义两个方面展开,以及结语部分。
正文部分主要包括节点定义和三角形单元定义两个子部分。
节点定义部分介绍了在三节点三角形单元中节点的定义和作用。
三角形单元定义部分则详细介绍了三角形单元的结构和数学表示,以及其在有限元分析中的应用。
三节点三角形单元matlab编程

1,'%d',1)
YOUNG=fscanf(FP1,'%e',1),POISS=fscanf(FP1,'%f',1),THICK=fscanf(FP1,'%f',1)
LNODS=fscanf(FP1,'%d',[3,NELEM])' % 单元定义数组
COORD=fscanf(FP1,'%f',[2,NPOIN])'
% 结点坐标数组
FORCE=fscanf(FP1,'%f',[3,NFORCE])' % 结点力数组
FIXED=fscanf(FP1,'%d',[3,inf])'
% 约束数组
ASTIF=ASSEMBLE(NPOIN,NELEM,YOUNG,POISS,THICK,COORD,LNODS) % 生成总刚
%总刚度矩阵
function ASTIF=ASSEMBLE(NPOIN,NELEM,YOUNG,POISS,THICK,COORD,LNODS)
% 张成特定大小总刚矩阵,并赋初值 0
ASTIF(1:2*NPOIN,1:2*NPOIN)=0;
% 组装总刚度矩阵
for i=1:NELEM
% 计算单刚
[ESTIF,SMATX]=FORMESTIF(i,COORD,LNODS,YOUNG,POISS,THICK)
总结点数, 单元数,
受约束点数, 结点力数 ,
第一组:
NPOIN=fscanf(FP1,'%d',1),NELEM=fscanf(FP1,'%d',1),
NFORCE=fscanf(FP1,'%d',1),NVFIX=fscanf(FP1,'%d',1)
现代设计方法4-3 三角形三节点平面单元
[m(x,y)][L]10
x 0
y 0
0 1
0 x
0y21c0i
0 ai
cj 0
0 aj
cm 0
0 am
0
bi
0 ci
0 bj 0 cj
0 bm 0 cm
N i( 0 x ,y )N i( 0 x ,y )N j( 0 x ,y )N j( 0 x ,y )N m ( 0 x ,y )N m ( 0 x ,y )
N i(x,y)2 1 (a ib ixciy)1b x
1
y
N j(x,y)2 (aj b jx cjy) 1 a
N m (x ,y ) 2 1 (a m b m x c m y ) 1 b x a y
精品课件
[N ] 1b x 0
0 1x
1y 0 a
0 1y
(1xy) ba 0
0
1
1 A
ui uj
xi xj
yi yj
1
2
1 A
1
ui uj
yi yj
1
3
1 A
1
xi xj
ui uj
um xm ym
1 um ym
1 xm um
(b)
1 xi yi A 1 xj yj
其中,
1 x y精品课件
m
m
对v同理可列出a4、a5、a6的方程 :
vi = a4+a5 xi+a6 yi
ci bi
(i, j, m)
2.3 由单元节点位移求单元的应力
物理方程
{s }=[D]{e}
而
{e }=[B]{d}e
{s } = [D][B]{d }e
西工大-有限元试题(附答案)
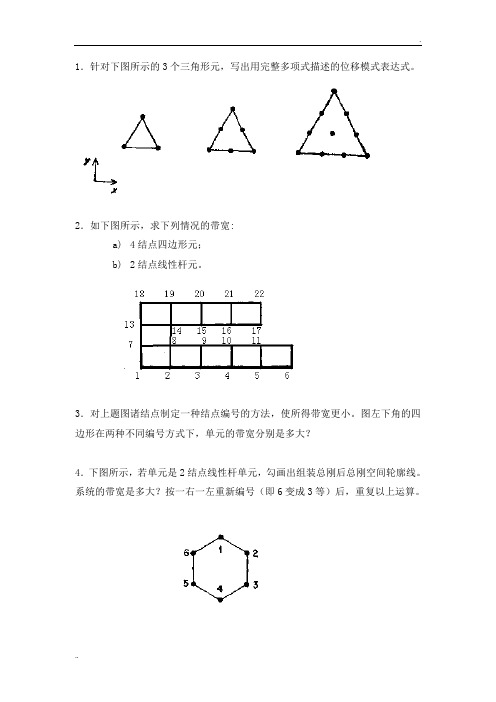
1.针对下图所示的3个三角形元,写出用完整多项式描述的位移模式表达式。
2.如下图所示,求下列情况的带宽:a)4结点四边形元;b)2结点线性杆元。
3.对上题图诸结点制定一种结点编号的方法,使所得带宽更小。
图左下角的四边形在两种不同编号方式下,单元的带宽分别是多大?4.下图所示,若单元是2结点线性杆单元,勾画出组装总刚后总刚空间轮廓线。
系统的带宽是多大?按一右一左重新编号(即6变成3等)后,重复以上运算。
5. 设杆件1-2受轴向力作用,截面积为A ,长度为L ,弹性模量为E ,试写出杆端力F 1,F 2与杆端位移21,u u 之间的关系式,并求出杆件的单元刚度矩阵)(][e k6.设阶梯形杆件由两个等截面杆件○1与○2所组成,试写出三个结点1、2、3的结点轴向力F 1,F 2,F 3与结点轴向位移321,,u u u 之间的整体刚度矩阵[K]。
7. 在上题的阶梯形杆件中,设结点3为固定端,结点1作用轴向载荷F 1=P ,求各结点的轴向位移和各杆的轴力。
8. 下图所示为平面桁架中的任一单元,y x ,为局部坐标系,x ,y 为总体坐标系,x 轴与x 轴的夹角为 。
(1) 求在局部坐标系中的单元刚度矩阵 )(][e k (2) 求单元的坐标转换矩阵 [T];(3) 求在总体坐标系中的单元刚度矩阵 )(][e k9.如图所示一个直角三角形桁架,已知27/103cm N E ⨯=,两个直角边长度cm l 100=,各杆截面面积210cm A =,求整体刚度矩阵[K]。
10. 设上题中的桁架的支承情况和载荷情况如下图所示,按有限元素法求出各结点的位移与各杆的内力。
11. 进行结点编号时,如果把所有固定端处的结点编在最后,那么在引入边界条件时是否会更简便些?12. 针对下图所示的3结点三角形单元,同一网格的两种不同的编号方式,单元的带宽分别是多大?13. 下图所示一个矩形单元,边长分别为2a 与2b ,坐标原点取在单元中心。
简支梁的有限单元法分析-三角形三节点单元

位移,由节点位移求单元应变、应力和节点力。
单元分析的步骤:
节点 (1) 位移
单元内部 各点位移
(2)
单元 (3) 应变
单元 应力
(4)
节点 力
单元分析
2.1 形函数
形函数反映了单元的位移形态,是坐标的函数。 三节点三角形单元的形函数为:
1 Ni ( x, y ) (ai bi x ci y )(i , j , m) 2A ai x j ym xm y j (i , j , m) bi y j ym ci xm x j
y j (0,2 )
x
m (0,0 ) i (2,0 )
三角形三节点单元
代入[D],[B]得三角形单元的单元刚度矩阵:
1 4 0 0 2 Et e [k ] 1 m2 m 4 1 4 m 4 对 1 m 8 1 m 8 0 1 m 8 1 m 8 称 1 m 8 0 1 m 8 1 m 8 1 4 3 m 8
A
由 { *}=[B]{ *}e
* e T e
得到 { *}T=({ *}e)T[B]T
* e T T e
({ } ) {F} ({ } ) [ B] D B tdxdy
A
三角形三节点单元,[B]为常量,单元厚度t也是常量,则
{F} [ B] D B tA
从结构中取出一个单元,如图其3个节点编 号是ni nj nm ,节点ni的2个自由度在结构自 由度的编号是2ni-1和2ni,在单元6个自由度 编号为1和2。
节点编号为
nj
1 51 ... ... 2 102 53 52 ... ... ... 561 ... ... 511
弹性力学及有限元考试复习简答题

弹性力学及有限元考试复习简答题1、简述有限单元法常分析的问题。
答:有限单元法是一种用于连续场分析的数值模拟技术,他不仅可以对机械、建筑结构的位移场和应力场进行分析,还可以对电磁学中的电磁场、传热学中的温度场、流体力学中的流体场进行分析。
2、在有限单元法中,位移模式应满足哪些基本条件。
答:1位移函数在单元节点的值应等于节点位移(即单元内部是连续的)2所选位移函数必须保证有限元的解收敛于真实解3、简述有限单元法结构刚度矩阵的特点。
答:对称矩阵奇异矩阵稀疏矩阵具有相对独立性4、简述有限单元法中单元刚度矩阵的性质。
答:1.单元刚度矩阵是对阵矩阵2.单元刚度矩阵的主对角线元素恒为正值3.单元刚度矩阵是奇异矩阵4.单元刚度矩阵仅与本身有关5、简述有限元法中选取单元位移函数(多项式)的一般原则。
答:必须假定一个函数,所假定的位移函数必须满足两个条件:其一,它在单元节点上的值应等于节点位移;其二,由该函数出发得到的有限元解收敛于真实解。
6、要保证有限单元法计算结果的收敛性,位移函数必须满足那些条件?答:1、完备性条件:要求单元的位移函数必须能够满足刚性位移和常量应变状态2、协调性条件:要求单元的位移函数在单元内部必须是连续函数,且必须保证相邻单元间位移协调9、用有限元法分析实际工程问题有哪些基本步骤?需要注意什么问题?1)建立实际工程问题的计算模型2)选择适当的分析工具侧重考虑以下几个方面1)前处理(Preproceing)2)求解(Solution)3)后处理(Potproceing10、在弹性力学中根据什么分别推导出平衡微分方程、几何方程、物理方程,这三个方程分别表示什么关系?答:根据静力学、几何学和物理学三方面条件,分别推导出平衡方程、几何方程和物理方程;三组方程分别表示:应力与载荷关系、应变与位移关系、应力与应变关系。
11、什么是平面应力问题?什么是平面应变问题?分别写出平面应力问题和平面应变问题的物理方程。
(同济大学)第7讲_三角形单元

0 ci bi
bj 0 cj
0 cj bj
bm 0 cm
⎧u ⎫ ⎡ N1 ⎨ ⎬=⎢ ⎩v ⎭ ⎣ 0
0 N1
N2 0
0 N2
N3 0
⎧ u1 ⎫ ⎪v ⎪ ⎪ 1⎪ 0 ⎤⎪ ⎪u2 ⎪ ⎪ ⎨ ⎬ N3 ⎥ ⎦ ⎪ v2 ⎪ ⎪u3 ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ v3 ⎭
1 Ni = (ai + bi x + ci y ) 2A
v ( x , y ) = N i ( x , y )vi + N j ( x , y )v j + N m ( x , y )vm
用单元节点位移和形函数表示的单元位移模式:
⎧u( x, y) ⎫ { f ( x, y)} = ⎨ ⎬ v ( x , y ) ⎩ ⎭
e
⎡ Ni ( x, y) 0 =⎢ Ni ( x, y) ⎢ ⎣ 0
Step3 单元刚度矩阵
弹性体的虚位移原理:在外力作用下,处于平衡状态 弹性体的虚位移原理: 的弹性体,当发生约束允许的任意微小的虚位移时, 则外力在虚位移上所作的功等于弹性体的变形位能当 虚位移发生时引起的增量,亦即等于整个体积内应力 在虚应变上所作之功。
y m Ym Xm
e e
y m
* vm * um
μ
0
1
⎥ ⎡ bi ⎥ 1 ⎢ 0 ⎥ 0 2A ⎢ ⎢ 1− μ ⎥ ⎣ ci ⎥ 2 ⎦ 0
0⎤ ci ⎥ ⎥ bi ⎥ ⎦
⎡ ⎢ bi E ⎢ = ⎢ μ bi 2 (1 − μ 2 ) A ⎢ 1− μ ci ⎢ ⎣ 2
⎤ μ ci ⎥ ⎥ ci ⎥ 1− μ ⎥ bi ⎥ 2 ⎦
( i, j, m )
u ( x, y ) 1 = [ ( a i u i + a j u j + a m u m ) + ( bi u i + b j u j + bm u m ) x + ( c i u i + c j u j + c m u m ) y ] 2A 1 = [ ( a i + bi x + c i y ) u i + ( a j + b j x + c j y ) u j + ( a m + bm x + c m y ) u m ] 2A = N i ( x , y )ui + N j ( x , y )u j + N m ( x , y )u m
一 三节点三角形单元

有限元课程总结一 三节点三角形单元 1位移函数移函数写成矩阵形式为:确定六个待定系数矩阵形式如下:[]{}em m j j i i m jim j iN v u v u v u N N N N N N v u δ=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧000002 单元刚度矩阵的计算1)单元应变和节点位移的关系由几何方程可以得到单元的应变表达式,{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂=m m j j i i m mjjiim j i m j i v u v u v u b c b c b c c c c b b b A x v y u y v x u 00000021ε⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧321111a a a y x y x y x u u u m m j j i i m j i ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m j i m j i m j i u u u c c c b b b a a a A a a a 21321⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m j i m jim ji 654v v v c c c b b b a a a A 21a a a2)单元应力与单元节点位移的关系[][][]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---==i i i i i ii i b c c b c b A E B D S 2121)1(22μμμμμ),,;,,(21212121)1(4]][[][][2m j i s m j i r b b c c cb bc b c c b c c b b A Et B D B K s r s r sr s r s r s r s r s r s T r rs ==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+-==μμμμμμμ3)单元刚度矩阵[][][][][][]Tm j iT m T j T i mm mj mi jm jj ji im ij ii e B B B D B B B tA K K K K K K K K K K ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=][][][][][][][][][3载荷移置1)集中力的移置如图3所示,在单元内任意一点作用集中力 {}⎭⎬⎫⎩⎨⎧=y x P P P图3由虚功相等可得,()()}{][}{}{}{**P N R TTe eTe δδ=由于虚位移是任意的,则 }{][}{P N R Te =2)体力的移置令单元所受的均匀分布体力为⎭⎬⎫⎩⎨⎧=y x p ρρ}{由虚功相等可得,()()⎰⎰=tdxdy p N R T TeTe }{][}{}{}{**δδ⎰⎰=tdxdy p N R T e }{][}{ 3)分布面力的移置设在单元的边上分布有面力{}TY X P ],[=,同样可以得到结点载荷,⎰=s T e tdsP N R }{][}{4. 引入约束条件,修改刚度方程并求解1)乘大数法处理边界条件图3-4所示的结构的约束和载荷情况,如图3-7所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(7-2)
(7-3)
令
x y , a b
在节点上的值为:
xi yi i , i (i , j , l , m ) a b
(i, j, l, m)
(7-4)
则式(7-3)可简写为
Ni (1 i )(1 i) / 4
将位移函数写成矩阵形式,即有与式(2-20)相同的形式
(7-12)
将[S]写成子矩阵形式
[S ] [Si S j Sl Sm ]
(7-13)
其中
ai (1 i ) bi (1 i ) E b (1 ) [ Si ] a ( 1 ) i i i i 4ab(1 2 ) 1 1 ai (1 i ) bi (1 i ) 2 2 (i, j, l , m) (7-14) 上式对应平面应力情形。对于平面应变情形,只需将其中 的E,作相应的改变即可。
u { f } [ N ]{ }e v
(7-5)
vl um vm ]T
式中
{ }e [ui vi u j
v j ul
(7-6)
[ N ] [ Ni I N j I Nl I N n I ]
其中,I为二阶单位矩阵。 2、应变矩阵 根据几何方程,可得与式(2-25)同样的形式
单元的位移函数可取为:
u a1 a2 x a3 y a4 xy v a5 a6 x a7 y a8 xy
(7-1)
在上式表示的位移模式中,a1, a2, a3, a5, a6, a7, a8 反映了单元的刚体位移和常 y 应变。在单元的边界(x=±a m l 或y =±a)上(或),位移是 b 按线性分布的。因此,相邻 x 单元在公共边上的位移是连 b 续的。这样,位移模式满足 j a a i 了解答收敛性的充分条件。 图7-3 在式(7-1)中代入节点位移和节点坐标后,可解出
可能达到较高的精度。图7-1悬臂梁分别采用高、低阶单元 计算就是一个典型的例子。
P
A B
h
4h 悬臂深梁
常应变单元:A=0.866 B=0.619
• •
解析解:A=1.0 B=1.0
• •
• •
图7-1
高阶单元:A=0.99 B=0.99
选择位移模式时,第2章提到要考虑解的收敛性,即要考虑
由此可见,[B]是、 的函数,即是x、y的函数。因此 单元中的应变不再是常数。
3、应力矩阵
根据应力-应变关系,可以计算单元中的应力,得到式(228)同样形式
{ } [ D]{ } [S ][ ]e
(7-11)
应力矩阵[S]具有与式(2-29)同样形式
[ S ] [ D][B]
式取完全二次式共6项。如
x2
x3 x4
1 x y
xy
y2
果某一阶次不能全取,则
应按对称性原则适当选取。
x2y xy2 y3 x3y x2y2 xy3 y4
图7-2 多项式选择的 怕斯卡三角形
例如在下节将要讨论的四 结点矩形单元中,位移 式不能取1,x,y,x2四项,
x3 x x2
1 y xy y2
第7章
平面问题高阶单元
7.1 位移模式阶次的选择 在前面两章中讨论了平面问题三结点三角形单元,其位 移模式的最高阶是坐标 x、 y的一次项。这种位移模式导致 单元常应变、常应力特性,单元应变矩阵、应力矩阵、刚 度矩阵均为常数矩阵,因此计算非常简单。但这种单元难 以反映应力梯度的迅速变化。要想提高计算精度,必须细 分网格,增加单元数和点数,因而加大输入数据的工作量 提高计算精度的另一条有效途径是采用高阶单元。由于 高阶单元的应变、应力不再是常数,因此采用少量单元就
{ } [ B]{ }e
(7-7)
(7-8)
把应变矩阵[B]写成子矩阵形式 其中
[B] [[Bi ] [B j ] [Bl ] [Bm ]]
(7-9)
0 b i (1 i ) 1 [ Bi ] 0 a i (1 i ) (i, j , l , m) (7-10) 4ab a i (1 i ) b i (1 i )
到位移模式的完备性和协调性。实际操作中,一般应考虑
位移模式的对称性。这是因为,有限元位移模式的选择实
由低价至高阶,顺序选取,组成多项式。多项式中的项数 等于单元节点自由度数。如三节点三角形单元,位移 模式取完全一次式,共3项。
际是以帕斯卡(Pascal)三解形基础上的(如图7-2所示),
六节点三角形单元,位移模
也不能取1,x,y, y2四项,
而应取1,x,y,xy四项。 7.2 四节点矩形单元
x4
x2y xy2 y3 x3y x2y2 xy3 y4
图7-2 多项式选择的 怕斯卡三角形
图7-3示出的矩形单元,边长分别为2a和2b。取4个角点为节
点,编号为i,j,l,m。将x轴和y轴置于单元的对称轴上。
1、位移函数
各待定系数(a1… a8)。将这些系数再代入式(7-1),可得:
u N i ui N j u j N l ul N mum v N i ui N j u j N l ul N mum
式中形函数为 :
1 x y N i 1 1 4 a b 1 x y N j 1 1 4 a b 1 x y N l 1 1 4 a b 1 x y N m 1 1 4 a b
4、单元刚度矩阵 单元刚度矩阵可采用式(2-33a)进行计算
[k ] [ B]T [ D ][B ]hdxdy
A
(2-33a)
在四节点矩形单元中,[k]是一个8×8的矩阵。将[k]写成分 块形式:
[kii ] [k ] ji [kli ] [kmi ] [kim ] [k jj ] [k jl ] [k jm ] [klj ] [kll ] [klm ] [kmj ] [kml ] [kmm ] [kij ] [kil ]
