数字信号处理的步骤与注意事项,并编写1024个采样点的FFT C语言程序
快速傅里叶变换FFT的C语言实现及应用

快速傅里叶变换FFT的C语言实现及应用快速傅里叶变换(Fast Fourier Transform, FFT)是一种快速计算离散傅里叶变换(Discrete Fourier Transform, DFT)的算法。
它能够在较短时间内计算出巨大数据集的傅里叶变换,广泛应用于信号处理、图像处理、通信等领域。
C语言是一种广泛应用于嵌入式系统和科学计算的编程语言,拥有高效、灵活和可移植等特点。
下面将介绍FFT的C语言实现及应用。
首先,我们需要了解离散傅里叶变换的定义。
离散傅里叶变换将一组离散的时域信号转换成一组对应的频域信号,可以表示为以下公式:X(k) = Σ[ x(n) * W^(kn) ]其中,X(k)是频域信号,x(n)是时域信号,W是单位复数旋转因子,其计算公式为W=e^(-j*2π/N),其中j是虚数单位,N是信号的长度。
实现FFT算法的关键在于计算旋转因子的值,一种常用的计算方法是采用蝶形算法(butterfly algorithm)。
蝶形算法将DFT分解成多个子问题的求解,通过递归调用可以快速计算出结果。
以下是一种基于蝶形算法的FFT实现的示例代码:```c#include <stdio.h>#include <math.h>typedef structfloat real;float imag;if (N <= 1)return;}for (int i = 0; i < N/2; i++)even[i] = signal[2*i];odd[i] = signal[2*i + 1];}fft(even, N/2);fft(odd, N/2);for (int k = 0; k < N/2; k++)signal[k].real = even[k].real + temp.real;signal[k].imag = even[k].imag + temp.imag;signal[k + N/2].real = even[k].real - temp.real; signal[k + N/2].imag = even[k].imag - temp.imag; }int maiint N = sizeof(signal) / sizeof(signal[0]);fft(signal, N);printf("频域信号:\n");for (int i = 0; i < N; i++)printf("%f + %fi\n", signal[i].real, signal[i].imag);}return 0;```以上代码实现了一个简单的4点FFT算法,输入时域信号为{1,0,1,0},输出为对应的频域信号。
基2时间抽取1024点FFT流图源程序

基2时间抽取1024点FFT流图源程序:#include<stdio.h>#include<math.h>#define pi 3.1415926#define N 10 //二进制位数#define K 10 //总级数#define L 1024 //点数struct Plural{ float R;float I; };//计算2的i次方intSquareI( inti ){int j;if(i==0) j=1;else for(j=1;i;i--)j=j*2;return j;}void WM(int e[],int k){inti,j,B,b;for(i=0;i<L;){B= SquareI(k);b= SquareI(k-1);if((i%B)==b){for(j=0;j<b;j++,i++)e[i]=j*SquareI(N-k);}else {e[i]=0;i++;}}}//计算旋转因子voidTwiddleFactor(intn,int e[],struct Plural Wn[]){ inti;for(i=0;i<L;i++){Wn[i].R=cos(2.0*pi*(e[i])/n);Wn[i].I=sin(-2.0*pi*(e[i])/n);}}//复数乘积voidPluralMultiple(struct Plural a[],struct Plural b[]){inti;float R,I;for(i=0;i<L;i++){R=a[i].R*b[i].R-a[i].I*b[i].I;I=a[i].R*b[i].I+a[i].I*b[i].R;a[i].R=R;a[i].I=I;}}voidnextarray(struct Plural x[],int k){inti,j,B,b;float R,I;for(i=0;i<L;){B= SquareI(k);b= SquareI(k-1);if((i%B)==0){for(j=0;j<b;j++,i++){R=x[i].R+x[i+SquareI(k-1)].R;I=x[i].I+x[i+SquareI(k-1)].I;x[i+SquareI(k-1)].R=x[i].R-x[i+SquareI(k-1)].R;x[i+SquareI(k-1)].I=x[i].I-x[i+SquareI(k-1)].I;x[i].R=R;x[i].I=I;}}else { i++;}}}//FFT倒序intFFTReverse( int k ){inti,j,a[N],b[N],kk,sum;for(i=0;i<N;i++){a[i]=k%2;k=k/2;}for(i=N-1,j=0;j<N;j++,i--){b[j]=a[i];}for(i=0,kk=0; i<N;i++){sum=SquareI(i); kk=kk+b[i]*sum;}returnkk;}//输入数组序列转换voidarrayFFTReverse(struct Plural y[],struct Plural x[]) {inti,kk;for(i=0;i<L;i++){kk=FFTReverse(i);x[kk].R=y[i].R;x[kk].I=y[i].I;}}//给数组赋值voidValuationCos(struct Plural Wn[]) //cos[k] { inti;for(i=0;i<L;i++){Wn[i].R=cos(2.0*pi*i/L);Wn[i].I=0;}}voidValuationRn(struct Plural Wn[]) //Rn[k] { inti;for(i=0;i<L;i++){Wn[i].R=1;Wn[i].I=0;}}voidValuationSin(struct Plural Wn[]) //sin[k] { inti;for(i=0;i<L;i++){Wn[i].R=sin(2.0*pi*i/L);Wn[i].I=0;}}void ValuationUnitimpluse(struct Plural Wn[]) //δ[k] { inti;Wn[0].R=1;Wn[0].I=0;for(i=1;i<L;i++){Wn[i].R=0;Wn[i].I=0;}}void main(){intll=0,i,k,e[L];struct Plural Wn[L],x[L];char c;printf("基2时间抽取1024点FFT流图\n\n");for(;;){printf("1.cos[k] 2.sin[k] 3.δ[k] 4.Rn[k] \n\n选择序号:");scanf(" %c",&c);switch(c){case '1':{ValuationCos(Wn);printf("\ncos[k]\n\n");break;}case '2':{ValuationSin(Wn);printf("\nsin[k]\n\n");break;}case '3':{ValuationUnitimpluse(Wn);printf("\nδ[k]\n\n");break;}case '4':{ValuationRn(Wn); printf("\nRn[k]\n\n");break;}default :{ValuationCos(Wn);printf("\ncos[k]\n\n");break;}}//数组转换arrayFFTReverse(Wn,x); //这里使用Wn[]是为了减少数组的个数,且Wn[]只是临时的for(k=1;k<=K;k++) //产生K级计算{WM(e, k); //产生Wn的上标TwiddleFactor(L,e,Wn); //产生Wn数组的值PluralMultiple(x,Wn); //计算x[]与Wn[]的复数相乘,结果放在x[]nextarray(x,k); //计算x[]加减,结果放在x[]}printf("结果\n\n");for(i=0;i<L;i++){if(x[i].I<0)printf("X[%d]=%1.0f%1.0fj\t",i,x[i].R,x[i].I);elseprintf("X[%d]=%1.0f+%1.0fj\t",i,x[i].R,x[i].I);ll++;if(ll==5) //每行输出5个{printf("\n");ll=0;}}printf("\n");}}。
数字信号处理实验FFT快速傅里叶变换C语言
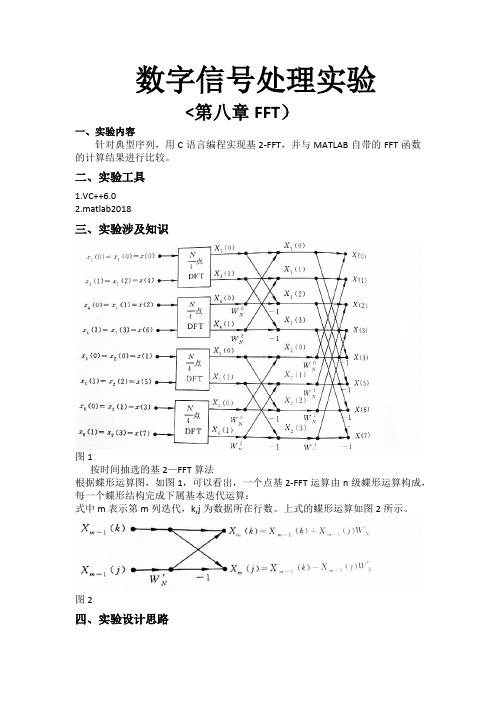
数字信号处理实验<第八章FFT)一、实验内容针对典型序列,用C语言编程实现基2-FFT,并与MATLAB自带的FFT函数的计算结果进行比较。
二、实验工具1.VC++6.02.matlab2018三、实验涉及知识图1按时间抽选的基2—FFT算法根据蝶形运算图,如图1,可以看出,一个点基2-FFT运算由n级蝶形运算构成,每一个蝶形结构完成下属基本迭代运算:式中m表示第m列迭代,k,j为数据所在行数。
上式的蝶形运算如图2所示。
图2四、实验设计思路首先,根据基2-FFT的算法特点,可以整理出程序设计的大致思路。
基2-FFT主要运用的就是蝶形运算来降低进行DFT运算时的运算量。
因为是基2,所以进行DFT计算的点数N必须的。
程序设计中主要解决3个问题,变址运算,复数运算,节点距离运算,及旋转因子的计算。
下面对这三个模块进行说明。
1.变址运算由蝶形图我们可以看出,FFT的输出X(k>是按正常顺序排列在存储单元中,即按X(0>,X(1>,…,X(7>的顺序排列,但是这时输入x(n>却不是按自然顺序存储的,而是按x(0>,x(4>,…,x(7>的顺序存入存储单元,所以我们要对输入的按正常顺序排列的数据进行变址存储,最后才能得到输出的有序的X(K>。
通过观察,可以发现,如果说输出数据是按原位序排列的话,那么输入数据是按倒位序排列的。
即如果输入序列的序列号用二进制数,则到位序就为。
我们需将输入的数据变为输出的倒位序存储,这里用雷德算法来实现。
下面给出雷德算法。
假如使用A[I]存的是顺序位序,而B[J]存的是倒位序。
例如 N = 8 的时候,倒位序顺序二进制表示倒位序顺序0 0 000 0004 1 100 0012 2 010 0106 3 110 0111 4 001 1005 5 101 1013 6 011 1107 7 111 111由上面的表可以看出,按自然顺序排列的二进制数,其下面一个数总是比其上面一个数大1,即下面一个数是上面一个数在最低位加1并向高位进位而得到的。
用c语言实现的FFT

一、对FFT的介绍1. FFT(Fast Fourier Transformation),即为快速傅里叶变换,是离散傅里叶变换的快速算法,它是根据离散傅里叶变换的奇、偶、虚、实等特性,对离散傅里叶变换的算法进行改进获得的。
2.FFT算法的基本原理FFT算法是把长序列的DFT逐次分解为较短序列的DFT。
按照抽取方式的不同可分为DIT-FFT(按时间抽取)和DIF-FFT(按频率抽取)算法。
按蝶形运算的构成不同可分为基2,基4,基8,以及任意因子的类型。
3.迭代关系4、本次程序的基本过程我们这次所研究的是数字信号处理中的FFT算法,我们这次所用的数字信号是复数类型的。
(1)所以首先,我们先定义了一个复数结构体,因为是进行复数的运算,我们又相继定义复数的加减乘运算的函数。
(2)紧接着,我们定义了进行FFT计算的fft()快速傅里叶变换函数initW() 初始化变换核函数即旋转因子的计算,change() 变址函数,output()输出傅里叶变换的结果的函数。
(3)定义主函数,并调用定义好的相关子函数,利用fft()中的蝶形运算以及change()函数来完成从时间域上选取的DIT-FFT。
二、FFT中码位倒置排序1、码位倒置的实现方法:(1)简单的利用按位与、或循环实现(2)利用公式推导的迭代方法2、为什么要进行码位倒置因为由于FFT的计算特性,如果按照正常顺序输入,而没有进行码位倒置的话,就会以乱序输出,就不便于我们后续对信号的相关性质进行研究了,所以DIT-FFT算法就是在进行FFT计算之前,进行分奇偶后的码位倒置运算,即二进制数的倒位。
3、倒位序由奇偶分组造成,以N=8为例,说明如下:三、蝶形运算由按照上述公式的规律进行逐级分解,直到2点DFT,如下是N=8时的蝶形算法分析图:四、FFT算法中蝶形算法的基本思想分析(1)我们知道N点FFT运算可以分成log2(N)级,每一级都有N/2个碟形,FFT的基本思想是用3层循环完成全部运算(N点FFT)。
C语言实现FFT

C语言实现FFT快速傅里叶变换(Fast Fourier Transform, FFT)是一种高效进行离散傅里叶变换(Discrete Fourier Transform, DFT)计算的算法。
它通过利用对称性和递归的方法,将O(n^2)的计算复杂度优化为O(nlogn)。
本文将介绍C语言实现FFT的基本步骤和代码。
首先,需要定义一个复数结构体来表示复数,包含实部和虚部两个成员变量:```ctypedef structdouble real; // 实部double imag; // 虚部```接着,需要实现FFT的关键函数,包括以下几个步骤:1. 进行位逆序排列(bit-reversal permutation):FFT中的输入数据需要按照位逆序排列,这里使用蝶形算法来实现位逆序排列。
先将输入序列按照索引位逆序排列,再将复数序列按照实部和虚部进行重新排列。
```cint i, j, k;for (i = 1, j = size / 2; i < size - 1; i++)if (i < j)temp = data[j];data[j] = data[i];data[i] = temp;}k = size / 2;while (j >= k)j=j-k;k=k/2;}j=j+k;}```2. 计算旋转因子(twiddle factor):FFT中的旋转因子用于对复数进行旋转变换,这里采用的旋转因子为e^( -2*pi*i/N ),其中N为DFT点数。
```cint i;double angle;for (i = 0; i < size; i++)angle = -2 * M_PI * i / size;twiddleFactors[i].real = cos(angle);twiddleFactors[i].imag = sin(angle);}```3.执行蝶形算法计算DFT:蝶形算法是FFT算法的核心部分,通过递归地将DFT问题一分为二,并将计算结果根据旋转因子进行两两合并,最终得到FFT结果。
C语言编写FFT程序

DSP 课程作业用C 语言编写FFT 程序1,快速傅里叶变换FFT 简介快速傅氏变换(FFT ),是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。
我们假设 x(n)为N 项的复数序列,由DFT 变换,任一X (m )的计算都需要N 次复数乘法和N-1次复数加法,而一次复数乘法等于四次实数乘法和两次实数加法,一次复数加法等于两次实数加法,即使把一次复数乘法和一次复数加法定义成一次“运算”(四次实数乘法和四次实数加法),那么求出N 项复数序列的X (m ),即N 点DFT 变换大约就需要N^2次运算。
当N=1024点甚至更多的时候,需要N2=1048576次运算,在FFT 中,利用WN 的周期性和对称性,把一个N 项序列(设N=2k,k 为正整数),分为两个N/2项的子序列,每个N/2点DFT 变换需要(N/2)2次运算,再用N 次运算把两个N/2点的DFT 变换组合成一个N 点的DFT 变换。
这样变换以后,总的运算次数就变成N+2(N/2)2=N+N2/2。
继续上面的例子,N=1024时,总的运算次数就变成了525312次,节省了大约50%的运算量。
而如果我们将这种“一分为二”的思想不断进行下去,直到分成两两一组的DFT 运算单元,那么N 点的DFT 变换就只需要Nlog2N 次的运算,N 在1024点时,运算量仅有10240次,是先前的直接算法的1%,点数越多,运算量的节约就越大,这就是FFT 的优越性。
2,FFT 算法的基本原理FFT 算法的基本思想:利用DFT 系数的特性,合并DFT 运算中的某些项,吧长序列的DFT —>短序列的DFT ,从而减少其运算量。
FFT 算法分类:时间抽选法DIT: Decimation-In-Time ;频率抽选法DIF: Decimation-In-Frequency按时间抽选的基-2FFT 算法1、算法原理设序列点数 N = 2L ,L 为整数。
数字信号处理的步骤与注意事项,并编写1024个采样点的FFT C语言程序

数字信号处理的步骤与注意事项,并编写1024个采样点的FFT C语言程序1. 数字信号处理1.1 数字信号处理概述数字信号处理是研究如何用数字或符号序列来表示信号以及如何对这些序列进行处理的一门学科。
随着计算机技术的发展,数字信号处理技术得到了越来越广泛的应用,它已成为现代科学技术必不可少的工具。
数字信号是数据序列,其处理实际上就是进行各种数学运算,如加、减、乘以及各种逻辑运算等等。
因此,数字信号处理既可以是软件处理也可以是硬件处理。
所谓软件处理,就是对所需要的运算编制程序,然后在计算机上实现,其处理灵活、方便。
所谓硬件处理,就是用加法器、乘法器、延时器以及它们的各种组合来构成数字电路,以实现所需要的运算。
硬件处理显然不如软件处理灵活方便,但能对数字信号进行实时处理。
近年来日益广泛采用的各种数字信号处理器(如TI TMS320系列、Philps Trimedia系列等)可以认为是软硬件处理方式的结合,这种处理时用数字信号处理芯片以及存储器来组成硬件电路,所需要的运算靠特定的汇编语言编程来实现。
因此,采用数字信号处理器既方便灵活,又能做到实时处理,所以数字信号处理器(DSP)已经越来越广泛地应用于包括通信在内的各个领域之中。
1.2 数字信号处理的优点(1)精度高数字系统的特性不因环境的变化而变化,计算精度是模拟系统所无法相比的,运算位数由8位提高到16位、32位、64位。
(2)可靠性高模拟系统中各种参数受温度、环境影响较大,因而易出现感应、杂散效应,甚至会出现震荡等等;而数字系统受温度、环境影响较小。
模拟信号受到干扰即产生失真,而数字信号由于只有两种状态,因此,所受的干扰只要在一定范围以内,就不会产生影响,这就是说,数字信号抗干扰能力强。
另外,如果用数字信号进行传输,在中继站还可以再生。
总的说来,信号的数字处理可靠性高。
(3)灵活性强可以通过改变数字信号系统的参数来改变系统的性能。
数字信号的灵活性还表现在可以利用一套计算设备同时处理多路相互独立的信号,即所谓的“时分复用”,这在数字电话系统中是非常有用的技术。
数字信号处理算法的使用注意事项与傅里叶分析

数字信号处理算法的使用注意事项与傅里叶分析数字信号处理(DSP)算法是处理数字信号的数学和计算方法。
它在许多领域中发挥着重要作用,包括通信、音频处理和图像处理等。
然而,在使用DSP算法时需要注意一些关键事项,以确保正确有效地处理信号。
本文将介绍一些使用DSP算法的注意事项。
首先,确保信号采样率正确。
采样率是指在单位时间内对信号进行采样的次数。
在使用DSP算法之前,必须明确信号的采样率,以便正确地对信号进行处理。
如果采样率设置不正确,可能会导致信号失真或信息丢失。
因此,在开始处理数字信号之前,需要了解信号的采样率,并将其作为算法输入的参数。
其次,选择适当的滤波器。
滤波器是DSP算法中的关键组件,用于去除信号中的噪声或不需要的频率成分。
选择适当的滤波器可以有效地提取所需信号,并减少干扰。
常见的滤波器类型包括低通、高通、带通和带阻滤波器。
在选择滤波器时,需要考虑信号的频率范围和所需滤波器响应的特点。
另外,合理选择傅里叶变换类型。
傅里叶变换是一种将信号从时域转换为频域的数学方法。
常用的傅里叶变换类型包括离散傅里叶变换(DFT)和快速傅里叶变换(FFT)。
DFT适用于对离散信号进行频谱分析,而FFT则是对连续信号进行频谱分析的快速算法。
在选择傅里叶变换类型时,需要根据信号类型和分析需求进行合理选择。
此外,注意对信号进行预处理。
信号预处理是在应用DSP算法之前对信号进行一系列操作,以准备信号进行处理。
常见的信号预处理方法包括去噪、均衡和幅度归一化等。
预处理可以提高信号的质量,并减少算法处理过程中的误差。
因此,在使用DSP算法时,应注意对信号进行适当的预处理。
最后,进行正确的结果解释和验证。
在使用DSP算法之后,需要正确解释和验证处理结果。
结果的解释需要考虑领域专业知识和特定应用的需求。
验证结果可以通过与已知结果对比、模拟实验等方式来实现。
确保结果的正确性和可靠性是使用DSP算法的关键。
总结起来,使用DSP算法时需要注意信号的采样率、滤波器选择、傅里叶变换类型、信号预处理和结果解释与验证等关键事项。
fft c语言程序

fft c语言程序快速傅里叶变换(Fast Fourier Transform,FFT)是一种计算机算法,它能够将一个离散的时间域信号转换为频谱域信号。
FFT算法是一种高效的计算傅里叶变换的方法,可以大大加快计算速度。
FFT算法是由高效的分治策略设计得来的。
它将傅里叶变换的计算分解为多个较小规模的子问题,然后逐步合并这些子问题的计算结果,最终得到原始问题的解。
因此,FFT算法的时间复杂度为O(n log n),其中n表示信号的长度。
相比之下,传统的傅里叶变换算法的时间复杂度为O(n^2),因此FFT算法在处理大规模信号时具有较大的优势。
在C语言中,我们可以使用库函数来实现FFT算法。
这些库函数通常提供了一些基本的操作,例如初始化FFT对象、进行离散傅里叶变换、进行逆变换等。
以下是一个简单的C语言程序,用于实现FFT算法:```c#include <stdio.h>#include <stdlib.h>#include <math.h>#include <complex.h>//计算离散傅里叶变换void fft(double complex buf[], int n){if (n <= 1)return;double complex *even = malloc(n / 2 * sizeof(double complex));double complex *odd = malloc(n / 2 * sizeof(double complex));for (int i = 0; i < n / 2; i++){even[i] = buf[2 * i];odd[i] = buf[2 * i + 1];}fft(even, n / 2);fft(odd, n / 2);for (int k = 0; k < n / 2; k++){double complex t = cexp(-I * 2 * M_PI * k / n) * odd[k]; buf[k] = even[k] + t;buf[k + n / 2] = even[k] - t;}free(even);free(odd);}//打印复数数组void print_complex(double complex buf[], int n){for (int i = 0; i < n; i++){printf("%.2f + %.2fi\n", creal(buf[i]), cimag(buf[i]));}}int main(void){int n = 8;double complex buf[] = {1.0 + 0.0 * I, 1.0 + 0.0 * I, 1.0 + 0.0 * I, 1.0 + 0.0 * I,0.0 + 0.0 * I, 0.0 + 0.0 * I, 0.0 + 0.0 * I, 0.0 + 0.0 * I};fft(buf, n);print_complex(buf, n);return 0;}```这个程序定义了两个函数:`fft`和`print_complex`。
FFT的C语言编程

i-2.878680 i-5.999998 i0.878680 i9.000000 i-7.121320
7.重复上述步骤 5-6,完成上机内容 3;
8.撰写上机实验报告。
四、参考程序
#include <stdio.h>
#include <math.h>
#define re 0
/* re=0,用 re 表示实部 */
temp[2]: 蝶形计算中的临时变量,temp[re]、temp[im]分别代表其实部和虚部;
*/
float arg,wreal,wimag; /* arg 存储旋转因子指数 p(数值上相差-2π/N)。wreal 存储 cos(arg),wimag 存储
-sin(arg) */
float tem,tr,ti;
for(k=j; k<N; k+=2*B) /*第 L 级具有相同旋转因子蝶形计算,每个蝶形相距 2L=2B 个点*/
{
/* 编写蝶蝶形计算的输入节点距离为 B */
/*
蝶形运算
x[i] = x[i + B]
x[i] + WNP x[i + = x[i] − WNP x[i
*/
}
}
/* 计算旋转因子说明 P = j * 2^ (M − L) 、 B = 2L−1 、 N = 2M
有 WNP
=
e−i
2π N
P
= e−i( jπ / B)
= e−iθ
= cosθ
− i sinθ
其中θ = jπ / B
下一个旋转因子旋转角度为 arg
e−iθ * e−i(arg) = (cosθ *cos(arg) − sinθ *sin(arg)) − i(cosθ *sin(arg) + sinθ *cos(arg))
实现FFT算法的C语言程序

实现FFT算法的C语言程序目前在许多嵌入式系统中要用到FFT运算,如以单片机为核心的交流采样系统、谐波运算、频谱分析等。
本文首先分析实数FFT算法的推导过程,然后给出一种验证过的具体实现FFT算法的C语言程序,可以直接应用于需要FFT 运算的单片机或DSP等嵌入式系统中。
一、倒位序算法分析按时间抽取(DIT)的FFT算法通常将原始数据倒位序存储,最后按正常顺序输出结果X(0),X(1),...,X(k),...。
假设一开始,数据在数组float dataR[128]中,我们将下标i表示为(b6b5b4b3b2b1b0)b,倒位序存放就是将原来第i个位置的元素存放到第(b0b1b2b3b4b5b6)b的位置上去.由于C语言的位操作能力很强,可以分别提取出b6、b5、b4、b3、b2、b1、b0,再重新组合成b0、b1、b2、b3、b4、b5、b6,即是倒位序的位置。
程序段如下(假设128点FFT):/* i为原始存放位置,最后得invert_pos为倒位序存放位置*/int b0=b1=b2=b3=b4=b5=6=0;b0=i&0x01; b1=(i/2)&0x01; b2=(i/4)&0x01;b3=(i/8)&0x01; b4=(i/16)&0x01; b5=(i/32)&0x01;b6=(i/64)&0x01; /*以上语句提取各比特的0、1值*/invert_pos=x0*64+x1*32+x2*16+x3*8+x4*4+x5*2+x6;对比教科书上的倒位序程序,会发现这种算法充分利用了C语言的位操作能力,非常容易理解而且位操作的速度很快。
二、实数蝶形运算算法的推导首先看一下图1所示的蝶形图。
图1:蝶形图蝶形公式:X(K) = X’(K) + X’(K+B)W PN ,X(K+B) = X’(K) - X’(K+B) W PN其中W PN= cos(2πP/N)- jsin(2πP/N)。
FFT的C语言算法实现

FFT的C语言算法实现FFT算法的基本思想是将一个N点离散信号转换成N个频率分量。
它使用了分治思想,通过递归将问题分解为较小规模的子问题,最终合并子问题的结果得到最终结果。
以下是FFT的C语言算法实现:```#include <stdio.h>#include <math.h>//计算复数的实部double real(double x)return x;//计算复数的虚部double imag(double x)return -x; // i的平方为-1//复数相加return a + b;//复数相乘return a * b;//快速傅里叶变换主函数void fft(double* real_input, double* imag_input, int N, double* real_output, double* imag_output)//如果输入序列长度为1,直接返回if (N == 1)real_output[0] = real(real_input[0]);imag_output[0] = imag(imag_input[0]);return;}//创建长度为N/2的偶数序列和奇数序列输入double* even_real_input = (double*)malloc(sizeof(double) * (N/2));double* even_imag_input = (double*)malloc(sizeof(double) * (N/2));double* odd_real_input = (double*)malloc(sizeof(double) * (N/2));double* odd_imag_input = (double*)malloc(sizeof(double) * (N/2));//将输入序列按奇偶分组for (int i = 0; i < N/2; i++)even_real_input[i] = real_input[2*i];even_imag_input[i] = imag_input[2*i];odd_real_input[i] = real_input[2*i+1];odd_imag_input[i] = imag_input[2*i+1];}//计算偶数序列的FFTdouble* even_real_output = (double*)malloc(sizeof(double) * (N/2));double* even_imag_output = (double*)malloc(sizeof(double) * (N/2));fft(even_real_input, even_imag_input, N/2, even_real_output, even_imag_output);//计算奇数序列的FFTdouble* odd_real_output = (double*)malloc(sizeof(double) * (N/2));double* odd_imag_output = (double*)malloc(sizeof(double) * (N/2));fft(odd_real_input, odd_imag_input, N/2, odd_real_output, odd_imag_output);//合并子问题的结果for (int i = 0; i < N/2; i++)double k_real = cos(2 * M_PI * i / N);double k_imag = sin(2 * M_PI * i / N);}//释放内存free(even_real_input);free(even_imag_input);free(odd_real_input);free(odd_imag_input);free(even_real_output);free(even_imag_output);free(odd_real_output);free(odd_imag_output);int mai//测试数据double real_input[] = {1, 2, 3, 4};double imag_input[] = {0, 0, 0, 0};int N = sizeof(real_input) / sizeof(double);double* real_output = (double*)malloc(sizeof(double) * N); double* imag_output = (double*)malloc(sizeof(double) * N);fft(real_input, imag_input, N, real_output, imag_output);//输出傅里叶变换结果for (int i = 0; i < N; i++)printf("%.2f + %.2fi\n", real_output[i], imag_output[i]);}//释放内存free(real_output);free(imag_output);return 0;```在FFT函数中,先判断输入序列的长度,如果长度为1,直接返回结果。
fft c语言程序

fft c语言程序快速傅里叶变换(FFT)是一种计算傅里叶变换的高效算法,广泛应用于信号处理、图像处理、数值分析等领域。
在这里,我将使用C语言来实现FFT算法。
首先,我们需要先理解傅里叶变换的原理。
傅里叶变换可以将一个函数从时域转换到频域,也可以将一个函数从频域转换到时域。
在C语言中,我们通常使用复数来表示傅里叶变换中的复数系数。
在使用C语言实现FFT算法之前,我们需要了解一些基本的数学概念和公式。
首先是复数的表示。
复数可以用实部和虚部表示,例如a+bi,其中a和b都是实数,i表示虚数单位。
在C语言中,我们可以使用结构体或数组来表示复数。
下面是一个使用数组表示复数的例子:ctypedef struct {double real;double imag;} Complex;傅里叶变换的公式可以表示为:cX(k) = Σ(x(n) * e^(-2πikn/N)) (0 <= k < N)其中X(k)表示频域上的复数系数,x(n)表示时域上的离散信号,N表示信号的长度,k表示频域上的位置。
基于这个公式,我们可以编写一个递归的FFT算法,如下所示:cvoid fft(Complex* input, Complex* output, int n, int s) {if (n == 1) {output[0].real = input[0].real;output[0].imag = input[0].imag;return;}Complex* even = (Complex*)malloc(n / 2 * sizeof(Complex));Complex* odd = (Complex*)malloc(n / 2 * sizeof(Complex));Complex* evenResult = (Complex*)malloc(n / 2 * sizeof(Complex));Complex* oddResult = (Complex*)malloc(n / 2 * sizeof(Complex));for (int i = 0; i < n / 2; i++) {even[i].real = input[2 * i].real;even[i].imag = input[2 * i].imag;odd[i].real = input[2 * i + 1].real;odd[i].imag = input[2 * i + 1].imag;}fft(even, evenResult, n / 2, 2 * s);fft(odd, oddResult, n / 2, 2 * s);for (int k = 0; k < n / 2; k++) {double angle = -2 * M_PI * k / n;Complex temp;temp.real = cos(angle);temp.imag = sin(angle);Complex mult = complexMultiply(temp, oddResult[k]);output[k].real = evenResult[k].real + mult.real;output[k].imag = evenResult[k].imag + mult.imag;output[k + n / 2].real = evenResult[k].real - mult.real;output[k + n / 2].imag = evenResult[k].imag - mult.imag;}free(even);free(odd);free(evenResult);free(oddResult);}Complex complexMultiply(Complex a, Complex b) {Complex result;result.real = a.real * b.real - a.imag * b.imag;result.imag = a.real * b.imag + a.imag * b.real;return result;}上述代码使用了递归的方式实现FFT算法。
fft c语言程序

fft c语言程序(原创实用版)目录1.FFT 的定义与作用2.C 语言程序的基本结构3.FFT 算法的原理4.FFT 算法的实现步骤5.FFT 程序的优缺点正文1.FFT 的定义与作用快速傅里叶变换(FFT)是一种高效的计算离散傅里叶变换(DFT)的算法。
DFT 是一种将时间域信号转换到频率域的方法,常用于信号处理、图像处理等领域。
然而,当信号长度很长时,DFT 的计算复杂度较高,因此,为了加速计算,提出了 FFT 算法。
2.C 语言程序的基本结构C 语言是一种广泛应用的编程语言,其具有较高的执行效率和灵活性。
编写 FFT C 语言程序,首先需要了解 C 语言的基本语法和结构,包括变量声明、函数定义、循环结构、条件语句等。
3.FFT 算法的原理FFT 算法的原理是将 DFT 分解成更小的子问题,并重复利用子问题的计算结果。
具体来说,如果将信号长度为 N 的 DFT 表示为:X_k = ∑_{n=0}^{N-1} x_n * e^(-j * 2 * pi * n * k / N)其中,x_n 是信号在时域上的值,X_k 是信号在频率域上的值。
那么,如果将信号长度分解为 2 的幂次方形式(如 N = 2^m),则可以将 DFT 分解为两个较短的 DFT 的加权和,即:X_k = ∑_{n=0}^{N/2-1} x_{2n} * e^(-j * 2 * pi * n * k / N) + e^(-j * 2 * pi * k) * ∑_{n=0}^{N/2-1} x_{2n+1} * e^(-j * 2 * pi * n * k / N)这样,计算复杂度就从 O(N^2) 降低到 O(NlogN)。
4.FFT 算法的实现步骤(1)确定信号长度 N,并判断是否为 2 的幂次方形式。
如果不是,则进行填充或截断,使其成为 2 的幂次方形式。
(2)按照 FFT 算法的原理,递归地将信号分解为较短的子信号,直到信号长度为 1。
用c语言实现的FFT

一、对FFT得介绍1、 FFT(Fast Fourier Transformation),即为快速傅里叶变换,就是离散傅里叶变换得快速算法,它就是根据离散傅里叶变换得奇、偶、虚、实等特性,对离散傅里叶变换得算法进行改进获得得。
2、FFT算法得基本原理FFT算法就是把长序列得DFT逐次分解为较短序列得DFT。
按照抽取方式得不同可分为DIT-FFT(按时间抽取)与DIF-FFT(按频率抽取)算法。
按蝶形运算得构成不同可分为基2,基4,基8,以及任意因子得类型。
3、迭代关系4、本次程序得基本过程我们这次所研究得就是数字信号处理中得FFT算法,我们这次所用得数字信号就是复数类型得。
(1)所以首先,我们先定义了一个复数结构体,因为就是进行复数得运算,我们又相继定义复数得加减乘运算得函数。
(2)紧接着,我们定义了进行FFT计算得fft()快速傅里叶变换函数initW() 初始化变换核函数即旋转因子得计算,change() 变址函数,output()输出傅里叶变换得结果得函数。
(3)定义主函数,并调用定义好得相关子函数,利用fft()中得蝶形运算以及change()函数来完成从时间域上选取得DIT-FFT。
EbodE。
二、FFT中码位倒置排序1、码位倒置得实现方法:(1)简单得利用按位与、或循环实现(2)利用公式推导得迭代方法2、为什么要进行码位倒置因为由于FFT得计算特性,如果按照正常顺序输入,而没有进行码位倒置得话,就会以乱序输出,就不便于我们后续对信号得相关性质进行研究了,所以DIT-FFT算法就就是在进行FFT计算之前,进行分奇偶后得码位倒置运算,即二进制数得倒位。
3、倒位序由奇偶分组造成,以N=8为例,说明如下:rAY2v。
三、蝶形运算由按照上述公式得规律进行逐级分解,直到2点DFT,如下就是N=8时得蝶形算法分析图:四、FFT算法中蝶形算法得基本思想分析(1)我们知道N点FFT运算可以分成log2(N)级,每一级都有N/2个碟形,FFT得基本思想就是用3层循环完成全部运算(N点FFT)。
c语言快速傅里叶变换处理数据

c语言快速傅里叶变换处理数据快速傅里叶变换(FFT)是一种用于处理数字信号的强大算法。
在C语言中,使用FFT可以对声音、图像、视频等数字信号进行处理和分析。
本文将介绍如何使用C语言进行快速傅里叶变换处理数据。
第一步是导入必要的头文件。
在C语言中,我们使用math.h头文件来进行数学运算,使用stdio.h头文件进行输入输出。
同时,我们需要使用一个专门的FFT库,例如FFTW或KISSFFT。
这些库可以在网上下载并导入到我们的程序中。
第二步是定义并初始化数据。
我们可以通过输入或读取文件来获取数据。
在本例中,我们将使用以下数组作为示例数据:float data[8] = {0, 1, 2, 3, 4, 3, 2, 1};第三步是使用FFT库进行FFT变换。
在这个例子中,我们使用FFTW库。
我们需要定义一个FFTW计划,然后使用fftw_plan_dft_1d 函数将数据传递给计划。
fftw_complex *fft_result;fftw_plan plan;fft_result = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * n);plan = fftw_plan_dft_1d(n, in, fft_result, FFTW_FORWARD, FFTW_ESTIMATE);fftw_execute(plan);第四步是对FFT结果进行后处理。
一般来说,处理后的FFT结果包括幅度谱和相位谱。
幅度谱表示信号中不同频率成分的强度,而相位谱表示这些频率成分之间的相对相位差。
我们可以使用以下代码来计算幅度谱:for (i = 0; i < n; i++) {double amplitude = sqrt(pow(fft_result[i][0], 2) +pow(fft_result[i][1], 2));printf('%d Hz: %f', i*fs/n, amplitude);}这段代码将输出不同频率成分的幅度。
fft c语言程序 -回复

fft c语言程序-回复你的要求是写一篇关于FFT(快速傅里叶变换)的C语言程序的文章,让我逐步解释该程序的实现过程。
下面是一个满足你要求的文章:标题:理解和实现FFT算法的C语言程序引言:FFT (快速傅里叶变换) 算法是一种重要的数学计算方法,用于将一个时间域函数转换为频域函数。
它在信号处理、图像处理和音频处理等领域广泛应用。
本文将通过一个C语言程序来逐步解释如何实现FFT算法。
第一部分:算法概述FFT算法的核心思想是将一个长度为N的复数序列进行分解,并将其转换为N个频率特征。
该算法的时间复杂度为O(NlogN),相比于传统的傅里叶变换算法具有更高的效率。
第二部分:C语言程序设计我们将使用C语言来实现FFT算法。
首先,需要引入一些基本的库函数。
c#include <math.h>#include <stdio.h>#include <stdlib.h>第三部分:全局变量和辅助函数的定义在程序中,我们需要定义一些全局变量和辅助函数来辅助实现FFT算法。
首先,我们需要定义复数结构体来表示复数:ctypedef struct {float real;float imag;} Complex;接下来,我们需要定义一些辅助函数,包括计算2的幂次方、位反转、获取频率以及计算FFT:cint get_power_of_two(int n) {int power = 0;while (pow(2, power) < n) {power++;}return power;}int bit_reverse(int x, int power) {int reversed = 0;for (int i = 0; i < power; ++i) {reversed <<= 1;reversed = (x & 1);x >>= 1;}return reversed;}float get_frequency(int k, int N, int fs) {return ((float)k * fs) / N;}Complex* compute_fft(Complex* x, int N, int power, int inverse) { Complex* X = (Complex*)malloc(sizeof(Complex) * N);for (int k = 0; k < N; ++k) {X[k].real = 0;X[k].imag = 0;for (int n = 0; n < N; ++n) {float angle = (inverse ? 1 : -1) * 2 * M_PI * k * n / N;float cos_val = cos(angle);float sin_val = sin(angle);X[k].real += x[n].real * cos_val - x[n].imag * sin_val;X[k].imag += x[n].real * sin_val + x[n].imag * cos_val;}}return X;}第四部分:主函数的实现在主函数中,我们可以通过输入一个时间域的复数序列并将其转换为频域函数。
整理的可用FFT原理及程序

FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。
一个模拟信号,经过ADC 采样之后,就变成了数字信号。
采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此啰嗦了。
采样得到的数字信号,就可以做FFT变换了。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。
为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N倍。
而每个点的相位呢,就是在该频率下的信号的相位。
第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理的步骤与注意事项,并编写1024个采样点的FFT C语言程序1. 数字信号处理1.1 数字信号处理概述数字信号处理是研究如何用数字或符号序列来表示信号以及如何对这些序列进行处理的一门学科。
随着计算机技术的发展,数字信号处理技术得到了越来越广泛的应用,它已成为现代科学技术必不可少的工具。
数字信号是数据序列,其处理实际上就是进行各种数学运算,如加、减、乘以及各种逻辑运算等等。
因此,数字信号处理既可以是软件处理也可以是硬件处理。
所谓软件处理,就是对所需要的运算编制程序,然后在计算机上实现,其处理灵活、方便。
所谓硬件处理,就是用加法器、乘法器、延时器以及它们的各种组合来构成数字电路,以实现所需要的运算。
硬件处理显然不如软件处理灵活方便,但能对数字信号进行实时处理。
近年来日益广泛采用的各种数字信号处理器(如TI TMS320系列、Philps Trimedia系列等)可以认为是软硬件处理方式的结合,这种处理时用数字信号处理芯片以及存储器来组成硬件电路,所需要的运算靠特定的汇编语言编程来实现。
因此,采用数字信号处理器既方便灵活,又能做到实时处理,所以数字信号处理器(DSP)已经越来越广泛地应用于包括通信在内的各个领域之中。
1.2 数字信号处理的优点(1)精度高数字系统的特性不因环境的变化而变化,计算精度是模拟系统所无法相比的,运算位数由8位提高到16位、32位、64位。
(2)可靠性高模拟系统中各种参数受温度、环境影响较大,因而易出现感应、杂散效应,甚至会出现震荡等等;而数字系统受温度、环境影响较小。
模拟信号受到干扰即产生失真,而数字信号由于只有两种状态,因此,所受的干扰只要在一定范围以内,就不会产生影响,这就是说,数字信号抗干扰能力强。
另外,如果用数字信号进行传输,在中继站还可以再生。
总的说来,信号的数字处理可靠性高。
(3)灵活性强可以通过改变数字信号系统的参数来改变系统的性能。
数字信号的灵活性还表现在可以利用一套计算设备同时处理多路相互独立的信号,即所谓的“时分复用”,这在数字电话系统中是非常有用的技术。
(4)便于大规模集成化数字部件具有高度的规范性,易于实现大规模集成化和大规模生产,数字系统体积小、重量轻。
(5)数字信号便于加密处理由于数字信号实际上为数据序列,因此便于加密运算处理。
(6)对于低频信号尤其优越处理低频信号的模拟元件如电感、电容等一般都体积较大、制作不易、适用不便。
如果转换成数字信号来进行处理,由于频率低,对数字部件的速度要求不高,因而容易实现。
数学处理当然也有不足之处。
目前,数字系统的速度还不能达到处理很高频率信号(例如射频信号)的要求。
但随着大规模集成电路、高速数字计算机的发展尤其是微处理器的发展,数字系统的速度将会越来越高,数字信号处理也会越来越显示出其优越性。
1.3 数字信号处理的步骤数字信号处理系统的框图,如图1所示:图1 数字信号处理系统框图由图1可知,数字信号处理主要有预处理、采样与A/D转换和计算机处理三大步骤。
(1)预处理预处理包括:a.隔离信号中的直流分量(如果所测信号中不应有直流分量)。
b.若信号经过调制,则应先行解调。
c.电压幅值调理,以便适宜于采样。
总是希望电压幅值峰—峰值足够大,以便充分利用A/D转换器的精度。
如12位的A/D转换器,其参考电压为±5V,若信号电平较低,转换后二进制数的高位都为0,仅在低位有值,其转换后的信噪比将很差,若信号电平绝对值超过5V,则转换中又将发生溢出,这是不允许的。
所以进入A/D的信号电平应适当调整。
(2)采样与A/D转换必要的滤波比提高信噪比,并滤去信号中的高频噪声。
采样与A/D转换包括采样、保持和量化。
(3)数字信号处理数字信号处理包括截断、加权、数字滤波和计算机信号分析四部分。
计算机只能处理有限长度的数据,所以首先要把长时间的序列截断,对截取的数字序列有时还要人为地进行加权(乘以窗函数)以成为新的有限长的序列。
对数据中的奇异点(由于强干扰或信号丢失所引起的数据突变)应予以剔除。
对温漂、时漂等系统性干扰所引起的趋势项(周期大于记录长度的频率成分)也应予以分离。
如有必要,还可以设计专门的程序来进行数字滤波。
然后把数据按给定的程序运行运算,完成各种分析。
1.4 数字信号处理的注意事项(1)采样间隔采样间隔的选择是一个重要的问题。
采样间隔太小(采样频率高),则对定长的时间记录来说其数字序列就很长,计算工作量迅速增大;如果数字序列长度较短,则只能处理较短的时间历程,可能产生较大的误差。
若采样间隔过大(采样频率低),则可能丢掉有用的信息,同时采样间隔过大还会引起混叠现象。
因此采样频率通常选为(3~4)f(h f为信号的最高频率)。
h(2)截断、泄露和窗函数截断就是讲信号乘以时域的有限宽矩形窗函数,由于窗函数是一个无限宽带的sinc函数,所以信号在截断后也必然成为无限宽带的信号,这种信号的能量在频率轴分布扩展的现象成为泄露,故信号截断必然导致误差。
为了减小截断的影响,常采用其他的时窗函数来对所截取的时域信号进行加权处理。
所选的窗函数应力求其频谱的主瓣宽度窄些、旁瓣幅度小些。
2.快速傅里叶变换(FFT)2.1 叶变换简介快速傅里有限长序列可以通过离散傅里叶变换(DFT)将其频域也离散化成有限长序列.但其计算量太大,很难实时地处理问题,因此引出了快速傅里叶变换(FFT). 1965 年,Cooley 和Tukey 提出了计算离散傅里叶变换(DFT)的快速算法,将DFT 的运算量减少了几个数量级。
从此,对快速傅里叶变换( FFT)算法的研究便不断深入,数字信号处理这门新兴学科也随FFT 的出现和发展而迅速发展。
根据对序列分解与选取方法的不同而产生了FFT 的多种算法,基本算法是基-2DIT 和基-2DIF。
FFT 在离散傅里叶反变换、线性卷积和线性相关等方面也有重要应用。
快速傅氏变换(FFT),是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。
快速傅立叶变换作为一种数学方法,已经广泛地应用在几乎所有领域的频谱分析中,而且经久不衰,因为信号处理方法没有先进和落后之分,只有经典和现代之别,在实际系统中用得最好的方法就是管用的方法。
换句话说,信号处理方法与应用背景和目的的贴近程度是衡量信号处理方法优劣的唯一标准。
FFT 是快速傅利叶变换(Fast FourierTransform 简称FFT)的英文缩写,它在当今科技世界中的应用相当活跃,无论是在时间序列分析领域中,还是在我国刚刚兴起的生物频谱治疗的研究与应用中,都有着重要的作用。
同时,它又是软件实现数字滤波器的必备组成部分之一。
FFT 算法的基本思想:利用DFT 系数的特性,合并DFT 运算中的某些项,把长序列的DFT —>短序列的DFT ,从而减少其运算量。
FFT 算法分类: 时间抽选法DIT: Decimation-In-Time ; 频率抽选法DIF: Decimation-In-Frequency 。
在此以按时间抽选的基-2FFT 算法为例进行说明。
2.2 算法原理N 为2 的整数幂的FFT 算法称基-2FFT 算法。
设N 点序列()x n ,n =0,1,2,…N-1 按n 的奇偶分成两个长为N/2的序列12()(2)()(21)x r x r x r x r ==+ r =0,1,2,…,2N -1由于2/2N N W W =则()x n 的DFT :111()()()()N N N nk nk nk NNNn n n X k x n Wx n Wx n W---=====+∑∑∑n 为偶数 n 为奇数=11222(21)00(2)(21)N N rk r k N Nr r x r W x r W--+==++∑∑=11221/22/20()()N N rk k rk N N N r r x r W W x r W --==+∑∑=12()()kN X k W X k + k =0,1,2,…,N-1 (1)其中:1()X k =12/20(2)N rk N r x r W -=∑=121/20()N rk N r x r W -=∑ (2)2()X k =12/20(21)N rk N r x r W -=+∑=122/20()N rk N r x r W -=∑ (3)按式(1)计算得到的只是()X k 的前一半项数的结果,即(0≤k ≤2N —1)。
由系数的周期性可推出()X k 的后一半值,即(2N ≤k ≤N —1):.(/2)/2/2r k N r k N NW W += (/2)/2k N k N k N N NNW W W W +=⋅=- (/2N N W =—1)又因为1()X k ,2()X k 是以2N 为周期的,可推出: 1122(/2)11/21/210(/2)()()()N N r k N rk N N r r X k N x r Wx r WX k --+==+===∑∑ (4)同理可得,2(/2)X k N +=2()X k (5) 由此可得N 点对应的DFT ()X k 的计算式子:1212()()()(/2)()()kN k NX k X k W X k X k N X k W X k =++=- k =0,1,2,…,2N -1 (6)上一式计算()X k 的前一半值,下一式计算()X k 的后一半值。
因此只要求出0~2N —1区间内各个整数k 值所对应的1()X k 和2()X k ,便可求出0到N-1点全部的()X k 值。
明显节约了运算量。
式中因子k N W 在复数乘法中起一个旋转的作用,称为旋转因子。
公式(6)的运算可以归结为两个复数a 、b 求得复数k N a bW +和k N a bW -。
用信号流程图的方法可以简单的表示为如图2所示。
这样的运算称为蝶形运算,在FFT 算法中占有核心的地位。
图2 时间抽选蝶形运算流图显然,每个蝶形运算对应于一次复数乘法和两次复数加法运算。
如果用DFT 方法直接计算出1()Xk 和2()Xk ,共需22N 次复数乘法运算,再作N/2次蝶形运算,又需N/2次复数乘法和N 次复数加法。
这样算出N 点DFT 共需要(2N +N )/2次复数乘法和(2N /2)+N 次复数加法。
当N 较大时,同直接计算N 点DFT 所需的2N 次复数乘加次数相比,几乎减少了一半的计算量。
假设N/2还是偶数,则1()Xk 和2()X k 这两个N/2点的DTF 计算,又分别可以通过计算N/4点DFT 和蝶形运算而得到。
