大学物理1质点运动学例题

合集下载

大学物理Ⅰ质点运动学试题(经典)

选择题1. 下列表述正确的是【】（A ）质点速度为零其加速度一定为零；（B ）质点具有恒定的速率一定有变化的速度；（C ）一质点具有沿x 轴正向的加速度而可以有沿x 轴负向的速度；（D ）质点具有恒定的速度但仍有变化的速率。

2. 某质点的运动规律为2xx dv kv t dt=-,式中的k 为大于零的常量.当t=0时,初速为,0x v 则速度xv 与时间t 的关系是【】（A ）021211x x v kt v += （B ）0221x x v kt v +-=（C ）0221x x v kt v +=（D ）021211x x v kt v +-= 3. 一质点从某一高度以v 的速度水平抛出，已知它落地时的速度为t v ,那么它运动的时间为【】（A ）t v v g -0 （B ）t v v g -02 （C ）t (v v )g -12220 （D ）t (v v )g-122202 4. 一质点在xoy 平面运动,其运动方程为j t b i t a r ωωsin cos +=式中a 、b 、ω皆为常量，则质点作【】（A ）匀速圆周运动；（B ）变速圆周运动；（C ）匀速直线运动；（D ）变速椭圆运动。

5. 用绳子系一物体，使它在铅直面内作圆周运动。

在圆周的最低点时物体受的力为：【】（A ）重力、向心力和离心力；（B ）重力和绳子拉力；（C ）重力和向心力；（D ）重力、绳子拉力和离心力。

（E ）开始随F 增大，达到某一最大值后，就保持不变。

6. 质量为0.25kg 的质点，受i t F =(N)的力作用，t=0时该质点以v =2jm/s 的速度通过坐标原点，该质点任意时刻的位置矢量是：【】（A ）22t i +2j m ；（B ）j t i t 2323+m ；（C ）j t i t 343243+m ；（D ）条件不足，无法确定。

7. 质量为m 的物体自空中落下，它除受重力外，还受到一个与速度平方成正比的阻力的作用。

大学物理题库-第1章-质点运动学(含答案解析)

大学物理题库第一章质点运动学一、选择题：1、在平面上运动的质点，如果其运动方程为j bt i at r22+= (其中b a ,为常数)，则该质点作[ ]（A ）匀速直线运动（B ）变速直线运动（C ）抛物线运动（D ）一般曲线运动2、质点以速度124-⋅+=s m t v 作直线运动，沿质点运动方向作ox 轴，并已知s t 3=时，质点位于m x 9=处，则该质点的运动方程为[ ](A) t x 2= (B) 2214t t x += (C) 123143-+=t t x (D) 123143++=t t x3、某雷达刚开机时发现一敌机的位置在j i96+处,经过3秒钟后，该敌机的位置在处,若i 、j分别表示直角坐标系中y x ,的单位矢量，则敌机的平均速度为[ ]（A ）j i 36+ （B ）j i 36-- （C ）j i -2 （D ）j i +-24、质点沿半径为R 的圆周作匀速率运动，每T 秒转一圈．在2T 时间间隔中，其平均速度大小与平均速率大小分别为(A) 2πR /T , 2πR/T ． (B) 0 , 2πR /T(C) 0 , 0． (D) 2πR /T , 0. ［］5、一质点在平面上作一般曲线运动，其瞬时速度为v，瞬时速率为v ，某一时间内的平均速度为v，平均速率为v ，它们之间的关系必定有：（A ）v v v,v == （B ）v v v,v =≠（C ）v v v,v ≠≠（D ）v v v,v ≠=[ ] 6、一运动质点的位置矢量为)y ,x (r，其速度大小为[ ](A)dt dr （B ）dt r d （C ）dt r d （D ）dtr d （E ）22)()(dt dydt dx +7、某物体的运动规律为t kv dtdv2-=,式中的k 为大于零的常数，当0=t 时，初速度为0v ，则速度v 与时间t 的函数关系是：[ ]（A ）0221v kt v += （B ） 0221v kt v +-=（C ） 021211v kt v += （D ） 021211v kt v +-=8、一质点作直线运动，某时刻的瞬时速度=v 2 m/s ，瞬时加速度2/2s m a -=，则一秒钟后质点的速度(A) 等于零． (B) 等于-2 m/s ．ji 612+(C) 等于2 m/s ． (D) 不能确定．［］ 9、质点作曲线运动，r 表示位置矢量，v 表示速度，a表示加速度，S 表示路程，a 表示切向加速度，下列表达式中，(1) a t = d /d v ， (2) v =t r d /d ， (3) v =t S d /d ， (4) t a t =d /d v．(A) 只有(1)、(4)是对的． (B) 只有(2)、(4)是对的． (C) 只有(2)是对的．(D) 只有(3)是对的．［］ 10、一质点在运动过程中，0=dtr d ,而=dtdv常数，这种运动属于[ ] （A ）初速为零的匀变速直线运动；（B ）速度为零而加速度不为零的运动；（C ）加速度不变的圆周运动；（D ）匀变速率圆周运动。

(完整版)大学物理01质点运动学习题解答

第一章质点运动学一选择题1．以下说法中，正确的选项是：（）A.一物体若拥有恒定的速率，则没有变化的速度；B.一物体拥有恒定的速度，但仍有变化的速率；C.一物体拥有恒定的加快度，则其速度不行能为零；D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。

解：答案是 D。

2.长度不变的杆 AB，其端点 A 以 v0匀速沿 y 轴向下滑动， B 点沿 x 轴挪动，则 B 点的速率为：（）A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解：答案是 C。

简要提示：设 B 点的坐标为 x， A 点的坐标为 y，杆的长度为l，则x2y2l 2对上式两边关于时间求导：dx dy0，因dxv，dyv0，所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。

3.如图示，路灯距地面高为 H，行人身高为 h，若人以匀速 v 背向路灯行走，灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为（）H h Hv h HA.vB.H H h H h 解：答案是 B 。

简要提示：设人头影子到灯杆的距离为 x ，则x s h ， x Hs ， x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。

4. 某质点作直线运动的运动学方程为x ＝ 3t-5t 3 + 6 (SI)，则该质点作A. 匀加快直线运动，加快度沿 x 轴正方向．B. 匀加快直线运动，加快度沿 x 轴负方向．C. 变加快直线运动，加快度沿 x 轴正方向．D. 变加快直线运动，加快度沿x 轴负方向．()解：答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出，已知它落地时的速度为v t ，那么它的运动时间是：（）v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解：答案是 C 。

大学物理上册第一章质点运动学习题及答案

第一章质点运动学一、简答题1、运动质点的路程和位移有何区别?答：路程是标量，位移是矢量；路程表示质点实际运动轨迹的长度，而位移表示始点指向终点的有向线段。

2、质点运动方程为()()()()k t z j t y i t x t r ++=，其位置矢量的大小、速度及加速度如何表示? 答：()()()t z t y t x r 222r ++==()()()k t z j t y i t xv ++= ()()()k t z j t y i t x a ++=3、质点做曲线运动在t t t ∆+→时间内速度从1v 变为到2v ，则平均加速度和t时刻的瞬时加速度各为多少? 答：平均加速度 t v v a ∆-=12 ，瞬时加速度()()dt v d t v v a t t lim t 120 =∆-=→∆4、画出示意图说明什么是伽利略速度变换公式? 其适用条件是什么?答：牵连相对绝对U V +=V ，适用条件宏观低速5、什么质点? 一个物体具备哪些条件时才可以被看作质点?答：质点是一个理想化的模型,它是实际物体在一定条件下的科学抽象。

条件：只要物体的形状和大小在所研究的问题中属于无关因素或次要因素,物体就能被看作质点。

二、选择题1、关于运动和静止的说法中正确的是 ( C )A 、我们看到的物体的位置没有变化，物体一定处于静止状态B 、两物体间的距离没有变化，两物体就一定都静止C 、自然界中找不到不运动的物体，运动是绝对的，静止是相对的D 、为了研究物体的运动，必须先选参考系，平时说的运动和静止是相对地球而言的2、下列说法中正确的是 ( D )A 、物体运动的速度越大，加速度也一定越大B 、物体的加速度越大，它的速度一定越大C 、加速度就是“加出来的速度”D 、加速度反映速度变化的快慢，与速度大小无关3、质点沿x 轴作直线运动，其t v-曲线如图所示，如s t 0=时，质点位于坐标原点，则s .t 54=时，质点在x 轴的位置为 ( B )A 、5 mB 、2 mC 、0 mD 、-2 m4、质点作匀速率圆周运动，则 ( B )A 、线速度不变B 、角速度不变C 、法向加速度不变D 、加速度不变5、质点作直线运动，某时刻的瞬时速度为s /m v 2=，瞬时加速度为22s /m a -=，则一秒钟后质点的速度 ( D )A 、等于0B 、等于s /m 2-C 、等于s /m 2D 、不能确定6、质点作曲线运动，r 表示位置矢量的大小，s 表示路程，z a 表示切向加速度的大小，v 表示速度的大小。

大学物理第一章质点运动学习题

n
1 2 间的关系为= v0t − bt ( SI)。 s 2，质点加速度的大小和方向。求：(1) 任意时刻t，质点加速度的大小和方向。任意时刻
求：
a
α
r aτ
R
R
τ
dt
r an
4
a = an + aτ =
2 2
(v0 − bt )4 + (− b )2
R2
r (v 0 − bt ) an a 与切向轴的夹角为 α = arctg = arctg (− Rb ) aτ
v v v v dr 解：v = = 2i − 2tj dt v v v v v t = 2 v2 = 2i − 4 j t = 0 v0 = 2i
v2 = 22 + 42 = 4.47m/ s 大小：大小：
−4 方向：方向： θ = arctan = −63o26′ 2
θ为 2与轴的夹角 v x
x = −t 2 (SI)
例5：一质点运动轨迹为抛物线：求：x= -4m时（t>0)粒子的时粒子的速度、速率、加速度。速度、速率、加速度。解： x= -4m时 t=2s 时
x t =2 dx vx = −4m s vx = = −2t dt t =2 dy 3 vy = −24m s vy = = −4t + 4t dt v v v 2 v = vx + v2 = 4 37 m s v = −4i − 24 j m/ s y 2 dvx d x −2 ax = s = = −2m ay = −12t 2 + 4 = −44(m −2 ) s 2 dt dt v v r a = −2i − 44 j m⋅ s−2
y = −t 4 + 2t 2(SI)

大学物理第一章质点运动学-习题及答案

第一章质点运动学1-1 一质点在平面上运动，已知质点位置矢量的表示式为j i r 22bt at += （其中b a ,为常量）则该质点作（A ）匀速直线运动（B ）变速直线运动（C ）抛物线运动（D ）一般曲线运动 [B]解：由j i rv bt at t 22d d +==知 v 随t 变化，质点作变速运动。

又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。

故该质点作变速直线运动。

1-2 质点作曲线运动，r 表示位置矢量，s 表示路程，t a 表示切向加速度，下列表达式中，① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v （A ）只有（1）、（4）是对的。

（B ）只有（2）、（4）是对的。

（C ）只有（2）是对的。

（D ）只有（3）是对的。

[D]解：由定义：t vt a d d d d ≠=v ； t r t s t v d d d d d d ≠==r ； t t v a d d d d v ≠=τ只有③正确。

1-3 在相对地面静止的坐标系内，A 、B 二船都以21s m -⋅的速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向。

今在A 船上设置与静止坐标系方向相同的坐标系（x ，y 方向单位矢用j i ,表示），那么在A 船上的坐标系中，B 船的速度（以1s m -⋅为单位）为（A ）j i 22+ （B ）j i 22+-（C ）j i 22-- （D ）j i 22- [B]解：由i v 2=对地A ，j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= （1s m -⋅）1-4 一质点沿x 方向运动，其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅，则当t 为3s 时，质点的速度1s m 23-⋅=v解：⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=，则在t 由0至4s 的时间间隔内，质点的位移大小为 8m ，在t 由0到4s 的时间间隔内质点走过的路程为 10m 。

大物1-4质点运动学习题

1大物习题练习一质点运动学（一）1.一质点的运动方程为r =t i +2t 3j (SI )，则t =1秒时的速度v =s m j i /)6(+，1至3秒内的平均速度为s m j i /)26( +，平均加速度为2/)24(s m j。

2.一质点在XOY 平面内运动，其运动方程为以下五种可能：（1）x=t ，y =19-2/t ；（2）x =2t ，y =18-3t ；（3）x =3t ，y =17-4t 2；（4）x =4sin 5t ，y =4cos 5t ；（5）x =5cos 6t ，y =6sin 6t 。

那么表示质点作直线运动的方程为 2 ，作圆周运动的为 4 ，作椭圆运动的方程为 5 ，作抛物线运动的方程为 3 ，作双曲线运动的方程为 1 。

（分别选择（1）（2）（3）（4）（5）填入空白处）。

3.（2）物体沿一闭合路径运动，经∆t 时间后回到出发点A ，如图1-3所示，初速度v 1，末速度v 2，且21v v=，则在∆t 时间内其平均速度v 与平均加速度a分别为：（1）00==a v ，（2）；，00≠=a v（3）00≠≠a v ，（4）00=≠a v，4.（3）质点作曲线运动，元位移d r ，元路程d s ，位移∆r ，路程∆s ，它们之间量值相等的是：（1）⎢∆r ⎢=⎢∆s ⎢；（2）⎢d r ⎢=∆s ；（3）⎢d r ⎢=d s ；（4）⎢d r ⎢=⎢∆r ⎢；（5）⎢∆r ⎢=d s 。

5.一质点沿OX 轴作直线运动，它在t 时刻的坐标是x=4.5t 2-2t 3(SI )试求（1）t =1秒末和2秒末的瞬时加速度，第二秒内质点的平均加速度；解：v=9t-6t 2, a=9-12t 所以：a1=-3, a2=-15 9-=a（2）第2秒内质点所通过的路程； y1=2.5, y2=2, y2.5=0 Δy=0.5 （3）填写下表中质点在0-3秒内的速率v 和加速度a 的方向变化情况。

大学物理第一章质点运动学-习题及答案

又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。

故该质点作变速直线运动。

（B ）只有（2）、（4）是对的。

（C ）只有（2）是对的。

（D ）只有（3）是对的。

[D]解：由定义：t vt a d d d d ≠=v ； t r t s t v d d d d d d ≠==r ； t t v a d d d d v ≠=τ只有③正确。

1-3 在相对地面静止的坐标系内，A 、B 二船都以21s m -⋅的速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向。

大学物理练习题_C1-1质点运动学（含答案解析）

本习题版权归西南交大理学院物理系所有《大学物理AI 》作业No.01运动的描述班级________学号________姓名_________成绩_______一、选择题1．一质点沿x 轴作直线运动，其v ~t 曲线如图所示。

若t ＝0时质点位于坐标原点，则t ＝4.5 s 时，质点在x 轴上的位置为[](A)0(B) 5 m(C) 2 m (D)－2 m (E)－5 m解：因质点沿x 轴作直线运动，速度v =x 2t 2v (m ⋅s -1)21O-112.5234 4.5t (s )d x，d t∆x =⎰d x =⎰v d tx 1t 1所以在v ~t 图中，曲线所包围的面积在数值上等于对应时间间隔内质点位移的大小。

横轴以上面积为正，表示位移为正；横轴以下面积为负，表示位移为负。

由上分析可得t＝4.5 s 时,位移∆x =x =1(1+2.5)⨯2-1(1+2)⨯1=2(m )22选C2．如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动。

设该人以匀速率v 0收绳，绳不伸长、ϖv湖水静止，则小船的运动是0[](A)匀加速运动(B)匀减速运动(C)变加速运动(D)变减速运动(E)匀速直线运动解：以水面和湖岸交点为坐标原点建立坐标系如图所示，且设定滑轮到湖面高度为h ，则xh 2+x 2d l x d x =-=v 0题意匀速率收绳有22d td t h +x 小船在任一位置绳长为l =d x h 2+x 2=-v 0故小船在任一位置速率为d t x 22d 2x 2h +2x =-v 0小船在任一位置加速度为a =，因加速度随小船位置变化，且d t 2x 3与速度方向相同，故小船作变加速运动。

选Cϖ3．一运动质点在某瞬时位于矢径r (x ,y )的端点处，其速度大小为[]d r (A)d t ϖd r (C)d tϖd r (B)d t(D)⎛d x ⎫⎛d y ⎫ ⎪+ ⎪d t d t ⎝⎭⎝⎭22ϖϖϖd x ϖd y ϖϖϖd r解：由速度定义v =及其直角坐标系表示v =v x i +v y j =i +j 可得速度大d t d t d t ϖ⎛d x ⎫⎛d y ⎫小为v =⎪+ ⎪d t d t ⎝⎭⎝⎭22精品文档选D4．一质点在平面上作一般曲线运动，其瞬时速度为v ，瞬时速率为v ，某一段时间内的平均速度为v ，平均速率为v ，它们之间的关系必定有[](A)v =v ,ϖϖϖϖϖ(B)v ≠v ,v =vv =v ϖϖϖϖ(C)v =v ,v ≠v (D)v ≠v ,v ≠vϖd s ϖd rϖϖ解：根据定义，瞬时速度为v =，瞬时速率为v =，由于d r =d s ，所以v =v 。

大学物理质点运动学习题（附答案）

第1章质点运动学习题及答案1．｜｜与有无不同?和有无不同? 和有无不同?其不同在哪里?试举例说明．r ∆r ∆t d d r dr dt t d d v dv dt解: ｜｜与不同. ｜｜表示质点运动位移的大小,而则表示质点运动时其径向长度的r ∆r ∆r ∆r ∆增量;和不同. 表示质点运动速度的大小,而则表示质点运动速度的径向分量;t d d r dr dt t d d r dr dtt d d v 和不同. 表示质点运动加速度的大小, 而则表示质点运动加速度的切向分量.dv dt t d d v dv dt2.质点沿直线运动，其位置矢量是否一定方向不变？质点位置矢量方向不变，质点是否一定做直线运动？解: 质点沿直线运动，其位置矢量方向可以改变;质点位置矢量方向不变，质点一定做直线运动.3.匀速圆周运动的速度和加速度是否都恒定不变？圆周运动的加速度是否总是指向圆心，为什么？解: 由于匀速圆周运动的速度和加速度的方向总是随时间发生变化的,因此,其速度和加速度不是恒定不变的;只有匀速圆周运动的加速度总是指向圆心,故一般来讲,圆周运动的加速度不一定指向圆心.4．一物体做直线运动，运动方程为，式中各量均采用国际单位制，求：（1）第二秒2362x t t =-内的平均速度（2）第三秒末的速度；（3）第一秒末的加速度；（4）物体运动的类型。

解: 由于: 232621261212x(t )t t dx v(t )t t dtdv a(t )t dt=-==-==-所以:（1）第二秒内的平均速度:1(2)(1)4()21x x v ms --==- （2）第三秒末的速度: 21(3)1236318()v ms -=⨯-⨯=- （3）第一秒末的加速度:2(1)121210()a ms -=-⨯= （4）物体运动的类型为变速直线运动。

5．一质点运动方程的表达式为，式中的分别以为单位，试求；（1）质点2105(t t t =+r i j ）,t r m,s 的速度和加速度；（2）质点的轨迹方程。

大学物理-质点运动学(答案)

一.选择题:［B］1、一质点沿x轴作直线运动，其v-t曲线如图所示，如t=0时，质点位于坐标原点，则t=4.5 s时，质点在x轴上的位置为(A) 5m．(B) 2m．(C) 0．(D) -2 m．(E) -5 m.(1 2.5)22(21)122()x m=+⨯÷-+⨯÷=提示：［C］2、如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率v收绳，绳不伸长、湖水静止，则小船的运动是(A) 匀加速运动．(B) 匀减速运动．(C) 变加速运动．(D) 变减速运动．(E) 匀速直线运动．提示：如图建坐标系，设船离岸边x米，222l h x=+22dx h xv i v idt x+==-vdv dv dxa idt dx==⋅=-［D］3、一运动质点在某瞬时位于矢径()yxr,的端点处, 其速度大小为(A)trdd(B)trdd(C)提示：,dx dyv i j vdt⎛⎫=+∴=⎪-12［ B ］4、质点沿半径为R 的圆周作匀速率运动，每T 秒转一圈．在2T 时间间隔中，其平均速度大小与平均速率大小分别为(A) 2πR /T , 2πR/T ． (B) 0 , 2πR /T(C) 0 , 0． (D) 2πR /T , 0.0rv ∆== 2s R =π ［ B ］5、在相对地面静止的坐标系内，A 、B 二船都以2 m/s 速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向．今在A 船上设置与静止坐标系方向相同的坐标系(x 、y 方向单位矢用i 、j表示)，那么在A 船上的坐标系中，B 船的速度（以m/s 为单位）为(A) 2i ＋2j ． (B) -2i ＋2j ． (C) －2i －2j ． (D) 2i －2j．提示：2(2)B A B A v v v j i →→→=+=+-地地［ D ］6、某人骑自行车以速率v 向西行驶，今有风以相同速率从北偏东30o方向吹来，人感到风从哪个方向吹来？(A)北偏东30︒ (B)北偏西60︒ (C) 北偏东60︒ (D) 北偏西30︒提示：根据v 风对人=v 风对地+v 地对人，三者的关系如图所示：这是个等边三角形，∴人感到风从北偏西300方向吹来。

质点运动学例题

R 位矢大小轨道方程为
r= x +y =R
2 2
θ
x
o
x2 + y2 = R2
位矢与x轴的夹角为θ 位矢与轴的夹角为θ 轴的夹角为
y sin ωt tanθ = = = tan ωt x cosωt
θ =ω t
r r r 速度 v = dr = −Rω sinωti + Rω cosωtr j dt
代入式（），式代入式（2），式（3）得
y
方法二: 取如图 o′x′y′坐标系，坐标原点在坐标系，
抛出点处，则式（抛出点处，则式（1）的分量式为 y′ 1 2 x′ = v0 cos βt′ + g sin αt′ v
2 1 2 y′ = v0 sin βt′ − g cosαt′ 2
o′
2v L= g
2
v0 o h
x
对时间t 求导：对时间求导：
dr dx 2r = 2x dt dt
dx r dr = dt x dt
代入(3) 式得: 代入式得
r r
vx = −v0
r r 2 − h2
= −v0
x +h x
2
2
(4)
根据加速度定义
d2 x a = 2 = v0 dt
故得: 故得
2 dx v0 h =− 3 2 2 dt x x +h
例 1.1: 一质点在 xoy 平面内运动 , 其运动函数为 x=Rcos ωt 和 y=Rsin ωt , 其中和ω为正值常量求质其中R和为正值常量. 点的运动轨道以及任一时刻它的位矢、速度和加速度. 点的运动轨道以及任一时刻它的位矢、速度和加速度 r r r 解： r = xi + yj y 位矢 r r (x, y) = Rcosωti + Rsinωtj

大学物理第一章质点运动学习题解详细完整

第一章质点运动学1–1 描写质点运动状态的物理量是 ;解：加速度是描写质点状态变化的物理量,速度是描写质点运动状态的物理量,故填“速度”;1–2 任意时刻a t =0的运动是运动；任意时刻a n =0的运动是运动；任意时刻a =0的运动是运动；任意时刻a t =0,a n =常量的运动是运动;解：匀速率；直线；匀速直线；匀速圆周;1–3 一人骑摩托车跳越一条大沟,他能以与水平成30°角,其值为30m/s 的初速从一边起跳,刚好到达另一边,则可知此沟的宽度为 )m/s 102=g ;解：此沟的宽度为m 345m 1060sin 302sin 220=︒⨯==g R θv1–4 一质点在xoy 平面内运动,运动方程为t x 2=,229t y -=,位移的单位为m,试写出s t 1=时质点的位置矢量__________；s t 2=时该质点的瞬时速度为__________,此时的瞬时加速度为__________;解：将s t 1=代入t x 2=,229t y -=得2=x m,7=y ms t 1=故时质点的位置矢量为j i r 72+=m由质点的运动方程为t x 2=,229t y -=得质点在任意时刻的速度为m/s 2d d ==t x x v ,m/s 4d d t tx y -==v s t 2=时该质点的瞬时速度为j i 82-=v m/s质点在任意时刻的加速度为0d d ==ta x x v ,2m/s 4d d -==t a y y v s t 2=时该质点的瞬时加速度为j 4-m/s 2;1–5 一质点沿x 轴正向运动,其加速度与位置的关系为x a 23+=,若在x =0处,其速度m/s 50=v ,则质点运动到x =3m 处时所具有的速度为__________;解：由x a 23+=得x xt x x t 23d d d d d d d d +===v v v v 故x x d )23(d +=v v积分得⎰⎰+=305d )23(d x x v v v则质点运动到x =3m 处时所具有的速度大小为 61=v m/s=s ；1–6 一质点作半径R =的圆周运动,其运动方程为t t 323+=θ,θ以rad 计,t 以s 计;则当t =2s 时,质点的角位置为________；角速度为_________；角加速度为_________；切向加速度为__________；法向加速度为__________;解： t =2s 时,质点的角位置为=⨯+⨯=23223θ22rad由t t 323+=θ得任意时刻的角速度大小为36d d 2+==t tθω t =2s 时角速度为 =+⨯=3262ω27rad/s任意时刻的角速度大小为t t12d d ==ωα t =2s 时角加速度为 212⨯=α=24rad/s 2t =2s 时切向加速度为=⨯⨯==2120.1t αR a 24m/s 2t =2s 时法向加速度为=⨯==22n 270.1ωR a 729m/s 2；1–7 下列各种情况中,说法错误的是 ;A ．一物体具有恒定的速率,但仍有变化的速度B ．一物体具有恒定的速度,但仍有变化的速率C ．一物体具有加速度,而其速度可以为零D ．一物体速率减小,但其加速度可以增大解：一质点有恒定的速率,但速度的方向可以发生变化,故速度可以变化；一质点具有加速度,说明其速度的变化不为零,但此时的速度可以为零；当加速度的值为负时,质点的速率减小,加速度的值可以增大,所以A 、C 和D 都是正确的,只有B 是错误的,故选B;1–8 一个质点作圆周运动时,下列说法中正确的是 ;A ．切向加速度一定改变,法向加速度也改变B ．切向加速度可能不变,法向加速度一定改变C ．切向加速度可能不变,法向加速度不变D ．切向加速度一定改变,法向加速度不变解：无论质点是作匀速圆周运动或是作变速圆周运动,法向加速度a n 都是变化的,因此至少其方向在不断变化;而切向加速度a t 是否变化,要视具体情况而定;质点作匀速圆周运动时,其切向加速度为零,保持不变；当质点作匀变速圆周运动时,a t 值为不为零的恒量,但方向变化；当质点作一般的变速圆周运动时,a t 值为不为零变量,方向同样发生变化;由此可见,应选B;1–9 一运动质点某瞬时位于位置矢量),(y x r 的端点处,对其速度大小有四种意见： 1t r d d 2t d d r 3t s d d 422d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 下述判断正确的是 ;A ．只有1,2正确B ．只有2,3正确C ．只有3,4正确D ．只有1,3正确解：tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中为质点的径向速度,是速度矢量沿径向的分量；t d d r 表示速度矢量；t s d d 是在自然坐标系中计算速度大小的公式；22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 是在真角坐标系中计算速度大小的公式;故应选C;1–10 一质点在平面上运动,已知质点位置矢量的表示式为j i r 22bt at +=其中a 、b 为常量,则该质点作 ;A ．匀速直线运动B ．变速直线运动C ．抛物线运动D ．一般曲线运动解：由j i r 22bt at +=可计算出质点的速度为j i bt at 22+=v ,加速度为j i b a 22+=a ;因质点的速度变化,加速度的大小和方向都不变,故质点应作变速直线运动;故选B;1–11 一小球沿斜面向上运动,其运动方程为S ＝5＋4t –t 2SI,则小球运动到最高点的时刻是 ;A ．t ＝4sB ．t ＝2sC ．t ＝8sD ．t ＝5s解：小球到最高点时,速度应为零;由其运动方程为S ＝5＋4t –t 2,利用ts d d =v 得任意时刻的速度为 t 24-=v令024=-=t v ,得s 2=t故选B;1–12 如图1-1所示,小球位于距墙MO 和地面NO 等远的一点A ,在球的右边,紧靠小球有一点光源S 当小球以速度V 0水平抛出,恰好落在墙角O 处;当小球在空中运动时,在墙上就有球的影子由上向下运动,其影子中心的运动是 ;A ．匀速直线运动B ．匀加速直线运动,加速度小于gC ．自由落体运动D ．变加速运动解：设A 到墙之间距离为d ;小球经t 时间自A 运动至B;此时影子在竖直方向的位移为S ;t V x 0=, 221gt y = 根据三角形相似得d S x y //=,所以得影子位移为2/V gt x yd S == 由此可见影子在竖直方向作速度为02V g 的匀速直线运动;故选A;1–13 在相对地面静止的坐标系内,A 、B 二船都以2m/s 的速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向;今在A 船上设置与静止坐标系方向相同的坐标系x 、y 方向单位矢量用i 、j 表示,那么在A 船上的坐标系中,B 船的速度以m/s 为单位为 ;A ．j i 22+B ．j i 22+-C ．j i 22--D ．j i 22+解：选B 船为运动物体,则B 船相对于地的速度为绝对速度j 2=v ,A 船相对于地的速度为牵连速度i 2=0v ,则在A 船的坐标系中,B 船相对于A 船的速度为相对速度v ';因v v v 0'+=,故j i 22+-='v ,因此应选B1–14 2004年1月25日,继“勇气”号之后,“机遇”号火星探测器再次成功登陆火星;在人类成功登陆火星之前,人类为了探测距离地球大约5103⨯km 的月球,也发射了一种类似四轮小车的月球探测器;它能够在自动导航系统的控制下行走,且每隔10s 向地球发射一次信号;探测器上还装着两个相同的减速器其中一个是备用的,这种减速器可提供的最大加速度为5m/s 2;某次探测器的自动导航系统出现故障,从而使探测器只能匀速前进而不再能自动避开障碍物;此时地球上的科学家必须对探测器进行人工遥控操作;下表为控制中心的显示屏的数据：图1-1y BM9:10:40 12 已知控制中心的信号发射与接收设备工作速度极快;科学家每次分析数据并输入命令最少需要3s;问： 1经过数据分析,你认为减速器是否执行了减速命令2假如你是控制中心的工作人员,应采取怎样的措施加速度需满足什么条件,才可使探测器不与障碍物相撞请计算说明;解：1设在地球和月球之间传播电磁波需时为0t ,则有s 10==c s t 月地从前两次收到的信号可知：探测器的速度为m/s 21032521=-=v 由题意可知,从发射信号到探测器收到信号并执行命令的时刻为9:10:34;控制中心第3次收到的信号是探测器在9:10:39发出的;从后两次收到的信号可知探测器的速度为m/s 2101232=-=v 可见,探测器速度未变,并未执行命令而减速;减速器出现故障;（2）应启用另一个备用减速器;再经过3s 分析数据和1s 接收时间,探测器在9:10:44执行命令,此时距前方障碍物距离s =2m;设定减速器加速度为a ,则有222≤=as v m,可得1≥a m/s 2,即只要设定加速度1≥a m/s 2,便可使探测器不与障碍物相撞;1–15 阿波罗16号是阿波罗计划中的第十次载人航天任务1972年4月16日,也是人类历史上第五次成功登月的任务;1972年4月27日成功返回;照片图1-2显示阿波罗宇航员在月球上跳跃并向人们致意;视频显示表明,宇航员在月球上空停留的时间是;已知月球的重力加速度是地球重力加速度的1/6;试计算宇航员在月球上跳起的高度;解：宇航员在月球上跳起可看成竖直上抛运动,由已知宇航员在空中停留的时间为,故宇航员从跳起最高处下落到月球表面的时间为t =,由于月球的重力加速度是地球的重力加速度的1/6,即g g 61M =,所以 m 43.0725.08.961212122M =⨯⨯⨯==t g h1–16 气球上吊一重物,以速度0v 从地面匀速竖直上升,经过时间t 重物落回地面;不计空气对物体的阻力,重物离开气球时离地面的高度为多少;解：方法一：设重物离开气球时的高度为x h ,当重物离开气球后作初速度为0v 的竖直上抛运动,选重物离开气球时的位置为坐标原点,则重物落到地面时满足图1-220021)(x x x gt h t h --=-v v 其中x h -表示向下的位移,0v x h 为匀速运动的时间,x t 为竖直上抛过程的时间,解方程得 gt t x 02v = 于是,离开气球时的离地高度可由匀速上升过程中求得,其值为)2()(000gt t t t h x x v v v -=-= 方法二：将重物的运动看成全程做匀速直线运动与离开气球后做自由落体运动的合运动;显然总位移等于零,所以0)(21200=--v v x h t g t 解得 )2(00g t t h x v v -=1–17 在篮球运动员作立定投篮时,如以出手时球的中心为坐标原点,作坐标系Oxy 如图1–3所示;设篮圈中心坐标为x ,y ,出手高度为H ,于的出手速度为0v ,试证明球的出手角度θ应满足⎥⎥⎦⎤⎢⎢⎣⎡+-±=)2(211tan 2022020v v v gx y g gx θ才能投入;证明：设出手后需用时t 入蓝,则有 θt t x x cos 0v v ==20221sin 21gt t gt t y y -=-=θv v 消去时间t ,得 θgx gx αx θgx θx y 22022022202tan 22tan cos 21tan v v v --=-= 图1-3整理得02tan tan 22022202=++-v v gx y θx θgx解之得⎥⎥⎦⎤⎢⎢⎣⎡+-±=)2(211tan 2022020v v v gx y g gx θ1–18 有一质点沿x 轴作直线运动,t 时刻的坐标为32254t t .x -=SI;试求：1第2s 内的平均速度；2第2s 末的瞬时速度；3第2s 内的路程;解：1将t =1s 代入32254t t .x -=得第1s 末的位置为m 5.225.41=-=x将t =2s 代入32254t t .x -=得第2s 末的位置为m 0.22225.4322=⨯-⨯=x则第2s 内质点的位移为0.5m 2.5m -m 0.212-==-=∆x x x第2s 内的平均速度-0.5m/s 10.5=-=∆∆=t x v 式中负号表示平均速的方向沿x 轴负方向;2质点在任意时刻的速度为269d d t t tx -==v 将s 2=t 代入上式得第2s 末的瞬时速度为 m/s 626292-=⨯-⨯=v式中负号表示瞬时速度的方向沿x 轴负方向;3由069d d 2=-==t t tx v 得质点停止运动的时刻为s 5.1=t ;由此计算得第1s 末到末的时间内质点走过的路程为m 875.05.25.125.15.4321=-⨯-⨯=s 第末到第2s 末的时间内质点走过的路程为m 375.10.25.125.15.4322=-⨯-⨯=s则第2s 内的质点走过的路程为m 25.2375.1875.021=+=+=s s s1–19 由于空气的阻力,一个跳伞员在空中运动不是匀加速运动;一跳伞员在离开飞机到打开降落伞的这段时间内,其运动方程为)e (/k t k t c b y -+-=SI,式中b 、c 和k 是常量,y 是他离地面的高度;问：1要使运动方程有意义,b 、c 和k 的单位是什么2计算跳伞员在任意时刻的速度和加速度;解：1由量纲分析,b 的单位为m,c 的单位为m/s,k 的单位为s;2任意时刻的速度为)e 1(d d /k t c ty -+-==v 当时间足够长时其速度趋于c -;任意时刻的加速度为k t kc t a /ed d -==v 当时间足够长时其加速度趋于零;1–20 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2d d v v K t-=,式中K 为常量;试证明电艇在关闭发动机后又行驶x 距离时的速度为Kx -=e 0v v 其中0v 是发动机关闭时的速度; 证明：由2d d v v K t-=得 2d d d d d d v v v v K xt x x -== 即x K d d -=vv 上式积分为⎰⎰-=x x K 0d d 0v v v v 得 Kx -=e 0v v1–21 一质点沿圆周运动,其切向加速度与法向加速度的大小恒保持相等;设θ为质点在圆周上任意两点速度1v 与2v 之间的夹角;试证：θe 12v v =;证明：因R a 2n v =,ta d d t v =,所以 t R d d 2v v =dsv v d d = 即vv d d =R s 对上式积分⎰⎰=2d d 0v v v v s R s得 12ln v v =R s 12ln v v ==R s θ 所以 θe 12v v =1–22 长为l 的细棒,在竖直平面内沿墙角下滑,上端A 下滑速度为匀速v ,如图1-4所示;当下端B 离墙角距离为xx<l 时,B 端水平速度和加速度多大解：建立如图所示的坐标系;设A 端离地高度为y ;∆AOB 为直角三角形,有222l y x =+ 方程两边对t 求导得 0d d 2d d 2=+t y y t x x所以B 端水平速度为 t y x y t x d d d d -=v xy =v x x l 22-= B 端水平方向加速度为v 222d /d d /d d d x tx y t y x t x-=232v x l -=1–23 质点作半径为m 3=R 的圆周运动,切向加速度为2t ms 3-=a ,在0=t 时质点的速度为零;试求：1s 1=t 时的速度与加速度；2第2s 内质点所通过的路程;图1-4解：1按定义ta d d t v =,得 t a d d t =v ,两端积分,并利用初始条件,可得 ⎰⎰⎰==t t t a t a 0t 0t 0d d d v v t t a 3t ==v当s 1=t 时,质点的速度为 m/s 3=v方向沿圆周的切线方向;任意时刻质点的法线加速度的大小为2222n m/s 39t Rt R a ===v 任意时刻质点加速度的大小为242n 2t m/s 99t a a a +=+=任意时刻加速度的方向,可由其与速度方向的夹角θ给出;且有22t n 33tan t t a a ===θ 当s 1=t 时有24m/s 23199=⨯+=a ,1tan =θ注意到0t >a ;所以得︒=45θ2按定义ts d d =v ,得t s d d v =,两端积分可得 ⎰⎰⎰==t t t s d 3d d v故得经t 时间后质点沿圆周走过的路程为C t s +=223 其中C 为积分常数;则第2s 内质点走过的路程为：m 5.4)123()223()1()2(22=+⨯-+⨯=-=∆C C s s s1–24 一飞机相对于空气以恒定速率v 沿正方形轨道飞行,在无风天气其运动周期为T ;若有恒定小风沿平行于正方形的一对边吹来,风速为)1(<<=k k V v ;求飞机仍沿原正方形对地轨道飞行时周期要增加多少解：依题意,设飞机沿如图1-5所示的ABCD 矩形路径运动,设矩形每边长为l ,如无风时,依题意有 vl T 4= 1 图1-5当有风时,设风的速度如图1-5所示,则飞机沿AB 运动时的速度为v v v k V +=+,飞机从A 飞到B 所花时间为vv k l t +=1 2 飞机沿CD 运动时的速度为v v v k V -=-,飞机从C 飞到D 所花时间为vv k l t -=2 3 飞机沿BC 运动和沿DA 运动所花的时间是相同的,为了使飞机沿矩形线运动,飞机相对于地的飞行速度方向应与运动路径成一夹角,使得飞机速度时的速度v 在水平方向的分量等于v k -,故飞机沿BC 运动和沿DA 运动的速度大小为222v v k -,飞机在BC 和DA 上所花的总时间为22232v v k lt -= 4综上,飞机在有风沿此矩形路径运动所花的总时间,即周期为2223212vv v v v v k l k l k l t t t T -+-++=++=' 5 利用1式,5式变为)1(4)4()1(4)11(22222k k T k k T T --≈--+='飞机在有风时的周期与无风时的周期相比,周期增加值为43)1(4)4(222T k T k k T T T T =---≈'-=∆。

质点运动学典型例题

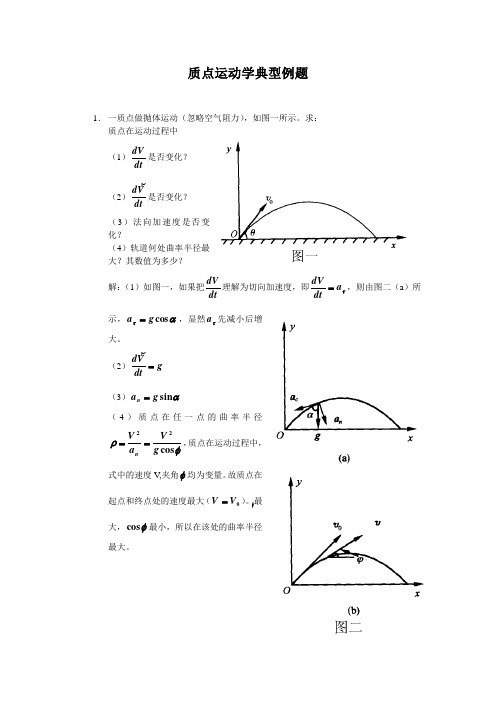
质点运动学典型例题1．一质点做抛体运动（忽略空气阻力），如图一所示。

求：质点在运动过程中（1）dtdV 是否变化？（2）dtV d 是否变化？（3）法向加速度是否变化？（4）轨道何处曲率半径最大？其数值为多少？解：（1）如图一，如果把dtdV 理解为切向加速度，即τa dt dV =，则由图二（a ）所示，ατcos g a =，显然τa 先减小后增大。

（2）g dtV d = （3）αsin g a n =（4）质点在任一点的曲率半径φρcos 22g V a V n ==，质点在运动过程中，式中的速度V,夹角φ均为变量。

故质点在起点和终点处的速度最大（0V V =）。

φ最大，φcos 最小，所以在该处的曲率半径最大。

上抛石块的位移和路程一石块以V=4.9m/s 的初速度向上抛出，经过2S 后，石块的位移y ∆________，路程S______.解：如图一，设定石块上抛的初始点为原点，竖直向上为正方向。

则其运动方程为2021gt t V y -= 2S 内的位移为m y 8.928.92129.42-=⨯⨯-⨯=，负号表明所求位移的方向为竖直向下，即物体在2S 内改变了运动方向。

先求物体到达最高点的时刻，即00=-=gt V dt dy ，S g V t 5.08.99.40=== 则总路程m L L L 25.12)5.1(8.921)5.0(8.9212221=⨯⨯+⨯⨯=+= 求解某一位置的速度质点沿x 轴正向运动，其加速度随位置变化的关系为2331x a +=，如果在x=0处，其速度为s m V /50=，那么，在x=3m 处的速度为多少？解：因为2331x V dx dV dt dx dx dV dt dV a +====s m V x x V x x V V dx x VdV V V /9)25333(2)23(2322)331(2320332023020=++=++=+=-+=⎰⎰宇宙速度众所周知，人造地球卫星和人造行星是人类认识宇宙的重大发展．但怎样才能把物体抛向天空，使之成为人造卫星或人造行星呢：）这取决于抛体的初速度。

质点运动学一章编写过的例题和习题

θ =vt R
∴a = a + a = v2 R
2 x 2 y
方向：方向：
指向圆心
v0 v ρ = ρmax = = an g cos θ
2
r en
r r a=g
x
o
g
g
ρ
思考：整个过程速度如何变化？分别就起点、思考：整个过程速度如何变化？分别就起点、终点以及最高点进行讨论。终点以及最高点进行讨论。
v0 6. 如图所示，在倾角为如图所示，在倾角为α=30°的斜坡上，以初速度发 °的斜坡上，射炮弹，设与斜坡的夹角为β=60°。求炮弹落地点离射炮弹，设与斜坡的夹角为 ° 发射点的距离L。发射点的距离。 y
r v0
dv (1) 是否变化？ dt r dv (2) 是否变化？ dt r (3)an是否变化？
y
r v
v v0
θ
P
r et
α
·
(4)轨道何处曲率半径最大？其值是多少？
r en
dv at = = − g sin α dt 2 v an = = g cos α
r r 抛体运动：a = g
o
x
ρ
答：
则：
r r r v = v0 + gt
t=0时时
若建立二维直角坐标系，若建立二维直角坐标系，以水平方向为 x 轴，则：
r r r 1 r 2 r = r0 + v 0 t + g t 2
r =g
r r a = − gj
v x = v0 x
x = x0 = 0 y = y0 = 0
可得分量形式：可得分量形式：
v x = v 0 cos β + gt sin α v y = v 0 sin β − gt cos α

(完整版)《大学物理》习题册题目及答案第1单元质点运动学

第一章力学的基本概念(一)质点运动学序号学号姓名专业、班级一选择题[ A ]1. 一小球沿斜面向上运动，其运动方程为285t t s -+=(SI)，则小球运动到最高点的时刻是：(A) s 4=t ;(B) s 2=t ; (C) s 8=t ;(D) s 5=t 。

[ D ]2. 一运动质点在某瞬时位于矢径 r (x,y)的端点处，其速度大小为 (A)dtdr(B) dt d r (C)dt d r (D)22)()(dt dy dt dx +[ D ]3. 某质点的运动方程x=3t-53t +6 (SI),则该质点作：（A ）匀加速直线运动，加速度沿x 轴正方向；（B ）匀加速直线运动，加速度沿x 轴负方向；（C ）变加速直线运动，加速度沿x 轴正方向；（D ）变加速直线运动，加速度沿x 轴负方向。

[ C ]4. 某物体的运动规律为dtdv=-k 2v t,式中k 为常数，当t=0时，初速度为0v ,则速度v 与时间的函数关系为：（A ） v=21k 2t +0v ; （B ） v=-21k 2t +0v（C ） v 1=21k 2t +01v（D ） v1=-21k 2t +01v[ D ]5. 一质点从静止出发，沿半径为1m 的圆周运动，角位移θ=3+92t ,当切向加速度与合加速度的夹角为︒45时，角位移θ等于：(A) 9 rad, （B ）12 rad, (C)18 rad, (D)3.5 rad[ D ]6. 质点作曲线运动，r 表示位置矢量，s 表示路径，t a 表示切向加速度，下列表达式中：（1）dt dv =a; (2)dt dr =v; (3)dtds=v; (4)dt d v =t a ,则，（A ）只有（1）、（4）是对的；（B ）只有（2）、（4）是对的；（C ）只有（2）是对的；（D ）只有（3）是对的。

二填空题1. 设质点在平面上的运动方程为r =Rcos t ωi +Rsin tωj ,R 、ω为常数，则质点运动的速度v =j t con R i t R ϖϖωωωω+-sin ，轨迹为半径为R 的圆。

大学物理 - 1-6章练习附答案

第一章质点运动学1、已知一质点作直线运动，其加速度为 a ＝4+3t 2s m -⋅，开始运动时，x ＝5 m ，v =0，求该质点在t ＝10s 时的速度和位置。

解：∵ t tva 34d d +==分离变量，得 t t v d )34(d += 积分，得 12234c t t v ++= 由题知，0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量， t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v2、质点沿x 轴运动，其加速度和位置的关系为 a ＝2+62x ，a 的单位为2s m -⋅，x 的单位为 m 。

质点在x ＝0处，速度为101s m -⋅,试求质点在任何坐标处的速度值。

解： ∵ xv v t x x v t v a d d d d d d d d ===分离变量： 2d (26)d v v adx x x ==+ 两边积分得c x x v ++=322221 由题知，0=x 时，100=v ,∴50=c∴ 13s m 252-⋅++=x x v第二章质点动力学1、质量为M 的大木块具有半径为R 的四分之一弧形槽，如图所示。

质量为m 的小立方体从曲面的顶端滑下，大木块放在光滑水平面上，二者都作无摩擦的运动，而且都从静止开始，求小木块脱离大木块时的速度。

解: m 从M 上下滑的过程中，机械能守恒，以m ，M ，地球为系统，以最低点为重力势能零点，则有222121MV mv mgR +=又下滑过程，动量守恒，以m 、M 为系统，则在m 脱离M 瞬间，水平方向有0=-MV mv联立以上两式，得2MgR v m M =+2、哈雷彗星绕太阳运动的轨道是一个椭圆。

大学物理第一章质点运动学习题

l030045060075 质点运动学一．选择题：１．质点的运动方程为)(5363SI t t x -+=，则该质点作［］（A ）匀加速直线运动，加速度沿Ｘ轴正方向．（B ）匀加速直线运动，加速度沿Ｘ轴负方向．（C ）变加速直线运动，加速度沿Ｘ轴正方向．（D ）变加速直线运动，加速度沿Ｘ轴负方向．２．质点在某瞬时位于矢径),(y x r的端点处其速度大小为［］(A)dt dr (B)dt r d (C)dt r d || (D) 22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx３．如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率0v 收绳，绳不伸长，湖水静止，则小船的运动是: ［］(A)匀加速运动（B ）匀减速运动 (C) 变加速运动 (D) 变减速运动 (E) 匀速直线运动４．一个质点在做匀速率圆周运动时［］（A ）切向加速度改变，法向加速度也改变．（B ）切向加速度不变，法向加速度改变．（C ）切向加速度不变，法向加速度也不变．（D ）切向加速度改变，法向加速度不变．5．如右图所示，几个不同倾角的光滑斜面，有共同的底边，顶点也在同一竖直面上．若使一物体（视为质点）从斜面上端由静止滑到下端的时间最短，则斜面的倾角应选［］(A)030． (B)045． (C)060． (D)075．６．一质点作直线运动，某时刻的瞬时速度s m v /2=，瞬时加速度2/2s m a -=，则一秒钟后质点的速度［］ (A) 等于零．(B) 等于s m /2-．(C) 等于s m /2．(D) 不能确定．)-7．质点沿半径为R 的圆周作匀速率运动，每t 秒转一圈．在t 2时间间隔中，其平均速度大小与平均速率大小分别为［］ (A)t R π2，t R π2． (B)0，t R π2．(C)0，0． (D)tRπ2，０．８．一质点沿x 轴作直线运动，其t v -曲线如下图所示，如0=t 时，质点位于坐标原点，则s t 5.4=时质点在x 轴上的位置为 (A) m 0． (B)m 5．(C) m 2． (D)m 2-． (E)m 5-．９．一小球沿斜面向上运动，其运动方程为)(452SI t t S -+=，则小球运动到最高点的时刻是［］ (A)s t 4=． (B)s t 2=． (C)s t 8=． (D)s t 5=．10．质点在平面上运动，已知质点位置矢量的表示式为)(22SI j bt i at r+=（其中a 、b 为常量），则该质点作［］ (A) 匀速直线运动． (B) 变速直线运动． (C) 抛物线运动． (D) 一般曲线运动．11．质点作曲线运动，r表示位置矢量，S 表示路程，t a 表示切向加速度，下列表达式中，(1)a dt dv =， (2)v dt dr =， (3)v dt ds =， (4)t a dtv d =||．（A ）只有(1)、(4)是对的． (B) 只有(2)、(4)是对的．（C ）只有(2)是对的．（D ）只有(3)是对的．［］ 12．下列说法中，哪一个是正确的？［］（Ａ）一质点在某时刻的瞬时速度是s m /2，说明它在此后s 1内一定要经过m 2的路程．（Ｂ）斜向上抛的物体，在最高点处的速度最小，加速度最大．（Ｃ）物体作曲线运动时，有可能在某时刻的法向加速度为零．（Ｄ）物体加速度越大，则速度越大．13．在相对地面静止的坐标系内，Ａ、Ｂ二船都是以s m /2的速率匀速行驶，Ａ船沿x 轴正向，Ｂ船沿y 轴正向，今在Ａ船上设置与静止坐标系方向相同的坐标系（x 、y 方向单位矢量用i、j表示），那么在Ａ船上的坐标系中，Ｂ船的速度为：［］（Ａ）j i 22+．（Ｂ）j i22+-．（Ｃ）j i22--．（Ｄ）j i 22-．14．某人骑自行车以速率v 向正西方向行驶，遇到由北向南刮的风（设风速大小也为v ），则他感到风是从［］（Ａ）东北方向吹来；（Ｂ）东南方向吹来；（Ｃ）西北方向吹来；（Ｄ）西南方向吹来．二．填空题：１．在XY 平面内有一运动的质点，其运动方程为)(5sin 105cos 10SI j t i t r+=，则t 时刻其速度=v___________，其切向加速度的大小=t a ___________；该质点运动的轨迹是_____________．２．一质点沿直线运动，其坐标x 与时间t 有如下关系：)(cos SI t Ae x t ωβ-=（A ，β皆为常数）：(1)任意时刻质点的加速度=a __________；(2)质点通过原点的时刻=t __________．３．一物体在某瞬时以速度0v从某点开始运动，在t ∆时间内，经一长度为Ｓ的路径后，又回到出发点，此时速度为0v-，则在这段时间内：(1)物体的平均速率是：____________；(2)物体的平均加速度是：___________．４．在一个转动的齿轮上，一个齿尖Ｐ沿半径为R 的圆周运动，其路程S 随时间的规律为2021bt t v S +=，其中0v 和b 都是正的常量，则t 时刻齿尖Ｐ的速度大小为____________，加速度大小为______________．５．质点沿半径为R 的圆周运动，运动方程为)(322SI t +=θ，则t 时刻质点的法向加速度大小为=n a _________；角加速度=β__________．６．在下列各图中质点M 作曲线运动，指出哪些运动是不可能的？７．一质点在平面上作曲线运动，其速率v 与路程S 的关系为)(12SI S v +=，则其切向加速度以路程S 来表示的表达式为=t a _______(SI)．８．已知质点运动方程为)()314()2125(32SI j t t i t t r++-+=当s t 2=时，=a ___________．９．一质点以060仰角作斜上抛运动，忽略空气阻力．若质点运动轨道最高点处的曲率半径为m 10，则抛出时初速度的大小为0v ___________．（重力加速度g 按2/10s m 计） 10．一质点作半径为m 1.0的圆周运动，其运动方程为：)(2142SI t +=πθ，则其切向加速度为=t a ____________．11．一质点沿半径R 的圆周运动，其路程S 随时间t 变化的规律为)(212SI ct bt S -=，式中b 、c 为大于零的常数，且Rc b >2．（１）质点运动的切向加速度=t a _____________；法向加速度=n a _____________．（２）质点经过=t _____________时，n t a a =． 12．试说明质点作何种运动时将出现下述各种情况（0≠v ）：（１）0≠t a ，0≠n a ；___________ ．（２）0≠t a ，0=n a ；__________．13．一物体作如右图所示的斜抛运动，测得在轨道Ａ点处速度v的大小为v ，其方向与水平方向成030的夹角，则物体在Ａ点的切向加速度=t a __________，轨道的曲率半径=ρ_____________．14．当一列火车以s m /10的速率向东行驶时，若相对于地面竖直下落的雨滴在列车的窗子上形成的雨迹偏离竖直方向030，则雨滴相对于地面的速率是____________；相对于列车的速率是______________．15．一物体作斜抛运动，初速度为0v，与水平方向夹角为θ，如右图所示．则物体达最高点处轨道的曲率半径ρ为______________．三．计算题：１．有一质点沿X 轴作直线运动，t 时刻的坐标为)(25.432SI t t x -=．试求：(1)第2秒内的平均速度；(2)第2秒末的瞬时速度；(3)第2秒内的路程．２．一质点沿X 轴运动，其加速度为)(4SI t a =，已知0=t 时，质点位于m X 100=处，初速度00=v ，试求其位置和时间的关系式．３．质点M 在水平面内运动轨迹如图所示，OA 段为直线，AB ，BC 段分别为不同半径的两个4/1)(5302SI t t S +=，求s t 2=时刻，质点Ｍ的切向４．由楼窗口以水平初速度0v 射出一发子弹，取枪口为坐标原点，沿0v方向为Ｘ轴，竖直向下为Ｙ轴，并取发射时s t 0=，试求：（1）子弹在任意时刻t 的位置坐标及轨迹方程；（2）子弹在t 时刻的速度，切向加速度和法向加速度．５．一物体悬挂在弹簧上作竖直振动，其加速度为ky a -=，式中k 为常量，y 是以平衡位置为原点所测得的坐标，假定振动的物体在坐标0y 处的速度为0v ，试求速度v 与坐标y 的函数关系式．６．一飞机驾驶员想往正北方向航行，而风以h km /60的速度由东向西刮来，如果飞机的航速(在静止空气中的速率)为h km /180，试问驾驶员应取什么航向？飞机相对于地面的速率为多少？试用矢量图说明．７．某物体的运动规律为t kv dt dv 2/-=，式中k 为大于零的常数，求速度v 与时间t 的函数关系式．M８．一质点沿x 轴运动，其加速度a 与位置坐标x 的关系为)(622SI x a +=，如果质点在原点处的速度为零，试求其在任意位置处的速度．９．一质点从静止开始作直线运动，开始加速度为a ，此后加速度随时间均匀增加，经过时间τ后，加速度为a 2，经过时间τ2，加速度为a 3，．．．．求经过时间τn 后，该质点的加速度和走过的距离．10．一质点沿半径为R 的圆周运动，质点所经过的弧长与时间的关系为)(212SI ct bt S +=，其中b 、c 是大于零的常量，求从0=t 开始到切向加速度与法向加速度大小相等时所经历的时间．11．当火车静止时，乘客发现雨滴下落方向偏向车头，偏角为030，当火车以s m /35的速率沿水平直线行驶时，发现雨滴下落方向偏向车尾，偏角为045，假设雨滴相对于地的速度保持不变，试计算雨滴相对于地的速度大小．。

大学物理质点运动例题

加速度的大小
2 a = at2 + an = 24 2 + 729 2 = 729m/s 2
设加速度与法向加速度的夹角为α 设加速度与法向加速度的夹角为，则
at 24 tan α = = = 0.0329 , ⇒ α = 1.9° an 729
例题2 质点沿半径为 R 的圆轨道运动，初速度为 0，加的圆轨道运动，初速度为v 例题度方向的夹角恒定，如图所示．速度与速度方向的夹角恒定，如图所示．求速度的大小与时间的关系．间的关系．解设加速度与速度方向的夹角 an 为α，则， tan α = at 即
则有
v v v v dr v= = ( −ωR sin ωt )i + (ωR cos ωt ) j dt v x = −ωRsinωt ; ωR ωt v y = ωRcosωt ωR ωt
2 2 速度的大小 v= vx + vy = (ωR sin ωt )2 + (ωR cos ωt )2 = Rω
v v v v = R cos ωti + R sin ωtv j r = xi + yj
(2) 由运动方程
消去
x = R cos ωt y = R sin ωt x 2 + y 2 = R2 t，可得质点的轨迹方程，可得质点的轨迹方程
可知，时质点的位置P （3）由运动方程可知，t=0 时质点的位置 0点的坐标为）运动方程可知
x
5
QHale Waihona Puke y =dvy dt= 12 ∴ d v y = 12 d t
Q v y (0) = 0 由初条件积分
∫
vy
0
d v y = ∫ 12 d t ∴ v y = 12 t

大学物理1质点运动学例题

大学物理Ⅰ质点运动学试题(经典)

大学物理题库-第1章-质点运动学(含答案解析)

(完整版)大学物理01质点运动学习题解答

大学物理上册第一章 质点运动学 习题及答案

大学物理第一章质点运动学习题

大学物理第一章 质点运动学-习题及答案

大物1-4质点运动学习题

大学物理第一章 质点运动学-习题及答案

大学物理练习题_C1-1质点运动学（含答案解析）

大学物理质点运动学习题（附答案）

大学物理-质点运动学(答案)

质点运动学例题

大学物理第一章质点运动学习题解详细完整

质点运动学典型例题

质点运动学一章编写过的例题和习题

(完整版)《大学物理》习题册题目及答案第1单元 质点运动学

大学物理 - 1-6章练习附答案

大学物理 第一章 质点运动学习题

大学物理质点运动例题

大学物理上册第一章质点运动学习题及答案

大学物理第一章质点运动学-习题及答案

大学物理第一章质点运动学-习题及答案

(完整版)《大学物理》习题册题目及答案第1单元质点运动学

大学物理第一章质点运动学习题