数字图像处理 几何运算
《数字图像处理》课程教学大纲

《数字图像处理》课程教学大纲课程代码:ABJD0619课程中文名称:数字图像处理课程英文名称:Dig让a1ImageProcessing课程性质:选修课程学分数:3学分课程学时数:48学时(32理论课时+16实验学时)授课对象:电子信息工程本课程的前导课程:高等数学,概率论,线性代数,数字信号处理,信息论,程序设计等一、课程简介数字图像处理是一门新兴的跨学科的前沿高科技,在军事、工业、科研、医学等领域获得了广泛应用,是国内外高校和科研院所的研窕生教育中一个重要的研究方向。
通过本课程的学习,同学们将掌握数字图像处理的基本理论与方法,包括图像变换、图像增强、图像分割、图像恢复、图像识别、图像压缩编码、数字图像处理系统及应用等内容。
二、教学基本内容和要求(-)数字图像处理方法概述教学内容:数字图像处理的研究对象、基本应用、研究内容等,数字图像的基本概念、彩色图像的调色板等概念。
课程的重点、难点:重点:CDIB类与程序框架结构介绍。
难点:调色板的基本概念和应用。
教学要求:D了解本课程研究的对象、内容及其在培养软件编程高级人才中的地位、作用和任务;2)了解数字图像处理的应用;3)理解数字图像的基本概念、与设备相关的位图(DDB)、与设备无关的位图(D1B);4)理解调色板的基本概念和应用;5)了解CD1B类与程序框架结构介绍;6)掌握位图图像处理技术。
(二)图像的几何变换教学内容:图像的几何变换种类以及概念,几何变换的实现原理和实施方法课程的重点、难点:重点:镜像变换。
难点:旋转。
教学要求:1)理解图像的缩放、平移、镜像变换、转置、旋转。
(三)图像灰度变换教学内容:直方图的概念、灰度的点运算(包含灰度信息的线性变化、指数变换等)、直方图的均匀化和规定化课程的重点、难点:重点:灰度直方图。
难点:灰度分布均衡化。
教学要求:1)了解非O元素取1法、固定阈值法、双固定阈值法的图像灰度变换;2)掌握灰度的线性变换、窗口灰度变换处理、灰度拉伸、灰度直方图、灰度分布均衡化。
14年数字图像处理考试重点

14年数字图像处理考试重点第一章1、基本概念(1)图像处理(image processing):是对图像信息进行加工以满足人的视觉或应用需求的行为。
(2)数字图像处理(digital image processing),就是利用计算机技术或其他数字技术,对图像信息进行某些数学运算和各种加工处理,以改善图像的视觉效果和提高图像实用性的技术。
(3)图像分析:通过对图像中不同对象进行分割来对图像中目标进行分类和识别的技术◆图像分析是比图像处理更高一级的计算处理过程。
◆图像分析的目的:是缩减对图像的描述,以使其更适合于计算机处理及对不同目标的分类。
◆图像分析的基本特征:输入是图像,输出是对输入图像进行描述的信息。
图像处理是对图像的低级处理阶段,图像分析是对图像的高一级的处理阶段。
图像的低级处理阶段和高一级的处理阶段是相互关联和有一定重叠性的。
1.2 数字图像处理系统的组成1.3 图像处理技术研究的内容包括图像变换,图像增强,图像恢复,图像压缩编码,图像分割与特征提取,形态学图像处理,彩色、多光谱及高光谱图像处理、图像的表示与描述等。
●图像变换(image transform)是简化图像处理过程和提高图像处理效果的基本技术,最典型的图像变换主要有傅里叶变换、离散余弦变换和小波变换等。
●图像增强(image enhancement)是或简单地突出图像中感兴趣的特征,或想方显现图像中那些模糊了的细节,以使图像更清晰地被显示或更适合于人或机器的处理与分析的一种技术。
●图像恢复(image restoration)是一种从图像退化的数学或概率模型出发,研究改进图像外观,从而使恢复以后的图像尽可能地反映原始图像的本来面目的一种技术,其目的是获得与景物真实面貌相像的图像。
●图像压缩编码(image compression)是在不损失图像质量或少损失图像质量的前提下,尽可能地减少图像的存储量,以满足图像存储和实时传输应用需求的一种技术。
数字图像处理课程设计基于Matlab的数字图像处理

数字图像处理课程设计--基于Matlab的数字图像处理数字图像处理课程设计基于Matlab的数字图像处理——图像的运算院系信息技术学院专业班级电气6班学号 201107111282姓名何英娜指导教师章瑞平课程设计时间 2012年11月目录一、摘要 (3)二、图像代数运算1、1图像的加法运算 (4)1、2图像的减法运算 (4)1、3图像的除法运算 (4)1、4绝对差值运算 (7)1、 5 图像的求补运算 (7)3三、图像的几何运算2、1 图像插值 (7)2、2图像的旋转 (8)2、3图像的缩放 (9)2、4图像的投影变换 (10)2、4图像的剪切 (11)四、课程设计总结与体会 (13)五、参考文献 (14)摘要图像运算涵盖程序设计、图像点运算、代数运算、几何运算等多种运算;设计目的和任务:1、熟悉图像点运算、代数运算、几何运算的基本定义和常见方法;2、掌握在MTLAB中对图像进行点运算、代数运算、几何运算的方法3、掌握在MATLAB中进行插值的方法4、运用MATLAB语言进行图像的插值缩放和插值旋转5、学会运用图像的投影变换和图像的剪切46、进一步熟悉了解MATLAB语言的应用,将数字图像处理更好的应用于实际7、通过各类算法加强图像各种属性、一、图像的几何运算何运算图像代数运算是指对两幅或两幅以上输入图像对应的像素逐个进行和差积商运算以产生增强效果的图像。
图像运算是一种比较简单有效的增强处理手段是图像处理中常用方法。
四种图像处理代数运算的数学表达式如下:C(x,y)=A(x,y)+B(x,y)C(x,y)=A(x,y)-B(x,y)C(x,y)=A(x,y)*B(x,y)C(x,y)=A(x,y)/B(x,y)1图像加法运算一般用于多幅图像求平均效果,以便有效降低具有叠加性的随机噪声,在matlab中imadd用于图像相加,其调用格式为z=imadd(X,Y);程序演示如下:I=imread('rice.png');subplot(2,2,1),imshow(I),title('原图像1'); J=imread('cameraman.tif');subplot(2,2,2),imshow(J),title('原图像52');K=imadd(I,J,'uint16'););subplot(2,2,3),imshow(K,[]),title('相加后图像'2、图像减法运算也称差分运算,是用于检测图像变化及运动物体的方法;用imsubtract函数实现。
数字图像处理-知识点总结

图像分类:根据图像空间坐标和幅度(亮度或色彩)的连续性可分为模拟(连续)图像和数字图像。
模拟图像是空间坐标和幅度都连续变化的图像,而数字图像是空间坐标和幅度均用离散的数字(一般是整数)表示的图像。
图像的数学表示:一幅图像所包含的信息首先表现为光的强度(intensity),即一幅图像可看成是空间各个坐标点上的光强度I 的集合,其普遍数学表达式为:I = f (x,y,z,λ,t) 式中(x,y,z)是空间坐标,λ是波长,t是时间,I是光点(x,y,z)的强度(幅度)。
上式表示一幅运动的(t)、彩色/多光谱的(λ)、立体的(x,y,z)图像。
图像的特点:1.空间有界:人的视野有限,一幅图像的大小也有限。
2.幅度(强度)有限:即对于所有的x,y都有0≤f(x,y) ≤Bm其中Bm为有限值。
图像三大类:在每一种情况下,图像的表示可省略掉一维,即1.静止图像:I = f(x,y,z, λ)2.灰度图像:I = f(x,y,z,t )3.平面图像:I = f(x,y,λ,t)而对于平面上的静止灰度图像,其数学表达式可简化为:I = f(x,y)数字图像处理的基本步骤:1.图像信息的获取:采用图像扫描仪等将图像数字化。
2.图像信息的存储:对获取的数字图像、处理过程中的图像信息以及处理结果存储在计算机等数字系统中。
3.图像信息的处理:即数字图像处理,它是指用数字计算机或数字系统对数字图像进行的各种处理。
4.图像信息的传输:要解决的主要问题是传输信道和数据量的矛盾问题,一方面要改善传输信道,提高传输速率,另外要对传输的图像信息进行压缩编码,以减少描述图像信息的数据量。
5.图像信息的输出和显示:用可视的方法进行输出和显示。
数字图像处理系统五大模块:数字图像处理系统由图像输入、图像存储、图像通信、图像处理和分析五个模块组成。
1.图像输入模块:图像输入也称图像采集或图像数字化,它是利用图像采集设备(如数码照相机、数码摄像机等)来获取数字图像,或通过数字化设备(如图像扫描仪)将要处理的连续图像转换成适于计算机处理的数字图像。
数字图像的几何运算

数字图像的几何运算
数字图像的几何运算是指对图像进行几何变换的操作。
几何变换包括平移、旋转、缩放、翻转等操作,通过这些操作可以改变图像的位置、角度、大小和方向。
数字图像的几何运算在图像处理、计算机视觉、图形学等领域有着广泛的应用。
平移是将图像沿着水平方向和垂直方向进行移动的操作。
平移变换可以通过将图像的像素点进行位移来实现。
对于二维图像而言,平移变换可以表示为:
T(x, y) = (x + dx, y + dy)
(x, y)为原始图像中的像素点坐标,(dx, dy)为平移向量。
对于彩色图像,需要对每个像素点的RGB分量进行平移。
垂直翻转变换可以表示为:
除了以上几种基本的几何运算,还有其他一些常用的几何运算,包括仿射变换、透视变换等。
这些运算可以通过矩阵运算来实现。
仿射变换可以通过将图像的像素点坐标进行线性变换来实现。
透视变换可以通过将图像的像素点坐标进行非线性变换来实现。
数字图像的几何运算在数字图像处理中有着广泛的应用。
在计算机视觉中,通过对图像进行几何运算可以实现目标检测、目标跟踪等功能。
在图形学中,通过对图像进行几何运算可以实现图形变换、图形合成等功能。
在图像处理中,通过对图像进行几何运算可以实现图像校正、图像增强等功能。
数字图像处理-图像基本运算
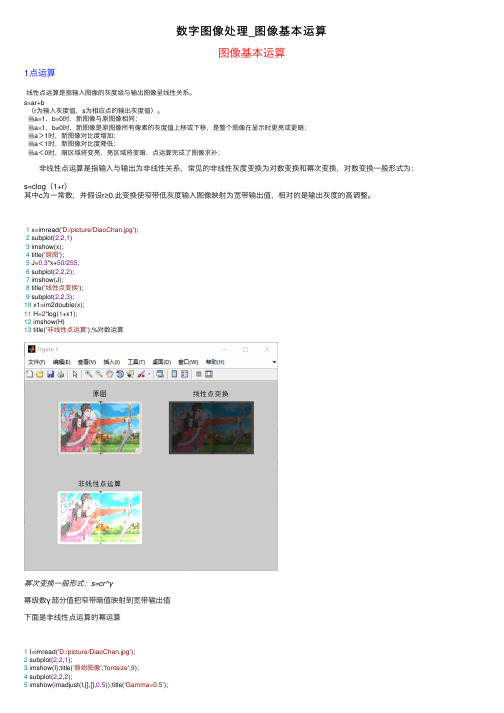
数字图像处理_图像基本运算图像基本运算1点运算线性点运算是指输⼊图像的灰度级与输出图像呈线性关系。
s=ar+b(r为输⼊灰度值,s为相应点的输出灰度值)。
当a=1,b=0时,新图像与原图像相同;当a=1,b≠0时,新图像是原图像所有像素的灰度值上移或下移,是整个图像在显⽰时更亮或更暗;当a>1时,新图像对⽐度增加;当a<1时,新图像对⽐度降低;当a<0时,暗区域将变亮,亮区域将变暗,点运算完成了图像求补; ⾮线性点运算是指输⼊与输出为⾮线性关系,常见的⾮线性灰度变换为对数变换和幂次变换,对数变换⼀般形式为:s=clog(1+r)其中c为⼀常数,并假设r≥0.此变换使窄带低灰度输⼊图像映射为宽带输出值,相对的是输出灰度的⾼调整。
1 x=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1)3 imshow(x);4 title('原图');5 J=0.3*x+50/255;6 subplot(2,2,2);7 imshow(J);8 title('线性点变换');9 subplot(2,2,3);10 x1=im2double(x);11 H=2*log(1+x1);12 imshow(H)13 title('⾮线性点运算');%对数运算幂次变换⼀般形式:s=cr^γ幂级数γ部分值把窄带暗值映射到宽带输出值下⾯是⾮线性点运算的幂运算1 I=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1);3 imshow(I);title('原始图像','fontsize',9);4 subplot(2,2,2);5 imshow(imadjust(I,[],[],0.5));title('Gamma=0.5');7 imshow(imadjust(I,[],[],1));title('Gamma=1');8 subplot(2,2,4);9 imshow(imadjust(I,[],[],1.5));title('Gamma=1.5');2代数运算和逻辑运算加法运算去噪处理1 clear all2 i=imread('lenagray.jpg');3 imshow(i)4 j=imnoise(i,'gaussian',0,0.05);5 [m,n]=size(i);6 k=zeros(m,n);7for l=1:1008 j=imnoise(i,'gaussian',0,0.05);9 j1=im2double(j);10 k=k+j1;11 End12 k=k/100;13 subplot(1,3,1),imshow(i),title('原始图像')14 subplot(1,3,2),imshow(j),title('加噪图像')15 subplot(1,3,3),imshow(k),title(‘求平均后的减法运算提取噪声1 I=imread(‘lena.jpg’);2 J=imnoise (I,‘lena.jpg’,0,0.02);3 K=imsubtract(J,I);4 K1=255-K;5 figure;imshow(I);7 figure;imshow(K1);乘法运算改变图像灰度级1 I=imread('D:/picture/SunShangXiang.jpg')2 I=im2double(I);3 J=immultiply(I,1.2);4 K=immultiply(I,2);5 subplot(1,3,1),imshow(I);subplot(1,3,2),imshow(J);6 subplot(1,3,3);imshow(K);逻辑运算1 A=zeros(128);2 A(40:67,60:100)=1;3 figure(1)4 imshow(A);5 B=zeros(128);6 B(50:80,40:70)=1;7 figure(2)8 imshow(2);9 C=and(A,B);%与10 figure(3);11 imshow(3);12 D=or(A,B);%或13 figure(4);14 imshow(4);15 E=not(A);%⾮16 figure(5);17 imshow(E);3⼏何运算平移运算实现图像的平移1 I=imread('lenagray.jpg');2 subplot(1,2,1);3 imshow(I);4 [M,N]=size(I);g=zeros(M,N);5 a=20;b=20;6for i=1:M7for j=1:N8if((i-a>0)&(i-a<M)&(j-b>0)&(j-b<N)) 9 g(i,j)=I(i-a,j-b);10else11 g(i,j)=0;12 end13 end14 end15 subplot(1,2,2);imshow(uint8(g));⽔平镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(i,N-j+1);7 end8 end9 subplot(122);imshow(uint8(g));垂直镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(M-i+1,j);7 end8 end9 subplot(122);imshow(uint8(g));图像的旋转1 x=imread('D:/picture/DiaoChan.jpg');2 imshow(x);3 j=imrotate(x,45,'bilinear');4 k=imrotate(x,45,'bilinear','crop');5 subplot(1,3,1),imshow(x);6 title(‘原图')7 subplot(1,3,2),imshow(j);8 title(‘旋转图(显⽰全部)')9 subplot(1,3,3),imshow(k);10 title(‘旋转图(截取局部)')⼏种插值法⽐较1 i=imread('lena.jpg');2 j1=imresize(i,10,'nearest');3 j2=imresize(i,10,'bilinear');4 j3=imresize(i,10,'bicubic');5 subplot(1,4,1),imshow(i);title(‘原始图像')6 subplot(1,4,2),imshow(j1);title(‘最近邻法')7 subplot(1,4,3),imshow(j2);title(‘双线性插值法')8 subplot(1,4,4),imshow(j3);title(‘三次内插法')放缩变换1 x=imread('D:/picture/ZiXia.jpg')2 subplot(2,3,1)3 imshow(x);4 title('原图');5 Large=imresize(x,1.5);6 subplot(2,3,2)7 imshow(Large);8 title('扩⼤为1.5');9 Small=imresize(x,0.1);10 subplot(2,3,3)11 imshow(Small);12 title('缩⼩为0.3');13 subplot(2,3,4)14 df=imresize(x,[600700],'nearest');15 imshow(df)16 title('600*700');17 df1=imresize(x,[300400],'nearest');18 subplot(2,3,5)19 imshow(df1)20 title('300*400');后记:(1)MATLAB基础知识回顾1:crtl+R是对选中的区域注释,ctrl+T是取消注释2:有的代码中点运算如O=a.*I+b/255 ,其中b除以255原因是:灰度数据有两种表式⽅法:⼀种是⽤unit8类型,取值0~255;另⼀种是double类型,取值0~1。
数字图像处理图像变换实验报告

实验报告实验名称:图像处理姓名:刘强班级:电信1102学号:1404110128实验一图像变换实验——图像点运算、几何变换及正交变换一、实验条件PC机数字图像处理实验教学软件大量样图二、实验目的1、学习使用“数字图像处理实验教学软件系统”,能够进行图像处理方面的简单操作;2、熟悉图像点运算、几何变换及正交变换的基本原理,了解编程实现的具体步骤;3、观察图像的灰度直方图,明确直方图的作用与意义;4、观察图像点运算与几何变换的结果,比较不同参数条件下的变换效果;5、观察图像正交变换的结果,明确图像的空间频率分布情况。
三、实验原理1、图像灰度直方图、点运算与几何变换的基本原理及编程实现步骤图像灰度直方图就是数字图像处理中一个最简单、最有用的工具,它描述了一幅图像的灰度分布情况,为图像的相关处理操作提供了基本信息。
图像点运算就是一种简单而重要的处理技术,它能让用户改变图像数据占据的灰度范围。
点运算可以瞧作就是“从象素到象素”的复制操作,而这种复制操作就是通过灰度变换函数实现的。
如果输入图像为A(x,y),输出图像为B(x,y),则点运算可以表示为:B(x,y)=f[A(x,y)]其中f(x)被称为灰度变换(Gray Scale Transformation,GST)函数,它描述了输入灰度值与输出灰度值之间的转换关系。
一旦灰度变换函数确定,该点运算就完全确定下来了。
另外,点运算处理将改变图像的灰度直方图分布。
点运算又被称为对比度增强、对比度拉伸或灰度变换。
点运算一般包括灰度的线性变换、阈值变换、窗口变换、灰度拉伸与均衡等。
图像几何变换就是图像的一种基本变换,通常包括图像镜像变换、图像转置、图像平移、图像缩放与图像旋转等,其理论基础主要就是一些矩阵运算,详细原理可以参考有关书籍。
实验系统提供了图像灰度直方图、点运算与几何变换相关内容的文字说明,用户在操作过程中可以参考。
下面以图像点运算中的阈值变换为例给出编程实现的程序流程图,如下:2、图像正交变换的基本原理及编程实现步骤数字图像的处理方法主要有空域法与频域法,点运算与几何变换属于空域法。
遥感数字图像处理-第6章 几何校正

二、几何校正原理
几何校正涉及两个过程: ➢ 一是空间位置(像元坐标)的变换 ➢ 二是像元灰度值的重新计算(重采样)
4
二、几何校正原理
坐标转换 (a)直接法;(b)间接法
5
三、几何校正步骤
几何精校正不需要空间位置变化数据,回避了成像的空间 几何过程,主要借助地面控制点实现校正。其主要校正步 骤为:
第6章
几何校正
几何校正
一、几何校正原理 二、几何校正步骤 三、几何校正类型 四、图像匹配 五、投影转换
难点:图像匹配 重点:几何校正方法
2
一、几何校正原理
几何校正和几何配准
➢ 几何配准是指将不同时间、不同波段、不同传感器系统所获得的同一 地区的图像(数据),经几何变换使同名像点在位置上和方位上完全 叠合的操作。
➢ 对畸变图像和基准图像建立统一的坐标系和地图投影。 ➢ 选择地面控制点(GCP),按照GCP选择原则,在畸变图像
和基准图像上寻找相同位置的地面控制点对。 ➢ 选择校正模型,利用选择的GCP数据求取校正模型的参数,
然后利用校正模型实现畸变图像和基准图像之间的像元坐 标变换。 ➢ 选择合适的重采样方法对畸变图像的输出图像像元进行灰 度赋值。 ➢ 几何校正的精度分析。
9
四、图像匹配
3.图像匹配方法 根据图像特征的选择,图像匹配方法一般可以分为基于灰
度的图像匹配和基于特征的图像匹配。
10
➢ 几何配准与几何校正的原理是完全相同的,即都涉及到空间位置(像 元坐标)变换和像元灰度值重采样处理两个过程。
➢ 二者的区别主要在于其侧重点不相同:几何校正注重的是数据 本身的处理,目的是为了对数据的一种真实性还原。而几何配 准注重的是图和图(数据)之间的一种几何关系,其目的是为 了和参考数据达成一致,而不考虑参考数据的坐标是否标准、 是否正确。也就是说几何校正和几何配准最本质的差异在于参 考的标准。另外,几何校正更像前期数据处理,几何配准更像 后期处理。
数字图像的几何运算

数字图像的几何运算数字图像的几何运算是指对图像进行平移、旋转、缩放和翻转等几何变换操作的过程。
这些几何运算可以改变图像的位置、方向、大小和形状,是数字图像处理中常用的操作之一。
本文将介绍几何运算的原理和应用,并讨论其在图像处理领域的重要性和作用。
一、几何运算的原理数字图像是由像素组成的二维矩阵,每个像素代表图像的一个点,包含了图像的颜色和位置信息。
几何运算是基于像素的位置信息对图像进行变换和调整的方法,可以通过修改像素的坐标来实现图像的平移、旋转、缩放和翻转等操作。
1. 平移平移是指将图像沿着水平和垂直方向进行移动,使得图像的位置发生变化。
平移操作可以通过修改像素的坐标来实现,将每个像素的坐标按照设定的平移量进行移动,从而改变图像的位置。
平移操作可以用以下公式表示:R’(x, y) = R(x-dx, y-dy)R(x, y)代表原始图像的像素,R’(x, y)代表平移后的图像像素,dx和dy分别代表水平和垂直方向的平移量。
二、几何运算的应用几何运算在数字图像处理中具有重要的应用价值,能够实现图像的位置、方向、大小和形状的调整,为图像处理提供了丰富的操作手段。
以下是几何运算的一些常见应用:1. 图像校正对于拍摄时出现的倾斜、扭曲等问题,可以通过旋转操作对图像进行校正,使得图像恢复到正常的状态。
图像校正能够提高图像的质量和美观度,减少图像处理时的误差和影响。
2. 图像增强通过缩放操作对图像进行放大或缩小,可以改变图像的大小和细节,使得图像更加清晰和细致。
图像增强能够提高图像的清晰度和可视性,使得图像更加逼真和吸引人。
3. 图像合成通过平移操作将多个图像进行位置调整,可以实现多个图像的合成和叠加,融合不同图像的信息和特点,生成新的图像内容。
图像合成能够实现图像的复杂处理和创意设计,为图像处理提供了更多的可能性。
4. 图像镜像通过翻转操作对图像进行镜像处理,可以改变图像的对称性和形状,生成镜像对称的图像。
数字图像处理实验06图像的几何变换

一、数字图像处理实验实验六 图像的几何变换一、实验目的学习和掌握图像几何空间变换和灰度插值的基本方法,对图像进行相应的几何变换操作。
二、实验内容1.编程实现图像的比例缩放。
2. 编程实现图像任意角度的旋转变换。
3. 分别用MATLAB 函数提供的三种插值方法实现图像的缩放和旋转。
三、实验原理图像的几何变换可以看成是像素在图像内的移动过程,该移动过程可以改变图像中物体对象(像素)之间的空间关系。
完整的几何运算需要由两个算法来实现:空间变换算法和灰度插值算法。
空间变换主要用来保持图像中曲线的连续性和物体的连通性,一般都采用数学函数形式来描述输入、输出图像相应像素间的空间关系。
空间变换一般定义为)],(),,([),(),(y x b y x a f y x f y x g =′′= (6.1)其中,f 表示输入图像,g 表示输出图像,坐标),(y x ′′指的是空间变换后的坐标,要注意这时的坐标已经不是原来的坐标),(y x 了,),(y x a 和),(y x b 分别是图像的x 和y 坐标的空间变换函数。
灰度级插值主要是对空间变换后的像素赋予灰度值,使之恢复原位置处的灰度值,在几何运算中,灰度级插值是必不可少的组成部分。
因为图像一般用整数位置处的像素来定义。
而在几何变换中,),(y x g 的灰度值一般由处在非整数坐标上的),(y x f 的值来确定,即g 中的一个像素一般对应于f 中的几个像素之间的位置,反过来看也是一样,即f 中的一个像素往往被映射到g 中的几个像素之间的位置。
下面介绍图像几何变换常用的方法。
1. 图像的缩放假设图像x 轴方向缩放比例fx ,y 轴方向缩放比例是fy ,那么原图中点),(00y x 对应于新图中的点),(11y x 的转换矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1100000010011y x f f y x y x (6.2) 其逆运算如下: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1100010********y x f f y x y x (6.3) 即: ⎩⎨⎧+=+=]5.0[]5.0[1010y x f y y f x x (6.4) 中括号表示对表达式取整。
MATLAB数字图像处理实验--图像基本运算

MATLAB数字图像处理实验--图像基本运算一、实验目的1.理解图像点运算、代数运算、几何运算的基本定义和常见方法;2.掌握在MTLAB中对图像进行点运算、代数运算、几何运算的方法;3.掌握在MATLAB中进行插值的方法4.运用MATLAB语言进行图像的插值缩放和插值旋转5.进一步熟悉了解MATLAB语言的应用。
二、实验设备与软件1.PC计算机系统2.MATLAB软件,包括图像处理工具箱(Image Processing Toolbox)3.实验图片三、实验内容及结果分析3.1图像的点运算选择pout.tif作为实验图像,实验原理及内容参照《MATLAB图像处理编程及应用》程序代码:I=imread('pout.tif');figure;subplot(1,3,1);imshow(I);title('原图');J=imadjust(I,[0.3;0.6],[0.1;0.9]);subplot(1,3,2);imshow(J);title('线性扩展');I1=double(I);I2=I1/255;C=2;K=C*log(1+I2);subplot(1,3,3);imshow(K);title('非线性扩展');M=255-I;figure;subplot(1,3,1);imshow(M);title('灰度倒置');N1=im2bw(I,0.4);N2=im2bw(I,0.7);subplot(1,3,2);imshow(N1);title('二值化阈值0.4');subplot(1,3,3);imshow(N2);title('二值化阈值0.7');执行结果:原图线性扩展非线性扩展灰度倒置二值化阈值0.4二值化阈值0.7实验1结果图3.2图像的代数运算选择两幅图像,一幅是原图像,一幅为背景图像,采用正确的图像代数运算方法,分别实现图像叠加、混合图像的分离和图像的局部显示效果。
实验二 图像基本运算

温州大学物理与电子信息工程学院数字图像处理 实验报告 课程名称:数字图像处理 班 级:电信二班 姓名: 施蒙皎 学号: 0911******* 实验地点:5B310 日期: 2011.11.10实验二 图像基本运算[实验目的和要求]1、 熟悉数字图像在计算的表达方式2、 掌握Matlab 对数字数字图像的点、代数、逻辑和几何运算[实验内容]1对一灰度图像,通过选择不同的灰度级变换函数s = T(r)实现图像的灰度范围线性扩展和非线性扩展,以及图像的灰度倒置和二值化。
2选择两幅图像,一幅是物体图像,一幅是背景图像,采用正确的图像代数运算方法,分别实现图像叠加、混合图像的分离和图像的局部显示效果(插值函数:imresize )。
3对一幅图像实现按比例缩小和不按比例任意缩小的效果,以及图像的成倍放大和不按比例放大效果。
4将一幅图像分别旋转045和090,与原图像对比,观察它们的区别。
问题:图像的旋转会导致图像的失真吗?若有,有什么办法可以解决这个问题? 实验结果及分析:1. I=imread('C:\Documents and Settings\Administrator\×ÀÃæ\lena.jpg'); K=I*20;J=double(I);J=2*log(J+1);l=255-I;subplot(2,3,1),imshow(I);subplot(2,3,2),imshow(K);subplot(2,3,3),imshow(J);subplot(2,3,4),imshow(l);A=rgb2gray(I);j=find(A<125);A(j)=0;j=find(A>=125);A(j)=255;subplot(2,3,5),imshow(A);2. a=imread('C:\Documents and Settings\Administrator\×ÀÃæ\lena.jpg'); b=imread('C:\Documents and Settings\Administrator\×ÀÃæ\an.jpg');c=imadd(a/2,b/2);s=(c-b/2)*2;g=(c-s/2)*2;d=imcrop(a,[150 100 200 200]);subplot(2,3,1),imshow(a);subplot(2,3,2),imshow(b);subplot(2,3,3),imshow(c);title('µþ¼ÓºóµÄͼÏñ');subplot(2,3,4),imshow(s);title('·ÖÀëºóµÄͼÏñ');subplot(2,3,5),imshow(g);title('·ÖÀëºóµÄͼÏñ');subplot(2,3,6),imshow(d);title('¾Ö²¿ÏÔʾ');3.成倍放大:a=imread('C:\Documents and Settings\Administrator\×ÀÃæ\lena.jpg'); b=imresize(a,2);c=imresize(a,0.5);figure(1)imshow(a);title('Ô-ͼ');figure(2)imshow(b);title('·Å´ó2±¶');figure(3)imshow(c);title('ËõСΪ1/2');不按比例放大:a=imread('C:\Documents and Settings\Administrator\×ÀÃæ\lena.jpg'); b=imresize(a,[25 64]);c=imresize(a,[90 150]);figureimshow(a);figureimshow(b);figureimshow(c);4. a=imread('C:\Documents and Settings\Administrator\×ÀÃæ\lena.jpg'); b=imrotate(a,45,'nearest');c=imrotate(a,90,'nearest');subplot(1,3,1),imshow(a);subplot(1,3,2),imshow(b);subplot(1,3,3),imshow(c);评定成绩:。
数字图像的几何运算

数字图像的几何运算数字图像的几何运算是图像处理中的一项重要技术,通过对原始图像进行一系列几何变换来改变图像的位置、姿态、大小、形状等方面,进而实现图像的增强、修复、配准、配对等应用。
数字图像的几何运算包括平移、旋转、缩放、翻转、仿射变换等多种运算,它们可以单独进行,也可以结合使用。
下面将介绍这些几何运算的原理和应用。
一、平移平移是将图像沿着指定的方向平移一定距离的操作,其公式为:x' = x + txy' = y + ty其中(x, y)为原始坐标,(x', y')为平移后的坐标,tx和ty分别表示在x和y方向上平移的像素数。
平移可以用来调整图像的位置,比如将图像居中、左右移动、上下移动等,对于某些需要对齐的图像,也可以通过平移使它们重合。
在实现时,可以通过对原始图像的每个像素进行平移,然后重新生成新图像的方式来实现。
二、旋转旋转是将图像绕一个点或一个轴线旋转一定角度的操作,其公式为:三、缩放缩放是将图像在水平、垂直或同时两个方向上缩小或放大的操作,其公式为:四、翻转在实现时,可以通过对原始图像的每个像素进行翻转,然后重新生成新图像的方式来实现。
翻转可以用来调整图像的朝向,比如将图像视角从左向右变为从右向左、将图像视角从上向下变为从下向上等。
在某些应用中,还常常需要同时对图像进行水平和垂直方向上的反转,以获取更加鲜明的效果。
五、仿射变换仿射变换是指将图像在平移、旋转、缩放和翻转的基础上进行进一步灵活变换的操作,其公式为:其中A、B、C、D、E、F分别为6个未知参数,需要根据实际情况进行确定。
仿射变换可以用来调整图像的形状和姿态,比如将图像从一个角度旋转至另一个角度或进行扭曲、变形等。
在实现时,可以通过对原始图像的每个像素进行仿射变换,然后重新生成新图像的方式来实现。
总结数字图像的几何运算是数字图像处理中的基础操作,它能够调整图像的位置、姿态、大小、形状等方面,为后续的图像处理提供重要支持。
数字图像的计算几何 拓扑和物理及其应用

精彩摘录
拓扑变换主要研究如何在保持图像形状特征的前提下对图像进行变换。拓扑流用于描述图像中形 状在时间上的变化,它可以揭示图像中形状之间的相互作用。代数拓扑则是对数字图像进行特征 提取和分类的重要工具,它通过对图像数据的代数运算来进行拓扑结构的分析。
数字图像物理理论是研究数字图像中像素之间的相互作用的理论。它涉及到电磁场理论、积分方 程和随机过程等方面的基础理论。电磁场理论是描述电磁波传播和相互作用的物理理论。在数字 图像处理中,电磁场理论可以用于实现图像的滤波和特征提取。积分方程在数字图像处理中主要 用于图像的建模和分析,例如在图像恢复和超分辨率重建等方面。随机过程是描述随机现象的理 论,它在数字图像处理中可以用于实现图像的降噪和分割等任务。
阅读感受
阅读感受
《数字图像的计算几何、拓扑和物理及其应用》是一本极具启发性的书籍,它全面而深入地介绍 了视觉场景中与计算几何学、拓扑学和物理学相关的内容。通过阅读这本书,我对数字图像有了 更深入的理解,也收获了许多有关图像技术的宝贵知识。
这本书的内容主要围绕目标形状信息的检测、表达和描述展开。其中,计算几何学的应用非常显 着。计算几何学在数字图像处理中起着至关重要的作用,尤其是在形状表达、特征提取和匹配等 方面。通过运用计算几何算法,我们可以更好地理解和分析图像中的几何结构。例如,书中的 “单元复合形”和“细丝”等概念,为我们提供了全新的视角来理解图像中的形状和结构。
目录分析
拓扑是研究几何图形或空间在连续变换下的性质的一门学科。在数字图像处理中,拓扑主要用于 图像分割、特征提取和模型建立等方面。通过对图像进行分割和特征提取,可以识别出图像中的 不同区域和特征,进而实现图像的分析和理解。同时,拓扑结构还可以用于建立图像模型,如拓 扑网格模型等,以更好地描述和表达图像数据。
图像的几何变换-数字图像处理

图像的几何变换
几何变换基础 图像比例缩放 图像平移 图像镜像 图像旋转 图像复合变换 透视变换 应用实例——几何畸变的
校正
图像的几何变换
4.1 几何变换基础
4.1.1 概述 图像的几何变换是指对原始图像按照需要产生大小、形
状和位置的变化。从图像类型来分,图像的几何变换有二维 平面图像的几何变换和三维图像的几何变换以及由三维向二 维平面的投影变换等。从变换的性质来分,有平移、比例缩 放、旋转、反射和错切等基本变换,透视变换等复合变换,以 及插值运算等。
图4-24-图像旋转之前进行的平移
图像的几何变换
按照上述行插值或列插值方法,原像素点(x=1,y=2)经旋 转30°后得到变换后的点(x'=2,y'=2),其后的空洞点(x',y'+1)可 以填充为(x',y'),即空洞点(2,3)可以用(2,2)点的值来代替。当 然,采用不同的插值方法所得到的空洞点的值是不同的,也可 以采用其他方法处理得到不同的空洞点填充效果。图 4-23 中的图像处理后的效果如图4-25 所示。
其逆运算为
图像的几何变换
图4-22 图像旋转θ角
图像的几何变换 用式(4-18)可以计算旋转后图像上像素的坐标。例如,对
图4-23所示大小为3×3的图像进行旋转,当θ=30°时,式(4-18) 为
变换后x、y 可能取的最小、最大值分别为
其变换过程如图4-23所示。
图像的几何变换
图4-23 图像旋转θ角度(30°)
2×3阶变换矩阵,其形式为
图像的几何变换
图像的几何变换 下面再验证点P(x,y)按照3×3的变换矩阵T 平移变换的
结果
智能数字图像处理-原理与技术 第3章 图像的基本运算与变形处理

几何运算 ➢ 几何运算就是改变图像中物体对象(像素)之间的空间关系,几何变换可以分为 位置变换(平移、镜像、旋转)、形状变换(放大、缩小)等。
5
代数与逻辑运算作用
降低或消除噪声 检测两幅图像之间的变化 图像叠加或合成 确定物体边界位置处的梯度
4. 图像的几何运算
2. 图像的代数运算
5. 图像的缩放及插值
3. 图像的逻辑运算
6. 图像变形技术
3
1.图像的基本运算
根据运算基本数学特征,常用的图像基本运算有: ➢ 代数运算 ➢ 逻辑运算 ➢ 几何运算 ➢ 图像缩放 ➢ 图像插值运算
4
代数、逻辑、几何运算基本简介
代数运算 ➢ 代数运算是指将两幅图像通过对应像素之间的加、减、乘、除运算得到输出图 像的方法。 ➢ 可以通过适当的组合,构成复合代数运算
6
2. 图像的代数运算
四种基本的代数运算:
运算规则:像素位置不变,A和B对应位置的像素灰度(或者颜色)进行计算 代数运算作用:
迭加:合成图像 相减:运动物体检测 相乘:提取或删掉图像某部分 相除:遥感多光谱图像相除,抵消一些入射分量
7
加运算
加法运算:两幅图像对应像素的灰度值或彩色分量进行相加
否则置为0 。
12
乘运算实例
乘运算实例1:扣取水流区域
乘运算实例2:扣取前景目标
13
相除运算
除法运算:就是两幅图像对应像素的灰度值或彩色分量进行相除。简单的除法运算可用于 改变图像的灰度级。
如果除数为0, 结果置为0.
两个图像相除实例 运算规则:像素位置不变,A和B对应位置的像素灰度(或者颜色)进行相除运算 主要用途:除法运算可用于校正非线性畸变的成像设备。
数字图像的几何运算

数字图像的几何运算数字图像的几何运算是数字图像处理中的重要环节,它主要涉及图像的平移、旋转、缩放和镜像等操作。
这些几何操作对于图像的变换和处理起着至关重要的作用,可以用于图像增强、图像拼接、图像对齐等各种应用中。
本文将重点介绍数字图像的几何运算方法及其应用。
1. 平移:平移是将图像沿着水平或垂直方向进行移动,其数学表示为:\[T(x, y) = (x + d_x, y + d_y)\]\(d_x\)和\(d_y\)分别表示水平和垂直方向的平移距离。
平移操作可以直接通过修改像素的坐标来实现,也可以通过插值的方法来实现更加精确的平移效果。
2. 旋转:旋转是将图像绕着某一点进行旋转,其数学表示为:\[R(x, y) = (x \cos \theta - y \sin \theta, x \sin \theta + y \cos \theta)\]\(\theta\)表示旋转角度。
旋转操作通常需要进行插值,以保证旋转后的图像质量。
3. 缩放:缩放是改变图像的尺寸,可以放大或者缩小图像,其数学表示为:\(s_x\)和\(s_y\)分别表示水平和垂直方向的缩放比例。
缩放操作通常需要进行插值,以保证图像的质量。
以上几种几何运算是数字图像处理中常用的基本操作,它们可以单独应用,也可以组合应用,以实现各种复杂的图像变换效果。
在实际应用中,这些几何运算通常需要搭配插值方法来保证图像质量,并且需要考虑到计算效率和存储空间的限制。
数字图像的几何运算在计算机视觉、图像处理、图像分析等领域有着广泛的应用。
下面将介绍几种典型的应用场景。
1. 图像配准:图像配准是将多幅图像进行对齐,以实现图像融合、图像融合等目的。
在图像配准中,通常需要进行平移、旋转和缩放等几何变换操作,以实现图像的对齐。
数字图像的几何运算是数字图像处理中的重要内容,它可以帮助我们实现各种图像处理任务,提高图像处理的效率和质量,拓展图像处理的应用领域。
希望本文对您有所帮助,谢谢阅读!。
HALCON数字图像处理-第5章 图像运算

HALCON数字图像处理
5.1 图像的代数运算
图像的代数运算也称为算数运算。即将多幅图像之间的像元
一一对应,并做相应的加、减、乘、除运算。图像之间的运算
也就是矩阵之间的运算。
四种运算的相应公式如下。
(1)加法运算:
C(x,y)=A(x,y)+B(x,y)
(5-1)
图像的加法运算可以用于图像合成,也可以通过该运算降低
3、图像乘法 HALCON数字图像处理
4、图像除法 HALCON数字图像处理
5.2 图像的几何变换
图像几何变换是指用数学建模方法来描述图像位置、大 小、形状等变化的方法,它通过数学建模实现对数字图像 进行几何变换的处理。图像几何变换主要包括图像平移变 换、比例缩放、旋转、仿射变换、透视变换和图像插值等, 其实质就是改变像素的空间位置或估算新空间位置上的像 素值。
仿射变换,要求读者从矩阵的角度去考虑,包括平移、 HA旋LC转ON、数缩字放图等像。处其理实在进行仿射变换的过程中,会涉及灰
每一种知识都需要努力, 都需要付出,感谢支持!
知识就是力量,感谢支持!
----谢谢大家!!
第5章
图像运算
◆ 5.1 ◆ 5.2 ◆ 5.3
图像的代数运算 图像的几何变换 基于HALCON的图像校正
HALCON数字图像处理
第5章
图像运算
图像运算指以图像为单位进行的搡作(该操作对图 像中的所有像素同时进行),运算的结果是得到一幅灰度分 布与原图像灰度分布不同的新图像(原图像指的是参与运算 的图像)。具体的运算主要包括算术和逻辑运算,它们通过 改变像素的值来达到图像增强的效果。算术和逻辑运算中每 次只涉及一个空间像素的位置,所以可以“原地”完成,即 在(x,y)位置做一个算术运算或逻辑运算的结果便可以存入 其中一个图像的相应位置,因为在之后的运算中那个位置不 会再使用。换句话说,设对两幅图像f(x,y) 和h(x,y)的 算术或逻辑运算的结果是g(x,y),则可直接将g(x,y)覆盖 f(x,y)或h(x,y),即从存放原输入图像的空间中直接得到 输出图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3 图像的几何运算实验名称:图像的几何运算实验内容:图像的几何运算与点运算相对立,几何运算的目的在于改变像素之间的空间位置和空间关系,但没有改变灰度等级值,包括两个独立的算法:空间变换和灰度插值。
其中空间变换又包括平移和镜像处理,应用空间变换和灰度插值算法可以实现对图像的缩放和旋转处理。
图像的几何中心作为坐标原点,x轴由左向右递增,Y轴由上至下递增。
因此,在进行图像旋转时,是以图像的几何中心为基准进行旋转的;在进行图像缩放时,也是以图像的几何中心为基准,其上下左右均等地向内收缩或向外扩大的。
这种坐标转换会使图像变换更自然。
另外,在进行几何运算的时候,保持原图像的尺寸大小不变,如果变换后的图像超出该尺寸,超出部分会被截断,而不足部分会以白色像素填充。
本此实验内容包括:图像平移、图像镜像、图像缩放、图像旋转。
实验步骤:1、界面设计如下:打开图像代码:private void open_Click(object sender, EventArgs e){OpenFileDialog opnDlg = new OpenFileDialog();opnDlg.Filter = "所有图像文件 | *.bmp; *.pcx; *.png; *.jpg; *.gif;" +"*.tif; *.ico; *.dxf; *.cgm; *.cdr; *.wmf; *.eps; *.emf|" +"位图( *.bmp; *.jpg; *.png;...) | *.bmp; *.pcx; *.png; *.jpg; *.gif; *.tif; *.ico|" + "矢量图( *.wmf; *.eps; *.emf;...) | *.dxf; *.cgm; *.cdr; *.wmf; *.eps; *.emf";opnDlg.Title = "打开图像文件";opnDlg.ShowHelp = true;if (opnDlg.ShowDialog() == DialogResult.OK){curFileName = opnDlg.FileName;try{curBitmap = (Bitmap)Image.FromFile(curFileName);}catch (Exception exp){MessageBox.Show(exp.Message);}}Invalidate();}关闭程序代码:private void close_Click(object sender, EventArgs e){this.Close();}Paint事件代码:private void Form1_Paint(object sender, PaintEventArgs e){Graphics g = e.Graphics;if (curBitmap != null){g.DrawImage(curBitmap, 160, 20, curBitmap.Width, curBitmap.Height);}}图像平移代码:private void translation_Click(object sender, EventArgs e){if (curBitmap != null){Translation traForm = new translation();if (traForm.ShowDialog() == DialogResult.OK){Rectangle rect = new Rectangle(0, 0, curBitmap.Width, curBitmap.Height); System.Drawing.Imaging.BitmapData bmpData = curBitmap.LockBits(rect, System.Drawing.Imaging.ImageLockMode.ReadWrite, curBitmap.PixelFormat);IntPtr ptr = bmpData.Scan0;int bytes = curBitmap.Width * curBitmap.Height;byte[] grayValues = new byte[bytes];System.Runtime.InteropServices.Marshal.Copy(ptr, grayValues, 0, bytes);int x = Convert.ToInt32(traForm.GetXOffset);int y = Convert.ToInt32(traForm.GetYOffset);byte[] tempArray = new byte[bytes];//Array.Clear(tempArray, 0, bytes);for (int i = 0; i < bytes; i++){tempArray[i] = 255;}for (int i = 0; i < curBitmap.Height; i++){if ((i + y) < curBitmap.Height && (i + y) > 0){for (int j = 0; j < curBitmap.Width; j++){if ((j + x) < curBitmap.Width && (j + x) > 0){tempArray[(j + x) + (i + y) * curBitmap.Width] = grayValues[j + i * curBitmap.Width];}}}}grayValues = (byte[])tempArray.Clone();System.Runtime.InteropServices.Marshal.Copy(grayValues, 0, ptr, bytes); curBitmap.UnlockBits(bmpData);}Invalidate();}}上段代码理解:在对图像进行处理之前,总要判断一下是否存在图像,如:if (curBitmap != null)在图像处理过程中,需要用户输入相关参数,这时候可以打开其他对话框的方式获取参数,如:if (traForm.ShowDialog() == DialogResult.OK),为什么要这么做?这样做可以判断参数是否有效输入。
我这里,这个对话框的名字有个名字,叫traForm,里面还有些代码的,看看namespace geometry_operations{public partial class translation : Form{public translation(){InitializeComponent();}private void start_Click(object sender, EventArgs e){this.DialogResult = DialogResult.OK;}private void close_Click(object sender, EventArgs e){this.Close();}public string GetXOffset{get{return xOffset.Text;}}public string GetYOffset{get{return yOffset.Text;}}private void translation_Load(object sender, EventArgs e){}}}上面的代码定义了two个属性:GetXOffset、GetYOffset,这里要好好看看怎么C#里面怎么为类定义属性的,其实语法很简单:Public 类型属性名称{get{获得属性值代码}set{设置属性值代码}}好好学习下!试着给它加个属性。
在对图像处理时,总要先获取图像的像素值,获取图像像素值的方法可以参照图象灰度化的内存法,代码为:Rectangle rect = new Rectangle(0, 0, curBitmap.Width, curBitmap.Height); System.Drawing.Imaging.BitmapData bmpData = curBitmap.LockBits(rect, System.Drawing.Imaging.ImageLockMode.ReadWrite, curBitmap.PixelFormat);IntPtr ptr = bmpData.Scan0;int bytes = curBitmap.Width * curBitmap.Height;byte[] grayValues = new byte[bytes];System.Runtime.InteropServices.Marshal.Copy(ptr, grayValues, 0, bytes);这样处理后就获得了一个图像灰度值得数组(注意:是1维的)下面的语句就是对图像灰度值得计算了,注意这时需要操作的图像实际上是个一维的数组grayValues,具体过程是这样的:先声名个临时的数组,并通过一个循环将数组初始化:byte[] tempArray = new byte[bytes];//Array.Clear(tempArray, 0, bytes);for (int i = 0; i < bytes; i++){tempArray[i] = 255;}关键的图像平移代码来啦!先看看?for (int i = 0; i < curBitmap.Height; i++){if ((i + y) < curBitmap.Height && (i + y) > 0){for (int j = 0; j < curBitmap.Width; j++){if ((j + x) < curBitmap.Width && (j + x) > 0){tempArray[(j + x) + (i + y) * curBitmap.Width] = grayValues[j + i * curBitmap.Width];}}}}这个对话框的代码:public mirror(){InitializeComponent();}private void startMirror_Click(object sender, EventArgs e) {this.DialogResult = DialogResult.OK;}private void close_Click(object sender, EventArgs e){this.Close();}public bool GetMirror{get{return horMirror.Checked;}}关键代码来了,实现镜像的功能的代码:private void mirror_Click(object sender, EventArgs e){if (curBitmap != null){mirror mirForm = new mirror();if (mirForm.ShowDialog() == DialogResult.OK){Rectangle rect = new Rectangle(0, 0, curBitmap.Width, curBitmap.Height); System.Drawing.Imaging.BitmapData bmpData = curBitmap.LockBits(rect, System.Drawing.Imaging.ImageLockMode.ReadWrite, curBitmap.PixelFormat);IntPtr ptr = bmpData.Scan0;int bytes = curBitmap.Width * curBitmap.Height;byte[] grayValues = new byte[bytes];System.Runtime.InteropServices.Marshal.Copy(ptr, grayValues, 0, bytes);int halfWidth = curBitmap.Width / 2;int halfHeight = curBitmap.Height / 2;byte temp;if (mirForm.GetMirror){for (int i = 0; i < curBitmap.Height; i++){for (int j = 0; j < halfWidth; j++){temp = grayValues[i * curBitmap.Width + j];grayValues[i * curBitmap.Width + j] = grayValues[(i + 1) * curBitmap.Width - 1 - j];grayValues[(i + 1) * curBitmap.Width - 1 - j] = temp;}}}else{for (int i = 0; i < curBitmap.Width; i++){for (int j = 0; j < halfHeight; j++){temp = grayValues[j * curBitmap.Width + i];grayValues[j * curBitmap.Height + i] =grayValues[(curBitmap.Height - j - 1) * curBitmap.Width + i];grayValues[(curBitmap.Height - j - 1) * curBitmap.Width + i] = temp;}}}System.Runtime.InteropServices.Marshal.Copy(grayValues, 0, ptr, bytes); curBitmap.UnlockBits(bmpData);}Invalidate();}}实验结果如下:3.图像缩放的代码private void zoom_Click(object sender, EventArgs e){if (curBitmap != null){zoom zoomForm = new zoom();if (zoomForm.ShowDialog() == DialogResult.OK){Rectangle rect = new Rectangle(0, 0, curBitmap.Width, curBitmap.Height); System.Drawing.Imaging.BitmapData bmpData = curBitmap.LockBits(rect, System.Drawing.Imaging.ImageLockMode.ReadWrite, curBitmap.PixelFormat);IntPtr ptr = bmpData.Scan0;int bytes = curBitmap.Width * curBitmap.Height;byte[] grayValues = new byte[bytes];System.Runtime.InteropServices.Marshal.Copy(ptr, grayValues, 0, bytes);double x = Convert.ToDouble(zoomForm.GetXZoom);double y = Convert.ToDouble(zoomForm.GetYZoom);int halfWidth = (int)(curBitmap.Width / 2);int halfHeight = (int)(curBitmap.Height / 2);int xz = 0;int yz = 0;int tempWidth = 0;int tempHeight = 0;byte[] tempArray = new byte[bytes];if (zoomForm.GetNearOrBil == true){for (int i = 0; i < curBitmap.Height; i++){for (int j = 0; j < curBitmap.Width; j++){tempHeight = i - halfHeight;tempWidth = j - halfWidth;if (tempWidth > 0){xz = (int)(tempWidth / x + 0.5);}else{xz = (int)(tempWidth / x - 0.5);}if (tempHeight > 0){yz = (int)(tempHeight / y + 0.5);}else{yz = (int)(tempHeight / y - 0.5);}tempWidth = xz + halfWidth;tempHeight = yz + halfHeight;if(tempWidth < 0 || tempWidth >= curBitmap.Width || tempHeight < 0 || tempHeight >= curBitmap.Height){tempArray[i * curBitmap.Width + j] = 255;}else{tempArray[i * curBitmap.Width + j] = grayValues[tempHeight * curBitmap.Width + tempWidth];}}}}else{double tempX, tempY, p, q;for (int i = 0; i < curBitmap.Height; i++){for (int j = 0; j < curBitmap.Width; j++){tempHeight = i - halfHeight;tempWidth = j - halfWidth;tempX = tempWidth / x;tempY = tempHeight / y;if (tempWidth > 0){xz = (int)tempX;}else{xz = (int)(tempX - 1);}if (tempHeight > 0){yz = (int)tempY;}else{yz = (int)(tempY - 1);}p = tempX - xz;q = tempY - yz;tempWidth = xz + halfWidth;tempHeight = yz + halfHeight;if (tempWidth < 0 || (tempWidth + 1) >= curBitmap.Width || tempHeight < 0 || (tempHeight + 1) >= curBitmap.Height){tempArray[i * curBitmap.Width + j] = 255;}else{tempArray[i * curBitmap.Width + j] = (byte)((1.0 - q) * ((1.0 - p) * grayValues[tempHeight * curBitmap.Width + tempWidth] + p * grayValues[tempHeight * curBitmap.Width + tempWidth + 1]) +q * ((1.0 - p) * grayValues[(tempHeight + 1) * curBitmap.Width + tempWidth] + p * grayValues[(tempHeight + 1) * curBitmap.Width + 1 + tempWidth]));}}}}grayValues = (byte[])tempArray.Clone();System.Runtime.InteropServices.Marshal.Copy(grayValues, 0, ptr, bytes); curBitmap.UnlockBits(bmpData);}Invalidate();}}4.图像旋转的代码private void rotation_Click(object sender, EventArgs e){if (curBitmap != null){rotation rotForm = new rotation();if (rotForm.ShowDialog() == DialogResult.OK){Rectangle rect = new Rectangle(0, 0, curBitmap.Width, curBitmap.Height); System.Drawing.Imaging.BitmapData bmpData = curBitmap.LockBits(rect, System.Drawing.Imaging.ImageLockMode.ReadWrite, curBitmap.PixelFormat);IntPtr ptr = bmpData.Scan0;int bytes = curBitmap.Width * curBitmap.Height;byte[] grayValues = new byte[bytes];System.Runtime.InteropServices.Marshal.Copy(ptr, grayValues, 0, bytes);int degree = Convert.ToInt32(rotForm.GetDegree);double radian = degree * Math.PI / 180.0;double mySin = Math.Sin(radian);double myCos = Math.Cos(radian);int halfWidth = (int)(curBitmap.Width / 2);int halfHeight = (int)(curBitmap.Height / 2);int xr = 0;int yr = 0;int tempWidth = 0;int tempHeight = 0;byte[] tempArray = new byte[bytes];double tempX, tempY, p, q;for (int i = 0; i < curBitmap.Height; i++){for (int j = 0; j < curBitmap.Width; j++){tempHeight = i - halfHeight;tempWidth = j - halfWidth;tempX = tempWidth * myCos - tempHeight * mySin;tempY = tempHeight * myCos + tempWidth * mySin;if (tempWidth > 0){xr = (int)tempX;}else{xr = (int)(tempX - 1);}if (tempHeight > 0){yr = (int)tempY;}else{yr = (int)(tempY - 1);}p = tempX - xr;q = tempY - yr;tempWidth = xr + halfWidth;tempHeight = yr + halfHeight;if(tempWidth < 0 || (tempWidth + 1) >= curBitmap.Width || tempHeight < 0 || (tempHeight + 1) >= curBitmap.Height){tempArray[i * curBitmap.Width + j] = 255;}else{tempArray[i * curBitmap.Width + j] = (byte)((1.0 - q) * ((1.0 - p) * grayValues[tempHeight * curBitmap.Width + tempWidth] + p * grayValues[tempHeight * curBitmap.Width + tempWidth + 1]) +q * ((1.0 - p) * grayValues[(tempHeight + 1) * curBitmap.Width + tempWidth] + p * grayValues[(tempHeight + 1) * curBitmap.Width + 1 + tempWidth]));}}}grayValues = (byte[])tempArray.Clone();System.Runtime.InteropServices.Marshal.Copy(grayValues, 0, ptr, bytes); curBitmap.UnlockBits(bmpData);}Invalidate();}实验结果如下:。
