离散数学chapter04-2014
离散数学第四章(第3讲)
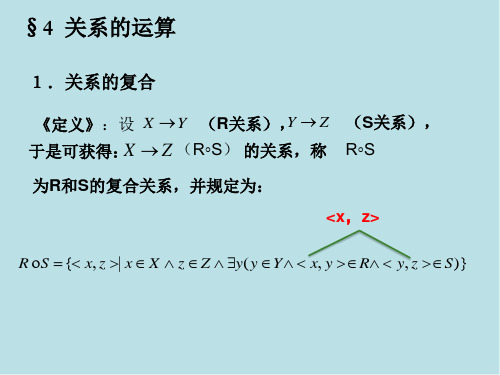
1.关系的复合
《定义》:设 X Y (R关系),Y Z (S关系),
于是可获得:X Z (R◦S) 的关系,称 R◦S
为R和S的复合关系,并规定为:
<x,z>
R S { x, z | x X z Z y( y Y x, y R y, z S)}
R S { x, z | x X z Z y( y Y x, y R y, z S)}
(R U Ix ) U (R U%Ix ) r(R) U r(%R) Sr(R)
例:设X={a,b,c},R={<a,b><c,c>}
(1)rs(R)=r{<a,b><b,a><c,c>}={<a,b><b,a><c,c><a,a><b,b>} sr(R)=s{<a,b><c,c><a,a><b,b>}={<a,b><b,a><c,c><a,a><b,b>}
例:设A={1,2,3,4,5},R,S均为A→A的关系,且 R={<1,2><3,4><2,2>} S={<4,2><2,5><3,1><1,3>}
则 R◦S={<1,5> <3,2> <2,5>} S◦R={<4,2> <3,2> <1,4>}
讨论: (1) RS ≠ SR,因此“◦”是不可交换的。 (2)RS为新的二元关系,且RS为X Z上的二元关系。
离散数学(微课版) 第4章

离散数学(微课版)第4章1. 引言在离散数学的第4章中,我们将讨论图论的基本概念和应用。
图论是研究图及其在现实生活中的应用的数学分支,它在计算机科学、网络设计、运筹学等领域中具有重要的应用价值。
本章将介绍图的定义、图的表示方法、图的遍历算法等内容。
2. 图的定义图由一组节点和一组节点之间的边构成。
节点通常表示现实世界中的对象,而边则表示对象之间的关系。
图可以用于描述各种问题,如社交网络中的用户关系、城市之间的交通网络等。
2.1 有向图和无向图图可以分为有向图和无向图两种类型。
在有向图中,边具有方向,表示节点之间的单向关系。
而在无向图中,边没有方向,表示节点之间的双向关系。
2.2 顶点和边图由顶点和边组成。
顶点是图的节点,用来表示对象。
边连接两个顶点,表示两个对象之间的关系。
2.3 路径和环路径是指在图中从一个顶点到另一个顶点的连接序列。
环是一条路径,其起点和终点相同。
3. 图的表示方法在计算机中,图可以用不同的数据结构来表示。
常见的表示方法包括:3.1 邻接矩阵邻接矩阵是用二维数组表示图的连接关系。
对于无向图,邻接矩阵是对称的,而对于有向图,则不对称。
A B CA010B101C010上述邻接矩阵表示了一个无向图,其中顶点A与顶点B相连,顶点B与顶点C相连。
3.2 邻接表邻接表是用链表表示图的连接关系。
对于每个顶点,邻接表保存了与其相连的其他顶点的信息。
A ->B -> NULLB -> A ->C -> NULLC -> B -> NULL上述邻接表表示了一个无向图,顶点A与顶点B相连,顶点B与顶点A、C相连,顶点C与顶点B相连。
4. 图的遍历算法图的遍历算法是指按照一定的方式访问图中的所有节点。
常见的图的遍历算法有深度优先搜索和广度优先搜索。
4.1 深度优先搜索深度优先搜索从起点开始,尽可能深地访问尚未访问的节点,直到无法继续深入为止,然后回溯到上一个节点,继续深入其他未访问的节点。
离散数学(第四章)解读.

§2.1 一阶逻辑命题符号化
例如,下列推理: 所有的人都是要死的。 苏格拉底是人。 苏格拉底是要死的。 众所周知,这是真命题。但在命题逻辑中,如 果用P,Q,R表示以上三个命题,则上述推理过 程为:(P∧Q)R。借助命题演算的推理理 论不能证明其为重言式。
§2.1 一阶逻辑命题符号化
原因:命题逻辑不能将命题之间的内在联系 和数量关系反映出来。 解决办法:将命题进行分解。
§2.1 一阶逻辑命题符号化
设谓词H表示“是劳动模范”, a表示个体名称 张明, b表示个体名称李华,c表示个体名称这只老 虎,那么H(a) 、 H(b)、 H(c)表示三个不同的命 题,但它们有一个共同的形式,即H(x).一般地, H(x)表示客体x具有性质H。这里x表示抽象的或 泛指的客体,称为个体变元,常用小写英文字 母x, y, z, …表示。相应地,表示具体或特定的客 体的词称为个体常项,常用小写英文字母a,b,c, …表示。
§2.1 一阶逻辑命题符号化
刻划一个个体性质的词称之为一元谓词 ,刻划 n 个个 体之间关系的词称之为n元谓词. 一般我们用大写英文字母表示谓词,用小写英文字 母表示客体名称,例如,将上述谓词分别记作大写 字母F、G、H、R,S则上述命题可表示为: (1) F(a) a:张明 (2) F(b) b:李华 (3) G(c) c:王红 (4) H(s,t) s:小李 t:小赵 (5) R(a,b,c) (6) S(a,b) a:阿杜 b:阿寺 其中(1)、(2)、 (3)为一元谓词, (4) 、 (6)为二元谓词 , (5)为三元谓词。
2.5谓词演算的推理理论(Inference theory of
predicate calculus)
§2.1 一阶逻辑命题符号化
离散数学第四章

代数系统
从这一章起到第七章涉及到的是近世代数的内容,本章介 绍的是代数系统的内容,后三章介绍的是几个重要的代数系统:
群,环,域,格.这些理论在计算机及物理,化学等学科都有重要应用.
§4.1 运 算
一 . 概念 本节将函数的讨论局限在集合An到集合A上. 定义1 设有非空集合A,函数f: An→A 称为A上的一个n元运算. n称为运算的阶. 若f: A2→A 则f是A上的一个二元运算
常用表格来表示一元运算和二元运算: ai a1 o(ai) o(a1) o a1 a2 … an o(a1,an)
a1 o(a1,a1) o(a1,a2)
.
. an 三
.
. o(an)
.
.
…
… o(an,an)
an o(an,a1) o(an,a2)
.关于运算的封闭性
定义2: 如果作用在一个集合A的元素的运算,其运算结果也
(4)单位元:加法有单位元;乘法有单位元;
(5)加法有逆元;
(6)消去律: 如果 i ≠0,任意 j,k∈I 由i · i · k= j, 称<J,+,· >是一个整环. 可以有 k= j ;
前述的<I,+ ,· <B,+,· <R,+,· <Q,+, · > > > >均为整环.再看一例:
例: 证明代数系统<Z3 , 3 , ⊙3 >是整环.其中 ⊙3 , 3的 定义如下:
=i+j- i.j+k- i k -j + i.j . k
i* ( j*k )=i*(k+j- k.j)=i+ (k+j- k.j)-i (k+j- k.j) =i+j- i.j+k- i k -j + i.j . k
离散数学第四章(第1讲)

第四章 二元关系
§1 序偶与笛卡尔积 §2 关系及其表示 §3 关系的性质 §4 关系的运算 §5 等价关系与划分 §6 相容关系与覆盖 §7 偏序关系
§1 序偶与笛卡尔乘积
1 序偶 《定义》由二个具有给定次序的客体所组成的序列
称为序偶。记作〈x,y〉 例:X—Y二维平面上的一个点的坐标〈x,y〉就
是一个序偶。
说明: (1)在序偶中二个元素要有确定的排列次序。 若ab时,则〈a,b〉〈b,a〉 若〈x,y〉=〈a,b〉(x=a y=b) (2) 多重序元: 三元组:〈〈x,y〉,z〉 =〈x,y,z〉 n元组: 〈〈〈〈x1,x2〉,x3〉…〉,xn〉= 〈x1,…,xn〉
ran R={a,b,c,d}
FLD R={1,2,3,4,a,b,c,d}
4.关系和笛卡尔乘积 笛卡尔乘积的任何子集都可以定义一种二元关系。 例:X={1,2,3,4},Y={1,2}
X Y {1,1 ,1,2 , 2,1 , 2,2 , 3,1 , 3,2 , 4,1 , 4,2 }
S1={<x,y>|x X yYx ≤ y}={<1,1><1,2><2,2>}
2 笛卡尔乘积 《定义》设A,B为二个任意集合,若序偶的第 一个成员(左元素)是A的一个元素,序偶的 第二个成员(右元素)是B的一个元素,则所 有这样的序偶构成的集合称为A和B的笛卡尔乘 积。
记作:A B={〈x,y〉|(xA)(yB)}
离散数学教学PPT第四章

但是从另一个角度看,每一个自然数都对应着一个平 方数;
所以,自然数和平方数是一样多的, 这 “一一对应” 的 规则也就是判断集合是否一样大的标准。
8
任何一个有限集合不能与其真子集等势。 另一种有限集、无限集的定义方法; 定义:如果存在一一对应的f: S→S,使得f(S)⊂S,
证明:必要条件已经在前面证明,下面证明其充分 条件。
反证法:
鸽洞原理
设一集合M含有与其等势的真子集M’,若M’为有限集, 设其元素个数为n,即|M|=n,则此时必有n>m;
但此时M与M’间由于元素个数不同而无法建立一一对应 的关系而产生矛盾。
17
有限集和无限集的重要定义 定义4.5 一集合存在与其等势的真子集,则称为无 限集,否则称为有限集。
“全体正整数的集合和全体有 理数的集合等势”是在数学上 很重要的一个例子,说明一个 实数中的稠密集可以和一个离 散集等势(稠密:在任意两个 元素之间存在第三个元素)
22
因为每个有理数都可以写成一个分数形式如下:
... -3/1 -2/1 --1/1 0/1 1/1 2/1 3/1 ... ... -3/2 -2/2 -1/2 0/2 1/2 2/2 3/2 ... ... -3/3 -2/3 -1/3 0/3 1/3 2/3 3/3 ...
任意一个小于1 的非负小数,取其二进制形式,比如 0.1101001, 如果将小数点后第 i 位对应的 0/1 看成是自然数 i 在某个集合中的 无/有,那么0.1101001就对应自然数的一个子集 {1, 2, 4, 7};
所以,任一个小数可以对应一个自然数的子集,当然,自然数的 一个子集,也可以很容易写出一个小数: [0,1) 之间的小数与自然 数 N 的所有子集的一一对应关系;
离散数学课件第四章 关系

关系的性质
例 2 (1) A上的全域关系EA,恒等关系IA及空关系都是A 上的对称关系;IA和 同时也是A上的反对称关系. (2)设A={1,2,3},则 R1={<1,1>,<2,2>}既是A上的对称关系,也是A上 的反对称关系; R2= {<1,1>,<1,2>,<2,1>}是对称的,但不是反对 称的; R3 ={<1,2>,<1,3>}是反对称的,但不是对称的; R4= {<1,2>,<2,1>,<1,3>}既不是对称的也不是 反对称的.
❖ 二、关系的表达方式 1. 集合表达式:列出关系中的所有有序对。 例 1 设A={1,2,3,4},试列出下列关系R的元素。 (1) R={<x,y> | x是y的倍数} (2) R={<x,y> | (x-y)2 A } (3) R={<x,y> | x/y是素数}
Discrete Mathematics
关系
第四章 二元关系
第一节 有序对与笛卡尔积
❖ 定义 1 由两个元素x和y(允许x=y)按顺序排列成 的二元组叫做一个有序对,记为<x, y>。
❖ 有序对的性质: 1.当 x ≠ y时,<x, y> ≠ <y, x>。 2.<x, y>=<u, v>的充分必要条件是 x=u且y=v。
Discrete Mathematics
笛卡尔积
❖ 定义 2 设A, B是集合。由A中元素作为第一元素,B 中元素作为第二元素组成的所有有序对的集合,称 为集合A与B的笛卡尔积(或直积),记为A×B。 即 A×B={<x,y>|x A y B}
离散数学第四章

标题 Discrete Mathematical Structures Note Chapter 04主题数学笔记-笛卡尔集和商集•有序对 (a, b)•笛卡尔集- A × B = { (a, b) | a ∈ A 且 b ∈ B }-例: A = { x, y }, B = {1, 2, 3}- A × B = { (x, 1), (x, 2), (x, 3), (y, 1), (y, 2),(y, 3) }•R2 = R × RYX此图可称为笛卡尔坐标系•A1 × A2 × … × A n = {(a1, a2 …, a n) | a i ∈ A , i = 1~n}•商集( 划分 )-A, P = {A1…A k}-满⾜足(1) A1 ∪ A2 ∪ … ∪ A k=A- (2) A i ∩ A j = ∅, i≠j-称P是A的⼀一个划分•例:A = Z, A1 = {m | m ∈ A, m是偶数},A2={m | m ∈ A, m是奇数}-P = Z-A1 = {m | m ∈ Z, m < 0}-A2 = {m | m ∈ N}-P = {A1, A2}-关系•R ≤ A × B, 称R 是从A 到B 上的⼀一个关系•若A =B 称R 是A 上的关系•∀(a, b) ∈ A × B• (a, b) ∈ R, 记做 aRb• (a, b) ∉ R, 记做 aRb •例:A = {x, y}, B = {1, 2, 3}• R = {(x, 1)}• |A × B| = 6• |P(A ×B)| = 26• A × B 称为全关系• (x, 1) ∈ R, xR1• (x, 2) ∈ R, xR1• a | b => a 能被b 整除-关系的定义域•Dom(R) = {a | (a, b) ∈ R} Dom 称为关系的定义域•Ran(R) = {b | (a, b) ∈ R} X 的R 关系集•R(X) = {b | (x, b) ∈ R}•若R 4 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 4), (3, 3), (4, 4)}• R 4(1) = {1, 2, 3, 4}• R 4(2) = {2, 4}• R 4(3) = {3}• R 4(4) = {4}-关系的矩阵• A = {a 1, a 2, …, a m }• B = {b 1,b 2, …, b n }• A × B = {(a i , b j ) | i = 1…m, j = 1~n}•|A × B| = m × n||•|P(A ×B)| = 2m ×n 1•(a i , b j ) ∈ R•(a i , b j ) ∉ R•M R = m ×n •其中“_”的值为0或1,若M R ∈ R 则为1• A = {x, y}, B = {1, 2, 3}•R = {(x, 2), (y, 3)}•MR = -习题4.2 4〜~12(⽼老师有提)-关系的有向图•R 是A 上的关系-顶点-有向边•(a, b) ∈ R, (b, c) ∈ R• -> ->•(b, b) ∈ R•例:A = {1, 2, 3, 4}, 且 aRb <=> a|b(a 能被b 整除)-R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}•背离顶点称出数(度)•指向顶点称进数(度)_,_,…_!_,_,…_⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪0,1,00,0,1⎧⎨⎩⎫⎬⎭①②③④①②③④出度4211-关系的路径(path)•路径R 是A 上的关系•序列π :a, x 1 …… x n-1, b•满⾜足:aRx, x 1Rx 2, …… x n-1Rb, 该π是从a 到b ⻓长度为n 的路径• A = {1, 2, 3, 4, 5}•R = {(1, 2), (2, 2), (2, 3), (2, 4), (2, 5), (4, 3), (5, 1),(5, 4)}•π1: 1, 2, 4•π2: 1, 2, 5 ,1•π3: 2, 2•π4: 1, 2, 2, 3-环:起点和终点相同的路径•恒等环:⻓长度为1的环•xRy: (x, y) ∈ R•xR 2y:从x 到y 有⼀一条⻓长度为2的路径•xR n y:从x 到y 有⼀一条⻓长度为n 的路径•xR ∞y:从x 到y 存在路径-定理:R 是A 上的关系|A|=n•则:(1) M R 2 = M R ⨀ M R• (2) M R n = M R ⨀ … ⨀M R•M R = •M R 2 = M R ⨀ M R 0 1 0 0 0 0 1 1 1 1 0 0 1 0 0 1 0 0 1 0⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟①②③⑤④•= •★此类题过程:(1) 写出R•(2) 写出M R •(3) ⽤用M R 去计算M R 2•(4) 画出R 2的有向图-复合路径(考填空)•π1: 1, 2, 5•π2: 5, 4, 3•π2o π1: 1, 2, 5, 4, 3•π1: a, x 1, … x n-1, b•π2: b, y 1, … y n-1, c•π2o π1: a, x 1, … x n-1, b, y 1, … y n-1, c-关系的性质•⾃自反性•⾃自反关系:∀ a ∈ A 有(a, a)∈R, 称R 是A 上的⾃自反关系• A = {1, 2, 3, 4}•R = {(1, 1), (2, 2), (3, 3), (4, 4)}, ⾃自少包含所有(a, a)-⾮非⾃自反关系•∀ a ∈ A, 有(a, a) ∉ R, 称R 是A 上的⾮非⾃自反关系•R = {(1, 2), (1, 1), (2, 2), (3, 3)}, 为⾮非⾃自反关系,且 为⾮非⾃自反关系•在关系阵中:(1) ⾃自反: m ii = 0 (2) ⾮非⾃自反: m ii = 0•在有向图中:(1) ⾃自反: 所有顶点都是恒等环 (2) ⾮非⾃自反: 有顶点不是恒等环-对称性•对称关系:∀ aRb 有bRa ,则R 是A 上的对称关系•⾮非对称关系:∃ aRb, 有bRa, 称R 是A 上的⾮非对称关系0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 0⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟|、1.2.3.4 制作2014年10⽉月27⽇日 星期⼀一-反对称关系•当a ≠ b 时, aRb 与bRa 不能同时成⽴立•在R 中, aRb 且bRa, 有a = b•如:R = {(1, 2), (4, 4)}-在关系矩阵中•对称矩阵:∀ m ij = 1 有 m ji = 1, 矩阵A 是对称矩阵 <=> A 的转置矩阵 A T = A•⾮非对称矩阵:m ii = 0, 且当m ij = 1有m ji = 0•反对称矩阵:当i ≠ i, ∀ m ij = 1有m ji = 0-在有向图中•对称:任意两个顶点间,要么没有边,要么有2个边,可⽤用下图表⽰示•⾮非对称:所有顶点都不是恒等环, 且任意两点间最多有⼀一边•反对称:任意两点最多有⼀一边-传递性•传递关系:对所有aRb, 且bRc 有aRc•定理:R 是A 上的关系, |A| = n 则R 是A 上的传递关系 <=> R 2 ≤ R•M R 2 = ⨀ = •R 2 = ∅ ≤ R•写出A = {(, ), (, )}•写出M R = ()•M R 2 = M R ⨀ M R•画出R 2的有向图•判断R 是否传递-等价关系•R 是⾃自反对称关系 0 1 0 0 0 0 0 0 0 0 0 0⎛⎝⎜⎜⎞⎠⎟⎟ 0 1 0 0 0 0 0 0 0 0 0 0⎛⎝⎜⎜⎞⎠⎟⎟ 0 0 0 0 0 0 0 0 0 0 0 0⎛⎝⎜⎜⎞⎠⎟⎟ab c•例: A = {1, 2, 3, 4}• R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (3, 4), (4, 3), (4, 4)}•M R = •m 11 = m 22 = m 33 = m 44 = 1, 则R 是⾃自反的•M R T = = M R , 则R 是对称的•M R 2 = M R ⨀ M R = = M R •R 2 = R, R 2 ∈ R, R 是传递的•例:A = Z, aRb <=> a ≣b(mod 2) 3≣5(mod 2)->3除2的余等于5除2的余•∀a ∈Z, a ≣a(mod 2), 则(a, a) ∈ R, ⾃自反•∀aRb, a ≣b(mod 2), b ≣a(mod 2), 则bRa, 对称• ∀aRb, 且bRc, a ≣b(mod 2), b = c(mod 2)有a ≣c(mod 2), 则aRc 传递-定理:P = {A 1, A 2, … A R }, 是A 的⼀一个划分, aRb <=> a 与b 在P 的同⼀一块A 之中, 则R 是A 上的⼀一个等价关系•R = {A 1×A 1∪A 2×A 2∪…∪A k ×A k }•例:A = Z, aRb <=> a ≣b(mod n ), A = {1, 2, 3, 4}, P = {{1, 2}, {3, 4}}, R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (4, 3), (4, 4)}•★等价类: R 是等价关系(P 147,21)•若R(x) = {b | (x, b) ∈ R}, 则称R(x)是x 的等价类•如R = {(1, 1), (1, 2), (2, 1), (2 ,2)}•R(1) = {1 ,2}1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟ 1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟ 1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟•R(2) = {1, 2}-定理:R是A上的等价关系, P = {R(a) | a ∈ A}, 则P是A上的⼀一个划分,记做A/R •满⾜足:(1) a∈A 的所有并集, R(a) = A• (2)。
[离散数学]第四章
![[离散数学]第四章](https://img.taocdn.com/s3/m/3e1ea8ab970590c69ec3d5bbfd0a79563c1ed418.png)
第四章代数代数又称为代数结构或代数系统,是用代数方法构造的数学模型。
代数系统对于研究各种数学问题和许多实际问题是很有用的,对计算机科学研究也有很大的实用意义,例如,在程序设计语言的语义研究中,数据结构的研究中,编码理论的研究中,系统生成与结构,语言代数,计算理论以及逻辑电路设计中均有重要的理论和实际意义。
§4.1 一般代数结构这一节开始讨论系统及系统的结构。
第一章与第二章着重讨论了一些集合,一般来讲,不论是什么系统,都是若干个集合按一定的条件构成。
构成的条件可以用列举法给出,更多的是由命题法和归纳法给出。
如果结出的若干个集合不是一些具体的集合,这些不具体的集合概念完全由命题来决定通用的概念,则这种构成系统的方法称为公理的方法。
所以这一节还有一个任务是向公理方法过渡。
4.1.1 代数运算关系是集合,函数是关系,函数是“单值”的关系也是集合。
下面定义的代数运算是一个特殊的函数。
定义4.1.1设X为非空集合,n∈I+,n→称为X上的n元运算,其中n为运算ω的阶(类型),记为n ω。
①函数ω:X X②X中的每一个元素称为X上的0元运算。
当n ω=1时,称ω为一元运算,例如实数集合R上的“负”运算;当n ω=2时,称ω为二元运算,例如R上的“+”和“*”运算。
二元运算在许多方面的研究中有着重要的意义,在后面二元运算用一个字母θ来表示。
实际上用的0元运算只是集合X中的某些特定的元素,例如R中的0和1。
在上一节中所定义的运算是一元运算。
由定义可以看出,所谓集合X上的n元运算,乃是指某种规则,对于X上的每一个n元序偶,规定了X中唯一的元素与之对应。
,,...,∈S,都有ω定义4.1.2设ω为X上的n元运算,S∈X,如果对于任意a a a n12,,...,‡)∈S,则称S关于ω封闭的。
(†a a a n12例如,考察自然数集合N上的加法运算“+”,显然非负偶数集合关于“+”是封闭的,但非负奇数关于“+”是不封闭的。
离散数学 第四章

f g
§2逆函数和复合函数
《定理》:函数的复合运算是可结合的,即如果f,g,h 均为函数,则有:
h ( g f ) (h g ) f
证明:函数也是一种二元关系, ∵二元关系的复合是满足结合律的, ∴函数的复合也是满足结合律的。
§2逆函数和复合函数
例:设 I
是负整数集合,定义二个双射函数f和g, f(x)= - x ={<-1,1><-2,2>…}, g(x)= x-1={<1,0><2,1>…},
f : I I
( f ( x)) (( x) 1) { 1,0 2,1 }
§2逆函数和复合函数
《定理》:若f是一双射函数,则 ( f 1 ) 1 f 证明:设任一 x, y f
y, x f 1
则
x, y ( f 1 ) 1 f
《定理》:设f: X→Y和g:Y→Z,且f和g均为双射函数,则有
( g f ) 1 f 1 g 1
(3)一个函数的反函数如果存在的话,则此函数一定是双 射函数,而入射,满射函数的逆关系均不满足函数的定义.
(4)为了和逆关系相区别,函数f的 “逆函数” 用1 来表示 f
1 f : X Y 是一双射函数,称 f : Y X 《定义》:设
为f的逆函数。 《定理》:如果f: X→Y是双射函数,则有: 1 : Y X f
§2逆函数和复合函数
《定理》:设f:X→Y和g:Y→Z是二个函数,于是复合函数
g f 是一个从X到Z的函数,对于每一个 x X 有:
( g f )( x) g ( f ( x))
证明:由定义可知 g f 是从X→Z的函数,即
离散数学第四章课件

无对称的偶对。
表示关系矩阵的主对角线两侧各有一个1且 对称,即有一个对称的偶对。
C1
n(n+1) 2
n(n+1) C 2 n(n+1) 2
表示关系矩阵的主对角线两侧全为1,
C1 + n(n+ +…+ 2
n(n+1) C 2 n(n+1) 2
于是
C0 n(n+1) 2 =
2
n(n+1) 2
四、反对称性 ⒈ 定义: 若xy(x∈A∧y∈A∧xRy∧yRx→x=y), 称R是反对称的。 例:设A={ a , b , c , d } R={ < a , b > , < a , c > , < b , b > , <b,d>,<c,c>,<c,d>, < d , d >}
⒉自反关系的关系矩阵的特征
R的关系矩阵的主对角线上的元素均为
1 ,则该关系就不具有自反性;
主对角线上有一个元素不为1,则该关
系就不具有自反性。
⒊ 自反关系的图的特征 自反关系的关系图中,每个顶点都有 自回路,则该关系具有自反性。
二、反自反性 ⒈ 定义:若x(x∈A xRx)则该关系是 反自反的。 ⒉ 具有反自反性的关系的关系矩阵的主对角
2 t1× t2 × … ×tn
五、关系的表示法-----通常有三种表示方法
⒈ 集合表示法: 因为关系也是集合,所以也可以用集合 的表示方法
例:A={ 2, 3,4,6 ,9,12 }上的整除关系
用特征描述法表示为
R={ < x , y > | x∈A ∧ y∈A ∧ x|y }
用穷举法表示为
R={ < 2 , 2 > , < 2 , 4 > , < 2 , 6 > ,
离散数学课件-第4章

哈塞图( Hasse 图)
我们可以使用下面的过程表示一个有穷集上的偏序。 从这个关系的有向图开始: (1)自反性:每个顶点都有自回路,省去。 (2)反对称性:两个顶点间只可能有一个箭头从左→ 右,或从下→上的方向从小到大安置顶点,可省略箭头。 (3)传递性:由于有(a,b),(b,c)∈R 则(a,c) ∈R 故只画(a,b),(b,c)对应的边,省略边(a,c)。
单击此处添加大标题内容
【example 10】 考虑小写英语字母串构成的集合。使用在字母表中的字母序,可以构成在串的集合上的字典顺序。 如果两个串第一次出现不同字母时,第一个串的字母先于第二个字母,或者如果第一个串和第二个串在所有的位都相同,但是第二个串有更多的字母,那么,第一个串小于第二个串。这种排序和字典使用的排序相同。例如 discreet < discrete 因为这两个串在第7位首次出现字母,并且 e< t. discreet < discreetness 因为这两个串前8个字母相同,但是第二个串更长。此外 discrete < discretion
添加标题
类似地,偏序集的一个元素叫做极小的,如果它不大于这个偏序集的任何其他元素。即a在偏序集(S, ≼ )中是极小的,如果不存在b∈S使得b<a。
【example 8】确定在偏序集(Z×Z,≼ )中是否有 (3, 5) < (4,8), (3,8)<(4,5) 和(4,9) <(4,11) ? 这里的≼ 是从Z上通常的≤关系构造的字典顺序。 Solution: 因为3<4,故而(3, 5) < (4,8), 且(3,8)<(4,5) 。因为(4,9)与(4,11) 的第一元素相同,但9<11,我们有(4,9) <(4,11) 。 下图明显地显示了Z+×Z+ 中比(3,4)小的有序对的集合。
离散数学第四章(第5讲)

例 设集合A = { a , b , c , d , e} , R 是A 上的偏序关系。
R = { < a , a > < a , b > < a , c > < a , d >< a , e > < b , b > < b , c> < b , e > < c , c > <c , e > < d , d > < d , e > < e , e >} ,求 盖住集COV A。
解: IA = { < a , a > < b , b > < c , c > < d , d> < e , e >}
R1 = R - IA = { < a , b > < a , c > < a , d >< a , e > < b , c >
< b , e > < c , e > < d , e >}
例:设A={2,3,4 , 6,8},则定义在A上的整除关系 R={<2,2><3,3><4,4><6,6><8,8><2,4><2,6> <2,8><3,6><4,8>},求COV A
解: IA = {<2,2><3,3><4,4><6,6><8,8>}
离散数学第四章

2018/10/27
4
初等代数学是指19世纪上半叶以前发展的方程理论,主要研究某 一方程(组)是否可解,如何求出方程所有的根(包括近似根), 以及方程的根有何性质等问题。 抽象代数学对于全部现代数学和一些其他科学领域都有重要的影 响。抽象代数的主要研究内容是研究各种代数结构, 它是在从较高 层次上, 撇开形式上很不相似的代数结构的个性, 抽象出其共性, 用统一的方法描述、研究与推理, 从而得到一些反映事物本质的结 论, 再把它们应用到那些系统中去。由于代数结构中运算个数以及 对运算要求的性质的不同, 从而产生了各种各样的代数结构, 这就 形成了抽象代数的不同分支, 其中最基本、最重要的分支是群、环 和域, 这也是离散数学课程抽象代数部分的重要研究内容 。
7
4.1 运算
定义1 设有非空集合A,函数f:An→A称为A上的一
个 n 元运算。特别,函数 f:A2 →A称为A上 的二元运算, f:A →A 称为A上的一元运算 。 例1 设有函数 f:N2 →N ,对于任意 (n1, n2)N2, f(n1,n2)=n1+n2 f(5,3)=8, f(3,5)=8, f(3,9)=12
。
求倒数的运算不能看作实数集R上的一元运算。
2018/10/27 9
例4 集合的并、交运算可以看作是全集合U的幂集2U
上的二元运算。求补集的运算可看作是2U上的一元运算。 对任意Si,Sj2U,
(Si , S j ) Si S j
(Si , S j ) Si S j
对任意Si2U , ( Si ) Si
本章在集合、关系和函数等概念基础上,研究更为复 杂的对象——代数系统,研究代数系统的性质和特殊的元 素,代数系统与代数系统之间的关系。如代数系统的同态、
离散数学_第_4_章习题解答讲解

第四章归结法原理习题与解答1. 用归结法证明:(1)(2)(3)(4)(5)(6)解(1) 首先将p→q,p→r,¬(p→q∧r)化为合取范式。
p→q⇔¬p∨qp→r⇔¬p∨r¬(p→q∧r)⇔¬(¬p∨(q∧r))⇔p∧(¬q∨¬r) 给出子句集{¬p∨q,¬p∨r,p,¬q∨¬r}的反驳如下。
⑴ ¬p∨q⑵ ¬p∨r⑶ p⑷ ¬q∨¬r⑸ q 由⑴和⑶由⑵和⑶⑹ r⑺ ¬r 由⑷和⑸⑻ □ 由⑹和⑺因此,p→q,p→r|=p→q∧r(2) 首先将p→r,q→r,¬(p∨q→r)化为合取范式。
p→r⇔¬p∨rq→r⇔¬q∨r¬(p∨q→r)⇔(p∨q)∧¬r给出子句集{¬p∨r,¬q∨r,p∨q,¬r}的反驳如下。
⑴ ¬p∨r⑵ ¬q∨r⑶ p∨q⑷ ¬r⑸ q∨r 由⑴和⑶ p→q,p→r|=p→q∧r p→r,q→r|=p∨q→r p→q∨r|=(p→q)→(p→r)p∧q→r|=(p→r)∨(q→r) p∨q∨r,p→r|=q∨r (p→q)→(p→r)|=p→(q→r)由⑵和⑸⑹ r⑺ □由⑷和⑹因此,p→r,q→r|=p∨q→r(3) 首先将p→q∨r,¬((p→q)∨(p→r))化为合取范式。
p→q∨r⇔¬p∨q∨r¬((p→q)∨(p→r))⇔¬((¬p∨q)∨(¬p∨r))⇔p∧¬q∧¬r 给出子句集{¬p∨q∨r,p,¬q,¬r}的反驳如下。
⑴ ¬p∨q∨r⑵ p⑶ ¬q⑷ ¬r⑸ q∨r 由⑴和⑵⑹ r 由⑶和⑸⑺ □ 由⑷和⑹因此,p→q∨r|=(p→q)∨(p→r)(4) 首先将p∧q→r,¬((p→r)∨(q→r))化为合取范式。
自考离散数学第4章

4.1 代数系统
定义4.1.8 设V=<S,f1,f2,...,fk>是代数系统,B S,且B对f1,f2,...,fk都是封闭的, B和S还含有相同的代数常数,则称<B,f1,f2,...,fk>是V的子代数系统,简称子 代数。
因为b=b,d=b2,a=b3.c=b4,e=b5,生成元为b;
因为c=c,a=c2,d=c3.b=c4,e=c5,生成元为c;
例:设A={a,b,c,d},*为A上的二元运算,
*
a
b
c
d
a
a
b
c
d
b
b
d
a
c
c
c
a
b
b
d
d
a
c
d
可以看出a为单位元。由a*a=a,b*c=a,c*b=a,d*b=a,
故a有逆元a;b有左逆元c,d;c有左逆元b;b有右逆元c;c有右逆元b;d有 右逆元b。其中b是c的逆元,c是b的逆元。
一个元素的左逆元不一定等于它的右逆元,而且一个元素可以有左(右)逆元 而没有右(左)逆元。一个元素的左右逆元也不一定是唯一的。
*
e
a
b
c
e
e
a
b
c
a
a
e
c
b
b
b
c
e
a
c
c
b
a
e
验证<G,*>是一个群。
解:*运算容易验证是可结合的,e是G中的单位元,对任意x G,x-1=x。G 关于*运算,构成一个群,这个群称作Klein四元群。
离散数学04

例题 n元谓词的符号化
例4.5 将下列命题符号化 (1)兔子比乌龟跑得快。 (2)有的兔子比所有的乌龟跑得快。 (3)并不是所有的兔子都比乌龟跑得快。 (4)不存在跑得同样快的两只兔子。
解:令 F(x):x是兔子, G(y):y是乌龟, H(x,y):x比y跑得快, L(x,y):x与y跑得同样快。
(1) “凡人都呼吸”应符号化为 x(M(x)→F(x))
(2) “有的人用左手写字”符号化为 x(M(x)∧G(x))
在使用全总个体域时,要将人从其他事物中区别出来,为此 结 引进了谓词M(x),称为特性谓词。 论 同一命题在不同的个体域中符号化的形式可能不同。
思考:在全总个体域中,能否将(1)符号化为 x(M(x)∧F(x))? 能否将15(2)符号化为x(M(x)→G(x))?
定义4.4 一阶语言F的合式公式定义如下:
(1) 原子公式是合式公式。
(2) 若A是合式公式,则(┐A)也是合式公式。
(3) 若A,B是合式公式,则(A∧B),(A∨B),(A→B),(AB) 也是合式公式。
(4) 若A是合式公式,则xA,xA也是合式公式。
(5) 只有有限次的应用(1)~(4)构成的符号串才是合式公式。
11
量词及相关概念
量词(quantifiers)是表示个体常项或个体变项之间数量关 系的词。
1. 全称量词:符号化为“”
日常生活和数学中所用的“一切的”、“所有的”、“每一 个”、“任意的”、“凡”、“都”等词可统称为全称量词 。
x表示个体域里的所有个体,xF(x)表示个体域里所有个体 都有性质F。
命题真值为假。 (2)有的人登上过月球。
令G(x):x登上过月球, M(x):x是人。命题符号化为 x(M(x)∧G(x))。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以(x)(P(x)∧Q(x))来描述是不可行的
取值与论域有关
总结:“所有的……都是……”,这类语句的形
式描述只能使用而不能使用∧
4.4.2 “有的实数是有理数”的形式化
翻译:存在一事物它是实数,而且是有理数.
判断一个公式是否为合式公式
合式公式 p, P(x,y)∨Q(x,y), (x)(A(x)B(x)), (x)(A(x)(y)B(x,y)) 非合式公式 (x)F(x)∧G(x), 违反第3条 (x)((x)F(x)), 违反第4条 (x)P(y), 违反第4条
4.4 自然语句的形式化
量词的运算优先级高于逻辑联结词
存在量词
举例 “有的事物是动物”
这命题中“有的”就是表示个体变元数量的词,“有的”的等义于 “存在” 形式化:(x)Q(x), 其中Q(x)表示x是动物
符号: (x)读作至少有一个x或存在一个x或有某
些x.所约束的变元是x
定义: 命题(x)Q(x)当且仅当在论域中至少有一个x0, Q(x0)为真时方为真.这就是存在量词的定义 性质: (x)Q(x)=F成立, 当且仅当对所有的x0D, 使Q(x0)=F 注意(x)(P(x)Q(x)) (x)P(x)Q(x)
这命题中的“凡”就是表示个体变元数量的词, 个体x的论域是包含一切事物的集合, 形式化:(x)P(x)
符号: (x)读作所有的x或任一x,一切x.所约束的个 体是x 定义: 命题(x)P(x)当且仅当对论域中的所有x来说, P(x)均为真时方为真. 性质: (x)P(x)=F成立, 当且仅当有一个x0D, 使P(x0) =F 注意(x)(P(x)Q(x)) (x)P(x)Q(x)
举例
“张三和李四是表兄弟”. “5大于3”. “张三比李四高”. “天津位于北京的东南”. “A在B上”. 其中“是表兄弟”是谓词. 其中“大于”是谓词. 其中“比……高”是谓词. 其中“位于……东南”是谓词. 其中“在……上”是谓词.
4.1.2 个体词
个体词(主词)
个体词是一个命题里表示思维对象的词 P(张三)中的张三是个体词或称个体常项 谓词P(x)中的变量x为个体变项或个体变元 有n个个体的谓词P(x1,…,xn)称n项(目、元)谓词 如果P是已赋有确定含义的谓词,就称为谓词常项 如果P表示任一谓词时,就称为谓词变项
n项(目、元)谓词
个体域
将个体变项的变化范围称为个体域或论域,以D表示 论域是重要的概念,同一谓词在不同论域下的描述形式可能不同,所取的真假 值也可能不同
约定
谓词逻辑的个体域除明确指明外,都认为是包括一切事物的一个最广的集合 谓词变项的变化范围,不做特别声明时,指一切关系或一切性质的集合
联结词可照搬 有的等值式推理式也可移植 但个体变元,谓词、量词等新概念,特别是个体论域常是无限 域,加大了处理难度 最简单又深刻的例子 在命题逻辑里一个公式不难判定它是否是重言式,真值表法是 能行的方法.然而在谓词逻辑里就没有一般的能行算法来判定 任一公式是不是普遍有效的(或称定理、永真式)
4.2 函数和量词 4.2.1 函数
以P(x)表示x是有理数,Q(x)表示x是实数,这句话
的形式描述应为
(x)(P(x)∧Q(x))
其真值与论域有关
设论域D中没有有理数,如D1={e,∏,张三,桌子},则为假 仅当论语D中包含有理数时方为真
若以(x)(Q(x)P(x))来描述,则在D1中也为真,错误
量词的辖域
量词所约束的范围称为量词的辖域.如
(x)R(x, y)中,R(x, y)是(x)的辖域 (x)((y)P(x, y))中,P(x, y)是(y)的辖域, (y)P(x, y)是(x)的 辖域
命题形式P(x), 在P确定为某个谓词常项时, 如P(x)表示x 是自然数, 如何化为命题?
约定函数符号用小写字母表示,如f,g,father,…
4.2.2 量词
用来表示个体数量的词是量词 可看作是对个体词所加的限制、约束的词
不是对数量的具体描述 是讨论两个最通用的数量限制词: “所有的”VS.“至少有一个”, “全称量词” VS. “存在量词”。
全称量词
举例 “凡事物都是运动的”
使用计算机来处理由自然语句或非形式化陈述的问题, 首要的工作是问题本身的形式描述 使用谓词逻辑描述以自然语句表达的问题,首先要将 问题分解成一些原子谓词,引入谓词符号,进而使用 量词、函数、联结词来构成合式公式
4.4.1 “所有的有理数都是实数”的形式 化
翻译:对任一x而言,如果x是有理数,那么x是实
命题逻辑的局限性
举例:凡有理数都是实数,2/7是有理数,所以2/7是实数
直观上看这样的推理应该是正确的。然而在命题逻辑里就不能描述 这种推理 设这三个命题分别以p, q, r表示,相应的推理形式为:(p q) r。由于对任意的p,q,r来说这推理形式并非重言式,也就是说这 个推理形式不是正确的 对这样的人们熟知的推理关系在命题逻辑中得不到正确的描述,自 然是命题逻辑的局限性
数
以P(x)表示x是有理数,Q(x)表示x是实数,则有 (x)(P(x)Q(x))
因为x的论域是一切事物的集合,所以x是有理数是 一个条件
当P(x)与Q(x)为此例中的谓词常项时,(x)(P(x)Q(x)) 的真值与论域无关
若D1含有有理数也含有非有理数,例如D1={1/2, ∏, 张三, 桌子}, 该式恒成立
例 张三是学生.李四是学生.
在命题逻辑里,这是两个不同的命题,只能分别以两个不同的 符号如p,q表示 然而这两个命题的共同点是,它们都有主词和谓词
主词“张三”、“李四”是不同的,而谓词“是学生”是相同的
现在强调它们的共同点.若以大写符号P表示“是学生”,这 样两个命题的共同性可由P来体现了,但主词还需区别开来, 便可把这两个命题分别写成P(张三) 和P(李四)
变元易名规则
变元易名规则:
(x)P(x)= (y)P(y) (x)(P(x)Q(x,y))≠(y)(P(y)Q(y,y))
4.3 合式公式
目的
限定所讨论的命题形式的范围 需考虑个体词、量词 限定在量词仅作用于个体变元 不允许量词作用于命题变项和谓词变项 也不讨论谓词的谓词 例如:不考虑下述公式 (p)(Q(x)p),量词作用于命题p (Q)(x)(Q(x)P(x)),量词作用于谓词Q(x) P(x,Q(y)),谓词的谓词
要认识这种推理规律,只有对简单命题做进一步剖析。这就需要 引入谓词、变量以及表示变量数量的量词(全称量词和存在量词, 分别表示一般的和个别的情况) ,进而研究它们的形式结构和逻 辑关系,这便构成了谓词逻辑
说明
约定
小写字母表示命题 大写字母表示谓词
内容仅限于一阶谓词逻辑或称狭谓词逻辑
4.1 谓词和个体词 4.1.1 谓词
明显地描述了这两个命题的共同点和不同点 一般地可引入变量x来表示主词,于是符号P(x)就表示“x是学 生”.通常把P(x)称作谓词
谓词描述性定义
一元谓词
在一个命题里,如果主词只有一个,这时表示该主词性质或属性的 词便称作谓词.这是一元(目)谓词,以P(x),Q(x),…表示
多元谓词
在一个命题里,如果主词多于一个,那么表示这几个主词间的关系 的词称作谓词.这是多元谓词,以P(x, y),Q(x, y),R(x, y, z), … 表示.
谓词的真值依赖于个体变元的论域
4.1.4 谓词逻辑与命题逻辑
可认为谓词逻辑是命题逻辑的推广,命题逻辑是谓词逻 辑的特殊情形
因为任一命题都可通过引入具有相应含义的谓词(个体词视为常 项)来表示 或认为一个命题是没有个体变元的零元谓词
命题逻辑中的很多概念、规则都可推广到谓词逻辑中延 用
关注一阶谓词逻辑,而不是高阶谓词逻辑
符号约定
命题变项:p, q, r, … 个体变项:x, y, z, … 个体常项:a, b, c, … 或者大写英文单词 谓词变项:P, Q, R, … 谓词常项:大写英文字母, 如GREAT 函数:f, g, … 或者小写英文单词 五个联结词:﹁, ∧, ∨, , 两个量词:, 括号:( )
个体变元x取为个体常项。如:P(2)=T是命题 将x量化。即(x)P(x)或者(x)P(x)都是命题
(x)P(x)表示论域D上任一x, x都是自然数 (x)P(x) = F (x)P(x)表示论域D上有一x, x是自然数
(x)P(x) = T 考虑命题形式P(x,y)如何用量化的方法化为命题?
4.2.3 约束变元和自由变元
在含有量词的命题形式里,必须区分个体词受量词的 约束还是不受量词的约束 若P(x)表示x是有理数,这时的变元x不受任何量词约束, 便称是自由的. (x)P(x)中的两处出现的变元x都受量词的约束,便 称作约束变元,或称被量词量化了的变元 命题形式(x)P(x)Q(y)中,变元x是约束的,而变元y 是自由的
在谓词逻辑中出现变量,自然也会考虑引入函数
函数是某个体域(不必是实数)到另一个体域的映射 不同于谓词:将个体映射为真假值 函数并不单独使用,是嵌入在谓词中
