全等三角形辅助线专业题材
全等三角形常见五种辅助线添法专训(学生版)

全等三角形常见五种辅助线添法专训【目录】辅助线添法一 倍长中线法辅助线添法二 截长补短法辅助线添法三 旋转法辅助线添法四 作平行线法辅助线添法五 作垂线法【经典例题一倍长中线法】【模型解读】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.【常见模型】1(2023春·吉林·八年级校考阶段练习)【阅读理解】数学兴趣小组活动时,老师提出如下问题:如图1,在△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明提出了如下解决方法,延长线段AD至点E,使DE=AD,连接BE.请根据小明的方法回答下列问题.(1)由已知和作图能得到△ADC≌△EDB的理由是.A.SSSB.SASC.AASD.HL(2)探究得出AD的取值范围.A.6<AD<8B.6≤AD≤8C.1<AD<7D.1≤AD≤7【问题解决】(3)如图2,在△ABC中,CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE.【变式训练】1(2022秋·甘肃庆阳·八年级校考期末)小明遇到这样一个问题,如图1,△ABC中,AB=7,AC=5,点D为BC的中点,求AD的取值范围.小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≅△CAD,经过推理和计算使问题得到解决.请回答:(1)小明证明△BED≅△CAD用到的判定定理是:(用字母表示);(2)AD的取值范围是;(3)小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.参考小明思考问题的方法,解决问题:如图3,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB= AC.2(2023·江苏·八年级假期作业)(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接CE.①证明△ABD≌△ECD;②若AB=5,AC=3,设AD=x,可得x的取值范围是;(2)如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF.3(2023·江苏·八年级假期作业)【观察发现】如图①,△ABC 中,AB =7,AC =5,点D 为BC 的中点,求AD 的取值范围.小明的解法如下:延长AD 到点E ,使DE =AD ,连接CE .在△ABD 与△ECD 中BD =DC∠ADB =∠EDCAD =DE∴△ABD ≅△ECD (SAS )∴AB =.又∵在△AEC 中EC -AC <AE <EC +AC ,而AB =EC =7,AC =5,∴<AE <.又∵AE =2AD .∴<AD <.【探索应用】如图②,AB ∥CD ,AB =25,CD =8,点E 为BC 的中点,∠DFE =∠BAE ,求DF 的长为.(直接写答案)【应用拓展】如图③,∠BAC =60°,∠CDE =120°,AB =AC ,DC =DE ,连接BE ,P 为BE 的中点,求证:AP ⊥DP .【经典例题二截长补短法】【模型分析】截长补短的方法适用于求证线段的和差倍分关系.截长:指在长线段中截取一段等于已知线段;补短:指将短线段延长,延长部分等于已知线段.该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程,截长补短法(往往需证2次全等).【模型图示】(1)截长:在较长线段上截取一段等于某一短线段,再证剩下的那一段等于另一短线段.例:如图,求证BE+DC=AD方法:①在AD上取一点F,使得AF=BE,证DF=DC;②在AD上取一点F,使DF=DC,证AF=BE (2)补短:将短线段延长,证与长线段相等例:如图,求证BE+DC=AD方法:①延长DC至点M处,使CM=BE,证DM=AD;②延长DC至点M处,使DM=AD,证CM=BE1(2023·江苏·八年级假期作业)把两个全等的直角三角形的斜边重合,组成一个四边形ACBD以D为顶点作∠MDN,交边AC、BC于M、N.(1)若∠ACD=30°,∠MDN=60°,∠MDN两边分别交AC、BC于点M、N,AM、MN、BN三条线段之间有何种数量关系?证明你的结论;(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?证明你的结论;(3)如图③,在(2)的条件下,若将M、N改在CA、BC的延长线上,完成图3,其余条件不变,则AM、MN、BN之间有何数量关系(直接写出结论,不必证明)【变式训练】1(2023·江苏·八年级假期作业)已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.(1)求∠AFC的度数;(2)若AD=6,CE=4,求AC的长.2(2023·江苏·八年级假期作业)在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.(1)如图②,当∠C≠90°,AD为△ABC的角平分线时,线段AB,AC,CD之间又有怎样的数量关系?不需要说明理由,请直接写出你的猜想.(2)如图③,当∠ACB≠90°,AD为△ABC的外角平分线时,线段AB,AC,CD之间又有怎样的数量关系?请写出你的猜想,并对你的猜想进行说明.3(2023·江苏·八年级假期作业)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=12∠BAD.(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由.(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.【经典例题三旋转法】【模型分析】旋转:将包含一条短边的图形旋转,使两短边构成一条边,证与长边相等.注:旋转需要特定条件(两个图形的短边共线),该方法常在半角模型中使用.【模型图示】例:如图,已知AB=AC,∠ABM=∠CAN=90°,求证BM+CN=MN方法:旋转△ABM至△ACF处,证NE=MN1(2022秋·湖北孝感·八年级统考期中)已知:△ABC≌△DEC,∠ACB=90°,∠B=32°.(1)如图1当点D在AB上,∠ACD.(2)如图2猜想△BDC与△ACE的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)【变式训练】1(2023春·全国·八年级专题练习)(1)如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系,并说明理由;(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF= 1∠BAD,此时(1)中的结论是否仍然成立?请说明理由.22(2021秋·天津和平·八年级校考期中)在△BAC中,∠BAC=90°,AB=AC,AE是过A的一条直线,BD⊥AE于点D,CE⊥AE于E,(1)如图(1)所示,若B,C在AE的异侧,易得BD与DE,CE的关系是DE=;(2)若直线AE绕点A旋转到图(2)位置时,(BD<CE),其余条件不变,问BD与DE,CE的关系如何?请予以证明;(3)若直AE绕点A旋转到图(3)的位置,(BD>CE),问BD与DE,CE的关系如何?请直接写出结果,不需证明.3(2021秋·河南周口·八年级统考期末)在Rt△ABC中,∠ACB=90°,CA=CB,点D是直线AB上的一点,连接CD,将线段CD绕点C逆时针旋转90°,得到线段CE,连接EB.(1)操作发现如图1,当点D在线段AB上时,请你直接写出AB与BE的位置关系为;线段BD、AB、EB的数量关系为;(2)猜想论证当点D在直线AB上运动时,如图2,是点D在射线AB上,如图3,是点D在射线BA上,请你写出这两种情况下,线段BD、AB、EB的数量关系,并对图2的结论进行证明;(3)拓展延伸若AB=5,BD=7,请你直接写出△ADE的面积.【经典例题四作平行线法】2(2022秋·江苏·八年级专题练习)如图所示:△ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD=CE,连接DE交BC于点M.求让:MD=ME【变式训练】4(2022秋·江苏·八年级专题练习)P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA =CQ,连PQ交AC边于D.(1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.5(2022秋·八年级课时练习)读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DB上,且∠BAE=∠CDE,求证:AB=CD分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证明AB =CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明.图(1):延长DE到F使得EF=DE图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F图(3):过C点作CF∥AB交DE的延长线于F.6(2023春·全国·七年级专题练习)已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M.请探究:(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;(3)如图(3),当点E在CA的延长线上,点D在线段AB上(点D不与A,B重合),DE所在直线与直线BC交于点M,若CE=2BD,请直接写出线段MD与线段ME的数量关系.【经典例题五作垂直法】1(2022秋·湖北武汉·八年级统考期中)我们定义:三角形一个内角的平分线所在的直线与另一个内角相邻的外角的平分线相交所成的锐角称为该三角形第三个内角的遥望角.(1)如图1,∠E是△ABC中∠A的遥望角.①直接写出∠E与∠A的数量关系;②连接AE,猜想∠BAE与∠CAE的数量关系,并说明理由.(2)如图2,四边形ABCD中,∠ABC=∠ADC=90°,点E在BD的延长线上,连CE,若已知DE=DC =AD,求证:∠BEC是△ABC中∠BAC的遥望角.【变式训练】1(2022秋·八年级课时练习)如图1,已知四边形ABCD,连接AC,其中AD⊥AC,BC⊥AC,AC =BC,延长CA到点E,使得AE=AD,点F为AB上一点,连接FE、FD,FD交AC于点G.(1)求证:△EAF≌△DAF;(2)如图2,连接CF,若EF=FC,求∠DCF的度数.已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠CDE.求证:AB=CD.分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.①如图1,延长DE到点F,使EF=DE,连接BF;②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G.(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.求证:AB=CD.分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形请用二种不同的方法证明.【重难点训练】4(2023·江苏·八年级假期作业)如图,AD为△ABC中BC边上的中线(AB>AC).(1)求证:AB-AC<2AD<AB+AC;(2)若AB=8cm,AC=5cm,求AD的取值范围.5(2023·江苏·八年级假期作业)如图1,在△ABC中,若AB=10,BC=8,求AC边上的中线BD的取值范围.(1)小聪同学是这样思考的:延长BD至E,使DE=BD,连接CE,可证得△CED≌△ABD.①请证明△CED≌△ABD;②中线BD的取值范围是.(2)问题拓展:如图2,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中,AB=BM,BC=BN,∠ABM=∠NBC=∠90°,连接MN.请写出BD与MN的数量关系,并说明理由.6(2023春·全国·七年级专题练习)【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:如图2,延长AD到点E,使DE=AD,连接BE.请根据小明的方法思考:(1)如图2,由已知和作图能得到△ADC≌△EDB的理由是.A.SSSB.SASC.AASD.ASA(2)如图2,AD长的取值范围是.A.6<AD<8B.6≤AD≤8C.1<AD<7D.1≤AD≤7【感悟】解题时,条件中若出现“中点”、“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论转化到同一个三角形中.【问题解决】(3)如图3,AD是△ABC的中线,BE交AC于点E,交AD于F,且AE=EF.求证:AC=BF.7(2023·江苏·八年级假期作业)(1)如图1,已知△ABC中,AD是中线,求证:AB+AC>2AD;(2)如图2,在△ABC中,D,E是BC的三等分点,求证:AB+AC>AD+AE;(3)如图3,在△ABC中,D,E在边BC上,且BD=CE.求证:AB+AC>AD+AE.8(2023·江苏·八年级假期作业)课堂上,老师提出了这样一个问题:如图1,在△ABC中,AD平分∠BAC交BC于点D,且AB+BD=AC,求证:∠ABC=2∠ACB,小明的方法是:如图2,在AC上截取AE,使AE=AB,连接DE,构造全等三角形来证明.(1)小天提出,如果把小明的方法叫做“截长法”,那么还可以用“补短法”通过延长线段AB构造全等三角形进行证明.辅助线的画法是:延长AB至F,使BF=,连接DF请补全小天提出的辅助线的画法,并在图1中画出相应的辅助线;(2)小芸通过探究,将老师所给的问题做了进一步的拓展,给同学们提出了如下的问题:如图3,点D在△ABC的内部,AD,BD,CD分别平分∠BAC,∠ABC,∠ACB,且AB+BD=AC.求证:∠ABC=2∠ACB.请你解答小芸提出的这个问题(书写证明过程);(3)小东将老师所给问题中的一个条件和结论进行交换,得到的命题如下:如果在△ABC中,∠ABC=2∠ACB,点D在边BC上,AB+BD=AC,那么AD平分∠BAC小东判断这个命题也是真命题,老师说小东的判断是正确的.请你利用图4对这个命题进行证明.9(2023春·江苏·八年级专题练习)如图,在锐角ΔABC中,∠A=60°,点D,E分别是边AB,AC上一动点,连接BE交直线CD于点F.(1)如图1,若AB>AC,且BD=CE,∠BCD=∠CBE,求∠CFE的度数;(2)如图2,若AB=AC,且BD=AE,在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM,连接MF,点N是MF的中点,连接CN.在点D,E运动过程中,猜想线段BF,CF,CN之间存在的数量关系,并证明你的猜想.10(2023·江苏·八年级假期作业)问题背景:如图1:在四边形ABCD中,AB=AD.∠BAD=120°.∠B=∠ADC=90°.E,F分别是BC.CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.(1)小王同学探究此问题的方法是:延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(直接写结论,不需证明)探索延伸:(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠ADF=180°.E,F分别是BC,CD上的点,且∠EAF=12∠BAD,(1)中结论是否仍然成立,并说明理由;(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=12∠BAD,(1)中的结论是否仍然成立?若成立,请证明:若不成立,请直接写出它们之间的数量关系.11(2023·全国·九年级专题练习)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=12∠BAD,线段EF、BE、FD之间的关系是;(不需要证明)(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=12∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=12∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.12(2023春·全国·七年级期末)(1)问题引入:如图1,点F是正方形ABCD边CD上一点,连接AF,将△ADF绕点A顺时针旋转90°与△ABG重合(D与B重合,F与G重合,此时点G,B,C在一条直线上),∠GAF的平分线交BC于点E,连接EF,判断线段EF与GE之间有怎样的数量关系,并说明理由.(2)知识迁移:如图2,在四边形ABCD中,∠ADC+∠B=180°,AB=AD,E,F分别是边BC,CD延长线上的点,连接AE,AF,且∠BAD=2∠EAF,试写出线段BE,EF,DF之间的数量关系,并说明理由.(3)实践创新:如图3,在四边形ABCD中,∠ABC=90°,AC平分∠DAB,点E在AB上,连接DE,CE,且∠DAB=∠DCE=60°,若DE=a,AD=b,AE=c,求BE的长.(用含a,b,c的式子表示)13(2022秋·八年级课时练习)如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,(1)求证:DP=DQ;(2)过P作PE⊥AC于E,若BC=4,求DE的长.14(2022秋·全国·八年级专题练习)如图,在△ABC中,AC=BC,AD平分∠CAB.(1)如图1,若ACB=90°,求证:AB=AC+CD;(2)如图2,若AB=AC+BD,求∠ACB的度数;(3)如图3,若∠ACB=100°,求证:AB=AD+CD.15(2023·全国·九年级专题练习)通过类比联想、引申拓展典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.【解决问题】如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,∠EAF =45°,连接EF ,则EF =BE +DF ,试说明理由.证明:延长CD 到G ,使DG =BE ,在△ABE 与△ADG 中,AB =AD∠B =∠ADG =90°BE =DG∴△ABE ≌△ADG 理由:(SAS )进而证出:△AFE ≌___________,理由:(__________)进而得EF =BE +DF .【变式探究】如图,四边形ABCD 中,AB =AD ,∠BAD =90°点E 、F 分别在边BC 、CD 上,∠EAF =45°.若∠B 、∠D 都不是直角,则当∠B 与∠D 满足等量关系________________时,仍有EF =BE +DF .请证明你的猜想.【拓展延伸】如图,若AB =AD ,∠BAD ≠90°,∠EAF ≠45°,但∠EAF =12∠BAD ,∠B =∠D =90°,连接EF ,请直接写出EF 、BE 、DF 之间的数量关系.。
全等三角形经典题型辅助线

全等三角形常见辅助线作法【例1】.已知:如图6,△BCE 、△ACD 分别是以BE 、AD 为斜边的直角三角形,且BE AD =,△CDE 是等边三角形.求证:△ABC 是等边三角形.【例2】、如图,已知BC > AB ,AD=DC 。
BD 平分∠ABC 。
求证:∠A+∠C=180°.一、线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。
1、倍长中线法【例. 3】如图,已知在△ABC 中,90C ︒∠=,30B ︒∠=,AD 平分BAC ∠,交BC 于点D 。
求证:2BD CD =证明:延长DC 到E ,使得CE=CD ,联结AE ∵∠ADE=60°∵∠C=90° ∴△ADE 为等边三角形 ∴AC ⊥CD ∴AD=DE ∵CD=CE ∵DB=DA∴AD=AE ∴BD=DE ∵∠B=30°∠C=90° ∴BD=2DC ∴∠BAC=60° ∵AD 平分∠BAC ∴∠BAD=30°∴DB=DA ∠ADE=60°DCBADCB EA【例 4.】 如图,D 是ABC ∆的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ∆的中线。
求证:2AC AE =。
证明:延长AE 到点F,使得EF=AE 联结DF在△ABE 和△FDE 中 ∴∠ADC=∠ABD+∠BDA BE =DE ∵∠ABE=∠FDE∠AEB=∠FED ∴∠ADC=∠ADB+∠FDE AE=FE 即 ∠ADC = ∠ADF ∴△ABE ≌ △FDE (SAS ) 在△ADF 和△ADC 中 ∴AB=FD ∠ABE=∠FDE AD=AD ∵AB=DC ∠ADF = ∠ADC ∴ FD = DC DF =DC∵∠ADC=∠ABD+∠BAD ∴△ ADF ≌ ADC(SAS) ∵ADB BAD ∠=∠ ∴AF=AC ∴AC=2AE【变式练习】、 如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证:AD 平分∠BAE.【小结】熟悉法一、法三“倍长中线"的辅助线包含的基本图形“八字型"和“倍长中线”两种基本操作方法,倍长中线,或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。
全等三角形辅助线专题

1、如图,在△ABC中,AD是∠BAC的角平分线,AC=AB+BD,求证:∠B=2∠C证明:在AC上截取AE=AB,连结DE∵AD是∠BAC的角平分线∴∠BAD=∠EAD在△BAD与△EAD中,有:AB=AE (已知)∠BAD=∠EAD (已证)AD=AD (公共边)∴△BAD≌△EAD (SAS)∴∠B=∠AED (全等三角形对应角相等)∵∠AED=∠EDC+∠C (三角形的外角等于不相邻的内角和)∴∠B=∠EDC+∠C (等量代换)∵△BAD≌△EAD (已证)∴BD=ED (全等三角形对应边相等)∵AC=AB+BD (已知)AB=AE (已知)BD=ED (已证)∴ED=CE (等量代换)∴∠C=∠EDC (等边对等角)∵∠B=∠EDC+∠C (已证)∴∠B=2∠C2、如图,在△ABC中,AD是∠BAC的角平分线,AB>AC,试判断AB-AC与BD-CD的大小并说明理由。
证明:在AB上截取AE=AC,连结DE∵AD是∠CAB的角平分线∴∠CAD=∠EAD在△CAD与△EAD中,有:AC=AE (已知)∠CAD=∠EAD (已证)AD=AD (公共边)∴△CAD≌△EAD (SAS)∴CD=ED (全等三角形对应边相等)∵AC=AE (已知)∴AB-AC=AB-AE=BE (等量代换)∵BD-CD=BD-DE<BE (三角形两边之差少于第三边)∴BD-CD=AB-AC3、如图,O为∠BAC内一点,且AB=AC,OB=OC,反向延长OB交AC于D,反向延长OC交AB于E,求证:AD=AE证明方法一:连结BC∵AB=AC,OB=OC∴∠ABC=∠ACB,∠OBC=∠OCB (等边对等角)∴∠ABC-∠OBC=∠ACB-∠OBC∴∠ABD=∠ACE在△ABD与△ACE中,有:∠ABD=∠ACE (已证)AB=AC (已知)∠A=∠A (公共角)∴△ABD≌△ACE (ASA)∴AD=AE (全等三角形对应边相等)证明方法二:连结AO在△AOB与△AOC中,有:OB=OC (已知)AB=AC (已知)AO=AO (公共边)∴△AOB≌△AOC (SSS)∴∠ABD=∠ACE (全等三角形对应角相等)在△ABD与△ACE中,有:∠ABD=∠ACE (已证)AB=AC (已知)∠BAC=∠CAB (公共角)∴△ABD≌△ACE (ASA)∴AD=AE (全等三角形对应边相等)4、在△ABC中,AB=6,AC=8,D是BC的中点。
中考数学第四章 三角形 重难 微专项3 全等三角形中常用的辅助线技巧

= ,
在△ACD和△AED中,ቐ ∠1 = ∠2,
= ,
∴△ACD≌△AED,
∴∠AED=∠C=90°,CD=ED.
重难·微专项3 全等三角形中常用的辅助线技巧
例题
又AC=BC,∴∠B=45°,∴∠EDB=∠B=45°,
∴DE=BE,∴CD=BE.
∴∠DBE=60°,
1
∴BD= BE,
2
∴TF=2BD,即BF-AB=2BD.
重难·微专项3 全等三角形中常用的辅助线技巧
突破点2 旋转
运用旋转的全等变换,可以把分散的条件集中到一个三角形中.
模型1
绕定点旋转60°,构造全等三角形
如图,△ABC为等边三角形,点P在△ABC内,将△ABP绕点A逆时针旋转
明剩下的线段等于另一条短线段.
补短法:延长短线段,使其延长部分等于另一条短线段,然后证明延长
后的线段等于长线段(或延长短线段,使延长后的线段等于长线段,然
后证明延长部分等于另一条短线段).
重难·微专项3 全等三角形中常用的辅助线技巧
例题
例1
如图,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于点D.
60°,得到△ACP',则△ABP≌△ACP',且△APP'为等边三角形.
重难·微专项3 全等三角形中常用的辅助线技巧
例题
例2
如图,在四边形ABCD中,AB=BC,∠ABC=60°,∠ADC=30°,则线段
AD,CD和BD之间的数量关系为 AD2+CD2=BD2 .
重难·微专项3 全等三角形中常用的辅助线技巧
∵BA=BT,∠ABT=60°,
全等三角形几种常见辅助线精典题型
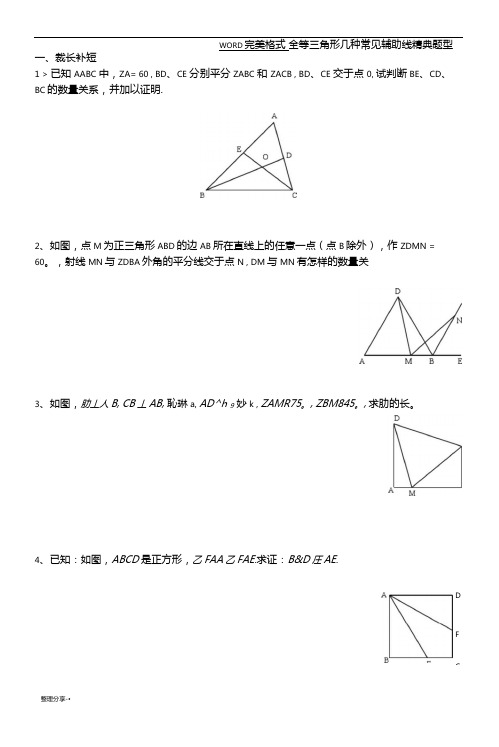
WORD完美格式全等三角形几种常见辅助线精典题型一、裁长补短1 > 已知AABC 中,ZA= 60 , BD、CE 分别平分ZABC 和ZACB , BD、CE 交于点0, 试判断BE、CD、BC的数量关系,并加以证明.2、如图,点M为正三角形ABD的边AB所在直线上的任意一点(点B除外),作ZDMN = 60。
,射线MN与ZDBA外角的平分线交于点N , DM与MN有怎样的数量关3、如图,肋丄人B, CB丄AB,恥琳a, AD^h 9妙k , ZAMR75。
, ZBM845。
, 求肋的长。
4、已知:如图,ABCD是正方形,乙FAA乙FAE.求证:B&D圧AE.DFC5、以AABC的ABj AC为边向三角形外作等边AABD、△ACE,连结CD、BE相交于点O.求证:0A平分ZDOE.6、如图所示,A ABC是边长为1的正三角形,ABDC是顶角为120。
的等腰三角形,以D为顶点作一个60。
的Z14DN,点M. N分别在AB、AC上, 求AAMN的周长.E是线段AD上的一7、如图所示,在AABC中,AB= AC , D是底边BC上的一点,点, 且ZBED = 2ZCED = ZBAC , 求证BD = 2CD •8、五边形力她疋中,AB^AE, BOWCD, ZABO^Z /4£»=180° ,求证:肋平分乙CDE二、全等与角度1、如图,在AABC 中,ZBAC = 60° , AD 是ZBAC 的平分线,且AC= AB + BD ,求ZABC 的度数.2、如图所示,在ZkABC中p AC = BC , ZC = 20°,又M在AC上,N在BC上,且满足ZBAN = 50° , ZABM = 60°, 求ZN14B •使DA=DB, 在AABC 外取一点E , 使ZDBE二ZDBC, 且3、在正4ABC内取一点DBE=BA, 求ZBED4.如图所示,在AABC 中,ZBAC = ZBCA= 44°, M为AABC内一点,使得ZMCA= SO*,ZMAC = 16 ,求ZBMC 的度数•5.如图:在AABC 内取一点M,使得ZMBA= 30*, ZMAB = 2 •设ZACB = 80 , AC = BC , 求ZAMC •6、如图,点M为正方形ABCD的边AB上任意一点,丄DM且与ZABC外角的平分线交于点N,MD与MN有怎样的数量关系?如是正五边形,正六边形呢?饗考答案:一.截长补短1、BE + CD = BC,理由是:在BC 上城取EF = BE,连结OF , 利用 SAS 证得 ABEO 竺 ABFO , A Z1 = Z2,V ZA=60°f ••• ZBOC = 90 + 丄ZA=12(r , ZDOE = 120\o・•・ ZA+ ZDOE = 180',・•・ ZAEO + ZADO = 180 , :. Zl + Z3=l 80° ,V Z2 + Z4=180 ,・・・Z1 = Z2,・*. Z3 = Z4 , 利用 AAS 证得 ACDO 竺 A CFO , /. CD = CF ,2、DM = MN.过点 M 作 MG 〃BD 交 AD 于点、G , AG=AM, A GD = 14B 又•/ZADM + ZDMA= 120° , ZDMA+ ZNMB = 120° AZADM = ZNMB ,而 ZDGM = ZK1BN = 120 , ・•・ AD GM 丝 A14BN , DM = MN .3、过点。
(完整版)全等三角形经典题型——辅助线问题

全等三角形问题中常见的辅助线的作法(含答案) 总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,D C BAED F CB A利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
专题07 全等三角形中的辅助线问题(原卷版)2022年中考数学二轮解题方法分类专项突破

专题07 全等三角形中的辅助线问题【类型】一、全等三角形中的辅助线问题-作平行线一、单选题1.如图,△ABC是边长为4的等边三角形,点P在AB上,过点P作PE△AC,垂足为E,延长BC至点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.1B.1.8C.2D.2.52.如图,△ABC是边长为2的等边三角形,点P在AB上,过点P作PE△AC,垂足为E,延长BC到点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.0.5B.0.9C.1D.1.25二、填空题3.如图,四边形ABCD中,AC与BD相交于点O,且AC△BD,AC=BD=CD,点P是△OCD角平分线的交点,点M是AB的中点,给出下列结论:△△CPD=135°;△BA=BP;△△P AC△△PDB;△S△ABP=S△DCP;CD.其中正确的是___.(填序号)△PM=12三、解答题4.P为等边△ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)证明:PD=DQ.(2)如图2,过P作PE△AC于E,若AB=6,求DE的长.=,连接DE交BC 5.如图所示:ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD CE于点M.求让:MD ME=6.读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DB上,且△BAE=△CDE,求证:AB=CD分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明.图(1):延长DE到F使得EF=DE图(2):作CG△DE于G,BF△DE于F交DE的延长线于F图(3):过C点作CF△AB交DE的延长线于F.7.如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,(1)求证:DP=DQ;(2)过P作PE△AC于E,若BC=4,求DE的长.8.如图,△ABC中,点D,E在边AB上,点F在边BC上,且AD=AC,EF=EC,△CEF=△A,连接DF.(1)在图1中找出与△ACE相等的角,并证明;(2)求证:△BDF=△EFC;(3)如图2,延长FD,CA交于点G,连接EG,若EG=AG,DE=kAE,求DGDF的值(用含k的代数式表示).9.P为等边△ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)证明:PD =DQ .(2)如图2,过P 作PE △AC 于E ,若AB =6,求DE 的长.【类型】二、全等三角形中的辅助线问题-作垂线一、单选题1.如图,AB =AD ,AC =AE ,90BAD CAE ∠=∠=,AH △BC 于H ,HA 的延长线交DE 于G ,下列结论:△DG =EG ;△BC =2AG ;△AH =AG ;△ΔΔABC ADE S S =,其中正确的结论为( )A .△△△B .△△△C .△△△D .△△△△二、填空题 2.如图,在Rt △ABC 中,△ACB =90°,AC =BC =4,点E 在AC 上,且AE =1,连接BE ,△BEF =90°,且BE =FE ,连接CF ,则CF 的长为____________3.如图,ABC 中,,90,(0,3), (1,0)AC BC ACB A C =∠=︒,则点B 的坐标为________.三、解答题4.已知△ACD=90°,MN是过点A的直线,AC=DC,且DB△MN于点B,如图易证BD+AB2=,过程如下:解:过点C作CE△CB于点C,与MN交于点E△△ACB+△BCD=90°,△ACB+△ACE=90°,△△BCD=△ACE.△DB△MN,△△ABC+△CBD=90°,CE△CB,△△ABC+△CEA=90°,△△CBD=△CEA.又△AC=DC,△△ACE△△DCB(AAS),△AE=DB,CE=CB,△△ECB为等腰直角三角形,△BE2=.又△BE=AE+AB,△BE=BD+AB,△BD+AB2=.(1)当MN绕A旋转到如图(2)位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并给予证明.(2)当MN绕A旋转到如图(3)位置时,BD、AB、CB满足什么样关系式,请直接写出你的结论.5.如图1,已知四边形ABCD,连接AC,其中AD△AC,BC△AC,AC=BC,延长CA到点E,使得AE=AD,点F为AB上一点,连接FE、FD,FD交AC于点G.(1)求证:△EAF△△DAF;(2)如图2,连接CF,若EF=FC,求△DCF的度数.6.如图,在四边形ABCD中,BC=CD,△BCD=α°,△ABC+△ADC=180°,A C、BD交于点E.将△CBA 绕点C顺时针旋转α°得到△CDF.(1)求证:△CAB=△CAD;(2)若△ABD=90°,AB=3,BD=4,△BCE的面积为S1,△CDE的面积为S2,求S1:S2的值.7.阅读下面的题目及分析过程,并按要求进行证明.已知:如图,点E是BC的中点,点A在DE上,且△BAE=△CDE.求证:AB=CD.分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.△如图1,延长DE到点F,使EF=DE,连接BF;△如图2,分别过点B、C作BF△DE,CG△DE,垂足分别为点F,G.(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.8.如图,已知AD为△ABC的中线,点E为AC上一点,连接BE交AD于点F,且AE=FE.求证:BF=AC.9.如图,阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DE上,且△BAE=△CDE.求证:AB=CD.分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形请用二种不同的方法证明.10.如图,已知△AOB=60°,在△AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.(1)当△DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当△DCE 绕点C 旋转到CD 与OA 不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由; (3)当△DCE 绕点C 旋转到CD 与OA 的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段OD 、OE 与OC 之间又有怎样的数量关系?请写出你的猜想,不需证明. 【类型】三、全等三角形中的辅助线问题-补全图形法一、解答题1.如图,ABC 中,AC =BC ,△ACB =90°,AD 平分△BAC 交BC 于点D ,过点B 作BE △AD ,交AD 延长线于点E ,F 为AB 的中点,连接CF ,交AD 于点G ,连接BG .(1)线段BE 与线段AD 有何数量关系?并说明理由;(2)判断BEG 的形状,并说明理由.2.如图1,在平面直角坐标系中,直线AB 分别交x 轴、y 轴于(,0) ,(0,)A a B b 两点,且,a b 满足2()|4|0a b a t ,且0,t t >是常数,直线BD 平分OBA ∠,交x 轴于点D .(1)若AB 的中点为M ,连接OM 交BD 于点N ,求证:ON OD =;(2)如图2,过点A 作AE BD ⊥,垂足为E ,猜想AE 与BD 间的数量关系,并证明你的猜想.3.如图,在△ABC 中,点D 为边BC 的中点,点E 在△ABC 内,AE 平分△BAC ,CE△AE 点F 在AB 上,且BF=DE(1)求证:四边形BDEF 是平行四边形(2)线段AB ,BF ,AC 之间具有怎样的数量关系?证明你所得到的结论4.已知,如图ABC ∆中,AB AC =,90A ∠=︒,ACB ∠的平分线CD 交AB 于点E ,90BDC ∠=︒, 求证:2CE BD =.5.(1)阅读理解:问题:如图1,在四边形ABCD 中,对角线BD 平分ABC ∠,180A C ∠+∠=︒.求证:DA DC =. 思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.方法1:在BC 上截取BM BA =,连接DM ,得到全等三角形,进而解决问题;方法2:延长BA 到点N ,使得BN BC =,连接DN ,得到全等三角形,进而解决问题.结合图1,在方法1和方法2中任选一种....,添加辅助线并完成证明. (2)问题解决:如图2,在(1)的条件下,连接AC ,当60DAC ∠=︒时,探究线段AB ,BC ,BD 之间的数量关系,并说明理由;(3)问题拓展:如图3,在四边形ABCD 中,180A C ∠+∠=︒,DA DC =,过点D 作DE BC ⊥,垂足为点E ,请直接写出线段AB 、CE 、BC 之间的数量关系.6.在△ABC 中,AB=AC ,将线段AC 绕着点C 逆时针旋转得到线段CD ,旋转角为α,且0180α<<,连接AD、BD.(1)如图1,当△BAC=100°,60α=时,△CBD 的大小为_________;(2)如图2,当△BAC=100°,20α=时,求△CBD的大小;(3)已知△BAC的大小为m(60120<<),若△CBD 的大小与(2)中的结果相同,请直接写出α的m大小.。
三角形全等证明常用辅助线作法(倍长中线、截长补短)
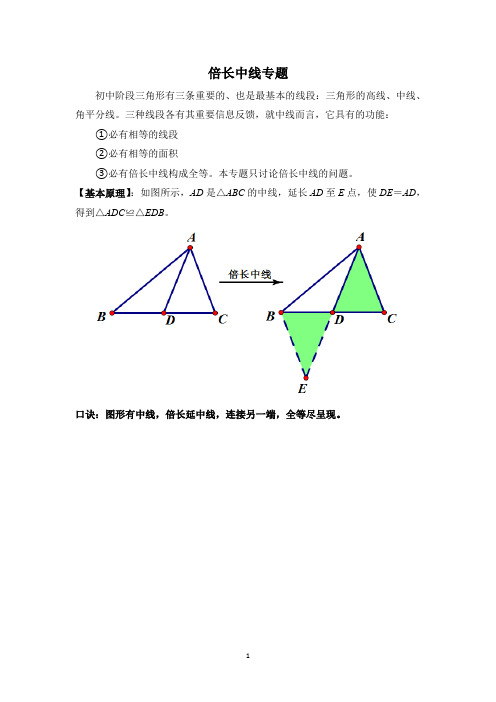
倍长中线专题初中阶段三角形有三条重要的、也是最基本的线段:三角形的高线、中线、角平分线。
三种线段各有其重要信息反馈,就中线而言,它具有的功能:①必有相等的线段②必有相等的面积③必有倍长中线构成全等。
本专题只讨论倍长中线的问题。
【基本原理】:如图所示,AD是△ABC的中线,延长AD至E点,使DE=AD,得到△ADC≌△EDB。
口诀:图形有中线,倍长延中线,连接另一端,全等尽呈现。
【模型实例】:如图,在△ABC 中,AD 是BC 边的中线,E 是AD 上一点,连接BE 并延长交AC 于F 点,AF=EF ,求证:AC=BE证明: 如图所示。
延长AD 至G 点,使DG=AD ,连接BG 。
在△ADC 与△GDB 中,⎪⎩⎪⎨⎧=∠=∠=CD BD GDB ADC GD AD∴△ADC ≌△GDB∴BG =AC ,∠1=∠G又因为AF=EF∴∠1=∠2=∠3∴∠3=∠G∴BG=BE (等角对等边)∴AC=BE②证全等①作倍长中线 ③列出需要用的结果④转化替代 ⑤得出结果【练习1】:如图,在在△ABC中,D为BC的中点,求证:AD+>AB2AC【练习2】:如图,在△ABC中,D为B C的中点,且AD是角平分线。
求证:AB=AC【练习3】:AD是△ABC的中线,分别以AB边、AC边为直角边向外作等腰直角三角形,求证:EF=2AD【练习4】:在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于F点。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论。
截长补短专题要证明两条线段之和等于第三条线段,可以采用“截长补短”法。
①截长法:把较长的线段截取一段等于两较短线中的一条;②补短法:把两条较短的线段补成一条,再证与长线段相等。
【模型实例】:如图,△ABC中,∠1=∠2,∠B=2∠C。
求证:AC=AB+BD 方法一:截长(利用角平分线构建全等三角形)分析:如图,在AC上截AE=AB,连接DE。
八年级(上)培优专刊资料三全等三角形辅助线作法

DCBAEDFCBA专题三 全等三角形辅助线作法一、“三线合一”法:等腰三角形底边上的高、中线、顶角的角平分线三线合一. 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题注意:有一个内角为60°的三角形一定是等边三角形二、倍长中线法:遇到三角形的中线,倍长中线,即延长中线使延长线段与原中线长相等,构造全等三角形。
例1、已知,如图△ABC 中,AB=5,AC=3,则中线AD 的取值范围是_________.例1图 例2图例2、如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF ,D 是中点,试比较BE+CF 与EF 的大小.例3、如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证:AD 平分∠BAE.E D CB A三、角平分线构造全等法:即利用角平分线构造全等三角形法。
遇到角平分线有三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,形成一对全等三角形。
所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
(3)可以在该角的两边上,距离角的顶点相等长度的位置上截取二点,然后从这两点再向角平分线上的某点作边线,构造一对全等三角形。
DCBA(一)角分线上点向角两边作垂线构全等1、如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交于点O ,求证:OE=OD例1. 如图2-1,已知AB>AD, ∠BAC=∠FAC,CD=BC 。
求证:∠ADC+∠B=180分析:可由C 向∠BAD 的两边作垂线。
近而证∠ADC 与∠B 之和为平角。
例2. 如图2-2,在△ABC 中,∠A=90 ,AB=AC ,∠ABD=∠CBD 。
求证:BC=AB+AD分析:过D 作DE ⊥BC 于E ,则AD=DE=CE ,则构造出全等三角形,从而得证。
辅助线——全等三角形专题训练

辅助线——全等三角形专题训练点G连接B,交MN于点H,连接DH,因为∠ABC为外角,所以∠ABH=∠ABC/2。
又∠HMD=90度,所以∠XXX=90度-∠ABH,即∠DMH=∠ABC/2。
因为∠XXX∠ABH,所以∠DGM=∠ABC/2,又因为∠DGM=∠MBN。
所以∠XXX∠ABC/2,所以∠NMB=90度-∠ABC/2,所以∠XXX∠NMB-∠DMH=90度-∠ABC/2-∠ABC/2=90度-∠ABC。
又因为∠MDN=90度,所以∠XXX=90度-∠MDN=∠ABC。
所以∠XXX∠XXX-∠XXX∠ABC-(90度-∠ABC)=2∠ABC-90度。
因为∠DGH=∠ABH=∠ABC/2,所以∠XXX∠DGM,所以DM=MN。
在等腰三角形ABC中,顶角A的度数为20度。
在边AB 上取点D,使得AD=BC。
求角BDC的度数。
解析:以AC为边向外作正三角形ACE,连接DE。
在三角形ABC和三角形EAD中,AD=BC,AB=EA,∠EAD=∠BAC+∠CAE=20+60=80=∠ABC。
因此,三角形ABC≌三角形EAD。
由此可得ED=EA=EC,因此三角形EDC 是等腰三角形。
由于∠AED=∠BAC=20度,因此∠CED=∠AEC-∠AED=60-20=40度。
从而∠DCE=70度,∠DCA=∠DCE-∠ACE=70-60=10度,因此∠XXX∠DAC+∠DCA=20+10=30度。
另解1:以AD为边在三角形ABC外部作等边三角形ADE,连接EC。
在三角形ACB和三角形CAE中,∠CAE=60度+20度=∠ACB,AE=AD=CB,AC=CA,因此三角形ACB≌三角形CAE,从而∠CAB=∠ACE,CE=AB=AC。
在三角形CAD和三角形CED中,AD=ED,CE=CA,CD=CD,因此三角形CAD≌三角形CED,从而∠ACD=∠ECD,∠XXX∠ACE=2∠ACD,因此∠ACD=10度,因此∠BDC=30度。
全等三角形几种常见辅助线精典题型

全等三角形几种常见辅助线精典题型This model paper was revised by the Standardization Office on December 10, 2020全等三角形几种常见辅助线精典题型一、截长补短1、已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.2、如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系 3、如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k ,∠AMD =75°,∠BMC =45°,求AB 的长。
4、已知:如图,ABCD 是正方形,∠FAD =∠FAE . 求证:BE +DF =AE .5、以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆,连结CD 、BE 相交于点O .求证:OA 平分DOE ∠.6、如图所示,ABC ∆是边长为1的正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.7、如图所示,在ABC ∆中,AB AC =,D 是底边BC 上的一点,E 是线段AD 上的一点,且2BED CED BAC ∠=∠=∠,求证2BD CD =.8、五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:AD 平分∠CDE二、全等与角度NEB M ADDO ECBAMDCBANMDCBAED CBACEDBA1、如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数.2、如图所示,在ABC ∆中,AC BC =,20C ∠=︒,又M 在AC 上,N 在BC 上,且满足50BAN ∠=︒,60ABM ∠=︒,求NMB ∠.3、 在正ABC ∆内取一点D ,使DA DB =,在ABC ∆外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.4、如图所示,在ABC ∆中,44BAC BCA ︒∠=∠=,M 为ABC ∆内一点,使得30MCA ︒∠=,16MAC ︒∠=,求BMC ∠的度数.5、如图:在ABC ∆内取一点M ,使得MBA ∠=30,10MAB ∠=.设80ACB ∠=,AC BC =,求AMC ∠.6、如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系如是正五边形,正六边形呢参考答案:一、截长补短1、BE CD BC +=,理由是:在BC 上截取BF BE =,连结OF ,利用SAS 证得BEO ∆≌BFO ∆,∴12∠=∠,∵60A ∠=︒,∴1901202BOC A ∠=+∠=,∴120DOE ∠=,∴180A DOE ∠+∠=,∴180AEO ADO ∠+∠=,∴13180∠+∠=,NMCBA4321FD OE CBA∵24180∠+∠=,∴12∠=∠,∴34∠=∠,利用AAS 证得CDO ∆≌CFO ∆,∴CD CF =,∴BC BF CF BE CD =+=+.2、DM MN =.过点M 作MG BD ∥交AD 于点G ,AG AM =,∴GD MB =又∵120ADM DMA +∠=∠,120DMA NMB +=∠∠∴ADM NMB =∠∠,而120DGM MBN ==∠∠,∴DGM MBN ∆∆≌,∴DM MN =.3、过点D 作BC 的垂线,垂足为E .∵∠AMD =75°,∠BMC =45° ∴∠DMC =60°∵DM =CM ∴CD =DM∵AD ⊥AB ,DE ⊥BC ,CB ⊥AB ,∠AMD =75°∴∠ADM =∠EDC ∴△ADM ≌△CDE ∴AD =DE故ABED 为正方形,AB =AD =h ,选D .4、延长CB 至M ,使得BM =DF ,连接AM .E MDCBAM F EDCB A∵AB =AD ,AD ⊥CD ,AB ⊥BM ,BM =DF ∴△ABM ≌△ADF∴∠AFD =∠AMB ,∠DAF =∠BAM ∵AB ∥CD∴∠AFD =∠BAF =∠EAF +∠BAE =∠BAE +∠BAM =∠EAM∴∠AMB =∠EAM ∴AE =EM =BE +BM =BE +DF .5、因为ABD ∆、ACE ∆是等边三角形,所以AB AD =,AE AC =,CAE ∠=60BAD ∠=,则BAE DAC ∠=∠,所以BAE DAC ∆∆≌, 则有ABE ADC ∠=∠,AEB ACD ∠=∠,BE DC =.在DC 上截取DF BO =,连结AF ,容易证得ADF ABO ∆∆≌,ACF AEO ∆∆≌. 进而由AF AO =.得AFO AOF ∠=∠;由AOE AFO ∠=∠可得AOF ∠=AOE ∠,即OA 平分DOE ∠. 6、如图所示,延长AC 到E 使CE BM =.在BDM ∆与CDE ∆中,因为BD CD =,90MBD ECD ∠=∠=,BM CE =, 所以BDM CDE ∆∆≌,故MD ED =.EABC DM N因为120BDC ∠=,60MDN ∠=,所以60BDM NDC ∠+∠=. 又因为BDM CDE ∠=∠,所以60MDN EDN ∠=∠=.在MND ∆与END ∆中,DN DN =,60MDN EDN ∠=∠=,DM DE =, 所以MND END ∆∆≌,则NE MN =,所以AMN ∆的周长为2.7、如图所示,作BED ∠的平分线交BC 于F ,又过A 作AH EF ∥交BE 于G ,交BC 于H ,则知12EAG DEF BEF AGE BAC ∠=∠=∠=∠=∠,从而GE AE =.又12AGE BED CED ∠=∠=∠,则AGB CEA ∠=∠.由ABE BAE BED BAC CAE BAE ∠+∠=∠=∠=∠+∠可得ABG CAE ∠=∠. 注意到AB CA =,故有ABG CAE ∆∆≌,从而BG AE =,AG CE =,于是BG GE =.又由AH EF ∥,有BH HF =,12GH EF =,且AH HDEF FD=. 而CED FED ∠=∠,从而1122CD EC AG AH GH AH HD FD EF EF EF EF FD -====-=-, 即1111122222CD HD FD HF FD BF FD BD =-=+=+=,故2BD CD =.8、延长DE 至F ,使得EF =BC ,连接AC .∵∠ABC +∠AED =180°,∠AEF +∠AED =180° ∴∠ABC =∠AEFGH F ED CB A∵AB=AE,BC=EF∴△ABC≌△AEF∴EF=BC,AC=AF∵BC+DE=CD∴CD=DE+EF=DF∴△ADC≌△ADF∴∠ADC=∠ADF即AD平分∠CDE.二、全等与角度1、如图所示,延长AB至E使BE BD=,连接ED、EC.由AC AB BD=+知AE AC=,而60BAC∠=,则AEC∆为等边三角形.注意到EAD CAD∠=∠,AD AD=,AE AC=,故AED ACD∆∆≌.从而有DE DC=,DEC DCE∠=∠,故2BED BDE DCE DEC DEC∠=∠=∠+∠=∠.所以20DEC DCE∠=∠=,602080ABC BEC BCE∠=∠+∠=+=【另解】在AC上取点E,使得AE AB=,则由题意可知CE BD=.在ABD∆和AED∆中,AB AE=,BAD EAD∠=∠,ABD EFCED C BAED C BAAD AD =,则ABD AED ∆∆≌,从而BD DE =,进而有DE CE =,ECD EDC ∠=∠,AED ECD EDC ∠=∠+∠=2ECD ∠.注意到ABD AED ∠=∠,则:1318012022ABC ACB ABC ABC ABC BAC ∠+∠=∠+∠=∠=-∠=,故80ABC ∠=︒.【点评】由已知条件可以想到将折线ABD “拉直”成AE ,利用角平分线AD 可以构造全等三角形.同样地,将AC 拆分成两段,之后再利用三角形全等亦可,此思路也是十分自然的.需要说明的是,无论采取哪种方法,都体现出关于角平分线“对称”的思想.上述方法我们分别称之为“补短法”和“截长法”,它们是证明等量关系时优先考虑的方法.2、过M 作AB 的平行线交BC 于K ,连接KA 交MB 于P .连接PN ,易知APB ∆、MKP ∆均为正三角形. 因为50BAN ∠=︒,AC BC =,20C ∠=︒,所以50ANB ∠=︒,BN AB BP ==,80BPN BNP ∠=∠=︒,则40PKN ∠=︒,180608040KPN ∠=︒-︒-︒=︒, 故PN KN =. 从而MPN MKN ∆∆≌.进而有PMN KMN ∠=∠,1302NMB KMP ∠=∠=︒3、如图所示,连接DC .因为AD BD =,AC BC =,CD CD =, 则ADC BDC ∆∆≌,故30BCD ∠=.而DBE DBC ∠=∠,BE AB BC ==,BD BD =,因此BDE BDC ∆∆≌, 故30BED BCD ∠=∠=.4、在ABC ∆中,由44BAC BCA ︒∠=∠=可得AB AC =,92ABC ︒∠=. 如图所示,作BD AC ⊥于D 点,延长CM 交BD 于O 点,连接OA ,则有30OAC MCA ︒∠=∠=,443014BAO BAC OAC ︒︒︒∠=∠-∠=-=,301614OAM OAC MAC ︒︒︒∠=∠-∠=-=,所以BAO MAO ∠=∠.又因为90903060AOD OAD COD ︒︒︒︒∠=-∠=-==∠, 所以120AOM AOB ∠=︒=∠.120BOM ∠=︒DECBAOD MCA B而AO AO =,因此ABO AMO ∆∆≌,故OB OM =.由于120BOM ︒∠=,则180302BOMOMB OBM ︒-∠∠=∠==︒,故180150BMC OMB ︒︒∠=-∠=5、如图所示,ABC ∆的高CH 与直线BM 交于点E ,则AE BE =. 而301020EAM EAB MAB ∠=∠-∠=-=,1402ACE ACB ∠=∠=,(9040)3020EAC CAH EAB ∠=∠-∠=--=,103040AME MAB MBA ∠=∠+∠=+=,由两角夹一边法则可知AME ACE ∆∆≌, 因此AM AC =,6、DM MN =.在AD 上截取AG AM =,∴DG MB =,∴45AGM =∠∴135DGM MBN ==︒∠∠,∴ADM NMB =∠∠, ∴DGM MBN ∆∆≌,∴DM MN =.EHABCMNCDEB M A。
全等三角形做辅助线 经典专题

1第十一讲 全等三角形作辅助线时间: 年 月 日 刘满江老师 学生签名:一、 兴趣导入二、 学前测试1.下列线段能围成三角形的是( ).A .7,5,12B .6,8,15C .4,5,6D .3,4,82.已知△ABC 的三个内角∠A 、∠B 、∠C 满足关系式∠B+∠C=3∠A ,则此三角形( ). A .一定有一个内角为︒45 B .一定有一个内角为︒60 C .一定是直角三角形 D .一定是钝角三角形 3.下列说法正确的是( ).A .三角形的内角中,至少有一个直角B .三角形的内角中,至少有一个钝角C .三角形的内角中,至少有两个锐角D .三角形的内角中,最多有两个锐角 4.如图,AB ∥FC ,DE=EF ,AB=15,CF=8,则BD 等于( ). A .8 B .7 C .6 D .55.下列条件中,不一定能使两三角形全等的是( ). A .两边一角对应相等 B .两角一边对应相等 C .三边对应相等 D .直角边和一个锐角对应相等6.如图,AB=B A '',∠A=∠A ',若△ABC ≌△C B A ''',还需要( ). A .∠B=∠B ' B .∠C=∠C ' C .AC=C A '' D .以上答案均可FED CBAC 'B 'A 'C B A第4题 第6题7.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( ).A .带①去B .带②去C .带③去D .带①②去8.如图,AB=CD ,DE=AF ,CF=BE ,∠AFB=︒80,∠CDE=︒60,那么∠ABC 等于( ). A .︒80 B .︒60 C .︒40 D .︒202F EDCBA第7题 第8题9.如图,MP=MQ ,PN=QN ,MN 交PQ 于O 点,则下列结论中,不一定正确的是( ). A .△MPN ≌△MQN B .∠PNM=∠QNM C .MO=NO D .∠MPN=∠MQN10.如图,AC=AD ,BC=BD ,O 是AB 上任一点,连结OC 、OD ,那么图中全等三角形的对数是( ). A .1 B .2 C .3 D .4O QP NM第9题 OD BCA第10题1.C 2.A 3.C 4.B 5.A 6.D 7.C 8.C 9.C 10.C三、方法培养知识讲解:1. 常见辅助线的作法有以下几种:1.遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”.2.遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”.3.遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.4.过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”5.截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.6.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.3EDFCBA☆专题:全等三角形专题(一)倍长中线(线段)造全等【例1】如图,ABC ∆中,F E 、分别在AC AB 、上,D DF DE ,⊥是中点,试比较CF BE +与EF的大小.【变式训练】如图,ABC ∆中,E AC DC BD ,==是DC 的中点,求证:AD 平分BAE ∠.E D CBA(二)截长补短【例2】如图,ABC ∆中,AD AC AB ,2=平分BAC ∠,且BD AD =,求证:AC CD ⊥.CDBA4EDCBA【变式训练】如图,EB EA BD AC 、,//分别平分CD DBA CAB ,,∠∠过点E ,求证:BD AC AB +=.(三)平移变换【例3】AD 为ABC ∆的角平分线,直线AD MN⊥于A .E 为MN 上一点,ABC ∆周长记为A P ,EBC ∆周长记为B P .求证B P >A P .【变式训练】如图,在ABC ∆的边上取两点E D 、,且CE BD =,求证:AE AD AC AB +>+.ED CBA5O EDCBA(四)借助角平分线造全等【例4】如图,已知在ABC ∆中,060=∠B ,ABC ∆的角平分线CE AD ,相交于点O ,求证:OD OE =.【变式训练】如图,ABC ∆中,AD 平分BC DG BAC ⊥∠,且平分AB DE BC ⊥,于AC DF E ⊥,于F . (1)说明CF BE =的理由;(2)如果b AC a AB ==,,求BE AE ,的长.四、强化练习1. 已知:如图2-7,在Rt △ABC 中,∠ACB=90° ,CD ⊥AB ,垂足为D ,AE 平分∠CAB 交CD 于F ,过F 作F H//AB 交BC 于H 。
(完整版)全等三角形经典题型——辅助线问题

(完整版)全等三⾓形经典题型——辅助线问题全等三⾓形问题中常见的辅助线的作法(含答案) 总论:全等三⾓形问题最主要的是构造全等三⾓形,构造⼆条边之间的相等,构造⼆个⾓之间的相等【三⾓形辅助线做法】图中有⾓平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
⾓平分线平⾏线,等腰三⾓形来添。
⾓平分线加垂线,三线合⼀试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三⾓形中两中点,连接则成中位线。
三⾓形中有中线,延长中线等中线。
1.等腰三⾓形“三线合⼀”法:遇到等腰三⾓形,可作底边上的⾼,利⽤“三线合⼀”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三⾓形3.⾓平分线在三种添辅助线4.垂直平分线联结线段两端5.⽤“截长法”或“补短法”:遇到有⼆条线段长之和等于第三条线段的长,6.图形补全法:有⼀个⾓为60度或120度的把该⾓添线后构成等边三⾓形7.⾓度数为30、60度的作垂线法:遇到三⾓形中的⼀个⾓为30度或60度,可以从⾓⼀边上⼀点向⾓的另⼀边作垂线,⽬的是构成30-60-90的特殊直⾓三⾓形,然后计算边的长度与⾓的度数,这样可以得到在数值上相等的⼆条边或⼆个⾓。
从⽽为证明全等三⾓形创造边、⾓之间的相等条件。
8.计算数值法:遇到等腰直⾓三⾓形,正⽅形时,或30-60-90的特殊直⾓三⾓形,或40-60-80的特殊直⾓三⾓形,常计算边的长度与⾓的度数,这样可以得到在数值上相等的⼆条边或⼆个⾓,从⽽为证明全等三⾓形创造边、⾓之间的相等条件。
常见辅助线的作法有以下⼏种:最主要的是构造全等三⾓形,构造⼆条边之间的相等,⼆个⾓之间的相等。
1)遇到等腰三⾓形,可作底边上的⾼,利⽤“三线合⼀”的性质解题,思维模式是全等变换中的“对折”法构造全等三⾓形.2)遇到三⾓形的中线,倍长中线,使延长线段与原中线长相等,构造全等三⾓形,D C BAED F CB A利⽤的思维模式是全等变换中的“旋转”法构造全等三⾓形.3)遇到⾓平分线在三种添辅助线的⽅法,(1)可以⾃⾓平分线上的某⼀点向⾓的两边作垂线,利⽤的思维模式是三⾓形全等变换中的“对折”,所考知识点常常是⾓平分线的性质定理或逆定理.(2)可以在⾓平分线上的⼀点作该⾓平分线的垂线与⾓的两边相交,形成⼀对全等三⾓形。
专题 全等三角形的常见辅助线

方法一作平行线法变式12.如图,△ABC 中,AB =AC ,在AB 上取一点E ,在AC 的延长线上取一点F ,使CF =BE ,连接EF ,交BC 于点D .求证:DE =DF 作平行,构造全等.利用的思维模式是全等变换中的“平移”.【例题1】1.△ABC 中,∠BAC =60°,∠C =40°,AP 平分∠BAC 交BC 于P ,BQ 平分∠ABC 交AC 于Q ,求证:AB +BP=BQ +AQ .(有多种辅助线作法).专题 全等三角形的常见辅助线变式23.如图,在Rt △ABC 中,∠ACB =90°,点D ,E 分别是边AB ,AC 的中点,延长BC 到点F ,使CF =12BC .连结CD 、EF ,那么CD 与EF 相等吗?请证明你的结论.变式34.如图所示,ABC ∆为等边三角形,边长为4,点O 为BC 边中点,120EOF ∠=︒,其两边分别交AB 和CA 的延长线于E ,F ,求AE AF -的值.变式45.如图,将一把三角尺放在边长为1的正方形ABCD 上使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q ,当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系?试证明你观察得到的结论.培优变式56.如图1,已知ABC 和EFC 都是等边三角形,且点E 在线段AB 上.(1)过点E 作//EG BC 交AC 于点G ,试判断AEG △的形状并说明理由;(2)求证://BF AC ;(3)如图2,若点D 在射线CA 上,且ED EC =,求证:AB AD BF =+.方法二作垂直法作垂直,构造全等.分为做1条垂直辅助线和2条垂直辅助线.可以利用通过作角平分线上的点两边的距离得全等,或截取等长线段得全等;思维模式是全等变换中的“轴对称”即“对折”.【例题2】7.如图,△ABC中,AB=2AC,AD平分∠BAC,且AD=BD.求证:CD⊥AC.变式18.如图所示,在四边形ABCD 中,AC 平分,DAB CD CB ∠=,求证:180B D ∠+∠= .变式29.已知:∠AOB+∠CPD =180°,OM 是∠AOB 的平分线,将三角板的直角顶P 在射线OM 上滑动,两直角边分别与OA 、OB 交于C 、D .求证:PC=PD .变式310.如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.变式411.如图,在梯形ABCD中,∠A=∠B=90°,点E为AB的中点,DE平分∠ADC.(1)求证:CE平分∠BCD;(2)求证:AD+BC=CD.培优变式512.已知如图,在△ABC中,以AB、AC为直角边,分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.(1)用圆规比较EM与FM的大小.(2)你能说明由(1)中所得结论的道理吗?方法三倍长中线法倍长中线主要用于证明全等三角形,其主要是在全等三角形的判定过程中,遇到一般三角形边上的中线或中点,考虑中线倍长;思维模式是全等变换中的“旋转”,可转移元素或将分散的条件聚集拢来.其主要的图形特征和证明方法如图:已知:在三角形ABC中,O为BC边中点,辅助线:延长AO到点D使AO=DO,结论:△AOB≌△DOC证明:延长AO到点D使AO=DO,由中点可知,OB=OC,在△AOB 和△DOC 中OA OD AOB DOC OB OC =⎧⎪∠=∠⎨⎪=⎩∴△AOB ≌△DOC同理在下图中仍能得到△AOB ≌△DOC规律总结:由倍长中线法证明三角形全等的过程一般均是用SAS 的方法,这是由于作出延长线后出现的对顶角决定的.补充:关于倍长中线的其他方法①向中线做垂直,易证△BEO ≌△CDO步骤:延长AO 到点D ,过点B ,C 分别向AD 作垂线,垂足为E ,D ,易证△BEO ≌△CDO (AAS )②过中线做任意三角形证明全等,易证△BDO ≌△CEO步骤:在AC 上任意选取一点E ,连接EO 并延长到点D ,使EO =DO ,连接BD ,易证△BDO ≌△CEO (SAS )点拨:倍长中线的思路:已知中线——作中线倍长线——证全等——找大小关系【例题3】13.如图,AD 是ABC 的中线,,E F 分别在边,AB AC 上(,E F 不与端点重合),且DE DF ⊥,则().A .BE CF EF+>B .BE CF EF +=C .BE CF EF+<D .BE CF +与EF 的长短关系不确定变式14.如图,901,2,AB CD BCD AB BC CD E ∠=︒=== ,,为AD 上的中点,则BE =______.变式15.如图,ABC ∆中,D 为BC 的中点,E 是AD 上一点,连接BE 并延长交AC 于F ,BE AC =,且9BF =,6CF =,那么AF 的长度为__.变式16.如图,E 是BC 的中点,点A 在DE 上,且∠BAE =∠CDE.求证:AB =CD .变式17.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.【探究与发现】(1)如图1,AD 是ABC 的中线,延长AD 至点E ,使ED AD =,连接BE ,证明:ACD EBD △≌△.【理解与应用】(2)如图2,EP 是DEF 的中线,若5EF =,3DE =,设EP x =,则x 的取值范围是________.(3)如图3,AD 是ABC 的中线,E 、F 分别在AB 、AC 上,且DE DF ⊥,求证:BE CF EF +>.培优变式18.问题探究:小红遇到这样一个问题:如图1,ABC 中,6AB =,4AC =,AD 是中线,求AD 的取值范围.她的做法是:延长AD 到E ,使DE AD =,连接BE ,证明BED CAD △≌△,经过推理和计算使问题得到解决.请回答:(1)小红证明BED CAD △≌△的判定定理是:__________________________________________;(2)AD 的取值范围是________________________;方法运用:(3)如图2,AD 是ABC 的中线,在AD 上取一点F ,连结BF 并延长交AC 于点E ,使AE EF =,求证:BF AC =.(4)如图3,在矩形ABCD 中,12AB BC =,在BD 上取一点F ,以BF 为斜边作Rt BEF △,且12EF BE =,点G 是DF 的中点,连接EG ,CG ,求证:=EG CG .方法四截长补短法基本方法已知条件在ABC 中,,AB AC AM >平分BAC∠辅助线作(1)在AB 上截取AD AC =;(2)把AC 延长到点E ,使AB AE =法可用结论截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长:在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;补短:将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段.理论依据(1)因为AM 平分BAC ∠,且AD AC =,所以(SAS)AMD AMC ≌;(2)因为AM 平分BAC ∠,且AE AB=,所以(SAS)AMB AME ≌【例题4】19.在ABC 中,60ABC ∠=︒,点D 、E 分别在AC 、BC 上,连接BD 、DE 和AE ;并且有AB BE =,AED C ∠=∠.(1)求CDE ∠的度数;(2)求证:AD DE BD +=.变式120.如图,在ABC 中,AD 为BAC ∠的平分线,如图,若2,12,7.2C B AB AC ∠=∠==,求线段CD 的长度.变式221.如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.(1)求证:DP=DB;(2)求证:DA+DB=DC;变式322.在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.(1)如图1,当点E在BC边的中点位置时,求证:AE=EM;(2)如图2,当点E在BC边的任意位置时,(1)中的结论是否成立?请说明理由.变式423.如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.(1)当点E在线段BD上移动时,如图(1)所示,求证:AE=EF;(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段AE与EF又有怎样的数量关系?请直接写出你的猜想,不需证明.变式524.如图1,在四边形ABCD 中,AB=AD ,∠B+∠ADC=180°,点E ,F 分别在四边形ABCD 的边BC ,CD 上,∠EAF=12∠BAD ,连接EF ,试猜想EF ,BE ,DF 之间的数量关系.(1)思路梳理将△ABE 绕点A 逆时针旋转至△ADG ,使AB 与AD 重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F ,D ,G 三点共线,易证△AFG ≌△AFE ,故EF ,BE ,DF 之间的数量关系为__;(2)类比引申如图2,在图1的条件下,若点E ,F 由原来的位置分别变到四边形ABCD 的边CB ,DC 延长线上,∠EAF=12∠BAD ,连接EF ,试猜想EF ,BE ,DF 之间的数量关系,并给出证明.(3)联想拓展如图3,在△ABC 中,∠BAC=90°,AB=AC ,点D ,E 均在边BC 上,且∠DAE=45°,若BD=1,EC=2,直接写出DE 的长为________________.培优变式625.通过类比联想、引申拓展典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.【解决问题】如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,连接EF ,则EF BE DF =+,试说明理由.证明:延长CD 到G ,使DG BE =,在ABE 与ADG △中,90AB AD B ADG BE DG =⎧⎪∠=∠=︒⎨⎪=⎩∴ABE ADG △≌△理由:(SAS )进而证出:AFE △≌___________,理由:(__________)进而得EF BE DF =+.【变式探究】如图,四边形ABCD 中,AB AD =,90BAD ∠=︒点E 、F 分别在边BC 、CD 上,45EAF ∠=︒.若B ∠、D ∠都不是直角,则当B ∠与D ∠满足等量关系________________时,仍有EF BE DF =+.请证明你的猜想.【拓展延伸】如图,若AB AD =,90≠︒∠BAD ,45EAF ∠≠︒,但12EAF BAD ∠=∠,90B D ∠=∠=︒,连接EF ,请直接写出EF 、BE 、DF 之间的数量关系.方法五补全图形法补全定理图形或基本图形,运用定理或基本结论解题.【例题5】26.如图,已知等腰直角三角形ABC 中,AB AC =,90BAC ∠=︒,BF 平分ABC ∠,CD BD ⊥交BF 的延长线于点D ,试说明:2BF CD =.变式127.如图,在ABC ∆中,,90,AC BC ACB BD =∠= 平分ABC ∠,且AE 垂直于BD 的延长线于点E ,求证:2BD AE =.变式228.如图,已知△ABC 中,AB =AC ,∠BAC =90°,直角EPF ∠的顶点P 是BC 中点,两边PE 、PF 分别交AB 、CA 的延长线于点E 、F .(1)求证:AE =CF ;(2)求证:△EPF 是等腰直角三角形;(3)求证:∠FEA +∠PFC =45°;(4)求证:S △PFC -S △PBE =12S △ABC .方法六旋转法常见通过旋转构造全等的情况1、等腰三角形的旋转2、等边三角形的旋转3、四边形旋转4、正方形旋转根据想要转换的线段以及“共顶点等线段"的特点锁定旋转目标,添加辅助线促成全等,实现线段或角度在位置上的变化,再根据题目中的具体条件从而解决问题.【例题6】29.如图,在四边形ABCD 中,AB =AD ,∠BAD =60°,∠BCD =120°,AC =2,则四边形ABCD 的面积为________变式130.在ABC 中,90,ACB CA CB ∠=︒=,点,E F 在AB 边上,45ECF ∠=︒.若10,15AE EF ==,则BF 的长为__________.变式231.如图,在Rt △ABC 和Rt △BCD 中,∠BAC =∠BDC =90°,BC =8,AB =AC ,∠CBD =30°,BD =M ,N 分别在BD ,CD 上,∠MAN =45°,则△DMN 的周长为_____.变式332.如图,等腰三角形ABC 中,BA BC =,ABC α∠=.作AD BC ⊥于点D ,将线段BD 绕着点B 顺时针旋转角α后得到线段BE ,连接CE .(1)求证:BE CE ⊥;(2)延长线段AD ,交线段CE 于点F .求CFA ∠的度数(用含有α的式子表示).培优变式433.阅读下面材料:小炎遇到这样一个问题:如图1,点E 、F 分别在正方形ABCD 的边BC ,CD 上,∠EAF=45°,连结EF ,则EF=BE+DF ,试说明理由.小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB ,AD 是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE 绕着点A 逆时针旋转90°得到△ADG ,再利用全等的知识解决了这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D 都不是直角,则当∠B与∠D满足_关系时,仍有EF=BE+DF;(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1,EC=2,求DE的长.。
全等三角形作辅助线经典例题

D CB AEDFCBA全等三角形作辅助线经典例题常见辅助线的作法有以下几种: 1) 遇到等腰三角形,可作底边上的高,利用“三线合一〞的性质解题,思维模式是全等变换中的“对折〞. 2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转〞. 3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折〞,所考知识点常常是角平分线的性质定理或逆定理. 4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移〞或“翻转折叠〞;〔遇垂线及角平分线时延长垂线段,构造等腰三角形〕 5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.一、倍长中线〔线段〕造全等1:,如图△ABC 中,AB=5,AC=3,那么中线AD 的取值X 围是_________.2:如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF ,D 是中点,试比拟BE+CF 与EF 的大小.3:如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证:AD 平分∠BAE.E D CB A中考应用1、以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆,EDCBADCBAPQCBA90,BAD CAE ∠=∠=︒连接DE ,M 、N 分别是BC 、DE 的中点.探究:AM 与DE 的位置关系及数量关系.〔1〕如图①当ABC ∆为直角三角形时,AM 与DE 的位置关系是,线段AM 与DE 的数量关系是;〔2〕将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ(0<θ<90)后,如图②所示,〔1〕问中得到的两个结论是否发生改变?并说明理由.二、截长补短1.如图,ABC ∆中,AB=2AC ,AD 平分BAC ∠,且AD=BD ,求证:CD ⊥AC2:如图,AD ∥BC ,EA,EB 分别平分∠CAB,∠DBA ,CD 过点E ,求证;AB =AD+BC3:如图,在ABC ,060BAC ∠=,040C ∠=,P ,Q 分别在BC ,CA 上,并且AP ,BQ分别是BAC ∠,ABC ∠的角平分线。
专题:三角形全等常用辅助线及模型(答案)

专题:三角形全等常用辅助线及模型※题型讲练考点一三角形全等常见辅助线一:倍长中线法1.如图,在△ABC中,D为BC的中点.(1)求证:AB+AC>2AD;(2)若AB=5,AC=3,求AD的取值范围.解:(1)延长AD至点E,使DE=AD,连接BE.∵D为BC的中点,∴CD=BD.又∵AD=ED,∠ADC=∠EDB,∴△ADC≌△EDB.∴AC=EB.∵AB+BE>AE,∴AB+AC>2AD.(2)∵AB-BE<AE<AB+BE,∴AB-AC<2AD<AB+AC.∵AB=5,AC=3,∴2<2AD<8.∴1<AD<4.2.如图,AB=AE,AB⊥AE,AD=AC,AD⊥AC,M为BC的中点,求证:(1)DE=2AM;(2) AM⊥DE.证明:(1)延长AM至点N,使MN=AM,连接BN.∵M为BC的中点,∴BM=CM.又∵AM=MN,∠AMC=∠NMB,∴△AMC≌△NMB(SAS),∴AC=BN,∠C=∠NBM,∴∠ABN=∠ABC+∠NBM=∠ABC+∠C=180°-∠BAC=∠EAD.∵AD=AC,AC=BN,∴AD=BN.又∵AB=AE,∴△ABN≌△EAD(SAS),∴DE=NA.又∵AM=MN,∴DE=2AM.(2)互余证法,证明略;3.如图,△ABC中,BD=AC,∠ADC=∠CAD,E是DC的中点,求证:AD平分∠BAE.解:延长AE到M,使EM=AE,连结DM易证△DEM≌△CEA∴∠C=∠MDE, DM=AC又BD=AC∴DM=BD,又∠ADB=∠C +∠CAD,∠ADM=∠MDE+∠ADC,∠ADC=∠CAD∴∠ADM=∠ADB∴△ADM≌△ADB∴∠BAD=∠MAD即AD平分∠BAE考点二三角形全等常见辅助线二:截长补短法1.如图,已知AP∥BC,∠PAB的平分线与∠CBA的平分线相交于点E,CE的延长线交AP于点D.求证:AD+BC=AB.证明:在AB上截取AF=AD,∵AE平分∠PAB,∴∠DAE=∠FAE,在△DAE和△FAE中,∴△DAE≌△FAE(SAS),∴∠AFE=∠ADE.∵AD∥BC,∴∠ADE+∠C=180°,∵∠AFE+∠EFB=180°,∴∠EFB=∠C.∵BE平分∠ABC,∴∠EBF=∠EBC,在△BEF和△BEC中,∴△BEF≌△BEC(AAS),∴BC=BF,∴AD+BC=AF+BF=AB.2.如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B =∠ADC=90°.E、F分别是BC、CD上的点,且∠EAF=60°.求证:EF=FD+BE.证明:如图,延长FD到点G,使DG=BE,连结AG.∵∠B=∠ADC=90°,∴∠B=∠ADG=90°.∵AB=AD,∴△ABE≌△ADG.∴AE=AG,∠BAE=∠DAG.又∵∠BAD=120°,∠EAF=60°,∴∠BAE+∠FAD=60°,∠DAG+∠FAD=60°.即∠GAF=60°,∴∠EAF=∠GAF=60°.∴△EAF≌△GAF.∴EF=GF=FD+DG,∴EF=FD+BE.考点三三角形全等常见模型一:一线三等角1.如图,在△ABC中,AB=AC,P、M分别在BC、AC边上,且∠APM=∠B,若AP=MP,求证:PB=MC.证明:∵∠B+∠BAP=∠APM+∠CPM,∠B=∠APM,∴∠BAP=∠CPM.∵AB=AC,∴△ABC为等腰三角形.∴∠B=∠C,又∵AP=PM,∴△APB≌△PMC.∴PB=MC 2.如图,一次函数y=-23x+4的图象分别与x轴、y轴交于点A,B,以AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.则过B,C两点的直线表达式为y=15x+4.3.(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E,则线段BD、CE、DE之间的关系是:DE=BD+CE ;(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问(1)中结论是否成立?若成立,请你给出证明;若不成立,请说明理由.图①图②解:(1)DE=BD+CE.(2)当α为任意钝角时,结论DE=BD+CE仍成立,理由:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,∴∠CAE=∠ABD,∵在△ADB和△CEA中,⎩⎨⎧∠ABD=∠CAE,∠BDA=∠AEC,AB=CA,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.考点四三角形全等常见模型二:手拉手1.如图,△ABC,△CDE是等边三角形,B,C,E三点在同一直线上,连接AE、BD交于点O.(1)求证:AE=BD;(2)求∠BOE的度数;(3)若BD和AC交于点M,AE和CD交于点N,求证:CM=CN.解:(1)∵△ABC和△DCE均为等边三角形,∴AC=BC,CE=CD,∠ACB=∠DCE=60°.∴∠BCD=∠ACE=120°.在△ACE和△BCD中,∴△ACE≌△BCD(SAS),∴AE=BD.(2) ∠BOE的度数为120°;(3)∵△ACE≌△BCD,∴∠CBD=∠CAE.∵∠ACN=180°-∠ACB-∠DCE=60°,∴∠BCM=∠ACN.在△BCM和△ACN 中,∴△BCM≌△ACN(ASA),∴CM=CN.2.如图,∠BAD =∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.(1)求证:BC=DE.(2)求∠EAF的度数;(3)若AC=10,求四边形ABCD的面积.解:(1)易证△ABC≌△ADE(SAS),∴BC=DE.(2) ∠EAF的度数为135°;(3) 四边形ABCD的面积=三角形ACE的面积=50.※课后练习1.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是D,E.AD=3,BE=1,则DE的长是 2 .2.如图,C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②∠AOB=60°;③AP=BQ;④DE=DP.其中正确的是①②③.(填序号)3.如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:AD=AE.证明:∵AB⊥AC,AD⊥AE,∴∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.在△ABD和△ACE中,∠BAD=∠CAE,AB=AC,∠ABD=∠ACE,∴△ABD≌△ACE,∴AD=AE.4.正方形ABCD中,E为BC上的一点,F为CD上的一点,∠EAF=45°,求证:BE+DF=EF.证明:延长EB使得BG=DF,连接AG,在△ABG和△ADF中,由AB=AD,∠ABG=∠ADF=90°,BG=DF,可得△ABG≌△ADF(SAS),∴∠DAF=∠BAG,AF=AG,又∵∠EAF=45°∴∠GAE=∠EAF=45°在△AEG和△AEF中,AE=AE,∠GAE=∠EAF,AG=AF∴△AEG≌△AEF(SAS),∴EF=GE= BG+BE即BE+DF=EF.5.如图,D是△ABC的边BC上的点,且CD=AB,∠ADB= ∠BAD,AE是△ABD的中线.求证:AC=2AE.解:延长AE到M ,使EM=AE,连结DM易证△DEM≌△BEA∴∠B=∠MDE, DM=AB又CD=AB∴DM=CD,又∠ADC=∠B+∠BAD,∠ADM=∠MDE+∠ADB,∠ADB=∠BAD∴∠ADM=∠ADC∴△ADM≌△ADC∴AC=AM=2AE6.如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC,∠ACB,AD,CE交于O.(1)求∠AOC的度数;(2)求证:AC=AE+CD.解:(1)∵∠1+∠2+∠3+∠4=180°-∠B=120°,∠1=∠2,∠3=∠4,∴∠2+∠3=60°,∴∠AOC=180°-60°=120°;(2)在AC上截取AF=AE,连接OF,∵AE=AF,∠1=∠2,AO=AO,∴△AEO≌△AFO(SAS),∴∠AOE=∠AOF,∵∠AOC=120°,∴∠AOE=∠DOC=60°,∴∠AOF=∠COF=60°,在△OFC和△ODC中,⎩⎨⎧∠FOC=∠DOC=60°,OC=OC,∠3=∠4,∴△OFC≌△ODC(ASA),∴FC=DC,∵AF+FC=AC,∴AC=AE+CD.7.Rt△ABC中,BC=AC,∠ACB=90°,D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上分别在点C 的两侧截取与线段CD相等的线段CE和CF,连接AE,BF.(1)当点D在线段AB上时(点D不与点A,B重合),如图1,线段BF,AD所在直线的位置关系为垂直,线段BF,AD的数量关系为相等.(2)当点D在线段AB的延长线上时,如图2,则(1)中的结论是否仍然成立?如果成立请证明;如果不成立,请说明理由.解:(2)成立.理由如下:∵CD⊥EF,∴∠DCF=90°,∵∠ACB=90°,∴∠DCF+∠BCD=∠ACB+∠BCD,即∠ACD=∠BCF,∵BC=AC,CD=CF,∴△ACD≌△BCF,∴AD=BF,∠BAC=∠FBC,∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.8.如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D 是中点,求证:BE+CF>EF.证明:延长FD至G,使得GD=DF,连接BG,EG∵在△DFC和△DGB中,DF=DG∠CDF=∠BDGDC=DB,∴△DFC≌△DGB(SAS),∴BG=CF,∵在△EDF和△EDG中DF=DG∠FDE=∠GDE=90°DE=DE∴△EDF≌△EDG(SAS),∴EF=EG在△BEG中,两边之和大于第三边,∴BG+BE>EG又∵EF=EG,BG=CF,∴BE+CF>EF.9.如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,按下列要求画图并回答:画∠MAB、∠NBA的平分线交于E(1)求∠AEB的度数;(2)过点E作一直线交AM于D,交BN于C,求证:DE=CE;(3)无论DC的两端点在AM、BN如何移动,只要DC经过点E,①AD+BC=AB;②AD+BC=CD谁成立?并说明理由.解:(1)∵AM∥BN,∴∠MAB+∠ABN=180°,又AE,BE分别为∠MAB、∠NBA的平分线,∴∠1+∠3=(∠MAB+∠ABN)=90°,∴∠AEB=180°-∠1-∠3=90°,即∠AEB为直角;(2)过E点作辅助线EF使其平行于AM,∵AM∥BN,EF∥BC,∴EF∥AD∥BC,∴∠AEF=∠4,∠BEF=∠2,∵∠3=∠4,∠1=∠2,∴∠AEF=∠3,∠BEF=∠1,∴AF=FE=FB,∴F为AB的中点,又EF∥AD∥BC,根据平行线等分线段定理得到E为DC中点,∴ED=EC;(3)由(2)中结论可知,无论DC的两端点在AM、BN如何移动,只要DC经过点E,总满足EF为梯形ABCD中位线的条件,所以总有AD+BC=2EF=AB.所以①成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学上册辅助线专题
教学目标:掌握各种类型的全等三角形的证明方法 教学重点:构造全等三角形 教学难点: 如何巧妙作辅助线 知识点: (一)截长补短型
(二)中点线段倍长问题
(三)蝴蝶形图案解决定值问题 (四)角平分线与轴对称
(五)等腰直角三角形,等边三角形 (六)双重直图案与全等三角形
典型例题讲练 重点例题:
一、截长补短型
如图,R T △CDA ≌RT △CDB,
①、若∠ACD=30°,∠MDN=60°,当∠MDN 绕点D 旋转时,AM 、MN 、BN 三条线段之间的关系式为______
②、若∠ACD=45°,∠MDN=45°,AM 、MN 、BN 三条线段之间的数量关系式为:______
③、由①②猜想:在上述条件下,当∠ACD 与∠MDN 满足什么条件时,上述关系式成立,证明你的结论。
二、中点线段倍长问题
如图△ABC 中,点D 是BC 边中点,过点D 作直线交AB 、CA 延长线于点E 、F 。
当AE=AF 时,求证BE=CF 。
B A
C
D M N ①
B
D A C M N ② A B C D M N ③
A
B
C D E F
三、蝴蝶形图案解决定值问题
1、如图,在R t △ACB 中,∠ACB=90°,CA=CB,D 是斜边AB 的中点,E 是DA 上一点,过点B 作BH ⊥CE 于点H ,交CD 于点F 。
(1) 求证:DE=DF.(2)若E 是线段BA 的延长线上一点,其它条件不变,
DE=DF 成立吗?画图说明。
2在△ABC 中,AB=AC,AD 和CE 是高,它们所在的直线相交于H 。
(1)如图1,若∠BAC=45°,求证:AH=2BD.
(2)如图2,若∠BAC=135°,(1)中的结论是否依然成立?请你在图2中画出图形并加以证明。
3,如图,等腰直角三角形ABC 中,AB=AC,∠BAC=90°,BE 平分∠ABC 交AC 于E ,过C 作CD ⊥BE 于D.求证BE=2CD.
(2) 连接AD ,求证:∠ADB=45°.
A
B C
D
E
F H
A
B C D E
H B A C C D B
A
E D B A E C
四、角平分线与轴对称 1、(1)如图①,R t △ABC 中,∠ACB=90°,∠BAC=60°,CD 平分∠ACB ,点E 为AB 上一点,且CE=BE ,PE ⊥AB 交CD 的延长线于P ,求∠PAC+∠PBC 的度数。
(2)如图②,R t △ABC 中,∠ACB=90°,∠BA C ≠45°,CD 平分∠ACB,点E 为AB 上一点,且CE=BE,PE ⊥AB 交CD 的延长线于P 。
(1)中结论是否成立,说明理由。
五、等腰直角三角形,等边三角形
1、如图①OA=2,OB=4,以A 点为顶点,AB 为腰在第三象限作等腰Rt △ABC 。
A
B
C D
E
P
A B
C D E
P
(2)如图②,P 为y 轴负半轴上一个动点,当P 点向y 轴负半轴向下运动时,若以P 点为顶点,PA 为腰作等腰Rt △APD ,过D 点作DE ⊥x 轴于E 点,求OP-DE 的值。
(3)如图③,已知点F 坐标为(-4,-4),当G 在y 轴的负半轴上沿负方向运动时,作Rt △FGH ,始终保持∠GFH=90°,FG 与y 轴负半轴交于点G(o,m),FH 与x 轴正半轴交于点H(n,o),当G 点在y 轴负半轴沿负方向运动时,求m+n 的值。
七、双重直图案与全等三角形
1、Rt △ABC 中,AB=AC,M 为BC 边上一点,连接AM ,过B 点作BN ⊥AM 交AC 于E 点,交AM 于D 点,在AC 上截取CF=AE,连接MF 并延长交BN 于N 点。
求证:∠AMB=∠CMF.
本次巩固题型
1、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=o
,且EF 交正方形外角DCG ∠的平分线CF 于点F ,求证:AE =EF . 经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.
A B
C
D
E F M
N
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
2、已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,
EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F . 当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证1
2
DEF CEF ABC S S S +=
△△△.
当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系?请写出你的猜想,不需证明.
A
D
F
C G
E B
图1
A
D
F C
G
E B 图2 A
D
F
G
B
图3
A E
C F
B D 图1
图3
A
D
F
E
C
B
A
D
B
C
E 图2
F
3.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母); (2)证明:DC BE .
图1
图2
(第22题)
4、在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为ABC V 外一点,且
︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上移动时,
BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.
图1 图2 图3
(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时
=L
Q
; (II )如图2,点M 、N 边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还
成立吗?写出你的猜想并加以证明;
(III ) 如图3,当M 、N 分别在边AB 、CA 的延长线上时, 若AN=x ,则Q= (用x 、L 表示).
5、已知四边形ABCD 中,AB AD ⊥,BC CD ⊥,AB BC =,120ABC =o
∠,
60MBN =o ∠,MBN ∠绕B 点旋转,它的两边分别交AD DC ,(或它们的延长线)
于E F ,.
当MBN ∠绕B 点旋转到AE CF =时(如图1),易证AE CF EF +=.
当MBN ∠绕B 点旋转到AE CF ≠时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE CF ,,EF 又有怎样的数量关系?请写出你的猜想,不需证明.
(图1) A B C
D E F
M N
(图2)
A B C
D E F
M N
(图3)
A
B
C D E F M
N
6、如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全
等三角形。
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC 中,∠ACB 是直角,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA
的平分线,AD 、CE 相交于点F 。
请你判断并写出FE 与FD 之间的数量关系; (2)如图③,在△ABC 中,如果∠ACB 不是直角,而(1)中的其它条件不变,请问,你
在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
信息反馈:
(第23题图)
O P A
M N
E B C
D
F A
E F B
D 图①
图② 图③
家长签字:。
