闭合导线坐标计算表格 有公式
测量,闭合导线等计算及表格

一.坐标计算以下为基本计算公式:直线上计算公式:已知该条直线的方位角à,已知直线的起点或终点的坐标,顺线路方向时,计算点的里程知道,直线的起点或终点的里程知道,可推算出计算点与直线的起点的直线距离d,(即计算点的里程减去起点的里程,逆线路方向时,为直线终点的里程减去计算点的里程),计算坐标增量:∆x=d×cosà∆y=d×cosà计算点的坐标为,直线的起点或终点坐标加上坐标增量,式中方位角à从直线起点算时,为已知即给定的方位角,而从终点算时,à为该段直线的起始方位角加上180度。
à+180à起点计算点终点第一种曲线为两段直线中加一圆曲线,指仅存在圆曲线,如下第1点。
1.圆曲线上计算点相对于ZY或YZ 点的弦长和偏角D=2 RSinδδ=90×L/(πR)δ---------圆曲线偏角D ---------弦长L --------为弧长α=α(zy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。
α=α(yz)-δα------------为计算点的方位角,此α为逆着线路方向计算时。
α(zy)、α(yz)---------为圆曲线的起始方位角。
一般为已知。
计算点相对与直圆点或圆直点的坐标增量:△x=D*COSα△y=D*SINα坐标增量计算完毕后,要算某一点的坐标,用直圆点或圆直点的坐标加上计算点与直圆点或圆直点的坐标增量,即为计算点的坐标。
缓和曲线同理。
第二种曲线为两段直线中始端加一缓和曲线,末端加一缓和曲线,两段缓和曲线中加一圆曲线,如下第2点。
2.缓和曲线上计算点相对于HY或YH点的弦长和偏角δ=L²/6RL0X1=L-(L^5/40R²L0²)Y1=L³/6RL0D=√(X1²+Y1²)α=α(hy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。
闭合导线测量的内业计算

角度闭合差的分配方法不同
陕西铁路工程职业技术学院公桥系
附合导线角度闭合差分配
α 12 2 B (1) β 2 β1
3
β
3
α A
AB
β
n-1
(n ) α C βn
cd
D
右角
v
f n
左角
v
f n
陕西铁路工程职业技术学院公桥系
闭合导线角度闭合差分配方法
陕西铁路工程职业技术学院公桥系
三.导线测量的内业 计算
闭合导线测量的内业计算
闭合导线与附合导线的区别之三
角度闭合差的计算不同
陕西铁路工程职业技术学院公桥系
附合导线角度闭合差计算
α 12 2 B (1) β 2 β1
3
β
3
α A
AB
β
n-1
(n ) α C βn
cd
D
右角 左角
f AB 右 n 180 CD f AB 左 n 180 CD
f f x2 f y2
B
D5B 0 5 2 4 3 D34
DB1
1 D12
5
D45
f y y测 y理 1
1 T 容许值 D f
图根导线
改正
fx vxi Di D
2
D23
4
1 T 2000
v yi 3 Di D
fy
检核
vx 0
(1)坐标增量计算 A
B DB1 0
xi ,i 1 Di cos i ,i 1 yi ,i 1 Di sin i ,i 1
1
B
D5B 5 2 4 3
闭合导线坐标计算(顺时针右内角)
B 127 25 38 127.4272222 -4.444444445 127.4259877 269.5280864 183.568
A 138 24 2 138.4005556 -4.444444445
和
—— —— —— 1260.011111
-40
已知α1= 0 0 1 0.000277778
4.978643 143.16446 4.957813765 143.14708 765.6561 605.9606
-88.37454 109.57122 -88.3950051 109.554144 770.6139 749.1076
-66.58147 26.744293 -66.591904 26.7355882 682.2189 858.6618 -160.6265 3.5615855 -160.64988 3.54209448 615.627 885.3974 -80.08118 -60.24492 -80.0957482 -60.2570738 454.9771 888.9395
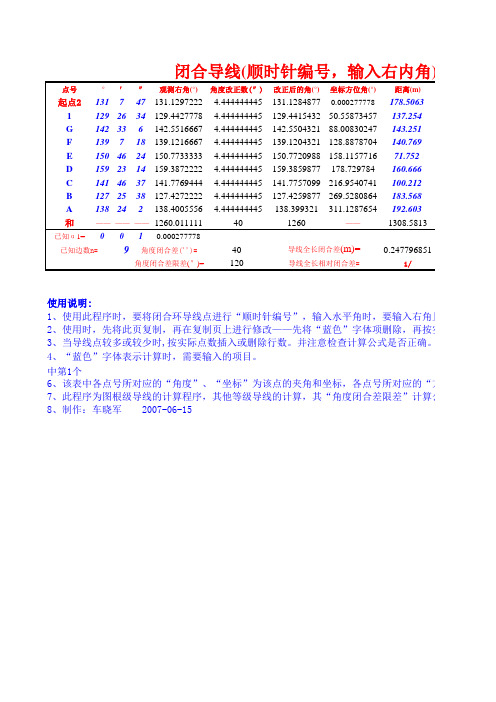
闭合导线(顺时针编号,输入右内角)坐标计算
点号
起点2 1 G
° ′ ″ 观测右角(°) 角度改正数(″) 改正后的角(°) 坐标方位角(°)
131 7 47 131.1297222 -4.444444445 131.1284877 0.000277778 129 26 34 129.4427778 -4.444444445 129.4415432 50.55873457 142 33 6 142.5516667 -4.444444445 142.5504321 88.00830247
-1.511931 -183.5618 -1.53862168 -183.584043 374.8813 828.6824
