六年级奥数专题找规律
六年级找规律奥数题

六年级找规律奥数题
题目:找出下面每行、每列和每个九宫格中的数字,并将它们组成一个四位数。
一行:357,892
一列:461,983
一个九宫格:289,417,982,357
要求:每个数字必须被4个数字整除,且这些数字不能重复。
解法:
首先观察题目中的数字,可以发现每行、每列和每个九宫格中的数字都是唯一的。
其次,我们可以使用穷举法来寻找符合条件的数字。
从行入手,如果行中的第一个数字是357,则该数字不能被4个数字整除,因此无法继续向下寻找。
同理,从列入手,如果列中的第一个数字是892,则该数字不能被4个数字整除,因此无法继续向下寻找。
因此,我们可以将这个行、列和九宫格中所有数字都排除掉,然后再从下一个行、列和九宫格中开始寻找符合条件的数字。
最后,我们使用计算机程序来解决这个问题,可以大大加快搜索的速度。
具体地,我们可以使用一个数组来表示符合条件的数字,使用一个循环来搜索整个数组。
在搜索过程中,我们需要检查每个数字是否被4个数字整除,如果符合条件,则将其加入数组中。
时间复杂度:O(n^3)
拓展:
这个问题可以推广到更大的数字规模。
例如,如果有n行、m列和n个九宫格,我们需要找到符合条件的n位数。
我们可以使用类似的方法来解决,即使用一个数组来表示符合条件的数字,使用一个循环来搜索整个数组。
在搜索过程中,我们需要检查每个数字是否被4个数字整除,如果符合条件,则将其加入数组中。
如果数字的规模很大,那么搜索的时间复杂度将变得非常高。
因此,我们需要使用更高效的算法来解决这个问题。
六年级上奥数第一讲找规律

六年级上奥数第一讲找规律第一讲 找规律给出几个具体的、特殊的数、式或图形,要求找出其中的变化规律,从而猜想出一般性的结论.解题的思路是实施特殊向一般的简化;具体方法和步骤是(1)通过对几个特例的分析,寻找规律并且归纳;(2)猜想符合规律的一般性结论;(3)验证或证明结论是否正确,下面通过举例来说明这些问题. 开篇小练习:1、有一列数,观察规律,并填写后面的数,-5,-2,1,4,_______,________,________。
2、有一组数为:1111111,,,,,,234567---- …找规律得到第11个数是_________,第n 个数是__________3、小凡在计算时发现,11×11=121,111×111=12321,1111×1111=1234321,他从中发现了一个规律。
你能根据他所发现的规律很快地写出 111111111×111111111=______吗? 答案是___________________________。
4、四个同学研究一列数:1,-3,5,-7,9,-11,13,……照此规律,他们得出第n 个数分别如下,你认为正确的是 ( )A.2n -1B.1-2nC.(1)(21)nn -- D.1(1)(21)n n +--5、如图,是用积木摆放一组图案,观察图形并探索:第五个图案中共有 块积木,第n 个图形中共有 块积木.6、观察数列1,1,2,3,5,8,x ,21,y ,……,则2x-y=____________7、观察下列各式:1234567822,24,28,216,232,264,2128,2256,======== …,请你根据上述规律,猜想108的末位数字是_________.8、观察下列各式:3211=3323332333321231236123410+=++=+++=典型例题:一、数字排列规律题1、下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 __ __2、请填出下面横线上的数字。
六年级奥数——找规律
(3)1,8,27,(),125,()
(4)3,6,9,15,24,(),63,()
2、按照规律在括号里画出每组的第32个图形。
(1)◎□○◎□○◎□○……()
(2)○○○□○○○□○○○□……()
(3)△△△○○△△△○○……()
3、六(2)班同学在六一国际儿童节按下面的规律在教室里挂上气球。
教学课题
探索规律
教学目标
掌握算式、数列及数图形中的规律,根据规律解答相关题目。
教学过程
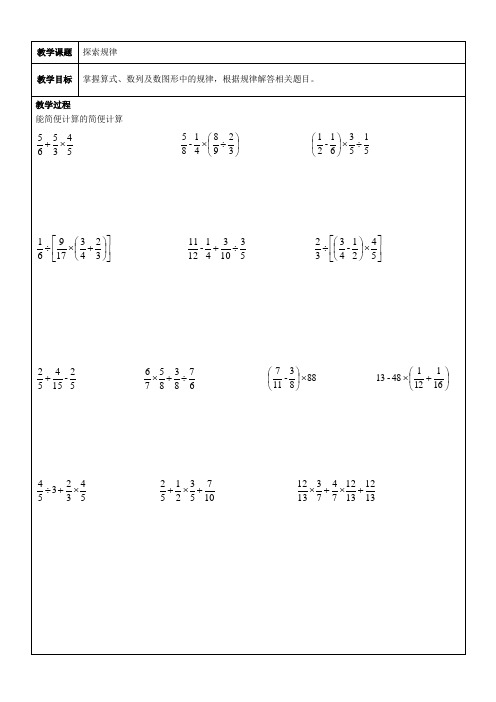
能简便计算的简便计算
探索规律
一、算式中的规律
在数学算式中探索规律,应认真观察算式的特点,再观察结果的特点,从而根据规律完成这一类题。如:
二、数列中的规律
按一定次数排列的一列数叫做数列
1、规律蕴涵在相邻两数的差和倍数中。
六、搭配中的规律
搭配问题的解题思路类似于乘法原理,即做一件事情,完成它需要分成n个步骤,做第一步有 中不同的方法,,做第二步有 中不同的方法…,做第 步有 中不同的方法,那么完成这件事有
例1:先观察下列各式,找出规律再填空。
(1)12345679×9=111111111
(2)12345679×18=222222222
例4:小明在一个正方形的棋盘里摆棋子,他先把最外层摆满,用了40个棋子,最外层每边有多少棋子?如果他要把整个棋盘摆满,还需要多少棋子?
例5:由1,2,3,4,5五个数字组成的五位数共有120个,将它们从小到大排列起来,第95个数是()。
跟踪练习
1、你能发现下列各组数的规律吗?
(1)8,11,14,17,(),23,26
如:12,15,17,30,22,45,27,60,…第1,3,5,…项依次相差5,第2,4,6,…项依次相差15。
(完整版)六年级数学经典找规律专题

找规律专题一.解答题(共 30 小题)1.( 2015?深圳)在生活中,经常把一些同样大小的圆柱管如图捆扎起来,下面我们来探索捆扎时绳子的长度,图中,每个圆的直径都是 8 厘米,当圆柱管放置放式是 “单层平放 ”时,100 个时需要绳子厘米( π取 3)2.( 2015?龙泉驿区校级三模)摆一个六边形需要六根小棒,摆 2 个六边形需要 11根小棒, 3 个需要 16 根小棒 ⋯问:摆 10 个六边形需要 根小棒,摆 100 个六边形需要 根小棒,摆 n 个六边形需要 根小棒.3.( 2015 春?淮安校级期中)用计算器计算,再根据规律编写一道算式并直接写出得数. (24+25) ×5= ; (872+873 )×5= ; (2830+2831 )×5= ;( + ) × = .4.( 2015 春?射阳县校级期中)根据规律填数. 9×9+9=90 9876×9+6=888905.( 2015 春?成都校级期中)如图表示 “宝塔”,它们的层数不同,但都是由一样大的小三角 形摆成的.仔细观察后,请回答:(1)五层的 “宝塔”最下层包含多少个小三角形?六层呢?七层呢? n 层呢? (2)整个五层 “宝塔”一共包含多少个小三角形?六层呢?七层呢? n 层呢?共几个面在外面7.( 2015 春?盐城校级期中)用小棒如图的方式搭正方搭 1 个正方形要 4 根小棒,搭 2 个正方形要 7 根小棒. (1)搭 3 个正方形要 根小棒; (2)搭 8 个正方形要 根小棒; (3)搭 n 个正方形要根小棒.(4)现有 2014 根小棒,可以搭个正方形.98×9+8=890 987×9+7=889098765×9+5= 987654 ×9+4=形.捆扎后的横截面积如图所示:6.( 2015 春?西安校级期中)仔细观察,根据发现的规律把表格填完整.第几幅图1 2 3 5 n8.(2015春?团风县期中)一串珠子按照 3 颗黑珠,2颗白珠, 3 颗红珠,2颗蓝珠的顺序排列.(1)第14 颗珠子是珠子.(2)第998 颗珠子是颜色珠子.9.(2015 春?射阳县校级期中)想一想,填一填.用上面的图形在左边表里框出5个数,先算出这5 个数的和,再想想算出的和与中间一个数有什么关系?如果5个数的和为795,请在上面图形里写出这 5 个数.10.(2015 春?威宁县校级期中)表中一共有50个奇数,黑线框出的5 个数之和是115;仔细观察后回答问题.(1)你能发现每次框出的 5 个数的和与中间数有什么关系吗?(2)如果框出5 个数的和要是375,应该怎么框?(先在图中框一框,并在下面用文字说明)(3)能框出和是295的 5 个数吗?为什么?(4)一共可以框出多少个大小不同的和?11.(2015 春?株洲校级月考)不计算,运用规律在横线上填上合适的数.7×9=6377×9=693777×9=69937777×9=69993 777777777×9=1÷7=0.142857142857 ⋯2÷7=0.285714285714 ⋯3÷7=0.428571428571 ⋯4÷7=0.575÷7=0.76÷7=7÷7=12.(2014?涟水县模拟)观察与计算.计算: 1+2+3+ ⋯+99+100+99+98+ ⋯+3+2+1=14.(2014?宝安区校级模拟)观察下面 3 题的规律,然后算出( 1)( 2)两小题的结果. 1+2+1=2 ×2=41+2+3+2+1=3 ×3=91+2+3+4+3+2+1=161) 1+2+3+ ⋯+99+100+99+ ⋯+3+2+1=15.(2014?绍兴)有些题目可以通过观察找出规律,知道答案.按照下图算式的规律不变,如果商是 123456,括号中的 “减数 ”应该是 . (3﹣3)÷27=0 (33 ﹣ 6) ÷27=1 (333﹣9)÷27=12(3333﹣12)÷27÷=123.16.(2014?武平县)观察图形找规律:1)按照图形变化规律填表:正方形个 12345数直角三角 048形个数2)如果画 8 个正方形能得到个直角三角形,画 n 个正方形能得到个直角三角形.序号 ①②③④⑤数列 A 13 5 7 9数列 B 0149⑩81+⋯ + + +1+ + +⋯+ + + =13.(2014?金寨县校级模拟)找规律,填表. 2)+17.(2014?东莞)探寻规律.用这种瓷砖来铺设地面. 如果铺成一个 2×2 的正方形图案 (如图 ?),其中完整的圆共有 5 个, 如果铺成一个 3×3 的正方形图案 (如图 ?),其中完整的圆共有 13 个,如果铺成一个 4×4 的正方形图案(如图 ④ ),其中完整的圆共有 25 个.若这样铺成 一个 10×10 的正方形图案,则其中完整的圆共有个.你要研究的问题是:正方体个数与拼成的长方体表面积之间的关系.根据你的发现填空.当正方体个数为 10 时,所拼成的长方体表面积是平方厘米.当正方体个数为 a 时,所拼成的长方体表面积是 平方厘米. 当拼成的长方体表面积是 202 平方厘米时,正方体个数是 .20.(2014?成都)有甲、乙两个同样的杯子,甲杯装满水,乙杯是空的.第一次将甲杯里的杯中的 倒回甲杯, ⋯,这样反复倒 2015 次后,甲杯中的水是原来的几分之几?18.(2014?东台市)准备( (2)一个挨着一个排成一都是棱长为 1 厘米的正方体.19.(2014?长沙)在如图所示的数表中,第 100 行左边的第一个数是,第二次将乙杯中水的倒回甲杯,第三次将甲杯中的 倒回乙杯,第四次将乙1)每个21.(2014?陕西校级模拟)有一列数 2, 9, 8,2, 6, ⋯从第 3 个数起,每个数都是前面两 个数乘积的个位数字.例如第四个数就是第二、第三两数乘积 9×8=72 的个位数字 2.问这 一列数第 1997 个数是几?, , , ⋯则 是第 个分数.23.(2014?临夏县模拟)找规律填数. 1,4, 9, 16,, ,49, ,81.24.(2014?湖南模拟)分析推理找规律① 1+2+1=4② 1+2+3+2+1=9③ 1+2+3+4+3+2+1=16④ 1+2+ ⋯+49+50+49+ ⋯+2+1=⑤ 1+2+⋯+(n ﹣1)+n+(n ﹣1)+⋯+2+1=(n 为自然数)2 2 225.(2014?江油市校级模拟) 1+3=4=22,1+3+5=9=32,1+3+5+7=16=4 2,⋯1+3+5+⋯+(2n ﹣1) =20132,则 n=.26.(2014?宁远县校级模拟)如图,第 6 个图形一共由 个小三角形组成,第 n个图形,一共由 个小角形组27.( 2014?广州模拟) 为了美化城市, 某商场在门前的空地上用花盆按如图所示的方式搭正 方形.28.( 2014?台湾模拟) 如图所示,按一定规律用棉花棒摆放图案:第一组的图案用棉花棒 2 枝,第二组用棉花棒 7 枝,第三组用棉花棒 15 枝,如此类推,问第二十组的图案用棉花 棒多少枝﹖29.( 2014?成都校级模拟)下面的小点按如图所示的规律摆放:第 1 个图形有 6 个小点,第 2 个图形有 10 个小点,第 3 个图形有 16 个小点,第 4 个图形有 24 个点 ⋯,依次规律,第 10 个图形中点的个数是,, ,,22.(2014?江油市校级模拟)有一串数,成.1)填写下表 正方形的层数 该层所需花盆的个数1 2 3 4 5 4 122)按这种规律搭下去,搭第 n (n 为正整数)层正方形,需要 盆花.30.(2014?海安县模拟)用小棒按照如下的方式摆图形.摆 1 个八边形需要8 根小棒,摆 2 个八边形需要15 根小棒,⋯摆50 个八边形需要根小棒;如果摆这样的八边形用了771 根小棒,你知道摆了个八边形.。
六年级奥数图形找规律学生版
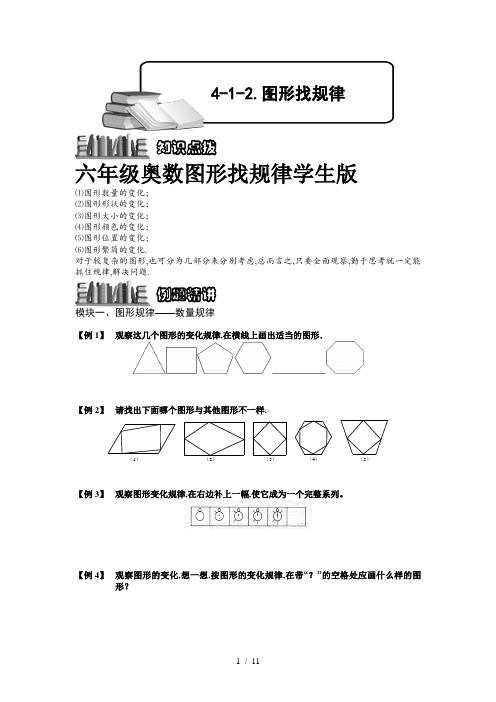
4-1-2.图形找规律知识点拨六年级奥数图形找规律学生版⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.例题精讲模块一、图形规律——数量规律【例 1】观察这几个图形的变化规律,在横线上画出适当的图形.【例 2】请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【例 4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【例 5】 观察下面的图形,按规律在“?”处填上适当的图形.(5)(4)(3)(2)(1)?【例 6】 观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【例 7】 观察下图中的点群,请回答:(1) 方框内的点群包含 个点;(2) 推测第10个点群中包含 个点; (3)前10个点群中,所有点的总数是 。
【例 8】观察下面由点组成的图形〈点群〉,请回答:〈1〉方框内的点群包含个点;〈2〉第〈10〉个点群中包含个点;〈3〉前十个点群中,所有点的总数是。
【例 9】下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:〈1〉五层的“宝塔”的最下层包含多少个小三角形?〈2〉整个五层“宝塔”一共包含多少个小三角形?【例 10】在纸上画5条直线,最多可有个交点。
模块二、图形规律——旋转、轮换型规律【例 11】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○ □ ☆△ ○ □ ☆△△ ○ □ ☆△ ○ □ ☆☆△ ○ □ ☆△ ○ □〈〉〈〉〈〉〈〉〈〉〈〉〈〉〈〉【例 12】下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.〈1〉?第1组第3组第2组〈2〉?第1组第3组第2组〈3〉★★★★★?第3组第2组第1组【例 13】 观察下图的变化规律,画出丙图.甲D CB A乙DABC丙【例 14】 图中的三个图形都是由A 、B 、C 、D 〈线段或圆〉中的两个组合而成,记为A ★B 、C ★D 、A ★D .请你画出表示A ★C 的图形.A ★BC ★DA ★D【例 15】 〈希望杯五年级一试第7题,6分〉下列四个图形是由四个简单图形A 、B 、C 、D〈线段和正方形〉组合〈记为*〉而成。
找规律知识点六年级

找规律知识点六年级一、数列和规律数列是由一系列按照一定规律排列的数字组成的序列。
在六年级的数学学习中,其中一个重要的知识点就是寻找数列中的规律。
通过观察数列中的数字变化规律,我们可以预测数列的下一个数字,甚至推导出数列的通项公式。
例如,考虑以下数列:2, 4, 6, 8, ...我们可以发现,每个数字都比前一个数字大2。
因此,可以得出这个数列的通项公式为:a_n = 2n,其中a_n表示数列中的第n个数字。
二、常见的数列规律1. 等差数列:在等差数列中,每个数字与前一个数字之差都是一个常数,这个常数称为公差。
例如,考虑以下数列:3, 6, 9, 12, ...我们可以发现,每个数字都比前一个数字大3。
因此,这个数列的公差为3。
可以得出通项公式为:a_n = 3n。
2. 等比数列:在等比数列中,每个数字与前一个数字的比值都相等,这个比值称为公比。
例如,考虑以下数列:2, 4, 8, 16, ...我们可以发现,每个数字都是前一个数字乘以2。
因此,这个数列的公比为2。
可以得出通项公式为:a_n = 2^n。
3. 斐波那契数列:斐波那契数列中的每个数字都是前两个数字之和。
例如,考虑以下数列:1, 1, 2, 3, 5, 8, ...我们可以发现,每个数字都是前两个数字之和。
可以得出通项公式为:a_n = a_(n-1) + a_(n-2),其中a_1 = 1,a_2 = 1。
三、寻找数列规律的方法1. 观察数列中数字之间的增减关系。
可以通过计算相邻数字的差值或者比值,判断数列是否具有等差或等比的规律。
2. 观察数列中数字之间的差值或比值是否保持恒定。
如果是恒定的,那么可以得出数列的通项公式。
3. 尝试使用已知的数列类型来逼近要寻找规律的数列。
有时候,一个数列可以被近似表示为某种已知的数列类型。
4. 利用递推公式或递推关系式来求解数列的规律。
递推公式描述了数列中每个数字与前面数字之间的关系。
四、数列规律的应用1. 预测数列未知部分的数字。
六年级奥数规律专题

第二章 规律专题(1)掌握等差数列的运用及变式,会总结数列的规律,并会用规律解决问题.例1 按规律填空:①2,4,6,8,10,···第100个数是( ),第101个数是( ),第n 个数是( ). ②3,6,9,12,15,···第100个数是( ),第101个数是( ),第n 个数是( ). 举一反三1. 4,8,12,16,20,···第100个数是( ),第101个数是( ),第n 个数是( ).2. 5,10,15,20,25,···第100个数是( ),第101个数是( ),第n 个数是( ).3. 7,14,21,28,35,···第100个数是( ),第101个数是( ),第n 个数是( )例2.按规律填空:①1,3,5,7,( ),( )···第100个数是( ),第101个数是( ),第n 个数是( ) ②2,6,10,14,( ),( )···第100个数是( ),第101个数是( ),第n 个数是( )举一反三1. 3,10,17,24,( ),( )···第100个数是( ),第101个数是( ),第n 个数是( )2. 1,4,7,10,( ),( )···第100个数是( ),第101个数是( ),第n 个数是( )3. 5,8,11,14,( ),( )···第100个数是( ),第101个数是( ),第n 个数是( ) 例3.按规律填空:①1,4,9,16,25,( ),( )···第n 个数是( ). ②3,4,6,9,13,18,( ),( ). 举一反三:1. 2,5,10,17,26,37,( ),( )···第n 个数是( ).2. 1,5,14,30,55,( ),( ).3. 1,5,11,19,29,( ),55.一.选择题1.下列一组数:2,6,10,14,( ),22,空格内应填( ). A.16 B.18 C.20 D.无法确定2.数列:19,17,15,13,( ),9,7中,空格内的数为( ). A.12 B.11 C.10 D.无法确定示范求解考点归纳学习思考自我检测3.根据下列规律:7a ,10a ,13a ,16a ,( ),21a ,空格内应填( ). A.18 B.19 C.18a D.19a二.填空题1.按规律填空:-1,4,-9,16,-25,36,( ),( ).2.根据下列数列规律填空:4,9,14,19,( ),( ).3.按规律填空:3,4,7,12,( ),28. 三.解答题1.观察下列各式数:0,3,8,15,24,……。
六年级数学奥数等差数列等比数列找规律填数

等差数列 知识导航: 把数列的第1项记为 ,第2项记为 ,……第 项记为 ,相邻两项的差(常数)记为 ,则有 ; ; ;……
1、在 这一列数中的第8个数是
2、观察规律填写第五、第六个数:1、4、7、10、 、 。
3、在8与36之间插入6个数,使它们同这两个数成等差数列。
找规律填数 知识导航: 1、利用等差数列求数。 2、利用等比数列求数。 3、利用周期性的特点找规律。 4、其他带有规律性的问题:如一列数1,1,2,3,5,8,13,…我们不难发现,后一个数是前两个数之和。 练习: 1、1,4,7,10, , 。 2、据报道目前用超级计算机找到的最大质数是 ,这个质数的末尾数字是( ) A、1 B、3 C、7 D、9 3、将连续奇数1,3,5,7,…2003,2005,排成表1形式,那么2005属于A,B,C,D,E中的 类。 4、将1,2,3,…,50,这50个数按表2的形式排列,则数50所在位置是A,B,C中的 处。 A B C D E 1 2 9 10 25 … A 1 3 5 4 3 8 11 24 …��13 11 9 7 5 6 7 12 23 …��15 17 19 16 15 14 13 22 …��27 25 23 21 17 18 19 20 21 …��29 31 33��������������41 39 37 35 C … … … … … B … … … … … 表1 表2 5、的末位数字是( ) A、2 B、4 C、6 D、8
4、已知一个等差数列的首项为5,公差是2,那么它的第10项、第15项各是多少?
5、梯子的最高一级宽32cm,最低一级宽110cm,中间还有9级,各级的宽度成等差数列,计算当中一级的宽。
等比数列 知识导航: 把数列的第1项记为 ,第2项记为 ,……第 项记为 ,相邻两项的比记为 ,则有 ; ; ;…… 1、根据规入括号内 19=1×9+(1+9);29=2×9+(2+9);39=3×9+(3+9); 那么1289= =N×9+(N+9)
六年级奥数专题:找规律

六年级奥数博题:找顺序之阳早格格创做共教们从三年级启初,便陆绝交战过许多“找顺序”的题目,比方创造图形、数字或者数表的变更顺序,创造数列的变更顺序,创造周期变更顺序等等.那一道的实质是通过创造某一问题的顺序,推导出该问题的估计公式.例1 供99边形的内角战.分解与解:三角形的内角战等于180°,但是99边形的内角战何如供呢?咱们把问题简化一下,先供四边形、五边形、六边形……的内角战,找一找其中的顺序.如上图所示,将四边形ABCD分成二个三角形,每个三角形的内角战等于180°,所以四边形的内角战等于180°×2= 360°;共理,将五边形ABCDE分成三个三角形,得到五边形的内角战等于180°×3=540°;将六边形ABCDEF分成四个三角形,得到六边形的内角战等于180°×4=720°.通过上头的图形及分解不妨创造,多边形被分成的三角形数,等于边数减2.由此得到多边形的内角战公式:n边形的内角战=180°×(n-2)(n≥3).有了那个公式,再供99边形的内角战便太简单了.99边形的内角战=180°×(99-2)=17460°.例2 四边形内有10个面,以四边形的4个顶面战那10个面为三角形的顶面,最多能剪出几个小三角形?分解与解:正在10个面中任与一面A,连结A与四边形的四个顶面,形成4个三角形.再正在剩下的9个面中任与一面B.如果B正在某个三角形中,那么连结B与B天方的三角形的三个顶面,此时三角形总数减少2个(睹左下图).如果B正在某二个三角形的大众边上,那么连结B与B天方边相对付的顶面,此时三角形总数也是减少2个(睹左下图).类似天,每减少一个面减少2个三角形.所以,共可剪出三角形 4+ 2× 9= 22(个).如果将例2的“10个面”改为n个面,其余条件没有变,那么由以上的分解可知,最多能剪出三角形4+2×(n-1)=2n+2=2×(n+1)(个).共教们皆了解圆柱体,如果将圆柱体的底里换成三角形,那么便得到了三棱柱(左下图);共理不妨得到四棱柱(下中图),五棱柱(左下图).如果底里是正三角形、正四边形、正五边形……那么相映的柱体便是正三棱柱、正四棱柱、正五棱柱……例3 n棱柱有几条棱?如果将没有相接的二条棱称为一对付,那么n棱柱公有几对付没有相接的棱?分解与解:n棱柱的底里战顶里皆是n边形,每个n边形有n个顶面,所以n棱柱公有2n个顶面.瞅察三棱柱、四棱柱、五棱柱的图形,不妨瞅出,每个顶面皆与三条棱贯串,而每条棱对接 2个顶面,所以n棱柱公有棱 2n×3÷2=3n (条).进一步瞅察不妨创造,n棱柱中每条棱皆与4条棱相接,与其余的3n-4-1 =(3n-5)条棱没有相接.公有3n条棱,所以没有相接的棱有 3n×(3n- 5)(条),果为没有相接的棱是成对付出现的,各估计一遍便沉复了一遍,所以没有相接的棱公有3n×(3n-5)÷2(对付).例4 用四条曲线最多能将一个圆分成几块?用100条曲线呢?分解与解:4条曲线时,咱们不妨试着绘,100条曲线便没有成能再绘了,所以必须觅找到顺序.如下图所示,一个圆是1块;1条曲线将圆分为2块,即减少了1块;2条曲线时,当2条曲线没有相接时,减少了1块,当2条曲线相接时,减少了2块.由此瞅出,要念分成的块尽管多,应当使后绘的曲线尽管与前里已绘的曲线相接.再绘第3条曲线时,应当与前里2条曲线皆相接,那样又减少了3块(睹左下图);绘第4条曲线时,应当与前里3条曲线皆相接,那样又减少了4块(睹左下图).所以4条曲线最多将一个圆分成1+1+2+3+4=11(块).由上头的分解不妨瞅出,绘第n条曲线时应当与前里已绘的(n—1)条曲线皆相接,此时将减少n块.果为一启初的圆算1块,所以n条曲线最多将圆分成1+(1+2+3+…+n)=1+n(n+1)÷2(块).当n=100时,可分成1+100×(100+1)÷2=5051(块).例5 用3个三角形最多不妨把仄里分成几部分?10个三角形呢?分解与解:仄里自己是1部分.一个三角形将仄里分成三角形内、中2部分,即减少了1部分.二个三角形没有相接时将仄里分成3部分,相接时,接面越多分成的部分越多(睹下图).由上图瞅出,新减少的部分数与减少的接面数相共.所以,再绘第3个三角形时,应使每条边的接面尽管多.对付于每个三角形,果为1条曲线最多与三角形的二条边相接,所以第3个三角形的每条边最多与前里2个三角形的各二条边相接,共可爆收3×(2×2)= 12(个)接面,即减少12部分.果此, 3个三角形最多不妨把仄里分成1+1+6+12= 20(部分).由上头的分解,当绘第n(n≥2)个三角形时,每条边最多与前里已绘的(n—1)个三角形的各二条边相接,共可爆收接面3×[(n—l)×2]=6(n—1)(个),能新减少6(n-1)部分.果为1个三角形时有2部分,所以n个三角形最多将仄里分成的部分数是2+6×[1+2+…+(n—1)]当n=10时,可分成2+3×10×(10—1)=272(部分).训练1.供12边形的内角战.2.五边形内有8个面.以五边形的5个顶面战那8个面为三角形的顶面,最多能剪出几个小三角形?3.已知n棱柱有14个顶面,那么,它有几条棱?4.n条曲线最多有几个接面?5.6条曲线与2个圆最多产死几个接面?6.二个四边形最多把仄里分成几部分?训练问案:1.1800°.2.19个.提示:与例2类似可得5+2×(8-1)=19(个).3.21条棱.提示:n棱柱有2n个顶面,3n条棱.4.n(n-1)÷2.解:1+2+3+…+(n-1)=n(n-1)÷2.5.41个.解:6条曲线有接面6×(6-1)÷2=15(个),每条曲线与二个圆各有2个接面,二个圆之间有2个接面,公有接面15+6×4+2=41(个).6.10部分.提示:睹左图.与例5类似,当绘第n(n≥2)个四边形时,每条边应与已绘的(n-1)个四边形的各2条边相接,共可爆收接面4×[(n-1)×2]=8(n-1)(个),新减少8(n-1)部分.果为1个四边形有2部分,所以n个四边形最多将仄里分成2+8×[1+2+…+(n-1)]=2+4n(n-1)(部分).。
六年级上册数学试题 - 奥数竞赛找规律填图形 全国通用(含答案)
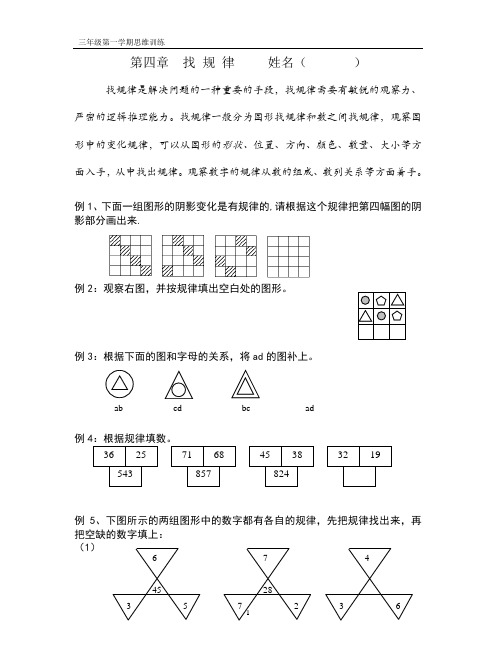
6 45 35 7 287 2 4 3 6第四章 找 规 律 姓名( )找规律是解决问题的一种重要的手段,找规律需要有敏锐的观察力、严密的逻辑推理能力。
找规律一般分为图形找规律和数之间找规律,观察图形中的变化规律,可以从图形的形状、位置、方向、颜色、数量、大小等方面入手,从中找出规律。
观察数字的规律从数的组成、数列关系等方面着手。
例1、下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来.例2:观察右图,并按规律填出空白处的图形。
例3:根据下面的图和字母的关系,将ad 的图补上。
例4:根据规律填数。
例5、下图所示的两组图形中的数字都有各自的规律,先把规律找出来,再把空缺的数字填上:(1)ab cd bcad 36 25 543 71 68 857 45 38 824 3219(2)例6:仔细观察下图,根据规律填出所缺的数。
例7:下面三块正方体的六个面,都是按相同的规律涂有红、黄、蓝、白、黑、绿六种颜色。
那么请你根据这一规律,白色的对面是什么颜色?红色的对面是什么颜色?黄色的对面是什么颜色?(1) (2) (3)练习:1、下面括号里两个数按一定规律组合,在( )里填上适当的数。
(1)、(8,7)、(6,9)(10、5)、( 、13 )。
(2)、(2,3)、(5,9)、(7、13)、( 、23 )。
(3)、(18,10)、(10,6)、(20、11)、( 、4(4)、 1、 2、 3、 6、 11、 20、( )2、仔细观察一右图,并按它的变化规律, 在“?”处填上适当的图。
3、在右图空格里填数白 黑 黄 绿 白 红 黄蓝 红 ? 3 12 6 4 16 8 5 206 124.下面的每一个图形都是由△,□,○中的两个构成的。
观察各图形与它下面的数之间的关系,“?”应当是几?5、找规律,从a,b,c,d,e中选入一幅图填入空格内.6. 找规律,画出第四幅图的答案.7、下图是由9个小人排列的方阵,但有一个小人没有到位,请你从右面的6个小人中,选一位小人放到问号的位置.你认为最合适的人选是()号.8、根据规律填数。
六年级-奥数-找规律(二)

第十九讲 找规律(二)【典型例题】例1、将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则①n = ;②第i 行第j 列的数为 (用i ,j 表示).第1列 第2列第3列… 第n 列第1行 123… n第2行 1+n 2+n 3+n … n 2 第3行 12+n22+n32+n… n 3… … … … … …例2、下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”最下层包含多少个小三角形?六层呢?七层呢?n 层呢?(2)整个五层“宝塔”一共包含多少个小三角形?六层呢?七层呢?n 层呢?例3、下图是由9个小人排列的方阵,但有一个小人没有到位,请你从下面图10—2中的6个小人中,选一位小人放到问号的位置,你认为最合适的人选是几号?例4、四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第五次交换位子后,小兔坐在第几号位子上?例5、杨老师在化学实验室做试验时,将水稻种子分组进行发芽试验;第1组取3粒,第2组取5粒,第3组取7粒……按此规律,那么请你推测第n 组应该有种子数是多少?【经典练习】1、观察下列图形,则第n 个图形中三角形的个数是( )A .22n +B .44n +C .44n -D .4n2、将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个……第1个 第2个 第3个小圆.3、观察下列等式:221.4135-=⨯; 222.5237-=⨯; 223.6339-=⨯; 224.74311-=⨯ …………则第n (n 是正整数)个等式为 .4、有一列数1234251017--,,,,…,那么第7个数是 . 5、王婧同学用火柴棒摆成如下的三个“中”字形图案,依此规律, 第n 个“中”字形图案需 根火柴棒.6、观察数表根据表中数的排列规律,则字母A 所表示的数是____________.7、如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是____________第1个图形 第2个图形 第3个图形 第4个图形…11 1 1 1 1 1 1 11-1-1-6-6-2-3-5-4-4-3 6 10 15 15 5 A 20- 18、下图是一组有规律的图案,第1个图案由4个基础图形组成,第2个 图案由7个基础图形组成……第n (n 是正整数)个图案中由 个基础图形组成.9、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个 .【课后作业】1、下图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = . (用n 的代数式表示s )2、下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“○”的个数为 .……n =1 n =2n =3(1)(2)(3)…………第1个第2个第3个(1)(2)(3)……3、用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有黑色瓷砖________块,第n 个图形中需要黑色瓷砖__________块(用含n 的代数式表示).4、将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第 行第 列.5、古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”. 从图1中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )A 、13 = 3+10B 、25 = 9+16C 、36 = 15+21D 、49 = 18+316、正整数按下图规律排列.请写出第20行,第21列的数字 .1 2 34=1+3 9=3+6 16=6+10图1…第一行第二行第三行第四行第五行第一列第二列第三列第四列第五列1 2 5 10 17 …4 3 6 11 18 …9 8 7 12 19 …16 15 14 13 20 …25 24 23 22 21 ………。
六年级找规律数学题

六年级找规律数学题一、数字规律1. 按规律填数:1,3,6,10,15,(),28。
- 解析:观察这组数字,1到3增加了2,3到6增加了3,6到10增加了4,10到15增加了5。
可以发现相邻两个数的差值在依次递增1。
那么15后面的数应该比15大6,即15 + 6 = 21。
验证一下,21到28增加了7,符合规律。
所以括号里应填21。
2. 数列:2,4,8,16,32,()。
- 解析:这组数列中,2×2 = 4,4×2 = 8,8×2 = 16,16×2 = 32。
可以得出规律是后一个数是前一个数的2倍。
所以括号里的数应该是32×2 = 64。
二、图形规律1. 用小棒按照如下方式摆三角形:摆1个三角形需要3根小棒;摆2个三角形需要5根小棒;摆3个三角形需要7根小棒……(1)摆10个三角形需要多少根小棒?- 解析:观察可得,摆1个三角形用3根小棒(3 = 2×1+1);摆2个三角形用5根小棒(5 = 2×2 + 1);摆3个三角形用7根小棒(7 = 2×3+1)。
可以总结出规律,摆n个三角形需要2n + 1根小棒。
当n = 10时,2×10+1 = 21根小棒。
(2)有21根小棒,可以摆多少个三角形?- 解析:根据前面总结的规律2n+1。
设可以摆n个三角形,则2n + 1 = 21,2n = 20,解得n = 10。
所以21根小棒可以摆10个三角形。
2. 下列图形是由同样大小的小圆圈按照一定规律所组成的,其中第1个图形中一共有6个小圆圈,第2个图形中一共有9个小圆圈,第3个图形中一共有12个小圆圈……(1)第5个图形中有多少个小圆圈?- 解析:观察图形,第1个图形有6 = 3×1+3个小圆圈;第2个图形有9 = 3×2 + 3个小圆圈;第3个图形有12 = 3×3+3个小圆圈。
可以得出规律,第n个图形有3n+3个小圆圈。
六年级奥数作找规律学生版

操作找规律知识点拨六年级奥数作找规律学生版在奥数中有一类“不讲道理”的题目,我们称之为“简单操作找规律”。
有一些对小学生来说很难证明的,但与证明相比,发现却是比较容易的。
这也是数学中的一种重要的思想,在以后的数学学习中会有一种先猜后证的解题方法。
这类题主要考查孩子们的发现能力。
例题精讲模块一,周期规律【例 1】四个小动物换座位.一开始,小鼠坐在第1号位子,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子.第一次上下两排交换.第二次是在第一次交换后再左右两排交换.第三次再上下两排交换.第四次再左右两排交换……这样一直换下去.问:第十次交换位子后,小兔坐在第几号位子上?〈参看下图〉【考点】操作找规律【难度】2星【题型】解答【关键词】华杯赛,初赛【解析】根据题意将小兔座位变化的规律找出来.可以看出:每一次交换座位,小兔的座位按顺时针方向转动一格,每4次交换座位,小兔的座位又转回原处.知道了这个规律,答案就不难得到了.第十次交换座位后,小兔的座位应该是第2号位子。
【答案】第2号【例 2】在1989后面写一串数字。
从第5个数字开始,每个数字都是它前面两个数字乘积的个位数字。
这样得到一串数字:1 9 8 9 2 8 6 8 8 42 ……那么这串数字中,前2005个数字的和是____________。
【考点】操作找规律【难度】2星【题型】填空【关键词】迎春杯,中年级,初试【解析】由题意知,这串数字从第5个数字开始,只要后面的连续两个数字与前面的连续两个数字相同,后面的数字将会循环出现。
1989︱286884︱28……由上图知,从第5个数字开始,按2,8,6,8,8,4循环出现。
()-÷=⋯,前2005个数字和是2005463333()()()+++++++++⨯+++271198816120311989286884333286=++=。
【答案】12031【例 3】先写出一个两位数62,接着在62右端写这两个数字的和8,得到628,再写末两位数字2和8的和10,得到62810,用上述方法得到一个有2006位的整数:628101123…,则这个整数的数字之和是。
找规律小学奥数题100道及答案(完整版)

找规律小学奥数题100道及答案(完整版)题目1:1,3,5,7,9,()答案:11(相邻两个数的差为2,依次递增)题目2:2,4,6,8,10,()答案:12(相邻两个数的差为2,依次递增)题目3:5,10,15,20,25,()答案:30(相邻两个数的差为5,依次递增)题目4:1,4,9,16,25,()答案:36(分别是1、2、3、4、5 的平方,下一个是 6 的平方)题目5:3,6,9,12,15,()答案:18(相邻两个数的差为3,依次递增)题目6:1,2,4,8,16,()答案:32(后一个数是前一个数的2 倍)题目7:2,6,12,20,30,()答案:42(相邻两个数的差依次为4、6、8、10、12)题目8:1,1,2,3,5,8,()答案:13(前两个数相加等于后一个数)题目9:3,4,7,11,18,()答案:29(前两个数相加等于后一个数)题目10:1,3,7,13,21,()答案:31(相邻两个数的差依次为2、4、6、8、10)题目11:2,5,10,17,26,()答案:37(相邻两个数的差依次为3、5、7、9、11)题目12:9,16,25,36,()答案:49(分别是3、4、5、6 的平方,下一个是7 的平方)题目13:1,8,27,64,()答案:125(分别是1、2、3、4 的立方,下一个是5 的立方)题目14:5,12,19,26,33,()答案:40(相邻两个数的差为7,依次递增)题目15:3,8,15,24,()答案:35(相邻两个数的差依次为5、7、9、11)题目16:2,3,5,8,13,()答案:21(前两个数相加等于后一个数)题目17:1,4,10,22,46,()答案:94(相邻两个数的差依次为3、6、12、24、48)题目18:1,5,14,30,55,()答案:91(相邻两个数的差依次为4、9、16、25、36)题目19:2,6,18,54,()答案:162(后一个数是前一个数的3 倍)题目20:7,14,28,56,()答案:112(后一个数是前一个数的2 倍)题目21:1,2,6,24,120,()答案:720(后一个数依次是前一个数乘2、3、4、5、6)题目22:3,5,9,17,33,()答案:65(相邻两个数的差依次为2、4、8、16、32)题目23:1,3,8,19,42,()答案:89(相邻两个数的差依次为2、5、11、23、47,这些差依次增加3、6、12、24)题目24:2,4,10,28,82,()答案:244(相邻两个数的差依次为2、6、18、54、162,后一个差是前一个差的 3 倍)题目25:5,9,17,33,65,()答案:129(相邻两个数的差依次为4、8、16、32、64)题目26:1,4,27,256,()答案:3125(分别是1、2、3、4 的1、2、3、4 次方,下一个是5 的 5 次方)题目27:1,6,21,66,201,()答案:606(相邻两个数的差依次为5、15、45、135、405,后一个差是前一个差的3 倍)题目28:3,8,15,24,35,()答案:48(相邻两个数的差依次为5、7、9、11、13)题目29:2,3,7,18,47,()答案:123(7 = 3×2 + 1,18 = 7×2 + 4,47 = 18×2 + 11,下一个数应为47×2 + 16 = 123)题目30:1,2,5,14,41,()答案:122(相邻两个数的差依次为1、3、9、27、81,后一个差是前一个差的3 倍)题目31:2,5,11,23,47,()答案:95(相邻两个数的差依次为3、6、12、24、48)题目32:4,9,16,25,36,()答案:49(分别是2、3、4、5、6 的平方,下一个是7 的平方)题目33:6,12,20,30,42,()答案:56(相邻两个数的差依次为6、8、10、12、14)题目34:1,3,7,15,31,()答案:63(相邻两个数的差依次为2、4、8、16、32)题目35:3,9,27,81,()答案:243(后一个数是前一个数的3 倍)题目36:5,13,25,41,()答案:61(相邻两个数的差依次为8、12、16、20)题目37:2,8,32,128,()答案:512(后一个数是前一个数的4 倍)题目38:7,16,29,46,()答案:67(相邻两个数的差依次为9、13、17、21)题目39:1,5,13,25,()答案:41(相邻两个数的差依次为4、8、12、16)题目40:6,18,54,162,()答案:486(后一个数是前一个数的3 倍)题目41:8,18,32,50,()答案:72(相邻两个数的差依次为10、14、18、22)题目42:1,4,13,40,()答案:121(相邻两个数的差依次为3、9、27、81)题目43:3,10,21,36,()答案:55(相邻两个数的差依次为7、11、15、19)题目44:5,15,45,135,()答案:405(后一个数是前一个数的3 倍)题目45:2,6,14,30,()答案:62(相邻两个数的差依次为4、8、16、32)题目46:9,25,49,81,()答案:121(分别是3、5、7、9 的平方,下一个是11 的平方)题目47:7,19,37,61,()答案:91(相邻两个数的差依次为12、18、24、30)题目48:4,12,36,108,()答案:324(后一个数是前一个数的3 倍)题目49:1,6,15,28,()答案:45(相邻两个数的差依次为5、9、13、17)题目50:8,20,36,56,()答案:80(相邻两个数的差依次为12、16、20、24)题目51:3,11,23,39,()答案:59(相邻两个数的差依次为8、12、16、20)题目52:6,15,35,77,()答案:143(相邻两个数的差依次为9、20、42、66,差依次增加11、22、24)题目53:2,9,28,65,()答案:126(分别是1、2、3、4 的立方加1,下一个是5 的立方加1)题目54:1,7,19,37,()答案:61(相邻两个数的差依次为6、12、18、24)题目55:5,16,29,46,()答案:67(相邻两个数的差依次为11、13、17、21)题目56:3,12,27,48,()答案:75(相邻两个数的差依次为9、15、21、27)题目57:7,18,33,52,()答案:77(相邻两个数的差依次为11、15、19、25)题目58:2,10,30,68,()答案:130(相邻两个数的差依次为8、20、38、62,差依次增加12、18、24)题目59:4,15,32,55,()答案:84(相邻两个数的差依次为11、17、23、29)题目60:6,21,42,72,()答案:106(相邻两个数的差依次为15、21、30、34)题目61:1,9,25,49,()答案:81(分别是1、3、5、7 的平方,下一个是9 的平方)题目62:8,24,48,80,()答案:120(相邻两个数的差依次为16、24、32、40)题目63:3,13,31,57,()答案:91(相邻两个数的差依次为10、18、26、34)题目64:5,19,41,71,()答案:105(相邻两个数的差依次为14、22、30、34)题目65:2,11,26,47,()答案:76(相邻两个数的差依次为9、15、21、29)题目66:9,27,51,81,()答案:117(相邻两个数的差依次为18、24、30、36)题目67:7,17,33,55,()答案:83(相邻两个数的差依次为10、16、22、28)题目68:4,14,30,52,()答案:78(相邻两个数的差依次为10、16、22、26)题目69:6,18,36,60,()答案:90(相邻两个数的差依次为12、18、24、30)题目70:1,11,27,51,()答案:81(相邻两个数的差依次为10、16、24、30)题目71:5,17,33,53,()答案:77(相邻两个数的差依次为12、16、20、24)题目72:3,14,31,58,()答案:91(相邻两个数的差依次为11、17、27、33)题目73:8,22,42,70,()答案:106(相邻两个数的差依次为14、20、28、36)题目74:2,13,30,53,()答案:84(相邻两个数的差依次为11、17、23、31)题目75:9,29,55,91,()答案:133(相邻两个数的差依次为20、26、36、42)题目76:7,20,39,64,()答案:95(相邻两个数的差依次为13、19、25、31)题目77:4,16,36,64,()答案:100(分别是2、4、6、8 的平方,下一个是10 的平方)题目78:3,15,33,57,()答案:87(相邻两个数的差依次为12、18、24、30)题目79:6,22,44,74,()答案:110(相邻两个数的差依次为16、22、30、36)题目80:1,13,29,53,()答案:89(相邻两个数的差依次为12、16、24、36)题目81:5,21,41,67,()答案:99(相邻两个数的差依次为16、20、26、32)题目82:8,26,50,82,()答案:118(相邻两个数的差依次为18、24、32、36)题目83:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目84:7,23,45,73,()答案:107(相邻两个数的差依次为16、22、28、34)题目85:2,14,32,56,()答案:88(相邻两个数的差依次为12、18、24、32)题目86:9,31,59,95,()答案:139(相邻两个数的差依次为22、28、36、44)题目87:6,24,48,84,()答案:126(相邻两个数的差依次为18、24、36、42)题目88:1,15,33,57,()答案:87(相邻两个数的差依次为14、18、24、30)题目89:5,23,47,77,()答案:113(相邻两个数的差依次为18、24、30、36)题目90:8,28,52,82,()答案:118(相邻两个数的差依次为20、24、30、36)题目91:3,19,41,69,()答案:105(相邻两个数的差依次为16、22、28、36)题目92:7,27,51,81,()答案:117(相邻两个数的差依次为20、24、30、36)题目93:4,18,38,66,()答案:100(相邻两个数的差依次为14、20、28、34)题目94:6,26,50,80,()答案:116(相邻两个数的差依次为20、24、30、36)题目95:2,16,36,60,()答案:90(相邻两个数的差依次为14、20、24、30)题目96:9,33,63,99,()答案:141(相邻两个数的差依次为24、30、36、42)题目97:8,28,56,92,()答案:136(相邻两个数的差依次为20、28、36、44)题目98:5,21,43,71,()答案:105(相邻两个数的差依次为16、22、28、34)题目99:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目100:7,25,49,79,()答案:115(相邻两个数的差依次为18、24、30、36)。
六年级找规律奥数题

六年级找规律奥数题找规律是奥数中常见的题型之一,要求学生通过观察数列或图形中的特点,找到其中的规律,并根据规律解答问题。
下面是几道六年级找规律的奥数题及其解题思路的相关参考内容:1. 题目: 2, 4, 8, 16, 32, ?解题思路:观察这个数列,可以发现每个数字都是前一个数字的2倍。
因此,下一个数字应该是32的2倍,即64。
答案:642. 题目: 3, 7, 15, 31, ?解题思路:观察这个数列,可以发现每个数字都是前一个数字的2倍再加1。
因此,下一个数字应该是31的2倍再加1,即63。
答案:633. 题目: 1, 2, 4, 7, 11, ?解题思路:观察这个数列,可以发现从第二个数字开始,每个数字都是前一个数字加上一个递增的数字。
第一个递增数字是1,第二个递增数字是2,第三个递增数字是3,以此类推。
因此,下一个数字应该是11加上递增数字4,即15。
答案:154. 题目: 1, 4, 9, 16, 25, ?解题思路:观察这个数列,可以发现每个数字都是前一个数字的平方。
因此,下一个数字应该是25的平方,即625。
答案:6255. 题目: 2, 5, 10, 17, ?解题思路:观察这个数列,可以发现每个数字都比前一个数字大2,4,6,8...。
因此,下一个数字应该比17大10,即27。
答案:276. 题目: 1, 4, 9, 16, 25, ?解题思路:观察这个数列,可以发现每个数字都是前一个数字的平方。
因此,下一个数字应该是25的平方,即625。
答案:6257. 题目: 1, 3, 6, 10, ?解题思路:观察这个数列,可以发现每个数字都是前一个数字加上一个递增的数字。
第一个递增数字是2,第二个递增数字是3,第三个递增数字是4...因此,下一个数字应该是10加上递增数字5,即15。
答案:15通过以上的例题可以看出,在解答找规律的问题时,可以通过观察数列或图形中数字的变化,找到其中的规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级奥数专题找规律
关键词:四边三角内角规律四边形奥数等于
同学们从三年级开始,就陆续接触过许多“找规律”的题目,例如发现图形、数字或数表的变化规律,发现数列的变化规律,发现周期变化规律等等.这一讲的内容是通过发现某一问题的规律,推导出该问题的计算公式.
例1 求99边形的内角和.
分析与解:三角形的内角和等于180°,可是99边形的内角和怎样求呢?我们把问题简化一下,先求四边形、五边形、六边形……的内角和,找一找其中的规律.
如上图所示,将四边形ABCD分成两个三角形,每个三角形的内角和等于180°,所以四边形的内角和等于180°×2= 360°;同理,将五边形ABCDE分成三个三角形,得到五边形的内角和等于180°×3=540°;将六边形ABCDEF分成四个三角形,得到六边形的内角和等于180°×4=720°.
通过上面的图形及分析可以发现,多边形被分成的三角形数,等于边数减2.由此得到多边形的内角和公式:
n边形的内角和=180°×(n-2)(n≥3).
有了这个公式,再求99边形的内角和就太容易了.
99边形的内角和=180°×(99-2)=17460°.
例2 四边形内有10个点,以四边形的4个顶点和这10个点为三角形的顶点,最多能剪出多少个小三角形?
分析与解:在10个点中任取一点A,连结A与四边形的四个顶点,构成4个三角形.再在剩下的9个点中任取一点B.如果B在某个三角形中,那么连结B与B所在的三角形的三个顶点,此时三角形总数增加2个(见左下图).如果B在某两个三角形的公共边上,那么连结B与B所在边相对的顶点,此时三角形总数也是增加2个(见右下图).
类似地,每增加一个点增加2个三角形.
所以,共可剪出三角形 4+ 2× 9= 22(个).
如果将例2的“10个点”改为n个点,其它条件不变,那么由以上的分析可知,最多能剪出三角形4+2×(n-1)=2n+2=2×(n+1)(个).
同学们都知道圆柱体,如果将圆柱体的底面换成三角形,那么便得到了三棱柱(左下图);同理可以得到四棱柱(下中图),五棱柱(右下图).
如果底面是正三角形、正四边形、正五边形……那么相应的柱体就是正三棱柱、正四棱柱、正五棱柱……
例3 n棱柱有多少条棱?如果将不相交的两条棱称为一对,那么n棱柱共有多少对不相交的棱?
分析与解:n棱柱的底面和顶面都是n边形,每个n边形有n个顶点,所以n棱柱共有2n个顶点.观
察三棱柱、四棱柱、五棱柱的图形,可以看出,每个顶点都与三条棱相连,而每条棱连接 2个顶点,所以
n棱柱共有棱 2n×3÷2=3n(条).
进一步观察可以发现,n棱柱中每条棱都与4条棱相交,与其余的3n-4-1 =(3n-5)条棱不相交.
共有3n条棱,所以不相交的棱有 3n×(3n- 5)(条),因为不相交的棱是成对出现的,各计算一遍就重
复了一遍,所以不相交的棱共有
3n×(3n-5)÷2(对).
例4 用四条直线最多能将一个圆分成几块?用100条直线呢?
分析与解:4条直线时,我们可以试着画,100条直线就不可能再画了,所以必须寻找到规律.如下图
所示,一个圆是1块;1条直线将圆分为2块,即增加了1块;2条直线时,当2条直线不相交时,增加
了1块,当2条直线相交时,增加了2块.由此看出,要想分成的块尽量多,应当使后画的直线尽量与前
面已画的直线相交.
再画第3条直线时,应当与前面2条直线都相交,这样又增加了3块(见左下图);画第4条直线时,应当与前面3条直线都相交,这样又增加了4块(见右下图).所以4条直线最多将一个圆分成1+1+2
+3+4=11(块).
由上面的分析可以看出,画第n条直线时应当与前面已画的(n—1)条直线都相交,此时将增加n块.因为一开始的圆算1块,所以n条直线最多将圆分成
1+(1+2+3+…+n)
=1+n(n+1)÷2(块).
当n=100时,可分成
1+100×(100+1)÷2=5051(块).
例5 用3个三角形最多可以把平面分成几部分?10个三角形呢?
分析与解:平面本身是1部分.一个三角形将平面分成三角形内、外2部分,即增加了1部分.两个三角形不相交时将平面分成3部分,相交时,交点越多分成的部分越多(见下图).
由上图看出,新增加的部分数与增加的交点数相同.所以,再画第3个三角形时,应使每条边的交点尽量多.对于每个三角形,因为1条直线最多与三角形的两条边相交,所以第3个三角形的每条边最多与前面2个三角形的各两条边相交,共可产生3×(2×2)= 12(个)交点,即增加12部分.因此, 3个三角形最多可以把平面分成
1+1+6+12= 20(部分).
由上面的分析,当画第n(n≥2)个三角形时,每条边最多与前面已画的(n—1)个三角形的各两条边相交,共可产生交点
3×[(n—l)×2]=6(n—1)(个),能新增加6(n-1)部分.因为1个三角形时有2部分,所以n个三角形最多将平面分成的部分数是
2+6×[1+2+…+(n—1)]
当n=10时,可分成2+3×10×(10—1)=272(部分).
练习16
1.求12边形的内角和.
2.五边形内有8个点.以五边形的5个顶点和这8个点为三角形的顶点,最多能剪出多少个小三角形?
3.已知n棱柱有14个顶点,那么,它有多少条棱?
4.n条直线最多有多少个交点?
5.6条直线与2个圆最多形成多少个交点?
6.两个四边形最多把平面分成几部分?。
