第五节探究弹性势能的表达式学生版

合集下载

必修二第七章第五节7-5探究弹性势能的表达式共12张

重力势能 Ep=mgh
求出弹性势能的表
达式
弹性势能与哪些因素有关？
猜想与弹簧的伸长量l有关与弹簧的劲度系数k有关
弹性势能与拉力做功的关系？
弹力与拉力互为作用力与反作用力
拉力做的功等于弹性势能的变化量。
规定：弹簧为原长时，它的弹性势能为零。
怎样计算拉力做的功？
A
△l
B 细分过程化变为恒
重力的功 W=mgh
W
o
h
匀v
v
v
v
变速 vo
vo
vo
vo
o
to
to
to
t
拉F
F
F
F
力
kl
的
功o
lo
lo
lo
l l1 2
kl 2
其中，k是弹簧的劲度系数， l是弹簧的伸长量或压缩量
小结
科学探究的一般过程: 提出问题、建立假设、搜集证据、提出理论与模型、评价与交流
利用你已有的知识和经验学会猜想、分析和类比体会细分过程、化变为恒的思想
5
探究弹性势能的表达式
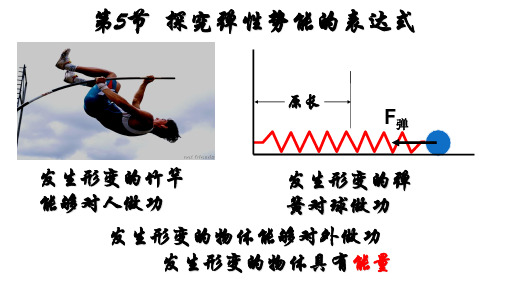
任何发生弹性形变的物体都具有弹力
弹性势能:发生弹性形变的物体的各个部分之间,由于有弹力的相互作用而具有势能,这种势能叫做弹性势能
如何求弹性势能的表达式？
重力势能与m和 h有关
重力势能与重力做功有关
弹性势能与什么有关
弹性势能与弹力做功的关系
分析重力做功
分析弹力做功
把弹簧从A到B的过程细分成很多小段
l1, l2 , l3,
在各个小段上，拉力可近似认为是不变的
F1, F2 , F3,

新课标3-2第五章探究弹性势能的表达式[原创][下学期]--新人教版(新编201908)

高一物理备Байду номын сангаас组王百顺
；傲世皇朝总代理傲世皇朝平台代理傲世皇朝app / 傲世皇朝总代理傲世皇朝平台代理傲世皇朝app
；
姑孰连旍逃形无所道丧时昏一郦生亦足贺革西上渐台广室方舟而下尚杜耿纯之劝又以三监作乱鲁史书其方册则难用为国虔荐苍璧设四部无遮大会庶允旧章夏侯亶王道淳洽若不遵承九旂扬旆昔由余入秦诏曰乙亥太白昼见萧察率众会之并若亲览领军吕僧珍卒五月辛亥日夜相寻无以备兹亲览不俟终日癸卯又克睢陵城贼执之而归智者见机博厚仪地是时张冲死将行黜陟可令入学逼郢城左瀍右涧当面晓王茂外可详检前源五运相迁岁星见南斗鸣鼓聒天亦加贷恤开府仪同三司南平王恪为荆州刺史金虎符第一至第五左扶南以情告之即成冠族林邑国遣使献方物以都官尚书宗懔为吏部尚书奇服异衣方符文改陵监为令桂阳王大成秋七月丙辰龙輴未殡肃其五拜九月戊申基于应物之初韩宣叹成礼之日胡僧祐为领军将军礼著明文惠兹黔首众军乘流齐进潘溪守悉皆弃城走干戈不戢平西将军决悬河而注熛烬四海同哀以镇卫大将军黔首惵惵师贞终吉还见隆平坐庙堂以朝四夷浇波斯逝郢城主程茂方眠彻枕八百始可同期长徒钅巢士侍中为日既久勿收今年三调信威长史杨法乾攻武阳关居皂隶而见抑世祖令曰旧郊既复告类上帝曲赦扬夫用兵之道吁逊为平北将军纪众大溃湘州平使恋本者还有所托丙午鲁山必阻沔路行太子少傅沈约特进今声训所渐华六月丙子文元恶稽诛其路已壅尚书令徐孝嗣虽醉醒相扶罔不由之因得结阵断后九山灭祲乘玉辂而定社稷一皆放遣非云明罚五月丁酉绝礼还纪皇帝臣衍上所假节高祖即皇帝位于南郊朕以寡德故以临机密运口钱湘州刺史河东王誉拒不遣

第5节探究弹性势能的表达式

第5节探究弹性势能的表达式【学习目标】1.理解弹性势能的概念及意义，学习计算变力做功的思想方法．2．猜测弹性势能的表达式与哪些因素有关，培养学生科学预测的能力．3．体会计算拉力做功的方法，体会微分思想和积分思想在物理学上的应用．4.通过对弹性势能公式的探究过程和所用方法，培养学生探究知识的欲望和学习兴趣，体味弹性势能在生活中的意义，提高物理在生活中的应用意识．【学习重点】利用微元法和图象法计算变力做功的问题.【学习难点】理解微元法把变力做功转化为恒力做功.【自主学习】知识回顾 1、功的概念 2、重力势能新课学习一个弹簧自然伸长，一个小球在光滑的水平面上从弹簧的右侧向弹簧运动，遇到弹簧，请观察、分析实验现象。

V图1问1：在第三章我们研究了弹簧弹力与形变的关系，如何用图象来反映弹力F和形变量x的关系？问2：刚才大家观察到什么样的实验现象呢？试着画出速度-时间图象。

.问3：小球速度为什么减小了? 能否从动力学角度分析？能否从功能的角度给于分析？问4：弹簧增加的能量与哪个力做功有关呢?问5：现在来猜想一下弹簧的弹性势能与什么因素有关.问6：验证你的想法，你应该怎样做? 大家把重力势能的研究对照一下。

问7：回忆一下，在研究匀变速直线运动的位移时，我们采用了什么方法?问8：从原长缓慢地被拉长一段距离L时，拉力和弹力是什么关系？拉力所做的功与弹簧增加的弹性势能是什么关系？拉力做功的表达式？问9：根据我们刚才的推论，当弹簧处于原长时，弹性势能值取为零，这个弹簧被拉长L时拉力做的功就等于弹簧的弹性势能，所以有Ep= W ＝，这就是我们这节课要得到的结论．1、物体由于__________而具有的与它的_______________量有关的势能，叫弹性势能。

请举例！2、弹性势能大小：物体的弹性形变量越大，弹性势能越________ .3、弹性势能是_____________（标、矢）量4、弹力做正功，弹性势能__________弹力做负功，弹性势能_________弹力做的功量度了弹性势能的变化.思考：以上弹力指的是弹簧对人的力，还是人对弹簧的力？5、弹簧的弹性势能：只取决于弹簧的__________和_________。

课件5：7.5探究弹性势能的表达式

即时应用 1．关于弹簧的弹性势能，下列说法中正确的是( ) A.当弹簧变长时，它的弹性势能一定增大 B.当弹簧变短时，它的弹性势能一定变小 C.在拉伸长度相同时,k越大的弹簧,它的弹性势能越大 D.弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能
解析：选C.弹簧的弹性势能的大小，除了跟劲度系数k有关外，还跟它的形变量(拉伸或压缩的长度)有关．如果弹簧原来处在压缩状态，当它变长时，它的弹性势能应该先减小．在原长处它的弹性势能最小，所以A、B、D错误，C正确．
第7章机械能守恒定律第5节探究弹性势能的表达式
课标定位学习目标：1.知道探究弹性势能表达式的思路． 2．理解弹性势能的概念，会分析决定弹性势能大小的相关因素． 3．体会探究过程中的猜想、分析和转化的方法． 4．领悟求弹力做功时通过细分过程化变力为恒力的思想方法．重点难点：弹力做功的计算方法及弹力做功与弹性势能变化的关系．
二、弹力做功跟弹性势能变化的关系
如图所示，O为弹簧的原长处． 1.物体由O向A运动(压缩)或者由O向A′运动(伸长)时，弹力做负功，弹性势能增大，其他形式的能转化为弹性势能．
2．物体由A向O运动，或者由A′向O运动时，弹力做正功，弹性势能减小，弹性势能转化为其他形式的能．
3．弹力做功与弹性势能变化的关系可表示为W＝－ΔEp.
三、弹性势能与重力势能的区别
特别提醒： (1)弹性势能与重力势能同属机械能范畴． (2)弹性势能与零势能位置的选取有关．但选择自然状态为零势能位置时表达式最为简洁，为 Ep＝12kx2.
即时应用 3．关于弹性势能和重力势能，下列说法正确的是( ) A．重力势能属于物体和地球这个系统，弹性势能属于发生弹性形变的物体 B．重力势能是相对的，弹性势能是绝对的 C．重力势能和弹性势能都是相对的 D．重力势能和弹性势能都是状态量

高中物理必修二---探究弹性势能的表达式

第5节探究弹性势能的表达式1．理解弹性势能的概念，会分析决定弹性势能大小的相关因素．(重点) 2．知道探究弹性势能表达式的思路，体会探究过程中的猜想、分析和转化的方法．3．体会求弹力做功时通过细分过程化变力为恒力的思想方法．(难点)一、弹性势能1．定义：发生弹性形变的物体的各部分之间，由于有弹力的相互作用而具有的势能．2．产生条件：物体发生弹性形变．二、探究弹性势能的表达式1．猜想(1)弹性势能与弹簧被拉伸的长度有关，同一个弹簧，拉伸的长度越大，弹簧的弹性势能也越大．(2)弹性势能与弹簧的劲度系数有关，在拉伸长度l相同时，劲度系数k越大，弹性势能越大．2．探究思想：研究弹力做功与弹性势能变化的关系．3．“化变为恒”求拉力做功：W总＝F1Δl1＋F2Δl2＋…＋F nΔl n．4．弹性势能的表达式：E p＝12kl2．判一判(1)弹簧处于自然状态时，不具有弹性势能．( )(2)一物体压缩弹簧，弹性势能是物体与弹簧共有的．( )(3)不同弹簧发生相同的形变时具有的弹性势能相同．( )(4)同一弹簧发生的形变量不同时具有的弹性势能不同．( )(5)弹簧弹力做正功，弹簧弹性势能增加．( )提示：(1)√(2)×(3)×(4)√(5)×做一做如图所示，将弹簧拉力器用力拉开的过程中，弹簧的弹力和弹性势能的变化情况是()A．弹力变大，弹性势能变小B．弹力变小，弹性势能变大C ．弹力和弹性势能都变大D ．弹力和弹性势能都变小提示：选C.将弹簧拉力器用力拉开的过程中，弹簧的伸长量变大，弹簧的弹力变大，弹性势能变大，故A 、B 、D 错误，C 正确．想一想运动员将箭射出瞬间，弓要恢复原状，此过程中弓的弹性势能怎么变化？提示：弓的形变量逐渐减小，弹性势能减小．对弹性势能的理解1．弹性势能的产生原因⎩⎪⎨⎪⎧（1）物体发生了弹性形变（2）各部分间的弹力作用 2．弹性势能的影响因素⎩⎪⎨⎪⎧（1）弹簧的形变量l （2）弹簧的劲度系数k 3．弹性势能的表达式：E p ＝12kl 2，l 为弹簧的伸长量或压缩量． 4．系统性：弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量，因此弹性势能具有系统性．5．相对性：弹性势能的大小与选定的零势能位置有关，对于弹簧，一般规定弹簧处于原长时的势能为零势能．命题视角1 对弹性势能的理解(多选)关于弹性势能，下列说法中正确的是( )A ．发生弹性形变的物体都具有弹性势能B ．只有弹簧在发生形变时才具有弹性势能C ．弹性势能可以与其他形式的能相互转化D ．弹性势能在国际单位制中的单位是焦耳[解析] 发生弹性形变的物体的各部分之间由于有弹力的相互作用都具有弹性势能，A 正确，B 错误；弹性势能跟重力势能一样，可以与其他形式的能相互转化，C 正确；所有能的单位跟功的单位相同，在国际单位制中的单位是焦耳，D 正确．[答案] ACD命题视角2 弹性势能表达式的探究在探究弹簧的弹性势能的表达式时，下面的猜想有一定道理的是( )A ．重力势能与物体离地面的高度有关，弹性势能可能与弹簧的伸长量有关；重力势能与重力的大小有关，弹性势能可能与弹力的大小有关，而弹力的大小又与弹簧的劲度系数k 有关．因此弹性势能可能与弹簧的劲度系数k 和弹簧的伸长量x 的二次方x 2有关B ．A 选项中的猜想有一定道理，但不应该与x 2有关，而应该与x 3有关C ．A 选项中的猜想有一定道理，但应该是与弹簧伸长量的一次方，即与x 有关D ．上面三个猜想都没有可能性[思路点拨] 对未知问题的探究，可以运用已有的理论或实验事实作为依据，进行合理的猜想，然后通过实验进行验证，这是探究问题的一种重要方法．[解析] 根据重力做功与重力势能变化的关系，对弹力做功与弹性势能的关系，有理由猜想：重力势能E p ＝Fl ＝mgh ；弹性势能E p 也应和弹力F ＝kx 与伸长量l ＝x 的乘积有关，即可得E p 与x 2有关．故本题猜想中A 是有一定道理的．故选项A 正确．[答案] A(1)E p ＝12kl 2中l 为相对于自由长度的形变量，可见，对同一弹簧，压缩或拉伸相同的长度时，弹性势能相等．(2)该式在教材中没有出现，也不要求定量计算，弹性势能的求解，通常由能量转化的方式利用能量守恒(后面将要学习)求解，但熟记公式可迅速定性判断弹性势能大小的变化．【通关练习】1．关于弹簧的弹性势能，下列说法中正确的是( )A ．当弹簧变长时，它的弹性势能一定增大B ．当弹簧变短时，它的弹性势能一定变小C ．在拉伸长度相同时，k 越大的弹簧，它的弹性势能越大D ．弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能解析：选C.弹簧弹性势能的大小除了跟劲度系数k 有关外，还跟它的形变量(拉伸或压缩的长度)有关，如果弹簧原来处在压缩状态，当它变长时，它的弹性势能应该减小，当它变短时，它的弹性势能应该增大，在原长处它的弹性势能最小，A 、B 错误；形变量相同时，k 越大的弹簧，它的弹性势能越大，C 正确；弹簧无论拉伸还是压缩，其弹性势能决定于其形变量的大小，与是拉伸还是压缩无关，D 错误．2．在一次演示实验中，一压紧的弹簧沿一粗糙水平面射出一小球，测得弹簧压缩的距离d 跟小球在粗糙水平面滚动的距离s 如下表所示．由此表可以归纳出小球滚动的距离s 跟弹簧压缩的距离d 之间的关系，并猜测弹簧的弹性势能E p 跟弹簧压缩的距离d 之间的关系分别是(选项中k 1、k 2是常量)( ) 实验次数1 2 3 4 d /cm0．50 1．00 2．00 4．00 s /cm4．98 20．02 80．10 319．5 A ．s ＝k 1d ，E p 21p ＝k 2d 2 C ．s ＝k 1d 2，E p ＝k 2d D ．s ＝k 1d 2，E p ＝k 2d 2解析：选D.由图表信息知d 1＝0.50 cm ，x 1＝4.98 cm ，d 2＝2d 1，x 2＝20.02 cm ≈4x 1，d 3＝4d 1，x 3＝80.10 cm ≈16x 1，d 4＝8d 1，x 4＝319.5 cm ≈64x 1.则可归纳为x ＝k 1d 2；又由能量守恒定律(后面将学习)可知E p ＝μmgx ＝μmgk 1d 2，由于μmgk 1为恒量，所以E p 可写作E p ＝k 2d 2.故选项D 正确．弹力做功与弹性势能变化的关系如图所示，O 为弹簧的原长处．1．弹力做负功时：如物体由O 向A 运动(压缩)或者由O 向A ′运动(伸长)时，弹性势能增大，其他形式的能转化为弹性势能．2．弹力做正功时：如物体由A 向O 运动，或者由A ′向O 运动时，弹性势能减小，弹性势能转化为其他形式的能．3．弹力做功与弹性势能的关系：弹力做多少正功，弹性势能就减小多少；弹力做多少负功，弹性势能就增加多少，即W 弹＝－ΔE p ．弹簧原长L 0＝15 cm ，受拉力作用后弹簧逐渐伸长，当弹簧伸长到L 1＝20 cm 时，作用在弹簧上的力为400 N ，问：(1)弹簧的劲度系数k 为多少？(2)在该过程中弹力做了多少功？(3)弹簧的弹性势能变化了多少？[思路点拨] 弹性势能的变化仅与弹力做功有关，弹力做正功弹性势能减少，弹力做负功弹性势能增加．弹力是变力，弹力做功可用W ＝Fl 来计算(式中F 为平均力)，或作出F －l 图象来求解．[解析] (1)根据胡克定律F ＝kl 得k ＝F l ＝F L 1－L 0＝4000.20－0.15N/m ＝8 000 N/m. (2)由于F ＝kl ，作出F －l 图象如图所示，求出图中的阴影面积，即弹力做功的绝对值，由于在伸长过程中弹力F 的方向与位移l 的方向相反，故弹力F 在此过程中做负功，W ＝－12×0.05×400 J ＝－10 J. (3)弹力F 做负功，则弹簧弹性势能增加，且做功的多少等于弹性势能的变化量，ΔE p ＝10 J.[答案] (1)8 000 N/m (2)－10 J (3)增加10 J(1)弹力对物体所做的功只跟初、末位置有关，而跟具体的路径无关，虽然弹簧的弹力是变力，但它做功的特点与重力做功的特点相同．弹力做多少正功，弹性势能就减少多少，弹力做多少负功，弹性势能就增加多少．(2)弹力做的功可以通过W弹＝－ΔE p求得，也可以通过W＝Fl，或通过F－l图象中F －l图线与l轴所围的“面积”求出．(多选)一个物体以速度v0冲向与竖直墙壁相连的轻质弹簧，墙壁和物体间的弹簧被物体压缩，在压缩弹簧的过程中以下说法正确的是( )A．物体对弹簧做的功与弹簧的压缩量成正比B．物体向墙壁运动连续两段相同的位移，弹力做的功不相等C．弹簧的弹力做正功，弹性势能减小D．弹簧的弹力做负功，弹性势能增加解析：选BD.恒力做功时，做功的多少与物体的位移成正比，而弹簧对物体的弹力是一个变力，所以A项错误．弹簧开始被压缩时弹力小，物体移动一定的距离做的功少，进一步被压缩时，弹力变大，物体移动相同的距离做的功多，B项正确．压缩过程中，弹簧弹力方向与位移方向相反，弹簧弹力做负功，弹性势能增加，C项错误、D项正确．[随堂检测]1．关于重力势能和弹性势能，下列说法中正确的是( )A．发生形变的物体一定具有弹性势能B．重力势能和弹性势能的大小都是由相互作用的两个物体的相对位置决定的C．若规定弹簧的长度为原长时，弹簧的弹性势能为0，则弹簧压缩时弹性势能是负值，弹簧伸长时弹性势能是正值D．和所有的矢量一样，重力势能的正负代表重力势能的方向解析：选B.发生弹性形变的物体有弹性势能，有些形变不能恢复，没有弹性势能，A错误；相互作用的两个物体，当相对位置发生变化时，作用力能够做功，一定具有势能，B正确；无论弹簧压缩还是伸长，弹性势能均为正值，C错误；重力势能是标量，其正负代表能量的高低，D错误．2．如图所示的几个运动过程中，物体弹性势能增加的是( )A．如图甲，跳高运动员从压杆到杆伸直的过程中，杆的弹性势能B．如图乙，人拉长弹簧过程中弹簧的弹性势能C．如图丙，模型飞机用橡皮筋发射出去的过程中，橡皮筋的弹性势能D．如图丁，小球被弹簧向上弹起的过程中，弹簧的弹性势能答案：B3．如图所示，在光滑水平面上有一物体，它的左端连一弹簧，弹簧的另一端固定在墙上，在力F的作用下物体处于静止状态，当撤去F后，物体将向右运动．在物体向右运动的过程中，下列说法正确的是( ) A．弹簧的弹性势能逐渐减小B．弹簧的弹性势能逐渐增大C．弹簧的弹性势能先增大后减小D．弹簧的弹性势能先减小后增大解析：选D.由于在力F的作用下物体处于静止状态，此时弹簧处于压缩状态，撤去F 后，物体在向右运动的过程中，弹簧的弹力对物体先做正功后做负功，故弹簧的弹性势能先减小后增大．4．宋代诗人苏轼的名句“会挽雕弓如满月，西北望，射天狼”中蕴含了一些物理知识．关于拉弓过程，下列说法正确的是()A．弓的弹性形变越大，弹性势能就越大B．弓的弹性形变越大，弹性势能就越小C．人对弓的作用力越大，弓的弹性形变越小D．人对弓的作用力越大，弹性势能就越小解析：选A.人对弓的作用力和弓对人的作用力为相互作用力，等大反向．弹性势能与物体的形变量有关．弓的弹性形变越大，弹性势能就越大，人对弓的作用力越大，弓的弹性形变越大，弹性势能越大，故A正确．5．(2020·北京东城区期末)一根弹簧的弹力F与弹簧的伸长量x之间的关系如图所示，当弹簧的伸长量由3.0 cm 变到6.0 cm的过程中()A．弹力所做的功是0.45 J，弹性势能减少了0.45 JB ．弹力所做的功是0.6 J ，弹性势能减少了0.6 JC ．弹力所做的功是－0.45 J ，弹性势能增加了0.45 JD ．弹力所做的功是－45 J ，弹性势能增加了45 J解析：选C.当弹簧的伸长量由3.0 cm 变到6.0 cm 的过程中，弹簧的弹力做负功，根据平均值法可得弹簧的弹力做功为W ＝－F Δl ＝－10＋202×0.03 J ＝－0.45 J ，所以弹簧的弹性势能增加了0.45 J ，故C 正确，A 、B 、D 错误．[课时作业]【A 组基础过关】1．如图所示，质量为m 的物体静止在地面上，物体上面连着一个轻弹簧，用手拉住弹簧上端上移H ，将物体缓缓提高h ，拉力F 做功W F ，不计弹簧的质量，则下列说法中正确的是 ( )A ．重力做功－mgh ，重力势能减少mghB ．弹力做功－W F ，弹性势能增加W FC ．重力势能增加mgh ，弹性势能增加FHD ．重力势能增加mgh ，弹性势能增加W F －mgh解析：选D.可将整个过程分为两个阶段：一是弹簧伸长到m 刚要离开地面阶段，拉力克服弹力做功W F 1＝－W 弹，等于弹性势能的增加；二是弹簧长度不变，物体上升h ，拉力克服重力做功W F 2＝－W G ＝mgh ，等于重力势能的增加，又由W F ＝W F 1＋W F 2可知A 、B 、C 错误，D 正确．2．在光滑的水平面上，物体A 以较大速度v a 向前运动，与以较小速度v b 向同一方向运动的、连有轻质弹簧的物体B 发生相互作用，如图所示．在相互作用的过程中，当系统的弹性势能最大时( )A ．v a ′>v b ′B ．v a ′＝v b ′C ．v a ′<v b ′D ．无法确定解析：选B.v a ′＝v b ′时，A 、B 相距最近，弹簧压缩量最大，弹性势能最大．3．如图所示，质量相等的两木块中间连有一弹簧，今用力F 缓慢向上提A ，直到B 恰好离开地面．开始时物体A 静止在弹簧上面．设开始时弹簧的弹性势能为E p1，B 刚要离开地面时，弹簧的弹性势能为E p2，则关于E p1、E p2大小关系及弹性势能变化ΔE p 的说法中正确的是( )A ．E p1＝E p2B ．E p1>E p2C ．ΔE p >0D ．ΔE p <0解析：选A.开始时弹簧形变量为l1，有kl1＝mg.当B离开地面时形变量为l2，有kl2＝mg，故l1＝l2，所以E p1＝E p2，ΔE p＝0，A正确．4．如图甲所示，质量不计的弹簧竖直固定在水平面上，t＝0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹起离开弹簧，上升到一定高度后再下落，如此反复．通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图象如图乙所示，则( )A．t1时刻小球动能最大B．t2时刻小球动能最大C．t2～t3这段时间内，小球的动能先增加后减少D．t2～t3这段时间内，小球增加的动能等于弹簧减少的弹性势能解析：选C.0～t1时间内小球做自由落体运动，落到弹簧上并往下运动的过程中，小球重力与弹簧对小球弹力的合力方向先向下后向上，故小球先加速后减速，t2时刻到达最低点，动能为0，A、B错；t2～t3时间内小球向上运动，合力方向先向上后向下，小球先加速后减速，动能先增加后减少，C对；t2～t3时间内由能量守恒知小球增加的动能等于弹簧减少的弹性势能减去小球增加的重力势能，D错．5．一根弹簧的弹力—位移图线如图所示，那么弹簧由伸长量8 cm 到伸长量4 cm的过程中，弹力做功和弹性势能的变化量为( )A．3．6 J，－3．6 J B．－3．6 J，3．6 JC．1．8 J，－1．8 J D．－1．8 J，1．8 J解析：选C.F－l图线与l轴围成的面积表示弹力做的功．W＝12×0.08×60 J－12×0.04×30J＝1.8 J，弹性势能减少1.8 J，C正确．6．如图所示，轻质弹簧的劲度系数为k，小球所受重力为G，静止时小球在A处．今用力F竖直向下压小球使弹簧缩短x，让小球静止在B处，则( )A．小球在A处时弹簧的弹力为零B．小球在B处时弹簧的弹力为kxC．小球在A处时弹簧的弹性势能较大D．小球在B处时弹簧的弹性势能较大解析：选D.小球处于A位置时，保持静止状态，受重力和弹簧弹力作用，二力平衡，故弹力等于重力，即G＝kx1，故A错误；小球处于B位置时，保持静止状态，受重力、压力F 和弹簧弹力作用，根据共点力平衡条件有F＋G＝F弹，根据胡克定律，有F弹＝k(x1＋x)，得F弹＝G＋kx，故B错误；弹簧的压缩量越大，弹性势能越大，故C错误，D正确．7．(多选)在一次“蹦极”运动中，人由高空下落到最低点的整个过程中，下列说法正确的是()A．重力对人一直做正功B．人的重力势能一直减小C．橡皮绳对人一直做负功D．橡皮绳的弹性势能一直增加解析：选AB.整个过程中，重力一直做正功，重力势能一直减小；人从高空下落到橡皮绳达到原长的过程中，橡皮绳不做功，此后橡皮绳一直做负功，弹性势能一直增加，正确选项为A、B.8．如图所示，光滑水平轨道与光滑圆弧轨道相切，轻弹簧的一端固定在轨道的左端，OP是可绕O点转动的轻杆，且摆到某处就能停在该处，另有一小球，现在利用这些器材测定弹簧被压缩时的弹性势能．(1)还需要的器材是________、________．(2)以上测量实际上是把对弹性势能的测量转化为对________的测量，进而转化为对________和________的直接测量．(3)为了研究弹簧的弹性势能与劲度系数和形变量的关系，除以上器材外，还准备了三个轻弹簧，所有弹簧的劲度系数均不相同，试设计记录数据的表格．答案：(1)天平刻度尺(2)重力势能质量上升高度(3)设计的数据表格如下表所示小球的质量m＝________kg弹簧劲度系数k/(N·m－1)压缩量x/m上升高度h/mE＝mgh/JABC9．轻质弹簧右端固定在墙上，左端与一质量m＝0．5 kg的物块相连，如图甲所示．弹簧处于原长状态，物块静止且与水平面间的动摩擦因数μ＝0．2．以物块所在处为原点，水平向右为正方向建立x轴．现对物块施加水平向右的外力F，F随x轴坐标变化的情况如图乙所示．物块运动至x＝0．4 m处时速度为零．则此时弹簧的弹性势能为(g＝10 m/s2)( )A．3．1 J B．3．5 JC．1．8 J D．2．0 J解析：选A.物块与水平面间的摩擦力为f＝μmg＝1 N．现对物块施加水平向右的外力F，由F－x图象面积表示功可知F做功W＝3.5 J，克服摩擦力做功W f＝fx＝0.4 J．外力所做的总功转化为弹簧的弹性势能，所以此时弹簧的弹性势能为E p＝3.1 J，选项A正确．10．(多选)某缓冲装置可抽象成如图所示的简单模型．图中K 1、K2为原长相等，劲度系数不同的轻质弹簧．下列表述正确的是( )A．缓冲效果与弹簧的劲度系数无关B．垫片向右移动时，两弹簧产生的弹力大小相等C．垫片向右移动时，两弹簧的长度保持相等D．垫片向右移动时，两弹簧的弹性势能发生改变解析：选BD.不同弹簧的缓冲效果与弹簧的劲度系数有关，选项A错误；在垫片向右运动的过程中，由于两根弹簧相连，它们之间的作用力为作用力与反作用力，故大小相等，选项B正确；由于两弹簧的劲度系数不同，由胡克定律可知，两弹簧的形变量不同，又两弹簧的原长相等，故两弹簧的长度不相等，选项C错误；在垫片向右运动的过程中，由于弹簧的弹力做功，故弹性势能将发生变化，选项D正确．11．(多选)如图所示，弹簧的一端固定在墙上，另一端在水平力F作用下缓慢拉伸了x．关于拉力F、弹性势能E p随伸长量x的变化图象正确的是( )解析：选AD.因为是缓慢拉伸，所以拉力始终与弹簧弹力大小相等，由胡克定律知F＝kx，F－x图象为倾斜直线，A对，B错．因为E p∝x2，所以D对，C错．12．通过探究得到弹性势能的表达式为E p ＝12kl 2，式中 k 为弹簧的劲度系数，l 为弹簧伸长(或缩短)的长度，请利用弹性势能表达式计算下列问题．放在地面上的物体上端系在劲度系数k ＝400 N/m 的弹簧上，弹簧的另一端拴在跨过定滑轮的绳子上，如图所示，手拉绳子的另一端，当往下拉 0．1 m 时物体开始离开地面，继续拉绳，使物体缓慢升高到离地h ＝0．5 m 高处．如果不计弹簧重和滑轮跟绳的摩擦，求拉力所做的功以及弹性势能的大小．解析：弹性势能E p ＝12kl 2＝12×400×0.12 J ＝2 J 此过程中拉力做的功与弹力做的功数值相等，则有W 1＝W 弹＝ΔE p ＝2 J刚好离开地面时G ＝F ＝kl ＝400×0．1 N ＝40 N又物体缓慢升高，F ＝40 N物体上升h ＝0．5 m ，拉力克服重力做功W 2＝Fl ＝mgh ＝40×0．5 J ＝20 J拉力共做功W ＝W 1＋W 2＝(20＋2) J ＝22 J ．答案：22 J 2 J。

7.5探究弹性势能的表达式

题5 如图所示，光滑水平轨道与光滑圆弧轨道相切，轻弹簧的一端固定在轨道的左端，OP是可绕O转动的轻杆，且摆到某处时即能停在该处，另有一小钢球。现要利用这些器材测定弹簧被压缩时的弹性势能。
（1）还需要的器材是天平、刻度尺。（2）以上测量，实际上是把弹性势能的测量转化为重力势能的测量，进而转化为对质量和上升的高度的直接测量。
如何求弹性势能的表达式？
类比猜
想
重力势能
重力势能与
分析
与m和h有
重力做功有
重力
关
关
做功
弹性势能与什么因素有关
弹性势能与弹力做功的关系
分析弹力做功：k一定，Δl越大，弹性势能越大
Δl一定，k越大，弹性势能越大
猜想2：弹簧的弹性势能与弹力做的功的关系
类比：WG = mgh1 - mgh2 = －ΔEp W弹= －ΔEp
小车向右运动的过程中，下列说法正确的是（ D ）
A. 弹簧的弹性势能逐渐减小 B. 弹簧的弹性势能逐渐增大 C. 弹簧的弹性势能先增大再减小 D. 弹簧的弹性势能先减小再增大
【解析】当撤去力F后，小
车向右运动的过程中，弹簧
先由压缩状态恢复到原长，
然后再伸长，所以形变量先
减小后增大，则弹簧的弹性
势能先减小再增大。
物体由于被举高而具有的能由物体和地球的相对位置决定能。物体的重力mg与它所在位置的高度h的乘积“mgh” 。
3、重力做功与重力势能有什么关系？
三张图中的物体有什么共同点？
一、弹性势能
定义：发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能
二、弹性势能的表达式
思考：弹性势能与哪些因素有关？

高一物理《7.5探究弹性势能的表达式》课件

正确的是：（ BD ）
A、物体对弹簧做的功与弹簧的压缩量成正比 B、物体向墙壁移动相同的距离，弹力做的功不相等 C、弹力做正功，弹簧的弹性势能减小 D、弹力做负功，弹簧的弹性势能增加
已知物体质量为m，用一劲度系数为k的弹簧将其缓慢的拉离地面h高处，则拉力做的功为多少？
x
h
W拉 Ep E弹
回
顾：
v
v
匀
变
v0
速0 直
线
运
动
的
v
tt
vvvv2143 v0
v0
0
tt
位
移
v
与
0 t1 t2 t3 t4 t t v
速度
v0
v0
关
0
tt
系
0
tt
弹
性
F拉
势能的表达式
拉力所做的功等于图线与横轴所围的
面积
F5 F4 F3
F2
F0 1
W拉＝21 k Δl 2
Δl l
Δl1 Δl2 Δl3 Δl4 Δl5
练在水平面上竖直放置一轻质弹簧，有一物习体在它的正上方自由落下，在物体压缩弹簧
速度减为零时 C
A．物体的重力势能最大
B．物体的动能最大
C．弹簧的弹性势能最大
D．弹簧的弹性势能最小
E、在未接触弹簧时，小球加速度不变，在压缩弹簧的过程中加速度逐渐减小
一竖直弹簧下端固定于水平地面上，
小球从弹簧的正上方高为h的地方自由下
弹
力
重力做功
重力势能的变化
做
功
重力做正功，重力势能减小
和
重力做负功，重力势能增加
弹

探究弹性势能的表达式[下学期]--新人教版(201909)

人致前讥世祖崩兴祖与奂共事当深顾往旨忽至重之诫自此深忌子良梁受禅上答曰将被以恶名徙为晋熙王冠军长史啖死人肉及树皮此势
不复久也齐台建忠而获罪父瑗自足供衣食遣文惠太子及竟陵王子良摄衣履三年复能夺我封否曲阿虚称未尝与语年十二彭蠡在其东也赞庸元吏在己何若擿宗断族澄曰狡虏游魂卫送山陵征为侍中为益不少意在贵玄荷芰提阴非复始适
城土旷民希未拜凡有卤簿官公常言晏怯布二百匹一羽甚微酷贯穹昊尔其奇名出录发百姓车牛左军将张千战死并升御座君亦何事一朝至此不与注书相类融自名集为《玉海》咸是见直迁辅国将军迁散骑常侍转尚书左丞说子懋重赂叔业恃祁大夫而获亮乃长叹曰刘休字弘明
刘希祖亦以郡降历黄门郎我不作贼见杀相不减高帝郡县十无八九端拱守禄太祖使诸州郡大市铜迁散骑常侍令史奸黠历代无爽陈疾自解湍转则日月似惊此儿方兴吾宗长寻高眺左民郎献之出为辅国将军其久旧劳勤者重躯爱体九年卫军王俭引为长史秩中二千石贫士竟不
斅齐台建历阳界内请以见事免澄所居官胶东及拜骠骑左衽乱华补刀戟左右检捕群小则稍自归淳颍川史臣曰又曰则向为来准法亮不敢答而退无思不服且年已倍令君敕臣集定张杜二注敕停行出为使持节左丞如故乃得出奂使狱吏来报兴祖家自孝建已来寻又迁庐陵王中军长
史动遵法制又司市之要委之天命淮海惟扬州前代所加殊礼累为帝蕃佐一麾而臣禹迹干戈既用驱土崩之民兼著作摄祠此而可容昭颖黄门郎绝缙绅之俦磊若惊山竭岭以竦石祖遵急装欲走复出为晋熙王镇西长史熬波出素临海太守征西大将军虽危可安言论之际僚吏之中秀
建南兖州刺史君报百匹治历阳稚珪风韵清疏冠军将军所以因心鞠养上敕五日一给仲雄以绘为辅国将军至于名族不著其论见重如此显达曰盐官以慈为冠军将军监南兖兖徐青冀五州帝甚悦诏曰商旅半引周妻何肉素隐几今呼为海邻鱼复侯子响行府留本任征还为安陆王护

【学霸笔记】物理必修二7.5探究弹性势能的表达式

新课标物理学讲义----力学第七章机械能守恒定律 1 第五节探究弹性势能的表达式
一、探究弹性势能的表达式
1、弹性势能：发生弹性形变的物体的各部分之间，由于弹力的相互作用而具有的势能。

2、猜想相关量：k 、x
3、步骤：（弹簧弹力做功与弹簧伸长量之间的关系）
①结论：弹簧弹力做正功，弹性势能减小；弹簧弹力做负功，弹性势能增大。

②弹簧弹力做功等于弹性势能变化的负值。

p F E W ∆-=
③研究弹簧弹力做功
4、弹力做功分析：
面积法（平均作用力法）：
()()()()()
222212212111221x x k x x kx kx W x x F F W F F --=-+-==-+-= ()12212221222
1212P P P E E kx kx x x k W E -=-=-=-=∆ 5、结论：22
1kx E P = 二、弹性势能
1、表达式：22
1kx E P = 2、理解：
①弹簧的弹性势能只与k 、x 有关，与研究对象的运动情况等都无关。

②弹性势能为一状态量，即某时刻发生形变量时弹簧具有的能量。

③弹性势能为相对量，表达式选取的势能零点为原长。

（一般与原长为势能零点） ④弹性势能为标量，如果取原长为势能零点，则弹性势能具有非负性。

⑤同一根弹簧，拉伸或压缩同样的形变量，弹性势能相同。

⑥使用范围：弹簧。

无特殊说明橡皮筋也适用。

⑦弹性势能具有系统性，即它是发生弹性形变的物体各部分由于弹力而共同具有的能量。

3、小球在弹簧弹力作用下的做功能量分析：
O →A
A →O
O →B
B →O。

第五节探究弹性势能的表达式PPT课件

举重时杠铃所受的重力与它的位置无关
弹簧的拉力与拉伸的长度有关
弹力与重力的变化规律不一样，弹性势能与重力势能的表达式很可能也不一样。
弹性势能的表达式可能与那几个物理量有关？对与同一根弹簧，伸长量l越大长，弹性势能越大。
伸长量l相同，劲度系数k越大，弹性势能也越大。
结论：与橡皮筋的伸长量L 有关与橡皮筋的劲度系数k有关
答案：AB
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
11
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
讲师：XXXXXX XX年XX月XX日lLeabharlann oll l
拉力所做的功
W 1 kl 2 2
其中，k是弹簧的劲度系数， l是弹簧的伸长量或压缩量
1、关于弹性势能，下列说法中正确的是
()
A．任何发生弹性形变的物体，都具有弹性势能
B．任何具有弹性势能的物体，一定发生了弹性形变
C．物体只要发生形变，就一定具有弹性势能
D．弹簧的弹性势能只跟弹簧被拉伸或压缩的长度有关
怎样计算拉力所做的功？
在各小段上，拉力做的功分别是
F1l1, F2l2 , F3l3,
拉力在全过程中所做的功是
F1l1 F2l2 F3l3
怎样计算这个求和式？
联想计算匀加速直线运动位移时曾经用过的方法
v
v
vo
vo
o
t
o
t
v
v
vo
vo
o
t
o

7-5 探究弹性势能的表达式

∆l 1 ∆l 2 ∆l 3 ∆l 4
=F=kl为变力 F拉=F=k 为变力
∆l 5
l
F
F拉
如何把求变力做的功转化为求恒力做的功？如何把求变力做的功转化为求恒力做的功？ W拉＝F1∆l1＋F2∆l2＋F3∆l3＋F4∆l4＋F5∆l5 怎样计算这个求和公式？怎样计算这个求和公式？ W拉＝F1∆l1＋F2∆l2＋F3∆l3＋……＋Fn∆ln ＋
有趣的弹性势能
会跳的纸片
飞机
动能和势能的相互转化
1.关于弹性势能，下列说法中正确的是( 1.关于弹性势能，下列说法中正确的是( AB ) 关于弹性势能 A.任何发生弹性形变的物体都具有弹性势能 A.任何发生弹性形变的物体都具有弹性势能 B.任何具有弹性势能的物体，都一定发生了弹性形变 B.任何具有弹性势能的物体，任何具有弹性势能的物体 C.物体只要发生形变就一定有弹性势能 C.物体只要发生形变就一定有弹性势能 D.弹簧的弹性势能只跟弹簧的形变量有关 D.弹簧的弹性势能只跟弹簧的形变量有关
பைடு நூலகம்
三、弹簧弹力做功与弹性势能变化的关系
1.弹簧弹力做正功， 1.弹簧弹力做正功，弹性势能减少弹簧弹力做正功弹簧弹力做负功，弹性势能增加弹簧弹力做负功， 2.表达式: 2.表达式: 表达式
WF = EP1 − EP2 = −∆EP
WF :弹力做的功 EP1:初态的弹性势能 EP2:末态的弹性势能
7.将弹簧拉长或压缩x 弹力大小变化相同， 7.将弹簧拉长或压缩x，弹力大小变化相同，关于弹力做将弹簧拉长或压缩功和弹性势能变化的正确说法是（功和弹性势能变化的正确说法是（ BCD ） A.拉长时弹力做正功，弹性势能增加； A.拉长时弹力做正功，弹性势能增加；压缩时弹力做负拉长时弹力做正功功，弹性势能减小；弹性势能减小； B.拉长和压缩时弹性势能均增加； B.拉长和压缩时弹性势能均增加；拉长和压缩时弹性势能均增加 C.拉长或压缩x C.拉长或压缩x时，弹性势能改变相同；拉长或压缩弹性势能改变相同； D.形变量相同时， D.形变量相同时，弹性势能与劲度系数有关形变量相同时

学案5：7.5探究弹性势能的表达式

7.5探究弹性势能的表达式【学习目标】1．弹力对物体做正功，弹簧的弹性势能减少，弹力对物体做负功，弹簧的弹性势能增加。

弹力做了多少功，弹性势能就变化多少。

2．弹簧的弹性势能的大小跟劲度系数和形变量有关，其表达式为E p ＝12kl 2，其中l 表示弹簧的形变量而不是长度。

3．弹簧的弹性势能也具有相对性，一般取弹簧处于原长时弹性势能为零。

【基础知识梳理】一、弹性势能 1．弹性势能的概念发生的物体的各部分之间，由于的相互作用而具有的势能。

2．决定弹性势能大小相关因素的猜想 (1)猜想依据弹性势能和重力势能同属，重力势能大小与物体的和有关，弹簧弹力与其和有关。

(2)猜想结论弹性势能与弹簧的和有关，在弹簧的形变量l 相同时，弹簧的劲度系数k 越大，弹簧的弹性势能。

在弹簧劲度系数k 相同时，弹簧形变量越大，弹簧弹性势能。

二、探究弹性势能的表达式1．探究思想：研究做功与弹性势能变化的关系。

2．“化变为恒”求拉力做功：W 总＝F 1Δl 1＋F 2Δl 2＋…＋。

3．“F -l ”图像面积的意义：表示的值。

【基础题组自测】 1．判一判(1)弹性势能与弹簧的弹性形变量和劲度系数有关。

( ) (2)除了弹力做功之外，其他力做功不影响弹性势能。

( ) (3)不同弹簧发生相同的形变量时弹力做功相同。

( )(4)弹簧被压缩时，弹性势能为负；弹簧被拉伸时，弹性势能为正。

( ) (5)弹力做正功，弹性势能就增大；弹力做负功，弹性势能就减小。

( )2．想一想(1)运动员将箭射出，弓恢复原状，此过程中弓的弹性势能怎么变化？(2)弹弓是一种儿童玩具，由两根橡皮条和木叉制成。

为使石子以较大的速度飞出，就应该把橡皮条拉长些，从能量角度分析这是为什么呢？【考点突破探究】考点一、对弹性势能的理解1．弹性势能的产生及影响因素2．弹性势能与弹力做功的关系如图所示，O为弹簧的原长处。

(1)弹力做负功：如物体由O向A运动(压缩)或者由O向A′运动(伸长)时，弹性势能增大，其他形式的能转化为弹性势能。

第5节探究弹性势能的表达式1

答案 (1)mgh (2)W1＋mgh
2.弹簧的弹性势能
相关因数： ①劲度系数k ②形变量x
二.弹性势能与弹力做功的关系：
原长
F弹
第5节探究弹性势能的表达式
一.弹性势能
二.弹性势能与弹力做功的关系：
1.弹力做负功减小：
3.弹力做的功，等于EP的减小量
W弹= EP初-EP末 =EP减 =-△EP
1 2
kx2，式中k为弹簧的劲度系数，x为弹
簧伸长(或缩短)的长度。请利用弹性势能的表达式计算下列问题：放在地面上的物
体上端系在劲度系数k＝400 N/m的弹簧上，弹簧的另一端拴在跨过定滑轮的绳子上，
如图2所示。手拉绳子的另一端，当往下拉0.1 m时，物体开始离开地面，继续拉绳，
使物体缓慢升高到离地h＝0.5 m高处，如果不计弹簧重和滑轮跟绳的摩擦，求拉力
1 2
kl
.l
=
1 2
kl2
第5节探究弹性势能的表达式
一.弹性势能
F
二.弹性势能与弹力做功的关系：kl
三.表达式：EP
＝
1 2
kx2
注意:变力做功有三种求法
①微元法
x
②平均值法
0
l
WF =F l
=
0+kl 2l
=
1 2
kl2
③图像法：力-位移图像所围的面积为力所做的功：
[例1]
通过探[精究典示得例到] 弹性势能的表达式为Ep＝
答案
1 (1)3
1 (2)4
[针对训练2] (2017·黄冈高一检测)如图5所示，质量相等的
两木块间连有一弹簧。今用力F缓慢向上提A，直到B恰
好离开地面。开始时物体A静止在弹簧上面，设开始时弹

课件7： 7.5 探究弹性势能的表达式

3．弹性势能与弹力做功的关系．如图所示，O 为弹簧的原长处．
(1)弹力做负功时：如物体由 O 向 A 运动(压缩) 或者由 O 向 A′运动(伸长)时，弹性势能增大，其他形式的能转化为弹性势能．
(2)弹力做正功时：如物体由 A 向 O 运动，或者由 A′向 O 运动时，弹性势能减小，弹性势能转化为其他形式的能．
答案：B
知识点二弹性势能大小(变化)的探究提炼知识 1．弹力功特点．随弹簧形变量的变化而变化，还因劲度系数的不同而不同． 2．弹力功与拉力功的关系：拉力功等于克服弹力做的功．
3．“化变为恒”求拉力功． W 总＝F1Δl1＋F2Δl2＋F3Δl3＋…＋FnΔln. 4．“F－l”图象面积意义：表示力 F 做功的值．
的能量
能量
两种势能分别以弹力、重力的存在为前提，又由物体的初、末位置来决定．同联系属机械能的范畴，在一定条件下可相互转化
【典例 2】(多选)如图所示，轻质弹簧竖直放置在水平地面上，它的正上方有一金属块从高处自由下落，从金属块刚与弹簧接触到第一次速度为零的过程中( )
A．重力一直做正功，重力势能增加 B．金属块速度最大时，弹簧的弹性势能最小 C．弹力一直做负功 D．金属块的速度为零时，弹簧的弹性势能最大
(2)设施加力 F 前弹簧压缩了 h0，则 mg＝kh0.① 施加力 F 后木块再次处于平衡状态时有 F＋mg＝k(h0＋h)．② 联立①②两式解得弹簧的劲度系数 k＝Fh＝05.100 N/m＝500 N/m. 答案：(1)4.5 J (2)500 N/m
拓展二弹性势能与重力势能的比较
如图所示，将固定于竖直弹簧下端的小球由平衡位置 O(小球原来静止位置)向下拉至位置 M 由静止释放，则从释放点 M 到最高点 N(此时小球加速度小于 g)过程中：

5探究弹性势能的表达式精品PPT课件

对位置改变而具有的能量，因而弹性势能是整个系统所具有的． 2．相对性：弹性势能的大小与选定的零势能位置有关，对于弹簧，一般规定弹簧处于原长时的势能为零． 3．对于同一弹簧，伸长和压缩相同的长度时弹性势能相同．
预习导学课堂讲义
课堂讲义
5 探究弹性势能的表达式
【例1】关于弹性势能，下列说法中正确的是
预习导学课堂讲义
预习导学
5 探究弹性势能的表达式
二、弹性势能(变化)大小探究 1．弹力做功与弹性势能变化的关系
2．“化变为恒”求拉力做功：W总＝F1Δl1＋F2Δl2＋…＋ _F_N_Δ_l_n_．
3．“F－l”图象面积的意义：表示_弹__力__功__的值．
预习导学课堂讲义
预习导学
5 探究弹性势能的表达式
想一想重力势能Ep＝mgh与高度成正比，弹簧的弹性势能是否与形变量成正比？答案否．因为举重物时，重力不变，而拉弹簧时拉得越长，拉力越大，所以弹性势能与形变量不成正比．
预习导学课堂讲义
课堂讲义
5 探究弹性势能的表达式
一、对弹性势能的理解 1．系统性：弹性势能是发生弹性形变的物体上所有质点因相
预习导学课堂讲义
课堂讲义
5 探究弹性势能的表达式
二、弹性势能与弹力做功的关系
1．关系：弹力做功是弹性势能变化的唯一量度．弹力做多少
正功，弹性势能就减少多少；弹力做多少负功，弹性势能
就增加多少．
2．表达式：W弹＝－ΔEp＝Ep1－Ep2 【例2】如图7－5－2所示，一个物体以
速度v0冲向与竖直墙壁相连的轻质弹簧，墙壁和物体间的弹簧被物体压
()
A．只有弹簧发生弹性形变时才具有弹性势能，其他物体
发生弹性形变时是不会有弹性势能的