十年高考真题不等式综合应用

合集下载

十年真题(2010_2019)高考数学真题分类汇编专题15不等式选讲文(含解析)

专题15不等式选讲历年考题细目表历年高考真题汇编1．【2019年新课标1文科23】已知a，b，c为正数，且满足abc＝1．证明：（1）a2+b2+c2；（2）（a+b）3+（b+c）3+（c+a）3≥24．【解答】证明：（1）分析法：已知a，b，c为正数，且满足abc＝1．要证（1）a2+b2+c2；因为abc＝1．就要证：a2+b2+c2；即证：bc+ac+ab≤a2+b2+c2；即：2bc+2ac+2ab≤2a2+2b2+2c2；2a2+2b2+2c2﹣2bc﹣2ac﹣2ab≥0（a﹣b）2+（a﹣c）2+（b﹣c）2≥0；∵a，b，c为正数，且满足abc＝1．∴（a﹣b）2≥0；（a﹣c）2≥0；（b﹣c）2≥0恒成立；当且仅当：a＝b＝c＝1时取等号．即（a﹣b）2+（a﹣c）2+（b﹣c）2≥0得证．故a2+b2+c2得证．（2）证（a+b）3+（b+c）3+（c+a）3≥24成立；即：已知a，b，c为正数，且满足abc＝1．（a+b）为正数；（b+c）为正数；（c+a）为正数；（a+b）3+（b+c）3+（c+a）3≥3（a+b）•（b+c）•（c+a）；当且仅当（a+b）＝（b+c）＝（c+a）时取等号；即：a＝b＝c＝1时取等号；∵a，b，c为正数，且满足abc＝1．（a+b）≥2；（b+c）≥2；（c+a）≥2；当且仅当a＝b，b＝c；c＝a时取等号；即：a＝b＝c＝1时取等号；∴（a+b）3+（b+c）3+（c+a）3≥3（a+b）•（b+c）•（c+a）≥3×8••24abc＝24；当且仅当a＝b＝c＝1时取等号；故（a+b）3+（b+c）3+（c+a）3≥24．得证．故得证．2．【2018年新课标1文科23】已知f（x）＝|x+1|﹣|ax﹣1|．（1）当a＝1时，求不等式f（x）＞1的解集；（2）若x∈（0，1）时不等式f（x）＞x成立，求a的取值范围．【解答】解：（1）当a＝1时，f（x）＝|x+1|﹣|x﹣1|，由f（x）＞1，∴或，解得x，故不等式f（x）＞1的解集为（，+∞），（2）当x∈（0，1）时不等式f（x）＞x成立，∴|x+1|﹣|ax﹣1|﹣x＞0，即x+1﹣|ax﹣1|﹣x＞0，即|ax﹣1|＜1，∴﹣1＜ax﹣1＜1，∴0＜ax＜2，∵x∈（0，1），∴a＞0，∴0＜x，∴a∵2，∴0＜a≤2，故a的取值范围为（0，2]．3．【2017年新课标1文科23】已知函数f（x）＝﹣x2+ax+4，g（x）＝|x+1|+|x﹣1|．（1）当a＝1时，求不等式f（x）≥g（x）的解集；（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．【解答】解：（1）当a＝1时，f（x）＝﹣x2+x+4，是开口向下，对称轴为x的二次函数，g（x）＝|x+1|+|x﹣1|，当x∈（1，+∞）时，令﹣x2+x+4＝2x，解得x，g（x）在（1，+∞）上单调递增，f（x）在（1，+∞）上单调递减，∴此时f（x）≥g（x）的解集为（1，]；当x∈[﹣1，1]时，g（x）＝2，f（x）≥f（﹣1）＝2．当x∈（﹣∞，﹣1）时，g（x）单调递减，f（x）单调递增，且g（﹣1）＝f（﹣1）＝2．综上所述，f（x）≥g（x）的解集为[﹣1，]；（2）依题意得：﹣x2+ax+4≥2在[﹣1，1]恒成立，即x2﹣ax﹣2≤0在[﹣1，1]恒成立，则只需，解得﹣1≤a≤1，故a的取值范围是[﹣1，1]．4．【2016年新课标1文科24】已知函数f（x）＝|x+1|﹣|2x﹣3|．（Ⅰ）在图中画出y＝f（x）的图象；（Ⅱ）求不等式|f（x）|＞1的解集．【解答】解：（Ⅰ）f（x），由分段函数的图象画法，可得f（x）的图象，如右：（Ⅱ）由|f（x）|＞1，可得当x≤﹣1时，|x﹣4|＞1，解得x＞5或x＜3，即有x≤﹣1；当﹣1＜x时，|3x﹣2|＞1，解得x＞1或x，即有﹣1＜x或1＜x；当x时，|4﹣x|＞1，解得x＞5或x＜3，即有x＞5或x＜3．综上可得，x或1＜x＜3或x＞5．则|f（x）|＞1的解集为（﹣∞，）∪（1，3）∪（5，+∞）．5．【2015年新课标1文科24】已知函数f（x）＝|x+1|﹣2|x﹣a|，a＞0．（Ⅰ）当a＝1时，求不等式f（x）＞1的解集；（Ⅱ）若f（x）的图象与x轴围成的三角形面积大于6，求a的取值范围．【解答】解：（Ⅰ）当a＝1时，不等式f（x）＞1，即|x+1|﹣2|x﹣1|＞1，即①，或②，或③．解①求得x∈∅，解②求得x＜1，解③求得1≤x＜2．综上可得，原不等式的解集为（，2）．（Ⅱ）函数f（x）＝|x+1|﹣2|x﹣a|，由此求得f（x）的图象与x轴的交点A（，0），B（2a+1，0），故f（x）的图象与x轴围成的三角形的第三个顶点C（a，a+1），由△ABC的面积大于6，可得[2a+1]•（a+1）＞6，求得a＞2．故要求的a的范围为（2，+∞）．6．【2014年新课标1文科24】若a＞0，b＞0，且．（Ⅰ）求a3+b3的最小值；（Ⅱ）是否存在a，b，使得2a+3b＝6？并说明理由．【解答】解：（Ⅰ）∵a＞0，b＞0，且，∴2，∴ab≥2，当且仅当a＝b时取等号．∵a3+b3 ≥224，当且仅当a＝b时取等号，∴a3+b3的最小值为4．（Ⅱ）∵2a+3b≥22，当且仅当2a＝3b时，取等号．而由（1）可知，2246，故不存在a，b，使得2a+3b＝6成立．7．【2013年新课标1文科24】已知函数f（x）＝|2x﹣1|+|2x+a|，g（x）＝x+3．（Ⅰ）当a＝﹣2时，求不等式f（x）＜g（x）的解集；（Ⅱ）设a＞﹣1，且当x∈[，]时，f（x）≤g（x），求a的取值范围．【解答】解：（Ⅰ）当a＝﹣2时，求不等式f（x）＜g（x）化为|2x﹣1|+|2x﹣2|﹣x﹣3＜0．设y＝|2x﹣1|+|2x﹣2|﹣x﹣3，则y，它的图象如图所示：结合图象可得，y＜0的解集为（0，2），故原不等式的解集为（0，2）．（Ⅱ）设a＞﹣1，且当x∈[，]时，f（x）＝1+a，不等式化为1+a≤x+3，故x≥a﹣2对x∈[，]都成立．故a﹣2，解得a，故a的取值范围为（﹣1，]．8．【2012年新课标1文科24】已知函数f（x）＝|x+a|+|x﹣2|①当a＝﹣3时，求不等式f（x）≥3的解集；②f（x）≤|x﹣4|若的解集包含[1，2]，求a的取值范围．【解答】解：（1）当a＝﹣3时，f（x）≥3 即|x﹣3|+|x﹣2|≥3，即，可得x≤1；，可得x∈∅；，可得x≥4．取并集可得不等式的解集为 {x|x≤1或x≥4}．（2）原命题即f（x）≤|x﹣4|在[1，2]上恒成立，等价于|x+a|+2﹣x≤4﹣x在[1，2]上恒成立，等价于|x+a|≤2，等价于﹣2≤x+a≤2，﹣2﹣x≤a≤2﹣x在[1，2]上恒成立．故当 1≤x≤2时，﹣2﹣x的最大值为﹣2﹣1＝﹣3，2﹣x的最小值为0，故a的取值范围为[﹣3，0]．9．【2011年新课标1文科24】设函数f（x）＝|x﹣a|+3x，其中a＞0．（Ⅰ）当a＝1时，求不等式f（x）≥3x+2的解集（Ⅱ）若不等式f（x）≤0的解集为{x|x≤﹣1}，求a的值．【解答】解：（Ⅰ）当a＝1时，f（x）≥3x+2可化为|x﹣1|≥2．由此可得x≥3或x≤﹣1．故不等式f（x）≥3x+2的解集为{x|x≥3或x≤﹣1}．（Ⅱ）由f（x）≤0得|x﹣a|+3x≤0此不等式化为不等式组或即或因为a＞0，所以不等式组的解集为{x|x}由题设可得1，故a＝210．【2010年新课标1文科24】设函数f（x）＝|2x﹣4|+1．（Ⅰ）画出函数y＝f（x）的图象：（Ⅱ）若不等式f（x）≤ax的解集非空，求a的取值范围．【解答】解：（Ⅰ）由于f（x），函数y ＝f （x ）的图象如图所示．（Ⅱ）由函数y ＝f （x ）与函数y ＝ax 的图象可知，极小值在点（2，1）当且仅当a ＜﹣2或a 时，函数y ＝f （x ）与函数y ＝ax 的图象有交点．故不等式f （x ）≤ax 的解集非空时，a 的取值范围为（﹣∞，﹣2）∪[，+∞）．考题分析与复习建议本专题考查的知识点为：解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．求解的一般方法是去掉绝对值，也可以借助数形结合求解.历年考题主要以解答题题型出现，重点考查的知识点为解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．预测明年本考点题目会比较稳定，备考方向以知识点解绝对值不等式、利用不等式恒成立求参数的值或范围，证明不等式为重点较佳.最新高考模拟试题 1．已知函数()22()f x x a x a R =-+-∈.（1）当2a =时，求不等式()2f x >的解集；（2）若[2,1]x ∈-时不等式()32f x x ≤-成立，求实数a 的取值范围．【答案】（1）2{|3x x <或()4cos(2)6f x x π=-；（2）空集. 【解析】解：（1）不等式()2f x >，即2222x x -+->.可得22222x x x ≥⎧⎨-+->⎩，或122222x x x <<⎧⎨-+->⎩或12222x x x ≤⎧⎨--+>⎩，解得23x <或2x >，所以不等式的解集为2{|2}3x x x <>或. （2）当[2,1]x ∈-时，220x -<，所以()22f x x a x =-+-，由()32f x x ≤-得1x a -≤，即11a x a -≤≤+，则1211a a -≤-⎧⎨+≥⎩，该不等式无解，所以实数a 的取值范围是空集（或者∅）.2．已知()221f x x x =-++．（1）求不等式()6f x <的解集；（2）设m 、n 、p 为正实数，且()3m n p f ++=，求证：12mn np pm ++≤．【答案】(1) ()1,3- (2)见证明【解析】（1）①2x ≥时，()24133f x x x x =-++=-，由()6f x <，∴336x -<，∴3x <，即23x ≤<，②12x -<<时，()4215f x x x x =-++=-，由()6f x <，∴56x -<，∴1x >-，即12x -<<， ③1x ≤-时，()42133f x x x x =---=-，由()6f x <，∴336x -<，∴1x >-，可知无解，综上，不等式()6f x <的解集为()1,3-；（2）∵()221f x x x =-++，∴()36f =，∴()36m n p f ++==，且,,m n p 为正实数∴()222222236m n p m n p mn mp np ++=+++++=，∵222m n mn +≥，222m p mp +≥，222n p np +≥， ∴222m n p mn mp np ++≥++，∴()()2222222363m n p m n p mn mp np mn mp np ++=+++++=≥++ 又,,m n p 为正实数，∴可以解得12mn np pm ++≤． 3．[选修4—5：不等式选讲]已知函数()|||2|(0)f x x m x m m =--+>. （1）当1m =，求不等式()1f x ≥的解集；（2）对于任意实数,x t ，不等式()21f x t t <++-恒成立，求实数m 的取值范围. 【答案】（1）113x x ⎧⎫-≤≤-⎨⎬⎩⎭；（2）()0,2 【解析】（1）当1m =时，()1f x ≥为：1211x x --+≥当1x ≥时，不等式为：1211x x ---≥，解得：3x ≤-，无解当112x -≤<时，不等式为：1211x x -+--≥，解得：13x ≤-，此时1123x -≤≤- 当12x <-时，不等式为：1211x x -+++≥，解得：1x -≥，此时112x -≤<-综上所述，不等式的解集为113x x ⎧⎫-≤≤-⎨⎬⎩⎭（2）对于任意实数x ，t ，不等式()21f x t t <++-恒成立等价于()()max min |2||1|f x t t <++- 因为|2||1||(2)(1)|3t t t t ++-≥+--=，当且仅当(2)(1)0t t +-≤时等号成立所以()min |2||1|3t t ++-=因为0m >时，()2f x x m x m =--+=2,23,22,m x m x m x x m x m x m ⎧+<-⎪⎪⎪--≤≤⎨⎪-->⎪⎪⎩，函数()f x 单调递增区间为(,)2m -∞-，单调递减区间为(,)2m-+∞ ∴当2m x =-时，()max 322m mf x f ⎛⎫=-= ⎪⎝⎭332m∴<，又0m >，解得：02m << ∴实数m 的取值范围()0,24．选修4-5不等式选讲已知关于x 的不等式20x m x -+≤的解集为{|2}x x ≤-，其中0m >. （1）求m 的值；（2）若正数a ，b ，c 满足a b c m ++=，求证：2222b c aa b c++≥.【答案】（1）2m =（2）见证明【解析】（1）由题意知：20x m x -+≤即20x m x m x ≥⎧⎨-+≤⎩或20x mm x x ≤⎧⎨-+≤⎩化简得：3x mm x ≥⎧⎪⎨≤⎪⎩或x m x m ≤⎧⎨≤-⎩ 0m > ∴不等式组的解集为{}x x m ≤- 2m ∴-=-，解得：2m =（2）由（1）可知，2a b c ++=由基本不等式有：22b a b a +≥，22c b c b +≥，22a c a c +≥三式相加可得：222222b c a a b c b c a a b c +++++≥++222b c a a b c a b c ∴++≥++，即：2222b c a a b c++≥ 5．选修4-5：不等式选讲已知函数()13f x x x a =+++ （1）当1a =-时，解不等式()2f x ≥；（2）若存在0x 满足00()211f x x ++<，求实数a 的取值范围. 【答案】(1) 1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或 (2) 24a << 【解析】（1）当1a =-时，()|1||31|f x x x =++-，当13x ≥时，不等式等价于1312x x ++-≥，解得12x ≥，12x ∴≥；当113x -<<时，不等式等价于1312x x +-+≥，解得0x ≤，10x ∴-<≤；当1x ≤-时，不等式等价于1312x x ---+≥，解得12x ≤-，1x -∴≤.综上所述，原不等式的解集为1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或. （2）由()00211f x x ++<，得003131x x a +++<，而()()000000313333333|3|x x a x x a x x a a +++=+++≥+-+=-，（当且仅当()()003330x x a ++≤时等号成立）由题可知min (()2|1|)1f x x ++<，即31a -<，解得实数a 的取值范围是24a <<. 6．已知函数()|2|f x ax =-.（Ⅰ）当4a =时，求不等式()|42|8f x x ++≥的解集；（Ⅱ）若[2,4]x ∈时，不等式()|3|3f x x x +-≤+成立，求a 的取值范围. 【答案】（I ）(,1][1,)-∞-+∞；（II ）[1,2]- 【解析】（I ）当4a =时，原不等式即|42||42|8x x -++≥，即|21||21|4x x -++≥. 当12x ≥时，21214x x -++≥，解得1x ≥，∴1x ≥；当1122x -≤≤时，12214x x -++≥，无解；当12x ≤-时，12214x x ---≥，解得1x ≤-，∴1x ≤-；综上，原不等式的解集为(,1][1,)-∞-+∞（II ）由()|3|3f x x x +-≤+得|2||3|3ax x x -+-≤+（*）当[2,3]x ∈时，（*）等价于|2|33|2|2ax x x ax x -+-≤+⇔-≤ 即22a x -≤，所以2222a x x -+≤≤+恒成立，所以813a -≤≤ 当(3,4]x ∈时，（*）等价于|2|33|2|6ax x x ax -+-≤+⇔-≤ 即48ax -≤≤，所以48a x x-≤≤恒成立，所以12a -≤≤ 综上，a 的取值范围是[1,2]-7．已知函数()21f x x x a =-++，()2g x x =+．（1）当1a =-时，求不等式()()f x g x <的解集；（2）设12a >-，且当1,2x a ⎡⎫∈-⎪⎢⎣⎭，()()f x g x ≤，求a 的取值范围．【答案】（1）()0,2；（2）11,23⎛⎤- ⎥⎝⎦【解析】（1）当1a =-时，不等式()()f x g x <化为：21120x x x -+---<当12x ≤时，不等式化为12120x x x -+---<，解得：102x <≤当112x <≤时，不等式化为21120x x x -+---<，解得：112x <≤ 当1x >时，不等式化为21120x x x -+---<，解得：12x << 综上，原不等式的解集为()0,2 （2）由12a x -≤<，得221a x -≤<，21210a x --≤-< 又102x a a ≤+<+则()()211f x x x a x a =--++=-++∴不等式()()f x g x ≤化为：12x a x -++≤+得21a x ≤+对1,2x a ⎡⎫∈-⎪⎢⎣⎭都成立 21a a ∴≤-+，解得：13a ≤又12a >-，故a 的取值范围是11,23⎛⎤- ⎥⎝⎦8．已知函数()|2|f x x =-．（Ⅰ）求不等式()|1|f x x x <++的解集；（Ⅱ）若函数5log [(3)()3]y f x f x a =++-的定义域为R ，求实数a 的取值范围．【答案】（I ）1,3⎛⎫+∞ ⎪⎝⎭（II ）(,1)-∞ 【解析】解：（I ）由已知不等式()|1|f x x x <++，得|2||1|x x x -<++，当2x ≥时，不等式为21x x x -<++，解得3x >-，所以2x ≥；当12x -<<时，不等式为21x x x -<++，解得13x >，所以123x <<；当1x ≤-时，不等式为21x x x -<--，解得3x >，此时无解．综上：不等式的解集为1,3⎛⎫+∞ ⎪⎝⎭．（II ）若5log [(3)()3]y f x f x a =++-的定义域为R ，则(3)()30f x f x a ++->恒成立． ∵|1||2|3|12|333x x a x x a a ++--≥+-+-=-，当且仅当[1,2]x ∈-时取等号． ∴330a ->，即1a <．所以实数a 的取值范围是(,1)-∞． 9．已知函数()123f x x x =-+-．（Ⅰ）解关于x 的不等式()4f x ≤；（Ⅱ）若()20f x m m -->恒成立，求实数m 的取值范围．【答案】（Ⅰ）111,3⎡⎤⎢⎥⎣⎦；（Ⅱ）()2,1-.【解析】解：（I ）当1x ≤时，不等式为：()1234x x -+-≤，解得1x ≥，故1x =．当13x <<时，不等式为：()1234x x -+-≤，解得1x ≥，故13x <<1＜x ＜3，当3x ≥时，不等式为：()1234x x -+-≤，解得113x ≤，故1133x ≤≤．综上，不等式()4f x ≤的解集为111,3⎡⎤⎢⎥⎣⎦．（II ）由()20f x m m -->恒成立可得()2m m f x +<恒成立．又()37,35,1337,1x x f x x x x x -≥⎧⎪=-+<<⎨⎪-+≤⎩，故()f x 在(],1-∞上单调递减，在()1,3上单调递减，在[)3,+∞上单调递增，∴()f x 的最小值为()32f =． ∴22m m +<，解得21m -<<．即m 的最值范围是()2,1-．10．已知函数()211f x x x =-++. （Ⅰ）解不等式()3f x ≥；（Ⅱ）记函数()f x 的最小值为m ，若,,a b c 均为正实数，且232a b c m ++=，求222a b c ++的最小值. 【答案】（Ⅰ）{}11x x x ≤-≥或；（Ⅱ）914. 【解析】（Ⅰ）由题意， 3,11()2,1213,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩，所以()3f x ≥等价于133x x ≤-⎧⎨-≥⎩或11223x x ⎧-<<⎪⎨⎪-≥⎩或1233x x ⎧≥⎪⎨⎪≥⎩.解得：1x ≤-或1x ≥，所以不等式的解集为{}11x x x ≤-≥或；（Ⅱ）由(1)可知,当12x =时, ()f x 取得最小值32,所以32m =，即233a b c ++=，由柯西不等式得2222222()(123)(23)9a b c a b c ++++≥++=，整理得222914a b c ++≥，当且仅当123a b c ==时, 即369,,141414a b c ===时等号成立.所以222a b c ++的最小值为914.11．已知函数()12f x x a x =+++. （Ⅰ）求1a =时，()3f x ≤的解集；（Ⅱ）若()f x 有最小值，求a 的取值范围，并写出相应的最小值. 【答案】（Ⅰ）[3,0]-；（Ⅱ）见解析. 【解析】（Ⅰ）当1a =时，232()12121231x x f x x x x x x --≤-⎧⎪=+++=-<<-⎨⎪+≥-⎩∵()3f x ≤当2x -≤时()233f x x =--≤解得32x -≤≤- 当21x -<<-时()13f x =≤恒成立当1x -≥时()233f x x =+≤解得10x -≤≤ 综上可得解集[3,0]-.（Ⅱ）(1)212()12(1)2121(1)211a x a x f x x a x a x a x a x a x -+--≤-⎧⎪=+++=-+--<<-⎨⎪+++≥-⎩当(1)0a -+>，即1a <-时，()f x 无最小值；当(1)0a -+=，即1a =-时，()f x 有最小值1-；当(1)0a -+<且10a -≤，即11a -<≤时， min ()(1)f x f a =-= 当(1)0a -+<且10a ->，即1a >时， min ()(2)1f x f =-= 综上：当1a <-时，()f x 无最小值；当1a =-时，()f x 有最小值1-；当11a -<≤时， min ()(1)f x f a =-= ；当1a >时， min ()(2)1f x f =-=； 12．选修4-5：不等式选讲已知函数()|23||1|f x x x =--+. （1）求不等式()6f x ≤的解集；（2）设集合M 满足：当且仅当x M ∈时，()|32|f x x =-，若,a b M ∈，求证：228223a b a b -++≤. 【答案】(1) {}210x x -≤≤；(2)见解析. 【解析】（1）()4,1323132,1234,2x x f x x x x x x x ⎧⎪-+<-⎪⎪=--+=-+-≤≤⎨⎪⎪->⎪⎩当1x <- 时，46x -+≤ ，得2x -≥ ，故21x -≤<-；当312x -≤≤时，326x -+≤ ，得43x ≥- ，故312x -≤<；当32x > 时，46x -≤ ，得10x ≤ ，故3102x <≤；综上，不等式()6f x ≤的解集为{}210x x -≤≤（2）由绝对值不等式的性质可知()231(23)(1)32f x x x x x x =--+≤-++=- 等价于23(1)32x x x -≤-++-，当且仅当(23)(1)0x x -+≤，即213x -≤≤时等号成立，故21,3M ⎡⎤=-⎢⎥⎣⎦所以221,133a b -≤≤-≤≤，所以222510(1),4(1)99a b ≤-≤-≤--≤-，即228(1)(1)3a b ---≤.13．[选修4—5：不等式选讲] 已知函数()31f x x m x m =---- （1）若1m =，求不等式()1f x <的解集.（2）对任意的x R ∈，有()(2)f x f ≤，求实数m 的取值范围. 【答案】（1）(,3)-∞；（2）1123m -≤≤ 【解析】（1）()141f x x x =---<，所以11441(4)11(4)1141x x x x x x x x x <≤≤>⎧⎧⎧⎨⎨⎨---<---<--+<⎩⎩⎩或或解之得不等式()1f x <的解集为(,3)-∞. (2)当131,2m m m +>>-时，由题得2必须在3m+1的右边或者与3m+1重合，所以1231,3m m ≥+∴≤，所以1123m -<≤，当131,2m m m +==-时，不等式恒成立，当131,2m m m +<<-时，由题得2必须在3m+1的左边或者与3m+1重合，由题得1231,3m m ≤+≥，所以m 没有解.综上，1123m -≤≤.14．已知()21f x x x =+-．（1）证明()1f x x +≥；（2）若,,a b c +∈R ，记33311134abc a b c +++的最小值为m ，解关于x 的不等式()f x m <．【答案】(1)见证明；(2) 2433x x ⎧⎫-<<⎨⎬⎩⎭【解析】（1）()2212211f x x x x x x +=+-≥-+=．当且仅当()2x 2x 10-≤,等号成立（2）∵3331113333334444abc abc abc abc m a b c abc +++≥=+≥==，当且仅当a=b=c 等号成立由不等式()3f x <即()213f x x x =+-<．由()31,01211,02131,2x x f x x x x x x x ⎧⎪-+≤⎪⎪=+-=-<<⎨⎪⎪-≥⎪⎩得：不等式()3f x <的解集为2433x x ⎧⎫-<<⎨⎬⎩⎭．15．选修4—5：不等式选讲已知函数()11f x x mx =++-，m R ∈。

十年真题(2010)高考数学真题分类汇编专题15不等式选讲文(含解析)

历年考题细目表题型年份考点试题位置解答题2019 不等式选讲2019年新课标1文科23解答题2018 综合测试题2018年新课标1文科23解答题2017 综合测试题2017年新课标1文科23解答题2016 综合测试题2016年新课标1文科24解答题2015 综合测试题2015年新课标1文科24解答题2014 综合测试题2014年新课标1文科24解答题2013 综合测试题2013年新课标1文科24解答题2012 综合测试题2012年新课标1文科24解答题2011 综合测试题2011年新课标1文科24解答题2010 综合测试题2010年新课标1文科24历年高考真题汇编十年真题（2010）高考数学真题分类汇编专题15不等式选讲文（含解析）1．【2019年新课标1文科23】已知a，b，c为正数，且满足abc＝1．证明：（1）a2+b2+c2；（2）（a+b）3+（b+c）3+（c+a）3≥24．【解答】证明：（1）分析法：已知a，b，c为正数，且满足abc＝1．要证（1）a2+b2+c2；因为abc＝1．就要证：a2+b2+c2；即证：bc+ac+ab≤a2+b2+c2；即：2bc+2ac+2ab≤2a2+2b2+2c2；2a2+2b2+2c2﹣2bc﹣2ac﹣2ab≥0（a﹣b）2+（a﹣c）2+（b﹣c）2≥0；∵a，b，c为正数，且满足abc＝1．∴（a﹣b）2≥0；（a﹣c）2≥0；（b﹣c）2≥0恒成立；当且仅当：a＝b＝c＝1时取等号．即（a﹣b）2+（a﹣c）2+（b﹣c）2≥0得证．故a2+b2+c2得证．（2）证（a+b）3+（b+c）3+（c+a）3≥24成立；即：已知a，b，c为正数，且满足abc＝1．（a+b）为正数；（b+c）为正数；（c+a）为正数；（a+b）3+（b+c）3+（c+a）3≥3（a+b）•（b+c）•（c+a）；当且仅当（a+b）＝（b+c）＝（c+a）时取等号；即：a＝b＝c＝1时取等号；∵a，b，c为正数，且满足abc＝1．（a+b）≥2；（b+c）≥2；（c+a）≥2；当且仅当a＝b，b＝c；c＝a时取等号；即：a＝b＝c＝1时取等号；∴（a+b）3+（b+c）3+（c+a）3≥3（a+b）•（b+c）•（c+a）≥3×8••24abc＝24；当且仅当a＝b＝c＝1时取等号；故（a+b）3+（b+c）3+（c+a）3≥24．得证．故得证．2．【2018年新课标1文科23】已知f（x）＝|x+1|﹣|ax﹣1|．（1）当a＝1时，求不等式f（x）＞1的解集；（2）若x∈（0，1）时不等式f（x）＞x成立，求a的取值范围．【解答】解：（1）当a＝1时，f（x）＝|x+1|﹣|x﹣1|，由f（x）＞1，∴或，解得x，故不等式f（x）＞1的解集为（，+∞），（2）当x∈（0，1）时不等式f（x）＞x成立，∴|x+1|﹣|ax﹣1|﹣x＞0，即x+1﹣|ax﹣1|﹣x＞0，即|ax﹣1|＜1，∴﹣1＜ax﹣1＜1，∴0＜ax＜2，∵x∈（0，1），∴a＞0，∴0＜x，∴a∵2，∴0＜a≤2，故a的取值范围为（0，2]．3．【2017年新课标1文科23】已知函数f（x）＝﹣x2+ax+4，g（x）＝|x+1|+|x﹣1|．（1）当a＝1时，求不等式f（x）≥g（x）的解集；（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．【解答】解：（1）当a＝1时，f（x）＝﹣x2+x+4，是开口向下，对称轴为x的二次函数，g（x）＝|x+1|+|x﹣1|，当x∈（1，+∞）时，令﹣x2+x+4＝2x，解得x，g（x）在（1，+∞）上单调递增，f（x）在（1，+∞）上单调递减，∴此时f（x）≥g（x）的解集为（1，]；当x∈[﹣1，1]时，g（x）＝2，f（x）≥f（﹣1）＝2．当x∈（﹣∞，﹣1）时，g（x）单调递减，f（x）单调递增，且g（﹣1）＝f（﹣1）＝2．综上所述，f（x）≥g（x）的解集为[﹣1，]；（2）依题意得：﹣x2+ax+4≥2在[﹣1，1]恒成立，即x2﹣ax﹣2≤0在[﹣1，1]恒成立，则只需，解得﹣1≤a≤1，故a的取值范围是[﹣1，1]．4．【2016年新课标1文科24】已知函数f（x）＝|x+1|﹣|2x﹣3|．（Ⅰ）在图中画出y＝f（x）的图象；（Ⅱ）求不等式|f（x）|＞1的解集．【解答】解：（Ⅰ）f（x），由分段函数的图象画法，可得f（x）的图象，如右：（Ⅱ）由|f（x）|＞1，可得当x≤﹣1时，|x﹣4|＞1，解得x＞5或x＜3，即有x≤﹣1；当﹣1＜x时，|3x﹣2|＞1，解得x＞1或x，即有﹣1＜x或1＜x；当x时，|4﹣x|＞1，解得x＞5或x＜3，即有x＞5或x＜3．综上可得，x或1＜x＜3或x＞5．则|f（x）|＞1的解集为（﹣∞，）∪（1，3）∪（5，+∞）．5．【2015年新课标1文科24】已知函数f（x）＝|x+1|﹣2|x﹣a|，a＞0．（Ⅰ）当a＝1时，求不等式f（x）＞1的解集；（Ⅱ）若f（x）的图象与x轴围成的三角形面积大于6，求a的取值范围．【解答】解：（Ⅰ）当a＝1时，不等式f（x）＞1，即|x+1|﹣2|x﹣1|＞1，即①，或②，或③．解①求得x∈∅，解②求得x＜1，解③求得1≤x＜2．综上可得，原不等式的解集为（，2）．（Ⅱ）函数f（x）＝|x+1|﹣2|x﹣a|，由此求得f（x）的图象与x轴的交点A（，0），B（2a+1，0），故f（x）的图象与x轴围成的三角形的第三个顶点C（a，a+1），由△ABC的面积大于6，可得[2a+1]•（a+1）＞6，求得a＞2．故要求的a的范围为（2，+∞）．6．【2014年新课标1文科24】若a＞0，b＞0，且．（Ⅰ）求a3+b3的最小值；（Ⅱ）是否存在a，b，使得2a+3b＝6？并说明理由．【解答】解：（Ⅰ）∵a＞0，b＞0，且，∴2，∴ab≥2，当且仅当a＝b时取等号．∵a3+b3 ≥224，当且仅当a＝b时取等号，∴a3+b3的最小值为4．（Ⅱ）∵2a+3b≥22，当且仅当2a＝3b时，取等号．而由（1）可知，2246，故不存在a，b，使得2a+3b＝6成立．7．【2013年新课标1文科24】已知函数f（x）＝|2x﹣1|+|2x+a|，g（x）＝x+3．（Ⅰ）当a＝﹣2时，求不等式f（x）＜g（x）的解集；（Ⅱ）设a＞﹣1，且当x∈[，]时，f（x）≤g（x），求a的取值范围．【解答】解：（Ⅰ）当a＝﹣2时，求不等式f（x）＜g（x）化为|2x﹣1|+|2x﹣2|﹣x﹣3＜0．设y＝|2x﹣1|+|2x﹣2|﹣x﹣3，则y，它的图象如图所示：结合图象可得，y＜0的解集为（0，2），故原不等式的解集为（0，2）．（Ⅱ）设a＞﹣1，且当x∈[，]时，f（x）＝1+a，不等式化为1+a≤x+3，故x≥a﹣2对x∈[，]都成立．故a﹣2，解得a，故a的取值范围为（﹣1，]．8．【2012年新课标1文科24】已知函数f（x）＝|x+a|+|x﹣2|①当a＝﹣3时，求不等式f（x）≥3的解集；②f（x）≤|x﹣4|若的解集包含[1，2]，求a的取值范围．【解答】解：（1）当a＝﹣3时，f（x）≥3 即|x﹣3|+|x﹣2|≥3，即，可得x≤1；，可得x∈∅；，可得x≥4．取并集可得不等式的解集为 {x|x≤1或x≥4}．（2）原命题即f（x）≤|x﹣4|在[1，2]上恒成立，等价于|x+a|+2﹣x≤4﹣x在[1，2]上恒成立，等价于|x+a|≤2，等价于﹣2≤x+a≤2，﹣2﹣x≤a≤2﹣x在[1，2]上恒成立．故当 1≤x≤2时，﹣2﹣x的最大值为﹣2﹣1＝﹣3，2﹣x的最小值为0，故a的取值范围为[﹣3，0]．9．【2011年新课标1文科24】设函数f（x）＝|x﹣a|+3x，其中a＞0．（Ⅰ）当a＝1时，求不等式f（x）≥3x+2的解集（Ⅱ）若不等式f（x）≤0的解集为{x|x≤﹣1}，求a的值．【解答】解：（Ⅰ）当a＝1时，f（x）≥3x+2可化为|x﹣1|≥2．由此可得x≥3或x≤﹣1．故不等式f（x）≥3x+2的解集为{x|x≥3或x≤﹣1}．（Ⅱ）由f（x）≤0得|x﹣a|+3x≤0此不等式化为不等式组或即或因为a＞0，所以不等式组的解集为{x|x}由题设可得1，故a＝210．【2010年新课标1文科24】设函数f（x）＝|2x﹣4|+1．（Ⅰ）画出函数y＝f（x）的图象：（Ⅱ）若不等式f（x）≤ax的解集非空，求a的取值范围．【解答】解：（Ⅰ）由于f（x），函数y ＝f （x ）的图象如图所示．（Ⅱ）由函数y ＝f （x ）与函数y ＝ax 的图象可知，极小值在点（2，1）当且仅当a ＜﹣2或a 时，函数y ＝f （x ）与函数y ＝ax 的图象有交点．故不等式f （x ）≤ax 的解集非空时，a 的取值范围为（﹣∞，﹣2）∪[，+∞）．考题分析与复习建议本专题考查的知识点为：解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．求解的一般方法是去掉绝对值，也可以借助数形结合求解.历年考题主要以解答题题型出现，重点考查的知识点为解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．预测明年本考点题目会比较稳定，备考方向以知识点解绝对值不等式、利用不等式恒成立求参数的值或范围，证明不等式为重点较佳.最新高考模拟试题 1．已知函数()22()f x x a x a R =-+-∈.（1）当2a =时，求不等式()2f x >的解集；（2）若[2,1]x ∈-时不等式()32f x x ≤-成立，求实数a 的取值范围．【答案】（1）2{|3x x <或()4cos(2)6f x x π=-；（2）空集. 【解析】解：（1）不等式()2f x >，即2222x x -+->.可得22222x x x ≥⎧⎨-+->⎩，或122222x x x <<⎧⎨-+->⎩或12222x x x ≤⎧⎨--+>⎩，解得23x <或2x >，所以不等式的解集为2{|2}3x x x <>或. （2）当[2,1]x ∈-时，220x -<，所以()22f x x a x =-+-，由()32f x x ≤-得1x a -≤，即11a x a -≤≤+，则1211a a -≤-⎧⎨+≥⎩，该不等式无解，所以实数a 的取值范围是空集（或者∅）.2．已知()221f x x x =-++．（1）求不等式()6f x <的解集；（2）设m 、n 、p 为正实数，且()3m n p f ++=，求证：12mn np pm ++≤．【答案】(1) ()1,3- (2)见证明【解析】（1）①2x ≥时，()24133f x x x x =-++=-，由()6f x <，∴336x -<，∴3x <，即23x ≤<，②12x -<<时，()4215f x x x x =-++=-，由()6f x <，∴56x -<，∴1x >-，即12x -<<， ③1x ≤-时，()42133f x x x x =---=-，由()6f x <，∴336x -<，∴1x >-，可知无解，综上，不等式()6f x <的解集为()1,3-；（2）∵()221f x x x =-++，∴()36f =，∴()36m n p f ++==，且,,m n p 为正实数∴()222222236m n p m n p mn mp np ++=+++++=，∵222m n mn +≥，222m p mp +≥，222n p np +≥，∴222m n p mn mp np ++≥++，∴()()2222222363m n p m n p mn mp np mn mp np ++=+++++=≥++又,,m n p 为正实数，∴可以解得12mn np pm ++≤．3．[选修4—5：不等式选讲]已知函数()|||2|(0)f x x m x m m =--+>.（1）当1m =，求不等式()1f x ≥的解集；（2）对于任意实数,x t ，不等式()21f x t t <++-恒成立，求实数m 的取值范围.【答案】（1）113x x ⎧⎫-≤≤-⎨⎬⎩⎭；（2）()0,2【解析】（1）当1m =时，()1f x ≥为：1211x x --+≥当1x ≥时，不等式为：1211x x ---≥，解得：3x ≤-，无解当112x -≤<时，不等式为：1211x x -+--≥，解得：13x ≤-，此时1123x -≤≤- 当12x <-时，不等式为：1211x x -+++≥，解得：1x -≥，此时112x -≤<- 综上所述，不等式的解集为113x x ⎧⎫-≤≤-⎨⎬⎩⎭（2）对于任意实数x ，t ，不等式()21f x t t <++-恒成立等价于()()max min |2||1|f x t t <++- 因为|2||1||(2)(1)|3t t t t ++-≥+--=，当且仅当(2)(1)0t t +-≤时等号成立所以()min |2||1|3t t ++-= 因为0m >时，()2f x x m x m =--+=2,23,22,m x m x m x x m x m x m ⎧+<-⎪⎪⎪--≤≤⎨⎪-->⎪⎪⎩，函数()f x 单调递增区间为(,)2m -∞-，单调递减区间为(,)2m -+∞ ∴当2m x =-时，()max 322m m f x f ⎛⎫=-= ⎪⎝⎭ 332m ∴<，又0m >，解得：02m << ∴实数m 的取值范围()0,24．选修4-5不等式选讲已知关于x 的不等式20x m x -+≤的解集为{|2}x x ≤-，其中0m >.（1）求m 的值；（2）若正数a ，b ，c 满足a b c m ++=，求证：2222b c a a b c++≥. 【答案】（1）2m =（2）见证明【解析】（1）由题意知：20x m x -+≤即20x m x m x ≥⎧⎨-+≤⎩或20x m m x x ≤⎧⎨-+≤⎩化简得：3x m m x ≥⎧⎪⎨≤⎪⎩或x m x m ≤⎧⎨≤-⎩ 0m > ∴不等式组的解集为{}x x m ≤-2m ∴-=-，解得：2m =（2）由（1）可知，2a b c ++= 由基本不等式有：22b a b a +≥，22c b c b+≥，22a c a c +≥ 三式相加可得：222222b c a a b c b c a a b c+++++≥++ 222b c a a b c a b c ∴++≥++，即：2222b c a a b c++≥ 5．选修4-5：不等式选讲已知函数()13f x x x a =+++（1）当1a =-时，解不等式()2f x ≥；（2）若存在0x 满足00()211f x x ++<，求实数a 的取值范围.【答案】(1) 1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或 (2) 24a << 【解析】（1）当1a =-时，()|1||31|f x x x =++-，当13x ≥时，不等式等价于1312x x ++-≥，解得12x ≥，12x ∴≥；当113x -<<时，不等式等价于1312x x +-+≥，解得0x ≤，10x ∴-<≤；当1x ≤-时，不等式等价于1312x x ---+≥，解得12x ≤-，1x -∴≤. 综上所述，原不等式的解集为1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或. （2）由()00211f x x ++<，得003131x x a +++<，而()()000000313333333|3|x x a x x a x x a a +++=+++≥+-+=-，（当且仅当()()003330x x a ++≤时等号成立）由题可知min (()2|1|)1f x x ++<，即31a -<，解得实数a 的取值范围是24a <<.6．已知函数()|2|f x ax =-.（Ⅰ）当4a =时，求不等式()|42|8f x x ++≥的解集；（Ⅱ）若[2,4]x ∈时，不等式()|3|3f x x x +-≤+成立，求a 的取值范围.【答案】（I ）(,1][1,)-∞-+∞；（II ）[1,2]-【解析】（I ）当4a =时，原不等式即|42||42|8x x -++≥，即|21||21|4x x -++≥. 当12x ≥时，21214x x -++≥，解得1x ≥，∴1x ≥；当1122x -≤≤时，12214x x -++≥，无解；当12x ≤-时，12214x x ---≥，解得1x ≤-，∴1x ≤-；综上，原不等式的解集为(,1][1,)-∞-+∞（II ）由()|3|3f x x x +-≤+得|2||3|3ax x x -+-≤+（*）当[2,3]x ∈时，（*）等价于|2|33|2|2ax x x ax x -+-≤+⇔-≤ 即22a x -≤，所以2222a x x -+≤≤+恒成立，所以813a -≤≤ 当(3,4]x ∈时，（*）等价于|2|33|2|6ax x x ax -+-≤+⇔-≤即48ax -≤≤，所以48a x x-≤≤恒成立，所以12a -≤≤ 综上，a 的取值范围是[1,2]-7．已知函数()21f x x x a =-++，()2g x x =+．（1）当1a =-时，求不等式()()f x g x <的解集；（2）设12a >-，且当1,2x a ⎡⎫∈-⎪⎢⎣⎭，()()f x g x ≤，求a 的取值范围．【答案】（1）()0,2；（2）11,23⎛⎤-⎥⎝⎦ 【解析】（1）当1a =-时，不等式()()f x g x <化为：21120x x x -+---< 当12x ≤时，不等式化为12120x x x -+---<，解得：102x <≤ 当112x <≤时，不等式化为21120x x x -+---<，解得：112x <≤ 当1x >时，不等式化为21120x x x -+---<，解得：12x <<综上，原不等式的解集为()0,2（2）由12a x -≤<，得221a x -≤<，21210a x --≤-< 又102x a a ≤+<+则()()211f x x x a x a =--++=-++∴不等式()()f x g x ≤化为：12x a x -++≤+得21a x ≤+对1,2x a ⎡⎫∈-⎪⎢⎣⎭都成立 21a a ∴≤-+，解得：13a ≤ 又12a >-，故a 的取值范围是11,23⎛⎤- ⎥⎝⎦8．已知函数()|2|f x x =-．（Ⅰ）求不等式()|1|f x x x <++的解集；（Ⅱ）若函数5log [(3)()3]y f x f x a =++-的定义域为R ，求实数a 的取值范围．【答案】（I ）1,3⎛⎫+∞ ⎪⎝⎭（II ）(,1)-∞【解析】解：（I ）由已知不等式()|1|f x x x <++，得|2||1|x x x -<++，当2x ≥时，不等式为21x x x -<++，解得3x >-，所以2x ≥；当12x -<<时，不等式为21x x x -<++，解得13x >，所以123x <<；当1x ≤-时，不等式为21x x x -<--，解得3x >，此时无解．综上：不等式的解集为1,3⎛⎫+∞ ⎪⎝⎭．（II ）若5log [(3)()3]y f x f x a =++-的定义域为R ，则(3)()30f x f x a ++->恒成立．∵，当且仅当[1,2]x ∈-时取等号．∴330a ->，即1a <．所以实数a 的取值范围是(,1)-∞．9．已知函数()123f x x x =-+-．（Ⅰ）解关于x 的不等式()4f x ≤；（Ⅱ）若()20f x m m -->恒成立，求实数m 的取值范围．【答案】（Ⅰ）111,3⎡⎤⎢⎥⎣⎦；（Ⅱ）()2,1-. 【解析】解：（I ）当1x ≤时，不等式为：()1234x x -+-≤，解得1x ≥，故1x =．当13x <<时，不等式为：()1234x x -+-≤，解得1x ≥，故13x <<1＜x ＜3，当3x ≥时，不等式为：()1234x x -+-≤，解得113x ≤，故1133x ≤≤．综上，不等式()4f x ≤的解集为111,3⎡⎤⎢⎥⎣⎦．（II ）由()20f x m m -->恒成立可得()2m m f x +<恒成立．又()37,35,1337,1x x f x x x x x -≥⎧⎪=-+<<⎨⎪-+≤⎩，故()f x 在(],1-∞上单调递减，在()1,3上单调递减，在[)3,+∞上单调递增， ∴()f x 的最小值为()32f =．∴22m m +<，解得21m -<<．即m 的最值范围是()2,1-．10．已知函数()211f x x x =-++.（Ⅰ）解不等式()3f x ≥；（Ⅱ）记函数()f x 的最小值为m ，若,,a b c 均为正实数，且232a b c m ++=，求222a b c ++的最小值.【答案】（Ⅰ）{}11x x x ≤-≥或；（Ⅱ）914. 【解析】（Ⅰ）由题意， 3,11()2,1213,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩，所以()3f x ≥等价于133x x ≤-⎧⎨-≥⎩或11223x x ⎧-<<⎪⎨⎪-≥⎩或1233x x ⎧≥⎪⎨⎪≥⎩.解得：1x ≤-或1x ≥，所以不等式的解集为{}11x x x ≤-≥或；（Ⅱ）由(1)可知,当12x =时, ()f x 取得最小值32, 所以32m =，即233a b c ++=，由柯西不等式得2222222()(123)(23)9a b c a b c ++++≥++=，整理得222914a b c ++≥，当且仅当123a b c ==时, 即369,,141414a b c ===时等号成立. 所以222a b c ++的最小值为914. 11．已知函数()12f x x a x =+++.（Ⅰ）求1a =时，()3f x ≤的解集；（Ⅱ）若()f x 有最小值，求a 的取值范围，并写出相应的最小值.【答案】（Ⅰ）[3,0]-；（Ⅱ）见解析.【解析】（Ⅰ）当1a =时，232()12121231x x f x x x x x x --≤-⎧⎪=+++=-<<-⎨⎪+≥-⎩∵()3f x ≤当2x -≤时()233f x x =--≤解得32x -≤≤-当21x -<<-时()13f x =≤恒成立当1x -≥时()233f x x =+≤解得10x -≤≤综上可得解集[3,0]-. （Ⅱ）(1)212()12(1)2121(1)211a x a x f x x a x a x a x a x a x -+--≤-⎧⎪=+++=-+--<<-⎨⎪+++≥-⎩当(1)0a -+>，即1a <-时，()f x 无最小值；当(1)0a -+=，即1a =-时，()f x 有最小值1-；当(1)0a -+<且10a -≤，即11a -<≤时， min ()(1)f x f a =-=当(1)0a -+<且10a ->，即1a >时， min ()(2)1f x f =-=综上：当1a <-时，()f x 无最小值；当1a =-时，()f x 有最小值1-；当11a -<≤时， min ()(1)f x f a =-= ；当1a >时， min ()(2)1f x f =-=；12．选修4-5：不等式选讲已知函数()|23||1|f x x x =--+.（1）求不等式()6f x ≤的解集；（2）设集合M 满足：当且仅当x M ∈时，()|32|f x x =-，若,a b M ∈，求证：228223a b a b -++≤. 【答案】(1) {}210x x -≤≤；(2)见解析.【解析】（1）()4,1323132,1234,2x x f x x x x x x x ⎧⎪-+<-⎪⎪=--+=-+-≤≤⎨⎪⎪->⎪⎩当1x <- 时，46x -+≤ ，得2x -≥ ，故21x -≤<-；当312x -≤≤时，326x -+≤ ，得43x ≥- ，故312x -≤<；当32x > 时，46x -≤ ，得10x ≤ ，故3102x <≤；综上，不等式()6f x ≤的解集为{}210x x -≤≤（2）由绝对值不等式的性质可知()231(23)(1)32f x x x x x x =--+≤-++=- 等价于23(1)32x x x -≤-++-，当且仅当(23)(1)0x x -+≤，即213x -≤≤ 时等号成立，故21,3M ⎡⎤=-⎢⎥⎣⎦所以221,133a b -≤≤-≤≤，所以222510(1),4(1)99a b ≤-≤-≤--≤-，即228(1)(1)3a b ---≤. 13．[选修4—5：不等式选讲]已知函数()31f x x m x m =----（1）若1m =，求不等式()1f x <的解集.（2）对任意的x R ∈，有()(2)f x f ≤，求实数m 的取值范围.【答案】（1）(,3)-∞；（2）1123m -≤≤ 【解析】（1）()141f x x x =---<，所以11441(4)11(4)1141x x x x x x x x x <≤≤>⎧⎧⎧⎨⎨⎨---<---<--+<⎩⎩⎩或或解之得不等式()1f x <的解集为(,3)-∞.(2) 当131,2m m m +>>-时，由题得2必须在3m+1的右边或者与3m+1重合，所以1231,3m m ≥+∴≤，所以1123m -<≤，当131,2m m m +==-时，不等式恒成立，当131,2m m m +<<-时，由题得2必须在3m+1的左边或者与3m+1重合，由题得1231,3m m ≤+≥，所以m 没有解. 综上，1123m -≤≤. 14．已知()21f x x x =+-．（1）证明()1f x x +≥；（2）若,,a b c +∈R ，记33311134abc a b c +++的最小值为m ，解关于x 的不等式()f x m <．【答案】(1)见证明；(2) 2433x x ⎧⎫-<<⎨⎬⎩⎭ 【解析】（1）()2212211f x x x x x x +=+-≥-+=．当且仅当()2x 2x 10-≤,等号成立（2）∵333333311131333333234444abc abc abc abc m a b c a b c abc abc +++≥+=+≥⋅==，当且仅当a=b=c 等号成立由不等式()3f x <即()213f x x x =+-<．由()31,01211,02131,2x x f x x x x x x x ⎧⎪-+≤⎪⎪=+-=-<<⎨⎪⎪-≥⎪⎩得：不等式()3f x <的解集为2433x x ⎧⎫-<<⎨⎬⎩⎭． 15．选修4—5：不等式选讲已知函数()11f x x mx =++-，m R ∈。

历年(2020-2024)全国高考数学真题分类(等式与不等式综合)汇编(附答案)

历年(2020-2024)全国高考数学真题分类(等式与不等式综合)汇编解不等式1．（2024∙全国新Ⅰ卷∙高考真题）已知集合{}355,{3,1,0,2,3}A xx B =-<<=--∣，则A B = （） A ．{1,0}- B ．{2,3} C ．{3,1,0}-- D ．{1,0,2}-2．（2024∙上海∙高考真题）已知,x ∈R 则不等式2230x x --<的解集为．3．（2023∙全国新Ⅰ卷∙高考真题）已知集合{}2,1,0,1,2M =--，{}260N x x x =--≥，则M N ⋂=（）A ．{}2,1,0,1--B ．{}0,1,2C ．{}2-D ．{}24．（2020∙全国∙高考真题）已知集合2{|340},{4,1,3,5}A x x x B =--<=-，则A B = （） A ．{4,1}- B ．{1,5} C ．{3,5}D ．{1,3}基本不等式1．（2024∙北京∙高考真题）已知()11,x y ，()22,x y 是函数2x y =的图象上两个不同的点，则（） A ．12122log 22y y x x ++ C ．12212log 2y y x x +<+ D ．12212log 2y y x x +>+ 2．（2021∙全国乙卷∙高考真题）下列函数中最小值为4的是（） A ．224y x x =++ B ．4sin sin y x x=+ C ．2y 22x x -=+D ．4ln ln y x x=+3．（2021∙全国新Ⅰ卷∙高考真题）已知1F ，2F 是椭圆C ：22194x y +=的两个焦点，点M 在C 上，则12MF MF ⋅的最大值为（） A ．13B ．12C ．9D ．64．（2020∙全国∙高考真题）设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b ab-=>>的两条渐近线分别交于,D E 两点，若ODE 的面积为8，则C 的焦距的最小值为（） A ．4B ．8C ．16D ．32参考答案解不等式1．（2024∙全国新Ⅰ卷∙高考真题）已知集合{}355,{3,1,0,2,3}A xx B =-<<=--∣，则A B = （） A ．{1,0}- B ．{2,3}C ．{3,1,0}--D ．{1,0,2}-【答案】A【详细分析】化简集合A ，由交集的概念即可得解.【答案详解】因为{{}|,3,1,0,2,3A x x B =<<=--，且注意到12<<，从而A B = {}1,0-. 故选：A.2．（2024∙上海∙高考真题）已知,x ∈R 则不等式2230x x --<的解集为．【答案】{}|13x x -<<【详细分析】求出方程2230x x --=的解后可求不等式的解集. 【答案详解】方程2230x x --=的解为=1x -或3x =，故不等式2230x x --<的解集为{}|13x x -<<，故答案为：{}|13x x -<<.3．（2023∙全国新Ⅰ卷∙高考真题）已知集合{}2,1,0,1,2M =--，{}260N x x x =--≥，则M N ⋂=（）A ．{}2,1,0,1--B ．{}0,1,2C ．{}2-D ．{}2【答案】C【详细分析】方法一：由一元二次不等式的解法求出集合N ，即可根据交集的运算解出．方法二：将集合M 中的元素逐个代入不等式验证，即可解出．【答案详解】方法一：因为{}(][)260,23,N x x x ∞∞=--≥=--⋃+，而{}2,1,0,1,2M =--，所以M N ⋂={}2-．故选：C ．方法二：因为{}2,1,0,1,2M =--，将2,1,0,1,2--代入不等式260x x --≥，只有2-使不等式成立，所以M N ⋂={}2-．故选：C ．4．（2020∙全国∙高考真题）已知集合2{|340},{4,1,3,5}A x x x B =--<=-，则A B = （） A ．{4,1}- B ．{1,5} C ．{3,5} D ．{1,3}【答案】D【详细分析】首先解一元二次不等式求得集合A ，之后利用交集中元素的特征求得A B ⋂，得到结果. 【答案详解】由2340x x --<解得14x -<<，所以{}|14A x x =-<<，又因为{}4,1,3,5B =-，所以{}1,3A B = ，故选：D.【名师点评】本题考查的是有关集合的问题，涉及到的知识点有利用一元二次不等式的解法求集合，集合的交运算，属于基础题目.基本不等式1．（2024∙北京∙高考真题）已知()11,x y ，()22,x y 是函数2x y =的图象上两个不同的点，则（） A ．12122log 22y y x x ++ C ．12212log 2y y x x +<+ D ．12212log 2y y x x +>+ 【答案】B【详细分析】根据指数函数和对数函数的单调性结合基本不等式详细分析判断AB ；举例判断CD 即可. 【答案详解】由题意不妨设12x x <，因为函数2x y =是增函数，所以12022x x <<，即120y y <<，对于选项AB ：可得121222222x xx x ++>=，即12122202x x y y ++>>，根据函数2log y x =是增函数，所以121212222log log 222x x y y x x+++>=，故B 正确，A 错误；对于选项D ：例如120,1x x ==，则121,2y y ==，可得()12223log log 0,122y y +=∈，即12212log 12y y x x +<=+，故D 错误；对于选项C ：例如121,2x x =-=-，则1211,24y y ==，可得()122223log log log 332,128y y +==-∈--，即12212log 32y y x x +>-=+，故C 错误，故选：B.2．（2021∙全国乙卷∙高考真题）下列函数中最小值为4的是（） A ．224y x x =++ B ．4sin sin y x x=+ C ．2y 22x x -=+ D ．4ln ln y x x=+【答案】C【详细分析】根据二次函数的性质可判断A 选项不符合题意，再根据基本不等式“一正二定三相等”，即可得出,B D 不符合题意，C 符合题意．【答案详解】对于A ，()2224133y x x x =++=++≥，当且仅当=1x -时取等号，所以其最小值为3，A 不符合题意；对于B ，因为0sin 1x <≤，4sin 4sin y x x=+≥=，当且仅当sin 2x =时取等号，等号取不到，所以其最小值不为4，B 不符合题意；对于C ，因为函数定义域为R ，而20x >，2422242x x xx y -=+=+≥=，当且仅当22x =，即1x =时取等号，所以其最小值为4，C 符合题意；对于D ，4ln ln y x x=+，函数定义域为()()0,11,+∞ ，而ln x R ∈且ln 0x ≠，如当ln 1x =-，5y =-，D 不符合题意．故选：C ．【名师点评】本题解题关键是理解基本不等式的使用条件，明确“一正二定三相等”的意义，再结合有关函数的性质即可解出．3．（2021∙全国新Ⅰ卷∙高考真题）已知1F ，2F 是椭圆C ：22194x y +=的两个焦点，点M 在C 上，则12MF MF ⋅的最大值为（） A ．13 B ．12C ．9D ．6【答案】C【详细分析】本题通过利用椭圆定义得到1226MF MF a +==，借助基本不等式212122MF MF MF MF ⎛+⎫⋅≤ ⎪⎝⎭即可得到答案．【答案详解】由题，229,4a b ==，则1226MF MF a +==，所以2121292MF MF MF MF ⎛+⎫⋅≤= ⎪⎝⎭（当且仅当123MF MF ==时，等号成立）．故选：C ．【名师点评】4．（2020∙全国∙高考真题）设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b ab-=>>的两条渐近线分别交于,D E 两点，若ODE 的面积为8，则C 的焦距的最小值为（） A ．4 B ．8 C ．16 D ．32【答案】B【详细分析】因为2222:1(0,0)x y C a b a b -=>>，可得双曲线的渐近线方程是b y x a=±，与直线x a =联立方程求得D ，E 两点坐标，即可求得||ED ，根据ODE 的面积为8，可得ab值，根据2c =等式，即可求得答案. 【答案详解】 2222:1(0,0)x y C a b a b -=>> ∴双曲线的渐近线方程是b y x a=±直线x a =与双曲线2222:1(0,0)x y C a b a b -=>>的两条渐近线分别交于D ，E 两点不妨设D 为在第一象限，E 在第四象限联立x ab y x a =⎧⎪⎨=⎪⎩，解得x a y b =⎧⎨=⎩ 故(,)D a b联立x ab y x a =⎧⎪⎨=-⎪⎩，解得x a y b =⎧⎨=-⎩ 故(,)E a b -∴||2ED b =∴ODE 面积为：1282ODE S a b ab =⨯==△双曲线2222:1(0,0)x y C a b a b-=>>∴其焦距为28c =≥==当且仅当a b ==∴C 的焦距的最小值：8故选：B.【名师点评】本题主要考查了求双曲线焦距的最值问题，解题关键是掌握双曲线渐近线的定义和均值不等式求最值方法，在使用均值不等式求最值时，要检验等号是否成立，考查了详细分析能力和计算能力，属于中档题.。

十年高考理科数学真题专题七不等式二十一不等式的综合应用及答案

专题七不等式第二十一讲不等式的综合应用2019年1.（2019天津理13）设0,0,25x y x y >>+=，则的最小值为 .2010-2018年一、选择题1．(2018北京)设集合{(,)|1,4,2},A x y x y ax y x ay =-+>-≥≤则A ．对任意实数a ，(2,1)A ∈B ．对任意实数a ，(2,1)A ∉C ．当且仅当0a <时，(2,1)A ∉D ．当且仅当32a ≤时，(2,1)A ∉ 2．（2017天津）已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+⎪⎩≥设a ∈R ，若关于x 的不等式()||2x f x a +≥在R 上恒成立，则a 的取值范围是A ．[2,2]- B．[2]- C．[2,- D．[- 3．（2015北京）设{}n a 是等差数列．下列结论中正确的是A ．若120a a +>，则230a a +>B ．若130a a +<，则120a a +<C ．若120a a <<，则2a >D ．若10a <，则()()21230a a a a -->4．（2015陕西）设()ln f x x =，0a b <<，若p f =，()2a bq f +=， 1(()())2r f a f b =+，则下列关系式中正确的是A ．q r p =C ．p r q =<D ．p r q => 5．（2014重庆）若b a ab b a +=+则）（,log 43log 24的最小值是A ．326+B ．327+C ．346+D ．347+ 6．（2013福建）若122=+yx ，则y x +的取值范围是A ．]2,0[B ．]0,2[-C ．),2[+∞-D ．]2,(--∞7．（2013山东）设正实数,,x y z 满足22340x xy y z -+-=．则当xyz取得最大值时， 212x y z+-的最大值为 A ．0 B ．1 C ．94D ．3 8．（2013山东）设正实数z y x ,,满足04322=-+-z y xy x ，则当zxy取得最大值时， 2x y z +-的最大值为A ．0B ．98C ．2D ．949．（2012浙江）若正数,x y 满足35x y xy +=，则34x y +的最小值是A ．245 B ．285C ．5D ．6 10．（2012浙江）若正数,x y 满足35x y xy +=，则34x y +的最小值是 A ．245 B ．285C ．5D ．6 11．（2012陕西）小王从甲地到乙地的时速分别为a 和b （a b <），其全程的平均时速为v ，则 A ．a v ab <)，1l 与函数2log y x =的图像从左至右相交于点,A B ，2l 与函数2log y x =的图像从左至右相交于,C D ．记线段AC 和BD 在x 轴上的投影长度分别为,a b ，当m 变化时，ba的最小值为 A ．2 B ．82 C ．34 D ．34413．（2011陕西）设0a b <<，则下列不等式中正确的是A ．2a b a b ab +<<，则下列不等式中，恒成立的是A ．222a b ab +>B．a b +≥ C．11a b +> D ．2b aa b +≥ 二、填空题15．(2018天津)已知,a b ∈R ，且360a b -+=，则128ab +的最小值为． 16．(2018浙江)已知λ∈R ，函数24,()43,x x f x x x x λλ-⎧=⎨-+<⎩≥，当2λ=时，不等式()0f x <的解集是___________．若函数()f x 恰有2个零点，则λ的取值范围是___________． 17．(2017北京)已知0x ≥，0y ≥，且1x y +=，则22x y +的取值范围是_______．18．（2017天津）若,a b ∈R ，0ab >，则4441a b ab++的最小值为___________．19．（2017江苏）某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年的总存储费用为4x 万元，要使一年的总运费与总存储费之和最小，则x 的值是． 20．（2017浙江）已知a ∈R ，函数4()||f x x a a x=+-+在区间[1，4]上的最大值是5，则a 的取值范围是．21．（2014浙江）已知实数,,a b c 满足0a b c ++=，2221a b c ++=，则a 的最大值是__； 22．（2014辽宁）对于0c >，当非零实数a ，b 满足22420a ab b c -+-=，且使|2|a b +最大时，124a b c++的最小值为． 23．（2014辽宁）对于0c >，当非零实数a ，b 满足224240a ab b c -+-=，且使|2|a b +最大时，345a b c-+的最小值为． 24．（2014湖北）某项研究表明：在考虑行车安全的情况下，某路段车流量F （单位时间内经过测量点的车辆数，单位：辆/小时）与车流速度v （假设车辆以相同速度v 行驶，单位：米/秒）、平均车长l （单位：米）的值有关，其公式为2760001820vF v v l=++．（Ⅰ）如果不限定车型， 6.05l =，则最大车流量为辆/小时；（Ⅱ）如果限定车型，5l =，则最大车流量比（Ⅰ）中的最大车流量增加辆/小时． 25．（2013天津）设a + b = 2， b >0，则当a = 时， 1||2||a a b+取得最小值. 26．（2013四川）已知函数()4(0,0)af x x x a x=+>>在3x =时取得最小值，则a =__． 27．（2011浙江）若实数,x y 满足221x y xy ++=，则x y +的最大值是____． 28．（2011湖南）设,x y R ∈，则222211()(4)x y y x++的最小值为． 29．（2010安徽）若0,0,2a b a b >>+=，则下列不等式对一切满足条件的,a b 恒成立的是 (写出所有正确命题的编号)． ①1ab ≤；； ③222a b +≥；④333a b +≥； ⑤112a b+≥专题七不等式第二十一讲不等式的综合应用答案部分2019年1.解析 0x >，0y >，25x y +=，===由基本不等式，==时，即3xy =，且25x y +=时，即31x y =⎧⎨=⎩或x y =⎧⎪⎨=⎪⎩2010-2018年1．D 【解析】点(2,1)在直线1x y -=上，4ax y +=表示过定点(0,4)，斜率为a -的直线，当0a ≠时，2x ay -=表示过定点(2,0)，斜率为1a的直线，不等式2x ay -≤表示的区域包含原点，不等式4ax y +>表示的区域不包含原点．直线4ax y +=与直线2x ay -=互相垂直，显然当直线4ax y +=的斜率0a ->时，不等式4ax y +>表示的区域不包含点(2,1)，故排除A ；点(2,1)与点(0,4)连线的斜率为32-，当32a -<-，即32a >时，4ax y +>表示的区域包含点(2,1)，此时2x ay -<表示的区域也包含点(2,1)，故排除B ；当直线4ax y +=的斜率32a -=-，即32a =时，4ax y +>表示的区域不包含点(2,1)，故排除C ，故选D ．解法二若(2,1)A ∈，则21422a a +>⎧⎨-⎩≤，解得32a >，所以当且仅当32a ≤时，(2,1)A ∉．故选D ．2．A 【解析】解法一函数()f x 的图象如图所示，当||2xy a =+的图象经过点(0,2)时，可知2a =±．当2x y a =+的图象与2y x x =+的图象相切时，由22x a x x+=+，得2240x ax -+=，由0∆=，并结合图象可得2a =，要使()||2xf x a +≥恒成立，当0a ≤时，需满足2a -≤，即20a -≤≤，当0a >时，需满足2a ≤，所以22a -≤≤．解法二由题意0x =时，()f x 的最小值2，所以不等式()||2xf x a +≥等价于 ||22xa +≤在R 上恒成立．当a =0x =，得|22x+>，不符合题意，排除C 、D ；当a =-0x =，得|22x->，不符合题意，排除B ；选A ．3．C 【解析】若{}n a 是递减的等差数列，则选项,A B 都不一定正确．若{}n a 为公差为0的等差数列，则选项D 不正确．对于C 选项，由条件可知{}n a 为公差不为0的正确数列，由等差中项的性质得1322a a a +=，由基本不等式得132a a +C 正确．4．B 【解析】∵0a b <<，∴2a b+()ln f x x =在(0,)+?上单调递增，故()2a bf f +<，即q p >，∵11(()())(ln ln )22r f a f b a b f p =+=+===，∴p r q =<．5．D 【解析】由已知得34a b ab +=，且0ab >，可知0,0a b >>，所以431a b +=(0,0a b >>)，4343()()77b aa b a b a b a b+=++=+++≥ 当且仅当43b aa b=时取等号．6．D 【解析】本题考查的是均值不等式．因为y x y x 222221⋅≥+=，即222-+≤yx ，所以2-≤+y x ，当且仅当yx 22=，即y x =时取等号． 7．B 【解析】由22340x xy y z -+-=，得2234z x xy y =-+．所以2214343xy xy x y z x xy y y x ==-++-1≤=，当且仅当4x y y x =，即2x y =时取等号此时22y z =，1)(max =zxy.xy y y z y x 2122212-+=-+)211(2)11(2yy x y -=-=1)221121(42=-+≤y y ，故选B.8．C 【解析】由22340x xy y z -+-=得2243x y xy z +-=，22443331z x y xyxy xy xy+=-≥=-=，当且仅当224x y =即2x y =时，zxy有最小值1，将2x y =代入原式得22z y =，所以22222224x y z y y y y y +-=+-=-+，当1y =时有最大值2．故选C ． 9．C 【解析】Q 35x y xy +=，135y x+=， 113131213(34)()()555x y x y y x y x +⋅+=++≥1132555⨯=. 10．C 【解析】Q 35x y xy +=，135y x+=， 113131213(34)()()555x y x y y x y x +⋅+=++≥1132555⨯=. 11．A 【解析】设从甲地到乙地所走路程为S ，则22211S ab v S Sa b a ba b===<=+++． ∵ a b <,∴ 2222ab a v a a b a=>=+,∴a v <<A ． 12．B 【解析】在同一坐标系中作出y m =，y =821m +(0m >)，2log y x =图像如下图，由2log x = m ，得122,2m mx x -==，2log x =821m +，得821821342,2m m x x +-+==．依题意得8218218218212222,22,22m m m mmm m m b a b a++--+--+-=-=-=-821821222m m mm +++==．8141114312122222m m m m +=++-≥-=++Q ，min ()82b a ∴=13．B 【解】（方法一）已知a b <2a bab +<，比较a ab因为22)()0a ab a a b -=-<，所以a ab <22()()0b ab b b a -=->ab b <；作差法：022a b b ab +--=>，所以2a b b +<，综上可得2a ba ab b +<<<；故选B ．（方法二）取2a =，8b =，4ab =，52a b +=，所以2a ba ab b +<<<．14．D 【解析】对于A 取1a b ==，此时2222a b ab +==，因此A 不正确；对于B 取1a b ==-，此时222a b ab +=-<=，因此B 不正确；对于C 取1a b ==-，此时1122a b ab+=-<=，因此C 不正确；对于D ，∵0ab >， ∴0b a >，0b a> ∴2b a b a a b a b+⋅=≥，D 正确．15．14【解析】由360a b -+=，得36a b =-，所以36331112222824ab b b --+=+=⨯=≥，当且仅当363122b b-=，即1b =时等号成立． 16．(1,4)；(1,3](4,)+∞U 【解析】若2λ=，则当2x ≥时，令40x -<，得24x <≤；当2x <时，令2430x x -+<，得12x <<．综上可知14x <<，所以不等式()0f x <的解集为(1,4)．令40x -=，解得4x =；令2430x x -+=，解得1x =或3x =．因为函数()f x 恰有2个零点，结合函数的图象（图略）可知13λ<≤或4λ>．17．1[,1]2【解析】由题意，22222211(1)2212()22u x y x x x x x =+=+-=-+=-+，且[0,1]x ∈，又0x =时，221u x y =+=，12x =时，22min 12u x y =+=，当1x =时，221u x y =+=，所以22x y +取值范围为1[,1]2．18．4【解析】44224141144a b a b ab ab ab ab+++=+≥≥ ，当且仅当222a b =，且12ab =，即22a =时取等号．19．30【解析】总费用为600900464()4240x x x x +⨯=+≥⨯，当且仅当900x x=，即30x =时等号成立．20．9(,]2-∞【解析】∵[1,4]x ∈，∴4[4,5]x x+∈ ①当5a ≥时，44()2224f x a x a a x a a x x =--+=---=-≤，所以()f x 的最大值245a -=，即92a =（舍去） ②当4a ≤时，44()5f x x a a x x x=+-+=+≤，此时命题成立．③当45a <<时，max ()max{|4|,|5|}f x a a a a =-+-+，则|4||5||4|5a a a a a a -+-+⎧⎨-+=⎩≥或|4||5||5|5a a a a a a -+<-+-+=，解得92a =或92a <，综上可得，实数a 的取值范围是9(,]2-∞．210a b c ++=得，a b c =--，则2222()2a b c b c bc =--=++ ()2222222b c b c b c +++=+≤，又2221a b c ++=，所以232a ≤，解得a ，故a22．－1【解析】设|2|a b +最大，则必须,a b 同号，因为22224463()2a b a b ab c ab c +++=++≤，故有2(2)4a b c +≤，22()2a b c +≥，当且仅当2a b =时取等号，此时2c b =，所以124a b c ++=2244114()112b b b +=+--≥．23．－2 【解析】设2a b t +=，则2a t b =-，因为224240a ab b c -+-=，所以将2a t b =-代入整理可得22630b tb t c -+-=①，由0∆≥解得t ≤2a b +取得最大值时，t =代入①式得b =2a t b =-得a = 所以345a b c -+=55c c +=222=--≥．当且仅当52c =时等号成立． 24．1900 100【解析】（Ⅰ）76000190020 6.0518F v v==⨯++，当且仅当11v =时等号成立．（Ⅱ）76000200020518F v v==⨯++，当且仅当10v =时等号成立．20001900100-=．25．－2【解析】∵1||2||a a b +=||||4||4||4||a b a a b a a b a a b++=++13114||4||44a a a a +=+-+=≥≥ 当且仅当||,04||b a a a b =<，即2,4a b =-=时取等号故1||2||a a b+取得最小值时，2a =-．26．36【解析】因为0,0x a >>，()44a f x x a x =+≥=，当且仅当4a x x=，即3x ==，解得36a =．27．3【解析】∵221x y xy ++=， ∴2()1x y xy +-=，即22()()12x y x y ++-≤，∴24()3x y +≤，3x y +≤． 28．9【解析】由柯西不等式可知2222211()(4)(12)9x y y x++≥+=．29．①③⑤【解析】令1a b ==，排除②④；由21a b ab =+≥≤，命题①正确；222()2422a b a b ab ab +=+-=-≥，命题③正确；1122a b a b ab ab++==≥，命题⑤正确．。

高考数学十年真题专题解析—不等式选讲

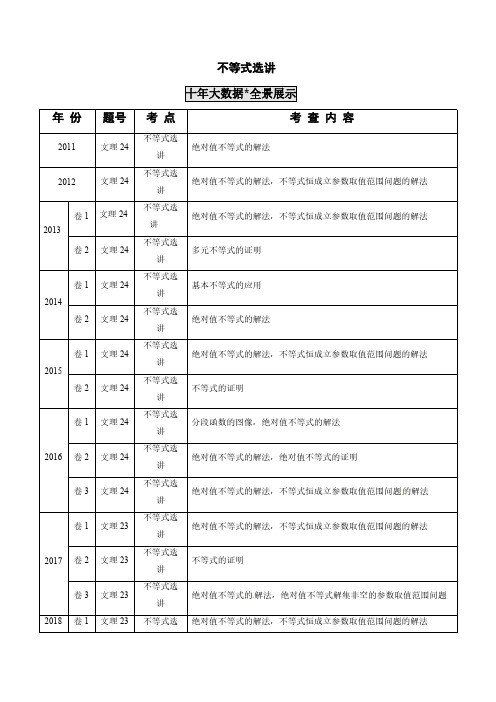
不等式选讲年份题号考点考查内容2011文理24不等式选讲绝对值不等式的解法2012文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法2013卷1文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲多元不等式的证明2014卷1文理24不等式选讲基本不等式的应用卷2文理24不等式选讲绝对值不等式的解法2015卷1文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲不等式的证明2016卷1文理24不等式选讲分段函数的图像，绝对值不等式的解法卷2文理24不等式选讲绝对值不等式的解法，绝对值不等式的证明卷3文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法2017卷1文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理23不等式选讲不等式的证明卷3文理23不等式选讲绝对值不等式的解法，绝对值不等式解集非空的参数取值范围问题2018卷1文理23不等式选绝对值不等式的解法，不等式恒成立参数取值范围问题的解法讲卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲绝对值函数的图象，不等式恒成立参数最值问题的解法2019卷1文理23不等式选讲三元条件不等式的证明卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件最值问题的解法，三元条件不等式的证明2020卷1文理23不等式选讲绝对值函数的图像，绝对值不等式的解法卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件不等式的证明考点出现频率2021年预测考点120绝对值不等式的求解23次考4次2021年主要考查绝对值不等式的解法、绝对值不等式的证明，不等式恒成立参数取值范围问题的解法等．考点121含绝对值不等式的恒成立问题23次考12次考点122不等式的证明23次考7次考点120绝对值不等式的求解1．(2020全国Ⅰ文理22)已知函数()3121f x x x =+--．(1)画出()y f x =的图像；(2)求不等式()()1f x f x >+的解集．【解析】(1)∵()3,1151,1313,3x x f x x x x x ⎧⎪+≥⎪⎪=--<<⎨⎪⎪--≤-⎪⎩，作出图像，如图所示：(2)将函数()f x 的图像向左平移1个单位，可得函数()1f x +的图像，如图所示：由()3511x x --=+-，解得76x =-，∴不等式的解集为7,6⎛⎫-∞- ⎪⎝⎭．2．(2020江苏23)设x ∈R ，解不等式2|1|||4x x ++≤．【答案】22,3⎡⎤-⎢⎥⎣⎦【思路导引】根据绝对值定义化为三个不等式组，解得结果．【解析】1224x x x <-⎧⎨---≤⎩ 或10224x x x -≤≤⎧⎨+-≤⎩或0224x x x >⎧⎨++≤⎩，21x ∴-≤<-或10x -≤≤或203x <≤，∴解集为22,3⎡⎤-⎢⎥⎣⎦．3．(2016全国I 文理)已知函数()|1||23|f x x x =+--．(I)在图中画出()y f x =的图像；(II)求不等式|()|1f x >的解集．【解析】(1)如图所示：(2)()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩，≤，，≥，()1f x >．当1x -≤，41x ->，解得5x >或3x <，1x -∴≤；当312x -<<，321x ->，解得1x >或13x <，113x -<<∴或312x <<；当32x ≥，41x ->，解得5x >或3x <，332x <∴≤或5x >．综上，13x <或13x <<或5x >，()1f x >∴，解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭ ，，，．4．(2014全国II 文理)设函数()f x =1(0)x x a a a++->(Ⅰ)证明：()f x ≥2；(Ⅱ)若()35f <，求a 的取值范围．【解析】(I)由0a >，有()f x 111()2x x a x x a a a a a=++-≥+--=+≥，∴()f x ≥2．(Ⅱ)1(3)33f a a=++-．当时a ＞3时，(3)f =1a a+，由(3)f ＜5得3＜a ＜5212；当0＜a ≤3时，(3)f =16a a-+，由(3)f ＜5得12＜a ≤3．综上：a 的取值范围是(152+，5212+)．5．(2011新课标文理)设函数()3f x x a x =-+，其中0a >．(Ⅰ)当1a =时，求不等式()32f x x ≥+的解集；(Ⅱ)若不等式()0f x ≤的解集为{}|1x x ≤-，求a 的值．【解析】(Ⅰ)当1a =时，()32f x x ≥+可化为|1|2x -≥，由此可得3x ≥或1x ≤-．故不等式()32f x x ≥+的解集为{|3x x ≥或1}x ≤-．(Ⅱ)由()0f x ≤得30x a x -+≤，此不等式化为不等式组30x ax a x ≥⎧⎨-+≤⎩或30x aa x x ≤⎧⎨-+≤⎩，即4x a a x ⎧⎪⎨⎪⎩≥≤或2x aax ⎧⎪⎨-⎪⎩≤≤，因为0a >，∴不等式组的解集为{}|2a x x ≤-，由题设可得2a-=1-，故2a =．考点121含绝对值不等式的恒成立问题6．(2020全国Ⅱ文理22)已知函数()221f x x a x a =-+-+．(1)当2a =时，求不等式()4f x ≥的解集；(2)若()4f x ≥，求a 的取值范围．【答案】(1)32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭；(2)(][),13,-∞-+∞ ．【思路导引】(1)分别在3x ≤、34x <<和4x ≥三种情况下解不等式求得结果；(2)利用绝对值三角不等式可得到()()21f x a ≥-，由此构造不等式求得结果．【解析】(1)当2a =时，()43f x x x =-+-．当3x ≤时，()43724f x x x x =-+-=-≥，解得：32x ≤；当34x <<时，()4314f x x x =-+-=≥，无解；当4x ≥时，()43274f x x x x =-+-=-≥，解得：112x ≥；综上所述：()4f x ≥的解集为32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭．(2)()()()()22222121211f x x a x a x ax a a a a =-+-+≥---+=-+-=-(当且仅当221a x a -≤≤时取等号)，()214a ∴-≥，解得：1a ≤-或3a ≥，a ∴的取值范围为(][),13,-∞-+∞ ．7．(2019全国II 文理23)[选修4-5：不等式选讲](10分)已知()|||2|().f x x a x x x a =-+--(1)当1a =时，求不等式()0f x <的解集；(2)若(,1)x ∈-∞时，()0f x <，求a 的取值范围．【解析】(1)当a=1时，()=|1| +|2|(1)f x x x x x ---．当1x <时，2()2(1)0f x x =--<；当1x ≥时，()0f x ≥，∴不等式()0f x <的解集为(,1)-∞．(2)因为()=0f a ，∴1a ≥．当1a ≥，(,1)x ∈-∞时，()=() +(2)()=2()(1)<0f x a x x x x a a x x -----∴a 的取值范围是[1,)+∞．8．(2018全国Ⅰ文理)已知()|1||1|f x x ax =+--．(1)当1a =时，求不等式()1f x >的解集；(2)若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围．【解析】(1)当1a =时，()|1||1|f x x x =+--，即2,1,()2,11,2, 1.--⎧⎪=-<<⎨⎪⎩≤≥x f x x x x 故不等式()1f x >的解集为1{|}2x x >．(2)当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立．若0≤a ，则当(0,1)x ∈时|1|1-≥ax ；若0a >，|1|1ax -<的解集为20x a <<，∴21≥a，故02<≤a ．综上，a 的取值范围为(0,2]．9．(2018全国Ⅱ文理)设函数()5|||2|=-+--f x x a x ．(1)当1a =时，求不等式()0≥f x 的解集；(2)若()1≤f x ，求a 的取值范围．【解析】(1)当1=a 时，24,1,()2,12,26, 2.+-⎧⎪=-<⎨⎪-+>⎩≤≤x x f x x x x 可得()0≥f x 的解集为{|23}-≤≤x x ．(2)()1≤f x 等价于|||2|4++-≥x a x ．而|||2||2|++-+≥x a x a ，且当2=x 时等号成立．故()1≤f x 等价于|2|4+≥a ．由|2|4+≥a 可得6-≤a 或2≥a ，∴a 的取值范围是(,6][2,)-∞-+∞ ．10．(2018全国Ⅲ文理)设函数()|21||1|f x x x =++-．(1)画出()y f x =的图像；(2)当[0,)x ∈+∞时，()f x ax b +≤，求a b +的最小值．【解析】(1)13,,21()2,1,23, 1.x x f x x x x x ⎧-<-⎪⎪⎪=+-<⎨⎪⎪⎪⎩≤≥()y f x =的图像如图所示．(2)由(1)知，()y f x =的图像与y 轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，故当且仅当3a ≥且2b ≥时，()f x ax b +≤在[0,)+∞成立，因此a b +的最小值为5．11．(2018江苏)若x ，y ，z 为实数，且226x y z ++=，求222x y z ++的最小值．【解析】由柯西不等式，得2222222()(122)(22)x y z x y z ++++++≥．因为22=6x y z ++，∴2224x y z ++≥，当且仅当122x y z ==时，不等式取等号，此时244333x y z ===，，，∴222x y z ++的最小值为4．12．(2017全国Ⅰ文理)已知函数2()4f x x ax =-++，()|1||1|g x x x =++-．(1)当1a =时，求不等式()()f x g x ≥的解集；(2)若不等式()()f x g x ≥的解集包含[1,1]-，求a 的取值范围．【解析】(1)当1a =时，不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤．①当1x <-时，①式化为2340x x --≤，无解；当11x -≤≤时，①式化为220x x --≤，从而11x -≤≤；当1x >时，①式化为240x x +-≤，从而11712x -+<≤，∴()()f x g x ≥的解集为117{|1}2x x -+-<≤．(2)当[1,1]x ∈-时，()2g x =，∴()()f x g x ≥的解集包含[1,1]-，等价于当[1,1]x ∈-时()2f x ≥．又()f x 在[1,1]-的最小值必为(1)f -与(1)f 之一，∴(1)2f -≥且(1)2f ≥，得11a -≤≤，∴a 的取值范围为[1,1]-．13．(2017全国Ⅲ文理)已知函数()|1||2|f x x x =+--．(1)求不等式()1f x ≥的解集；(2)若不等式2()f x x x m -+≥的解集非空，求m 的取值范围．【解析】(1)3,1()21,123,2x f x x x x -<-⎧⎪=--⎨⎪>⎩≤≤，当1x <-时，()f x 1≥无解；当x -12≤≤时，由()f x 1≥得，x -211≥，解得x 12≤≤；当＞2x 时，由()f x 1≥解得＞2x ．∴()f x 1≥的解集为{}x x 1≥．(2)由()f x x x m -+2≥得m x x x x +---+212≤，而x x x x x x x x +---+--+2212+1+2≤x ⎛⎫ ⎪⎝⎭2355=--+244≤，且当32x =时，2512=4x x x x +---+，故m 的取值范围为5-，4⎛⎤∞ ⎥⎝⎦．14．(2016全国III 文理)已知函数()|2|f x x a a =-+(Ⅰ)当a=2时，求不等式()6f x ≤的解集；(Ⅱ)设函数()|21|g x x =-，当x ∈R 时，()()3f x g x +≥，求a 的取值范围．【解析】(Ⅰ)当2a =时，()|22|2f x x =-+．解不等式|22|26x -+ ，得13x - ，因此()6f x ≤的解集为{|13}x x - ．(Ⅱ)当x R ∈时，()()|2||12|f xg x x a a x +=-++-|212|x a x a -+-+ |1|a a =-+，当12x =时等号成立，∴当x R ∈时，()()3f x g x + 等价于|1|3a a -+ ．①当1a 时，①等价于13a a -+ ，无解．当1a >时，①等价于13a a -+ ，解得2a ．∴a 的取值范围是[2,)+∞．15．(2015全国I 文理)已知函数()|1|2||f x x x a =+--，0a >．(Ⅰ)当1a =时，求不等式()1f x >的解集；(Ⅱ)若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围．【解析】(Ⅰ)当1a =时，不等式()1f x >化为|1|2|1|10x x +--->，当1x -≤时，不等式化为40x ->，无解；当11x -<<时，不等式化为320x ->，解得213x <<；当1x ≥时，不等式化为20x -+>，解得12x <≤．∴()1f x >的解集为2{|2}3x x <<．(Ⅱ)有题设可得，12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--⎨⎪-++>⎩≤≤，∴函数()f x 图象与x 轴围成的三角形的三个顶点分别为21(,0),(21,0),(,1)3a A B a C a a -++，ABC ∆的面积为22(1)3a +．有题设得22(1)63a +>，故2a >．∴a 的取值范围为(2,)+∞．16．(2014全国I 文理)若0,0ab >>，且11a b +=．(Ⅰ)求33a b +的最小值；(Ⅱ)是否存在,a b ，使得236a b +=？并说明理由．【解析】(I)11a b =+≥，得2ab ≥，且当a b ==时取等号．故33ab+≥≥，且当a b ==∴33a b +的最小值为(II)由(I)知，23a b +≥．由于6>，从而不存在,a b ，使得236a b +=．16．(2013全国I 文理)已知函数()f x =|21||2|x x a -++，()g x =3x +．(Ⅰ)当a =-2时，求不等式()f x ＜()g x 的解集；(Ⅱ)设a ＞-1，且当x ∈[2a -，12)时，()f x ≤()g x ，求a 的取值范围．【解析】(Ⅰ)当a =-2时，不等式()f x ＜()g x 化为|21||22|30x x x -+---<，设函数y =|21||22|3x x x -+---，y =15, 212, 1236, 1x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩，其图像如图所示，从图像可知，当且仅当(0,2)x ∈时，y ＜0，∴原不等式解集是{|02}x x <<．(Ⅱ)当x ∈[2a -，12)时，()f x =1a +，不等式()f x ≤()g x 化为13a x ++≤，∴2x a -≥对x ∈[2a -，12)都成立，故2a -≥2a -，即a ≤43，∴a 的取值范围为(-1，43]．17．(2012新课标文理)已知函数|2|||)(-++=x a x x f ．(Ⅰ)当|3-=a 时，求不等式()3f x 的解集；(Ⅱ)若()|4|f x x - 的解集包含]2,1[，求a 的取值范围．【解析】(1)当3a =-时，()3323f x x x ⇔-+- 2323x x x ⎧⇔⎨-+-⎩ 或23323x x x <<⎧⇔⎨-+-⎩ 或3323x x x ⎧⇔⎨-+-⎩ 1x ⇔ 或4x ．(2)原命题()4f x x ⇔- 在[1,2]上恒成立24x a x x ⇔++-- 在[1,2]上恒成立22x a x ⇔--- 在[1,2]上恒成立30a ⇔- ．考点122不等式的证明18．(2020全国Ⅲ文理23)设,,,0,1a b c a b c abc ∈++==R ．(1)证明：0ab bc ca ++<；(2)用{}max ,,a b c 表示,,a b c 的最大值，证明：{}3max ,,4a b c ≥【答案】(1)证明见解析(2)证明见解析．【思路导引】(1)根据题设条件,0=++c b a 两边平方，再利用均值不等式证明即可；(2)思路一：不妨设max{,,}a b c a =，由题意得出0,,0a b c ><，由()222322b c b c bc a a a bc bc+++=⋅==，结合基本不等式，即可得出证明．思路二：假设出c b a ,,中最大值，根据反证法与基本不等式推出矛盾，即可得出结论．【解析】(1)证明：().0,02=++∴=++c b a c b a ,0222222=+++++∴ca ac ab c b a 即()222222c b a ca bc ab ++-=++.0,0222<++∴<++∴ca bc ab ca bc ab (2)证法一：不妨设max{,,}a b c a =，由0,1a b c abc ++==可知，0,0,0a b c ><<，1,a b c a bc =--= ，()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=，当且仅当b c =时，取等号，a ∴≥，即max{,,}a b c ．证法二：不妨设403<<<≤c b a ，则,4,41133>=-->=c b a c ab而1132a b ->--≥>==矛盾，∴命题得证．19．(2019全国I 文理23)已知a ，b ，c 为正数，且满足abc=1．证明：(1)222111a b c a b c++≤++；(2)333()()()24a b b c c a +++≥++．【解析】(1)因为2222222,2,2a b ab b c bc c a ac +≥+≥+≥，又1abc =，故有222111ab bc ca a b c ab bc ca abc a b c ++++≥++==++，∴222111a b c a b c++≤++．(2)因为, , a b c 为正数且1abc =，故有333()()()a b b c c a +++++≥=3(+)(+)(+)a b b c ac 3≥⨯⨯⨯=24．∴333()()()24a b b c c a +++++≥．20．(2019全国III 文理23)设,,x y z ∈R ，且1x y z ++=．(1)求222(1)(1)(1)x y z -++++的最小值；(2)若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a ≤-或1a ≥-．【解析】(1)由于2[(1)(1)(1)]x y z -++++222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤≤-++++⎣⎦，故由已知得2224(1)(1)(1)3x y z -++++≥，当且仅当x=53，y=–13，13z =-时等号成立．∴222(1)(1)(1)x y z -++++的最小值为43．(2)由于2[(2)(1)()]x y z a -+-+-222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤-+-+-⎣⎦ ，故由已知2222(2)(2)(1)()3a x y z a +-+-+- ，当且仅当43a x -=，13a y -=，223a z -=时等号成立，因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +．由题设知2(2)133a + ，解得3a - 或1a - ．21．(2017全国Ⅱ文理)已知0a >，0b >，332a b +=，证明：(1)()()554a b a b ++≥；(2)2a b +≤．【解析】(1)556556()()a b a b a ab a b b ++=+++3323344()2()a b a b ab a b =+-++()22244ab a b =+-≥．(2)∵33223()33a b a a b ab b +=+++23()ab a b =++23()2()4a b a b +≤++33()24a b +=+，∴3()8a b +≤，因此2a b +≤．22．(2017江苏)已知a ，b ，c ，d 为实数，且224a b +=，2216c d +=，证明8ac bd +≤．【解析】证明：由柯西不等式可得：22222()()()ac bd a b c d +++≤，因为22224,16,a b c d +=+=∴2()64ac bd +≤，因此8ac bd +≤．23．(2016全国II 文理)已知函数()1122f x x x =-++，M 为不等式()2f x <的解集．(I)求M ；(II)证明：当a ，b M ∈时，1a b ab +<+．【解析】(I)当12x <-时，()11222f x x x x =---=-，若112x -<<-；当1122x -≤≤时，()111222f x x x =-++=<恒成立；当12x >时，()2f x x =，若()2f x <，112x <<．综上可得，{}|11M x x =-<<．(Ⅱ)当()11a b ∈-，，时，有()()22110a b -->，即22221a b a b +>+，则2222212a b ab a ab b +++>++，则()()221ab a b +>+，即1a b ab +<+，证毕．24．(2015全国II 文理)设,,,a b c d 均为正数，且a b c d +=+，证明：(Ⅰ)若ab >cd ，则a b c d +>+；(Ⅱ)a b c d +>+是||||a b c d -<-的充要条件．【解析】(Ⅰ)∵2()2a b a b ab +=++，2()c d c d cd +=++由题设a b c d +=+，ab cd >得22()a b c d >+a b c d +>(Ⅱ)(ⅰ)若||||a b c d -<-，则22()()a b c d -<-，即22()4()4a b ab c d cd +-<+-．因为a b c d +=+，∴ab cd >，由(Ⅰ)得a b c d >(ⅱ)a b c d +>则22(a b c d >+，即a b ab c d cd ++>++因为a b c d +=+，∴ab cd >，于是2222()()4()4()a b a b ab c d cd c d -=+-<+-=-．因此||||a b c d -<-．a b c d +>||||a b c d -<-的充要条件．25．(2013全国II 文理)设,,a b c 均为正数，且1a b c ++=，证明：(Ⅰ)13ab bc ca ++≤；(Ⅱ)2221a b c b c a++≥．【解析】(Ⅰ)2222222,2,2a b ab b c bc c a ca +≥+≥+≥得222a b c ab bc ca ++≥++，由题设得()21a b c ++=，即2222221a b c ab bc ca +++++=，∴()31ab bc ca ++≤，即13ab bc ca ++≤．(Ⅱ)∵2222,2,2a b c b a c b a c b c a +≥+≥+≥，∴222()2()a b c a b c a b c b c a +++++≥++，即222a b c a b c b c a ++≥++，∴2221a b c b c a ++≥．。

不等式高考真题(含答案)

【2010课标卷】设函数f(x)=241x -+（Ⅰ)画出函数(x)的图像；（Ⅱ）若不等式f(x)≤的解集非空，求a 的取值范围.【答案】【2011课标卷】设函数()3f x x a x =-+,其中0a >。

（Ⅰ）当1a =时，求不等式()32f x x ≥+的解集（Ⅱ）若不等式()0f x ≤的解集为{}|1x x ≤- ，求a 的值。

解：（Ⅰ）当1a =时，()32f x x ≥+可化为|1|2x -≥。

由此可得 3x ≥或1x ≤-。

故不等式()32f x x ≥+的解集为{|3x x ≥或1}x ≤-。

( Ⅱ) 由()0f x ≤得： 30x a x -+≤此不等式化为不等式组30x a x a x ≥⎧⎨-+≤⎩或30x a a x x ≤⎧⎨-+≤⎩ 即 4x a a x ≥⎧⎪⎨≤⎪⎩或2x a a a ≤⎧⎪⎨≤-⎪⎩ 因为0a >，所以不等式组的解集为{}|2ax x ≤- 由题设可得2a-= 1-，故2a =【2012课标卷】已知函数()2f x x a x =++-（1）当3a =-时，求不等式()3f x ≥的解集；（2）若()4f x x ≤-的解集包含[1,2]，求a 的取值范围。

【解析】（1）当3a =-时，()3323f x x x ≥⇔-+-≥2323x x x ≤⎧⇔⎨-+-≥⎩或23323x x x <<⎧⇔⎨-+-≥⎩或3323x x x ≥⎧⇔⎨-+-≥⎩ 1x ⇔≤或4x ≥（2）原命题()4f x x ⇔≤-在[1,2]上恒成立24x a x x ⇔++-≤-在[1,2]上恒成立22x a x ⇔--≤≤-在[1,2]上恒成立30a ⇔-≤≤【2013课标Ⅰ卷】已知函数()f x |21||2|x x a -++()g x 3x +.（Ⅰ）当a =2时，求不等式()f x ＜()g x 的解集；（Ⅱ）设a ＞-1,且当x ∈[2a -，12)时，()f x ≤()g x ,求a 的取值范围. 【解析】当a 2时，不等式()f x ＜()g x 化为|21||22|30x x x -+---<，设函数y =|21||22|3x x x -+---，y =15, 212, 1236, 1x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩，其图像如图所示，从图像可知，当且仅当(0,2)x ∈时，y ＜0∴原不等式解集是{|02}x x <<.（Ⅱ）当x ∈[2a -，12)时，()f x =1a +，不等式()f x ≤()g x 化为13a x +≤+， ∴2x a ≥-对x ∈[2a -，12)都成立，故2a -≥2a -，即a ≤43， ∴a 的取值范围为（-1，43].【2013课标Ⅱ卷】设a b c 、、均为正数，且1a b c ++=，证明：（Ⅰ）13ab bc ac ++≤；（Ⅱ）2221a b c b c a ++≥【2014课标Ⅰ卷】若0,0a b >>，且11ab a b +=. (Ⅰ) 求33a b +的最小值；（Ⅱ）是否存在,a b ，使得236a b +=？并说明理由.【解析】：(Ⅰ) 由112ab a b ab=+≥，得2ab ≥，且当2a b ==时等号成立，故3333342a b a b +≥=，且当2a b ==时等号成立，∴33a b +的最小值为42. （Ⅱ）由62326a b ab =+≥，得32ab ≤，又由(Ⅰ)知2ab ≥，二者矛盾，所以不存在,a b ，使得236a b +=成立.【2014课标Ⅱ卷】设函数()f x =1(0)x x a a a++-> （Ⅰ）证明：()f x ≥2；（Ⅱ）若()35f <，求a 的取值范围.【2015课标Ⅰ卷】已知函数()12,0f x x x a a =+--> .（I ）当1a = 时求不等式()1f x > 的解集；（）若()f x 图像与x 轴围成的三角形面积大于6，求a 的取值范围.（Ⅱ）由题设可得，12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--≤≤⎨⎪-++>⎩，所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21(,0)3a A -，(21,0)B a +，(,+1)C a a ，所以△的面积为22(1)3a +. 由题设得22(1)3a +＞6，解得2a >.所以a 的取值范围为（2，+∞）. 【2015课标Ⅱ卷】设,,,abcd 均为正数，且a b c d +=+，证明：（Ⅰ）若ab cd >a b c d >a b c d >是a b c d -<-的充要条件．【解析】（Ⅰ）因为2)2a b a b ab =++，2(2c d c d cd =++，由题设a b c d +=+，ab cd >，得22(a b c d >a b c d >．（Ⅱ）（ⅰ）若a b c d -<-，则22()()a b c d -<-．即22()4()4a b ab c d cd +-<+-．因为a b c d +=+，所以ab cd >a b c d >+ a b c d >+22()a b c d +>.即2a b ab ++>2c d cd ++a b c d +=+，所以ab cd >.于是22()()4a b a b ab -=+-2()4c d cd <+-2()c d =-．因此a b c d -<-.a b c d >是a b c d -<-的充要条件．。

十年高考理数真题专题不等式(原卷)

第七章不等式一．基础题组1. 【 2009 全国卷Ⅰ，理 3】不等式 |x 1 | ＜ 1 的解集为（）x 1A.{x|0 ＜ x ＜ 1 } ∪{x|x ＞ 1}B.{x|0 ＜ x ＜1}C.{x|-1 ＜x ＜ 0}D.{x|x＜ 0}x － y －1，2.【 2012 全国，理 14】设 x ， y满足拘束条件x ＋ y 3，，则 z x y的取值范围为 __________ ．＝－ 2 x 0，y 0,x y ≥ 0，3.4.【 2008 全国 1，理 13 】若 x ， y 满足拘束条件x y3 02x y 的最大值为．≥ ，则 z 0 ≤ x ≤ ，32 x y1,【 2 006 全国，理 14】设 z2 y x ，式中变量 x 、y 满足以下条件 3x2y 23, 则 z 的最大值为。

y1,5. 【 2005 全国 1，理 13】若正整数 m 满足 10 m 1 2512 10m , 则 m ________ .(lg 2 0.3010)二．能力题组x y 1,1. 【 2014 课标Ⅰ，理 9】不等式组2y的解集为 D,有下边四个命题：x 4,p 1 : (x, y) D, x 2 y 2 ， p 2 : (x, y)D, x 2 y 2 ，p 3 : (x, y) D, x 2 y 3 p 4 : (x, y) D, x2 y1，此中的真命题是（）A ． p 2 , p 3B ． p 1 , p 2C ． p 1 , p 3D ． p 1, p 42.【 2005 全国 1，理 9】在座标平面上，不等式组yx 1,（）y所表示的平面地域的面积为3 | x | 1A ． 2B ．3C ．3 2D ． 22 2x 1 0，则y的最大值为 .3. 【2015高考新课标1，理 15】若x, y满足拘束条件x y 0x y 4x 0三．拔高题组1.全国新课标，理 13】若变量x y3 2x y 9 则z x ＋ 2 y 的最小值为 __________ ．【 2011 ，满足拘束条件＝6 x y 9。

2010-2019历年高考数学《不等式综合应用》真题汇总含解析

2010-2019历年高考数学《不等式综合应用》真题汇总含解析专题七不等式第二十一讲不等式综合应用2019年1.（2019天津文13）设0x >，0y >，24x y +=，则(1)(21)x y xy++的最小值为__________.2010-2018年一、选择题1．(2018北京)设集合{(,)|1,4,2},A x y x y ax y x ay =-+>-≥≤则A ．对任意实数a ，(2,1)A ∈B ．对任意实数a ，(2,1)A ∉C ．当且仅当0a <时，(2,1)A ∉D ．当且仅当32a ≤时，(2,1)A ∉ 2．(2018浙江)已知1a ，2a ，3a ，4a 成等比数列，且1234123ln()a a a a a a a +++=++．若11a >，则A ．13a a <，24a a ，24a a <C ．13a a <，24a a >D ．13a a >，24a a >3．（2017天津）已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+⎪⎩≥设a ∈R ，若关于x 的不等式()||2x f x a +≥在R 上恒成立，则a 的取值范围是A ．[2,2]- B．[2]- C．[2,- D．[- 4．（2015福建）若直线1(0,0)x ya b a b+=>>过点(1,1)，则a b +的最小值等于 A ．2 B ．3 C ．4 D ．5 5．（2015湖南）若实数,a b满足12a b+=，则ab 的最小值为 AB ．2C ．D ．46．（2014重庆）若b a ab b a +=+则）（,log 43log 24的最小值是A ．326+B ．327+C ．346+D ．347+ 7．（2013福建）若122=+yx ，则y x +的取值范围是A ．]2,0[B ．]0,2[-C ．),2[+∞-D ．]2,(--∞8．（2013山东）设正实数,,x y z 满足22340x xy y z -+-=．则当xyz取得最大值时，212x y z+-的最大值为 A ．0 B ．1 C ．94D ．3 9．（2013山东）设正实数z y x ,,满足04322=-+-z y xy x ，则当zxy取得最大值时，2x y z +-的最大值为A ．0B ．98 C ．2 D ．9410．（2012浙江）若正数,x y 满足35x y xy +=，则34x y +的最小值是A ．245 B ．285C ．5D ．6 11．（2012陕西）小王从甲地到乙地的时速分别为a 和b （a b <），其全程的平均时速为v ，则 A ．a v ab <)，1l 与函数2log y x =的图像从左至右相交于点,A B ，2l 与函数2log y x =的图像从左至右相交于,C D ．记线段AC 和BD 在x 轴上的投影长度分别为,a b ，当m 变化时，ba的最小值为 A ．2 B.82 C.384 D. 34413．（2011陕西）设0a b <<，则下列不等式中正确的是A ．2a b a b ab +<<，则下列不等式中，恒成立的是A ．222a b ab +>B．a b +≥ C．11a b +> D ．2b aa b+≥ 二、填空题15．(2018天津)已知,a b ∈R ，且360a b -+=，则128ab+的最小值为． 16．(2018天津)已知a ∈R ，函数22220()220x x a x f x x x a x ⎧++-⎪=⎨-+->⎪⎩，≤，，．若对任意[3,)x ∈-+∞，()||f x x ≤恒成立，则a 的取值范围是____．17．（2017天津）若a ，b ∈R ，0ab >，则4441a b ab++的最小值为．18．（2017山东）若直线1(00)x ya b a b+=＞，＞过点(1,2)，则2a b +的最小值为． 19．（2017江苏）某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年的总存储费用为4x 万元，要使一年的总运费与总存储费之和最小，则x 的值是． 20．（2017北京）能够说明“设a ，b ，c 是任意实数．若a b c >>，则a b c +>”是假命题的一组整数a ，b ，c 的值依次为____________________． 21．（2017浙江）已知a ∈R ，函数4()||f x x a a x=+-+在区间[1，4]上的最大值是5，则a 的取值范围是．22．（2017江苏）在平面直角坐标系xOy 中，(12,0)A -，(0,6)B ，点P 在圆O ：2250x y +=上，若20PA PB ⋅u u u r u u u r≤，则点P 的横坐标的取值范围是．23．（2015重庆）设,0a b >，5a b +=________．24．(2015山东)定义运算“⊗”：22x y x y xy-⊗=（,x y ∈R ，0xy ≠）．当0x >，0y >时，(2)x y y x ⊗+⊗的最小值为．25．（2014浙江）已知实数,,a b c 满足0a b c ++=，2221a b c ++=，则a 的最大值是__； 26．（2014辽宁）对于0c >，当非零实数a ，b 满足22420a ab b c -+-=，且使|2|a b +最大时，124a b c++的最小值为． 27．（2014辽宁）对于0c >，当非零实数a ，b 满足224240a ab b c -+-=，且使|2|a b +最大时，345a b c-+的最小值为． 28．（2014湖北）某项研究表明：在考虑行车安全的情况下，某路段车流量F （单位时间内经过测量点的车辆数，单位：辆/小时）与车流速度v （假设车辆以相同速度v 行驶，单位：米/秒）、平均车长l （单位：米）的值有关，其公式为2760001820vF v v l=++．（Ⅰ）如果不限定车型， 6.05l =，则最大车流量为辆/小时；（Ⅱ）如果限定车型，5l =，则最大车流量比（Ⅰ）中的最大车流量增加辆/小时． 29．（2013天津）设a + b = 2，b >0，则当a = 时， 1||2||a a b+取得最小值. 30．（2013四川）已知函数()4(0,0)af x x x a x=+>>在3x =时取得最小值，则a =__． 31．（2011浙江）若实数,x y 满足221x y xy ++=，则x y +的最大值是____． 32．（2011湖南）设,x y R ∈，则222211()(4)x y y x++的最小值为． 33．（2010安徽）若0,0,2a b a b >>+=，则下列不等式对一切满足条件的,a b 恒成立的是 (写出所有正确命题的编号)． ①1ab ≤；； ③222a b +≥；④333a b +≥； ⑤112a b+≥．答案部分 2019年1.解析0x >，0y >，24x y +=，而()()1212212552x y xy x y xy xy xy xyxy ++++++===+.由基本不等式有42x y =+…所以02xy <<（当且仅当22x y ==时，即2x =，1y =时，等号成立）.所以552xy…，5592222xy ++=…，所以()()121x y xy++的最小值为92.2010-2018年1．D 【解析】解法一点(2,1)在直线1x y -=上，4ax y +=表示过定点(0,4)，斜率为a -的直线，当0a ≠时，2x ay -=表示过定点(2,0)，斜率为1a 的直线，不等式2x ay -≤表示的区域包含原点，不等式4ax y +>表示的区域不包含原点．直线4ax y +=与直线2x ay -=互相垂直，显然当直线4ax y +=的斜率0a ->时，不等式4ax y +>表示的区域不包含点(2,1)，故排除A ；点(2,1)与点(0,4)连线的斜率为32-，当32a -<-，即32a >时，4ax y +>表示的区域包含点(2,1)，此时2x ay -<表示的区域也包含点(2,1)，故排除B ；当直线4ax y +=的斜率32a -=-，即32a =时，4ax y +>表示的区域不包含点(2,1)，故排除C ，故选D ．解法二若(2,1)A ∈，则21422a a +>⎧⎨-⎩≤，解得32a >，所以当且仅当32a ≤时，(2,1)A ∉．故选D ．2．B 【解析】解法一因为ln 1x x -≤(0x >)，所以1234123ln()a a a a a a a +++=++1231a a a ++-≤，所以41a -≤，又11a >，所以等比数列的公比0q <．若1q -≤，则212341(1)(10a a a a a q q +++=++）≤，而12311a a a a ++>≥，所以123ln()0a a a ++>，与1231234ln()0a a a a a a a ++=+++≤矛盾，所以10q -<<，所以2131(1)0a a a q -=->，2241(1)0a a a q q -=-<，所以13a a >，24a a <，故选B ．解法二因为1x e x +≥，1234123ln()a a a a a a a +++=++，所以123412312341a a a a e a a a a a a a +++=++++++≥，则41a -≤，又11a >，所以等比数列的公比0q <．若1q -≤，则212341(1)(10a a a a a q q +++=++）≤，而12311a a a a ++>≥，所以123ln()0a a a ++>与1231234ln()0a a a a a a a ++=+++≤矛盾，所以10q -<<，所以2131(1)0a a a q -=->，2241(1)0a a a q q -=-<，所以13a a >，24a a <，故选B ．3．A 【解析】解法一函数()f x 的图象如图所示，当||2xy a =+的图象经过点(0,2)时，可知2a =±．当2x y a =+的图象与2y x x =+的图象相切时，由22x a x x +=+，得2240x ax -+=，由0∆=，并结合图象可得2a =，要使()||2xf x a +≥恒成立，当0a ≤时，需满足2a -≤，即20a -≤≤，当0a >时，需满足2a ≤，所以22a -≤≤．解法二由题意0x =时，()f x 的最小值2，所以不等式()||2x f x a +≥等价于||22xa +≤在R 上恒成立．当a =0x =，得|22x+>，不符合题意，排除C 、D ；当a =-0x =，得|22x->，不符合题意，排除B ；选A ．4．C 【解析】解法一 ∵1x y a b +=(0,0)a b >>过点(1,1)，所以111a b +=，所以111a b =+=≥(当且仅当2a b ==时去等号)2．又a b +≥当且仅当2a b ==时去等号)，所以4a b +≥(当且仅当2a b ==时去等号)．解法二∵1x y a b +=(0,0)a b >>过点(1,1)，所以111a b +=，所以11()()224a b a b a b a b b a +=++=+++=≥(当且仅当2a b ==时去等号)．5．C 【解析】解法一由已知122b aa b ab ++==0,0a b >>，∴2b a =+≥ab ≥解法二由题意知0,0a b >>，∴12a b =+≥ab ≥6．D 【解析】由已知得34a b ab +=，且0ab >，可知0,0a b >>，所以431a b += (0,0a b >>)，43()()a b a b a b +=++=4377b aa b +++≥．当且仅当43b aa b =时取等号． 7．D 【解析】本题考查的是均值不等式．因为y x y x 222221⋅≥+=，即222-+≤yx ，所以2-≤+y x ，当且仅当yx 22=，即y x =时取等号． 8．B 【解析】由22340x xy y z -+-=，得2234z x xy y =-+．所以2214343xy xy x y z x xy y y x ==-++-1≤=，当且仅当4x y yx =，即2x y =时取等号此时22y z =，1)(max =z xy.xy y y z y x 2122212-+=-+)211(2)11(2y y x y -=-=1)221121(42=-+≤y y ，故选B.9．C 【解析】由x 2－3xy ＋4y 2－z ＝0得x 2＋4y 2－3xy ＝z ，22443331z x y xy xy xy xy +=-≥=-=，当且仅当x 2＝4y 2即x ＝2y 时，zxy 有最小值1，将x ＝2y 代入原式得z ＝2y 2，所以x ＋2y －z ＝2y ＋2y －2y 2＝－2y 2＋4y ，当y ＝1时有最大值2.故选C.10．C 【解析】Q 35x y xy +=，135y x +=，113131213(34)()()555x y x y y x y x +⋅+=++≥1132555⨯=.11．A 【解析】设从甲地到乙地所走路程为S，则22211S ab v S S a b a ba b===<=+++∵ a b <,∴ 2222ab a v aa b a =>=+,∴a v <<选A.12．B 【解析】在同一坐标系中作出y m =，y =821m +(0m >)，2log y x=图像如下图，由2log x= m ，得122,2m mx x -==，2log x = 821m +，得821821342,2m m x x +-+==.依照题意得8218218218212222,22,22m m mm m m mm b a b a++--+--+-=-=-=-821821222m m mm +++==.8141114312122222m m m m +=++-≥-=++Q ，min()82b a ∴=13．B 【解】（方法一）已知a b <2a bab +<，比较a ab ，因为22)()0a ab a a b -=-<，所以a ab <22()()0b ab b b a -=->ab b ；作差法：022a b b a b +--=>，所以2a bb +<，综上可得2a b a ab b +<<；故选B ．（方法二）取2a =，8b =4ab =，52a b +=，所以2a ba ab b+<<<．14．D 【解析】对于A 取1a b ==，此时2222a b ab +==，因此A 不正确；对于B 取1a b ==-，此时222a b ab +=-<=，因此B 不正确；对于C 取1a b ==-，此时1122a b ab +=-<=，因此C 不正确；对于D ，∵0ab >，∴0b a >，0ba >，∴22b a b a a b a b +⋅=≥，D 正确．15．14【解析】由360a b -+=，得36a b =-，所以36331112222824a b b b --+=+=⨯=≥，当且仅当363122b b -=，即1b =时等号成立．16．1[,2]8【解析】当30x -≤≤时，()||f x x ≤恒成立等价于222x x a x++--≤恒成立，即232a x x --+≤恒成立，所以2min (32)2a x x --+=≤；当0x >时()||f x x ≤恒成立等价于222x x a x -+-≤恒成立，即22x x a -+≥恒成立，所以2max 1()28x x a -+=≥．综上，a 的取值范围是1[,2]8．17．4【解析】44224141144a b a b ab ab ab ab +++=+≥≥ ，当且仅当222a b =，且12ab =，即22a =，24b =时取等号. 18．8【解析】由题意有121a b+=，所以1242(2)()448b a a b a b a b a b +=++=+++=≥．当且仅当4b a a b =，即4b =，2a =时等号成立． 19．30【解析】总费用为600900464()4240x x x x +⨯=+≥⨯=，当且仅当900x x =，即30x =时等号成立．20．-1，-2，-3（答案不唯一）【解析】因为“设a ，b ，c 是任意实数．若a b c >>，则a b c +>”是假命题，则它的否定“设a ，b ，c 是任意实数．若a b c >>，则a b c +≤”是真命题，由于a b c >>，所以2a b c +>，又a b c +≤，所以0c <，因此a ，b ，c 依次取整数-1，-2，-3，满足a b c +≤．()123,1233->->--+-=->-相矛盾，所以验证是假命题．21．9(,]2-∞【解析】∵[1,4]x ∈，∴4[4,5]x x +∈①当5a ≥时，44()2224f x a x a a x a a x x =--+=---=-≤，所以()f x 的最大值245a -=，即92a =（舍去）②当4a ≤时，44()5f x x a a x x x =+-+=+≤，此时命题成立．③当45a <<时，max ()max{|4|,|5|}f x a a a a =-+-+，则 |4||5||4|5a a a a a a -+-+⎧⎨-+=⎩≥或|4||5||5|5a a a a a a -+<-+-+=，解得92a =或92a <，综上可得，实数a 的取值范围是9(,]2-∞． 22．[-【解析】设(,)P x y ，由20PA PB ⋅u u u r u u u r ≤，得250x y -+≤，x如图由250x y -+≤可知，P 在¼MN 上，由2225050x yx y-+=⎧⎨+=⎩，解得(1,7)M，(5,5)N--，所以P点横坐标的取值范围为[-．23．【解析】24a b=+++92+≤9418a b=+++=．当且仅当13a b+=+且5a b+=，即73,22a b==时等号成立．24．【解析】由新定义运算知，2222(2)4(2)(2)2y x y xy xy x xy--⊗==，因为00x y>>，，所以，22222242(2)222x y y x x yx y y xxy xy xy xy--+⊗+⊗=+=≥=，当且仅当x=时，(2)x y y x⊗+⊗．25．【解析】由0a b c++=得，a b c=--，则2222()2a b c b c bc=--=++()2222222b c b c b c+++=+≤，又2221a b c++=，所以232a≤，解得a，故a的最大值为．26．－1【解析】设|2|a b+最大，则必须,a b同号，因为22224463()2a ba b ab c ab c+++=++≤，故有2(2)4a b c+≤，22()2a bc+≥，当且仅当2a b=时取等号，此时2c b=，所以124a b c++=2244114()112b b b+=+--≥．27．－2【解析】设2a b t+=，则2a t b=-，因为224240a ab b c-+-=，所以将2a t b =-代入整理可得22630b tb t c -+-=①，由0∆≥解得t ，当2a b +取得最大值时，t =代入①式得b =2a t b =-得a = 所以345a b c -+=55c c =222=--≥．当且仅当52c =时等号成立．28．1900 100【解析】（Ⅰ）76000190020 6.0518F v v ==⨯++，当且仅当11v = 时等号成立．（Ⅱ）76000200020518F v v ==⨯++，当且仅当10v =时等号成立． 20001900100-=．29．－2【解析】∵1||2||a a b +=||||4||4||4||a b a a b a a b a a b ++=++13114||4||44a a a a +=+-+=≥≥ 当且仅当||,04||b a a a b =<，即2,4a b =-=时取等号故1||2||a a b +取得最小值时，2a =-．30．36【解析】因为0,0x a >>，()44a f x x a x =+≥=，当且仅当4a x x =，即3x ==，解得36a =．31．【解析】∵221x y xy ++=， ∴2()1x y xy +-=，即22()()12x y x y ++-≤，∴24()3x y +≤，3x y +≤． 32．9【解析】由柯西不等式可知2222211()(4)(12)9x y y x ++≥+=．33．①③⑤【解析】令1a b ==，排除②④；由21a b ab =+≥⇒≤，命题①正确；222()2422a b a b ab ab +=+-=-≥，命题③正确；1122a b a b ab ab ++==≥，命题⑤正确．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

不等式
不等式的综合应用
2019年
1.（2019天津理13）设0,0,25x y x y >>+=，
则
1)
的最小值
为 .
2010-2018年
一、选择题
1．(2018北京)设集合{(,)|1,4,2},A x y x y ax y x ay =-+>-≥≤则
A ．对任意实数a ，(2,1)A ∈
B ．对任意实数a ，(2,1)A ∉
C ．当且仅当0a <时，(2,1)A ∉
D ．当且仅当3
2
a ≤
时，(2,1)A ∉ 2．（2017天津）已知函数||2,1,
()2
, 1.x x f x x x x +<⎧⎪
=⎨+⎪⎩
≥设a ∈R ，若关于x 的不等式()||2x f x a +≥在R 上恒成立，则a 的取值范围是
A ．[2,2]- B
．[- C
．[- D
．[- 3．（2015北京）设{}n a 是等差数列．下列结论中正确的是
A ．若120a a +>，则230a a +>
B ．若130a a +<，则120a a +<
C ．若120a a <<
，则2a >
D ．若10a <，则()()21230a a a a -->
4．（2015陕西）设()ln f x x =，0a b <<
，若p f =，(
)2
a b
q f +=， 1
(()())2
r f a f b =+，则下列关系式中正确的是
A ．q r p =
C ．p r q =<
D ．p r q =>
5．（2014重庆）若b a ab b a +=+则）
（,log 43log 24的最小值是
A ．326+
B ．327+
C ．346+
D ．347+ 6．（2013福建）若122=+y
x ，则y x +的取值范围是
A ．]2,0[
B ．]0,2[-
C ．),2[+∞-
D ．]2,(--∞
7．（2013山东）设正实数,,x y z 满足2
2
340x xy y z -+-=．则当
xy
z
取得最大值时， 212
x y z
+-的最大值为 A ．0 B ．1 C ．
9
4
D ．3 8．（2013山东）设正实数z y x ,,满足0432
2
=-+-z y xy x ，则当
z
xy
取得最大值时， 2x y z +-的最大值为
A ．0
B ．
9
8
C ．2
D ．
94
9．（2012浙江）若正数,x y 满足35x y xy +=，则34x y +的最小值是
A ．
245 B ．28
5
C ．5
D ．6 10．（2012浙江）若正数,x y 满足35x y xy +=，则34x y +的最小值是 A ．
245 B ．285
C ．5
D ．6 11．（2012陕西）小王从甲地到乙地的时速分别为a 和b （a b <），其全程的平均时速为v ，
则
A ．a v <)，1l 与函数2log y x =的
图像从左至右相交于点,A B ，2l 与函数2log y x =的图像从左至右相交于,C D ．记线段AC 和BD 在x 轴上的投影长度分别为,a b ，当m 变化时，
b
a
的最小值为
A ．
B ．
C ．
D ．13．（2011陕西）设0a b <<，则下列不等式中正确的是
A ．2a b a b +<<
，则下列不等式中，恒成立的是
A ．2
2
2a b ab +>
B
．a b +≥ C
．
11a b +>
D ．2b a
a b +≥ 二、填空题
15．(2018天津)已知,a b ∈R ，且360a b -+=，则1
28
a
b +
的最小值为． 16．(2018浙江)已知λ∈R ，函数24,()43,x x f x x x x λ
λ-⎧=⎨-+<⎩
≥，当2λ=时，不等式()0
f x <的解集是___________．若函数()f x 恰有2个零点，则λ的取值范围是___________． 17．(2017北京)已知0x ≥，0y ≥，且1x y +=，则22x y +的取值范围是_______．
18．（2017天津）若,a b ∈R ，0ab >，则4441
a b ab
++的最小值为___________．
19．（2017江苏）某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年
的总存储费用为4x 万元，要使一年的总运费与总存储费之和最小，则x 的值是． 20．（2017浙江）已知a ∈R ，函数4
()||f x x a a x
=+
-+在区间[1，4]上的最大值是5，则a 的取值范围是．
21．（2014浙江）已知实数,,a b c 满足0a b c ++=，2221a b c ++=，则a 的最大值是__； 22．（2014辽宁）对于0c >，当非零实数a ，b 满足2
2
420a ab b c -+-=，且使|2|
a b +最大时，
124
a b c
++的最小值为． 23．（2014辽宁）对于0c >，当非零实数a ，b 满足2
2
4240a ab b c -+-=，且使|2|a b +最大时，
345
a b c
-+的最小值为． 24．（2014湖北）某项研究表明：在考虑行车安全的情况下，某路段车流量F （单位时间内
经过测量点的车辆数，单位：辆/小时）与车流速度v （假设车辆以相同速度v 行驶，单位：米/秒）、平均车长l （单位：米）的值有关，其公式为2760001820v
F v v l
=
++．
（Ⅰ）如果不限定车型， 6.05l =，则最大车流量为辆/小时；
（Ⅱ）如果限定车型，5l =，则最大车流量比（Ⅰ）中的最大车流量增加辆/小时． 25．（2013天津）设a + b = 2， b >0，则当a = 时， 1||
2||a a b
+
取得最小值. 26．（2013四川）已知函数()4(0,0)a
f x x x a x
=+
>>在3x =时取得最小值，则a =__． 27．（2011浙江）若实数,x y 满足2
2
1x y xy ++=，则x y +的最大值是____． 28．（2011湖南）设,x y R ∈，则22
2211()(4)x y y x
+
+的最小值为． 29．（2010安徽）若0,0,2a b a b >>+=，则下列不等式对一切满足条件的,a b 恒成立的
是 (写出所有正确命题的编号)．
①1ab ≤； ≤； ③222a b +≥；
④3
3
3a b +≥； ⑤
11
2a b
+≥。