力学竞赛考试范围2014

合集下载

力学竞赛考试范围

全国周培源大学生力学竞赛考试范围（参考）理论力学一、基本部分(一) 静力学(1) 掌握力、力矩和力系的基本概念及其性质。

能熟练地计算力的投影、力对点的矩和力对轴的矩。

(2) 掌握力偶、力偶矩和力偶系的基本概念及其性质。

能熟练地计算力偶矩及其投影。

(3) 掌握力系的主矢和主矩的基本概念及其性质。

掌握汇交力系、平行力系与一般力系的简化方法、熟悉简化结果。

能熟练地计算各类力系的主矢和主矩。

掌握重心的概念及其位置计算的方法。

(4) 掌握约束的概念及各种常见理想约束力的性质。

能熟练地画出单个刚体及刚体系受力图。

(5) 掌握各种力系的平衡条件和平衡方程。

能熟练地求解单个刚体和简单刚体系的平衡问题。

(6) 掌握滑动摩擦力和摩擦角的概念。

会求解考虑滑动摩擦时单个刚体和简单平面刚体系的平衡问题。

(二)运动学(1) 掌握描述点运动的矢量法、直角坐标法和自然坐标法，会求点的运动轨迹，并能熟练地求解点的速度和加速度。

(2) 掌握刚体平移和定轴转动的概念及其运动特征、定轴转动刚体上各点速度和加速度的矢量表示法。

能熟练求解定轴转动刚体的角速度、角加速度以及刚体上各点的速度和加速度。

(3) 掌握点的复合运动的基本概念，掌握并能应用点的速度合成定理和加速度合成定理。

(4) 掌握刚体平面运动的概念及其描述，掌握平面运动刚体速度瞬心的概念。

能熟练求解平面运动刚体的角速度与角加速度以及刚体上各点的速度和加速度。

(三)动力学(1) 掌握建立质点的运动微分方程的方法。

了解两类动力学基本问题的求解方法。

(2) 掌握刚体转动惯量的计算。

了解刚体惯性积和惯性主轴的概念。

(3) 能熟练计算质点系与刚体的动量、动量矩和动能；并能熟练计算力的冲量（矩），力的功和势能。

(4) 掌握动力学普遍定理(包括动量定理、质心运动定理、对固定点和质心的动量矩定理、动能定理)及相应的守恒定理，并会综合应用。

(5) 掌握建立刚体平面运动动力学方程的方法。

了解其两类动力学基本问题的求解方法。

2014年国际工程力学学竞赛试题参考答案(个人赛)

国际工程力学竞赛试题参考答案（2014）评分标准：该赛事最后结果会扣分很多。

在步骤分的设置上，仅仅设置少数几个关键步的中间量的结果。

仅仅关键步骤的中间结果正确才有该步骤的分。

若该步骤方程正确，得到的中间量的结果错误是，仍不得分。

故要想获得高分，需要最终结果正确。

所以处，首先要保证计算结果的正确率，然后，再追求完成题目数。

--------------------【题1】------------------【提醒】摩擦问题，若仅仅是求临界力，按照教材的方法，其求出的值必然是极值。

而若是求尺寸，若这个尺寸仅时发生临界（必须需要同时补充2个方程）的情形，还需要补充上=221πϕϕ=+（在上面任意一个不等式条件中，加上=）【同学2：推荐】解法合理，结果正确。

--------------------【题2】--------------------------------------【题3】------------------见培训6运动学视频讲解。

由加速度关系垂直BA杆方向投影得所以该题特色：找准动点动系。

【提醒】1）任何一个刚体以外的点相对该刚体有相对该题，若用动点动系法，可以取2轮的轮心为动点.但坐标求导法更简单。

具体方法可参考教材。

--------------------【题6】------------------[提醒按百度翻译来理解。

该题“Find out the ve locity which should be given to the center of the disk at its lower position for the decreasing ofthe normal cylinder pressure force in1.5times for the position of the isk when the angleφ=60°.”意思为：最低点压力是60度时的1.5倍。

2016新编全国周培源大学生力学竞赛考试范围（参考）

全国周培源大学生力学竞赛考试范围（参考）理论力学一、基本部分(一) 静力学(1) 掌握力、力矩和力系的基本概念及其性质。

能熟练地计算力的投影、力对点的矩和力对轴的矩。

(2) 掌握力偶、力偶矩和力偶系的基本概念及其性质。

能熟练地计算力偶矩及其投影。

(3) 掌握力系的主矢和主矩的基本概念及其性质。

掌握汇交力系、平行力系与一般力系的简化方法、熟悉简化结果。

能熟练地计算各类力系的主矢和主矩。

掌握重心的概念及其位置计算的方法。

(4) 掌握约束的概念及各种常见理想约束力的性质。

能熟练地画出单个刚体及刚体系受力图。

(5) 掌握各种力系的平衡条件和平衡方程。

能熟练地求解单个刚体和简单刚体系的平衡问题。

(6) 掌握滑动摩擦力和摩擦角的概念。

会求解考虑滑动摩擦时单个刚体和简单平面刚体系的平衡问题。

(二)运动学(1) 掌握描述点运动的矢量法、直角坐标法和自然坐标法，会求点的运动轨迹，并能熟练地求解点的速度和加速度。

(2) 掌握刚体平移和定轴转动的概念及其运动特征、定轴转动刚体上各点速度和加速度的矢量表示法。

能熟练求解定轴转动刚体的角速度、角加速度以及刚体上各点的速度和加速度。

(3) 掌握点的复合运动的基本概念，掌握并能应用点的速度合成定理和加速度合成定理。

(4) 掌握刚体平面运动的概念及其描述，掌握平面运动刚体速度瞬心的概念。

能熟练求解平面运动刚体的角速度与角加速度以及刚体上各点的速度和加速度。

(三)动力学(1) 掌握建立质点的运动微分方程的方法。

了解两类动力学基本问题的求解方法。

(2) 掌握刚体转动惯量的计算。

了解刚体惯性积和惯性主轴的概念。

(3) 能熟练计算质点系与刚体的动量、动量矩和动能；并能熟练计算力的冲量（矩），力的功和势能。

(4) 掌握动力学普遍定理(包括动量定理、质心运动定理、对固定点和质心的动量矩定理、动能定理)及相应的守恒定理，并会综合应用。

(5) 掌握建立刚体平面运动动力学方程的方法。

了解其两类动力学基本问题的求解方法。

第八届重庆大学大学生力学竞赛考试范围

附件2：第八届重庆大学大学生力学竞赛考试范围（参考）理论力学部分一、基本部分(一) 静力学(1) 掌握力、力矩和力系的基本概念及其性质。

能熟练地计算力的投影、力对点的矩和力对轴的矩。

(2) 掌握力偶、力偶矩和力偶系的基本概念及其性质。

能熟练地计算力偶矩及其投影。

(3) 掌握力系的主矢和主矩的基本概念及其性质。

掌握汇交力系、平行力系与一般力系的简化方法、熟悉简化结果。

能熟练地计算各类力系的主矢和主矩。

掌握重心的概念及其位置计算的方法。

(4) 掌握约束的概念及各种常见理想约束力的性质。

能熟练地画出单个刚体及刚体系受力图。

(5) 掌握各种力系的平衡条件和平衡方程。

能熟练地求解单个刚体和简单刚体系的平衡问题。

(6) 掌握滑动摩擦力和摩擦角的概念。

会求解考虑滑动摩擦时单个刚体和简单平面刚体系的平衡问题。

(二)运动学(1) 掌握描述点运动的矢量法、直角坐标法和自然坐标法，会求点的运动轨迹，并能熟练地求解点的速度和加速度。

(2) 掌握刚体平移和定轴转动的概念及其运动特征、定轴转动刚体上各点速度和加速度的矢量表示法。

能熟练求解定轴转动刚体的角速度、角加速度以及刚体上各点的速度和加速度。

(3) 掌握点的复合运动的基本概念，掌握并能应用点的速度合成定理和加速度合成定理。

(4) 掌握刚体平面运动的概念及其描述，掌握平面运动刚体速度瞬心的概念。

能熟练求解平面运动刚体的角速度与角加速度以及刚体上各点的速度和加速度。

(三)动力学(1) 掌握建立质点的运动微分方程的方法。

了解两类动力学基本问题的求解方法。

(2) 掌握刚体转动惯量的计算。

了解刚体惯性积和惯性主轴的概念。

(3) 能熟练计算质点系与刚体的动量、动量矩和动能；并能熟练计算力的冲量（矩），力的功和势能。

(4) 掌握动力学普遍定理(包括动量定理、质心运动定理、对固定点和质心的动量矩定理、动能定理)及相应的守恒定理，并会综合应用。

(5) 掌握建立刚体平面运动动力学方程的方法。

全国周培源力学竞赛试题

全国周培源力学竞赛试题周培源力学竞赛是以力学为主题的全国性竞赛，旨在考察学生对力学基础知识的掌握和应用能力。

以下为相关参考内容，包括力学的基本概念、公式和解题思路等。

一、力学基本概念：1. 物体：具有一定质量和形状的实体。

2. 运动：物体在空间中的位置随时间的变化。

3. 弹力：弹性物体受到扭曲或拉伸后，恢复原状的能力。

4. 动力学：研究物体运动的动力学定律和力的作用规律等。

5. 静力学：研究物体在静止状态下的平衡条件与力的作用规律等。

6. 力：使物体发生变化或改变状态的推动或阻碍作用。

7. 质点：假设物体无限小且质量集中，只具有位置和质量两个性质。

8. 牛顿第一定律：质点在无外力作用下保持匀速直线运动或静止。

9. 牛顿第二定律：力是质点受到的推动或阻碍作用，与质点的加速度成正比。

10. 牛顿第三定律：相互作用的两个物体所受的力大小相等、方向相反。

二、力学公式：1. 速度公式：速度 = 位移 / 时间，单位为米每秒（m/s）。

2. 加速度公式：加速度 = （终速度 - 初始速度）/ 时间，单位为米每秒平方（m/s²）。

3. 牛顿第二定律公式：力 = 质量 ×加速度，单位为牛顿（N）。

4. 力矩公式：力矩 = 力 ×距离，单位为牛顿米（Nm）。

5. 动能公式：动能 = 1/2 ×质量 ×速度²，单位为焦耳（J）。

6. 力的合成公式：合成力大小= √（力₁² + 力₂² + ... + 力ₙ²）。

三、力学解题思路：1. 建立坐标系和力图。

对于空间力学问题，可以建立一个适当的坐标系，并根据问题所给的力的方向和大小，绘制力图。

2. 利用牛顿第二定律解题。

根据题目所要求的问题，建立合适的坐标系，并根据牛顿第二定律公式进行计算，求出所需的未知量。

3. 引入力矩和转动定律解题。

对于转动问题，除了考虑物体的质量和加速度外，还要考虑到力对物体的转动作用。

2014年第十届湖南省大学生力学竞赛试题和答案

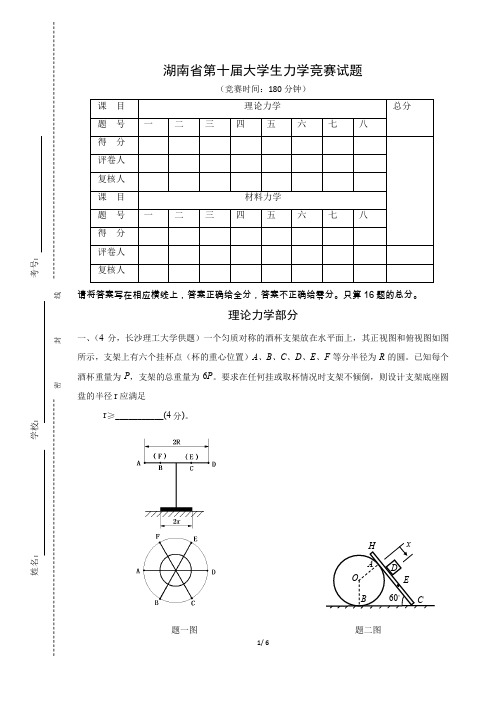
湖南省第十届大学生力学竞赛试题（竞赛时间：180分钟）课目理论力学题号一二三四五六七八总分得分评卷人复核人课目材料力学题号一二三四五六七八得分评卷人复核人请将答案写在相应横线上，答案正确给全分，答案不正确给零分。

只算16题的总分。

理论力学部分一、（4分，长沙理工大学供题）一个匀质对称的酒杯支架放在水平面上，其正视图和俯视图如图所示，支架上有六个挂杯点（杯的重心位置）A 、B 、C 、D 、E 、F 等分半径为R 的圆。

已知每个酒杯重量为P ，支架的总重量为6P 。

要求在任何挂或取杯情况时支架不倾倒，则设计支架底座圆盘的半径r 应满足r ≥___________(4分)。

题一图题二图密封线二、（8分，湖南大学供题）如图所示，均质轮O 置于水平面上，杆HC 垂直轮轴O 搁置于轮和平面上，杆与水平面倾角为60°，轮与杆及水平面之间的接触点A 、B 和 C 处均有摩擦，使得杆与轮保持静止。

现将不计大小的物块D 轻置于杆HC 上的A 点，并由静止沿杆无摩擦加速下滑。

设轮、杆与物块D 质量均为m ，杆的重心位于AC 中点E ，AC 长为l ，试分析下述问题:（1）轮与杆保持静止的条件之一是其两者之间的静摩擦因数最小应为（3分）；（2）设A 与C 处的摩擦足够大，则维持B 处不滑动的最小静摩擦因数值等于（5分）。

三、（5分，湖南农业大学供题）一半径为r 的半圆柱放在另一半径为R 固定于水平面的半圆柱上，如图所示。

静止时上面一个半圆柱的重心C 与接触点A 的距离为d ，并假定任意接触处不会发生相对滑动。

试求该系统在图示位置稳定平衡时d 的最大值为（5分）。

题三图题四图四、（10分，国防科技大学供题）图示平面机构中杆OA 以等角速度 0作定轴转动，半径为r 的滚轮在杆OA 上作纯滚动，O 1B 杆绕O 1轴转动并与轮心B 铰接，在图示瞬时O 、B 在同一水平线上，且 O 1B 长为2r ，处于在铅垂位置，则此瞬时（1）滚轮的角速度大小为（3分）；（2）滚轮的角加速度大小为（7分）。

2014四川省孙训方力学竞赛参考解答

FNA 3P 3 P[cos sin (1 )] 0 2 3 D O1 A O3
P P
E O 2 C FSB
y x
PB
FNB
解得
tan 1
3 32.37 3 3
FSA
FNA
故平衡时斜面倾角的最大值为
32.37
O3 D O1 A
2、平衡时圆盘 O1 与 O2 之间铰链 C 沿圆盘公切线方向的约束力与倾角的关系取整体为研究对象由
r
dr , ve r ，由系统机械能守恒和对转轴 z dt
mr 02 (J z ) 0 ( J z mr 2 ) 4
，
(A) (B)
将 r r0 代入式(A)和(B)得当质点 A 运动到盘沿 B 时圆盘的角速度
3 0 4
质点 M 的速度和相对速度
va
对式（B）求导得
3 2 r00 , 4
vr r
3 r00 4
0 m (2r02 r 2 ) 2m rr
3 将 r r0 时， 0 和 vr 4
r
3 r00 代入上式解得 4
当质点 A 运动到盘沿 B 时，圆盘的角加速度
3 02 8
2
四、解： =
当 F 处于最左端时，压杆的轴力最大，
五、解：1）使用叠加原理在均布载荷 q 作用时：向下
在钢索预紧力作用时：
向上
（拉力）
8分 6分
绝对值 2）不能在钢索预紧力作用时： 6分
,
向下；
即预紧力仍然使 C 截面挠度向下，无法向上；而 q 的作用，C 的挠度向下。
六、解： 1）在杆 2 和杆 4 顶端力作用下：每根杆上端铰接处出现切向力在杆 3 顶端的力作用下：设每杆均受压平衡方程：

本科生力学竞赛试题及答案

本科生力学竞赛试题及答案一、选择题（每题3分，共30分）1. 在经典力学中，牛顿第一定律又称为：A. 惯性定律B. 作用力与反作用力定律C. 力与加速度定律D. 万有引力定律答案：A2. 一个物体的质量为2kg，受到10N的力作用，产生的加速度为：A. 5 m/s²B. 10 m/s²C. 20 m/s²D. 4 m/s²答案：A3. 根据胡克定律，弹簧的弹力F与弹簧的形变量x成正比，比例系数k为弹簧的劲度系数。

当弹簧伸长2m时，弹力为100N，则弹簧的劲度系数k为：A. 50 N/mB. 100 N/mC. 200 N/mD. 25 N/m答案：A4. 一个物体从静止开始自由下落，忽略空气阻力，其下落过程中的加速度为：A. 9.8 m/s²B. 0 m/s²C. 2 m/s²D. 19.6 m/s²答案：A5. 在国际单位制中，力的单位是以哪位科学家的名字命名的？A. 牛顿B. 爱因斯坦C. 伽利略D. 阿基米德答案：A6. 一个物体在水平面上做匀速直线运动，其受到的摩擦力为10N，那么推力的大小为：A. 0 NB. 10 NC. 20 ND. 不能确定答案：B7. 根据能量守恒定律，一个物体从高处自由下落到地面，其势能转化为：A. 动能B. 内能C. 电能D. 化学能答案：A8. 在斜面上下滑的物体，其受到的重力分量可以分解为：A. 垂直于斜面的压力B. 沿斜面向下的力C. 垂直于斜面的力D. 沿斜面向下的力和垂直于斜面的力答案：D9. 一个物体在水平面上以恒定的加速度加速运动，其受到的合外力与速度的方向：A. 相反B. 相同C. 不确定D. 垂直答案：B10. 两个物体之间的万有引力与它们的质量乘积成正比，与它们之间的距离的平方成反比。

这个定律是由哪位科学家提出的？A. 牛顿B. 爱因斯坦C. 伽利略D. 阿基米德答案：A二、简答题（每题10分，共40分）11. 什么是动量守恒定律？请举例说明。

第六届大学生力学竞赛试题-理论力学

湖南省第六届大学生力学竞赛试题一一理论力学题号-一一二二二四五六七总分得分评卷人复核人请将答案写在相应横线上，答案正确给全分，答案不正确给零分。

、综合题（16 分）1 •长度为I ，重P 为1kN 的匀质板搁在倾角为60°的V 型水渠上，如图所示。

板与斜面间的摩擦角为15o 试求可以通过该桥人的最大体重题1.1图2•连杆滑块机构中，OA=2I,AB=I,杆OA 在图示平面内绕0轴以匀角速度「°转动。

试3•—匀质圆盘半径为R ,质量为m ,放在光滑的水平平面上。

初始时以匀角速度绕盘边缘一点A 转动。

当转动到图示位置时，突然释放 A 点，固定盘边缘上的B 点，再释放4 •图示机构，曲柄 OA 可绕O 轴定轴转动，AB 杆穿过套筒C ，OC 连线水平，其中OA=r ，AB=4r ，OA 曲柄作用大小为 M 的顺时针力偶，初始时刻曲柄OA 处于铅垂位置，C 为AB 中点，在AB 杆的B 端施加一力P 可使系统在该位置平衡，为了使力P 最小，可以改变其方向，若不计各处摩擦，试求平衡时力P 的最小值为（4分）。

求当角'=0时，AB 杆的角速度为（4 分）。

B 点。

试求此后圆盘运动的角速度为-■（4 分）。

线密Q=I（4 分）。

题1.3图、正方体边长为a，力F i, F2大小均为F，该力系对轴CA •之矩为_____________________分）；该力系简化可能得到的最小主矩为（6分）R题3图题三图三、（4分+4分+7分=15分）图示均质轮轴重量为G,半径为R,轮轴上鼓轮半径为r，在鼓轮上缠绕轻质绳经过定滑轮系以重物，各处摩擦因数均为f,二角已知，试求平衡时重物的最大重量G o 0四、图示平面机构中，滑块 C 与滚轮A 用杆和铰链连接，A 为轮心，套筒绕0轴转动，图示瞬时0在AB 中点，：• =60o, BC_AB 。

已知0、C 在同一水平线上，AB=20cm , V A 为常数，且V A =16cm/s ，试求该瞬时AB 杆的角速度为（4分），滑块C 的速度大小为 ________ （4分），AB 杆的角加速度为小为 ____________________ （ 4分）。

全国周培源大学生力学竞赛考试范围

力学是工程和各门科学的基础，也是想成长为优秀的科学家和工程师必受的入门教育和锻炼。

第八届周培源全国大学生力学竞赛团体赛将于2011年在清华举行。

该项竞赛旨在促进大学生从本阶段就开始了解与接触高水平的科研和重大工程课题，培养大学生的动手能力和创新能力，培养团队合作精神，丰富校园文化。

个人建议：先看看以前的竞赛题目，自身感觉一下难度，把握一下试题的侧重点和自身的薄弱点。

然后进行复习：材料力学和理论力学，再有一本竞赛练习册和大纲进行对应练习，最后用真题进行模拟，考察自己的实际能力，查缺补漏，争取在比赛中有好的成绩。

附：全国周培源大学生力学竞赛考试范围（参考）理论力学一、基本部分(一) 静力学(1) 掌握力、力矩和力系的基本概念及其性质。

能熟练地计算力的投影、力对点的矩和力对轴的矩。

(2) 掌握力偶、力偶矩和力偶系的基本概念及其性质。

能熟练地计算力偶矩及其投影。

(3) 掌握力系的主矢和主矩的基本概念及其性质。

掌握汇交力系、平行力系与一般力系的简化方法、熟悉简化结果。

能熟练地计算各类力系的主矢和主矩。

掌握重心的概念及其位置计算的方法。

(4) 掌握约束的概念及各种常见理想约束力的性质。

能熟练地画出单个刚体及刚体系受力图。

(5) 掌握各种力系的平衡条件和平衡方程。

能熟练地求解单个刚体和简单刚体系的平衡问题。

(6) 掌握滑动摩擦力和摩擦角的概念。

会求解考虑滑动摩擦时单个刚体和简单平面刚体系的平衡问题。

(二)运动学(1) 掌握描述点运动的矢量法、直角坐标法和自然坐标法，会求点的运动轨迹，并能熟练地求解点的速度和加速度。

(2) 掌握刚体平移和定轴转动的概念及其运动特征、定轴转动刚体上各点速度和加速度的矢量表示法。

能熟练求解定轴转动刚体的角速度、角加速度以及刚体上各点的速度和加速度。

(3) 掌握点的复合运动的基本概念，掌握并能应用点的速度合成定理和加速度合成定理。

(4) 掌握刚体平面运动的概念及其描述，掌握平面运动刚体速度瞬心的概念。

物理竞赛--力学

物理竞赛--力学力学作为物理学的重要分支，研究物体在运动过程中的力学规律和物理现象。

力学竞赛则是运用力学知识和技能来解决各种力学难题和挑战，是展示物理学学生实力的重要途径。

下面将重点介绍力学竞赛的一些内容和技巧。

一、竞赛类型和内容力学竞赛类型较多，包括个人赛、团队赛、定向赛、综合赛等。

针对不同竞赛类型，竞赛内容也各不相同。

一般来说，力学竞赛包括以下几个方面：1.牛顿力学牛顿力学是力学的基础知识，包括运动学和动力学。

要熟练掌握牛顿定律、动量守恒定律、角动量守恒定律等基本概念，以及如何应用这些概念解决各种物理问题。

2.万有引力万有引力是物理学中重要的概念，是了解天体运动的必要条件。

要熟悉万有引力定律，掌握行星运动的法则和计算方法。

3.能量守恒定律能量守恒定律是物理学中非常重要的概念，可以应用于解决各种复杂的物理问题。

要了解各种能量形式的定义和计算方法，掌握能量转化和能量守恒的基本理论。

4.波动波动是力学中非常重要的概念，包括机械波和电磁波。

要熟悉波的基本性质，掌握波的传播规律和反射、折射等现象的原理和计算方法。

二、竞赛技巧和经验1. 首先要熟悉竞赛的考试形式和内容，了解竞赛的评分标准和题目难度系数，制定科学合理的备考计划。

2. 注重基础知识的掌握，掌握牛顿力学、万有引力、能量守恒定律等基本概念和计算方法，做到熟练掌握应用。

3. 多做一些历年的竞赛试题和模拟试题，了解各种题型和难题，熟悉解题技巧，积累解题经验。

4. 训练自己的思维逻辑和分析能力，培养发现问题和解决问题的能力。

力学竞赛一般要求考生能够结合具体情况分析问题和制定解决方案，因此这方面训练非常重要。

5. 与同学、老师、专业教练等一起讨论和学习，共同探讨和解决物理难题。

参加一些物理学术会议和论坛，了解最新的物理研究成果和动态。

三、竞赛评价标准力学竞赛评价标准一般包括以下几方面：1. 基础知识和技能的掌握程度，包括牛顿力学、万有引力、能量守恒定律等基本概念和计算方法的熟练掌握，以及自由落体、弹性碰撞、动量、角动量、振动等基本物理现象的分析和解决能力。

2014年第31届全国部分地区大学生物理竞赛试卷与答案

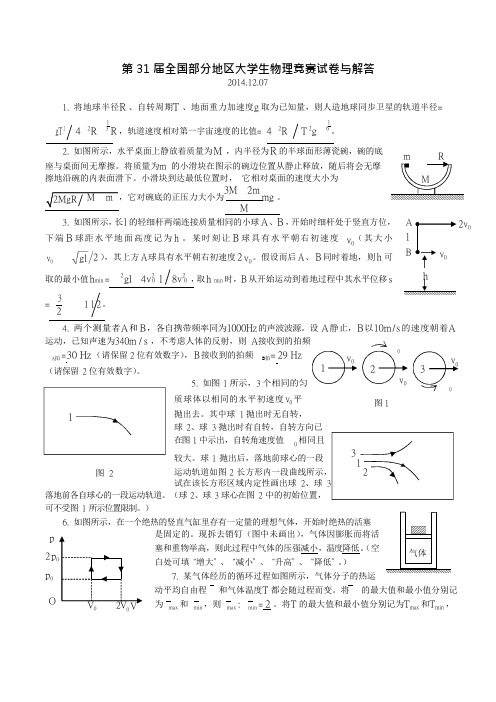
1 1 v 0 v 0 min 0 0 min 第 31 届全国部分地区大学生物理竞赛试卷与解答2014.12.071. 将地球半径R 、自转周期T 、地面重力加速度g 取为已知量，则人造地球同步卫星的轨道半径=gT 242R 3R ，轨道速度相对第一宇宙速度的比值=4 2R T 2g 62. 如图所示，水平桌面上静放着质量为M ，内半径为R 的半球面形薄瓷碗，碗的底座与桌面间无摩擦。

将质量为m 的小滑块在图示的碗边位置从静止释放，随后将会无摩擦地沿碗的内表面滑下。

小滑块到达最低位置时，它相对桌面的速度大小为3M 2mm g 。

M3. 如图所示，长l 的轻细杆两端连接质量相同的小球A 、B ，开始时细杆处于竖直方位， A 下端 B 球距水平地面高度记为 h 。

某时刻让 B 球具有水平朝右初速度（其大小 l2v 0v 0 2 ），其上方 A 球具有水平朝右初速度2。

假设而后A 、 B 同时着地，则h 可 B 取的最小值h =2 gl 4v 2l 8v 2，取h 时，B 从开始运动到着地过程中其水平位移s h4. 两个测量者A 和B ，各自携带频率同为1000Hz 的声波波源。

设 A 静止，B 以10m / s 的速度朝着A 运动，已知声速为340m / s ，不考虑人体的反射，则 A 接收到的拍频A 拍= 30 Hz （请保留 2 位有效数字），B 接收到的拍频B 拍= 29 Hz（请保留 2 位有效数字）。

图 25. 如图 1 所示，3 个相同的匀质球体以相同的水平初速度v 0 平图 1抛出去。

其中球 1 抛出时无自转，球 2、球 3 抛出时有自转，自转方向已在图 1 中示出，自转角速度值 0 相同且较大。

球 1 抛出后，落地前球心的一段31运动轨道如图 2 长方形内一段曲线所示， 2试在该长方形区域内定性画出球 2、球 3落地前各自球心的一段运动轨道。

（球 2、球 3 球心在图 2 中的初始位置，可不受图 1 所示位置限制。

十四届周培源力学竞赛题解

十四届周培源力学竞赛题解摘要：1.周培源力学竞赛概述2.竞赛题目难度及评分标准3.竞赛对学生能力的培养4.竞赛的报名方式及考试范围5.竞赛奖励及获奖名单公布6.竞赛的影响和意义正文：第十四届周培源力学竞赛是一项面向全国大学生的学科竞赛，旨在培养力学人才、服务教学、促进高等学校力学基础课程的改革与建设。

该竞赛由教育部高等教育司委托，中国力学学会和周培源基金会共同主办，全国各地的高校力学协会协办。

本次竞赛的题目难度被许多参赛者认为比清华大学出的题目还难，计算量也非常大。

根据评分标准，有得分机会的地方最多只有40 分，且可能没有同情分。

广东省上一届12 分就能获得国三，因此，本届竞赛有希望拿分的题目可能只有20 多分。

尽管题目难度较大，但竞赛对学生能力的培养是非常有益的。

它不仅能够培养学生灵活运用基础知识、分析和解决问题的能力，还可以激发学生学习力学的兴趣，发现力学创新人才。

本次竞赛采用闭卷笔试方式，考试范围包括理论力学和材料力学两门课程的理论和实验。

报名方式为加入QQ 群了解报名详情，报名截止日期为2023 年4 月14 日晚10 点。

考试将于2023 年5 月21 日在西南交通大学（犀浦校区）举行。

竞赛的奖励非常丰厚，全国竞赛个人赛特等奖5 名，一等奖0.3%（15 名），二等奖0.5%（25 名）；全国三等奖和优秀奖以各省（市）分赛区报名人数为基数，以各省（市）阅卷成绩评选出三等奖5%，优秀奖15%。

获奖者名单将在周培源大学生力学竞赛网站和《力学与实践》杂志上公布，由全国竞赛组委会授予证书。

总的来说，周培源力学竞赛对于培养力学人才、推动力学基础课程改革具有重要的影响和意义。

2014年第31届全国中学生物理竞赛复赛试题及答案(全Word版)

For personal use only in study and research; not for commercial use第31届全国中学生物理竞赛复赛理论考试试题2014年9月20日说明：所有答案（包括填空）必须写在答题纸上，写在试题纸上无效。

一、（12分）2013年6月20日，“神舟十号”女航天员王亚平在“天宫一号”目标飞行器里成功进行了我国首次太空授课. 授课中的一个实验展示了失重状态下液滴的表面张力引起的效应. 视频中可发现漂浮的液滴处于周期性的“脉动”中（平时在地球表面附近，重力的存在会导致液滴下降太快，以至于很难观察到液滴的这种“脉动”现象）. 假设液滴处于完全失重状态，液滴的上述“脉动”可视为液滴形状的周期性的微小变化（振动），如图所示. （1）该液滴处于平衡状态时的形状是__________；（2）决定该液滴振动频率f 的主要物理量是________________________________________；（3）按后面括号中提示的方法导出液滴振动频率与上述物理量的关系式.（提示：例如，若认为,,a b c 是决定该液滴振动频率的相互独立的主要物理量，可将液滴振动频率f 与,,a b c 的关系式表示为αβγ∝f a b c ，其中指数,,αβγ是相应的待定常数.）二、(16分) 一种测量理想气体的摩尔热容比/p V C C γ≡的方法（Clement-Desormes 方法）如图所示：大瓶G 内装满某种理想气体，瓶盖上通有一个灌气（放气）开关H ，另接出一根U 形管作为压强计M ．瓶内外的压强差通过U 形管右、左两管液面的高度差来确定. 初始时，瓶内外的温度相等，瓶内气体的压强比外面的大气压强稍高，记录此时U 形管液面的高度差i h ．然后打开H ，放出少量气体，当瓶内外压强相等时，即刻关闭H . 等待瓶内外温度又相等时，记录此时U 形管液面的高度差f h ．试由这两次记录的实验数据i h 和f h ，导出瓶内气体的摩尔热容比γ的表达式．（提示：放气过程时间很短，可视为无热量交换；且U 形管很细，可忽略由高差变化引起的瓶内气体在状态变化前后的体积变化）三、（20分）如图所示，一质量为m 、底边AB 长为b 、等腰边长为a 、质量均匀分布的等腰三角形平板，可绕过光滑铰链支点A 和B 的水平轴x 自由转动；图中原点O 位于AB 的中点，y 轴垂直于板面斜向上，z 轴在板面上从原点O 指向三角形顶点C .今在平板振动的液滴上任一给定点000M (,0,)x z 加一垂直于板面的拉力Q .（1）若平衡时平板与竖直方向成的角度为ϕ，求拉力Q 以及铰链支点对三角形板的作用力N A 和N B ；（2）若在三角形平板上缓慢改变拉力Q 的作用点M 的位置，使平衡时平板与竖直方向成的角度仍保持为ϕ，则改变的作用点M 形成的轨迹满足什么条件时，可使铰链支点A 或B 对板作用力的垂直平板的分量在M 变动中保持不变？四、（24分）如图所示，半径为R 、质量为m 0的光滑均匀圆环，套在光滑竖直细轴OO ￠上，可沿OO ￠轴滑动或绕OO ￠轴旋转．圆环上串着两个质量均为m 的小球. 开始时让圆环以某一角速度绕OO ￠轴转动，两小球自圆环顶端同时从静止开始释放．（1）设开始时圆环绕OO ￠轴转动的角速度为ω0，在两小球从环顶下滑过程中，应满足什么条件，圆环才有可能沿OO ￠轴上滑？（2）若小球下滑至30θ=︒（θ是过小球的圆环半径与OO ￠轴的夹角）时，圆环就开始沿OO ￠轴上滑，求开始时圆环绕OO ￠轴转动的角速度ω0、在30θ=︒时圆环绕OO ￠轴转动的角速度ω和小球相对于圆环滑动的速率v .五、（20分）如图所示，现有一圆盘状发光体，其半径为5cm ，放置在一焦距为10cm 、半径为15cm 的凸透镜前，圆盘与凸透镜的距离为20cm ，透镜后放置一半径大小可调的圆形光阑和一个接收圆盘像的光屏．图中所有光学元件相对于光轴对称放置．请在几何光学近轴范围内考虑下列问题，并忽略像差和衍射效应．（1（21）中圆盘（3）若将圆形光阑移至凸透镜后方18cm 处，回答（2）中的问题；（4）圆形光阑放置在哪些位置时，圆盘像的大小将与圆形光阑的半径有关？（5）若将图中的圆形光阑移至凸透镜前方6cm 处，回答（2）中的问题.六、（22分）如图所示，一电容器由固定在共同导电底座上的N 片可旋转金属板N +1片对顶双扇形薄金属板和固定在可旋转的导电对称轴上的N 片对顶双扇形薄金属板组成，所有顶点共轴，轴线与所有板面垂直，两组板面各自在垂直于轴线的平面上的投影重合，板面扇形半径均为R ，圆心角均为0θ（02πθπ≤<）；固定金属板和可旋转的金属板相间排列，两相邻金属板之间距离均为s ．此电容器的电容C 值与可旋转金属板的转角θ有关．已知静电力常量为k ．（1）开始时两组金属板在垂直于轴线的平面上的投影重合，忽略边缘效应，求可旋转金属板的转角为θ（00θθθ-≤≤）时电容器的电容()C θ；（2）当电容器电容接近最大时，与电动势为E 的电源接通充电（充电过程中保持可旋转金属板的转角不变），稳定后断开电源，求此时电容器极板所带电荷量和驱动可旋转金属板的力矩；（3）假设02πθ=，考虑边缘效应后，第（1）问中的()C θ可视为在其最大值和最小值之间光滑变化的函数式中，max C 可由第（1）问的结果估算，而min C 是因边缘效应计入的，它与max C 的比值λ是已知的．若转轴以角速度m ω匀速转动，且m t θω=，在极板间加一交流电压0cos V V t ω=．试计算电容器在交流电压作用下能量在一个变化周期内的平均值，并给出该平均值取最大值时所对应的m ω．七、（26分）Z-箍缩作为惯性约束核聚变的一种可能方式，近年来受到特别重视，其原理如图所示．图中，长20 mm 、直径为5m μ的钨丝组成的两个共轴的圆柱面阵列，瞬间通以超强电流，钨丝阵列在安培力的作用下以极大的加速度向内运动, 即所谓自箍缩效应；钨丝的巨大动量转移到处于阵列中心的直径为毫米量级的氘氚靶球上，可以使靶球压缩后达到高温高密度状态，实现核聚变．设内圈有N 根钨丝（可视为长直导线）均匀地分布在半径为r 的圆周上，通有总电流7210A =⨯内I ；外圈有M 根钨丝，均匀地分布在半径为R 的圆周上，每根钨丝所通过的电流同内圈钨丝．已知通有电流i 的长直导线在距其r 处产生的磁感应强度大小为m ik r，式中比例常量772210T m/A 210N /A m k --=⨯⋅=⨯．（1）若不考虑外圈钨丝，计算内圈某一根通电钨丝中间长为L ∆的一小段钨丝所受到的安培力；（2）若不考虑外圈钨丝，内圈钨丝阵列熔化后形成了圆柱面，且箍缩为半径0.25cm r =的圆柱面时，求柱面上单位面积所受到的安培力，这相当于多少个大气压？（3）证明沿柱轴方向通有均匀电流的长圆柱面，圆柱面内磁场为零，即通有均匀电流外圈钨丝的存在不改变前述两小题的结果；（4）当1N >>时, 则通有均匀电流的内圈钨丝在外圈钨丝处的磁感应强度大小为m Ik R内，若要求外圈钨丝柱面每单位面积所受到的安培力大于内圈钨丝柱面每单位面积所受到的安培力，求外圈钨丝圆柱面的半径R 应满足的条件；（5）由安培环路定理可得沿柱轴方向通有均匀电流的长圆柱面外的磁场等于该圆柱面上所有电流移至圆柱轴后产生的磁场，请用其他方法证明此结论. （计算中可不考虑图中支架的影响）八、（20分）天文观测表明，远处的星系均离我们而去．着名的哈勃定律指出，星系离开我们的速度大小v =HD ，其中D 为星系与我们之间的距离，该距离通常以百万秒差距（Mpc ）为单位；H 为哈勃常数，最新的测量结果为H =67.80km/(s ⋅Mpc)．当星系离开我们远去时，它发出的光谱线的波长会变长（称为红移）．红移量z 被定义为λλλ'-=z ，其中λ￠是我们观测到的星系中某恒星发出的谱线的波长，而λ是实验室中测得的同种原子发出的相应的谱线的波长，该红移可用多普勒效应解释．绝大部分星系的红移量z 远小于1，即星系退行的速度远小于光速．在一次天文观测中发现从天鹰座的一个星系中射来的氢原子光谱中有两条谱线，它们的频率ν'分别为4.549⨯1014Hz 和6.141⨯1014Hz ．由于这两条谱线处于可见光频率区间，可假设它们属于氢原子的巴尔末系，即为由n > 2的能级向k =2的能级跃迁而产生的光谱．（已知氢原子的基态能量013.60 eV =-E ，真空中光速82.99810m/s =⨯c ，普朗克常量346.62610J s -=⨯⋅h ，电子电荷量19 1.60210C -=⨯e ）（1）该星系发出的光谱线对应于实验室中测出的氢原子的哪两条谱线？它们在实验室中的波长分别是多少？（2）求该星系发出的光谱线的红移量z 和该星系远离我们的速度大小v ；（3）求该星系与我们的距离D ．第31届全国中学生物理竞赛复赛理论考试试题解答2014年9月20日一、（12分）（1）球形（2）液滴的半径r 、密度ρ和表面张力系数σ（或液滴的质量m 和表面张力系数σ）（3）解法一假设液滴振动频率与上述物理量的关系式为αβγρσ=f k r ①式中，比例系数k 是一个待定常数. 任一物理量a 可写成在某一单位制中的单位[]a 和相应的数值{}a 的乘积{}[]=a a a . 按照这一约定，①式在同一单位制中可写成由于取同一单位制，上述等式可分解为相互独立的数值等式和单位等式，因而 [][][][]αβγρσ=f r ② 力学的基本物理量有三个：质量m 、长度l 和时间t ，按照前述约定，在该单位制中有 {}[]=m m m ，{}[]=l l l ，{}[]=t t t 于是[][]-=f t 1 ③ [][]=r l ④ [][][]ρ-=m l 3 ⑤将③④⑤⑥式代入②式得即[][][][]αββγγ--+-=t l m t 132 ⑦ 由于在力学中[]m 、[]l 和[]t 三者之间的相互独立性，有30αβ-=， ⑧ 0βγ+=， ⑨ 21γ= ⑩ 解为311,,222αβγ=-=-= ?将?式代入①式得=f ? 解法二假设液滴振动频率与上述物理量的关系式为αβγρσ=f k r ①式中，比例系数k 是一个待定常数. 任一物理量a 可写成在某一单位制中的单位[]a 和相应的数值{}a 的乘积{}[]=a a a . 在同一单位制中，①式两边的物理量的单位的乘积必须相等[][][][]αβγρσ=f r ②力学的基本物理量有三个：质量M 、长度L 和时间T ，对应的国际单位分别为千克（kg ）、米（m ）、秒（s ）. 在国际单位制中，振动频率f 的单位[]f 为s -1，半径r 的单位[]r 为m ，密度ρ的单位[]ρ为3kg m -⋅，表面张力系数σ的单位[]σ为1212N m =kg (m s )m kg s ----⋅⋅⋅⋅=⋅，即有[]s -=f 1 ③ []m =r ④ []kg m ρ-=⋅3 ⑤ []kg s σ-=⋅2 ⑥ 若要使①式成立，必须满足()()s m kg m kg s (kg)m s βγαβγαβγ---+--=⋅⋅=⋅⋅13232 ⑦由于在力学中质量M 、长度L 和时间T 的单位三者之间的相互独立性，有0βγ+=， ⑨ 21γ= ⑩ 解为311,,222αβγ=-=-= ?将?式代入①式得f = ? 评分标准：本题12分. 第（1）问2分，答案正确2分；第（2）问3分，答案正确3分；第（3）问7分，⑦式2分，?式3分，?式2分（答案为f、f =f 也给这2分）.二、(16分)解法一：瓶内理想气体经历如下两个气体过程：其中，000000(,,,),(,,,,,,)i i f f f p V T N p V T N p V T N )和(分别是瓶内气体在初态、中间态与末态的压强、体积、温度和摩尔数．根据理想气体方程pV NkT =，考虑到由于气体初、末态的体积和温度相等，有f f iip N p N =①另一方面，设V '是初态气体在保持其摩尔数不变的条件下绝热膨胀到压强为0p 时的体积，即此绝热过程满足1/00i V p V p γ⎛⎫= ⎪'⎝⎭②由状态方程有0i p V N kT '=和00f p V N kT =，所以 0f iN V N V ='③联立①②③式得1/0fi i p p p p γ⎛⎫= ⎪⎝⎭④ 此即lnln i i fp p p p γ=⑤由力学平衡条件有0i i p p gh ρ=+ ⑥0f f p p gh ρ=+ ⑦式中，00p gh ρ=为瓶外的大气压强，ρ是U 形管中液体的密度，g 是重力加速度的大小.由⑤⑥⑦式得00ln(1)ln(1)ln(1)if i h h h hh h γ+=+-+⑧利用近似关系式：1, ln(1)xx x +≈当，以及 0/1, /1i f h h h h ，有000///i ii f i fh h h h h h h h h γ==--⑨评分标准：本题16分．①②③⑤⑥⑦⑧⑨式各2分．解法二：若仅考虑留在容器内的气体：它首先经历了一个绝热膨胀过程ab ，再通过等容升温过程bc 达到末态其中，100000(,,),(,,,,)i f p V T p V T p V T )和(分别是留在瓶内的气体在初态、中间态和末态的压强、体积与温度．留在瓶内的气体先后满足绝热方程和等容过程方程1100ab: γγγγ----=i p T p T①00bc://=f p T p T②由①②式得1/0fi i p p p p γ⎛⎫= ⎪⎝⎭③ 此即lnln i i fp p p p γ=④由力学平衡条件有0i i p p gh ρ=+ ⑤0f f p p gh ρ=+ ⑥式中，00p gh ρ=为瓶外的大气压强，ρ是U 形管中液体的密度，g 是重力加速度的大小．由④⑤⑥式得00ln(1)ln(1)ln(1)if i h h hh h γ+=+-+⑦利用近似关系式：1, ln(1)xx x +≈当，以及 0/1, /1i f h h h h ，有000///i ii f i fh h h h h h h h h γ==--⑧评分标准：本题16分．①②式各3分，④⑤⑥⑦⑧式各2分．三、（20分）（1）平板受到重力C P 、拉力0M Q 、铰链对三角形板的作用力N A 和N B ，各力及其作用点的坐标分别为：C (0,sin ,cos )ϕϕ=--mg mg P ，(0,0,)h ；0M (0,,0)Q =Q ， 00(,0,)x z ；A A A A (,,)x y z N N N =N ，(,0,0)2b； B B B B (,,)x y z N N N =N ， (,0,0)2b-式中是平板质心到x 轴的距离.平板所受力和（对O 点的）力矩的平衡方程为A B x0=+=∑xxF N N① A B sin 0ϕ=++-=∑yyyF Q N N mg② A B cos 0ϕ=+-=∑zzzF N N mg③ 0sin 0xM mgh Q z ϕ=-⋅=∑④ B A 022=-=∑y zz b bM N N⑤0A B 022z yy b bM Q x N N =⋅+-=∑⑥联立以上各式解得sin mgh Q z ϕ=， A B x x N N =-，000sin 21()2Ay mg h b x N b z z ϕ⎡⎤=-+⎢⎥⎣⎦，000sin 21()2By mg h b x N b z z ϕ⎡⎤=--⎢⎥⎣⎦即0M 0sin (0,,0)mgh z ϕ=Q ，⑦0A A 002sin 1(,1(),cos )22x x mg h b N mg b z z ϕϕ⎡⎤=-+⎢⎥⎣⎦N ，⑧0B A 002sin 1(,1(),cos )22x x mg h b N mg b z z ϕϕ⎡⎤=---⎢⎥⎣⎦N⑨（2）如果希望在M(,0,)x z 点的位置从点000M (,0,)x z 缓慢改变的过程中，可以使铰链支点对板的作用力By N 保持不变，则需 sin 21()2By mg h b x N b z z ϕ⎡⎤=--=⎢⎥⎣⎦常量 ⑩M 点移动的起始位置为0M ，由⑩式得0022-=-b x b x z z z z? 或00022b x b x zz z ⎛⎫-=- ⎪⎝⎭ ? 这是过A(,0,0)2b 点的直线. (*)因此，当力M Q 的作用点M 的位置沿通过A 点任一条射线(不包含A 点)在平板上缓慢改变时，铰链支点B 对板的作用力By N 保持不变. 同理，当力M Q 的作用点M 沿通过B 点任一条射线在平板上缓慢改变时，铰链支点A 对板的作用力Ay N 保持不变. 评分标准：本题20分．第（1）问14分，①式1分，②③④⑤⑥式各2分，⑦⑧⑨式各1分；第（2）问6分，⑩?式各1分，(*) 2分，结论正确2分. 四、（24分）（1）考虑小球沿径向的合加速度. 如图，设小球下滑至? 角位置时，小球相对于圆环的速率为v ，圆环绕轴转动的角速度为? ．此时与速率v 对应的指向中心C 的小球加速度大小为 21a R=v① 同时，对应于圆环角速度?，指向OO ?轴的小球加速度大小为2(sin )sin R a R ωωθθ= ②该加速度的指向中心C 的分量为22(sin )sin R a a R ωωθθ== ③该加速度的沿环面且与半径垂直的分量为23(sin )cos cot R a a Rωωθθθ== ④由①③式和加速度合成法则得小球下滑至? 角位置时，其指向中心C 的合加速度大小为2212(sin )v ωθ=+=+R R a a a R R⑤在小球下滑至? 角位置时，将圆环对小球的正压力分解成指向环心的方向的分量N 、垂直于环面的方向的分量T . 值得指出的是：由于不存在摩擦，圆环对小球的正压力沿环的切向的分量为零. 在运动过程中小球受到的作用力是N 、T 和mg . 这些力可分成相互垂直的三个方向上的分量：在径向的分量不改变小球速度的大小，亦不改变小球对转轴的角动量；沿环切向的分量即sin θmg 要改变小球速度的大小；在垂直于环面方向的分量即T 要改变小球对转轴的角动量，其反作用力将改变环对转轴的角动量，但与大圆环沿'OO 轴的竖直运动无关. 在指向环心的方向，由牛顿第二定律有22(sin )cos R R N mg ma mRωθθ++==v ⑥ 合外力矩为零，系统角动量守恒，有202(sin )L L m R θω=+ ⑦式中L 0和L 分别为圆环以角速度?0和?转动时的角动量．如图，考虑右半圆环相对于轴的角动量，在?角位置处取角度增量??，圆心角??所对圆弧l ∆的质量为m l λ∆=∆（02m Rλπ≡），其角动量为 2sin L m r l rR Rr z R S ωλωθλωλω∆=∆=∆=∆=∆ ⑧式中r 是圆环上? 角位置到竖直轴OO ?的距离，S ∆为两虚线间窄条的面积．⑧式说明，圆弧l ∆的角动量与S ∆成正比. 整个圆环（两个半圆环）的角动量为2200122222m R L L R m R R πωωπ=∆=⨯=∑ ⑨[或：由转动惯量的定义可知圆环绕竖直轴OO ?的转动惯量J 等于其绕过垂直于圆环平面的对称轴的转动惯量的一半，即2012J m R = ⑧则角动量L 为2012L J m R ωω== ⑨ ]同理有200012L m R ω= ⑩力N 及其反作用力不做功；而T 及其反作用力的作用点无相对移动，做功之和为零；系统机械能守恒. 故22012(1cos )2[(sin )]2k k E E mgR m R θωθ-+⨯-=⨯+v ?式中0k E 和k E 分别为圆环以角速度0ω和ω转动时的动能．圆弧l ∆的动能为整个圆环（两个半圆环）的动能为22220011222224k k m R E E R m R R πωωπ=∆=⋅⋅⋅⋅=∑ ? [或：圆环的转动动能为22201124k E J m R ωω== ? ]同理有2200014k E m R ω= ?根据牛顿第三定律，圆环受到小球的竖直向上作用力大小为2cos N θ，当02cos N m g θ≥ ?时，圆环才能沿轴上滑．由⑥⑦⑨⑩?? ?式可知，?式可写成2220000220cos 6cos 4cos 102(4sin )ωθθθθ⎡⎤-+--≤⎢⎥+⎣⎦m R m m m m gm m ?式中，g 是重力加速度的大小.（2）此时由题给条件可知当=30θ︒时，?式中等号成立，即有或00(m m ω=+ ?由⑦⑨⑩?式和题给条件得0000200+4sin +m m m m m m ωωωθ=== ? 由?????式和题给条件得v ?评分标准：本题24分．第（1）问18分，①②③④⑤式各1分，⑥⑦式各2分，⑨⑩式各1分，?式2分，??式各1分，?式2分，?式1分；第（2）问6分，???式各2分．五、（20分）（1）设圆盘像到薄凸透镜的距离为v . 由题意知：20cm u =, 10cm f =，代入透镜成像公式111u f+=v ① 得像距为20cm =v ② 其横向放大率为1uβ=-=-v③ 可知圆盘像在凸透镜右边20cm ，半径为5cm ，为圆盘状，圆盘与其像大小一样. （2）如下图所示，连接A 、B 两点，连线AB 与光轴交点为C 点，由两个相似三角形AOC ∆与BB'C ∆的关系可求得C 点距离透镜为15cm. 1分若将圆形光阑放置于凸透镜后方6cm 处，此时圆形光阑在C 点左侧. 1分当圆形光阑半径逐渐减小时，均应有光线能通过圆形光阑在B 点成像，因而圆盘像的形状及大小不变，而亮度变暗. 2分此时不存在圆形光阑半径a r 使得圆盘像大小的半径变为（1）中圆盘像大小的半径的一半．1分（3）若将圆形光阑移至凸透镜后方18cm 处，此时圆形光阑在C 点（距离透镜为15cm ）的右侧. 由下图所示，此时有:利用两个相似三角形CRR'∆与CBB'∆的关系，得 CR'52RR'=BB'=5cm 3cm CB'5r -=⨯⨯= ④ 可见当圆盘半径3cm r =（光阑边缘与AB 相交）时，圆盘刚好能成完整像，但其亮度变暗． 4分若进一步减少光阑半径，圆盘像就会减小．当透镜上任何一点发出的光都无法透过光阑照在原先像的一半高度处时，圆盘像的半径就会减小为一半，如下图所示．此时光阑边缘与AE相交，AE 与光轴的交点为D ，由几何关系算得D 与像的轴上距离为207cm. 此时有利用两个相似三角形DRR'∆与DEE'∆的关系，得 D R '20/72R R '=E E '= 2.5c m 0.75c m D E '20/7a r -=⨯⨯= ⑤ACOBB' CRBR'B'可见当圆形光阑半径a r =0.75cm ，圆盘像大小的半径的确变为（1）中圆盘像大小的半径的一半． 3分（4）只要圆形光阑放在C 点（距离透镜为15cm ）和光屏之间，圆盘像的大小便与圆形光阑半径有关． 2分（5）若将图中的圆形光阑移至凸透镜前方6cm 处，则当圆形光阑半径逐渐减小时，圆盘像的形状及大小不变，亮度变暗； 2分同时不存在圆形光阑半径使得圆盘像大小的半径变为（1）中圆盘像大小的半径的一半． 1分评分标准：第（1）问3分，正确给出圆盘像的位置、大小、形状，各1分；第（2）问5分，4个给分点分别为1、1、2、1分；第（3）问7分，2个给分点分别为2、3分；第（4）问2分，1个给分点为2分；第（5）问3分，2个给分点分别为2、1分．六、（22分）（1）整个电容器相当于2N 个相同的电容器并联，可旋转金属板的转角为θ时1()2()C NC θθ=①式中1()C θ为两相邻正、负极板之间的电容1()()4A C ksθθπ=②这里，()A θ是两相邻正负极板之间相互重迭的面积，有2000200200200012(2), 212(), 02()12(), 0212(2), 2R R A R R θπθθθπθθθπθθθθθπθθππθθθ⎧⨯--≤≤-⎪⎪⎪⨯+-≤≤⎪=⎨⎪⨯-≤≤-⎪⎪⎪⨯--<<⎩当当当当③由②③式得2000200120020001(2), 41(), 04()1(), 041(2), 4R ks R ksC R ks R ksθπθθθππθθθπθπθθθθπθπθππθθθπ⎧--≤≤-⎪⎪⎪+-≤≤⎪=⎨⎪-≤≤-⎪⎪⎪--<<⎩当当当当④由①④式得DRER' E'20002002002000(2), 2(), 02()(), 02(2), 2N R ks N R ks C N R ks N R ksθπθθθππθθθπθπθθθθπθπθππθθθπ⎧--≤≤-⎪⎪⎪+-≤≤⎪=⎨⎪-≤≤-⎪⎪⎪--<<⎩当当当当⑤（2）当电容器两极板加上直流电势差E 后，电容器所带电荷为()()θθ=Q C E⑥当0θ=时，电容器电容达到最大值max C ，由⑤式得20max2NR C ksθπ=⑦充电稳定后电容器所带电荷也达到最大值max Q ，由⑥式得20max2NR Q E ksθπ= ⑧断开电源，在转角θ取0θ=附近的任意值时，由⑤⑧式得，电容器内所储存的能量为2222max 0000() 2()4()θθθθπθθπθθ==-≤≤--Q NR E U C ks 当⑨设可旋转金属板所受力矩为()T θ（它是由若干作用在可旋转金属板上外力i F 产生的，不失普遍性，可认为i F 的方向垂直于转轴，其作用点到旋转轴的距离为i r ，其值i F 的正负与可旋转金属板所受力矩的正负一致），当金属板旋转θ∆（即从θ变为θθ+∆）后，电容器内所储存的能量增加U ∆，则由功能原理有()()()θθθθ∆=∆=∆=∆∑∑i i i i T Fr F l U⑩式中，由⑨⑩式得22200020()() 4()θθθθθπθθπθθ∆==-≤≤-∆-NR E U T ks 当?当电容器电容最大时，充电后转动可旋转金属板的力矩为2204θθπ=∆⎛⎫== ⎪∆⎝⎭U NR E T ks ?（3）当0cos V V t ω=，则其电容器所储存能量为[]222max min max min 02max min max min 020max min max min max min max min 2012111()()cos2cos 222111()()cos2(1cos2)422()()cos2()cos2()cos2cos28{(8m m m m U CV C C C C t V t C C C C t V t V C C C C t C C t C C t t V ωωωωωωωω=⎡⎤=++-⎢⎥⎣⎦⎡⎤=++-+⎢⎥⎣⎦=++++-+-=max min max min max min max min )()cos2()cos21()[cos2()cos2()]}2m m m C C C C t C C t C C t t ωωωωωω++++-+-++- ?由于边缘效应引起的附加电容远小于max C ，因而可用⑦式估算max C ．如果m ωω≠，利用⑦式和题设条件以及周期平均值公式cos2=0 cos2=0, cos2()=0, cos2()=0m m m t t t t ωωωωωω+-,?可得电容器所储存能量的周期平均值为2221max min 001(1)()832NR U C C V V ksλ+=+=?如果m ωω=，?式中第4式右端不是零，而是1．利用⑦式和题设条件以及周期平均值公式的前3式得电容器所储存能量的周期平均值为222222max min 0max min 0max min 00111(3)()()(3)8161664NR U C C V C C V C C V V ks λ+=++-=+= ?由于边缘效应引起的附加电容与忽略边缘效应的电容是并联的，因而max C 应比用⑦式估计max C 大；这一效应同样使得min 0C >；可假设实际的max min ()C C -近似等于用⑦式估计max C ．如果m ωω≠，利用⑦式和题设条件以及周期平均值公式cos2=0 cos2=0, cos2()=0, cos2()=0m m m t t t t ωωωωωω+-,?可得电容器所储存能量的周期平均值为2221max min 001(12)()832NR U C C V V ksλ+=+=?[如果m ωω=，?中第4式右端不是零，而是1．利用⑦式和题设条件以及周期平均值公式?的前3式得电容器所储存能量的周期平均值为 222222max min 0max min 0max min 00111(34)()()(3)8161664NR U C C V C C V C C V V ksλ+=++-=+= ?]212 U U U >因为，则最大值为，所对应的m ω为m ωω=?评分标准：本题22分．第（1）问6分，①②式各1分，③⑤式各2分；第（2）问9分，⑥⑦⑧⑨⑩式各1分（⑩式中没有求和号的，也同样给分；没有力的符号，也给分），??式各2分；第（3）问7分，??式各2分，???式各1分．七、（26分）（1）通有电流i 的钨丝（长直导线）在距其r 处产生的磁感应强度的大小为m iB k r =① 由右手螺旋定则可知，相应的磁感线是在垂直于钨丝的平面上以钨丝为对称轴的圆，磁感应强度的方向沿圆弧在该点的切向，它与电流i 的方向成右手螺旋．两根相距为d 的载流钨丝（如图（a ））间的安培力是相互吸引力，大小为2m k Li F B Li d∆=∆=② 考虑某根载流钨丝所受到的所有其他载流钨丝对它施加的安培力的合力．由系统的对称性可知，每根钨丝受到的合力方向都指向轴心；我们只要将其他钨丝对它的吸引力在径向的分量叠加即可．如图，设两根载流钨丝到轴心连线间的夹角为ϕ，则它们间的距离为2sin2d r ϕ=③由②③式可知，两根载流钨丝之间的安培力在径向的分量为22sin 2sin(/2)22m m r k Li k Li F r rϕϕ∆∆== ④它与ϕ无关，也就是说虽然处于圆周不同位置的载流钨丝对某根载流钨丝的安培力大小和方向均不同，但在径向方向上的分量大小却是一样的；而垂直于径向方向的力相互抵消．因此，某根载流钨丝所受到的所有其他载流钨丝对它施加的安培力的合力为222(1)(1)22-∆-∆==m m N k L I N k Li F r rN 内⑤ 其方向指向轴心．（2）由系统的对称性可知，所考虑的圆柱面上各处单位面积所受的安培力的合力大小相等，方向与柱轴垂直，且指向柱轴．所考虑的圆柱面，可视为由很多钨丝排布而成，N 很大，但总电流不变．圆柱面上ϕ∆角对应的柱面面积为s r L ϕ=∆∆⑥ 圆柱面上单位面积所受的安培力的合力为22(1)24m N N k Li N F P s r Lϕππ-∆∆==∆⑦由于1N ，有22(1)-=N N i I 内 ⑧ 由⑦⑧式得224π=m k I P r 内⑨ 代入题给数据得1221.0210N/m P =⨯ ⑩ 一个大气压约为5210N/m ，所以710atm P ≈ ?即相当于一千万大气压．图(a)（3）考虑均匀通电的长直圆柱面内任意一点A 的磁场强度. 根据对称性可知，其磁场如果不为零，方向一定在过A 点且平行于通电圆柱的横截面. 在A 点所在的通电圆柱的横截面（纸面上的圆）内，过A 点作两条相互间夹角为微小角度θ∆的直线，在圆上截取两段微小圆弧L 1和L 2，如图（b ）所示. 由几何关系以及钨丝在圆周上排布的均匀性，通过L 1和L 2段的电流之比/I I 12等于它们到A 点的距离之比/l l 12：111222==I L l I L l ? 式中，因此有1212=m m I I k k l l ? 即通过两段微小圆弧在A 点产生的磁场大小相同，方向相反，相互抵消．整个圆周可以分为许多“对”这样的圆弧段，因此通电的外圈钨丝圆柱面在其内部产生的磁场为零，所以通电外圈钨丝的存在，不改变前述两小题的结果．（4）由题中给出的已知规律，内圈电流在外圈钨丝所在处的磁场为=m IB k R内? 方向在外圈钨丝阵列与其横截面的交点构成的圆周的切线方向，由右手螺旋法则确定．外圈钨丝的任一根载流钨丝所受到的所有其他载流钨丝对它施加的安培力的合力为222(1)(2)+ 22-∆∆+=∆=m m m M k L I I k I k L I I I F L RM M R RM外外内外内外外 ?式中第一个等号右边的第一项可直接由⑤式类比而得到，第二项由?式和安培力公式得到.因此圆柱面上单位面积所受的安培力的合力为22(2)24ϕπϕπ+∆==∆∆外外内外外m F k I I I M P R L R ? 若要求2222244ππ+>外内外内（）m m k I I I k I R r ? 只需满足<R r ?（5）考虑均匀通电的长直圆柱面外任意一点C 的磁场强度. 根据对称性可知，长直圆柱面上的均匀电流在该点的磁场方向一定在过C 点且平行于通电圆柱的横截面（纸面上的圆），与圆的径向垂直，满足右手螺旋法则. 在C 点所在的通电圆柱的横截面内，过C 点作两条相互间夹角为微小角度θ∆的直线，在圆上截取两段微小圆弧3L 和4L ，如图（c ）所示. 由几何关系以及电流在圆周上排布的均匀性，穿过3L 和4L 段的电流之比34/I I 等于它们到C 点的距离之比34/l l ：333444I L l I L l == ? 式中，33CL l =，44CL l =，CO l =. 由此得33443434I I I I l l l l +==+ ?考虑到磁场分布的对称性，全部电流在C 点的磁感应强度应与CO 垂直. 穿过3L 和4L 段的电流在C 点产生的磁感应强度的垂直于CO 的分量之和为设过C 点所作的直线34CL L 与直线CO 的夹角为θ，直线34CL L 与圆的半径4OL 的夹角为α（此时，将微小弧元视为点）. 由正弦定理有。

2014年湖南省第十届力学竞赛竞赛试题备选

2014年湖南省第十届力学竞赛竞赛试题备选
一．对称桁架，受载荷P作用。

已知各杆材料相同，横截面面积也相同。

材料许用应力为[σ]，横截面面积为A，杆长及角度如图所示。

1，在准确加工、装配的情况下，桁架中各杆的受力为F N1=F N2= （1分），F N3= （1分）
为了使各杆同时到达材料的许用应力[σ]，我们采用加装配应力的办法，即预先将杆3做长δ，在进行强制装配。

2，δ与各杆伸长量之间满足的协调方程是：（2分）
3，δ= （2分）
4，此时，该桁架能承受的最大载荷为[P]= （2分）
解答：
二．简支梁AB，跨度为4a，离某一刚性水平面的距离为δ0，当作用于梁上的两个载荷P逐渐增加时，迫使梁的中间段CD与平面A'B'接触。

已知δ0，EI及接触段长度a
1.载荷P= （3分）
2.梁A端的转角θA= （3分）
解答：。

第十三届全国大学生力学竞赛试题

第一部分基础题部分（共60 分）第1 题 (18分)铅垂面内的机构如图所示，由直角杆ABC 、A 1BC 1、CDE 、C 1DE 1铰接而成，销钉A 1可沿固定水平滑槽运动，AB=BC=A 1B= BC 1=CD= C 1D=a ，DE= DE 1=2a 。

1）已知图示瞬时AB 与水平线AA 1的夹角为φ，ABC 的角速度为ω，求CDE 和C 1DE 1的角速度CDE ω、11C DE ω；（5分）2）已知ABC 上作用力偶M ，E 和E 1点通过刚度为k 、原长为2a 的弹簧连接，均质杆DE 和DE 1的质量均为m ，忽略其它杆的质量和各处摩擦。

为使系统在45ϕ=的位置平衡，求销钉A 1上的水平力F ；（5分）3）若在上述平衡位置突然撤去力F ，求该瞬时ABC 的角加速度ABC α。

（8分）第1题图ABCDC 1A 1E ω kφFM图(a)为可在火星上滚动的无轮缘车轮，由n 根直杆在中点固结而成。

假设n =3，各杆质量均为2m 、长度均为2R ，相邻杆间的夹角均为600，如图(b)所示。

车轮在铅垂面内向右滚动，杆件各端点依次与路面发生完全塑性碰撞，且不发生相对滑动。

端点A 与路面碰撞前、后瞬时车轮的角速度分别记为0A ω、1A ω，端点B 与路面碰撞前、后瞬时车轮的角速度分别记为0B ω、1B ω。

已知重力加速度为g 。

1）求1B ω与0B ω的比值；（3分）2）如图(b)所示，假设路面上与端点A 、B 、C 碰撞的三个点位于同一高度，求车轮能够由图中实线位置滚动到虚线位置的1A ω的最小值；（4分）3）车轮沿倾角为θ（30θ<）的斜面向下滚动，如图(c)所示，为使11=B A ωω，求θ应满足的关系式。

（5分）（a ）（b ）（c ）第2题图BFOAB ＇＇A ＇C ＇O ＇ωA 1ABCDEFOθωA 1平面杆系结构由四根材料相同的圆截面直杆组成，其中杆AC与杆BC长度相同、直径均为d1=20mm，杆CD与杆CE长度相同、直径均为d2=40mm，设计尺寸如图（a）所示。

力学竞赛考试范围2014