弹性力学常用公式
弹性力学公式

2°斜截面上的正应力:全应力矢量p N 在外法线方向n 上的投影即为斜截面上的正应力σN :=r r m n ⋅r r r r r r nσ=n p n ⋅()()x y z p ip j p k li j k ++++(){}{}x T x y z y n p p l p m p n lmn p n p ⎧⎫⎪⎪=++==⎨⎬l zx yxx ττσ⎫⎧⎟⎞⎜⎛z p ⎪⎪⎩⎭}){(}{)(n n n m n ml ij Tzyzxzzy y xyσστττστ=⎪⎭⎪⎬⎪⎩⎪⎨⎟⎟⎠⎜⎜⎝=即}){(}{n n ij T N σσ=(2-15)j 3°斜截面上的切应力:全应力矢量p N 在斜截面内的投影即斜截面上的切应力分量为:||n n n p τ=×r r ++216或2222222()()n n n x y z x y z p p p p p l p m p n τσ=−=++−(2-16)τxσz4-4、弹塑性力学中常用的简化力学模型44、弹塑性力学中常用的简化力学模型σA B分析计算有困难与实际符合较好1、理想弹塑性模型:o εεsσ⎨⎧>=≤=ss sE E εεεσεεεσ当当s理想弹塑性力学模型⎩Bσ1tg −2、线性强化弹塑性力学模型As σ1E 计算复杂⎨⎧>−+=≤=ss s s E E εεεεσσεεεσ当当)(1εoEtg 1−sε⎩型线性强化弹塑性力学模3、幂强化力学模型:σ1=n 参数少想弹性模型n A n<<=εσ100=n 便于分析理想塑性模型当理想弹性模型当A n A n ====σεσ01ε1幂强化力学模型4、刚塑性力学模型(理想塑性模型)在应力到达屈服极限之前应变为零。
AσB分析计算容易oε刚塑性力学模型5σ(刚塑性力学模型)5.理想塑性力学模型σssσσ=ε6.σ6.理想弹性力学模型εσE =ε4-6、常用屈服条件:对屈服条件的研究已有两个世纪。
弹力功的公式

弹力功的公式弹性功可以通过公式来进行描述和计算,其公式可以根据物体受力的不同情况而有所不同。
在本文中,我们将探讨弹力功的相关公式,并对其进行详细介绍。
弹性功的一般定义在弹性力学中,弹性功通常被定义为物体受力变形过程中存储的能量。
当物体受到外力作用时,如果发生弹性变形,就会产生弹性势能,这部分能量就是弹性功。
弹性功的计算一般可以通过外力对物体做功的计算来实现。
弹性功的一般公式弹性功的一般公式可以表示为:\[W = \int F \cdot dx\]在这里,W代表弹性功,F代表外力,dx代表物体在受力作用下发生的位移。
根据这个公式,我们可以将物体在受力变形过程中所做的功来计算弹性功。
弹性势能与弹性功在弹性力学中,物体受到外力会产生弹性变形,而这部分变形会使得物体产生弹性势能。
而弹性功就是描述这部分弹性势能的能量转换和传递。
当物体受到外力变形时,就会存储一定的弹性势能,这部分势能可以通过弹性功来计算。
同时,在物体发生弹性恢复时,这部分势能就会转化为弹性功来完成能量的传递。
当物体的变形是弹性的时,可以使用弹性势能的表达式来计算弹性功。
弹性势能的一般表达式可以描述为:\[PE = \frac{1}{2} kx^2\]在这里,PE代表弹性势能,k代表弹簧系数,x代表物体在受力作用下的位移。
在这个表达式中,我们可以看到弹性势能与物体的位移的平方成正比,这也就说明了弹性势能与物体受力变形的程度相关。
对于弹性势能,我们可以通过对其微分来得到弹性力的表达式,其一般可以表示为:\[F = -\frac{dPE}{dx} = -kx\]在这个表达式中,F代表弹性力,k代表弹簧系数,x代表物体的位移。
这个表达式也说明了弹性力与物体位移成反比,而且符合胡克定律的描述。
弹性力与物体的位移方向相反,并且与位移成线性关系。
将上述弹性势能的表达式代入到弹性功的一般表达式中,我们可以得到弹性功与外力作用下的物体位移的公式:\[W = \int F \cdot dx = \int (-kx) \cdot dx\]通过对上述积分表达式的计算,我们可以得到物体受力变形过程中存储的弹性功。
弹性力学公式范文

弹性力学公式范文弹性力学是研究材料在外力作用下的变形和恢复能力的一门学科。
弹性力学公式描述了材料的弹性性质和力学行为。
以下是一些常用的弹性力学公式:1. Hooke定律:Hooke定律描述了线弹性材料在小变形范围内的应力-应变关系。
它可以表示为:σ=Eε其中σ是应力,E是弹性模量,ε是应变。
2.应变能密度:弹性体变形时,有一部分外力的功以弹性能量的形式储存。
应变能密度U可以通过以下公式计算:U=(1/2)σε其中σ是应力,ε是应变。
3.杨氏模量:杨氏模量是度量材料在受拉应力下的刚性程度的物理量。
它可以表示为:E=σ/ε其中E是杨氏模量,σ是应力,ε是应变。
4.剪切模量:剪切模量是度量材料在受剪应力下的变形程度的物理量。
它可以表示为:G=τ/ε其中G是剪切模量,τ是剪切应力,ε是应变。
5.泊松比:泊松比是表示材料在受拉应力下沿垂直方向收缩的程度的无量纲物理量。
它可以表示为:ν=-ε_t/ε_l其中ν是泊松比,ε_t是横向应变,ε_l是纵向应变。
6.拉伸应变:拉伸应变是材料在受拉应力下的线性变形程度的物理量。
它可以表示为:ε=(L-L_0)/L_0其中ε是拉伸应变,L是材料受拉时的长度,L_0是未受拉时的长度。
7.压缩应变:压缩应变是材料在受压应力下的线性变形程度的物理量。
它可以表示为:ε=(L_0-L)/L_0其中ε是压缩应变,L是材料受压时的长度,L_0是未受压时的长度。
8.杨氏弹性模量:杨氏弹性模量是一种描述材料刚性程度的物理量,它可以表示为:E=(σ_2-σ_1)/(ε_2-ε_1)其中E是杨氏弹性模量,σ_2和σ_1分别是应力的最大值和最小值,ε_2和ε_1分别是相应的应变的最大值和最小值。
9.线性弹性模量:线性弹性模量是材料在小应变范围内的弹性行为的物理量。
它可以表示为:E=σ/ε其中E是线性弹性模量,σ是应力,ε是应变。
10.应力张量:应力张量描述了材料中各个方向上的内部力状态。
它可以表示为:σ=[σ_11σ_12σ_13;σ_21σ_22σ_23;σ_31σ_32σ_33]其中σ是应力张量,σ_ij是各个分量。
弹性力学公式

2°斜截面上的正应力:全应力矢量p N 在外法线方向n 上的投影即为斜截面上的正应力σN :=r r m n ⋅r r r r r r nσ=n p n ⋅()()x y z p ip j p k li j k ++++(){}{}x T x y z y n p p l p m p n lmn p n p ⎧⎫⎪⎪=++==⎨⎬l zx yxx ττσ⎫⎧⎟⎞⎜⎛z p ⎪⎪⎩⎭}){(}{)(n n n m n ml ij Tzyzxzzy y xyσστττστ=⎪⎭⎪⎬⎪⎩⎪⎨⎟⎟⎠⎜⎜⎝=即}){(}{n n ij T N σσ=(2-15)j 3°斜截面上的切应力:全应力矢量p N 在斜截面内的投影即斜截面上的切应力分量为:||n n n p τ=×r r ++216或2222222()()n n n x y z x y z p p p p p l p m p n τσ=−=++−(2-16)τxσz4-4、弹塑性力学中常用的简化力学模型44、弹塑性力学中常用的简化力学模型σA B分析计算有困难与实际符合较好1、理想弹塑性模型:o εεsσ⎨⎧>=≤=ss sE E εεεσεεεσ当当s理想弹塑性力学模型⎩Bσ1tg −2、线性强化弹塑性力学模型As σ1E 计算复杂⎨⎧>−+=≤=ss s s E E εεεεσσεεεσ当当)(1εoEtg 1−sε⎩型线性强化弹塑性力学模3、幂强化力学模型:σ1=n 参数少想弹性模型n A n<<=εσ100=n 便于分析理想塑性模型当理想弹性模型当A n A n ====σεσ01ε1幂强化力学模型4、刚塑性力学模型(理想塑性模型)在应力到达屈服极限之前应变为零。
AσB分析计算容易oε刚塑性力学模型5σ(刚塑性力学模型)5.理想塑性力学模型σssσσ=ε6.σ6.理想弹性力学模型εσE =ε4-6、常用屈服条件:对屈服条件的研究已有两个世纪。
弹性力学基本公式

弹性力学基本公式✧ Scalar product(dot product):cos u v u v θ⋅= i i u v u v ⋅=✧ Vector product(cross product):w u v =⨯ sin w u v θ= 123123123e e e M R F r r rf f f =⨯= ✧ Gradient of a scalar field:i iG grad e x ϕϕϕ∂==∇=∂ 1/2ϕϕϕ∇=∇⋅∇ ✧ Divergence of a vector:312123v v v v divv x x x ∂∂∂∇⋅==++∂∂∂ ✧ Curl of a vector:✧ 123123123e e e v curlv x x x v v v ∂∂∂∇⨯==∂∂∂ ✧ Other relations between partial derivatives of ϕ, ψand v :2222222123x x x ϕϕϕϕϕ∂∂∂∇⋅∇=++=∇∂∂∂()ϕψϕψψϕ∇=∇+∇ ()v v v ϕϕϕ∇⋅=∇⋅+⋅∇ ()0curlgrad ϕϕ=∇⨯∇= ()0divcurlv v =∇⋅∇⨯=✧ Kronecker deltaij δ (also called substitution operator)ij j ji j i v v v δδ== 3i j i j δδ= i j i j e e δ⋅= kk ij ik jk ij ij σσδδσδ==✧ Alternating tensorijk ε (third order tensor)ijk j k i u v e u v ε=⨯ ()ijk i j k u v w u v w ε=⋅⨯ i j k i s t j s k t j εεδδδδ=- 6i j k k j i εε=-✧ Transformation of coordinates:'ij i j l e e =⋅ 'i i j j e l e = 'i j i j e l e= ir jr ri rj ij l l l l δ== 'i i j j v l v = 'i ji j v l v = 'i ij j x l x = 'i j i j x l x = ''ji ij j i x x l x x ∂∂==∂∂ ✧ Stress vector nT with cutting plane n :ni ij j T n σ=✧ Cauchy formulae for stress:nnn i i ij i j T n T n n n σσ=⋅== 222()nnn S T σ=-✧ Principal stress:From the equation ni i ij j i T n n n σσσ= ⇒=, we can calculate the direction of principal stresses. From the equation 321230I I I σσσ-+-=, we can get the principal stresses.1112233I σσσ=++ 1113222311122313332332122I σσσσσσσσσσσσ=++ 1112133212223313233I σσσσσσσσσ= ✧ Octahedral stresses:222112233123111()33oct n n n I σσσσσσσ=++=++=1223132221/22()3oct ττττ=++=✧ Stress deviator tensor: ✧ij ij ij s p σδ=+ 1231()3p σσσ=++11122331230J s s s s s s =++=++=222222212132322212132311()()()()261()()()6ij ji x y y z x z xyyz xz J s s s s s s s s σσσσσστττσσσσσσ⎡⎤==-++=-+-+-+++⎣⎦⎡⎤=-+-+-⎣⎦333312312311()33xxy xzij jk ki yxy yz zxzy zs J s s s s s s s s s s s ττττττ===++=✧ Relations between I i and J i :22121(3)3J I I =- 3311231(2927)27J I I I I =-+ 1ij ij I δσ∂=∂ 2ij ij J s σ∂=∂ 3223i k k ji j ij J s s J δσ∂=-∂ ✧ Stress on hydrostatic axis and deviatoric plane:123(,,)ON OP n σσσ→→=⋅=⋅== (,,)ON ON n p p p →→=⋅=222123()NP s s s →=++= 123(,,)N P s s s →= ✧ Equations of equilibrium:,0ij j i F σ+= i j j iσσ= ✧ Stain vector nδ with cutting plane n :ni ij j n δε=✧ Cauchy formulae for stress:nnn i i ij i j n n n n εδδε=⋅== 222n nϑδε=- ✧ Principal strain:From the equation ni i ij j i n n n δεεε= ⇒=, we can calculate the direction of principal stresses. From the equation 321230I I I εεε-+-=, we can get the principal stresses. ✧ Strain-Displacement relationships: ✧ Lagrangian description: ,,,,1()2ij i j j i r i r j u u u u ε=++ 其中,i i j ju u x ∂=∂ 22212x u u v w x x x x ε⎡⎤∂∂∂∂⎛⎫⎛⎫⎛⎫=+++⎢⎥ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦122xy xy u v u u v v w w y x x y x y x y γε⎡⎤∂∂∂∂∂∂∂∂==++++⎢⎥∂∂∂∂∂∂∂∂⎣⎦等等 ✧ Eulerian description: ////1()2ij i j j i r i r j u u u u ε=++ 其中/i i j ju u ξ∂=∂ ✧ 备注:应变张量是指pure deformation ,而转动张量是指rigid body rotation 。
弹性力的计算

弹性力的计算弹性力是力学中的重要概念之一,用于描述弹性物体受力后的变形情况。
在物理学和工程学中,我们常常需要计算弹性力以理解和预测物体的行为。
本文将介绍弹性力的计算方法及其应用。
1. 弹性力的概念弹性力是一种具有恢复性的力,它使物体返回到其原始形态或位置。
当物体受到外力作用后发生变形,弹性力将通过内部的分子力恢复物体的形状。
弹性力遵循胡克定律,即弹性力与物体的变形成正比,反向作用于物体,使其恢复原状。
2. 弹性力的计算方法弹性力的计算涉及应力和应变的概念。
应力是物体受力后单位面积上的力的作用,常用符号σ表示,计算公式为:σ = F / A其中,F为作用在物体上的力,A为物体上受力的面积。
应变是物体受力后的变形程度,常用符号ε表示,计算公式为:ε = ΔL / L其中,ΔL为物体受力后的长度变化,L为物体的原始长度。
根据胡克定律,弹性力与应变成正比。
弹性力的计算公式为:F = k * ΔL其中,k为弹性系数,表示物体的弹性特性,ΔL为物体的长度变化。
3. 弹性系数的计算弹性系数是衡量物体弹性性质的重要参数。
常见的弹性系数有弹簧常数、杨氏模量、剪切模量等。
3.1 弹簧常数弹簧常数是弹簧系统中描述弹性力的参数,用符号k表示。
弹簧常数的计算公式为:k = F / Δx其中,F为弹簧所受的力,Δx为弹簧的伸长或压缩距离。
3.2 杨氏模量杨氏模量是衡量物体弹性和刚性的参数,用符号E表示。
杨氏模量的计算公式为:E = σ / ε其中,σ为应力,ε为应变。
4. 弹性力的应用弹性力的计算在许多领域都有广泛应用。
例如,在结构工程中,可以使用弹性力的计算方法来预测建筑物受力后的变形情况,以确保结构的安全性。
在材料科学中,弹性力的计算可用于研究材料的弹性变形和应力分布。
此外,在机械工程中,弹性力的计算可用于设计弹簧、减震器等装置。
总结:弹性力是具有恢复性的力,用于描述物体受力后的变形情况。
通过计算应力和应变,可以得到弹性力的大小。
弹性力学公式

①平衡微分方程:⎪⎪⎩⎪⎪⎨⎧=+∂∂+∂∂=+∂∂+∂∂00yxy y x yxx Y x y f y x τστσ②平面问题中一点应力状态:()()⎪⎩⎪⎨⎧-+-=++=xy x y n xy y x n m l lm lm m l τσσττσσσ22222⎪⎩⎪⎨⎧+=+=xyy y xyx x l m p m l p τστσ 222122xyyx yx τσσσσσσ+⎪⎪⎭⎫ ⎝⎛-±+=221minmax σστ-±=;xxyxy xtg tg σστατσσα--=-=1211;③平面问题几何方程:yu x v yv xu xy y x ∂∂+∂∂=∂∂=∂∂=γεε,,④平面应力问题物理方程:()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==+=+-=-=-=01211zxyzxyxyyx zxyyyxxEEEEγγτμγσσμεμσσεμσσε;;应变问题E=E/(1-μ *μ);μ=μ/(1-μ) ⑤相容方程:yx xyxyyx ∂∂∂=∂∂+∂∂γεε22222⑥应力边界条件:()()()()⎪⎩⎪⎨⎧=+=+y s xy s y xsyx s x f l m f m l τστσ圣维南原理:⎰⎰⎰⎰⎰⎰--=--=--==⎩⎨⎧==⎩⎨⎧==⎩⎨⎧=222222222222)()()()()()(hh Sy hh l x xy hh x h h l x x hh Nx hh l x x F dy y f dy M ydy y f ydy F dy y f dy τσσ 应力函数表示的相容方程()()⎪⎪⎭⎫⎝⎛∂∂+∂∂+=+⎪⎪⎭⎫⎝⎛∂∂+∂∂y f xf y xy x yxμσσ12222 ⑦应力函数与应力分量: yx y f xx f yxyy yx x∂∂Φ∂-=-∂Φ∂=-∂Φ∂=22222,,τσσ应力函数表示的相容方程024422444=∂Φ∂+∂∂Φ∂+∂Φ∂yyx x按位移求解平面应力问题时所用的基本微分方程:)2121(10)2121(1222222222222=+∂∂∂++∂∂-+∂∂-=+∂∂∂++∂∂-+∂∂-y x f yx u xv yv E f yx v yu xu E μμμμμμ按位移法求解平面问题时所用的应力分量:)()1(2),(1),(122yu xvE xu yv E y v xu E xy yx∂∂+∂∂+-=∂∂+∂∂-=∂∂+∂∂-=μτμμσμμσ①极坐标平衡微分方程:⎪⎪⎩⎪⎪⎨⎧=++∂∂+∂∂=+-+∂∂+∂∂02101ϕϕϕϕϕϕτϕστσσϕτσf f ρρρρρρρρρρρρ ②极坐标几何方程:⎪⎪⎩⎪⎪⎨⎧-∂∂+∂∂=∂∂+=∂∂=ρρρρρ,ρρρρρρϕϕϕϕϕϕγϕεεu u u u u u 11③极坐标平面应力物理方程:()()()⎪⎪⎩⎪⎪⎨⎧+==-=-=ϕϕϕϕϕϕτμτγμσσεμσσερρρρρρE G EE 1211,1④极坐标中的应力分量⎪⎪⎩⎪⎪⎨⎧∂∂+∂∂∂-=∂∂=∂∂+∂∂=ϕϕτσϕσϕϕφρρφρρφφρρφρρρ222222211,11 ⑤极坐标中的相容方程:011222222=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂φρρρρϕ 应力分量的坐标转换式:⎪⎪⎩⎪⎪⎨⎧-+-=-+=++=)sin (cos cos sin )(,cos sin 2cos sin ,cos sin 2sin cos 222222ϕϕτϕϕσστϕϕτϕσϕσσϕϕτϕσϕσσϕϕxy x y xy y x xy y x ρρ⎪⎪⎩⎪⎪⎨⎧-+-=++=-+=)sin (cos cos sin )(,cos sin 2cos sin ,cos sin 2sin cos 222222ϕϕτϕϕσστϕϕτϕσϕσσϕϕτϕσϕσσρϕϕρρϕϕρρϕϕρxyy x ⑥轴对称问题: 应力分量简化为:0122====ρρρ,ρφ,ρφρϕϕϕττσσd d d d相容方程化简为:01222=⎪⎪⎭⎫⎝⎛+φρρρd d d d 应力函数:D C B A +++=22ln ln ρρρρφ轴对称的应力分量:()()⎪⎪⎪⎩⎪⎪⎪⎨⎧==+++-=+++=02ln 232ln 2122ρρρρρρρϕϕϕττσσCB AC B A轴对称的位移分量(平面应力):()()()()()⎪⎪⎩⎪⎪⎨⎧+-+=++⎥⎦⎤⎢⎣⎡-+-+--++-=ϕϕϕϕϕμμμμϕcos sin 4sin cos 12311ln 1211K I H E B u K I C B B A E u ρρρρρρρρ ⑧圆环或圆筒受均布压力:2222212222222221222211111111q Rr rq rR Rq Rr rq rR R-+--+=------=ρρ,ρρρϕσσ半平面体在边界上受集中力: )sin sin cos (cos 2ϕϕσββπρρ+-=F ,⑨圆孔的孔边应力集中: 0=ϕσ, ==ρρϕϕττ0双向受拉:0112222==⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛-=ρρρ,ρ,ρϕϕϕττσσr q rq相对沉陷:ρπηs EF ln2=一向受拉一向受压:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛--==⎪⎪⎭⎫ ⎝⎛+-=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=22224422223112sin 312cos 3112cos ρρρρρρρρrr q r q r r q ϕττϕσϕσϕϕϕ顶端受集中力的楔形体0)sin sin sin sin cos cos (2==-++-=ϕϕτσααϕβααϕβρσρρ,Fϕστϕσσϕσσρϕρ2sin 21sincos 22===xyyx,,平面问题的有限元法:{}{}tdxdyF Tσεδ⎰⎰=**exyy xxyyx mmj ji i mymx jy jx iyix N y x v y x u d v uv uv u F F F F F F F δγεεετσσσδ=⎭⎬⎫⎩⎨⎧=====),(),(,,,,*******单元分析:)(21;;;i j j i j m i m j i j m m j i c b c b A x x c y y b y x y x a -=-=-=-=⎥⎦⎤⎢⎣⎡==m ji m jii N NN N N N N A y x N 000000;21),(),,.(21;21;3m j i im ds N ij ds N A dxdy N imi iji Ai ===⎰⎰⎰⎰eeeeek FDB S S D B δδεσδε=====;;;⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=2)1(010112μμμμE D 弹性矩阵 [];0021;⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==i ii ii mj ib c c b A B B B B B 几何矩阵 应力转换矩阵:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==2)1(2)1()1(2;2ii iiii i mjib c c b c b A ES S SS S μμμμμ单元刚度矩阵:⎢⎢⎢⎣⎡-+-+-+-+-==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==sr s r rs r s s r s r s r s r sT rrs mm mjmi jm jjjiim ij iiTeb bc c bc c b b c c b c c b b A Et DBB k k k k k kk k k k DBtA B k21212121)1(42μμμμμμμ分布体力向节点移置:⎰⎰⎰⎰⎰⎰===Ay i Liy Ax i Lix ATeL dxdyf y x N t F dxdy f y x N t F fdxdy Nt F ),(,),(;分布面力向节点移置:⎰⎰⎰⎰⎰⎰===σσσS x i Lix S x i Lix S TeL dsf y x N t F ds f y x N t F ds f Nt F ),(;),(;∑=ee rrkK 11 r 指单元位于节点1的顶点的局部编码 ∑=ee rsq kK 1 r 指单元位于节点1的顶点的局部编码,s 是单元位于节点q 的顶点的局部编码。
高中物理弹力公式

高中物理弹力公式
高中物理中涉及到弹性力的公式是胡克定律,也被称为弹簧定律。
它描述了弹性体(如弹簧、弹性绳等)受到拉伸或压缩时所产生的弹力与其形变的关系。
弹力是指在恢复力的作用下,物体受力变形后,恢复到原始形状时所产生的力。
胡克定律的数学表示为:
F = -kx
其中,
F 表示弹力(单位为牛顿) k 是弹簧系数,也叫做弹性系数或弹性常数(单位为牛顿/米)x 表示弹簧或弹性体的形变(单位为米)
胡克定律表明,弹性力的大小与形变是成正比的,且方向与形变相反。
即,当物体受到拉伸或压缩时,弹力的方向与形变方向相反,且弹力的大小与形变成正比。
这个公式在解析和计算弹簧的行为、弹性体的形变与弹力之间的关系时经常使用。
通过实验或测量,可以确定弹簧系数k的值,并利用胡克定律来计算弹簧的形变或弹力。
它在物理学中应用广泛,帮助解释了许多与弹性体相关的现象和实验。
弹性力学公式总结
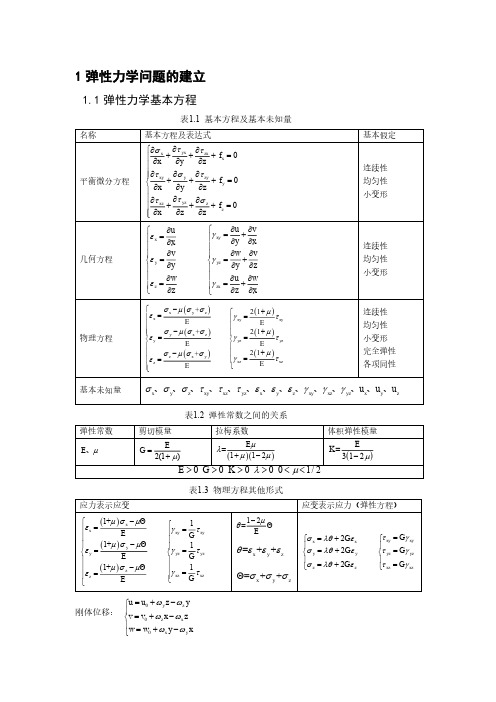
名称 表达式
平面应力问题
x
E xy x + y 、 y 1 E 2 y + x 、 xy 2 1E 1 2
平面应变问题则 E
E 2 1 1
2.3 平面问题的协调方程
名称 以 应 力 表 示 以应变表示 常体力 一般情况 平面应力问题
xy zx yz 2 x + =2 y x yz x z yz xy 2 y xy + =2 x y xz y z 2 yz + zx xy =2 z y z xy z x
n3
z'
表1.9 转轴时应力、应变的转换 应力转换
应变转换
T
' = L L
' = L L
l1 L l2 l3 m1 m2 m3 n1 n2 n3
x 1 2 xy 1 xz 2 1 xy 2
表1.7 用应力表示应变的协调方程
一般情况
f y f z f x 2 1 2 1 x 2 2 x 1 x y z f y 2 1 f f 2 x z 1 y 2 2 y 1 y x z 2 1 2 1 2 f z f y f x z z 2 1 z y x 常体力等式右侧改为0
z 向尺寸远大于 xOy 平面内的尺寸
(等截面长柱体)
弹性力学公式经典版

任意斜截面上的应力Cauchy 公式:T x = σ x l + τ xy m + τ zx n 、T y = τ xy l+ σ y m +τ zy n 、T y =τ xz l+τ y z m +σ z n弹性体的应力边界条件:x yx zx xy y zy xz yz z l m n X l m n Y l m n Z στττστττσ⎫++=⎪⎪++=⎬⎪+++⎪⎭主应力、应力张量、不变量当一点处于某种应力状态时, 在过该点的所有截面中, 一般情况下存在着三个互相垂直的特殊截面, 在这些截面上没有剪应力, 这种剪应力等于零的截面称为过该点的 主平面 , 主平面上的正应力称为该点的 主应力 , 主平面的法线所指示方向称为该点的 主方向。
静力平衡方程几何方程:物理方程三个基本原理:解的唯一性原理、叠加原理、圣维南原理。
圣维南原理:由作用在物体局部边界表面上的自平衡力系,所引起的应力和应变,在远离作用区的地方将衰减到可以忽略不计的程度。
另一种提法:如果把物体局部边界表面上的力系,使用分布不同但静力等效(主失相等,绕一点的主矩也相等)的力系来代替,则这种等效代换处理使得物体内的应力分布仅在作用区附近有显著影响,而在远离作用区的地方所受影响很小,可以忽略不计。
为什么要用:1、在弹性力学的边值问题中,要求在边界上任意点,应力与面力相等,方向一致,往往难以满足。
2、有时只知道边界面上的合力和合力矩,并不知道面力的分布形式。
因此,在弹性力学问题的求解过程中,一些边界条件可以通过某种等效形式提出。
其要点有两处: 一、两个力系必须是按照刚体力学原则的“等效”力系(主矢量和主矩分别等于对应面力的主矢量和主矩); 二、替换所在的表面必须小,并且替换导致在小表面附近失去精确解。
Cauchy 公式: P x = σ x l + τ xy m +τ zx n p y = τ xy l+σ y m +τ zy n p y =τ xz l+τ y z m +σ zn(n z n T nT στ=边界条件:()()()x xy xz s xxy y yz s y xz yz z s zl m n T l m n T l m n T στττστττσ++=++=++= 平衡微分方程:000yx x zxx xy y zyy yz xz zz F x y z F x y z F x y zτσττστττσ∂∂∂+++=∂∂∂∂∂∂+++=∂∂∂∂∂∂+++=∂∂∂ 主应力、不变量,偏应力不变量321231230x y zx xy y z zxyz yx y zy xz x z x xy xzyx y yzzx zy z I I I I I I σσσσσσστσστττσττσσσττστττσ-+-==++=++= 1231();3m i i m s σσσσσσ=++=-()()()112322222223016()6x y y z z x xy yz zx J s s s J J σσσσσστττ=++=⎡⎤=-+-+-+++⎢⎥⎣⎦=偏应力张量行列式的秩八面体812381()3σσσστ=++等效应力σ体积应变x y z θεεε=++12312()Ev vεσσσ-=++ 几何方程:;;;x xy y yz z xy u u v x y x v v w y z y w u w z z xεγεγεγ∂∂∂==+∂∂∂∂∂∂==+∂∂∂∂∂∂==+∂∂∂ 12ij ij εγ=变形协调方程22222y xyx xy y xετε∂∂∂+=∂∂∂物理方程()()()12(1);12(1);12(1);x x y z xy xy y y x z yz yz z z y x zx zx v v E Ev v E Ev v E Eεσσσγτεσσσγτεσσσγτ+⎡⎤=-+=⎣⎦+⎡⎤=-+=⎣⎦+⎡⎤=-+=⎣⎦偏应力与偏应变的关系 3;2m m ij ij K s Ge σε==平面应变问题()()()()()'x '''''''2111111112(1)2(1);0;110;x y x y y y x y x xy xyxy z zy zx zy zx z x y v v v v Ev v v v E v v E E E v E v v v v εσσσσεσσσσγττεγγττσσσ⎡⎤=-=--⎣⎦-⎡⎤=-=--⎣⎦-++=====--=====+ 平面应力问题()()()x 11;2(1)01;0x y y y x xy xyzy zx zy zx z x y z v v E E v Evεσσεσσγτγγττεσσσ=-=-+======-+= 平面问题方程: 平衡方程:00yxx x xy yy F x y F x yτστσ∂∂++=∂∂∂∂++=∂∂ 几何方程;;x y xy u v u vx y y xεεγ∂∂∂∂===+∂∂∂∂边界条件;x yx x xy y y l m T l m T σττσ+=+=位移边界条件;x x y y u u u u ==协调方程平面应变22222y xyx xy y xετε∂∂∂+=∂∂∂平面应力222220;0;0z z zxy x yεεε∂∂∂===∂∂∂ 平面问题应力解(直角坐标系)22222x x y y xy F xy F y x xyϕσϕσϕτ∂=-∂∂=-∂∂=-∂协调方程:222222222()()()0x y x y x yϕσσ∂∂∂∂+=++=∂∂∂∂ 平面问题应力解(极坐标系) 平衡微分方程:10210r r r r r r F r r r F r r rθθθθθθτσσσθτστθ∂-∂+++=∂∂∂∂+++=∂∂ 几何方程:1;1r r r r r u u u r r r u u u r r rθθθθθεεθγθ∂∂==+∂∂∂∂=+-∂∂ 本构方程:()()r 11;2(1)r r rrv v E E v Eθθθθθεσσεσσγτ=-=-+= 变形协调:22222211()0r r rr θ∂∂∂++=∂∂∂已知应力函数ϕ,求应力 2222222211;111()r r r r r r r r r r r θθϕϕϕσσθϕϕϕϕτθθθ∂∂∂=+=∂∂∂∂∂∂∂=-+=-∂∂∂∂∂ 极坐标求解的对称问题2222ln ln (12ln )2(32ln )2r A r Br r cr D Ar C r Ar Crθϕσσ=+++=+++=-+++B B b B 0q ,q ,a =中间有空洞,位移单值要求环内力环外力()()()()2222222222222222222221''''''a b (1)(1)b b (1)(1)D u D r r1121ln 1113cos sin 4sin cos r a br a br b a q q a b r b a r b aq q b a r b a rA u v v Br r r E v Cr I K EBr u Hr I K E θσσθθθθθ=-----=+-+--=+⎡⎤=-++--⎢⎥⎣⎦+-++=+-+位移:平面应变下:()()[]()()[]r (1)112(1)112r r Eu u u u Eu u u u θθθσεεσεε=-++-=-++-。
弹性力学知识点总结

弹性力学知识点总结弹性力学是力学的一个重要分支,研究固体物体的变形和回复过程。
在本文中,将对弹性力学的几个重要概念和原理进行总结和介绍。
1. 弹性模量弹性模量是衡量固体物体抵抗形变的能力的物理量。
根据胡克定律,弹性模量E可以通过应力σ和应变ε的比值得到:E = σ/ε。
其中,应力表示受力物体单位面积上的力的大小,应变表示物体在应力作用下产生的形变程度。
2. 胡克定律胡克定律是弹性力学的基本原理,描述了理想弹性体在弹性应变范围内的力学行为。
根据胡克定律,应变与应力成正比。
即ε = σ/E,其中E为杨氏模量。
3. 杨氏模量杨氏模量是衡量固体材料抗拉性能的物理量,表示固体在单位面积上受到的拉力与单位长度的伸长量之比。
杨氏模量的定义为:E =F/AΔL/L0,其中F为受力物体的拉力,A为受力物体的横截面积,ΔL为拉伸后的长度增量,L0为原始长度。
4. 泊松比泊松比是衡量固体材料体积收缩性的物理量。
泊松比定义为物体在一轴方向上受力引起的形变量与垂直方向上的形变量之比。
公式表示为:μ = -εlateral/εaxial。
5. 应力-应变关系弹性力学中的应力-应变关系描述了材料在受力作用下的力学行为。
对于弹性材料,应力与应变成线性关系,即应力和应变成比例。
6. 弹性极限弹性极限是指固体材料可以弹性变形的最大程度。
超过弹性极限后,材料将会发生塑性变形。
7. 弹性势能弹性势能是指物体在形变后能够恢复到初始状态的能力。
弹性势能可以通过应变能来表示,其大小等于物体在受力作用下形变所储存的能量。
8. 弹性波传播弹性波是在固体中传播的一种机械波。
根据介质的不同,弹性波可以分为纵波和横波。
9. 斯内尔定律斯内尔定律描述了弹性力学体系中应力与应变之间的关系。
根据斯内尔定律,弹性变形是由应力和应变之间的线性关系所描述的。
10. 压力容器设计弹性力学在压力容器设计中起着重要作用。
根据弹性力学的原理,可以计算压力容器在不同压力下的变形情况,从而设计出满足安全要求的容器结构。
弹性力学常用公式

弹性力学常用公式一,三维空间应力:n x n x •=)(),(σσ,[][][][]Tβσβσ=',)(0,i i j ij u f ••=+ρσ应变:()i j j i ij u u ,,21+=ε,协调方程: 0,,,,=--+ik jl jl ik ij kl kl ij εεεε 线性本构方程:Hooke 定律 kl ijkl ij C εσ=,各向同性:ij kk ij ij ij kk ij ij EE G δσυσυεδλεεσ-+=+=1 ,2 边界条件:σS S B u ⋃=∂,φσ=⋂S S u ;i S i u u u=,i S jij X n =σσ二、平面问题本构方程平面应变平面应力平面应力(极坐标系)αβαβαβδλεεσkk G +=2, 平面应力 平面应变:21υ-→E E 、υυυ-→1 xyxyx y y y x x G G G γτευυευυσευυευυσ=-+--=-+--=)1(21)1(2)1(21)1(2 xyxyx y y y x x G G Gγτυεευσυεευσ=+-=+-=)(12)(12 θθθθθγτυεευσυεευσr r r r r G G G=+-=+-=)(12)(12 0)()(==+=+=zx zx y x y x z ττεελσσυσ===zx zx z ττσ0=z σ 0==θττz zrαβαβαβδσυσυεkk EE -+=1 xyxy xy x y y y x x GE E τεγσυυσυεσυυσυε12)1(1)1(122==---=---= xyxy xy x y y y x x GEEτεγυσσευσσε12)(1)(1==-=-=θθθθθτγυσσευσσεr r r r r GE E1)(1)(1=-=-====zy zx z γγε)(==+-=zy zx y x z Eγγσσυε )(θσσυε+-=r z E0==θγγz zr协调方程:y x y x xy x y ∂∂∂=∂∂+∂∂γεε22222,0112112222222=∂∂-∂∂-∂∂+∂∂∂-∂∂+∂∂θγεεθγθεεθθθθr r r r r r r r r r r r r ))(1()(,,2y y x x y x f f ++-=+∇νσσ,如x x V f ,-=,y y V f ,-=,引入Airy 应力函数:V yy x +=,φσV xx y +=,φσ,xy xy,φτ-=22222y x ∂∂+∂∂=∇,4422444222yy x x ∂∂+∂∂∂+∂∂=∇∇极坐标系:02101=++∂∂+∂∂=+-+∂∂+∂∂θθθθθθτθστσσθτσf r r r f r r r r r r r r r r v r v u r ru v r r u r r rr r θθθθθθγθεε-∂∂+∂∂=+∂∂=∂∂=11 , ⎪⎭⎫⎝⎛∂∂∂∂-=∂∂=∂∂+∂∂=θφτφσθφφσθθr r rr r r r r 1 ,1122222 V 222)1(∇--=∇∇νφ,22222211θ∂∂+∂∂+∂∂=∇r r r r , ⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛θθθθσττσθθθθσττσθθθcos sin sin cos cos sin sin cos r r ry xyxy x三,柱形杆自由扭转位移:yz u α-=,xz v α=,),(y x w αψ=,02=∇ψ(翘曲函数),y x zx ααψγ-=,,x y zy ααψγ+=, 应力:zx y zx G γφτ==,,zy x zy G γφτ=-=,,其余应力、应变分量均为0,αφG 22-=∇(应力函数)边界条件:σS B =∂上0=+y zy x zx n n ττ→ )(y x y y x x xn yn n n -=+αψψ,C =φ 扭矩:t zx zyt D dxdy y x M αττ=-=⎰⎰Ω)(, ∑⎰⎰+=Ωii i t A dxdy M φφ22,抗扭刚度:22d d t D Gx y x y x y y x ψψΩ⎛⎫∂∂=++- ⎪∂∂⎝⎭⎰⎰; 薄膜比例:S q z /2-=∇,0|=Ω∂z狭长矩形杆:313t D Ga δ=,max 23t M a τδ=;开口薄壁杆:313n t i i i G D a δ==∑,max 313i t i n i i i M a δτδ==∑; 闭口薄壁管:2tM A τδ=, ()24t M ds GA s αδ=⎰,等厚闭口薄壁管:24t M sGA αδ=四,能量原理与近似解法虚功原理:i i i i ij ij VS Vf u dV p u dS dV σδδσδε+=⎰⎰⎰余虚功原理:ui i ij ij S Vu p dS dV δεδσ=⎰⎰总势能:()()i ij i i i i VVS u W dV f u dV p u dS σε∏=--⎰⎰⎰,i S iu u u =,kl ij ijkl ij C W εεε21)(=; 总余能:()()uc ij c ij i i VS W dV p u dS σσ∏=-⎰⎰,0,=+i j ij f σ,i S jij p n =σσ,kl ij ijkl ij c C W σσσ121)(-=;0=∏+∏c近似解法(Ritz 法与Galerkin 法):齐次化,找基函数,求近似最小值。
第二章弹性力学的基本方程

, , 1, 2
由此,向量 a可表示为
3
a a1e1 a2e2 a3e3 ai ei i 1
三阶线性代数方程组
a11x a12 y a13 z P1
a21
x
a22
y
a23
z
P2
a31
x
a32
y
a33
z
P3
可表示为
ai1x1 ai2 x2 ai3x3 Pi
(c) 非循环序列:i, j, k中有两个以上得指标取
相同值
e112 e222 e323 0
利用置换符号可以简化公式
(1)行列式
a11 a12 a13 a a21 a22 a23
( xix j
) ,ij
例如:
xi
,i
ui x j
ui, j
2ui x j xk
ui, jk
ui xi
ui,i
u1,1
u2,2
u3,3
f xi
dxi
f ,i dxi
f ,1dx1
f ,2 dx2
f ,3dx3
4、 克罗内克(Kroneker)符号
定义: ij ei e j cos(ei ˆ e j )
Fx
1 dh 3
0
同理可得:
Tx xl yx m zx n Ty xyl y m zy n Tz xzl yz m z n
上式称为斜面应力公式,又称Cauchy公式。
2、斜面上得正应力与剪应力
Tν Txl Tym Tz n
xl 2 y m 2 z n 2 2 xylm 2 yz mn 2 zx nl
ei
弹性力学公式范文

弹性力学公式范文弹性力学是研究物体在外力作用下产生的变形和应力的学科。
弹性力学公式是描述物体在弹性变形过程中的应力、应变、模量等物理量之间的关系的数学公式。
下面将介绍几个常用的弹性力学公式。
1.宕度公式:在物体在外力作用下发生弹性变形时,物体的宕度δ与外力F、物体应力σ及物体截面面积A之间的关系可以用宕度公式表示。
宕度公式的数学表达式为:δ=F*L/AE其中,δ为宕度,F为外力,L为物体的长度,A为物体的截面面积,E为物体的弹性模量,也称为杨氏模量。
2.应力-应变关系:物体在受力的作用下发生弹性变形时,物体的应变与物体的应力之间存在线性关系,可以用应力-应变关系来描述。
应力-应变关系的数学表达式为:σ=E*ε其中,σ为应力,E为弹性模量,ε为应变。
3.长度变化公式:物体在受力的作用下发生弹性变形时,物体的长度会发生变化。
物体长度变化量ΔL与受力F、物体初始长度L、物体的截面面积A及物体的弹性模量E之间存在线性关系,可以用长度变化公式来表示。
长度变化公式的数学表达式为:ΔL=F*L/AE4.胡克定律:胡克定律是描述物体在弹性变形过程中应力和应变之间的关系的基本定律。
根据胡克定律,当物体在弹性范围内发生弹性变形时,物体的应力与物体的应变之间存在线性关系,数学表达式为:σ=E*ε其中,σ为应力,E为弹性模量,ε为应变。
5.纵波传播速度公式:在弹性介质中,纵波的传播速度v与介质的弹性模量E和密度ρ之间存在关系,可以用纵波传播速度公式来表示。
纵波传播速度公式的数学表达式为:v=√(E/ρ)其中,v为纵波的传播速度,E为弹性模量,ρ为介质的密度。
这些是弹性力学中的一些常用公式,它们描述了物体在弹性变形过程中的应力、应变、模量等物理量之间的关系。
通过这些公式,我们可以更好地理解和分析物体在受力下的变形和力学行为。
弹性材料的弹性常数计算

弹性材料的弹性常数计算弹性常数是描述材料在受力时的弹性性质的物理参数。
在弹性力学中,常用的弹性常数有弹性模量、泊松比和剪切模量等。
本文将介绍如何计算弹性材料的弹性常数。
一、弹性模量的计算弹性模量是衡量材料抵抗形变的能力的物理量。
常见的弹性模量有杨氏模量、体积模量和剪切模量。
1. 杨氏模量杨氏模量(Young's modulus)是描述材料在拉伸或压缩过程中的弹性性质的重要参数。
它定义为单位截面积上的拉应力与相应的拉应变之比。
计算公式为:E = (F/A) / (ΔL/L0)其中,E为杨氏模量,F为施加在材料上的力,A为材料的初始横截面积,ΔL为材料的长度变化,L0为材料的初始长度。
2. 体积模量体积模量(Bulk modulus)是描述材料在受到体积变化时的抵抗能力的参数。
它定义为单位体积的压力增量与相应的体积变化之比。
计算公式为:K = -ΔV / (V * ΔP)其中,K为体积模量,ΔV为材料的体积变化,V为材料的初始体积,ΔP为施加在材料上的压力增量。
3. 剪切模量剪切模量(Shear modulus)是描述材料抵抗剪切形变的能力的参数。
它定义为单位面积上的剪切应力与相应的剪切应变之比。
计算公式为:G = (F/A) / (Δx / L)其中,G为剪切模量,F为施加在材料上的力,A为材料的初始横截面积,Δx为材料的横向位移,L为材料的初始长度。
二、泊松比的计算泊松比(Poisson's ratio)是描述材料在拉伸或压缩过程中横向收缩或膨胀的程度的物理量。
它定义为横向应变与纵向应变之比。
计算公式为:ν = -Δd / (d0 * ΔL/L0)其中,ν为泊松比,Δd为材料的横向位移,d0为材料的初始横向尺寸,ΔL为材料的长度变化,L0为材料的初始长度。
根据以上的计算公式,可以通过适当的实验测量或者模拟计算来得到材料的弹性常数。
不同类型的材料在相同应变情况下具有不同的弹性常数,这些值对材料的使用和设计具有重要的指导意义。
弹力大小计算公式

弹力大小计算公式
弹力大小,也称为弹性系数,是描述材料性能的重要参数,可以应用于工程设计和计算。
它定义为材料在拉伸或压缩状态下弹性回弹能力的系数。
可以用下面的公式表示:弹性系数= ε / δ,ε是当前变形量,δ则是弹性变形量。
在材料力学实验中,弹性系数可以通过拉伸和压缩实验来测量。
应用不同的材料,体积不变的条件下拉伸或压缩,并根据力与变形的关系,计算出材料的弹性系数。
例如,在实验过程中,我们给一根材料施加了0.1N 的力,然后材料变形了0.08mm,那么这种材料的弹力系数等于ε / δ= 0.1M / 0.08mm=12.5M。
另外,弹性系数也可以通过计算的方法来测量,并应用于实际工程中。
例如,利用拉伸和压缩测试数据来预测材料的弹性系数,可以使用有限元法。
有限元法是构建材料模型,建立其在受力条件下的数学状态方程,并将均匀分布的节点分割成一些区域,然后对这些区域的力学状态进行求解,从而实现材料弹力的计算。
总之,弹力大小计算公式是Ε/δ,通过实验与计算可以得出材料的弹性系数。
弹性系数是描述材料的弹性和强度的重要参数,它可以用于工程设计与计算,并且为后续工作提供更加准确的指导。
弹力的计算公式

弹力的计算公式弹力是物体因形变而产生的力,它是一种复杂的物理现象,可以通过一些简单的公式来描述和计算。
在本文中,我们将探讨弹力的计算公式及其应用。
弹力的计算公式可以通过胡克定律来描述。
胡克定律是描述弹簧弹力的基本定律,它可以用数学公式表示为:F = -kx。
其中,F代表弹力的大小,k代表弹簧的弹性系数,x代表弹簧的形变量。
这个公式告诉我们,弹力的大小与弹簧的弹性系数成正比,与形变量成反比。
这个公式是描述弹簧弹力的基本公式,也可以用于其他形式的弹力计算。
除了弹簧弹力,弹力还可以表现为其他形式,比如弹簧板的弯曲弹力、气体的弹性压力等。
对于这些不同形式的弹力,我们可以使用不同的计算公式来描述。
对于弹簧板的弯曲弹力,我们可以使用以下公式来计算:F = kx。
其中,F代表弯曲弹力的大小,k代表弹性系数,x代表板的形变量。
这个公式告诉我们,弯曲弹力的大小与弹性系数成正比,与形变量成正比。
这个公式可以用于描述弹簧板在受力后产生的弯曲弹力。
对于气体的弹性压力,我们可以使用以下公式来计算:P = F/A。
其中,P代表气体的压力,F代表气体对容器壁的弹力,A代表容器壁的面积。
这个公式告诉我们,气体的压力与气体对容器壁的弹力成正比,与容器壁的面积成反比。
这个公式可以用于描述气体在容器中产生的弹性压力。
除了以上几种形式的弹力,还有许多其他形式的弹力,比如弹簧振子的振动力、弹性材料的拉伸力等。
对于这些不同形式的弹力,我们可以根据具体情况使用相应的计算公式来描述和计算。
弹力的计算公式不仅可以用于描述弹力的大小,还可以用于解决一些实际问题。
比如,在工程中,我们可以使用弹力的计算公式来设计弹簧系统、弹簧板系统、气体容器等,以满足不同的工程需求。
在物理实验中,我们可以使用弹力的计算公式来测量弹簧的弹性系数、弹簧板的弯曲弹性系数等,以验证理论模型。
在日常生活中,我们也可以使用弹力的计算公式来解决一些实际问题,比如汽车悬挂系统的设计、弹簧床的设计等。
弹性力学公式大全-知识归纳整理

xyy x N ml m l τσσσ222++= x y N mp lp -=τ xy y x N lm m l γεεε++=22求切应力公式:()()xyx y N m l lm τσστ22++-= 几何方程在平面中的简化形式:⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+∂∂=∂∂=∂∂=y u x v y vx u xy y x γεε最大位移:()22maxv u uN +=平面应力方程(物理方程):()()()⎪⎪⎪⎭⎪⎪⎪⎬⎫+=-=-=xy xy x yy y xx EE E τμγμσσεμσσε1211 平面应变方程:()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫+=⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛---=xy xy x y y y x x E E E τμγσμμσμεσμμσμε12111122 应力边界问题中:()()()()⎪⎭⎪⎬⎫=+=+y s xy s y x s yx s x f l m f m l τστσ 位移边界:⎭⎬⎫==v v u u x x应力分量:()()()⎪⎪⎪⎭⎪⎪⎪⎬⎫+=+-=+-=xy xy x y y y xx E E E γμτμεεμσμεεμσ121122 弹性方程:()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=y u x v E x u y v E y v x u E xy y x μτμμσμμσ121122 知识归纳整理平面问题的平衡微分方程:⎪⎪⎭⎪⎪⎬⎫=+∂∂+∂∂=+∂∂+∂∂00y xy y x yx x f x y f x x τστσ 弹性方程简化:⎪⎪⎭⎪⎪⎬⎫=+⎪⎪⎭⎫ ⎝⎛∂∂∂++∂∂-+∂∂-=+⎪⎪⎭⎫⎝⎛∂∂∂++∂∂-+∂∂-021211021211222222222222y x f y x u x v y v E f y x v y u x u E μμμμμμ位移表示平面微分方程:⎪⎪⎭⎪⎪⎬⎫=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-y ss x s s f y u x v l x u y v m E f x v y u m y v x u l E21121122μμμμμμ应变:y x x y xy y x ∂∂∂=∂∂+∂∂γεε22222 平面应力:()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+-=+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂y f x f y x y x y x μσσ12222 平面应变:()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂--=+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂y f x f y x y x y x μσσ112222 ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫∂∂Φ∂-=-∂Φ∂=-∂Φ∂=y x y f x x f y xy y y x x 22222τσσ 024422444=∂Φ∂+∂∂Φ∂+∂Φ∂yy x x ⎪⎪⎭⎪⎪⎬⎫++--=+-=022022v x x EI M y EI M v u y xy EIM u ωμω ⎪⎪⎪⎭⎪⎪⎪⎬⎫-=-+-=+++-=x h q xy h q q y h q y h q K Hy y h q y x h q xy y x 2362232264623333323τσσ ⎪⎪⎪⎭⎪⎪⎪⎬⎫=-==0xy y x y EI M y EI M γμεε ⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂+∂∂-=∂∂=∂∂0y ux v y EI M y v y EI Mx u μ ()()⎪⎪⎭⎪⎪⎬⎫+-=+=x f y EI M v y f xy EI M u 2212μ ()()012=++dy y df x EI M dx x df ()()x EI M dx x df dy y df +=-21 求知若饥,虚心若愚。
弹性力学公式总结

弹性力学公式总结弹性力学是研究物体在受力后的形变与应变关系的力学分支。
在弹性力学中,常使用一些公式来描述物体的力学性质。
下面是一些弹性力学中常用的公式:1. 应变(strain)公式:应变是物体在受力后发生的形变相对于初始状态的比例。
应变可以分为线性应变和剪切应变两种类型。
线性应变公式:ε=ΔL/L其中,ε表示线性应变,ΔL表示长度变化,L表示初始长度。
剪切应变公式:γ=Δθ其中,γ表示剪切应变,Δθ表示切变角度的变化。
2. 应力(stress)公式:应力是物体表面上的内力,是由外力作用于物体上的单位面积所产生的力。
法向应力公式:σ=F/A其中,σ表示法向应力,F表示受力,A表示作用面积。
切向应力公式:τ=F/A其中,τ表示切向应力,F表示受力,A表示作用面积。
3.长度变形公式:受力作用下,物体的长度会发生变化,有两种类型:拉伸和压缩。
拉伸变形公式:ΔL=FL/AE其中,ΔL表示长度变化,F表示受力,L表示初始长度,A表示截面积,E表示弹性模量。
压缩变形公式:ΔL=-FL/AE4.钢材弹性模量公式:钢材弹性模量是衡量材料抵抗外力而形变的能力指标。
E=σ/ε其中,E表示弹性模量,σ表示法向应力,ε表示线性应变。
5.线性弹性体系恢复力公式:恢复力是物体受到外力作用后恢复到初始状态所产生的力。
F=kΔx其中,F表示恢复力,k表示弹性系数,Δx表示位移。
6.钢丝绳伸长公式:钢丝绳在受拉伸力作用下会发生伸长。
ΔL=FL/EA其中,ΔL表示伸长长度,F表示受力,L表示初始长度,A表示截面积,E表示钢丝绳的弹性模量。
7.矩形梁弯曲公式:在作用力下,矩形梁会发生弯曲。
M = -EI(d^2y / dx^2)其中,M表示弯曲力矩,E表示杨氏模量,I表示截面惯性矩,y表示梁的纵轴位移,x表示位置。
这些公式是弹性力学中的一些基本公式,用于描述物体在受力后的形变与应变关系,以及恢复力、弯曲等力学性质。
掌握这些公式对于深入理解和研究弹性力学具有重要意义。
