一年级下册数学试题-奥数思维讲练:第十二讲 巧填数阵图 (含答案)全国通用
一年级数学巧填数阵图

一年级数学巧填数阵图
1、一年级数学巧填数阵图11.
2、填数,使每条线上的三个数之和都得15.
3、在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数
之和都是18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
5、在下面的○中填上适当的数,使每条线上的三个数相加都等于15.
提高篇
1、把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
2、把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和
都等于1 2.
3、把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数
相加的和都为12.
提高篇
1、把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
2、把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和
都等于1 2.
3、把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数
相加的和都为12.。
(完整word版)奥数一年级教案第十二讲巧填数阵图教师

巧填数阵图数学乐园晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!基础篇数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.拓展练习(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.【答案】【答案】在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:方法二:从斜行来考虑:要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.拓展练习在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.【答案】【答案】把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:提高篇把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.拓展练习把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为 12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:拓展练习把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.【教学思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个正方形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.【教学思路】这道题的答案不唯一.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.【答案】【答案】把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.【答案】【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.使用数字0,1,2,3,4,5,6,7,8, 9求和.而且同一个数在一幅图中不能重复出现.【答案】【答案】把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.【答案】练习十二1.在下面的○里填上适当的数,使每条线上的三个数之和都是12.【答案】2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.【答案】4.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.【答案】5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【答案】6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.【答案】小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
最新一年级数学巧填数阵图

一年级数学巧填数阵图
1、一年级数学巧填数阵图11.
2、一年级数学巧填数阵图15.
3、在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数
之和都是18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
5、在下面的○中填上适当的数,使每条线上的三个数相加都等于15.
6、在下面的○里填上适当的数,使每条线上的三个数之和都是12.
提高篇
1、把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
2、把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和
都等于1 2.
3、把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数
相加的和都为12.。
一年级奥数巧填数阵图.doc

第十二讲巧填数阵图芈肃数学乐园蒄蒁晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子 . 一个雪精灵告诉她们:“你们只要能够把 1~ 7 这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了. ”你能帮她们填一填吗?.蚇螃小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法. 下面我们就一起来学习吧!芁薀基础篇膆使用数字0, 1, 2, 3, 4, 5,6, 7, 8, 9 做加法 . 在每一道题中,同一个数字不能重复出现.蒃莃螈薆芄拓展练习莄(1) 填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.肀羅在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.羄膁要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?腿虿拓展练习螄在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.芃薁把 1, 2, 3,4, 5, 6 六个数,分别填入○内,使每条线上 3 个数的和相等.膈蒅肀提高篇把 3, 4, 5, 6, 7 这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.蚀薇拓展练习芅把 2, 3, 4, 5, 6 这五个数分别填入圆圈中,使每条线上三个数相加的和都等于 1 2.肁螈把 1, 2, 3, 4, 5, 7 分别填入○里,使每一个大椭圆上的四个数之和等于13.羇羆把 1, 2, 3, 4, 5, 6, 7 这七个数分别填入○里,使每条直线上的三个数相加的和都为12.膃膀莆拓展练习把 1~ 9 这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于 15.蚆羀把 2, 3, 4, 5,6, 7, 8 这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.艿袅拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?蒆羂我会做一做蚁蕿把 1, 2, 3,4, 5, 6, 7 这 7 个数分别填入右图中,使得每条直线上的 3 个数的和相等.羃肃蝿练习十二羈 1.在下面的○里填上适当的数,使每条线上的三个数之和都是12.蚃袀袈 2. 把 3~ 8 这 6 个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.莈蒃羂 3.把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.芀螇膄羃荿 4.把3,4,5,7,9,11,13这七个数分别填入○ 里,使每条直线上的三个数相加的和都为20.芆袄螀 5.将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.螁蚆蚅袂 6. 把数字 1, 2, 3, 5, 6, 7,9 填在下面的○里,使每边上的和为15.衿荿莅袃羈螈小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.膅这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细蚁心和有耐心 .莀现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”. 小朋友,这可真不容易哦!膈袆螂。
(完整word版)一年级数学巧填数阵图
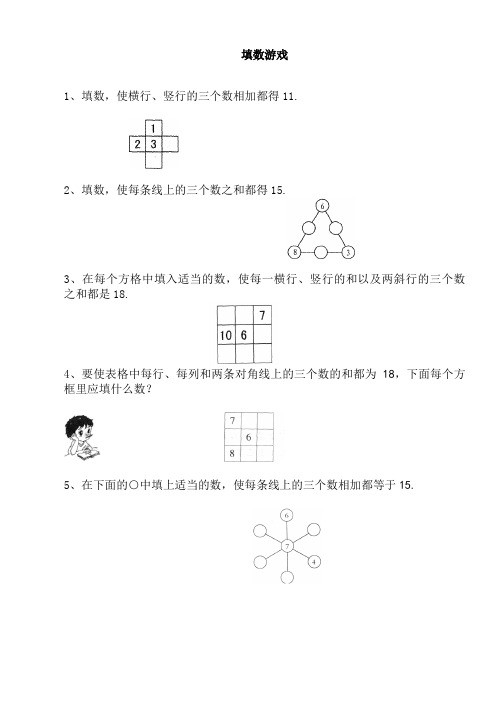
填数游戏
1、填数,使横行、竖行的三个数相加都得11.
2、填数,使每条线上的三个数之和都得15.
3、在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
5、在下面的○中填上适当的数,使每条线上的三个数相加都等于15.
6、在下面的○里填上适当的数,使每条线上的三个数之和都是12.
提高篇
1、把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
2、把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.
3、把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.。
小学奥数教程:数阵图_全国通用(含答案)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.复合型数阵图【例 1】 由数字1、2、3组成的不同的两位数共有9个,老师将这9个数写在一个九宫格上,让同学选数,每个同学可以从中选5个数来求和.小刚选的5个数的和是120,小明选的5个数的和是111.如果两人选的数中只有一个是相同的,那么这个数是_____________.313233212223131211【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】迎春杯,中年级,决赛,3题 【分析】 这9个数的和:111213212223313233++++++++10203031233198=++⨯+++⨯=()()由小刚和小明选的数中只有一个是相同的,可知他们正好把这9个数全部都取到了,且有一个数取了两遍.所以他们取的数的总和比这9个数的和多出来的部分就是所求的数.那么,这个数是12011119833+-=.【答案】33【例 2】 如图1,圆圈内分别填有1,2,……,7这7个数。
如果6个三角形的顶点处圆圈内的数字的和是64,那么,中间圆圈内填入的数是 。
例题精讲知识点拨教学目标5-1-3-2.数阵图【考点】复合型数阵图 【难度】3星 【题型】填空【关键词】希望杯,五年级,复赛,第5题,5分 【解析】 2 【答案】2【例 3】 如下图(1)所示,在每个小圆圈内填上一个数,使得每一条直线上的三个数的和都等于大圆圈上三个数的和.(1)17894【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为叙述方便,先在每个圆圈内标上字母,如图(2),(2)a cb49817则有a+4+9=a+b+c (1)b+8+9=a+b+c (2)c+17+9=a+b+c (3) (1)+(2)+(3):(a+b+c )+56=3(a+b+c ),a+b+c=28,则 a=28-(4+9)=15,b=28-(8+9)=11,c=28-(17+9)=2解:见图.1789411215【答案】1789411215【例 4】 请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为了叙述方便,将各圆圈内先填上字母,如图(2)所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k(A+B+C )+(A+F+G )+(A+D+E )+(B+D+F )+(C+E+G )=5k ,3A+2B+2C+2D+2E+2F+2G=5k ,2(A+B+C+D+E+F+G )+A=5k ,2(1+2+3+4+5+6+7)+A=5k ,56+A=5k.,因为56+A 为5的倍数,得A=4,进而推出k=12,因为在1、2、3、5、6、7中,1+5+6=7+3+2=12,不妨设B=1,F=5,D=6,则C=12-(4+1)=7,G=12-(4+5)=3,E=12-(4+6)=2.,解:得到一个基本解为:(见图)7654321【答案】7654321【例 5】 在左下图的每个圆圈中填上一个数,各数互不相等,每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。
(完整word)一年级数学巧填数阵图
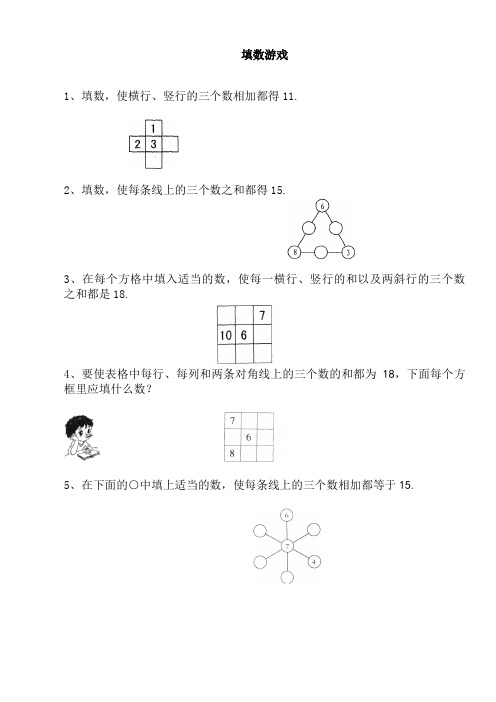
填数游戏
1、填数,使横行、竖行的三个数相加都得11.
2、填数,使每条线上的三个数之和都得15.
3、在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
5、在下面的○中填上适当的数,使每条线上的三个数相加都等于15.
6、在下面的○里填上适当的数,使每条线上的三个数之和都是12.
提高篇
1、把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
2、把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.
3、把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.。
(完整)一年级数学巧填数阵图
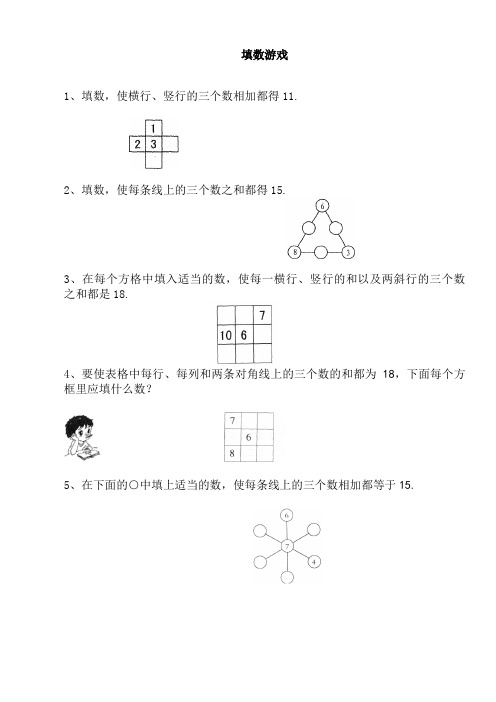
填数游戏
1、填数,使横行、竖行的三个数相加都得11.
2、填数,使每条线上的三个数之和都得15.
3、在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
5、在下面的○中填上适当的数,使每条线上的三个数相加都等于15.
6、在下面的○里填上适当的数,使每条线上的三个数之和都是12.
提高篇
1、把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
2、把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.
3、把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.。
一年级奥数巧填数阵图名师制作优质教学资料

第十二讲巧填数阵图
数学乐园
晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数
之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.
小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不
是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!
基础篇
使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.
拓展练习
(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.
在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.
要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
拓展练习
在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.
把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
提高篇
把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.
拓展练习
把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于 1 2.
把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.。
(完整版)奥数一年级教案第十二讲巧填数阵图教师

巧填数阵图数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.数学乐园晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!基础篇使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.拓展练习(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.【答案】【答案】在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:方法二:从斜行来考虑:要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.拓展练习在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.【答案】【答案】把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:提高篇把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.拓展练习把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为 12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:拓展练习把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.【教学思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个正方形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.【教学思路】这道题的答案不唯一.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.【答案】【答案】把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.【答案】【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.使用数字0,1,2,3,4,5,6,7,8, 9求和.而且同一个数在一幅图中不能重复出现.【答案】【答案】把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.【答案】练习十二1.在下面的○里填上适当的数,使每条线上的三个数之和都是12.【答案】2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.【答案】4.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.【答案】5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【答案】6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.【答案】小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
奥数 一年级 教案 第十二讲 巧填数阵图 学生

第十二讲巧填数阵图
数学乐园
晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线
?.
现
竖行的三个数相加都得15.
在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.
要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么
数?
拓展练习
在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.
把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
15.
这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.
拓展练习
把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数
之和都等于15.
把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.
拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?
把1.
在下面的○里填上适当的数,使每条线上的三个数之和都是
2.个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为
3. 这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.
4.把311,13这七个数分别填入20.
5. 14.
“围。
(完整版)奥数一年级教案第十二讲巧填数阵图教师

巧填数阵图数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习忧若有些过难 .但这节课我们可是希望经过一些简单的填数字游戏,使学生初步感知到什么样的是数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思想能力.在激励学生去研究方法的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,经过找数阵中的要点数来找到解题的钥匙.在今后的不休学习中,能把这类方法灵便应用到本质中去.数学乐园晶晶和莹莹抵达了雪精灵国,天空中各处飘着洁白剔透的雪花,就像下面图中的样子. 一个雪精灵告诉她们:“你们只要能够把1~ 7 这七个数填在雪花的七个花瓣上,使每三个位于同素来线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了. ”你能帮她们填一填吗?.【授课思路】在开课的时候,老师可经过故事引入,激发学生对填数游戏的兴趣. 让学生初步感知什么是数阵 . 因为填数阵有必然的难度,因此在这里我们不需要马上让孩子完成这个题,能够放在最今后解决这个问题 .小朋友们,你喜欢这样的填数字游戏吗?要想正确的填出图中的每一个数,可不是一件简单的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法. 下面我们就一起来学习吧!基础篇使用数字 0, 1, 2, 3, 4, 5,6, 7, 8, 9 做加法 . 在每一道题中,同一个数字不能够重复出现.【授课思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填. 从前我们已经有过这样的练习,学生有了必然的基础 . 这道题的答案不仅一个,我们只要修业生能找到其中的一种就达到要求了 .( 1)右边两个圆的和应该是9,因此里可填(0, 9)( 2, 7)( 3, 6) .( 2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4 ,因此剩下两边上两个数能够填(0, 7),( 1,6),( 3, 4)(3) 7+6=13, 15-13=2 ,因此第 2 条线中间填 2. 左边第一条线: 15-7=8 ,0+8=3+5,数字不重复共两种填法 . 第三条线 15-6=9 , 0+9=4+5,数字不重复共两种填法( 4) 6+4=10, 13-10=3 ,因此第 2 条线最下是3,. 左边第一条线:13-6=7 , 0+7=2+5,数字不重复共两种解法 . 第三条线: 13-3=10 ,1+9=2+8,数字不重复共两种解法.拓展练习(1) 填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.【答案】【答案】在每个方格中填入合适的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.【授课思路】方法一:填数时,第一要看哪一行已经有了两个数,尔后用18 减去这两个数,就得出这一行的第三个数 . 填数的序次以下:方法二:从斜行来考虑:要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?【授课思路】第一我们要找到填这个表格的打破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填 . 找到这个打破口,后边就简单多了 . 方法一:从竖行下手 . 方法二:分别从两条对角线下手 .拓展练习在以下两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.【答案】【答案】把 1, 2, 3,4, 5, 6 六个数,分别填入○内,使每条线上 3 个数的和相等.【授课思路】比较三个已知数 1,2,3,和 1 比 2 大 1,3 大 2. 还剩下三个数 4,5,6 要我们来填, 5+6=116+4=10 5+4=9 ,要使每边和相等, 5+6+1=6+4+2=5+4+3=12,答案以下:提高篇把 3, 4, 5, 6, 7 这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.【授课思路】方法一:察见解. 要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数. 观察这五个数 3,4, 5,6, 7,我们发现 4 和 6,3 和 7 能够组成 10,它们分别再加上多出来的 5 都得 15,因此中间这个数应该填 5,上下,左右能够分别填 4 和 6, 3 和 7,如图:方法二:观察这些图,简单发现,中间方框中的数比较特别,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”. 只要我们确定了中间的“重叠数”填几,其余空格就简单了. 那么横行 3 个数的和加上竖列 3 个数之和就等于所要填入的 5 个数的和与重叠数的和. 于是( 3+4+5+6+7) +重叠数 =15+15,重叠数 =30-25=5 ,因此中间的这个数应该填5,在剩下的 4 个数 3, 4, 6, 7 中,只有 3+7=4+6=10,填法如图 .建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这类方法对于今后数字大的题就很难掌握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要修业生马上掌握,但是要让学生明确解答这样的题要从重叠数开始下手解析,今后练得多了就能贯通融会了. 若是老师感觉这几个数太大学生不简单接受,还可以够改成更小的数.拓展练习把 2, 3, 4, 5, 6 这五个数分别填入圆圈中,使每条线上三个数相加的和都等于 1 2.【答案解析】中间○即为特其余重叠数,因为它既是横线上的数,又是竖线上的数横行加上竖行之和应为12+12=24 ,而 2+3+4+5+6=20,中间的要多加一次,因此应为. 中间的数填什么呢4.?把 1,2, 3, 4, 5, 7 分别填入○里,使每一个大椭圆上的四个数之和等于13.【授课思路】方法一:察见解,在这 6 个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察 1, 2, 3, 4, 5,7 中 1 是公共数,这时我们发现2+7 和 4+5 都等于 9,因此剩下的 3 也应该是公共数, 2 和 7,4 和 5 应该分别填在这两个圆的左边和右边. 经检验每个大椭圆上的四个数这和等于13.方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,其余这 6 个数相加的和是1+2+3+4+5+7=22,26 和 22 之间相差的是什么呢?只有中间的这两个重叠数被多加了 1 次,这相差的 4 应该是两个重叠数的和,1+3=4,因此中间的这两个重叠数应该是 1 和 3. 剩下的数2+7=4+5=9.把 1, 2, 3, 4, 5, 6, 7 这七个数分别填入○里,使每条直线上的三个数相加的和都为12.【授课思路】方法一:察见解,在1, 2,3, 4, 5,6,7 这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是 4 时, 1+7=2+6=3+5=8, 8+4=12,如图:方法二:因为图中共有 3 条直线,因此中心的重叠数重叠了2=12+12+12. 重叠数 =(36-28 )÷ 2=8. 那么中间的数应该填数的和等于12-4=8 的有 1+7=2+6=3+5,如图:2 次,于是(14 剩下的 6 个数1+2+3+4+5+6+7) +重叠数×1,2,3,5,6, 7,中, 2 个拓展练习把1~ 9 这九个数字填入以下圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于 15.把 2, 3, 4, 5,6, 7, 8 这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.【授课思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+ 重叠数 =19+19.重叠数 =3,那么中间圆圈里面应该填 3. 剩下的数中2+6+8=4+5+7=19-3=16 ,因此每个正方形中,剩下的三个数应该填:2, 6,8 或 4, 5, 7. 详尽填法以下:拓展:若是使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把 1, 2, 3,4, 5, 6, 7 这 7 个数分别填入右图中,使得每条直线上的 3 个数的和相等.【授课思路】这道题的答案不唯一.附加题(老师可依照自己的课堂进度灵便办理讲义内容,附加题仅供老师参照使用. )在空格内填上合适的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】【授课思路】若是有充足的时间,建议这题可放在例 3 的后边做一个加深,这道题也主若是利用加减法之间的关系来解答的. 这个题我们要从已知三个加数的第二列下手开始填,先计算出这三个加数的和,再用64 减去这三个加数的和就获取了这第四个加数.用图中已有的三个数填满其余的空格,每个数字必定使用三次.使得每行、每列和两条对角线上的三个数之和相等.【答案】【答案】把 1~ 9 这九个数字填入以下圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于 15.【答案】【授课思路】这道题可参照放在例 6 的后边,做一个拓展 . 在例 6 的基础上,我们只要要调动四条边上各数的地址就可以考据出结果 .使用数字0, 1, 2, 3, 4, 5,6, 7, 8, 9 求和 . 而且同一个数在一幅图中不能够重复出现.【答案】【答案】把 1~ 11 这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.【答案】练习十二1. 在下面的○里填上合适的数,使每条线上的三个数之和都是12.【答案】2. 把 3~ 8 这 6 个数,填在以下列图中使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 把 1, 2,3, 4, 5 这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.【答案】4.把3,4,5,7,9,11,13这七个数分别填入○ 里,使每条直线上的三个数相加的和都为20.【答案】5.将1,2,3,4,5,6这6个数分别填入以下列图中,使两个大圆上 4 个数的和都等于14.【答案】6. 把数字 1,2, 3, 5, 6, 7, 9 填在下面的○里,使每边上的和为15.【答案】小朋友,你在少年宫里走过“勇敢者的道路”吗?道路曲折,充满困难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易经过,需要小朋友细心和有耐心 ..现在请小朋友用一枝铅笔,依照图中箭头的方向画出通行路线,而且线条不能够碰到两边的“围墙”小朋友,这可真不简单哦!。
奥数-一年级-教学导案-第十二讲-巧填数阵图-学生

奥数-一年级-教案-第十二讲- 巧填数阵图-学生作者:日期: 2第十二讲巧填数阵图晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子 •一个雪精灵告诉她们:“你们只要能够把1〜7这七个数填在雪花的七个花瓣上, 使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了• ”你能帮她们填一填吗?.,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法 下面我们就一起来学习吧!每边上的和为10 毎边匕的和为9小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数每边匕的和为13拓展练习填数,使横行、竖行的三个数相加都得11. (2) 填数,使每条线上的三个数之和都得15.在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?七7在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于门把5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于:拓展练习15.2, 3, 4, 5, 6六个数,分别填入O 内,使每条线上3个数的和相等.把3, 4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.:拓展练习1 2.1〜9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都6J>把 1 , 2,13.O 里,使每条直线上的三个数相加的和都为12.:拓展练习R-3, 4, 5, 6, 7这七个数分别填入等于15.819我会做一做o o12拓展:如果使两个正方形中四个数之和相等 I Ff21,又应该怎样填?1.在下面的O 里填上适当的数,使每条线上的三个数之和都是练习十把2, 3, 4, 5, 6, 7, 8这七个数分别填入圆圈中,使两个正方形中四个数之和相等把1, 2, 3, 4, 5, 6, 7这7个数分别填入右图中,使得每条直线上的3个数的和相等°183 104 5 把3将1 6.把数字使得每行、每列和两条对角线上的三个数的和都为2.把3〜8这6个数,填在下图中4个数的和都等于14把1 , 2, 3, 4, 5这五个数分别填入下面的O 里,使横行、竖行的三个数相加都得2, 3, 4, 5, 6这6个数分别填入下图中,使两个大圆 1, 2, 3, 5, 6, 7, 9填在下面的O 里,使每边上的和为154, 5, 7, 9, 11, 13这七个数分别填入 O 里,使每条直线上的三个数相加的和都为 20.□ □_□ ~小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻 •但是,它能培养小朋友的勇敢精神和不怕困难的毅力 •这里有两幅图,也叫“勇敢者的道路” •图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙” 小朋友,这可真不容易哦!为> ^YAYO勇敢者的游戏》1:亡结y Sg $亡□丄■■'Dy 0亡叩卍电,"4"。
巧填数阵图

巧填数阵图1.从1~13这十三个数中挑出十二个数,填入下图的小方格内,使每一横行的四个数的和相等,每一竖列的三个数的和也相等。
2.如图,“好、伙、伴、助、手、参、谋”这7个汉字分别代表1至7这7个数字,已知3条直线上的3个数相加、1个圆周上的3个数相加,所得的5个和相同,那么,“好”字代表多少?3.4个小三角形顶点处有6个圆圈。
若这些圆圈中分别填上6个质数,它们的和是20,且每个小三角形顶点上的和相等,完成该数阵图。
4.下图中有大、小六个正方形,将1~9九个数分别填入圈内,使每个正方形角上的四个数的和都相等。
5.下图中四个圆相交分割成阴影部分以及A、B、C、D、E、F、G、H、I九个空白部分,将1~9九个数填入这九个部分,使每个圆内四个数字之和都等于24,并要求I部分填入的是偶数。
6.下图的6条线分别连接着9个圆圈,其中一个圆圈里的数是6,请你选9个连续自然数(包括6在内)填入圆圈内,使每条线上各数的和都等于23。
7.请在下图的7个小圆圈内各填入一个自然数,使得图中给出的每个数都是相邻两个圆圈中所填数的差(大数减小数),并且所填的7个数之和是1997。
8.下图是奥林匹克的五环标志,其中a,b,c,d,e,f,g,h,i处分别填入整数1至9,如果每一个圆环内所填的各数之和都相等,那么这个相等的和最大是多少,最小是多少?9.有10个连续的自然数,9是其中第三大的数,现在把这10个数填到下图的10个方格中,每格内填一个数,要求图中3个2×2的正方形中的4个数之和相等,那么,这个和数的最小值是多少?10.能否将数0,1,2,…,9分别填入下图的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等?11.如下图,大三角形被分成了9个小三角形,试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形3条边的每5个数相加的和相等,问这5个数的和最大可能是多少?12.下图包括6个加法算式,要在圆圈里填上不同的自然数,使6个算式都成立,那么最右边的圆圈中的数最少是多少?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二讲巧填数阵图
数学乐园
晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.
【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.
小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不
是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!
基础篇
使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.
数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是
数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法
的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关
键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.
【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.
(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).
(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)
(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法
(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.
拓展练习
(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.
【答案】【答案】
在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.
【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:
方法二:从斜行来考虑:
要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.
拓展练习
在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.
【答案】
【答案】
把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.
【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:
提高篇
把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.
【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:
方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.
建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.
拓展练习
把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.
【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为 12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.
把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.
【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.
方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.
把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.
【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:
方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:
拓展练习
把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.
把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.
【教学思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个正方形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:
拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?
我会做一做
把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.
【教学思路】这道题的答案不唯一.
附加题
(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)
在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.
【答案】
【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.
用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.
【答案】【答案】
把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.
【答案】
【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.
使用数字0,1,2,3,4,5,6,7,8, 9求和.而且同一个数在一幅图中不能重复出现.
【答案】【答案】
把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.
【答案】
练习十二
1.在下面的○里填上适当的数,使每条线上的三个数之和都是1
2.
【答案】
2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.
【答案】
3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.
【答案】
4.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.
【答案】
5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.
【答案】
6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.
【答案】
小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.
这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细
心和有耐心.
现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
