力学第三章习题课
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
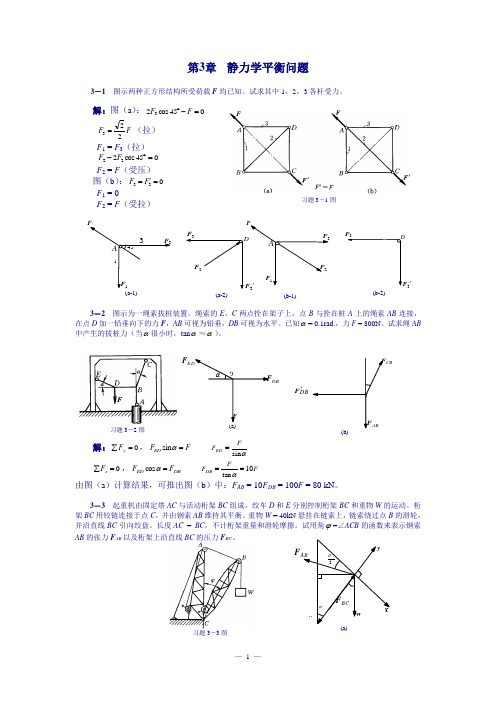
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
理论力学课后习题第三章解答

理论力学课后习题第三章解答3.1解 如题3.1.1图。
均质棒受到碗的弹力分别为,棒自身重力为。
棒与水平方向的夹角为。
设棒的长度为。
由于棒处于平衡状态,所以棒沿轴和轴的和外力为零。
沿过点且与轴平行的合力矩为0。
即:①②③ 由①②③式得:④ 又由于即⑤ 将⑤代入④得:图题1.3.11N ,2N G θl x y A z 0sin 2cos 21=-=∑θθN N F x0cos 2sin 21=-+=∑G N N Fyθθ0cos 22=-=∑θlG c N M i ()θθ22cos 1cos 22-=c l ,cos 2c r =θrc 2cos =θ3.2解 如题3.2.1图所示,均质棒分别受到光滑墙的弹力,光滑棱角的弹力,及重力。
由于棒处于平衡状态,所以沿方向的合力矩为零。
即①由①②式得:所以()cr c l 2224-=o图题1.3.21N 2N G y 0cos 2=-=∑G N Fyθ0cos 22cos 2=-=∑θθlG d N M z ld=θ3cos 31arccos ⎪⎭⎫ ⎝⎛=l d θ3.3解 如题3.3.1图所示。
棒受到重力。
棒受到的重力。
设均质棒的线密度为。
由题意可知,整个均质棒沿轴方向的合力矩为零。
3.4解 如题3.4.1图。
轴竖直向下,相同的球、、互切,、切于点。
设球的重力大小图题1.3.32AB i G ag ρ=1i G bgρ=2ρz ()BH BF G OD G M z --⋅=∑21sin θ=0sin cos 2sin 2=⎪⎭⎫ ⎝⎛--θθρθρa b gb a ga aba b 2tan 22+=θ图题1.3.4Ox A B C B C D为,半径为,则对、、三个球构成的系统来说,在轴方向的合力应为零。
即:①对于球,它相对于过点与轴平行的轴的合力矩等于零。
即:②由式得:3.5解 如题3.5.1图。
梯子受到地面和墙的弹力分别为,,受地面和墙的摩擦力分别为,。
大学物理第三章刚体力学基础习题答案

方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞,系统机械能守恒: 2 2 2 1 1 2 2 又: J M 2l Ml 12 3 6mu M 3m u 联立可得: v M 3m l M 3m
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后,经过t1时间到达了额定 转速,此时相应的角速度为 0。当关闭电源后,经 过t2时间风扇停转。已知风扇转子的转动惯量为 J, 并假定摩擦力矩和电机的电磁力矩均为常量,试根据 已知量推算电机的电磁力矩。 解: 设电机的电磁力矩为M,摩擦力矩为Mf
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得: a 22 k
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
结构力学第三版王焕定第3章习题及参考答案
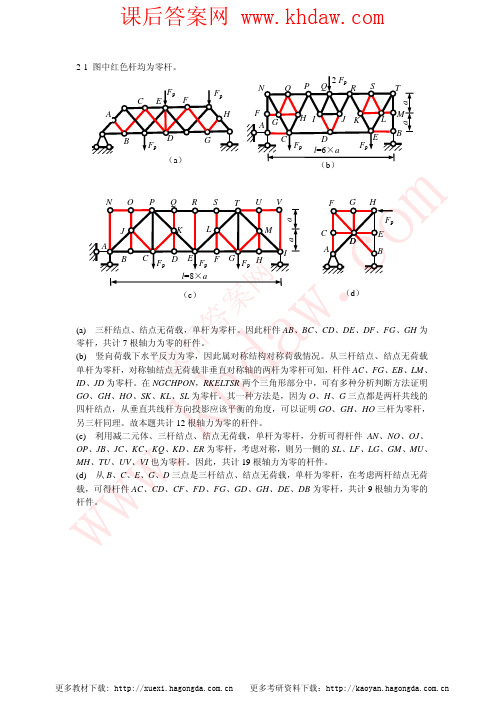
w.
cos α = 2 5
隔离体(b)
FN7 = FN8 = 35 kN
FN6 = FN5 = 65 kN
更多考研资料下载:
co
FN10
FN4
FN3
α α
隔离体(d)
m
40 kN FN4
课后答案网
2-2(b) Fp
θ
再取结点 B 作隔离体
FN4 = 26.67 kN
ww
更多教材下载:
w.
kh
更多考研资料下载:
da
课
后
答
w.
案 网
5 FN3 = − FN1 =33.33 kN 3 4 FN2 = FN1 = − 26.67 kN 3
1 0 8
12
13 6
4 5
7 4×2.5 m
17.5 kN 依次取结点为隔离体,受力图如下所示。 10 kN FN1 FN2
32.5 kN
2×1.25 m
2-2(a) 先求反力,结果如图所示。 10 kN 2
40 kN 3
α
FN8
FN1
α α
α
FN5
案 网
17.5 kN 隔离体(a)
FN9
32.5 kN 隔离体(c)
FN 2 = −30 2 kN=42.42 kN
FN3 = −15 2 kN= − 21.21 kN
更多教材下载:
更多考研资料下载:
co
FN4 45o FN1 FN3 (c)隔离体图
2-6(b)取 2、3 杆件相交的结点作隔离体图(a)所示,往FN2方向投影,列方程得:
( FN3 − FN4 ) sin 2α − 40 kN × cos α = 0, FN3 = 20 kN/sinα + FN4 = − 27.951 kN
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第3章 静力学平衡问题

FP
FP
FA
FB
习题 3-13 图
解:分析轴承受力为一组平行力系,由平衡方程:
习题 3-13 解图
∑ M B (F ) = 0 : − FP ×1380 − FA ×1020 + (G + Pδ ) × 640 = 0
解得, FA = 6.23kN (↑)
∑ Fy = 0 : FP + FA − (G + Pδ ) = 0
∑ M B (F ) = 0 : FT 50 − FW (300 cos 60D + 200) = 0
FT = 100(300 cos 60D + 200) / 50 = 700N
FT
FT
习题 3-17 图
Fw
习题 3-17 解图
∑ Fx = 0 : FT sin 30D − FB cosθ = 0 ∑ Fy = 0 : FT cos 30D − FB sinθ − FW = 0
α
FQ Cx FN
习题 3-11b 解图
取节点C为研究对象,见习题3-11b解图,
∑ Fy = 0 : F'BC cosα = FN
∴ FN
=
FP cosα 2 sin α
=
FP 2 tan α
=
3 × 15 2×2
= 11.25kN
3-12 蒸汽机的活塞面积为0.1m2,连杆AB长2m,曲柄BC长0.4m。在图示位置时, 活塞两侧的压力分别为p0=6.0×105Pa, p1=1.0×105Pa, ∠ABC=90D 。试求连杆AB作用于曲柄 上 的 推 力 和 十 字 头 A对 导 轨 的压力(各部件之间均为光滑接触)。
习题 3-14 解图
结构力学第03章习题课

集中力 作用点
集中力
铰处和自由端
偶作用点 有力偶 无力偶
剪水 力平 图线
斜 直 线
Q
为 零 处
有突变(突 变值等于该 集中力的 值)
如 变 号
无变化
无变化 无变化
弯 矩 图
斜 直 线
抛物线 (凸向 与q指向
相同)
有 极 值
有尖角(尖 角方向与集 中力指向相 同)
有 极 值
有突变 (突
变值等于该 集中力偶 值)
等于该 力偶值
为 零
(2)增量关系
DN = -Px DQ = -Py DM = m
(3)积分关系
NB = N A -
xB xA
q
x
dx
QB = QA -
xB xA
q
y
dx
M B = M A +
xBQdx
xA
.
3-6
二、分段叠加法作弯矩图
1、叠加原理 由各力分别产生的效果(内力、应力、变形、位移等)的 总和等于各力共同作用时所产生的效果。
(5) 内力图的绘制规定同前。
.
3-9
3、力学特性 (1) 具有超静定结构、静定结构两者的优点,截面弯矩 小,抗弯刚度好;
(2) 避开了超静定结构的缺点,不受温度变化、支座移 动(沉陷)的影响;
(3) 要保证较好的力学特性,关键是中间铰的设置。
四、静定刚架
1、刚架的特点
(1) 由直杆组成的结构(一般梁与柱刚结而成); (2) 结点全部或部分为刚结点; (3) 刚结点承受和传递弯矩,结点处各杆无相对转动; (4) 弯矩是刚架的主要内力。
该体系的组成次序为先固定
DF和GH,再固定FG和HI。因此 基本部分为DF和GH,附属部分为 FG和HI。
gxt3第三章工程力学课后题答案
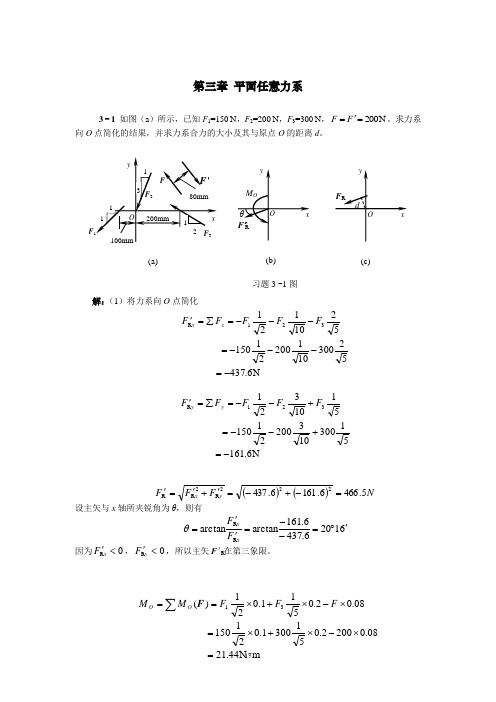
第三章 平面任意力系3-1 如图(a )所示,已知F 1=150N ,F 2=200N ,F 3=300N ,N 200='=F F 。
求力系向O 点简化的结果,并求力系合力的大小及其与原点O 的距离d 。
解:(1)将力系向O 点简化N6.43752300101200211505210121321R-=---=---=∑='F F F F F x xN6.16151300103200211505110321321R-=+--=+--=∑='F F F F F y y()()N F F F y x 5.4666.1616.437222R 2R R=-+-='+'='设主矢与x 轴所夹锐角为θ,则有61206.4376.161arctanarctanRR '︒=--=''=x y F F θ因为0R <'x F ,0R <'y F ,所以主矢F 'R在第三象限。
08.02002.0513001.02115008.02.0511.021)(31⨯-⨯+⨯=⨯-⨯+⨯==∑F F F M M O O F(a)(b) (c)将力系向O 点简化的结果如图(b )。
(2)因为主矢和主矩都不为零,所以此力系可以简化为一个合力如图(c ),合力的大小mm 96.4504596.05.46644.21N 5.466RR R ====='=m F M d F F o3-2重力坝的横截面形状如图(a )所示。
为了计算的方便,取坝的长度(垂直于图面)l =1m 。
已知混凝土的密度为2.4×103 kg/m 3,水的密度为1×103 kg/m 3,试求坝体的重力W 1,W 2和水压力P 的合力F R ,并计算F R 的作用线与x 轴交点的坐标x 。
解:(1)求坝体的重力W 1,W 2和水压力P 的大小kNN dy y dy y q P mN y dyy dy y q 5.9922105.9922245108.9)45(108.9)()45(108.9)45(8.91011)(3234534533=⨯=⨯⨯=⋅-⨯=⋅=-⨯=-⨯⨯⨯⨯⨯=⎰⎰(2)将坝体的重力W 1,W 2和水压力P 向O 点简化,则kN 5.9922R==∑='P F F x xkN 3057621168940821R-=--=--=∑='W W F F y y()kN 7.32145305765.9922222R 2R R=-+='+'='y x F F FkN N W kN N W 2116810211688.9104.2136)545(2194081094088.9104.218)545(332331=⨯=⨯⨯⨯⨯⨯+==⨯=⨯⨯⨯⨯⨯+=(a) (b) (c)设主矢与x 轴所夹锐角为θ,则有︒=-=''= 02.725.992230576arctanarctanRR x y F F θ因为0R >'x F ,0R <'y F ,所以主矢F 'R在第四象限,如图(b )。
土力学-第三章-土体中的应力计算 习题课 张丙印

L B
,
z B
)p
4F(12.5,2)p
p
x
C点:矩形荷载CDFH的附加应力
zC
Ksp
F(
L B
,
z B
)p
F(12.5,2)p
0.25zA 13.73kPa
y
L B
z
M
z 18
方法及讨论 –有效应力计算
课堂讨论题4:有效应力计算
板桩 基坑
k=5.0×10-6 m/s sat=1.8g/cm3
《土力学1》之习题课2
第三章习题讨论课
张丙印
清华大学土木水利学院 岩土工程研究所
第三章:习题讨论课
主要内容: • 习题讨论 • 小测验(30分钟) • 方法讨论 • 概念及难点
• 作业中的问题评述
• 附加应力计算 • 有效应力计算 • 太沙基固结模型
• 其它问题讨论
小测验 30分钟
3
方法及讨论 –有效应力计算与渗流固结
A点总应力:A=110kPa 孔隙水压力:u=60+10h kPa 有效应力:A=50-10h
粘土层发生流土: A=50-10h=0 h=5m
14
方法及讨论 – 附加应力计算
智者乐水 仁者乐山
课堂讨论题3:附加应力计算法
对如图所示的条形基础,作用有均布荷载p。已知A(基础中心 点)和B两点以下4m处的垂直附加应力分别为zA=54.9kPa和 zB=40.9kPa。求C点以下4m和8m处的垂直附加应力是多少?
8
方法及讨论 –有效应力计算与渗流固结
智者乐水 仁者乐山
d) 如发生渗流固结现象,画出t=0时的超静孔隙水压力分布。
T=0
T= 超静孔隙 (稳定渗流) 水压力
理论力学习题答案第三章

第三章思考题解答3.1 答:确定一质点在空间中得位置需要3个独立变量,只要确定了不共线三点的位置刚体的位置也就确定了,故须九个独立变量,但刚体不变形,此三点中人二点的连线长度不变,即有三个约束方程,所以确定刚体的一般运动不需3n 个独立变量,有6个独立变量就够了.若刚体作定点转动,只要定出任一点相对定点的运动刚体的运动就确定了,只需3个独立变量;确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量,确定任一点在平面上的位置需二个独立变量,共需三个独立变量;知道了定轴转动刚体绕转动轴的转角,刚体的位置也就定了,只需一个独立变量;刚体的平动可用一个点的运动代表其运动,故需三个独立变量。
3.2 答物体上各质点所受重力的合力作用点即为物体的重心。
当物体的大小远小于地球的线度时物体上各质点所在点的重力加速度都相等,且方向彼此平行即重力场为均匀场,此时质心与重心重合。
事实上但物体的线度很大时各质点所在处g 的大小是严格相等,且各质点的重力都指向地心,不是彼此平行的,重心与质心不和。
答 当物体为均质时,几何中心与质心重合;当物体的大小远小于地球的线度时,质心与重心重合;当物体为均质且大小远小于地球的线度时,三者都重合。
3.4 答 主矢F 是力系各力的矢量和,他完全取决于力系中各力的大小和方向,故主矢不随简化中心的位置而改变,故而也称之为力系的主矢;简化中心的位置不同,各力对简化中心的位矢i r 也就不同则各力对简化中心的力矩也就不同,故主矩随简化中心的位置而变,被称之为力系对简化中心的主矩。
分别取O 和O '为简化中心,第i 个力i F 对O 和O '的位矢分别为i r 和i r ',则i r =i r '+O O ',故()()iii ii i O F O O r F r M ⨯'-'=⨯'=∑∑'()∑∑⨯'-⨯'=ii ii i F O O F r ∑⨯'+=ii o F O O M即o o M M ≠'主矢不变,表明刚体的平动效应不变,主矩随简化中心的位置改变,表明力系的作用对刚体上不同点有不同的转动效应,但不改变整个刚体的转动规律或者说不影响刚体绕质心的转动。
普通物理学教程力学课后答案高等教育出版社第三章-动量定理及其守恒定律

第三章 动量定理及其守恒定律习题解答3.5.1 质量为2kg 的质点的运动学方程为j t t i t r ˆ)133(ˆ)16(22+++-=ρ(单位:米,秒), 求证质点受恒力而运动,并求力的方向大小。
解:∵j i dt r d a ˆ6ˆ12/22+==ρρ, j ia m F ˆ12ˆ24+==ρρ 为一与时间无关的恒矢量,∴质点受恒力而运动。
F=(242+122)1/2=125N ,力与x 轴之间夹角为:'34265.0/︒===arctg F arctgF x y α3.5.2 质量为m 的质点在o-xy 平面内运动,质点的运动学方程为:j t b i t a r ˆsin ˆcos ωω+=ρ,a,b,ω为正常数,证明作用于质点的合力总指向原点。
证明:∵r j t b it a dt r d a ρρρ2222)ˆsin ˆcos (/ωωωω-=+-== r m a m F ρρρ2ω-==, ∴作用于质点的合力总指向原点。
3.5.3 在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷粒,一方面逐出秸杆,筛面微微倾斜,是为了从较低的一边将秸杆逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才可能将谷粒筛出,若谷粒与筛面静摩擦系数为0.4,问筛沿水平方向的加速度至少多大才能使谷物和筛面发生相对运动?解:以地为参考系,设谷物的质量为m ,所受到的最大静摩擦力为 mg f oμ=,谷物能获得的最大加速度为2/92.38.94.0/s m g m f a o =⨯===μ ∴筛面水平方向的加速度至少等于3.92米/秒2,才能使谷物与筛面发生相对运动。
μ1μ23.5.3 题图 3.5.4题图3.5.4 桌面上叠放着两块木板,质量各为m 1 ,m 2,如图所示,m 2和桌面间的摩擦系数为μ2,m 1和m 2间的摩擦系数为μ1,问沿水平方向用多大的力才能把下面的木板抽出来。
解:以地为参考系,隔离m 1、m 2,其受力与运动情况如图所示,其中,N 1'=N 1,f 1'=f 1=μ1N 1,f 2=μ2N 2,选图示坐标系o-xy ,对m 1,m 2分别应用牛顿二定律,有0212222211111111=--=--=-=g m N N a m N N F g m N a m N μμμ 解方程组,得()2221211211/m g m g m g m F a ga μμμμ---==要把木板从下面抽出来,必须满足12a a >,即gm g m g m g m F 12221211μμμμ>---()()g m m F 2121++>∴μμ3.5.5 质量为m 2的斜面可在光滑的水平面上滑动,斜面倾角为α,质量为m 1的运动员与斜面之间亦无摩擦,求运动员相对于斜面的加速度及其对斜面的压力。
流体力学第三章课后习题答案

流体⼒学第三章课后习题答案⼀元流体动⼒学基础1.直径为150mm 的给⽔管道,输⽔量为h kN /7.980,试求断⾯平均流速。
解:由流量公式vA Q ρ= 注意:()vA Q s kg h kN ρ=?→//A Qv ρ=得:s m v /57.1=2.断⾯为300mm ×400mm 的矩形风道,风量为2700m 3/h,求平均流速.如风道出⼝处断⾯收缩为150mm ×400mm,求该断⾯的平均流速解:由流量公式vA Q = 得:A Q v =由连续性⽅程知2211A v A v = 得:s m v /5.122=3.⽔从⽔箱流经直径d 1=10cm,d 2=5cm,d 3=2.5cm 的管道流⼊⼤⽓中. 当出⼝流速10m/ 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速解:(1)由s m A v Q /0049.0333==质量流量s kg Q /9.4=ρ (2)由连续性⽅程:33223311,A v A v A v A v ==得:s m v s m v /5.2,/625.021==4.设计输⽔量为h kg /294210的给⽔管道,流速限制在9.0∽s m /4.1之间。
试确定管道直径,根据所选直径求流速。
直径应是mm 50的倍数。
解:vA Q ρ= 将9.0=v ∽s m /4.1代⼊得343.0=d ∽m 275.0 ∵直径是mm 50的倍数,所以取m d 3.0= 代⼊vA Q ρ= 得m v 18.1=5.圆形风道,流量是10000m 3/h,,流速不超过20 m/s 。
试设计直径,根据所定直径求流速。
直径规定为50 mm 的倍数。
解:vA Q = 将s m v /20≤代⼊得:mm d 5.420≥ 取mm d 450= 代⼊vA Q = 得:s m v /5.17=6.在直径为d 圆形风道断⾯上,⽤下法选定五个点,以测局部风速。
设想⽤和管轴同⼼但不同半径的圆周,将全部断⾯分为中间是圆,其他是圆环的五个⾯积相等的部分。
大学物理课后习题答案第三章

第3章 力学基本定律与守恒律 习题及答案1.作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j6-m ·s -1的物体,回答这两个问题. 解: (1)若物体原来静止,则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理, 12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ,(s 20='t 舍去)2.一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入,得 ba I 22= (3)由动量定理可求得子弹的质量202bv a v I m == 3.如图所示,一质量为m 的球,在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。
《流体力学》徐正坦主编课后答案第三章

第三章习题简答3-1 已知流体流动的速度分布为22y x u x -= ,xy u y 2-=,求通过1,1==y x 的一条流线。
解:由流线微分方程yx u dyu dx =得dy u dx u x y =则有 dy y x xydx )(222-=-两边积分可得C y y x yx +-=-3322即0623=+-C y x y将x=1,y=1代入上式,可得C=5,则 流线方程为05623=+-y x y3-3 已知流体的速度分布为⎭⎬⎫==-=-=tx x u ty y u y x 00εωεω(ω>0,0ε>0)试求流线方程,并画流线图。
解:由流线微分方程yx u dyu dx =得dy u dx u x y =则有 tydy txdx 00εε-=两边积分可得C y x +-=22流线方程为C y x =+223-5 以平均速度s m v /5.1=流入直径为D=2cm 的排孔管中的液体,全部经8个直径d=1mm 的排孔流出,假定每孔出流速度依次降低2%,试求第一孔与第八孔的出流速度各为多少?题3-5图解:由题意得:v 2=v 1(1-2%),v 3=v 1(1-2%)2,…,v 8=v 1(1-2%)7 根据质量守恒定律可得282322212832144444dv d v d v d v D v Q Q Q Q Q πππππ⋅+⋅⋅⋅+⋅+⋅+⋅=⋅+⋅⋅⋅+++=sm d vD v v d v v v v d D v /4.80)98.01(001.002.002.05.1)98.01()98.01(98.01)98.01(4)(448228221812832122=-⨯⨯⨯=--⋅=∴--⋅=+⋅⋅⋅+++⋅=⋅πππ则 v 8=v 1(1-2%)7=80.4×(1-2%)7=69.8m/s3-6 油从铅直圆管向下流出。
管直径cm d 101=,管口处的速度为s m v /4.11=,试求管口处下方H=1.5m 处的速度和油柱直径。
工程力学 同济 2版 第三章静力学专题

[例7] 由不计自重的三根直杆组成的A字形支架置于光滑地面 上,如图 a) 所示,杆长AC=BC=L=3 m,AD=BE=L/5,支架 上有作用力F1=0.8 kN,F2=0.4 kN,求横杆DE的拉力及铰C和A 、B处的反力。
(a)
(b)
(c)
23
解 A字形支架由三根直杆组成,要求横杆DE的拉力和铰C的 反力,必须分开研究,又DE为二力杆,所以可分别研究AC和BC 两部分,但这两部分上A、B、C、D、E处都有约束反力,且未 知量的数目都多于3个。用各自的平衡方程都不能直接求得未知 量。如果选整个系统为研究对象,则可一次求出系统的外约束 反力。 (1) 先取整体为研究对象,在其上作用有主动力Fl和F2,A、 B处均为光滑面约束,而A处是两个方向上受到约束,因而约束 反力有FAx,FAy和FB,并选取坐标轴如图 b) 所示。列出平衡方 程
目
录
§3-1 物体系统的平衡问题
§3-2 特殊构架—平面桁架
2
§3-1 物体系统的平衡问题
一、静定与超静定的概念 我们学过: ∑X = 0
平面汇交力系
力偶系 平面 任意力系
Y ∑ =0
两个独立方程,只能求两个独立未知数。
一个独立方程,只能求一个独立未知数。 三个独立方程,只能求三个独立未知数。
m ∑
i
=0
X ∑ =0 Y ∑ =0
m ∑
O
( Fi ) = 0
当:独立方程数目≥未知数数目时,是静定问题(可求解) 独立方程数目<未知数数目时,是静不定问题(超静定问题)
3
[例 ]
静定(未知数三个)
静不定(未知数四个)
静不定问题在强度力学(材力,结力,弹力)中用位移协 调条件来求解。
03 力学:第三章 动量与角动量-课堂练习及部分习题解答

Zhang Shihui
题.设行星的质量为m,它绕太阳运动的角动量为L0,试 推导行星绕太阳运动的掠面速度(即行星的矢径单位时 间内扫过的面积)表达式 。 解:在dt的时间内,矢r 处的速度 v 同向 Δr v 与 夹角为 θ ,即 与 夹角为 θ r r Δ r r h θ Δr 顶点到 r 的距离 h = Δr sin θ 1 在dt的时间内,矢径扫过的面积 ΔS = r Δr sin θ 2 L0 1 1 dS 1 L= ΔtÆ0, dr = vdt 故 = r v sin θ = r × v = 2m 2m 2 dt 2
r
地心O
M = r ×F =0 r1 R + l1 因此,角动量守恒 r1mv1 = r2 mv2⇒ v2 = v1 = v1 r2 R + l2
v
因万有引力F始终沿地心指向卫星, 与矢径方向相同,故
学习指导·第三章 动量和角动量·典型例题第4题
Zhang Shihui
题. 匀质的柔软细绳铅直悬挂着,绳的下端刚好触到水平地 面上。如把绳的上端释放,绳将落到地面上。试证明:在 绳下落过程中,任意时刻作用于地面的压力(大小),等 于已落到地面上的绳重量的三倍。 解:设单位绳长的质量为λ。t时刻已经落到地面 的绳长为x,这部分绳子对地面的压力N0 = (λ x) g 此外,即将接触地面的质元dm对地面的冲量dp 会产生一个额外的冲力F (注:质元长dx,下落 的距离为x) 。设此瞬间质元的速度为v,则
m
解:水平方向M和m组成的系统所受合外 力为零,因此质心在水平方向不受外力作 用,质心水平方向分量保持不变,等于0
Μ
mΔx + M ΔX mx + MX ⇒ Δxc = =0 xc = m+M m+M
弹性力学简明教程(第四版)第三章课后习题答案

③在 x=0,x=l 的次要边界上,面力可写成主矢、主矩形式: x=0 上 x=l 上
x向主矢:FN1 = y向主矢:FS1 = 主矩:M 1 =
h/2 -h/2
h/2
h / 2 h/2
f x dy 0, f y dy F ,
FN2 FS2
h/2
h / 2 h/2
h / 2
④在次要边界 x l 上,分布面力为
f x x l x x l f y x l xy
主矩: 弹性体边界上的面力分布及在次要上面力的主矢和主矩如图所示
M'
x x l ydy h / 2 2blydy 0 h / 2
(3) cxy
3
将应力函数代入公式(2-24) ,得应力分量表达式
x 6cxy, y 0, xy yx 3cy 2
考察应力边界条件,主要边界,由公式(2-15)得
y
在
h h h f x y bh, f y y 0 2 2 2 主要边界,上边界上,面力为
在
y
h h h f x y bh, f y y 0 2 2 2 ,下边界上,面力为
面力的主矢、主矩为 x 向主矢
Fx
x x l dy h / 2 6clydy 0 h / 2
h/2 h / 2
h/2
h/2
y 向主矢:
Fy
h/2
y x l
dy
h/2
h/2
h / 2
ch 3cy dy 1 4
2
3
主矩:
结构力学课后练习题+答案

第三章 静定结构的位移计算
一、判断题:
1、虚位移原理等价于变形谐调条件,可用于求体系的位移。 2、按虚力原理所建立的虚功方程等价于几何方程。 3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内 力,但会有位移且位移只与杆件相对刚度有关。 4、求图示梁铰 C 左侧截面的转角时,其虚拟状态应取:
P 2I
I
I
6m
2I
I
I
6m
8m
25、用力法计算图示结构并作 M 图。EI =常数。
20 kN
4m
3m
4m
3m
26、用力法计算图示结构并作 M 图。EI =常数。
P
P
l
l /2 l /2
l
l /2 l /2
27、利用对称性简化图示结构,建立力法基本结构(画上基本未知量)。E =常数。
—— 33 ——
B A
l
2l
23、求图示刚架 C 点的水平位移 CH ,各杆 EI = 常数 。
2kN/m C
3m
4m
4m
24、求图示刚架 B 的水平位移 BH ,各杆 EI = 常数 。
7kN/m
B
q
4m
3m 4m
25、求图示结构 C 截面转角。已知 :q=10kN/m , P=10kN , EI = 常数 。
8、用力法作图示结构的 M 图。
28 kN 3
C
4kN/m
EI 3m
A
EI
B
3m
9、用力法作图示排架的 M 图。已知 A = 0.2 m2 ,I = 0.05 m4 ,弹性模量为 E0 。
—— 29 ——
工程力学第三章:平面任意力系

水平尾翼的约束。
车刀
利用平面任意力系的简化讨论固定端约束(以雨搭为例):
Fi
A
雨搭
雨搭
简化为一个平面任意力系
MA
A
FA
雨搭
FAy
MA
A
FAx
雨搭
向A处简化,简化结果是 一个主矢加一个主矩
主矢方向待定,用两正交分 量表示
例1:已知F1=150N,F2=200N,F3=300N,F=F ́=200N。求此力 系向原点O简化的结果,并求力系的合力。
2
M=0
FR′≠0
3
M=0
合力
合力
合力作用线通过简化中心
合力作用线距离简化中心距离
4
M≠0
d M O / FR
第三种和第四种结果属于同一种情形。是简化中心选择的不同 引起的。
四、合力矩定理
可以证明,M O ( FR ) M O ( Fi )
i 1
n
由于简化中心可任取,因此上式有普遍意义,可描述为:平 面任意力系的合力对作用面内任一点之矩等于力系中各分力 对于同一点之矩的代数和。
4、在列平衡方程时,最好将力矩方程的矩心取为两个未知力的 交点,而对投影方程的投影轴的选取,应尽可能使其与某些未知 力垂直,为什么? 答:避免解联立方程,使方程尽量简单。
5、在等腰直角三角形上的A、B、C三点分别作用三个力,各力 的大小和方向如图所示。问该力系是否平衡?为什么?
问题引入:平面任意力系研究物体或物系在受到相关力系作用
下的平衡问题。
吊车:工程中吊车的
起重载荷如何进行计
算?
破碎机:鄂式破碎机是矿山机械中常见的机械设备,颚板作用 给矿石的作用力应如何进行计算?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(m − M )v0 − 2 MvM v= m+M
因为M>>m,即有:
v = − v0 − 2vM = 29.6km / s
第三章练习题2
解答2
(1)对0 ≤ x ≤ l,有:Fx = k1 (l − x), 1 2 k1 x − k1lx x 2 对x < 0, 有:Fx = k1 (l − x) − k 2 x E p ( x) = ∫ Fx dx =
解答5
代数后得: v1x=2.17m/s, v1y=2.49m/s, v2=1.08m/s 故v1=3.30m/s 碰后小球最高位置相对原碰撞点的高度为: hmax=v1y2/2g=0.32m
设碰后小球将落于地面,则其间历时 v1 y + 2(hmax + H ) / g = 0.773s t= g 此段时间内小球水平向右的位移和斜面体水平向左的位移量分别为 lm = v1x t = 1.68m, lM = v2t = 0.835m 如小球落于地面,则要求lm + lM > H cot θ = 3.73m 显然不成立
第三章练习题6
解答6
车厢系中,小球右滑或左滑离开圆柱面的方位角如图所示,应有 mu '2 1 mg cos φ = , mu '2 = mgR(1 − cos φ ) R 2 可解得 : cos φ = 2 , u ' = 2 gR 3 3 地面系中,小球初速u0 = v0 , 右滑或左滑离开圆柱面时的速度u可 分解为水平x方向与竖直y方向分量,各为: u x = v0 ± u ' cos φ , u y = u ' sin φ 过程中圆柱面支持力N对小球做功: 1 1 2 2 2 W = m(u x + u y ) − mgR(1 − cos φ ) + mv0 2 2 2 2 可算得:W = ± mv0 gR , (+:右行滑离; :左行滑离) − 3 3
• 补充题2 系统如图示,滑轮不动,滑轮与绳间无摩擦,绳的 质量线密度为常量λ,且有m1+ λh1>m2+ λh2。 试求m1下行加速度a和半圆部分绳中张力T 的角分 布。
解答
分析ϕ角处微元的受力 T (ϕ + ∆ϕ ) − T (ϕ ) − ∆ϕRλg cos ϕ (重力分力) = ∆ϕRλa dT = ∆ϕRλ (a + g cos ϕ ) 积分得T − T2 = ∫ Rλ (a + g cos ϕ )dϕ = ϕRλa + Rλg sin ϕ
1 5
1 v⊥ = =5 v// 2 µ
2 gH v⊥ 2 gH , 此时t N > ∆t f , 有 tan φ = = v0 v0
第三章练习题4
解答4
• 分析:下降H/4时,小重物下降速度大于0
对于系统与地面构成的大系统,有机械能守恒 1 [λ (πR + H ) + m]v02 = 1 [λ (πR + H ) + H ]v 2 + λ H g ( H − H ) − mg H 2 2 4 4 4 1 m = λH 2 为使小重物在H / 4处v > 0,要求 1 [λ (πR + H ) + m]v02 > λ H g ( H − H ) − mg H 2 4 4 4 H g 即v0 > 2 2πR + 3H
T = T2 + ϕRλa + Rλg sin ϕ
第二次作业题选讲2
• 补充题7 光滑的细长直管道绕着它的某一固定部位P在水平面上旋转, 转动角速度始终为常量ω。质量为m的小球开始时静止在管 内P处,后因受到微小的扰动离开P点沿着管道运动。试求 小球与P相距x时,管壁受小球的作用力大小N。
解答
以管为参考系,小球径dv dt dv dv dx dv = = v = xω 2 dt dx dt dx
第三章练习题5
解答5
m碰到M前竖直向下速度为u0 = 2 gh 碰后m速度v1有水平分量v1x , 竖直分量v1 y , M碰后水平速度为v2 水平方向动量m守恒:mv1x = Mv2 m碰撞后前后沿斜面方向速度不变:v1x cos θ − v1 y sin θ = u0 sin θ 由e涉及的m,M法向碰撞关系,有:1x sin θ + v1 y cos θ ) + v2 sin θ = eu0 cos θ (v 由以上三式可解得 (1 + e) sin θ cos θ v1x = u0 2 m 1 + M sin θ (1 + e) cos 2 θ − 1u0 v1 y = 2 m 1 + M sin θ (1 + e) sin θ cos θ v2 = u0 2 M m + sin θ
0
1 E p ( x) = ∫ Fx dx = (k1 + k 2 ) x 2 − k1lx x 2 (2)对0 ≤ x ≤ l,有:Fx = k1 (l − x),
0
1 2 1 2 E p ( x) = ∫ Fx dx = k1 x − k1lx + k1l x 2 2 对x < 0, 有:Fx = k1 (l − x) − k 2 x
0
ϕ
令ϕ = π , T1 = T2 + πRλa 对两端进行受力分析 (m1 + λh1 ) g − T1 = (m1 + λh1 )a T2 − (m2 + λh2 ) g = (m2 + λh2 )a 所以a = m1 − m2 + λ (h1 − h2 ) g , T2 = (m2 + λh2 )( g + a ) m1 + m2 + λ (h1 + h2 + Rπ )
弹弓效应
弹弓效应:小天体或航天飞行器借助于大质量天体的重力来获得 更大的动能. 行星、宇宙飞船 二体系统 万有引力 交换轨道能量与动量 动量守恒、能量守恒 宇宙飞船能量增加、 动量增加,周期变长 双曲线轨道
应用举例:1997年发射的“卡西尼”号,经过四次“弹弓效应” 加速,获得足够能量到达土星。
解答1
l
E p ( x) = ∫
0
x
1 1 2 2 Fx dx = (k1 + k 2 ) x − k1lx + k1l 2 2
第三章习题3
• 长平板在水平方向上以恒定的速率v0朝右运动,板上方H 高处有一个小球从静止自由下落与平板碰撞。已知球与 平板间摩擦因数u=0.1,小球反弹高度仍为H,试确定小 球反弹抛射角Φ与正切tanΦ与 H 之间的函数关系。
力学第三章习题课
助教:王钟堂 2011-4-14
前两次作业完成情况
• 第一次作业未交同学:
• 00746143 00986037 00986042 1000010494
• 第二次作业未交同学:
• 00746143 00986037 1000011003 1000011055 1000062701
第二章作业题选讲1
v 2 x 0 0
∫ vdv = ω ∫
xdx, v = xω
小球在水平面垂直于管方向上有向下的科氏力Fcor Fcor = 2mvω = 2mxω 2 竖直方向上受壁弹力N ⊥ = mg
2 故N = Fcor 2 + N ⊥ = 4m 2 x 2ω 4 + m 2 g 2
机械能定理
元功: dW = F • dl 质点动能定理(W=△Ek) 保守力 势能 质点组机械能定理(△E=W内 +W ) 质点系动能定理(W内+W =△Ek)
解答3
解:设碰撞时间∆t N内正碰力平均值为N,小球受摩擦力作用 时间记为∆t f ,平均摩擦力为f,必有:∆t N ≤ ∆t f 小球碰撞前竖直方向速度为v⊥ = 2 gH , 碰撞过程的冲量、动量关系为 N∆t N = 2mv⊥ , f ∆t f = mv// , v// 是小球碰后的水平速度 若∆t N = ∆t f ,则可得 f = µ N,v// = 2 µv⊥ = 2µ 2 gH 真实的v// 不可超过v 0,要求2µv⊥ ≤ v 0 故∆t N = ∆t f 的条件是v 0 ≥ 2 µ 2 gH 所以当v 0 ≥ 2µ 2 gH = 1 2 gH ,有 tan φ = 5 当v 0 < 2 µ 2 gH =
质点组动能变化定理 机械能守恒定律 碰撞:弹性vs非弹性
一维&二维
第三章练习题1
• “弹弓效应”是航天技术中增大宇宙探测速率的一种有效 方法,如图所示,土星以相对太阳的轨道速率vM=9.6km/s 运行,一空间探测器以相对于太阳的速率v0=10.4km/s迎 向土星飞行,由于土星的引力,探测器绕过土星沿着河原 来相反的方向离去,试求探测器离去时相对于太阳的速率 v。
