高考数学140冲刺专题：29立体几何中的最值问题含解析38

合集下载

高考立体几何与导数结合求最值的例题分析

高考立体几何与导数结合求最值的例题分析在高中数学中，立体几何和微积分是两个重要的分支。

它们的结合使用可以解决许多实际问题。

本文将主要讨论如何使用立体几何和导数结合求解一个实际问题的例子。

问题描述有一块铁皮，它的形状如下图所示。

其中ABCD为矩形底面，EF为底面中线，AEB和DFC为两个底面上的直角三角形。

现在我们要从这块铁皮中切出一个正方体，使得这个正方体的体积最大。

image-1image-1解题思路为了求解这个问题，我们可以通过以下几个步骤来完成：1.设正方体的边长为x，则正方体的体积为V(x)=x3。

我们需要求解使得V(x)最大的x。

2.画出问题的立体图形，如下所示。

我们可以使用立体几何中的相关定理求出图形中各个部分的长度。

3.找到求最大值的方法。

根据导数的定义，函数V(x)的导数V′(x)表示函数V(x)在点x处的变化率。

当导数为零时，函数处于极值点，可以通过求解导数为零的方程求得函数的最大值。

image-2image-2求出图形中各部分的长度根据图形中的几何关系，我们可以求出各个部分的长度，如下所示：1.左侧斜面的高度 $AD=BF=\\frac{\\sqrt{2}}{2}AB$。

2.后侧斜面的高度 $AE=\\frac{1}{2}AB$。

3.前侧斜面的高度 $CF=\\frac{1}{2}AB$。

4.底面半长 $AF=\\frac{1}{2}AB$。

求解导数为零的方程我们已经知道了正方体的体积为V(x)=x3，其中x表示正方体的边长。

现在我们需要求解函数在什么条件下达到最大值。

根据高中数学中的微积分知识，函数在极值点处的导数为零。

因此，我们可以通过求解导数为零的方程来确定正方体边长的最大值。

首先求出导数V′(x)：V′(x)=3x2令V′(x)=0，解得x=0或 $x=\\pm\\sqrt{\\frac{1}{3}}$。

因为x表示的是正方体的边长，所以x必须为正数。

因此，我们可以得到正方体的边长为 $\\sqrt{\\frac{1}{3}}$ 时体积最大。

立体几何中的最值问题

在 △Ａ中，由余弦定理，得ＡＡ一１１。
于点Ｄ，则ＰＤ上ＢＣ，且球０与面ＰＢＣ的切点Ｅ在
故截面ＡＡＤＥ周长的最小值为ｌ１。
说明：对于几何体表面上两点距离的最值问题，
ＰＤｋ
现考虑截面ＰＡＤ（如图
一 … ｔ一。
过点０作Ｏ０上平面ＡＢＣ，垂足为０ｌ，设００１一
ｚ，则点Ｄ到平面ＡＢＣ的距离为１＋。
所以
１ ·
ＰＯ￣－
一
因为０１Ａ一０１Ｂ＝＝＝０１Ｃ＝￣／１６一ｚ。，所以Ｓ△ＡＢｃ≤
２
一（ｔａｎｚ一专）。＋丢。故当ｔａｎ。一号时，。取得最小值为８。
解：当Ａ，Ｂ，ｃ三点固定时，要使四面体ＡＢＣＤ
‘）
０１Ｄｔａｎ２０一
，ＡＤ一
的体积最大，则点Ｄ到平面ＡＢＣ的距离应最大。由
于点Ｄ在以０为球心，１为半径的球面上运动，故当３０。Ｄ：＝＝３ｃｏｔ０。从而，正三角形ＡＢＣ的边长为ｎ一Ｄ０上平面ＡＢＣ时，四面体ＡＢＣＤ的体积最大。
形面积为最大，且最大面积为Ｒ。。
‘士
例４如图３，四棱锥
ＡＢＣＤ的底面是平行四边形，过
点Ａ和侧棱ＳＣ的中点Ｍ作平
面分别交侧棱ＳＢ，ＳＤ于点Ｐ，．
Ｔ，
Ｑ，求
的最大值和最小值。

高中数学立体几何中的最值问题

高中数学立体几何中的最值问题在高中数学的学习中，立体几何一直是一个重点和难点，而其中的最值问题更是让许多同学感到头疼。

这类问题往往需要我们综合运用空间想象力、几何知识以及数学方法来求解。

接下来，让我们一起深入探讨立体几何中的最值问题。

一、常见类型及解法1、距离最值问题（1）两点间距离最值在立体几何中，求两点间距离的最值，常常需要我们将空间中的两点转化到同一平面内。

例如，在长方体中，求异面直线上两点的最短距离，就需要通过平移将其转化为共面直线，然后利用平面几何中的知识求解。

（2）点到直线距离最值求点到直线的距离最值时，通常要找到点在直线上的投影。

如果直线是某一平面的斜线，那么可以通过作垂线找到投影，再利用勾股定理计算距离。

（3）点到平面距离最值对于点到平面的距离最值，一般可以利用空间向量法。

先求出平面的法向量，然后通过向量的数量积来计算点到平面的距离。

2、面积最值问题（1）三角形面积最值在立体几何中，涉及三角形面积的最值问题，可能需要考虑三角形的边长关系或者角度大小。

例如，已知三角形的两边及其夹角，当夹角为直角时，面积最大。

（2）四边形面积最值对于四边形，如平行四边形，其面积可以表示为底边乘以高。

当底边长度固定时，高取得最大值时面积最大；或者当四边形的对角线相互垂直时，面积等于对角线乘积的一半。

3、体积最值问题（1）柱体体积最值对于柱体，如圆柱、棱柱，其体积等于底面积乘以高。

当底面积不变时，高最大则体积最大；反之，高最小时体积最小。

（2）锥体体积最值锥体体积为三分之一底面积乘以高。

在求解锥体体积最值时，需要关注底面积和高的变化。

二、例题分析例 1：在棱长为 2 的正方体 ABCD A1B1C1D1 中，E、F 分别是棱AB、BC 的中点，求点 A1 到直线 EF 的距离。

解：连接 A1C1、C1F、EF，因为 A1C1 平行于 EF，所以点 A1 到直线 EF 的距离等于点 A1 到直线 C1F 的距离。

高三数学立体几何中的最值问题复习

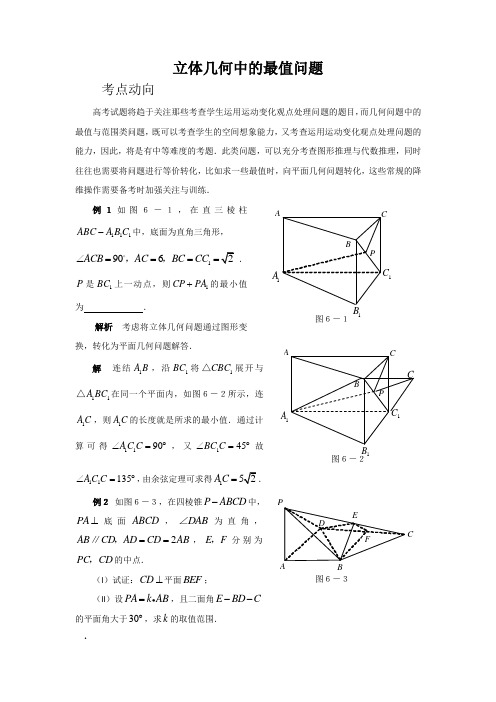
突破立体几何之《立体几何中的最值问题》考点动向高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难度的考题．此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练．例１如图６－１，在直三棱柱111ABC A B C -中，底面为直角三角形，1906ACB AC BC CC ∠==== ，，．P 是1BC 上一动点，则1CP PA +的最小值为．解析考虑将立体几何问题通过图形变换，转化为平面几何问题解答．解连结1A B ，沿1BC 将1CBC △展开与11A BC △在同一个平面内，如图６－２所示，连1AC ，则1AC 的长度就是所求的最小值．通过计算可得1190AC C ∠=︒，又145BC C ∠=︒故11135AC C ∠=︒，由余弦定理可求得1AC =．例２如图６－３，在四棱锥P ABCD -中，PA ⊥底面A B C D ，DAB ∠为直角，2A B C D A D C D A B ==，∥，E F ，分别为PC CD ，的中点．（I ）试证：CD ⊥平面BEF ；（II ）设PA k AB =，且二面角E BD C --的平面角大于30︒，求k 的取值范围．解析对（I ），可以借助线面垂直的判定定理，或者借助平面的法向量及直线的方向A1A 11图６－１AC PB1A1C1B图６－２C C图６－３向量解答；对（II ），关键是确定出所求二面角的平面角．解法１（I ）证：由已知DF AB ∥且DAB ∠为直角，故ABFD 是矩形，从而CD BF ⊥．又PA ⊥底面ABC D ，CD AD ⊥，故由三垂线定理知CD PD ⊥．在PDC △中，E ，F 分别为PC ，CD 的中点，故EF PD ∥，从而CD EF ⊥，由此得CD ⊥面BEF ．（II ）连接AC 交BF 于G ，易知G 为AC 的中点，连接EG ，则在PAC △中易知EG PA ∥．又因PA ⊥底面ABCD ，故EG ⊥底面ABCD ．在底面ABCD 中，过G 作GH BD ⊥，垂足为H ，连接EH ，由三垂线定理知EH BD ⊥，从而EHG ∠为二面角E BD C --的平面角．设AB a =，则在PAC△中，有1122EG PA ka ==．以下计算GH ，考虑底面的平面图（如图６－５），连接GD ，因1122BD S BD GH GB DF == △G ，故GB DFGH BD = ．在ABD △中，因AB a =，2AD a =，得BD =．而1122GB FB AD a ===，DF AB =，从而得GB AB GH BD ===．因此1tan kaEG EHG GH ===．故0k >知EHG ∠是锐角，故要使30EHG >∠，必须tan 3023>=，解之得，k的取值范围为15k >．解法２（I ）如图６－６，以A 为原点，AB 所在直线为x 轴，AD 所在直线为y 轴，AP 所在直线为z 轴建立空间直角坐标系，设AB a =，则易知点A ，B ，C ，D ，F 的坐标分别为()000A ，，，()00B a ，，，()220C a a ，，，()020D a ，，，()20F a a ，，．C图６－４图６－５A从而(200)(020)DC a BF a ==，，，，，，0DC BF = ，故DC BF ⊥ ．设PA b =，则(00)P b ，，，而E 为PC 中点，故2b E a a ⎛⎫ ⎪⎝⎭，，，从而02b B E a ⎛⎫= ⎪⎝⎭ ，，．0DC BE = ，故D C B E⊥．由此得CD BEF ⊥面．（II ）设E 在xOy 平面上的投影为G ，过G 作GH BD ⊥垂足为H ，由三垂线定理知EH BD ⊥．从而EHG ∠为二面角E BD C --的平面角．由PA k AB = 得(00)P ka ，，，2ka E a a ⎛⎫ ⎪⎝⎭，，，(0)G a a ，，．设(0)H x y ，，，则(0)(20)GH x a y a BD a a =--=- ，，，，，，由0GH BD =得()2()0a x a a y a --+-=，即2x y a -=-． ①又因(0)BH x a y =- ，，，且BH 与BD的方向相同，故2x a ya a-=-，即22x y a +=． ②由①②解得3455x a y a ==，，从而21055GH a a GH ⎛⎫=--= ⎪⎝⎭，，，．tan ka EG EHG GH=== ．由0k >知EHG ∠是锐角，由30EHG ∠>︒，得t a n t a n30E H G >︒，>．故k的取值范围为k >． [规律小结]立体几何中的最值与范围，需要首先确定最值或范围的主体，确定题目中描述的相关变动的量，根据必要，可确定是利用几何方法解答，还是转化为代数（特别是函数）问题解答．其中的几何方法，往往是进行翻折变换，这时可以想象实际情形，认为几何体是利用硬纸等折图６－６成的，可以动手翻折的，在平时做练习时，不妨多动手试试，培养自己的空间想象能力，在考试时就可以不动手，动脑想就可以了．特别注意变动的过程，抓住变动的起始与终了等特殊环节．考点误区分析（１）这类问题容易成为难点，关键是学生的空间想象能力缺乏，或者对问题的转化方向不明确．因此，要注意常见的转化方向，如化立体几何问题为平面几何问题，或化立体几何问题为代数问题等，根据题目特征进行转化．（２）对题目所描述的情形没有清醒的认识也是造成错解的主要原因，注意产生量的变化的主要原因是什么，相关的数量和位置关系都做怎样的变化，抓住问题的关键，才能顺利解决问题．同步训练１．如图６－７，在直三棱柱111ABC A B C -中，AB BC ==12BB =， 90=∠ABC ，,E F分别为111,AA C B 的中点，沿棱柱的表面从E 到F 两点的最短路径的长度为．２．有两个相同的直三棱柱，高为a2，底面三角形的三边长分别为)0(5,4,3>a a a a ．用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则a 的取值范围是__________．３．如图６－８，正四面体ABCD 的棱长为1，棱AB ∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是．［参考答案］１．［解析］分别将111A B C △沿11A B 折到平面11ABB A 上；将111A B C △沿11AC 折到平面11ACC A 上；将11BCC B 沿1BB 折到平面11ABB A 上；将11BCC B 沿1CC 折到平面11ACC AA图６－７1A 1E图６－８上，比较其中EF 长即可．［答案］2２．［解析］可知，全面积最小的是四棱柱面积为22428a +，全面积最小的是三棱柱面积为21248a +，解2212482428a a +>+即可．［答案］3150<<a ．３．［解析］当CD 所在的直线与平面α平行时，所求射影面积最大，为1122AB CD ⨯=；当CD 所在的直线与平面α垂直时，所求射影面积最小，可求得为4．［答案］1[]42．。

立体几何的最值问题

立体几何最值问题立体几何是数学中的一个重要分支，它研究的是空间图形的性质和数量关系。

在立体几何中，我们经常遇到最值问题，即寻找某个量的最大值或最小值。

本文将介绍立体几何中最值问题的几个方面：1.立体几何位置关系立体几何中的位置关系是指空间中点、线、面之间的相对位置。

解决位置关系问题需要运用空间想象和逻辑推理。

在立体几何中最值问题中，位置关系往往与距离、角度等问题交织在一起，需要综合考虑多种因素。

2.立体几何中的距离立体几何中的距离是指空间中两点之间的直线距离，或者是点与线、线与面之间的距离。

在解决最值问题时，我们需要考虑如何利用距离公式来计算最短路径、最大距离等。

3.立体几何中的体积立体几何中的体积是指空间中封闭图形的体积，或者是两个平面图形之间的距离。

计算体积需要运用体积公式，而解决最大或最小面积问题则需要考虑如何调整图形的形状和大小。

4.立体几何中的最短路径立体几何中的最短路径问题是指寻找空间中两点之间的最短距离。

解决这类问题需要运用距离公式和几何定理，有时还需要借助对称、旋转等技巧。

5.立体几何中的最大/最小面积立体几何中的最大/最小面积问题通常涉及到平面图形在空间中的展开和折叠。

解决这类问题需要运用面积公式和平面几何定理，同时要注意图形的对称性和边长之间的关系。

6.立体几何中的角度问题立体几何中的角度问题是指空间中两条直线或两个平面之间的夹角。

解决这类问题需要运用角度公式和空间向量，同时要注意图形的对称性和边长之间的关系。

7.立体几何中的轨迹问题立体几何中的轨迹问题是指一个点或一条线在空间中按照一定规律移动所形成的轨迹。

解决这类问题需要运用轨迹方程和运动学原理，同时要注意轨迹的形状和大小随时间的变化情况。

专题38 立体几何中的距离、截面、折叠问题(解析版)

因为平面 ,所以 ,所以为二面角的平面角．
结合图1可知, 为中点,故 ,从而
所以 ,所以二面角的平面角的余弦值为．
向量法:以点为原点,建立空间直角坐标系如图所示,
则 , , ，所以 ,
设为平面的法向量,则 ,即 ,
解得 ,令 ,得，由(Ⅰ)知, 为平面的一个法向量,
所以，即二面角的平面角的余弦值为．
2、平面外一点P到平面α的距离：如图，已知平面α的法向量为n，A是平面α内的定点，P是平面α外一点，过点P作平面α的垂线l，交平面α于点Q，则n是直线l的方向向量，且点P到平面α的距离PQ＝＝＝
基本题型：
1．(多选)已知正方体ABCD-A1B1C1D1的棱长为1，点E，O分别是A1B1，A1C1的中点，点P在正方体内部且满足＝＋＋，则下列说法正确的是()
【解析二】由题意可知，该平面与在正方体的截面为对边平行的六边形，如图所示，则截面面积为
所以当时，
7．（2017新课标Ⅰ）如图，圆形纸片的圆心为，半径为5 cm，该纸片上的等边三角形的中心为．、、为圆上的点，，，分别是以，，为底边的等腰三角形。沿虚线剪开后，分别以，，为折痕折起，，，使得、、重合，得到三棱锥。当的边长变化时，所得三棱锥体积(单位： )的最大值为_______。
所以，，，．
得，．
设平面的法向量，平面的法向量，
平面与平面夹角为，则，得，取，
，得，取，从而，
即平面与平面夹角的余弦值为．
9．（2015浙江）如图，已知，是的中点，沿直线将翻折成，所成二面角的平面角为，则
10．（2012浙江）已知矩形，，．将沿矩形的对角线所在的直线进行翻折，在翻折过程中，

厉兵秣马，2019高考数学立体几何必考压轴题及解析，冲刺140必备

厉兵秣马，2019高考数学立体几何必考压轴题及解析，冲刺140必备高中数学的立体几何很抽象，一直让不少学生头疼。

然而，每年的高考都会至少考一题立体几何，且往往是分值高的大题，如果没有迎难而上的勇气，一下子就会被别人甩下将近20分；相反，如果你能搞定立体几何，那你就等于甩开了数以万计被立体几何打败的学生，有助你考上理想大学。

高考对于立体几何的考查重点集中在以下几个方面：①几何的机构特征和三视图、直观图，重点是三视图。

②点、线、平面之间的位置关系，重点是平行关系、垂直关系和异面直线③空间的角度，重点是二面角、直线和平面所成的角、异面直线所成的角④空间向量，一般是以解答题的形式出现，这是立体几何考查的一个重要点。

下面是小编为同学们整理的2019年高考数学立体几何必考压轴题及答案解析，希望同学们一定要给予足够的重视！由于篇幅有限文中无法全部为同学们展示，所以，如果同学们需要完整版的话可以点小编的头像私信咨询小编哦~！私信：立体几何高中数学《立体几何》压轴题及答案解析在高一的时候，同学们开始学习立体几何“三视图”时，大家都会觉得这个内容非常难学.这块内容之所以难学其本质的原因是大家空间想象力不够，对空间几何体直观图的框架呈现方式没有深入理解，另平行投影的原理及三视图的边界意义是还原几何体的重点.三视图作为高考数学立体几何部分的核心考点之一，关键是如何还原几何体．涉及立体几何所有知识点：包括空间几何体（棱锥、棱柱、棱台、圆锥、圆柱、圆台、球）的直观图画法；三视图的投影原理（平行投影：长对正、高平齐、宽相等）；截面的做法（平面的基本性质的应用）；常见几何体的概念及相关计算公式（表面积和体积等）.还原几何体过程中还会考虑到空间点、线、面位置关系的判断等，如线面平行、线面垂直的判定定理与性质定理.立体几何中的动态问题或最值问题，这类问题往往困扰成绩比较好的同学，一般成绩较弱的同学其实这类问题就果断放弃了.究其原因，这类问题的知识覆盖面广，很多同学在这方面缺乏专项的训练，常常在解题时没有明确的思路，无从下手.即使偶尔能做对，也是凭着运气成分，并不是实力使然，也不能100%的做对.。

立体几何最值问题-高考数学一题多解

立体几何最值问题-高考数学一题多解一、攻关方略事物的空间形成，总是表现为不同维数且遵循由低维到高维的发展规律，所谓升维策略，就是把维数、抽象水平较低的或局部的问题转化为维数、抽象水平较高或整体性较强的整体间的关系问题，通过对整体性质或关系的考虑，使原问题获得解决的策略，如平面图形通过翻折或旋转成为空间图形就是二维向三维的转化与变换．在解题时，考虑把高维空间的问题转化为低维空间的问题，这种处理问题的方法叫降维法，也可称之为降维策略，如将立体几何问题转化为平面几何问题．实际上，许多立体几何问题如求空间角、空间距离等，通常总是转化为平面内的问题，通过计算来解决的，当然将空间角、空间距离转变为平面角、平面上点线距离这一步是需要证明的．在立体几何学习中经常碰到几何体中有变角或变动的线段，此时必须根据题意列出沟通已知量与变量之间的关系，运用函数与方程的思想来处理，立体几何中由于动点的变化引起的最值，通常建立关于与动点相关的角度的目标函数，转化为函数最值问题求解．若在空间图形中建立空间直角坐标系，利用向量坐标法，结合条件得到方程（组），则可用解方程（组）求出结果，利用函数与方程的思想方法还可以解空间图形中涉及线面关系、面面关系的探究性问题．真可谓：翻折旋转二维升三，空间问题降维处理．点动角变牵动图形，立几最值函数搞定．1．如图所示，圆形纸片的圆心为O ，半径为5cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，DBC △、ECA △、FAB 分别是以BC 、CA 、AB 为底边的等腰三角形，沿虚线剪开后，分别以BC 、CA 、AB 为折痕折起DBC △、ECA △、FAB ，使得D 、E 、F 重合，得到三棱锥．当ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为______．【针对训练】2．点P 在ABC 所在平面α外，PA α⊥，PB PC ==，3tan 2PBC ∠=，则点A 到平面PBC 的距离的最大值是______．3．如图所示，在ABC 中，2AB BC ==，120ABC ∠=︒．若平面ABC 外的点P 和线段AC 上的点D ，满足PD DA =，PB BA =，则四面体P BCD -的体积的最大值是______．4．已知底面边长为2的正三棱锥-P ABC ，其表面展开图是123PP P ，如图所示，求123PP P 的各边长及此三棱锥的体积V ．5．已知球的直径4SC =，A 、B 是该球面上的两点，30ASC BSC ∠=∠=︒，则三棱锥S ABC -的体积的最大值为______．（2021全国新高考Ⅰ卷19）6．已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，D 为棱11A B 上的点．11BF A B ⊥（1）证明：BF DE ⊥；（2）当1B D 为何值时，面11BB C C 与面DFE 所成的二面角的正弦值最小?（2022新高考1卷）7．已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且333l ≤≤）A ．8118,4⎡⎤⎢⎥⎣⎦B ．2781,44⎡⎤⎢⎥⎣⎦C ．2764,43⎡⎤⎢⎥⎣⎦D ．[18,27]（2022年全国乙卷（文数）第12题）8．已知球O 的半径为1，四棱锥的顶点为O ，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（）A ．13B ．12C D ．2（2022年全国乙卷（文数）第18题）9．如图，四面体ABCD 中，AD CD ⊥，AD CD =，ADB BDC ∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2AB BD ==，60ACB ∠=︒，点F 在BD 上，当AFC △的面积最小时，求三棱锥F ABC -的体积．10．如图，已知平面四边形ABCD ，AB=BC=3，CD=1，ADC=90°．沿直线AC 将ACD 翻折成ACD '△，直线AC 与BD '所成角的余弦的最大值是________.11．已知四边形ABCD ，2AB BD DA ===，BC CD ==ABD △沿BD 折起，使二面角A BD C --的大小在5,66ππ⎡⎤⎢⎥⎣⎦内，则直线AB 与CD 所成角的余弦值取值范围是（）A ．08⎡⎢⎣⎦，B ．08⎡⎢⎣⎦，C ．01⎡⎫⎪⎢⎪⎣⎦⎣⎭ D ．88⎢⎣⎦，参考答案：1．3【分析】先求得所求三棱锥体积的表达式，然后利用导数或基本不等式求得体积的最大值.【详解】解法一：由题意可知，折起后所得三棱锥为正三棱锥，当ABC 的边长变化时，设ABC 的边长为()0a a >cm ，则ABC 的面积为24a ．DBC △的高为56a -，则正三棱锥的高为=∴2503->，∴0a <<．∴所得三棱锥的体积213412V a =⨯=．令45253t a a =-，则34100t a ='，由0t '=，得a =此时所得三棱锥的体积最大，为3．解法二：如图所示，连接OD 交BC 于点G ，由题意知，OD BC ⊥，OG 是等边三角形ABC 内切圆半径，21π1sin 3232BC BC OG ⨯⨯=⨯⨯，解得OG =，∴OG 的长度与BC 的长度成正比．设OG x =，则BC =，5DG x =-，2132ABC S x =⨯=△，则所得三棱锥的体积2213V =⨯=令()452510f x x x =-，50,2x ⎛⎫∈ ⎪⎝⎭．则()3410050f x x x '=-，令()0f x '≥，即4320x x -≤，得02x <≤．则当50,2x ⎛⎫∈ ⎪⎝⎭时，()()280f x f =≤，∴V ≤．∴所求三棱锥的体积的最大值为3．解法三：如图所示，连接OE 交AC 于点H ，连接AO 、OC ，设OH x =．则AC =，5EH x =-，三棱锥D ABC -2ABC S = ，D ABC V -=2≤=，当且仅当104x x =-，即2x =时取等号．∴所求三棱锥的体积的最大值为3．【点睛】本题为平面图形折叠成空间图形，当折叠终止时，几何体是一个正三棱锥，这个正三棱锥底面边长是一个变元，从而导致三棱锥体积的变化，特别要提醒的是，在折叠问题中，必须注意到折叠过程中哪些要素在变化，哪些要素始终保持不变，其中不变要素见核心要素．根据平面图形的性质，寻找不变的数量关系以及直线与直线平行和垂直的位置关系，是解决折叠问题的突破口，因此折叠问题要通过变图、想图、构图、用图的过程，积极思考，体会解题程序方向性，直击问题的本质，折叠问题既要看清平面转化为空间的过程，又要了解三维空间图形问题的平面化处理，两者是互通的．在建立体积表达式的函数模型之后，结合函数思想求最值，通常用导数法，也可考虑运用基本不等式的方法．策略一:以动正三角形AEC 的边长为变元建立函数关系式，运用导数法求其最大值.策略二:以动正三角形ABC 的中心到边的距离为变元建立函数关系式，运用导数法求其最大值.策略三:以动正三角形ABC 的中心到边的距离为变元建立函数关系式，运用基本不等式求最大值，注意等号成立的条件.2【分析】法一，取BC 的中点D ，连接AD 、PD ，设ADP θ∠=，用θ的正余弦表示AD ，PD ，再利用等体积法求解作答.法二，作PD BC ⊥于点D ，连接AD ，作AF PD ⊥于点F ，证明AF ⊥平面PBC ，再利用均值不等式求解作答.【详解】解法一，取BC 的中点D ，连接AD 、PD ，如图，因PB PC =，则PD BC ⊥，而3tan2PBC ∠=，有sin PBC ∠=则有sin PD PB PBC =⋅∠=PA ⊥平面ABC ，,AD BC ⊂平面ABC ，则PA AD ⊥，PA BC ⊥，又,,PA PD P PA PD ⋂=⊂平面PAD ，因此BC ⊥平面PAD ，AD ⊂平面PAD ，则AD BC ⊥，在Rt PAD △中，令(0,)2ADP πθ∠=∈，sin ,cos PA PD AD PD θθ==，设点A 到平面PBC 的距离为h ，11,22PBC ABC S BC PD S BC AD =⋅=⋅ ，由A PBC P ABC V V --=得：1133PBC ABC S h S PA ⋅=⋅ ，即1122BC PD h BC AD PA ⋅⋅=⋅⋅，于是得cos sin 2AD PA PD PD h PD PD θθθ⋅⋅==，当且仅当22=πθ，即4πθ=时取等号，所以点A 到平面PBC解法二，在PBC 中，作PD BC ⊥于点D ，连接AD ，作AF PD ⊥于点F，如图，PA ⊥平面ABC ，BC ⊂平面ABC ，则PA BC ⊥，又,,PA PD P PA PD ⋂=⊂平面PAD ，因此BC ⊥平面PAD ，而BC ⊂平面PBC ，则有平面PAD ⊥平面PBC ，又平面PAD ⋂平面PBC PD =，AF ⊂平面PAD ，因此AF ⊥平面PBC ，即AF 就是点A 到平面PBC 的距离，而3tan 2PBC ∠=，有sin PBD ∠=sin PD PB PBD =⋅∠=，在Rt PAD △中，22211()1222PA AD PD PA AD AF PD PD PD PD +⋅=≤==当且仅当3PA AD ==时取等号，所以点A 到平面PBC3．12##0.5【分析】先求得四面体P BCD -体积的表达式，利用基本不等式或函数的单调性求得体积的最大值.【详解】解法一：由2AB BC ==，120ABC ∠=︒，可得AC =要求四面体P BCD -的体积，关键是寻找底面三角形BCD 的面积BCD S △和点P 到平面BCD 的距离h ，易知2h ≤．设AD x =，则DP x =，DC x =，()12sin 3022DBC xS x =⨯⨯⨯︒=△，其中(0,x ∈，且h x ≤．∴2111366622P BCDBCD x x x x V S h h x -⎛⎫-+=⨯=≤≤= ⎪ ⎪⎝⎭△．当且仅当x x =，即x =P BCD -的体积的最大值是12．解法二：设PD AD x ==，∵PB PA =，PBD ABD ≌△△，1133P BCD BCD V S h -=⨯=△（h 为三棱锥P BCD -的高）．当平面PBD ⊥平面BDC 时，使四面体PBCD 的体积较大．作PH BD ⊥，垂足为H ，则PH ⊥平面BCD ，sin sin h PH PD PDB x ADB ==⋅∠=⋅∠．此时，()211sin sin sin 662P BCDx x V ADB ADB ADB -=⋅∠≤∠=∠⎝⎭，当且仅当x =1sin 2P BCD V ADB -=∠，当90ADB ∠=︒，即AD BD ⊥时，P BCD V -最大值为12．解法三：∵13P BCD BCD V S h -=⨯△（h 为三棱锥P BCD -的高），在ABC 中，2AB BC ==，120ABC ∠=︒，则AC =30BAC BCA ∠=∠=︒，设(0PD DA x x ==<<，则DC x =-，1sin 22BCD xS BC CD BCA =⨯⋅∠=△．在ABD △中，由余弦定理，有2222cos BD AD AB AD AB BAC =+-⋅∠．代入整理得BD =PBD △中，由余弦定理，有222cos 2PB BD PD PBD PB BD+-∠=⋅，代值整理得cos PBD ∠∴sin PBD ∠=．过P 作PM BD ⊥，垂足为M ，则PM 为四面体P BCD -的高．∴sin h PM PB PBM ==∠故111336P BCDBCD V S h -===△，t =，∵0x <<12t ≤<，∴224x t -=-．2141466P BCDt V t t t--⎛⎫=⨯=- ⎪⎝⎭在[)1,2t ∈上单调递减．∴当1t =，即x =P BCD -的体积最大为1411612P BCD V --=⨯=．4．1213234PP PP P P ===，3【分析】由12APB CBP ≌△△，分析可得123PP P 是边长为4的正三角形，再由13P ABC ABC S PO V -=⋅ 结合题干数据求解即可.【详解】由题图可知1P 、B 、2P 三点共线，∴12APBCBP ≌△△．∵60ABC ∠=︒，∴1260ABP CBP ∠=∠=︒，1APB △和2CBP △都是正三角形．∴124PP =．同理可知其他两边长也是4，∴123PP P 是边长为4的正三角形．折叠后是棱长为2的正四面体-P ABC ，如图所示．设顶点P 在底面内的投影为O ，连结BO 并延长，交AC 于点D ，则D 为AC 的中点，O 为ABC 的重心，PO ⊥底面ABC ．AO AB ==，PO ==．故133P ABC ABC V S PO -=⋅=△．5．2【分析】过AB 作与SC 垂直的截面ABM ．通过13S ABC ABM V SC S -=⋅△，分析即得解.【详解】过AB 作平面ABM SC ⊥且SC 平面ABM M =，如图所示，由题意知SAC 、SBC △均为直角三角形．∵4SC =，30ASC BSC ∠=∠=︒，故SAC SBC ≅ ，∴SA =，2CA =，∴SA ACAM BM SC⋅==．∴2141sin 2sin 2332S ABCABM V SC S AMB AMB -=⋅=⨯⨯∠=∠≤△．∴三棱锥S ABC -体积的最大值为2．故答案为：26．（1）证明见解析；（2）112B D =【分析】（1）方法二：通过已知条件，确定三条互相垂直的直线，建立合适的空间直角坐标系，借助空间向量证明线线垂直；（2）方法一：建立空间直角坐标系，利用空间向量求出二面角的平面角的余弦值最大，进而可以确定出答案；【详解】（1）[方法一]：几何法因为1111,//BF AB AB AB ⊥，所以BF AB ⊥．又因为1AB BB ⊥，1BF BB B ⋂=，所以AB ⊥平面11BCC B ．又因为2AB BC ==，构造正方体1111ABCG A B C G -，如图所示，过E 作AB 的平行线分别与AG BC ，交于其中点,M N ，连接11,AM BN ，因为E ，F 分别为AC 和1CC 的中点，所以N 是BC 的中点，易证1Rt Rt BCF B BN ≅ ，则1CBF BBN ∠=∠．又因为1190BBN BNB ∠+∠=︒，所以1190CBF BNB BF BN ∠+∠=︒⊥，．又因为111111,BF AB BN AB B ⊥= ，所以BF ⊥平面11A MNB ．又因为ED ⊂平面11A MNB ，所以BF DE ⊥．[方法二]【最优解】：向量法因为三棱柱111ABC A B C -是直三棱柱，1BB ∴⊥底面ABC ，1B B AB ∴⊥11//A B AB ，11BF A B ⊥，BF AB ∴⊥，又1BB BF B ⋂=，AB ∴⊥平面11BCC B ．所以1,,BA BC BB 两两垂直．以B 为坐标原点，分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系，如图．()()()0,0,0,2,0,0,0,2,0,B A C ∴()()()1110,0,2,2,0,2,0,2,2B A C ，()()1,1,0,0,2,1E F ．由题设(),0,2D a （02a ≤≤）．因为()()0,2,1,1,1,2BF DE a ==--，所以()()0121120BF DE a ⋅=⨯-+⨯+⨯-=，所以BF DE ⊥．[方法三]：因为11BF A B ⊥，11//A B AB ，所以BF AB ⊥，故110BF A B ⋅= ，0BF AB ⋅=，所以()11BF ED BF EB BB B D ⋅=⋅++ ()11=BF B D BF EB BB ⋅+⋅+ 1BF EB BF BB =⋅+⋅ 11122BF BA BC BF BB ⎛⎫=--+⋅ ⎪⎝⎭11122BF BA BF BC BF BB =-⋅-⋅+⋅ 112BF BC BF BB =-⋅+⋅111cos cos 2BF BC FBC BF BB FBB =-⋅∠+⋅∠1=2202-⨯⨯，所以BF ED ⊥．（2）[方法一]【最优解】：向量法设平面DFE 的法向量为(),,m x y z =，因为()()1,1,1,1,1,2EF DE a =-=--，所以00m EF m DE ⎧⋅=⎨⋅=⎩ ，即()0120x y z a x y z -++=⎧⎨-+-=⎩．令2z a =-，则()3,1,2m a a =+-因为平面11BCC B 的法向量为()2,0,0BA =，设平面11BCC B 与平面DEF 的二面角的平面角为θ，则cos m BA m BA θ⋅=⋅==当12a =时，2224a a -+取最小值为272，此时cos θ=所以()minsin θ=112B D =．[方法二]：几何法如图所示，延长EF 交11A C 的延长线于点S ，联结DS 交11B C 于点T ，则平面DFE 平面11B BCC FT =．作1BH FT ⊥，垂足为H ，因为1DB ⊥平面11BB C C ，联结DH ，则1D H B ∠为平面11BB C C 与平面DFE 所成二面角的平面角．设1,B D t =[0,2],t ∈1B T s =，过1C 作111//CG AB 交DS 于点G ．由111113C S C G SA A D ==得11(2)3C G t =-．又1111B D BT C G C T=，即12(2)3t s s t =--，所以31t s t =+．又111B H BT C F FT =，即11B H =，所以1B H =所以DH ==则11sin B D DHB DH∠===所以，当12t =时，()1min 3sin 3DHB ∠=．[方法三]：投影法如图，联结1,FB FN，DEF 在平面11BB C C 的投影为1BN F ，记面11BB C C 与面DFE 所成的二面角的平面角为θ，则1cos B NF DEFS S θ=．设1(02)BD t t =≤≤，在1Rt DB F中，DF ==在Rt ECF中，EF =D 作1B N 的平行线交EN 于点Q ．在Rt DEQ △中，DE ==在DEF 中，由余弦定理得222cos 2DF EF DE DFE DF EF+-∠=⋅=，sin DFE ∠1sin 2DFE S DF EF DFE =⋅∠ =13,2B NF S = 1cos B NF DFES S θ==，sin θ，当12t =，即112B D =，面11BB C C与面DFE 所成的二面角的正弦值最小，最小值为3．【整体点评】第一问，方法一为常规方法，不过这道题常规方法较为复杂，方法二建立合适的空间直角坐标系，借助空间向量求解是最简单，也是最优解；方法三利用空间向量加减法则及数量积的定义运算进行证明不常用，不过这道题用这种方法过程也很简单，可以开拓学生的思维.第二问：方法一建立空间直角坐标系，利用空间向量求出二面角的平面角是最常规的方法，也是最优方法；方法二：利用空间线面关系找到，面11BB C C 与面DFE 所成的二面角，并求出其正弦值的最小值，不是很容易找到；方法三：利用面DFE 在面11BB C C 上的投影三角形的面积与DFE △面积之比即为面11BB C C 与面DFE 所成的二面角的余弦值，求出余弦值的最小值，进而求出二面角的正弦值最小，非常好的方法，开阔学生的思维．7．C【分析】设正四棱锥的高为h ，根据题意求出正四棱锥的底面边长与高的关系，再利用导数求解即可.【详解】设球体的半径为R ，由题知：34363R ππ=，所以球的半径3R =.设正四棱锥的底面边长为2a ，高为h ，则222222l h a h =+=+，22232(3)a h =+-,所以26h l =，2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭，设()641=936x f x x ⎛⎫- ⎪⎝⎭，3x ≤≤，所以()5233112449696x x f x x x ⎛⎫⎛⎫-'=-= ⎪⎝⎭⎝⎭，当3x ≤≤()0f x ¢>，()f x 为增函数，当x <≤()0f x '<，()f x 为减函数，所以当l =时，正四棱锥的体积V 取最大值，最大值为643，又3l =时，274V =，l =814V =,所以正四棱锥的体积V 的最小值为274，所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦，.故选：C 8．C【分析】令四棱锥底面四边形外接圆半径为r ，用r 表示四棱锥的高及底面四边形面积最大值，再借助导数求解作答.【详解】设该四棱锥底面四边形为ABCD ，平面ABCD 截球O 所得小圆半径为r ，则球心O到平面ABCD 的距离h =设四边形ABCD 对角线,AC BD 的夹角为α，则1sin 2ABCD S AC BD α=⋅，于是得该四棱锥的体积：12sin 22sin 36623ABCD V S h BD r r rπα=⋅=⋅≤⋅⋅=当且仅当对角线,AC BD 是截面小圆互相垂直的两条直径，即四边形ABCD 为正方形时取等号，令2(0,1)r x =∈，有23r =23(),(0,1)f x x x x =-∈，求导得：22()233()3f x x x x x '=-=-，当203x <<时，()0f x '>，当213x <<时，()0f x '<，因此函数()f x 在2(0,)3上单调递增，在2(,1)3上单调递减，当23x =时，23max 224()(()3327f x =-=，从而当223r =时，max 222(333r =⨯⨯max V =，此时3h ==，故选：C9．(1)证明见解析；【分析】（1）利用线面垂直的判定定理可得AC ⊥平面BED ，然后根据面面垂直的判定定理可得平面BED ⊥平面ACD ；（2）首先判断出三角形AFC 的面积最小时F 点的位置，然后求得F 到平面ABC 的距离，从而求得三棱锥F ABC -的体积或利用等积法及锥体的体积公式即得.【详解】（1）AD CD = ，ADB BDC ∠=∠，BD BD =，ADB CDB ∴≅ ，AB BC ∴=，又E 为AC 的中点．AC BE ∴⊥，AD CD = ，E 为AC 的中点．AC DE ∴⊥，又BE DE E = ，BE ⊂平面BED ，DE ⊂平面BED ，AC ∴⊥平面BED ，又AC ⊂ 平面ACD ，∴平面BED ⊥平面ACD ；（2）方法一：依题意2AB BD BC ===，60ACB ∠=︒，三角形ABC 是等边三角形，所以2,1,AC AE CE BE ====由于,AD CD AD CD =⊥，所以三角形ACD 是等腰直角三角形，所以1DE =，所以222DE BE BD +=，即DE BE ⊥，由于AC BE E ⋂=，,AC BE ⊂平面ABC ，所以DE ⊥平面ABC ，由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅ ，所以AF CF =，所以EF AC ⊥，由于12AFC S AC EF =⋅⋅ ，所以当EF 最短时，三角形AFC 的面积最小，过E 作EF BD ⊥，垂足为F ，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得2EF =，所以13,222DF BF DF ===-=，所以34BF BD =，过F 作FH BE ⊥，垂足为H ，则//FH DE ，又DE ⊥平面ABC ，所以FH ⊥平面ABC ，且34FH BF DE BD ==，所以34FH =，所以111323324F ABC ABC V S FH -=⋅⋅=⨯⨯=方法二：AB BC = ，60ACB ∠=︒，2AB =ABC ∴ 是边长为2的等边三角形，BE ∴=连接EF ，由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅ ，所以AF CF =，所以EF AC ⊥，由于12AFC S AC EF =⋅⋅ ，所以当EF 最短时，三角形AFC 的面积最小，即EF BD ⊥时，AFC △的面积最小，,,2AD CD AD CD AC ⊥== ，E 为AC 的中点，∴1DE =，222DE BE BD +=，BE ED ∴⊥，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得2EF =，∴32BF ，113222BEF S BF EF ∴=⋅=⋅11233F ABC A BEF C BEF BEF V V V S AC ---∴=+=⋅=⋅= .10．6【分析】取AC 中点O ，连接OB ，过点O 作Oz ⊥平面ABC ，以点O 为原点建立空间直角坐标系，设二面角D AC B '--的大小为α，把直线A C 与BD '所成角的余弦表示为α的函数，求出函数最大值作答.【详解】在ACD 中，90ADC ∠= ，1,CD AD ==则AC =，过D 作DH AC ⊥于H ，连接D H '，如图，显然D H AC '⊥，ACD 绕直线AC 旋转过程中，线段DH 绕点H 在垂直于直线AC 的平面γ内旋转到D H '，取AC 中点O ，连接OB ，因3AB BC ==，有OB AC ⊥，OB =，,663CD ADD H DH CH OH AC⋅'=====，过点O 作Oz ⊥平面ABC ，以点O 为原点，射线,,OB OA Oz 分别为,,x y z 轴非负半轴，建立空间直角坐标系，则A ，B ，(0,2C -，显然有//Oz 平面γ，设二面角D AC B '--的大小为[0,]απ∈，有(,,sin )636D αα'-，则有(,sin )6236BD αα=--' ，CA的方向向量为(0,1,0)n = ，设直线AC 与BD '所成的角为θ，于是得||cos |cos ,|||||n BD n BD n BD θ'⋅'=〈〉=='因[0,]απ∈，则1cos 1α-≤≤，于是得cos 6θ=，当且仅当cos 1α=取等号，所以直线AC 与BD '11．A【分析】取BD 中点O ，连接AO ，CO ，以O 为原点建立空间直角坐标系，利用二面角A BD C --的大小θ的正余弦表示,AB CD的坐标，利用空间向量建立函数关系求解作答.【详解】取BD 中点O ，连接AO ，CO ，而AB =BD =DA =2，BC =CD，则CO ⊥BD ，AO ⊥BD ，且CO =1，AOAOC ∠是二面角A BD C --的平面角，令5[,]66AOC ππθ∠=∈，显然有BD ⊥平面AOC ，BD ⊂平面BCD ，则平面AOC ⊥平面BCD ，在平面AOC 内过O 作Oz OC ⊥，而平面AOC I 平面BCD OC =，因此Oz ⊥平面BCD ，即射线,,OC OD Oz 两两垂直，以O 为原点，射线,,OC OD Oz 分别为,,x y z轴非负半轴，建立空间直角坐标系，如图，则(0,1,0),(1,0,0),(0,1,0)B C D -，)A θθ，,1,),(1,1,0)BA CD θθ==-，设直线AB 与CD 所成的角为α，则||cos |cos ,|||||AB CD AB CD AB CD α⋅=〈〉==，由5[,66ππθ∈得：cos [,]22θ∈，15122θ-≤≤，则5|1|[0,2θ∈，于是得cos[0,]α∈，8.所以直线AB与CD 所成角的余弦值取值范围是[0,]8故选：A答案第18页，共18页。

立体几何中的最值问题

AB + BD = AC + CD = 2a，显然△ABD≌ △ACD，所以BE = CE．
取 BC 中点 F，∴ EF⊥BC，EF⊥AD，四面体 ABCD 的体积的最大值，只需 EF 最大即可，
当△ABD 是等腰直角三角形时几何体的体积最大． ∵ AB + BD = AC + CD = 2a，
∴ AB = a，所以 EB = 槡a2 － c2 ，EF = 槡a2 － c2 － 1，
棱 AA1 的长的最小值为
．
解析设 AA1 = m，AE = x，以 D 为坐标
原点建系，则 D（ 0，0，0），E（ a，0，x），B（ a，
a，0）
所，C以1 （ E→0B，a=，m（ 0）
，，a，－
x）
，E→C1
=
（
－ a，a，m － x），
所以 x2 － mx + a2 = 0，x∈［0，m］．
点评本题求的是动点到两个定点距离和的最值问
题，采用了补型的技巧，化曲为直，将折线的最值转化为直
线的最值得解，这是动点距离和中常用的技巧．
题型二棱长最值问题
例 2 长方体 ABCD － A1 B1 C1 D1 的底
面是边长为 a 的正方形，若在侧棱 AA1 上
至少存在一点 E，使得 ∠C1 EB = 90°，则侧
解题技巧与方法
126
JIETI JIQIAO YU FANGFA
立体几何中的最值问题
◎孙岳炜（山东省寿光现代中学，山东寿光 262700）
立体几何中的最值问题一般是指有关距离的最值、角
的最值或面积的最值的问题．在立体几何中，计算几何体的

立体几何解析几何最值问题

立体几何解析几何最值问题立体几何和解析几何都是数学中的分支领域，它们在研究物体的形状、位置和运动等方面有着不同的方法和应用。

在解析几何中，最值问题是其中一个重要的问题类型，它涉及到找到函数在特定区域内的最大值或最小值。

在立体几何中，我们研究的是空间中的物体，比如点、线、面、体等。

解析几何则是研究平面几何与坐标系统之间的关系，通常使用坐标点来表示点、线、曲线等。

解析几何中最值问题的解决方法通常是通过求导来进行。

我们可以将问题转化为一个函数，然后求该函数的导数，找到导数为0的点，再通过比较得出最大值或最小值。

这种方法在求解平面最值问题时非常有效。

而在立体几何中，最值问题通常涉及到体积、面积或长度等量的最大化或最小化。

解决这类问题可以利用几何性质和定理来进行推导和求解。

比如，要求一个几何体的体积的最大值，我们可以通过寻找几何体的特定形状的体积公式以及几何性质来得出最优解。

具体地说，在立体几何中，最值问题的解决方法可以归纳如下：1.求解体积最大问题：对于已知形状的几何体，我们可以通过推导体积公式，并利用一些方法来求解体积的最大值。

例如，求解一个长方体在给定表面积约束条件下的最大体积，我们可以设长方体的长、宽、高分别为x、y、z，然后利用约束条件和体积公式写出等式，最后通过求解方程组可得到最优解。

2.求解表面积最小问题：类似地，我们可以通过推导表面积公式，并利用一些方法来求解表面积的最小值。

例如，求解一个包含给定体积的圆柱体的表面积最小值，我们可以设圆柱体的底面半径为r、高度为h，然后通过体积公式将h表示为r的函数，并利用表面积公式得到表面积的表达式，最后求解表面积的最小值。

3.求解长度最短问题：有时候我们需要找到连接两个点的最短路径，可以利用几何性质和定理求解。

例如，求解从一个点到直线的最短距离，我们可以利用点到直线的距离公式，并通过求导的方法求解最短距离的点。

总而言之，立体几何和解析几何最值问题的求解方法有所不同，但都可以通过推导公式、利用几何性质和定理以及求导等方法来解决。

2024年高考数学压轴题专项训练：立体几何压轴题十大题型汇总(解析版)(共65页)(1)

立体几何压轴题十大题型汇总命题预测本专题考查类型主要涉及点立体几何的内容，主要涉及了立体几何中的动点问题，外接球内切球问题，以及不规则图形的夹角问题，新定义问题等。

预计2024年后命题会继续在以上几个方面进行。

高频考法题型01几何图形内切球、外接球问题题型02立体几何中的计数原理排列组合问题题型03立体几何动点最值问题题型04不规则图形中的面面夹角问题题型05不规则图形中的线面夹角问题题型06几何中的旋转问题题型07立体几何中的折叠问题题型08不规则图形表面积、体积问题题型09立体几何新定义问题题型10立体几何新考点题型01几何图形内切球、外接球问题解决与球相关的切、接问题，其通法是作出截面，将空间几何问题转化为平面几何问题求解，其解题思维流程如下：(1)定球心：如果是内切球，球心到切点的距离相等且为球的半径；如果是外接球，球心到接点的距离相等且为半径；(2)作截面：选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系)，达到空间问题平面化的目的；(3)求半径下结论：根据作出截面中的几何元素，建立关于球的半径的方程，并求解.1(多选)(23-24高三下·浙江·开学考试)如图，八面体的每个面都是正三角形，并且4个顶点A ,B ,C ,D 在同一个平面内，如果四边形ABCD 是边长为2的正方形，则()A.异面直线AE 与DF 所成角大小为π3B.二面角A -EB -C 的平面角的余弦值为13C.此八面体一定存在外接球D.此八面体的内切球表面积为8π3【答案】ACD=|OA |=|OB |=|OC |=|OD |可判断C 项，运用等体积法求得内切球的半径，进而可求得内切球的表面积即可判断D 项.【详解】连接AC 、BD 交于点O ，连接OE 、OF ，因为四边形ABCD 为正方形，则AC ⊥BD ，又因为八面体的每个面都是正三角形，所以E 、O 、F 三点共线，且EF ⊥面ABCD ，所以以O 为原点，分别以OB 、OC 、OE 为x 轴、y 轴、z 轴建立空间直角坐标系O -xyz ，如图所示，则O (0,0,0)，A (0,-2,0)，B (2,0,0)，C (0,2,0)，D (-2,0,0)，E (0,0,2)，F (0,0,-2)，对于A 项，AE =(0,2,2)，DF=(2,0,2)，设异面直线AE 与DF 所成角为θ，则cos θ=|cos AE ,DF |=|AE ⋅DF||AE ||DF |=22×2=12，所以θ=π3，即异面直线AE 与DF 所成角大小为π3，故A 项正确；对于B 项，BE =(-2,0,2)，BA =(-2,-2,0)，BC=(-2,2,0)，设面ABE 的一个法向量为n=(x 1,y 1,z 1)，则n ⋅BE=0n ⋅BA =0 ⇒-2x 1+2z 1=0-2x 1-2y 1=0，取x 1=1，则y 1=-1，z 1=1，则n=(1,-1,1)，设面BEC 的一个法向量为m=(x 2,y 2,z 2)，则n ⋅BE=0n ⋅BC =0⇒-2x 2+2z 2=0-2x 2+2y 2=0，取x 2=1，则y 2=1，z 2=1，则m=(1,1,1)，所以cos n ,m =n ⋅m |n ||m |=1-1+13×3=13，又因为面ABE 与BEC 所成的二面角的平面角为钝角，所以二面角A -EB -C 的平面角的余弦值为-13，故B 项错误；对于C 项，因为|OE |=|OF |=|OA |=|OB |=|OC |=|OD |=2，所以O 为此八面体外接球的球心，即此八面体一定存在外接球，故C 项正确；对于D 项，设内切球的半径为r ，则八面体的体积为V =2V E -ABCD =2×13S ABCD ⋅EO =2×13×2×2×2=823，又八面体的体积为V =8V E -ABO =8V O -ABE =8×13S EAB ⋅r =8×13×12×22×sin π3×r =833r ，所以833r =823，解得r =63，所以内切球的表面积为4πr 2=4π×632=8π3，故D 项正确.故选：ACD .2(2024·浙江宁波·二模)在正四棱台ABCD -A 1B 1C 1D 1中，AB =4,A 1B 1=2,AA 1=3，若球O 与上底面A 1B 1C 1D 1以及棱AB ,BC ,CD ,DA 均相切，则球O 的表面积为()A.9πB.16πC.25πD.36π【答案】C【分析】根据勾股定理求解棱台的高MN =1,进而根据相切，由勾股定理求解球半径R =52，即可由表面积公式求解.【详解】设棱台上下底面的中心为N ,M ,连接D 1B 1,DB ，则D 1B 1=22,DB =42，所以棱台的高MN =B 1B 2-MB -NB 1 2=3 2-22-2 2=1,设球半径为R ,根据正四棱台的结构特征可知：球O 与上底面A 1B 1C 1D 1相切于N ,与棱AB ,BC ,CD ,DA 均相切于各边中点处，设BC 中点为E ，连接OE ,OM ,ME ,所以OE 2=OM 2+ME 2⇒R 2=R -1 2+22，解得R =52，所以球O 的表面积为4πR 2=25π，故选：C3(2024·河北石家庄·二模)已知正方体的棱长为22，连接正方体各个面的中心得到一个八面体，以正方体的中心O 为球心作一个半径为233的球，则该球O 的球面与八面体各面的交线的总长为()A.26πB.463π C.863π D.46π【答案】B【分析】画出图形，求解正方体的中心与正八面体面的距离，然后求解求与正八面体的截面圆半径，求解各个平面与球面的交线、推出结果.【详解】如图所示，M 为EF 的中点，O 为正方体的中心，过O 作PM 的垂线交于点N ，正八面体的棱长为2，即EF =2，故OM =1，OP =2，PM =3，则ON =63，设球与正八面体的截面圆半径为r ，如图所示，则r =2332-ON 2=2332-632=63，由于MN =ZN =33，NJ =NI =63，所以IJ =233，则∠INJ =π2，平面PEF 与球O 的交线所对应的圆心角恰为π2，则该球O 的球面与八面体各面的交线的总长为8×14×2π×63 =463π故选：B 4(多选)(2022·山东聊城·二模)用与母线不垂直的两个平行平面截一个圆柱，若两个截面都是椭圆形状，则称夹在这两个平行平面之间的几何体为斜圆柱．这两个截面称为斜圆柱的底面，两底面之间的距离称为斜圆柱的高，斜圆柱的体积等于底面积乘以高．椭圆的面积等于长半轴与短半轴长之积的π倍，已知某圆柱的底面半径为2，用与母线成45°角的两个平行平面去截该圆柱，得到一个高为6的斜圆柱，对于这个斜圆柱，下列选项正确的是()A.底面椭圆的离心率为22B.侧面积为242πC.在该斜圆柱内半径最大的球的表面积为36πD.底面积为42π【答案】ABD【分析】不妨过斜圆柱的最高点D 和最低点B 作平行于圆柱底面的截面圆，夹在它们之间的是圆柱，作出过斜圆柱底面椭圆长轴的截面，截斜圆柱得平行四边形，截圆柱得矩形，如图，由此截面可得椭圆面与圆柱底面间所成的二面角的平面角，从而求得椭圆长短轴之间的关系，得离心率，并求得椭圆的长短轴长，得椭圆面积，利用椭圆的侧面积公式可求得斜椭圆的侧面积，由斜圆柱的高比圆柱的底面直径大，可知斜圆柱内半径最大的球的直径与圆柱底面直径相等，从而得其表面积，从而可关键各选项．【详解】不妨过斜圆柱的最高点D 和最低点B 作平行于圆柱底面的截面圆，夹在它们之间的是圆柱，如图，矩形ABCD 是圆柱的轴截面，平行四边形BFDE 是斜圆柱的过底面椭圆的长轴的截面，由圆柱的性质知∠ABF =45°，则BF =2AB ，设椭圆的长轴长为2a ，短轴长为2b ，则2a =2⋅2b ，a =2b ，c =a 2-b 2=a 2-22a 2=22a ，所以离心率为e =c a =22，A 正确；EG ⊥BF ，垂足为G ，则EG =6，易知∠EBG =45°，BE =62，又CE =AF =AB =4，所以斜圆柱侧面积为S =2π×2×(4+62)-2π×2×4=242π，B 正确；2b =4，b =2，2a =42，a =22，椭圆面积为πab =42π，D 正确；由于斜圆锥的两个底面的距离为6，而圆柱的底面直径为4，所以斜圆柱内半径最大的球的半径为2，球表面积为4π×22=16π，C 错．故选：ABD ．5(21-22高三上·湖北襄阳·期中)在正方体ABCD -A 1B 1C 1D 1中，球O 1同时与以A 为公共顶点的三个面相切，球O 2同时与以C 1为公共顶点的三个面相切，且两球相切于点F .若以F 为焦点，AB 1为准线的抛物线经过O 1，O 2，设球O 1，O 2的半径分别为r 1，r 2，则r1r 2=.【答案】2-3/-3+2【分析】首先根据抛物线的定义结合已知条件得到球O 2内切于正方体，设r 2=1，得到r 1=2-3，即可得到答案.【详解】如图所示：根据抛物线的定义，点O 2到点F 的距离与到直线AB 1的距离相等，其中点O 2到点F 的距离即半径r 2，也即点O 2到面CDD 1C 1的距离，点O 2到直线AB 1的距离即点O 2到面ABB 1A 1的距离，因此球O 2内切于正方体.不妨设r 2=1，两个球心O 1，O 2和两球的切点F 均在体对角线AC 1上，两个球在平面AB 1C 1D 处的截面如图所示，则O 2F =r 2=1，AO 2=AC 12=22+22+222=3，所以AF =AO 2-O 2F =3-1.因为r 1AO 1=223，所以AO 1=3r 1，所以AF =AO 1+O 1F =3r 1+r 1，因此(3+1)r 1=3-1，得r 1=2-3，所以r1r 2=2- 3.故答案为：2-3题型02立体几何中的计数原理排列组合问题1(2024·浙江台州·二模)房屋建造时经常需要把长方体砖头进行不同角度的切割，以契合实际需要.已知长方体的规格为24cm ×11cm ×5cm ，现从长方体的某一棱的中点处作垂直于该棱的截面，截取1次后共可以得到12cm ×11cm ×5cm ，24cm ×112cm ×5cm ，24cm ×11cm ×52cm 三种不同规格的长方体.按照上述方式对第1次所截得的长方体进行第2次截取，再对第2次所截得的长方体进行第3次截取，则共可得到体积为165cm 3的不同规格长方体的个数为()A.8B.10C.12D.16【答案】B【分析】根据原长方体体积与得到的体积为165cm 3长方体的关系，分别对长宽高进行减半，利用分类加法计数原理求解即可.【详解】由题意，V 长方体=24×11×5=8×165，为得到体积为165cm 3的长方体，需将原来长方体体积缩小为原来的18，可分三类完成：第一类，长减半3次，宽减半3次、高减半3次，共3种；第二类，长宽高各减半1次，共1种；第三类，长宽高减半0,1,2 次的全排列A 33=6种，根据分类加法计数原理，共3+1+6=10种. 故选：B2(2023·江苏南通·模拟预测)在空间直角坐标系O -xyz 中，A 10,0,0 ,B 0,10,0 ,C 0,0,10 ，则三棱锥O -ABC 内部整点(所有坐标均为整数的点，不包括边界上的点)的个数为()A.C 310B.C 39C.C 210D.C 29【答案】B【分析】先利用空间向量法求得面ABC 的一个法向量为n =1,1,1 ，从而求得面ABC 上的点P a ,b ,c 满足a +b +c =10，进而得到棱锥O -ABC 内部整点为Q s ,t ,r 满足3≤s +t +r ≤9，再利用隔板法与组合数的性质即可得解.【详解】根据题意，作出图形如下，因为A 10,0,0 ,B 0,10,0 ,C 0,0,10 ，所以AB =-10,10,0 ,AC=-10,0,10 ，设面ABC 的一个法向量为n=x ,y ,z ，则AB ⋅n=-10x +10y =0AC ⋅n=-10x +10z =0，令x =1，则y =1,z =1，故n=1,1,1 ，设P a ,b ,c 是面ABC 上的点，则AP=a -10,b ,c ，故AP ⋅n=a -10+b +c =0，则a +b +c =10，不妨设三棱锥O -ABC 内部整点为Q s ,t ,r ，则s ,t ,r ∈N *，故s ≥1,t ≥1,r ≥1，则s +t +r ≥3，易知若s +t +r =10，则Q 在面ABC 上，若s +t +r >10，则Q 在三棱锥O -ABC 外部，所以3≤s +t +r ≤9，当s +t +r =n ,n ∈N *且3≤n ≤9时，将n 写成n 个1排成一列，利用隔板法将其隔成三部分，则结果的个数为s ,t ,r 的取值的方法个数，显然有C 2n -1个方法，所有整点Q s ,t ,r 的个数为C 22+C 23+⋯+C 28，因为C r n +C r -1n =n !r !n -r !+n !r -1 !n +1-r !=n +1-r n !+rn !r !n +1-r !=n +1 !r !n +1-r!=C rn +1，所以C 22+C 23+⋯+C 28=C 33+C 23+⋯+C 28=C 34+C 24+⋯+C 28=⋯=C 38+C 28=C 39.故选：B .【点睛】关键点睛：本题解决的关键是求得面ABC 上的点P a ,b ,c 满足a +b +c =10，从而确定三棱锥O -ABC 内部整点为Q s ,t ,r 满足3≤s +t +r ≤9，由此得解.3(2024·重庆·模拟预测)从长方体的8个顶点中任选4个，则这4个点能构成三棱锥的顶点的概率为()A.2736B.2935C.67D.3235【答案】B【分析】首先求出基本事件总数，再计算出这4个点在同一个平面的概率，最后利用对立事件的概率公式计算可得.【详解】根据题意，从长方体的8个顶点中任选4个，有C 48=70种取法，“这4个点构成三棱锥的顶点”的反面为“这4个点在同一个平面”，而长方体有2个底面和4个侧面、6个对角面，一共有12种情况，则这4个点在同一个平面的概率P =1270=635，所以这4个点构成三棱锥的概率为1-635=2935.故选：B ．4(多选)(2024·重庆·模拟预测)如图，16枚钉子钉成4×4的正方形板，现用橡皮筋去套钉子，则下列说法正确的有(不同的图形指两个图形中至少有一个顶点不同)()A.可以围成20个不同的正方形B.可以围成24个不同的长方形(邻边不相等)C.可以围成516个不同的三角形D.可以围成16个不同的等边三角形【答案】ABC【分析】利用分类计算原理及组合，结合图形，对各个选项逐一分析判断即可得出结果.【详解】不妨设两个钉子间的距离为1，对于选项A ，由图知，边长为1的正方形有3×3=9个，边长为2的正方形有2×2=4个，边长为3的正方形有1个，边长为2的正方形有2×2=4个，边长为5的有2个，共有20个，所以选项A 正确，对于选项B ，由图知，宽为1的长方形有3×3=9个，宽为2的长方形有4×2=8个，宽为3的长方形有5个，宽为2的有2个，共有24个，所以选项B 正确，对于选项C ，由图知，可以围成C 316-10C 34-4C 33=516个不同的三角形，所以选项C 正确，对于选项D ，由图可知，不存在等边三角形，所以选项D 错误，故选：ABC .5(2024·上海浦东新·模拟预测)如图ABCDEF -A B C D E F 为正六棱柱，若从该正六棱柱的6个侧面的12条面对角线中，随机选取两条，则它们共面的概率是．【答案】611【分析】根据题意，相交时分为：在侧面内相交，两个相邻面相交于一个点，相隔一个面中相交于对角线延长线上，分别分析几种情况下对角线共面的个数，再利用古典概型的概率计算公式，计算结果即可．【详解】由题意知，若两个对角线在同一个侧面，因为有6个侧面，所以共有6组，若相交且交点在正六棱柱的顶点上，因为有12个顶点，所以共有12组，若相交且交点在对角线延长线上时，如图所示，连接AD ，C D ，E D ，AB ，AF ，先考虑下底面，根据正六边形性质可知EF ⎳AD ⎳BC ，所以E F ⎳AD ⎳B C ，且B C =E F ≠AD ，故ADC B 共面，且ADE F 共面，故AF ，DE 相交，且C D ，AB 相交，故共面有2组，则正六边形对角线AD 所对应的有2组共面的面对角线，同理可知正六边形对角线BE ，CF 所对的分别有两组，共6组，故对于上底面对角线A D ，B E ，C F 同样各对两组，共6组，若对面平行，一组对面中有2组对角线平行，三组对面共有6组，所以共面的概率是6+12+12+6C 212=611．故答案为：611．题型03立体几何动点最值问题空间几何体中线段和差最值以及几何体中的轨迹问题，以及线线角和线面角的求解，综合性较强，难度较大，解答时要发挥空间想象，明确空间的位置关系，结合空间距离，确定动点的轨迹形状；结合等体积法求得点到平面的距离，结合线面角的定义求解.1(多选)(2024·浙江台州·二模)已知正方体ABCD -A 1B 1C 1D 1的棱长为1，P 为平面ABCD 内一动点，且直线D 1P 与平面ABCD 所成角为π3，E 为正方形A 1ADD 1的中心，则下列结论正确的是()A.点P 的轨迹为抛物线B.正方体ABCD -A 1B 1C 1D 1的内切球被平面A 1BC 1所截得的截面面积为π6C.直线CP 与平面CDD 1C 1所成角的正弦值的最大值为33D.点M 为直线D 1B 上一动点，则MP +ME 的最小值为11-266【答案】BCD【分析】对于A ，根据到D 点长度为定值，确定动点轨迹为圆；对于B ，理解内切球的特点，计算出球心到平面的距离，再计算出截面半径求面积；对于C ，找到线面所成角的位置，再根据动点的运动特点(相切时)找到正弦的最大值；对于D ，需要先找到P 点位置，再将立体问题平面化，根据三点共线距离最短求解.【详解】对于A ，因为直线D 1P 与平面ABCD 所成角为π3，所以DP =1tan π3=33.P 点在以D 为圆心，33为半径的圆周上运动，因此运动轨迹为圆.故A 错误.对于B ，在面BB 1D 1D 内研究，如图所示O 为内切球球心，O 1为上底面中心，O 2为下底面中心，G 为内切球与面A 1BC 1的切点.已知OG ⊥O 1B ，OG 为球心到面A 1BC 1的距离.在正方体中，O 1B =62，O 2B =22，O 1O 2=1.利用相似三角形的性质有OG O 2B =OO 1O 1B，即OG 22=1262，OG =36.因此可求切面圆的r 2=122-362=16，面积为π6.故B 正确.对于C ，直线CP 与平面CDD 1C 1所成角即为∠PCD ，当CP 与P 点的轨迹圆相切时，sin ∠PCD 最大.此时sin ∠PCD =13=33.故C 正确.对于D ，分析可知，P 点为BD 和圆周的交点时，MP 最小.此时可将面D 1AB 沿着D 1B 翻折到面BB 1D 1D 所在平面.根据长度关系，翻折后的图形如图所示.当E ,M ,P 三点共线时，MP +ME 最小.因为O 2P =33-22，O 1O 2=1，所以最小值为12+33-222=11-266，故D 正确.故选：BCD2(多选)(2024·江苏扬州·模拟预测)如图，在棱长为1的正方体ABCD -A 1B 1C 1D 1中，M 为平面ABCD 内一动点，则()A.若M 在线段AB 上，则D 1M +MC 的最小值为4+22B.平面ACD 1被正方体内切球所截，则截面面积为π6C.若C 1M 与AB 所成的角为π4，则点M 的轨迹为椭圆D.对于给定的点M ，过M 有且仅有3条直线与直线D 1A ,D 1C 所成角为60°【答案】ABD迹方程判断C ，合理转化后判断D 即可.【详解】对于A ，延长DA 到E 使得AE =2，则D 1M +MC =EM +MC ≥EC =4+22，等号在E ,M ,C 共线时取到；故A 正确，对于B ，由于球的半径为12，球心到平面ACD 1的距离为36，故被截得的圆的半径为14-112 =66，故面积为π66 2=π6，故B 正确，对于C ，C 1M 与AB 所成的角即为C 1M 和C 1D 1所成角，记CM =xCD +yCB ，则x 2+y 2+1=2(y 2+1)，即x 2-y 2=1，所以M 的轨迹是双曲线；故C 错误，对于D ，显然过M 的满足条件的直线数目等于过D 1的满足条件的直线l 的数目，在直线l 上任取一点P ，使得D 1P =D 1A =D 1C ，不妨设∠PD 1A =π3，若∠PD 1C =π3，则AD 1CP 是正四面体，所以P 有两种可能，直线l 也有两种可能，若∠PD 1C =2π3，则l 只有一种可能，就是与∠AD 1C 的角平分线垂直的直线，所以直线l 有三种可能.故选：ABD3(多选)(2023·安徽芜湖·模拟预测)已知正方体ABCD -A 1B 1C 1D 1的棱长为2，棱AB 的中点为M ，过点M 作正方体的截面α，且B 1D ⊥α，若点N 在截面α内运动(包含边界)，则()A.当MN 最大时，MN 与BC 所成的角为π3B.三棱锥A 1-BNC 1的体积为定值23C.若DN =2，则点N 的轨迹长度为2πD.若N ∈平面A 1BCD 1，则BN +NC 1 的最小值为6+23【答案】BCD【分析】记BC ,CC 1,C 1D ,D 1A 1,A 1A 的中点分别为F ,H ,G ,F ,E ，构建空间直角坐标系，证明M ,F ,H ,G ,F ,E 共面，且DB 1⊥平面MEFGHI ，由此确定平面α，找到MN 最大时N 的位置，确定MN 与BC 所成角的平面角即可判断A ，证明A 1BC 1与平面α平行，应用向量法求M 到面A 1BC 1的距离，结合体积公式，求三棱锥A 1-BNC 1的体积，判断B ；根据球的截面性质确定N 的轨迹，进而求周长判断C ，由N ∈平面A 1BCD 1确定N 的位置，通过翻折为平面图形，利用平面几何结论求解判断D .【详解】记BC ,CC 1,C 1D ,D 1A 1,A 1A 的中点分别为F ,H ,G ,F ,E ，连接EF ,FG ,GH ,HI ,IM ,ME ，连接GM ,FI ，因为FG ∥A 1C 1,A 1C 1∥AC ,AC ∥MI ，又FG =12A 1C 1 =12AC =MI 所以FG ∥MI ，FG =MI ，所以四边形FGIM 为平行四边形，连接FI ,MG ，记其交点为S ，根据正方体性质，可构建如下图示的空间直角坐标系，则A (2,0,0)，A 1(2,0,2)，B (2,2,0)，C 1(0,2,2)，B 12,2,2 ,M (2,1,0)，E (2,0,1)，F (1,0,2)，G (0,1,2)，H (0,2,1)，I (1,2,0)，S 1,1,1 ，因为DB 1 =2,2,2 ，SM =1,0,-1 ，SI =0,1,-1 ，SH =-1,1,0 ，SG =-1,0,1 ，SF =0,-1,1 ，SE =1,-1,0 ，所以DB 1 ⋅SM =0，DB 1 ⋅SI =0，DB 1 ⋅SH =0，DB1 ⋅SG =0，DB 1 ⋅SF =0，DB 1 ⋅SE =0所以M ,E ,F ,G ,H ,I 六点共面，因为DB 1 =2,2,2 ，MI =-1,1,0 ，ME =0,-1,1 ，所以DB 1 ⋅MI =-2+2+0=0，DB 1 ⋅ME =0-2+2=0，所以DB 1 ⊥MI ，DB 1 ⊥ME ，所以DB 1⊥MI ,DB 1⊥ME ，又MI ,ME ⊂平面MEFGHI ，所以DB 1⊥平面MEFGHI ，故平面MEFGHI 即为平面α，对于A ，N 与G 重合时，MN 最大，且MN ⎳BC 1，所以MN 与BC 所成的角的平面角为∠C 1BC ，又BC =CC 1 ,∠BCC 1=90°，所以∠C 1BC =π4，故MN 与BC 所成的角为π4，所以A 错误；对于B ，因为所以DB 1 =2,2,2 ，A 1C 1 =-2,2,0 ，BC 1=-2,0,2 ，所以DB 1 ⋅A 1C 1 =-4+4+0=0，DB 1 ⋅BC 1 =-4+0+4=0，所以DB 1 ⊥A 1C 1 ，DB 1 ⊥BC 1 ，所以DB 1⊥A 1C 1,DB 1⊥BC 1，又A 1C 1,BC 1⊂平面A 1BC 1，所以DB 1⊥平面A 1BC 1，又DB 1⊥平面MEFGHI ，所以平面A 1BC 1∥平面MEFGHI ，所以点N 到平面A 1BC 1的距离与点M 到平面A 1BC 1的距离相等，所以V A 1-BNC 1=V N -A 1BC 1=V M -A 1BC 1，向量DB 1 =2,2,2 为平面A 1BC 1的一个法向量，又MB =(0,1,0)，所以M 到面A 1BC 1的距离d =DB 1 ⋅MB DB 1=33，又△A 1BC 1为等边三角形，则S △A 1BC 1=12×(22)2×32=23，所以三棱锥A 1-BNC 1的体积为定值13×d ×S △A 1BC 1=23，B 正确；对于C ：若DN =2，点N 在截面MEFGHI 内，所以点N 的轨迹是以D 为球心，半径为2的球体被面MEFGHI 所截的圆(或其一部分)，因为DS =1,1,1 ，DB 1 =2,2,2 ，所以DB 1 ∥DS ，所以DS ⊥平面MEFGHI ，所以截面圆的圆心为S ，因为DB 1 =2,2,2 是面MEFGHI 的法向量，而DF =(1,0,2)，所以D 到面MEFGHI 的距离为d =m ⋅DFm=3，故轨迹圆的半径r =22-(3)2=1，又SM =2，故点N 的轨迹长度为2πr =2π，C 正确.对于D ，N ∈平面A 1BCD 1，N ∈平面MEFGHI ，又平面A 1BCD 1与平面MEFGHI 的交线为FI ，所以点N 的轨迹为线段FI ，翻折△C 1FI ，使得其与矩形A 1BIF 共面，如图，所以当B ,N ,C 1三点共线时，BN +NC 1 取最小值，最小值为BC 1 ，由已知C 1I =C 1F =5，BI =1，FI =22，过C 1作C 1T ⊥BI ，垂足为T ，则C 1T =2，所以IT=C 1I2-C 1T 2=3=BT 2+C T 2=3+12+2=6+23，所以BN +NC 1 的最小值为6+23，D 正确；故选：BCD【点睛】关键点点睛：本题解决的关键在于根据截面的性质确定满足条件的过点M 的截面位置，再结合异面直线夹角定义，锥体体积公式，球的截面性质，空间图形的翻折判断各选项.4(多选)(2024·福建厦门·一模)如图所示，在五面体ABCDEF 中，四边形ABCD 是矩形，△ABF 和△DCE 均是等边三角形，且AB =23，EF =x (x >0)，则()A.EF ⎳平面ABCDB.二面角A -EF -B 随着x 的减小而减小C.当BC =2时，五面体ABCDEF 的体积V (x )最大值为272D.当BC =32时，存在x 使得半径为32的球能内含于五面体ABCDEF 【答案】ACD【分析】A 由线面平行的判定证明；B 设二面角A -EF -B 的大小为2α，点F 到面ABCD 的距离为h ，则tan α=3h，分析取最小值的对应情况即可判断；C 把五面体ABCDEF 补成直三棱柱FGI -EKJ ，取AB ,GI 的中点M ,H ，设∠FMH =θ0<θ≤π2，则MH =3cos θ,FH =3sin θ，结合V (x )=V FGI -EKJ -2V F -ABIG 并应用导数研究最值；D 先分析特殊情况：△ABF 和△DCE 所在平面均垂直于面ABCD 时构成正三棱柱ABF -DCE ，再借助左视图、正视图研究内切圆半径分析一般情况判断.【详解】A ：由题设BC ⎳AD ，AD ⊂面ADEF ，BC ⊄面ADEF ，则BC ⎳面ADEF ，由面BCEF ∩面ADEF =EF ，BC ⊂面BCEF ，则BC ⎳EF ，BC ⊂面ABCD ，EF ⊄面ABCD ，则EF ⎳平面ABCD ，对；B ：设二面角A -EF -B 的大小为2α，点F 到面ABCD 的距离为h ，则tan α=3h，点F 到面ABCD 的距离，仅在面FAB ⊥面ABCD 时取得最大值，当EF =x =BC 时tan α取最小值，即α取最小值，即二面角A -EF -B 取最小值，所以EF =x ∈(0,+∞)，二面角先变小后变大，错；C ：当BC =2，如图，把五面体ABCDEF 补成直三棱柱FGI -EKJ ，分别取AB ,GI 的中点M ,H ，易得FH ⊥面ABCD ，FM =3，设∠FMH =θ0<θ≤π2，则MH =3cos θ,FH =3sin θ，V (x )=V ABCDEF =V FGI -EKJ -2V F -ABIG =12×23×3sin θ×(2+6cos θ)-2×13×3sin θ×23×3cos θ=63sin θ+63sin θcos θ，令f (θ)=0⇒2cos 2θ+cos θ-1=0，可得cos θ=12或cos θ=-1(舍)，即θ=π3，0<θ<π3，f (θ)>0，f (θ)递增，π3<θ≤π2，f(θ)<0，f (θ)递减，显然θ=π3是f (θ)的极大值点，故f (θ)max =63×32+63×32×12=272.所以五面体ABCDEF 的体积V (x )最大值为272，C 对；D ：当BC =32时，△ABF 和△DCE 所在平面均垂直于面ABCD 时构成正三棱柱ABF -DCE ，此时正三棱柱内最大的求半径r =34<32，故半径为32的球不能内含于五面体ABCDEF ，对于一般情形，如下图示，左图为左视图，右图为正视图，由C 分析结果，当五面体ABCDEF 体积最大时，其可内含的球的半径较大，易知，当∠FMH =π3时，FH =332,IH =3,IF =392，设△FIG 的内切圆半径为r 1，则12×332×23=12r 1×23+2×392 ，可得r 1=332+13>32，另外，设等腰梯形EFMN 中圆的半径为r 2，则r 2=34tan π3=334>r 1=332+13，所以，存在x 使半径为32的球都能内含于五面体ABCDEF ，对.故选：ACD【点睛】关键点点睛：对于C 通过补全几何体为棱柱，设∠FMH =θ0<θ≤π2得到五面体ABCDEF 的体积关于θ的函数；对于D 从特殊到一般，结合几何体视图研究内切圆判断最大半径是否大于32为关键.5(多选)(2024·广西南宁·一模)在边长为2的正方体ABCD -A 1B 1C 1D 1中，动点M 满足AM =xAB+yAD +zAA 1 ，(x ,y ,z ∈R 且x ≥0,y ≥0,z ≥0)，下列说法正确的是()A.当x =14,z =0,y ∈0,1 时，B 1M +MD 的最小值为13B.当x =y =1,z =12时，异面直线BM 与CD 1所成角的余弦值为105C.当x +y +z =1，且AM =253时，则M 的轨迹长度为42π3D.当x +y =1,z =0时，AM 与平面AB 1D 1所成角的正弦值的最大值为63【答案】AD【分析】对于A ，确定M 的位置，利用侧面展开的方法，求线段的长，即可判断；对于B ，利用平移法，作出异面直线所成角，解三角形，即可判断；对于C ，结合线面垂直以及距离确定点M 的轨迹形状，即可确定轨迹长度；对于D ，利用等体积法求得M 点到平面AB 1D 1的距离，结合线面角的定义求得AM 与平面AB 1D 1所成角的正弦值，即可判断.【详解】对于A ，在AB 上取点H ，使AH =14AB ，在DC 上取点K ，使DK =14DC ，因为x =14,z =0,y ∈0,1 ，即AM =14AB +yAD ，故M 点在HK 上，将平面B 1HKC 1与平面AHKD 沿着HK 展开到同一平面内，如图：连接B 1D 交HK 于P ，此时B ,P ,D 三点共线，B 1M +MD 取到最小值即B 1D 的长，由于AH =14AB =12,∴BH =32，则B 1H =22+32 2=52，故AB 1=52+12=3,∴B 1D =(B 1A )2+AD 2=32+22=13，即此时B 1M +MD 的最小值为13，A 正确；对于B ，由于x =y =1,z =12时，则AM =AB +AD +12AA 1 =AC +12CC 1 ，此时M 为CC 1的中点，取C 1D 1的中点为N ，连接BM ,MN ,BN ，则MN ∥CD 1,故∠BMN 即为异面直线BM 与CD 1所成角或其补角，又MN =12CD 1=2,BM =22+12=5,BN =(BC 1)2+(C 1N )2=8+1=3，故cos ∠BMN =BM 2+MN 2-BN 22BM ⋅MN =5 2+2 2-3225⋅2=-1010，而异面直线所成角的范围为0,π2，故异面直线BM 与CD 1所成角的余弦值为1010，B 错误；对于C ，当x +y +z =1时，可得点M 的轨迹在△A 1BD 内(包括边界)，由于CC 1⊥平面ABCD ，BD ⊂平面ABCD ，故CC 1⊥BD ，又BD ⊥AC ，AC ∩CC 1=C ,AC ,CC 1⊂平面ACC 1，故BD ⊥平面ACC 1，AC 1⊂平面ACC 1，故BD ⊥AC 1，同理可证A 1B ⊥AC 1,A 1B ∩BD =B ,A 1B ,BD ⊂平面A 1BD ，故AC 1⊥平面A 1BD ，设AC 1与平面A 1BD 交于点P ，由于V A -A 1BD =V A 1-ABD =13×12×2×2×2=43，△A 1BD 为边长为22的正三角形，则点A 到平面A 1BD 的距离为AP =4313×34×22 2=233，若AM =253，则MP =AM 2-AP 2=223，即M 点落在以P 为圆心，223为半径的圆上，P 点到△A 1BD 三遍的距离为13×32×22=63<223，即M 点轨迹是以P 为圆心，223为半径的圆的一部分，其轨迹长度小于圆的周长42π3，C 错误；因为当x +y =1,z =0时，AM =AB +AD，即M 在BD 上，点M 到平面AB 1D 1的距离等于点B 到平面AB 1D 1的距离，设点B 到平面AB 1D 1的距离为d ，则V B -AB 1D 1=V D 1-ABB 1=13S △ABB 1⋅A 1D 1=13×12×2×2×2=43，△AB 1D 1为边长为22的正三角形，即13S △A 1BD ⋅d =13×34×22 2×d =43，解得d =233，又M 在BD 上，当M 为BD 的中点时，AM 取最小值2，设直线AM 与平面AB 1D 1所成角为θ,θ∈0,π2，则sin θ=d AM =233AM≤2332=63，即AM 与平面AB 1D 1所成角的正弦值的最大值为63，D 正确，故选：AD【点睛】难点点睛：本题考查了空间几何体中线段和差最值以及几何体中的轨迹问题，以及线线角和线面角的求解，综合性较强，难度较大，解答时要发挥空间想象，明确空间的位置关系，难点在于C ，D 选项的判断，对于C ，要结合空间距离，确定动点的轨迹形状；对于D ，要结合等体积法求得点到平面的距离，结合线面角的定义求解.题型04不规则图形中的面面夹角问题利用向量法解决立体几何中的空间角问题，关键在于依托图形建立合适的空间直角坐标系，将相关向量用坐标表示，通过向量的坐标运算求空间角，其中建系的关键在于找到两两垂直的三条直线．1(2024·浙江台州·二模)如图，已知四棱台ABCD -A 1B 1C 1D 1中，AB =3A 1B 1，AB ∥CD ，AD ⊥AB ，AB =6，CD =9，AD =6，且AA 1=BB 1=4，Q 为线段CC 1中点，(1)求证：BQ ∥平面ADD 1A 1；(2)若四棱锥Q -ABB 1A 1的体积为3233，求平面ABB 1A 1与平面CDD 1C 1夹角的余弦值.【答案】(1)证明见解析(2)217【分析】(1)分别延长线段AA 1，BB 1，CC 1，DD 1交于点P ，将四棱台补成四棱锥P -ABCD ，取DD 1的中点E ，连接QE ，AE ，由四边形ABQE 为平行四边形，得到BQ ∥AE ，然后利用线面平行的判定定理证明；(2)先证明AD ⊥平面ABB 1A 1，再以A 为坐标原点，以直线AB 为x 轴，以直线AD 为y 轴，建立空间直角坐标系，求得平面CDD 1C 1的法向量为m =x ,y ,z ，易得平面ABB 1A 1的一个法向量为n=0,1,0 ，然后由cos m ,n=m ⋅n m n 求解.【详解】(1)证明：如图所示：分别延长线段AA 1，BB 1，CC 1，DD 1交于点P ，将四棱台补成四棱锥P -ABCD .∵A 1B 1=13AB ，∴PC 1=13PC ，∴CQ =QC 1=C 1P ，取DD 1的中点E ，连接QE ，AE ，∵QE ⎳CD ⎳AB ，且QE =123+9 =6=AB ，∴四边形ABQE 为平行四边形.∴BQ ∥AE ，又AE ⊂平面ADD 1A 1，BQ ⊄平面ADD 1A 1，∴BQ ∥平面ADD 1A 1；(2)由于V Q -ABB 1A 1=23V C -ABB 1A 1，所以V C -ABB 1A 1=163，又梯形ABB 1A 1面积为83，设C 到平面ABB 1A 1距离为h ，则V C -ABB 1A 1=13S 梯形ABB 1A 1⋅h =163，得h =6.而CD ∥AB ，AB ⊂平面ABB 1A 1，CD ⊄平面ABB 1A 1，所以CD ∥平面ABB 1A 1，所以点C 到平面ABB 1A 1的距离与点D 到平面ABB 1A 1的距离相等，而h =6=AD ，所以AD ⊥平面ABB 1A 1.以A 为坐标原点，以直线AB 为x 轴，以直线AD 为y 轴，建立空间直角坐标系，易得△PAB 为等边三角形，所以A 0,0,0 ，B 6,0,0 ，C 9,6,0 ，D 0,6,0 ，P 3,0,33设平面CDD 1C 1的法向量为m=x ,y ,z ，则m ⋅DP=x ,y ,z ⋅3,-6,33 =3x -6y +33z =0m ⋅DC=x ,y ,z ⋅9,0,0 =9x =0，得x =0，y =32z ，不妨取m =0,3,2 ，又平面ABB 1A 1的一个法向量为n=0,1,0 .则，平面ABB 1A 1与平面CDD 1C 1夹角的余弦值为217.2(2024·浙江杭州·二模)如图，在多面体ABCDPQ 中，底面ABCD 是平行四边形，∠DAB =60°,BC=2PQ =4AB =4,M 为BC 的中点，PQ ∥BC ,PD ⊥DC ,QB ⊥MD ．(1)证明：∠ABQ =90°；(2)若多面体ABCDPQ 的体积为152，求平面PCD 与平面QAB 夹角的余弦值．【答案】(1)证明见解析；(2)31010．【分析】(1)根据余弦定理求解DM =3，即可求证DM ⊥DC ，进而根据线线垂直可证明线面垂直，即可得线线垂直，(2)根据体积公式，结合棱柱与棱锥的体积关系，结合等体积法可得PM =h =33，即可建立空间直角坐标系，求解法向量求解.【详解】(1)在△DCM 中，由余弦定理可得DM =DC 2+MC 2-2DC ⋅MC cos60°=3，所以DM 2+DC 2=CM 2，所以∠MDC =90°，所以DM ⊥DC ．又因为DC ⊥PD ，DM ∩PD =D ,DM ,DP ⊂平面PDM ,所以DC ⊥平面PDM ,PM ⊂平面PDM ．所以DC ⊥PM ．由于PQ ⎳BM ,PQ =BM =2,所以四边形PQBM 为平行四边形，所以PM ∥QB ．又AB ∥DC ，所以AB ⊥BQ ，所以∠ABQ =90°．(2)因为QB ⊥MD ，所以PM ⊥MD ，又PM ⊥CD ，DC ∩MD =D ,DC ,MD ⊂平面ABCD ,所以PM ⊥平面ABCD ．取AD 中点E ，连接PE ，设PM =h ．设多面体ABCDPQ 的体积为V ，则V =V 三棱柱ABQ -PEM +V 四棱锥P -CDEM =3V A -PEM +V 四棱锥P -CDEM =3V P -AEM +V 四棱锥P -CDEM=S △AEM ×h +13S 四边形CDEM ×h =S △AEM ×h +132S △AEM ×h =53S △AEM ×h =53×12×2×1×sin 2π3h =152．解得PM =h =33．建立如图所示的空间直角坐标系，则A -3,2,0 ,B -3,1,0 ,C 3,-1,0 ，D 3,0,0 ,P 0,0,33 ,Q -3,1,33 ,M 0,0,0 ．则平面QAB 的一个法向量n=1,0,0 ．所以CD =0,1,0 ,PD=3,0,-33 ，设平面PCD 的一个法向量m=x ,y ,z ，则m ⋅CD=0,n ⋅PD =0,即y =0,3x -33z =0, 取m=3,0,1 ．所以cos θ=m ⋅n m ⋅n=31010．。

立体几何动点最值问题

立体几何动点最值问题
立体几何动点最值问题是指在立体几何空间中，给定一些特定条件下，求一个动点的某个值的最大或最小值。

这类问题广泛应用于建筑设计、机械工程、地理测量等领域。

在解决立体几何动点最值问题时，通常需要利用几何性质和数学方法进行分析和求解。

下面以两个典型的问题为例进行拓展说明。

问题一：在一个正方体中，找到离一个定点最远的顶点。

解答：首先，我们找到这个正方体的中心点，然后根据对称性可以知道，离中心点最远的顶点就是通过连接中心点和一个面的对角线的顶点。

因此，我们可以通过计算这个对角线的长度，并找出最长的对角线来确定离定点最远的顶点。

问题二：在一个球体上，找到离球心最远的点。

解答：根据球体的几何性质，离球心最远的点是球体表面上的点。

因此，我们可以通过计算球心到球面上各点的距离，并找出最大距离的点来确定离球心最远的点。

在实际应用中，立体几何动点最值问题的解决往往需要结合具体的条件和约束条件进行分析和求解。

这些问题可能涉及到线段、面积、体积等几何量的计算，以及最优化等数学方法的运用。

因此，解决这类
问题需要理解立体几何的基本概念和性质，并熟练掌握相关的计算和求解技巧。

高考数学复习压抽题专项突破—立体几何中最值问题

高考数学复习压抽题专项突破—立体几何中最值问题一．方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力。

最值问题一般涉及到距离、面积、体积、角度等四个方面。

此类问题多以规则几何体为载体，涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从三个方面思考：一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解；二是根据几何体的结构特征，变动态为静态，直观判断在什么情况下取得最值；三是将几何体平面化，如利用展开图，在平面几何图中直观求解.二．解题策略类型一空间角的最值问题【例1】（2020·浙江高三期末）如图，四边形ABCD ，4AB BD DA ===，BC CD ==现将ABD ∆沿BD 折起，当二面角A BD C --的大小在2[,]33ππ时，直线AB 和CD 所成角为α，则cos α的最大值为（）A ．2268B ．6224C ．2268+D ．2264+【答案】C【解析】取BD 中点O ，连结AO ，CO ，∵AB ＝BD ＝DA ＝4．BC ＝CD =CO ⊥BD ，AO ⊥BD ，且CO ＝2，AO =，∴∠AOC 是二面角A ﹣BD ﹣C 的平面角，以O 为原点，OC 为x 轴，OD 为y 轴，过点O 作平面BCD 的垂线为z 轴，建立空间直角坐标系，B （0，﹣2，0），C （2，0，0），D （0，2，0），设二面角A ﹣BD ﹣C 的平面角为θ，则2,33ππθ⎡⎤∈⎢⎥⎣⎦，连AO 、BO ，则∠AOC ＝θ，A（0θθ，），∴()2BA θθ= ，，()220CD =- ，，，设AB 、CD 的夹角为α，则cosαAB CD AB CD ⋅==⋅ ，∵2,33ππθ⎡⎤∈⎢⎥⎣⎦，∴cos 1122θ⎡⎤∈-⎢⎥⎣⎦，，∴|1θ|∈[0，1+32]．∴cos α的最大值为2268．故选：C．【指点迷津】空间的角的问题，只要便于建立坐标系均可建立坐标系，然后利用公式求解.解本题要注意，空间两直线所成的角是不超过90度的.几何问题还可结合图形分析何时取得最大值.【举一反三】[来1．（2020·广东高考模拟）在正方体1111ABCD A B C D -中，E 是侧面11ADD A 内的动点，且1B E //平面1BDC ，则直线1B E 与直线AB 所成角的正弦值的最小值是()A ．13B ．33C ．12D ．22【答案】B【解析】以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z轴，建立空间直角坐标系，设正方体1111ABCD A B C D -中棱长为1，设E(a,0，c)，0a 1≤≤，0c 1≤≤，1B (1,1，1)，B(1,1，0)，D(0,0，0)，1C (0,1，1)，()1B E a 1,1,c 1=--- ，DB (1,= 1，0)，1DC (0,=1，1)，设平面1DBC 的法向量n (x,= y ，z)，则1n DB 0n DC 0x y y z⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x 1=，得()n 1,1,1=- ，1B E // 平面1BDC ，1B E n a 11c 10∴⋅=-++-=，解得a c 1+=，()222a c a c 2ac 12ac ∴+=+-=-，2a c 1ac 24+⎛⎫≤= ⎪⎝⎭，设直线1B E 与直线AB 所成角为θ，AB (0,= 1，0)，11AB B E cosθAB B E⋅∴==⋅ 2a c 1ac 24+⎛⎫≤= ⎪⎝⎭，322ac 2∴-≥，1222ac 3∴≤-，sinθ∴==3==≥=．∴直线1B E 与直线AB 所成角的正弦值的最小值是33．故选B ．2．（2020·河南高三月考（理））如图，在菱形ABCD 中，∠ABC ＝60°，E ，F 分别是边AB ，CD 的中点，现将△ABC 沿着对角线AC 翻折，则直线EF 与平面ACD 所成角的正切值最大值为()AB．3C．3D ．2【答案】D【解析】如图，以AC 的中点O 为坐标原点，建立空间直角坐标系，设二面角B AC D --为θ，可证BOD ∠=θ，设棱形的边长为4，则()0,2,0A -，(),0,B θθ，),Eθθ-，()0,2,0C，()D，)F)FE θθ∴=-- ，易知平面ACD 的法向量()0,0,1n = 设直线EF 与平面ACD 所成角为α，则()()()222222231cos 3sin 3sin sin 106cos 253cos 3cos 143sin n FE n FE θθθαθθθθ⎛⎫⋅- ⎪==== ⎪---++⋅⎝⎭令()2153x f x x-=-，()1,1x ∈-，()()()()()22231331033535x x x x f x x x ---+'==--则()0f x '>时113x -<<即()f x 在11,3⎛⎫- ⎪⎝⎭上单调递增；()0f x '<时113x <<即()f x 在1,13⎛⎫ ⎪⎝⎭上单调递减；()max 1239f x f ⎛⎫∴== ⎪⎝⎭，()2max 1sin 3α∴=则()2max 2cos 3α=()222max sin 1tan cos 2ααα∴==，()max 2tan 2α∴=，故选：D 3．AB 是圆锥 S O 的直径，SB 是它的一条母线，E 、F 是SB 的两个三等分点（E 点靠近S 点），C 点在圆O 上运动（不与A 、B 两点重合），则二面角 --E AC F 的平面角为α则tan α的最大值是_______．【解析】设圆锥的高为,,h BC a =如图所示，二面角E AC B --的平面角为1,EDN α=∠，二面角F AC B --的平面角为2FGH α=∠，则1221233tan ,tan 25536h h h h a a a a αα====，设1222tan t,tan 55h h t a a αα====,所以12223335555tan tan()221211555t t t t t t t t ααα-=-===≤+⨯++.所以tan max α==.类型二空间距离的最值问题【例2】（2020银川一中模拟）正方体1111ABCD A B C D 的棱长为1,M 、N 分别在线段11A C 与BD 上,MN 的最小值为【答案】1【解析】分析：方法一,该题可以结合正方体的结构特征,将其转化为两异面直线的距离来求；方法二,可设出变量,构建相应的函数,利用函数的最值求解；方法三,建立空间直角坐标系,利用点的坐标以及距离公式表示出目标函数,然后利用函数方法求解最值.方法一（定义转化法）因为直线11A C 与BD 是异面直线,所以当MN 是两直线的共垂线段时,MN 取得最小值。

怎样求解立体几何最值问题

立体几何中的最值问题具有较强的综合性，对同学们的空间想象能力和运算能力有较高的要求.常见的立体几何最值问题有线段最值问题、面积最值问题以及体积最值问题.下面结合实例来谈一谈这三类立体几何最值问题的解法.一、线段最值问题立体几何中的线段最值问题比较常见，通常要求某条线段的最大值或最小值.求解立体几何中的线段最值问题，需先将该线段视为平面几何图形的一条边，然后根据平面几何图形的性质，如平行四边形的性质、等腰三角形的性质、直角三角形的性质，确定该条边的最大、小值，或根据勾股定理、正余弦定理求得该线段的表达式，运用函数的性质、基本不等式求得最值.例1.如图1，在三棱锥P -ABC 中，PA ⊥底面ABC ，△ABC 为等边三角形，PA =AB =2，点N 为BC 的中点.若点M 为△ABC 内一点，且∠MPA =30°，则MN 的最小值为____.图1图2分析：由于点A 为定点，点M 为动点，且∠MPA =30°，故AM 为定值，则可推断出点M 的轨迹为一段圆弧.将求MN 的最值问题转化为圆上的点到圆心的距离问题，根据圆的性质即可求出最值.解：如图2，连接AM ，AN ，∵PA ⊥底面ABC ,∴PA ⊥AM ，∵∠MPA =30°，PA =2，∴AM =，∴点M 的轨迹在以A 为圆心，AM 为半径的圆弧，∵△ABC 为等边三角形，AB =2，点N 为BC 的中点，∴AN =3,∴MN 的最小值为3-=.将点M 视为圆弧上的一点，将MN 看作圆内的一条线段，便可将立体几何中的线段问题转化为平面内的距离问题，利用平面几何图形的性质来解题.二、面积最值问题立体几何中的面积最值问题往往和截面有关，这类问题的求解思路为：①将已知的线段、角及其关系转化到截面上；②利用勾股定理、正余弦定理，求得在截面上的各条线段、角的大小；③根据平面几何图形的面积公式求得几何图形面积的表达式；④利用函数的性质、基本不等式等求得最值.例2.某圆锥的母线长为2，底面半径为3，则过该圆锥顶点的平面截此圆锥所得截面的面积最大值为____.图3分析：首先作出截面△SMN ，如图3所示，然后对未知变量做出假设，设OP =x ，再根据三角形的面积公式求出截面的面积，利用二次函数的性质即可求得最值.解：由题意可知SB =2，设OP =x ()0≤x ≤3，在Rt△SOB 中，SO =SB 2-OB 2=1，在Rt△SOP 中，SP =SO 2+OP 2=1+x 2，连接OM ，如图3，则MN =2OM 2-OP 2=2()32-x2，故S △SMN =12MN ∙SP ×23-x 2=-()x 2-12+4，因此，当x =1时，△SMN 的面积最大，其值为2.三、体积最值问题立体几何中的体积最值问题较为复杂.要求得最值，需先根据题意确定变化的量，如动点、动直线、动平面，然后设出相应的参数，将其视为自变量，求出几何体体积的表达式，再根据函数的性质、基本不等式求得最值.还可以通过分析几何图形，找到几何体的体积取得最值时的情形，根据简单几何体的体积公式求得最值.方法集锦46思路探寻例3.如图4所示，在三棱锥P -ABC 中，BC ⊥平面PAC ，PA ⊥AB ，PA =AB =4，且E 为PB 的中点，AF ⊥PC 于F .当AC 变化时，三棱锥P -AEF 体积的最大值是_____.解：在三棱锥P -ABC 中，由BC ⊥平面PAC ，得BC ⊥AC ，∵AB =4，∴AC 2+BC 2=AB 2=16,∴V P -AEF =V E -PAF =13∙BC2∙S △PAF ，易知△PAF ~△PCA ，∴S △PAF S △PCA =PA 2PC 2=PA 2PA 2+AC 2，∵S △PAC =12AC ∙PA ，PA =4，∴S △PAF =32AC16+AC 2，∴V E -PAF =163∙AC ∙BC16+AC 2,设AC =a ，0<a <4，∴BC =16-a 2，∴V E -PAF =163∙，令m =a 2+16，易知16<m <32，∴V E -PAF =163∙，令x =1m ∈æèöø0,116，VE -PAF =163∙-512x 2+48x -1，由二次函数f ()x =-512x 2+48x -1性质可得，当x =364时，f ()x 有最大值18，∴VE -PAF 最大值为163×.由于AC 为动直线，故三棱锥P -AEF 体积也随之发生变化.需首先设出参数，根据已知条件和三棱锥的体积公式得到三棱锥P -AEF 的表达式，然后根据相似三角形的性质求出S △PAF 的表达式，再根据二次函数的性质求得最值.通过上述分析不难发现，大部分的立体几何最值问题都需借助平面几何知识来求解.因此求解立体几何最值问题时，可根据题意和几何图形的特点，将点、线、面及其关系转化到同一个平面内，然后利用平面几何知识列出关系式，再根据函数的性质、基本不等式求得最值.（作者单位：江苏省如皋市第一中学）求曲线的方程问题在圆锥曲线中比较常见.此类问题侧重于考查圆锥曲线的定义、几何性质以及一元二次方程的性质.求解曲线的方程问题的方法有很多种，如定义法、相关点法、消参法、数形结合法等.那么，如何选择合适的方法进行求解呢?下面结合实例加以说明.一、定义法运用定义法求解曲线的方程问题，主要是根据椭圆、双曲线、抛物线、圆的定义来求解.这就要求同学们熟练掌握椭圆、双曲线、抛物线、圆的定义，根据这些定义来建立关系式，求得曲线的方程.例1.已知双曲线x 2a 2-y 2b2=1()a >0,b >0的焦距为4，F 1，F 2分别是双曲线的左、右焦点，点P 是双曲线在第一象限上的点，且 PF 1∙PF 2=0，|| PF 1∙|| PF 2=6，求双曲线的方程.解：由题意可得||F 1F 2=4,c =2，∵ PF 1∙ PF 2=0，∴PF 1⊥PF 2,||PF 12+||PF 22=16,由||PF 1-||PF 2=2a 可得||PF 12+||PF 22-2||PF 1||PF 2=4a 2，∵||PF 12+||PF 22=16，|| PF 1∙|| PF 2=6，图447。

第04讲立体几何中最值问题-培优辅导冲刺高考讲义突破140

一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练．
立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载
体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类
问题一般可从三个方面思考：一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化
【反馈】 1、在三棱锥 P-ABC 中，PA⊥面 ABC，AB⊥AC 且 AC=1，AB=2，PA=3，过 AB 作截面交 PC 于 D，则截面 ABD 的最小面积为（）
1
10
A.
10
35
B.
5
3 10
C.
10
5
D.
5
2、如图，在正四棱柱 ABCD A1B1C1D1 中， AB 1, AA1 2 ，点 P 是平
D. 2 3
【反馈】 1、如图，在棱长为 1 的正方体 ABCD-A1B1C1D1 中，点 E、F 分别是棱 BC，CC1 的中点，P 是侧面 BCC1B1 内一点，若 A1P∥平面 AEF，则线段 A1P 长度的取值范围是_____ 。
1、如图所示,在空间直角坐标系中,D 是坐标原点,有一棱长为 a 的正方体 ABCD A1B1C1D1 , E 和 F 分别是体
第 04 讲立体几何中最值问题
高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类
问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难
度的考题．此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求

高中数学立体几何中的最值问题专题辅导

高中数学立体几何中的最值问题海红楼立体几何主要研究空间中点、线、面之间的位置关系，与空间图形有关的线段、角、体积等最值问题常常在试题中出现。

下面举例说明解决这类问题的常用方法。

一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中，SO ⊥平面ABCD 于O ，SO=2，底面边长为2，点P 、Q 分别在线段BD 、SC 上移动，则P 、Q 两点的最短距离为（）A. 55B. 552C. 2D. 1解析：如图1，由于点P 、Q 分别在线段BD 、SC 上移动，先让点P 在BD 上固定，Q 在SC 上移动，当OQ 最小时，PQ 最小。

过O 作OQ ⊥SC ，在Rt △SOC 中，552=OQ 中。

又P 在BD 上运动，且当P 运动到点O 时，PQ 最小，等于OQ 的长为552，也就是异面直线BD 和SC 的公垂线段的长。

故选B 。

图1二、定性分析法求最值例2. 已知平面α//平面β，AB 和CD 是夹在平面α、β之间的两条线段。

AB ⊥CD ，AB=3，直线AB 与平面α成30°角，则线段CD 的长的最小值为______。

解析：如图2，过点B 作平面α的垂线，垂足为O ，连结AO ，则∠BAO=30°。

过B 作BE//CD 交平面α于E ，则BE=CD 。

连结AE ，因为AB ⊥CD ，故AB ⊥BE 。

则在Rt △ABE 中，BE=AB ·tan ∠BAE ≥AB ·tan ∠BAO=3·tan30°=3。

故3≥CD 。

图2三、展成平面求最值例3. 如图3-1，四面体A-BCD 的各面都是锐角三角形，且AB=CD=a ，AC=BD=b ，AD=BC=c 。

平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ，则四边形PQRS 的周长的最小值是（）A. 2aB. 2bC. 2cD. a+b+c图3-1解析：如图3-2，将四面体的侧面展开成平面图形。

2019届高三数学备考冲刺140分问题29立体几何中的最值问题含解析

问题29立体几何中的最值问题一、考情分析立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从两个方面思考：一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解；二是直接法,即根据几何体的结构特征或平面几何中的相关结论,直接判断最值.纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理．二、经验分享1.解决立体几何中的最值问题常见方法有：(1)建立函数法是一种常用的最值方法，很多情况下，我们都是把这类动态问题转化成目标函数，最终利用代数方法求目标函数的最值.解题途径很多，在函数建成后，可用一次函数的端点法；二次数的配方法、公试法；有界函数界值法（如三角函数等）及高阶函数的拐点导数法等.(2)公理与定义法通常以公理与定义作依据，直接推理问题的最大值与最小值，一般的公理与定理有：两点之间以线段为最短，分居在两异面直线上的两点的连线段中，以它们的公垂线段为短.球面上任意两点间的连线中以过这两点与球心的平面所得圆的劣弧长为最短等.如果直接建立函数关系求之比较困难，而运用两异面直线公垂线段最短则是解决问题的捷径.(3)解不等式法是解最值问题的常用方法、在立体几何中同样可利用不等式的性质和一些变量的特殊不等关系求解：如最小角定理所建立的不等关系等等.(4)展开体图法是求立体几何最值的一种特殊方法，也是一种常用的方法，它可将几何题表面展开，也可将几何体内部的某些满足条件的部分面展开成平面，这样能使求解问题，变得十分直观，由难化易.(5)变量分析法是我们要透过现象看本质，在几何体中的点、线、面，哪些在动，哪些不动，要分析透彻，明白它们之间的相互关系，从而转化成求某些线段或角等一些量的求解最值总题的方法.除了上述5种常用方法外，还有一些使用并不普遍的特殊方法，可以让我们达到求解最值问题的目的，这就是：列方程法、极限思想法、向量计算法等等其各法的特点与普遍性，大家可以通过实例感受其精彩内涵与思想方法所在.2.决定棱锥体积的量有两个，即底面积和高，当研究其体积的最值问题时，若其中有一个量确定，则只需另一个量的最值；若两个量都不确定，可通过设变量法，将体积表示为变量的函数解析式，利用函数思想确定其最值；将空间问题转化为平面问题是转化思想的重要体现，通过旋转到一个平面内，利用两点之间距离最短求解3.解决几何体体积最值问题的方法(1) 根据条件建立两个变量的和或积为定值,利用基本不等式求体积的最值；通过建立相关函数式,将所求的最值问题转化为函数的最值问题求解,此法应用最为广泛；由图形的特殊位置确定最值,如垂直求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．4.解题时，通常应注意分析题目中所有的条件，首先应该在充分理解题意的基础上，分析是否能用公理与定义直接解决题中问题；如果不能，再看是否可将问题条件转化为函数，若能写出确定的表意函数，则可用建立函数法求解；再不能，则要考虑其中是否存在不等关系，看是否能运用解等不式法求解；还不行则应考虑是否可将其体图展开成平面，这样依次从本文所标定的方法顺序思考，必能找到解题的途径三、题型分析(一) 距离最值问题1.空间中两点间距离的最值问题A C与BD上,求MN的最小值.【例1】正方体的棱长为1,M、N分别在线段11【分析】方法一,该题可以结合正方体的结构特征,将其转化为两异面直线的距离来求；方法二,可设出变量,构建相应的函数,利用函数的最值求解；方法三,建立空间直角坐标系,利用点的坐标以及距离公式表示出目标函数,然后利用函数方法求解最值.A C与BD是异面直线,所以当MN是两直线的共垂线段时,MN 【解析】方法一（定义转化法）因为直线11取得最小值.取11A C 的中点P ,BD 的中点Q .则线段PQ 就是两异面直线11A C 与BD 的共垂线段.下证明之.在矩形11BDD B 中,PQ 为中位线,所以1//PQ BB ,又因为1BB ⊥平面ABCD ,所以PQ ⊥平面ABCD又因为BD ⊆平面ABCD ,所以PQ BD ⊥.同理可证11PQ A C ⊥,而, ,所以线段PQ 就是两异面直线11A C 与BD 的共垂线段,且1PQ =.由异面直线公垂线段的定义可得,故MN 的最小值为1.方法二：（参数法）如图,取11A C 的中点P ,BD 的中点Q .则线段PQ 就是两异面直线11A C 与BD 的共垂线段.由正方体的棱长为1可得1PQ =.连结AC ,则11//AC A C ,所以BQC ∠为两异面直线11A C 与BD 所成角.在正方形ABCD 中,AC BD ⊥,所以.过点M 作MH AC ⊥,垂足为H ,连结NH ,则//MH PQ ,且.设PM m =,QN t =,则QH m =.在Rt QNH ∆中,,在Rt MHN ∆中,.显然,当0m n ==时,2MN 取得最小值1,即MN 的最小值为1.方法三：（向量法）如图,以D 为坐标原点,分别以射线DA 、DC 、1DD 为x 、y 、z 轴建立空间直角坐标系.设DN m =,1A M n =.则,即；,即.所以,故当m n ==时,2MN 取得最小值1,即MN 的最小值为1.【点评】空间中两点距离的最值,最基本的方法就是利用距离公式建立目标函数,根据目标函数解析式的结构特征求解最值.对于分别在两个不同对象上的点之间距离的最值,可以根据这两个元素之间的关系,借助立体几何中相关的性质、定理等判断并求解相应的最值.如【典例1】中的两点分别在两条异面直线上,显然这两点之间距离的最小值即为两异面直线的公垂线段的长度.另外注意直线和平面的距离,两平面的距离等的灵活运用.【小试牛刀】【湖南省长沙市2019届上学期高三统一检测】设正方体的棱长为，为的中点，为直线上一点，为平面内一点，则，两点间距离的最小值为（）A． B． C． D．【答案】B【解析】结合题意，绘制图形结合题意可知OE是三角形中位线，题目计算距离最短，即求OE与两平行线的距离，，所以距离d，结合三角形面积计算公式可得，解得，故选B。

立体几何中的最值问题答案

立体几何中的最值问题答案立体几何中的最值问题一、线段长度最短或截面周长最小问题例1. 正三棱柱ABC —A 1B 1C 1中，各棱长均为2，M 为AA 1中点，N 为BC 的中点，则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.解析： (1)从侧面到N ，如图1，沿棱柱的侧棱AA 1剪开，并展开，则MN ＝22AN AM +＝22)12(1++＝10(2)从底面到N 点，沿棱柱的AC 、BC 剪开、展开，如图2.则MN ＝??-+120cos 222AN AM AN AM ＝21312)3(122++＝34+∵34+＜10 ∴m in MN ＝34+.例2.如图，正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。

点M 在AC 上移动，点N 在BF 上移动，若CM=BN=a ).20(<（2）当a 为何值时，MN 的长最小；（3）当MN 长最小时，求面MNA 与面MNB 所成的二面角α的大小。

解析：（1）作MP ∥AB 交BC 于点P ，NQ ∥AB 交BE 于点Q ，连接PQ ，依题意可得MP ∥NQ ，且MP=NQ ，即MNQP 是平行四边形。

∴MN=PQ,由已知，CM=BN=a,CB=AB=BE=1,∴2==BF AC ,21,21a BQ a CP ==, 即2aBQ CP ==, ∴=+-==22)1(BQ CP PQ MN )20(21)22()2()21(222<<+-=+-a a a a （2）由（1）知: 2222==MN a 时，当，的中点时，分别移动到即BF AC N M ,, 22的长最小，最小值为MN(3)取MN 的中点G ，连接AG 、BG ，∵AM=AN,BM=BN ，∴AG ⊥MN,BG ⊥MN ，∴∠AGB 即为二面角α的平面角。

又46==BG AG ，所以由余弦定理有31464621)46()46(cos 22-=?-+=α。

立体几何中的最值

立体几何最值问题立体几何主要研究空间中点、线、面之间的位置关系，与空间图形有关的线段、角、体积等最值问题常常在试题中出现。

下面举例说明解决这类问题的常用方法。

一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中，SO ⊥平面ABCD 于O ，SO=2，底面边长为2，点P 、Q 分别在线段BD 、SC 上移动，则P 、Q 两点的最短距离为（）A. 55 B. 552 C. 2 D. 1二、定性分析法求最值例2. 已知平面α//平面β，AB 和CD 是夹在平面α、β之间的两条线段。

AB ⊥CD ，AB=3，直线AB 与平面α成30°角，则线段CD 的长的最小值为______。

三、展成平面求最值例3. 如图3-1，四面体A-BCD 的各面都是锐角三角形，且AB=CD=a ，AC=BD=b ，AD=BC=c 。

平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ，则四边形PQRS 的周长的最小值是（）A. 2aB. 2bC. 2cD. a+b+c图3-1四、利用向量求最值例4. 在棱长为1的体ABCD-EFGH 中，P 是AF 上的动点，则GP+PB 的最小值为_______。

一、线段长度最短或截面周长最小问题例1. 正三棱柱ABC —A 1B 1C 1中，各棱长均为2，M 为AA 1中点，N 为BC 的中点，则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.例2.如图，形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。

点M 在AC 上移动，点N 在BF 上移动，若CM=BN=a ).20(<<a （1）求MN 的长；（2）当a 为何值时，MN 的长最小；（3）当MN 长最小时，求面MNA 与面MNB 所成的二面角α的大小。

例3. 如图，边长均为a 的形ABCD 、ABEF 所在的平面所成的角为)20(πθθ<<。

专题突破立体几何之《立体几何中的最值问题》

立体几何中的最值问题考点动向高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难度的考题．此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练．例１如图６－１，在直三棱柱111ABC A B C -中，底面为直角三角形，1906ACB AC BC CC ∠===，，．P 是1BC 上一动点，则1CP PA +的最小值为．解析考虑将立体几何问题通过图形变换，转化为平面几何问题解答．解连结1A B ，沿1BC 将1CBC △展开与11A BC △在同一个平面内，如图６－２所示，连1A C ，则1A C 的长度就是所求的最小值．通过计算可得1190A C C ∠=︒，又145BC C ∠=︒故11135A C C ∠=︒，由余弦定理可求得1AC = 例２如图６－３，在四棱锥P ABCD -中，PA ⊥底面ABCD ，DAB ∠为直角，2AB CD AD CD AB ==，∥，E F ，分别为PC CD ，的中点．（I ）试证：CD ⊥平面BEF ；（II ）设PA k AB =，且二面角E BD C --的平面角大于30︒，求k 的取值范围．·A1A 11图６－１AC PB1A1C1B图６－２C BC图６－３解析对（I ），可以借助线面垂直的判定定理，或者借助平面的法向量及直线的方向向量解答；对（II ），关键是确定出所求二面角的平面角．解法１（I ）证：由已知DF AB ∥且DAB ∠为直角，故ABFD 是矩形，从而CD BF ⊥．又PA ⊥底面ABCD ，CD AD ⊥，故由三垂线定理知CD PD ⊥．在PDC △中，E ，F 分别为PC ，CD 的中点，故EF PD ∥，从而CD EF ⊥，由此得CD ⊥面BEF ．（II ）连接AC 交BF 于G ，易知G 为AC 的中点，连接EG ，则在PAC △中易知EG PA ∥．又因PA ⊥底面ABCD ，故EG ⊥底面ABCD ．在底面ABCD 中，过G 作GH BD ⊥，垂足为H ，连接EH ，由三垂线定理知EH BD ⊥，从而EHG ∠为二面角E BD C --的平面角．设AB a =，则在PAC △中，有1122EG PA ka ==．以下计算GH ，考虑底面的平面图（如图６－５），连接GD ，因1122BD S BD GH GB DF ==△G ，故GB DFGH BD =．在ABD △中，因AB a=，2AD a =，得BD =．而1122GB FB AD a ===，DF AB =，从而得55GB AB GH a BD a===．因此1tan 2kaEG EHG k GH ===． ~故0k >知EHG ∠是锐角，故要使30EHG >∠，必须3tan 3023>=，解之得，k 的取值范围为15k >．BC图６－４图６－５解法２（I ）如图６－６，以A 为原点，AB 所在直线为x 轴，AD 所在直线为y 轴，AP 所在直线为z 轴建立空间直角坐标系，设AB a =，则易知点A ，B ，C ，D ，F 的坐标分别为()000A ，，，()00B a ，，，()220C a a ，，，()020D a ，，，()20F a a ，，．从而(200)(020)DC a BF a ==，，，，，，0DC BF =，故DC BF ⊥．设PA b =，则(00)P b ，，，而E 为PC 中点，故2b E a a ⎛⎫ ⎪⎝⎭，，，从而02b BE a ⎛⎫= ⎪⎝⎭，，．0DC BE =，故DC BE ⊥．由此得CD BEF ⊥面．（II ）设E 在xOy 平面上的投影为G ，过G 作GH BD ⊥垂足为H ，由三垂线定理知EH BD ⊥．从而EHG ∠为二面角E BD C --的平面角．由PA k AB =得(00)P ka ，，，2ka E a a ⎛⎫ ⎪⎝⎭，，，(0)G a a ，，．设(0)H x y ，，，则(0)(20)GH x a y a BD a a =--=-，，，，，，由0GH BD =得()2()0a x a a y a --+-=，即2x y a -=-． ①又因(0)BH x a y =-，，，且BH 与BD 的方向相同，故2x a ya a-=-，即22x y a +=． ②由①②解得3455x a y a ==，，从而215055GH a a GH a ⎛⎫=--= ⎪⎝⎭，，，． (2tan 25kaEGEHG k GH===．由0k >知EHG ∠是锐角，由30EHG ∠>︒，得tan tan30EHG >︒，即23k >．图６－６故k的取值范围为k >． [规律小结]立体几何中的最值与范围，需要首先确定最值或范围的主体，确定题目中描述的相关变动的量，根据必要，可确定是利用几何方法解答，还是转化为代数（特别是函数）问题解答．其中的几何方法，往往是进行翻折变换，这时可以想象实际情形，认为几何体是利用硬纸等折成的，可以动手翻折的，在平时做练习时，不妨多动手试试，培养自己的空间想象能力，在考试时就可以不动手，动脑想就可以了．特别注意变动的过程，抓住变动的起始与终了等特殊环节．考点误区分析（１）这类问题容易成为难点，关键是学生的空间想象能力缺乏，或者对问题的转化方向不明确．因此，要注意常见的转化方向，如化立体几何问题为平面几何问题，或化立体几何问题为代数问题等，根据题目特征进行转化．（２）对题目所描述的情形没有清醒的认识也是造成错解的主要原因，注意产生量的变化的主要原因是什么，相关的数量和位置关系都做怎样的变化，抓住问题的关键，才能顺利解决问题．同步训练１．如图６－７，在直三棱柱111ABC A B C -中，AB BC ==12BB =， 90=∠ABC ，,E F分别为111,AA C B 的中点，沿棱柱的表面从E 到F 两点的最短路径的长度为．》２．有两个相同的直三棱柱，高为a2，底面三角形的三边长分别为)0(5,4,3>a a a a ．用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则a 的取值范围是__________．３．如图６－８，正四面体ABCD 的棱长为1，棱AB ∥平面α，则正四面体上的所有点在平面αA图６－７1A 1E图６－８内的射影构成的图形面积的取值范围是．［参考答案］１．［解析］分别将111A B C △沿11A B 折到平面11ABB A 上；将111A B C △沿11A C 折到平面11ACC A 上；将11BCC B 沿1BB 折到平面11ABB A 上；将11BCC B 沿1CC 折到平面11ACC A 上，比较其中EF 长即可．．２．［解析］可知，全面积最小的是四棱柱面积为22428a +，全面积最小的是三棱柱面积为21248a +，解2212482428a a +>+即可．［答案］3150<<a ．３．［解析］当CD 所在的直线与平面α平行时，所求射影面积最大，为1122AB CD ⨯=；当CD 所在的直线与平面α．［答案］1]2．。

高考数学140冲刺专题：29立体几何中的最值问题含解析38

高考立体几何与导数结合求最值的例题分析

立体几何中的最值问题

高中数学立体几何中的最值问题

高三数学立体几何中的最值问题复习

立体几何的最值问题

专题38 立体几何中的距离、截面、折叠问题(解析版)

厉兵秣马，2019高考数学立体几何必考压轴题及解析，冲刺140必备

立体几何最值问题-高考数学一题多解

立体几何中的最值问题

立体几何解析几何最值问题

2024年高考数学压轴题专项训练：立体几何压轴题十大题型汇总(解析版)(共65页)(1)

立体几何动点最值问题

高考数学复习压抽题专项突破—立体几何中最值问题

怎样求解立体几何最值问题

第04讲 立体几何中最值问题-培优辅导冲刺高考讲义突破140

高中数学立体几何中的最值问题专题辅导

2019届高三数学备考冲刺140分问题29立体几何中的最值问题含解析

立体几何中的最值问题答案

立体几何中的最值

专题突破立体几何之《立体几何中的最值问题》

第04讲立体几何中最值问题-培优辅导冲刺高考讲义突破140