热力学与统计物理学第五章玻耳兹曼统计

合集下载

热力学与统计物理答案第五章

第五章不可逆过程热力学简介5.1 带有小孔的隔板将容器分为两半. 容器与外界隔绝，其中盛有理想气体. 两侧气体存在小的温度差T ∆和压强差p ∆，而各自处在局部平衡. 以n dn J dt =和u dU J dt=表示单位时间内从左侧转移到右侧的气体的物质的量和内能. 试导出气体的熵产生率公式，从而确定相应的动力. 解: 以下标1，2标志左、右侧气体的热力学量. 当两侧气体物质的量各有12,dn dn ，内能各有12,dU dU 的改变时，根据热力学基本方程，两侧气体的熵变分别为1111112222221,1.dS dU dn T T dS dU dn T T μμ=-=- （1）由熵的相加性知气体的熵变为12.dS dS dS =+ （2）容器与外界隔绝必有12120,0.dn dn dU dU +=+=值得注意，在隔板带有小孔的情形下，物质和内能都会发生双向的传递，1dn 和1dU 是物质的量和内能双向传递的净改变，2dn 和2dU 亦然. 我们令1212,.dU dU dU dn dn dn ==-==-在两侧气体只存在小的温度差T ∆和压强差p ∆的情形下，我们令1212,;,.T T T T T μμμμμ=+∆==+∆=气体的熵变可以表示为11,dS dU dn T T T T T T μμμ+∆⎛⎫⎛⎫=--- ⎪ ⎪+∆+∆⎝⎭⎝⎭ （3）熵产生率为11dS dU dn dt T T T dt T T T dtμμμ+∆⎛⎫⎛⎫=--- ⎪ ⎪+∆+∆⎝⎭⎝⎭22.T dU T T dnT dt T dtμμ∆∆-∆≈-+⋅ （4）以u dU J dt =表示内能流量，2u T X T ∆=-表示内能流动力，n dnJ dt=表示物质流量，2n T T X T μμ∆-∆=表示物质流动力，熵产生率即可表示为标准形式.u u n n dSJ X J X dt=⋅+⋅ （5）5.2 承前5.1题，如果流与力之间满足线性关系，即,,().u uu u un n n nu u nn n nu unJ L X L X J L X L X L L =+=+=昂萨格关系（a ）试导出n J 和u J 与温度差T ∆和压强差p ∆的关系.（b ）证明当0T ∆=时，由压强差引起的能流和物质流之间满足下述关系：.u unn nuJ L J L = （c ）证明，在没有净物质流通过小孔，即0n J =时，两侧的压强差与温度差满足,un m nnmL H L pTTV -∆=∆其中m H 和m V 分别是气体的摩尔焓和摩尔体积. 以上两式所含unnnL L 可由统计物理理论导出（习题7.14，7.15）. 热力学方法可以把上述两效应联系起来.解: 如果流与力之间满足线性关系,,u uu u un n n nu u nn n J L X L X J L X L X =+=+ （1）将习题5.1式（5）的,u n X X 代入可得22,u uu un T T T J L L T T μμ∆∆-∆⎛⎫=-+ ⎪⎝⎭22.n nu nn T T T J L L T T μμ∆∆-∆⎛⎫=-+ ⎪⎝⎭（2）（a ）根据式（3.2.1），有,m m S T V p μ∆=-∆+∆ （3）代入式（2）可得2222,.m m u uu un m m n nu nn H T V T p T J L L T T H T V T p T J L L T T ∆-∆∆⎛⎫=-+ ⎪⎝⎭∆-∆∆⎛⎫=-+ ⎪⎝⎭（4）式（4）给出了,u n J J 和两侧气体的温度差T ∆和压强差p ∆的关系，其中m m H TS μ=+是气体的摩尔焓. （b ）当0T ∆=时，由式（4）得.u unn nnJ L J L = （5）式（5）给出，当两侧气体有相同的温度0T ∆=但存在压强差p ∆时，在压强驱动下产生的能流与物质流的比值.（c ）令式（4）的第二式为零，可得.nu unm m nn nnm m L LH H L L pTV T V T--∆==∆ （6）最后一步利用了昂萨格关系un nu L L =. 这意味着，当两侧的压强差与温度差之比满足式（6）时，将没有净物质流过小孔，即0n J =，但却存在能流，即0.u J ≠昂萨格关系使式（6）和式（5）含有共同的因子unnnL L 而将两个效应联系起来了. 统计物理可以进一步求出比值un nn L L 从而得到u nJJ 和p T ∆∆的具体表达式，并从微观角度阐明过程的物理机制（参看习题7.14和7.15）.5.3 流体含有k 种化学组元，各组元之间不发生化学反应. 系统保持恒温恒压，因而不存在因压强不均匀引起的流动和温度不均匀引起的热传导. 但存在由于组元浓度在空间分布不均匀引起的扩散. 试导出扩散过程的熵流密度和局域熵产生率.解: 在流体保持恒温恒压因而不存在流动和热传导且k 种化学组元不发生化学反应的情形下，热力学基本方程（5.1.4）简化为.ii idS dn Tμ=-∑（1）局域熵增加率为.i i i n St T tμ∂∂=-∂∂∑ （2）由于不发生化学反应，各组元物质的量保持不变，满足守恒定律()01,2,,.ii n i k t∂+∇⋅==∂ J （3）代入式（2），有i i i St Tμ∂=∇⋅∂∑J.i ii i i iT Tμμ⎛⎫⎛⎫=∇⋅-⋅∇ ⎪ ⎪⎝⎭⎝⎭∑∑J J （4）系统的熵增加率为i i i i i i dS d d dt T T μμττ⎛⎫⎛⎫=∇⋅-⋅∇ ⎪ ⎪⎝⎭⎝⎭∑∑⎰⎰J J.ii i i iid d T T μμτ⎛⎫=⋅-⋅∇ ⎪⎝⎭∑∑⎰⎰ J J σ （5）与式（5.1.6）比较，知熵流密度为.iS i iTμ=-∑J J （6）局域熵产生率为.ii iΘT μ⎛⎫=⋅∇- ⎪⎝⎭∑J （7）5.4 承前5.3题，在粒子流密度与动力呈线性关系的情形下，试就扩散过程证明最小熵产生定理.解: 5.3题式（7）已求得在多元系中扩散过程的局域熵产生率为.ii iΘTμ=-⋅∇∑J （1）系统的熵产生率为.ii iP d Tμτ=-⋅∇∑⎰J （2）在粒子流密度与动力呈线性关系的情形下，有,ii i L T μ⎛⎫=-∇ ⎪⎝⎭J （3）所以，有2,i i iP L d T μτ⎛⎫=-∇ ⎪⎝⎭∑⎰ （4）则1212i ii ii i idP L d dt T T t d T t μμτμτ∂⎛⎫⎛⎫=-∇⋅-∇ ⎪ ⎪∂⎝⎭⎝⎭∂⎛⎫=⋅-∇ ⎪∂⎝⎭∑⎰∑⎰J1122.i i i i i i d d T t T t μμττ⎧∂⎫∂⎛⎫⎛⎫=∇⋅-+∇⋅⋅⎨⎬ ⎪ ⎪∂∂⎝⎭⎝⎭⎩⎭∑∑⎰⎰J J （5）上式第一项可化为边界上的面积分. 在边界条件下随时间变化的情形下，此项为零. 在恒温恒压条件下，有,ji i j j n t n tμμ∂∂∂=∂∂∂∑再利用扩散过程的连续性方程（习题5.3式（3）），可将式（5）表为,1.j i i i j j n n dP d dt T n t tμτ∂∂∂=-∂∂∂∑⎰ （6）现在讨论式（6）中被积函数的符号. 由于系统中各小部分处在局域平衡，在恒温恒压条件下，局域吉布斯函数密度g 应具有极小值，即它的一级微分0,i i ig n δμδ==∑二级微分2,0,ii j i jjg n n n μδδδ∂=≥∂∑（7）其中用了式（4.1.11）.应当注意，i μ作为1,,,,k T p n n 的函数，是1,,k n n 的零次齐函数，因此式（6）和式（7）中的ijn μ∂∂不是完全独立的，要满足零次齐函数的条件（习题 4.2）0.ijjjn n μ∂=∂∑ （8）比较式（6）和式（7），注意它们都同样满足式（8），知式（6）的被各函数不为负，故有0.dPdt≤ （9）这是多元系中扩散过程的最小熵产生定理.5.5 系统中存在下述两个化学反应：123A X 2X,B X C.k k k ++→假设反应中不断供给反应物A 和B ，使其浓度保持恒定，并不断将生成物C 排除. 因此，只有X 的分子数密度X n 可以随时间变化. 在扩散可以忽略的情形下，X n 的变化率为2X 1A X 2X 3B X .dn k n n k n k n n dt =--'引入变量312A B X 22,,,,k k t k t a n b n X n k k '==== 上述方程可以表为()2.dXa b X X dt=-- 试求方程的定常解，并分析解的稳定性. 解: 反应1A X 2X k +−−→的反应速率与1A ,k n 和X n 成正比，反应后增加一个X 分子；反应22X A X k −−→+的反应速率与2k 和2X n 成正比，反应后减少一个X 分子. 反应3B XC k +−−→的反应速率与3B ,k n 和X n 成正比，反应后减少一个X 分子. 在扩散可以忽略的情形下，X n 的变化率为2X 1A X 2X 3B X .dn k n n k n k n n dt=-+ （1）引入变量312A B X 22,,,,k k t k t a n b n X n k k '==== 式（1）可以表为()2.dXa b X X dt=-- （2）方程（2）的定常解0X 满足00,dXdt=即()000.X a b X --=⎡⎤⎣⎦ （3）方程（3）有两个解：01020,.X X a b ==- （4）下面用线性稳定性分析讨论这两个定常解的稳定性. 假设发生涨落，解由0X 变为0.X X X =+∆ （5）将式（5）代入式（2），准确到X ∆的一次项，有()02X dX a b X X dt∆=-∆-∆()02.a b X X =--∆ （6）设t X Ce ω=，代入式（6），得02.a b X ω=-- （7）（a ）对于定常解010,X =有.a b ω=-如果0,a b -<有0,ω<则发生涨落X ∆后，X ∆会随时间衰减，使X 回到01.X 所以定常解01X 是稳定的. 反之，如果0,a b ->则0,ω>涨落将随时间增长，定常解01X 是不稳定的. （b ）对于常解02,X a b =-有 .a b ω=-+由于02X 是X 分子的浓度，02X 应是正实数（020X =不必再考虑），必有,a b >因而0.ω<所以定常解02X 是稳定的.5.6 系统中存在下述两个化学反应：123A X 3X,B X C.k k k +→+−−→假设反应中不断供给反应物A 和B ，使其浓度保持恒定，并不断将生成物C 排除，因此只有X 的浓度X n 可以发生改变. 假设扩散可以忽略，试写出X n 的变化率方程，求方程的定常解，并分析解的稳定性.解: 与5.5题类似，对于题设的化学反应，组元X 的变化率方程为3X 1A X 2X 3B X 22.dn k n n k n k n n dt=--' （1）令312A B X 22,,,k k t k t a n b n X n k k '====，可将式（1）表为()322dXa b X X dt=-- （2）式（2）的定常解0X 满足00dXdt=，即()200220.X a b X --= （3）式（3）有两个解：01020.X X ==（4）现在用线性稳定性分析讨论这两个定常解的稳定性. 假设发生涨落，解由0X 变为0,X X X =+∆ （5）代入式（2），保留X ∆的线性项，得()2026.dX a b X X X dt∆=-∆-∆ （6）令t X Ce ω∆=，代入式（6），有2026.a b X ω=-- （7）（a ）对于定常解010,X =有2.a b ω=-如果20,a b ->01X 是不稳定的. 如果20,a b -<01X 是稳定的.（b ）对于定常解02X =注意02X 是X 的浓度，是正实数（020X =不必再考虑），故只取“+”号，且20,a b ->由式（7）知0.ω<因此定常解02X =.补充题 1 浸没在热源中的导线存在电流密度为e J 的真流电流. 已知欧姆定律e E σ=J 适用. 试求在此单纯的电导过程中的熵流密度和局域熵产生率.解: 考虑导线的一个体积元. 体积元中电子的数密度n 满足物质守恒定律0,n nt∂+∇⋅=∂J （1） n J 是电子流密度. 以e -表示电子的电荷，电荷密度()e n ρ=-，电流密度().e n e =-J J 与式（1）相应的电荷守恒定律为0.e tρ∂+∇⋅=∂J （2）体积元中内能密度u 的变化满足能量守恒定律0,u ut∂+∇⋅=∂J （3） u J 是内能流密度，它是热流密度q J 和电子流所携带的能流密度n μJ 之和，即.u q n μ=+J J J （4）将式（4）代入式（3），有 ().q n u tμ∂=-∇⋅-∇⋅∂J J （5）根据热力学基本方程（5.1.4），局域熵密度的增加率为1.S u n t T t T t μ∂∂∂=-∂∂∂ （6）将式（1）和式（5）代入式（6），有()()11q n n S t T T Tμμ∂=-∇⋅-∇⋅+∇⋅∂J J J 1.q n q T T T μ⎛⎫⋅∇=-∇⋅+⋅∇- ⎪⎝⎭J J J （7）在导体性质均匀和温度均匀的情形下，有 10,T ∇= e e V μμ∇=∇=-∇，V 是电势，所以q eV S t T T ⎛⎫⋅∇∂=-∇⋅- ⎪∂⎝⎭J J 2,q E T T σ⎛⎫=-∇⋅+ ⎪⎝⎭J （8）最后一步用了欧姆定律.将式（8）对系统（导线）积分，得系统的熵增加率为2q dS E d d dt T Tσττ=-∇⋅+⎰⎰J 2,qE d d T T σστ=-⋅+⎰⎰ J （9）最后一步利用高斯定理将右方第一项换为面积分. 由此可知，焦耳热效应导致的局域熵产生率为2.E ΘT σ= （10）熵流密度为 .q S T =J J （11）热量和熵都从导线流入热源. 如果焦耳效应产生的热量能及时从导线流出，则2.q E σ∇⋅=J由式（9）知，熵增加率为零，系统处在定常状态.补充题2 承上题，在电流密度与动力呈线性关系的情形下，试就单纯的电导过程证明最小熵产生定理.解: 上题式（8）已证明，在单纯的电导过程中，局域熵产生率为.e V ΘT ⋅∇=-J （1）在电流密度e J 与动力V T ∇-呈线性关系的情形下，有 ,e V L T ∇⎛⎫=- ⎪⎝⎭J （2） L 是动理系数.系统的熵产生率为 .e V p Θd d T ττ∇⎛⎫==⋅- ⎪⎝⎭⎰⎰J （3）熵产生率的变化率为12222e e e dp V V L d dt T T tV d T t V V d d T t T t ττττ∇∂⎛⎫⎛⎫=--∇ ⎪⎪∂⎝⎭⎝⎭∂⎛⎫=-⋅∇ ⎪∂⎝⎭∂∂⎛⎫=-∇⋅+∇⋅ ⎪∂∂⎝⎭⎰⎰⎰⎰J J J 22.e e V V d d T t T tστ∂∂=-⋅+∇⋅∂∂⎰⎰ J J （4）式（4）右方第一项在系统（导线）表面上求面积分. 假设电源电压没有涨落，在导线与电源的接头上，0V t∂=∂；电流不从导线的其余表面漏出，0.e d σ⋅=J 因此式（4）的面积分为零，有 22.e dp V V d d dt T t T t tρττ∂∂∂=∇⋅=-∂∂∂⎰⎰J （5）第二步利用了电荷守恒定律习题5.3式（2）.虽然电源电压是稳定的，导线内的涨落可能使其中的电势发生改变：()()(),,,V x t V x V x t =+∇(),V x t ∇是涨落电势，相应的涨落电荷密度为(),.x t ρ∇ 在电磁效应可以忽略的情形下，二者满足泊松方程()()201,,,V x t x t ρε∇∆=-∆ （6）0ε是真空介电常量. 将式（6）求对时间t 的偏导数，注意()(),,,,V V x t t t x t t tρρ∂∂∆=∂∂∂∂∆=∂∂ 代入式（5）可得202.dP V V d dt T t t ετ∂∂=∇∂∂⎰ （7）根据格林公式()2d d nψφψφψτφ∂∇+∇⋅∇=⋅∂⎰⎰ σ 令其中的V tφψ∂==∂，即有 22.V V V V V d d d t t t t n t ττ∂∂∂∂∂∂⎛⎫∇=-∇+⋅ ⎪∂∂∂∂∂∂⎝⎭⎰⎰⎰ σ （8）与式（4）中面积分等于零相类似，上式中的面积分也等于零，所以有 202.dP V d dt T t ετ∂⎛⎫=-∇ ⎪∂⎝⎭⎰ （9）上式意味着，如果导线内部发生涨落使0V t ∂∇≠∂，导线中存在的线性电导过程将使系统的熵产生率减小，直到熵产生率达到极小为止，这是单纯电导过程的最小熵产生定理.。

热力学与统计物理第五章知识总结

热⼒学与统计物理第五章知识总结§5.1 热⼒学量的统计表达式我们根据Bolzman分布推导热⼒学量的统计表达式⼀、配分函数粒⼦的总数为令（1）名为配分函数，则系统的总粒⼦数为（2）⼆、热⼒学量1、内能（是系统中粒⼦⽆规则运动的总能量的统计平均值）由（1）（2）得（3）此即内能的统计表达式2、⼴义⼒，⼴义功由理论⼒学知取⼴义坐标为y时，外界施于处于能级上的⼀个粒⼦的⼒为则外界对整个系统的⼴义作⽤⼒y为（4）此式即⼴义作⽤⼒的统计表达式。

⼀个特例是（5）在⽆穷⼩的准静态过程中，当外参量有dy的改变时，外界对系统所做的功为（6）对内能求全微分，可得（7）（7）式表明，内能的改变分为两项：第⼀项是粒⼦的分布不变时，由于能级的改变⽽引起的内能变化；地⼆项是粒⼦能级不变时，由于粒⼦分布发⽣变化⽽引起的内能变化。

在热⼒学中我们讲过，在⽆穷⼩过程中，系统在过程前后内能的变化dU等于在过程中外界对系统所作的功及系统从外界吸收的热量之和：（8）与（6）（7）式相⽐可知，第⼀项代表在准静态过程中外界对系统所作的功，第⼆项代表在准静态过程中系统从外界吸收的热量。

这就是说，在准静态过程中，系统从外界吸收的热量等于粒⼦在其能级上重新分布所增加的内能。

热量是在热现象中所特有的宏观量，它与内能U和⼴义⼒Y不同。

3、熵1）熵的统计表达式由熵的定义和热⼒学第⼆定律可知（9）由和可得⽤乘上式，得由于引进的配分函数是，的函数。

是y的函数，所以Z是，y的函数。

LnZ的全微分为：因此得（10）从上式可看出：也是的积分因⼦，既然与都是的积分因⼦，我们可令（11）根据微分⽅程关于积分因⼦的理论，当微分式有⼀个积分因⼦时，它就有⽆穷多个积分因⼦，任意两个积分因⼦之⽐是S的函数（dS是⽤积分因⼦乘微分式后所得的全微分）⽐较（9）、（10）式我们有积分后得（12）我们把积分常数选为零，此即熵的统计表达式。

2）熵函数的统计意义由配分函数的定义及得由玻⽿兹曼分布得所以（13）此式称为Boltzman关系，表明某宏观状态的熵等于玻⽿兹曼k乘以相应的微观状态数的对数。

热力学与统计物理学第五章玻耳兹曼统计

多大？
( d ) ( ) L 3 4 2 m 3 / 2 d 3 / 2 3 / 2 3
L3
4
2
m
3 /2
1
d
3 / 2
1
3
py
L3
4 3
2
m
3
/2
1
3 2
d
1
L 3 2 2 m 3 / 2 1 / 2 d 11
§5.1 玻耳兹曼统计分布律
)
() ... dq1dq2dqrdp1dp2dpr
Hε
等能面就像 “洋葱”
在
等
能
X
面上
√
画
格
子？
10
【例题5.1】处于边长为L的立方容器内由单原子分子组成
的理想气体，粒子的能量表示为： H
1 2m
p
2 x
p
2 y
p
2 z
解：根据相体积定义
H 等能面所维的相体积是
空间范围
L
pz
果真如此吗？如果普朗克所言不虚，那么科学争论在科学思想发展史上的意义就要大打折扣了。普朗克为人平和、正直，被誉为“学林古柏”，其高尚的人品是值得人们敬仰的，但并不是他所说的每一句话都是正确的，哪怕这句话多次被人们引用。
由此可见，玻耳兹曼就是他自己发明的“孤立系统的熵增加
原理”的牺牲品。
7
第五章玻耳兹曼统计
因此而自杀！
6
科学史话(5) “普朗克定律”（一个现代科学的绊脚石）
其表述如下：“一个新的科学真理照例不能用说服对手，等他们表示意见说‘得益匪浅’这个办法来实行。恰恰相反，只能是等到对手们渐渐死亡，使得新的一代开始熟悉真理时才能贯彻。”对普朗克来说，学术争论没有多少诱惑力，因为他认为它们不能产生什么新东西。由于上述说法后来又被学界有重大影响的其他学者，如托马斯·库恩等多次引证，它熟，那么当今统计物理还有那些问题要研究？

玻尔兹曼统计分布

玻尔兹曼统计分布玻尔兹曼统计分布是热力学和统计物理学中的一个重要概念，它描述了粒子在能级间的分布情况。

玻尔兹曼统计分布是基于玻尔兹曼分布定律得出的，该定律指出在热平衡状态下，粒子在各能级上的分布服从玻尔兹曼分布。

玻尔兹曼统计分布的推导是基于两个基本假设。

首先，假设粒子之间是无相互作用的，其能量仅由粒子的内能决定。

其次，假设粒子在不同能级上的分布是独立的，即一个粒子在某个能级上的分布不会影响其他粒子在相同能级上的分布。

基于这两个假设，我们可以得到玻尔兹曼统计分布的表达式。

玻尔兹曼统计分布可以用来描述各种不同的系统，例如理想气体、固体、液体等。

对于理想气体来说，玻尔兹曼统计分布可以用来计算不同能级上的粒子数。

根据统计物理学的基本原理，处于热平衡的理想气体中，各个能级上的粒子数与该能级对应的能量有关。

在玻尔兹曼统计分布中，粒子在某个能级上的分布概率与该能级的能量成负指数关系。

具体而言，粒子在第i个能级上的概率P(i)可以用玻尔兹曼因子e^(-E(i)/kT)表示，其中E(i)为第i个能级的能量，k为玻尔兹曼常数，T为系统的温度。

玻尔兹曼统计分布可以通过计算每个能级上的粒子数与总粒子数的比例来得到。

玻尔兹曼统计分布在理解和描述各种物理现象中起着重要作用。

例如，在研究固体的热容时，可以利用玻尔兹曼统计分布计算不同能级上的粒子数，并进一步计算总的内能和热容。

另外，玻尔兹曼统计分布也可以用来解释光谱线的强度分布、电子能级跃迁等现象。

玻尔兹曼统计分布是热力学和统计物理学中的一个重要概念，它描述了粒子在能级间的分布情况。

通过玻尔兹曼统计分布，我们可以计算不同能级上的粒子数，并进一步理解和解释各种物理现象。

玻尔兹曼统计分布在研究和应用中具有广泛的意义，对于理解物质的性质和行为具有重要的启示作用。

热力学统计物理玻耳兹曼统计

义
粒子处在该
能级的几率
有效状态数
al
N Z1
l
e
l
al
el l
N
Z1
el l el l
玻耳兹
曼因子粒子总是优先占据较低能级；温度升高，占据该能级的几率增大。
Z1——有效状态和一个粒子所有可能达到的有效状态的总和。
热统西华大学理化学院
6
f e s
l 能量为εl的一个量子态s上的平均粒子数
p
3.粒子配分函数的经典表达式
处元于内能层的l 粒l内子，数运为动：状态处于相体积
al
l
h0r
fs
l h0r
e l
N Z1
l
h0r
el
l x
Z1
l
el l
h0r
al
N Z1
l
h0r
el
取 l 足够小，求和可化为积分：
Z1
el d
h0r
e ( p,q) dq1dq2 dqr dp1dp2 dpr h0r
l l
FD l l! BE
l
l
l
e l
ln
l l
l
对于满足非兼并条件的处
于平衡态（最可几分布） lnFD lnBE l ln l lnl !
的非定域（玻色、费米）系统，通过对所对应的系统微观状态数目取对数，得到了微观状态数目的对数ln与系统包含的粒子数
l
l
l ln l l ln l 1
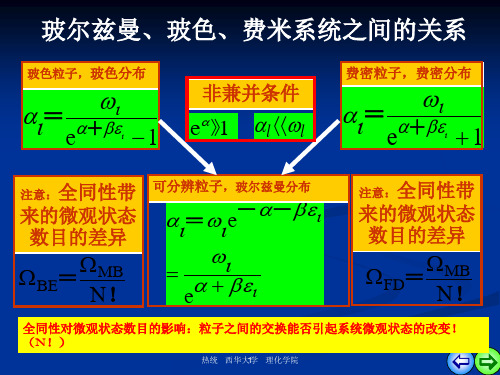
玻尔兹曼、玻色、费米系统之间的关系
玻色粒子，玻色分布
＝
e＋
1
非兼并条件
e》1 l l
费密粒子，费密分布

热力学与统计物理答案

第一章热力学的基本规律习题试求理想气体的体胀系数α,压强系数β和等温压缩系数T κ; 解：由得：nRT PV=V nRTP P nRT V ==; 所以,TP nR V T V V P 11)(1==∂∂=α习题试证明任何一种具有两个独立参量的物质p T ,,其物态方程可由实验测得的体胀系数α及等温压缩系数T κ,根据下述积分求得:⎰-=)(ln dp dT V T κα如果1Tα=1T p κ=,试求物态方程;解：因为0),,(=p V T f ,所以,我们可写成),(p T V V =,由此,dp p V dT T V dV T p )()(∂∂+∂∂=,因为T T p p VV T V V )(1,)(1∂∂-=∂∂=κα 所以,dp dT VdVdp V dT V dVT T κακα-=-=,所以,⎰-=dp dT VT καln ,当p T T /1,/1==κα.习题测得一块铜块的体胀系数和等温压缩系数分别为1510*85.4--=K α和1710*8.7--=n T p κ,T κα,可近似看作常量,今使铜块加热至10°C;问1压强要增加多少np才能使铜块体积不变 2若压强增加100n p ,铜块的体积改多少解：分别设为V xp n ∆;,由定义得：所以,410*07.4,622-=∆=V p xn习题描述金属丝的几何参量是长度L ,力学参量是张力η,物态方程是0),,(=T L f η实验通常在n p 1下进行,其体积变化可忽略;线胀系数定义为ηα)(1T L L ∂∂=等杨氏摸量定义为T LA L Y )(∂∂=η其中A 是金属丝的截面积,一般说来,α和Y 是T 的函数,对η仅有微弱的依赖关系,如果温度变化范不大,可看作常数;假设金属丝两端固定;试证明,当温度由1T 降2T 时,其张力的增加为)(12T T YA --=∆αη解：),(,0),,(T L L T L f ηη==所以,dT TLd L dL T ηηη)()(∂∂+∂∂= 因AY L L L L T T T =∂∂∂∂=∂∂)(;)(1)(ηηη所以,)(12T T YA --=∆αη习题在C ︒25下,压强在0至1000n p 之间,测得水的体积13263)10046.010715.0066.18(---⨯+⨯-=mol cm p p V 如果保持温度不变,将1mol 的水从1n p 加压至1000n p ,求外界所做的功;解：外界对水做功: 习题解：外界所作的功：习题抽成真空的小匣带有活门,打开活门让气体充入;当压强达到外界压强p 0时将活门关上;试证明：小匣内的空气在没有与外界交换热量之前,它的内能U 与原来大气中的0U 之差为000V p U U =-,其中0V 是它原来在大气中的体积;若气体是理想气体,求它的温度和体积;解：假设先前的气体状态是P 0,dV 0,T 0内能是u 0,当把这些气体充入一个盒子时,状态为P 0,dV,T 这时的内能为u,压缩气体所做的功为：00dV p ,依绝热过程的热力学第一定律,得()000000=+-⎰dV P U U V积分得000V p U U=-对于理想气体,上式变为()001vRT T T vc V=-故有()01T R c T c V V +=所以001V T c c T VPγ==对于等压过程0101V T T V V γ==习题热泵的作用是通过一个循环过程将热量从温度较低的环境传送扫温度较高的物体上去;如果以理想气体的逆卡诺循环作为热泵的循环过程,热泵的效率可以定义为传送到高温物体的热量与外界所作的功的比值;试求热泵的效率;如果将功直接转化为热量而令高温物体吸收,则“效率”为何解：A →B 等温过程B →C 绝热过程 C →D 等温吸热D →A 绝热,2111Q Q Q A Q -==η由绝热过程泊松方程：1211--=r Cr B V T V T ；1112--=r Ar DV T V T∴D AC B V V V V =；CDB A V V V V =∴212212212111T T T T T T T T T T T -+=-+-=-=η将功A 直接转化为热量1Q ,令高温物体吸收;有A=Q 1∴11==AQ η; 习题假设理想气体的C p 和C V 之比γ是温度的函数,试求在准静态绝热过程中T 和V 的关系;该关系试中要用到一个函数FT ,其表达式为：解：准静态绝热过程中：0=dQ,∴pdV dU -=1对于理想气体,由焦耳定律知内能的全微分为dT C dU v =2物态方程VnRT P nRT pV =⇒=32,3代入1得：dV VnRTdTC V -=其中1-=γnR C V ()dTVdV⎰⎰-=-11γ关系式γ为T 的函数∴V -1为T 的函数;∴VT F 1)(=1)(=V T F ; 第二章均匀物质的热力学性质习题已知在体积保持不变的情况下,一气体的压强正比于其绝对温度.试证明在温度保持不变时,该气体的熵随体积而增加; 解：由题意得：)()(V f T V k p +=;因V 不变,T 、p 升高,故kV >0T V S )(∂∂=V Tp)(∂∂=k VkV >0 由于kV >0,当V 升高时或V 0→V ,V >V 0,于是⇒T 不变时,S 随V 的升高而升高;设一物质的物态方程具有以下形式T V f P)(=,试证明其内能与体积无关;解：T V f P)(=,V T V U ∂∂),(T =T V T P)(∂∂-p =)()(V Tf V Tf -=0得证;习题求证：ⅰHP S )(∂∂<0ⅱU VS)(∂∂>0证VdP TdS dH +=等H 过程:H HVdP TdS )()(-=⇒PS ∂∂H=-TV <0V >0;T >0由基本方程：PdV TdS dU-=dV T pdU T dS +=⇒1;⇒VS ∂∂U =Tp>0.习题已知T VU)(∂∂=0,求证T p U )(∂∂=0;解T V U )(∂∂=T V T p )(∂∂-p ;⇒T V U )(∂∂=0;V TpT p )(∂∂= T VU )(∂∂=),(),(T V T U ∂∂=),(),(T p T U ∂∂),(),(T V T p ∂∂=0=T p U )(∂∂T Vp)(∂∂ ∵T Vp)(∂∂≠0;⇒T p U )(∂∂=0;习题试证明一个均匀物体在准静态等过程中熵随体积的增减取决于等压下温度随体积的增减;解：F =U-TS ,将自由能F 视为P ,V 的函数;F =Fp ,V=⎪⎭⎫⎝⎛∂∂p V S ()()p V p S ,,∂∂=()()⋅∂∂p T p S ,,()()p V p T ,,∂∂()()()()p T p V p T p S ,,,,∂∂∂∂==pp T V T S ⎪⎭⎫⎝⎛∂∂⎪⎭⎫⎝⎛∂∂由关系T C p=p T S ⎪⎭⎫ ⎝⎛∂∂;⇒=⎪⎭⎫⎝⎛∂∂pV S ⋅T C p pV T ⎪⎭⎫ ⎝⎛∂∂; 习题试证明在相同的压强降落下,气体在准静态绝热膨胀中的温度降落大于在节流过程中的温度降落;提示:证明S p T ⎪⎪⎭⎫⎝⎛∂∂-Hp T ⎪⎪⎭⎫⎝⎛∂∂>0证：()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂==⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂==dS S H dp p H H T dp p T dH H T dp p T dT H p T T dS S T dp p T dT S p T T p S p H p Hp S),(1),(联立1,2式得：Sp T ⎪⎪⎭⎫⎝⎛∂∂-H p T ⎪⎪⎭⎫ ⎝⎛∂∂=p H T ⎪⎭⎫ ⎝⎛∂∂S p H ⎪⎪⎭⎫ ⎝⎛∂∂=pST H p H ⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂=pS C p H ⎪⎪⎭⎫⎝⎛∂∂据：pdV TdS dU-=熵不变时,dS =0,pdV dU -=Vdp TdS dH +=Sp H ⎪⎪⎭⎫⎝⎛∂∂=V⇒S p T ⎪⎪⎭⎫ ⎝⎛∂∂-Hp T ⎪⎪⎭⎫ ⎝⎛∂∂=0>p C V；原题得证;习题一弹簧在恒温下的恢复力X 与其伸长x 成正比,即.X =-Ax ；今忽略弹簧的热膨胀,试证明弹簧的自由能F 、熵S 和内能U 的表达式分别为；解：),();(,x T U U T A A Ax X==-==dU dT T U x ⎪⎭⎫ ⎝⎛∂∂+dx x U T⎪⎭⎫⎝⎛∂∂⇒+-=;)(xdx T A SdT dF S T F x -=⎪⎭⎫ ⎝⎛∂∂;=x T A )(Tx F ⎪⎭⎫ ⎝⎛∂∂-=⇒S XT F ⎪⎭⎫⎝⎛∂∂=dT T dB x dT T dA )()(212--由于TS U F-=,）（2 dS S T dp p H H T p T p S p H ⎪⎭⎫⎝⎛∂∂+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂⋅⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂==⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-dT dB T T B x dT T dA T T A )()()(212∵X =0时,U =0,即不考虑自身因温度而带来的能量;实际上,dT dB TT B -)(=0或dTdBT T B -)(=)0,(T U 即得：2)()(21)0,(),(x dT T dA T T A T U X T U ⎥⎦⎤⎢⎣⎡-=-221)0,(),(Ax T F T X F +=;dT dA x T S T X S 2)0,(),(2-= 进而求U ∆略;代入abd c V V V V V aT uV U=⇒==；4习题如下图所示,电介质的介电常数EDT =)(ε与温度有关,试求电路为闭路时电介质的热容量与充电后再令电路断开后的热容量之差;解：当电路闭合时,电容器电场恒定当电路断开时,电容器电荷恒定D T TED S )()(∂∂-=∂∂,因而习题已知顺磁物质的磁化强度为：H TCm =,若维持物质温度不变,使磁场由0增至H,求磁化热;解：;H TCm =mV M =；TH S ⎪⎭⎫ ⎝⎛∂∂⇒=0μV H T m ⎪⎭⎫ ⎝⎛∂∂=H T C ⎪⎭⎫⎝⎛-20μ等T 下：22000H T CV HdH T C V S T Q H μμ⋅-=-=∆=∆⎰习题已知超导体的磁感应强度()00=+=m H B μ；求证:ⅰC m 与m 无关,只是T 的函数,其中C m 是在磁化强度m 保持不变时的热容量；ⅱ0202U m dT C U m +-=⎰μ；ⅲ0S dT TC S m+=⎰解：超导体()m H m H M B-=⇒=+=00ⅰT C H=HT S ⎪⎭⎫ ⎝⎛∂∂∵m H-=；T C C m H ==⇒HT S ⎪⎭⎫⎝⎛∂∂ⅱHdM TdS dU0μ+=;mV M =代入m C 表达式,其中U 0 为0K 时的内能;ⅲ由ii 中已应用了dT C TdSm =⇒T C T S mm=⎪⎭⎫⎝⎛∂∂；⇒0S dT TC S m+=⎰〈忽略因体积变化带来的影响〉; 习题实验测得顺磁介质的磁化率)(T χ;如果忽略其体积的变化,试求特性函数fm,t,并导出内能和熵;解：显然χ只与T 有关；)(T χ=TH m ⎪⎭⎫⎝⎛；()T H m m ,=HdMTdS dU 0μ+=;TS U f -=;SdT TdS dU df --=⇒HdM SdT df 0μ+-=;⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=dT T m dH H m V dM H T()H T V H f χμ0=⎪⎭⎫⎝⎛∂∂；()()()T f m V T f H T V f 02002022+=+=⇒χμχμ f 既已知：-=S ()02202S dT T d m V T f m+⋅=⎪⎭⎫⎝⎛∂∂χχμ HdMTdS dU 0μ+=；TS U f -=第三章单元系的相变习题试由0>vC 及0)(<∂∂T V p 证明0>p C 及0)(<∂∂S Vp; 证T C C V p =-⇒VT p ⎪⎭⎫⎝⎛∂∂pT V ⎪⎭⎫ ⎝⎛∂∂ =P C p T H ⎪⎭⎫ ⎝⎛∂∂=pT S T ⎪⎭⎫⎝⎛∂∂;=V C V T U ⎪⎭⎫⎝⎛∂∂V T S T ⎪⎭⎫ ⎝⎛∂∂= ⇒=⎪⎭⎫ ⎝⎛∂∂T V p V S p ⎪⎭⎫ ⎝⎛∂∂T V S ⎪⎭⎫ ⎝⎛∂∂+SV p ⎪⎭⎫⎝⎛∂∂1=⎪⎭⎫ ⎝⎛∂∂V T p VS p ⎪⎭⎫ ⎝⎛∂∂TT S ⎪⎭⎫⎝⎛∂∂2 ⇒=⎪⎭⎫ ⎝⎛∂∂S V T -VS p ⎪⎭⎫⎝⎛∂∂⇒V C V T S T ⎪⎭⎫ ⎝⎛∂∂=；即0>=⎪⎭⎫⎝⎛∂∂VV C T S T . 于是：0>=⎪⎭⎫⎝⎛∂∂T V p +⎪⎭⎫⎝⎛∂∂SV p 正数于是：SV p ⎪⎭⎫⎝⎛∂∂<0 0>V C ;因而0>P C习题求证：1-=⎪⎭⎫⎝⎛∂∂n V T ,μV T n S ,⎪⎭⎫ ⎝⎛∂∂；2-=⎪⎪⎭⎫ ⎝⎛∂∂nT p ,μp T n V ,⎪⎭⎫⎝⎛∂∂ 证：1开系吉布斯自由能dn Vdp SdT dG μ++-=,),(T V p p =⇒VS T G n V +-=⎪⎭⎫⎝⎛∂∂,VT p ⎪⎭⎫⎝⎛∂∂① V V G nT =⎪⎭⎫⎝⎛∂∂,T V p ⎪⎭⎫⎝⎛∂∂② μ=⎪⎭⎫⎝⎛∂∂VT n G ,③ 由式①⇒n V n V T G T p V S ,⎪⎭⎫ ⎝⎛∂∂-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂=V T n S ,⎪⎭⎫ ⎝⎛∂∂nV T ,⎪⎭⎫ ⎝⎛∂∂-=μ第1式得证;习题试证明在相变中物质摩尔内能的变化为：⎪⎪⎭⎫⎝⎛⋅-=∆dp dT T p L u1如果一相是气相,可看作理想气体,另一相是凝聚相,试将公式化简; 解V p S T U∆-∆=∆VT L dT dp ∆=；S T L ∆=；dp dT T p L L U ⋅⋅-=∆⇒⎪⎪⎭⎫⎝⎛⋅-=dp dT T p L 1 习题在三相点附近,固态氨的蒸气压单位为a P 方程为：Tp 375492.27ln -= 液态氨的蒸气压方程为：Tp 306338.24ln -=,试求氨三相点的温度和压强,氨的汽化热、升华热及在三相点的熔解热;解：1固态氨的饱和蒸气压方程决定了固态-气态的相平衡曲线；液态氨的饱和蒸气压方程决定了氨的液态-气态的相平衡曲线;三相点是两曲线的交点,故三相点温度3T 满足方程：TT 306338.24375492.27-=-；由此方程可解出3T ,计算略； 2相变潜热可由RTLA p -=ln与前面实验公式相比较得到： 3754=RL S,从而求出S L ；类似可求出Q L ；计算略； 3在三相点,有r Q SL L L +=,可求得r L ,计算略;习题蒸汽与液相达到平衡;以dTdv 表在维持两相平衡的条件下,蒸汽体积随温度的变化率;试证明蒸汽的两相平衡膨胀系数为⎪⎭⎫ ⎝⎛-=⋅RT L T dT dv v 111; 解αV ～0.方程近似为：TVLT p ≈∆∆,V —气相摩尔比容;Vp T L T V V 11⋅∆=∆⋅⇒①气相作理想气体,pV=RT ②T R V p pV ∆=∆+∆⇒③联立①②③式,并消去△p 、P 得：TL TV VVP T R ∆=⋅∆-∆21RT LRT T V V -=⎪⎭⎫ ⎝⎛∆∆⇒；⎪⎭⎫ ⎝⎛-=-=⎪⎭⎫ ⎝⎛∂∂=⇒RT L T RT T T V V P 111112α 习题证明爱伦费斯公式：()()()()1212k k dT dp --=αα；()()()())(1212αα--=Tv c c dT dpp p 证：对二级相变0)(=∆dS ；即()2dS -()1dS =00)(=∆dV ；即()2dV -()1dV =0()2dS()dT T S ⎪⎪⎭⎫ ⎝⎛∂∂=2()dp p S ⎪⎪⎭⎫ ⎝⎛∂∂+1；()1dS ()dT T S ⎪⎪⎭⎫ ⎝⎛∂∂=1()dp p S ⎪⎪⎭⎫ ⎝⎛∂∂+1 )(0dS ∆=()2dS=-()1dS⇒()()=⎥⎦⎤⎢⎣⎡∂∂-∂∂dT T S TS 12()()dp p S p S ⎥⎦⎤⎢⎣⎡∂∂-∂∂-12 ()()()()⎥⎦⎤⎢⎣⎡∂∂-∂∂⎥⎦⎤⎢⎣⎡∂∂-∂∂-=⇒p S p S T S T S dT dp 1212;将pp T S T C ⎪⎭⎫ ⎝⎛∂∂=代入得;()()[]()()pS p S C C T dT dppP ∂∂-∂∂--=12121①即为：()-∂∂p S 2()()()()121αα--=∂∂V pS ；代入①得：()()()()1212αα--=TV C C dT dp p P类似地,利用0)(=∆dV 可证第二式;略第四章多元系的复相平衡和化学平衡习题若将U 看作独立变数T ,V ,n 1,…n k 的函数,试证明：1VUV n U n Ui ii∂∂+∂∂=∑；2VUv n U u i i i∂∂+∂∂=证：1),,,(),,,(11k k n n V T U n n V T U λλλλ=根据欧勒定理,f x fx iii=∂∂∑,可得 2i ii i i i i i iiu n V Uv n U n V U V n U n U∑∑∑=∂∂+∂∂=∂∂+∂∂=)( 习题证明),,,(1k i n n p T μ是k n n ,1的零次齐函数,0=⎪⎪⎭⎫⎝⎛∂∂∑j ij j n n μ; 证：),,,(),,,(11k m k n n p T n n p T μλλλμ=,化学势是强度量,必有m =0,习题二元理想溶液具有下列形式的化学势：其中g i T ,P 为纯i 组元的化学势,x i 是溶液中i 组元的摩尔分数;当物质的量分别为n 1、n 2的两种纯液体在等温等压下合成理想溶液时,试证明混合前后 1吉布斯函数的变化为)ln ln (2211x n x n RT G+=∆2体积不变0=∆V3熵变)ln ln (2211x n x n R S +-=∆4焓变0=∆H ,因而没有混合热;5内能变化如何解： 1222211112211ln ),(ln ),( x RT n p T g n x RT n p T g n n n n G i ii +++=+==∑μμμ所以22110ln ln x RT n x RT n G G G+=-=∆2p G V ∂∂=；0)(=∂∆∂=∆∴pG V ; 3T G S ∂∂-= ；2211ln ln )(x R n x R n TG S --=∂∆∂-=∆∴ 4TSH G -=50=∆-∆=∆V p H U习题理想溶液中各组元的化学势为：i i ix RT P T g ln ),(+=μ；(1) 假设溶质是非挥发性的;试证明,当溶液与溶剂蒸发达到平衡时,相平衡条件为其中'1g 是蒸汽的摩尔吉布斯函数,g 1是纯溶剂的摩尔吉布斯函数,x 是溶质在溶液中的摩尔分数; (2) 求证：在一定温度下,溶剂的饱和蒸汽压随溶液浓度的变化率为 (3) 将上式积分,得)1(0x p p x -=其中p 0是该温度下溶剂的饱和蒸汽压,p x 是溶质浓度为x 时的饱和蒸汽压;该公式称为拉乌定律; 解：1设“1”为溶剂,())1ln(,'111x RT P T g g -+==μ2由⇒=∂∂v p g Tp x x RT p g p g ⎪⎪⎭⎫⎝⎛∂∂--⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂)1(1'1Tp x ⎪⎪⎭⎫⎝⎛∂∂ -=⇒v v ')1(x RT-Tp x ⎪⎪⎭⎫ ⎝⎛∂∂；v’—蒸汽相摩尔热容 v —凝聚相摩尔热容故有v’-v ≈v’,又有pv’=RT 代入⇒ Tx p ⎪⎭⎫⎝⎛∂∂x p --=1 3积分2式得拉乌定律习题的气体A 1和n 0v 2mol 的气体A 2的混合物在温度T 和压强p 下所占体积为V 0,当发生化学变化,0A A A A 22114433=--+νννν；并在同样的温度和压强下达到平衡时,其体积为V e ;试证明反应度为证：未发生化学变化时,有当发生化学变化时,原来有n 0v 1mol 的气体A 1,反应了n 0v 1εmol,未反应1-εn 0v 1mol,n 0v 2mol 的气体A 2,反应了εn 0v 2mol,未反应1-εn 0v 2mol,生成εn 0v 3molA 3和εn 0v 4molA 4,有习题根据第三定律证明,在T →0时;表面张力系数与温度无关;即0→dTd σ; 证：表面膜系统,dA SdT Fσ+-=S T F A -=⎪⎭⎫ ⎝⎛∂∂⇒;σ=⎪⎭⎫⎝⎛∂∂T A F=⎪⎭⎫ ⎝⎛∂∂T A S AT ⎪⎭⎫⎝⎛∂∂-σ;而实际上σ与A 无关,即=⎪⎭⎫⎝⎛∂∂TA S dT d σ-T →0时,根据热力学第三定律；()0lim 0=∆→TT S于是得：dT d σ0=⎪⎭⎫⎝⎛∂∂-=TA S ；原式得证; 习题试根据第三定律证明,在T →0时,一级相变两平衡曲线的斜率dTdp为零;证：VS dT dp ∆∆=；T →0；000=⎪⎭⎫⎝⎛∆∆=⎪⎭⎫⎝⎛→→T T V S dT dp ()0lim 0=∆→TT S ；原式得证;习题设在压强p 下,物质的熔点为T 0,相变潜热为L ,固相的定压热容量为C p ,液相的定压热容量为C p ’.试求液体的绝对熵表达式;解：为计算T 温度,p 压强下,液体绝对熵,可假想如下图过程;p液相 ABC 固相T 0T①A →B,等压过程：⎰=∆→0T p BA TdT C S②B 点相变过程.0T L S B =∆相变③B →C,等压过程：⎰=∆→TT p CB TdT C S 0'于是∑=∆+=S S S)0(⎰T p TdT C 0T L+⎰+TT p T dT C 0'习题试根据第三定律讨论图ab 两图中哪一个是正确的图上画出的是顺磁性固体在H =0和H=H i 时的S-T 曲线;解：图b 正确;拒热力学第三定律;T →0；S 0=0;且T →0,0=⎪⎭⎫⎝⎛∂∂Tx S ；即0K 附近,S 在等温过程中的变化与任何其它参量无关;第五章不可逆过程热力学简介习题带有小孔的隔板将容器分为两半,容器与外界隔绝,其中盛有理想气体,两侧气体存在小的温差ΔT 和压强差Δp 而各自处于局域平衡;以dt dn J n=和dtdUJ u =表示单位时间内通过小孔从一侧转移到另一侧的气体的物质的量和内能;试导出熵产生率公式,从而确定相应的动力; 解：根据热力学基本方程∑-=iii dn dU Tdsμ得dtdn T dt dU T dt ds i i i ∑-=μ11设温度为T +ΔT 的一侧熵为s 1;温度为T 的一侧熵为s 2,则因为0 ;0='+='+n d dn U d dU所以dn n d dU U d -='-=';,dtdnT dt dU T dt ds μ+-=12熵产生率 dt ds dt ds dt s d i 21+==dtdnT dt dU T dt dn T T dt dU T T μμμ+-∆+∆+-∆+11 =dtdn T T T dt dU T T T ⎪⎭⎫ ⎝⎛-∆+∆+-⎪⎭⎫⎝⎛-∆+μμμ11=⎪⎭⎫ ⎝⎛∆-⎪⎭⎫⎝⎛∆T J T J n u μ1 相应的动力22 ,1T T T T X T T T X n u μμμ∆-∆=⎪⎭⎫ ⎝⎛∆-=∆-=⎪⎭⎫ ⎝⎛∆=第六章近独立粒子的最概然分布习题试证明,对子一维自由粒子,再长度L 内,在ε到εεd +的能量范围内,量子态数为：证：一维自由粒子,x P 附近的量子态为x dP hLdn =；x x x x x dP m dP m m m dP P d m P εεεε21222+=⋅+==⇒= 于是;()εεεεd mh Ld D2+=而±P x对应同一能量ε,于是：()mh L m h L D εεε2222=⎪⎪⎭⎫ ⎝⎛⨯=习题试证明,对于二维自由粒子,在长度L 2内,在ε到εεd +的能量范围内,量子态数为证：二维；在P x ,P y 附近dP x dP y 区间上内的粒子数;ϕPdPd hSdP dP h S dn y x 22==s －面积因mP 22=ε只与P 有关P >0,故对ϕ积分可得：()⎪⎪⎭⎫ ⎝⎛==m P h S PdP h S d D 222222ππεε,επd h mSm 22= ()22hmS D πε=⇒s=L 2习题在极端相对论情形下,粒子的能量动量关系为cp =ε;试求在体积V 内,在ε到εεd +的能量范围内能量范围内三维粒子的量子态数; 解：φθθd dpd p hV dp dp dp h V dn z y x sin 233==由于cp =ε只与p 有关,与θ、φ无关,于是以上已经代入了cdp d cp =⇒=εε于是,32)(4)(hc V D επε=习题设系统含有两种粒子,其粒子数分别为N 和N ’.粒子间的相互作用很弱,可看作是近独立的;假设粒子可分辨,处在一个个体量子态的粒子数不受限制;试证明, 在平衡态下两种粒子的最概然分布分别为：le a l lβεαω--=和'--'='l e a l lβεαω;其中l ε和'l ε是两种粒子的能级,l ω和'l ω是能级简并度;证：粒子A 能级,粒子数分布：l ε——{a l }——简并度l ω 粒子B 能级,粒子数分布：'l ε——{a ’l }——简并度'l ω由21Ω⋅Ω=Ω21ln ln ln Ω+Ω=Ω即使Ω最大,()11ln ΩΩ,()22ln ΩΩ达到最大;l e a l l εβαω''-'-'='注：'l a δ与l a δ在此情况下独立讨论,若将一系作为子系统,意味总能守恒,于是参照教材玻尔兹曼分布证明……0ln ln =⎪⎭⎫ ⎝⎛''+-''-'⎪⎪⎭⎫ ⎝⎛''+-⎪⎪⎭⎫ ⎝⎛⇒∑∑∑∑∑∑l l l l l l l l l llla a a a a a a a δεδεβδαδωδαδω同一0β,原题得证;这也是满足热平衡的要求;第七章玻耳兹曼统计习题根据公式∑∂∂-=lllVa Pε证明,对于非相对论粒子：)()2(21222222z y x n n n Lm m p s ++== π,z y x n n n ,,=0,±1,±2,…有VU p 32=,上述结论对玻耳兹曼分布、玻色分布和费米分布都成立;证：∑∂∂-=lllVa Pε=⎥⎦⎤⎢⎣⎡++∂∂-∑)()2(212222z y x lln n n L m V a π=⎥⎦⎤⎢⎣⎡++∂∂-∑)()2(222223z y x l l n n n L m L V a π 其中Va ul l ε∑=;V ~3L 对同一l ,222zy x n n n ++=m a ll21∑-2)2( π)(222z y x n n n ++)32(35--V =m a ll21∑-22222)()2(L n n n z y x ++ π)32(3532--V V =V U32习题试根据公式∑∂∂-=lllVa Pε证明,对于极端相对论粒子：21222)(2z y x n n n L c cp ++== πε,z y x n n n ,,=0,±1,±2,…有VU p 31=,上述结论对玻耳兹曼分布、玻色分布和费米分布都成立;证：∑∂∂-=ll lVa Pε；对极端相对论粒子21222)(2z y x n n n Lc cp ++== πε类似得31212)()2(-∑∂∂-=∑V n V a P i ll π=VUVV a ll l 31)31(3431-=---∑ε 习题当选择不同的能量零点时,粒子第l 个能级的能量可以取为ll *εε或,以∆表示二者之差=∆l l εε-*;试证明相应的配分函数存在以下关系11Z e Z ∆-*=β,并讨论由配分函数Z 1和Z 1求得的热力学函数有何差别; 证：配分函数∑-=le Z l βεω1以内能U 为例,对Z 1:1ln Z NUβ∂∂-=对Z 1:()U N e N Z NU Z +∆=∂∂-=∂∂-=-1ln ln 1**βββ习题试证明,对于遵从玻尔兹曼分布的系统,熵函数可以表示为式中P s是总粒子处于量子态s 的概率,1Z e N e P ss s βεβεα---==,∑s对粒子的所有量子态求和;证法一：出现某状态s ψ几率为P s设S 1,S 2,……S k 状态对应的能级s 'ε；设S k+1,S k+2,……S w 状态对应的能级s 'ε；类似………………………………；则出现某微观状态的几率可作如下计算：根据玻尔兹曼统计Ne P sS βεα--=；显然NP s 代表粒子处于某量子态S 下的几率,Se NP Sβεα--=;于是Se βεα--∑代表处于S 状态下的粒子数;例如,对于s 'ε能级⎪⎪⎭⎫⎝⎛∑=--'K S S S S e 1βεα个粒子在s 'ε上的K 个微观状态的概率为：类似写出：()⎪⎪⎭⎫ ⎝⎛''∑=''=''--k S S S s e S PS P1βεα ………………………………………………等等; 于是N 个粒子出现某一微观状态的概率; 一微观状态数P1=Ω,基于等概率原理将Se NP Sβεα--=带入S SS P P kN S ln ∑-=⇒；习题固体含有A 、B 两种原子;试证明由于原子在晶体格点的随机分布引起的混合熵为k S=㏑[][][])1ln()1(ln !)1(!!x x x x N x N N N x --+-=-κ其中N 是总原子数,x 是A原子的百分比,1-x 是B 原子的百分比;注意x<1,上式给出的熵为正值; 证：显然[]!)1()!(!!!!21x N Nx N n n N -==ΩS=k ㏑Ω=-N k [])1ln()1(ln x x x x --+=)1()1(ln x x x x Nk ---；由于)1()1(x xx x--＜1,故0〉S ；原题得证;习题气体以恒定的速度沿方向作整体运动;试证明,在平衡状态下分子动量的最概然分布为证：设能级l ε这样构成：同一l ε中,P z 相同,而P x 与P y 在变化,于是有：∑==0p a p p l z参照教材玻耳兹曼分布证明；有E N βδαδδ--Ωln -z p γ,其中）（22221Z y x lp p p m++=ε 由1知:N dp dp dp ehV z y x p z=⎰---γβεα3 将l ε代入并配方得:=N dp dp dp e hV z y x m p mm z y x =⎰+-+---2)(2)()22(3βγβεεββγα其中mp m p y y xx 2,222==εε整个体积内,分布在z z z y y y x x x dp p p dp p p dp p p +→+→+→,,内分子数为：由条件3知⎰=0),,(Np dp dp dp p p p f pz y x z y x z计算得 =z m p my x dp em dp dp emkTz y x ⎰⎰+-+--2)(2)(23)()21(βγβεεββγπ=0p Ndp dp fdp m zy x =-⎰βγ0p m -=⇒βγ代入得出分布：[]3)(22022"hdp dp Vdp ezy x p p p p mz y x-++--βα其中βγαα22'm -=,0p m -=βγ习题试根据麦克斯韦速度分布率导出两分子的相对速度12v v v r-=和相对速率rr v v =的概率分布,并求相对速率的平均值r v ;解：两分子的相对速度r v在rz ry rx dv dv dv 内的几率2122111])()()()[(23211)()2()()()(2212121212121--∞∞-+++++++-===⎰⎰⎰⎰kTm edv dv dv e kT m v V v V v d v V rx rz z ry y rx x z y x v kT m zy x v v v v v v v v v kT mr r ππ 同理可求得z y v v 11,分量为2122)(2--kTm ery v kT m π和2122)(2--kTm er v kT m π引进2m=μ,速度分布变为r r v kT mdv v e kT r 22232)2(-πμ 利用球极坐标系可求得速率分布为：r r v kT m dv v e kTr22232)2(4-πμπ 相对速率平均值v kT dv v e v kT v r r v kT m r r r28)2(4220232===-∞⎰πμπμπ习题试证明,单位时间内碰到单位面积上,速率介于v 与dv v +之间的分子数为：dv v e kTm n d kTmv 322/32)2(-=Γππ证：在斜圆柱体内,分速度为z v 的v 方向的分子数为:对于:0,,积分得从对从+∞→+∞→∞-z y x v v vdt 时间碰撞到ds 面积上的分子数dv v v +→=dsdt d dvd v ekTm n kTmv ϕθθπππcos )2(2/032202\32⎰⎰-得到：若只计算介于dv v v +→分子数则为：只对φθ,积分习题分子从器壁小孔射出,求在射出的分子束中,分子平均速度和方均根速度;解：dvv e kT m n dvv e kT m n v kT nv v kT m3022/30422/322)2()2(⎰⎰∞+-+∞-=ππππ；变量代换⇒==dx mkTdv x n kT m2;2 习题已知粒子遵从经典玻耳兹曼分布,其能量表达式为：bx ax p p p mz y x ++++=2222)(21ε其中b a ,是常数,求粒子的平均能量; 解：ab a b a bx x a m p 4)4(222222-+++=ε习题气柱的高度为H ,截面为S ,在重力场中;试求解此气柱的内能和热容量;解：配分函数⎰-++-=z y x mgz p p p mdp dp dxdydzdp ehZ z y x ββ)(232221 设⎥⎦⎤⎢⎣⎡=mg m hS A 1)2(2/33π；[]mgH e A Z ββ--+-=1ln ln )2/5(ln ln习题试求双原子理想气体的振动熵;解：振动配分函数ωβωβ ---=e e Z V 12/1代入式)1ln(2/ln 1ωβωβ ----=⇒e Z代入熵计算式V V k T Nk Nk S θωθ=+=⇒其中)./ln(;习题对于双原子分子,常温下kT 远大于转动的能级间距;试求双原子分子理想气体的转动熵; 解转动配分函数212 βI Z r=);/ln(;/1ln ;2ln ln 121r T Nk Nk S Z I Z θβββ+=⇒-=∂∂=其中r k I h θ=22习题气体分子具有固有电偶极矩0d ,在电场ε下转动能量的经典表达式为：θεθεφθcos )sin 1(210222d p p I r -+=,证明在经典近似下转动配分函数：解：经典近似下,rε视为准连续能量配分函数⎰⎰⎰⎰⎰⋅==∞∞-+⋅---πφθεβθβθβφθβεφθφθθ20cos sin 21222102211d dp d edp ehd d dp dpe hZ d I p Ir利用π=⎰∞∞--dx ex 2习题同19题,试证在高温10≤εβd 极限下,单位体积电偶极矩电极化强度为：εξkT d 320=; 解：电极化强度)1(1ln 0000001εβββεβξεβεβεβεβ--+=∂∂=--d d d d ee e d e d Z N 高温极限下,0→β,保留至20)(εβd εεβkTnd d 222020=⇒;其中VN n =习题试求爱因斯坦固体的熵;解：将ωβωβh h eeZ ---=121,代入至S 表达式即得,注意N 取3N;略第九章系综理论习题证明在正则分布中熵可表为∑-=ss s k S ρρln 其中sE s e Zβρ-=1是系统处在s 态的概率; 证：)ln (ln ββ∂∂-=Z Z k S多粒子配分函数)1(1ss E s E e Z e Z ββρ--=⇒=∑由1知[]s s s s s E Z E Z E Z esρβρβρβln ln 1;ln ln +=-+=-⇒=-代至2得[]∑∑+=+=∂∂ssss s s Z Z Z ρρββρρββln 1ln 1ln ln 1ln ;于是∑-=⎪⎪⎭⎫⎝⎛∂∂-=s ss k Z Z k Sρρββln ln ln习题试用正则分布求单原子分子理想气体的物态方程,内能和熵证：()222121;iziy ix Ni s sE p p p mE eZs++==∑∑=-β符号∏=i iz iy ix dp dp dp dp符号∏=i ii i dz dy dx dq 利用式V NTk V Z Z Z P =∂∂=∂∂=⇒βββ1ln 1类似求S U ,;习题体积内盛有两种组元的单原子混合理想气体,其摩尔数为1n 和2n ,温度为T ; 试由正则分布导出混合理想气体的物态方程,内能和熵;解：习题利用范氏气体的配分函数,求内能和熵;解：Q m N Z N 2/32!1⎪⎪⎭⎫ ⎝⎛=βπ()⎰⎰⎰-----++=-=∂∂⇒dr f V N V dr e V N NTk U dr e V N Q N N N N 12121212122/3;22βφβφφφβ一般认为dr f VN 1222较小；习题利用德拜频谱求固体在高温和低温下配分函数对数Z ln ,从而求内能和熵; 解：式德拜频谱B ND 93=ω 对于振动())(1ln 1ln ln ln 2020020x d e e B d D e e e Z D D =⎪⎪⎪⎭⎫ ⎝⎛-+-=⎪⎪⎪⎭⎫ ⎝⎛-+=⎰⎰-----ωβωωβφωωωωβωβωωβωββφ 代换 S 计算略高温近似,∞→T ,0→ωβ()N N +--=ωββφ ln 30计算略习题用巨正则分布导出单原子分子理想气体的物态方程,内能,熵和化学势; 解：参照关于玻耳兹曼体系配分函数的处理过渡到连续能量分布得: 利用热力学式可求得kT N pV =,kT N U 23=等略注:l ε--------单粒子处于l 能级的能量;习题利用巨正则分布导出玻耳兹曼分布; 解：∑∑--=ΞN S E N s eβα；由于玻耳兹曼系,粒子可分辨,从而为简单起见,考虑无简并有简并情况完全可类似处理于是：(){}∏∞=+-=Ξ0ex p l a l l eβα即对无简并情况()l e a l βεα+-=对有简并者,类似处理可得()l e a l lβεαω+-=略 l ω——简并度。

热力学统计第五章

整个系统的微观状态数等于两个部分的微观状态数的乘积
系统的熵为S
1 2
S k ln 1 2 S1 S2
当整个系统达到平衡状态后，它的微观状态数为，熵 S
S k ln
第五章粒子的经典与量子分布
第20页
扬州大学物理科学与技术学院
是在所给定的孤立系条件下与最可几分布相对应的微观状
l
l
假设所有的 l 都很大
ln l! l ln l 1
第4页
第五章粒子的经典与量子分布
扬州大学物理科学与技术学院
ln Nln N 1 l ln l 1 l ln l
l
l
N ln N l ln l l ln l
l
l
为了求得使 ln 为极大的分布，令 l 有 l 的变化。
ln 将有 ln 的变化，
第五章粒子的经典与量子分布
§5.1 玻耳兹曼分布
§5.2 热力学公式 §5.3 玻色分布和费米分布 §5.4 经典公式 §5.5 理想气体的热力学函数 §5.6 Maxwell速度分布律 §5.7 能量均分定理及其应用 §5.8 固体热容量 §5.9 顺磁性固体
1
扬州大学物理科学与技术学院
§5-1 玻耳兹曼分布
s
s
e s 1
其中对粒子的所有量子状态s求和。
s
第五章粒子的经典与量子分布
第26页
扬州大学物理科学与技术学院
e 1 玻色分布和费米分布都过渡到玻耳兹曼分布
的一级微分等于零，即 ln ＝0 且 ln 二级微分小于零。
2 ln
l
ln
l l
l
l
l 2
l
l 0
这就证明了玻耳兹曼分布是使为极大的分布。

热力学统计物理第五章课件

J LX 在许多情形下往往有几种力与几种流同时存在，这时将出现不同过程的交叉现象。而上式相应推广为
J k Lkl X l
l

上式称为线性唯象律，系数Lkl称为动理系数。 Lkl等于一个单位的第l 种动力所引起的第k 种流量，一般是局域强
度量的函数。
统计物理学可以证明，适当选择流量和动力，可使局域熵产生率表达为

J q T
其中κ是导热系数。
扩散过程的经验规律是菲克定律。以 J n表示混合物中某组元物质在单位时间内流过单位截面的粒子数，称为粒子流密度。菲克定律指出，粒子流密度与该组元的浓度梯度成正比，即

Jn D n 其中n是该组元的浓度，D是扩散系数。
导电过程的经验规律是欧姆定律。
把在单位时间内通过单位截面所输运的物理量（分子
数、电荷量、动量和能量等）统称为热力学流，以 J

表示。
把引起物理量输运的物体中某种性质的梯度（浓度梯度、电势梯度、速度梯度、温度梯度等）统称为热力学力，以 X 表示。在各向同性物体中上述各种输运过程的经验规律都可以表述为“流量与动力成正比”，即
物体中温度不均匀引起能量的输运，称为热传导过程；混合物中各组元浓度不均匀引起物质的输运，称为扩散过程；流体流动时速度不均匀引起动量的输运，称为粘滞现象；导体中的电势差引起电荷的输运，称为导电过程…
对于一系列输运过程都建立了经验规律。热传导过程的经验规律是傅里叶定律。
以 J q表示单位时间内流过单位截面的热量，称为热流密度。傅里叶定律指出，热流密度与温度梯度成正比，即
如果系统内部发生的过程可逆，熵产生
diS=0 如果系统内部发生的过程不可逆，熵产生

热力学统计物理第五章课件

此式是能量守恒定律的表达式，其中J u 是内能流密度。
由基本方程可知，当粒子数密度增加dn时，内能密度的增加为μdn，μ是一个粒子的化学势。因此当存在粒子流时，内能流密度可以表示为
ቤተ መጻሕፍቲ ባይዱ

Ju J q J n
即内能流密度是热流密度与粒子流携带的能流密度之和。
把上式代入内能密度的连续性方程，得 u J q J n t
第五章不可逆过程热力学简介
§5.1 局域平衡熵流密度与局域熵产生率
在第一章中根据热力学第二定律得到不等式 dQ dS T 式中等号适用于可逆过程，不等号适用于不可逆过程。
将上式中dS推广为下述等式
dS=deS+diS 式中deS是由于系统与外界交换物质和能量所引起的系统熵变，是可正可负的；diS表示系统内部发生的过程引起的熵产生，不能取负值。
根据系统熵的积分式，整个系统熵的增加率可表为 dS d s = sd d J s d dt dt t 利用高斯定理将右方第一项化为面积分，得 dS = J s d d dt 上式右方第一项表示单位时间通过系统表面从外界流入的熵，第二项表示单位时间内系统各体积元的熵产生之和。将上式与 dS=deS+diS 比较可得 de S di S = Js d ， = d dt dt 由于在任何宏观区域中熵产生都是正定的，故有Θ≥0。

T 1 T Jq Jq 2 2 0 T T T 由于导热系数恒正，热传导过程中局域熵产生率Θ是正定

2
的。例2 如果系统内部除了温度不均匀外，化学势也不均匀，

统计物理第五章

统计物理（Statistical Physics）黄建明电子工程学院北京邮电大学，北京100876北京邮电大学北京1008761J. –M. Huang目录第章热力学的基本规律第一章第二章均匀物质的热力学性质第三章近独立粒子的最概然分布第四章玻耳兹曼统计第五章玻色统计和费米统计第六章系综理论2J. –M. Huang第五章玻色统计和费米统计§5.1 热力学量的统计表达式51§5.2 弱简并理想玻色气体和费米气体§5.3 玻色－爱因斯坦凝聚：强简并理想玻色气体§5.子5.4 光子气体§5.5 金属中的自由电子气体：强简并理想费米气体3J. –M. Huang11ln ln e e ωΞ≡Ξ≡−⇒Ξ=−−()()ln ll lllN ∂=−Ξ∑∏∏4J. –M. Huangα∂∂yβpdVW −=δVp ∂Ξ∂=⇒ln 1β5J. –M. Huangln d d dy d βαΞ=++y dU Ydy dN βααββ∂∂∂⇒−+ln ln ln d αβαβ⎛⎞⎛⎞∂Ξ∂Ξ=Ξ−−⎜⎟⎜⎟∂∂⎝⎠⎝⎠6J. –M. Huang()+≡Ξ≡Ξl e1−−=ΦN TS U μ()∑∏∏−−+=Ξll llleβεαω1ln ln Ξ−=Φ⇒ln kT 7J. –M. Huang系统的内能为：()∫∫∞+∞+±=±=02323301221)(βεαβεαεεπεεεed m h V ge d D U 8J. –M. Huang⎝⎠⎣⎦311242U NkT e α−⎡⎤⇒=±⎢⎥⎣⎦9J. –M. Huang效的排斥作用；3）玻色统计的附加内能为负：量子统计关联使玻色粒子间出现等效的吸引作用。

10J. –M. HuangkT kT−−),(11 n T eeμμ=⇒11 J. –M. Huang()32232021612.22612.221n mk T e dx x c x ππ=⇒×=−∫∞12J. –M. Huangd ∞2()ne m h T n T T kTc=−+⇒−→<∫=021233012)(0εεεεπμ13J. –M. Huang子将全部处在的最低能级。

热力学与统计物理第5章

3 2 1 2
例子5: 例子 :
经典极限条件
∑
n
对子相空间的积分
子系的一个量子态 (自由度是 r) ) 一维谐振子: 一维谐振子:经典情况
ε =
p 2 2 m ε p 2 2 m + 1 + m ω 2 x 2 2ε
2 2
大小为h r的相格体积
x
2
= 1
m ω
2ε ; b = 2mε a= 2 mω 2πε 面积:S = πab = =
εn
(五)近独立体系微观状态的量子描述 1.系统粒子的描述
(1)全同粒子组成的系统:就是由具有完全相同的属性(相全同粒子组成的系统:就是由具有完全相同的属性( 同的质量,电荷,自旋等等)的同类粒子组成的系统; 同的质量,电荷,自旋等等)的同类粒子组成的系统; (2)近独立粒子组成的系统:是指系统中粒子之间相互作用很近独立粒子组成的系统: 相互作用的平均能量远小于单个粒子的平均能量, 弱,相互作用的平均能量远小于单个粒子的平均能量,因而可以忽略粒子之间的相互作用, 忽略粒子之间的相互作用,将整个系统的能量表达为单个粒子的 N 能量之和: 能量之和: E = ∑εi
p2 1 2 2 ε= + mω x 2m 2 ( x, p ) p x + =1 2ε 2 mε mω 2 能量ε可以在(0,+∞)任意取值
2 2
2,粒子的量子描述 ,
德布罗意关系: 德布罗意关系:
ε = hω
p = hk
不确定(测不准关系不确定测不准)关系: 测不准关系:
qp ≈ h
薛定谔方程: 薛定谔方程:
第五章, 第五章,统计物理学的基本概念
(一) 等概率原理 (统计物理学唯一的假设一统计物理学唯一的假设) 统计物理学唯一的假设

波尔兹曼常数-228.6-概述说明以及解释

波尔兹曼常数-228.6-概述说明以及解释1.引言1.1 概述波尔兹曼常数是一个与热力学及统计力学密切相关的物理量。

它代表了自然界中微观粒子与热力学宏观量之间的桥梁，具有重要的理论和实际意义。

在热力学中，我们研究的是大规模物体的性质和行为，如温度、压力、能量等。

而在微观粒子的世界中，如原子、分子等微观粒子的尺度，我们则需要运用统计力学来描述它们的特性。

波尔兹曼常数正是连接这两个层面的关键因子。

波尔兹曼常数通常用字母"k"表示，其数值约为1.38×10^-23 J/K。

它与能量之间的关系是光速c、普朗克常数h等基本物理常数的组合。

波尔兹曼常数在统计力学中的运用十分广泛，是描述微观粒子的行为和性质的重要工具。

波尔兹曼常数的物理意义十分丰富。

首先，它与热量和温度之间的关系密切相关。

根据统计物理学的理论，温度是描述粒子热运动状态的度量，而波尔兹曼常数则将微观粒子的能量和温度联系了起来。

其次，波尔兹曼常数还与熵的概念息息相关。

熵是描述系统的无序程度的量度，在热力学和信息论中具有重要的地位，而波尔兹曼常数则是熵的计算中必不可少的参数。

波尔兹曼常数的应用广泛且深入。

在材料科学中，它被用来研究热传导、热导率等热学性质；在天文学中，它用于分析恒星核反应和宇宙背景辐射等现象；在电子学中，波尔兹曼常数与电子的行为和电导率之间有着密切的联系。

总之，波尔兹曼常数在各个学科领域起着至关重要的作用。

本文将对波尔兹曼常数的定义和背景进行介绍，探讨其在物理学中的物理意义，以及它在各个领域的应用，旨在阐明波尔兹曼常数在科学研究和实际应用中的重要性。

通过深入理解波尔兹曼常数，我们能更好地理解自然界的微观世界，并应用于解决实际问题。

1.2文章结构文章结构部分的内容应该是对整篇文章涉及的主要内容进行简要介绍和概括。

以下是一个可能的编写方式：在本次长文中，我们将重点讨论波尔兹曼常数的相关内容。

首先，在引言部分概述了整篇文章的内容和目的，接着将在正文中详细阐述波尔兹曼常数的定义和背景，以及它在物理学中的重要性和意义。

物理论文玻尔兹曼统计

摘要：玻尔兹曼统计是对全同近独立粒子体系提出的平衡统计力学理论，在热力学统计物理中具有极其重要的地位和作用。

玻尔兹曼指出全同粒子是可以分辨的，粒子运动是轨道运动，是可以被跟踪的。

在一个量子态上的粒子数分布是不受限制。

玻尔兹曼统计的发展分为几个历程，而在每个历程的时代，玻尔兹曼统计无疑的都有很重要的作用。

对于玻尔兹曼统计的研究有着必然性和重要性。

关键词：玻尔兹曼；统计；粒子的力学态；相格目录摘要 (I)ABSTRACT ..................................................................................................... I I0 引言 (1)1 统计物理学是热运动的微观理论 (1)2 玻尔兹曼统计所描述的统计规律 (1)2.1玻尔兹曼统计的具体描述 (1)2.2玻尔兹曼统计的发展历程 (2)2.3等几率假设于统计力学的作用 (2)3 热力学量得统计表达 (3)4 玻尔兹曼统计应用举例 (4)5 结论 (6)参考文献 (7)0 引言玻尔兹曼统计是量子物理学中最典型的一种分布，为量子统计物理学奠定了基础，玻尔兹曼分布指出全同粒子是可以进行分辨的，粒子运动是轨道运动，是可以被跟踪的。

其分布不遵从泡利不相容原理，即处在一个量子态上的粒子数是不受限制。

1 统计物理学是热运动的微观理论统计物理学是热运动的微观理论。

深入到热运动的本质，物质的宏观性质是大量微观粒子运动的集体表现，宏观物理量是微观物理量的统计平均。

对物质的微观结构作以某些假设之后，可求得具体物质的特性。

其局限性：由于对物质的微观结构所作的往往是简化的模型假设，所得理论结果也往往是近似的[1]。

使用玻尔兹曼统计的对象，也是对实际体系所形成的理想模型，以便建立统计理论。

在这里，本来是使体系得以建成的基本因素的粒子间相互作用，被平衡态已经建成的假定所代替了。

热力学统计物理各章重点总结

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载热力学统计物理各章重点总结地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容第一章概念系统：孤立系统、闭系、开系与其他物体既没有物质交换也没有能量交换的系统称为孤立系；与外界没有物质交换，但有能量交换的系统称为闭系；与外界既有物质交换，又有能量交换的系统称为开系；平衡态平衡态的特点：1.系统的各种宏观性质都不随时间变化；2.热力学的平衡状态是一种动的平衡，常称为热动平衡；3.在平衡状态下，系统宏观物理量的数值仍会发生或大或小的涨落；4.对于非孤立系，可以把系统与外界合起来看做一个复合的孤立系统，根据孤立系统平衡状态的概念推断系统是否处在平衡状态。

准静态过程和非准静态过程准静态过程：进行得非常缓慢的过程，系统在过程汇总经历的每一个状态都可以看做平衡态。

非准静态过程，系统的平衡态受到破坏内能、焓和熵内能是状态函数。

当系统的初态A和终态B给定后，内能之差就有确定值，与系统由A到达B所经历的过程无关;表示在等压过程中系统从外界吸收的热量等于态函数焓的增加值。

这是态函数焓的重要特性克劳修斯引进态函数熵。

定义:热容量：等容热容量和等压热容量及比值定容热容量:定压热容量:循环过程和卡诺循环循环过程（简称循环）：如果一系统由某个状态出发，经过任意一系列过程，最后回到原来的状态，这样的过程称为循环过程。

系统经历一个循环后，其内能不变。

理想气体卡诺循环是以理想气体为工作物质、由两个等温过程和两个绝热过程构成的可逆循环过程。

可逆过程和不可逆过程不可逆过程：如果一个过程发生后,不论用任何曲折复杂的方法都不可能使它产生的后果完全消除而使一切恢复原状。

可逆过程：如果一个过程发生后，它所产生的后果可以完全消除而令一切恢复原状。

热力学与统计物理学第五章 玻耳兹曼统计

热力学与统计物理答案第五章

热力学与统计物理第五章知识总结

热力学与统计物理学第五章 玻耳兹曼统计

玻尔兹曼统计分布

热力学统计物理玻耳兹曼统计

热力学与统计物理答案

热力学统计第五章

热力学统计物理 第五章 课件

热力学统计物理 第五章 课件

统计物理第五章

热力学与统计物理第5章

波尔兹曼常数-228.6-概述说明以及解释

物理论文 玻尔兹曼统计

热力学统计物理各章重点总结

热力学与统计物理学第五章玻耳兹曼统计

热力学与统计物理学第五章玻耳兹曼统计

热力学统计物理第五章课件

热力学统计物理第五章课件

物理论文玻尔兹曼统计