人教版数学九年级下册26.1二次函数(2)ppt课件
合集下载
26.1二次函数课件(共26张PPT)

想一想
生活问题数学化
果园共有(100+x)棵树,平均每棵树结 (600-5x)个橙子,因此果园橙子的总产量 y=(100+x)(600-5x)=-5x² பைடு நூலகம்100x+60000 在上述问题中,种多少棵橙子树,可以使果 园橙子的总产量最多?
X/棵 Y/个
你能根据表格中的数据作出猜想 吗
1
2
3
4
5 6
=30a-a²
= -a²+30a .
是二次函数关系式.
小试牛刀
心动不如行动
如果函数y=
0或3 则k的值一定是______
x
k 3k 2
2
+kx+1是二次函数,
如果函数y=(k-3) x +kx+1是二 0 次函数,则k的值一定是______
k 2 3k 2
小结
拓展
回
味
无
穷
定义中应该注意的几个问题:
设人民币一年定期储蓄的年利率是x,一年到 期后,银行将本金和利息自动按一年定期储蓄转 存.如果存款是100元,那么请你写出两年后的本 息和y(元)的表达式(不考虑利息税).
?
y=100(x+1)² =100x² +200x+100
思索归纳
二次函数
y=-5x²+100x+60000 y=100x²+200x+100
想一想
源于生活的数学
某果园有100棵橙子树,每一棵树平均结600 个橙子.现准备多种一些橙子树以提高产量,但 是如果多种树,那么树之间的距离和每一棵树所 接受的阳光就会减少.根据经验估计,每多种一 棵树,平均每棵树就会少结5个橙子.
数学:26.1《二次函数》(第2课时)课件(人教新课标九年级下)

又想起朋友说市中心还有一家属于国家正规医院,看的也非常好。打听到位置,离得不是太远,便步行而去。走到医院门口的不远处,就看到一个环形的高楼矗立在眼前,里面全是病房和科室,前 台一番咨询后,才在二楼的转角处找到了那个皮肤科,女医生看了看说是过敏性皮炎,然后叮嘱我不要吃辛辣食品,不要用任何化妆品,还说她开的药若用了不管用,还得做过敏源的检查,检查费得一 千多,听的我心里如长了草一样难受。最后她同样是开了一大串天文数字一样的处方单,让我去取药,走到楼梯处见四处无人便用手机偷偷拍下那个处方单,心里想着回去让我们镇上的李医生看看她这 处方里配的是啥药,拍完后便辗转到一楼的药房窗口,把处方单递了进去,双手抓着窗棱看着女护士在计算机上噼噼啪啪的摁着键盘上的数,随着她手指快速的敲击计声我的心也跟着跳起来,我像等着 宣判一样的睁着仅有一条缝的眼睛望着女护士的手,终于,她停下敲击声的手在纸上挥笔写着什么,然后头也没抬的说398……一时我抓着窗棱的两只手不知该放哪里,就一个脸过敏,就得好几百,此时 的心疼胜过脸疼。踌躇了一下,我决定还是故伎重演,二话没说就撤了。
经朋友介绍说市里有一家私人医院,专门看各类皮肤病的,无奈打车直接去了这家皮肤科。一下车就看见两扇透亮的玻璃门上贴着红色的字样——“专治各类皮肤问题。”推门进去,右侧是药房, 左侧是吧台。白色的地板光可鉴人。往里走便是一个小小的院落,放着长条椅,台阶上全是各类绿色植物,环境甚是优越。因前面还有其他病人叫进了他的诊疗室。经过一番仔细的询问,那医生便给我开了一整张处方单的药,密密麻麻的写着洋文一样的字,我一个都不认得,拿着药单到药房一划价485,一听药价吓了一跳,只 好委婉的说待会过来拿,逃一样的离开了那个诊所。千人斩
数学:26.1《二次函数》(第2课时)课件(人教新课标九年级下)

源地的改变过程B.病原体的改变场所过程C.病人的改变场所过程D.携带者的改变场所过程E.医院改变场所的过程 下列说法中,是不正确的。A.一般的分布式系统是建立在计算机网络之上的,因此分布式系统与计算机网络在物理结构上基本相同B.分布式操作系统与网络操作系统的设计思想是不同的,但是它们的结构、工作方式与功能是相同的C.分布式系统与计算机网络的主要区别不在它们的物理结构,而是在 D.分布式系统是一个建立在网络之上的软件系统,这种软件保证了系统的高度一致性与透明性 咯血时垂体后叶素的止血机制是A.凝血B.减少肺血管收缩C.加强肺小动脉收缩D.对血小板的影响E.对病人有镇静作用 关于免疫溶血法测量补体活性的说法正确的是A.常用于替代途径各成分的测定B.抗原为SRBCC.实验中有一组补体系统参与反应D.不是以50%溶血作为指示终点E.检测补体的蛋白含量 1951年8月,经政务院批准,中国农业银行正式成立。A.正确B.错误 恶心与呕吐病史采集要点。 高血压的诊断标准为血压A.≥l25/75mmHgB.>130/80mmHgC.≥l35/80mmHgD.>140/85mmHgE.≥l40/90mmHg 外阴鳞状上皮细胞增生最主要的症状是A.外阴疼痛B.外阴瘙痒C.白带增多D.外阴皮疹E.外阴结节 关于服务群众对企业的作用,下列表述不正确的是A、有利于提升企业的竞争力B、有利于扩大企业的影响力C、服务群众是企业的一项重要内容和原则。D、服务群众是服务员的事儿,和企业没关系。 屈原,名,字原,战国后期国人。 河南省海拔最低处在固始县___出省处,仅23.2米。A.黄河B.长江C.海河D.淮河 原度酒的酒精含量,在贮存过程中,物质间的化学反应要快一些,也就是老熟速度些。 船舱破损前,舱内货物越多,则渗透率。A.越大B.越小C.不变D.不定 1904年1月,清政府颁布并实施,这标志着中国现代教育和体育制度的正式确立。A、《钦定学堂章程》B、《奏定学堂章程》C、《新学制课程标准》D、《学校体育指导纲要》 人类最原始的基本需要是A.生理需要B.尊重需要C.爱与归属的需要D.安全需要E.自我实现的需要 引起继发性腹膜炎的病因不包括A.急性阑尾炎B.溃疡穿孔C.胆囊穿孔D.肝硬化腹水感染E.手术污染 关节结核的早期X线主要表现是A.以骨质破坏为主B.以骨质增生为主C.骨质增生与破坏并存D.局限性脱钙E.关节间隙消失 小儿体格发育最快的时期是.A.新生儿期B.婴儿期C.幼儿期D.学龄前期E.学龄期 机件的真实大小应以图样上所注的尺寸为依据,与图形的大小及绘图的准确度无关A.正确B.错误 《办法》分几章?几条?有那些主要内容? 低钾血症心电图最早的改变是A.ST段降低B.T波降低、变平或倒置C.Q-T间期延长D.U波E.QRS增宽 潜伏性感染与病原携带状态的主要区别A.每种感染性疾病都存在B.病原体一般不排出体外C.体内存在病原体D.不出现临床症状E.以上都不是 某患者,因右肝占位引起右膈肌升高,胸片如图,查体心肺无异常症状。首先应考虑A.肺部炎症B.肺水肿C.肺转移瘤D.肺纤维化E.盘状肺不张 交叉反应率(CRR)是属于下列哪种类型的质量指标()A.精密度B.准确度C.灵敏度D.特异性E.稳定性 患者,男,55岁,进行性尿频、排尿困难1年。应首先考虑的是A.急性前列腺炎B.膀胱结石C.前列腺增生症D.肾结石E.尿道结石 根据企业所得税法的规定,下列说法中正确的是。A.企业接受捐赠收入,按合同约定日期确认收入B.被投资企业将股权(票)溢价所形成的资本公积转为股本的,作为投资方企业的股息、红利收入C.租赁合同规定的租赁期限跨年度的,且租金提前一次性支付的,出租人要一次性确认收入D.非营利组 他单位或者个人捐赠的收入为免税收入 《医疗机构从业人员行为规范》适用于哪些人员?A.医疗机构的医生、护士、药剂、医技人员B.医疗机构的医护及后勤人员C.医疗机构的管理、财务、后勤等人员D.药学技术人员E.医疗机构内所有从业人员 腹泻病史采集要点。 下列活动中,属于企业财务管理中长期投资的有。A.购买衍生金融工具B.购买机器设备C.购买长期债券D.对子公司进行增资 腰穿的禁忌证为A.小脑肿瘤B.病毒性脑膜炎C.腰椎外伤畸形并颅内感染D.蛛网膜下腔出血E.腰部局部皮肤发炎 患者男性。因全身乏力、厌油腻、恶心、尿色逐渐加深2周入院。既往无病毒性肝炎病史,无家族史。生化报告:GPT180U/L,GOT90U/L,TBil89μmol/L,抗-HAV阴性。抗-HEV阴性。抗-HBe(+),抗-HBc(+)。根据病史及生化报告应首先考虑A.HAV感染B.HBV感染C.HCV感染D.HDV感 感染 制作泵轴的材料要求有足够的强度、和耐磨性等良好的综合机械性能。A、刚度B、塑性C、耐磁性D、较好的伸长率 加工合同 关于美曲膦酯(敌百虫)中毒患者的急救措施不妥的是A.对受污染的皮肤和头发用大量清水擦洗B.口服中毒者用清水反复洗胃C.喷洒农药时中毒患者应马上脱去污染衣物D.眼部污染者用2%碳酸氢钠连续冲洗E.早期足量反复给予阿托品解毒 一个中年女性,晨起突然出现嘴歪、视物双影来诊。查体:神清语利,右侧眼球外展不能,露齿时口角左偏,右侧额纹、鼻唇沟消失,伸舌左偏、舌肌无萎缩,左侧上、下肢中枢性偏瘫,左侧偏身深、浅感觉障碍。其病变部位可能是A.左侧脑桥B.右侧脑桥C.右侧内囊D.左侧延髓E.右侧脑桥及左侧延
初三二次函数ppt课件ppt课件

轴是$x = - \frac{b}{2,利用描点法可以 绘制出二次函数的图像。
与x轴交点
当$\Delta > 0$时,二次函数的 图像与x轴有两个交点;当
$\Delta = 0$时,二次函数的图 像与x轴只有一个交点;当
$\Delta < 0$时,二次函数的图 像与x轴没有交点。
理解二次函数的基本 概念和图像表示。
能够运用二次函数解 决实际问题。
掌握二次函数的性质 ,包括开口方向、顶 点坐标和对称轴。
课程计划
通过PPT演示,引导学生了解 二次函数的概念和图像表示。
通过例题讲解,帮助学生掌握 二次函数的性质和应用。
组织课堂练习和讨论,加深学 生对二次函数的理解和应用能 力。
二次函数的表达式
01
02
03
表达式
二次函数的表达式为$y = ax^{2} + bx + c$,其中 $a \neq 0$。
各项的意义
$a$是二次项系数,$b$ 是一次项系数,$c$是常 数项。
如何确定表达式
通过已知条件,利用待定 系数法可以确定二次函数 的表达式。
二次函数的图像
图像特点
二次函数的图像是一个抛物线, 其顶点坐标是$( - \frac{b}{2a}, \frac{4ac - b^{2}}{4a})$,对称
06
参考资料
初三二次函数ppt课件
初三二次函数的概念
介绍二次函数的基本定义、表达式和 图像特征。
初三二次函数的图像和性质
详细描述了如何绘制二次函数的图像 ,并分析了图像的开口方向、顶点坐 标、对称轴和增减性等性质。
初三二次函数的实际应用
通过实例和练习题,展示了二次函数 在解决实际问题中的应用,如最值问 题、行程问题等。
与x轴交点
当$\Delta > 0$时,二次函数的 图像与x轴有两个交点;当
$\Delta = 0$时,二次函数的图 像与x轴只有一个交点;当
$\Delta < 0$时,二次函数的图 像与x轴没有交点。
理解二次函数的基本 概念和图像表示。
能够运用二次函数解 决实际问题。
掌握二次函数的性质 ,包括开口方向、顶 点坐标和对称轴。
课程计划
通过PPT演示,引导学生了解 二次函数的概念和图像表示。
通过例题讲解,帮助学生掌握 二次函数的性质和应用。
组织课堂练习和讨论,加深学 生对二次函数的理解和应用能 力。
二次函数的表达式
01
02
03
表达式
二次函数的表达式为$y = ax^{2} + bx + c$,其中 $a \neq 0$。
各项的意义
$a$是二次项系数,$b$ 是一次项系数,$c$是常 数项。
如何确定表达式
通过已知条件,利用待定 系数法可以确定二次函数 的表达式。
二次函数的图像
图像特点
二次函数的图像是一个抛物线, 其顶点坐标是$( - \frac{b}{2a}, \frac{4ac - b^{2}}{4a})$,对称
06
参考资料
初三二次函数ppt课件
初三二次函数的概念
介绍二次函数的基本定义、表达式和 图像特征。
初三二次函数的图像和性质
详细描述了如何绘制二次函数的图像 ,并分析了图像的开口方向、顶点坐 标、对称轴和增减性等性质。
初三二次函数的实际应用
通过实例和练习题,展示了二次函数 在解决实际问题中的应用,如最值问 题、行程问题等。
26.1 第1课时 反比例函数的图象 课件(共21张PPT)数学人教版九年级下册

(1) 当 k > 0 时,双曲线的两支分别位于第一、三 象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四 象限,在每一象限内,y 随 x 的增大而增大.
k 的正负决定反比例函 数图象的位置和增减性
当堂练习
1.已知反比例函数 y m 2 的图象在第一、三
y
4 x
的图象.
解析:通过刚刚的学习可知画图象的三个步骤为
列表
描点
连线
需要注意的是在反比例函数中自变量 x 不能为 0.
解:列表如下
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
y
…2 3
0.8 1
4 3
2
4 -4 -2 - 4 -1
3
-0.8 - 2 …
3
y
y=
4 x
6
5 4 3
为(-1,3),则它们的另一个交点坐标是
( C)
A. (1,3)
y
B. (3,1) C. (1,-3)
x O
D. (-1,3)
4.已知反比例函数y k 的图象经过点 A (2,3). x
(1) 求这个函数的表达式;
解:∵ 反比例函数 y k 的图象经过点 A(2,3), x
∴ 把点 A 的坐标代入表达式,得 3 k , 2
例3 已知反比例函数的图象经过点 A (2,6). (1) 这个函数的图象位于哪些象限?y 随 x 的增大如
何变化?
解:因为点 A (2,6) 在第一象限,所以这个函数的 图象位于第一、三象限; 在每一个象限内,y 随 x 的增大而减小.
(2) 点B(3,4),C( 2 1 , 4 4),D(2,5)是否在这个
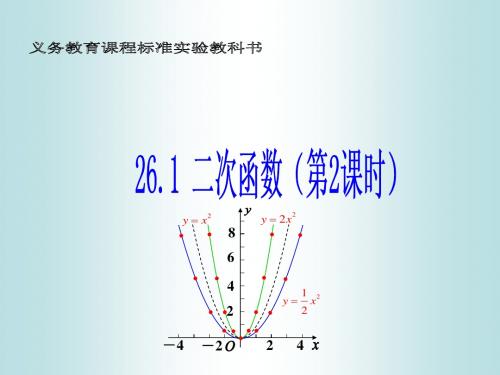
26.1二次函数(第2课时)
y= x
2
当a>0时,在对称轴的 时 左侧, 随着 随着x的增大而 左侧,y随着 的增大而 减小。 减小。 当a>0时,在对称轴的 时 右侧, 随着 随着x的增大而 右侧,y随着 的增大而 增大。 增大。 当a<0时,在对称轴的 时 左侧, 随着 随着x的增大而 左侧,y随着 的增大而 增大。 增大。 当x=-2时,y=4 时 当x=1时,y=1 时 当x=-1时,y=1 时 当x=2时,y=4 时
1 y = x 2 , y = 2 x 2 的图象. 在同一直角坐标系中, 的图象. 例1 在同一直角坐标系中,画出函数 2 分别填表,再画出它们的图象, 解:分别填表,再画出它们的图象,如图
x
···
-4
-3
-2
-1
0
1
2
3
4
··· ··· ··· ···
1 2 ··· y= x 2
x
8
··· -2 ···
9 6 3 -3 3
y轴是抛物线 = x 2 的对称轴,抛物线 = x 2 与它的对称轴的交点(0, 轴是抛物线y 的对称轴,抛物线y 与它的对称轴的交点( , 轴是抛物线 0)叫做抛物线 = x2 的顶点,它是抛物线 = x 2 的最低点. 抛物线y 的顶点,它是抛物线y 最低点. )叫做抛物线 实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线 实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线 都有对称轴 的顶点.顶点是抛物线的最低点或最高点 最低点或最高点. 的顶点.顶点是抛物线的最低点或最高点.
相同点:开口都向上,顶 相同点:开口都向上, 点是原点而且是抛物线的 最低点, 最低点,对称轴是 y 轴 不同点: 要越大, 不同点:a 要越大,抛 物线的开口越小. 物线的开口越小.
26.1.3 实际问题与二次函数课件(2) (新人教版九年级下)

-10
o
C
10
B x
练习2.某涵洞是抛物线形,它的截面如图 26.2.9所示,现测得水面宽1.6m,涵洞顶 点O到水面的距离为2.4m,问距水面1.5米 处水面宽是否超过1米?
A
B
3:根据实际问题建立函数的表 达式解决实际问题
一座拱桥的示意图如 图,当水面宽4m时, 桥洞顶部离水面2m。 已知桥洞的拱形是抛 物线,(1)求该抛物 线的函数解析式。(2) 若水面下降1米,水面 宽增加多少米?
在这个问题中,总利润是不是一个变量?如果 是,它随着哪个量的改变而改变? 若设每件售价为x元,总利润为W元。你能列出 函数关系式吗? 解:设每箱售价为x元时获得的总利润为W元. w =(x-40) [300-10(x-60)] (40<x<90) =(x-40)(900-10x) =-10x2+1300x-36000 =-10(x2-130x)-36000 =-10[(x-65)2-4225)-36000 =-10(x-65)2+6250
平面直角坐标系建立的不同,所得的抛物线的 解析式相同吗? 最终的解题结果一样 哪一种取法求得的函数解析式最简单?
做一做 如图所示,有一座抛物线型拱桥,在正常水位AB时,水 面宽20米,水位上升3米,就达到警戒线CD,这时水面宽 为10米。 (1)求抛物线型拱桥的解析式。 (2)若洪水到来时,水位以每小时0.2米的速度上升, 从警戒线开始, 在持续多少小时才能达 到拱桥顶? (3)若正常水位时,有一艘 C D
A
C
B
y M(0,2) 1m o B (2,0)x D
C
(2)水面下降1米,即当y=-1时 -0.5x2+2=-1 解得x1=-√6 x2=√6 CD=︱x1-x2︳=2√6 水面宽增加 CD-AB=(2√6-4)米
o
C
10
B x
练习2.某涵洞是抛物线形,它的截面如图 26.2.9所示,现测得水面宽1.6m,涵洞顶 点O到水面的距离为2.4m,问距水面1.5米 处水面宽是否超过1米?
A
B
3:根据实际问题建立函数的表 达式解决实际问题
一座拱桥的示意图如 图,当水面宽4m时, 桥洞顶部离水面2m。 已知桥洞的拱形是抛 物线,(1)求该抛物 线的函数解析式。(2) 若水面下降1米,水面 宽增加多少米?
在这个问题中,总利润是不是一个变量?如果 是,它随着哪个量的改变而改变? 若设每件售价为x元,总利润为W元。你能列出 函数关系式吗? 解:设每箱售价为x元时获得的总利润为W元. w =(x-40) [300-10(x-60)] (40<x<90) =(x-40)(900-10x) =-10x2+1300x-36000 =-10(x2-130x)-36000 =-10[(x-65)2-4225)-36000 =-10(x-65)2+6250
平面直角坐标系建立的不同,所得的抛物线的 解析式相同吗? 最终的解题结果一样 哪一种取法求得的函数解析式最简单?
做一做 如图所示,有一座抛物线型拱桥,在正常水位AB时,水 面宽20米,水位上升3米,就达到警戒线CD,这时水面宽 为10米。 (1)求抛物线型拱桥的解析式。 (2)若洪水到来时,水位以每小时0.2米的速度上升, 从警戒线开始, 在持续多少小时才能达 到拱桥顶? (3)若正常水位时,有一艘 C D
A
C
B
y M(0,2) 1m o B (2,0)x D
C
(2)水面下降1米,即当y=-1时 -0.5x2+2=-1 解得x1=-√6 x2=√6 CD=︱x1-x2︳=2√6 水面宽增加 CD-AB=(2√6-4)米
26.1.2二次函数y=x2的图像1

1. 二次函数的图像都是抛物线. 2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点. (2)当a>0时,抛物线的开口向上,顶点是 抛物线的最低点;(0,0) 当a<0时,抛物线的开口向下,顶点是 抛物线的最高点;(0,0) |a|越大,抛物线的开口越小;
y
a>0
一般地,二次函数y=ax2 的图象是抛物线 _______, 对称 轴是Y ____ 原点 . 轴 ,顶点是______ 当a>0时,抛物线的开口_____ 向上 ,顶点是抛物线的 低 点,当x < 0时,y随x的增大而_______, 减小 最___ 当 增大 x > 0时,y随x的增大而_______, ;a越大,抛物 越小 ; 线的开口_____ 向下 ,顶点是抛物线的 当a<0时,抛物线的开口_____ 高 点,当x < 0时,y随x的增大而_______, 增大 最___ 当 减小 x > 0时,y随x的增大而_______, ;a越大,抛物 越大 ; 线的开口_____
当a<0时,抛物线的开口向 下 顶点是抛物线的最____ 高 点, ____, a越大,抛物线的开口越 大 . ____ │a│越大抛物线开口越小
1 2 y x 2
x
-5 -4 -3 -2 -1 o 1 2 3 4 5
a<0
-3 -2 -1
1
y
1 2
0 -1 -2 -3 -4
3x
1 y x2 2
y 2 x 2
a>0 一般地,抛物线 y=ax2 的对称 原点 .当 y轴 ,顶点是______ 轴是____ a>0时,抛物线的开口向上 _____,
y 2 x 2y
二次函数第二课时PPT课件(数学人教版九年级下册)

二次函数(第二课时)
授课教师:XX 日期:XX年XX月XX日
数学初中
学习目标
1 会用函数观点看一元二次方程和一元二次不等式,建 立知识之间的联系;
2 会利用函数图象解决问题,进一步体会数形结合思想; 3 灵活运用函数与方程的有关知识解决问题,提高分析
和解决问题的能力.
数学初中
用函数观点看一元二次方程、不等式
b2 4ac 0
b2 4ac 0
b2 4ac 0
数学初中
用函数观点看一元二次方程、不等式
解一元二次方程aaxx2+2+bbxx++cc==0m(a(≠a0≠)0) 解一元二次方不程等a式x2a+xb2x++bcx=+mc>(am≠(0a)≠0)
数
当二次函数y=ax2+bx+c的函函数数值值yy==0m 时,求自变量x的值.
数学初中
例题讲解
例2.二次函数 y=ax2+bx+c (a≠0)的图象如图所示,对称轴为直线x=-1, 与x 轴的一个交点为 (1,0),与 y轴的交点为 (0,3).
3 关于x的方程ax2+bx+c=3 (a≠0)的解 为 x=-2或0 .
4 若 关于x的方程ax2+bx+c=k (a≠0)有两个 不 相等的实数根,则k的取值范围为 k<4 .
一元二次方程 令y=0 二次函数 令y>0 一元二次不等式
ax2+bx+c=0(a≠0)
y=ax2+bx+c(a≠0)
ax2+bx+c>0(a≠0)
数 当二次函数y=ax2+bx+c的 函数值y=0时,求自变量x的值.
授课教师:XX 日期:XX年XX月XX日
数学初中
学习目标
1 会用函数观点看一元二次方程和一元二次不等式,建 立知识之间的联系;
2 会利用函数图象解决问题,进一步体会数形结合思想; 3 灵活运用函数与方程的有关知识解决问题,提高分析
和解决问题的能力.
数学初中
用函数观点看一元二次方程、不等式
b2 4ac 0
b2 4ac 0
b2 4ac 0
数学初中
用函数观点看一元二次方程、不等式
解一元二次方程aaxx2+2+bbxx++cc==0m(a(≠a0≠)0) 解一元二次方不程等a式x2a+xb2x++bcx=+mc>(am≠(0a)≠0)
数
当二次函数y=ax2+bx+c的函函数数值值yy==0m 时,求自变量x的值.
数学初中
例题讲解
例2.二次函数 y=ax2+bx+c (a≠0)的图象如图所示,对称轴为直线x=-1, 与x 轴的一个交点为 (1,0),与 y轴的交点为 (0,3).
3 关于x的方程ax2+bx+c=3 (a≠0)的解 为 x=-2或0 .
4 若 关于x的方程ax2+bx+c=k (a≠0)有两个 不 相等的实数根,则k的取值范围为 k<4 .
一元二次方程 令y=0 二次函数 令y>0 一元二次不等式
ax2+bx+c=0(a≠0)
y=ax2+bx+c(a≠0)
ax2+bx+c>0(a≠0)
数 当二次函数y=ax2+bx+c的 函数值y=0时,求自变量x的值.
人教版九年级数学下册26.1.2第1课时反比例函数的图象和性质课件

y k(k>0)的图象上, x
若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y随x的增大而减小.
①当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解; ②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有y1<0<y2. ∴a-1<0,a+1>0, 解得:-1<a<1.
,4
4 5
),D(2,5)是否在这个函数的图象上?
解:设这个反比例函数的解析式为 y k ,因为点A(2,6)在其图象上,所
x
以有 6 k ,解得k=12.
2
所以反比例函数的解析式为 y 12 .
x
因为点B,C的坐标都满足该解析式,而点 D的坐标不满足,所以点B,C在
这个函数的图象上,点D不在这个函数的图象上.
结论吗?
一般地,当k>0时,对于反比例函数
y
k x
,由函数图象,并结合解析式,
我们可以发现:
(1)函数图象分别位于第一、第三象限; (2)在每一个象限内,y随x的增大而减小.
归纳: 反比例函数 y k (k>0) 的图象和性质:
x
●由两条曲线组成,且分别位于第一、三象限 它们与 x 轴、y 轴都不相交;
例1 画出反比例函数y 6 与 y 12 的图象.
x
x
提示:画函数的图象步骤一般分为:列表 →描点→连线. 需要注意的是在反比例函 数中自变量 x 不能为 0.
解:列表如下:
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
y
6 x
… -1
-1.2
-1.5
-2
-3
-6
6
《二次函数》26.1.课件(第2课时)(人教版九年级下)

x ··· -4 -3 -2 -1 0 1 2 3 4 ···
y 1 x2 ··· 2
8
4.5
2 0.5 0 0.5 2 4.5
8
···
x
·· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
y 2x2 · 8 4.5 2 0.5 0 0.5 2 4.5 8
·· ·
y x2
画最简单的二次函数 y = x2 的图象
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x ··· -3 -2 -1 0
1
2
3 ···
y = x2 ··· 9 4 1 0 1 4 9 ···
2. 根据表中x,y的数值在坐标平面中描点(x,y)
3. 如图,再用平滑曲线顺次连接
9 6 3
-3
3
y轴是抛物线y = x 2 的对称轴,抛物线y = x 2 与它的对称轴的交点(0, 0)叫做抛物线y = x2 的顶点,它是抛物线y = x 2 的最低点.
实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线 的顶点.顶点是抛物线的最低点或最高点.
例解1:在分同别一填直表角,坐再标画系出中它,们画的出图函象数,如y 图12 x2, y 2x2 的图象.
9
各点,就得到y = x2 的图象.
6
3
-3
3
二次函数 y = x2的图象是一条曲线,它的形状类似于投篮球时球在空中 所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线 y = x2 ,
二次函数的图象都是抛物线, 它们的开口或者向上或者向下. 一般地, 二次函数 y = ax2 + bx + c(a≠0)的图象叫做抛物线y = ax2 + bx + c
初三二次函数ppt课件ppt课件ppt课件

03
二次函数的图像变换
平移变换
总结词
平移变换是指二次函数的图像在平面坐标系 中沿x轴或y轴方向进行移动。
详细描述
平移变换包括沿x轴方向的左移和右移,以 及沿y轴方向的上移和下移。对于一般形式 的二次函数y=ax^2+bx+c,当b≠0时,图 像为抛物线。当b>0时,图像向右平移b/2a个单位;当b<0时,图像向左平移 |b|/2a个单位。
总结词
顶点式二次函数解析式是y=a(xh)^2+k,其中(h,k)为函数的顶点。
详细描述
顶点式二次函数解析式表示的是一个 开口向上或向下的抛物线,其顶点为 (h,k)。该形式简化了函数的对称轴和 顶点,便于分析函数的性质。
交点式二次函数解析式
总结词
交点式二次函数解析式是y=a(x-x1)(x-x2),其中x1、x2为函数与x轴的交点。
02
二次函数的解析式
一般二次函数解析式
总结词
一般二次函数解析式是y=ax^2+bx+c,其中a、b、c为常数 ,且a≠0。
详细描述
一般二次函数解析式是二次函数的基本形式,它可以表示任 意二次函数。其中a控制函数的开口方向和开口大小,b控制 函数的对称轴,c为函数与y轴的交点。
顶点式二次函数解析式
值的变化。
04
二次函数的实际应用
最大利润问题
总结词
通过建立二次函数模型,解决最大利润问题。
详细描述
在生产和经营过程中,常常需要寻求最大利润。通过将实际问题转化为数学模型,利用二次函数求导 数的方法,可以找到获得最大利润的条件和对应的最大利润值。
抛物线形拱桥问题
总结词
利用二次函数解析式表示抛物线形拱桥的形 状,进而解决相关问题。
九年级数学下册26.1二次函数课件

§26.1二次函数
你知道吗?
函数
k k ≠0 y=kx+b (k ≠0) y = x
一次函数
反比例函数
二次函数
一条直线
双曲线
? ?
源于生活的数学 引入1:某果园有100棵橙子树,每一棵树平
均结600个橙子.现准备多种一些橙子树以提高产 量,但是如果多种树,那么树之间的距离和每一棵 树所接受的阳光就会减少.根据经验估计,每多种 一棵树,平均每棵树就会少结5个橙子.
解:(1) k
1时 y 是 x 的一次函数.
(2)当 k 2 k 0即 k 0 且 k 1 时 y是 x 的二次函数
小结 拓展 定义中应该注意的几个问题:
1.定义:一般地,形如y=ax²+bx+c(a,b,c是常 数,a≠0)的函数叫做x的二次函数.
y=ax²+bx+c(a,b,c是常数,函数
y= (m+1)x
m 2m 1
2
+(m-3)x+m
是二次函数?
2
具有着 这样的性质:当x<0时,函数值y随x的增大而减小; 当x>0时,函数值y随x的增大而增大;当x=0时,函数 取得最小值,最小值y=0.
2 y ax (a 0) 图象的这些特点表明,函数
思考
观察函数 与 的图象,试作出类似的概括,即 思考:若a<0时,抛物线 y ax2 有什么特点?它反映了函 数 y ax2 (a 0) 具有哪些性质? 将你思考的结果填在下面方框内,并与同伴交流.
假设果园增种x棵橙子树,果园橙子的 总产量为y(个),那么请你写出y与x之间的 关系式.
源于生活的数学 解:设果园共有(100+x)棵树,平均
你知道吗?
函数
k k ≠0 y=kx+b (k ≠0) y = x
一次函数
反比例函数
二次函数
一条直线
双曲线
? ?
源于生活的数学 引入1:某果园有100棵橙子树,每一棵树平
均结600个橙子.现准备多种一些橙子树以提高产 量,但是如果多种树,那么树之间的距离和每一棵 树所接受的阳光就会减少.根据经验估计,每多种 一棵树,平均每棵树就会少结5个橙子.
解:(1) k
1时 y 是 x 的一次函数.
(2)当 k 2 k 0即 k 0 且 k 1 时 y是 x 的二次函数
小结 拓展 定义中应该注意的几个问题:
1.定义:一般地,形如y=ax²+bx+c(a,b,c是常 数,a≠0)的函数叫做x的二次函数.
y=ax²+bx+c(a,b,c是常数,函数
y= (m+1)x
m 2m 1
2
+(m-3)x+m
是二次函数?
2
具有着 这样的性质:当x<0时,函数值y随x的增大而减小; 当x>0时,函数值y随x的增大而增大;当x=0时,函数 取得最小值,最小值y=0.
2 y ax (a 0) 图象的这些特点表明,函数
思考
观察函数 与 的图象,试作出类似的概括,即 思考:若a<0时,抛物线 y ax2 有什么特点?它反映了函 数 y ax2 (a 0) 具有哪些性质? 将你思考的结果填在下面方框内,并与同伴交流.
假设果园增种x棵橙子树,果园橙子的 总产量为y(个),那么请你写出y与x之间的 关系式.
源于生活的数学 解:设果园共有(100+x)棵树,平均
九年级数学下册《二次函数》课件(2) 新人教版

的图象如图所示。 2
2
(1)抛物线①②③④分别对应哪个函数?
y
y
x
2
①
② y 1 x2
2
x
③
y
1 2
x
2
④
y x2
归纳:
(1 )一条抛物线,对称轴:y轴 (直线:x=0) 顶点是坐标原点(0,0)
(2)a>0时,开口向上,顶点是最低点,当x=0函 数有最小值y=0,a越大开口越小;
a<0时,开口向下,顶点是最高点,当x=0函数有最 大值y=0,a越大开口越大。
-1
23
-2
y43来自21x
-2 -1
01 2
-1
-2
这节课你有什么 收获与体会
(3)增减性: a>0时x <0函数值y随增大x而 减小,x >0函数值y随x增大而增大;
a<0时x <0函数值y随增大x而增大,x >0函数 值y随x增大而减小。
练习
1、函数 y 3x2 的图象是_抛_物_线__,开口方向
_下__,对称轴是_y__轴。顶点坐标(_0_,0_)_,x<0时, 函数值y随增大而__ 增,大x>0时,函数值随增大而
二次函数 y ax2
的图象和性质
在同一直角坐标系中,画出函数 y 1 x2 和 2
y 2x2 的图象
解:分别列表,再画它们的图象 x … -4 -3 -2 -1 0 1 2 3 4 …
y 1 x2 2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 … y 2x2
在同一直角坐标系中,画出函数 y 1 x2 和 2
y 2x2 的图象
解:分别列表,再画它们的图象 x … -4 -3 -2 -1 0 1 2 3 4 … y 1 x2 … 8 4.5 2 0.5 0 0.5 2 4.5 8 …
初中数学九年级下册《26.1二次函数》PPT课件 (2)

随堂练习 在实践中感悟
1.下列函数中,哪些是二次函数?
怎么判断?(1)((5y3=))y3=((s(x=是 是(-x31) )+)-²23+t)²1²-x²((42))yy((不不xx2是是1))1xx
(不是)
(6) v=10πr²
(是)
知道就做别
2随.用堂练总习长为60m的篱笆客围成气矩形场地,场
地面积S(mபைடு நூலகம்)与矩形一边长a(m)之间的关系
是什么?是函数关系吗?是哪一种函数?
解:S=a(
60 2
-
a)=a(30-a)
=30a-a²
是=二-a²次+函30数a .关系式.
小试牛刀 心 动 不 如 行 动
如果函数y= xk2 3k 2 +kx+1是二次函数, 则k的值一定是__0_或__3_
如果函数y=(k-3) xk2 3k 2+kx+1是二 次函数,则k的值一定是___0___
小结 拓展 回 味 无 穷
定义中应该注意的几 1b.,定c是个义常:问数一,题般a≠地:0,)形的如函y数=叫ax做²x+的b二x+次c函(a数,
. y=ax²+bx+c(a,b,c是常数,a≠0)
的几种不同表示形式: (1)y=ax² --------- (a≠0,b=0,c=0,).
60420 60455 60480 60495 60500 604956048060455 60420
y ……
……
例题欣赏
数学真奇妙
你发现了吗?
60495 60500 60495
60480
60480
60455
60455
初中数学九年级下册《26.2二次函数的图象与性质》PPT课件 (2)

1.5
1
0.5
-2
-1
1
2
x
… –1.5 –1
y=2x2
… 4.5 2
y=2x2+1 … 5.5 3
(1)二次函数 y=2x²+1 的图 象与二次函数
y=2x²的图象有 什么关系?
-6
-4
-2
–0.5 0 0.5 1 1.5 … 0.5 0 0.5 2 4.5 … 1.5 1 1.5 3 5.5 …
5.已知一个二次函数图像的顶点在y轴上,并 且离原点1个单位,图像经过点(–1,0),求该 二次函数解析式。
y 1 x2 2
6.已知抛物线
,把它向下平移,得到
的抛物线与x轴交于A、B两点,与y轴交于C
点,若⊿ABC是直角三角形,那么原抛物线
通过本堂课的学习
我学会了… … 我体会到… … 我感到困惑的是… …
2
1.5
1
0.5
y 3x2 1
1
2
- 0.5
-1
1… 3… 2…
在同一直角坐标系中画出函
数
y 1 x2
y 1 x2 2 3
5 4
y
3 y 1 x2 2
3
3 2
的图像
1
x
–5 –4 –3 –2 –1 O –1
–2
y 1 x2 2
–3
3
–4
–5
12345 y 1 x2 2 3
7
6
5
y 2x2 1
4
3
2
y 2x2
1
2
4
6
x y=3x2 y=3x2–1
… –1 –0.6 … 3 1.08 … 2 0.08
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的 顶点。顶点是抛物线的最低点或最高点。
1 例1 在同一直角坐标系中,画出函数y= 2 x2,y=2x2的图象。
x y= x2
x
… …
…
-4
-3
9 2
-1.5
-2
-1
1 2
-0.5 0
0
1
1 2
0.5
2
3
9 2
1.5
4
… …
…
1 2
8
-2
2
-1
顶点是原点。 2、当a>0,图象开口向上。 3、顶点是抛物线的最高点。 4、a越大开口越大反之越小。
抛物线y=ax2: 1、抛物线y=ax2 的对称轴是y轴, 顶点是原点。 2、当a<0,图象开口向下。
3、顶点是抛物线的最高点。
4、a越大开口越大反之越小。
y 2x2
yx
2
1 2 y x 2
一次函数的图象是一条直线,反比例函数的图象是双 曲线,二次函数的图象是什么形状呢?通常怎样画一个函 数的图象? 我们来画最简单的二次函数y=x2的图象。
x … … -3 -2 -1 0 1 2
4
9
x y=x2
… …
-3
-2
-1
0
1
2
3
… …
9
4 y
9 8
1
0
1 y=x2
4
9
7
6
5
4
3
2
1
-8
-6
-4
-2 -1
2
4
6
8
x
二次函数 y x 的图象是一 条曲线,叫做抛物线。实际上,二 次函数的图象都是抛物线,它们的 开口或者向上或者向下。
2
yx
2
y ax 2 bx c 一般地,二次函数 y ax 2 bx c。 的图象叫做抛物线
y轴是抛物线 y x 的对称轴, y x 2 与它的对称轴的交 抛物线 2 点(0,0)叫做抛物线 y x 的顶点,它是抛物线 y x 2 的最低 点。
观察y=ax2的图象, 它有什么特点?
动画演示
1 2 y x 2
y x2
y 2 x 2
y轴 原点 最低点 减小 向上 越小 增大
向下
最高点 增大 x轴 小 减小
谈谈你这节课的收获?
0
2
1
8
2
y=2x2
…
8
9 2
2
y
9
1 2
0
y=2x2
1 2
21 2 y= 2 x2
9
8
…
8
7
6
5
4
3
2
1
-6
-4
-2
0
2
4
6
x
函数 y
象相比,有什么共同点和不同点?
1 2 x , y 2 x 2 的图象与函数 y 2
x (图中的虚线图形)的图
2
抛物线y=ax2:
1、抛物线y=ax2 的对称轴是y轴,
每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的 顶点。顶点是抛物线的最低点或最高点。
1 例1 在同一直角坐标系中,画出函数y= 2 x2,y=2x2的图象。
x y= x2
x
… …
…
-4
-3
9 2
-1.5
-2
-1
1 2
-0.5 0
0
1
1 2
0.5
2
3
9 2
1.5
4
… …
…
1 2
8
-2
2
-1
顶点是原点。 2、当a>0,图象开口向上。 3、顶点是抛物线的最高点。 4、a越大开口越大反之越小。
抛物线y=ax2: 1、抛物线y=ax2 的对称轴是y轴, 顶点是原点。 2、当a<0,图象开口向下。
3、顶点是抛物线的最高点。
4、a越大开口越大反之越小。
y 2x2
yx
2
1 2 y x 2
一次函数的图象是一条直线,反比例函数的图象是双 曲线,二次函数的图象是什么形状呢?通常怎样画一个函 数的图象? 我们来画最简单的二次函数y=x2的图象。
x … … -3 -2 -1 0 1 2
4
9
x y=x2
… …
-3
-2
-1
0
1
2
3
… …
9
4 y
9 8
1
0
1 y=x2
4
9
7
6
5
4
3
2
1
-8
-6
-4
-2 -1
2
4
6
8
x
二次函数 y x 的图象是一 条曲线,叫做抛物线。实际上,二 次函数的图象都是抛物线,它们的 开口或者向上或者向下。
2
yx
2
y ax 2 bx c 一般地,二次函数 y ax 2 bx c。 的图象叫做抛物线
y轴是抛物线 y x 的对称轴, y x 2 与它的对称轴的交 抛物线 2 点(0,0)叫做抛物线 y x 的顶点,它是抛物线 y x 2 的最低 点。
观察y=ax2的图象, 它有什么特点?
动画演示
1 2 y x 2
y x2
y 2 x 2
y轴 原点 最低点 减小 向上 越小 增大
向下
最高点 增大 x轴 小 减小
谈谈你这节课的收获?
0
2
1
8
2
y=2x2
…
8
9 2
2
y
9
1 2
0
y=2x2
1 2
21 2 y= 2 x2
9
8
…
8
7
6
5
4
3
2
1
-6
-4
-2
0
2
4
6
x
函数 y
象相比,有什么共同点和不同点?
1 2 x , y 2 x 2 的图象与函数 y 2
x (图中的虚线图形)的图
2
抛物线y=ax2:
1、抛物线y=ax2 的对称轴是y轴,
