简谈常见的算法分析设计策略 算法设计
谈谈用枚举算法解决问题的编程思路与步骤方法

谈谈用枚举算法解决问题的编程思路与步骤方法一.问题上海市普通高中在信息科技学科中开展《算法与程序设计》教学,教材中有一章名为“算法实例”的内容,其中有一节介绍“枚举算法”。
教材中关于枚举算法的描述:有一类问题可以采用一种盲目的搜索方法,在搜索结果的过程中,把各种可能的情况都考虑到,并对所得的结果逐一进行判断,过滤掉那些不合要求的,保留那些符合要求的。
这种方法叫做枚举算法(enumerative algorithm)。
枚举法就是按问题本身的性质,一一列举出该问题所有可能的解,并在逐一列举的过程中,检验每个可能解是否是问题的真正解,若是,我们采纳这个解,否则抛弃它。
在列举的过程中,既不能遗漏也不应重复。
生活和工作中,人们经常会不经意间运用“枚举算法”的基本原理,进行问题的解决。
比如,让你用一串钥匙,去开一把锁,但是不知道具体是用哪一把钥匙,你就会一把一把地挨个地逐个尝试,最终打开锁为止。
又如,要对1000个零件,进行合格检验,等等。
二.用枚举算法的思想编写程序的思路与步骤枚举算法,归纳为八个字:一一列举,逐个检验。
在实际使用中,一一列举;采用循环来实现,逐个检验:采用选择来实现。
下面,通过一个问题的解决来说明这一类问题的解决过程的方法与步骤;例1:在1—2013这些自然数中,找出所有是37倍数的自然数。
这个问题就可以采用枚举算法来解决:1).一一列举;采用循环来实现;循环需要确定范围:本循环控制变量假设用i,起始值是1,终止值是2013。
2).逐个检验:采用选择来实现;选择需要列出判断的关系表达式:i Mod 37 = 0这样,就可以写出整个求解的VB代码:Dim i As IntegerFor i = 1 To 2013If i Mod 37 = 0 ThenPrint iEnd IfNext i说白了,用枚举算法解决问题,其实是利用计算机的高速度这一个优势,就好比上题完全可以使用一张纸和一支笔,采用人工的方法完成问题的解,从1开始,一一试除以37,这样计算2013次,也可以找到问题的答案。
人工智能工程师面试题

人工智能工程师面试题在当今科技飞速发展的时代,人工智能领域的需求日益增长,对于人工智能工程师的要求也越来越高。
为了选拔出优秀的人才,面试环节至关重要。
以下是一些可能在人工智能工程师面试中出现的问题:一、基础知识1、请简要介绍一下人工智能的发展历程和主要的里程碑事件。
这道题旨在考察面试者对人工智能领域的整体了解程度,以及对历史发展脉络的掌握。
一个优秀的人工智能工程师应该对该领域的起源、重要突破和当前的发展趋势有清晰的认识。
2、解释什么是机器学习,以及它与人工智能的关系。
机器学习是人工智能的核心组成部分,了解面试者对机器学习的定义和其在人工智能中的地位的理解,能够判断他们的基础知识是否扎实。
3、列举几种常见的机器学习算法,并简述它们的适用场景。
常见的算法如决策树、支持向量机、朴素贝叶斯等。
了解面试者能否根据不同的问题选择合适的算法,反映出他们的实际应用能力。
二、技术能力1、谈谈你在深度学习方面的经验,包括使用过的框架(如TensorFlow、PyTorch 等)。
深度学习是当前人工智能的热门领域,熟悉相关框架并具有实际项目经验是非常重要的。
2、如何处理数据不平衡的问题?在实际应用中,数据不平衡是常见的挑战,考察面试者的解决思路和方法。
3、介绍一下你在模型优化方面的经验,例如正则化、超参数调整等。
模型优化是提高模型性能的关键,了解面试者的优化技巧和实践经验。
三、项目经验1、请描述一个你参与过的最具挑战性的人工智能项目,你在其中承担的角色以及遇到的问题和解决方案。
通过这个问题,可以了解面试者在实际项目中的能力、团队协作和解决问题的能力。
2、在项目中,如何确保模型的准确性和可靠性?考察面试者对模型评估和验证的方法,以及对模型质量的把控能力。
3、如果项目进度紧张,你会如何安排工作以确保按时完成任务?这道题可以考察面试者的时间管理和任务分配能力。
四、问题解决能力1、假设你在训练模型时遇到了严重的过拟合问题,你会采取哪些措施来解决?过拟合是常见的问题,考察面试者的应对策略和分析问题的能力。
浅谈程序设计语言中算法的教学

在对程序设计语言的教学上,注重学生对语言语句的理解、
波浪式地推进学生在认知过程中的情感变化, 激发学生的创
使用,往往忽视 了 算法的理解、设计、 表示 因此,造成 了 新 学 习意识 例 如:编程 判断一个教是 否为 写出了 正确
的算 法。对于后两个 问题,经过启发 、弓导 , 部分 学生写 I 有 出 了算法 ( 如流程 图 ) :
、
增加算法设 计内容 授课量,提高学生对算法设计 的
认识和重视
目前的计算机程序设计语言教材中, 关于算法的内容大 都 比较少,教师在授课过程中分配的课时也就响应的比较 少.因此,给学生造成了 这样一种错觉:算法及算法设计在
算法设计是计算机程序设计的核心内容, 算法是程序设
计 中解决实 际问题 的方法和步骤。 合理 的算法不仅 可以节约
1 、循循善诱,激发学生算法学习意识 在程序基本结构学习中, 学生对循环结构的理解和应用
空间、 提高程序的执行效率,而且是提高学生程序设计能力 感到有一定的困难。在教学过程中,设计一定的氛围,合理
牛思先 河南济源职业技术学院
摘 要:算法设计是计算机程序设计语言中的核心内容,合理的算法不仅可以节约空间、提高程序的执行效率,而且是提
算法工 具 高学生程序设 计能力的关键 .本文通过对算法的认识 、表 示、分析 来探讨如何做好程序设计语言 中算法 的教学。 关键词 :算 法设 计 程序设 计
这样 一种局 面:学生在学校学 习期间学 习了多种程序设计语 谓 “ 回文教”是指一个数从前往后和从后往前是 一 的,例 样
软件工程师常见面试题

软件工程师常见面试题在当今竞争激烈的就业市场中,软件工程师的岗位备受青睐。
而面试则是通往这一岗位的关键环节,面试官通常会通过一系列问题来评估候选人的技术能力、解决问题的能力、团队协作能力以及沟通能力等。
以下是一些常见的软件工程师面试题:一、技术基础类1、谈谈你对面向对象编程(OOP)的理解,以及其三大特性(封装、继承、多态)在实际开发中的应用。
面向对象编程是一种编程范式,它将数据和操作数据的方法封装在一起,形成对象。
封装可以隐藏对象的内部实现细节,只暴露必要的接口,提高了代码的安全性和可维护性。
继承允许子类继承父类的属性和方法,实现代码的复用和扩展。
多态则使得同一个方法在不同的对象上有不同的实现方式,增强了程序的灵活性和可扩展性。
比如,在一个图形绘制的程序中,可以定义一个父类“Shape”,然后派生出子类“Circle”、“Rectangle”等,通过多态,可以用统一的接口来绘制不同的图形。
2、解释一下什么是数据库索引,以及它的作用和可能带来的弊端。
数据库索引是一种数据库结构,用于加快数据的查询和检索速度。
它就像一本书的目录,通过索引可以快速定位到所需的数据,而不必全表扫描。
索引的作用显著,能够大大提高查询效率,特别是在处理大型数据表时。
然而,索引也并非完美无缺。
创建和维护索引需要消耗系统资源,过多的索引会增加数据插入、更新和删除的开销。
此外,对于很少用于查询或者数据量较小的表,创建索引可能得不偿失。
3、请简述一下常见的排序算法(如冒泡排序、快速排序、归并排序等)的时间复杂度和空间复杂度,并比较它们的优缺点。
冒泡排序的时间复杂度为 O(n²),空间复杂度为 O(1)。
它的优点是实现简单,易于理解,缺点是效率较低。
快速排序的平均时间复杂度为 O(nlogn),最坏情况为 O(n²),空间复杂度为 O(logn)到 O(n)。
它在大多数情况下效率很高,但在最坏情况下性能不佳。
归并排序的时间复杂度为 O(nlogn),空间复杂度为 O(n)。
计算方法有哪些

计算方法有哪些计算方法是指在数学和科学领域中,用来解决问题和得出结果的一种具体步骤或程序。
在日常生活和工作中,我们经常会用到各种不同的计算方法来进行数值计算、数据分析和问题求解。
下面将介绍一些常见的计算方法。
首先,我们来谈谈基本的算术计算方法。
加法、减法、乘法和除法是最基础的四则运算,是我们日常生活中最常用的计算方法。
通过这些基本的算术计算方法,我们可以进行简单的数值计算,比如计算购物的总价、计算工资收入等。
其次,还有一些高级的数学计算方法,比如代数运算、几何计算、微积分等。
代数运算包括了代数式的化简、方程的求解、不等式的推导等,是解决代数问题的重要方法。
几何计算则涉及到图形的面积、体积、角度等计算,常用于解决几何问题。
微积分则是研究变化的一种数学工具,包括了导数、积分等。
另外,统计学中也有一些常见的计算方法,比如平均值的计算、标准差的计算、相关系数的计算等。
这些统计计算方法常用于数据分析和科学研究中,可以帮助我们更好地理解数据的特征和规律。
除了数学和统计学中的计算方法,计算机科学领域也有许多重要的计算方法,比如算法设计、数据结构的应用、复杂度分析等。
算法设计是指设计和分析解决问题的方法和步骤,是计算机科学中的核心内容。
数据结构则是指数据的组织、存储和管理方式,不同的数据结构适用于不同的计算问题。
此外,工程领域也有一些特殊的计算方法,比如有限元分析、概率论计算等。
有限元分析是一种工程结构强度和稳定性的计算方法,常用于工程设计和材料研究中。
概率论计算则是指利用概率理论进行风险评估、可靠性分析等工程计算。
总的来说,计算方法是解决问题和得出结果的重要手段,涵盖了数学、统计学、计算机科学、工程等多个领域。
不同的计算方法适用于不同的问题和场景,我们需要根据具体情况选择合适的计算方法来进行计算和分析。
通过灵活运用各种计算方法,我们可以更好地解决问题、提高工作效率,实现个人和社会的发展和进步。
浅谈高中《算法与程序设计》教学

原 理来 分 析 、 决 某 些 相 关 的 问题 。 象化 教 学 设 计要 注意 几个 解 形
环 节 . 当 地处 理 这 些 环 节 . 能 达 到想 要 的 效果 。 先 . 象 化 恰 才 首 形 模 型 要 恰 当 , 选 择 贴 近 学生 生 活 的 , 现 实 意 义 的实 例 , 且 要 有 而 形 象 化描 述 算 法 时 . 将 过程 清 楚 地 表达 出来 。其 次 , 程 序形 要 在 象化 解 释 时 , 使 描 述 跟 上 面 的模 型 一一 对 应 起 来 。 另外 , 要 在教 学 中 还 必 须 明 确 , 象 是 为 了 达 到抽 象 , 象 教 学 不 是 目 的 , 形 形 而 是 启迪 学 生思 维 和 想象 的手 段 。要 在考 虑 到 学 生可 接 受 的 基 础
体 系 , 握 知识 的规 律 性 , 思 维能 力 得 到 更 高 的发 展 。 掌 使
3 基 于 “ 务 驱 动” 小组 协 作 学 习模 式 提 升 教 学质 量 任 的
基 于 “ 务驱 动 ” 任 的小 组 协 作 学 习的 教 学 模式 可 以激 发 学 习 兴 趣 。 生 在 完 成 任务 的过 程 中 。 激 发 学生 求 知 欲 和学 习 的 主 学 能 动 性 , 更 容 易调 动 学 生学 习 的激 情 和 内在 潜 力 。 它 教学 中根 据学 生 实 际设 计 任 务 . 学 生 在完 成 任 务 体验 到 成 就 感 和优 越 感 , 让 从 而增 强学 生 学 习 的 自信 心 。 同 时还 可 以培 养学 生 团队 协 作 精神 和 创新 能力 。 种 方法 能够 很好 地 培 养 学 生 的 自学 能 力 、 作 与 这 合 创 新 精神 , 大地 提 高 了学 生 的动 手 能力 。 极 算 法 与 程 序设 计 的课 程 教 学需 要 教 师 有极 高 的教 学 水 平 和 综合 的教 学 艺 术 。 只有 不 断 探 索 、 断学 习 、 断总 结 、 断 创新 不 不 不
小学数学_两位数乘两位数笔算乘法教学设计学情分析教材分析课后反思

笔算两位数乘两位数学习内容:人教版三年级下册第46页例1,两位数乘两位数的笔算乘法(不进位)。
教材分析“两位数乘两位数的笔算乘法”这一教学内容,是在学生掌握了两位数乘一位数笔算乘法的算理和计算法则的基础上进行教学的。
本单元是按口算——笔算的顺序编排的,“两位数乘数整十数是“笔算”的基础,“笔算”又是“两位数乘整十数口算和乘一位数的”的巩固和应用。
笔算的教学又分为进位和不进位两个层次,本课时只学习不进位的笔算乘法,重点是让学生掌握乘的顺序及第二个积的书写位置,理解笔算两位数乘两位数的算理,从而使学生能解决与之相关的实际问题,还为四年级学习三位数乘两位数及混合运算做准备。
因此,本课时是本单元的重点,也是全册的一个重点,对今后进一步学习起着举足轻重的作用。
教学目标知识与技能:进一步理解乘法的意义,在理解算理的基础上,掌握两位数乘两位数的计算方法,能正确进行计算。
培养学生运用转化的方法主动学习新知识的能力,训练学生掌握优化策略的数学思想和方法。
过程与方法:通过借助点子图,让学生通过观察算一算、说一说,理解两位数乘两位数的算理;让学生经历探究发现“两位数乘两位数”算法的全过程,体验解决问题的策略的多样化,渗透“转化”的数学思想。
情感态度与价值观:通过学生自己提出问题,解决问题,获得成功解决数学问题的喜悦,增强学生学习数学的自信心。
【学情分析】学生在学习本课之前已经熟练掌握了两位数乘一位数的计算方法,能够理解其算理。
在以往的教学中,面对“两位数乘两位数”这个新知识时,学生们的反应有所不同,有部分学生立刻想到了拆数的方法,通过口算解决;有部分学生能在他人的帮助下计算出正确结果;还有的学生直接想到了竖式,可是在计算过程中遇到困难,学生在计算中就无法继续进行下去了。
针对这些情况,本节课的难点就是让学生经历探究算法的过程,借助直观手段,帮助学生理解算理、掌握算法,提升学生的计算能力。
【教学策略选择与设计】引导学生通过自主学习、合作探究出两位数乘两位数的笔算方法。
浅谈小学信息技术课程中计算思维的培养

浅谈小学信息技术课程中计算思维的培养计算思维是指通过分解问题、抽象问题、模式识别和算法设计等方式,将问题转化为计算机可以理解和解决的形式,在解决问题的过程中运用逻辑推理、算法设计和问题求解等能力。
在当今信息时代,计算思维被认为是一种重要的思维方式,对于培养学生创新思维、解决问题的能力以及提升信息技术应用能力具有重要意义。
因此,在小学信息技术课程中培养学生的计算思维已成为一项必要的任务。
要培养学生的计算思维,需要重视以下几个方面。
1.培养学生的分解问题能力。
分解问题是将复杂问题分解为多个较简单的子问题,从而有助于解决问题的能力。
在小学信息技术课程中,可以通过设计一系列的编程项目或者问题让学生分解问题。
例如,可以设计一个小程序,要求学生实现控制机器人在迷宫中找到出口。
这样的问题可以通过分解为多个步骤,例如如何前进一步,如何判断是否到达出口等,从而培养学生的分解问题能力。
2.培养学生的抽象问题能力。
抽象问题即将问题中的关键信息和特征提取出来,形成一个更为简化和一般化的问题,进而解决问题的能力。
在小学信息技术课程中,可以通过设计一些抽象问题的任务来培养学生的抽象问题能力。
例如,可以设计一个任务,要求学生设计一个简单的游戏,规定游戏中需要用到的各种元素和规则,从而培养学生的抽象问题能力。
再次,培养学生的模式识别能力。
模式识别是指发现或构建问题中的规律和模式,通过对规律进行抽象和推广,来解决与问题相关的其他问题的能力。
在小学信息技术课程中,可以通过设计一些模式识别的任务来培养学生的模式识别能力。
例如,可以设计一个任务,要求学生通过给定的一些示例,发现其中的规律和模式,从而解决其他类似的问题。
3.培养学生的算法设计能力。
算法设计是指基于问题要求和约束条件,设计出能够解决问题的具体步骤和操作的能力。
在小学信息技术课程中,可以通过设计一些算法设计的任务来培养学生的算法设计能力。
例如,可以设计一个任务,要求学生设计一个程序,能够计算两个数的最大公约数,从而培养学生的算法设计能力。
算法设计与分析教学大纲

02
分而治之篇I
课时
2.1归并排序
2.2递归式求解
2.3最大子数组问题I
第2章单元测验
03
分而治之篇II
课时
3.1逆序对计数问题
3.2快速排序
3.3次序选择问题
3.4阿里巴巴副总裁李飞飞博士访谈:双十一背后的大数据算法
04
动态规划篇I
课时
4.1 0-1背包问题
4.2最大子数组问题II
第4章单元测验
本课程具有对基础知识要求少、对核心方法讲解细、对算法本质剖析深、对产业需求分析准的特点。无论你是你是零基础的算法初学者,还是在算法刷题中困惑的求职者,相信本课程都将通过详细易懂的实例剖析降低理解难度,通过相关问题的归纳总结揭示算法本质,助你真正学懂算法!
帮助学生掌握算法的定义、性质和表示方法,能够熟练使用伪代码对算法进行描述;
05
动态规划篇II
课时
5.1最长公共子序列问题
5.2最长公共子串问题
5.3编辑距离问题
第5章单元测验
06
动态规划篇III
课时
6.1钢条切割问题
6.2矩阵链乘法问题
6.3滴滴出行副总裁叶杰平博士访谈:海量共享出行的算法设计
第6章单元测验
07
贪心策略篇
课时
7.1部分背包问题
7.2霍夫曼编码
7.3活动选择问题
7.4任务调度问题
第7章单元测验
08
图算法篇I
课时
8.1图的基本概念
8.2广度优先搜索
8.3深度优先搜索
第8章单元测验
09
图算法篇II
课时
9.1有向图的深度优先搜索
9.2图中环路的存在性判断
小学数学_三位数除以一位数(中间或末尾有0的除法)教学设计学情分析教材分析课后反思

《三位数除以一位数商中间有0除法》教学设计教学流程2.估算428÷4的商比100大一些。
3.用竖式计算四、抽象概括,总结提升:1.交流竖式计算,弄清算理。
谈话:用十位上的2除以4不够商1,怎么办?学生交流,师小结:当用十位上的2除以4不够商1时,可以在十位上商0占位。
谈话:我发现同学们列的竖式有两种形式(出示下面两个竖式)你认为哪种写法简便呢?为什么2除以4不够商1,在十位商0后,0乘以4得0可以不写呢?你喜欢哪种写法?2.自主解决“平均每小时生产多少千克果脯”,理解十位上0除以一个数应在十位商0的算理,掌握计算方法。
(1)独立思考,探索新知。
谈话:这个问题怎样解决?学生说出算式后,师板书:204÷2谈话:204÷2怎样算呢?同学们有信心自己解决吗?(2)全班交流,深化算法。
谈话:谁愿意说说你的算法?大部分学生会用竖式计算,在竖式计算前,引导学生先估算商,重点让学生说一说十位上0除以2时该商几?商在什么位上?二次备课《三位数除以一位数商末尾有0的除法》教学设计学情分析一、知识基础学生在前阶段已经掌握了基本的表内乘法、除法的口算、笔算、估算方法,学习本节知识时相对难度较低,重点让学生在信息窗中发现有价值的数学信息,提出有关的数学问题,学生自主探究,掌握两三位数除以一位数的除法。
二、年龄特点三年级孩子的一般年龄在9-10岁。
这一阶段的孩子有了一些合理性的独立思考和主见,是培养学习能力、意志品质和学习习惯的最佳时期。
老师要及时观察学生的变化,不要随意改变孩子的行为。
要从他的角度体会当时的心理状态,鼓励孩子自己寻找解决问题的办法。
三年级数学下册教材分析本册教材使用的是的新教材,共设八个单元,按照课程标准设定的知识与技能的四个领域,本册教材精选了学生进一步发展所必需的重要数学知识以及基本的数学思想方法作为教学内容,注意加强各部分之间的联系。
在“数与代数”领域两、三位数除以一位数、两数乘两位数和解决问题为主要教学内容,同时安排了认识年月日、小数的初步认识。
系统技术面试题目(3篇)

第1篇一、基础知识1. 请简要描述操作系统、数据库和计算机网络的基本概念及其在系统开发中的应用。
2. 解释什么是线程、进程和协程,以及它们之间的区别。
3. 描述内存管理的基本原理,包括页面置换算法和垃圾回收机制。
4. 简述TCP/IP协议栈的工作原理,以及TCP和UDP协议的区别。
5. 请解释什么是缓存,以及缓存机制在系统优化中的应用。
6. 介绍数据库的基本概念,包括关系型数据库和非关系型数据库的特点。
7. 描述SQL语言的基本语法,包括SELECT、INSERT、UPDATE和DELETE语句。
8. 解释什么是分布式系统,以及其在系统架构设计中的应用。
9. 简述负载均衡的原理和常用算法,如轮询、随机和最少连接数等。
10. 描述分布式事务的基本概念,以及常见的解决方案。
二、系统架构设计1. 请简要描述微服务架构和单体架构的区别,以及它们各自的优势和劣势。
2. 介绍RESTful API设计原则,以及如何设计RESTful API。
3. 描述分布式系统中的CAP定理和BASE理论,以及它们在系统设计中的应用。
4. 请解释什么是服务发现和配置中心,以及它们在分布式系统中的作用。
5. 简述分布式锁的实现原理,以及常用的分布式锁算法。
6. 介绍缓存雪崩和缓存穿透的原理,以及如何解决这些问题。
7. 描述数据库分库分表的原理和常用策略,如水平切分和垂直切分。
8. 请解释什么是数据一致性和数据隔离,以及它们在分布式系统中的应用。
9. 描述分布式系统中的幂等性设计,以及如何实现幂等性。
10. 介绍负载均衡和反向代理的作用,以及常用的负载均衡算法。
三、系统性能优化1. 描述系统性能优化的常用方法,如缓存、数据库优化、网络优化等。
2. 介绍JVM性能调优的基本原理,包括垃圾回收、内存分配和线程管理等。
3. 请解释什么是数据库索引,以及如何选择合适的索引。
4. 描述SQL语句优化技巧,如避免全表扫描、减少表连接等。
5. 简述分布式系统中的缓存穿透和缓存雪崩的解决方法。
例谈算法初步的综合应用
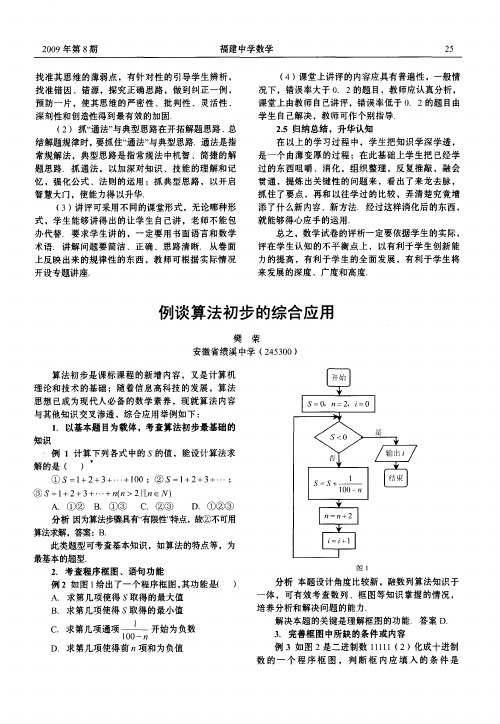
4 与不等 式结合 . 2 例 5用 程序 框图 把求 解一 般一 元 二次不 等式 。 + > > ) + c 0 0 的过程表示 出来. 分析 把解不等式 的过程用程序框 图表示 , 命题 思路新颖 ,而 且能更好 的检测逻辑思维能力. 解 如图4 .
即可 ,故答案 c .
2( 0】 9年第 8 期
福建 中学数学
2 5
找准其思 维的薄弱点 ,有针对 性 的引导 学生辨析 ,
找准错 因 、错源 ,探 究正确 思路 ,做 到纠正一例 ,
预防一片 ,使其 思维的严密性 、批判性 、灵活性 、 深刻性和 创造性得到最有效 的加 固. ( 2)抓“ 法” 通 与典型思路在开拓解题思路 、 总
例谈算法初 步 的综合应用
樊 荣
安徽省绩溪 中学 ( 4 3 0 250 )
算 法初 步是课标课 程 的新 增 内容 ,又是计算机 理论和技 术的基础 ;随着信息 高科 技 的发展 ,算 法 思想 已成 为现代人 必备的数学 素养 ,现就 算法 内容
与其他知识交叉渗透 ,综合应用举例如下 : l _以基本题 目 为载体 ,考查算法初步最基础 的
2
( 2)工 资在 (6 0 2 0 1 .属 于第一级 ,所 1 0 , 10 时
C. > 4 D. f 5
A.
>5
B.
<4
以①输 出 ( 6 0 × % =0 5 ~lo ) 5 . 一8 0 0. ( 3)工 资在 (1 0 3 o 1 ,属于 第二级 ,所 2o ,60时 以②输 出 5 0 5 一2 0 ) 1% =01 8 应 0 × %+ 10 × 0 . 一15,
开设专题讲座.
( 课堂上讲评 的内容应具有普遍性 ,一般情 4) 况下 ,错误率大于 0 .2的题 目,教师应认 真分析 , 课 堂上 由教师 自己讲评 .错误 率低于 0 .2的题 目由 学生 自己解 决 ,教师可作个别指导. 2 归纳 总结 ,升华认知 . 5 在 以上 的学 习过程 中,学生把知 识学 深学透 , 是 一个 由薄变厚 的过程 ;在此基础 上学生把 已经学 过 的东西咀 嚼 、消化 .组 织整理 .反 复推敲 ,融会 贯 通 ,提炼 出关 键性 的问题来 ,看 出了来龙 去脉 , 抓 住了要点 ,再和 以往学 过的 比较 ,弄清楚究 竟增 添了什 么新 内容 、新方 法.经过这样消化后 的东西, 就 能够得心应 手的运用 . 总 之,数学试卷 的评析一定要依据学生 的实际, 评在 学生认知 的不 平衡点 上 ,以有利 于学生创新 能 力的提 高 ,有利 于学生 的全 面发展 ,有利于学 生将 来发展 的深度 、广度和高度.
市场容量计算法

市场容量计算法方法一:占比加权法估算酒类市场容量常用的单位有三种,一种是以重量单位计算,如全国白酒市场容量三百多万吨,多用在宏观报告中,我们一线的营销人员很少接触到。
第二种是以箱、件、瓶为单位估算,如H市区中档纸箱啤酒年销售量两百万件、W大酒店11月消费红酒总量为1394瓶,这种单位在啤酒和终端销售预测多用。
第三种最为常见,以销售额估算,其中又分为厂家出价、市场批发价、进终端价、终端售价等等的区别,不同的时机、不同的角度会有不同的用途。
生产商肯定考虑厂家出厂价容量,经销商以市场批发价为统计基点,终端配送商习惯采用进终端价,而城调队和终端更喜欢用终端售价。
怎样既简单又准确地估算市场容量呢?我的方法是,将几个(5-7个)主流品牌的销售总额相加,然后估算他们的权重,一般都是七成到八成之间,最后就能估算出总容量了。
数学公式是:(主流品牌A销售额+主流品牌B销售额+主流品牌C销售额+主流品牌D销售额+主流品牌E销售额)÷权重数=市场总容量约数。
这个权重数,基本上可以用几大品牌市场占有率之和来表示。
比如你要知道浙江葡果酒的总量,我们只要了解到几个主流品牌的年销售总额,总市场容量就八九不离十了。
王朝葡萄酒两亿余,威龙一亿余,张裕五六千万,沙城长城、华夏长城、烟台长城总量一亿,新天、香格里拉等其他品牌七千万左右,5.5亿元/80%≈7亿元,可以估算出浙江市场红酒总额在七个亿左右.点评:用这种方法,区域越小,数据越准确;区域越大,权重数越难估算,关键在于权值的估算和推定。
权值推定可以通过收集三家相关企业的报告,然后结合经销商访谈,对数据进行进一步修正,最后得出比较合适的市场占有率情况。
此方法适用于成熟产品进入成熟市场.方法二:核心精算法区域市场的容量测算总是不准确的,根据不同的营销策略我们可以选择不同的计算方法。
选择方法也不复杂:尽量将容易失真的部分控制在营销策略中无关紧要的部分。
某些产品销售渠道、消费场所、消费时间比较集中,此时,如果采用统计式的计算方法偏差就非常的大。
自动驾驶汽车的道德算法设计

自动驾驶汽车的道德算法设计随着科技的飞速发展,自动驾驶汽车正逐渐从科幻走向现实。
然而,在这一令人兴奋的进步背后,隐藏着一系列复杂而棘手的道德和伦理问题,其中道德算法的设计尤为关键。
当我们谈到自动驾驶汽车的道德算法,其实就是在探讨在不可避免的危险情况下,车辆应该如何做出决策,以最大程度地减少伤害和损失。
这可不是一个简单的“二选一”问题,而是涉及到众多因素的权衡和考量。
想象一下这样的场景:自动驾驶汽车在高速行驶中突然面临一个无法避免的碰撞。
它的选择是撞向一群正在过马路的行人,还是转向撞上路边的建筑物,从而可能危及车内乘客的生命?这是一个极端但并非不可能发生的情况,而道德算法就需要为车辆提供一个决策的依据。
那么,如何设计这样一种道德算法呢?首先,我们需要明确一些基本的道德原则。
例如,“保护生命”应该是首要的原则,但这又引发了一个问题:如何界定生命的价值?是车内乘客的生命更重要,还是行人的生命更重要?一种常见的观点是,应该平等地对待每一个生命,不因为身份、地位或者所处的位置而有所区别。
但在实际情况中,要实现这种绝对的平等是非常困难的。
比如,如果车内是一位孕妇或者是一位正在执行紧急救援任务的医生,那么在决策时是否应该给予他们更多的权重?此外,道德算法的设计还需要考虑到社会的整体利益。
如果一辆自动驾驶汽车总是选择保护车内乘客而不顾及行人的安全,那么公众可能会对这种技术产生恐惧和抵制,从而阻碍自动驾驶技术的推广和应用。
相反,如果车辆总是优先考虑行人的安全,那么可能会导致车主不愿意购买和使用自动驾驶汽车,这也不利于技术的发展。
除了生命的价值和社会利益,道德算法还需要考虑到文化和地域的差异。
不同的文化对于道德和伦理问题有着不同的看法和价值观。
在一些文化中,个人的权利和自由被视为至高无上的;而在另一些文化中,集体的利益和和谐更为重要。
因此,自动驾驶汽车的道德算法需要具有一定的灵活性和适应性,能够根据不同的文化和地域背景进行调整和优化。
核心素养下“数的运算”教学策略——以《分数除法》教学为例

教海寻理教育实践2021-02·湖北教育运算在数学课程的各个学段中,都占了很大的比重。
运算能力的培养不仅可以提高学生计算的正确率,而且有助于学生灵活地选用方法,寻求简洁合理的运算途径解决问题。
笔者以《分数除法》教学为例,谈培养学生运算能力的具体办法。
一、利用现实情境,找准运算依据分数除法的计算是一个难点,教师要充分了解学生的知识起点,利用现实的问题情境,促进学生已有知识的正迁移,增强对分数除法的意义的理解。
课始,教师出示问题情境:把一张纸的45平均分成2份,每份是这张纸的几分之几,怎样列式?学生回答:算式是45÷2,可是怎样计算45÷2呢?学生初学分数除法,不易理解45÷2的意义,笔者从学生的知识起点出发,先创设8张纸平均分成2份的情境,让学生回忆整数中平均分用除法,再引导学生认同45张纸平均分成2份也用除法,促进学生理解分数除以整数和整数除以整数的意义是一样的。
这样设计,使学生利用现实情境理解分数除法列式的依据,这也是正确运算的第一步。
二、借助直观模型,深入理解算理深入理解算理可以帮助学生明白计算的道理,提高学生计算的正确率。
但算理是抽象的,教师可以借助直观模型引导学生理解算理。
例如,在教学45÷2的算理时,笔者设计了让学生用长方形纸折一折的活动,引导学生把一张纸的45平均分成2份,并根据自己的折法算出45÷2等于多少。
学生通过独立思考、小组交流后,展示了以下两种算法:方法1:方法2:45÷2=4÷25=2545÷2=45×12=25笔者根据学生的思维特点,采用手脑并用、数形结合的策略,让学生体会到45÷2两种不同算法的算理,即“把45平均分成2份,可以把4个15平均分成2份,所以45÷2=4÷25=25”或者“把45平均分成2份,每份就是45的12,也就是45×12,所以45÷2=45×12=25”。
初中数学 分数四则运算的简便算法的教学设计

学生已经学习了分数的混合运算的简便运算的基础上进行教学的,整数混合运算的简便运算.
四、教学方法
要求:实施教学方法时建议使用各种教具及电子白板、交互电视、电子书包等信息化环境。
五、教学过程
一、利用旧知,导入新课
分数混合运算要考虑哪些?请同学们类比于分数混合运算的知识.
二、探究新知
1、计算
过渡语:经过课前的谈话,我了解到同学们的兴趣很广泛。相信大家也参加了不少的兴趣小组吧!
附件二(2):教学设计模板
分数四则运算的简便算法的教Fra bibliotek设计课程名称
分数四则运算的简便算法
课时
1课时
学段学科
六年级
教材版本
人教版
作者
李艳梅
学校
风华中学
一、教学目标
1、体会运用运算律使得分数混合运算更简便。2、利用分数乘除法解决日常生活中的实际问题,发展应用意识。
二、教学重难点
利用运算律灵活简便运算。
三、学情分析
你能谈一谈你的想法吗?混合运算先要如何思考?
生:先考虑运算顺序,先乘除,除化乘,然后就是乘法的混合运算。混合的运算的计算方法要注意类比于分数乘法混合运算。
、2、用简便算法解决下面的问题
3、合作交流
师:谁能把自己的想法和全班同学交流一下?让学生分析、解决问题,教师加以适当引导。
师:通过上面计算你有什么收获?
生:
1、把小数转化为分数进行约分或通分计算
2、把除法转化为乘法运算,运用运算律寻找简便算法
注意:除法没有运算律
(三)巩固练习
(要求:学生独立完成,教师巡视,个别指导,集体反馈,及时纠正)
师:看到同学们学得这么认真,智慧老人邀请大家到智慧屋里去坐客。你们愿意吗?
浅谈小学数学高年级算理和算法有机结合的教学策略

浅谈小学数学高年级算理和算法有机结合的教学策略摘要:小学阶段作为学生的启迪阶段,一直具有重要的作用。
在小学学段的数学教学过程中,提高学生的计算能力是我们教学的核心,这将会对学生的未来发展具有积极作用。
为了更好的提高计算方面的教学质量,我们需要将算理和算法两者进行有机的结合。
本文主要从小学计算教学中算理和算法的内在联系入手,进而对如何促进算理和算法有机结合提几点建议,供业内人士的借鉴与参考。
关键词:小学数学高年级算理算法众所周知,小学学段的教育将会为学生的学习打下基础,甚至影响学生的一生。
数学作为基础学科之一,加上其独特的学科特点,决定了数学教学的特殊性。
基于此,我们必须要将多种教学方式方法应用到实际教学中,将算理与算法进行有机结合,更有效的辅助数学教学。
我将结合人教版五年级的数学教学大纲,就小学数学高年级算理和算法的有机结合展开全面研究。
一、算理和算法概念的相关概述我们都知道,算理和算法是数学教学中的典型术语,两者之间既存在着联系,又有所不同。
算理主要是指在数学计算过程中存在的各种道理,即在计算过程中的固定公式,可以辅助解题,进而提高解题效率。
算法则主要是指数学计算方法,直白来讲就是将复杂的数学题目利用算法向简单化转变,并且在后期人为的加入某些计算法则。
只有相对应的位数才能进行加减运算,这便是数理。
算法体现在加减运算中就是计算过程的竖化形式转变,可以更便利和有效的进行计算结果的检验,相同的位数进行相加,满十则需要进一,这便是对算法的大致概述。
二、小学数学教学中算理和算法的内在联系分析我们用最直白的话来讲,算理就是客观存在的规律,算法则是提高运算效率的计算方法。
算理主要是由一系列的定律、概念等组成,算法主要是我们总结的计算方法。
算理和算法之间存在着密切的联系,两者之间相辅相成、互为补充,算理能够为我们提供最基本的计算思路,进而促进计算过程的及时性和科学性,提高运算的正确度。
算法为计算过程提供了高效快捷的计算方法,算理为算法提供了理论支撑,算法是算理的精练与概括。
小学数学_除数是整数的小数除法教学设计学情分析教材分析课后反思

除数是整数的小数除法教学设计一、创设情境,自主探索谈话:同学们,还记得三峡水电站吗?在第一单元,我们通过三峡水电站学习了小数除法,今天我们就再次走进三峡水电站,去探究其中的奥秘!课件出示信息窗1谈话:谁来介绍一下三峡大坝的蓄水情况?学生读信息。
提问:根据这些信息,你能提出一个数学问题吗?根据学生提出的问题,有选择地进行板书问题:水位平均每天上升多少米?提问:该怎样解决这个问题?说说你列式的根据。
引导学生理解小数除法的意义。
随学生回答板书算式:9.84÷3=二、算法交流,分析比较1.比较发现提问:这个算式和我们以前学的有什么不同?预设:被除数是小数引出本节课的课题—小数除法(板书)2.尝试解决,估算取值范围谈话:动脑想象,这该怎么做呢?可以先估计一下,水位平均每天上升多少米?估算:9÷3=3,9.84比9多,所以每天上升3米多。
谈话:估算的结果可以帮助我们大概了解商的取值范围,要求出准确的数值,咱还得计算。
3.小组合作,研究计算方法谈话:咱们进行小组合作,讨论这道题应该怎么做。
要求:(1)在组内交流自己的算法,说说为什么这样计算(2)小组长负责记录(3)每组选出两名同学准备在班内交流。
小组讨论交流4.交流方法,渗透转化思想谈话:哪个小组来交流一下你们组的方法。
预设1:先乘以100,再除以100提问:为什么这样做?让学生体会将被除数变成整数这一转化的方法预设2:竖式交流竖式计算的方法,引导学生体会捂住小数点不看以及商的点点在哪里。
谈话:对比这两种方法,你有什么发现?预设:都是变成整数来的小结:大家在不知不觉的运用了一种很重要的数学方法—转化,把不熟悉的小数转化成整数除法来计算。
(板书)提问:你认为转化有什么好处?引导学生感受到转化会把不会的知识转化成我们会的知识来解决。
三、沟通优化,促进发展分析竖式,理解算理课件出示竖式提问:谁来说说商的小数点应该点在哪儿?预设:按照整数除法来做的,最后还要缩小到原来的1/100,就点在个位后面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简谈常见的算法分析设计策略项波波,09713043(安徽中医学院信息工程学院,安徽合肥 230031 )摘要:对于计算机科学来说,算法分析与设计是至关重要的。
怎样分析算法的“好”于“坏”,怎样设计算法,并以广泛用于计算机科学中,这要我们了解掌握各种算法分析设计策略。
本文阐述有哪些算法分析设计策略,说明各个策略的特点、方法。
总结算法设计分析的各种分析设计策略,加深对各种算法分析设计的应用,学会运用各种算法设计分析问题。
关键字:算法分析与设计、实质、特点、要求。
Jane talk about common algorithm analysis design strategyXIANG bo bo, 09713043(School of Medical and Information Engineering , Traditional Chinese Medicine Of Anhui University , Hefei , an hui 230031 China )Abstract: for computer science for, the algorithm analysis and design is very important. How to analysis algorithm of "good" in the "bad", how to design algorithm, and widely used in computer science, this to our understanding of all kinds of the algorithm analysis design strategy. This paper analyzes what algorithm design strategy, explain the characteristics of various strategies and methods. Summary analysis algorithm design kinds of analysis design strategy, deepen our understanding of the various algorithm analysis and design of the application, and learn to use all kinds of algorithm design analysis problem.Key word: algorithm analysis and design, the essence, the characteristic, the requirements.中图分类号:TU 411.01文献标识码:A0、引言我们一般常见的几种算法分析设计策略主要有:递归算法、动态规划、贪心算法、回溯法、分支限界法。
接下来我主要介绍一下这几种算法。
1.1递归算法:直接或间接地调用自身的算法称为递归算法。
用函数自身给出定义的函数称为递归函数。
递归算法的实质:递归算法的实质:是把问题转化为规模缩小了的同类问题的子问题。
然后递归调用函数(或过程)来表示问题的解。
递归算法的特点:递归算法解决问题的特点:(1) 递归就是在过程或函数里调用自身。
(2) 在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口。
(3) 递归算法解题通常显得很简洁,但递归算法解题的运行效率较低。
所以一般不提倡用递归算法设计程序。
(4) 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。
递归次数过多容易造成栈溢出等。
所以一般不提倡用递归算法设计程序。
递归算法举例:描述:把一个整数按n(2<=n<=20)进制表示出来,并保存在给定字符串中。
比如121用二进制表示得到结果为:“11 11001”。
参数说明:s: 保存转换后得到的结果。
n: 待转换的整数。
b: n进制(2<=n<=20)voidnumbconv(char *s, int n, int b){int len;if(n == 0) {strcpy(s, "");return;}/* figure out first n-1 digits */numbconv(s, n/b, b);/* add last digit */len = strlen(s);s[len] = "0123456789ABCDEFGH IJKLMNOPQRSTUVWXYZ"[n%b];s[len+1] = '\0';}voidmain(void){char s[20];int i, base;FILE *fin, *fout;fin = fopen("palsquare.in", "r");fout = fopen("palsquare.out", "w ");assert(fin != NULL && fout != N ULL);fscanf(fin, "%d", &base);/*PLS set START and END*/for(i=START; i <= END; i++) {numbconv(s, i*i, base);fprintf(fout, "%s\n", s);}exit(0);}1.2 分治法在计算机科学中,分治法是一种很重要的算法。
字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)分治策略:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。
分治法所能解决的问题一般具有以下几个特征:1) 该问题的规模缩小到一定的程度就可以容易地解决2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解;4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
分治法在每一层递归上都有三个步骤:分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题合并:将各个子问题的解合并为原问题的解。
它的一般的算法设计模式如下:Divide-and-Conquer(P)1. if |P|≤n02. then return(ADHOC(P))3. 将P分解为较小的子问题P1 ,P2 ,...,Pk4. for i←1 to k5. do yi ← Divide-and-Conq uer(Pi) △递归解决Pi6. T ← MERGE(y1,y2,...,yk)△合并子问题7. return(T)其中|P|表示问题P的规模;n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。
ADHOC(P)是该分治法中的基本子算法,用于直接解小规模的问题P。
因此,当P的规模不超过n0时直接用算法ADHOC(P)求解。
算法MERGE(y1,y2,...,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,...,Pk的相应的解y1,y2,...,yk合并为P的解。
1.3 递归与分治如果原问题可分割成k个子问题,1<k≤n ,且这些子问题都可解并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。
由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。
在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。
这自然导致递归过程的产生。
分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
1.4 动态规划动态规划算法通常用于求解具有某种最优性质的问题。
在这类问题中,可能会有许多可行解。
每一个解都对应于一个值,我们希望找到具有最优值的解。
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。
若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。
如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。
我们可以用一个表来记录所有已解的子问题的答案。
不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。
这就是动态规划法的基本思路。
具体的动态规划算法多种多样,但它们具有相同的填表格式。
动态规划适用条件:任何思想方法都有一定的局限性,超出了特定条件,它就失去了作用。
同样,动态规划也并不是万能的。
适用动态规划的问题必须满足最优化原理和无后效性。
1.最优化原理(最优子结构性质)最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。
简而言之,一个最优化策略的子策略总是最优的。
一个问题满足最优化原理又称其具有最优子结构性质。
2.无后向性将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。
换句话说,每个状态都是过去历史的一个完整总结。
这就是无后向性,又称为无后效性。
3.子问题的重叠性动态规划将原来具有指数级复杂度的搜索算法改进成了具有多项式时间的算法。
其中的关键在于解决冗余,这是动态规划算法的根本目的。
动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。
1.5 贪心算法所谓贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。
