(心理学研究方法)10第十章-独立和相关样本t检验
独立样本T检验课件

独立性
两个样本之间相互独立,没有关联性 ,即一个样本的数据不会对另一个样 本的数据产生影响。
目的与意义
比较两组数据的均值差异
通过独立样本t检验,可以比较两组数据的均值是否存在显 著差异,从而判断不同组别之间的差异是否具有统计学上 的意义。
探索潜在的分组因素
在研究过程中,有时需要探索不同分组之间的差异,独立 样本t检验可以帮助我们确定这些差异是否具有统计学上的 显著性。
假设检验
独立样本t检验是一种假设检验方法,通过设定原假设和备 择假设,进行统计推断,以决定是否拒绝原假设或接受备 择假设。
02
独立样本t检验的步骤
数据准备
确定样本来源
明确实验或调查的样本来 源,确保数据具有代表性 。
数据收集
按照研究目的和范围收集 数据,确保数据准确性和 完整性。
数据筛选与整理
对数据进行筛选,排除异 常值和缺失值,并进行数 据整理,使其满足分析要 求。
样本量的大小对独立样本t检验的结果具有重要影响。较小的样本量可能会导致 结果的不稳定和不可靠,而较大的样本量则可以提供更准确和可靠的结果。
确定合适的样本量
在进行分析之前,需要根据研究目的、研究设计和数据情况,确定合适的样本量 。如果样本量不足,可能需要重新收集数据或采用其他统计方法。
05
独立样本t检验的案例分析
数据正态性检验
正态分布检验
使用统计量或图形方法检验数据 是否符合正态分布,如直方图、 P-P图、Q-Q图等。
异常值处理
若数据不符合正态分布,需对异 常值进行处理,如用中位数或平 均数进行替代。
方差齐性检验
方差齐性检验方法
选择适当的方差齐性检验方法,如 Bartlett检验或Levene检验。
(心理学研究方法)10第十章-独立和相关样本t检验

95%பைடு நூலகம்信区间
t值,自由度和p值
效应大小
D=均值差/差值的标准差 =2.836/1.006=2.82
非常大的效应
见练习1-体重数据
实验目的:比较被试在的减肥锻炼前后, 甘油三酯的量是否有差异(tg0与tg4)?体 重是否有改变(wgt0与wgt4)?
方法学:被试有16名,参加了4个月的减肥 训练
方差齐性结果的P>0.05,显示学生组和老年组数据方差齐性。
概括数据
集中趋势 离散趋势
对集中趋势和离散趋势进行 文字描述: 大学生组的词汇回忆的均值 是45.58(SD=10.46),老 年组的词汇回忆测均值是 64.04(SD=12.27)。
方差齐性(当方差不齐时, 需要对自由度进行校正)
1、当样本量每组大于30,可以 不用理会数据是什么分布,可以 用t分布。 2、当样本量每组小于30,对样 本数据进行explore,如果近似 正态的话,间接代表了总体也具 有正态性特征。
如果不符合正态的话,那么不能 用t分布。这种情况可能需要替换 极端值或数据转换,转换为正态 分布。
练习3
假定一个抑郁疗法研究的结果如下(实验 组和对照组的数据符合正态分布):
实验组(接受新疗法治疗)抑郁量表得分 平均值=24,标准差=4.5,N1=5;对照组平 均值=30,标准差=9.4,N2=15;
问题:
1、用哪种统计分析方法,判断抑郁新疗法 是否有效?
2、手算:计算t值,置信区间和效应量大小 。
Log转换后的数据分布
实验组和对照组 的正态性检验的 P<0.05,不符
合正态分布
实验组和对照组的直方图不符 合左右对称和中间高耸,因此
不符合正态分布
独立样本T检验课件

目录
• 独立样本t检验概述 • 独立样本t检验的步骤 • 独立样本t检验的应用场景 • 独立样本t检验的注意事项 • 独立样本t检验案例分析 • 独立样本t检验总结与展望
01
独立样本t检验概述
Chapter
定义与概念
定义
独立样本t检验(Independent Sample t-test)是一种统计假设 检验,用于比较两个独立样本的 均值是否存在显著差异。
概念
独立样本t检验基于假设,即两个 样本的总体分布都是正态分布, 且两个总体方差齐性。
目的与用途
目的
通过独立样本t检验,我们可以判断两个样本的均 值是否存在显著差异,从而支持或否定原假设。
用途
独立样本t检验在科学、工程、医学等领域广泛应 用,用于检验实验组和对照组之间的差异是否具有 统计学意义。
假设与条件
解读结果
如果p值小于显著性水平(通常为0.05),则拒绝原假设,认为两组样本的均值存在 显著差异。
如果p值大于显著性水平,则无法拒绝原假设,认为两组样本的均值不存在显著差异 。
根据需要,可以进一步进行方差分析(ANOVA)等统计方法来比较两组样本的差异 。
03
独立样本t检验的应用场景
Chapter
案例三
目的
检验一个样本是否显著不 同于另一个样本。
数据
两个样本数据,每个样本 包含多个观察值。
方法
使用独立样本t检验进行分 析。
案例三
步骤
1. 收集数据:收集两个样本数据,每个样本包含 多个观察值。
2. 数据清洗:对数据进行清洗,包括处理缺失值 、异常值和离群点等。
案例三
01
3. 数据转换
相关样本、独立样本均值分析之比较
相关样本、独立样本均值分析之比较在实际应用中,我们经常需要比较两个或者多个总体是否有显著差异,比如两个或者多个班级的学习成绩是否有显著差异;针对同一种疾病,两种或多种药物的疗效是否有显著差异;两种或者多种投资的收益是否有显著差异,等等。
实际上这类问题主要还是比较总体之间的平均水平是否存在显著差异。
本文将对这类问题的多种应用场景进行分门别类,帮助大家识别不同的应用场景,进而便于选取对应的正确的分析方法。
分类是人们认识和解决问题最基本的方法之一。
在使用数据分析工具过程中,人们往往需要先界定清楚自己所面临问题的应用场景是怎样的,比如是两样本,还是多样本,是独立样本,还是相关样本,是参数检验还是非参数检验,只有分析清楚了当前的应用场景,才可以选取正确的分析方法。
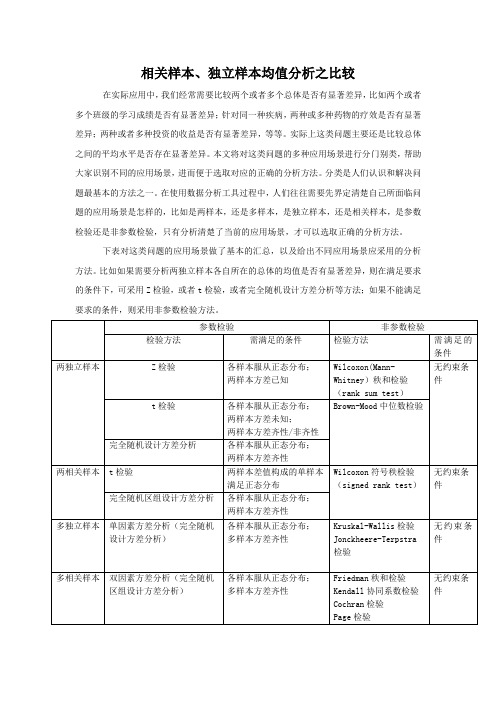
下表对这类问题的应用场景做了基本的汇总,以及给出不同应用场景应采用的分析方法。
比如如果需要分析两独立样本各自所在的总体的均值是否有显著差异,则在满足要求的条件下,可采用Z检验,或者t检验,或者完全随机设计方差分析等方法;如果不能满足要求的条件,则采用非参数检验方法。
说明:1、对于两独立样本的t检验来说,在两样本方差齐性与非齐性两种场景下,t检验统计量与自由度是不同的。
2、Excel工具提供了Z检验方法,而在SPSS工具中,没有提供Z检验的方法,因为t检验方法可以代替Z检验方法。
3、Kruskal-Wallis是双边检验,而Jonckheere-Terpstra是单边检验。
4、Friedman和kendall实际上是同一种检验场景,完全可以使用同一个检验统计量,只是由不同的统计学家给出了两个不同的检验统计量,这两个统计量其实可以互换。
5、与Friedman秩和检验相比,Page检验用于位置参数是否存在趋势的检验,也就是单边检验。
6、Cochran检验:对由二元定性数据构成的完全随机区组设计进行位置参数检验。
T检验单样本与独立样本

T检验单样本与独立样本T检验是一种常用的统计方法,用于比较两组数据之间的差异是否显著。
在实际应用中,T检验可以分为单样本T检验和独立样本T检验两种情况。
本文将分别介绍单样本T检验和独立样本T检验的原理、应用场景以及计算方法。
## 单样本T检验单样本T检验用于检验一个样本的均值是否与已知的总体均值存在显著差异。
在进行单样本T检验时,需要满足以下假设:- 零假设(H0):样本均值与总体均值无显著差异。
- 备择假设(H1):样本均值与总体均值存在显著差异。
进行单样本T检验的步骤如下:1. 提出假设:设定零假设和备择假设。
2. 收集数据:获取样本数据。
3. 计算T值:根据样本数据计算T值。
4. 确定显著性水平:设定显著性水平(通常为0.05)。
5. 判断结果:比较计算得到的T值与临界T值,判断是否拒绝零假设。
## 独立样本T检验独立样本T检验用于比较两组独立样本的均值是否存在显著差异。
在进行独立样本T检验时,同样需要满足零假设和备择假设。
独立样本T检验的步骤如下:1. 提出假设:设定零假设和备择假设。
2. 收集数据:获取两组独立样本数据。
3. 计算T值:根据两组样本数据计算T值。
4. 确定显著性水平:设定显著性水平(通常为0.05)。
5. 判断结果:比较计算得到的T值与临界T值,判断是否拒绝零假设。
在实际应用中,单样本T检验常用于分析一个样本的均值是否与总体均值存在显著差异,例如某一产品的平均质量是否符合标准要求;而独立样本T检验常用于比较两组独立样本的均值,例如男性和女性在某项指标上的平均差异是否显著。
总之,T检验是一种重要的统计方法,可以帮助研究者判断样本数据之间的差异是否具有统计学意义。
通过合理应用T检验,可以更准确地进行数据分析和决策制定。
希望本文对T检验的单样本和独立样本应用有所帮助。
独立样本t检验spss的步骤

独立样本t检验spss的步骤独立样本t检验SPSS的步骤概述:独立样本t检验(Independent Samples t-test)是一种常见的统计方法,用于比较两组独立样本的均值是否存在显著差异。
在SPSS (Statistical Package for the Social Sciences)软件中进行独立样本t检验是一项相对简单而又方便的任务。
本文将详细介绍如何使用SPSS进行独立样本t检验的步骤。
步骤一:准备数据和SPSS环境在进行独立样本t检验之前,首先需要准备好需要进行比较的两组数据以及将其输入到SPSS软件中。
确保数据的格式正确,即每一组数据都应该是一个单独的变量。
打开SPSS软件,并在数据编辑器中将这两组数据输入到不同的变量列中。
步骤二:指定假设在进行独立样本t检验之前,需要明确要比较的两组数据的假设。
独立样本t检验有一对假设需要检验,分别是零假设(H0)和备择假设(H1)。
零假设(H0):两组数据的均值相等。
备择假设(H1):两组数据的均值不相等。
步骤三:进行独立样本t检验在SPSS软件中,进行独立样本t检验需要使用“Analyze”和“Compare Means”菜单。
按照以下步骤进行操作:1. 选择菜单栏中的“Analyze”。
2. 选择“Compare Means”。
3. 在“Compare Means”菜单下,选择“Independent-Samples T Test”。
在弹出的对话框中,将需要比较的两组数据变量选择到“Test Variables”框中。
点击“箭头”按钮将其移至“Grouping Variable”框中。
点击“OK”按钮,SPSS将自动为你进行独立样本t检验,并生成相应的结果报告。
步骤四:解读结果SPSS生成的独立样本t检验结果报告包含了一些关键的统计信息。
以下是一些常见的结果:1. “Mean Difference”(平均数差异):表示两组数据均值之间的差异。
T检验独立样本与配对样本

T检验独立样本与配对样本T检验是一种常用的统计方法,用于比较两个样本之间的差异是否显著。
在实际应用中,常常需要进行独立样本的T检验和配对样本的T 检验。
本文将分别介绍独立样本T检验和配对样本T检验的原理、应用场景和计算方法。
一、独立样本T检验独立样本T检验用于比较两个独立样本的均值是否存在显著差异。
例如,我们想要比较男性和女性的平均身高是否有显著差异,就可以使用独立样本T检验。
1. 原理独立样本T检验的原理是基于两个独立样本的均值差异和样本方差的比较。
假设我们有两个样本,分别记为样本1和样本2,样本1的均值为μ1,样本2的均值为μ2,样本1的方差为σ1^2,样本2的方差为σ2^2。
独立样本T检验的原假设为“两个样本的均值相等”,备择假设为“两个样本的均值不相等”。
2. 应用场景独立样本T检验适用于以下场景:- 比较两个独立样本的均值是否存在显著差异;- 样本数据满足正态分布假设;- 两个样本的方差相等或近似相等。
3. 计算方法进行独立样本T检验的计算方法如下:- 计算两个样本的均值和方差;- 计算T值,T值的计算公式为:T = (x1 - x2) / sqrt(s1^2/n1 + s2^2/n2),其中x1和x2分别为样本1和样本2的均值,s1和s2分别为样本1和样本2的标准差,n1和n2分别为样本1和样本2的样本容量;- 根据自由度和显著性水平查找T分布表,确定临界值;- 比较计算得到的T值和临界值,判断是否拒绝原假设。
二、配对样本T检验配对样本T检验用于比较同一组样本在不同条件下的均值差异是否显著。
例如,我们想要比较同一组学生在考试前和考试后的平均成绩是否有显著差异,就可以使用配对样本T检验。
1. 原理配对样本T检验的原理是基于同一组样本在不同条件下的均值差异和样本方差的比较。
假设我们有一组样本,记为样本1和样本2,样本1和样本2是同一组样本在不同条件下的观测值。
配对样本T检验的原假设为“两个样本的均值相等”,备择假设为“两个样本的均值不相等”。
T检验分为三种方法

T检验分为三种方法
T检验是一种常见的统计推断方法,它用于比较两个样本之间的差异。
T检验分为三种方法:独立样本T检验、配对样本T检验和单样本T检验。
下面将对这三种方法进行介绍。
1.独立样本T检验:
独立样本T检验用于比较两个不相关的样本之间的均值差异。
要进行
独立样本T检验,首先需要收集两个独立的样本数据,然后根据这些数据
计算出两个样本的均值和方差。
T检验的原假设是这两个样本的均值相等,备择假设是这两个样本的均值不相等。
根据计算的T值和自由度,可以计
算出P值,从而判断原假设是否成立。
2.配对样本T检验:
配对样本T检验用于比较同一个样本在不同条件下的均值差异。
配对
样本T检验适用于两种情况:一是两个样本是相关的,例如同一个受试者
在不同时间点的数据;二是两个样本是配对的,例如同一组受试者在不同
条件下的数据。
在配对样本T检验中,计算的T值和自由度与独立样本T
检验类似,根据P值判断原假设是否成立。
3.单样本T检验:
单样本T检验用于判断一个样本的均值是否与一个已知的总体均值相等。
在单样本T检验中,收集一个样本的数据,计算样本的均值和标准差。
T检验的原假设是样本的均值等于总体的均值,备择假设是样本的均值不
等于总体的均值。
根据计算的T值和自由度,计算P值,从而判断原假设
是否成立。
总的来说,T检验是一种常用的统计方法,可以用于比较两个样本均值是否有差异,并判断这种差异是否显著。
根据实际问题的需求,可以选择独立样本T检验、配对样本T检验或单样本T检验来进行分析。
独立样本和相关样本的区别于联系
说到样本和总体的概念,大家应该不陌生。
如果只有一组样本,通常就叫one sample test,这是与总体比较,看是否显著。
这我就不多说了。
如果有2组样本,就存在样本与样本的比较,其实是他们各自代表的总体的比较。
对于2组样本,很多人对独立样本和相关样本非常迷惑,光是字面意思就够令人费解的了。
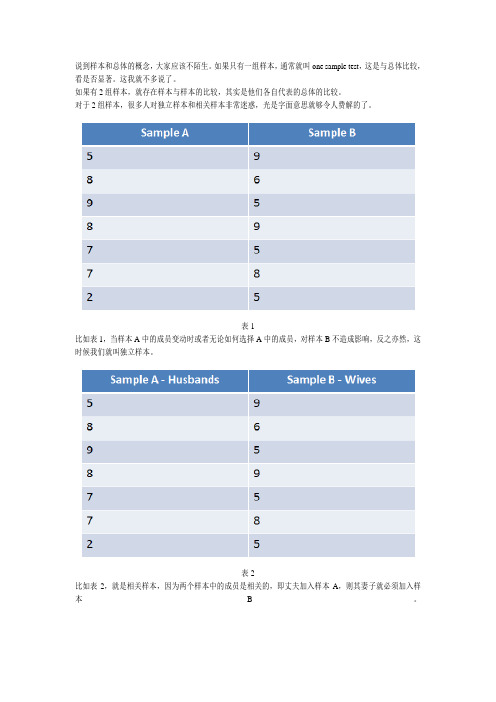
表1
比如表1,当样本A中的成员变动时或者无论如何选择A中的成员,对样本B不造成影响,反之亦然,这时候我们就叫独立样本。
表2
比如表2,就是相关样本,因为两个样本中的成员是相关的,即丈夫加入样本A,则其妻子就必须加入样本B。
再如表3,也属于相关样本。
之前和之后都是同一个样本。
独立样本t检验的应用

独立样本t检验的应用一、引言独立样本t检验是一种常用的统计方法,用于比较两个独立样本之间的均值是否存在显著差异。
在许多领域中,如医学、社会科学、教育等,独立样本t检验被广泛应用于研究和实践中,以验证假设和推断总体的差异。
本文将从实际应用的角度,介绍独立样本t检验在不同领域中的具体应用。
二、医学领域应用在医学研究中,独立样本t检验常被用来比较两种不同药物或治疗方法的疗效。
以某种疾病的治疗为例,研究者可以分成两组,一组接受药物A治疗,另一组接受药物B治疗。
然后,通过独立样本t检验来比较两组患者治疗后的平均病情得分。
如果通过检验发现两组患者的病情得分存在显著差异,就可以得出药物A和药物B对疾病疗效的差异。
三、教育领域应用在教育研究中,独立样本t检验被广泛应用于比较不同教学方法的效果。
例如,研究者想要比较传统教学法和创新教学法对学生学习成绩的影响。
研究者可以将学生随机分成两组,一组接受传统教学法,另一组接受创新教学法。
然后通过独立样本t检验,比较两组学生的平均成绩是否存在显著差异,以得出不同教学方法对学生成绩的影响。
四、商业领域应用在市场调研中,独立样本t检验可以用来比较不同群体之间的消费行为差异。
假设一个公司想要了解男性和女性对于一种新产品的喜好程度是否存在显著差异。
他们可以通过随机抽样,在男性和女性两个群体中各选取一定数量的样本,然后针对这些样本进行问卷调查,最后利用独立样本t检验来比较两组样本之间的平均喜好程度是否有显著差异。
五、社会科学领域应用在社会科学研究中,独立样本t检验可以用来比较不同群体之间的态度、观点或行为差异。
以一项心理学研究为例,研究者想要比较不同年龄群体对于环境保护的态度是否存在差异。
他们可以通过随机抽样,在不同年龄段选取一定数量的样本,并利用问卷调查来收集他们的态度数据。
最后,通过独立样本t检验,比较不同年龄群体的平均态度得分是否存在显著差异,以验证不同年龄群体对环境保护态度的差异。
独立样本t检验定义值

独立样本t检验定义值全文共四篇示例,供读者参考第一篇示例:独立样本t检验是一种用于比较两组平均值是否有显著差异的统计方法。
在实际应用中,我们经常需要比较两组数据的平均值,以确定它们之间是否存在显著性差异。
我们可能想知道一个新的药物是否比现有药物更有效,或者想了解男性和女性在某一特定指标上的差异。
在这些情况下,我们可以使用独立样本t检验来进行分析。
独立样本t检验的基本思想是比较两组独立样本的平均值是否存在显著差异。
在进行检验时,我们首先建立一个原假设(H0)和一个备择假设(H1)。
原假设通常是两组样本的平均值相等,备择假设则是两组样本的平均值不相等。
然后,我们计算两组样本的平均值和标准差,并使用t值来比较两组样本的差异性。
如果t值的显著性水平小于给定的显著性水平(通常为0.05),我们可以拒绝原假设,接受备择假设,说明两组样本的平均值存在显著差异。
在进行独立样本t检验时,我们需要满足一些前提条件。
两组样本必须是独立的,即两组样本中的数据点之间没有关联性。
两组样本必须满足正态分布,即每组样本的数据符合正态分布。
两组样本的方差必须相等,即两组样本的方差具有相同的值。
如果样本不满足这些前提条件,我们可以考虑使用非参数检验方法来进行分析。
独立样本t检验在实际应用中有着广泛的应用。
在医学研究中,我们可以使用独立样本t检验来比较不同治疗方法的效果;在教育研究中,我们可以使用独立样本t检验来比较不同教学方法的效果;在市场研究中,我们可以使用独立样本t检验来比较不同产品的销售效果。
通过独立样本t检验,我们可以得出科学的结论和建议,为决策提供依据。
独立样本t检验是一种用于比较两组平均值是否有显著差异的统计方法。
在实际应用中,我们可以通过独立样本t检验来分析不同组别之间的差异性,为我们的研究和决策提供科学依据。
希望通过本文的介绍,读者对独立样本t检验有了更深入的了解,能够在实践中灵活运用这一方法,取得更好的研究效果。
独立样本T检验

【下载本文档,可以自由复制内容或自由编辑修改内容,更多精彩文章,期待你的好评和关注,我将一如既往为您服务】独立样本T检验要求被比较的两个样本彼此独立,既没有配对关系,要求两个样本均来自正态分布,要求均值是对于检验有意义的描述统计量。
例如:男性和女性的工资均值比较分析——比较均值——独立样本T检验。
分析身高大于等于155厘米与身高小于155的两组男生的体重和肺活量均值之间是否有显著性差异。
组统计量身高N 均值标准差均值的标准误>= 155.00 13 40.838 5.1169 1.4192 体重< 155.00 16 34.113 3.8163 .9541>= 155.00 13 2.4038 .40232 .11158 肺活量< 155.00 16 2.0156 .42297 .10574 基本信息的描述方差齐次性检验(详见下面第二个例题)和T检验的计算结果。
从sig(双侧)栏数据可以看出,无论两组体重还是肺活量,方差均是齐的,均选择假设方差相等一行数据进行分析得出结论。
体重T检验结果,sig(双侧)=0.000,小于0.01,拒绝原假设。
两组均值之差的99%上、下限均为正值,也说明两组体重均值之差与0的差异显著。
由此可以得出结论,按身高155.0分组的两组体重均值差异,在统计学上高度显著。
肺活量T检验的结果,sig(双侧)=0.018,大于0.01,。
两组均值之差的上下限为一个正值,一个负值,也说明差值的99%上下限与0的差异不显著。
由此可以得出结论,按身高155.0分组烦人两组肺活量均值差异在99%水平上不显著,均值差异是由抽样误差引起的。
以性别作为分组变量,比较当前工资salary变量的均值方差齐性检验(levene检验)结果,F值为119.669,显著性概率为p<0.001,因此结论是两组方差差异显著,及方差不齐。
在下面的T 检验结果中应该选择假设方差不相等一行的数据作为本例的T检验的结果数据,另一航是假设方差相等的T检验的据算数据,不取这个结果。
(完整word版)T检验分为三种方法

T 检验分为三种方法:1. 单一样本t 检验( One-sample t test ),是用来比较一组数据的平均值和一个数值有无差异。
例如,你选取了5 个人,测定了他们的身高,要看这五个人的身高平均值是否高于、低于还是等于1.70m ,就需要用这个检验方法。
2. 配对样本t 检验( paired-samples t test ),是用来看一组样本在处理前后的平均值有无差异。
比如,你选取了5 个人,分别在饭前和饭后测量了他们的体重,想检测吃饭对他们的体重有无影响,就需要用这个t 检验。
注意,配对样本t 检验要求严格配对,也就是说,每一个人的饭前体重和饭后体重构成一对。
3. 独立样本t 检验( independent t test ),是用来看两组数据的平均值有无差异。
比如,你选取了5 男 5 女,想看男女之间身高有无差异,这样,男的一组,女的一组,这两个组之间的身高平均值的大小比较可用这种方法。
总之,选取哪种t 检验方法是由你的数据特点和你的结果要求来决定的。
t 检验会计算出一个统计量来,这个统计量就是t 值,spss 根据这个t 值来计算sig 值。
因此,你可以认为t 值是一个中间过程产生的数据,不必理他,你只需要看sig 值就可以了。
sig 值是一个最终值,也是t 检验的最重要的值。
sig 值的意思就是显著性 (significance ),它的意思是说,平均值是在百分之几的几率上相等的。
一般将这个sig 值与0.05 相比较,如果它大于0.05 ,说明平均值在大于5%的几率上是相等的,而在小于95% 的几率上不相等。
我们认为平均值相等的几率还是比较大的,说明差异是不显著的,从而认为两组数据之间平均值是相等的。
如果它小于0.05 ,说明平均值在小于5% 的几率上是相等的,而在大于95%的几率上不相等。
我们认为平均值相等的几率还是比较小的,说明差异是显著的,从而认为两组数据之间平均值是不相等的。
独立样本t检验的原理

独立样本t检验的原理统计学作为一门重要的数理学科,在现代社会中扮演着越来越重要的角色。
其中,检验方法作为统计学中最基本的方法之一,被广泛应用于各个领域。
其中,独立样本t检验作为常用的统计方法之一,在医学、生物学、社会学等领域中得到了广泛的应用。
本文将详细介绍独立样本t检验的原理。
1. 独立样本t检验的基本概念独立样本t检验是一种比较两个样本的方法,其基本概念如下:1.1 独立样本独立样本是指两个样本之间没有任何关系,互相独立采样。
例如,在比较两种药物的疗效时,两组患者之间没有任何关系,互相独立采样,因此这两组患者就是独立样本。
1.2 方差齐性方差齐性是指两个样本所代表的总体方差相等。
这是独立样本t检验的基本假设之一。
如果两个样本所代表的总体方差不同时,就需要采用非独立样本t检验进行比较。
1.3 均值差均值差是指两个样本中样本均值的差值,也就是总体均值的差值的估计值。
独立样本t检验的目的就是比较这个均值差是否有显著的差异。
2. 独立样本t检验原理的具体步骤独立样本t检验的原理可以概括为以下几个步骤:2.1 假设检验首先进行假设检验。
独立样本t检验的假设检验包括零假设和备择假设。
零假设是指两个样本所代表的总体具有相同的均值,备择假设则是指两个样本所代表的总体均值不相同。
2.2 计算t值然后计算t值。
t值是指独立样本均值差的标准误的比值,用来评估两个样本所代表的总体均值差的显著性。
其中,标准误是指均值差的标准差,用来描述均值差的离散程度。
2.3 计算自由度计算自由度。
自由度是指样本容量与样本方差之间的关系,用来描述样本所代表的总体的最大容量。
自由度越大,样本所代表的总体容量就越大,可靠性就越高。
2.4 计算p值计算p值。
p值是指在假设检验之下,样本差异产生的概率。
p 值越小,样本差异就越显著。
2.5 结论判定最后进行结论判定。
如果p值小于显著性水平α,就拒绝零假设,接受备择假设,即两个样本所代表的总体均值不相同;反之,则接受零假设,认为两个样本所代表的总体均值相同。
研究生独立样本T检验

Page 8
t 检验可以判断两组数据平均数间的差异显著
性,而方差分析既可以判断两组又可以判断多组数
据平均数之间的差异显著性。
有人说,我们可以把多组数据化成n个两组数据(化整 为零),用n次t检验来完成这个多组数据差异显著性的判 断。
Page 9
对多个处理进行平均数差异显著性检验时,采用t检验法的缺点:
F
Page 13
多重比较(multiple comparisons)
常用方法
最小显著 差数法
最小显著 极差法
least significant difference
LSD法
least significant 法的实质是两个平均数相比较的t检验法。
LSR法克服了LSD法的局限性,采用不同平均数
独立样本T检验
成组数据平均数的比较
如果两个样本的各个变量是从各自总体中随机
抽取的,两个样本之间的变量没有任何关联,即两
个抽样样本彼此独立,则不论两样本的容量是否相
同,所得数据皆为成组数据。两组数据以组平均数 作为相互比较的标准,来检验其差异的显著性。 根据两样本所属的总体方差是否已知和样本大 小不同而采用不同的检验方法。
间用不同的显著差数标准进行比较,它可用于平均 数间的所有相互比较。
Page 15
最小显著极差法(LSR法)
是指不同平均数间用不同的显著差数标准进行
比较,可用于平均数间的所有相互比较。
新复极差法
(New multiple rang method) SSR法
Page 16
q 检验
(q-test)
因此,在实际计算中:
Page 2
Page 3
Page 4
心理学 相关样本的t检验

• 统计前提 • 比较 • 论文形式报告结果
匹配样本的定义
两个样本,其中一个样本的每一个个体与另一 样本中的每个个体匹配(配对)。匹配的作用 是使两个个体在研究者要控制的特定的变量上 等同(或近似等同)。
In a matched-subjects study, each individual in one sample is matched with a subject in the other sample. The matching is done so that the two individuals are equivalent (or nearly equivalent) with respect to a specific variable that the researcher would like to control.
第3步:确定检验的自由度 df=n- 1 = 9 –1 =8
第4步:查表求临界t分数 tcrit = 1.86
• 前言 • 相关概念
– 相关样本 – 匹配样本
• 相关样本的意义 • 相关样本的检验
– D分布 – 公式 – 步骤
• 统计前提 • 比较 • 论文形式报告结果
第5步 计算样本的实际t分数
• 前言 • 相关概念
– 相关样本 – 匹配样本
• 相关样本的意义 • 相关样本的检验
– D分布 – 公式 – 步骤
• 统计前提 • 比较 • 论文形式报告结
果
相关样本t检验的统计前提
1 在每一种处理条件内,观察都彼此独 立
2 差异分数的总体分布是正态的
• 前言 • 相关概念
– 相关样本 – 匹配样本
第十章 t检验

如果是单侧检验,则在查t 如果是单侧检验,则在查t 界值表时应查单侧 查 t 界值表,单侧 界值表, , , P < 0.05,按 0.05, 的检验水准,拒绝H 的检验水准,拒绝H0,接受 差别有统计学意义, H1,差别有统计学意义,可认为该地难产儿出生体 重大于一般新生儿。 重大于一般新生儿。
第一节
单样本均数的 t 检验
亦称样本均数与总体均数比较的 t 检验,检验 检验, 的目的是推断该样本来自的总体均数 µ 与已知的总 体均数 µ0 是否相等。 是否相等。
一般为已 知的理论 值、标准 值或经过 大量观察 所得到的 稳定值。 稳定值。
例10-1 通过以往大规模调查,已知某地新生儿出生 10- 通过以往大规模调查, 体重均数为3.30kg,今从该地难产儿中随机抽取35 体重均数为3.30kg,今从该地难产儿中随机抽取35 名难产儿,测得其平均出生体重为3.42kg, 名难产儿,测得其平均出生体重为3.42kg,标准差 0.40kg, 为0.40kg,问该地难产儿出生体重是否与一般新生 儿出生体重不同 ?
H0: µ = µ0 = 3.30kg (难产儿出生体重总体均数与一般 30kg
新生儿出生体重总体均数相等) 新生儿出生体重总体均数相等); 30kg H1: µ > µ0 = 3.30kg (难产儿出生体重总体均数大于一般 新生儿); 新生儿) 单侧
如果有理由认为难产儿出生体重的总体均数不会小于一 般新生儿, 可采用单侧检验, 般新生儿,例10-1可采用单侧检验,即: 可采用单侧检验
确定采用双侧检验还是单侧检验, 确定采用双侧检验还是单侧检验,必须在研究 设计阶段根据专业知识预先确定, 设计阶段根据专业知识预先确定,不能在假设检验 结果出来之后随意挑选。 结果出来之后随意挑选。
t检验的逻辑机理和实施步骤

T检验的逻辑机理和实施步骤1. 什么是T检验?T检验是一种用于比较两个样本均值是否有显著差异的统计方法。
它是以计算分析两个样本之间的差异,从而推断总体差异情况的一种假设检验方法。
T检验分为独立样本T检验和相关样本T检验两种形式。
独立样本T检验用于比较两个独立样本组的均值是否有显著差异,而相关样本T检验用于比较同一样本在不同条件下的均值变化是否有显著差异。
2. T检验的逻辑机理T检验的逻辑机理基于以下几个关键概念:2.1 样本均值与总体均值的比较T检验通过比较样本均值和总体均值之间的关系,来判断两个样本是否存在显著差异。
它首先计算两个样本的均值,并将其与总体均值进行比较。
2.2 方差的估计T检验中还需要对总体的方差进行估计。
为了保证估计的准确性,T检验使用样本方差来近似总体方差。
样本方差能够提供总体方差的一个良好估计。
2.3 自由度的计算T检验中的自由度是指样本数据在计算中可以任意变动的程度。
自由度的计算与样本大小和样本独立性有关。
自由度越大,T检验的结果越可信。
2.4 假设检验的实施T检验是一种假设检验方法,其中包括原假设和备择假设。
原假设通常为两个样本均值相等,而备择假设为两个样本均值不相等。
通过计算得到的T值和临界值作比较,可以判断原假设是否成立。
3. T检验的实施步骤进行T检验需要经过以下几个主要步骤:3.1 收集和整理数据首先需要收集相关的样本数据,并根据需要进行整理。
确保数据的准确性和可靠性,以便进行后续的分析。
3.2 设定假设根据具体的研究问题和实验设计,设定原假设和备择假设。
原假设通常为两个样本均值相等,备择假设为两个样本均值不相等。
3.3 计算T值根据样本数据的均值、样本大小和样本方差估计值,计算得到T值。
T值可以通过计算公式来获得,公式的具体形式取决于T检验的类型。
3.4 计算临界值根据设定的显著性水平和自由度,确定临界值。
临界值是判断原假设是否成立的参考标准。
3.5 比较T值和临界值将计算得到的T值与临界值进行比较。
t检验知识点总结

t检验知识点总结在进行T检验之前,我们需要明确所要分析的问题,确定需要比较的两组数据,以及所使用的数据类型。
T检验分为独立样本T检验和配对样本T检验两种,分别适用于不同的数据类型。
独立样本T检验是用于比较两组独立样本均值是否有显著差异的方法。
它假设两组样本是相互独立的,而且数据呈正态分布,方差相等。
在进行独立样本T检验时,我们需注意检验方差齐性的问题,可以使用Levene检验或Bartlett检验进行检验。
配对样本T检验是用于比较同一组样本在不同条件下的表现是否有显著差异的方法。
它假设两组数据是成对的,即每个观测值在两个条件下都有对应的数值。
在进行配对样本T检验时,我们需要首先计算每对观测值的差值,然后对这些差值进行T检验。
在进行T检验之前,我们还需要明确假设检验的原假设和备择假设。
原假设通常是两组样本均值相等,备择假设则是两组样本均值不相等。
根据所得的T值和自由度,我们可以使用T分布表或统计软件计算出检验的P值,以判断两组样本均值是否有显著差异。
在进行T检验时,我们还需要注意以下几点:1. 样本容量:T检验对样本容量要求不高,通常当样本容量大于30时,T检验的效果会更稳定。
2. 数据正态性:T检验假设数据呈正态分布,因此需要对数据进行正态性检验。
在数据不符合正态分布时,可以使用非参数检验方法进行分析。
3. 数据方差性:T检验假设两组数据的方差相等,因此需要进行方差齐性检验。
当方差不相等时,可以使用修正的T检验方法进行分析。
总的来说,T检验是一种简单而有效的假设检验方法,适用于比较两组样本均值是否有显著差异的情况。
在进行T检验时,我们需要明确问题、选择合适的方法、进行假设检验、并对结果进行解释和判断。
通过合理使用T检验方法,我们可以更好地从数据中获取有效信息,做出正确的决策。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相关样本t检验
Spss中数据的排列方式:按被试排列,每 个被试的结果成对排列 Spss中数据的分析方法:analyzecompare means-paired sample t test
判断是否正态
相关样本t检验
相关样本t检验结果
数据描述
两变量的相关程度
样本差值的标准 差:可用于计算 效应大小
思考题
1、这个数据满足t检验的条件吗?请说明 理由。 2、如果不符合t检验要用什么办法处理? 3、这是一个学生毕业论文的数据,得出的 t值和P值,你看出有什么错误了吗?
练习1
独立样本t检验
独立样本t检验分析结果
检验方差是否齐性,计算结果是 P<0.05,表明方差非齐性,因此用第二 行分析结果(自由度进行校正)
练习3
假定一个抑郁疗法研究的结果如下(实验 组和对照组的数据符合正态分布): 实验组(接受新疗法治疗)抑郁量表得分 平均值=24,标准差=4.5,N1=5;对照组 平均值=30,标准差=9.4,N2=15; 问题: 1、用哪种统计分析方法,判断抑郁新疗法 是否有效? 2、手算:计算t值,置信区间和效应量大 小。
1、用哪种统计分析方法? 2、把统计分析结果用文字表示。根据统计检验的p值、 置信区间,你觉得这项减肥训练能帮助降低体重吗? 3、假如你根据已有的资料认为,这项训练肯定具有减 肥功能,但是你的结果却不支持这样的结论。于是,你 认为,可能实验设计上出现了问题。你觉得可以对实验 设计做哪些改进,以增加出现统计显著性的可能性?
Log转换后的数据分布
实验组和对照组 的正态性检验的 P<0.05,不符 合正态分布
实验组和对照组的直方图不符 合左右对称和中间高耸,因此 不符合正态分布
Log转换后的数据分布
实验组和对照组的数据远离对 角线分布,因此不符合正态分 布。
平方根转换
实验组和对照组的直方图不符 合左右对称和中间高耸,因此 不符合正态分布
1、符合被试内设计 2、只有1个自变量,且这个自变 量只有2个水平。 如单组前测-后测设计
总体正态。
要求和独立样本t检验一致。 1、当样本量小于30,两组数据 都要满足正态。 2、当样本量很大,大于30,可 以不用理会数据的分布。
相关样本t检验-示例
实验目的:共有30个被试,同时对疼痛词 汇和中性词汇进行唤醒度评分,疼痛词汇 和中性词汇是否有差别。
练习2——数据转换的结论
数据经过转换后也不符合正态分布。 所以,也不能用转换后的数据进行t检验。
解决方法:需要使用非参数检验——秩和检验的方法 (以后再讲如何操作)。
练习3
思考题
这是一个学生毕业论文的数据,得出的t值 和P值,你看出有什么错误了吗?
1、数据的自由度是相同的,所以同一个t分布 。T值越大,P值就越小。所以数据出错。 2、t = -0.065,p =0.051,p是错误的。当t 分布趋近于正态分布时,z值1.96(接近于2 ),才能产生显著性。
explore
explore
数据探索的结果
1、实验组和对照组对疼痛词汇的得分均不 符合正态, 2、且每组的样本量没有超过30 所以,两组数据没有符合总体正态的特征。 因此,不能用独立样本t检验来处理数据。
练习2
练习2——数据转换
尝试log转换(Y+1),以及平方根转换( Y+0.5) 分别对转换后的数据进行分析是否符合正 态
1、用哪种分析方法? 2、把统计分析结果用文字表示。并计算效应 量。根据统计检验的p值、置信区间和效应量 ,你觉得这项减肥有实际意义吗?详细说明理 由。
见练习2-减肥训练数据
实验目的:比较被试在的减肥锻炼前后,体重是否 有改变(wgt0与wgt4)? 方法学:训练组16人,对照组16人。训练组参加 了4个月的减肥训练,对照组没有参加训练。 统计:
95%置信区间
t值,自由度和p值
效应大小
D=均值差/差值的标准差 =2.836/1.006=2.82 非常大的效应
见练习1-体重数据
实验目的:比较被试在的减肥锻炼前后, 甘油三酯的量是否有差异(tg0与tg4)? 体重是否有改变(wgt0与wgt4)? 方法学:被试有16名,参加了4个月的减肥 训练 统计:
了解数据
ቤተ መጻሕፍቲ ባይዱ
用箱形图判断是否有错误值和极端值
何时运用独立样本t检验
适用条件:
当有两个样本时,两样本是 独立的(因变量是等距/等 比数据)。
两总体正态(样本平均数的 差值才符合正态)
1、被试间设计 2、只有1个自变量,且这个自变 量只有2个水平
方差齐性(当方差不齐时, 需要对自由度进行校正)
1、当样本量每组大于30,可以 不用理会数据是什么分布,可以 用t分布。 2、当样本量每组小于30,对样 本数据进行explore,如果近似 正态的话,间接代表了总体也具 有正态性特征。 如果不符合正态的话,那么不能 用t分布。这种情况可能需要替换 极端值或数据转换,转换为正态 分布。
数据分析的步骤
数据分析的三步骤
1
• 了解数 据
输入错误 极端值 数据正态分布 是否数据转换
2
• 概括数 据
集中趋势 离散趋势
3
• 证实数 据所揭 示的意 义
相关样本t检验
公式t=(拔x1-拔x2)/sD/根号n
相关样本t检验
适用条件
当有两个样本时,两样 本是相关的(因变量是 等距/等比数据)。
Z分布
t分布
本章内容
独立和相关样本t检验
独立样本t检验
置信区间 效应大小 研究的实际意义与统计意义
相关样本t检验
前提 步骤 置信区间 效应大小
独立样本t检验——示例
实验目的:比较大学生组和老年组的词汇 量是否有差别?
例子:比较不同年龄段词汇量是否有差异
大学生组:59、31、47、43、54、42、38 、44、48、57、42、48、30、41、59、 23、 62、27、53、51、39、38、 50、 58、 56、 45 老年组: 70、59、68、68、57、66、78 、 78、64、43、53、83、74、69、 59、 44、73、65、32、 60、 54、 64、 82、 62、 62、 78
