相似三角形基本图形及练习题-绝对经典

合集下载

经典相似三角形练习题(附参考答案)

经典练习题相似三角形（附答案)一.解答题（共３０小题)１.如图，在△AＢC中，DE∥BC，EF∥AＢ，求证:△ＡDE∽△ＥＦＣ.2.如图，梯形ABCD中,AＢ∥CD,点F在BC上,连DF与AB的延长线交于点G.（1)求证:△CDF∽△BＧF;(２)当点F是BC的中点时，过Ｆ作EF∥ＣD交ＡD于点E，若ＡB＝6cm,EF=４cm,求CD的长.3.如图，点D，E在BC上,且FD∥ＡB,ＦＥ∥AC.求证:△ABC∽△ＦＤE.4.如图，已知Ｅ是矩形ABCD的边CD上一点,BＦ⊥AＥ于Ｆ,试说明:△ＡBF∽△EAD.５．已知：如图①所示，在△ABC和△ADE中,ＡB=AC，AD＝AE，∠BAＣ=∠DＡＥ,且点B,A，Ｄ在一条直线上，连接BE，ＣD,Ｍ,N分别为BE,CＤ的中点.(1)求证：①BE=ＣD;②△AMN是等腰三角形;（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形．请直接写出（1)中的两个结论是否仍然成立；（３）在（２）的条件下,请你在图②中延长EＤ交线段BC于点P.求证:△PＢD∽△AＭN.6．如图,E是▱ABＣD的边BA延长线上一点,连接EＣ，交ＡD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形,并任选一对相似三角形给予证明．7．如图,在4×３的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（１)填空:∠AＢC＝_________ °，ＢC= ＿__＿＿____ ;(2)判断△AＢC与△DEＣ是否相似，并证明你的结论．8.如图,已知矩形ＡBCD的边长AB=3cm，BC=6cｍ．某一时刻，动点M从A点出发沿AB方向以１cm/s 的速度向Ｂ点匀速运动;同时，动点N从D点出发沿ＤA方向以２ｃm/s的速度向A点匀速运动，问: (1)经过多少时间,△AMN的面积等于矩形ABＣD面积的？(２）是否存在时刻ｔ,使以A,M,N为顶点的三角形与△ACＤ相似?若存在,求t的值;若不存在，请说明理由.9．如图，在梯形ABCD中，若AB∥DＣ,AD=BＣ，对角线ＢＤ、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；(注意：全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明．1０．如图△ＡBC中,D为ＡC上一点，CD=2ＤA，∠ＢAＣ=45°,∠BＤＣ=60°,CE⊥ＢD于E,连接AE. (1)写出图中所有相等的线段，并加以证明；(2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由;(3）求△BEC与△BEＡ的面积之比．1１.如图，在△ABC中，AB=AC=a，M为底边ＢC上的任意一点，过点M分别作AB、ＡC的平行线交ＡＣ于P，交AB于Q．（1)求四边形AQＭP的周长;（２)写出图中的两对相似三角形(不需证明);（3)M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论.12．已知：P是正方形ABＣD的边ＢC上的点,且BP=３PC,M是CD的中点，试说明：△ＡＤＭ∽△MCP．13．如图,已知梯形ABＣD中,AD∥BC,AＤ=2，AB=ＢC＝8，CD＝10．(1）求梯形ＡＢＣD的面积Ｓ;(2)动点Ｐ从点B出发，以1cｍ/s的速度,沿B⇒A⇒D⇒C方向,向点C运动；动点Q从点C出发，以１ｃm/s的速度,沿C⇒D⇒Ａ方向,向点A运动，过点Ｑ作QＥ⊥BC于点E．若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束，设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABＣD的周长平分？若存在，请求出t 的值;若不存在，请说明理由;②在运动过程中,是否存在这样的t，使得以P、A、D为顶点的三角形与△CQＥ相似？若存在,请求出所有符合条件的t的值；若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的ｔ的值；若不存在，请说明理由．１４．已知矩形AＢCＤ,长BC=１2cm,宽ＡB=8ｃm,P、Q分别是AB、BC上运动的两点.若Ｐ自点A出发，以1cｍ/ｓ的速度沿AB方向运动,同时，Q自点Ｂ出发以2cm/s的速度沿ＢC方向运动,问经过几秒,以Ｐ、Ｂ、Q为顶点的三角形与△BＤC相似？15．如图,在△ABC中,AB=10cm,BC＝20cm，点Ｐ从点A开始沿AB边向B点以2ｃｍ/s的速度移动，点Ｑ从点Ｂ开始沿BC边向点Ｃ以4cｍ/s的速度移动，如果P、Q分别从A、B同时出发,问经过几秒钟，△ＰBQ与△ＡBC相似．16．如图,∠ＡＣB=∠ＡDＣ=9０°,AC=，AD=2．问当AＢ的长为多少时，这两个直角三角形相似.17．已知，如图,在边长为a的正方形ABCＤ中,M是ＡD的中点，能否在边AB上找一点N（不含A、Ｂ)，使得△ＣＤM与△ＭAN相似?若能，请给出证明,若不能，请说明理由．１8．如图在△AＢC中，∠C=９0°，BC=８cｍ,AC=6cm，点Q从B出发，沿BC方向以2ｃm/s的速度移动,点Ｐ从C出发,沿ＣA方向以1ｃm/s的速度移动.若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBＡ相似?19.如图所示，梯形ＡBCD中，AD∥BC，∠A=90°，AB=7,AD=２，BC=3,试在腰ＡB上确定点Ｐ的位置，使得以P,A，D为顶点的三角形与以P，B，C为顶点的三角形相似．２0.△ＡＢC和△ＤEF是两个等腰直角三角形,∠A=∠D=90°，△DEF的顶点Ｅ位于边BC的中点上．（1）如图1,设DE与AＢ交于点M,EF与AＣ交于点N，求证：△BEＭ∽△CNE;（2）如图2,将△ＤEF绕点Ｅ旋转，使得DE与ＢA的延长线交于点M,EＦ与AC交于点N,于是，除(1）中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.2１.如图，在矩形ABCD中,AB=15ｃm，BＣ=1０cm，点P沿AＢ边从点Ａ开始向Ｂ以2cm／ｓ的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发，用t（秒)表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似.２2.如图,路灯(P点）距地面8米,身高1.6米的小明从距路灯的底部(Ｏ点)20米的A点，沿ＯA所在的直线行走１4米到Ｂ点时，身影的长度是变长了还是变短了？变长或变短了多少米？23.阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是: _____＿___ ;(2）请在下图中画出测量示意图；(3)设树高AB的长度为x，请用所测数据（用小写字母表示)求出x.24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为６0ｃｍ.乙组：如图2,测得学校旗杆的影长为900cm.丙组:如图3，测得校园景灯（灯罩视为球体,灯杆为圆柱体,其粗细忽略不计）的高度为2０0cｍ，影长为１５6cm.任务要求：(1）请根据甲、乙两组得到的信息计算出学校旗杆的高度;（2)如图３,设太阳光线ＮH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示：如图3,景灯的影长等于线段NG的影长；需要时可采用等式1562＋2082＝26０2)2５．阳光通过窗口照射到室内,在地面上留下2．７m宽的亮区（如图所示）,已知亮区到窗口下的墙脚距离ＥC=8．7m,窗口高ＡB=1.8m,求窗口底边离地面的高BC.26．如图,李华晚上在路灯下散步.已知李华的身高AB=ｈ,灯柱的高OP＝Ｏ′Ｐ′=l,两灯柱之间的距离O Ｏ′=m．（1）若李华距灯柱OP的水平距离OA=a,求他影子AC的长;（2）若李华在两路灯之间行走,则他前后的两个影子的长度之和（DA+ＡC)是否是定值请说明理由;（3）若李华在点A朝着影子(如图箭头)的方向以v１匀速行走，试求他影子的顶端在地面上移动的速度ｖ2．2７.如图①,分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S１，S２,Ｓ3表示,则不难证明S1=S２＋S３.(１）如图②,分别以直角三角形ABＣ三边为边向外作三个正方形，其面积分别用S1，Ｓ２，S３表示，那么S １，S2，S3之间有什么关系；（不必证明)(２)如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用Ｓ1,Ｓ2,Ｓ3表示，为使Ｓ1,S2,S ３之间仍具有与(2）相同的关系,所作三角形应满足什么条件证明你的结论；(４）类比(1)，(2），(3）的结论,请你总结出一个更具一般意义的结论．２8．已知：如图,△AＢＣ∽△ADＥ,AＢ=1５,AC＝9,BＤ＝5.求ＡE.29．已知:如图Rt△ＡBC∽Rt△BＤC，若AB＝3,ＡC=4.(1）求ＢD、CＤ的长;（2)过Ｂ作ＢE⊥ＤＣ于E,求BE的长.30.（１)已知，且３x+4z﹣2y＝４０，求x,y,z的值；(2)已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为5６0cm,求它们的周长.参考答案与试题解析一．解答题(共３0小题）1.如图,在△ABC中，DE∥BC，EF∥AＢ，求证：△AＤＥ∽△EFC.考点：相似三角形的判定；平行线的性质。

初三数学相似三角形典例及练习(含答案)

初三数学相似三角形（一）相似三角形是初中几何的一个重点，同时也是一个难点，本节复习的目标是：1。

理解线段的比、成比例线段的概念，会根据比例线段的有关概念和性质求线段的长或两线段的比，了解黄金分割.2. 会用平行线分线段成比例定理进行有关的计算、证明，会分线段成已知比。

3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。

4. 能熟练运用相似三角形的有关概念解决实际问题本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。

本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。

相似三角形是平面几何的主要内容之一,在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现，分值一般在10%左右，有时也单独成题,形成创新与探索型试题；有利于培养学生的综合素质。

（二）重要知识点介绍： 1。

比例线段的有关概念：在比例式：：中，、叫外项，、叫内项，、叫前项，a b cda b c d a d b c a c ==() b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC,使AC 2=AB ·BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质: ①基本性质：a b cdad bc =⇔= ②合比性质：±±a b c d a b b c d d=⇒= ③等比性质：……≠……a b c d m n b d n a c m b d n a b===+++⇒++++++=()03。

平行线分线段成比例定理：①定理：三条平行线截两条直线，所得的对应线段成比例，如图：l 1∥l 2∥l 3。

则，，，…AB BC DE EF AB AC DE DF BC AC EFDF===②推论：平行于三角形一边的直线截其他两边(或两边的延长线）所得的对应线段成比例。

相似三角形典型例题30道

相似三角形典型例题30道1: 在△ABC中，DE是平行于BC的线段，且AD/DB = 2/3。

求DE/BC的比值。

2: 已知△PQR与△XYZ相似，PQ = 6，XY = 9，求QR 与YZ的比值。

3: 在△ABC中，D、E分别是AB、AC上的点，且DE平行于BC，已知AD = 3，DB = 6，求AE与EC的比值。

4: 已知两个相似三角形的面积比为4:9，求它们对应边的比。

5: 在△XYZ中，MN是平行于XY的线段，且XM = 4，MY = 6，求MN/XY的比值。

6: 在△ABC中，AD是BC的中线，且AE是AB的延长线，若AE与BC相交于点F，求AF与FB的比值。

7: 在△DEF中，GH平行于EF，已知DE = 8，DF = 10，求GH/EF的比值。

8: 在一个相似三角形中，若大三角形的周长是36，小三角形的周长是24，求它们的面积比。

9: 在△JKL中，MN平行于JK，若JM = 3，MK = 5，求MN/JK的比值。

10: 如果两个相似三角形的对应边长分别为5和15，求它们的面积比。

11: 在△ABC中，AD是BC的中线，且DE平行于BC，已知AD = 4，BC = 8，求DE的长度。

12: 已知相似三角形的对应边长比为1:4，求它们的周长比。

13: 在△PQR中，S是PQ的中点，若ST平行于QR，求PS与PQ的比值。

14: 在相似三角形中，若小三角形的每条边长为5，大三角形的对应边长为15，求它们的面积比。

15: 在一个三角形中，若一条边的延长线与另一边的平行线相交，则形成的两小三角形与原三角形相似，求相似比。

16: 在△XYZ中，若XY = 10，XZ = 15，YZ = 12，求△XYZ的周长。

17: 已知△ABC与△DEF相似，若AB = 4，DE = 8，求AC与DF的比值。

18: 在△GHI中，JK平行于GH，若GJ = 5，GH = 20，求JK的长度。

19: 在相似三角形中，若一个三角形的面积是36，另一个三角形的面积是144，求其对应边的比。

初中数学经典相似三角形练习题(附参考答案)

经典演习题类似三角形【1 】一．解答题（共30小题）1．如图,在△ABC中,DE∥BC,EF∥AB,求证：△ADE∽△EFC．2．如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延伸线交于点G．（1）求证：△CDF∽△BGF;（2）当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长．3．如图,点D,E在BC上,且FD∥AB,FE∥AC．求证：△ABC∽△FDE．4．如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试解释：△ABF∽△EAD．5．已知：如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,衔接BE,CD,M,N分离为BE,CD的中点．（1）求证：①BE=CD;②△AMN是等腰三角形;（2）在图①的基本上,将△ADE绕点A按顺时针偏向扭转180°,其他前提不变,得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立;（3）在（2）的前提下,请你在图②中延伸ED交线段BC于点P．求证：△PBD∽△AMN．6．如图,E是▱ABCD的边BA延伸线上一点,衔接EC,交AD于点F．在不添加帮助线的情形下,请你写出图中所有的类似三角形,并任选一对类似三角形赐与证实．7．如图,在4×3的正方形方格中,△ABC和△DEF的极点都在边长为1的小正方形的极点上．（1）填空：∠ABC=_________°,BC=_________;（2）断定△ABC与△DEC是否类似,并证实你的结论．8．如图,已知矩形ABCD的边长AB=3cm,BC=6cm．某一时刻,动点M从A点动身沿AB偏向以1cm/s的速度向B点匀速活动;同时,动点N从D点动身沿DA偏向以2cm/s的速度向A点匀速活动,问：（1）经由若干时光,△AMN的面积等于矩形ABCD面积的？（2）是否消失时刻t,使以A,M,N为极点的三角形与△ACD类似？若消失,求t的值;若不消失,请解释来由．9．如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD.AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情形,并求出拔取到的两个三角形是类似三角形的概率是若干;（留意：全等算作类似的特例）（2）请你任选一组类似三角形,并给出证实．10．如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,衔接AE．（1）写出图中所有相等的线段,并加以证实;（2）图中有无类似三角形？如有,请写出一对;若没有,请解释来由;（3）求△BEC与△BEA的面积之比．11．如图,在△ABC中,AB=AC=a,M为底边BC上的随意率性一点,过点M分离作AB.AC的平行线交AC于P,交AB于Q．（1）求四边形AQMP的周长;（2）写出图中的两对类似三角形（不需证实）;（3）M位于BC的什么地位时,四边形AQMP为菱形并证实你的结论．12．已知：P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试解释：△ADM∽△MCP．13．如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10．（1）求梯形ABCD的面积S;（2）动点P从点B动身,以1cm/s的速度,沿B⇒A⇒D⇒C偏向,向点C活动;动点Q从点C动身,以1cm/s的速度,沿C⇒D⇒A偏向,向点A活动,过点Q作QE⊥BC于点E．若P.Q两点同时动身,当个中一点到达目标地时全部活动随之停止,设活动时光为t秒．问：①当点P在B⇒A上活动时,是否消失如许的t,使得直线PQ将梯形ABCD的周长等分？若消失,请求出t的值;若不消失,请解释来由;②在活动进程中,是否消失如许的t,使得以P.A.D为极点的三角形与△CQE类似？若消失,请求出所有相符前提的t的值;若不消失,请解释来由;③在活动进程中,是否消失如许的t,使得以P.D.Q为极点的三角形正好是以DQ为一腰的等腰三角形？若消失,请求出所有相符前提的t的值;若不消失,请解释来由．14．已知矩形ABCD,长BC=12cm,宽AB=8cm,P.Q分离是AB.BC上活动的两点．若P自点A动身,以1cm/s 的速度沿AB偏向活动,同时,Q自点B动身以2cm/s的速度沿BC偏向活动,问经由几秒,以P.B.Q为极点的三角形与△BDC类似？15．如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开端沿AB边向B点以2cm/s的速度移动,点Q从点B 开端沿BC边向点C以4cm/s的速度移动,假如P.Q分离从A.B同时动身,问经由几秒钟,△PBQ与△ABC类似．16．如图,∠ACB=∠ADC=90°,AC=,AD=2．问当AB的长为若干时,这两个直角三角形类似．17．已知,如图,在边长为a的正方形ABCD中,M是AD的中点,可否在边AB上找一点N（不含A.B）,使得△CDM 与△MAN类似？若能,请给出证实,若不克不及,请解释来由．18．如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B动身,沿BC偏向以2cm/s的速度移动,点P从C动身,沿CA偏向以1cm/s的速度移动．若Q.P分离同时从B.C动身,试探讨经由若干秒后,以点C.P.Q为极点的三角形与△CBA类似？19．如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上肯定点P的地位,使得以P,A,D 为极点的三角形与以P,B,C为极点的三角形类似．20．△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的极点E位于边BC的中点上．（1）如图1,设DE与AB交于点M,EF与AC交于点N,求证：△BEM∽△CNE;（2）如图2,将△DEF绕点E扭转,使得DE与BA的延伸线交于点M,EF与AC交于点N,于是,除（1）中的一对类似三角形外,可否再找出一对类似三角形并证实你的结论．21．如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开端向B以2cm/s的速度移动;点Q沿DA边从点D开端向点A以1cm/s的速度移动．假如P.Q同时动身,用t（秒）暗示移动的时光,那么当t为何值时,以点Q.A.P为极点的三角形与△ABC类似．22．如图,路灯（P点）距地面8米,身高1.6米的小明从距路灯的底部（O点）20米的A点,沿OA地点的直线行走14米到B点时,身影的长度是变长了照样变短了？变长或变短了若干米？23．阳光亮媚的一天,数学兴致小组的同窗们去测量一棵树的高度（这棵树底部可以到达,顶部不轻易到达）,他们带了以下测量对象：皮尺,标杆,一副三角尺,小平面镜．请你在他们供给的测量对象中选出所需对象,设计一种测量计划．（1）所需的测量对象是：_________;（2）请鄙人图中画出测量示意图;（3）设树高AB的长度为x,请用所测数据（用小写字母暗示）求出x．24．问题布景在某次活动课中,甲.乙.丙三个进修小组于统一时刻在阳光下对校园中一些物体进行了测量．下面是他们经由过程测量得到的一些信息：甲组：如图1,测得一根竖立于平地,长为80cm的竹竿的影长为60cm．乙组：如图2,测得黉舍旗杆的影长为900cm．丙组：如图3,测得校园景灯（灯罩视为球体,灯杆为圆柱体,其粗细疏忽不计）的高度为200cm,影长为156cm．义务请求：（1）请依据甲.乙两组得到的信息盘算出黉舍旗杆的高度;（2）如图3,设太阳光线NH与⊙O相切于点M．请依据甲.丙两组得到的信息,求景灯灯罩的半径．（友谊提醒：如图3,景灯的影长等于线段NG的影长;须要时可采取等式1562+2082=2602）25．阳光经由过程窗口照耀到室内,在地面上留下2.7m宽的亮区（如图所示）,已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC．26．如图,李华晚上在路灯下漫步．已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的程度距离OA=a,求他影子AC的长;（2）若李华在两路灯之间行走,则他前后的两个影子的长度之和（DA+AC）是否是定值请解释来由;（3）若李华在点A朝着影子（如图箭头）的偏向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2．27．如图①,分离以直角三角形ABC三边为直径向外作三个半圆,其面积分离用S1,S2,S3暗示,则不难证实S1=S2+S3．（1）如图②,分离以直角三角形ABC三边为边向外作三个正方形,其面积分离用S1,S2,S3暗示,那么S1,S2,S3之间有什么关系;（不必证实）（2）如图③,分离以直角三角形ABC三边为边向外作三个正三角形,其面积分离用S1.S2.S3暗示,请你肯定S1,S2,S3之间的关系并加以证实;（3）若分离以直角三角形ABC三边为边向外作三个一般三角形,其面积分离用S1,S2,S3暗示,为使S1,S2,S3之间仍具有与（2）雷同的关系,所作三角形应知足什么前提证实你的结论;（4）类比（1）,（2）,（3）的结论,请你总结出一个更具一般意义的结论．28．已知：如图,△ABC∽△ADE,AB=15,AC=9,BD=5．求AE．29．已知：如图Rt△ABC∽Rt△BDC,若AB=3,AC=4．（1）求BD.CD的长;（2）过B作BE⊥DC于E,求BE的长．30．（1）已知,且3x+4z﹣2y=40,求x,y,z的值;（2）已知：两类似三角形对应高的比为3：10,且这两个三角形的周长差为560cm,求它们的周长．参考答案与试题解析一．解答题（共30小题）1．如图,在△ABC中,DE∥BC,EF∥AB,求证：△ADE∽△EFC．考点：类似三角形的剖断;平行线的性质.菁优网版权所有专题：证实题.剖析：依据平行线的性质可知∠AED=∠C,∠A=∠FEC,依据类似三角形的剖断定理可知△ADE∽△EFC．解答：证实：∵DE∥BC,∴DE∥FC,∴∠AED=∠C．又∵EF∥AB,∴EF∥AD,∴∠A=∠FEC．∴△ADE∽△EFC．点评：本题考核的是平行线的性质及类似三角形的剖断定理．2．如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延伸线交于点G．（1）求证：△CDF∽△BGF;（2）当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长．考点：类似三角形的剖断;三角形中位线定理;梯形.菁优网版权所有专题：几何分解题.剖析：（1）应用平行线的性质可证实△CDF∽△BGF．（2）依据点F是BC的中点这一已知前提,可得△CDF≌△BGF,则CD=BG,只请求出BG的长即可解题．解答：（1）证实：∵梯形ABCD,AB∥CD,∴∠CDF=∠FGB,∠DCF=∠GBF,（2分）∴△CDF∽△BGF．（3分）（2）解：由（1）△CDF∽△BGF,又F是BC的中点,BF=FC,∴△CDF≌△BGF,∴DF=GF,CD=BG,（6分）∵AB∥DC∥EF,F为BC中点,∴E为AD中点,∴EF是△DAG的中位线,∴2EF=AG=AB+BG．∴BG=2EF﹣AB=2×4﹣6=2,∴CD=BG=2cm．（8分）点评：本题重要考核了类似三角形的剖断定理及性质,全等三角形的剖断及线段的等量代换,比较庞杂．3．如图,点D,E在BC上,且FD∥AB,FE∥AC．求证：△ABC∽△FDE．考点：类似三角形的剖断.菁优网版权所有专题：证实题.剖析：由FD∥AB,FE∥AC,可知∠B=∠FDE,∠C=∠FED,依据三角形类似的剖断定理可知：△ABC∽△FDE．解答：证实：∵FD∥AB,FE∥AC,∴∠B=∠FDE,∠C=∠FED,∴△ABC∽△FDE．点评：本题很简略,考核的是类似三角形的剖断定理：（1）假如两个三角形的两个角对应相等,那么这两个三角形类似;（2）假如一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形类似;（3）假如一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形类似．4．如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试解释：△ABF∽△EAD．考点：类似三角形的剖断;矩形的性质.菁优网版权所有专题：证实题.剖析：依据两角对应相等的两个三角形类似可解．解答：证实：∵矩形ABCD中,AB∥CD,∠D=90°,（2分）∴∠BAF=∠AED．（4分）∵BF⊥AE,∴∠AFB=90°．∴∠AFB=∠D．（5分）∴△ABF∽△EAD．（6分）点评：考核类似三角形的剖断定理,症结是找准对应的角．5．已知：如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,衔接BE,CD,M,N分离为BE,CD的中点．（1）求证：①BE=CD;②△AMN是等腰三角形;（2）在图①的基本上,将△ADE绕点A按顺时针偏向扭转180°,其他前提不变,得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立;（3）在（2）的前提下,请你在图②中延伸ED交线段BC于点P．求证：△PBD∽△AMN．考点：类似三角形的剖断;全等三角形的剖断;等腰三角形的剖断;扭转的性质.菁优网版权所有专题：几何分解题.剖析：（1）因为∠BAC=∠DAE,所以∠BAE=∠CAD,又因为AB=AC,AD=AE,应用SAS可证出△BAE≌△CAD,可知BE.CD是对应边,依据全等三角形对应边上的中线相等,可证△AMN是等腰三角形．（2）应用（1）中的证实办法仍然可以得出（1）中的结论,思绪不变．（3）先证出△ABM≌△ACN（SAS）,可得出∠CAN=∠BAM,所以∠BAC=∠MAN（等角加等角和相等）,又∵∠BAC=∠DAE,所以∠MAN=∠DAE=∠BAC,所以△AMN,△ADE和△ABC都是顶角相等的等腰三角形,所以∠PBD=∠AMN,所以△PBD∽△AMN（两个角对应相等,两三角形类似）．6．如图,E是▱ABCD的边BA延伸线上一点,衔接EC,交AD于点F．在不添加帮助线的情形下,请你写出图中所有的类似三角形,并任选一对类似三角形赐与证实．考点：类似三角形的剖断;平行四边形的性质.菁优网版权所有专题：凋谢型.剖析：依据平行线的性质和两角对应相等的两个三角形类似这一剖断定理可证实图中类似三角形有：△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF．解答：解：类似三角形有△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF．（3分）如：△AEF∽△BEC．在▱ABCD中,AD∥BC,∴∠1=∠B,∠2=∠3．（6分）∴△AEF∽△BEC．（7分）点评：考核了平行线的性质及类似三角形的剖断定理．7．如图,在4×3的正方形方格中,△ABC和△DEF的极点都在边长为1的小正方形的极点上．（1）填空：∠ABC=135°°,BC=;（2）断定△ABC与△DEC是否类似,并证实你的结论．考点：类似三角形的剖断;正方形的性质.菁优网版权所有专题：证实题;网格型.剖析：（1）不雅察可得：BF=FC=2,故∠FBC=45°;则∠ABC=135°,BC==2;（2）不雅察可得：BC.EC的长为2.,可得,再依据其夹角相等;故△ABC∽△DEC．解答：解：（1）∠ABC=135°,BC=;（2）类似;∵BC=,EC==;∴,;∴;又∠ABC=∠CED=135°,∴△ABC∽△DEC．点评：解答本题要充分应用正方形的特别性质．留意在正方形中的特别三角形的应用,搞清晰矩形.菱形.正方形中的三角形的三边关系,可有助于进步解题速度和精确率．8．如图,已知矩形ABCD的边长AB=3cm,BC=6cm．某一时刻,动点M从A点动身沿AB偏向以1cm/s的速度向B点匀速活动;同时,动点N从D点动身沿DA偏向以2cm/s的速度向A点匀速活动,问：（1）经由若干时光,△AMN的面积等于矩形ABCD面积的？（2）是否消失时刻t,使以A,M,N为极点的三角形与△ACD类似？若消失,求t的值;若不消失,请解释来由．考点：类似三角形的剖断;一元二次方程的应用;分式方程的应用;正方形的性质.菁优网版权所有专题：动点型.剖析：（1）关于动点问题,可设时光为x,依据速度暗示出所涉及到的线段的长度,找到相等关系,列方程求解即可,如本题中应用,△AMN的面积等于矩形ABCD面积的作为相等关系;（2）先假设类似,应用类似中的比例线段列出方程,有解的且相符题意的t值即可解释消失,反之则不消失．解答：解：（1）设经由x秒后,△AMN的面积等于矩形ABCD面积的,则有：（6﹣2x）x=×3×6,即x2﹣3x+2=0,（2分）解方程,得x1=1,x2=2,（3分）经磨练,可知x1=1,x2=2相符题意,所以经由1秒或2秒后,△AMN的面积等于矩形ABCD面积的．（4分）（2）假设经由t秒时,以A,M,N为极点的三角形与△ACD类似,由矩形ABCD,可得∠CDA=∠MAN=90°,是以有或（5分）即①,或②（6分）解①,得t=;解②,得t=（7分）经磨练,t=或t=都相符题意,所以动点M,N同时动身后,经由秒或秒时,以A,M,N为极点的三角形与△ACD类似．（8分）点评：重要考核了类似三角形的剖断,正方形的性质和一元二次方程的应用以及解分式方程．要控制正方形和类似三角形的性质,才会灵巧的应用．留意：一般关于动点问题,可设时光为x,依据速度暗示出所涉及到的线段的长度,找到相等关系,列方程求解即可．9．如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD.AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情形,并求出拔取到的两个三角形是类似三角形的概率是若干;（留意：全等算作类似的特例）（2）请你任选一组类似三角形,并给出证实．考点：类似三角形的剖断;概率公式.菁优网版权所有专题：凋谢型.剖析：（1）采取列举法,列举出所有可能消失的情形,再找出类似三角形即可求得;①与③,②与④类似;（2）应用类似三角形的剖断定理即可证得．解答：解：（1）任选两个三角形的所有可能情形如下六种情形：①②,①③,①④,②③,②④,③④（2分）个中有两组（①③,②④）是类似的．∴拔取到的二个三角形是类似三角形的概率是P=（4分）证实：（2）选择①.③证实．在△AOB与△COD中,∵AB∥CD,∴∠CDB=∠DBA,∠DCA=∠CAB,∴△AOB∽△COD（8分）选择②.④证实．∵四边形ABCD是等腰梯形,∴∠DAB=∠CBA,∴在△DAB与△CBA中有AD=BC,∠DAB=∠CAB,AB=AB,∴△DAB≌△CBA,（6分）∴∠ADO=∠BCO．又∠DOA=∠COB,∴△DOA∽△COB（8分）．点评：此题考核概率的求法：假如一个事宜有n种可能,并且这些事宜的可能性雷同,个中事宜A消失m种成果,那么事宜A的概率P（A）=,即类似三角形的证实．还考核了类似三角形的剖断．10．附加题：如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,衔接AE．（1）写出图中所有相等的线段,并加以证实;（2）图中有无类似三角形？如有,请写出一对;若没有,请解释来由;（3）求△BEC与△BEA的面积之比．考点：类似三角形的剖断;三角形的面积;含30度角的直角三角形.菁优网版权所有专题：分解题.剖析：（1）依据直角三角形中30度角所对的直角边是斜边的一半,可知CD=2ED,则可写出相等的线段;（2）两角对应相等的两个三角形类似则可断定△ADE∽△AEC;（3）请求△BEC与△BEA的面积之比,从图中可看出两三角形有一公共边可作为底边,若求得高之比可知面积之比,由此需作△BEA的边BE边上的高即可求解．解答：解：（1）AD=DE,AE=CE．∵CE⊥BD,∠BDC=60°,∴在Rt△CED中,∠ECD=30°．∴CD=2ED．∵CD=2DA,∴AD=DE,∴∠DAE=∠DEA=30°=∠ECD．∴AE=CE．（2）图中有三角形类似,△ADE∽△AEC;∵∠CAE=∠CAE,∠ADE=∠AEC,∴△ADE∽△AEC;（3）作AF⊥BD的延伸线于F,设AD=DE=x,在Rt△CED中,可得CE=,故AE=．∠ECD=30°．在Rt△AEF中,AE=,∠AED=∠DAE=30°,∴sin∠AEF=,∴AF=AE•sin∠AEF=．∴．点评：本题重要考核了直角三角形的性质,类似三角形的剖断及三角形面积的求法等,规模较广．11．如图,在△ABC中,AB=AC=a,M为底边BC上的随意率性一点,过点M分离作AB.AC的平行线交AC于P,交AB于Q．（1）求四边形AQMP的周长;（2）写出图中的两对类似三角形（不需证实）;（3）M位于BC的什么地位时,四边形AQMP为菱形并证实你的结论．考点：类似三角形的剖断;菱形的剖断.菁优网版权所有专题：分解题.剖析：（1）依据平行四边形的性质可得到对应角相等对应边相等,从而不难求得其周长;（2）因为∠B=∠C=∠PMC=∠QMB,所以△PMC∽△QMB∽△ABC;（3）依据中位线的性质及菱形的剖断不难求得四边形AQMP为菱形．解答：解：（1）∵AB∥MP,QM∥AC,∴四边形APMQ是平行四边形,∠B=∠PMC,∠C=∠QMB．∵AB=AC,∴∠B=∠C,∴∠PMC=∠QMB．∴BQ=QM,PM=PC．∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a．（2）∵PM∥AB,∴△PCM∽△ACB,∵QM∥AC,∴△BMQ∽△BCA;（3）当点M中BC的中点时,四边形APMQ是菱形,∵点M是BC的中点,AB∥MP,QM∥AC,∴QM,PM是三角形ABC的中位线．∵AB=AC,∴QM=PM=AB=AC．又由（1）知四边形APMQ是平行四边形,∴平行四边形APMQ是菱形．点评：此题重要考核了平行四边形的剖断和性质,中位线的性质,菱形的剖断等常识点的分解应用．12．已知：P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试解释：△ADM∽△MCP．考点：类似三角形的剖断;正方形的性质.菁优网版权所有专题：证实题.剖析：欲证△ADM∽△MCP,经由过程不雅察发明两个三角形已经具备一组角对应相等,即∠D=∠C,此时,再求夹此对应角的双方对应成比例即可．解答：证实：∵正方形ABCD,M为CD中点,∴CM=MD=AD．∵BP=3PC,∴PC=BC=AD=CM．∴．∵∠PCM=∠ADM=90°,∴△MCP∽△ADM．点评：本题考核类似三角形的剖断．辨认两三角形类似,除了要控制界说外,还要留意精确找出两三角形的对应边.对应角,可应用数形联合思惟依据图形供给的数据盘算对应角的度数.对应边的比．本题中把若干线段的长度用统一线段来暗示是求线段是否成比例时经常应用的办法．13．如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10．（1）求梯形ABCD的面积S;（2）动点P从点B动身,以1cm/s的速度,沿B⇒A⇒D⇒C偏向,向点C活动;动点Q从点C动身,以1cm/s的速度,沿C⇒D⇒A偏向,向点A活动,过点Q作QE⊥BC于点E．若P.Q两点同时动身,当个中一点到达目标地时全部活动随之停止,设活动时光为t秒．问：①当点P在B⇒A上活动时,是否消失如许的t,使得直线PQ将梯形ABCD的周长等分？若消失,请求出t的值;若不消失,请解释来由;②在活动进程中,是否消失如许的t,使得以P.A.D为极点的三角形与△CQE类似？若消失,请求出所有相符前提的t的值;若不消失,请解释来由;③在活动进程中,是否消失如许的t,使得以P.D.Q为极点的三角形正好是以DQ为一腰的等腰三角形？若消失,请求出所有相符前提的t的值;若不消失,请解释来由．考点：类似三角形的剖断;三角形三边关系;等腰三角形的剖断;勾股定理;直角梯形.菁优网版权所有专题：动点型;凋谢型.剖析：（1）求面积要先求梯形的高,可依据两底的差和CD的长,在直角三角形顶用勾股定理进行求解,得出高后即可求出梯形的面积．（2）①PQ等分梯形的周长,那么AD+DQ+AP=BC+CQ+BP,已知了AD,BC的长,可以用t来暗示出AP,BP,CQ,QD的长,那么可依据上面的等量关系求出t的值．②本题要分三种情形进行评论辩论：一,当P在AB上时,即0＜t≤8,假如两三角形类似,那么∠C=∠ADP,或∠C=∠APD,那么在△ADP中依据∠C的正切值,求出t的值．二,当P在AD上时,即8＜t≤10,因为P,A,D在一条直线上,是以构不成三角形．三,当P在CD上时,即10＜t≤12,因为∠ADC是个钝角,是以△ADP是个钝角三角形是以不成能和直角△CQE类似．分解三种情形即可得出相符前提的t的值．（3）和（2）雷同也要分三种情形进行评论辩论：一,当P在AB上时,即0＜t≤8,等腰△PDQ以DQ为腰,是以DQ=DP或DQ=PQ,可以经由过程构建直角三角形来暗示出DP,PQ的长,然后依据得出的等量关系来求t的值．二,当P在AD上时,即8＜t≤10,因为BA+AD=CD=10,是以DP=DQ=10﹣t,是以DP,DQ恒相等．三,当P在CD上时,即10＜t≤12,情形同二．分解三种情形可得出等腰三角形以DQ为腰时,t的取值．点评：本题重要考核了梯形的性质以及类似三角形的剖断和性质等常识点,要留意（2）中要依据P,Q的不合地位,进行分类评论辩论,不要漏解．14．已知矩形ABCD,长BC=12cm,宽AB=8cm,P.Q分离是AB.BC上活动的两点．若P自点A动身,以1cm/s 的速度沿AB偏向活动,同时,Q自点B动身以2cm/s的速度沿BC偏向活动,问经由几秒,以P.B.Q为极点的三角形与△BDC类似？考点：类似三角形的剖断;矩形的性质.菁优网版权所有专题：几何动点问题;分类评论辩论.剖析：要使以P.B.Q为极点的三角形与△BDC类似,则要分两两种情形进行剖析．分离是△PBQ∽△BDC或△QBP∽△BDC,从而解得所需的时光．解答：解：设经x秒后,△PBQ∽△BCD,因为∠PBQ=∠BCD=90°,（1）当∠1=∠2时,有：,即;（2）当∠1=∠3时,有：,即,∴经由秒或2秒,△PBQ∽△BCD．点评：此题考核了类似三角形的剖断及矩形的性质等常识点的分解应用．15．如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开端沿AB边向B点以2cm/s的速度移动,点Q从点B 开端沿BC边向点C以4cm/s的速度移动,假如P.Q分离从A.B同时动身,问经由几秒钟,△PBQ与△ABC类似．考点：类似三角形的剖断;一元一次方程的应用.菁优网版权所有专题：动点型.剖析：设经由t秒后,△PBQ与△ABC类似,依据旅程公式可得AP=2t,BQ=4t,BP=10﹣2t,然后应用类似三角形的性质对应边的比相等列出方程求解即可．解答：解：设经由秒后t秒后,△PBQ与△ABC类似,则有AP=2t,BQ=4t,BP=10﹣2t,当△PBQ∽△ABC时,有BP：AB=BQ：BC,即（10﹣2t）：10=4t：20,解得t=2.5（s）（6分）当△QBP∽△ABC时,有BQ：AB=BP：BC,即4t：10=（10﹣2t）：20,解得t=1．所以,经由2.5s或1s时,△PBQ与△ABC类似（10分）．解法二：设ts后,△PBQ与△ABC类似,则有,AP=2t,BQ=4t,BP=10﹣2t分两种情形：（1）当BP与AB对应时,有=,即=（2）当BP与BC对应时,有=,即=,解得t=1s所以经由1s或2.5s时,以P.B.Q三点为极点的三角形与△ABC类似．点评：本题分解了旅程问题和三角形的问题,所以学生日常平凡学过的常识要会融会起来．16．如图,∠ACB=∠ADC=90°,AC=,AD=2．问当AB的长为若干时,这两个直角三角形类似．考点：类似三角形的剖断.菁优网版权所有专题：分类评论辩论.剖析：假如一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形类似．在Rt△ABC和Rt△ACD,直角边的对应需分情形评论辩论．解答：解：∵AC=,AD=2,∴CD==．要使这两个直角三角形类似,有两种情形：（1）当Rt△ABC∽Rt△ACD时,有=,∴AB==3;（2）当Rt△ACB∽Rt△CDA时,有=,∴AB==3．故当AB的长为3或3时,这两个直角三角形类似．点评：本题考核类似三角形的剖断．辨认两三角形类似,除了要控制界说外,还要留意精确找出两三角形的对应边.对应角,可应用数形联合思惟依据图形供给的数据盘算对应角的度数.对应边的比．17．已知,如图,在边长为a的正方形ABCD中,M是AD的中点,可否在边AB上找一点N（不含A.B）,使得△CDM 与△MAN类似？若能,请给出证实,若不克不及,请解释来由．考点：类似三角形的剖断;正方形的性质.菁优网版权所有专题：探讨型;分类评论辩论.剖析：两个三角形都是直角三角形,还只需知足一对角对应相等或夹直角的双方对应成比例即可解释两个三角形类似．若DM与AM对应,则△CDM与△MAN全等,N与B重合,不合题意;若DM与AN对应,则CD：AM=DM：AN,得AN=a,从而肯定N的地位．解答：证实：分两种情形评论辩论：①若△CDM∽△MAN,则=．∵边长为a,M是AD的中点,∴AN=a．②若△CDM∽△NAM,则．∵边长为a,M是AD的中点,∴AN=a,即N点与B重合,不合题意．所以,能在边AB上找一点N（不含A.B）,使得△CDM与△MAN类似．当AN=a时,N点的地位知足前提．点评：此题考核类似三角形的剖断．因不明白对应关系,所以需分类评论辩论．18．如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B动身,沿BC偏向以2cm/s的速度移动,点P从C动身,沿CA偏向以1cm/s的速度移动．若Q.P分离同时从B.C动身,试探讨经由若干秒后,以点C.P.Q为极点的三角形与△CBA类似？考点：类似三角形的剖断.菁优网版权所有专题：分解题;动点型.。

相似三角形经典题(含答案)

相似三角形经典习题例1 从下面这些三角形中，选出相似的三角形．例2 已知：如图，ABCD 中，2:1:=EB AE ，求AEF ∆与CDF ∆的周长的比，如果2cm 6=∆AEF S ，求CDF S ∆．例3 如图，已知ABD ∆∽ACE ∆，求证：ABC ∆∽ADE ∆．例4 下列命题中哪些是正确的，哪些是错误的？（1）所有的直角三角形都相似．（2）所有的等腰三角形都相似．（3）所有的等腰直角三角形都相似．（4）所有的等边三角形都相似．例5 如图，D 点是ABC ∆的边AC 上的一点，过D 点画线段DE ，使点E 在ABC ∆的边上，并且点D 、点E 和ABC ∆的一个顶点组成的小三角形与ABC ∆相似．尽可能多地画出满足条件的图形，并说明线段DE 的画法．例6 如图，一人拿着一支刻有厘米分画的小尺，站在距电线杆约30米的地方，把手臂向前伸直，小尺竖直，看到尺上约12个分画恰好遮住电线杆，已知手臂长约60厘米，求电线杆的高．例7 如图，小明为了测量一高楼MN 的高，在离N 点20m 的A 处放了一个平面镜，小明沿NA 后退到C 点，正好从镜中看到楼顶M 点，若5.1=AC m ，小明的眼睛离地面的高度为1.6m ，请你帮助小明计算一下楼房的高度（精确到0.1m ）．例8 格点图中的两个三角形是否是相似三角形，说明理由．例9 根据下列各组条件，判定ABC ∆和C B A '''∆是否相似，并说明理由：（1）,cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A ．（2）︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A ．（3）︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB ．例10 如图，下列每个图形中，存不存在相似的三角形，如果存在，把它们用字母表示出来，并简要说明识别的根据．例11 已知：如图，在ABC ∆中，BD A AC AB ,36,︒=∠=是角平分线，试利用三角形相似的关系说明AC DC AD ⋅=2．例12 已知ABC ∆的三边长分别为5、12、13，与其相似的C B A '''∆的最大边长为26，求C B A '''∆的面积S ．例13 在一次数学活动课上，老师让同学们到操场上测量旗杆的高度，然后回来交流各自的测量方法．小芳的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C 处（如图），然后沿BC 方向走到D 处，这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上，又测得C 、D 两点的距离为3米，小芳的目高为1.5米，这样便可知道旗杆的高．你认为这种测量方法是否可行？请说明理由．例14．如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A ，再在河的这一边选点B 和C ，使BC AB ⊥，然后再选点E ，使BC EC ⊥，确定BC 与AE 的交点为D ，测得120=BD 米，60=DC 米，50=EC 米，你能求出两岸之间AB 的大致距离吗？例15．如图，为了求出海岛上的山峰AB 的高度，在D 和F 处树立标杆DC 和FE ，标杆的高都是3丈，相隔1000步（1步等于5尺），并且AB 、CD 和EF 在同一平面内，从标杆DC 退后123步的G 处，可看到山峰A 和标杆顶端C 在一直线上，从标杆FE 退后127步的H 处，可看到山峰A 和标杆顶端E 在一直线上．求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少？（古代问题）例16 如图，已知△ABC 的边AB ＝32，AC ＝2，BC 边上的高AD ＝3．（1）求BC 的长；（2）如果有一个正方形的边在AB 上，另外两个顶点分别在AC ，BC 上，求这个正方形的面积．相似三角形经典习题答案例1．解 ①、⑤、⑥相似，②、⑦相似，③、④、⑧相似例2．解 ABCD Θ是平行四边形，∴CD AB CD AB =,//，∴AEF ∆∽CDF ∆，又2:1:=EB AE ，∴3:1:=CD AE ，∴AEF ∆与CDF ∆的周长的比是1：3．又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ，∴)cm (542=∆CDF S ．例3 分析由于ABD ∆∽ACE ∆，则CAE BAD ∠=∠，因此DAE BAC ∠=∠，如果再进一步证明AECAAD BA =，则问题得证．证明 ∵ABD ∆∽ACE ∆，∴CAE BAD ∠=∠．又DAC BAD BAC ∠+∠=∠Θ，∴CAE DAC DAE ∠+∠=∠， ∴DAE BAC ∠=∠． ∵ABD ∆∽ACE ∆，∴AEACAD AB =．在ABC ∆和ADE ∆中，∵AEACAD AB ADE BAC =∠=∠,，∴ABC ∆∽ADE ∆ 例4．分析（1）不正确，因为在直角三角形中，两个锐角的大小不确定，因此直角三角形的形状不同．（2）也不正确，等腰三角形的顶角大小不确定，因此等腰三角形的形状也不同．（3）正确．设有等腰直角三角形ABC 和C B A '''，其中︒='∠=∠90C C ，则︒='∠=∠︒='∠=∠45,45B B A A ，设ABC ∆的三边为a 、b 、c ，C B A '''∆的边为c b a '''、、，则a c b a a c b a '=''='==2,,2,，∴a ac c b b a a '=''=',，∴ABC ∆∽C B A '''∆．（4）也正确，如ABC ∆与C B A '''∆都是等边三角形，对应角相等，对应边都成比例，因此ABC ∆∽C B A '''∆．答：（1）、（2）不正确．（3）、（4）正确．例5．解：画法略．例6．分析本题所叙述的内容可以画出如下图那样的几何图形，即60=DF 厘米6.0=米，12=GF 厘米12.0=米，30=CE 米，求BC ．由于ADF ∆∽ACAF EC DF AEC =∆,，又ACF ∆∽ABC ∆，∴BC GFEC DF =，从而可以求出BC 的长．解 EC DF EC AE //,⊥Θ，∴EAC DAF AEC ADF ∠=∠∠=∠,，∴ADF ∆∽AEC ∆．∴ACAFEC DF =．又EC BC EC GF ⊥⊥,，∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//， ∴AGF ∆∽ABC ∆，∴BC GF AC AF =，∴BCGFEC DF =．又60=DF 厘米6.0=米，12=GF 厘米12.0=米，30=EC 米，∴6=BC 米．即电线杆的高为6米．例7．分析根据物理学定律：光线的入射角等于反射角，这样，BCA ∆与MNA ∆的相似关系就明确了．解因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,，所以BCA ∆∽MNA ∆．所以AC AN BC MN ::=，即5.1:206.1:=MN ．所以3.215.1206.1≈÷⨯=MN （m ）．说明这是一个实际应用问题，方法看似简单，其实很巧妙，省却了使用仪器测量的麻烦．例8．分析这两个图如果不是画在格点中，那是无法判断的．实际上格点无形中给图形增添了条件——长度和角度．解在格点中BC AB EF DE ⊥⊥,，所以︒=∠=∠90B E ，又4,2,2,1====AB BC DE EF ．所以21==BC EF AB DE ．所以DEF ∆∽ABC ∆．说明遇到格点的题目一定要充分发现其中的各种条件，勿使遗漏．例9．解（1）因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ，所以ABC ∆∽C B A '''∆；（2）因为︒=∠-∠-︒=∠41180B A C ，两个三角形中只有A A '∠=∠，另外两个角都不相等，所以ABC ∆与C B A '''∆不相似；（3）因为12,=''='''∠=∠C B BC B A AB B B ，所以ABC ∆相似于C B A '''∆．例10．解（1）ADE ∆∽ABC ∆ 两角相等；（2）ADE ∆∽ACB ∆ 两角相等；（3）CDE ∆∽CAB ∆ 两角相等；（4）EAB ∆∽ECD ∆ 两边成比例夹角相等；（5）ABD ∆∽ACB ∆ 两边成比例夹角相等；（6）ABD ∆∽ACB ∆ 两边成比例夹角相等．例11．分析有一个角是65°的等腰三角形，它的底角是72°，而BD 是底角的平分线，∴︒=∠36CBD ，则可推出ABC ∆∽BCD ∆，进而由相似三角形对应边成比例推出线段之间的比例关系．证明 AC AB A =︒=∠,36Θ，∴︒=∠=∠72C ABC ．又BD Θ平分ABC ∠，∴︒=∠=∠36CBD ABD ．∴BC BD AD ==，且ABC ∆∽BCD ∆，∴BC CD AB BC ::=，∴CD AB BC ⋅=2，∴CD AC AD ⋅=2．说明（1）有两个角对应相等，那么这两个三角形相似，这是判断两个三角形相似最常用的方法，并且根据相等的角的位置，可以确定哪些边是对应边．（2）要说明线段的乘积式cd ab =，或平方式bc a =2，一般都是证明比例式，b dc a =，或caa b =，再根据比例的基本性质推出乘积式或平方式．例12分析由ABC ∆的三边长可以判断出ABC ∆为直角三角形，又因为ABC ∆∽C B A '''∆，所以C B A '''∆也是直角三角形，那么由C B A '''∆的最大边长为26，可以求出相似比，从而求出C B A '''∆的两条直角边长，再求得C B A '''∆的面积．解设ABC ∆的三边依次为，13,12,5===AB AC BC ，则222AC BC AB +=Θ，∴︒=∠90C ．又∵ABC ∆∽C B A '''∆，∴︒=∠='∠90C C ．212613==''=''=''B A AB C A AC C B BC ，又12,5==AC BC ，∴24,10=''=''C A C B ． ∴12010242121=⨯⨯=''⨯''=C B C A S ．例13．分析判断方法是否可行，应考虑利用这种方法加之我们现有的知识能否求出旗杆的高．按这种测量方法，过F作AB FG ⊥于G ，交CE 于H ，可知AGF ∆∽EHF ∆，且GF 、HF 、EH 可求，这样可求得AG ，故旗杆AB 可求．解这种测量方法可行．理由如下：设旗杆高x AB =．过F 作AB FG ⊥于G ，交CE 于H （如图）．所以AGF ∆∽EHF ∆．因为3,30327,5.1==+==HF GF FD ，所以5.1,25.15.3-==-=x AG EH ．由AGF ∆∽EHF ∆，得HF GF EH AG =，即33025.1=-x ，所以205.1=-x ，解得5.21=x （米）所以旗杆的高为21.5米．说明在具体测量时，方法要现实、切实可行．例14. 解：︒=∠=∠∠=∠90,ECD ABC EDC ADB Θ，∴ABD ∆∽ECD ∆，1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB （米），答：两岸间AB 大致相距100米．例15. 答案：1506=AB 米，30750=BD 步，（注意：AK FEFHKE AK CD DG KC ⋅=⋅=,．）例16. 分析：要求BC 的长，需画图来解，因AB 、AC 都大于高AD ，那么有两种情况存在，即点D 在BC 上或点D 在BC 的延长线上，所以求BC 的长时要分两种情况讨论．求正方形的面积，关键是求正方形的边长．解：（1）如上图，由AD ⊥BC ，由勾股定理得BD ＝3，DC ＝1，所以BC ＝BD ＋DC ＝3＋1＝4．如下图，同理可求BD ＝3，DC ＝1，所以BC ＝BD －CD ＝3－1＝2．（2）如下图，由题目中的图知BC ＝4，且162)32(2222=+=+AC AB ，162=BC ，∴222BC AC AB =+．所以△ABC 是直角三角形．由AE G F 是正方形，设G F ＝x ，则FC ＝2－x ， ∵G F ∥AB ，∴AC FCAB GF =，即2232x x -=． ∴33-=x ，∴3612)33(2-=-=AEGF S 正方形．如下图，当BC ＝2，AC ＝2，△ABC 是等腰三角形，作CP ⊥AB 于P ，∴AP ＝321=AB ，在Rt △APC 中，由勾股定理得CP ＝1， ∵GH ∥AB ，∴△C GH ∽△CBA ，∵x x x -=132，32132+=x ∴121348156)32132(2-=+=GFEH S 正方形因此，正方形的面积为3612-或121348156-．。

相似三角形经典题(含答案)

相似三角形经典题(含答案)相似三角形经典习题例1 从下面这些三角形中，选出相似的三角形．例2 已知：如图，ABCD 中，2:1:=EB AE ，求AEF ∆与CDF ∆的周长的比，如果2cm 6=∆AEFS，求CDFS∆．例3 如图，已知ABD ∆∽ACE ∆，求证：ABC ∆∽ADE ∆．例4 下列命题中哪些是正确的，哪些是错误的？（1）所有的直角三角形都相似．（2）所有的等腰三角形都相似．（3）所有的等腰直角三角形都相似．（4）所有的等边三角形都相似．例5 如图，D点是ABC∆的边AC上的一点，过D点画线段DE，使点E在ABC∆的一个顶点组成∆的边上，并且点D、点E和ABC的小三角形与ABC∆相似．尽可能多地画出满足条件的图形，并说明线段DE的画法．例6 如图，一人拿着一支刻有厘米分画的小尺，站在距电线杆约30米的地方，把手臂向前伸直，小尺竖直，看到尺上约12个分画恰好遮住电线杆，已知手臂长约60厘米，求电线杆的高．例7 如图，小明为了测量一高楼MN 的高，在离N 点20m 的A 处放了一个平面镜，小明沿NA 后退到C 点，正好从镜中看到楼顶M 点，若5.1=AC m ，小明的眼睛离地面的高度为1.6m ，请你帮助小明计算一下楼房的高度（精确到0.1m ）．例8 格点图中的两个三角形是否是相似三角形，说明理由．例9 根据下列各组条件，判定ABC ∆和C B A '''∆是否相似，并说明理由：（1）,cm 4,cm 5.2,cm 5.3===CA BC AB cm28,cm 5.17,cm 5.24=''=''=''A C C B B A ．（2）︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A ．（3）︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB ．例10 如图，下列每个图形中，存不存在相似的三角形，如果存在，把它们用字母表示出来，并简要说明识别的根据．例11 已知：如图，在ABC ∆中，BD A AC AB ,36,︒=∠=是角平分线，试利用三角形相似的关系说明ACDC AD ⋅=2．例12 已知ABC ∆的三边长分别为5、12、13，与其相似的C B A '''∆的最大边长为26，求C B A '''∆的面积S ．例13 在一次数学活动课上，老师让同学们到操场上测量旗杆的高度，然后回来交流各自的测量方法．小芳的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处（如图），然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E 恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，这样便可知道旗杆的高．你认为这种测量方法是否可行？请说明理由．例14．如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A，再在河的这一边选点B和C，使BCAB⊥，然后再选点E，使BCBD米，=EC⊥，确定BC与AE的交点为D，测得120 EC米，你能求出两岸之间AB的大致距离吗？=60DC米，50=例15．如图，为了求出海岛上的山峰AB的高度，在D和F 处树立标杆DC和FE，标杆的高都是3丈，相隔1000步（1步等于5尺），并且AB、CD和EF在同一平面内，从标杆DC 退后123步的G处，可看到山峰A和标杆顶端C在一直线上，从标杆FE退后127步的H处，可看到山峰A和标杆顶端E 在一直线上．求山峰的高度AB及它和标杆CD的水平距离BD 各是多少？（古代问题）例16 如图，已知△ABC的边AB＝32，AC＝2，BC边上的高AD＝3．（1）求BC的长；（2）如果有一个正方形的边在AB上，另外两个顶点分别在AC，BC上，求这个正方形的面积．相似三角形经典习题答案例1．解 ①、⑤、⑥相似，②、⑦相似，③、④、⑧相似例2．解 ABCD Θ是平行四边形，∴CD AB CD AB =,//，∴AEF ∆∽CDF ∆，又2:1:=EB AE ，∴3:1:=CD AE ，∴AEF ∆与CDF ∆的周长的比是1：3．又)cm (6,)31(22==∆∆∆AEF CDFAEF S SS，∴)cm (542=∆CDFS．例3 分析由于ABD ∆∽ACE ∆，则CAE BAD ∠=∠，因此DAE BAC ∠=∠，如果再进一步证明AECAAD BA =，则问题得证．证明 ∵ABD ∆∽ACE ∆，∴CAE BAD ∠=∠．又DAC BAD BAC ∠+∠=∠Θ，∴CAE DAC DAE ∠+∠=∠， ∴DAE BAC ∠=∠．∵ABD ∆∽ACE ∆，∴AEACAD AB =．在ABC ∆和ADE ∆中，∵AEACAD AB ADE BAC =∠=∠,，∴ABC ∆∽ADE ∆ 例4．分析（1）不正确，因为在直角三角形中，两个锐角的大小不确定，因此直角三角形的形状不同．（2）也不正确，等腰三角形的顶角大小不确定，因此等腰三角形的形状也不同．（3）正确．设有等腰直角三角形ABC 和C B A '''，其中︒='∠=∠90C C ，则︒='∠=∠︒='∠=∠45,45B B A A ，设ABC ∆的三边为a 、b 、c ，C B A '''∆的边为c b a '''、、，则a c b a a c b a '=''='==2,,2,，∴a ac c b b aa '=''=',，∴ABC ∆∽C B A '''∆．（4）也正确，如ABC ∆与C B A '''∆都是等边三角形，对应角相等，对应边都成比例，因此ABC ∆∽C B A '''∆．答：（1）、（2）不正确．（3）、（4）正确．例5．解：画法略．例6．分析本题所叙述的内容可以画出如下图那样的几何图形，即60=DF 厘米6.0=米，12=GF 厘米12.0=米，30=CE 米，求BC ．由于ADF ∆∽ACAF EC DF AEC =∆,，又ACF ∆∽ABC ∆，∴BC GF EC DF =，从而可以求出BC 的长．解ECDF EC AE //,⊥Θ，∴EAC DAF AEC ADF ∠=∠∠=∠,，∴ADF ∆∽AEC ∆．∴ACAFEC DF =．又EC BC EC GF ⊥⊥,，∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//，∴AGF ∆∽ABC ∆，∴BC GF AC AF =，∴BCGFEC DF =．又60=DF 厘米6.0=米，12=GF 厘米12.0=米，30=EC 米，∴6=BC 米．即电线杆的高为6米．例7．分析根据物理学定律：光线的入射角等于反射角，这样，BCA ∆与MNA ∆的相似关系就明确了．解因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,，所以BCA ∆∽MNA ∆．所以AC AN BC MN ::=，即5.1:206.1:=MN ．所以3.215.1206.1≈÷⨯=MN （m ）．说明这是一个实际应用问题，方法看似简单，其实很巧妙，省却了使用仪器测量的麻烦．例8．分析这两个图如果不是画在格点中，那是无法判断的．实际上格点无形中给图形增添了条件——长度和角度．解在格点中BC AB EF DE ⊥⊥,，所以︒=∠=∠90B E ，又4,2,2,1====AB BC DE EF ．所以21==BC EF AB DE ．所以DEF ∆∽ABC ∆．说明遇到格点的题目一定要充分发现其中的各种条件，勿使遗漏．例9．解（1）因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ，所以ABC ∆∽C B A '''∆；（2）因为︒=∠-∠-︒=∠41180B A C ，两个三角形中只有A A '∠=∠，另外两个角都不相等，所以ABC ∆与C B A '''∆不相似；（3）因为12,=''='''∠=∠C B BC B A AB B B ，所以ABC ∆相似于C B A '''∆．例10．解（1）ADE ∆∽ABC ∆ 两角相等；（2）ADE ∆∽ACB∆ 两角相等；（3）CDE ∆∽CAB ∆ 两角相等；（4）EAB ∆∽ECD ∆ 两边成比例夹角相等；（5）ABD ∆∽ACB ∆两边成比例夹角相等；（6）ABD ∆∽ACB ∆ 两边成比例夹角相等．例11．分析有一个角是65°的等腰三角形，它的底角是72°，而BD 是底角的平分线，∴︒=∠36CBD ，则可推出ABC ∆∽BCD ∆，进而由相似三角形对应边成比例推出线段之间的比例关系．证明 AC AB A =︒=∠,36Θ，∴︒=∠=∠72C ABC ．又BD Θ平分ABC ∠，∴︒=∠=∠36CBD ABD ．∴BC BD AD ==，且ABC ∆∽BCD ∆，∴BC CD AB BC ::=，∴CDAB BC⋅=2，∴CDAC AD⋅=2．说明（1）有两个角对应相等，那么这两个三角形相似，这是判断两个三角形相似最常用的方法，并且根据相等的角的位置，可以确定哪些边是对应边．（2）要说明线段的乘积式cd ab =，或平方式bca=2，一般都是证明比例式，b d c a =，或caa b =，再根据比例的基本性质推出乘积式或平方式．例12分析由ABC ∆的三边长可以判断出ABC ∆为直角三角形，又因为ABC ∆∽C B A '''∆，所以C B A '''∆也是直角三角形，那么由C B A '''∆的最大边长为26，可以求出相似比，从而求出C B A '''∆的两条直角边长，再求得C B A '''∆的面积．解设ABC ∆的三边依次为，13,12,5===AB AC BC ，则222AC BC AB +=Θ，∴︒=∠90C ．又∵ABC ∆∽C B A '''∆，∴︒=∠='∠90C C ．212613==''=''=''B A AB C A AC C B BC ，又12,5==AC BC ，∴24,10=''=''C A C B ． ∴12010242121=⨯⨯=''⨯''=C B C A S ．例13．分析判断方法是否可行，应考虑利用这种方法加之我们现有的知识能否求出旗杆的高．按这种测量方法，过F 作ABFG ⊥于G ，交CE 于H ，可知AGF ∆∽EHF ∆，且GF 、HF 、EH可求，这样可求得AG ，故旗杆AB 可求．解这种测量方法可行．理由如下：设旗杆高x AB =．过F 作AB FG ⊥于G ，交CE 于H （如图）．所以AGF ∆∽EHF ∆．因为3,30327,5.1==+==HF GF FD ，所以5.1,25.15.3-==-=x AG EH ．由AGF ∆∽EHF ∆，得HF GF EH AG =，即33025.1=-x ，所以205.1=-x ，解得5.21=x （米）所以旗杆的高为21.5米．说明在具体测量时，方法要现实、切实可行．例14. 解：︒=∠=∠∠=∠90,ECD ABC EDC ADB Θ，∴ABD ∆∽ECD ∆，1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB （米），答：两岸间AB 大致相距100米．例15. 答案：1506=AB 米，30750=BD 步，（注意：AK FEFHKE AK CD DG KC ⋅=⋅=,．）例16. 分析：要求BC 的长，需画图来解，因AB 、AC 都大于高AD ，那么有两种情况存在，即点D 在BC 上或点D 在BC 的延长线上，所以求BC 的长时要分两种情况讨论．求正方形的面积，关键是求正方形的边长．解：（1）如上图，由AD ⊥BC ，由勾股定理得BD ＝3，DC ＝1，所以BC ＝BD ＋DC ＝3＋1＝4．如下图，同理可求BD ＝3，DC ＝1，所以BC ＝BD －CD ＝3－1＝2．（2）如下图，由题目中的图知BC ＝4，且162)32(2222=+=+AC AB，162=BC ，∴222BC AC AB=+．所以△ABC 是直角三角形．由AE G F 是正方形，设G F ＝x ，则FC ＝2－x ， ∵G F ∥AB ，∴ACFCAB GF =，即2232x x -=． ∴33-=x ，∴3612)33(2-=-=AEGF S 正方形．如下图，当BC ＝2，AC ＝2，△ABC 是等腰三角形，作CP ⊥AB 于P ，∴AP ＝321=AB ，在Rt △APC 中，由勾股定理得CP ＝1，∵GH ∥AB ，∴△C GH ∽△CBA ，∵xxx -=132，32132+=x ∴121348156)32132(2-=+=GFEH S 正方形因此，正方形的面积为3612-或121348156-．。

相似三角形典型模型及例题

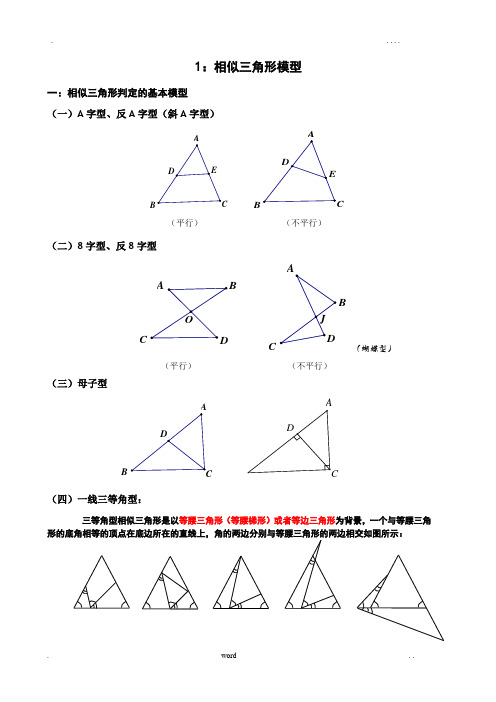
1：相似三角形模型一：相似三角形判定的基本模型（一）A字型、反A字型（斜A字型）B（平行）（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景，一个与等腰三角形的底角相等的顶点在底边所在的直线上，角的两边分别与等腰三角形的两边相交如图所示：（五）一线三直角型：三直角相似可以看着是“一线三等角”中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的基本图形如下：当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。

（六）双垂型：CAD二：相似三角形判定的变化模型旋转型：由A字型旋转得到8字型拓展CB EDA共享性一线三等角的变形GAB CE F一线三直角的变形2：相似三角形典型例题（1）母子型相似三角形例1：如图，梯形ABCD中，AD∥BC，对角线AC、BD交于点O，BE∥CD交CA延长线于E．求证：OEOAOC⋅=2．例2：已知：如图，△ABC中，点E在中线AD上, ABCDEB∠=∠．求证：（1）DADEDB⋅=2；（2）DACDCE∠=∠．例3：已知：如图，等腰△ABC中，AB＝AC，AD⊥BC于D，CG∥AB，BG分别交AD、AC于E、F．求证：EGEFBE⋅=2．1、如图，已知AD为△ABC的角平分线，EF为AD的垂直平分线．求证：FCFBFD⋅=2．A CDEB2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

初中数学经典相似三角形练习题附参考答案

经典练习题相似三角形（附答案）一．解答题（共30小题）1．如图，在△中，∥，∥，求证：△∽△．2．如图，梯形中，∥，点F在上，连与的延长线交于点G．（1）求证：△∽△；（2）当点F是的中点时，过F作∥交于点E，若6，4，求的长．3．如图，点D，E在上，且∥，∥．求证：△∽△．4．如图，已知E是矩形的边上一点，⊥于F，试说明：△∽△．5．已知：如图①所示，在△和△中，，，∠∠，且点B，A，D在一条直线上，连接，，M，N分别为，的中点．（1）求证：①；②△是等腰三角形；（2）在图①的基础上，将△绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长交线段于点P．求证：△∽△．6．如图，E是▱的边延长线上一点，连接，交于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．7．如图，在4×3的正方形方格中，△和△的顶点都在边长为1的小正方形的顶点上．（1）填空：∠°，；（2）判断△与△是否相似，并证明你的结论．8．如图，已知矩形的边长3，6．某一时刻，动点M从A点出发沿方向以1的速度向B点匀速运动；同时，动点N从D点出发沿方向以2的速度向A点匀速运动，问：（1）经过多少时间，△的面积等于矩形面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△相似？若存在，求t的值；若不存在，请说明理由．9．如图，在梯形中，若∥，，对角线、把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．10．如图△中，D为上一点，2，∠45°，∠60°，⊥于E，连接．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△与△的面积之比．11．如图，在△中，，M为底边上的任意一点，过点M分别作、的平行线交于P，交于Q．（1）求四边形的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于的什么位置时，四边形为菱形并证明你的结论．12．已知：P是正方形的边上的点，且3，M是的中点，试说明：△∽△．13．如图，已知梯形中，∥，2，8，10．（1）求梯形的面积S；（2）动点P从点B出发，以1的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1的速度，沿C⇒D⇒A方向，向点A运动，过点Q作⊥于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线将梯形的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．14．已知矩形，长12，宽8，P、Q分别是、上运动的两点．若P自点A 出发，以1的速度沿方向运动，同时，Q自点B出发以2的速度沿方向运动，问经过几秒，以P、B、Q为顶点的三角形与△相似？15．如图，在△中，10，20，点P从点A开始沿边向B点以2的速度移动，点Q从点B开始沿边向点C以4的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△与△相似．16．如图，∠∠90°，，2．问当的长为多少时，这两个直角三角形相似．17．已知，如图，在边长为a的正方形中，M是的中点，能否在边上找一点N（不含A、B），使得△与△相似？若能，请给出证明，若不能，请说明理由．18．如图在△中，∠90°，8，6，点Q从B出发，沿方向以2的速度移动，点P从C出发，沿方向以1的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△相似？19．如图所示，梯形中，∥，∠90°，7，2，3，试在腰上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．20．△和△是两个等腰直角三角形，∠∠90°，△的顶点E位于边的中点上．（1）如图1，设与交于点M，与交于点N，求证：△∽△；（2）如图2，将△绕点E旋转，使得与的延长线交于点M，与交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．21．如图，在矩形中，15，10，点P沿边从点A开始向B以2的速度移动；点Q沿边从点D开始向点A以1的速度移动．如果P、Q同时出发，用t （秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O 点）20米的A点，沿所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：；（2）请在下图中画出测量示意图；（3）设树高的长度为x，请用所测数据（用小写字母表示）求出x．24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80的竹竿的影长为60．乙组：如图2，测得学校旗杆的影长为900．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200，影长为156．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段的影长；需要时可采用等式1562+2082=2602）25．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离8.7m，窗口高1.8m，求窗口底边离地面的高．26．如图，李华晚上在路灯下散步．已知李华的身高，灯柱的高′P′，两灯柱之间的距离′．（1）若李华距灯柱的水平距离，求他影子的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．27．如图①，分别以直角三角形三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S123．（1）如图②，分别以直角三角形三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．28．已知：如图，△∽△，15，9，5．求．29．已知：如图△∽△，若3，4．（1）求、的长；（2）过B作⊥于E，求的长．30．（1）已知，且34z﹣240，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560，求它们的周长．参考答案与试题解析一．解答题（共30小题）1．如图，在△中，∥，∥，求证：△∽△．考点：相似三角形的判定；平行线的性质。

相似三角形知识点及典型例题

相似三角形知识点及典型例题知识点归纳:1、三角形相似的判定方法（1）定义法：对应角相等，对应边成比例的两个三角形相似。

（2 ）平行法：平行于三角形一边的直线和其它两边（或两边的延长线）相交，所构成的三角形与原三角形相似。

（3 ）判定定理1 :如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

简述为：两角对应相等，两三角形相似。

（4 ）判定定理2 :如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。

简述为：两边对应成比例且夹角相等，两三角形相似。

（5 ）判定定理3 :如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。

简述为：三边对应成比例，两三角形相似。

（6 ）判定直角三角形相似的方法：①以上各种判定均适用。

②如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。

③直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。

#直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。

每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

如图，Rt △ABC中，/ BAC=90 °, AD是斜边BC上的高，则有射影定理如下：(1)( AD ) 2=BD DC , (2)( AB ) 2=BD •BC ,典型例题:例1 如图，已知等腰厶ABC 中，AB = AC , AD 丄BC 于D , CG IIAB , BG 分别交 AD , AC 于E 、F ,求证：BE 2= EF EG 证明：如图，连结 EC,V AB = AC , AD 丄BC ,•••/ABC = ZACB , AD 垂直平分 BC•••BE = EC ,/1 =/2 , A /ABC- /1 =/ACB- Z2 ,即/3 =/4，又 CG //AB ,「./G = /3 ,二/4 = /GCE EF又v/CEG = /CEF , •••©EF S /EC , • EG = CE•••EC 2 = EG - EF ,故 EB 2=EF EG【解题技巧点拨】本题必须综合运用等腰三角形的三线合一的性质，线段的垂直平分线的性质和相似三角形的基本图形来得到证明•而其中利用线段的垂直平分线的性质得到 BE=EC ，把原来处在同一条直线上的三条线段 BE , EF , EC 转换到相似三角形的基本图形中是证明本题的关键。

中考中相似三角形的常见模型及典型例题

1.相似的基本模型：
（1）A字、8字；（3）角平分线；（5）一线三等角；（7）内接矩形；
2.基本辅助线：
（2）反A、反8；（4）旋转型；（6）线束模型；（8）相似比与面积比。
（1）作平行线构造A字、8字；（2）作垂线构造直角三角形相似
3.基本问题类型：
（1）证明相似；
（2）求线段长；
（1）若点P在线段CB上，且BP=6，求线段CQ的长；（2）若BP=x，CQ=y,求y与x的关系式，并求出自变量x的取值范围。
例 9 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CD，
AD与BE相交于点F. （1）求证：△ABD≌△BCE；（2）求证：△ABE∽△FAE；
（3）当AF=7，DF=1时，求BD的长。
（量得BN=70cm）
C
C
DME
DME
A PN F
B
A PN F
B
1.如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80 毫米，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？
A
A
M
EN
H
KG
∟
B Q DPC
B
E
DF C
E
AB AC BC
B
C （2）公共边平方=共线边之积：AC 2 AE • AB
反A字型【模型2】反“A”字型＆反“8”字型
（Ⅱ）DE拉下来经过点C，又称之为母子型，为相似常考模型：
A
A
E
B
C
AC2 AED • BC
AC2 CD • CB
AD2 BD • CD

相似三角形(基本图形

相似三角形（基本图形）复习一、基本图形梳理 1、如图（1），已知CA=8,CB=6，AB=5，CD=4(1)若CE= 3，则DE=____(2)如图（2）若CE=316，则DE=____.2、如图（3），在⊿ABC 中，D 为AC 边上一点，∠DBC=∠A ，BC= ，AC=3，则CD 的长为（）（A ）1 （B ）2 （C ）（D ） 3、如图（4），∠ABC=90， BD ⊥AC 于D ，DC=4，AD=9，则BD 的长为（）（A ）36 （B ）16 （C ）6 （D ）4、如图，F 、C 、D 共线，BD ⊥FD, EF ⊥FD ，BC ⊥EC ,若DC=2，BD=3，FC=9,则EF 的长为（）（A ）6 （B ）16 （C ）26 （D ）二、归纳基本图形三、典型例题在△ABC 中，E 是 AB 上一点，AE ＝2，BE ＝3，AC ＝4，在 AC 上取一点 F ，使△AEF 与△ABC 相似，求 AF 长回思：1. “△AEF 与△ABC 相似”与“△AEF ∽△ABC ”的异同点 2. 基本图形变式训练：在△ABC 中，E 是 AB 上一点，AB ＞AC ，在另一边上取一点 F ，使所得三角形与原三角形相似。

请画出满足条件的示意图。

反馈练习：1、EABCD 边BC 的延长线上的点，连接AE 交边CD 于F, 则图中有______对相似三角形2、如图，在平行四边形ABCD 中，E 是AD 上一点，连结CE 并延长交BA 的延长线于点F ，则下列结论中错误的是（）A. ∠AEF ＝∠DECB. FA:CD ＝AE:BCC. FA:AB ＝FE:ECD. AB ＝DC3、已知如图，在△ABC 中，P 为AB 上一点，在下列四个条件中：①∠ACP=∠B ②∠APC =∠ACB ③AC 2=AP ∙AB ④ AB ∙CP=AC ∙CB ，能满足△APC 和△ACB 相似的条件是( ) A. ④ B. ①③④ C.②③④. D. ①②③4、已知，如图6所示，△ABC 中，AB=AC ，D为AB 上的点，E 为AB延长线上的点，且。

经典相似三角形练习题(附参考答案)

经典练习题一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC=_________ °，BC= _________ ；（2）判断△ABC与△DEC是否相似，并证明你的结论．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．10．如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC 于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．17．已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：_________ ；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）25．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．28．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．29．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．30．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．参考答案与试题解析一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC=135°°，BC= ；（2）判断△ABC与△DEC是否相似，并证明你的结论．BC==22、，可得BC=∵BC=EC=；∴，∴8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．面积的面积的则有：（×3×6，即面积的因此有①，或t=（t=t=都符合题意，同时出发后，经过秒或9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．P=，即相似三角形的证明．还考查了相似三角形的判定．10．附加题：如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．CE=．AE=∴sin∠AEF=，∴AF=AE•sin∠AEF=∴．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC 于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．∴QM=PM=AB=12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．∴CM=MD=∴PC=BC=AD=∴．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．（AB=∴tan∠ADP=tan∠C==∴=，∴t=∴tan∠APD=tan∠C==，∴=∴t=∴t=t=时，△PAD∴PD=∵CE=t QE=t∴QH=BE=8﹣t t∴PH=t﹣t=t∴PQ=，，，＞∴t=t=14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？时，有：；时，有：∴经过15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．=，即=，解得对应时，有=，即=，解得16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．解：∵AC=∴CD==时，有=，∴AB=时，有=，∴AB==3317．已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．a①若△CDM∽△MAN，则=．∴AN=②若△CDM∽△NAM，则AN=18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？或时，两三角形相似．）当时，，∴x=；）当时，，∴x=．所以，经过秒或秒后，两三角形相似．19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．∴=，∴=，∴=，∴=，∴=，∴AP=．AP=时，由BP=，∴=，、20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．∴．∴，中有21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似．，所以，所以；=，即，；=，即，t=时，以点22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？∴，，23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．∴，∴，∴．24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）∴，即，与①类似得：，即∴（∴，与①类似得：，∴，，∴MN=r（25．（2007•白银）阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．AE∥BD，所以△ECA∽△DCB，则有∴．∴，26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．∵，∴，∴解得：∴，，即．∴．同理可得：，∴=是定值．）可知，即，∴同理可得：∴，由等比性质得：∴，所以人影顶端在地面上移动的速度为．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）。

相似三角形经典例题(练习)

一、如何证明三角形相似例1、如图：点G 在平行四边形ABCD 的边DC 的延长线上,AG 交BC 、BD 于点E 、F ，则△AGD ∽ ∽ 。

例2、已知△ABC 中，AB=AC ，∠A=36°，BD 是角平分线，求证：△ABC ∽△BCD例3：已知，如图，D 为△ABC 内一点连结ED 、AD ，以BC 为边在△ABC 外作∠CBE=∠ABD，∠BCE=∠BAD求证：△DBE∽△ABC例4、矩形ABCD 中，BC=3AB ，E 、F ，是BC 边的三等分点，连结AE 、AF 、AC ，问图中是否存在非全等的相似三角形？请证明你的结论。

二、如何应用相似三角形证明比例式和乘积式例5、△ABC 中，在AC 上截取AD ，在CB 延长线上截取BE ，使AD=BE ，求证：DF AC=BC FE例6：已知：如图，在△ABC 中，∠BAC=900，M 是BC 的中点，DM⊥BC 于点E ，交BA 的延长线于点D 。

例7：如图△ABC 中，AD 为中线，CF 为任一直线，CF 交AD 于E ，交AB 于F ，求证：AE ：ED=2AF ：FB 。

过D 点作DG∥AB 交FC 于G 则△AEF∽△DEG。

（平行于三角形一边的直线截其它两边或两边的延长线所得三角形与原三角形相似）（1）∵D 为BC 的中点，且DG∥BF∴G 为FC 的中点则DG 为△CBF 的中位线，（2）将（2）代入（1）得：三、如何用相似三角形证明两角相等、两线平行和线段相等。

边AB 和AD 上的点，且。

求证：例8：已知：如图E 、F 分别是正方形ABCD 的∠AEF=∠FBD例9、在平行四边形ABCD 内，AR 、BR 、CP 、DP 各为四角的平分线，••DG AFDE AE =BF DG 21=FBAF BF AF DE AE 221==31==AD AF AB EB A B C D E FG 1234ABC D AB C D E FK A B CD E FCDRAC E ABCDEFO 123ABCDFGE求证：SQ ∥AB ，RP ∥BC例10、已知A 、C 、E 和B 、F 、D 分别是∠O 的两边上的点，且AB ∥ED ，BC ∥FE ，求证：AF ∥CD例11、直角三角形ABC 中，∠ACB=90°，BCDE 是正方形，AE 交BC 于F ，FG ∥AC 交AB 于G ，求证：FC=FG例12、Rt △ABC 锐角C 的平分线交AB 于E ，交斜边上的高AD 于O ，过O 引BC 的平行线交AB 于F ，求证：AE=BF（答案）例1分析：关键在找“角相等”，除已知条件中已明确给出的以外，还应结合具体的图形，利用公共角、对顶角及由平行线产生的一系列相等的角。

《相似三角形》经典练习题(附答案)

相似三角形经典练习题（附答案）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC=_________ °，BC= _________ ；（2）判断△ABC与△DEC是否相似，并证明你的结论．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s 的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．10．如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC 的平行线交AC于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q 从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t 秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s 的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．17．已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s 的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C 出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB 上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q 同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：_________ ；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）25．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．28．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．29．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．30．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．参考答案与试题解析1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．考点：相似三角形的判定；平行线的性质。

(完整版)相似三角形基本知识点+经典例题(完美打印版)

相似三角形知识点与经典题型知识点1 有关相似形的概念(1)形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形。

(2)如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形．相似多边形对应边长度的比叫做相似比(相似系数)．知识点2 比例线段的相关概念（1）如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=．注：在求线段比时，线段单位要统一.（2）在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段，简称比例线段．注：①比例线段是有顺序的，如果说a 是d c b ,,的第四比例项，那么应得比例式为：a d c b =．②()a ca b c d b d ==在比例式：：中，a 、d 叫比例外项，b 、c 叫比例内项, a 、c 叫比例前项，b 、d 叫比例后项，d 叫第四比例项,如果b=c ，即 a b b d =：：那么b 叫做a 、d 的比例中项，此时有2b ad =。

(3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项，即2AC AB BC =⋅,叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AB AC 215-=≈0.618AB．即12AC BC AB AC ==简记为：长短＝全长注:黄金三角形：顶角是360的等腰三角形。

黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质（注意性质立的条件：分母不能为0)（1) 基本性质：①bc ad d c b a =⇔=::；②2::a b b c b a c =⇔=⋅．注：由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =，除了可化为d c b a ::=,还可化为d b c a ::=，b a d c ::=,c a d b ::=，c d a b ::=,b d a c ::=,a b c d ::=，a c b d ::=．（2）更比性质（交换比例的内项或外项)：()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩，交换内项，交换外项．同时交换内外项 (3）反比性质(把比的前项、后项交换）： a c b db d a c=⇔=．(4）合、分比性质：a c abc db d b d±±=⇔=．注：实际上，比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立．如：⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=dc dc b a b a c cd a a b d c b a 等等．（5)等比性质：如果)0(≠++++====n f d b nm f e d c b a ，那么b an f d b m e c a =++++++++ ．注：①此性质的证明运用了“设k 法”（即引入新的参数k ）这样可以减少未知数的个数,这种方法是有关比例计算变形中一种常用方法．②应用等比性质时，要考虑到分母是否为零．③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数，再利用等比性质也成立．如:baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322；其中032≠+-f d b ．知识点4 比例线段的有关定理1。

相似三角形基本图形及练习题_绝对经典

A DB D A相似中的基本图形练习相似三角形是初中数学中重要的内容，应用广泛，可以证明线段的比例式；也可证明线段相等、平行、垂直等；还可计算线段的长、比值，图形面积及比值。

而识别（或构造）A 字型、X 字型、母子相似型、旋转型等基本图形是解证题的关键。

1．A 字型及变形△ABC 中， AD=2，BD=3，AE=1 （1）如图1，若DE ∥BC ，求CE 的长（2）如图2，若∠ADE=∠ACB ，求CE 的长2.X 字型及变形（1）如图1，AB ∥CD ，求证：AO ：DO=BO ：CO（2）如图2，若∠A=∠C ，求证：AO ×DO=BO ×CO3. 母子相似型及变形（1）如右图，在△ABC 中， AD 把△ABC 分成两个三角形△BCD 和△CAD ，当∠ACD =∠B 时，说明△CAD 与△ABC 相似。

说明：由于小三角形寓于大三角形中，恰似子依母怀，故被称为“母子三角形”（2）如图， Rt △ABC 中，CD ⊥AB, 求证：AC ²=ADxAB,CD ²=ADxBD,4. 旋转型如图，若∠ADE=∠B ，∠BAD=∠CAE ，说明△ADE 与△ABC 相似练习题1、如图1，在△ABC 中，中线BE 、CD 相交于点G ，则BCDE = ；S △GED ：S △GBC = ；2、如图2，在△ABC 中， ∠B=∠AED ，AB=5，AD=3，CE=6，则AE= ；3、如图3，△ABC 中，M 是AB 的中点，N 在BC 上，BC=2AB ，∠BMN=∠C ，则△ ∽△ ，相似比为，NCBN= ； 4、如图4，在梯形ABCD 中，AD ∥BC ，S △ADE ：S △BCE =4：9，则S △ABD ：S △ABC = ；5、如图5，在△ABC 中，BC=12cm ，点D 、F 是AB 的三等分点，点E 、G 是AC 的三等分点，则DE+FG+BC= ；二、选择题6、如图，在△ABC 中，高BD 、CE 交于点O ，下列结论错误的是（） A 、CO ·CE=CD ·CA B 、OE ·OC=OD ·OB C 、AD ·AC=AE ·AB D 、CO ·DO=BO ·EO7、如图，D 、E 分别是△ABC 的边AB 、AC 上的点， AD BD =CEAE=3，且∠AED=∠B ，则△AED 与△ABC 的面积比是（） A 、1：2 B 、1：3 C 、1：4 D 、4：98、已知，如图，在△ABC 中，DE ∥BC ，AD=5，BD=3，求S △ADE ：S △ABC 的值。