几何体中的截面问题(修订版)精选-共6页
高中数学截面问题方法总结

高中数学截面问题方法总结高中数学里的截面问题啊,那可真是有点头疼呢!但别怕,咱一起来好好捋一捋。
你想想看,截面就像是给一个立体图形来个“切片”。
要解决这类问题,首先得对各种立体图形特别熟悉,就像了解自己的手掌纹路一样。
比如说正方体吧,那可是最常见的啦。
要找正方体的截面,你就得发挥想象力,把自己想象成一个小蚂蚁,在正方体里爬来爬去,看看能截出个啥形状。
有时候可能是个三角形,有时候是个四边形,甚至还可能是个五边形或者六边形呢!这多神奇呀!再比如棱柱、棱锥这些家伙,它们的截面可就更复杂啦。
这时候就得仔细分析它们的特点,看看从哪里下“刀”合适。
这就好比切蛋糕,你得找准位置才能切出漂亮的一块儿。
还有啊,画图可太重要啦!把图形画出来,就好像把难题给“抓”到了眼前,能更清楚地看到问题所在。
别小看这一笔一划,有时候就是这简单的几笔,能让你豁然开朗呢!做截面问题的时候,可别死脑筋哦。
要多角度去思考,就像孙悟空一样,七十二变,总有一个角度能找到答案。
还有个小技巧,那就是找特殊点和特殊线。
这些特殊的地方往往就是解决问题的关键。
就像黑暗中的一盏明灯,一下子就能照亮你解题的路。
比如说,在一个三棱锥里,找到顶点和底边的中点连线,这可能就是一个重要的截面呢。
哎呀,说了这么多,其实关键还是要多练习呀!只有多做几道题,才能真正掌握这些方法。
就像学骑自行车,一开始可能会摔倒,但多骑几次,不就熟练了嘛!总之呢,高中数学的截面问题虽然有点难,但只要我们用心去学,去思考,就一定能把它拿下!加油吧,同学们!让我们一起在数学的海洋里畅游,把这些难题都当成是我们前进路上的小怪兽,一个一个地打败它们!相信自己,我们一定行!。
立体几何截面问题

立体几何中的截面问题剖析用平面去截一个几何体,截面的情况可以帮助我们更好地认识几何体,对于一个几何体不同切截方式,所以得截面可能出现不同的情况.以正方体为例:平面截正方体的截面图形三角形:四边形五边形六边形类型一:与截面有关的求值问题1、在棱长为2的正方体1111ABCD A B C D -中,M 是棱11A D 的中点,过1C ,B ,M 作正方体的截面,则这个截面的面积为( )A .352B .358C .92D .982、体积为216的正方体1111ABCD A B C D -中,点M 是线段11D C 的中点,点N 在线段11B C 上,//MN BD ,则正方体1111ABCD A B C D -被平面AMN 所截得的截面面积为( )A.27172 B .21172 C .15172 D .13172正三棱柱111ABC A B C -中,所有棱长均为2,点,E F 分别为棱111,BB A C 的中点,若过点,,A E F 作一截面,则截面的周长为( )A .425133+B .225133+ C .2513+ D .13252+反馈练习: 1、在棱长为2的正方体1111D C B A ABCD -中,E 是正方形C C BB 11的中心,M 为11D C 的中点,过M A 1的平面α与直线DE 垂直,则平面α截正方体1111D C B A ABCD -所得的截面面积为( )A .23B .26C .225D .32、如图,在正方体````ABCD A B C D -中,平面垂直于对角线AC ,且平面截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S ,周长为l ,则( )A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值类型二:与截面有关的最值问题1、已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .433B .332C .423D .232、如图,在棱长为2的正方体1111ABCD A B C D -中,,,E F G 分别是棱1,,AB BC CC 的中点,P 是底面ABCD 内一动点,若直线1D P 与平面EFG 不存在公共点,则三角形1PBB 的面积的最小值为( )A .22B .1C .2D .2反馈练习:1、如图,已知四面体ABCD 为正四面体,22AB =,E ,F 分别是AD ,BC 中点.若用一个与直线EF 垂直,且与四面体的每一个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为______________2、有一容积为33a cm 的正方体容器1111ABCD A B C D -,在棱AB 、1BB 和面对角线1BC 的中点各有一小孔E 、F 、G ,若此容器可以任意放置,则其可装水的最大容积是( )A .3312a cmB .3378a cmC .331112a cmD .334748a cm类型三:与球有关的截面问题1、已知正四面体A BCD -的棱长为62,M ,N 分别是AC ,AD 上的点,过MN 作平面α,使得AB ,CD 均与α平行,且AB ,CD 到α的距离分别为2,4,则正四面体A BCD -的外接球被α所截得的圆的面积为( )A .11πB .18πC .26πD .27π2、已知圆锥1SO 的顶点和底面圆周均在球O 的球面上,且该圆锥的高为8,母线12SA =,点B 在SA 上,且3SB BA =,则过点B 的平面被该球O 截得的截面面积的最小值为( ) A .27πB .36πC .54πD .81π反馈练习:1、已知正三棱锥A BCD -的外接球是球O ,正三棱锥底边3BC =,侧棱23AB =,点E 在线段BD 上,且BE DE =,过点E 作球O 的截面,则所得截面圆面积的取值范围是( ) A .9,34ππ⎡⎤⎢⎥⎣⎦ B .[]2,3ππ C .11,44ππ⎡⎤⎢⎥⎣⎦ D .9,44ππ⎡⎤⎢⎥⎣⎦2、如图所示,正方体ABCD ﹣A 1B 1C 1D 1的棱长为6,则以正方体ABCD ﹣A 1B 1C 1D 1的中心为顶点,以平面AB 1D 1截正方体外接球所得的圆为底面的圆锥的全面积为 .。
立体几何中的截面(解析版)

立体几何中的截面(解析版)在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱、圆锥、球、棱柱、棱锥、长方体、正方体等),得到的平面图形。
总共有三种截面方式,分别为横截、竖截、斜截。
我们需要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
正六面体的基本斜截面不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
圆柱体的基本截面也有其特殊性质。
我们可以运用线、面平行的判定定理与性质求截面问题,或者结合线、面垂直的判定定理与性质定理求正方体中截面问题。
此外,我们还可以灵活运用一些特殊图形与几何体的特征,“动中找静”,如正三角形、正六边形、正三棱锥等。
建立函数模型也是求最值问题的一种方法。
在一个透明的塑料制成的长方体内灌进一些水,固定底面一边于地面上,再将倾斜,有四个命题。
其中,水的部分始终呈棱柱状,棱AD始终与水面平行,当倾斜到如图5(2)时,BE·BF是定值。
水面的面积在转动过程中会改变,而BC//FG//A1D1,所以A1D1//面EFGH。
因此,正确的命题序号为①③④。
一个容积为1立方单位的正方体,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G。
若此可以任意放置,则该可装水的最大容积是多少?分析本题,不能用一个平面去截一个正方体,使得截面为五边形。
进一步地,截面也不能为正五边形。
这是因为正方体的每个面都是正方形,而五边形无法与正方形相切。
因此,无论如何调整平面的位置,都不能得到五边形的截面。
而且OE=OC是抛物线的直线准线,所以焦点F在OC上,且OF=OC=1.故选:D二、完形填空在数学课上,老师讲到一个有趣的问题:如何用一个平面去截一个正方体所得截面不能是一个正五边形。
这个问题引起了我的思考,我开始想象一个平面在正方体中穿过的情景。
我发现,如果截面是一个正五边形,那么这个五边形的五条边必须分属于正方体的五个不同的面。
但是,正方体的每两个相对的面是平行的,所以这五条边中必有两条边是平行的。
高考数学立体几何截面问题

高考数学立体几何截面问题在高考数学立体几何中,截面问题是一个重要的考点。
本文将从以下几个方面对截面问题进行讲解:截面的形状和性质、截面与几何体的关系、截面与投影的关系以及截面与面积的关系。
一、截面的形状和性质1.截面的形状截面是指通过一个平面与一个几何体相交,所得的交线。
截面的形状可能是一个点、一条直线、一个平面多边形或一个圆。
在解决立体几何问题时,我们需要根据题目所给的条件,判断出截面的形状,并进一步解决问题。
2.截面的性质截面的性质包括以下几点:(1)截面是平面图形,其形状取决于几何体和截面的位置关系。
(2)截面与几何体的边界相交,但不穿过几何体的内部。
(3)截面与几何体的表面平行,因此可以运用平行投影的知识来研究截面的性质。
二、截面与几何体的关系1.截面与正方体的关系正方体的截面有三种情况:三角形、矩形和五边形。
当截面与正方体的中心轴平行时,可以得到一个正方形;当截面与正方体的中心轴垂直时,可以得到一个三角形;当截面与正方体的中心轴斜交时,可以得到一个矩形或五边形。
长方体的截面也有三种情况:三角形、矩形和五边形。
当截面与长方体的中心轴平行时,可以得到一个矩形;当截面与长方体的中心轴垂直时,可以得到一个三角形;当截面与长方体的中心轴斜交时,可以得到一个梯形或不规则四边形。
三、截面与投影的关系1.投影的定义及性质投影是指将一个几何体投射到一个平面上的结果。
投影的性质包括以下几点:(1)投影是直线与平面相交的结果。
(2)投影的长度等于被投影线段的长度。
(3)投影的方向与被投影线段的方向相同或相反。
2.截面与投影的关系截面与投影之间存在一定的关系。
如果一个几何体在一个平面上的投影是一个多边形,那么这个多边形的形状就取决于该几何体的形状以及它与平面的相对位置。
因此,在解决立体几何问题时,我们需要通过判断几何体在某一平面上的投影来推断出它的形状和性质。
四、截面与面积的关系1.面积的定义及计算方法面积是指一个平面图形所占的面积大小。
立体几何中的截面(解析版)

专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________分析当长方体容器绕BC边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG,但EH与FG的距离EF在变,所以水面EFGH的面积在改变,故②错误;在转动过程中,始终有BC//FG//A1D1,所以A1D1//面EFGH,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BCBFBEV⋅⋅=21水是定值,又BC是定值,所以BE·BF是定值,即④正确。
立体几何中的截面问题

立体几何中的截面问题一.基本原理:过正方体(长方体)上三点做截面.1.三点中有两点共面例1.如图,在正方体ABCD-A 1B 1C 1D 1中,E,F,G 分别在AB,BC,DD 1上,求作过E,F,G 三点的截面.思路:当三点中有两点共面时,做截面的思路就是先找共面两点所在直线与该平面所有的棱交点,而这些交点由同时在另外一个平面中,即该截面和正方体某个侧面的交点,这样利用公理1,逐次相连找到所有的交点,即可得到截面.解析:作法:①.由于F E ,共面,在底面AC 内,过F E ,作直线EF ,与DA 于L ,显然,此时L 即在侧面D A 1内,又在欲求截面内,而该截面与侧面D A 1又交于点G ,根据公理1,截面与侧面D A 1交于L .同理,过F E ,作直线EF 与DC 的延长线交于M ,此时M 即在侧面1DC 内,又在欲求截面内,根据公理1,截面与侧面1DC 交于M .②在侧面D A 1内,连接LG 交1AA 于K .③在侧面1DC 内,连接GM 交1CC 于H .④连接FH KE ,.则五边形EFHGK EFHGK 即为所求的截面.练习1.(三点两两共面)P,Q,R 三点分别在直四棱柱AC 1的棱BB 1,CC 1和DD 1上,试画出过P,Q,R 三点的截面作法.解析:作法:(1)连接QP,QR 并延长,分别交CB,CD 的延长线于E,F.(2)连接EF 交AB 于T,交AD 于S.(3)连接RS,TP.则五边形PQRST 即为所求截面.例2.(三点所在的棱两两异面)如图,长方体1111D C B A ABCD -中,R Q P ,,分别为111,,CC AB D A 上三点,求过这三点的截面.分析:此题的难点在于R Q P ,,三点均不在同一个侧面(底面)中,这样我们就暂时无法通过侧面(底面)中连线与棱的交点来找到截面的边界点,于是需要先做出一个平面来,让上面三点RQ P ,,中有两点共面,这就转化成例1的情形,从而解决问题.解:如图,作1//BB QE 交11B A 与E ,则1,RC QE 确定一个平面,转化为例1的情形.连接QR EC ,1,交于点F ;连接PF 交1111,B A D C 延长线于H G ,;连接HQ 交11,BB AA 延长线于J I ,;连接JR 交BC 于K .则KRGPIQK 为所作截面.例3.利用平行关系确定截面在三棱锥A BCD -中,AB CD a ==,截面MNPQ 与AB ,CD 都平行,则截面MNPQ 的周长等于()A.2a B.4a C.a D.无法确定解析:设AM k CM=,因为//AB 平面MNPQ ,平面ABC 平面MNPQ MN =,AB Ì平面ABC ,所以//MN AB ,同理可得//PQ AB ,//MQ CD ,//NP CD ,故四边形MNPQ 为平行四边形,所以11MN PQ AB AB k ==+,1MQ NP k CD CD k ==+.因为AB CD a ==,所以1a MN PQ k==+,1ak MQ NP k ==+,所以四边形MNPQ 的周长为2211a ak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭.故选:A.二.截面的的画法小结1.确定截面的主要依据有(1)平面的四个公理及推论.(2)直线和平面平行的判定和性质.(3)两个平面平行的性质.2.作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程。
几何体截面归类十四种(解析版)

几何体截面归类十四种1.目录重难点题型归纳⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1【题型一】截面做法基础1:平行线法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1【题型二】截面做法基础2:相交线法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5【题型三】截面形状判定⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9【题型四】求截面周长⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11【题型五】求截面面积⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14【题型六】截面分两部分体积⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16【题型七】与线、面平行的截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯19【题型八】与直线、平面垂直的截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯21【题型九】外接球截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯23【题型十】内切球截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯25【题型十一】“动点”型截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯28【题型十二】截面与角度⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯34【题型十三】与截面有关的最值⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯36【题型十四】截面综合应用⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯39好题演练⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯42 1.重难点题型归纳重难点题型归纳题型一:截面做法基础1:平行线法【典例分析】1已知正方体ABCD -A 1B 1C 1D 1的体积为1,点M 在线段BC 上(点M 异于B 、C 两点),点N 在CC 1上满足CN =C 1N ,若平面AMN 截正方体ABCD -A 1B 1C 1D 1所得的截面为五边形,则线段BM 的取值范围是( )A.0,12B.12,1C.13,1D.12,13【答案】B【分析】由正方体的性质及面面平行的性质分析截面与上底面A 1B 1C 1D 1的两条边A 1D 1和C 1D 1有交点,然后作出截面AMNTS ,由相似形得出A 1S =2CM =2(1-BM ),从而可得BM 的范围.【详解】因为截面过A 点,那么它只能与正方体的过点A 的三个面中两个面有交线,因此截面的边只能在正方体ABCD -A 1B 1C 1D 1的两个侧面ABB 1A 1和侧面ADD 1A 1的其中一个上(已经有一条边是AM ),从而截面必与上底面A 1B 1C 1D 1有交线,由面面平行的性质定理知这个交线与直线AM 平行,如下图,在B 1C 1上取点P ,使得B 1P =BM ,连接PM 可得平行四边形BMPB 1,则PM ⎳BB 1且PM =BB 1,而BB 1与AA 1平行且相等,得PM ⎳AA 1且PM =AA 1,从而AMPA 1是平行四边形,所以A 1P ⎳AM ,在A 1D 1上取A 1Q =C 1P 得平行四边形A 1PC 1Q ,因此有A 1P ⎳C 1Q ,如下图,截面是五边形AMNTS ,由面面平行的性质定理得AS ⎳MN ,因为两个角∠A 1AS 和∠MNC 的两边分别平行,且它们都是锐角,所以∠A 1AS =∠CNM ,而∠AA 1S =∠NCM =90°,所以△AA 1S ∼△NCM ,所以AA 1NC =A 1S CM,CN =C 1N ,因此有CN =12CC 1=12AA 1,所以A 1S =2CM ,所以A 1S =2CM =2(1-BM ),0<2(1-BM )<1,12<BM <1,故选:B .方法归纳【技法指引】】基础模型:如下图E 、F 是几等分点,不影响作图。
立体几何截面问题的十种题型(解析版)
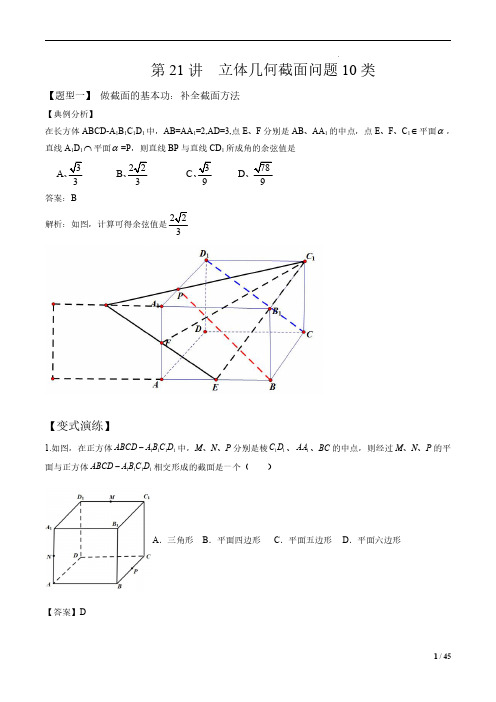
第21讲立体几何截面问题10类【题型一】做截面的基本功:补全截面方法【典例分析】在长方体ABCD-A 1B 1C 1D 1中,AB=AA 1=2,AD=3,点E 、F 分别是AB 、AA 1的中点,点E 、F 、C 1∈平面α,直线A 1D 1⋂平面α=P ,则直线BP 与直线CD 1所成角的余弦值是3378 A22 C B 3 D 3 99、、、、答案:B解析:如图,计算可得余弦值是3【变式演练】1.如图,在正方体1111ABCD A B C D -中,M 、N 、P 分别是棱11C D 、1AA 、BC 的中点,则经过M 、N 、P 的平面与正方体1111ABCD A B C D -相交形成的截面是一个()A .三角形B .平面四边形C .平面五边形D .平面六边形【答案】D分别取11A D 、AB 、1C C 的中点、、F H E ,连接MF 、FN 、NH 、HP 、PE 、EM 、11A C 、AC 、NE 、1A B ,先证明、、、H P M F 四点共面,再证明N ∈平面HPMF ,P ∈平面HPMF 可得答案.【详解】如图,分别取11A D 、AB 、1C C 的中点、、F H E ,连接MF 、FN 、NH 、HP 、PE 、EM 、11A C 、AC 、NE 、1A B ,且M 、N 、P 分别是棱11C D 、1AA 、BC 的中点,所以11//A C FM 、//HP AC ,且11//A C AC ,所以//HP FM ,即、、、H P M F 四点共面,因为11//=,F BP F BP A A ,所以四边形1A FPB 是平行四边形,所以1//A B FP ,又因为1//A B NH ,得//NH FP ,且FP ⊂平面HPMF ,H ∈平面HPMF ,所以NH ⊂平面HPMF ,得N ∈平面HPMF ,因为11//=,M H MC B C BH ,所以四边形1C MHB 是平行四边形,所以1//C B MH ,又因为1//C B EP ,得//MH EP ,又MH ⊂平面HPMF ,P ∈平面HPMF ,所以PE ⊂平面HPMF ,得E ∈平面HPMF ,所以、、、、、H P E M F N 六点共面,平面六边形HPEMFN 即为经过M 、N 、P 与正方体1111ABCD A B C D -相交形成的截面,故选:D.2.如图,在正方体1111ABCD A B C D -中,E 是棱1CC 的中点,则过三点A 、D1、E 的截面过()A .AB 中点B .BC 中点C .CD 中点D .BB1中点【答案】B根据截面特点结合正方形结构性质求解.【详解】取BC 的中点F ,连接EF ,AF ,如图,则1EF AD ∥,所以F 在截面上,故选:B3.如图正方体1111ABCD A B C D -,棱长为1,P 为BC 中点,Q 为线段1CC 上的动点,过A 、P 、Q 的平面截该正方体所得的截面记为Ω.若1CQ CC λ→→=,则下列结论错误的是()A .当102λ∈⎛⎫⎪⎝⎭,时,Ω为四边形B .当12λ=时,Ω为等腰梯形C .当3,14λ⎛⎫∈ ⎪⎝⎭时,Ω为六边形D .当1λ=时,Ω的面积为2【答案】C 【分析】根据题意,依次讨论各选项,作出相应的截面,再判断即可.【详解】解:当102λ<<时,如下图1,Ω是四边形,故A 正确;当12λ=时,如下图2,Ω为等腰梯形,B 正确:当314λ<<时,如下图3,Ω是五边形,C 错误;当1λ=时,Q 与1C 重合,取11A D 的中点F ,连接AF ,如下图4,由正方体的性质易得1////BM PC AF ,且=1PC AF ,截面Ω为1APC F 为菱形,其面积为112AC PF ⋅,D 正确.故选:C【题型二】截面形状的判断【典例分析】一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是()A .B .C .D .【答案】B 【分析】根据题意可知,该三棱锥为正四面体,内切球与各面相切于各个面的中心,即可判断出选项B 正确.【详解】如图所示:因为三棱锥的各棱长均相等,所以该三棱锥为正四面体,内切球与各面相切于各个面的中心,即可知过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是.故选:B .【变式演练】1.如图,正四棱锥P ABCD -的高为12,AB =E ,F 分别为PA ,PC 的中点,过点B ,E ,F 的截面交PD 于点M ,截面EBFM 将四棱锥分成上下两个部分,规定BD为主视图方向,则几何体CDAB FME -的俯视图为()A .B .C .D .【答案】C 【分析】根据主视图所给方向即可知俯视图中底面正方形,计算可知M 点投影位置,即可得出答案.【详解】研究平面DPB ,设AC 与BD 的交点为O ,BM 与EF 交点为N,,E F 为,PA PC 的中点,N ∴为PO 的中点,12PO =,6ON OB ∴==,又因为12tan 26PO PDB OD ∠===,过点M 作MG DB ⊥,设GB x =,45NBO ∠=︒ ,GB MG x ∴==,又12DB = ,12DG x ∴=-,tan 212xPDB x∠==-,8x GB ∴==,DG ∴为4个格,GB 为8个格,故选:C 2.用一个平面去截正方体,所得截面不.可能是()A .直角三角形B .直角梯形C .正五边形D .正六边形【答案】ABC 【分析】根据正方体的几何特征,我们可分别画出用一个平面去截正方体得到的几何体的图形,然后逐一与四个答案中的图形进行比照,即可判断选项.【详解】当截面为三角形时,可能出现正三角形,但不可能出现直角三角形;截面为四边形时,可能出现矩形,平行四边形,等腰梯形,但不可能出现直角梯形;当截面为五边形时,不可能出现正五边形;截面为六边形时,可能出现正六边形,故选:ABC.3.在正方体1AC 中,M 为AB 中点,N 为BC 中点,P 为线段1CC 上一动点(不含C )过M 、N 、P 与正方体的截面记为α,则下面三个判断,其中正确判断的序号有______.①当P 为1CC 中点时,截面α为六边形;②当112CP CC <时,截面α为五边形;③当截面α为四边形时,它一定是等腰梯形;【答案】①③.【分析】①延长MN 交AD 于M ',交CD 于N ',延长N P '交11C D 于T ,取11A D 的中点S ,连接M S '交1AA 于P ',连接11,AC A C ,结合图形即可判断;②延长MN 交AD 于M ',交CD 于N ',连接1N D '交1CC 于P ,连接1M D '交1AA 于P ',此时截面α为五边形,求出1CPCC 即可判断;③当截面α为四边形时,点P 与点1C 重合,判断四边形11A MNC 的形状即可.【详解】解:如图①,延长MN 交AD 于M ',交CD 于N ',延长N P '交11C D 于T ,取11A D 的中点S ,连接M S '交1AA 于P ',连接11,AC A C ,因为M 为AB 中点,N 为BC 中点,所以MN AC ∕∕,同理11ST A C ∕∕,又因11AC A C ∕∕,所以ST MN ∕∕,同理,SP PN MP PT ''∕∕∕∕,所以,,,,,S T P N M P '共面,此时六边形STPNMP '为截面α,所以截面α为六边形;故①正确;如图②,延长MN 交AD 于M ',交CD 于N ',连接1N D '交1CC 于P ,连接1M D '交1AA 于P ',此时截面α为五边形因为11CD C D ∕∕,所以11CPN C PD ' ∽,所以11112CP CN C P C D '==,即113CP CC =,所以当113CP CC ≤时,截面α为五边形;故②错误;当截面α为四边形时,点P 与点1C 重合,如图,由①得,11MN A C ∕∕,所以四边形11A MNC 即为截面α,设正方体的棱长为1,则12NC =,12MA =,所以11NC MA =,所以四边形11A MNC 是等腰梯形;故③正确.故答案为:①③.【题型三】平行关系确定截面【典例分析】在三棱锥A BCD -中,AB CD a ==,截面MNPQ 与AB ,CD 都平行,则截面MNPQ 的周长等于()A .2aB .4aC .aD .无法确定【答案】A 【分析】由线面平行的性质定理确定截面MNPQ 的形状,再利用三角形相似的性质求截面MNPQ 的周长.【详解】设AMk CM=,因为//AB 平面MNPQ ,平面ABC 平面MNPQ MN =,AB Ì平面ABC ,所以//MN AB ,同理可得//PQ AB ,//MQ CD ,//NP CD ,故四边形MNPQ 为平行四边形,所以11MN PQ AB AB k ==+,1MQ NP k CD CD k==+.因为AB CD a ==,所以1aMN PQ k ==+,1ak MQ NP k==+,所以四边形MNPQ 的周长为2211aak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭.故选:A.【变式演练】1.在正方体1111ABCD A B C D -中,与AC 平行,且过正方体三个顶点的截面是___________和___________.【答案】平面11AC D 平面11A C B【分析】根据题意,结合图形,得出与AC 平行,且过正方体三个顶点的截面是平面11AC D ,平面11A C B .【详解】解:在正方体1111ABCD A B C D -中,与AC 平行,且过正方体三个顶点的截面是平面11AC D ,平面11A C B .11//AA CC ,11AA CC =,∴四边形11ACC A 是平行四边形;11//AC A C ∴,又AC ⊂/平面11AC D ,11AC ⊂平面11ACD ,//AC ∴平面11AC D ;同理//AC 平面11A C B .故答案为:平面11AC D ,平面11A CB .2.若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有()A .0条B .1条C .2条D .4条【答案】C 【分析】由平行四边形的性质有两对边平行且相等,再应用线面平行的判定可确定线面平行,由线面平行的性质、判定即可知有几条棱与平面α平行.【详解】如下图示,若平面α即为面HEGF 为平行四边形,即//HE FG 且HE FG =,//EG HF 且EG HF =,又HE ⊂面ACD ,FG ⊄面ACD ,则//FG 面ACD ,而FG ⊂面ABD ,面ABD ⋂面ACD AD =,∴//FG AD ,由线面平行判定易知://AD 平面α;同理可得//EG BC ,易得//BC 平面α.∴该三棱锥与平面α平行的棱有AD 、BC ,共2条.故选:C3.如图是一个以 A 1B 1C 1为底面的直三棱柱被一平面所截得的几何体,截面为 ABC .已知AA 1=4,BB 1=2,CC 1=3.在边AB 上是否存在一点O ,使得OC ∥平面A 1B 1C 1.【答案】存在【分析】取AB 的中点O ,连接OC ,可证明11//,OD CC OD CC =,即四边形ODC 1C 是平行四边形,所以OC ∥C 1D ,由线线平行证明线面平行,即得证【详解】存在,取AB 的中点O ,连接OC ,作OD ∥AA 1交A 1B 1于点D ,连接C 1D ,则OD ∥BB 1∥CC 1.因为O 是AB 的中点,所以OD=12(AA 1+BB 1)=3=CC 1,则四边形ODC 1C 是平行四边形,所以OC ∥C 1D.又C 1D ⊂平面C B 1A 1,且OC ⊄平面C 1B 1A 1,所以OC ∥平面A 1B 1C 1.即在边AB 上存在一点O ,使得OC ∥平面A 1B 1C 1.【题型四】垂直关系确定的截面【典例分析】已知正三棱柱(底面为正三角形的直棱柱)111ABC A B C -的体积为AB =D 是11B C 的中点,点P 是线段1A D 上的动点,过BC 且与AP 垂直的截面α与AP 交于点E ,则三棱锥P BCE -的体积的最小值为A 2B .32C .2D .52【答案】A 【分析】由正三棱柱111ABC A B C -的体积为AB =12AA =,由于P ABC P BCE A BCE V V V ---==+,所以要使三棱锥P BCE -的体积最小,则三棱锥E ABC -的体积最大,设BC 的中点为F ,作出截面如图所示,可得点E 在以AF 为直径的圆上,从而可求出点E 到底面ABC 距离的最大值,进而可求得三棱锥P BCE -的体积的最小值【详解】如图所示,因为正三棱柱111ABC A B C -的体积为AB =(214AA ⨯⨯=,即12AA =,因为(21234P ABC P BCE A BCE V V V ---=⨯⨯=+,所以要使三棱锥P BCE -的体积最小,则三棱锥E ABC -的体积最大,设BC 的中点为F ,作出截面如图所示,因为AP α⊥,所以AE EF ⊥,所以点E 在以AF 为直径的圆上,所以点E 到底面ABC 1322=,所以三棱锥P BCE -的体积的最小值为(21332-⨯⨯=.故选:A.【变式演练】1.如图,ABCD A B C D ''''-为正方体,任作平面α与对角线AC '垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l ,则()A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值【答案】B【分析】将正方体切去两个正三棱锥'A A BD -与'''C D B C -后,得到一个以平行平面'A BD 与''D B C 为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱''A B 剪开,展开在一个平面上,得到一个平行四边形''11A B B A ,考查'E 的位置,确定,S l【详解】解:将正方体切去两个正三棱锥'A A BD -与'''C D B C -后,得到一个以平行平面'A BD 与''D B C 为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱''A B 剪开,展开在一个平面上,得到一个平行四边形''11A B B A ,如图所示而多边形W 的周界展开后便成为一条与'1A A 平行的线段(如图中'1E E ),显然,''11E E A A =,所以l 为定值,当'E 位于''A B 中点时,多边形W 为正六边形,而当'E 称到'A 时,W 为正三角形,则当周长这定值l 的正六22,所以S 不是定值,故选:B 2.正方体1111ABCD A B C D -,的棱长为4,已知1AC ⊥平面α,1AC β⊂,则关于α、β截此正方体所得截面的判断正确的是()A .α截得的截面形状可能为正三角形B .1AA 与截面αC .α截得的截面形状可能为正六边形D .β截得的截面形状可能为正方形【答案】ABC【分析】首先根据已知条件确定截面,αβ,然后根据选项依次判断正误即可.【详解】如图因为正方体1111ABCD A B C D -∴AC BD ⊥,1BD CC ⊥,又∵1AC CC C = ∴BD ⊥平面11ACC A 又∵1AC ⊂平面11ACC A ∴1AC BD ⊥同理:11AC A D ⊥又∵1A D BD D ⋂=∴1AC ⊥平面1A BD ∴平面α可以是平面1A BD ,又因为11A D BD A B ==∴1A BD 为等边三角形,故A 正确取111111,,,,,A D D D CD CB BB A B 的中点,,,,,E G P K H F 并依次连接易知11=2EG A D ∥,因为EG ⊄平面1A BD ,1A D ⊂平面1A BD ∴=EG ∥平面1A BD 同理:GP 平面1A BD 又因为EG GP G = 且EG ⊂平面EGPKHF ,GP ⊂平面EGPKHF ∴平面EGPKHF ∥平面1A BD ∴平面α可以是平面EGPKHF ∵=EG GP PK KH HF FE ====∴六边形EGPKHF 是正六边形,故C 正确以平面α是平面1A BD 为例计算:设A 到平面1A BD 的距离为h等体积法求距离∵11A A BD A ABD V V --=,∴111133A BD ABD h S AA S ⋅⋅=⋅⋅又因为11=2A BD S ⨯ ,1=44=82ABD S ⨯⨯∴=3h 则1AA 与平面1A BD所成角的正弦值为1=3h AAB 正确对于D 选项:由于直线1AC β⊂,在正方体上任取点但异于1,A C ,与1,A C 可构成平面β,但是截面的形状都不是正方形,故D 错误故选:ABC3.已知正方体1111ABCD A B C D -的棱长为2,M 为1AA 的中点,平面α过点1D 且与CM 垂直,则()A .CM BD⊥B .//BD 平面αC .平面1//C BD 平面αD .平面α截正方体所得的截面面积为92【答案】ABD【分析】分析出BD ⊥面ACM ,可判断选项A ;取AD 的中点E ,由平面几何知识可知,1DM D E ⊥,从而判断出CM ⊥面11B D EF ,即平面α截正方体所得的截面为梯形11B D EF ,从而可判断剩余的三个选项.【详解】连接AC ,则AC BD ⊥,又因为BD AM ⊥,AC AM A ⊥=,所以BD ⊥面ACM ,又因为CM ⊂面ACM ,所以BD ⊥CM ,故选项A 正确;取AD 的中点E ,AB 的中点F ,连接1D F ,EF ,1B F ,DM ,11B D ,在正方形11ADD A 中,由平面几何知识可知,1DM D E ⊥,又因为1CD D E ⊥,CD DM D ⋂=,所以1D E ⊥面CDM ,所以1D E CM ⊥,又因为BD ⊥CM ,所以11B D CM ⊥,又因为1111D E B D D ⋂=,所以CM ⊥面11B D EF ,即平面α截正方体所得的截面为梯形11B D EF ,所以显然//BD 平面α,选项B 正确;平面1C BD 与平面α不平行,选项C 错误;在梯形11B D EF 中,11B D =EF =11B F D E ==所以梯形的高为2,所以梯形11B D EF 的面积为92,即平面α截正方体所得的截面面积为92,故选项D 正确.故选:ABD.【题型五】求截面周长【典例分析】如图,在正方体1111ABCD A B C D -中,4AB =,E 为棱BC 的中点,F 为棱11A D 的四等分点(靠近点1D ),过点,,A E F 作该正方体的截面,则该截面的周长是___________.【分析】首先根据面面平行的性质定理作出过点,,A E F 的正方体的截面,从而求截面的周长.【详解】如图,取11C D 的中点H ,取1CC 上靠近点1C 的三等分点G ,连接,,,,AE EG GH HF FA ,易证//,//AE HF AF EG ,则五边形AEGHF 为所求截面.因为4AB =,所以111182,3,1,3BE CE C H D H A F D F CG =======,143C G =则103AE EG ==,5,GH HF AF ===故该截面的周长是AE EG GH HF AF ++++【变式演练】1.正三棱柱ABC ﹣A 1B 1C 1中,所有棱长均为2,点E ,F 分别为棱BB 1,A 1C 1的中点,若过点A ,E ,F 作一截面,则截面的周长为()A .B .C .D .2【答案】B【分析】根据题意先作出截面,进而算出截面各边的长度,最后得到答案.【详解】如图,在正三棱柱111ABC A B C -中,延长AF 与CC 1的延长线交于M ,连接EM 交B 1C 1于P ,连接FP ,则四边形AEPF 为所求截面.过E 作EN 平行于BC 交CC 1于N ,则N 为线段CC 1的中点,由1MFC 相似于MAC △可得MC 1=2,由1MPC △相似于MEN 可得:111242,2333PC PC B P =⇒==,在1Rt AA F 中,112,1AA A F ==,则AF ==,在Rt ABE △中,2,1AB BE ==,则AE ==1Rt B EP 中,1121,3B E B P ==,则PE =在1C FP 中,11141,,603C F C P FC P ==∠=︒,由余弦定理:2224413121cos 60339PF ⎛⎫=+-⨯⨯⨯︒= ⎪⎝⎭,则PF ==故选:B.2.已知在棱长为6的正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是棱C 1D 1,B 1C 1的中点,过A ,E ,F 三点作该正方体的截面,则截面的周长为________.【答案】【分析】根据正方体的性质作出截面图形,进而算出周长.【详解】如图,延长EF ,A 1B 1,相交于点M ,连接AM ,交BB 1于点H ,延长FE ,A 1D 1,相交于点N ,连接AN ,交DD 1于点G ,连接FH ,EG ,可得截面为五边形AHFEG .因为ABCD -A 1B 1C 1D 1是棱长为6的正方体,且E ,F 分别是棱C1D 1,B 1C 1的中点,由中位线定理易得:EF =AG =AH =EG=FH AH +HF +EF +EG +AG =故答案为:+3.已知直三棱柱111ABC A B C -的侧棱长为2,AB BC ⊥,2AB BC ==.过AB 、1BB 的中点E 、F 作平面α与平面11AA C C 垂直,则所得截面周长为()A .+B C .D .【答案】C【分析】确定平面α与各棱的交点位置,计算出截面各边边长,由此可得出所得截面周长.【详解】如下图所示,取AC 的中点J ,连接BJ ,取AJ 的D ,连接DE ,取11A C 的中点K ,连接KJ 、1B K ,AB BC = ,J 为AC 的中点,则BJ AC ⊥,1AA ⊥ 平面ABC ,BJ ⊂平面ABC ,1BJ AA ∴⊥,1AC AA A ⋂=,BJ ∴⊥平面11AA C C ,D Q 、E 分别为AJ 、AB 的中点,则//DE BJ 且12DE BJ =,DE ∴⊥平面11AA C C ,DE ⊂ 平面DEF ,所以,平面DEF ⊥平面11AA C C ,所以,平面α即为平面DEF ,设平面α交11B C 于点I ,在直棱柱111ABC A B C -中,11//AA CC 且11AA CC =,所以,四边形11AA C C 为平行四边形,11//AC A C ∴且11AC A C =,J 、K 分别为AC 、11A C 的中点,1//AJ A K 且1AJ A K =,所以,四边形1AA KJ 为平行四边形,1//KJ AA ∴且1KJ AA =,11//BB AA 且11BB AA =,1//KJ BB ∴且1KJ BB =,所以,四边形1BB KJ 为平行四边形,//DE BJ ,DE ⊄平面1BB KJ ,BJ ⊂平面1BB KJ ,//DE ∴平面1BB KJ ,设平面α 平面1BB KJ FG =,DE ⊂ 平面α,所以,//DE FG ,//FG BJ ∴,//BF GJ ,所以,四边形BFGJ 为平行四边形,可得11122GJ BF BB KJ ===,所以,G 为KJ 的中点,延长DG 交11A C 于点H ,//DJ KH ,所以,DJG HKG ∠=∠,JDG KHG ∠=∠,又JG KG = ,所以,DJG HKG ≅△△,11122HK DJ AJ KC ∴===,H ∴为1KC 的中点,因为平面//ABC 平面111A B C ,平面α 平面ABC DE =,平面α 平面111A B C IH =,//DE IH ∴,//DE BJ ,1//BJ B K ,//DE IH ,1//IH B K ∴,I ∴为11B C 的中点,AB BC ⊥,2AB BC ==,则AC ==J 为AC的中点,12BJ AC ∴==122DE BJ ==,同理2IH =,因为直棱柱111ABC A B C -的棱长为2,F 为1BB 的中点,1112BF BB ∴==,由勾股定理可得EF ==IF =,1//KJ BB 且12KJ BB ==,1BB ⊥平面ABC ,KJ ∴⊥平面ABC ,AC ⊂ 平面ABC ,KJ AC ∴⊥,G 、D 分别为KJ 、AJ 的中点,则112GJ KJ ==,122DJ AJ ==,由勾股定理可得DG,同理GH =因此,截面的周长为22DE IH EF IF DH ++++=++.故选:C.【题型六】求截面面积【典例分析】已知正四棱柱1111ABCD A B C D -中,1124BE BB ==,143AB AA =,则该四棱柱被过点1A ,C ,E 的平面截得的截面面积为______.【答案】【分析】在1DD 上取点F ,使得12D F =,连接1,A F CF ,则四边形1A ECF 是平行四边形,由勾股定理可得11,,A E CE A C ,再结合余弦定理与面积公式即可求解【详解】由题意,正四棱柱1111ABCD A B C D -中,1124BE BB ==,143AB AA =,可得1118,2AA BB CC BE ====,在1DD 上取点F ,使得12D F =,连接1,A F CF ,则有11,//A F CE A F CE =,所以四边形1A ECF是平行四边形,由勾股定理可得11A E CE A C ======所以2221111cos 210A E CE A C A EC A E CE +-∠==-⨯,所以1sin 10A EC ∠=,所以四边形1A ECF 是平行四边形的面积为11sin 1210A E EC A EC ⨯⨯∠==,故答案为:【变式演练】1.正方体1111ABCD A B C D -的棱长为2,E 是棱1DD 的中点,则平面1AC E 截该正方体所得的截面面积为()A .5B .C .D .【答案】D【分析】作出示意图,设F 为1BB 的中点,连接1,,AF FC EF ,易得平面1AC E 截该正方体所得的截面为1AFC E ,再计算其面积.【详解】如图所示,设F 为1BB 的中点,连接1,AF FC ,设G 为1CC 的中点,连接,EG GB ,由//EG AB 且EG AB =,得ABGE 是平行四边形,则//AE BG 且AE BG =,又1//BG C F 且1BG C F =,得1//AE C F 且1AE C F =,则1,,,A E C F 共面,故平面1AC E 截该正方体所得的截面为1AFC E .又正方体1111ABCD A B C D -的棱长为2,11AF FC EC EA ===,1AC =EF =1EF AC ⊥,故1AFC E 的面积为12S =⨯=故选:D.2.在棱长为a 的正方体1111ABCD A B C D -中,E 为1AA 的中点,则过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面面积为()A 2B .298aC .24aD 2【答案】B【分析】取11A D 中点F ,连接BE 、EF 、1C F 、1BC 、1AD ,证明出1//EF BC ,故四点B 、1C 、E 、F 共面,所以过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面为等腰梯形1EFC B ,根据已知,即可求解.【详解】取11A D 中点F ,连接BE 、EF 、1C F 、1BC 、1AD ,因为11//AB C D 且11AB C D =,所以,四边形11ABC D 为平行四边形,所以,11//AD BC ,E 、F 分别为1AA 、11A D 的中点,所以,1//EF AD 且112EF AD a =,所以,1//EF BC ,故B 、1C 、E 、F 四点共面,所以过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面为等腰梯形1EFC B ,其中2EF a =,1BC =,12BE C F a =,过点E 、F 在平面1BC FE 内分别作1BC 的垂线,垂足点分别为G 、H ,因为1BE C F =,1EBG FC H ∠=∠,12EGB FHC π∠=∠=,所以,1Rt EBG Rt FHC ≅△△,故1BG C H =,在平面1BC FE 内,因为1EG BC ⊥,1FH BC ⊥,1//EF BC ,所以,四边形EFHG 为矩形,则GH EF a =,所以,112BC EF BG C H a -==,所以,梯形1BC FE 的高4h a ==,梯形1B CFE 的面积2192428a S a a ⎫=⨯⨯=⎪⎪⎭.故选:B.3.已知正方体1111ABCD A B C D -的棱长为2,点P 在线段1CB 上,且12B P PC =,平面α经过点1,,A P C ,则正方体1111ABCD A B C D -被平面α截得的截面为___________,其面积为___________.【答案】四边形1AECQ 【分析】第一空,先画出1,,A P C 所在平面,由平面11//AA DD 平面11BB CC 得出1//AQ EC ,1//AQ EC ,1A E C Q ,,,四点共面,即为所求截面;第二空由已知条件可求出11AE EC AC ==1AEC 的面积,再乘以2可得截面的面积.【详解】如图所示:1,,A P C 确定一个平面α,因为平面11//AA DD 平面11BB CC ,所以1//AQ EC ,同理1//AQ EC ,所以四边形1AEC Q 是平行四边形.即正方体被平面截的截面.因为12B P PC =,所以112C B CE =,即1EC EB ==所以11AE EC AC ===由余弦定理得:22211111cos 25AE EC AC AEC AE EC +-∠==⨯,所以1sin AEC ∠,所以1AEC Q S四边形1112sin 22AE EC AEC =⨯⨯⨯∠=故答案为:四边形1AEC Q。
立体几何的截面问题

立体几何的截面问题
嘿,咱来聊聊立体几何的截面问题啊!比如说,你怎么知道一个几何体被某个平面截了之后,截面会是什么形状呢?这就好像你切一块蛋糕,你能想象出不同的切法会得到什么样的切面吗?这多有意思呀!
再想想,如何找到截面与几何体各个面的交线呢?这不就像是在一个复杂的迷宫里找特定的通道一样吗?
还有哦,截面面积怎么求呢?哇,这可不是个简单的事儿呢,就像要算出一个奇形怪状的图形有多大一样难。
比如说一个三棱锥,它的截面面积能那么容易就求出来吗?
而且呀,截面问题里还常常会有最值问题呢!哎呀呀,就好像要在一堆选择里找到那个最棒的、最特别的一样,得绞尽脑汁去思考呢!
不同的几何体,截面的情况也完全不同呢!这就像不同性格的人面对同样的事情会有不同的反应,你说神奇不神奇?咱可不能小瞧了这立体几何的截面问题呀!。
立体几何中的 截面问题

立体几何中的截面问题立体几何中的截面问题一、引言1·1 概述本文档将详细介绍立体几何中的截面问题。
截面问题是立体几何中常见的问题类型之一,涉及到在给定几何体上进行切割,求解切割平面与几何体的交线或截面的形状、性质等问题。
1·2 目的本文档的目的是为读者提供关于立体几何中截面问题的全面了解,包括截面的定义、不同几何体的截面特征、相关定理和推论的证明方法、截面问题的应用等。
1·3 适用范围本文档适用于对立体几何有一定了解的读者,特别是对截面问题感兴趣的学生、教师和研究人员。
二、截面的定义与分类2·1 截面的定义截面是指一个平面与立体几何体相交所得的曲线、线段或点集。
2·2 平行截面与垂直截面根据切割平面与几何体的相对位置,我们可以将截面分为平行截面和垂直截面两种类型。
三、不同几何体的截面特征3·1 球体的截面3·1·1 截面形状球体的截面是一个圆或一个点。
3·1·2 截面性质球体的截面是等面积的,并且与球心的连线垂直于截面。
3·2 圆柱体的截面3·2·1 截面形状圆柱体的截面可以是一个圆、一个椭圆、一条直线或两个平行线段。
3·2·2 截面性质圆柱体的截面与轴线平行或垂直,并且截面上的点到轴线的距离是恒定的。
3·3 圆锥体的截面3·3·1 截面形状圆锥体的截面可以是一个圆、一个三角形、一个直线或两个平行线段。
3·3·2 截面性质圆锥体的截面与轴线平行或垂直,并且截面上的点到轴线的距离是变化的。
3·4 正多面体的截面3·4·1 截面形状正多面体的截面可以是一个正多边形、一个多边形、一个直线或两个平行线段。
3·4·2 截面性质正多面体的截面与对称轴平行或垂直,并且截面上的点到对称轴的距离是恒定的。
二轮复习第32讲 立体几何中的截面问题

第32讲立体几何中的截面问题一.选择题(共13小题)1.(2021•诸暨市校级期中)过正方体ABCD-A1B1C1D1的棱AB、BC的中点E、F作一个截面,使截面与底面ABCD所成二面角为45°,则此截面的形状为( )A.三角形或五边形B.三角形或四边形C.正六边形D.三角形或六边形【解答】解:过棱AB、BC的中点E、F作正方体AC1的截面,∵二面角D1-EF-D,二面角B1-EF-B都大于450,∴当截面为EFHJIG时,如下图所示时,为六边形,当截面为EFM时,如下图所示时,为三边形,故选:D.2.(2021•黄陵县校级二模)如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )A.直线AC与直线EC′所成角为45°B.点E到平面OCD′的距离为12C.四面体O EA′B′在平面ABCD上的射影是面积为16的三角形D.过点O,E,C的平面截正方体所得截面的面积为62【解答】解:对于A,连结A′C′,A′E,C′E,则A′C′⎳AC,∴∠A′C′E为直线AC与直线EC′所成角,在△A′C′E中,A′C′=2,A′E=C′E=5 2,∴cos∠A′C′E=2+54-542×2×52=105,∴直线AC与直线EC′所成角的余弦值为105,故A错误;对于B,连结CD′,A′B,则O∈平面BCD′A′,∴B′到平面BCD′A′的距离为12AB′=22,∴E到平面BCD′A′的距离为24,故B错误;对于C,O在底面ABCD的射影为正方形ABCD的中心,A′的射影为A,B′和E在底面的射影为B,∴四面体O EA′B′在平面ABCD上的射影是面积为14的三角形,故C错误;对于D,取DD′中点F,连结A′E,A′F,CE,CF,则菱形CEA′F是过O,C,E的平面与正方体的截面,∵EF=2,A′C=3,∴截面面积S=12×2×3=62.故D正确.故选:D.3.(2021•张家口期末)在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为棱AB,C1D1的中点,G为棱CC1靠近C点的三等分点,用过点E,F,G的平面截正方体,则截面图形的周长为( )A.13+223B.10+223C.13+226D.143【解答】解:根据题意作出截面如图,利用勾股定理和对边相等易得周长为10+223,故选:B.4.(2021春•天心区校级月考)在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1,C1D1的中点,过点A、C、E、F的截面与平面BDD1B1的交线为m,则异面直线m、CC1所成角的正切值为( ) A.2B.324C.22D.24【解答】解:如图所示,O,O1分别为上下底面中心,G=EF∩B1D1.∵E,F分别为A1D1,C1D1的中点,∴G为GO1的中点.则∠GOO1为异面直线m、CC1所成角.tan∠GOO1=GO1OO1=14×21=24,故选:D.5.(2021春•瑞金市月考)在棱长为4的正方体ABCD-A1B1C1D1中,点E,F分别为AA1,CC1的中点,则过B,E,F三点的平面与正方体各个面的交线组成的平面多边形的面积为( )A.42B.86C.63D.125【解答】解:连接ED1,FD1,显然有ED1⎳BF,FD1⎳BE,故过B,E,F三点的截面多边形为平行四边形BED1F,又BE=BF,∴四边形BED1F为菱形,∵正方体棱长为4,故EF=42,BD1=43,∴菱形BED1F的面积为12×42×43=86.故选:B.6.(2021•丽水期末)斜线段AB与平面α所成的角为60°,B为斜足,点P是平面α上的动点且满足∠PAB=60°,则动点P的轨迹是( )A.直线B.抛物线C.椭圆D.双曲线的一支【解答】解:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.此题中平面α上的动点P满足∠PAB=60°,可理解为P在以AB为轴的圆锥的侧面上,再由斜线段AB与平面α所成的角为60°,可知P的轨迹符合圆锥曲线中抛物线定义.故可知动点P的轨迹是抛物线.故选:B.7.(2021•泉州模拟)设四棱锥P-ABCD的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( )A.不存在B.只有1个C.恰有4个D.有无数多个【解答】证明:由侧面PAD与侧面PBC相交,侧面PAB与侧面PCD相交,设两组相交平面的交线分别为m,n,由m,n确定的平面为β,作α与β平行且与四条侧棱相交,交点分别为A1,B1,C1,D1则由面面平行的性质定理得:A1B1⎳m⎳D1C1,A1D1⎳n⎳B1C1,从而得截面必为平行四边形.由于平面α可以上下移动,则这样的平面α有无数多个.故选:D.8.(2021•西湖区校级模拟)如图,ABCD-A′B′C′D′为正方体,任作平面α与对角线AC′垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )A.S为定值,l不为定值B.S不为定值,l为定值C.S与l均为定值D.S与l均不为定值【解答】解:将正方体切去两个正三棱锥A-A′BD与C′-D′B′C后,得到一个以平行平面A′BD与D′B′C为上、下底面的几何体V,V的每个侧面都是等腰直角三角形,截面多边形W的每一条边分别与V的底面上的一条边平行,将V的侧面沿棱A′B′剪开,展平在一张平面上,得到一个▱A′B′B1A1,如图而多边形W的周界展开后便成为一条与A′A1平行的线段(如图中E′E1),显然E′E1=A′A1,故l为定值.当E′位于A′B′中点时,多边形W为正六边形,而当E′移至A′处时,W为正三角形,易知周长为定值l的正六边形与正三角形面积分别为324l2与336l2,故S不为定值.故选:B.9.(2021•安徽二模)已知正四面体的中心与球心O重合,正四面体的棱长为26,球的半径为5,则正四面体表面与球面的交线的总长度为( )A.4πB.82πC.122πD.12π【解答】解:∵正四面体A-BCD的中心与球心O重合,正四面体的棱长为26,取CD中点E,连结BE,AE,过A作AF⊥底面BCD,交BE于F,则BE=AE=(26)2-(6)2=32,BF=23BE=22,DF=13BE=2,AF=(26)2-(22)2=4,设正四面体内切球半径为r,则(4-r)2=(22)2+r2,解得正四面体内切球半径为r=1,∵球的半径为5,∴由球的半径知球被平面截得小圆半径为r1=5-1=2,故球被正四面体一个平面截曲线为三段圆弧,且每段弧所对中心角为30°,∴正四面体表面与球面的交线的总长度为:4×3×30°360°×2π×2=4π.故选:A.10.(2021春•浙江期中)如图所示,一个圆柱形乒乓球筒,高为12厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )A.154B.32C.265D.15【解答】解:不妨设椭圆方程为x2a2+y2b2=1(a>b>0),由题意得2a=12-4 b=2,解得a=4,b=2,c=16-4=23,∴该椭圆的离心率为e=c a=234=32.故选:B.11.(2021秋•翠屏区校级期末)如图,A为平面α内一定点,AB是平面α的定长斜线段,A为斜足,若点P 在平面α内运动,使ΔABP面积为定值,则动点P的轨迹是( )A.圆B.两条平行线C.一条直线D.椭圆【解答】解:因为三角形面积为定值,以定长斜线段AB为底,则得P到直线AB的距离为定值,分析可得,点P在以AB为轴线的圆柱面与平面α的交线上,且α与圆柱的轴线斜交,由平面与圆柱面的截面的性质判断,可得P的轨迹为椭圆;故选:D.12.(2021春•江西期中)已知AB是平面α的斜线段,A为斜足,若AB与平面α成60°角,过定点B的动直线l与斜线AB成60°角,且交α于点P,则动点P的轨迹是( )A.圆B.椭圆C.双曲线D.抛物线【解答】解:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.此题AB与平面α成60°角,过定点B的动直线l与斜线AB成60°角,且交α于点P,故可知动点P的轨迹是抛物线.故选:D.13.(2021•滨州一模)如图,斜线段AB与平面α所成的角为π4,B为斜足.平面α上的动点P满足∠PAB =π6,则点P的轨迹为( )A.圆B.椭圆C.双曲线的一部分D.抛物线的一部分【解答】解:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.参考上图:此题中平面α上的动点P满足∠PAB=π6,可理解为P在以AB为轴的圆锥的侧面上,再由斜线段AB与平面α所成的角为π4,可知P的轨迹符合圆锥曲线中椭圆定义,故可知动点P的轨迹是椭圆.故选:B.二.多选题(共5小题)14.(2021春•湖南期末)已知在正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC上的中点,过E,F 的平面α与底面ABCD所成的锐二面角为60°,则正方体被平面α所截的截面形状可能为( )A.三角形B.四边形C.五边形D.六边形【解答】解:如图所示:设正方体的棱长为4a,在BB1上取一点G使得平面EFG与平面ABCD所成的锐二面角为60°,因为E,F分别为棱AB,BC的中点,所以EG=FG,连接BD交EF于点N,连接AC,所以EF⊥BN,且N为EF的中点,BN=14BD,所以GN⊥EF,所以∠GNB为平面EFG与平面ABCD所成的锐二面角为60°,所以GB=tan60°⋅BN=3×14×42a=6a,所以GBBB1=6a4a=64,所以此时平面EFG为平面α,所以平面α为三角形,故A正确;在AA1和CC1上分别取点M和点H,使得AM=CH,取MH,AC的中点K,O,则KO⊥平面ABCD,又因为EF⊂平面ABCD,所以KO⊥EF又NO⊥EF,所以EF⊥平面KNO,又因为KN⊂平面KNO,所以∠KNO为平面MEFH与平面ABCD所成的锐二面角为60°,所以KO=tan60°⋅ON=3×14×42a=6a,所以KO BB 1=MA AA 1=CH CC 1=6a 4a =64,延长FH 交B 1C 1于T ,延长EM 交B 1A 1于S ,连接ST 交A 1D 1于Q ,交C 1D 1于P ,连接HP ,MQ ,则平面MEFHPQ 为平面α,所以平面α为六边形,故D 正确.故选:AD .15.(2021•唐山三模)将边长为2的正方形ABCD 沿对角线BD 折成直二面角A -BD -C ,如图所示,点E ,F 分别为线段BC ,AD 的中点,则( )A .AC 与EF 所成的角为45°B .EF ⊥BCC .过EF 且与BD 平行的平面截四面体A -BCD 所得截面的面积为2D .四面体A -BCD 的外接球的表面积为8π【解答】解:如图建立空间直角坐标系,则A (0,0,2),C (0,2,0),B (2,0,0),D (-2,0,0),E 22,22,0 ,F -22,0,22.对于A ,∵AC =(0,2,-2),EF =-2,-22,22 ,∴cos <AC ,EF >=AC ⋅EF |AC ||EF |=-33,故A 错;对于B ,∵BC =(-2,2,0),∴BC ⋅EF =2-1=1≠0,故B 错;对于C ,取CD 中点为M ,AB 的中点为N ,过EF 且与BD 平行的平面截四面体A -BCD 所得截面为矩形EMFN ,EM =12DB =2,MF =12AC =1,故截面的面积为2,故C 正确;对于D ,四面体ABCD 的外接球的球心为O ,半径为R =2,所以表面积为4πR 2=8π,所以D 对.故选:CD.16.(2021•雁峰区校级模拟)由四个三角形围成的多面体称为四面体,对棱相等的四面体称为等腰四面体.已知如图等腰四面体ABCD中,AB=CD,AD=BC,AC=BD,E,F,G,H分别是棱AB,BC,CD,DA的中点.下面结论中,正确的有( )A.直线EG,FH有可能是异面直线B.EG⊥ABC.过直线EG的平面截四面体外接球所得截面面积为定值D.共顶点A的三个侧面面角和(∠BAC+∠CAD+∠DAB)等于180°【解答】解:如图所示:对于A:由于E、F、G、H为各边的中点,所以:EF⎳AC⎳HG,所以E、F、G、H四点共面,故A错误;对于B:由于BD=AC,BC=AD,CD=CD,所以ΔACD≅ΔBCD,所以∠ACD=∠BDC,故ΔACG≅ΔBDG,所以AG=BG,由于点E为AB的中点,所以EG⊥AB,故B正确;对于C:把四面体ABCD补形为长方体,则四面体与长方体外接球为同一个球,球心为EG的中点,所以截面为球的大圆,其面积为定值,故C正确;对于D:四个面全等,设一个面的三个内角为α、β、γ、则共顶点的三个侧面的内角和为α+β+γ=180°,故D 正确;故选:BCD.17.(2021•江苏模拟)正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F在侧面CDD1C1上运动,且满足B1 F⎳平面A1BE.以下命题正确的有( )A.侧面CDD1C1上存在点F,使得B1F⊥CD1B.直线B1F与直线BC所成角可能为30°C.平面A1BE与平面CDD1C1所成锐二面角的正切值为22D.设正方体棱长为1,则过点E,F,A的平面截正方体所得的截面面积最大为62【解答】解:作辅助线,I、J、N,分别为所在棱中点,P点为A1E与AD延长线交点,BP连线交CD于G,则G为CD中点,K为IJ中点,L为A1B与A1B交点;对于A,当F取IJ中点K时,B1K⊥IJ,IJ⎳CD1所以B1K⊥CD1,B1K⎳LM,LM⊂平面A1BE,B1K⎳平面A1BE,所以A对;对于B,当点F与点I或点J重合时,B1F与直线BC所成的角最大,所以tan∠C1B1F=12<33=tan30°,所以B不对;对于C,平面AA1B1B⎳平面CDD1C1,所以平面A1BE与平面CDD1C1所锐二面角,即为平面A1BE与平面AA1B1B所成锐二面角,二面角的平面角即为∠PLA,其正切值为APAL=222=22,所以C对;对于D,因为过点E,F,A的平面截正方体所得的截面面积最大的截面为菱形AEC1N,其面积为12EN⋅AC1=122⋅3=62,所以D对.故选:ACD.18.(2021•新罗区校级月考)如图,AB是平面α的斜线段,A为斜足,点C满足|BC|=λ|AC|(λ>0),且在平面α内运动,则有以下几个命题,其中正确的命题是( )A.当λ=1时,点C的轨迹是线段B.当λ=1时,点C的轨迹是一条直线C.当λ=2时,点C的轨迹是圆D.当λ=2时,点C的轨迹是椭圆【解答】解:在ΔABC中,点C满足|BC|=λ|AC|(λ>0),当λ=1时,即|BC|=|AC|,则C在过AB的中点且垂直直线AB的平面β与平面α的交线上,即点C的轨迹是一条直线,故A错误,B正确;当λ=2时,|BC|=2|AC|,设点B在平面α内的射影为D,连接BD,AD,CD,设|BD|=h,|AD|=2a,则|BC|=|CD|2+h2,在平面α内,以AD所在直线为x轴,以AD的中垂线为y轴,建立如图所示坐标系:设C(x,y),则A(-a,0),D(a,0),所以|CA|=(x+a)2+y2,|CD|=(x-a)2+y2,|CB|=(x-a)2+y2+h2,则(x-a)2+y2+h2=2(x+a)2+y2,整理可得x+5 3a2+y2=169a2+h23,即C的轨迹是圆,故C正确,D错误;故选:BC.三.填空题(共9小题)19.(2021春•邵阳县期末)已知正方体的棱长为1,每条棱所在的直线与平面α所成的角相等,则平面α截正方体所得的截面面积的最大值为 334 .【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且是正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长2 2,α截此正方体所得截面最大值为:6×34×222=334.故答案为:334.20.(2021•上海模拟)如图,圆锥VO 的母线长为l ,轴截面VAB 的顶角∠AVB =150°,则过此圆锥的顶点作该圆锥的任意截面VCD ,则ΔVCD 面积的最大值是 12l 2 ,此时∠VCD = .【解答】解:过此圆锥的顶点作该圆锥的任意截面VCD ,则ΔVCD 面积的最大值时是等腰直角三角形时,且顶角为90°,三角形VCD 中,VC =VD =l ,所以此时S ΔVCD =12⋅l 2⋅sin90°=12l 2,且∠VCD =45°故答案分别为:12l 2,45°.21.(2021•闵行区校级月考)如图所示,点P ,Q ,R 分别在正方体ABCD -A 1B 1C 1D 1的棱AB ,BC ,CC 1上,AP =5,PB =15,BQ =15,CR =10,那么正方体被平面PQR 所截得的截面面积是 525 .【解答】解:连接AC ,因为BP =BQ ,所以PQ ⎳AC ,如图,过点R 作平行于PQ 的直线交AA 1于点U ,连接PU ,过点R 作SR ⎳UP 交C 1D 1于点S ,过点U 作TU ⎳RQ 交A 1D 1于点T ,连接ST ,则六边形PQRSTU 为平面PQR 与正方体的交线组成的多边形,UR 的中点是正方体的中心,所以六边形PQRSTU 上的点关于正方体的中心对称,因此六边形PQRSTU 的面积是梯形PQRU 的2倍,易知UR =202,PQ =152,PU =55,所以梯形PQRU 的高h =(55)2-552 2=1522.故所求面积为(202+152)×1522=525.故答案为:525.22.过正四面体ABCD 的顶点A 作一个形状为等腰三角形的截面,且使截面与底面BCD 所成的角为75°,这样的截面共可作出 18 个.【解答】解:作正四面体A -BCD 的高AO ,连接BO 交CD 于E ,连接AE .则E 为CD 的中点,O 为△等边三角形BCD 的中心.∴BE ⊥CD ,AE ⊥CD ,∴∠AEB 为二面角A -CD -B 的平面角.设AB =2,则BE =3,∴OE =13BE =33,OB =23BE =233.∴AO =AB 2-BO 2=263.∴tan ∠AEB =AO OE=22.∵tan75°=sin75°cos75°=6+226-22=2+3>22,∴∠AEB <75°.在平面BCD 内,以O 为圆心,以OA ∙tan75°为半径作圆O ,则圆O 在ΔBCD 内部.∴若截面AMN 与底面BCD 所成角为75°,则截面AMN 与平面BCD 的交线为圆O 的切线.(1)若圆O 的切线与ΔBCD 的一边平行,如图1所示:则存在6个符合条件的截面三角形AMN .(2)若圆O 的切线过三角形的顶点,不妨设过点B ,交CD 于M ,如图2所示:则由ΔACM ≅ΔBCM 可得AM =BM ,故截面ABM 为符合条件的截面三角形,显然存在6个这样的截面三角形.(3)若圆O 的切线MN 与三角形BCD 的两边相交,不妨设与NC 交于M ,与CD 交于N ,且BM =CN ,如图3所示:显然ΔABM ≅ΔACN ,故而AM =AN ,∴截面AMN 为符合条件的截面三角形.显然这样的截面也有6个.综上,符合条件的截面共有18个.故答案为:18.23.(2021春•绍兴期末)已知四面体ABCD 的所有棱长均为4,点O 满足OA =OB =OC =OD ,则以O 为球心,2为半径的球与四面体ABCD 表面所得交线总长度为 1633π .【解答】解:∵正四面体A -BCD 的中心与球心O 重合,正四面体的棱长为4,取CD 中点E ,连结BE ,AE ,过A 作AF ⊥底面BCD ,交BE 于F ,则BE =4sin60°=23,BF =23BE =433,∴AF =AB 2-BF 2=463,又(AF -OF )2=OF 2+BF 2,∴OF =63,由球的半径知球被平面截得小圆半径为r =(2)2-63 2=233.而ΔABC 的内切圆半径为233,故球被正四面体一个平面截曲线为圆弧,∴正四面体表面与球面的交线的总长度为:4×2π×233=1633π.故答案为:1633π.24.(2021春•开福区校级月考)以棱长为26的正四面体中心点O 为球心,以R (0<R <3)为半径的球面与正四面体的表面相交得到若干个圆(或圆弧)的总长度的取值范围是 (0,82π] .【解答】解:将S -ABC 正四面体看作是正方体的6条面对角线围成的正四面体,设正方体棱长为a ,则2a =26,故a =23,于是正四面体的外接球半径为3a 2=3,又正四面体的体积为V S -ABC =a 3-4×13×12a 2×a =a 33=83,表面积为S 表=4×34×(26)2=243,设正四面体的内切球半径为r 1,则13×243×r 1=83,解得r 1=1.设三角形ABC 的内切圆半径为r 2,圆心为O ′,D 为BC 的中点,则∠O ′BD =30°,BD =6,故r 2=O ′D =2,此时R =r 12+r 22=3,(1)当0<R ≤1时,球面与正四面体无交点或相切,此时圆弧总长度为0;(2)当1<R ≤3时,球面与正四面体的每个面交线均为相等的圆,设圆的半径为r ,则0<r ≤2,故当r =2时,圆弧总长度取得最大值,最大值为4×2π×2=82π;(3)当3<R <3时,球面与正四面体的每个面的交线均为三段相等的圆弧,不妨设其中一段为EF,如图所示:设∠DO ′E =α,显然0<α<π3,O ′E =2cos α,∠EO ′F =2π3-α =2π3-2α,于是EF 的长为f (α)=2π3-2α ∙O ′E =2π3-2α ∙2cos α,∴f ′(α)=-22cos α+22π3-22α sin αcos 2α=22π3sin α-αsin α-cos α cos 2α,令g (α)=π3sin α-αsin α-cos α0<α<π3 ,则g ′(α)=π3cos α-αcos α=π3-α cos α>0,∴g (α)在0,π3 上单调递增,故g (α)<g π3 =-12<0,∴f ′(α)<0,故f (α)在0,π3 上单调递减,∴f (α)<f (0)=22π3,故当3<R <3时,圆弧总长度小于22π3×3×4=82π.综上,圆(或圆弧)的总长度的取值范围是:(0,82π].故答案为:(0,82π].25.(2021春•金山区校级期中)设正方体ABCD -A 1B 1C 1D 1的棱长为2,α为过直线BD 1的平面,则α截该正方体的截面面积的取值范围是 [26,42] .【解答】解:以点D 1为坐标原点,建立空间直角坐标系如图所示,则B (2,2,2),D 1(0,0,0),设α与棱CC 1的交点为P ,与棱AA 1的交点为G ,则四边形BGD 1P 为平行四边形,在平面α内过点P 作BD 1的垂线,垂足为Q ,则截面的面积S =|BD 1 ||PQ |=23|PQ |,设Q (x ,x ,x ),P (0,2,y ),则D 1B =(2,2,2),PQ =(x ,x -2,x -y ),因为D 1B ⋅PQ =0,所以2x +2(x -2)+2(x -y )=0,所以3x -y -2=0,所以y =3x -2,因为0≤3x -2≤2,所以23≤x ≤43,又|PQ |=x 2+(x -2)2+(x -y )2=6x 2-12x +8=6(x -1)2+2,有23≤x ≤43,可得2≤|PQ |≤263,所以26≤S ≤42,则α截该正方体的截面面积的取值范围是[26,42].故答案为:[26,42].26.(2021春•杨浦区校级期末)如图,顶点为P 的圆锥的轴截面是等腰直角三角形,母线PA =4,O 是底面圆心,B 是底面圆内一点,且AB ⊥OB ,C 为PA 的中点,OD ⊥PB ,垂足为D ,当三棱锥O -PCD 的体积最大时,OB = 263 .【解答】解:AB ⊥OB ,可得PB ⊥AB ,即AB ⊥面POB ,所以面PAB ⊥面POB .OD ⊥PB ,则OD ⊥面PAB ,OD ⊥DC ,OD ⊥PC ,又,PC ⊥OC ,所以PC ⊥面OCD .即PC 是三棱锥P -OCD 的高.PC =OC =2.而ΔOCD 的面积在OD =DC =2时取得最大值(斜边=2的直角三角形).当OD =2时,由PO =22,知∠OPB =30°,OB =PO tan30°=263.故答案为:263.27.(2021•东阳市校级月考)顶点为P 的圆锥的轴截面是等腰直角三角形,A 是底面圆周上的点,B 是底面圆内的点,O 为底面圆圆心,AB ⊥OB ,垂足为B ,OH ⊥PB ,垂足为H ,且PA =4,C 是PA 的中点,则当三棱锥O -HPC 的体积最大时,OB 的长为 263 .【解答】解:∵AB ⊥OB ,AB ⊥OP ,∴AB ⊥PB ,∵OH ⊥PB ,∴面PAB ⊥面POB ,∴OH ⊥HC ,OH ⊥PA ,∵C 是PA 的中点,∴OC ⊥PA ,∴当HO =HC 时,S ΔHOC 最大,即V O -HPC =V P -HCO 最大,此时,HO =2,∴HO =12OP ,∴∠HPO =30°,∴OB =OP ∙tan30°=263,故答案为:263.四.解答题(共3小题)28.如图,G 是正方体ABCD -A 1B 1C 1D 1的棱的DD 1延长线上的一点,E 、F 是棱AB 、BC 的中点,试分别画出:(1)过点G 、A 、C 的平面与正方体表面的交线;(2)过点E、F、D1的平面与正方体表面的交线.【解答】解:如图,过点A、C、G的平面为平面AC1H,过点G、A、C的平面与正方体表面的交线分别为:AH,HI,IC,AC.(2)如图,过点E、F、D1的平面为平面EFRD1O,过点E、F、D1的平面与正方体表面的交线分别为:D1O,OE,EF,FR.RD1.29.如图,已知底面为平行四边形的四棱锥P-ABCD中,平面MNGH与直线PB和直线AC平行,点E为PD的中点,点F在CD上,且DF:FC=1:2.(1)求证:四边形MNGH是平行四边形;(2)求作过EF作四棱锥P-ABCD的截面,使PB与截面平行(写出作图过程,不要求证明).截面的定义:用一个平面去截一个几何体,平面与几何体的表面的交线围成的平面图形.【解答】证明:(1)∵平面MNGH与直线PB平行,MH⊂平面MNGH,NG⊂平面MNGH,又MH与PB共面于平面PAB,NG与PB共面于平面PBC,∴MH⎳PB,NG⎳PB,∴MH⎳NG,∵平面MNGH与直线AC平行,MN⊂平面MNGH,HG⊂平面MNGH,又MN与AC共面于ABCD,HG与AC共面于PAC,∴MN ⎳AC ,HG ⎳AC ,∴MN ⎳HG ,∴四边形MNGH 是平行四边形.解:(2)延长FO ,与AB 交于点G ,延长FE ,与面PAB 交于点S (直线l 为平面PAB 和平面PCD 的交线),连接SG ,与PA 交于点H ,连接HE .平面EFGH 为所求截面,PB ⎳截面EFGH .30.(2021•邢台月考)如图,在边长为3的正方体ABCD -A 1B 1C 1D 1中,点P ,Q ,R 分别在棱AB ,B 1C 1,D 1D 上,且AP =B 1Q =D 1R =1.(1)求点D 到平面PQR 的距离;(2)若平面PQR 与线段AC 1的交点为N ,求AN AC 1的值.【解答】解:(1)以点D 为坐标原点,分别以DA ,DC ,DD 1 的方向为x ,y ,z 轴的正方向,建立空间直角坐标系D -xyz ,则A (3,0,0),P (3,1,0),R (0,0,2),Q (2,3,4),C 1(0,3,3),PQ =(-1,2,3),PR =(-3,-1,2),AP =(0,1,0),AC 1 =(-3,3,3),DR =(0,0,2),设平面PQR 的法向量为m =(x ,y ,z ),则m ⋅PQ =0m ⋅PR =0 ,代入可得-x +2y +3z =0-3x -y +2z =0 ,令x =1,则y =-1,z =1,所以m =(x ,y ,z ),故点D 到平面PQR 的距离为m ⋅DR |m |=23=233.(2)因为点N 在平面PQR 内,可设PN =mPQ +nPR (其中m ,n 为常数,又AN 与AC 1 共线,可设AN =kAC 1,由图可得AN =AP +PN =AP +mPQ +nPR =kAC 1 ,即(0,1,0)+m (-1,2,3)+n (-3,-1,2)=k (-3,3,3),整理得-m -3n =-3k ①1+2m -n =3k ②3m +2n =3k ③,由①③可得2m =n ④,由②③可得m +3n ⑤,联立④⑤解得m=17n =27 ,代入②可得k =13,所以AN =13AC 1 ,即AN AC 1=13.。
高中总复习二轮数学精品课件 专题四 立体几何 素养提升微专题(五) 截面问题

21
3
2
-12
=
2 3
>1,故球
3
O 与正方体 ABCD-A1B1C1D1 的每个面的交线均为四段圆弧,易求得每段圆
π
π
2π
弧所对的圆心角为6,故每个面上的四段圆弧所对的圆心角之和为6 ×4= 3 ,
2π
2 3
故每个面上的交线长为 3 × 3
4 3π
|1 |sin∠CA1N=
时,Smin=
6
2
< 2.
6
综上所述,截面面积的最小值为 2 .
2( 2 -
+ 1) =
2
1 2
- 2
3
+4
,当
1
t=2
4.如图,正方体ABCD-A1B1C1D1的棱长为2,P为BC的中点,Q为CC1的中点,则
过点A,P,Q的平面α截该正方体所得截面的周长为
.
答案 2 5+3 2
A.1
5
B.4
)
6
C. 2
D. 2
答案 C
解析 以A为坐标原点,AB,AD,AA1所在直线分别为x轴、y轴、z轴,建立空间
直角坐标系如图所示,则
A(0,0,0),A1(0,0,1),B(1,0,0),B1(1,0,1),C(1,1,0),C1(1,1,1),D(0,1,0),D1(0,1,1).
设点P(1,t,t),其中0≤t≤1.
· =-1+tz=0,得
1
z= >1,不合题意.
设平面 α 交棱 AB 于点 M(x,0,0),则=(x-1,-1,0),由 ·=x-1-(t-1)=0,得
第32讲 立体几何中的截面问题(解析版)

第32讲 立体几何中的截面问题参考答案与试题解析一.选择题(共13小题)1.(2021•诸暨市校级期中)过正方体1111ABCD A B C D -的棱AB 、BC 的中点E 、F 作一个截面,使截面与底面ABCD 所成二面角为45︒,则此截面的形状为( ) A .三角形或五边形 B .三角形或四边形 C .正六边形D .三角形或六边形【解答】解:过棱AB 、BC 的中点E 、F 作正方体1AC 的截面, 二面角1D EF D --,二面角1B EF B --都大于045,∴当截面为EFHJIG 时,如下图所示时,为六边形,当截面为EFM 时,如下图所示时,为三边形, 故选:D .2.(2021•黄陵县校级二模)如图所示,点O 为正方体ABCD A B C D ''''的中心,点E 为棱B B '的中点,若1AB =,则下面说法正确的是( )A .直线AC 与直线EC '所成角为45︒B .点E 到平面OCD '的距离为12C .四面体O EA B ''在平面ABCD 上的射影是面积为16的三角形D .过点O ,E ,C 【解答】解:对于A ,连结A C '',A E ',C E ',则//AC AC '',AC E ∴∠''为直线AC 与直线EC '所成角,在△A C E ''中,A C ''=A E C E '='=,552cos A C E +-∴∠''== ∴直线AC 与直线EC ',故A 错误; 对于B ,连结CD ',A B ',则O ∈平面BCD A '',B ∴'到平面BCD A ''的距离为12AB '=E ∴到平面BCD A '',故B 错误; 对于C ,O 在底面ABCD 的射影为正方形ABCD 的中心,A '的射影为A ,B '和E 在底面的射影为B ,∴四面体O EA B ''在平面ABCD 上的射影是面积为14的三角形,故C 错误; 对于D ,取DD '中点F ,连结A E ',A F ',CE ,CF ,则菱形CEA F '是过O ,C ,E 的平面与正方体的截面,2EF =A C '∴截面面积12S =.故D 正确. 故选:D .3.(2021•张家口期末)在棱长为1的正方体1111ABCD A B C D -中,E ,F 分别为棱AB ,11C D 的中点,G 为棱1CC 靠近C 点的三等分点,用过点E ,F ,G 的平面截正方体,则截面图形的周长为( )A B C D .143【解答】解:根据题意作出截面如图,, 故选:B .4.(2021春•天心区校级月考)在棱长为1的正方体1111ABCD A B C D -中,E ,F 分别为11A D ,11C D 的中点,过点A 、C 、E 、F 的截面与平面11BDD B 的交线为m ,则异面直线m 、1CC 所成角的正切值为( )A B C D 【解答】解:如图所示,O ,1O 分别为上下底面中心,11G EFB D =.E ,F 分别为11A D ,11C D 的中点,G ∴为1GO 的中点.则1GOO ∠为异面直线m 、1CC 所成角.11114tan 1GO GOO OO ∠===故选:D .5.(2021春•瑞金市月考)在棱长为4的正方体1111ABCD A B C D -中,点E ,F 分别为1AA ,1CC 的中点,则过B ,E ,F 三点的平面与正方体各个面的交线组成的平面多边形的面积为( ) A.B.C.D.【解答】解:连接1ED ,1FD ,显然有1//ED BF ,1//FD BE , 故过B ,E ,F 三点的截面多边形为平行四边形1BED F , 又BE BF =,∴四边形1BED F 为菱形, 正方体棱长为4,故EF =1BD =∴菱形1BED F的面积为12⨯故选:B .6.(2021•丽水期末)斜线段AB 与平面α所成的角为60︒,B 为斜足,点P 是平面α上的动点且满足60PAB ∠=︒,则动点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支【解答】解:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.此题中平面α上的动点P 满足60PAB ∠=︒,可理解为P 在以AB 为轴的圆锥的侧面上, 再由斜线段AB 与平面α所成的角为60︒,可知P 的轨迹符合圆锥曲线中抛物线定义. 故可知动点P 的轨迹是抛物线. 故选:B .7.(2021•泉州模拟)设四棱锥P ABCD -的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面(α )A .不存在B .只有1个C .恰有4个D .有无数多个【解答】证明:由侧面PAD 与侧面PBC 相交,侧面PAB 与侧面PCD 相交, 设两组相交平面的交线分别为m ,n , 由m ,n 确定的平面为β, 作α与β平行且与四条侧棱相交, 交点分别为1A ,1B ,1C ,1D 则由面面平行的性质定理得: 1111////A B m D C ,1111////A D n B C ,从而得截面必为平行四边形.由于平面α可以上下移动,则这样的平面α有无数多个. 故选:D .8.(2021•西湖区校级模拟)如图,ABCD A B C D -''''为正方体,任作平面α与对角线AC '垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l ,则( )A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值【解答】解:将正方体切去两个正三棱锥A A BD -'与C D B C '-''后,得到一个以平行平面A BD '与DBC ''为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱A B ''剪开,展平在一张平面上,得到一个11A B B A '',如图而多边形W 的周界展开后便成为一条与1A A '平行的线段(如图中1)E E ',显然11E E A A '=',故l 为定值.当E '位于A B ''中点时,多边形W 为正六边形,而当E '移至A '处时,W 为正三角形,易知周长为定值l 22,故S 不为定值. 故选:B .9.(2021•安徽二模)已知正四面体的中心与球心O 重合,正四面体的棱长为,则正四面体表面与球面的交线的总长度为( )A .4πB .C .D .12π【解答】解:正四面体A BCD -的中心与球心O 重合,正四面体的棱长为 取CD 中点E ,连结BE ,AE ,过A 作AF ⊥底面BCD ,交BE 于F ,则BE AE =23BF BE ==,13DF BE ==4AF =,设正四面体内切球半径为r ,则222(4)r r -=+,解得正四面体内切球半径为1r =,,∴由球的半径知球被平面截得小圆半径为12r =,故球被正四面体一个平面截曲线为三段圆弧,且每段弧所对中心角为30︒,∴正四面体表面与球面的交线的总长度为:304(322)4360ππ︒⨯⨯⨯⨯=︒. 故选:A .10.(2021春•浙江期中)如图所示,一个圆柱形乒乓球筒,高为12厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )A B C D .15【解答】解:不妨设椭圆方程为22221(0)x y a b a b+=>>,由题意得21242a b =-⎧⎨=⎩,解得4a =,2b =,c ==∴该椭圆的离心率为c e a =. 故选:B .11.(2021秋•翠屏区校级期末)如图,A 为平面α内一定点,AB 是平面α的定长斜线段,A 为斜足,若点P 在平面α内运动,使ABP ∆面积为定值,则动点P 的轨迹是( )A .圆B .两条平行线C .一条直线D .椭圆【解答】解:因为三角形面积为定值,以定长斜线段AB 为底,则得P 到直线AB 的距离为定值,分析可得,点P 在以AB 为轴线的圆柱面与平面α的交线上,且α与圆柱的轴线斜交, 由平面与圆柱面的截面的性质判断,可得P 的轨迹为椭圆; 故选:D .12.(2021春•江西期中)已知AB 是平面α的斜线段,A 为斜足,若AB 与平面α成60︒角,过定点B 的动直线l 与斜线AB 成60︒角,且交α于点P ,则动点P 的轨迹是( ) A .圆B .椭圆C .双曲线D .抛物线【解答】解:用垂直于圆锥轴的平面去截圆锥,得到的是圆; 把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.此题AB 与平面α成60︒角,过定点B 的动直线l 与斜线AB 成60︒角,且交α于点P , 故可知动点P 的轨迹是抛物线. 故选:D .13.(2021•滨州一模)如图,斜线段AB 与平面α所成的角为4π,B 为斜足.平面α上的动点P 满足6PAB π∠=,则点P 的轨迹为( )A .圆B .椭圆C .双曲线的一部分D .抛物线的一部分【解答】解:用垂直于圆锥轴的平面去截圆锥,得到的是圆; 把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线. 参考上图:此题中平面α上的动点P 满足6PAB π∠=,可理解为P 在以AB 为轴的圆锥的侧面上, 再由斜线段AB 与平面α所成的角为4π, 可知P 的轨迹符合圆锥曲线中椭圆定义, 故可知动点P 的轨迹是椭圆. 故选:B .二.多选题(共5小题)14.(2021春•湖南期末)已知在正方体1111ABCD A B C D -中,点E ,F 分别为棱AB ,BC 上的中点,过E ,F 的平面α与底面ABCD 所成的锐二面角为60︒,则正方体被平面α所截的截面形状可能为( )A .三角形B .四边形C .五边形D .六边形【解答】解:如图所示:设正方体的棱长为4a ,在1BB 上取一点G 使得平面EFG 与平面ABCD 所成的锐二面角为60︒,因为E ,F 分别为棱AB ,BC 的中点, 所以EG FG =,连接BD 交EF 于点N ,连接AC , 所以EF BN ⊥,且N 为EF 的中点, 14BN BD =, 所以GN EF ⊥,所以GNB ∠为平面EFG 与平面ABCD 所成的锐二面角为60︒,所以1tan 604GB BN =︒⋅⨯=,所以1GB BB ==, 所以此时平面EFG 为平面α, 所以平面α为三角形,故A 正确;在1AA 和1CC 上分别取点M 和点H ,使得AM CH =, 取MH ,AC 的中点K ,O , 则KO ⊥平面ABCD , 又因为EF ⊂平面ABCD , 所以KO EF ⊥又NO EF ⊥, 所以EF ⊥平面KNO , 又因为KN ⊂平面KNO ,所以KNO ∠为平面MEFH 与平面ABCD 所成的锐二面角为60︒,所以1tan 604KO ON =︒⋅⨯=,所以111KO MA CH BB AA CC ==== 延长FH 交11B C 于T ,延长EM 交11B A 于S ,连接ST 交11A D 于Q ,交11C D 于P , 连接HP ,MQ ,则平面MEFHPQ 为平面α, 所以平面α为六边形,故D 正确. 故选:AD .15.(2021•唐山三模)将边长为2的正方形ABCD 沿对角线BD 折成直二面角A BD C --,如图所示,点E ,F 分别为线段BC ,AD 的中点,则( )A .AC 与EF 所成的角为45︒B .EF BC ⊥C .过EF 且与BD 平行的平面截四面体A BCD -D .四面体A BCD -的外接球的表面积为8π【解答】解:如图建立空间直角坐标系,则(0A ,0,(0C ,0),B 0,0),(D 0,0),E ,0),(F 0.对于A ,(0AC =,,,(EF =-,,,cos ,||||AC EF AC EF AC EF ⋅∴<>==-,故A 错;对于B ,(BC =-0),∴2110BC EF ⋅=-=≠,故B 错;对于C ,取CD 中点为M ,AB 的中点为N ,过EF 且与BD 平行的平面截四面体A BCD -所得截面为矩形EMFN ,12EM DB ==112MF AC ==C 正确;对于D ,四面体ABCD 的外接球的球心为O ,半径为R =, 所以表面积为248R ππ=,所以D 对. 故选:CD .16.(2021•雁峰区校级模拟)由四个三角形围成的多面体称为四面体,对棱相等的四面体称为等腰四面体.已知如图等腰四面体ABCD 中,AB CD =,AD BC =,AC BD =,E ,F ,G ,H 分别是棱AB ,BC ,CD ,DA 的中点.下面结论中,正确的有( )A .直线EG ,FH 有可能是异面直线B .EG AB ⊥C .过直线EG 的平面截四面体外接球所得截面面积为定值D .共顶点A 的三个侧面面角和()BAC CAD DAB ∠+∠+∠等于180︒ 【解答】解:如图所示:对于A :由于E 、F 、G 、H 为各边的中点,所以:////EF AC HG ,所以E 、F 、G 、H 四点共面,故A 错误;对于B :由于BD AC =,BC AD =,CD CD =,所以ACD BCD ∆≅∆,所以ACD BDC ∠=∠,故ACG BDG ∆≅∆,所以AG BG =,由于点E 为AB 的中点,所以EG AB ⊥,故B 正确; 对于C :把四面体ABCD 补形为长方体,则四面体与长方体外接球为同一个球,球心为EG 的中点,所以截面为球的大圆,其面积为定值,故C 正确;对于D :四个面全等,设一个面的三个内角为α、β、γ、则共顶点的三个侧面的内角和为180αβγ++=︒,故D 正确; 故选:BCD .17.(2021•江苏模拟)正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥ B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C所成锐二面角的正切值为D .设正方体棱长为1,则过点E ,F ,A【解答】解:作辅助线,I 、J 、N ,分别为所在棱中点,P 点为1A E 与AD 延长线交点,BP 连线交CD 于G ,则G 为CD 中点,K 为IJ 中点,L 为1A B 与1A B 交点;对于A ,当F 取IJ 中点K 时,1B K IJ ⊥,1//IJ CD所以11B K CD ⊥,1//B K LM ,LM ⊂平面1A BE ,1//B K 平面1A BE ,所以A 对; 对于B ,当点F 与点I 或点J 重合时,1B F 与直线BC 所成的角最大,所以111tan tan302C B F ∠==︒,所以B 不对; 对于C ,平面11//AA B B 平面11CDD C ,所以平面1A BE 与平面11CDD C 所锐二面角, 即为平面1A BE 与平面11AA B B 所成锐二面角,二面角的平面角即为PLA ∠,其正切值为AP AL ==C 对; 对于D ,因为过点E ,F ,A 的平面截正方体所得的截面面积最大的截面为菱形1AEC N ,其面积为112EN AC ⋅=,所以D 对. 故选:ACD .18.(2021•新罗区校级月考)如图,AB 是平面α的斜线段,A 为斜足,点C 满足||||(0)BC AC λλ=>,且在平面α内运动,则有以下几个命题,其中正确的命题是( )A .当1λ=时,点C 的轨迹是线段B .当1λ=时,点C 的轨迹是一条直线C .当2λ=时,点C 的轨迹是圆D .当2λ=时,点C 的轨迹是椭圆【解答】解:在ABC ∆中,点C 满足||||(0)BC AC λλ=>,当1λ=时,即||||BC AC =,则C 在过AB 的中点且垂直直线AB 的平面β与平面α的交线上,即点C 的轨迹是一条直线,故A 错误,B 正确;当2λ=时,||2||BC AC =,设点B 在平面α内的射影为D ,连接BD ,AD ,CD ,设||BD h =,||2AD a =,则||BC =在平面α内,以AD 所在直线为x 轴,以AD 的中垂线为y 轴,建立如图所示坐标系: 设(,)C x y ,则(,0)A a -,(,0)D a ,所以||CA =||CD ||CB整理可得2516()222393h x a y a ++=+,即C 的轨迹是圆,故C 正确,D 错误;故选:BC .三.填空题(共9小题)19.(2021春•邵阳县期末)已知正方体的棱长为1,每条棱所在的直线与平面α所成的角相等,则平面α截正方体所得的截面面积的最大值为. 【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且是正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长2,α截此正方体所得截面最大值为:26..20.(2021•上海模拟)如图,圆锥VO 的母线长为l ,轴截面VAB 的顶角150AVB ∠=︒,则过此圆锥的顶点作该圆锥的任意截面VCD ,则VCD ∆面积的最大值是 212l ,此时VCD ∠= .【解答】解:过此圆锥的顶点作该圆锥的任意截面VCD ,则VCD ∆面积的最大值时是等腰直角三角形时,且顶角为90︒,三角形VCD 中,VC VD l ==, 所以此时2211sin9022VCD S l l ∆=⋅⋅︒=,且45VCD ∠=︒故答案分别为:212l ,45︒.21.(2021•闵行区校级月考)如图所示,点P ,Q ,R 分别在正方体1111ABCD A B C D -的棱AB ,BC ,1CC 上,5AP =,15PB =,15BQ =,10CR =,那么正方体被平面PQR 所截得的截面面积是 525 .【解答】解:连接AC ,因为BP BQ =,所以//PQ AC ,如图,过点R 作平行于PQ 的直线交1AA 于点U ,连接PU ,过点R 作//SR UP 交11C D 于点S ,过点U 作//TU RQ 交11A D 于点T ,连接ST ,则六边形PQRSTU 为平面PQR 与正方体的交线组成的多边形,UR 的中点是正方体的中心,所以六边形PQRSTU 上的点关于正方体的中心对称,因此六边形PQRSTU 的面积是梯形PQRU 的2倍,易知UR =,PQ =PU =,所以梯形PQRU 的高h ==故所求面积为525=. 故答案为:525.22.过正四面体ABCD 的顶点A 作一个形状为等腰三角形的截面,且使截面与底面BCD 所成的角为75︒,这样的截面共可作出 18 个.【解答】解:作正四面体A BCD -的高AO ,连接BO 交CD 于E ,连接AE . 则E 为CD 的中点,O 为△等边三角形BCD 的中心.BE CD ∴⊥,AE CD ⊥,AEB ∴∠为二面角A CD B --的平面角.设2AB =,则BE =,13OE BE ∴=23OB BE =AO ∴=.tan AOAEB OE∴∠==.sin 75tan 752cos75︒︒===︒75AEB ∴∠<︒.在平面BCD 内,以O 为圆心,以tan75OA ︒为半径作圆O ,则圆O 在BCD ∆内部.∴若截面AMN 与底面BCD 所成角为75︒,则截面AMN 与平面BCD 的交线为圆O 的切线.(1)若圆O 的切线与BCD ∆的一边平行,如图1所示:则存在6个符合条件的截面三角形AMN .(2)若圆O 的切线过三角形的顶点,不妨设过点B ,交CD 于M ,如图2所示:则由ACM BCM ∆≅∆可得AM BM =,故截面ABM 为符合条件的截面三角形, 显然存在6个这样的截面三角形.(3)若圆O 的切线MN 与三角形BCD 的两边相交,不妨设与NC 交于M ,与CD 交于N ,且BM CN =, 如图3所示:显然ABM ACN ∆≅∆,故而AM AN =,∴截面AMN 为符合条件的截面三角形.显然这样的截面也有6个. 综上,符合条件的截面共有18个. 故答案为:18.23.(2021春•绍兴期末)已知四面体ABCD 的所有棱长均为4,点O 满足OA OB OC OD ===,则以O ABCD 表面所得交线总长度为. 【解答】解:正四面体A BCD -的中心与球心O 重合,正四面体的棱长为4, 取CD 中点E ,连结BE ,AE ,过A 作AF ⊥底面BCD ,交BE 于F ,则4sin 60BE =︒=23BF BE ==,AF ∴=又222()AF OF OF BF -=+,OF ∴=由球的半径知球被平面截得小圆半径为r ==而ABC ∆, 故球被正四面体一个平面截曲线为圆弧,∴正四面体表面与球面的交线的总长度为:42π⨯=..24.(2021春•开福区校级月考)以棱长为O 为球心,以(03)R R <<为半径的球面与正四面体的表面相交得到若干个圆(或圆弧)的总长度的取值范围是 (0,] .【解答】解:将S ABC -正四面体看作是正方体的6条面对角线围成的正四面体,设正方体棱长为a =a =3=,又正四面体的体积为332114323S ABC a V a a a -=-⨯⨯⨯==,表面积为24S ==表设正四面体的内切球半径为1r ,则1243⨯1r =11r =.设三角形ABC 的内切圆半径为2r ,圆心为O ',D 为BC 的中点,则30O BD ∠'=︒,BD =,故2r O D ='=,此时R(1)当01R <时,球面与正四面体无交点或相切,此时圆弧总长度为0; (2)当13R<时,球面与正四面体的每个面交线均为相等的圆,设圆的半径为r ,则02r <,故当r42π⨯=; (33R <时,球面与正四面体的每个面的交线均为三段相等的圆弧, 不妨设其中一段为EF ,如图所示:设DO E α∠'=,显然03πα<<,O E '22()233EO F ππαα∠'=-=-, 于是EF 的长为222()(2)(2)33cos fO E ππαααα=-'=-, 22)sin 2(sin sin cos )33()f cos cos πααααααααα-+---∴'==, 令()sin sin cos (0)33g ππαααααα=--<<,则()cos cos ()cos 033g ππαααααα'=-=->,()g α∴在(0,)3π上单调递增,故1()()032g g πα<=-<,()0f α∴'<,故()f α在(0,)3π上单调递减,()(0)3f f α∴<=, 3R <<34⨯=. 综上,圆(或圆弧)的总长度的取值范围是:(0,]. 故答案为:(0,].25.(2021春•金山区校级期中)设正方体1111ABCD A B C D -的棱长为2,α为过直线1BD 的平面,则α截该正方体的截面面积的取值范围是 .【解答】解:以点1D 为坐标原点,建立空间直角坐标系如图所示, 则(2B ,2,2),1(0D ,0,0),设α与棱1CC 的交点为P ,与棱1AA 的交点为G , 则四边形1BGD P 为平行四边形,在平面α内过点P 作1BD 的垂线,垂足为Q , 则截面的面积1||||23||S BD PQ PQ ==, 设(Q x ,x ,)x ,(0P ,2,)y , 则1(2,2,2),(,2,)D B PQ x x x y ==--,因为10D B PQ ⋅=,所以22(2)2()0x x x y +-+-=, 所以320x y --=,所以32y x =-, 因为0322x -,所以2433x,又2||PQ x = 有2433x,可得262||3PQ , 所以642S ,则α截该正方体的截面面积的取值范围是.故答案为:.26.(2021春•杨浦区校级期末)如图,顶点为P 的圆锥的轴截面是等腰直角三角形,母线4PA =,O 是底面圆心,B 是底面圆内一点,且AB OB ⊥,C 为PA 的中点,OD PB ⊥,垂足为D ,当三棱锥O PCD -的体积最大时,OB =.【解答】解:AB OB ⊥,可得PB AB ⊥,即AB ⊥面POB ,所以面PAB ⊥面POB . OD PB ⊥,则OD ⊥面PAB ,OD DC ⊥,OD PC ⊥,又,PC OC ⊥,所以PC ⊥面OCD .即PC 是三棱锥P OCD -的高.2PC OC ==.而OCD ∆的面积在OD DC ==2=的直角三角形).当OD 时,由PO =,知30OPB ∠=︒,tan30OB PO =︒.. 27.(2021•东阳市校级月考)顶点为P 的圆锥的轴截面是等腰直角三角形,A 是底面圆周上的点,B 是底面圆内的点,O 为底面圆圆心,AB OB ⊥,垂足为B ,OH PB ⊥,垂足为H ,且4PA =,C 是PA 的中点,则当三棱锥O HPC -的体积最大时,OB 的长为 . 【解答】解:AB OB ⊥,AB OP ⊥,AB PB ∴⊥,OH PB ⊥,∴面PAB ⊥面POB ,OH HC ∴⊥,OH PA ⊥, C 是PA 的中点,OC PA ∴⊥,∴当HO HC =时,HOC S ∆最大,即O HPC P HCO V V --=最大,此时,HO =12HO OP ∴=,30HPO ∴∠=︒,tan 30OB OP ∴=︒=,.四.解答题(共3小题)28.如图,G 是正方体1111ABCD A B C D 的棱的1DD 延长线上的一点,E 、F 是棱AB 、BC 的中点,试分别画出:(1)过点G 、A 、C 的平面与正方体表面的交线; (2)过点E 、F 、1D 的平面与正方体表面的交线.【解答】解:如图,过点A 、C 、G 的平面为平面1AC H , 过点G 、A 、C 的平面与正方体表面的交线分别为:AH ,HI ,IC ,AC .(2)如图,过点E 、F 、1D 的平面为平面1EFRD O , 过点E 、F 、1D 的平面与正方体表面的交线分别为: 1D O ,OE ,EF ,FR .1RD .29.如图,已知底面为平行四边形的四棱锥P ABCD-中,平面MNGH与直线PB和直线AC 平行,点E为PD的中点,点F在CD上,且:1:2DF FC=.(1)求证:四边形MNGH是平行四边形;(2)求作过EF作四棱锥P ABCD-的截面,使PB与截面平行(写出作图过程,不要求证明).截面的定义:用一个平面去截一个几何体,平面与几何体的表面的交线围成的平面图形.【解答】证明:(1)平面MNGH与直线PB平行,MH⊂平面MNGH,NG⊂平面MNGH,又MH与PB共面于平面PAB,NG与PB共面于平面PBC,MH NGNG PB,//∴,MH PB//∴,//平面MNGH 与直线AC 平行,MN ⊂平面MNGH ,HG ⊂平面MNGH , 又MN 与AC 共面于ABCD ,HG 与AC 共面于PAC , //MN AC ∴,//HG AC ,//MN HG ∴,∴四边形MNGH 是平行四边形.解:(2)延长FO ,与AB 交于点G ,延长FE ,与面PAB 交于点S (直线l 为平面PAB 和平面PCD 的交线), 连接SG ,与PA 交于点H ,连接HE .平面EFGH 为所求截面, //PB 截面EFGH .30.(2021•邢台月考)如图,在边长为3的正方体1111ABCD A B C D -中,点P ,Q ,R 分别在棱AB ,11B C ,1D D 上,且111AP B Q D R ===. (1)求点D 到平面PQR 的距离;(2)若平面PQR 与线段1AC 的交点为N ,求1ANAC 的值.【解答】解:(1)以点D 为坐标原点,分别以DA ,DC ,1DD 的方向为x ,y ,z 轴的正方向,建立空间直角坐标系D xyz -,则(3A ,0,0),(3P ,1,0),(0R ,0,2),(2Q ,3,4),1(0C ,3,3),(1,2,3)PQ =-,(3,1,2)PR =--,(0,1,0)AP =,1(3,3,3)AC =-,(0,0,2)DR =,设平面PQR 的法向量为(,,)m x y z =, 则00m PQ m PR ⎧⋅=⎪⎨⋅=⎪⎩,代入可得230320x y z x y z -++=⎧⎨--+=⎩,令1x =,则1y =-,1z =,所以(,,)m x y z =, 故点D 到平面PQR的距离为2||||3m DR m ⋅== (2)因为点N 在平面PQR 内,可设PN mPQ nPR =+(其中m ,n 为常数,又AN 与1AC 共线,可设1AN k AC =,由图可得1AN AP PN AP mPQ nPR k AC =+=++=, 即(0,1,0)(1m +-,2,3)(3n +-,1-,2)(3k =-,3,3), 整理得33123323m n k m n k m n k --=-⎧⎪+-=⎨⎪+=⎩①②③,由①③可得2m n =④, 由②③可得3m n +⑤,联立④⑤解得1727m n ⎧=⎪⎪⎨⎪=⎪⎩,代入②可得13k =,所以113AN AC =,即113AN AC =.。
立体几何中的截面解析版

专题13 立体几何中的截面1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体〔包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等〕,得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的根本斜截面:3、圆柱体的根本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
技能1.结合线、面平行的判定定理与性质性质求截面问题; 技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜测法求最值问题:要灵活运用一些特殊图形与几何体的特征,"动中找静〞:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是〔〕分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,应选D 。
例2 如图,在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器内灌进一些水,固定容器底面一边BC 于地面上,再将容器倾斜,随着倾斜程度的不同,有以下四个命题: ① 水的局部始终呈棱柱状; ② 水面EFGH 的面积不改变; ③ 棱A 1D 1始终与水面EFGH 平行;ACBD④ 当容器倾斜到如图5〔2〕时,BE·BF 是定值; 其中正确的命题序号是______________分析当长方体容器绕BC 边转动时,盛水局部的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水局部呈直三棱柱时如图5〔2〕,因为BC BF BE V ⋅⋅=21水是定值,又BC 是定值,所以BE·BF 是定值,即④正确。
立体几何中的截面问题

线段DD1上靠近D的三等分点,若正四棱柱ABCD-A1B1C1D1被过点A1,M,N的平
面所截,则所得截面的周长为
(B)
A.10+8 2
B.10+7 2
C.9+8 2
D.9+7 2
【解析】 如图,延长 C1C 至 Q,使得 CQ=1,连接 MQ,NQ, 则四边形 A1MQN 为平行四边形.记 MQ 与 BC 交于点 R,NQ 与 CD 交于点 P,则截面为五边形 A1NPRM.易得 A1N=4 2,A1M =5,MR= 32+32=3 2,NP= 22+832=130,PR= 12+432 =53,故所得截面的周长为 A1M+MR+PR+PN+A1N=5+3 2 +53+130+4 2=10+7 2.
球心
O
到平面
MNPQ
的距离
d
=
EG
=
1 2
EC1
.
设
正
方
体
ABCDA1B1C1D1 的棱长为 2 2,则 R=12EF= 2,d=EG=12EC1=1,所以球 O 被平面 MNPQ 所截的小圆半径 r= R2-d2= 2-1=1,所以球 O 被平面 MNPQ 所截的小
圆面积为 πr2=π.又易知 NM=2,PN=2 2,所以该正方体被平面 MNPQ 所截得的
图(1)
PQ⊂底面A1B1C1D1,所以PQ⊥CC1.因为A1C1,CC1⊂平面A1C1CA,A1C1∩CC1= C1,所以PQ⊥平面A1C1CA.因为CE⊂平面A1C1CA,所以PQ⊥CE,即l⊥CE.
1 (2023·汕头二模节选)如图,在正方体ABCDA1B1C1D1中, 直线l⊂平面A1B1C1D1,l∩A1C1=E,A1E=3EC1. (2)设点A与(1)中所作直线l确定平面α.请在图中作出平面α截正方 体ABCDA1B1C1D1所得的截面,并写出作法.
立体几何中的截面(解析版)

专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________分析当长方体容器绕BC边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EHA CBDBC BF BE V ⋅⋅=21水例3 有一容积为1 立方单位的正方体容器ABCD-A 1B 1C 1D 1,在棱AB 、BB 1及对角线B 1C 的中点各有一小孔E 、F 、G ,若此容器可以任意放置,则该容器可装水的最大容积是( )A .21 B .87 C .1211 D .4847 分析 本题很容易认为当水面是过E 、F 、G 三点的截面时容器可装水的容积最大图(1),最大值为8712121211=⋅⋅⋅-=V 立方单位,这是一种错误的解法,错误原因是对题中“容器是可以任意放置”的理解不够,其实,当水平面调整为图(2)△EB 1C 时容器的容积最大,最大容积为1211112121311=⋅⋅⋅⋅-=V ,故选C 。
立体几何中截面问题

立体几何中截面问题(周长、面积、体积、长度)1.在正方体 ABCD - A 1B 1C 1D 1 中,E ,F 分别为棱 AB ,BC 的中点,过点 D 1 ,E ,F 作该正方体的截面,截面将正方体分成两部分,则较小部分与较大部分的体积的比值为 ( )2.已知正方体 ABCD - A 1B 1C 1D 1 的棱长为 2 ,直线 AC 1 ⊥ 平面α ,平面α 截此正方体所得截面中,正确的说法是( )A .截面形状可能为四边形B .截面形状可能为五边形C .截面面积最大值为32D .截面面积最大值为 233 3.正方体 ABCD -- A 1B 1C 1D 1,E 、F 分别是 AA 1 、CC 1 的中点,P 是CC 1 上的动点(包括 端点),过 E 、D 、P 作正方体的截面,若截面为四边形,则 P 的轨迹是( )A .线段C 1FB .线段CFC .线段CF 和一点C 1D .线段C 1F 和一点 C4.已知圆锥的高为 1,母线长为 5 ,则过此圆锥顶点的截面面积的最大值( )5.如下图,正方体 ABCD - A 1B 1C 1D 1 的棱长为 1,E ,F ,G 分别为棱 AB , A 1D 1,C 1D 1 的中点,经过 E ,F ,G 三点的平面被正方体所截,则截面图形的面积为( )6.如上图,在正方体 ABCD - A `B `C `D ` 中,平面 垂直于对角线 AC ,且平面 截得正方体的六个表面得到截面六边形,记此截面六边形的面积为 S ,周长为l ,则( )A . S 为定值, l 不为定值B . S 不为定值, l 为定值C . S 与l 均为定值D . S 与l 均不为定值7.已知正方体ABCD - A1B1C1D1 棱长为4,P 是AA1中点,过点D1作面α 满足CP ⊥ 平面α ,则平面α 与正方体ABCD - A1B1C1D1的截面周长为()第7题第8题第9题8.如图,在直三棱柱ABC - A1B1C1中,AC = BC = CC1= 6,AC ⊥ BC ,E、F 分別为BB1,A1C1中点,过点A、E、F 作三棱柱的截面交B1C1于M,则EM =9.在长方体A B C D - A1 B1C1 D1 中,AB = AD = 4, AA2 = 2 ,过点A1作平面α 与A B, A D 分别交于M,N 两点,若AA1与平面α 所成的角为45︒ ,则截面A1MN 面积的最小值是()10.已知圆锥SO1 的顶点和底面圆周均在球O 的球面上,且该圆锥的高为8. 母线SA =12 ,点B 在SA上,且SB = 2BA ,则过点B 的平面被该球O 截得的截面面积的最小值为()11.在直三棱柱ABC - A1B1C1 中,M 是BB1 上的点,AB = 3 ,BC = 4,AC = 5,CC1= 7 ,过三点A、M 、C1作截面,当截面周长最小时,截面将三棱柱分成的两部分的体积比为().12.已知正方体ABCD - A1B1C1D1 的体积为8,点M 在线段BC 上(点M 异于B、C 两点),点N 为线段CC1的中点,若平面AMN 截正方体ABCD - A1B1C1D1所得的截面为五边形,则线段BM 长度的取值范围是______.13.已知正方体ABCD - A1B1C1D1的棱长为1,E ,F ,G 分别是棱AB ,BC ,CC1的中点,过E ,F ,G 三点作该正方体的截面,点M 为底面ABCD 内一动点.若MD1与该截面平行,则直线MD1与CC1所成角的余弦值的最大值为______.答案:1、47252、D3、C4、25 5、433 6、B 7、2654 8、13 9、24 10、32π 11、1110 12、(1,2) 13、36。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何体中的的截面问题1.定义及相关要素用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线.此平面与几何体的棱的交集(交点)叫做截点. 2.作多面体的截面方法(交线法):该作图关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.题型一、截面的形状1.P 、Q 、R 三点分别在直四棱柱AC 1的棱BB 1、CC 1和DD 1上,试画出过P 、Q 、R 三点的截面.1解答:(1)连接QP 、QR 并延长,分别交CB 、CD 的延长线于E 、F . (2)连接EF 交AB 于T,交AD 于S .(3)连接RS 、TP 。
则多边形PQRST 即为所求截面。
2.已知P 、Q 、R 分别是四棱柱ABCD ―A 1B 1C 1D 1的棱CD 、DD 1和AA 1上的点,且QR 与AD 不平行,求作过这三点的截面.2解答: (1)连接QP 并延长交DA 延长线于点I 。
(2)在平面ABCD 内连接PI 交AB 于点M 。
(3)连接QP、RM。
则四边形PQRM即为所求。
注:①若已知两点在同一平面内,只要连接这两点,就可以得到截面与多面体的一个面的截线。
②若面上只有一个已知点,应设法在同一平面上再找出第二确定的点。
③若两个已知点分别在相邻的面上,应找出这两个平面的交线与截面的交点。
3.一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是ACBD3答案:D解析:考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D 。
题型二、截面面积、长度等计算4.过正方体1111D C B A ABCD -的对角线1BD 的截面面积为S ,S max 和S min 分别为S 的最大值和最小值,则m inm axS S 的值为 ( ) A .23 B .26 C .332 D .362 4答案:C解析:设M 、N 分别为AA 1、CC 1的中点.易证截面BMD 1N1D1D 5. 如图,已知球O 是棱长为1 的正方体ABCD ﹣A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为 . 5答案:解析:平面ACD 1是边长为的正三角形,且球与以点D 为公共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积,则由图得,△ACD 1内切圆的半径是×tan30°=,则所求的截面圆的面积是π××=.6.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )A .1BCD .26答案:C解析:1O 与2O 的公共弦为AB ,球心为O,AB 中点为C , 则四边形C OO O 21为矩形,12||||,O O OC =||2,OA = 所以||1,||AC AC OC OC =⊥∴==7.已知正四棱锥P —ABCD 的棱长都等于a ,侧棱PB 、PD 的中点分别为M 、N ,则截面AMN 与底面ABCD 所成二面角大小的正切值为 . 7答案:12O2OCO2解析:过A 在平面ABCD 内作直线l BD //,连接AC,BD 交于O ,连接PO ,MN .记PO 、MN 交于O‘.因为PB 、PD 的中点分别为M 、N ,所以MN //BD ,因为l BD //,所以l MN //,A l ∈,所以l ⊂平面AMN , l =平面AMN∩平面ABCD .易知O AO '∠即为面AMN 与底面ABCD 所成二面角的平面角.1tan 242AO PO a O O O AO ''==⇒=⇒= 8.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S 。
则下列命题正确的是_____ ①当102CQ <<时,S 为四边形 ②当12CQ =时,S 为等腰梯形 ③当34CQ =时,S 与11C D 的交点R 满足1113C R =④当314CQ <<时,S 为六边形⑤当1CQ =时,S8答案: ①②③⑤解析:CQ DT PQ AT PQ AT T D D 22//1=⇒=且,则相交于设截面与. 对①,时当210.<<CQ ,则.10<<DT 所以截面S 为四边形,且S 为梯形.所以为真. 对②, 1 = DT ,21.时当=CQ 重合与1,D T ,截面S 为四边形.,11Q D AP APQD =所以截面S 为等腰梯形. 所以为真. 对③, 时当43.=CQ .31.21,23,411111====⇒R C T D DT QC 利用三角形相似解得所以为真. 对④, 2 DT 23,143.<<<<时当CQ .截面S 与线段1111C D ,D A 相交,所以四边形S 为五边形.所以为假.对⑤,A G APC G D A S C CQ 111111,Q 1.即为菱形相交于中点与线段截面重合与时,当=.对角线长度分别为.2632的面积为,和S 所以为真.9.如图,1111D C B A ABCD -为正方体。
任作平面α与对角线C A '垂直,使得α与正方体的每个面都有公共点,记这样得到 的截面多边形的面积为S ,周长为l .则( ) A .S 为定值,l 不为定值 B .S 不为定值,l 为定值 C .S 与l 均为定值D .S 与l 均不为定值9答案:B解析:将正方体切去两个正三棱锥A A BD '-与C D B C '''-后,得到一个以平行平面A BD '与D B C ''为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱A B ''剪开,展平在一张平面上,得到一个平行四边形11A B B A '',而多边形W 的周界展开后便成为一条与1A A '平行的线段(如图中1E E '),显然11A A E E ''=,故l 为定值。
题型三、截面图形的计数10.设四棱锥 P ABCD - 的底面不是平行四边形, 用平面α去截此四棱锥, 使得截面四边形是平行四边形, 则这样的平面α( )A. 不存在B. 只有1个C. 恰有4个D. 有无数多个 10答案:D解析:设四棱锥的两组不相邻的侧面的交线为m ,n ,直线m 、n 确定了平面β,作与β平行的平面α与四棱锥侧棱相截,则截得的四边形是平行四边形.这样的平面α有无数多个. 11.过正四面体ABCD 的顶点A 做一个形状为等腰三角形的截面,且使截面与底面BCD 成75角,问这样的截面可作几个?11答案:6个.解析:可以证明正四面体的棱、侧面与底面成角均小于75度,这样过顶点与底面成75度角,且平行与底面一条边的 截面也就是符合题意的截面,有两个。
三条边就是6个。
题型四、截面图形的性质12.如图4,在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器内灌进一些水,固定容器底面一边BC 于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:① 水的部分始终呈棱柱状; ② 水面EFGH 的面积不改变; ③ 棱A 1D 1始终与水面EFGH 平行;④ 当容器倾斜到如图4(2)时,BE ·BF 是定值; 其中正确的命题序号是______________ 12答案:①③④解析 当长方体容器绕BC 边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BC BF BE V ⋅⋅=21水是定值,又BC 是定值,所以BE ·BF 是定值,即④正确。
13.有一容积为1 立方单位的正方体容器ABCD-A 1B 1C 1D 1,在棱AB 、BB 1及对角线B 1C 的中点各有一小孔E 、F 、G ,若此容器可以任意放置,则该容器可装水的最大容积是 A .21 B .87 C .1211D .484713答案:C解析:本题很容易认为当水面是过E 、F 、G 三点的截面时容器可装水的容积最大图6(1),最大值为8712121211=⋅⋅⋅-=V 立方单位,这是一种错误的解法,错误原因是对题中“容器是可以任意放置”的理解不够,其实,当水平面调整为图6(2)△EB 1C 时容器的容积最大,最大容积为1211112121311=⋅⋅⋅⋅-=V . 14.(08年江西)如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a 升水时,水面恰好经过正四棱锥的顶点P 。
如果将容器倒置,水面也恰好过点P (图2)。
有下列四个命题: A .正四棱锥的高等于正四棱柱高的一半 B .将容器侧面水平放置时,水面也恰好过点PC .任意摆放该容器,当水面静止时,水面都恰好经过点PD .若往容器内再注入a 升水,则容器恰好能装满 其中真命题是: 14答案:BD解析:a 升水对应的体积为V ,则正四棱锥的体积2V,正四棱柱的体积为522V V V V ++=AB C HA 1B 1C 1D 1E FGDA B CD A 1B 1C 1D 1EFG H图4(2)图4(1)C 1A BCD A 1D 1 B 1EG F 图(2)C 1A B C D A 1D 1 B 1EGF 图(1)图12图容器的盛水量为2V.易知所盛水的容积为容器容量的一半,故D正确,于是A错误;水平放置时由容器形状的对称性知水面经过点P,故B正确;C的错误可由图1中容器位置向右边倾斜一些可推知点P将露出水面。
