【F】普通年金终值例子
复利现值、终值、年金现值终值公式、实例

解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式为:ii A i A i A i A i A P nn n ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21Λ 式中的分式ii n -+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。
它是普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1.递延年金现值公式为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1) 或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2) 上述(1)公式是先计算出n 期的普通年金现值,然后减去前s 期的普通年金现值,即得递延年金的现值,公式(2)是先将些递延年金视为(n-s)期普通年金,求出在第s 期的现值,然后再折算为第零期的现值。
普通年金

P A表示现值(现额),F A表示终值,i表示年利率,n表示年数,而(1+i)^-n表示1+i的-n次方,A表示每年收入或支出金额,其中(1+i)^-n=1/(1+i)^n.普通年金及案例年金的含义:年金是指每隔相同时间(一年、半年、一季度)收入或支出相等金额的款项普通年金:又称为后付年金。
它是指每期末收付等额款项的年金终值(F):是指一定量的货币按规定利率折算的未来价值(本利和)现值(P):是指一定量未来的货币按规定利率折算的现在价值货币时间价值的表达式=终值-现值普通年金公式={(1+i)^n-1}/i*AFAP={1-(1+i)^-n}/i*AA普通年金终值举例公司有科研项目,分5年投资,每年末投入400000元,预计5年后该项目投资向银行借款,借款利率为12%。
该项目的投资总额为多少?F={(1+i)^n-1}/i*AA={(1+12%)^5-1}/12%*400000=0.7623416832/12%*400000=6.35284736*400000=2541138.944年偿债基金含义:是为在未来某一时点偿还一定数额的债务,现在应存入多少钱。
计算公式:它是年金终值的逆运算/{[(1+i)^n-1]/i}A=FA公司决定从今年起建立年偿债基金,即在今后5年内每年末存入银行等额款项,偿还第六年初到期的公司债务3000000元.若银行存款利率为10%,每年复利一次.公司每年末存入银行的等额款项?A=F/{[(1+i)^n-1]/i}A=3000000/{[(1+10%)^5-1]/10%}=3000000/6.1051=491392.442384普通年金普通年金现值举例购房总房款为100万元,如果首付30%,年利率为8%,银行提供20年按揭。
购房贷款70万元,每年应付款多少?每月付款多少?={1-(1+i)^-n}/i*APA70={1-(1+8%)^-20}/8%*A70=(1-0.2145482)/0.08*AA=70/9.81814732A =7.12965(万元)每年应付款A =7.12965万元)每月付款A/12=0.5941375(万元)。
普通年金终值的计算公式为

保险产品通常具有保障和投资双重功能,其中投资型保险产品如万能险、分红险等,与普通年金终值类 似,都具有长期投资和复利效应。但保险产品的投资收益受保险公司经营状况和市场环境等因素影响, 存在一定风险。
应用场景举例
养老规划
个人在年轻时通过购买养老保险 或进行普通年金终值投资,为退 休后的生活提供稳定的收入来源 。
后续年份累计金额
按照上述方法,逐年计算每一年的累计金额,直到达到投 资期限的最后一年。
汇总得出最终结果
• 将所有年份的累计金额相加,得出普通年金终值的最终结 果。这个结果表示在投资期限结束时,投资者将获得的总 额。
04 风险评估与防范措施建 议
市场风险识别及评估方法论述
风险识别
通过收集和分析市场数据、投资者行为、政策变化等信息,识别可能对普通年 金终值产生不利影响的风险因素。
计算公式中各个参数的含义和影响因素
在普通年金终值的计算公式中,A代表每期支付的年金金 额,i代表利率水平,n代表支付期数。这些参数的变化都 会对普通年金终值产生影响。例如,当利率上升时,普通 年金终值会相应增加;当期数增加时,普通年金终值也会 增加。
学员心得体会分享交流环节
要点一
学员对课程内容的理 解和掌握情况
普通年金终值的计算 公式为
汇报人:XX
目录
CONTENTS
• 普通年金终值概念及意义 • 普通年金终值计算原理 • 具体计算步骤与实例演示 • 风险评估与防范措施建议 • 实际操作中注意事项及技巧分享 • 总结回顾与展望未来发展趋势
01 普通年金终值概念及意 义
定义与特点
普通年金终值定义
普通年金终值是指在一定期限内,按 照固定利率和固定时间间隔进行等额 投资,到期时所能累积的总金额。
普通年金终值与现值
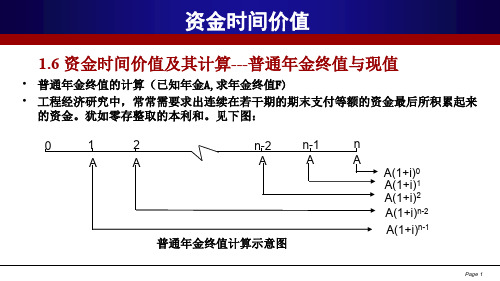
•普通年金终值的计算(已知年金A,求年金终值F)•工程经济研究中,常常需要求出连续在若干期的期末支付等额的资金最后所积累起来的资金。
犹如零存整取的本利和。
见下图:1.6 资金时间价值及其计算---普通年金终值与现值A(1+i)1 A(1+i)2 01 2 n-2 n-1 n AAAAAA(1+i)0 普通年金终值计算示意图A(1+i)n-2 A(1+i)n-1•由上图可知:年金终值的计算公式为:F=A(1+i)0+A(1+i)1+A(1+i)2+……+A(1+i)n-2+A(1+i)n-1…(1) 将(1)式两边同时乘上(1+i)得:F(1+i) = A(1+i)1+A(1+i)2+A(1+i)3 + ……+A(1+i)n-1+A(1+i)n …(2) 将(2)式减去(1)式得:F .i=A(1+i)n -A=A[(1+i)n -1]1.6资金时间价值及其计算---普通年金终值与现值(1+i)n-1[F= A ] …… (3) i1.6 资金时间价值及其计算---普通年金终值与现值(3)式中方括号中的数值,通常称作“年金终值系数”,记作(F/A,i,n)。
上式也可写作: F=A(F/A,i,n)[例3]假设某项目在5年建设期内每年年末向银行借款100万元,借款年利率为10%,问该项目竣工时应付本息的总额是多少?1.6 资金时间价值及其计算---普通年金终值与现值•年偿债基金的计算(已知年金终值F,求年金A)•年偿债基金的计算实际上是年金终值的逆运算。
其计算公式为:i ]A=F[(1+i)n-1上式也可写作:A=F(A/F,i,n)或:A=F[1/(F/A,i,n)]1.6 资金时间价值及其计算---普通年金终值与现值•年偿债基金的计算(已知年金终值F,求年金A)•[例4]:假设某企业有一笔4年后到期的借款,数额为1000万元,为此设置偿债基金,年复利率为10%,到期一次还清借款,问每年应存入的金额是多少?•普通年金现值的计算(已知年金A,求年金现值P)1.6 资金时间价值及其计算---普通年金终值与现值AAAA12 n-1 n P=A (1+i)-1+A (1+i)-2+A (1+i)-(n-1)+……..+A (1+i)-n =A[1-(1+i) –n / i]A (1+i)-1 A (1+i)-2A (1+i)-(n-1) A (1+i)-n假定这一系列收益会永远持续下去则有: P=A / i (永续年金)1.6 资金时间价值及其计算---普通年金终值与现值•上式中方括号内的数值称作“年金现值系数”,记作(P/A,i,n), •即:P=A(P/A,i,n)•[例5]租入某设备,每年年末需要支付租金120元,年复利率为10%,问5年内应支付的租金总额的现值是多少?1.6 资金时间价值及其计算---普通年金终值与现值•年资本回收额的计算(已知年金现值P,求年金A)•年金现值的逆运算,计算公式:A=P[i/1-(1+i)-n]•式中方括号内的数值称作“资本回收系数”记作(A/P,i,n)上式也可写作:•A=P (A/P,i,n)或A=P [1/(P/A,i,n)]•[例6]:某企业现在借得1000万元的贷款,在十年内以年利率12%均匀偿还,每年应付的金额是多少?。
复利现值、终值、年金现值终值公式、实例

某投资项目预测得净现金流量见下表(万元),设资金基本贴现率为10%,则该项目得净现金值为()万元解:本例因为涉及到年金当中得递延年金,所以将年金系列一起先介绍,然后解题年金,就是指一定时期内每次等额收付款得系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生得时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其她得在后面介绍。
一、普通年金,就是指从第一期起,在一定时期内每期期末等额发生得系列收付款项,又称后付年金。
1、普通年金现值公式为:ii A i A i A i A i A P nn n ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21Λ 式中得分式ii n-+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关得数值,上式也可写作:P=A (P/A ,i ,n )、 2、例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付得租金总额得现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金,就是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生得系列等额收付款项。
它就是普通年金得特殊形式,凡不就是从第一期开始得年金都就是递延年金。
1、递延年金现值公式为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1) 或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2) 上述(1)公式就是先计算出n 期得普通年金现值,然后减去前s 期得普通年金现值,即得递延年金得现值,公式(2)就是先将些递延年金视为(n-s)期普通年金,求出在第s 期得现值,然后再折算为第零期得现值。
普通年金现值与终值计算

F=A+A×(1+i)+A×(1+i)2+…+A×(1+i)n-1
①
等F×式(两1边+同i)乘=A(×1(+i)1+,i)则+有A×:(1+i)2+A×(1+i)3 +…+A×(1+i)n
②
②-①得: n
F=A×1-(1+i)-1
普通年金终值系数, 记做(F/A,i,n)
24
24
24
24
0 2018
2019 2020
2021
支付价款的现值=24×(P/A,10%,4)=24×3.1699=76.08(万元)
〖注意〗上期期末和下期期初是同一个时点,2019年年初相当于2018年年末;
(2)普通年金终值 对于等额收付n次的普通年金而言,其终值是指各期等额收付金额在第n期期 末的复利终值之和。
A
A
A
0
1
2
3
普通年金现值是指普通年金中各期等额收付金额在第一期期初(0时点)的 复利现值之和。
普通年金现值 P=A×(P/A, i, n)
A AA
......
AA
0 1 23
nБайду номын сангаас1 n
P=A×(1+i) -1 +A×(1+i) -2 +A×(1+i)-3 +... +A×(1+i)-n
①
等式两边同乘(1+i):
普通年金现值与终值的计算
主讲人:
终值和现值的计算
1、年金的含义:定期、等额的系列收付款项,年金的符号为A [注意]年金中收付的间隔时间不一定是1年,可以是半年、1个月等等; 2、年金包括普通年金、预付年金、递延年金、永续年金等;
年金终值和现值得计算

4.永续年金
[例题]:拟建立一项永久性奖学金,每年计划 颁发1万元奖金,若利率为10%,现在应存入 多少钱? P=1/10%=10万元 [例题]:如果有一股优先股,每季分得股息3 元,而利率是年利6%,对于一个准备购买这 种股票的人来说,他愿意出多少前来购买此优 先股? i=6%/4=1.5% P=3/1.5%=200元
3 延期年金 [例题]:某企业向银行借入一笔款项,银行的 贷款利率是8%,银行规定前10年不用还本付 息,但是从第11年到第20年每年年末偿还本息 1000元,问这笔款项的现值应为多少?
P=1000﹡(P/A, 8%, 10) ﹡(P/F, 8%, 10) =100A﹡﹡(P/A, 8%, 20)-A ﹡ (P/A, 8%, 10) =1000﹡(9.818−6.710)=3107 元
PVA=A﹡ (P/A, 8%, 3) =5000﹡2.577=12885元
1.3普通年金现值 [例题]:某企业打算购置一台柴油机更新目前 使用的汽油机,每月可节省燃料费用60元,但 柴油机比汽油机高1500元。请问柴油机是用多 少年才合算?(假设年利率为12%,每月复利 一次)
1500≤60﹡ (P/A, 1%, n) 25≤ (P/A, 1%, n) 查表得:n=30月
A= P/ (P/A, 12%, 8)=2000/4.968=402.6万元
2.1先付年金终值
[例题]:某人每年年初存入1000元,存 款利率i=8%,问第10年末的本利和应是 多少?
F=1000﹡(F/A,8%,10) ﹡(1+8%) =1000﹡14.408﹡1.08=15645元 F=1000﹡ (F/A,8%,11) −1000 =1000﹡(16.645−1)=15645元
复利现值终值年金现值终值公式实例

复利现值终值年金现值终值公式实例集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]某投资项目预测的净现金流量见下表(万元),设资金基本贴现率为10%,则该项目的净现金值为()万元解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式为:ii A i A i A i A i A P nn n ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21 式中的分式ii n -+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。
它是普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1.递延年金现值公式为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1) 或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2)上述(1)公式是先计算出n 期的普通年金现值,然后减去前s期的普通年金现值,即得递延年金的现值,公式(2)是先将些递延年金视为(n-s)期普通年金,求出在第s 期的现值,然后再折算为第零期的现值。
复利现值、终值、年金现值终值公式、实例

解:本例因为涉及到年金当中的递延年金, 所以将年金系列一起先介 绍,然后解题年金 ,是指一定时期内每次等额收付款的系列款项, 通常记作 A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及 零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同, 可 分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介 绍普通年金与递延年金,其他的在后面介绍。
一、普通年金 ,是指从第一期起,在一定时期内 每期期末 等额发生的 系列收付款项,又称后付年金。
1. 普通年金现值公式为 :式中的分式 1 (1 i ) 称作“年金现值系数”,记为(P/A ,i ,n ), i可通过直接查阅 “1 元年金现值表” 求得有关的数值, 上式也可写作:P=A (P/A , i ,n ). 2. 例子: 租入某设备,每年年末需要支付租金 120 元,年复利 利率为 10%,则 5 年内应支付的租金总额的现值为:、递延年金 ,是指第一次收付款发生时间 与第一期无关 ,而隔若干P A (1 i)A (1 i) 2 A (1 i) ( n 1) A (1 i) n 1 (1 i) A 1 (1 i) n 120 1 (1 10%)10% 120 3.7908 455(元)期(假设为 s 期, s ≥1),后才开始发生的系列等额收付款项。
它是 普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1. 递延年金现值公式为 :期的普通年金现值 ,即得递延年金的现值,公式( 2)是先将些递延年金视为 (n-s ) 期普通年金,求出在第 s期的现值,然后再折算为第零期的现值。
=1000×(元)PAns1 (1 i ) n 1 (1 i) s A (P/ A,i,n) (P/ A,i,s) 1) 或P A 1 (1 i)(ns)i (1 i) A (P/ A,i,n s) (P/F,i,s)2) 上述 1)公式是先 计算出 n 期的普通年金现值,然后减去前 s2. 例子:某人在年初存入一笔资金,存满 5 年后每年年末取出1000 元,至第 10 年末取完,银行存款利率为 10%。
普通年金终值公式推导过程

普通年金终值公式推导过程嘿,朋友们!今天咱来唠唠普通年金终值公式的推导过程。
咱就说啊,年金就好像是一列排好队的小士兵,每个时期都规规矩矩地站在那里,等着给咱效力呢!普通年金就是这列小士兵中最常见的那种。
那普通年金终值是啥呢?就好比你每年都存一笔钱,到最后这些钱加起来一共能有多少。
那怎么算出来呢?咱就一步步来。
假设每年存 A 元,利率是 i,存了 n 年。
第一年存的 A 元到最后会变成多少呢?那当然是 A(1+i)^(n-1)呀,就像小士兵经过长时间的训练变得更强大了。
第二年存的 A 元呢,会变成 A(1+i)^(n-2)。
这么一直推下去,最后一年存的 A 元还是 A 元呢。
那把这些都加起来不就是普通年金终值嘛!这不就像把这些变强了的小士兵的力量都汇总到一起嘛!你说是不是很形象?那加起来怎么算呢,咱可以用等比数列求和公式呀。
你看,这过程是不是挺有意思的?就像搭积木一样,一块一块往上堆,最后就堆出了一个漂亮的城堡。
普通年金终值公式不就是这样嘛,通过一步步的推导,把看似复杂的东西变得清晰明了。
咱再想想,如果没有这个公式,那要算出这些年金的终值得多麻烦呀,得一个一个去算,还容易出错。
有了这个公式,就像有了一把万能钥匙,轻轻一转,门就开了。
而且啊,这个公式在生活中用处可大了呢!比如你计划着未来养老,每年存点钱,那你就可以用这个公式算算到时候能有多少钱,心里不就有底了嘛!或者你想做个长期的投资,也可以用它来预估收益呀。
所以说呀,普通年金终值公式可真是个好东西,它让我们能更清楚地看到未来,能更好地规划我们的生活。
大家可得好好理解它,让它为我们的生活服务呀!这就是我对普通年金终值公式推导过程的讲解啦,你们觉得咋样呢?是不是很通俗易懂呀!。
普通年金终值现值及年金的计算有图解

课程网站:http:\\
其中:
1 in 1
i
是普通年金为1元、利率为i、经过n期的年金终值 记作(F/A,i,n) 可以通过查阅“年金终值系数表”取得相关系数。
课程网站:http:\\
【同步训练2-3】收益再投资
江南公司连续3年每年年末获得分红100万元,用 于再投资,在投资报酬率为10%的情况下,则 该项分红在第3年末累计为多少?
331
【同步训练2-2】 年金终值系数与复利终值系数关系
如果已知
(F/P,10%,1)=1.10 (F/P,10%,2)=1.21 你能求出(F/A,10%,3)的值
吗?
课程网站:http:\\
普通年金终值计算公式的推导
每年的支付金额为A;利率为I;期数为n; 则按复利计算的普通年金终值F为:
你能求出(P/A,10%,3)的值 吗?
课程网站:http:\\
普通年金现值公式的推导:
由于:
P A1 i 1 A1 i 2 A1 i 3 ...... A1 i n
等式两边同乘(1+i):
1 iP A1 i0 A1 i 1 A1 i 2 ...... A1 i (n1)
A,10%,3
30.21万元
在银行利率为10%时,每年存入30.21万元,3年 后可得100万元,用来还清债务。
课程网站:http:\\
四、年资本回收额的计算
年资本回收额(Capital Recovery),是指在约 定年限内等额收回初始投入资本或清偿所欠的债 务。
即根据年金现值计算的年金,即已知现值求年金。
课程网站:http:\\
年金
年金是(Annuity)指等额、定期的系列收支。
