北京市海淀区2012届高三下学期期中练习文科数学试题(2012海淀一模)

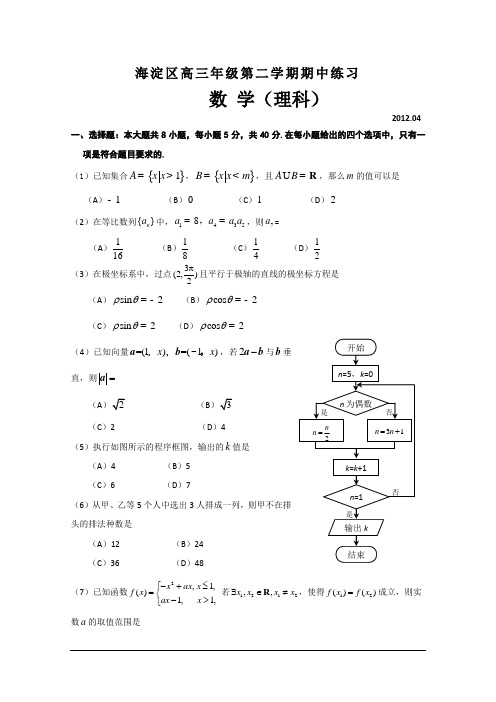
海淀区高三年级第二学期期中练习数 学（文科）2012.04一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知集合2{|1}A x x ==，{|(2)0}B x x x =-<，那么AB =（A ）Æ （B ） {1}- （C ）{1} （D ）{1,1}- （2）在等比数列{}n a 中，26a =，318a =-，则1234a a a a +++=（A ）26（B ）40 （C ）54（D ）80（3）已知向量=(12=(1)x x +-,a b ,),. 若a 与b 垂直，则||b =（A ）1 （B（C ）2 （D ）4（4）过双曲线221916x y -=的右焦点，且平行于经过一、三象限的渐近线的直线方程是 （A ）34150x y +-= （B ）34150x y --= （C ）43200x y -+= （D ）43200x y --=（5）执行如图所示的程序框图，输出的k 值是（A ）5 （B ）6 （C ）7 （D ）8（6）若满足条件020x y x y y a -≥⎧⎪+-≤⎨⎪≥⎩的整点(,)x y 恰有9个，其中整点是指横、纵坐标都是整数的点，则整数a 的值为（A ）3- （B ） 2- （C ）1- （D ）0（7）已知函数2,1,()1,1,x ax x f x ax x ⎧-+≤=⎨->⎩若1212,,x x x x ∃∈≠R ，使得12()()f x f x =成立，则实数a 的取值范围是（A ）2a < （B ）2a >（C ）22a -<< （D ）2a >或2a <-（8）在棱长为1的正方体''''ABCD A B C D -中，若点P 是棱上一点，则满足'2PA PC +=的点P 的个数为（A ）4 （B ）6 （C ）8 （D ）12二、填空题：本大题共6小题，每小题5分，共30分，把答案填在题中横线上. （9）复数2i1i-在复平面内所对应的点的坐标为 . （10）若tan 2α=，则sin 2α= .（11）以抛物线24y x =上的点0(,4)x 为圆心，并过此抛物线焦点的圆的方程是 .（12已知三条侧棱两两垂直的正三棱锥的俯视图如图所示，那么此三棱锥的体积是 ，左视图的面积是 .（13）设某商品的需求函数为1005Q P =-，其中,Q P 分别表示需求量和价格，如果商品需求弹性EQ EP大于1（其中'EQ Q P EP Q=-，'Q 是Q 的导数），则商品价格P 的取值范围是 .（14）已知函数1,,()0,.x f x x ìÎïï=íïÎïîR Q Q ð 则()()______f f x =； 下面三个命题中，所有真命题的序号是 . ① 函数()f x 是偶函数；② 任取一个不为零的有理数T ，()()f x T f x +=对x ∈R 恒成立；③ 存在三个点112233(,()),(,()),(,()),A x f x B x f x C x f x 使得ABC ∆为等边三角形.三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.A'B'C'D'ABCD俯视图（15）（本小题满分13分）已知函数()sin sin()3f x x x π=+-. （Ⅰ）求()f x 的单调递增区间；（Ⅱ）在ABC ∆中，角A ，B ，C 的对边分别为,,a b c .已知()f A =a =，试判断ABC ∆的形状.（16）（本小题满分13分）某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0,100]，样本数据分组为[0,20)，[20,40)，[40,60)，[60,80)，[80,100].（Ⅰ）求直方图中x 的值；（Ⅱ）如果上学所需时间不少于1小时的学生可申请在学校住宿，请估计学校600名新生中有多少名学生可以申请住宿.(17)（本小题满分14分）已知菱形ABCD 中，AB =4， 60BAD ∠=（如图1所示），将菱形ABCD 沿对角线BD 翻折，使点C 翻折到点1C 的位置（如图2所示），点E ，F ，M 分别是AB ，DC 1，BC 1的中点． （Ⅰ）证明：BD //平面EMF ； （Ⅱ）证明：1AC BD ⊥；（Ⅲ）当EF AB ⊥时，求线段AC 1 的长．(18)（本小题满分13分）已知函数211()ln (0)22f x a x x a a =-+∈≠且R . （Ⅰ）求()f x 的单调区间；ABCD图1M FEABC 1D图2（Ⅱ）是否存在实数a ，使得对任意的[)1,x ∈+∞，都有()0f x ≤？若存在，求a 的取值范围；若不存在，请说明理由. （19）（本小题满分13分）已知椭圆:C 2222 1 (0)x y a b a b+=>>的右顶点(2,0)A ，，O 为坐标原点. （Ⅰ）求椭圆C 的方程；（Ⅱ）已知P （异于点A ）为椭圆C 上一个动点，过O 作线段AP 的垂线l 交椭圆C 于点,E D ，求DE AP的取值范围.（20）（本小题满分14分）对于集合M ，定义函数1,,()1,.M x M f x x M -∈⎧=⎨∉⎩对于两个集合M ，N ，定义集合{()()1}M N M N x f x f x ∆=⋅=-. 已知A ={2，4，6，8，10}，B ={1，2，4，8，16}. （Ⅰ）写出(1)A f 和(1)B f 的值，并用列举法写出集合A B ∆； （Ⅱ）用Card (M )表示有限集合M 所含元素的个数.（ⅰ）求证：当()()Card X A Card X B ∆+∆取得最小值时， 2X Î； （ⅱ）求()()Card X A Card X B ∆+∆的最小值.海淀区高三年级第二学期期中练习数 学（文科）参考答案及评分标准 2012．04一.选择题：本大题共8小题，每小题5分，共40分.二.填空题：本大题共6小题，每小题5分，共30分. （9）(1,1)- （10）45（11）22(4)(4)25x y -+-=（12（13）(10,20) （14）1 ①②③ 三.解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤. （15）（本小题满分13分）解：（Ⅰ）()sin sin()3f x x x π=+-1sin sin 22x x x =+- ………………………………………2分3sin 22x x =-1cos 22x x ÷ç÷=-ç÷ç÷)6x π=-. ………………………………………4分 由22,262k x k k πππππ-<-<+?Z ， 得：222,33k x k k ππππ-<<+?Z . 所以 ()f x 的单调递增区间为2(2,2)33k k ππππ-+，k ÎZ . ………………………………………6分（Ⅱ）因为 ()2f A =，所以)62A π-=.所以1sin()62A π-=. ………………………………………7分因为 0A π<<，所以 5666A πππ-<-<. 所以 3A π=. ………………………………………9分 因为 sin sin a bA B=，a =， 所以 1sin 2B =. ………………………………………11分因为 a b >，3A π=，所以 6B π=.所以 2C π= .所以 ABC ∆为直角三角形. ………………………………………13分(16)（本小题满分13分） 解：（Ⅰ）由直方图可得200.025200.0065200.0032201x ⨯+⨯+⨯+⨯⨯=.所以0.0125x =. ………………………………………6分（Ⅱ）由直方图可知，新生上学所需时间不少于1小时的频率为：0.003220=0.12创. ………………………………………9分因为 6000.1272⨯=.所以 600名新生中有72名学生可以申请住宿.………………………………………13分(17)（本小题满分14分）证明：（Ⅰ）因为点,F M 分别是11,C D C B 的中点，所以//FM BD ． ………………………………………2分 又FM ⊂平面EM F ，BD ⊄平面EM F ,所以//BD 平面EM F ． ………………………………………4分（Ⅱ）在菱形ABCD 中，设O 为,AC BD 的交点,则AC BD ⊥． ………………………………………5分 所以 在三棱锥1C ABD -中，1,C O BD AO BD ⊥⊥.又 1,C OAO O =所以 BD ⊥平面1AOC ． ………………………………………7分O M FEABC 1D又 1AC ⊂平面1AOC ，所以 BD ⊥1AC ． ………………………………………9分（Ⅲ）连结1,DE C E ．在菱形ABCD 中，,60DA AB BAD =∠=，所以 ABD ∆是等边三角形.所以 DA DB =． ………………………………………10分因为 E 为AB 中点，所以 DE AB ⊥． 又 EF AB ⊥，EF DE E =．所以 AB ⊥平面DEF ，即AB ⊥平面1DEC ．………………………………………12分又 1C E ⊂平面1DEC ，所以 AB ⊥1C E ．因为 ,4AE EB AB ==，1BC AB =，所以 114AC BC ==． ………………………………………14分 (18)（本小题满分13分）解：（Ⅰ）()f x 的定义域为(0,)+∞.2'()a x af x x x x-+=-=. ………………………………………2分当0a <时，在区间(0,)+∞上，'()0f x <.所以 ()f x 的单调递减区间是(0,)+∞. ………………………………………3分当0a >时，令'()0f x =得x =x =.函数()f x ,'()f x 随x 的变化如下：所以 ()f x 的单调递增区间是，单调递减区间是)+∞.………………………………………6分综上所述，当0a <时， ()f x 的单调递减区间是(0,)+∞；M FEABC 1D当0a >时，()f x 的单调递增区间是，单调递减区间是)+∞. （Ⅱ）由（Ⅰ）可知：当0a <时, ()f x 在[1,)+∞上单调递减.所以()f x 在[1,)+∞上的最大值为(1)0f =，即对任意的[1,)x ∈+∞，都有()0f x ≤. ………………………………………7分当0a >时，① 1≤，即01a <≤时，()f x 在[1,)+∞上单调递减.所以()f x 在[1,)+∞上的最大值为(1)0f =，即对任意的[1,)x ∈+∞，都有()0f x ≤. ………………………………………10分② 1>，即1a >时，()f x 在上单调递增，所以 (1)f f >.又 (1)0f =，所以 0f >，与对于任意的[1,)x ∈+∞，都有()0f x ≤矛盾.………………………………………12分综上所述，存在实数a 满足题意，此时a 的取值范围是(,0)(0,1]-∞.………………………………………13分（19）（本小题满分13分）解：（Ⅰ）因为 (2,0)A 是椭圆C 的右顶点，所以 2a =.又2c a =，所以 c = 所以 222431b a c =-=-=.所以 椭圆C 的方程为2214x y +=. ………………………………………3分 （Ⅱ）当直线AP 的斜率为0时，||4AP =，DE 为椭圆C 的短轴，则||2DE =. 所以||1||2DE AP =. ………………………………………5分当直线AP 的斜率不为0时，设直线AP 的方程为(2)y k x =-，00(,)P x y ，则直线DE 的方程为1y x k=-. ………………………………………6分 由 22(2),14y k x x y =-⎧⎪⎨+=⎪⎩得224[(2)]40x k x +--=. 即2222(14)161640k x k x k +-+-=.所以 202162.41k x k +=+所以 20282.41k x k =+-………………………………………8分所以||AP ==即 ||AP =.类似可求||DE =所以2||||DE AP==………………………………………11分设t =则224k t =-，2t >.22||4(4)1415(2).||DE t t t AP t t-+-==> 令2415()(2)t g t t t -=>，则22415'()0t g t t +=>. 所以 ()g t 是一个增函数.所以2||41544151||22DE t AP t -⨯-=>=. 综上，||||DE AP 的取值范围是1[,)2+?. ………………………………………13分（20）（本小题满分14分）（Ⅰ）解：(1)=1A f ，(1)=1B f -，{1,6,10,16}A B ∆=.………………………………………3分（Ⅱ）设当()()Card X A Card X B ∆+∆取到最小值时，X W =. （ⅰ）证明：假设2W Ï，令{2}Y W=.那么 ()()Card Y A Card Y B ∆+∆()1()1Card W A Card W B =∆-+∆-()()Card W A Card W B <∆+∆.这与题设矛盾.所以 2W Î，即当()()Card X A Card X B ∆+∆取到最小值时，2X Î. ………………………………………7分（ⅱ）同（ⅰ）可得：4W Î且8W Î.若存在a X Î且a AB Ï，则令{}X Z a =ð.那么()()Card Z A Card Z B ∆+∆()1()1Card X A Card X B =∆-+∆-()()Card X A Card X B <∆+∆.所以 集合W 中的元素只能来自AB .若a AB Î且a A B Ï，同上分析可知：集合X 中是否包含元素a ，()()Card X A Card X B ∆+∆的值不变.综上可知，当W 为集合{1,6,10,16}的子集与集合{2,4,8}的并集时，()()Card X A Card X B ∆+∆取到最小值4.………………………………………14分。