§7.5 载流导线在磁场中所受的力
合集下载
载流导线在磁场中所受的力
04
载流导线在磁场中的受力分析
单根导线受力分析
总结词
当单根载流导线处于磁场中时， 会受到安培力的作用。
详细描述
安培力的大小与导线中电流的大 小、导线的长度以及磁场强度成 正比，方向垂直于导线与磁感线 构成的平面。
多根导线受力分析
总结词
当多根载流导线处于同一磁场中时，每根导线都会受到安培力的作用，且各导线之间的安培力相互影 响。
谢谢您的聆听
THANKS
磁场和电流之间存在相互作用，当导 线在磁场中放置时，导线会受到力的 作用，这个力被称为洛伦兹力。
02
安培力
安培力的定义
总结词
安培力是指通电导线在磁场中受到的 力。
详细描述
当导线中流过电流时，导线会受到磁 场对其的作用力，这个力即为安培力 。安培力的大小与电流、磁场强度以 及导线在磁场中的放置角度有关。
安培力的方向
总结词
安培力的方向由左手定则确定。
详细描述
通过左手定则可以判断安培力的方向。具体来说，伸开左手，让拇指与其余四 指垂直，并处于同一平面内；然后让磁感线穿过掌心，四指指向电流的方向， 则拇指所指的方向即为安培力的方向。
安培力的计算公式
总结词
安培力的计算公式为F = BILsinθ。
详细描述
详细描述
对于平行放置的多根导线，安培力的大小与导线之间的距离、导线的长度、电流大小以及磁场强度有 关。
磁场对通电导体的影响
总结词
磁场不仅会对载流导线施加力，还会对导线的电流产生影响。
详细描述
磁场对通电导体的影响表现在霍尔效应和磁致伸缩效应等方面。霍尔效应是指通电导线在磁场中受到横向力，导 致电子在垂直于电流和磁场的平面上聚集，从而在导线两端产生电压差。磁致伸缩效应则是指磁场的变化会导致 导线长度和直径的变化，从而引起导线的形变和应力。
毕-萨定律
已知:
圆形导线,半径 a
电流强度为 I ,
a I
x
P
求:P点的磁感应强度?
解： 任取电流元 I dl 它在空间一点产生 的磁场dB
I dl a I
r
x
dB P
x
μ o Idl sin a dB = r2 4 μ o Idl = 4 r2
π
π
a = 90
0
方向如图
由对称性： B y = B z =0
所以: F I ab B sin a IBR
方向
三. 磁场对载流线圈的作用
l1
l2
I
B
均匀磁场 载流线圈放入磁场中, 1.线圈所受的合外力?
2.线圈所受的合外力矩?
F1
l1 l2 I
B
上下两导线受力如图, 大小相等，方向相反 在同一条直线上
F1 F2 0
F2
dF Idl B
解: 1）.对称性分析 知内部场沿轴向,如图
方向与电流成右手螺旋关系
2）.做对称性环路 ...............B B dl B内 dl B dl
ab bc
L
B外 dl B dl
cd da
a
b
d
c
注意到:
F
L
Id l B ILB sin a
例.2
已知:均匀磁场,
I
内放半圆形导线， 半径为R,电流强度为I，
b B
a
导线两端连线与 磁感强度方向夹角a=30°，
求:此段圆弧电流受的磁力。
1.在电流上任取电流元 Id l
圆形导线,半径 a
电流强度为 I ,
a I
x
P
求:P点的磁感应强度?
解： 任取电流元 I dl 它在空间一点产生 的磁场dB
I dl a I
r
x
dB P
x
μ o Idl sin a dB = r2 4 μ o Idl = 4 r2
π
π
a = 90
0
方向如图
由对称性： B y = B z =0
所以: F I ab B sin a IBR
方向
三. 磁场对载流线圈的作用
l1
l2
I
B
均匀磁场 载流线圈放入磁场中, 1.线圈所受的合外力?
2.线圈所受的合外力矩?
F1
l1 l2 I
B
上下两导线受力如图, 大小相等，方向相反 在同一条直线上
F1 F2 0
F2
dF Idl B
解: 1）.对称性分析 知内部场沿轴向,如图
方向与电流成右手螺旋关系
2）.做对称性环路 ...............B B dl B内 dl B dl
ab bc
L
B外 dl B dl
cd da
a
b
d
c
注意到:
F
L
Id l B ILB sin a
例.2
已知:均匀磁场,
I
内放半圆形导线， 半径为R,电流强度为I，
b B
a
导线两端连线与 磁感强度方向夹角a=30°，
求:此段圆弧电流受的磁力。
1.在电流上任取电流元 Id l
大学物理课件-磁场对载流导线的作用
载流导线在磁场中会受到力的作用，这种力被称为安培力。安培力是由于导线中的自由电子与晶格之间的相互作用，使得导线在宏观上表现出受到磁场力的作用。安培定律是关于电流元在பைடு நூலகம்场中受力的基本规律，它表述为：一个电流元在磁场中所受的磁场力等于电流元与磁感应强度的矢量积。具体公式为dF=Idl×B，其中dF表示电流元所受的安培力，Idl表示电流元，B表示磁感应强度。通过积分可以求得有限长载流导线在磁场中受力的大小和方向。在均匀磁场中，直载流导线所受的安培力大小为F=IlBsinθ，其中I表示电流强度，l表示导线长度，B表示磁感应强度，θ表示电流方向与磁场方向的夹角。对于弯曲的平面导线或不规则形状的导线，可以通过将其分割成若干电流元并分别计算受力，再进行矢量合成来求得总受力。此外，文档还通过多个具体例题详细解析了如何应用安培定律和公式计算载流导线在磁场中的受力情况。最后，介绍了电磁轨道炮的原理，它是一种利用电流间相互作用的安培力将弹头发射出去的武器。
研究磁场中载流导线的受力和力矩计算方法
● 01
第1章 研究磁场中载流导线 的受力和力矩计算方法
研究背景及意义
研究磁场中载流导线 的受力和力矩计算方 法对于电磁理论的发 展具有重要意义。磁 场对导线的影响在电 力输送、磁悬浮等领 域具有广泛应用。本 章将介绍磁场中导线 受力和力矩计算的重 要性，并探讨这一研 究领域的现实意义。
磁场基础知识回顾
● 06
第六章 总结与展望
研究成果总结
导线受力计 算方法研究
成果
详细分析了磁场 中导线的受力情
况
贡献和影响
研究成果对相关 领域的影响和应
用
创新性和重 要性
强调研究工作的 创新和重要性
力矩计算方 法研究成果
对磁场中导线的 力矩进行全面计
算和分析
存在问题与改进建议
问题分析
研究中存在的问 题和不足
力矩来源
磁场对导线的扭转力 导线自身电流所受的力
变化规律
不同情况下导线力矩的特 点 受力平衡时力矩的关系
具体步骤
导线力矩计算的实例演示 应用导线力矩计算的案例
磁场中载流导线的受力和力矩计 算方法
磁场中载流导线的受力和力矩计算是电磁学中的 重要课题，涉及到磁场与导线相互作用的物理规 律。通过对导线在磁场中受力和力矩的计算方法 进行研究，可以更好地理解导线的运动规律及其 在实际工程中的应用。
表达对研究团队的感激之 情
未来展望
展望未来与合作机会
研究成果展示
研究磁场中载流导线 的受力和力矩计算方 法，对工程实践具有 重要价值。
感谢观看
THANKS
磁场基本概 念
磁感线、磁通量 等
磁场作用原 理
洛伦兹力、磁场 力等
导线作用
导线在磁场中的 运动特点
载流长直导线在磁场中所受的力讲解
範例6
邊長5 m、4 m、3 m 的直角三 角形電路，通以2 A電流，置於 方向向右且強度3 T的均勻磁場 中。若電路的平面與磁場方向 平行，則整個線圈所受之淨磁 力與淨磁力矩各為何？ (A) 磁 力0、磁力矩0 (B) 磁力18 N、 磁力矩0 (C) 磁力18 N、磁力矩 36 N．m (D) 磁力0、磁力矩36 N．m (E) 磁力24 N、磁力矩 72 N．m 。
及磁場的方向，即指離另
一導線的方向。
a兩導線之間的磁力為量值相等、方向相反的斥力。 換言之，兩平行載流直導線若電流方向相反時，則 兩導線互相 排斥 。
F 0i1i2 L 2 d
※安培的定義
上述公式被用來定義SI制單位中的電流的單位 --安培。如兩載相同電流的無限長細直導線， 互相平行排列，在真空中相距 1 公尺，而導 線上每公尺的作用力為 2×10－7 牛 頓，則導 線上電流的值定為 1 安培。
如下圖所示，將四種導線的首尾相接：
(1)甲導線的長度為 4L 所受磁力
L
所 受 的 磁 力 i 4 L B
2L
4iLB
Hale Waihona Puke L4L(2)乙導線的長度為 2L 所受磁力
L
2L
2L 2L
所 受 的 磁 力 i 2 L B
L
L L
LL
2iLB
2L
2L
L
L
LL
2L
2L
(1)甲 導 線 所 受 的 磁 力 4iLB。 (2)乙 導 線 所 受 的 磁 力 2iLB。
( 4 ) F d a 4 2 0 .5 s in 9 0 2 2 ( N ) ， 方 向 平 行 於 O c 。
(2 )F b c4 1 0 .5 sin9 0 2 (N )， 方 向 平 行 於 b O (即 x軸 方 向 )。 (3 )F cd42 0 .5 sin4 5 2 (N )， 方 向 平 行 於 zO (即 z軸 方 向 ) 。 (4 )F d a42 0 .5 sin9 0 22 (N )， 方 向 平 行 於 O c 。
载流导线在磁场中所受的力
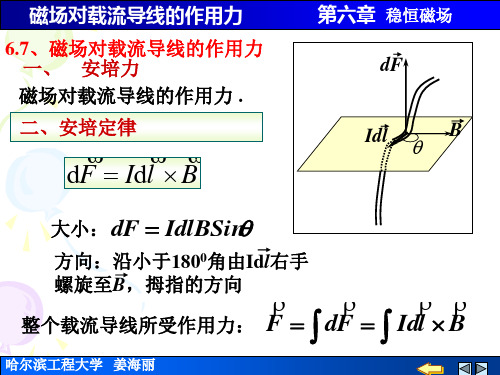
可得 0 4 π 10
7
7
N A
H m
2
1
4 π 10
0 I1 I 2
2π d
问 若两直导线电流方向相反 二者之间的作用力如何？
哈尔滨工程大学 姜海丽
F2 d F2 y d F2 sin
y
Id l
d
B
C
Id l
BI dl sin
0
I B
0
F1
r o
A
因 dl rd
x
F2 BIr
π 0
0
sin d
F2 BI ( 2 r cos 0 ) j BI AB j 故 F F1 F2 0 由于 F1 BI AB j
第六章 稳恒磁场
例 3 半径为 R 载有电流 I 2的导体圆环与电流为 I 1 的长直导线 放在同一平面内（如图）， 直导线与圆心 相距为 d ，且 R < d 两者间绝缘 , 求 作用在圆电流上 的磁场力. y 0 I1 B 解 B d F y dF 2 π d R cos d
.
d F BI 2 d l
0 I1 I 2
2π
dl d R cos
I1
d
dF x
I 2dl
dl Rd
dF
O R
I2
x
0 I1 I 2
2π
Rd d R cos
哈尔滨工程大学 姜海丽
磁场对载流导线的作用力
d F x d F cos
第六章 稳恒磁场
90 , sin 1
d F2 B1 I 2 d l 2
大学物理之载流导线在磁场中所受的力_图文_图文
例 2 如图一通有电流 的闭合回路放
在磁感应强度为 的均匀磁场中，回路平
面与磁感强度 垂直 .回路由
直导线 AB 和半径为
的圆弧导线 BCA 组成 ，
C
电流为顺时针方向,
求磁场作用于闭合
B
A
导线的力.
o
解 根据对称性分析
C
B
A
o
因
C
由于
B
A
故
o
例3：求一无限长直载流导线的磁场对另一直载流导
线ab的作用力。 已知：I1、I2、d、L
解：
a
b
x
d
L
例 3 半径为 载有电流 的导体圆
环与电流为 的长直导线 放在同一平
面（如图），直导
线与圆心相距为 d ，
d
且 R < d 两者间绝缘 ,
求 作用在圆电流上的
磁场力.
OR
解
.
d
OR
.
d
OR
.
d
OR
二 磁场作用于载流线圈的磁力矩
如图 均匀磁场中有 一矩形载流线圈 MNOP
M
P
大学物理之载流导线在磁场中所受的力_图文_ 图文.ppt
一般情况
导线是曲线 , 磁场为非均匀场。 导线上各长度元 上的速度 不相同
电流源受力
整个导线L上受磁场力
均匀磁场 直线电流
L
例 1 求如图不 规则的平面载流导线 在均匀磁场中所受的 力，已知 和 .
解 取一段电流元
P L
P L
结论 任意平面载流导线在均匀磁场 中所受的力 , 与其始点和终点相同的载流 直导线所受的磁场力相同；任意形状闭合 载流线圈在均匀磁场中受合力为零。
电磁学课件载流导线在磁场中所受的力
Bdr
2
2
2
2
右方第二和第三项都涉及到全微分绕闭合路径的积分，
故这两项均为零，于是我们得到
L
(
I 2
Lr
dr )
B
m
B
7
令电流圈的磁矩方向与磁场B的方向夹角为 ，它
受到的力矩之值为
L mBsin
这力矩将使磁矩朝磁场方向转动.如同电偶极子 p 与
电场中的互作用能
Wi
pE
pE cos
弧导线的力.
yB
C
Ir
B
A
o
x
4
磁场对载流线圈作用的力矩
5
电流圈 受到相对于通过O点的轴 的力矩为
L L r dF I L r (dl B)
(2.7-2)
如果磁场B 是均匀的，并注意到
a (b c) b(c a) c(a b)
d[r (r B)] dr (r B) r (dr B) r (dr B) dr (B r ) B(r dr )
dl dr
1
dr (B
r)
1
dr (B
r)
1
Bdr 2
2
2
2
1
(r
dr )
B
1
r (B
dr )
1
dr (B
r)
1
Bdr 2
2
2
2
2
1
(rdr ) 来自B1d[r (r
B)]
1
Bdr 2
2
2
2
6
r
(dr
B)
1
(r
dr )
B
1
d[r (r
B)]
载流导线在磁场中所受的力磁场对载流线圈的作用
载流导线在磁场中所受的力磁场对载流线圈的作用
物理作业
当一个载流线圈进入到磁场中，磁场会对载流线圈的回路造成影响，引起电流的流动。
1、电流流动
当一个载流线圈进入磁场中，其载体上的电压在机械施加电势差的基础上，受磁场的作用产生另外的电势差，由于存在电势差，就会有电流流动，这就是受磁场作用的结果。
根据霍尔定律，当电流流动时，磁场中的磁感应强度会受到影响，只要有电流流动就会改变磁场中的磁感应强度，进而引起磁场的变化。
2、磁场
当载流线圈进入磁场中时，会产生磁力，这个磁力会对载流线圈的回路造成影响，使其具有电磁能。
电磁能的大小取决于磁力大小，磁力的大小又取决于磁场的强度和磁力矢量的方向，所以，磁场的强度和方向对电磁能的大小起着关键性作用。
3、电磁对抗
当载流线圈进入到磁场中时，磁场会影响载流线圈的回路，使其具有电磁能，电磁能的大小取决于电压和磁力的大小，因此，载流线圈在磁场中的电磁能可以用电压和磁力两个度量表示。
当磁场和电压产生相互作用时，载流线圈会受到电磁对抗的作用，它会发出声音或震动，从而受到磁场的影响。
4、磁通率
当载流线圈进入到磁场中时。
大学物理之7-8载流导线在磁场中所受的力
06
参考文献
参考文献
[1] 张三. "磁场对电 流的作用力". 物理学 基础, 2010, 25(7): 123-135.
[3] 王五. "磁场与电 流相互作用的基础研 究". 物理研究, 2018, 40(7): 98-109.
[2] 李四. "载流导线 在磁场中的受力分析 ". 物理实验教程, 2015, 30(8): 234245.
100%
结果讨论
讨论实验误差来源，如导线弯曲 、磁场不均匀等，并提出改进措 施。
80%
结论总结
总结实验结果，得出导线在磁场 中所受的力与电流和磁场强度的 关系，加深对安培力定律的理解 。
05
结论
主要发现
载流导线在磁场中受到的力与 磁场强度、电流强度以及导线 在磁场中的放置角度有关。
当导线垂直于磁场放置时，受 到的力最大；当导线与磁场平 行放置时，受到的力为零。
动量
动量是描述物体运动状态的物理量，其大小等于物体的质量与速度的乘积，方 向与速度方向相同。单位是千克米每秒（Kg m/s），国际单位制中的基本单位。
04
实验与观察
实验设计
实验目标
通过观察载流导线在磁场中的受力情况，验证安培 力定律。
实验原理
依据安培力定律，当导线中通有电流时，导线将受 到垂直于导线方向上的磁场力。
磁场对放入其中的电流或磁体产生作用力，即洛伦 兹力或安培力。
磁场强度、磁感应强度和磁感线是描述磁场的主要 物理量。
载流导线的定义与性质
02
01
03
载流导线是指内部通过电流的导线，其电流可以是直 流或交流。
载流导线在磁场中会产生受到力的作用，这个力称为 洛伦兹力或安培力。
§7.8 载流导线在磁场中所受的力(打印稿)
Bo
0I1
2R
方向：
小线圈： pm I2S2 I2 r 2
I1
当小线圈转到θ 位置时：
M pm B M pmB sin
I2 r2B sin
I2 r R
· 13 ·
Chapter 7. 稳恒电流与稳恒磁场
§7.8 载流导线在磁场中所受的力
由于：R
>>
r，则：
I
· 10 ·
Chapter 7. 稳恒电流与稳恒磁场
§7.8 载流导线在磁场中所受的力
二、载流线圈所受的磁力矩
匀强磁场中： Fi 0
但合力矩： Mi 0 !
F1 F2 IBb
合力矩：M Mi
2F1
a 2
cos(2
பைடு நூலகம்
)
BIab sin
B
Bo
0I1
2R
M I2 r 2
0I1
2R
sin
/2
W Md
0
I2
r2
0 I1
2R
/2
sin
d
I1
0
0r2
2R
I1I2
(解毕 )
I2 r R
· 14 ·
Chapter 7. 稳恒电流与稳恒磁场
§7.8 载流导线在磁场中所受的力
1. 安培定律：
z oa
0
Idl
B bx
F I Bab sin
(
B
在xoz平面内)
·7 ·
Chapter 7. 稳恒电流与稳恒磁场
流导线在磁场中所受的力(1)
A
0
x
2021/4/10
15
第十一章 恒定磁场
11 – 8 载流导线在磁场中所受的力
物理学教程 （第二版）
二 磁场对载流线圈的力矩
如图 均匀磁场中有一矩形载流线圈MNOP
MN l2
NO
l1
F1 BIl2 F1 F2
F3 P
M
F2
I
B
F3 BIl1 sin(π )
F1
N F4
O en
B1
0 I1 2x
,
2
7
第十一章 恒定磁场
11 – 8 载流导线在磁场中所受的力
物理学教程 （第二版）
dF I 2dxB 1 sin
分割的所有电流元受力
方向都向上，离 I1 近的电流 元受力大，离 I1 远的电流元 受力小，所以 I2 受到的安培
I1 dF x dx o
I2 x
力为：
aL
F dF
M BISsin
M
ISen
B
m
B
线圈有N 匝时
M
NISen
B （适用于任意线圈）
2021/4/10
17
第十一章 恒定磁场
11 – 8 载流导线在磁场中所受的力
物理学教程 （第二版）
讨论
1）en方向与 B 相同 2）方向相反
稳定平衡
不稳定平衡
3）方向垂直 力矩最大
++++++
I
++++++
I B
F⊙
解：由均匀磁场中曲线电流受力的结论：
半圆形电流受到的安培力相当于沿直径
0
x
2021/4/10
15
第十一章 恒定磁场
11 – 8 载流导线在磁场中所受的力
物理学教程 （第二版）
二 磁场对载流线圈的力矩
如图 均匀磁场中有一矩形载流线圈MNOP
MN l2
NO
l1
F1 BIl2 F1 F2
F3 P
M
F2
I
B
F3 BIl1 sin(π )
F1
N F4
O en
B1
0 I1 2x
,
2
7
第十一章 恒定磁场
11 – 8 载流导线在磁场中所受的力
物理学教程 （第二版）
dF I 2dxB 1 sin
分割的所有电流元受力
方向都向上，离 I1 近的电流 元受力大，离 I1 远的电流元 受力小，所以 I2 受到的安培
I1 dF x dx o
I2 x
力为：
aL
F dF
M BISsin
M
ISen
B
m
B
线圈有N 匝时
M
NISen
B （适用于任意线圈）
2021/4/10
17
第十一章 恒定磁场
11 – 8 载流导线在磁场中所受的力
物理学教程 （第二版）
讨论
1）en方向与 B 相同 2）方向相反
稳定平衡
不稳定平衡
3）方向垂直 力矩最大
++++++
I
++++++
I B
F⊙
解：由均匀磁场中曲线电流受力的结论：
半圆形电流受到的安培力相当于沿直径
载流导体在磁场中一定受到磁场力的作用吗
载流导体在磁场中一定受到磁场力的作用吗
载流导体在磁场中不一定受到磁场力的作用。
只有载流导体与磁场存在一定夹角时才有磁场力，如果导体和磁场的夹角为0或180度，则没有磁场力磁场力包括磁场对运动电荷作用的洛仑兹力和磁场对电流作用的安培力磁场力现象中涉及3个物理量的方向：磁场方向、电荷运动方向、洛仑兹力方向磁场方向、电流方向、安培力方向。
磁场
磁场，物理概念，是指传递实物间磁力作用的场。
磁场是由运动着的微小粒子构成的，在现有条件下看不见、摸不着。
磁场具有粒子的辐射特性。
磁体周围存在磁场，磁体间的相互作用就是以磁场作为媒介的，所以两磁体不用在物理层面接触就能发生作用。
由于磁体的磁性来源于电流，电流是电荷的运动，因而概括地说，磁场是相对于观测点运动的电荷的运动的电场的强度与速度，带来的观测点处电荷所受力
的变化的表现。
用现代物理的观点来考察，物质中能够形成电荷的终极成分只有电子（带单位负电荷）和质子（带单位正电荷）。
因此负电荷就是带有过剩电子的带电物体，正电荷就是带有过剩质子的带电物体。
运动电荷产生磁场的真正场源是运动电子或运动质子所产生的磁场。
例如电流所产生的磁场就是在导线中运动的电子所产生的磁场。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a o
l
a
0 I1 I 2 dx 2 x
I2
x x dx
B1
x
0 I1 I 2 a l F ln 竖直向上。 2 a (解毕 )
0 I1 2 x
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 7 / 25 .
课堂练习 已知：I1、I2、a，求单位长度上两导线间的
a
(安培定律)
a
I
dl
B
B
☻ dF 大小： dF Idl B sin
方向：右手定则。 ☻电流元 Id 沿电流方向，故上 l
I
S
v
I
dl
B
式的积分方向亦为电流方向。
fm
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
I 2dl B1
0 I1 I 2 a l F ln 竖直向上。 2 a (解毕 )
a
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 8 / 25 .
课堂练习 已知：I1、I2、a，求单位长度上两导线间的
相互作用力。
提示：取元如图所示： I 2dl 0 I1 B1 dF2 I 2dl B1
2 a dF2 0 I1 I 2 Fl dl 2 a
I1
dF2
I2
I 2dl B1
答案：
相互吸引。
SI 制中安培定义 ： 真空中两根∞载流直
导线间距为 1m ，通以相同大小的稳恒电流，
a
若导线上作用力为2×10－7 N/m，则每根导
线中电流为1A。
Chapter 14. 稳恒磁场
Facba 0
R
R
b 2 R
B a
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
B
F1
I en
F2
I
en
M
S sin BIab sin
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 18 / 25 .
磁偶极矩 ( 磁矩 )：
pm IS en
则磁力矩：
( A· m2 )
B
a
b
M pm B
b
M pm B
I en
F2
☻上两式对任意形状的载流线
圈都成立。
B
F1
I
en
M
☻当θ = 0 时线圈处于最稳定状态。
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 20 / 25 .
例 如图，已知：I1、I2、R >> r，大线圈固定 。求当小
x
F I B ab sin
( B 在xoz平面内)
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 12 / 25 .
推论1：在匀强磁场B中，载流直导线所受的磁力： 大小：F I B l 方向：l B
a F I B b
dq I neSdl neSv dt dl / v
v
I
dl
B
fm
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 4 / 25 .
导线受到的磁力即为安培力：
I b
dF Idl B b F Id l B
线圈从如图位置转到相互垂直时磁力矩作的功。
解 大线圈在其圆心处产生的磁场：
0 I1 Bo 方向： 2R 2 p I S I r 小线圈： m 2 2 2
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 9 / 25 .
试证：在匀强磁场B中，任意形状的载流导线所受的磁
力为 F I ab B sin 。已知：I 、θ 。
证明 建立坐标系如图所示 dF Idl B ˆ dl dx ˆ i dy ˆ j dz k ˆ B B cos ˆ i B sin k
I
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 14 / 25 .
课堂练习 如图，匀强磁场B中，求该载流导线所受到的
磁力。已知：B、R、I 。
提示：用一导线将ab连接起来，则：
I 推论2：在匀强磁场 B 中，任意 c 形状的闭合载流线圈所 受到的磁力为零！
☻ dF 大小： dF Idl B sin
方向：右手定则。 ☻电流元 Id 沿电流方向，故上 l
a o
l
I2
x x dx
B1
x
0 I1 2 x
式的积分方向亦为电流方向。
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 6 / 25 .
I en
F2
B
F1
I
en
M
S sin sin M BIab
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 19
则磁力矩：
( A· m2 )
B
a
P. 15 / 25 .
课堂练习 如图，匀强磁场B中，求该载流导线所受到的
磁力。已知：B、R、I 。
提示：用一导线将ab连接起来，则：
Facba 0
Facba Facb Fba
答案： Facb 2IBR
I c
例 已知：I1、I2、l、a，求两导线间的相互作用力。 解 建立坐标系如图所示 j dF I 2dl B1 I 2dl B1 sin 90o ˆ
0 I1 dF dFy I I22dx dl B1 2 x
F Fy
a l
y
I1
I 2 d l dF
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 1 / 25 .
§14.4 载流导线在磁场中所受
的力
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 2 / 25 .
一、安培力 安培定律
电流元 Idl 受力：dF dF dN fm
相互作用力。
2 a dF2 0 I1 I 2 答案： Fl dl 2 a a l 0 I1 I 2 F Fy dx 2 x a
提示：取元如图所示： I 2dl 0 I1 B1 dF2 I 2dl B1
相互吸引。
I1
dF2
I2
Fz dFz IBx dy 0
0
0
F I B ab sin
Chapter 14. 稳恒磁场
§14. 4 载流导线在磁场中所受的力 作者：杨茂田
P. 13 / 25 .
推论1：在匀强磁场B中，载流直导线所受的磁力： 大小：F I B l 方向：l B 推论2：在匀强磁场 B 中，任意
Fy dFy IB cos dz IB sin dx
0 0
xb xa
IB ab sin
y
I
dFz I ( By dx Bx dy ) IBx dy
Fz dFz IBx dy 0
0 0
Idl B
z
o a
b
Fy dFy IB cos dz IB sin dx
0 0
xb xa
IB ab sin
y
I
dFz I ( By dx Bx dy ) IBx dy ˆ B B cos ˆ i B sin k z dFx I ( Bz dy By dz) IBz dy
P. 5 / 25 .
例 已知：I1、I2、l、a，求两导线间的相互作用力。 解 建立坐标系如图所示 j dF I 2dl B1 I 2dl B1 sin 90o ˆ
0 I1 dF dFy I I22dx dl B1 2 x
y
I1
I 2 d l dF
a
F I
形状的闭合载流线圈所
受到的磁力为零！
B b B
y
I
Idl B
z
o a
b
x
dFx I ( Bz dy By dz) IBz dy
Fx dFx IBz dy 0