三角函数公式全集合

合集下载

(完整word版)三角函数公式全集合

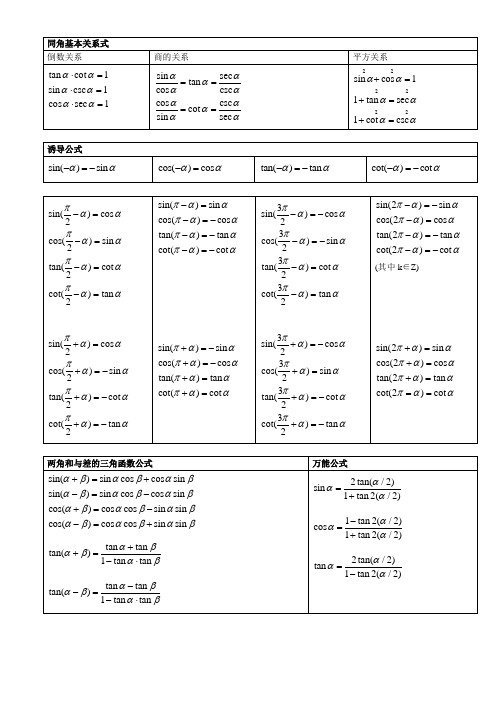
三角函数1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b)cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)] tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)]3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) - sin(b) = 2sin[(a - b)/2]cos[(a + b)/2]cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2]cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(a)cos 2a = cos2a - sin2a = 2cos2a - 1= 1 - 2sin2a6.半角公式sin2a = （1 – cos 2a）/ 2cos2a = （1 + cos 2a）/ 2tan a = [1 – cos 2a] /sin 2a = sin 2a / [1 + cos 2a ]7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]三角函数公式三角函数是数学中属于初等函数中的超越函数的一类函数。

(完整版)三角函数公式大全

三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ,记：22y x r +=，正弦函数：r y=αsin 余弦函数：r x =αcos 正切函数：x y =αtan余切函数：y x =αcot 正割函数：xr=αsec余割函数：yr=αcsc二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割,左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ,1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角,终边相同的角的同一三角函数的值相等:sin（2kπ＋α）＝sinα cos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanα cot（2kπ＋α)＝cotα (其中k∈Z) 公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin（π＋α）＝－sinα cos（π＋α）＝－cosα tan（π＋α）＝tanα cot（π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系： sin（－α）＝－sinα cos（－α）＝cosα tan(－α）＝－tanα cot（－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin（π－α）＝sinα cos（π－α）＝－cosα tan（π－α）＝－tanα cot(π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系:sin（απ-2）＝cosα cos（απ-2）＝sinα tan（απ-2）＝cotα cot（απ-2）＝tanα公式六:απ+2与α的三角函数值之间的关系:sin（απ+2）＝cosα cos（απ+2）＝－sinαtan(απ+2)＝－cotα cot（απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系：sin(απ-23）＝－cosα cos（απ-23）＝－sinαtan（απ-23)＝cotα cot（απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin(απ+23）＝－cosα cos（απ+23）＝sinαtan（απ+23）＝－cotα cot（απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin（2π－α)＝－sinα cos(2π－α）＝cosα tan（2π－α)＝－tanα cot（2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

最全的三角函数公式

最全的三角函数公式三角函数是数学中一个重要的概念，广泛应用于几何、物理和工程等领域。

在本文中，我将为您介绍最全的三角函数公式，包括基本公式、倒数公式、和角公式、和差公式、倍角公式、半角公式、和积公式、和商公式以及其他一些特殊的三角函数公式。

一、基本公式1. 正弦公式：sinθ = 对边/斜边2. 余弦公式：cosθ = 邻边/斜边3. 正切公式：tanθ = 对边/邻边二、倒数公式1. 余切公式：cotθ = 邻边/对边2. cosec公式：cscθ = 1/sinθ3. sec公式：secθ = 1/cosθ三、和角公式1. 正弦和：sin(α+β) = sinαcosβ + cosαsinβ2. 余弦和：cos(α+β) = cosαcosβ - sinαsinβ3. 正切和：tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)四、差角公式1. 正弦差：sin(α-β) = sinαcosβ - cosαsinβ2. 余弦差：cos(α-β) = cosαcosβ + sinαsinβ3. 正切差：tan(α-β) = (tanα - tanβ)/(1 + tanαtanβ)五、倍角公式1. 正弦倍角：sin2θ = 2sinθcosθ2. 余弦倍角：cos2θ = cos²θ - sin²θ3. 正切倍角：tan2θ = 2tanθ/(1 - tan²θ)六、半角公式1. 正弦半角：sin(θ/2) = ±√[(1 - cosθ)/2]2. 余弦半角：cos(θ/2) = ±√[(1 + cosθ)/2]3. 正切半角：tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)] （其中分母不等于0）七、和积公式1. 正弦和积：sin(α+β) = 2sin(α/2)cos(β/2)2. 余弦和积：cos(α+β) = 2cos(α/2)cos(β/2)3. 正切和积：tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)八、和商公式1. 正弦和商：sin(α+β) = sinαcosβ + cosαsinβ/cosαcosβ - sinαsinβ2. 余弦和商：cos(α+β) = cosαcosβ - sinαsinβ/cosαcosβ + sinαsinβ3. 正切和商：tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)九、其他特殊公式1. 倍角余弦1：cos2θ = 1 - 2sin²θ2. 倍角余弦2：cos²θ = （1 + cos2θ）/23. 倍角正弦：sin2θ = 2sinθcosθ4. 差角正切：tan(α-β) = (tanα - tanβ)/(1 + tanαtanβ)这些三角函数公式是三角学中最基本且最重要的公式。

三角函数运算公式大全

以下是三角函数公式的个人归纳，请查收~诱导公式(1)sinx=sin(x+2kπ)cosx=cos(x+2kπ)tanx=tan(x+2kπ)k∈Z原理：终边相同的角同一三角函数值相同（或可用三角函数图像的周期性验证）(2)sin(-x)=-sinxcos(-x)=cosx tan(-x)=-tanx(3)sin(π+x)=-sinx cos(π+x)=-cosx tan(π+x)=tanx(4)sin(π-x)=sinx cos(π-x)=-cosxtan(π-x)=-tanx原理：三角函数值中，正弦一二象限为正，余弦一四象限为正，正切一三象限为正（终边）(5)sin(π/2+x)=cosxcos(π/2+x)=-sinxtan(π/2+x)=-cotx(6)sin(π/2-x)=cosxcos(π/2-x)=sinxtan(π/2-x)=cotx(7)展开公式sin(3π/2+x)=sin(π+π/2+x)=-sin(π/2+x)=-cosx cos(3π/2+x)=cos(π+π/2+x)=-cos(π/2+x)=sinx tan(3π/2+x)=-cotxsin(3π/2-x)=sin(π+π/2-x)=-sin(π/2-x)=-cosx cos(3π/2-x)=cos(π+π/2-x)=-cos(π/2-x)=-sinx tan(3π/2-x)=cotx两角公式(1)两角和差公式sin(x+y)=sinxcosy+sinycosxsin(x-y)=sinxcosy-sinycosxcos(x+y)=cosxcosy-sinxsinycos(x-y)=cosxcosy+sinxsinytan(x+y)=sin(x+y)/cos(x+y)=sinxcosy+sinycosx/cosxcosy-sinxsiny=tanx+tany/1-tanxtanytan(x-y)=sin(x-y)/cos(x-y)=sinxcosy-sinycosx/cosxcosy+sinxsiny=tanx-tany/1+tanxtany证明：单位圆作图(2)二倍角公式sin2x=2sinxcosx推导：sin2x=sin(x+x)=sinxcosx+cosxsinx=2sinxcosxcos2x=(cosx)²-(sinx)²=2cos²x-1=1-2sin²x (sin²x+cos²x=1)推导：cos2x=cos(x+x)=cosxcosx-sinxsinx=cos²x-sin²xtan2x=sin2x/cos2x=2sinxcosx/cos²x-sin²x=2tanx/1-tan²x*三倍角公式sin3x=sin(2x+x)=sin2xcosx+cos2xsinx=2sinx(1-sin²x)+(1-2sin²x)sinx=3sinx-4sin³xcos3x=cos(2x+x)=cos2xcosx-sinxsin2x=(2cos²x-1)cosx-2cosx(1-cos²x)=4cos³x-3cosxtan3x=sin3x/cos3x=tanxtan(π/3+x)tan(π/3-x)(3)半角公式sin²(x/2)=(1-cosx)/2cos²(x/2)=(1+cosx)/2tan²(x/2)=1-cosx/1+cosx推导：cosx=2cos²(x/2)-1=1-2sin²(x/2)(4)辅助角公式asinx+bcosx=√(a²+b²)[asinx/√(a²+b²)+bcosx/√(a²+b²)]原理：配凑为sin²m+cos²m的形式，值域为[-√(a²+b²),√(a²+b²)] (5)两角推诱导例sin(π+x)=sinπcosx+sinxcosπ=-sinxcos(π+x)=cosπcosx-sinπsinx=-cosxsin(π-x)=sinπcosx-sinxcosπ=sinxcos(π-x)=cosπcosx+sinπsinx=-cosx与二次函数的那些事儿(1)变量法e.g.求f(x)=sinx+cos2x的值域解：由题f(x)=sinx+1-2sin²x......将sinx看做熟悉的变量f(x)=-2(sin²x-1/2sinx+1/16-1/16)+1=-2(sinx-1/4)²+9/8......化为熟悉的顶点式∵sinx∈[-1,1]......注意定义域（尤其是题目如果给出角范围）∴当sinx=1/4时，有f(x)最大值9/8；当sinx=-1时，有f(x)最小值-2 ∴f(x)值域为[-2,9/8](2)换元法e.g.求f(x)=sinx+cosx+sinxcosx的值域解：由题,令t=sinx+cosx=√2sin(x+π/4) t∈[-√2,√2]f(x)=t+sinxcosx∵t²=1+2sinxcosx∴sinxcosx=(t²-1)/2即f(x)=t+t²/2-1/2......换元，注意定义域接下来由二次函数解即可(3)公式法对于复合函数或不等式而言，需要注意其单调性与奇偶性，综合运用公式、定理与方程思想。

三角函数的公式大全

三角函数的公式大全1、两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)2、倍角公式tan2A = 2tanA/(1-tan² A)Sin2A=2SinA•CosACos2A = Cos^2 A–Sin² A=2Cos² A—1=1—2sin^2 A3、三倍角公式sin3A = 3sinA-4(sinA)³;cos3A = 4(cosA)³ -3cosAtan3a = tan a • tan(π/3+a)• tan(π/3-a)4、半角公式sin(A/2) = √{(1–cosA)/2}cos(A/2) = √{(1+cosA)/2}tan(A/2) = √{(1–cosA)/(1+cosA)}cot(A/2) = √{(1+cosA)/(1-cosA)} ?tan(A/2) = (1–cosA)/sinA=sinA/(1+cosA) 5、和差化积sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosB6、积化和差sin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)]7、诱导公式sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2-a) = cos(a)cos(π/2-a) = sin(a)sin(π/2+a) = cos(a)cos(π/2+a) = -sin(a)sin(π-a) = sin(a)cos(π-a) = -cos(a)sin(π+a) = -sin(a)cos(π+a) = -cos(a)tgA=tanA = sinA/cosA8、万能公式sin(a) = [2tan(a/2)] / {1+[tan(a/2)]²}cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]²}tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}9、其它公式a•sin(a)+b•cos(a) = [√(a²+b²)]*sin(a+c) [其中，tan(c)=b/a] a•sin(a)-b•cos(a) = [√(a²+b²)]*cos(a-c) [其中，tan(c)=a/b] 1+sin(a) = [sin(a/2)+cos(a/2)]²;1-sin(a) = [sin(a/2)-cos(a/2)]²;10、其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)11、双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tg h(a) = sin h(a)/cos h(a)12、公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）= sinαcos（2kπ＋α）= cosαtan（2kπ＋α）= tanαcot（2kπ＋α）= cotα13、公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= -sinαcos（π＋α）= -cosαtan（π＋α）= tanαcot（π＋α）= cotα14、公式三：任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα15、公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα16、公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα17、公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2+α）= cosαcos（π/2+α）= -sinαtan（π/2+α）= -cotαcot（π/2+α）= -tanαsin（π/2-α）= cosαcos（π/2-α）= sinαtan（π/2-α）= cotαcot（π/2-α）= tanαsin（3π/2+α）= -cosαcos（3π/2+α）= sinαtan（3π/2+α）= -cotαcot（3π/2+α）= -tanαsin（3π/2-α）= -cosαcos（3π/2-α）= -sinαtan（3π/2-α）= cotαcot（3π/2-α）= tanα√表示根号,包括{……}中的内容18、三角函数记忆口诀三角函数是函数，象限符号坐标注。

三角函数公式大全

三角函数公式大全三角函数是数学中重要的概念，它们在几何、物理、工程等领域都有广泛的应用。

下面将详细介绍一些常用的三角函数公式。

1. 正弦函数（sine function）：正弦函数是一个周期函数，它表示角度为x的点在单位圆上的y坐标。

正弦函数的公式如下：sin(x) = y，其中-1≤y≤12. 余弦函数（cosine function）：余弦函数也是一个周期函数，它表示角度为x的点在单位圆上的x坐标。

余弦函数的公式如下：cos(x) = x，其中-1≤x≤13. 正切函数（tangent function）：正切函数表示角度为x的点在单位圆上的斜率。

正切函数的公式如下：tan(x) = sin(x)/cos(x)。

4. 余切函数（cotangent function）：余切函数表示角度为x的点在单位圆上斜率的倒数。

余切函数的公式如下：cot(x) = 1/tan(x) = cos(x)/sin(x)。

5. 正割函数（secant function）：正割函数表示角度为x的点在单位圆上的x坐标的倒数。

正割函数的公式如下：sec(x) = 1/cos(x)。

6. 余割函数（cosecant function）：余割函数表示角度为x的点在单位圆上的y坐标的倒数。

余割函数的公式如下：csc(x) = 1/sin(x)。

7. 和差公式（sum and difference formulas）：和差公式用于计算两个角的正弦、余弦和正切的和或差。

具体公式如下：sin(A±B) = sin(A)cos(B) ± cos(A)sin(B)cos(A±B) = cos(A)cos(B) ∓ sin(A)sin(B)tan(A±B) = (tan(A) ± tan(B))/(1∓tan(A)tan(B))8. 倍角公式（double angle formulas）：倍角公式用于计算一个角的正弦、余弦和正切的两倍。

(完整版)三角函数公式汇总

(完整版)三角函数公式汇总介绍三角函数是数学中重要的概念，可用来描述角的性质和在各个学科中的应用。

三角函数包括正弦（sin）、余弦（cos）、正切（tan）等，它们之间存在一系列的基本关系和公式。

本文档将详细介绍常见的三角函数公式，以帮助读者更好地理解和应用三角函数。

正弦函数（sin）定义正弦函数是一个周期为2π的周期函数，定义域为实数集，值域为[-1, 1]。

公式1. 正弦函数的周期性公式为：sin(x + 2kπ) = sin(x)，其中 k ∈ Z。

2. 正弦函数的关系公式有：- 反正弦函数：x = arcsin(y)，其中 y ∈ [-1, 1]。

- 正弦函数的平方和公式：sin^2(x) + cos^2(x) = 1。

余弦函数（cos）定义余弦函数是一个周期为2π的周期函数，定义域为实数集，值域为[-1, 1]。

公式1. 余弦函数的周期性公式为：cos(x + 2kπ) = cos(x)，其中 k ∈Z。

2. 余弦函数的关系公式有：- 反余弦函数：x = arccos(y)，其中 y ∈ [-1, 1]。

- 余弦函数的平方和公式：sin^2(x) + cos^2(x) = 1。

正切函数（tan）定义正切函数是一个周期为π的周期函数，定义域为实数集。

公式1. 正切函数的周期性公式为：tan(x + kπ) = tan(x)，其中 k ∈ Z。

2. 正切函数的关系公式有：- 反正切函数：x = arctan(y)，其中 y ∈ R。

其他三角函数公式1. 余切函数（cot）与正切函数的关系式：cot(x) = 1/tan(x)。

2. 正割函数（sec）与余弦函数的关系式：sec(x) = 1/cos(x)。

3. 余割函数（csc）与正弦函数的关系式：csc(x) = 1/sin(x)。

应用领域三角函数广泛应用于工程、物理、计算机图形学等领域。

例如，在三角形的计算中，可以利用正弦、余弦、正切等函数来求解各种角度和边长。

三角函数公式大全

三角函数公式大全一、正弦函数公式。

正弦函数是最基本的三角函数之一，其公式如下：sinθ = 对边/斜边。

其中，θ为角度，对边为与角度θ相对的直角三角形的边长，斜边为直角三角形的斜边长度。

正弦函数的图像是一个周期性的波动曲线，具有一定的对称性和周期性。

二、余弦函数公式。

余弦函数是另一个重要的三角函数，其公式如下：cosθ = 邻边/斜边。

其中，θ为角度，邻边为与角度θ相邻的直角三角形的边长，斜边为直角三角形的斜边长度。

余弦函数的图像也是一个周期性的波动曲线，与正弦函数的图像有一定的相似性。

三、正切函数公式。

正切函数是三角函数中的另一个重要概念，其公式如下：tanθ = 对边/邻边。

其中，θ为角度，对边为与角度θ相对的直角三角形的边长，邻边为与角度θ相邻的直角三角形的边长。

正切函数的图像也是一个周期性的波动曲线，但与正弦函数和余弦函数的图像有着明显的不同。

四、三角函数的基本关系。

在学习三角函数时，还需要了解三角函数之间的基本关系，如正弦函数与余弦函数、正切函数与余切函数之间的关系。

这些关系可以通过三角恒等式来表示，如sin^2θ + cos^2θ = 1，tanθ = sinθ/cosθ等。

五、三角函数的诱导公式。

三角函数的诱导公式是指通过某个角的正弦、余弦、正切等函数值，来推导其他角的正弦、余弦、正切等函数值的公式。

例如，利用角度为θ的正弦函数值，可以求得角度为π/2-θ的余弦函数值，从而得到诱导公式sin(π/2-θ) = cosθ。

六、三角函数的图像和性质。

除了掌握三角函数的公式外，还需要了解三角函数的图像和性质。

正弦函数、余弦函数、正切函数等在坐标平面上的图像特点，以及它们的周期、对称性、增减性等性质都是非常重要的。

七、三角函数在实际问题中的应用。

三角函数在实际问题中有着广泛的应用，如在航海、测量、建筑等领域都需要用到三角函数的知识。

掌握三角函数公式和性质，能够帮助我们更好地解决实际问题。

总结。

高中三角函数公式大全整理版

高中三角函数公式大全整理版以下是高中三角函数公式大全：sin30°=1/2，sin45°=√2/2，sin60°=√3/2，cos30°=√3/2，cos45°=√2/2，cos60°=1/2，tan30°=√3/3，tan45°=1，tan60°=√3，cot30°=√3，cot45°=1，cot60°=√3/3.这些公式可以用来计算不同角度的三角函数值。

还有一些特殊角度的三角函数值：sin15°=（√6-√2）/4，sin75°=（√6+√2）/4，cos15°=（√6+√2）/4，cos75°=（√6-√2）/4.这些值可以通过sin（45°±30°）=sin45°cos30°±cos45°sin30°推导得出。

正弦定理是一个重要的三角函数公式，可以用来计算三角形中的各个边和角度之间的关系。

在△ABC中，a / sin A = b / sin B = c / sin C = 2R，其中，R为△___的外接圆的半径。

两角和公式包括sin(A+B)、sin(A-B)、cos(A+B)和cos(A-B)，可以用来计算两个角度的三角函数之和或差的值。

另外，tan(A+B)可以用1-___表示，tan(A-B)可以用1+___表示。

倍角公式包括tan2A、sin2A和cos2A，可以用来计算一个角度的两倍角的三角函数值。

此外，sin3A、cos3A和tan3A 也是三个重要的三角函数公式，可以用来计算一个角度的三倍角的三角函数值。

半角公式包括sin(A/2)、cos(A/2)、tan(A/2)和cot(A/2)，可以用来计算一个角度的一半角的三角函数值。

另外，和差化积公式可以用来将两个三角函数的和或差转化为一个三角函数的积。

(完整版)大学用三角函数公式大全.docx

倒数关系：tan α ·cot α=1sin α ·cscα=1cosα ·secα=1cosα/sin α=cot α=cscα/sec α1+cot^2( α)=csc^2( α)tan α *cotα=1一个特殊公式（s ina+sin θ） * （sina- sin θ） =sin （a+θ） *sin （ a- θ）二倍角公式正弦sin2A=2sinA ·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=（2tanA） / （ 1-tan^2(A) ）万能公式sin α=2tan( α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α /2)]tan α=2tan( α/2)/[1-tan^2(α/2)]半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))半角公式sin^2( α/2)=(1 - cosα)/2cos^2( α/2)=(1+cos α)/2tan^2( α/2)=(1 - cosα)/(1+cos α)tan( α/2)=sin α/(1+cos α)=(1 - cosα)/sinα和差化积sin θ+sin φ = 2 sin[(θ+φ)/2] cos[(θ -φ)/2]sin θ - sin φ = 2 cos[(θ+φ)/2] sin[(θ -φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ -φ)/2]cosθ - cosφ = - 2 sin[(θ+φ)/2] sin[(θ -φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)两角和公式tan( α+β)=(tan α+tan β)/(1 - tan αtan β)tan( α - β)=(tan α - tan β)/(1+tanαtanβ)cos( α+β)=cos αcosβ - sin αsin βcos( α - β)=cos αcosβ+sin αsin βsin( α+β)=sin αcosβ+cosαsin βsin( α - β)=sin αcosβ - cosαsin β双曲函数sh a = [e^a-e^(-a)]/2ch a = [e^a+e^(-a)]/2th a = sin h(a)/cos h(a)sin （π /2+ α） = cos αcos（π /2+ α） = - sin αtan （π /2+ α） = - cot αcot （π /2+ α） = - tan αsin （π /2 - α） = cos αcos（π /2 - α） = sin αtan （π /2 - α） = cot αcot （π /2 - α） = tan α三角函数的诱导公式（六公式）公式一sin(- α) =- sin αtan (-α)= - tanα公式二 sin( π/2 - α) = cos αcos( π/2 - α) = sinα公式三sin( π/2+ α) = cos αcos( π/2+ α) =- sin α公式四 sin( π - α) = sinαcos( π - α) =- cosα公式五 sin( π+α) =- sin αcos( π+α) =- cosα公式六 tanA= sinA/cosAtan （π /2+ α） =－cot αtan （π /2 －α） =cot αtan （π－α） =－tan αtan （π +α） =tan α诱导公式记背诀窍：奇变偶不变，符号看象限万能公式sin α=2tan( α/2)/[1+(tan(α/2))2]cosα=[1 - (tan( α/2))2]/[1+(tan(α/2))2] tan α=2tan( α/2)/[1 - (tan( α/2))2]其它公式(1)(sin α)^2+(cos α)^2=1 （平方和公式）(2)1+(tan α)^2=(sec α)^2(3)1+(cot α)^2=(csc α)^2(4)对于任意非直角三角形，总有tanA+tanB+tanC=tanAtanBtanC(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2;+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)（sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)(seca)^2+(csca)^2=(seca)^2(csca)^2和差化积及积化和差用还原法结合上面公式可推出（换(a+b)/2与(a-b)/2）两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)反三角函数公式arcsin(-x)=-arcsinxarccos(-x)= π－arccosxarctan(-x)=-arctanxarccot(-x)= π－arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π /2，π/2〕时，有 arcsin(sinx)=x当x∈〔 0, π〕,arccos(cosx)=xx∈(—π /2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=xx〉0,arctanx= π-arctan1/x,arccotx/2 类似若(arctanx+arctany)∈(—π /2，π/2),则 arctanx+arctany=arctan(x+y/1-xy)三角函数求导：(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/ -x^2)√(1(arccosx)'=-1/ √ (1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)基本求导公式⑴ (C )0 （C 为常数）⑵ ( x n ) nx n 1 ；一般地， (x )x1。

(完整版)大学用三角函数公式大全

倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1cosα/sinα=cotα=cscα/secα1+cot^2(α)=csc^2(α）tan α *cot α=1一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=（2tanA）/（1-tan^2(A)）万能公式sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))半角公式sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)两角和公式tan(α+β)=(tanα+tanβ)/(1-tanαtanβ）tan(α-β)=(tanα-tanβ)/(1+tanαtanβ）cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ　-cosαsinβ双曲函数sh a = [e^a-e^(-a)]/2ch a = [e^a+e^(-a)]/2th a = sin h(a)/cos h(a)sin（π/2+α）= cosαcos（π/2+α）= -sinαtan（π/2+α）= -cotαcot（π/2+α）= -tanαsin（π/2-α）= cosαcos（π/2-α）= sinαtan（π/2-α）= cotαcot（π/2-α）= tanα三角函数的诱导公式（六公式）公式一sin(-α) = -sinαtan (-α)=-tanα公式二sin(π/2-α) = cosαcos(π/2-α) = sinα公式三sin(π/2+α) = cosαcos(π/2+α) = -sinα公式四sin(π-α) = sinαcos(π-α) = -cosα公式五sin(π+α) = -sinαcos(π+α) = -cosα公式六tanA= sinA/cosAtan（π/2+α）=－cotαtan（π/2－α）=cotαtan（π－α）=－tanαtan（π+α）=tanα诱导公式记背诀窍：奇变偶不变，符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))2]cosα=[1-(tan(α/2))2]/[1+(tan(α/2))2]tanα=2tan(α/2)/[1-(tan(α/2))2]其它公式(1) (sinα)^2+(cosα)^2=1（平方和公式）(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2(4)对于任意非直角三角形，总有tanA+tanB+tanC=tanAtanBtanC(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2;+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)（sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)(seca)^2+(csca)^2=(seca)^2(csca)^2和差化积及积化和差用还原法结合上面公式可推出（换(a+b)/2与(a-b)/2）两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π－arccosxarctan(-x)=-arctanxarccot(-x)=π－arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π/2，π/2〕时，有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=x-arctan1/x,arccotx类似x〉0,arctanx=π/2若(arctanx+arctany)∈(—π/2，π/2),则arctanx+arctany=arctan(x+y/1-xy)三角函数求导：(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx-x^2)(arcsinx)'=1/√(1(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)基本求导公式⑴0)(C （C 为常数）⑵1)(n n nx x ；一般地，1)(x x 。

三角函数公式大全

三角函数公式大全一、基本定义及性质1. 正弦函数（sin）：sin A = 对边 / 斜边cos A = 临边 / 斜边tan A = 对边 / 临边余切函数（cot）：cot A = 临边 / 对边2.零度三角函数：sin 0° = 0, cos 0° = 1, tan 0° = 0, cot 0° = ∞3.π/6弧度三角函数：sin (π/6) = 1/2, cos (π/6) = √3/2, tan (π/6) = 1/√3, cot (π/6) = √34.π/4弧度三角函数：sin (π/4) = √2/2, cos (π/4) = √2/2, tan (π/4) = 1, cot (π/4) = 15.π/3弧度三角函数：sin (π/3) = √3/2, cos (π/3) = 1/2, tan (π/3) = √3, cot (π/3) = 1/√36.相反角关系：sin (-A) = -sin A, cos (-A) = cos A, tan (-A) = -tan A, cot (-A) = -cot A7.90°三角函数：sin 90° = 1, cos 90° = 0, tan 90° = ∞, cot 90° = 08.π/2弧度三角函数：sin (π/2) = 1, cos (π/2) = 0, tan (π/2) = ∞, cot (π/2) = 09.倒数关系：sin (π - A) = sin A, cos (π - A) = -cos A, tan (π - A) = -tan A, cot (π - A) = -cot A10.余角关系：sin (π/2 - A) = cos A, cos (π/2 - A) = sin A, tan (π/2 -A) = cot A, cot (π/2 - A) = tan A二、和差与倍角公式1.和差公式：sin (A ± B) = sin A cos B ± cos A sin Bcos (A ± B) = cos A cos B ∓ sin A sin Btan (A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B)2.二倍角公式：sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)三、万能角公式（三角函数的倒数、减角公式、二倍角公式的推广形式）1.正弦函数倒数公式：csc A = 1 / sin A2.余弦函数倒数公式：sec A = 1 / cos A3.正切函数倒数公式：cot A = 1 / tan A4.减角公式：sin (A - B) = sin A cos B - cos A sin Bcos (A - B) = cos A cos B + sin A sin Btan (A - B) = (tan A - tan B) / (1 + tan A tan B)5.二倍角公式推广形式：sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)四、积和差公式1.积公式：sin A sin B = (1/2)[cos(A-B) - cos(A+B)]cos A cos B = (1/2)[cos(A-B) + cos(A+B)]sin A cos B = (1/2)[sin(A-B) + sin(A+B)]2.差公式：sin A - sin B = 2 cos[(A+B)/2] sin[(A-B)/2]cos A - cos B = -2 sin[(A+B)/2] sin[(A-B)/2]sin A + sin B = 2 sin[(A+B)/2] cos[(A-B)/2]cos A + cos B = 2 cos[(A+B)/2] cos[(A-B)/2]五、其他重要性质1. 正弦函数的周期：2π，即sin (x + 2π) = sin x余弦函数的周期：2π，即cos (x + 2π) = cos x2.正弦函数的奇偶性：sin (-x) = -sin x，即 sin 函数是奇函数sin (π + x) = -sin x，即 sin 函数是周期为2π的周期函数3.余弦函数的奇偶性：cos (-x) = cos x，即 cos 函数是偶函数cos (π + x) = -cos x，即 cos 函数是周期为2π的周期函数4.正弦函数和余弦函数的间接关系：sin^2 x + cos^2 x = 1。

三角函数公式(最全)

1、正弦定理
正弦定理变形可得：
五、其他公式
2、余弦定理
对于如图所示的边长为a、b、c而相应角为α、β、γ的△ABC，有：
3、降幂公式
sin²α=[1-cos(2α)]/2 cos²α=[1+cos(2α)]/2 tan²α=[1-cos(2α)]/[1+cos(2α)]
4、三角和
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+ cosα·cosβ·sinγ-sinα·sinβ·sinγ
ln(1+x)=x-x2/2+x3/3-…+(-1)k-1xk/k, x∈(-1,1)
sin x = x-x3/3!+x5/5!-…+(-1)k-1x2k-1/(2k-1)!+…, x∈R
cos x = 1-x2/2!+x4/4!-…+(-1)kx2k/(2k)!+…, x∈R
arcsin x = x + x3/(2*3) + (1*3)x5/(2*4*5) + (1*3*5)x7/(2* 4*6*7)…+(2k+1)!!*x2k+1/(2k!!*(2k+1))+…, x∈(-1,1)（!!表示双阶乘）
1
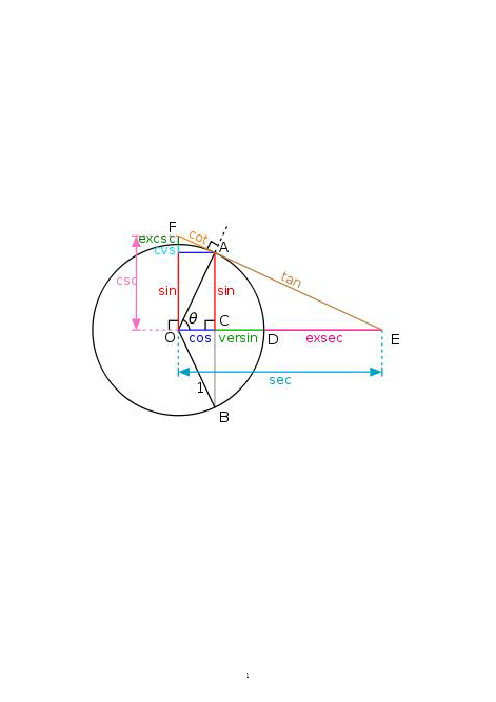
一、定义公式
三角函数公式
锐角三角函数任意角三角函数
正弦（sin）余弦（cos）正切（tan或tg）余切（cot或ctg）正割（sec）余割（csc）正弦（sin）余弦（cos）正切（tan或tg）余切（cot或ctg）正割（sec）余割（csc）
1、倒数关系
二、函数关系

数学常用三角函数公式全集

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotAcotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=AA cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a -cosa+cosb = 2cos2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+ 积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式sin(-a) = -sinacos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sinacos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +-tana=2)2(tan 12tan2a a- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =asin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinαcos （2kπ＋α）= cosαtan （2kπ＋α）= tanαcot （2kπ＋α）= cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin （π＋α）= -sinαcos （π＋α）= -cosαtan （π＋α）= tanαcot （π＋α）= cotα公式三：任意角α与 -α的三角函数值之间的关系：sin （-α）= -sinαcos （-α）= cosαtan （-α）= -tanαcot （-α）= -cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinαcos （π-α）= -cosαtan （π-α）= -tanαcot （π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinαcos （2π-α）= cosαtan （2π-α）= -tanαcot （2π-α）= -cotα公式六：2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosαcos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z) 正弦定理 a/sinA=b/sinB=c/sinC=2R 注：其中 R 表示三角形的外接圆半径余弦定理 b2=a2+c2-2accosB 注：角B 是边a 和边c 的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A乘法与因式分解a 2-b 2=(a+b)(a-b)a 3+b 3=(a+b)(a 2-ab+b 2)a 3-b 3=(a-b)(a 2+ab+b 2)三角不等式 |a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|某些数列前n 项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n -1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3圆的标准方程(x-a)2+(y-b)2=r2注：（a,b）是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0抛物线标准方程y2=2px直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。

(完整版)三角函数公式大全

三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ，记：22y x r +=，正弦函数：r y =αsin 余弦函数：r x =αcos 正切函数：x y=αtan 余切函数：y x =αcot 正割函数：xr=αsec 余割函数：y r =αcsc 二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ，1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）＝sinα cos （2kπ＋α）＝cosαtan （2kπ＋α）＝tanα cot （2kπ＋α）＝cotα (其中k ∈Z)公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin （π＋α）＝－sinα cos （π＋α）＝－cosα tan （π＋α）＝tanα cot （π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系：sin （－α）＝－sinα cos （－α）＝cosα tan （－α）＝－tanα cot （－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin （π－α）＝sinα cos （π－α）＝－cosα tan （π－α）＝－tanα cot （π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系：sin （απ-2）＝cosα cos （απ-2）＝sinα tan （απ-2）＝cotα cot （απ-2）＝tanα公式六：απ+2与α的三角函数值之间的关系：sin （απ+2）＝cosα cos （απ+2）＝－sinα tan （απ+2）＝－cotα cot （απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系： sin （απ-23）＝－cosα cos （απ-23）＝－sinαtan （απ-23）＝cotα cot （απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin （απ+23）＝－cosα cos （απ+23）＝sinαtan （απ+23）＝－cotα cot （απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin （2π－α）＝－sinα cos （2π－α）＝cosα tan （2π－α）＝－tanα cot （2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值，等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

三角函数公式整合版(把文库里大概整合了一下)

基本初等函数求导公式(1) 0)(='C (2) 1)(-='μμμx x(3) x x cos )(sin ='(4) x x sin )(cos -='(5)x x 2sec )(tan =' (6)x x 2csc )(cot -=' (7) x x x tan sec )(sec ='(8) x x x cot csc )(csc -='(9)a a a xx ln )(=' (10) xx e e =')((11)a x x a ln 1)(log ='(12)x x 1)(ln ='，(13)211)(arcsin x x -='(14)211)(arccos x x --='(15)21(arctan )1x x '=+(16)21(arccot )1x x '=-+函数的和、差、积、商的求导法则设)(x u u =，)(x v v =都可导，则（1）v u v u '±'='±)( （2）u C Cu '=')(（C 是常数）（3）v u v u uv '+'=')(（4） 2v v u v u v u '-'='⎪⎭⎫ ⎝⎛反函数求导法则：若函数)(y x ϕ=在某区间y I 内可导、单调且0)(≠'y ϕ，则它的反函数)(x f y =在对应区间x I 内也可导，且)(1)(y x f ϕ'=' 或 dy dx dx dy 1=复合函数求导法则：设)(u f y =，而)(x u ϕ=且)(u f 及)(x ϕ都可导，则复合函数)]([x f y ϕ=的导数为dx dudu dy dx dy ∙=或)()(x u f y ϕ'∙'='。

三角函数公式全集归纳

三角函数公式全集归纳1. 基本公式- 正弦函数公式：$\sin(\alpha + \beta) = \sin\alpha\cos\beta +\cos\alpha\sin\beta$- 余弦函数公式：$\cos(\alpha + \beta) = \cos\alpha\cos\beta -\sin\alpha\sin\beta$- 正切函数的和差公式：$\tan(\alpha \pm \beta) =\dfrac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha\tan\beta}$ - 正弦函数的二倍角公式：$\sin(2\alpha) = 2\sin\alpha\cos\alpha$ - 余弦函数的二倍角公式：$\cos(2\alpha) = \cos^2\alpha -\sin^2\alpha$- 正切函数的二倍角公式：$\tan(2\alpha) = \dfrac{2\tan\alpha}{1 - \tan^2\alpha}$- 正弦函数的倍角公式：$\sin(n\alpha) = 2^{n-1}\sin\alpha\sqrt{1-\sin^2\alpha}\sqrt{1-\sin^2(2\alpha)}\cdot...\cdot\sqrt{1-\sin^2((n-1)\alpha)}$- 余弦函数的倍角公式：$\cos(n\alpha) = 2^{n-1}\cos^n\alpha - \binom{n}{2}2^{n-3}\cos^{n-2}\alpha\sin^2\alpha + ... + \cos^n\alpha$- 正切函数的倍角公式：$\tan(n\alpha) = \dfrac{\binom n1\tan\alpha - \binom n 3\tan^3\alpha + \binom n 5\tan^5\alpha - ...}{1 - \binom n 2\tan^2\alpha + \binom n 4\tan^4\alpha - ...}$2. 三角函数的关系- 正切函数与正弦函数的关系：$\tan\alpha =\dfrac{\sin\alpha}{\cos\alpha}$- 正弦函数与余弦函数的关系：$\sin^2\alpha + \cos^2\alpha = 1$ - 余切函数与正弦函数的关系：$\cot\alpha =\dfrac{\cos\alpha}{\sin\alpha} = \dfrac{1}{\tan\alpha}$- 正切函数与余切函数的关系：$\tan\alpha\cot\alpha = 1$3. 特殊角公式- 30度角的正弦值：$\sin30^\circ = \dfrac{1}{2}$- 30度角的余弦值：$\cos30^\circ = \dfrac{\sqrt{3}}{2}$- 30度角的正切值：$\tan30^\circ = \dfrac{1}{\sqrt{3}}$- 45度角的正弦值：$\sin45^\circ = \dfrac{\sqrt{2}}{2}$- 45度角的余弦值：$\cos45^\circ = \dfrac{\sqrt{2}}{2}$- 45度角的正切值：$\tan45^\circ = 1$- 60度角的正弦值：$\sin60^\circ = \dfrac{\sqrt{3}}{2}$- 60度角的余弦值：$\cos60^\circ = \dfrac{1}{2}$- 60度角的正切值：$\tan60^\circ = \sqrt{3}$以上是常见的三角函数公式，掌握了这些公式可以更好地理解和应用三角函数在数学和科学中的相关问题。

三角函数合成公式

三角函数合成公式三角函数是数学中一类有关角度测量的概念函数，其中包括正弦函数，余弦函数和正切函数。

三角函数合成（或称合成函数）是指将三角函数按一定规则组合后形成的函数。

它有助于我们更好地理解及应用三角函数，同时也为数学中的很多问题提供了有用的方法。

正弦函数与余弦函数合成正弦函数和余弦函数的合成是指将正弦函数和余弦函数结合在一起形成的函数。

其公式如下：sin(x) + cos(x) = 1两边作求导操作，即可算出新函数的导数：cos(x) - sin(x) = 0正弦函数与正切函数合成正弦函数和正切函数的合成是指将正弦函数和正切函数结合在一起形成的函数。

其公式如下：sin(x) * tan(x) = 1/cos(x)两边作求导操作，即可算出新函数的导数：cos(x) + tan(x) * sin(x) = 0余弦函数与正切函数合成余弦函数和正切函数的合成是指将余弦函数和正切函数结合在一起形成的函数。

其公式如下：cos(x) * tan(x) = sin(x)两边作求导操作，即可算出新函数的导数：sin(x) - tan(x) * cos(x) = 0应用三角函数的合成对我们的数学研究有着重要的作用，它可以为解决许多有关曲线研究提供有用的方法，而解决这些曲线研究又可以帮助我们解决许多实际问题。

例如，在水力学研究中，函数f（x）=sin(x) +cos(x)可以用来描述水流的动态变化，这有助于我们对水流进行研究并分析水流的变化趋势。

此外，在摄影术中，函数f（x）=sin(x) *tan(x)可以用来表示镜头的光学性能，从而方便我们对摄影术的研究。

总结三角函数合成是指将三角函数按一定规则组合在一起形成的函数，可以分为正弦函数与余弦函数合成，正弦函数和正切函数合成，余弦函数和正切函数合成三种。

三角函数合成对我们的数学研究有着重要的作用，可以为解决许多有关曲线研究提供有用的方法，而解决这些曲线研究又可以帮助我们解决许多实际问题，因此三角函数合成具有重要的意义。