月考复习题1(2018.4.1)
2018年下学期高一年级第一次月考试卷

2018年下学期高一年级第一次月考试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页。
时量120分钟,总分120第Ⅰ卷第一部分听力(共两节,满分20分)第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What will the woman do today?A. See her mother.B. Do some shopping.C. Go to t he beach.2. What are the speakers talking about?A. A boy.B. A school.C. A dictionary.3. What is Snowball?A. A horse.B. A goat.C. A rabbit.4. Who was the woman’s best friend later at college?A. Susan.B. Alisa.C. Linda.5. Where are the plane tickets?A. On the shelf.B. In the handbag.C. On the desk.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第六段材料,回答第6至7题。
What time is it now probably?A. 9:30pm.B.9:45pm.C. 10:00pm.7. How will the woman go home?A. By car.B. By bus.C. On foot.听第七段材料,回答第8至9题。
2018年六年级数学4月份月考试卷

_________学校班级考号姓名_________________◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆ 2018年春六年级数学第二次月考试卷 时间:90分钟 满分:100分 一、认真填写,我最棒!( 每空1分,共18分 ) 1、 月球表面夜间的平均温度是零下150℃,记作( )℃。
2、 6∶2 =21∶( ) 1.6∶4=( )∶2.5 3、如果3a=4b ,那么a∶b=( ) 4、一个圆柱体的底面直径4分米,高0.5分米,它的侧面积是( )平方分米;它的表面积是( )平方分米;它的体积是( )立方分米。
5、在○里填上“>”“<”或“=”。
0 ○—1.5 41- ○ 31- 1 ○ —1 —0.25 ○ 0.05 6、圆柱有( )条高,圆锥有( )高。
7、把地面15千米的距离用3厘米的线段画在地图上,那么,这幅地图的比例尺是( ). 8、一个圆锥体与和它等底等高的圆柱体体积相差30立方厘米,这个圆锥体的体积是( )立方厘米。
9、一个圆锥的体积是18立方分米,高是6分米,底面积是( )。
10、在比例尺为1∶2000的地图上,6厘米的线段代表实际距离( )米,实际距离180米在图上要画( )厘米。
二、 慎重选择,对号入座。
(每题1分,共10分 ) 1、一个圆柱的底面半径是2 cm ,高是12.56 cm ,它的侧面沿高剪开是( )。
A.长方形 B. 正方形 C.平行四边形 2.一架客机从北京飞往上海,飞行速度和所用时间( ) A.成正比例 B. 成反比例 C.不成比例 3、圆柱的体积一定,它的高和( )成反比例。
A. 底面半径 B. 底面积 C. 底面周长 4、下面各组的两个比不能组成比例的是( ) A. 7:8和14:16 B.0.6:0.2和3:1 C.19:110 和10:9 5、在x=7y 中,x 和y ( ) A.成正比例 B. 成反比例 C.不成比例 6、压路机的前轮转动一周能压多少路面就是求压路机前轮的( ) A.侧面积 B. 表面积 C.体积 7、下面图形中,( )是圆柱的展开图。
届高三数学(理)第一次月考模拟试卷及答案

届高三数学(理)第一次月考模拟试卷及答案2018届高三数学(理)第一次月考模拟试卷及答案高考数学知识覆盖面广,我们可以通过多做数学模拟试卷来扩展知识面!以下是店铺为你整理的2018届高三数学(理)第一次月考模拟试卷,希望能帮到你。
2018届高三数学(理)第一次月考模拟试卷题目一、选择题(本题共12道小题,每小题5分,共60分)1.已知全集U=R,A={x|x2﹣2x<0},B={x|x≥1},则A∪(∁UB)=( )A.(0,+∞)B.(﹣∞,1)C.(﹣∞,2)D.(0,1)2.已知集合A={1,2,3,4},B={y|y=3x﹣2,x∈A},则A∩B=()A.{1}B.{4}C.{1,3}D.{1,4}3.在△ABC中,“ >0”是“△ABC为锐角三角形”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.下列说法错误的是( )A.命题“若x2﹣4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2﹣4x+3≠0”B.“x>1”是“|x|>0”的充分不必要条件C.若p且q为假命题,则p、q均为假命题D.命题p:“∃x∈R使得x2+x+1<0”,则¬p:“∀x∈R,均有x2+x+1≥0”5.已知0A.a2>2a>log2aB.2a>a2>log2aC.log2a>a2>2aD.2a>log2a>a26.函数y=loga(x+2)﹣1(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m>0,n>0,则 + 的最小值为( )A.3+2B.3+2C.7D.117.已知f(x)是定义在R上的偶函数,在[0,+∞)上是增函数,若a=f(sin ),b=f(cos ),c=f(tan ),则( )A.a>b>cB.c>a>bC.b>a>cD.c>b>a8.若函数y=f(x)对x∈R满足f(x+2)=f(x),且x∈[-1 ,1]时,f(x)=1﹣x2,g(x)= ,则函数h(x)=f(x)﹣g(x)在区间x∈[-5 ,11]内零点的个数为( ) A.8 B.10 C.12 D.149设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1= ,an=f(n)(n∈N*),则数列{an}的前n 项和Sn的取值范围是( )A.[ ,2)B.[ ,2]C.[ ,1)D.[ ,1]10.如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )A . B.C. D.11.设函数f(x)=(x﹣a)|x﹣a|+b,a,b∈R,则下列叙述中,正确的序号是( )①对任意实数a,b,函数y=f(x)在R上是单调函数;②对任意实数a,b,函数y=f(x)在R上都不是单调函数;③对任意实数a,b,函数y=f(x)的图象都是中心对称图象;④存在实数a,b,使得函数y=f(x)的图象不是中心对称图象.A.①③B.②③C.①④D.③④12.已知函数,如在区间(1,+∞)上存在n(n≥2)个不同的数x1,x2,x3,…,xn,使得比值= =…= 成立,则n的取值集合是( )A.{2,3,4,5}B.{2,3}C.{2,3,5}D.{2,3,4}第II卷(非选择题)二、填空题(本题共4道小题,每小题5分,共20分)13.命题:“∃x∈R,x2﹣x﹣1<0”的否定是 .14.定义在R上的奇函数f(x)以2为周期,则f(1)= .15.设有两个命题,p:x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0};q:函数y=lg(ax2﹣x+a)的定义域为R.如果p∨q为真命题,p∧q为假命题,则实数a的取值范围是 .16.在下列命题中①函数f(x)= 在定义域内为单调递减函数;②已知定义在R上周期为4的函数f(x)满足f(2﹣x)=f(2+x),则f(x)一定为偶函数;③若f(x)为奇函数,则 f(x)dx=2 f(x)dx(a>0);④已知函数f(x)=ax3+bx2+cx+d(a≠0),则a+b+c=0是f(x)有极值的充分不必要条件;⑤已知函数f(x)=x﹣sinx,若a+b>0,则f(a)+f(b)>0.其中正确命题的序号为 (写出所有正确命题的序号).三、解答题(本题共7道小题,第1题12分,第2题12分,第3题12分,第4题12分,第5题12分,第6题10分,第7题10分,共70分)17.已知集合A={x|x2﹣4x﹣5≤0},函数y=ln(x2﹣4)的定义域为B.(Ⅰ)求A∩B;(Ⅱ)若C={x|x≤a﹣1},且A∪(∁RB)⊆C,求实数a的取值范围.18.已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(1)求实数a,b的值;(2)解关于x的不等式: >0(c为常数).19.已知函数f(x)= 是定义在(﹣1,1)上的奇函数,且f( )= .(1)确定函数f(x)的解析式;(2)证明f(x)在(﹣1,1)上是增函数;(3)解不等式f(t﹣1)+f(t)<0.20.已知关于x的不等式x2﹣(a2+3a+2)x+3a(a2+2)<0(a∈R).(Ⅰ)解该不等式;(Ⅱ)定义区间(m,n)的长度为d=n﹣m,若a∈R,求该不等式解集表示的区间长度的最大值.21.设关于x的方程2x2﹣ax﹣2=0的两根分别为α、β(α<β),函数(1)证明f(x)在区间(α,β)上是增函数;(2)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小.选做第22或23题,若两题均选做,只计第22题的分。
八年级数学下2018年4月月考1

1蒙阴高都镇中心学校 姓名 班级 考号座号中心学校2018年 4月月考八年级数学试卷2018.04A.9B. 7C. 20D.312 ).A .①和②B .②和③C .①和④D .③和④ 3、若代数式1-x x 有意义,则实数x 的取值范围是( )A. x ≠ 1B. x ≥0C. x >0D. x ≥0且x ≠1 4、如图字母B 所代表的正方形的面积是 ( )A. 12B. 13C. 144D. 1945、 如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD 的面积是 ( ) A.12 B. 24 C. 312D. 3166、如图某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多少米?A 4B 8C 9 D77、三角形的三边长分别为6,8,10,它的最长边上的高为( ) A.6 B.4.8 C.2.4 D.88、.在平行四边形ABCD 中,∠A:∠B:∠C:∠D 的值可以是( ) A.1:2:3:4 B.1:2:2:1 C.1:2:1:2 D.1:1:2:29、已知x 、y 为正数,且│x 2-4│+(y 2-3)2=0,如果以x 、y 的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )A 、5B 、25C 、7D 、15 10、.如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C ′处,折痕为EF ,若AB=6,BC=10,则DE 的值为( )A 、8B 、3.2C 、 4.8D 、611、8、菱形ABCD 中,AB=15,∠ADC=120°,则B 、D 两点之间的距离为( ). A .15B .3215C .7.5D .31512、. 如图,在矩形ABCD 中,AD=2AB ,点M 、N 分别在边AD 、BC 上,连接BM 、DN.若四边形MBND 是菱形,则MDAM 等于( )A.83 B.32 C.53 D.54二、填空题:(每小题3分,共15分)13.在布置新年联欢会的会场时,小虎准备把同学们做的拉花用上,他搬来了一架高为2.5米的梯子,要想把拉花挂在高2.4米的墙上,小虎应把梯子的底端放在距离墙________米处.14.如图3,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M 在CH 上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A 爬到点M,需要爬行的最短距离是多少15如图,ABCD 且使ABCD 成为菱形.(只需添加一个即可) 16 .如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF.若菱形ABCD 的边长为2cm ,∠A=120°,则EF= .17.如图,矩形ABCD 中,AB =3,BC =4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B ′处,当△CEB ′为直角三角形时,BE 的长为_________. 三、解答题 18.计算:(每小题4分,共16分) (1)、 )(ba b ba 1223÷⋅ (2)、+(3)、(27+52)(52-27) (4)、(2)(2-12)(18+48); E C D B A B ′ O F E DB A5米3米A NM DBCA12题图 10题图5题图 6题图219、(本题5分)如图,四边形ABCD 中,AB=3cm,BC=4cm,CD=12cm,DA=13cm, 且度.求四边形ABCD 的面积.20. (本题6分)如图,四边形ABCD 是菱形,对角线AC 与BD 相交于O,AB =6,AO =4,求BD 的长和四边形ABCD 的面积21. (本题6分)先化简,后计算:11()b a bb a a b ++++,其中12a =,12b =.22.(本题6分)如图:已知D 、E 、F 分别是△ABC 各边的中点, 求证:AE 与DF 互相平分. 23. (本题8分)在矩形ABCD 中,将点A 翻折到对角线BD 上的点M 处,折痕BE 交AD 于点E .将点C 翻折到对角线BD 上的点N 处,折痕DF 交BC 于点F . (1)求证:四边形BFDE 为平行四边形;(2)若四边形BFDE 为菱形,且AB =4cm,BC=3cm ,求NF 的长.24. (本题10分)如图,在□ABCD 中,F 是AD 的中点,延长BC 到点E ,使CE=21BC ,连结DE ,CF 。
2018届九年级数学4月月考试题
广东省××市××区2018届九年级数学4月月考试题说明:l .本卷共4页,满分为120分,考试用时为100分钟.一、选择题(本大题共10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,请将下列各题的正确选项填写在答题卡相应的位置上. 1.sin60°的值为( ) A .B .C .D .2.在△ABC 中,∠C=90°,AB=10,cosA=,则BC 的长为( ) A .6B .7.5C .8D .12.53.已知⊙O 的半径为3,圆心O 到直线l 的距离为2,则直线l 与⊙O 的位置关系是() A .相交B .相切C .相离D .不能确定 4.二次函数3)1(2+-=x y ( )A .有最大值1B .有最小值1C .有最大值3D .有最小值3 5.如图,⊙O 是△ABC 的外接圆,已知∠ACO=30°, 则∠B 的度数是( ) A .30°B.45°C.60°D.75°6.三角形的内心是三角形内切圆的圆心,它也是三角形( ) A .三条高线的交点B .三边垂直平分线的交点 C .三边中线的交点D .三条内角平分线的交点 7.正六边形ABCDEF 内接于⊙O ,正六边形的周长是12, 则⊙O 的半径是( ) A .B .2C .2D .28.二次函数c bx ax y ++=2的图象如图所示,则下列结论中错误的是( ) A .函数有最小值 B .0<cC .当﹣1<x <2时,y >0D .当x <时,y 随x 的增大而减小9.如图,边长为1的小正方形网格中,⊙O的值是()EA BCA .B .C .D .10.当ab >0时,2ax y =与b ax y +=的图象大致是( )A .B .C .D .二、填空题(本大题共6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应的位置上.11.在Rt △ABC 中,∠C =90°,AC=3,BC=4,则sinA=.12.已知扇形的圆心角是120°,半径是6cm ,则它的面积是_____(结果保留π). 13.抛物线122-=x y 的对称轴是.14.如图,四边形ABCD 内接于⊙O ,DA=DC ,∠CBE=50°,则∠DAC 的大小为度.15.已知二次函数m x x y ++-=22的部分图象如图,则关于x 的一元二次方程022=++-m x x 的解为.16.把直尺、三角尺和圆形螺母按如图所示放置于桌面上,∠CAB=60°,若量出AD=8cm ,则圆形螺母的外直径是.三、解答题(一)(本大题共3小题,每小题6分,共18分)请在答题卡相应位置上作答. 17.计算:0360tan 2)21(12)14.3(--++--π18.求二次函数1422+--=x x y 的顶点坐标,并说出此函数的两条性质.19.如图,AB 与⊙O 相切于点C ,OA=OB ,⊙O 的直径为8cm ,AB=10cm ,求OA 长.四、解答题(二)(本大题共3小题,每小题7分,共21分)请在答题卡相应位置上作答.20.如图,一条公路的转弯处是一段圆弧().(1)用直尺和圆规作出所在圆的圆心O;(要求保留作图痕迹,不写作法)(2)若的中点C到弦AB的距离为20m,AB=80m,求所在圆的半径.21.一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为 2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.(1)求抛物线的表达式;(2)一辆货车高4m,宽4m,能否从该隧道内通过,为什么?22.如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:≈1.414,≈1.732).五、解答题(三)(本大题共3小题,每小题9分,共27分)请在答题卡相应位置上作答.23. 为了美化生活环境,小兰的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y 平方米. (1)用含有x 的代数式表示BC 的长,BC=米;(2)求y 与x 的函数关系式,写出自变量x 的取值范围; (3)当x 为何值时,y 有最大值?最大值为多少?24.如图,在Rt △ABC 中,∠A=90°,O 是BC 边上一点,以O 为圆心的半圆与AB 边相切于点D ,与AC 、BC 边分别交于点E 、F 、G ,连接OD ,已知BD=2,AE=3, tan ∠BOD=.(1)求⊙O 的半径OD ; (2)求证:AE 是⊙O 的切线; (3)求图中两部分阴影面积的和.25.如图,抛物线c bx x y ++-=2交x 轴于点A (﹣3,0)和点B ,交y 轴于点C (0,3). (1)求抛物线的函数表达式;(2)若点P 在抛物线上,且S △AOP =4S △BOC ,求点P 的坐标;(3)如图b ,设点Q 是线段AC 上的一动点,作DQ ⊥x 轴,交抛物线于点D ,则线段DQ 长度的最大值是_________(直接填空,不写过程).参考答案及评分标准一、选择题(每题3分,共30分)二、填空题:(每题4分,共24分) 11.4512.12π cm 213.直线x=0或y 轴14. 15. 121,3x x =-= 16.三、解答题:(一)(本大题3小题,每小题6分,共18分) 17. 解:原式=32)8(321--++............4分=-7..........6分18.解: ∵y=﹣2x 2﹣4x+1=﹣2(x+1)2+3,............3分 ∴顶点坐标为(﹣1,3),............4分 其性质有:①开口向下,②有最大值3,.......6分19.解:连接OC ;......1分 ∵AB 与⊙O 相切于点C , ∴OC ⊥AB ,......2分∵OA=OB ,∴AC=BC=5,......3分 在Rt △AOC 中,(cm ).......5分答:OA 的长为............6分四、解答题(二)(本大题共3小题,每小题7分,共21分) 20.解:(1)如图1,...........2分∴点O 为所求;...........3分(2)连接OA ,OC ,OC 交AB 于D ,如图2,∵C 为的中点, ∴OC ⊥AB ,∴AD=BD=AB=40,...........4分设⊙O 的半径为r ,则OA=r ,OD=OD ﹣CD=r ﹣20, 在Rt △OAD 中,∵OA 2=OD 2+AD 2, ∴r 2=(r ﹣20)2+402,...........5分 解得r=50,...........6分即所在圆的半径是50m ............7分21.(1)解:设抛物线的解析式为y=a (x ﹣h )2+k ,..........1分 ∵顶点(4,6),∴y=a (x ﹣4)2+6, ∵它过点(0,2),∴a (0﹣4)2+6=2, 解得a=﹣,..........3分 ∴设抛物线的解析式为21(4)64y x =--+;..........4分 (2)当x=2时或当x=6时,y=5>4, ∴该货车能通过隧道...........7分22.解:过点A 作AH ⊥CD ,垂足为H ,..........1分由题意可知四边形ABDH为矩形,∠CAH=30°,∴AB=DH=1.5,BD=AH=6,在Rt△ACH中,tan∠CAH=,∴CH=AH•tan∠CAH,∴CH=AH•tan∠CAH=6tan30°=6×=2,..........3分∵DH=1.5,∴CD=2+1.5,..........5分在Rt△CDE中,∵∠CED=60°,sin∠CED=,∴CE==4+≈5.7(米),..........6分答:拉线CE的长约为5.7米...........7分五、解答题(三)(本大题共3小题,每小题9分,共27分)23.解:(1)由题意可得,BC=32﹣2x,..........1分(2)由题意可得,y=x(32﹣2x)=﹣2x2+32x,.........4分∵,∴11≤x<16,即y与x的函数关系式是y=﹣2x2+32x(11≤x<16);..........6分(3)∵y=﹣2x2+32x=﹣2(x﹣8)2+128,11≤x<16,..........7分∴x=11时,y取得最大值,此时y=110,即当x=11时,y取得最大值,最大值为110...........9分24.解:(1)∵AB与圆O相切,..........1分∴OD⊥AB,在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3;..........3分(2)连接OE,..........4分∵AE=OD=3,AE∥OD,∴四边形AEOD为平行四边形,..........5分∴AD∥EO,∵DA⊥AE,∴OE⊥AC,又∵OE为圆的半径,∴AE为圆O的切线;..........6分(3)∵OD∥AC,∴=,即=,∴AC=7.5,∴EC=AC﹣AE=7.5﹣3=4.5,..........7分∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG=×2×3+×3×4.5﹣=3+﹣=...........9分25.解:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得,..........1分解得...........2分故该抛物线的解析式为:y=﹣x2﹣2x+3...........3分(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).∵S△AOP=4S△BOC,∴×3×|﹣x2﹣2x+3|=4××1×3...........4分整理,得(x+1)2=0或x2+2x﹣7=0,解得x=﹣1或x=﹣1±2...........5分则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2,﹣4)或(﹣1﹣2,﹣4);..........7分(3)QD有最大值...........9分。
2018.4.1南平市事业单位考试真题与答案解析(2)

(4.1)笔试题本总分: 150分时限:150分钟(本试题题本用后收回,请不要在题本上作答)第一题单项选择题(每题2分,共90分)(下面每题的备选答案中,只有一项是正确答案,请将所选答案的字母填写在答题纸上)1.______是对马克思列宁主义、毛泽东思想、邓小平理论、“三个代表”重要思想、科学发展观的继承和发展,是马克思主义中国化最新成果,是党和人民实践经验和集体智慧的结晶,是中国特色社会主义理论体系的重要组成部分,是全党全国人民为实现中华民族伟大复兴而奋斗的行动指南,必须长期坚持并不断发展。
A.习近平新时代中国特色社会主义思想B.全面推进依法治国的总目标C.“五位一体”总体布局D.“四个全面”战略布局2.党的十九大的主题是: ______,高举中国特色社会主义伟大旗帜,决胜全面建成小康社会,夺取新时代中国特色社会主义伟大胜利,为实现中华民族伟大复兴的中国梦不懈奋斗。
A.不忘初心,继续前进B.不忘初心,牢记使命C.不忘初心,方得始终D.不忘初心,砥砺前行3.党的十九大报告指出,经过长期努力,中国特色社会主义进入了______,这是我国发展新的历史方位。
A.新时代B.新纪元C.新阶段D.新时期4.党的十九大报告指出,我国社会主要矛盾已经转化为人民日益增长的______需要和______的发展之间的矛盾。
A.美好生活不充分不平衡B.幸福生活不平衡不充分C.幸福生活不充分不平衡D.美好生活不平衡不充分5.中国特色社会主义最本质的特征是______.A.中国共产党领导B.坚持人民当家做主C.坚持改革开放D.坚持新发展理念答案1-5:ABADA6.必须坚持以____为中心的发展思想,不断促进人的全面发展,全体人民共同富裕。
A.人民B.科学C.群众D.改革7.实施乡村振兴战略的目标任务是:到2050年,乡村全面振兴,农业强、农村美、_____全面实现。
A.产业旺B.生态好C.生活富D.农民富8.2018年3月7日上午,中共中央总书记、国家主席、中央军委主席习近平参加十三届全国人大一次会议广东代表团审议时强调指出,发展是第一要务,_____是第一资源,创新是第一动力。
2018届高三4月月考 精品
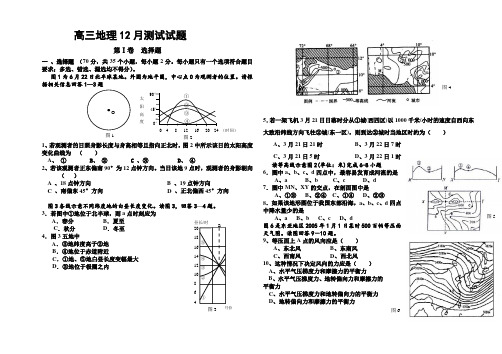
图1① 0 4 8 12 16 20 24 (时间)图2太阳高度④ ② ③ 90° 45° 0°高三地理12月测试试题第Ⅰ卷 选择题一 、选择题 (70分,共35个小题,每小题2分。
每小题只有一个选项符合题目要求;多选、错选、漏选均不得分)。
图1为6月22日北半球某地。
外圆为地平圈,中心点O 为观测者的位置。
请根据相关信息回答1—3题1、若观测者的日照身影长度与身高相等且指向正北时,图2中所示该日的太阳高度变化曲线为 ( )A 、 ①B 、 ②C 、③D 、 ④2、若该观测者正东偏南90°为12点钟方向。
当日该地9点时,观测者的身影朝向( )A 、18点钟方向B 、19点钟方向C 、南偏东45°方向D 、正北偏西45°方向图3各线示意不同纬度地的白昼长度变化。
读图3,回答3—4题。
3.若图中①地位于北半球,则a 点时刻应为 A .春分 B .夏至 C .秋分 D .冬至4.图3五地中 A .③地纬度高于②地 B .④地位于赤道附近C .①地、⑤地白昼长度变幅最大D .②地位于极圈之内5.若一架飞机3月21日日落时分从①城(西四区)以1000千米/小时的速度自西向东大致沿纬线方向飞往②城(东一区),则到达②城时当地区时约为( )A 、3月21日21时B 、3月22日7时C 、3月21日5时D 、3月22日1时读等高线示意图2(单位:米)完成6-8小题6.图中a 、b 、c 、d 四点中,最容易发育成河流的是A 、aB 、bC 、cD 、d 7.图中MN 、XY 的交点,在剖面图中是A 、①③B 、②④C 、①④D 、②③8.如果该地形图位于我国东部沿海,a 、b 、c 、d 四点中降水量少的是A 、aB 、bC 、cD 、d图6是东亚地区2005年1月1日某时500百帕等压面天气图。
读图回答9-10题。
9、等压面上A 点的风向应是( )A 、东北风B 、东南风C 、西南风D 、西北风10、这种情况下决定风向的力应是( ) A 、水平气压梯度力和摩擦力的平衡力B 、水平气压梯度力、地转偏向力和摩擦力的平衡力C 、水平气压梯度力和地转偏向力的平衡力D 、地转偏向力和摩擦力的平衡力图3月份a昼长/时46 8 1012 14161820 ⑤ ④ ③ ②①图4图5图6图7中a 为纬线,P 、Q 两地经度相同,相距800千米。
201804高一数学月考试题.doc

1.C. ---------- 2 1D.一2 6函数/(x ) = 2sin ((72¥ +(p )(\(p\ <的图像如图所示,那么( 10 〃A. co — —, (p——116 厂 。
兀 10 71 B. CD — , (D — 11 6 D. co = 2,(p =—12把正确答案的代号填在括号2017-2018学年度第二学期模块考试 高一月考数学试题(2018. 4) 考试时间120分钟满分150分第I 卷(选择题,共60分)一'选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四 个选项中,只有一个是符合要求的,sin (-120°)等于(2、 已知扇形的周长是6 cm,面积是2 cn?,则扇形的圆心角的弧度数是(A. 1 或4B. 1C. 4D. 8 a3、 已知。
为第二象限角,贝1]分所在的象限是()A.第一或第二象限B.第二或第三象限C.第一或第三象限D.第二或第四象限4、 已知点P (sina —cosa, tana )在第一象限,则在[0,2兀]内a 的取值范围是() A.(.,容B.(兀,*C.(孚 })D.(.,壹)U (7T, |兀)71 3 71 3TI5、 已知 cos (万+□)=§, 且 万~),贝0 tanot = ( )A 4「3 八 3 、 3 AR B 标 C. -4 D. ±47、函数y = cos%|tan%| (-—< x<-)的大致图象是()' 1 1 2 22kn + —,Ikn + — ,k eZ227 5/r 7 11〃 ki ----- --------- 12 12 C 15 8、下列函数中,以〃为周期且在区间[o,上为增函数的函数是()A. y = sin —B. y = sinxC. y = -tanxD. y = -cos 2x 9、 设g (x )是将函数/(x ) = cos2x 向左平移:个单位得到的,则g (;)等于()A. 1B. ---C. 0D. —12 10、 函数y=3sin ](-2,的单调递增区间是( )A 、 2k 兀 ---------,2k/c — ,k E ZB 、22 ,k E Z D 、 kzr ----- ,k/c H -- ,k E ZL 12 12jrr11、 已知加= sinS+§®>0)的图象与 尸一1的图象的相邻两交点间的距离为兀,要得 到y =fi x )的图象,只需把y=cos2工的图象() A.向右平移书个单位B.向右平移普个单位C.向左平移苦个单位D.向左平移普个单位7T TT 12、 已知函数y (x ) = 2sin5(口>0)在区间[一亍彳]上的最小值是一2,则口的最小值为()23 A.^ B.^ C. 2 D. 3第II 卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13、 设 a>0,角 a 的终边经过点 P (-3Q ,4Q ),那么 sinot+2cosa=14、若角a 的终边落在直线v =—x 上,则/,血,的值等于sin 2a cosaB 知sinot 是方程5A 2 — 7x — 6 = 0的根,且a 是第三象限角,则 3冗 3兀 9sin (—a —^-)cos (~2~—o )tan (兀—a )cos (壹一 a )sin (壹 + a )1920、16、 下面有5个命题:①分针每小时旋转21弧度;②若a 、P 是第一象限角且a 邛,则~、 sinx/(X ) = \ 兀 571tanavtan";;③ 函数 l + cosx 是奇函数;④尤=§是函数y=sin (2x+^-)的一条 对称轴方程;⑤函数y=sin (2x+|)的图象关于点(含,0)成中心对称图形其中,真命题的编号是 (写出所有真命题的编号)三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明 过程或演算步骤.)17、 (10分)已知扇形。
