半导体异质结
异质结和半导体

异质结是指由两个不同材料组成的半导体结构,其中每个材料的能带结构不同。
异质结是一种重要的半导体结构,具有许多独特的性质和应用,例如在光电器件、太阳能电池、激光器、晶体管等领域中都有广泛的应用。
半导体是指一种物质,其电子能级介于价带和导带之间,形成禁带,使得半导体在导电方面表现出特殊的性质。
半导体材料的导电性质可以通过掺杂等手段进行调节,从而实现各种电子器件的制造。
常见的半导体材料包括硅、锗、氮化镓等。
异质结和半导体之间有着密切的联系。
在半导体器件中,异质结通常用于构建晶体管、太阳能电池等器件的结构。
例如,在PN结中,P型半导体和N型半导体之间形成一个异质结,可以实现电子和空穴的分离,实现电流的控制。
另外,在太阳能电池中,异质结也是关键的组成部分,可以实现光的吸收和电子空穴对的分离。
异质结

N AND pn n ≈ k BT ln 1 2 = k BT ln 2 ni2 n1 p1 n1
即内建电势取决于两种半导体载流子浓度的比值。具体到pN结,取 决于N型半导体中的多子(电子)与p型中的少子(电子)浓度比。
§2.3 半导体异质结
根据《半导体物理》的结论,p区和N区各自的内建电势分别是 2 eN A x 2 eN N x N p , VDN = VDp = 2ε p 2ε N 若近似认为,正负电荷在耗尽层是均匀分布的,则电中性条件为
Space charge region
Vo
(f)
x
nno ni
npo
(c)
PE(x) eVo Hole PE(x)
pno
ρnet
x=0 M x
x Electron PE(x)
(g)
eNd
W 杴p Wn
x
(d)
eV 杴o
-eNa
Properties of the junction. pn
§2.3 半导体异质结
由两种性质带隙宽度不同的半导体材料通过一定的生长方法所形成一突变异质结pn1pn结的形成与能带图窄带隙的p型半导体与宽带隙的n型半导体生长一起时界面处出现了载流子的浓度差于是n中的电子向p中扩散相反p中的空穴也会向n中扩散在界面形成空间电荷内建电场e扩散迁移23半导体异质结1960年anderson用能带论分析了pn结的形成与有关问题直观而深刻并得到一些十分有用的结论称为anderson模型
3、载流子的输运 Anderson模型:零偏压时,由N向p越过势垒VDN的电子流应与从p到 N越过势垒∆Ec-VDp的电子流相等,即
∆E − eVDp eV = B2 exp − DN B1 exp − c k T k BT B D N D N B1 = e ⋅ n 2 10 , B2 = e ⋅ n1 20 Ln 2 Ln1 Ln1 = Dn1τ e1 , Ln 2 = Dn 2τ e 2
(15)半导体异质结

n0 p0 N N e
Eg kBT
异型同质PN结注入比
ND和NA —— N区和P区掺杂浓度
jn Dn Lp N D j p D p Ln N A
异型异质PN结
( E g ) N ( E g ) P k BT
异质PN结注入比
j n Dn L p N D e j p D p Ln N A
异 质 结
同质结 —— 由同种半导体材料构成N区或P区,形成的PN结
异质结 —— 两种带隙宽度不同的半导体材料生长在同一块 单晶上形成的结 同型异质结 —— 结的两边导电类型相同:NN,PP
异型异质结 —— 结的两边导电类型不相同:NP,PN
两种材料未构成异质PN结之前的能级图
两种半导体材料构成异质PN结之后的能级图
Ei
异质结的“窗口效应” 异质结的窗口效应 —— 有效地减小电子-空穴的复合率
E
异质PN结界面处导带底和价带顶不连续 —— 差值
—— 两种材料的费密能级 不同,电子从高费密能级 材料流向低费密能级材料, 形成PN结势垒 —— 形成异质结时,能 带在界面处间断,在势垒 的一侧出现尖峰,另一侧 出现峡谷
异质结的“注入比” P区的电子电流密度
N区的空穴电流密度
PN结注入比
热平衡条件 Ei源自 Ei—— 强电场将电子扫向N区 —— 强电场将空穴扫向P区
—— N区带负电 —— P区带正电
Ei
—— 上下电极 产生电压
E
异质结的“窗口效应” —— 光子能量小于宽带隙的N型层__ 过N型层,在带隙较窄的P型层被吸收 —— 同质PN结制作光电 池,缺陷引起的表面复合 和高掺杂层中载流子寿命 低等因素 —— 使得一些电子-空穴 对不能到达强电场区域 ,可以透
第3章 异质结构

1
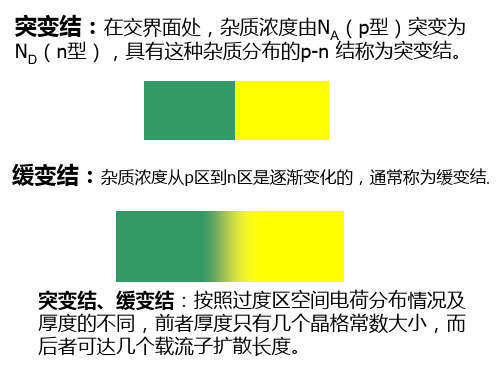
突变结:在异质结界面附近,两种材料的组
分、掺杂浓度发生突变,有明显的空间电荷 区边界,其厚度仅为若干原子间距。
缓变结:在异质结界面附近,组分和掺杂浓
度逐渐变化,存在有一过渡层,其空间电荷 浓度也逐渐向体内变化,厚度可达几个电子 或空穴的扩散长度。
同型异质结:导电类型相同的异质结
如:N‐AlxGa1‐xAs/n‐GaAs, p‐GexSi1‐x/p‐Si
EC1
EC2 EC2
VDN EV 2 EV2
VDp Eg2
EDp Eg Eg2
EC
2
eND 2 2
eNA ( 21 xN 2
xp x)2 (xN x)2
x xp xp ≤x 0
0 x ≤xN xN x
x xp xp ≤x 0 0 x ≤xN
eV D F1 F2 F
依据这一分析,很容易发现异质结界面无论是导带还是价 带都会出现不连续性。导带底和价带顶的这种不连续性 分别为EC和EV:
Eg Ec Ev (Eg 2 Eg1)
Ec 1 2 Ev Eg Ec Eg
1. 异质结的带隙差等于导带差同价带差之和。 2. 导带差是两种材料的电子亲和势之差。 3. 而价带差等于带隙差减去导带差。
16
8
17
自建电场E的作用下,电子和空穴的飘移电流分别为:
ins n E ne n E
ips p E pe p E
从泊松(Poisoon)方程出发,利用D =(E)=式,推导出 电子和空穴的扩散电流分别为:
i nd
eDn
dn dx
i pd
eD p
dp dx
流经异质i结n 界i面ns 的i空nd 穴 电ne流 n等E于空eD穴n的ddn飘x 移电流:
半导体光电子学第2章_异质结
x1 φ1
EC1
ΔEC
Eg1
F1
EV1
ΔEV
p
图2.1-1
x2 φ2
真空能级
EC2 F2
Eg2
EV2
N
②两种材料形成异质结后应处于同一平衡系统中,因而各自的费米能 级应相同; ③画出空间电荷区(由内建电势可求空间电荷区宽度),φ值在空间 电荷区以外保持各自的值不变; ④真空能级连续与带边平行(弯曲总量为两边费米能级之差,每侧弯 曲程度由费米能级与本征费米能级之差决定,由掺杂浓度决定); ⑤而各自的χ、Eg不变。原来两种材料导带、价带位置之间的关系在 交界处不变。(即:ΔEc、ΔEv、Eg、Eg不变)
一、非平衡状态下的pn结 1、外加电压下,pn结势垒的变化及载流子的运动。
正向偏压
P-N结加正向偏压V (即P区接电源正极,N区接负极)
势垒区内载流子浓度很小,电阻很大,势垒区外的P区和N 区中载流子浓度很大,电阻很小,所以外加正向偏压基本 降落在势垒区。
正向偏压在势垒区中产生了与内建电场方向相反的电场,因而 减弱了势垒区中的电场强度,这就表明空间电荷相应减少。故 势垒区的宽度也减小,同时势垒高度从qVD下降为q(VD-V)。
这时,P-N结中有统 一的费米能级EF,P-N结 处于平衡状态,其能带图 如图所示。
能带相对移动的原因 是P-N结空间电荷区中存 在内建电场的结果。
由于整个半导体处于 平衡状态,因此在半 导体内各处的Fermi 能级是一样的。可以 看到,这时由于势垒 的存在,电子和空穴 也没有机会复合
如果一个半导体的两端加一个电压, 由于电场的作用,使得能带整体沿 着电场方向倾斜。电子和空穴的势 能也发生变化,电子势能逆着电场 方向降低,而空穴势能顺着电场方 向降低。所以电子和空穴向两个相 反方向移动。
第九章半导体异质结结构

汇报人:XX
目录
• 异质结基本概念与特性 • 异质结制备技术与方法 • 异质结器件物理基础 • 异质结在光电器件中应用 • 异质结在微纳电子器件中应用 • 异质结性能优化与未来发展趋势
01
异质结基本概念与特性
异质结定义及分类
定义
由两种或两种以上不同半导体材料组 成的结,称为异质结。
异质结界面态与缺陷
界面态
异质结界面处存在悬挂键、界面电荷等界面态,对异质结的电学性能和稳定性 产生重要影响。
缺陷
异质结在制备过程中可能引入位错、层错等缺陷,影响异质结的晶体质量和电 学性能。
典型异质结材料及性质
Si-Ge异质结
具有高迁移率、低噪声等优点,广泛应用于高速 、高频电子器件。
GaAs-AlGaAs异质结
异质结发光二极管原理
通过异质结的能带结构和载流子限制作用,实现电子 和空穴的复合发光。
常见异质结发光二极管结构
如GaN基异质结发光二极管、量子点/有机物异质结发 光二极管等,具有高亮度、高色纯度等优点。
光电探测器中的异质结结构
异质结光电探测器原理
利用异质结的能带结构和内建电场,实现光 信号到电信号的转换。
和选择性。
MEMS器件
03
将异质结结构与MEMS技术相结合,实现微型化、集成化的生
物传感器件。
其他微纳电子器件中的异质结应用
光电探测器
利用异质结的能带结构和光电效应,实现高性能的光电转换。
太阳能电池
通过设计异质结的能级匹配和光吸收特性,提高太阳能电池的转 换效率。
热电转换器件
利用异质结的热电效应,实现热能和电能之间的转换。
04
异质结在光电器件中应用
半导体异质结

半导体异质结
半导体异质结是半导体物理和材料学中最基础的概念之一,它指的是不同半导体材料之间的界面,物理上的结构是彼此分离的。
半导体异质结是由不同结构或物理本征的半导体分子构成的。
这样的结构可以产生半导体物质的能带变化,从而影响传输特性。
半导体异质结是由一方阳离子和另一方阴离子电荷配对构成的,这样就可以形成一个稳定的电势阻挡,使得流动的电子和空穴在其中穿梭,电流才能传递。
另一方面,由于空穴和电子的转移率不同,半导体异质结可以用来控制光电子器件的传输特性,例如在光子晶体中的发射率。
此外,半导体异质结还可以用于降低半导体器件,降低输出功耗,提高效率。
半导体异质结

异质结半导体异质结构一般是由两层以上不同材料所组成,它们各具不同的能带隙。
这些材料可以是GaAs 之类的化合物,也可以是Si-Ge之类的半导体合金。
按异质结中两种材料导带和价带的对准情况可以把异质结分为Ⅰ型异质结和Ⅱ型异质结两种,两种异质结的能带结构如图1所示。
如图1(a)所示,I型异质结的能带结构是嵌套式对准的,窄带材料的导带底和价带顶都位于宽带材料的禁带中,ΔEc和ΔEv的符号相反,GaAlAs/GaAs和InGaAsP/InP都属于这一种。
在Ⅱ型异质结中,ΔEc和ΔEv的符号相同。
具体又可以分为两种:一种如图1(b)所示的交错式对准,窄带材料的导带底位于宽带材料的禁带中,窄带材料的价带顶位于宽带材料的价带中。
另一种如图1(c)所示窄带材料的导带底和价带顶都位于宽带材料的价带中[14]。
Ⅱ型异质结的基本特性是在交界面附近电子和空穴空间的分隔和在自洽量子阱中的局域化。
由于在界面附近波函数的交叠,导致光学矩阵元的减少,从而使辐射寿命加长,激子束缚能减少。
由于光强和外加电场会强烈影响Ⅱ型异质结的特性,使得与Ⅰ型异质结相比,Ⅱ型异质结表现出不寻常的载流子的动力学和复合特性,从而影响其电学、光学和光电特性及其器件的参数。
在Ⅰ型异质结中能级的偏差量具有不同的符号,电子和空穴是在界面的同一侧(窄带材料一侧)由受热离化而产生的。
这种情况下只有一种载流子被束缚在量子阱中(n-N结构中的电子,p-P结构中的空穴)。
Ⅱ型异质结能级的偏差量具有相同的符号,电子和空穴是在界面的不同侧由受热离化而产生的。
两种载流子被束缚在自洽的量子阱中,因此在Ⅰ型异质结中载流子复合发生在窄带材料一侧,Ⅱ型异质结中载流子复合主要是借助界面的隧道而不是窄带材料一侧。
不同半导体的能隙宽度可根据使用的要求做适当调整,办法可以是取代半导体元素(例如,用In或者Al代替Ga,用P、Sb或N代替As),也可以通过改变合金的成分。
有多种方法可用于形成不同半导体层之间的突变界面,例如分子束外延法(MBE)和金属有机化学沉积法(MOCVD)。
微电子器件 第4版 第 5 章 半导体异质结器件

材料1
材料2
由两种不同材料所构成的结就是异质结。如果这两种材料都是 半导体,则称为半导体异质结;如果这两种材料是金属和半导 体,则称为金属-半导体接触,这包括Schottky结和欧姆接触。
• 半导体异质结可根据界面情况分成三种 • 晶格匹配突变异质结;当两种半导体的晶格常数近似
V
k0T
EC
n10
exp
qV k0T
在稳定情况下,P型区半导体中注入的少子的运动连续性方
程是
Dn1
d
2n1 x
dx 2
n1x n10
n1
0
其通解是
Ec 1 2
n1x
n10
A exp
x Ln1
B exp
x Ln1
应用边界条件
n1x
n10
n10
exp
qV k0T
1
exp
制作步骤:
1、在GaAs衬底上采用MBE(分子束外延)等技术连续 生长出高纯度的GaAs层和n型AlGaAs层;
2、然后进行台面腐蚀以隔离有源区;
3、 接着制作Au·Ge/Au 的源、漏欧姆接触 电极,并通过反应 等离子选择腐蚀去 除栅极区上面的n型 GaAs层;
4、最后在n型AlGaAs 表面积淀Ti/Pt/Au栅 电极。
HEMT是通过栅极下面的肖特基势垒来控制GaAs/AlGaAs 异质结的2-DEG的浓度而实现控制电流的。
由于肖特基势垒的作用和电子向未掺杂的GaAs层转移,栅极 下面的N型AlGaAs层将被完全耗尽。
转移到未掺杂GaAs层中的 电子在异质结的三角形势阱 中即该层表面约10nm范围 内形成2-DEG;这些2-DEG 与处在AlGaAs层中的杂质 中心在空间上是分离的,不
半导体物理学第九章知识点

半导体物理学第九章知识点第9章半导体异质结构第6章讨论的是由同⼀种半导体材料构成的p-n结,结两侧禁带宽度相同,通常称之为同质结。
本章介绍异质结,即两种不同半导体单晶材料的结合。
虽然早在1951年就已经提出了异质结的概念,并进⾏了⼀定的理论分析⼯作,但是由于⼯艺⽔平的限制,⼀直没有实际制成。
直到⽓相外延⽣长技术开发成功,异质结才在1960年得以实现。
1969年发表了第⼀个⽤异质结制成激光⼆极管的报告之后,半导体异质结的研究和应⽤才⽇益⼴泛起来。
§9.1 异质结及其能带图⼀、半导体异质结异质结是由两种不同的半导体单晶材料结合⽽成的,在结合部保持晶格的连续性,因⽽这两种材料⾄少要在结合⾯上具有相近的晶格结构。
根据这两种半导体单晶材料的导电类型,异质结分为以下两类:(1)反型异质结反型异质结是指由导电类型相反的两种不同的半导体单晶材料所形成的异质结。
例如由p型Ge与n型Si构成的结即为反型异质结,并记为pn-Ge/Si或记为p-Ge/n-Si。
如果异质结由n型Ge 与p型Si形成,则记为np-Ge/Si或记为n-Ge/p-Si。
已经研究过许多反型异质结,如pn-Ge/Si;pn-Si/GaAs;pn-Si/ZnS;pn-GaAs/GaP;np-Ge/GaAs;np-Si/GaP等等。
(2)同型异质结同型异质结是指由导电类型相同的两种不同的半导体单晶材料所形成的异质结。
例如。
在以上所⽤的符号中,⼀般都是把禁带宽度较⼩的材料名称写在前⾯。
⼆、异质结的能带结构异质结的能带结构取决于形成异质结的两种半导体的电⼦亲和能、禁带宽度、导电类型、掺杂浓度和界⾯态等多种因素,因此不能像同质结那样直接从费⽶能级推断其能带结构的特征。
1、理想异质结的能带图界⾯态使异质结的能带结构有⼀定的不确定性,但⼀个良好的异质结应有较低的界⾯态密度,因此在讨论异质结的能带图时先不考虑界⾯态的影响。
(1)突变反型异质结能带图图9-1(a)表⽰禁带宽度分别为E g1和E g2的p型半导体和n型半导体在形成异质pn结前的热平衡能带图,E g1 E g2。
半导体光电子学第2章_异质结

势垒区电场减弱,
破坏了载流子的扩散 运动和漂移运动之间 的平衡,削弱了漂移 运动,使扩散电流大 于漂移电流。
所以在加正向偏 压时,产生了电子从N 区向P区以及空穴从P 区到N区的净扩散电流。
由于pn结阻碍多数载流子的定向移动,因此从电路性质看,它 是高阻区。如果在半导体两端有外加电压,那么电压基本上都 施加在pn结上。现在在半导体加一个电压V,p区结电源正极, n区接负极,形成正向偏置。外加电压基本上都施加在pn结上, 这也等于在pn上施加一个外加电场E。外加电场的方向与内置 电场E0的方向相反,总电场E0-E比原来的电场小了。这削弱了 电子和空穴的势垒,由原来的eV0变为e(V0-V)。同时空间电荷 区宽度变窄,由原来的w0变为w。
x1 φ1
EC1
ΔEC
Eg1
F1
EV1
ΔEV
p
图2.1-1
x2 φ2
真空能级
EC2 F2
Eg2
EV2
N
②两种材料形成异质结后应处于同一平衡系统中,因而各自的费米能 级应相同; ③画出空间电荷区(由内建电势可求空间电荷区宽度),φ值在空间 电荷区以外保持各自的值不变; ④真空能级连续与带边平行(弯曲总量为两边费米能级之差,每侧弯 曲程度由费米能级与本征费米能级之差决定,由掺杂浓度决定); ⑤而各自的χ、Eg不变。原来两种材料导带、价带位置之间的关系在 交界处不变。(即:ΔEc、ΔEv、Eg、Eg不变)
不论是n型或p型半导体材料,若Fermi能级都处于禁带 中。——轻掺杂半导体。 这时在外加电压作用下电子和空穴虽然也能复合产生光子, 但是由于载流子浓度有限,形成不了粒子数反转和受激辐射。 这种材料只能用于发光二极管。 为了使半导体材料在外界作用下实现粒子数反转,必须对半 导体进行重掺杂,使n型的Fermi能级处于导带中,p型的 Fermi能级处于价带中。
半导体异质结构

半导体异质结构1半导体异质结及其能带图异质结由两种不同的半导体单晶材料组成的结,称为异质结。
半导体异质结的能带图反型异质结指由导电类型相反的两种不同的半导体单晶材料所形成的异质结。
例如p型Ge与n型GaAs所形成的结——p-nGe-GaAs(或(p)Ge-(n)GaAs)——一般把禁带宽度较小的半导体材料写在前面。
同型异质结指由导电类型相同的两种不同的半导体单晶材料所形成的异质结。
例如n型Ge与n型GaAs所形成的结——p-pGe-GaAs(或(p)Ge-(p)GaAs)突变型异质结一种半导体材料向另一种半导体材料的过渡只发生于几个原子距离范围内不考虑界面态时的能带图突变反型异质结能带图由于n型半导体的费米能级较高,电子将从n型半导体流向p型半导体,同时空穴在与电子相反方向流动,直至Ef=Ef1=Ef2——热平衡状态。
此时,材料交界面的两边形成了空间电荷区(即势垒区或耗尽层)。
n型半导体一侧为正空间电荷区,p型半导体一侧为负空间电荷区,且电荷数相等(由于不考虑界面态),空间电荷区间产生电场,也称为内建电场,所以电子在空间电荷区中各点有附加电势能,使空间电荷区中的能带发生了弯曲。
尖峰与凹口能带突变突变同型异质结能带图形成异质结时,由于禁带宽度大的n型半导体的费米能级比禁带宽度小的高,所以电子将从前者流向后者。
结果在禁带宽度小的n型半导体一边形成了电子的积累层,而另一边形成了耗尽层。
对于反型异质结,两种半导体材料的交界面两边都成为了耗尽层;而在同型异质结中,一般必有一边成为积累层。
尖峰与凹口能带突变考虑界面态时的能带图1.形成异质结的两种半导体材料的晶格失配,需要引入界面态。
2.由于晶格失配,在两种半导体材料的交界面处产生了悬挂键,引入界面态。
3.当具有金刚石结构的晶体的表面能级密度在10¹³cm-²以上时,在表面处的费米能级位于禁带宽度的越1/3处——巴丁极限。
4.对于n型半导体,悬挂键起受主作用,因此表面处的能带向上弯曲。
半导体光电子学§2.1 异质结及其能带图

加正向偏压 vf 时,外加电场与内建电场方
向相反,空间电荷相应减少,势垒区宽度减少, 扩散运动超过了漂移运动 qvD q(vD vf ) , 载流子扩散运动超过了漂移运动→成为正向电流。
→n 区电子进入p区成为p区非平衡少数载流子。 →非平衡少数载流子的电注入。
扩散过程中与多子相遇而不断复合→一个扩散长度 后复合完毕。
x1
Ec1
1
VDP
F
Ev1
xp
内建电场
VD VDP VDN
Ec
Ev xn
Eg1 Eg2
VDN
x1 x2
Ec2 1 2
Ev 2
x1 Eg1 x2 Eg 2
④ p-n结 p- n: n型和p型样占接触在一起p- n结。 n区电子向p区扩散→n区剩下电离施主,形成带 正电荷区。 p区孔穴向n区扩散→p区剩下电离受主,形成带 负电荷区。
第二章 异质结
§2 – 1 异质结及其能带图
①异质结:两种禁带宽度不同的半导体材料,通过一定 的生长方法所形成的结。
②分 类
按电荷分布 按掺杂类型
突变结
缓变结 同型异质结 p-P,n-N
异型异质结 p-N,n-P
③ 能带图 界面上静电场是不连续的;功函数Φ;电子
亲和势X 电子势能增加方向
真空能级
3.同型异质结材料费米能级有差别 → 扩散
4. Eg: X: Φ:
不同, 能带不同
F:
x1
Ec1
Ev1
1
Ec Eg1
Ev
-+
x1 x2 1 2 x1 Eg1 x2 Eg 2
1
2 Ec2
-+
第九章 半导体异质结

当半导体表面存在足够大的界面态时,半导体表面的状态完全由界面态电 荷决定,与功函数等没有关系。
⑴ 当表面态为施主态时:(被电子占据时呈电中性,释放电子后呈正电性)
对于n型半导体:
E
电子积累
正
在半导体表面处形成很薄的多子积累层。
电
荷
高低
二、计入界面态的影响
对于P型半导体:
在半导体表面形成耗尽 层,层内电荷为电离受主。 该耗尽层很厚,其厚度由掺 杂浓度决定。
(c)
二、计入界面态的影响
界面态不同,在界面形成的势垒也不同,此时 界面态起决定性的作用,而界面两侧半导体材料的 固有性质(如功函数、电子亲和能、介电常数等) 对界面势垒没有影响,这是由于界面态上大量电荷 的屏蔽作用所致。
三、突变反型异质结的接触电势差
设:构成异质结的两种半导体材料即P型和N型中的杂质都是均匀分布的,其
第九章
半导体异质结的组成与生长
第九章 Part 1
9.1 半导体异质结的一般性质 9.2 半导体异质结的能带结构 9.3 异质PN结的注入特性 9.4 理想突变异质结的伏安特性
9.1 半导体异质结的一般性质
由两种不同的半导体单晶材料形成的PN结称为异质结。
1951年由Gubanov首先提出了异质结的概念;
B1
VD Va
1/2
式中第一项为由界面态影响在空间电荷区产生的电荷量,第二项为不考虑界 面态时的空间电荷区电荷量。
二、计入界面态的影响
分析空间电荷区宽度的变化:
令L1=x0-x1, L2=x2-x0,L1、L2为P区和N区的耗尽层宽度,
则 Q1、Q2可改写为:
qNAL1 qNDL2
1NAQIS 1NA 2ND
半导体光电子学异质结

半导体光电子学异质结引言半导体光电子学异质结是半导体器件中的一种重要结构,其特殊的层状组合能够实现光电转换和电子输运功能的有效集成。
本文将对半导体光电子学异质结的基本原理、应用领域和未来发展方向进行详细介绍。
基本原理半导体光电子学异质结的基本原理源于不同材料间的价带和禁带差异导致的能带弯曲。
在正向偏置情况下,载流子在异质结中会因能带曲率而发生漂移,在逆向偏置时则会发生空间电荷屏蔽效应。
这些特性使得半导体光电子学异质结能够对光信号进行高效转换。
应用领域半导体光电子学异质结在光电器件中有着广泛的应用。
以下是一些常见的应用领域:光伏电池光伏电池是半导体光电子学异质结最常见的应用之一。
通过将光线照射到光伏电池上,光能被转换为电能。
光伏电池的效率取决于异质结界面的设计和材料的选择。
光电探测器光电探测器利用了半导体光电子学异质结的光电转换特性,可以将光信号转换为电信号。
它们在光通信、光谱测量等领域中发挥着重要作用。
光发射器光发射器利用半导体光电子学异质结中的电流注入和复合过程,将电能转换成光能。
它们在光通信领域中被广泛应用,能够实现高速、高效的光信号传输。
光放大器光放大器是利用半导体光电子学异质结结构实现光信号放大的器件。
它们在光通信中具有重要地位,能够帮助信号在光纤中传输更远的距离。
未来发展方向半导体光电子学异质结领域仍然存在许多挑战和发展机遇。
以下是一些可能的未来发展方向:新型材料尽管现有的半导体材料已经取得了令人瞩目的成果,但仍然有许多材料可以探索。
通过研究和开发新型材料,可以进一步改善异质结的光电转换效率和稳定性。
结构优化异质结的结构优化是提高器件性能的关键。
通过精确控制界面的形貌和材料的晶格匹配,可以降低界面态和缺陷的影响,提高器件的效率和稳定性。
新型器件设计除了上述常见的应用领域,半导体光电子学异质结还有许多潜在的应用,如光存储器、光计算、光传感器等。
发展新型器件设计是推动半导体光电子学异质结前进的关键。
第九章半导体异质结结构

面的时悬挂键密度为
Ns
4
3
a22 a12 a12a22
(9-8)
同理(110)晶面,悬挂键密度为
Ns
4
2
a22 a12 a12a22
(9-9)
School of Electronic Engineering & Optoelectronic Techniques
同理(110)晶面,悬挂键密度为
School of Electronic Engineering & Optoelectronic Techniques
如果从一种半导体材料向另一种半导体材料得过渡只发生 于几个原子范围内,则称为突变型异质结。如果发生于几 个扩散长度范围内,则称为缓变形异质结。 1.不考虑界面态时的能带图 (1)突变反型异质结能带图
d
2V1 ( x) dx2
qN A1
1
x1 x x0
d 2V2 (x) qND2
dx2
2
x0 x x2
将(9-15)(9-16)积分一次得
dV1(x) dx
qN A1x
1
C1
x1 x x0
dV2 (x) dx
qN D 2 x
2
C2
x0 x x2
(9-15) (9-16)
(9-28) (9-29) (9-30) (9-31)
School of Electronic Engineering & Optoelectronic Techniques
交界面处引入界面态。
9.1.2 突变反型异质结的接触电势差及势垒区宽度
以突变pn异质结为例
设p型和n型半导体中的杂志都是均匀分布的,则交界面两 边的势垒区中的电荷密度可以写成
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正反向势垒异质结的伏安特性
• 势阱中的电子要往右边输运,需要克服高度为∆Ec–qVD1的 势垒 • 右边n型区导带中的电子要往左边输运,需要克服的势垒 高度为qVD2 • 但左边的空穴要通过异质结所需越过的势垒却很高,为 qVD1+qVD2–∆Ev • 这种异质结几乎不存在整流特性
多量子阱和超晶格中电子的波函数 由于两种构成材料的禁带宽度不同,当窄禁带材料的厚度 小于电子的德布罗意波长时,这种材料即成为载流子的势阱
量子阱效应
量子约束效应:量子阱中电子的能级间距与阱宽的平方成反比,对于由 一、量子约束效应 夹在宽禁带材料之间的窄禁带材料薄层构成的量子阱,当薄层狭窄到 足以使电子状态量子化 共振隧穿效应:当入射电子的能量与中间量子阱中的分立能级一致时, 二、共振隧穿效应 其隧穿概率可接近于1,而能量不一致时,其隧穿概率则几乎为零 声子约束效应:在量子阱或超晶格中,声子态也有类似于电子态的量 三、声子约束效应 子约束效应 微带效应:超晶格中各量子阱之问的势垒较薄,各量子阱中的束缚能 四、微带效应 级互相耦合,形成微带
ϕ ( z ) = Az sin(k z z )(k z = π n / Lz ; n = ±1, ±2, ±3⋯)
满足边界条件的波函数(z=0及z=Lz处恒为零)的能量 Ez是量子化的
ℏ 2π 2 2 Ez = En = n * 2 2m⊥ Lz (n = 1, 2,3,⋯)
* m⊥ 为z方向的有效质量;n为量子数,能量本征值与量子数n的平方成正比
耗尽层宽度随着结电压的变化而变化,微分电容C=dQ/dV,
1 2
dQ qε1ε 2 N A1 N D 2 C= = dVa 2(ε1 N A1 + ε 2 N D 2 )(VD − V )
(1/C2)和V呈线性关系,
可以从直线在电压轴上的截距求得势垒高度VD
考虑界面态时的能带图
−( Ec1 − EFn ) n1 = N c1 exp kT
−( Ec 2 − EFn n2 = N c 2 exp kT
Nc1~Nc2
n1 Ec 2 − Ec1 ≈ exp n2 kT
实现激光器所要求的粒子数反转条件
由于Ec1<Ec2,故n1>n2
−(qVD − ∆ Ec ) n10 = n20 exp kT
加正向偏压时, p型半导体势垒区边界处的少子浓度
−( qVD − qV − ∆ Ec ) qV n1 (− x1 ) = n20 exp = n10 exp kT kT qD n qV J n = n1 10 exp 电子电流密度 − 1 Ln1 kT
加正向电压后的p-GaAs-N-AlxGal-xAs异质结 当异质结上施加的正向电压足够大时, p区电子为少数载流子, 其准费米能级随电子浓度的上升很快 ,结两边的电子准费米能级可达一致。 由于P区导带底比N区导带底更接近费米能级,故P区导带的电子浓度高于N区
以n1和n2分别表示P区和N区的电子浓度 Ec1和Ec2分别表示p区和N区的导带底能值 Nc1和Nc2分别表示两种半导体导带底有效态密度
3.3 量子阱与二维电子气
量子阱: 量子阱:在量子力学中,能够对电子的运动产生某种约束并 使其能量量子化的势场 二维电子气( ):一般是指在两个方向上可以自由运动, 二维电子气(2DEG): ): 而在第三个方向上的运动受到限制的电子群。
图3.11半导体量子阱示意图
对处于无限深方势阱中的粒子 ,假定势阱的宽度为Lz,求解 薛定谔方程,则波函数的解为 Ψ ( x, y, z ) = ψ ( x, y )ϕ ( z ) 在z方向上
多层量子阱LED LED结构 蓝光 InGaN/GaN 多层量子阱LED结构
Active Layer
P electrode
P-type GaN:Mg 0.5µm
P-type Al0.1Ga0.9N:Mg 100nm 3-4µm
Transparent electrode N electrode 5-period In0.3Ga0.7N/GaN SLs (2.5nm/4.0nm) GaN buffer layer: 30nm
N-type GaN: Si 3-4µm
Substrate Sapphire or Si
ZnMgO/ZnO 多层量子阱LED结构 多层量子阱LED结构 LED
周期性波长 u = [ ( L1-L2)λ / [2(sin θ1一sinθ2) 式中λ为所使用的X 射线波长;L为反射级数; θ表示衍射角 L=0对 应于 布拉 格 (Bragg)反射峰,若在较 低 角 度的 第 一 条 伴 线 取 为 L= -1,则在较高角度的第 一条伴线即取L= +1。 上图超晶格的调制 波长为13nm,而下图超晶 格的调制波长为11nm。随 着调制波长的增加,伴线变 得越靠近Bragg峰。
Ln1为电子扩散长度,Dn1为电子扩散系数 n型半导体中少数载流子的浓度p20 加正向电压时
−( qVD + ∆ Ev p20 = p10 exp kT
−(qVD − V + ∆ Ev qV p2 ( x2 ) = p10 exp = p20 exp kT kT
ZnO掺杂能带示意图
第3章 半导体异质结 章
• pn结的两边是采用同一种材料,称为同质结 结的两边是采用同一种材料, 结的两边是采用同一种材料 • 由两种不同的半导体单晶材料组成的结,则称为异质结 由两种不同的半导体单晶材料组成的结, N和P表示宽带半导体,n和p表示窄带半导体 p型GaAs与P型AlGaAs ,同型异质结 p型GaAs与N型AlGaAs,异型异质结
总电流
注入比: 注入比: 是指pn结加正向电压时,n区向p区注入的电子流与
p区向n区注入的空穴流之比
J n qDn1 Lp1n10 Dn1 Lp 2 n12i n20 = = 2 p qD p 2 Ln1 p20 D p 2 Ln1 n2i p10
同质结注入比
J n Dn L p N D = J p D p Ln N A
3.1 异质结及其能带图
一些Ⅲ-Ⅴ族化合物及几种Ⅱ-Ⅵ族化合物的禁带宽度和晶格常数
异质结的形成
晶格匹配越好, 晶格匹配越好,界面态密度越低 晶格失配 定义
2(a2 − a2 ) ∆a = a2 + a1 a
a1和a2分别是两种材料的晶格常数 (a2>a1),a为平均值
三元合金的禁带宽度和晶格常数 用三元或四元化合物半导体来制作出晶格匹配非常完美的异质结。
∆ Ev = ( Eg1 − Eg 2 ) − ( χ1 − χ 2 )
(a)异质结形成之前平衡能带图(b)形成之后的平衡能带图 )异质结形成之前平衡能带图( ) 特点:在界面处就会出现能带的弯曲, 特点:在界面处就会出现能带的弯曲,发生导带及价带的不连续
异质结耗尽层宽度的计算
• 假设条件:在热平衡下,界面两端的费米能级相同 禁带宽度Eg和电子亲和能皆非杂质浓度的函(非简并) • 导带边缘的不连续和价带边缘的不连续不会受杂质浓度影响 • 能带的弯曲量VD(扩散电势)为两种半导体功函数之差
• 空穴的电流密度
qD p 2 p20 qV Jp = exp kT Lp 2
− 1
Lp2为空穴扩散长度,Dp2为空穴扩散系数
Dn1n10 D p 2 p20 qV + J = Jn + J p = q exp L Lp 2 kT n1 − 1
(a)p-n异质 (b)n-p异质结 a p-n b n-p
(c)p-p异质结 (d)n-n异质结
渐变异质结的能带图
3.2 异型异质结的电学特性
半导体异质结的电流电压关系比同质结复杂 突变异质结的伏安特性和注入特性
(a)负反向势垒(b)正反向势垒
负反向势垒异质结的伏安特性
p型半导体中少数载流子的浓度n10 n型半导体中多数载流子的浓度n20
界面态的影响
如果考虑界面态,载流子将通过界面态发生复合,复合电流为
Ein qV J ∝ exp − exp kT kT
− 1
Ein代表界面态的能级深度,V是外加电压
异质结的超注入现象
超注入现象:指在异质结中由宽带半导体注入到窄带半导体中 的少数载流子浓度可以超过宽带半导体中多数载流子浓度
2ε1ε 2 N D 2VD ( x0 − x1 ) = qN A1 (ε1 N A1 + ε 2 N D 2 )
当外加偏压时,用(VD–V)替换VD 内建电势的大部分降落在杂质浓度较低的一侧, 内建电势的大部分降落在杂质浓度较低的一侧,其耗尽层宽度也较宽
同质结中势垒高度V 同质结中势垒高度 D的计算
二维电子气的态密度
态密度:单位能量间隔内允许存在的状态数 在三维情况下,态密度和能量呈抛物线关系,通过k空间来求 能量空间的状态密度, 二维电子气只需要把三维求解中的体积转化为二维的面积 设势阱平面在x, y方向的长度分别为Lx和Ly, 2 每个状态所占的面积为 2π ) (
s= Lx Ly
k空间的等能曲线是一个圆,对于圆环状面积对应的状态数等于
2π kdk / s = kdk Lx Ly 2π
单位实空间中对应的状态数为
kdk / 2π
倒空间中的面积元
2DEG中电子的状态密度与能量的关系
3.4 多量子阱与超晶格
(a) 半导体量子阱
