届高三数学一轮复习强化训练精品――基本算法语句、算法案例 doc
【江苏南通名校】高三数学一轮复习:基本算法语句和算法案例

课堂互动讲练
【解】 法一:用“While 语句”表示如 下:
s←1 i←2 While i≤100
a←1/i s←s+a i←i+1 Wend Print “1+12+13+14+…+1100=”;s End
课堂互动讲练
法二:用“Until 语句”表示如
S1 Print “圆面积为”;S2
End
课堂互动讲练
考点二
条件语句的嵌套 一般形式
条件语句
课堂互动讲练
对应的程序框图为
课堂互动讲练
例2 如图,在边长为4的 正方形ABCD的边上有 一点P,沿着折线BCD A由点B(起点)向点A(终 点)运动.设点P运动的 路程为x,△APB的面积 为y,求y与x之间的函 数关系式.并画出程序 框图,写出程序.
课堂互动讲练
例1 下列程序的运行结果为_________. m=1 n=2 p=3 p=m n=p m=n Print m,n,p End
课堂互动讲练
【思路点拨】 此程序主要以赋值语 句来设计,变量的值等于最近一次赋给 它的值.
【解析】 首先对变量m,n,p分别 赋值1,2,3,然后将变量m的值赋给p,再 将变量p的值赋给n,最后将变量n的值赋 给m,所以最后的变量m,n,p的值都等 于1,所以运行结果输出为1,1,1.
课堂互动讲练
4=504, 504-84=420,420-84=336,336-8
4=252, 252-84=168,168-84=84,13分 所以840与1764的最大公约数是84.1
4分
课堂互动讲练
【点评】 求最大公约数的方法: (1)辗转相除法就是用大数除以小数, 再用小数除以余数,如此继续下去直到 较大的数能被较小的数整除为止,这个 较小的数就是所求的最大公约数. (2)更相减损术是以较大的数减去较 小的数,接着把所得的差与较小的数比 较,并以大数减小数直到大数减小数的 差等于小数时停止,这个小数就是最大 公约数.
高三数学一轮复习 第九章 第2课时 基本算法语句、算法案例与框图课件

输入信息
语句
一般格式
功能
输出 _P_R_I_N__T_“__提__示__内__ 输出_常__量__、__变___量__ 语句 _容__”__;__表__达__式___ 的__值___和__系__统__信__息__
赋值 语句
__变__量__=__表__达__式___
将表达式所代表的 值_赋__给__变___量__
1.四位二进制数 1 111(2)表示的十进制数是
()
A.4
B.15
C.64
D.127
解 析 : 1 111(2)= 1×23+ 1×22+ 1×21+ 1×20=8+4+2+1=15.
答案: B
2.用“辗转相除法”求得 168 和 486 的最大
公约数是( )
A.3
B.4
C.6
D.16
解析: 486=2×168+150,168=1×150 +18,
某工种按工时计算工资,每月总工资=每月劳 动时间(小时)×每小时工资,从总工资中扣除 10%作公积金,剩余的为应发工资,当输入劳 动时间和每小时工资数时,试编写一程序输出 应发工资.
解析: 算法分析:第一步,输入月劳动时 间 t 和每小时工资 a; 第二步,求每月总工资 y=每月劳动时间 t× 每小时工资 a; 第三步,求应发工资 z=每月总工资 y×(1 -10%);
答案: 21 4
练规范、练技能、练速度
人教版八年级上
Unit 4 What’s the best movie theater?
课时4 Section B (2a-2e)
二、根据句意,用括号内所给词的适当形式填空。 6. We are looking for the best singers and the most exciting
高三数学(文)一轮复习课件:基本算法语句、算法案例与框图

2.更相减损术与辗转相除法不同,但二者的算法理论却 是相似的,主要区别是一个是减法运算,一个是除法运 算,实质都是一个递推的过程.用秦九韶方法计算多项式 的值,关键是将多项式改写,然后由内向外依次计算. 3.进位制 将k进制数转化为10进制的数的方法和将10进制数转化为 k进制数的算法操作性很强,要掌握算法步骤,并熟练转 化.要熟练应用“除基数,倒取余,一直除到商为0”.
1 2 23 3 4
99 100
图,写出用基本语句编写的程序_____.
【解析】这是一个累加求和问题,共 99 项相加,可设计一个计数变量, 一个累加变量,用循环结构实现这一算法.程序框图如图所示:
2/18/2020
程序如下:
2/18/2020
【变式训练】 3.将下列程序用DO-LOOP UNTIL循环 语句重新编写出来,并说明解决的是什么数学问题.
a=0 j=1 WHILE j<=5
a=(a+j)MOD 5 j=j+1
WEND
PRINT a
END
2/18/2020
4.(2014·陕西模拟)以下给出了一个程序,根据该程序回答:
INPUT x IF x<3 THEN
y=2*x
ELSE IF x>3 THEN y=x*x-1
ELSE y=2
END IF
2/18/2020
【变式训练】 1.(1)请写出图1运算输出的结果为
.
a=2
b=3
c=a+b
b=a+c-b
PRINT“a=,b=,c=”;a,b,c
2/18/2020
(2)为了在运行图2的程序之后得到结果y=16,则键盘输
入的x应该是
.
2015届高三数学一轮复习教案:2基本算法语句 必修三

必修Ⅲ-02 基本算法语句1、的格式为:INPUT “提示内容”;变量的格式为: PRINT “提示内容”;变量的格式为:变量=表达式,如“x=y”表示。
计算机执行赋值语句时,先计算“=”边表达式的值,然后把这个值赋给“=”边的变量。
2、条件语句的两种形式:IF 条件THEN IF 条件THEN语句体语句1END IF ELSE语句2END IF第一种:先对条件进行判断若条件结果为,则执行表达式后面的语句,否则直接跳过语句执行其他语句,条件语句中必须用结尾。
第二种:如果条件为真,则执行语句1,如果条件为假,则执行语句2。
3、循环语句的两种形式:直到型(UNTIL)语句当型(WHILE)语句DO WHILE 条件循环体循环体LOOP UNTIL 条件WEND(1)直到型(UNTIL)语句,这种语句是先然后进行条件的判定,如果继续执行循环体。
直到直接跳到UNTIL语句后。
(2)当型(WHILE)语句,是在执行循环体之前先,如果条件为真,继续执行循环体。
否则直接跳到WEND语句后。
例1、 (2009年湖南高中学业水平考试)若运行下右图的程序,则输出的结果是( )A 4B 9C 13D 22例2、 关于语句:INPUT “提示内容”;变量,下列说法不正确的是( )A 、提示内容可以是中文也可以是英文B 、语句可以给出多个变量赋值C 、提示内容一般是提示用户输入什么样的信息D 、这是一个输出语句例3、下列给出输入、输出语句正确的是( )○1输入语句INPUT a;b;c ○2输入语句INPUT x=3 ○3输出语句PRINT a=4 ○4输出语句PRINT 20,3*2 A 、○1○2 B 、○2○3 C 、○3○4 D 、○4 例4、下列关于条件语句说法正确的是 ( )A 条件语句中必须有ELSE 和END IFB 条件语句中可以没有END IFC 条件语句中可以没有ELSE,但是必须有END IFD 条件语句中可以没有END IF,但必须有ELSE例5、请完成一个程序,对于函数()221(0),25(0)x x f x x x ⎧-≥⎪=⎨-<⎪⎩输入x 的值,输出相应的函数值。
【创新设计】高三数学一轮复习 10-2基本算法语句、算法案例课件 文 苏教版

________.
解析:从程序知函数y=
,因
≥4.
所以当n=2时,x取最小值4,从而函数y取得最小值17.
答案:17
在一个算式中如果出现有规律的多次相加或相乘时,可以考虑用循环语句编写 算法的伪代码,在编写时即可以用当型循环也可以用直到型循环.
【例3】 设计一个计算
的算法,写出伪代码,并
画出流程图.
第2课时 基本算法语句、算法案例
1.了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循 环 语句的含义.
2.并能用它们解决简单的问题. 3.通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的
贡献.
【命题预测】 1.条件语句和循环语句将会成为高考考查的重点,三种题型均可涉及,以中、
解析:运算结果为:1+3+5+7+9=25. 答案:25
3.(苏北四市高三第三次联考)如图,给出一个算法的伪代码,则f(-3)+f(2)= ________.
解析:根据算法可知f(-3)=4×(-3)=-12,f(2)=22=4,所以f(-3)+f(2) =-8. 答案:-8
4.下列伪代码运行的结果是________. 答案:105
所以圆的面积S2=πR2=
因此可以用顺序结构实现这一算法.
解:伪代码如下:
流程图如下:
变式1:编写一个程序,要求输入两个正数a和b的值,输出ab与ba的值.
解:解法一: 伪代码为:
解法二:伪代码为:
条件语句一般用在需要对条件进行判断的算法设计中,求分段函数的函数 值往往用条件语句编写程序.
【例2】 已知分段函数y=
5.阅读所给的伪代码,并写出a=3,b=5时的计算结果a=________. 答案:
高三一轮复习丛书48基本算法语句 算法案例

高三文科数学一轮复习 基本算法语句 算法案例 (必修3 选修1-2)- 153 -基本算法语句 算法案例【知识要点】1. 输入语句的格式:INPUT “提示内容”; 变量. 例如: INPUT “x =”; 2. 输出语句的一般格式:PRINT “提示内容”;表达式. 例如:PRINT “S=”;S 3.赋值语句的一般格式:变量=表达式. 赋值语句中的“=”称作赋值号赋值语句左边只能是变量名字,而不是表达式,右边表达式可以是一个常量、变量 或含变量的运算式。
不能利用赋值语句进行代数式的演算。
4.条件语句 5.循环语句6.求最大公约数:(1)辗转相除法;(2)更相减损术7.秦九韶算法用秦九韶算法求一般多项式f(x)= a n x n +a n-1x n-1+….+a 1x+a 0当x=x 0时的函数值, 递推公式:v 0=a n ,v k =v k -1+a n -k (k=1,2,…n) 8.进位制(1)一般地,若k 是一个大于一的整数,那么以k 为基数的k 进制可以表示为:110()110...(0,0,...,,)n n k n n a a a a a k a a a k --<<≤<,如34(5)表示5进制数。
(2)进位制间的转换:非十进制数转换为十进制数:0111011.........)(.....a k a k a k a k a a a a n n n n n n +⨯++⨯+⨯=---; 十进制数转换成非十进制数 :“除k 取余法”。
【典例解析】 例1:右边程序运行结果为( ) A .7 B .6 C .5 D .4【巩固练习】(1)“IF —THEN —ELSE ”语句 格式: IF 条件 THEN 语句1 ELSE 语句2 END IF(2)“IF —THEN ”语句格式: IF 条件 THEN 语句 END IF (1)当型循环语句 当型(WHILE 型)语句的一般格式为:WHILE 条件 循环体WEND(2)直到型循环语句 直到型(UNTIL 型)语句的一般格式为: DO 循环体LOOP UNTIL 条件高三文科数学一轮复习 基本算法语句 算法案例 (必修3 选修1-2)- 154 - 一选择题:1.如果以下程序运行后s 值是336,那么在程序中until 后面的条件应为 ( )i=8 s=1 Do s ←s ×i i = i -1Loop UntilA. 6>iB. 7>iC. 6<iD. 7<i2.用秦九韶算法求多项式a x a x a x f n n +++=-11)(时,求)( x f 需要算乘方、乘法、加 法的次数分别为 A.n n n n ,),1(21+ B.n n n ,2, C.n n ,2,0 D. n n ,,0 ( )二.填空题:3. (2)1011的十进制数:_______________;十进制数250的二进制数为:____________.4.5.用秦九韶算法求1510105)(2+++++=x x x x x x f 当2-=x 的值时. 4v = 三.解答题6.:现将某科的成绩分为3个等级:不低于80分为A ,低于60分为C ,其余为B ,试用 语句表示输出学生相应的成绩等级的算法语句。
高三数学一轮复习 第9单元 9.2 基本算法语句与算法案例课件 理 新人教A版

按照从内到外的顺序,依次计算多项式x=3时的值: v0=7,v1=7×3+6=27,v2=27×3+5=86,v3=86×3+4=262, v4=262×3+3=789,v5=789×3+2=2 369,v6=2 369×3+1=7 108, v7=7 108×3+0=21 324,
∴当x=3时,多项式的值为21 324.
9.2
基本算法语句与算法案例
(理解几种基本算法语句:输入语句、输出语句、赋值 语句、条件语句、循环语句的含义)
1.赋值语句与输入、输出语句 (1)赋值语句的一般格式是:
(2)输入语句的一般格式是:
(3)输出语句我们主要介绍PRINT,其一般格式为:
2.条件语句
(1)IF-THEN-ELSE语句的一般格式为:
(2)IF-THEN语句的一般格式是:
3.循环语句
(1)WHILE语句的一般格式:
(2)UNTIL语句的一般格式:
4.算法案例
(1)辗转相除法:辗转相除法是用于 求两数最大公约数 的一种方法,这种算法 是由欧几里得在公元前300年左右首先提出的,因而又叫 欧几里得算法 . (2)秦九韶算法 秦九韶算法是我国南宋数学家秦九韶在他的代表作 《数书九章》 中提出的一 种用于计算 多项式的值 的方法.
∴168和264的最大公约数为24.
解法二:采用更相减损术
264-168=96,168-96=72,96-72=24,72-24=48,48-24=24,
∴168和264的最大公约数为24. (2)根据秦九韶算法,把多项式改写成如下形式: f(x)=((((((7x+6)x+5)x+4)x+3)x+2)x+1)x,
依分析可知程序框图如图所示:
程序如下:
对于累加求和、累积求积问题,自然想到用循环语句设计算法,算法的设计又
高三数学一轮复习必备精品16:基本算法语句

高三数学一轮复习必备精品16:基本算法语句第16讲基本算法语句一.【课标要求】1.经历将具体问题的程序框图转化为程序语句的过程,理解几种基本算法语句――输入语句、输出语句、赋值语句、条件语句、循环语句,进一步体会算法的基本思想;2.通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献。
二.【命题走向】算法是高中数学课程中的新内容,本章的重点是算法的概念和算法的三种逻辑结构预测2021年高考对本章的考察是:以选择题或填空题的形式出现,分值在5分左右,本讲考察的热点是识别程序和编写程序三.【要点精讲】1.输入语句输入语句的格式:INPUT “提示内容”;变量例如:INPUT “x=”; x功能:实现算法的输入变量信息(数值或字符)的功能。
要求:(1)输入语句要求输入的值是具体的常量;(2)提示内容提示用户输入的是什么信息,必须加双引号,提示内容“原原本本”的在计算机屏幕上显示,提示内容与变量之间要用分号隔开;(3)一个输入语句可以给多个变量赋值,中间用“,”分隔;输入语句还可以是““提示内容1”;变量1,“提示内容2”;变量2,“提示内容3”;变量3,??”的形式。
例如:INPUT“a=,b=,c=,”;a,b,c。
2.输出语句输出语句的一般格式:PRINT“提示内容”;表达式例如:PRINT“S=”;S功能:实现算法输出信息(表达式)要求:(1)表达式是指算法和程序要求输出的信息;(2)提示内容提示用户要输出的是什么信息,提示内容必须加双引号,提示内容要用分号和表达式分开。
(3)如同输入语句一样,输出语句可以一次完成输出多个表达式的功能,不同的表达式之间可用“,”分隔;输出语句还可以是“提示内容1”;表达式1,“提示内容2”;表达式2,“提示内容3”;表达式3,??”的形式;例如:PRINT “a,b,c:”;a,b,c。
3.赋值语句赋值语句的一般格式:变量=表达式赋值语句中的“=”称作赋值号作用:赋值语句的作用是将表达式所代表的值赋给变量;要求:(1)赋值语句左边只能是变量名字,而不是表达式,右边表达式可以是一个常量、变量或含变量的运算式。
高三数学一轮复习第9知识块第2讲基本算法语句与算法案例课件

答案:B
4.二进制的数1 011化为十进制的数为________,十进制的数1 011化为二进 制的数为________. 解析:1 011(2)=1×23+0×22+1×21+1×20=8+3=11.
故1 011(10)=1 111 110 011(2). 答案:11 1 111 110 011
第2讲 基本算法语句与算法案例
【考纲下载】
理解几种基本算法语句——输入语句、输出语句、赋值语句、条 件语句、循环语实现算法的 输入 和 输出 功能.其一般格式
为:
输入语句: INPUT“提示内容”;变量
.
输出语句: PRINT“提示内容”;表达式 .
A.
B.
C.
D.
答案:B
2.当a=3时,下面的程序段输出的结果是( )
A.9
B.3
C.10
D.6
解析:根据条件3<10,故y=2×3=6.
答案:D
3.用辗转相除法计算60与48的最大公约数时,需要做的除法次数是( )
A.1
B.2
C.3
D.4
解析:∵60=48×1+12,48=12×4+0,
故只需要两步计算.
下,用辗转相除法求最大公约数步骤较少,用更相减损术步骤较多,但运算简易, 解题时要灵活运用.
2.求一元n次多项式的值用秦九韶算法,首先要对n次多项式改写,然后由内向外 逐次计算,要确保中间结果的准确性.非十进制之间的转化是以十进制数为桥
梁.
【例4】 (1)利用辗转相除法或更相减损术求168和264的最大公约数. (2)用秦九韶算法求多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x当x=3 时的值. 思维点拨:(1)264作为大数,168作为小数,利用辗转相除法或更相减损 术都可以求两数的最大公约数. (2)根据秦九韶算法原理,将所给多项式改写,然后由内到外逐次计算即 可.
高三数学第一轮复习专题---算法与程序框图、基本算法语句
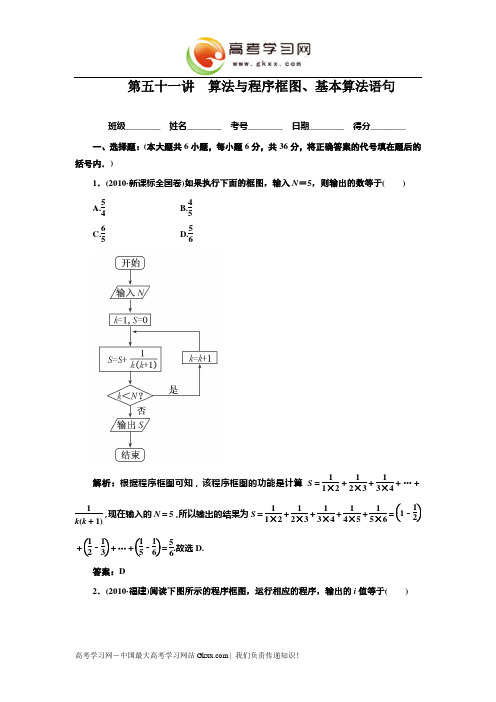
第五十一讲 算法与程序框图、基本算法语句班级________ 姓名________ 考号________ 日期________ 得分________ 一、选择题:(本大题共6小题,每小题6分,共36分,将正确答案的代号填在题后的括号内.)1.(2010·新课标全国卷)如果执行下面的框图,输入N =5,则输出的数等于( ) A.54 B.45 C.65D.56解析:根据程序框图可知,该程序框图的功能是计算S =11×2+12×3+13×4+…+1k (k +1),现在输入的N =5,所以输出的结果为S =11×2+12×3+13×4+14×5+15×6=⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫15-16=56.故选D. 答案:D2.(2010·福建)阅读下图所示的程序框图,运行相应的程序,输出的i 值等于( )A.2 B.3C.4 D.5解析:当i=1时,a=1×2=2,s=0+2=2,i=1+1=2;由于2>11不成立,故a=2×22=8,s=2+8=10,i=2+1=3;由于10>11不成立,故a=3×23=24,s=10+24=34,i =3+1=4;34>11成立,故输出的i=4.答案:C3.(2010·天津)阅读如图所示的程序框图,运行相应的程序,则输出s的值为()A.-1B.0 C.1D.3解析:第一次执行s=1×(3-1)+1=3,i=2;第二次执行s=3×(3-2)+1=4,i=3;第三次执行s=4×(3-3)+1=1,i=4;第四次执行s=1×(3-4)+1=0;i=5>4,结束循环,故输出的结果是0,选B.答案:B4.(2010·辽宁)如果执行右面的程序框图,输入n=6,m=4,那么输出的p等于()A.720 B.360C.240 D.120解析:k=2,p=12;k=3,p=60;k=4,p=360,k=4时不满足k<m,所以输出的p=360.答案:B5.如图是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为()A.S=S*(n+1) B.S=S*x n+1C.S=S*n D.S=S*x n解析:由题意可知,输出的是10个数的乘积,故循环体应为S=S*x n,所以选D.答案:D6.(2010·天津)阅读如图所示的程序框图,若输出s的值为-7,则判断框内可填写()A.i<3? B.i<4?C.i<5? D.i<6?解析:由题意可知i=1,s=2→s=1,i=3→s=-2,i=5→s=-7,i=7,因此判断框内应为i<6?.答案:D二、填空题:(本大题共4小题,每小题6分,共24分,把正确答案填在题后的横线上.)7.(2010·安徽)如图所示,程序框图(算法流程图)的输出值x=________.解析:当x =1时,执行x =x +1后x =2;当x =2时,执行x =x +2后x =4,再执行x =x +1后x =5;当x =5时,执行x =x +1后x =6;当x =6时,执行x =x +2后x =8,再执行x =x +1后x =9;当x =9时,执行x =x +1后x =10;当x =10时,执行x =x +2后x =12,此时12>8,因此输出的x 的值为12.答案:128.(2010·山东)执行如图所示的程序框图,若输入x =4,则输出y 的值为________.解析:当x =4时,y =1,|1-4|=3>1,此时x =1; 当x =1时,y =-12,⎪⎪⎪⎪-12-1=32>1,此时x =-12;当x =-12时,y =-54,⎪⎪⎪⎪-54+12=34<1, 故此时输出y 的值为-54.答案:-549.定义某种运算S =a ⊗b ,运算原理如图所示.则式子:(2tan 5π4)⊗lne +lg100⊗(13)-1的值是________.解析:原式=2⊗1+2⊗3=2×(1+1)+2×(3-1)=8. 答案:810.(2010·广东)某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n 位居民的月均用水量分别为x 1,…,x n (单位:吨).根据如图所示的程序框图,若n =2,且x 1,x 2分别为1,2,则输出的结果s 为________.解析:i =1时,s 1=0+x 1=1,s 2=0+x 21=1,s =11×⎝⎛⎭⎫1-11×12=0;i=2时,s1=1+x2=3,s2=1+x22=5,s=12×⎝⎛⎭⎫5-12×32=14;i=3时,结束循环,输出s=1 4.答案:1 4三、解答题:(本大题共3小题,11、12题13分,13题14分,写出证明过程或推演步骤.)11.如图,设计算法求底面边长为4,侧棱长为5的正四棱锥的侧面积及体积,并画出相应的程序框图.解:解法一:先求体积,V=13Sh,S=a2,高h=l2-R2,R=22a,斜高h′=l2-a24,从而求得S侧=4×12a·h′=2ah′.由解法一可得算法一:S1 a=4,l=5;S2 R=22a;S3 h=l2-R2,S=a2;S4 V=13Sh;S5 输出V;S6 h′=l2-a2 4;S7 S侧=2ah′;S8 输出S侧.解法二:推导出利用a和l表达的侧面积及体积公式,然后代入求解.由解法二得算法二:S1 a=4,l=5;S3 V=13a2l2-a22;S4 输出S侧,V.算法一程序框图如图1;算法二程序框图如图2.评析:利用公式求解问题,先写出公式,看公式中的条件是否满足,若不满足,先求出需要的量,看要求的量需根据哪些条件求解,需要的条件必须先输入,或将已知条件全部输入,求出未知的量,然后将公式中涉及的量全部代入求值即可.利用算法和程序框图,能够规范思维,可以锻炼书面表达的能力,先求什么,后求什么,无论是用算法表达,还是用程序框图表达,都是一目了然,非常清晰的,所以把这种方法用于我们平时的做题会使解题的思路简练、易懂、有逻辑性.12.2008年某地森林面积为1000 km2,且每年增长5%,到哪一年该地森林面积超过2000 km2.请设计一个程序,并画出程序框图.解:需要一个累加变量和一个计数变量,将累加变量的初值设为1000,计数变量从0开始取值.程序框图为:程序为:13.用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1当x=2时的值.分析:利用秦九韶算法一步一步地代入运算,注意本题中有几项不存在,在计算时,我们应该将这些项添加上,比如含有x3这一项可看作0·x3.解:根据秦九韶算法,把多项式改写成如下形式f(x)=8x7+5x6+0·x5+3·x4+0·x3+0·x2+2x+1=((((((8x+5)x+0)x+3)x+0)x+0)x+2)x+1.v0=8;v1=8×2+5=21;v2=21×2+0=42;v3=42×2+3=87;v4=87×2+0=174;v5=174×2+0=348;v6=348×2+2=698;v7=698×2+1=1397.∴当x=2时,多项式的值为1397.评析:秦九韶算法是多项式求值的优秀算法,秦九韶算法的特点:(1)化高次多项式求值为一次多项式求值;(2)减少了运算次数,提高了效率;(3)步骤重复执行,容易用计算机实现.利用秦九韶算法计算多项式的值关键是能正确地将所给多项式改写,然后由内向外逐次计算,由于后项计算用到前项的结果,故应认真、细心,确保中间结果的准确性.若在多项式中有几项不存在时,可将这些项的系数看成0,即把这些项看做0·x n.高考学习网-中国最大高考学习网站 | 我们负责传递知识!。
高考数学 15.2 基本算法语句与算法案例

15、算法初步15.2 基本算法语句与算法案例【知识网络】1.理解用伪代码表示的几种基本算法语句:赋值语句、输入语句、输出语句、条件语句、循环语句。
2.能用自然语言、流程图和伪代码表述算法,会用“While循环”和“For循环”语句或GoTo语句实施循环(注意:优先使用While和For语句,尽量少用GoTo语句)。
【典型例题】[例1](1)下列问题所描述出来的算法,其中不包含条件语句的为()A.读入三个表示三条边长的数,计算三角形的面积B.给出两点的坐标,计算直线的斜率C.给出一个数x,计算它的常用对数的值D.给出三棱锥的底面积与高,求其体积(2)设计一个计算1×3×5×7×9×11×13的算法.图中给出了程序的一部分,则在横线①上不能填入下面的那一个数?答:()A.13B.13.5C.14D.14.5(3)若mod(m,3)=1,则m的取值不可以是()A.2005 B.2006 C.2008 D.2020(4)下面的表述:①6←p;②t←3×5+2;③b+3←5;④p←((3x+2)-4)x+3;⑤a←a3;⑥x,y,z←5;⑦ab←3;⑧x ←y+2+x .其中正确表述的赋值语句有 . (注:要求把正确的表述全填上)(5)下面程序的运行结果为4[例2] 某百货公司为了促销,采用打折的优惠办法:每位顾客一次购物①在100元以上者(含100元,下同),按九五折优惠; ②在200元以上者,按九折优惠; ③在300元以上者,按八五折优惠; ④在500元以上者,按八折优惠. 试写出算法、画出流程图、伪代码,以求优惠价.[例3] 定义运算“!”为:n!=1×2×3×…×n ,其中n 为正整数,并且读作“n 的阶乘”,例如,5!=1×2×3×4×5=120,10!=9!×10= 3628800. 计算2007!写出算法分析与伪代码,并画出流程图。
2020届高三数学一轮复习强化训练精品――基本算法语句算法案例

. 要求输入 l 的值,输出
x 1, 例 2 〔14 分〕分段函数 y= 0,
x 1, 的函数值,并画出流程图 . 解 伪代码如下: Read x If x< 0 Then
y ← - x +1 Else
If x =0 Then y← 0
Else y ←x+1
End If End If Print y
⑦打印 n, z;
⑧程序终止 .
由语句⑦打印出的数值为
、.
答案 8 7 682 2. 按照下面的算法进行操作:
S1 x←2ቤተ መጻሕፍቲ ባይዱ35
S2 y←Int 〔x〕
S3 Print y
最后输出的结果是
.
答案 2
3. 读下面的伪代码:
Read x
If x > 0 Then
Print x
Else
Print - x
End If
〔1〕图 1 的运行结果为 〔2〕图 2 的运行结果为 答案 〔1〕7 〔2〕6
; .
图1
图2
4. 以下给出的是用条件语句编写的一个伪代码,该伪代码的功能是
.
Read x If x< 3 Then
y← 2× x Else
If x> 3 Then y← x2-1
Else y← 2
End If End If Print y End
2020 届高三数学一轮复习强化训练精品 ――基本算法语句算 法案例
基础自测
1. 下面是一个算法的操作讲明:
①初始值为 n←0, x ←1, y← 1, z ←0;
②n← n+1;
③x← x +2;
④y← 2y;
⑤z← z +xy ;
高三数学一轮复习教案:算法案例 必修三

必修Ⅲ—03 算法案例1、所谓辗转相除法,就是对于给定的两个数,用 除以 。
若余数不为零,则将 构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时的 就是原来两个数的最大公约数。
2、更相减损术是我国古代数学专著 中介绍的一种求两数最大公约数的方法。
其过程是:对于两个给定的两数,用 , 接着把所得的 和 比较,并以大数减小数,继续这个操作,直到所得的数 为止,则这个数就是所求的最大公约。
3、秦九韶算法是我国南宋数学家 在他的代表作 中提出的一种用于计算一元n 次多项式的值的方法。
()1110n n n n a x a x a x a --=++++把一个n 次多项式f x 改写成如下形式:()()()()()()()1110121102312101210n n n n n n n n n n n n n n n a x a x a x a a x a x a x a a x a x a x a x a a x a x a x a x a ----------=++++=++++=+++++==++++f x 求多项式的值时,首先计算最内层括号内一次多项式的值,即0n v a = ,1v = ,2v = ,3v =,n v = 。
4、进位制:是人们为了计数和运算方便而约定的记数系统.“满十进一”就是十进制,“满二进一”就是二进制,“满k 进一”就是 进制,几进制的基数就是几。
k 进制数的基数是 。
在k 进制中,共有 个数字符号。
他们是 。
5、把k 进制化成十进制数的运算规则是()1210n n k a a a a a -=6、将一个十进制数a 化为等值k 进制数b 的算法步骤(除k 取余法):第一步:将给定的十进制整数除以基数 , 便是等值的k 进制数b 的最 位。
第二步:将上一步的 再除以基数k , 便是等值的k 进制数b 的 位。
第三步:重复第二步,直到最后所得的 等于0为止。
各次除得到的便是k 进制数b 的各位数,最后一次的余数是 位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010届高三数学一轮复习强化训练精品――基本算法语句、算法案例
1.下面是一个算法的操作说明: ①初始值为n ←0,x ←1,y ←1,z ←0; ②n ←n +1; ③x ←x +2; ④y ←2y ; ⑤z ←z +xy ;
⑥如果z >7 000,则执行语句⑦;否则回到语句②继续执行; ⑦打印n ,z ; ⑧程序终止.
由语句⑦打印出的数值为 、 . 答案 8 7 682
2.按照下面的算法进行操作: S1 x ←2.35 S2 y ←Int (x ) S3 Print y
最后输出的结果是 . 答案 2
3.读下面的伪代码: Read x If x >0 Then
Print x Else
Print -x End If
这个伪代码表示的算法的功能是 . 答案 输入一个数,输出其绝对值
4.下面是一个算法的伪代码.如果输入的x 的值是20,则输出的y 的值是 .
答案
150
基础自测
5.与下列伪代码对应的数学表达式是 . Read n e ←0 S ←1
For I From 1 To n Step 1 S ←S ×I e ←e +1/S End for Print e 答案 S =1+!21+!31+…+!
1n
例1 设计算法,求用长度为l 的细铁丝分别围成一个正方形和一个圆时的面积.要求输入l 的值,输出 正方形和圆的面积. 解 伪代码如下: Read l S 1←(l ×l )/16 S 2←(l ×l )/(4×3.14) Print S 1 Print S 2 End
例2 (14分)已知分段函数y =⎪⎩⎪
⎨⎧>+=<+-0
,10,
00
,
1x x x x x ,编写伪代码,输入自变量x 的值,输出其相应 的函数值,并画出流程图. 解 伪代码如下:
流程图如图所示:
Read x If x <0 Then y ←-x +1 Else
If x =0 Then
y ←0 Else
y ←x +1 End If End If Print y End
7分
例3 编写一组伪代码计算1+21+3
1
+…+00011,并画出相应的流程图.
解 伪代码如下: i ←1 S ←0
While i ≤1 000 S ←S +1/i i ←i +1 End While Print S End
流程图如图所示:
1.下面的表述: ①6←p ; ②t ←3×5+2; ③b +3←5;
④p ←((3x +2)-4)x +3; ⑤a ←a 3
; ⑥x ,y ,z ←5; ⑦ab ←3; ⑧x ←y +2+x .
其中正确表述的赋值语句有 . (注:要求把正确的表述的序号全填上) 答案 ②④⑤⑧
2.某百货公司为了促销,采用打折的优惠办法: 每位顾客一次购物
①在100元以上者(含100元,下同),按九五折优惠; ②在200元以上者,按九折优惠; ③在300元以上者,按八五折优惠; ④在500元以上者,按八折优惠.
试写出算法、画出流程图、伪代码,以求优惠价. 解 设购物款为x 元,优惠价为y 元, 则优惠付款公式为y =⎪⎪⎪⎩⎪
⎪⎪
⎨⎧≥<≤<≤<≤<500
,
8.0500
300,85.0300200,
9.0200100,95.0100,
x x x x x x x x x x 算法分析: S1 输入x 的值;
S2 如果x <100,输出y ←x ,否则转入S3; S3 如果x <200,输出y ←0.95x ,否则转入S4; S4 如果x <300,输出y ←0.9x ,否则转入S5; S5 如果x <500,输出y ←0.85x ,否则转入S6; S6 输出y ←0.8x .
3.某玩具厂1996年的生产总值为200万元,如果年生产增长率5%,计算最早在哪一年生产总值超过300万元.试写出伪代码.
解 伪代码如下: n ←1 996 p ←1.05 a ←200 While a ≤
300
a←a×p
n←n+1
End While
Print n
End
一、填空题
1.伪代码
a←3
b←5
Print a+b
的运行结果是 .
答案8
2.为了在运行下面的伪代码后输出y=16,应输入的整数x的值是 .
Read x
If x<0 Then
y←(x+1)2
Else
y←1-x2
End If
Print y
答案-5
3.写出下列伪代码的运行结果.
图1 图2 (1)图1的运行结果为;
(2)图2的运行结果为 .
答案(1)7 (2)6
4.以下给出的是用条件语句编写的一个伪代码,该伪代码的功能是 .
答案 求下列函数当自变量输入值为x 时的函数值f (x ),其中f (x )=⎪⎩⎪
⎨⎧>-=<3
,
13,
23,22
x x x x x 5.下面是一个算法的伪代码,其运行的结果为 .
答案 2 500
6.如图所示,该伪代码表示的作用是 .
答案 求三个数中最大的数
7.如图(1)是某循环流程图的一部分,若改为图(2),则运行过程中I 的值是
.
答案 1
8.图中算法执行的循环次数为 .
答案 333 二、解答题
9.用条件语句描述下面的算法流程图.
解 Read x If x <0 Then
y ←2×x +3 Else
If x >0 Then
y ←2×x -5 Else
y ←0 End If End If Print y
End
10.请设计一个问题,使得该问题的算法如已知的伪代码所示.
解 已知圆O 内有一个边长为a 的圆的内接正方形,求圆的面积比正方形的面积大多少? 11.有一个算法如下: S1 输入x ; S2 判断x >0
是:z ←1;否:z ←-1; S3 z ←1+z ; S4 输出z .
试写出上述算法的流程图及相应的伪代码. 解
12.一个小朋友在一次玩皮球时,偶然发现一个现象:球从某高度落下后,每次都反弹回原高度的3
1
,再落下,再反弹回上次高度的
3
1
,如此反复.假设球从100 cm 处落下,那么第10次下落的高度是多少?在第10次落地时共经过多少路程?试用伪代码表示其算法. 解 伪代码如图所示:。
