重庆市2011年初中毕业暨高中招生考试数学试数学试卷及答案
重庆市2011年初中毕业暨高中招生考试
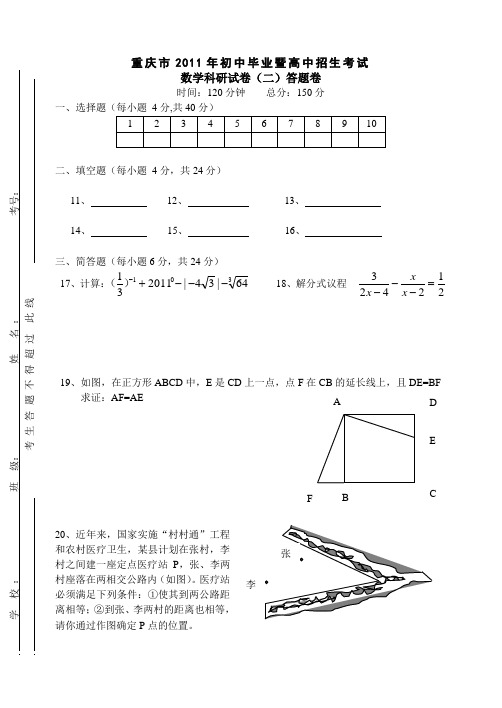
重庆市2011年初中毕业暨高中招生考试数学科研试卷(二)答题卷时间:120分钟 总分:150分一、选择题(每小题 4分,共40分)二、填空题(每小题 4分,共24分)11、 12、 13、14、 15、 16、三、简答题(每小题6分,共24分)17、计算:30164|34|201131---+-)( 18、解分式议程 212423=---x x x19、如图,在正方形ABCD 中,E 是CD 上一点,点F求证:AF=AE20、近年来,国家实施“村村通”工程和农村医疗卫生,某县计划在张村,李村之间建一座定点医疗站P ,张、李两村座落在两相交公路内(如图)。
医疗站必须满足下列条件:①使其到两公路距离相等;②到张、李两村的距离也相等,请你通过作图确定P 点的位置。
B FCD E四、简答题 (每小题10分,共40分)21、化简求值:11)1152-+÷----a a a a a (,其中13-=a22、如图,直线AD 交坐标轴于B 和C ,交双曲线于A 和D ,OB =OC =2,AB =BC =CD1) 求直线和双曲线的解析式,2) 请你连接AO 和DO ,并求出△AOD 的面积。
23、科技创新必须从娃娃抓起,我校为了培养小能人,小发明家,开展了全校的小制作比赛,作品上交时间为2010年3月1日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每组的件数进行统计,绘制成如图所示的统计图。
已知从左到右各矩形的高度比为2:3:4:6:1,其中第四小组有2人交了1件作品,5人交了2件作品,2人交了3件作品。
请你回答:1)本次活动共有 件作品参赛;其中第四小组平均每人交了 件作品; 2)经评比,第一组和第五组分别有3件和9件作品获奖,那么第一组和第五组的获奖率分别为 和 ;3)小制作评比结束后,组委会评出了4件最优秀的作品A 、B 、C 、D ,决定从中选出两件进行全校展示,请用树状图列表法求出刚好展示作品A 和作品C 的概率。
2011中考重庆市数学卷

重庆市2011年初中毕业暨高中招生考试数学试题(全卷共五个大题,满分150分,考试时间120分钟)参考公式:抛物线的2(0)y ax bx c a =++≠顶点坐标为24(,)24b ac b a a --,对称轴公式为2b x a=-。
一.选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1.在-6,0,3,8这四个数中,最小的数是( )A . -6 B .0 C .3 D . 8 2.计算()23a的结果是( ) A . a B . a 5 C .a 6D . 9a3.下列图形中,是中心对称图形的是( )4. 如图,AB ∥CD ,︒=∠90C ,︒=∠60CAD ,则∠BAD 的度数等于( ) 5.下列调查中,适宜采用抽样方式的是( ) A . 调查我市中学生每天体育锻炼的时间 B . 调查某班学生对“五个重庆”的知晓率 C . 调查一架“歼20”隐形战机各零部件的质量 D . 调查广州亚运会100米参赛运动员兴奋剂的使用情况6.如图,⊙O 是△ABC 的外接圆,∠OCB =400,则∠A 的度数等于( )A .60°B . 50°C .45°D .40°A.BCD7. 已知抛物线2(0)y ax bx c a =++≠在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( )A .0>aB . 0<bC .0<cD . 0>++c b a8.为了建设社会主义新农村,我市积极推进“行政村通畅工程”。
张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按完成了两村之间的道路改造。
下面能反映该工程尚未改造的道路里程y (公里)与时间x (天)的函数关系的大致图象是( )9.下列图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,……则第⑥个图形中平行四边形的个数为( )A .55B . 42C . 41D . 29 10. 如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE 。
2011重庆中考数学2篇

2011重庆中考数学2011重庆中考数学试卷,共分为两篇。
每篇字数要求为3000字,接下来将分别介绍这两篇试题内容。
第一篇:数与代数1. 下列四个数的分数值从小到大依次是多少?A. 0.3B. 1/3C. \sqrt{3}D. 0.3333...答案:B < A < D < C2. 已知a,b,c是正数,且满足a+b+c=6. 若a^2+b^2+c^2=14,则a+b的最大值为多少?答案:当a=b=1, c=4时,a+b的值最大,即a+b=2+2=4。
3. 如果一个数的20%等于另一个数的30%,这两个数的比值是多少?答案:设这两个数分别为x和y,则可以列出等式0.2x=0.3y。
根据等式,可以得出比值x:y=3:2。
4. 已知函数f(x)的定义域为R,且对于任意实数x,有f(x+3)=2f(x)-1。
若f(0)=2,则f(-21)的值为多少?答案:将x=0代入已知等式,则f(3)=2f(0)-1=2×2-1=3。
类似地,可以得出f(6)=2f(3)-1=2×3-1=5,f(9)=2f(6)-1=2×5-1=9,依次类推,可以得出f(0)=2,f(3)=3,f(6)=5,f(9)=9。
由此可得出规律,当x为3的倍数时,f(x)的值也为3的倍数。
因为-21是3的倍数,所以f(-21),其值为3的倍数,即答案为9。
5. 在空间直角坐标系中,下列说法中正确的是:A. 全部的点都在一条直线上B. 存在一个点在x轴上,其他点在y轴上C. 至少有三个点在同一个平面上D. 每一个点的坐标都是整数答案:C第二篇:几何与概率1. 如图,ABCD为一个平行四边形,其中AE=BC,R为AB的中点,连接RC,交AD于点F。
则比值BF:AF为多少?答案:根据平行四边形的性质可知,AE平行于BC,AF平行于BC,所以△ABF和△EDC是相似的。
根据相似三角形的性质,可得出BF:AF=CD:ED=DC:DC=1:1。
2011重庆江津中考数学

重庆市江津区2011年初中毕业生学业暨高中招生考试数 学 试 卷(本卷共四个大题 满分:150分 考试时间:120分钟)温馨提示:试卷各题答案用钢笔或圆珠笔书写在答题卷上,不得在试卷上直接作答. 一、选择题 (本大题共10个小题,每小题4分,共40分)每个小题的下面给出了代号为A 、B 、C 、D 四个答案,其中只有一个答案是正确的,请将正确答案的代号填到答题卷上. 1.( 2011重庆江津, 1,4分)2-3的值等于( ) A.1 B.-5 C.5 D.-1· 【答案】D ·2. ( 2011重庆江津, 2,4分)下列式子是分式的是( ) A.2x B.1+x x C. y x +2 D. 3x 【答案】B. 3. ( 2011重庆江津, 3,4分)已知3是关于x 的方程2x -a=1的解,则a 的值是( ) A.-5 B.5 C.7 D.2 【答案】B · 4·( 2011重庆江津, 4,4分)直线y=x -1的图像经过象限是( ) A.第一、二、三象限 B.第一、二、四象限 C.第二、三、四象限 D.第一、三、四象限【答案】D5. ( 2011重庆江津, 5,4分)下列说法不正确...是( ) A.两直线平行,同位角相等; B 两点之间直线最短C.对顶角相等;D.半圆所对的圆周角是直角· 【答案】B ·6. ( 2011重庆江津, 6,4分)已知如图,A 是反比例函数xky =的图像上的一点,AB ⊥x 轴于点B,且△ABO 的面积是3,则k 的值是( ) A.3 B.-3 C.6 D.-6·第6题图… A 1AA 2 A 3 BB 1 B 2 B 3C 2 C 1 C 3D 2 D 1 D 3 第10题图【答案】C ·7. ( 2011重庆江津, 7,4分)某课外学习小组有5人,在一次数学测验中的成绩分别是120、100、135、100、125,则他们的成绩的平均数和众数分别是( )A.116和100B.116和125C.106和120D.106和135· 【答案】A ·8. ( 2011重庆江津, 8,4分)已知如图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB 、CD 交于O 点,对于各图中的两个的两个三角形而言,下列说法正确的是( )A.都相似B.都不相似C.只有(1)相似D.只有(2)相似【答案】A ·9. ( 2011重庆江津, 9,4分)已知关于x 的一元二次方程(a -1)x 2-2x+1=0有两个不相等的实数根,则a 的取值范围是( )A.a<2 B,a>2 C.a<2且a ≠1 D.a<-2·【答案】C ·10. ( 2011重庆江津, 10,4分)如图,四边形ABCD 中,AC=a,BD=b,且AC ⊥BD,顺次连接四边形ABCD 各边中点,得到四边形A 1B 1C 1D 1,再顺次连接四边形A 1B 1C 1D 1各边中点,得到四边形A 2B 2C 2D 2……,如此进行下去,得到四边形A n B n C n D n .下列结论正确的有( ) ①四边形A 2B 2C 2D 2是矩形; ②四边形A 4B 4C 4D 4是菱形; ③四边形A 5B 5C 5D 5的周长4b a +; ④四边形A n B n C n D n 的面积是12+n abA.①②B.②③C.②③④D.①②③④ 【答案】C ·二、填空题(本大题共10个小题,每小题4分,共40分)请将正确答案直接填在答题卷上.11. ( 2011重庆江津, 11,4分)今年长江中下游旱情严重,某地村民吃水都成问题,(1) A B C DO4 36 8(2)第8题图一消防大队决定支援灾区,为灾区人民送去饮用水13万吨,用科学记数法表示为____________吨.【答案】1.3×10512. ( 2011重庆江津, 12,4分)因式:2x 3-x 2=______________. 【答案】x 2(2x-1)·13. ( 2011重庆江津, 13,4分)在梯形ABCD 中,AD ∥BC,中位线长为5,高为6,则它的面积是___________.【答案】30·14. ( 2011重庆江津, 14,4分)函数21-=x y 中x 的取值范围是___________.【答案】x >2· 15. ( 2011重庆江津, 15,4分)在Rt △ABC 中,∠C=90º,BC=5,AB=12,sinA=_________. 【答案】125· 16·( 2011重庆江津, 16,4分)已知如图,在圆内接四边形ABCD 中,∠B=30º,则∠D=____________.【答案】150°·17. ( 2011重庆江津, 17,4分)在一个袋子里装有10个球,6个红球,3个黄球,1个绿球,这些球除颜色外、形状、大小、质地等完全相同,充分搅匀后,在看不到球的条件下,随机从这个袋子中摸出一球,不是红球....的概率是__________. 【答案】52· 18. ( 2011重庆江津, 18,4分)将抛物线y=x 2-2x 向上平移3个单位,再向右平移4个单位等到的抛物线是_______.【答案】y=(x-5)2+2 或 y=x 2-10x+27· 19·( 2011重庆江津, 19,4分)如图,点A 、B 、C 在直径为32的⊙O 上,∠BAC=45º,则图中阴影的面积等于______________,(结果中保留π).第16题图第19题图【答案】2343-π 20. ( 2011重庆江津, 20,4分)如图,在平面直角坐标系中有一矩形ABCD,其中(0,0),B(8,0),C(0,4,) 若将△ABC 沿AC 所在直线翻折,点B 落在点E 处,则E 点的坐标是__________.【答案】(245,325) 三、解答题(本大题共3个小题,21小题18分,22、23小题各10分,共38分)21.(18分)计算(每小题6分)(1) ( 2011重庆江津, 21(1),6分)( 31)-1-∣-2∣+2sin30º +(23-)º 【答案】(1) 原式=3-2+2×21+1=3·(2) ( 2011重庆江津, 21(2),6分)解不等式组⎩⎨⎧<->+13223x xx 并把解集在数轴上表示出来· 【答案】(2)由①得,x >-2; 由②得x <4. ∴原不等式组的解集是-2<x <4· 在数轴上表示为 :(3) ( 2011重庆江津, 21(3),6分)先化简,再求值:)121(212-+÷+-x x x ,其中31=x · 【答案】(3)原式=2212)1)(1(+--÷+-+x x x x x =)1(22)1)(1(+-+⨯+-+x x x x x =1-x ·把31=x 代入得 原式=1-31=32· 22. ( 2011重庆江津, 22,10分)在△ABC 中,AB=CB,∠ABC=90º,F 为AB 延长线上一点,点E 在BC 上,且AE=CF.(1)求证:Rt △ABE ≌Rt △CBF;-2 4(2)若∠CAE=30º,求∠ACF 度数.【答案】(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.在Rt △ABE 和Rt △CBF 中,∵AE=CF, AB=BC, ∴Rt △ABE ≌Rt △CBF(HL)(2)∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠ACB=45°. ∵∠BAE=∠CAB-∠CAE=45°-30°=15°.由(1)知 Rt △ABE ≌Rt △CBF , ∴∠BCF=∠BAE=15°, ∴∠ACF=∠BCF+∠ACB=45°+15°=60°.23. ( 2011重庆江津, 23,10分)A 、B 两所学校在一条东西走向公路的同旁,以公路所在直线为x 轴建立如图所示的平面直角坐标系,且点A 的坐标是(2,2),点B 的坐标是(7,3).(1)一辆汽车由西向行驶,在行驶过程中是否存在一点C,使C 点到A 、B 两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.(2)若在公路边建一游乐场P,使游乐场到两校距离之各最小,通过作图在图中找出建游乐场的位置,并求出它的坐标.【答案】(1)存在满足条件的点C: 作出图形,如图所示,作图略;(2)作出点A 关于x 轴的对称点A /(2,-2), 连接A /B ,与x 轴的交点即为所求的点P. 设A /B 所在的直线的解析式为: y=kx+b, 把A /(2,-2), B(7,3)分别代入得:⎩⎨⎧-=+=+2237b k b k 解得:⎩⎨⎧-==41b k ·所以: y=x-4·当y=0时,x=4,所以交点P 为(4,0)·四、解答题 (本在题共3个掌上小题,第24、25小题各10分,共32分)24. ( 2011重庆江津, 24,10分)在“传箴言”活动中,某党支部对全体党员在一个B CEF第22题图.A(2, 2).B(7, 3) y O x第23题图月内所发箴言条数情况进行了统计,并制成了如下两幅不完整的统计图.(1)求该支部党员在这一个月内所发箴言的平均条数是多少?并将该条形统计图补充完整; (2)如果发了三条箴言的党员中有两位男党员,发了四条箴言的党员有两位女党员,在发了三条箴言和四条箴言的党员中分别选出一位参加区委组织的“传箴言”活动总结会,请你用列表或树状图的方法,求出所选两位党员恰好是一男一女的概率.【答案】(1)由图形可知,总人数为:3÷20﹪=15(人) 发两条的人数:15-2-5-3-2=3(人)· 图形如图平均条数=(1×2+2×3+3×5+4×3+5×2)÷15=3(条)· (2)树状图∴P (一男一女)=157·25. ( 2011重庆江津, 25,10分)已知双曲线xk y与抛物线y=zx 2+bx+c 交于A(2,3)、条数第24题图条数四条 三条男 男 男 男 男 男 男 女 女 女 女 女 女 女 女 女 女 女 女 女B(m,2)、c(-3,n)三点.(1)求双曲线与抛物线的解析式;(2)在平面直角坐标系中描出点A 、点B 、点C,并求出△ABC 的面积,【答案】(1)把点A(2,3)代入xky =得 :k=6· ∴反比例函数的解析式为:xy 6=· 把点B(m,2)、C(-3,n)分别代入xy 6=得: m=3,n=-2·把A(2,3)、B(3,2)、C(-3,-2)分别代入y=ax 2+bx+c 得:⎪⎩⎪⎨⎧-=+-=++=++239239324c b a c b a c b a 解之得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=33231c b a ∴抛物线的解析式为:y=-332312++x x · (2)描点画图 S △ABC =21(1+6)×5-21×1×1-21×6×4=1221235--=5· 26. ( 2011重庆江津, 26,12分) 在“五个重庆”建设中,为了提高市民的宜居环境,某区规划修建一个文化广场(平面图形如图所示),其中四边形ABCD 是矩形,分别以AB 、BC 、CD 、DA 边为直径向外作半圆,若整个广场的周长为628米,高矩形的边长AB=y 米,BC=x 米.(注:取π=3.14)(1)试用含x 的代数式表示y;(2)现计划在矩形ABCD 区域上种植花草和铺设鹅卵石等,平均每平方米造价为428元,在四个半圆的区域上种植草坪及铺设花岗岩,平均每平方米造价为400元; ①设该工程的总造价为W 元,求W 关于x 的函数关系式;②若该工程政府投入1千万元,问能否完成该工程的建设任务?若能,请列出设计方案,若第25题图 第25题图不能,请说明理由?③若该工程在政府投入1千万元的基础上,又增加企业募捐资金64·82万元,但要求矩形的边BC 的长不超过AB 长的三分之二,且建设广场恰好用完所有资金,问:能还完成该工程的建设任务?若能,请列出所有可能的设计方案,若不能,请说明理由·【答案】(1) 由题意得πy+πx=6·28∵π=3.14 ∴3.14y+3.14x=628.∴x+y=200.则 y=200-x; (2) ①w=428xy+400π(2y )2+400π(2x )2=428x(200-x)+400×3.14×4)200(2x -+400×3.14×42x=200x 2-40000x+12560000;②仅靠政府投入的1千万不能完成该工程的建设任务,其理由如下:由①知 w=200(x-100)2+1.056×107>107, 所以不能; ③由题意得 x ≤32y, 即x ≤32(200-x) 解之得 x ≤80 ∴0≤x ≤80.又根据题意得 w=200(x-100)2+1.056×107=107+6.482×105整理得 (x-100)2=441 解之得 x 1=79, x 2=121 (不合题意舍去) ∴只能取 x=79, 则y=200-79=121所以设计的方案是: AB 长为121米,BC 长为79米,再分别以各边为直径向外作半圆·ABC D 第26题。
2011重庆市中考数学及答案

重庆市2011年初中毕业暨高中招生考试数学试题(本卷共五个大题,满分150分,考试时间120分钟)参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-b2a,4ac-b24a),对称轴公式为x=-b2a.一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1.(2011四川重庆,1,4分)在-6,0,3,8 这四个数中,最小的数是( ) A.-6 B.0 C.3 D.8【答案】A2.(2011四川重庆,2,4分)计算(a3)2的结果是( )A.a B.a5C.a6 D.a9【答案】C3.(2011四川重庆,3,4分)下列图形中,是中心对称图形的是( )A.B.C.D.【答案】B4.(2011四川重庆,4,4分)如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )A.60°B.50°C.45°D.40°【答案】D5 .(2011四川重庆,5,4分)下列调查中,适宜采用抽样调查方式的是( )A.调查我市中学生每天体育锻炼的时间B.调查某班学生对“五个重庆”的知晓率C.调查一架“歼20”隐形战机各零部件的质量D.调查广州亚运会100米决赛参赛运动员兴奋剂的使用情况【答案】A6.(2011四川重庆,6,4分)如图,⊙O是△A BC的外接圆,∠OCB=40°则∠A的度数等于( )A.60°B.50°C.40°D.30°【答案】B7.(2011四川重庆,7,4分)已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )A.a>0 B.b<0 C.c<0 D.a+b+c>0【答案】D8.(2011四川重庆,8,4分)为了建设社会主义新农村,我市积极推进“行政村通畅工程”,张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造.下面能反映该工程尚未改造道路里程y(公里)与时间x(天)的函数关系的大致图像是( )A.B.C.D.【答案】A9.(2011四川重庆,9,4分)下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,……,则第⑥个图形中平行四边形的个数为( )……图①图②图③图④A.55 B.42 C.41 D.29【答案】C10.(2011四川重庆,10,4分)如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =3.其中正确结论的个数是( )A .1B .2C .3D .4【答案】C二、填空题:(本大题6个小题,每小题4分,共24分)在每小题中,请将答案直接填在答题卷中对应的横线上.11.(2011四川重庆,11,4分)据第六次全国人口普查结果显示,重庆市常住人口约2880万人.将数2880万用科学记数法表示为 万.【答案】2.88×10312.(2011四川重庆,12,4分)如图,△ABC 中,DE ∥BC ,DE 分别交边AB 、AC 于D 、E 两点,若AD :AB =1:3,则△ADE 与△ABC 的面积比为 .【答案】1:913.(2011四川重庆,13,4分)在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵树分别是:10,9,9,10,11,9.则这组数据的众数是 .【答案】914.(2011四川重庆,14,4分)在半径为4π的圆中,45°的圆心角所对的弧长等于 .【答案】115.(2011四川重庆,15,4分)有四张正面分别标有数字-3,0,1,5的不透明卡片,它们除数字不同外其余相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a ,则使关于x 的分式方程1-ax x -2+2= 12-x有正整数解的概率为 . 【答案】1416.(2011四川重庆,16,4分)某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成.乙种盆景由10朵红花、12朵黄花搭配而成.丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用了 朵.【答案】4380三、解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤,将解答书写在答题卷中对应的位置上.17.(2011四川重庆,17,6分)计算:|-3|+(-1)2011×(π-3)0-327+(12)-2 【答案】原式=3+(-1)×1-3+4=318.(2011四川重庆,18,6分)解不等式2x -3<x +13,并把解集在数轴上表示出来. 【答案】由2x -3<x +13得6x -9<x +1,5 x <10,x <2,所以解集为x <2,解集在数轴上表示如下:19.(2011四川重庆,19,6分)如图,点A 、F 、C 、D 在同一直线上,点B 和点E 分别在直线AD 的两侧,且AB =DE ,∠A =∠D ,AF =DC .求证:BC ∥EF .【证明】∵AF =DC ,∴AC =DF ,又∠A =∠D ,AB =DE ,∴△ABC ≌△DEF ,∴∠ACB =∠DFE ,∴BC ∥EF .20.(2011四川重庆,20,6分)为进一步打造“宜居重庆”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M 到广场的两个入口A 、B 的距离相等,且到广场管理处C 的距离等于A 和B 之间距离的一半,A 、B 、C 的位置如图所示.请在答题卷的原图上利用尺规作出音乐喷泉M 、位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)【答案】四、解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,将解答书写在答题卷中对应的位置上.21.(2011四川重庆,21,10分)先化简,再求值:(x -1x -x -2x +1)÷2x 2-x x 2+2x +1,其中x 满足x 2-x -1=0.【答案】原式=(x -1x -x -2x +1)÷2x2-x x2+2x +1 = (x -1)( x +1)- x( x -2)x( x +1)÷2x2-x x2+2x +1=2x -1x(x +1)×(x +1)2 2x -1=x+1x2当x2-x -1=0时,x2=x +1,原式=1.22.(2011四川重庆,22,10分)如图,在平面直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象与反比例函数y =xm (m ≠0)的图象交于二、四象限内的A 、B 两点,与x 轴交于C 点,点B 的坐标为(6,n ),线段OA =5,E 为x 轴负半轴上一点,且s i n ∠AOE =45. (1)求该反比例函数和一次函数;(2)求△AOC 的面积.【答案】(1)过A 点作AD ⊥x 轴于点D ,∵sin ∠AOE = 45,OA =5, ∴在Rt △ADO 中,∵sin ∠AOE =AD AO =AD 5= 45, ∴AD =4,DO =OA2-DA2=3,又点A 在第二象限∴点A 的坐标为(-3,4),将A 的坐标为(-3,4)代入y =m x ,得4=m -3∴m =-12,∴该反比例函数的解析式为y =-12x , ∵点B 在反比例函数y =-12x 的图象上,∴n =-126=-2,点B 的坐标为(6,-2),∵一次函数y =kx +b(k≠0)的图象过A 、B 两点, ∴⎩⎨⎧-3k +b=4, 6k +b =-2,∴⎩⎪⎨⎪⎧k =-23, b =2∴该一次函数解析式为y =-23x +2. (2)在y =-23x +2中,令y =0,即-23x +2=0,∴x=3, ∴点C 的坐标是(3,0),∴OC =3, 又DA=4,∴S △AOC =12×OC×AD =12×3×4=6,所以△AOC 的面积为6. 23.(2011四川重庆,23,10分)为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.【答案】(1)4÷20﹪=20(个);20-2-3-4-5-4=2(个),(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4(名).答:该校平均每班有4名留守儿童.(2)因为只有2名留守儿童的班级只有甲班和乙班两个,设甲班的2名留守儿童为a1,a2,乙班的2由表格可知:共有12种情况,符合条件的有a1 a2、a1a2、b1 b2、b1b2四种,4÷12=13.答:所选两名留守儿童来自同一个班级的概率为13.24.(2011四川重庆,24,10分)如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F.点G为BC中点,连结EG、AF.(1)求EG的长;(2)求证:CF=AB+AF.【答案】(1) 解∵BD⊥CD,∠DCB=45°,∴∠DBC=∠DCB=45°,∴CD=DB=2,∴CB=DB2+CD2=22,∵CE ⊥AB 于E ,点G 为BC 中点,∴EG =12CB =2.(2)证明:证法一:延长BA 、CD 交于点H ,∵BD ⊥CD ,∴∠CDF =∠BDH =90°, ∴∠DBH +∠H =90°,∵CE ⊥AB 于E ,∴∠DCF +∠H =90°,∴∠DBH =∠DCF ,又CD =BD ,∠CDF =∠BDH ,∴△CDF ≌△BDH(ASA), DF =DH , CF = BH =BA +AH ,∵AD ∥BC ,∴∠DBC =∠ADF =45°,∠HDA =∠DCB =45°,∴∠ADF =∠HAD ,又DF =DH ,DA =DA ,∴△ADF ≌△ADH(SAS),∴AF =AH ,又CF =BH =BA +AH ,∴CF =AB +AF .证法二:在线段 DH 上截取CH=CA ,连结DH .∵BD ⊥CD ,BE ⊥CE ,∴∠EBF +∠EFB =90°,∠DCF +∠DFC =90°.又∠EFB=∠DFC ,∴∠EBF=∠DCF .又BD=CD ,BA=CH ,∴△ABD ≌△HCD .∴AD=HD ,∠ADB=∠HDC .又AD ∥BC ,∴∠ADB =∠DBC =45°.∴∠HDC =45°.∴∠HDB =∠BDC -∠HDC =45°.∴∠ADB =∠HDB .又AD=HD , DF=DF ,∴△ADF ≌△HDF ,∴AF =HF .∴CF =CH +HF=AB +AF .五、解答题:(本大题2个小题,第25小题10分,第26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卷中对应的位置上.25.(2011四川重庆,25,10分)某企业为重庆计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x ≤9,且x取整数),10至12月的销售量p2(万件)p2=-0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;(3)今年1至5月,每件配件的原材料价格均比去年12月上涨60元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少0.1 a%.这样,在保证每月上万件配件销量的前提下,完成1至5月的总利润1700万元的任务,请你参考以下数据,估算出a的整数值.(参考数据:992=9801,982=9604,972=9409,962=9216,952=9025)【答案】(1)y1 与x之间的函数关系式为y1=20x+540,y2与x之间满足的一次函数关系式为y2=10x+630.(2)去年1至9月时,销售该配件的利润w=p1(1000-50-30-y1)=(0.1x+1.1)(1000−50−30−20x−540)=(0.1x+1.1)(380−20x)=-2x2+160x+418=-2( x-4)2+450,(1≤x≤9,且x取整数)∵-2<0,1≤x≤9,∴当x=4时,w最大=450(万元);去年10至12月时,销售该配件的利润w=p2(1000-50-30-y2)=(-0.1x+2.9)(1000-50-30-10x-630)=(-0.1x+2.9)(290-10x)=( x-29)2,(10≤x≤12,且x取整数),当10≤x≤12时,∵x<29,∴自变量x增大,函数值w减小,∴当x=10时,w最大=361(万元),∵450>361,∴去年4月销售该配件的利润最大,最大利润为450万元.(3)去年12月份销售量为:-0.1×12+0.9=1.7(万件),今年原材料的价格为:750+60=810(元),今年人力成本为:50×(1+20﹪)=60(元),由题意,得5×[1000(1+a ﹪)-810-60-30]×1.7(1-0.1a ﹪)=1700,设t= a ﹪,整理,得10t2-99t+10=0,解得t=99±940120,∵972=9409,962=9216,而9401更接近9409.∴9401=97.∴t1≈0.1或t2≈9.8,∴a1≈10或a2≈980.∵1.7(1-0.1a ﹪)≥1,∴a2≈980舍去,∴a ≈10.答:a 的整数值为10.26.(2011四川重庆,26,12分)如图,矩形ABCD 中,AB =6,BC =23,点O 是AB的中点,点P 在AB 的延长线上,且BP =3.一动点E 从O 点出发,以每秒1个单位长度的速度沿OA 匀速动动,到达A 点后,立即以原速度沿AO 返回;另一动点F 从P 点出发,以每秒1个单位长度的速度沿射线P A 匀速动动,点E 、F 同时出发,当两点相遇时停止运动.在点E 、F 的运动过程中,以EF 为边作等边△EFG ,使△EFG 和矩形ABCD 在射线P A 的同侧,设动动的时间为t 秒(t ≥0).(1)当等边△EFG 的边FG 恰好经过点C 时,求运动时间t 的值;(2)在整个运动过程中,设等边△EFG 和矩形ABCD 重叠部分的面积为S ,请直接写出S 与t 之间的函数关系式和相应的自变量t 的取值范围;(3)设EG 与矩形ABCD 的对角线AC 的交点为H ,是否存在这样的t ,使△AOH 是等腰三角形?若存在,求出对应的t 的值;若不存在,请说明理由.【答案】(1)当等边△EFG 的边FG 恰好经过点C 时(如图),∠CFB =60°,BF =3-t ,在Rt △CBF 中,BC =23,∴tan ∠CFB =BC BF ,∴tan 60°=23BF,∴BF =2,∴t =3-t =2,∴t =1.(2)当0≤t <1时,S= 2 3 t +43;当1≤t <3时,S=32 t 2+3 3 t +732;当3≤t <4时,S= -4 3 t +203;当4≤t <6时,S= 3 t2-12 3 t +363.(3)存在,理由如下:在Rt △ABC 中,tan ∠CAB =BC AB =33,∴∠CAB=30°. 又∵∠HEO=60°,∴∠HAE=∠AHE=30°.∴AE=HE=3-t 或t -3.(ⅰ)当AH=AO=3时(如图②),过点E 作EM ⊥AH 于M ,则AM=12AH=32.在Rt △AME 中,cos ∠MAE =AM AE ,即cos 30°=32AE ,∴AE=3, 即3-t=3或t -3=3,t=3-3或3+3.(ⅱ)当HA=HO 时(如图③),则∠HOA=∠HAO=30°,又∵∠HEO=60°,∴∠EHO=90°.∴EO=2HE=2AE .又∵AE +EO=3,∴AE +2AE=3.∴AE=1.即3-t=1或t -3=1,t=2或4.(ⅲ)当OH=OA 时(如图④),则∠OHA=∠OAH=30°,∴∠HOB=60°=∠HEB .∴点E 和O 重合,∴AE=3.即3-t=3或t -3=3,t=6(舍去)或t=0.综上所述,存在5个这样的值,使△AOH 是等腰三角形,即: t=3-3或t=3+3或t=2或t=4或t=0.。
2011年重庆市中考数学试卷及答案

③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°-∠FGC=∠GFC+∠GCF,
B、调查某班学生对“五个重庆”的知晓率,采用全面调查,
C、调查一架“歼20”隐形战机各零部件的质量,采用全面调查,
D、调查广州亚运会100米参赛运动员兴奋剂的使用情况,采用全面调查,
故选A.点评:本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查,比较简单.
∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
④错误.
过F作FH⊥DC,
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴ = ,
EF=DE=2,GF=3,
∴Hale Waihona Puke G=5, ∴ = = ,
∴S△FGC=S△GCE-S△FEC= ×3×4- ×4×( ×3)= ≠3.
故选C.点评:本题综合性较强,考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算,有一定的难度.
答题:冯延鹏老师 隐藏解析体验训练收藏试题试题纠错下载试题试题篮6、如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
2011年重庆市中考数学试题(WORD解析版)

2011年重庆市中考数学试题一.选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1、(2011•重庆)在﹣6,0,3,8这四个数中,最小的数是()A、﹣6B、0C、3D、8考点:有理数大小比较。
专题:计算题。
分析:根据正数大于0,0大于负数,正数大于负数,两负数绝对值大的反而小,解答即可.解答:解:∵8>3>0>﹣6,∴最小的数是﹣6.故选A.点评:本题考查了有理数大小的比较,熟记:正数大于0,0大于负数,正数大于负数,两负数绝对值大的反而小.2、(2011•重庆)计算(a3)2的结果是()A、aB、a5C、a6D、a9考点:幂的乘方与积的乘方。
专题:计算题。
分析:根据幂的乘方法则:底数不变,指数相乘.(a m)n=a mn(m,n是正整数)计算即可.解答:解:(a3)2=a3×2=a6.故选C.点评:本题考查了幂的乘方,注意:①幂的乘方的底数指的是幂的底数;②性质中“指数相乘”指的是幂的指数与乘方的指数相乘,这里注意与同底数幂的乘法中“指数相加”的区别.3、(2011•重庆)下列图形中,是中心对称图形的是()A、B、C、D、考点:中心对称图形。
专题:数形结合。
分析:根据中心对称图形的定义来判断:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.解答:解:A、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;B、将此图形绕某一点旋转180度正好与原来的图形重合,所以这个图形是中心对称图形;C、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;D、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形.故选B.点评:本题主要考查中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.4、(2011•重庆)如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于()A、60°B、50°C、45°D、40°考点:平行线的性质。
重庆中考数学试题解析版.doc

重庆市2011年中考数学试卷—解析版一.选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1、(2011•重庆)在﹣6,0,3,8这四个数中,最小的数是()A、﹣6B、0C、3D、8考点:有理数大小比较。
专题:计算题。
分析:根据正数大于0,0大于负数,正数大于负数,两负数绝对值大的反而小,解答即可.解答:解:∵8>3>0>﹣6,∴最小的数是﹣6.故选A.点评:本题考查了有理数大小的比较,熟记:正数大于0,0大于负数,正数大于负数,两负数绝对值大的反而小.2、(2011•重庆)计算(a3)2的结果是()A、aB、a5C、a6D、a9考点:幂的乘方与积的乘方。
专题:计算题。
分析:根据幂的乘方法则:底数不变,指数相乘.(a m)n=a mn(m,n是正整数)计算即可.解答:解:(a3)2=a3×2=a6.故选C.点评:本题考查了幂的乘方,注意:①幂的乘方的底数指的是幂的底数;②性质中“指数相乘”指的是幂的指数与乘方的指数相乘,这里注意与同底数幂的乘法中“指数相加”的区别.3、(2011•重庆)下列图形中,是中心对称图形的是()A、B、C、D、考点:中心对称图形。
专题:数形结合。
分析:根据中心对称图形的定义来判断:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.解答:解:A、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;B、将此图形绕某一点旋转180度正好与原来的图形重合,所以这个图形是中心对称图形;C、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;D、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形.故选B.点评:本题主要考查中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.4、(2011•重庆)如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于()A、60°B、50°C、45°D、40°考点:平行线的性质。
2011年重庆市中考数学真题试卷及答案(word版,答案扫描)

《新课程导航》遵义市2010年初中毕业生学业(升学)综合练习题数学(四)试题卷(本试卷总分150分,考试时间120分钟)注意事项:1. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2. 答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3. 答非选择题时,必须使用0.5毫米黑色签字笔将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试卷上答题无效。
5. 考试结束后,将试卷和答题卡一并交回。
一、选择题(本题共10小题,每小题3分,共30分。
在每小题给出的四个答案中,只有一项是符合题目要求的,请用2B 铅笔把答题卡上对应题目的答案标号涂黑、涂满。
)1. 如果零上3C 记为+3C ,那么零下3C 记作( )A .3-B . 6-C . 3C -D . 6C -2.我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是( )从左面看A .B .C .D .3. 某位同学一次掷出的三个骰子全是“6”的事件是( )A .不可能事件B .必然事件C . 不确定事件,可能性较大D . 不确定事件,可能性较小4.不等式组201x x -<⎧⎨>-⎩的解集是 ( ) A .1x >- B .2x <- C . 12x -<< D . 2x <5. 下列运算正确的是( )A .326a a a ⋅=B . ()22a a -=C .325a a a +=D . ()235a a =6. 如图,P 是反比例函数8y x=在第一象限分支上的一个动点,PA x ⊥轴,随着x 的逐渐增大,△APO 的面积将( )CA 'A y A .减小B .增大C . 不变D . 无法确定7.某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车沿相同路线前往,如图,12l l ,分别表示步行和骑自行车前往目的地所走的路程y (千米)与所用时间x (分钟)之间的函数图形,则以下判断错误的是( )A .骑自行车的同学比步行的同学晚出发30分钟B .步行的速度是6千米/时C .骑车的同学从出发到追上步行的同学用了20分钟D . 骑车的同学和步行的同学同时到达目的地l 2l 1605450306第7题yxO B 第8题A FE D C OB 第10题A ED C O8.如图,正方形ABCD 中,点E 、F 分别为AB 、BC 的中点,AF 与DE 相交于点O ,则AO DO 等于( )A.13B.12C.23D.2559.一根蜡烛在凸透镜下成一实像,物距u ,像距v 和凸透镜的焦距f 满足关系式:111u v f+=,若u =30厘米,f =5厘米,则像距v 的值是( )A .6厘米B .5厘米C .4厘米D .10厘米10.如图,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE 、BD 的延长线交于点C ,若CE=2,则图中阴影部分的面积是( )A.433π-B.23π C.233π- D.13π二、填空题(本大题共8小题,每小题4分,共32分。
2011中考数学试题答题卷

重庆市2011年初中毕业暨高中招生考试
数 学 试 题 答 题 卷
(全卷共五个大题,满分150分,考试时间120分钟)
注意事项:
1.试题的答案用钢笔或圆珠笔书写在答题卷上,不得在试卷上直接作答. 2.答题前将答题卷上密封线内的各项内容写清楚. 3.考试结束,由监考人员将试题和答题卷一并收回.
参考公式:抛 物 线2
(0)y ax bx c a =++≠的 顶点坐标为2
4(,)24b ac b a a --,对称轴公式为 2b x a
=-.
一、选择题:(每小题4分,共40分)
二、填空题:(每小题4分,共24分)
11. . 12. .
13. . 14. .
15. . 16. .
三、解答题:(本大题4个小题,每小题6分,共24分)
17.
18. 19.
20.(注:请务必用铅笔作图)
19题图
A
B
C
F D
E B
20题图
四、解答题:(本大题4个小题,每小题10分,共40分)
21.
22.
23.
全校留守儿童人数条形统计图
24.
A C
E
F
G D
24题图
五、解答题:(本大题2个小题,第25小题10分,第26小题12
分,共22分)
25.
26.
F
26题图
备用图。
2011重庆中考数学试卷--解析版

∴ =,
4页脚内容
K1+478~K1+5888 段左侧片石混凝土挡土墙第 1 部分
EF=DE=2,GF=3, ∴ EG=5,
∴ == ,
∴ S△ FGC=S△ GCE﹣S△ FEC= ×3×4﹣ ×4×( ×3)= ≠3.
故选 C.
点评:本题综合性较强,考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平 行线的判定,三角形的面积计算,有一定的难度.
∵ ∠ OCB=40°,∠ C0B=180°﹣∠ OBC﹣∠ 0CB,
∴ ∠ COB=100°;
又∵ ∠ A= ∠ C0B(同弧所对的圆周角是所对的圆心角的一半),
∴ ∠ A=50°, 故选 B. 点评:本题考查了圆周角定理:同弧所对的圆周角是所对的圆心角的一半.解题时,借用了等腰三角形的两 个底角相等和三角形的内角和定理. 7、(2011•重庆)已知抛物线 y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确
A、55
B、42
C、41
D、29
考点:规律型:图形的变化类。
专题:规律型。
分析:由于图②5 个=1+2+2,图③11 个=1+2+3+2+3,图④19=1+2+3+4+2+3+4,由此即可得到第⑥个图形
中平行四边形的个数.
解答:解:∵ 图②平行四边形有 5 个=1+2+2,
图③平行四边形有 11 个=1+2+3+2+3,
解答:解:∵ 抛物线的开口向下,
∴ a<0;
又∵ 抛物线的对称轴在 y 轴的右侧,
重庆 -解析版

重庆市2011年中考数学试卷—解析版一.选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1、(2011•重庆)在﹣6,0,3,8这四个数中,最小的数是()A、﹣6B、0C、3D、8考点:有理数大小比较。
专题:计算题。
分析:根据正数大于0,0大于负数,正数大于负数,两负数绝对值大的反而小,解答即可.解答:解:∵8>3>0>﹣6,∴最小的数是﹣6.故选A.点评:本题考查了有理数大小的比较,熟记:正数大于0,0大于负数,正数大于负数,两负数绝对值大的反而小.2、(2011•重庆)计算(a3)2的结果是()A、aB、a5C、a6D、a9考点:幂的乘方与积的乘方。
专题:计算题。
分析:根据幂的乘方法则:底数不变,指数相乘.(a m)n=a mn(m,n是正整数)计算即可.解答:解:(a3)2=a3×2=a6.故选C.点评:本题考查了幂的乘方,注意:①幂的乘方的底数指的是幂的底数;②性质中“指数相乘”指的是幂的指数与乘方的指数相乘,这里注意与同底数幂的乘法中“指数相加”的区别.3、(2011•重庆)下列图形中,是中心对称图形的是()A、B、C、D、考点:中心对称图形。
专题:数形结合。
分析:根据中心对称图形的定义来判断:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.解答:解:A、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;B、将此图形绕某一点旋转180度正好与原来的图形重合,所以这个图形是中心对称图形;C、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;D、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形.故选B.点评:本题主要考查中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.4、(2011•重庆)如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于()A、60°B、50°C、45°D、40°考点:平行线的性质。
2011重庆潼南中考数学及答案

【答案】B
10.(2011重庆潼南县,10,4分)如图,在平面直角坐标系中,四边形OABC是菱形, 点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间t秒(0≤t≤4),则能大致反映S与t的函数关系的图像是( )
重庆潼南县20分,考试时间120分钟)
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(- , ),对称轴公式x=- .
一、选择题:(本大题10个小题,每个小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号涂在答题卡中对应的位置.
A.1cm B.4cm C.5cm D.6cm
【答案】D
8.(2011重庆潼南县,8,4分)目前,全球淡水资源日益减少,提倡全社会节约用水,据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是( )
【答案】C
二、填空题:(本大题6个小题,每小题4分,共24分)
11.(2011重庆潼南县,11,4分)如图,数轴上A、B两点分别对应实数a、b,则a、b的大小关系为.
【答案】b>a
12.(2011重庆潼南县,12,4分)据统计,2010年11月1日调查中国总人口为1 339 000 000人,用科学计数法表示1 339 000 000为.
【答案】5cm
15.(2011重庆潼南县,15,4分)某地居民生活用电基本价格为0.50元/度,规定每月基本用电量为a度,超过部分电量的每度电价比基本用电量的每度电价增加20%收费,某用户在5月份用电100度,共交电费56元,则a的值=.
2011年重庆市中考数学试题及答案详细解析(word版)

一.选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1、(2011•重庆)在﹣6,0,3,8这四个数中,最小的数是()A、﹣6B、0C、3D、82、(2011•重庆)计算(a3)2的结果是()A、aB、a5C、a6D、a93、(2011•重庆)下列图形中,是中心对称图形的是()A、B、C、D、4、(2011•重庆)如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于()A、60°B、50°C、45°D、40°5、(2011•重庆)下列调查中,适宜采用抽样方式的是()A、调查我市中学生每天体育锻炼的时间B、调查某班学生对“五个重庆”的知晓率C、调查一架“歼20”隐形战机各零部件的质量D、调查广州亚运会100米参赛运动员兴奋剂的使用情况6、(2011•重庆)如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于()A、60°B、50°C、40°D、30°7、(2011•重庆)已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是()A、a>0B、b<0C、c<0D、a+b+c>08、(2011•重庆)为了建设社会主义新农村,我市积极推进“行政村通畅工程”.张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的函数关系的大致图象是()A、B、C、D、9、(2011•重庆)下列图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,…则第⑥个图形中平行四边形的个数为()A、55B、42C、41D、2910、(2011•重庆)如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE 沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是()A、1B、2C、3D、4二.填空题:(本大题6个小题,每小题4分,共24分)11、(2011•重庆)据第六次全国人口普查结果显示,重庆常住人口约为2880万人.将数2880万用科学记数法表示为 2.88×103万.12、(2011•重庆)如图,△ABC中,DE∥BC,DE分别交边AB、AB于D、E两点,若AD:AB=1:3,则△ADE与△ABC的面积比为1:9.13、(2011•重庆)在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,9,9,10,11,9.则这组数据的众数是9.14、(2011•重庆)在半径为的圆中,45°的圆心角所对的弧长等于1.15、(2011•重庆)有四张正面分别标有数学﹣3,0,1,5的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数学记为a,则使关于x的分式方程有正整数解的概率为.16、(2011•重庆)某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用了4380朵.二.解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤)17、(2011•重庆)|﹣3|+(﹣1)2011×(π﹣3)0﹣+.18、(2011•重庆)解不等式2x﹣3<,并把解集在数轴上表示出来.19、(2011•重庆)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.20、(2011•重庆)为进一步打造“宜居重庆”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)四.解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤21、(2011•重庆)先化简,再求值:,其中x满足x2﹣x﹣1=0.22、(2011•重庆)如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=.(1)求该反比例函数和一次函数的解析式;(2)求△AOC的面积.23、(2011•重庆)为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.24、(2011•重庆)如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C 作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.(1)求EG的长;(2)求证:CF=AB+AF.五.解答题:(本大题2个小题,第25题10分,第26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤.25、(2011•重庆)某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式p1=0.1x+1.1(1≤x≤9,且x取整数)10至12月的销售量p2(万件)与月份x满足函数关系式p2=﹣0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;(3)今年1至5月,每件配件的原材料价格均比去年12月上涨60元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少0.1a%.这样,在保证每月上万件配件销量的前提下,完成了1至5月的总利润1700万元的任务,请你参考以下数据,估算出a的整数值.(参考数据:992=9901,982=9604,972=9409,962=9216,952=9025)26、(2011•重庆)如图,矩形ABCD中,AB=6,BC=2,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F 的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S 与t之间的函数关系式和相应的自变量t的取值范围;(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形?若存大,求出对应的t的值;若不存在,请说明理由.一.选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1、(2011•重庆)在﹣6,0,3,8这四个数中,最小的数是()A、﹣6B、0C、3D、8考点:有理数大小比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市2011年初中毕业暨高中招生考试
数学试题
(全卷共五个大题,满分150分,考试时间120分钟)
参考公式:抛物线的2
(0)y ax bx c a =++≠顶点坐标为2
4(,)24b ac b a a
--,对称轴公式为2b x a =-。
一.选择题:(本大题10个小题,每小题4分,共40分)
1.在-6,0,3,8这四个数中,最小的数是( )
A . -6
B 、0
C 、3
D 8 2.计算()
2
3a
的结果是( )
A 、 a
B 、 a 5
C 、a 6
D 、 a 9
3.下列图形中,是中心对称图形的是( )
4.如图,AB/∥CD ,∠∠C =800,∠CAD =600
,则∠BAD 的度数等于( ) 5.下列调查中,适宜采用抽样方式的是( ) A 调查我市中学生每天体育锻炼的时间 B 调查某班学生对“五个重庆”的知晓率
C 调查一架“歼20”隐形战机各零部件的质量
D 调查广州亚运会100米参赛运动员兴奋剂的使用情况
6.如图,⊙O 是△ABC 的外接圆,∠OCB =400
,则∠A 的度数等于( )
A 600
B 500
C 、400
D 、30
7.已知抛物线2(0)y ax bx c a =++≠在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( ) A 、a>0 B b<0 C c<0 D a+b+c>0
8.为了建设社会主义新农村,我市积极推进“行政村通畅工程”。
张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按完成了两村之间的道路改造。
下面能反映该工程尚未改造的道路里程y (公里)与时间x (天)的函数关系的大致图象是( )
9.下列图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,……则第⑥个图形中平行四边形的个数为( )
B C
D
A B C
D
A 55
B 42
C 41
D 29
10.如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE 。
将△ADE 沿对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF 。
下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF;④S △FGC =3. 其中正确结论的个数是( ) A 1 B 2 C 、3 D 、4 二.填空题:(本大题6个小题,每小题4分,共24分)
11.据第六次全国人口普查结果显示,重庆常住人口约为2880万人。
将数2880万用科学记数法表示为 万。
12.如图,△ABC中,DE∥BC,DE分别交边AB、AB于D、E两点,若AD:AB=1:3,则△ADE与△ABC的面积比为 。
13.在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是: 10,9,9,10,11,9.则这组数据的众数是 。
14、在半径为4π
的圆中,450
的圆心角所对的弧长等于 。
15.有四张正面分别标有数学-3,0,1,5的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数学记为a ,则使关于x 的分式方程1122
2ax x x
-+=--有正整数解的概率
为 。
16.某步行街摆放有若干盆甲、乙、丙三种造型的盆景。
甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙咱盆景由10朵红花、18朵黄花和25朵紫花搭配而成。
这些盆景一共用了2900朵红花,3750朵紫花,由黄花一共用了 朵。
二.解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤) 17.()
(
)2
2011
13132π-⎛⎫
-+-⨯- ⎪⎝⎭
18.解不等式1233
x x +- ,并把解集在数轴上表示出来。
19.如图,点A 、F 、C 、D 在同一直线上,点B 和点E 分别在直线AD 的两侧,且AB=DE ,∠A=∠D ,AF=DC 。
求证:BC ∥EF 。
20.为进一步打造“宜居重庆”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求意象喷泉M 到广场的两个入口A 、B 的距离相等,且到广场管理处C 的距离等于A 和B 之间距离的一半,A 、B 、C 的位置如图所示。
请在答题卷的原图上利用尺规作图作出音乐喷泉M 的位置。
(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
四.解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤
21.先化简,再求值:22
122 121x x x x x x x x ---⎛⎫-÷ ⎪+++⎝⎭
,其中x 满足x 2-x-1=0.
22.如图,在平面直角坐标系x0y 中,一次函数y=kx+b(k ≠0)的图象与反比例函数()0m
y m x
=
≠的图象交于二、四象限内的A 、B 两点,与x 轴交于C 点,点B 的坐标为(6,n )。
线段OA=5,E 为x 轴上一点,且sin ∠AOE=45 。
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC 的面积。
23.为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率。
24.如图,梯形ABCD 中,AD ∥BC ,∠DCB=450
,CD=2,BC ⊥CD 。
过点C 作CE ⊥AB 于E ,交对角线BD 于F ,点G 为
BC 中点,连结EG 、AF 。
(1)求EG 的长;
(2)求证:CF=AB+AF 。
五.解答题:(本大题2个小题,第25题10分,第26小题12分,共22分)
25.某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x (1≤x ≤9,且x 取整数)之间的函数关系如下表:
x (10≤x ≤12,且x 取整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x 之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x 之间满足的一次函数关系式;
(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式p1=0.1x+1.1(1≤x≤9,且x取整数)10至12月的销售量p2(万件)与月份x满足函数关系式p2=-0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1至5月,每件配件的原材料价格均比去年12月上涨60元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少0.1a% 。
这样,在保证每月上万件配件销量的前提下,完成了1至5月的总利润1700万元的任务,请你参考以下数据,估算出a的整数值。
(参考数据:992=9901,982=9604,972=9409,962=9216,952=9025)
26.如图,矩形ABCD中,AB=6,BC= 点O是AB的中点,点P在AB的延长线上,且BP=3。
一动点E从O点
出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧。
设运动的时间为t秒(t≥0)。
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t ,使△AOH是等腰三角形?若存大,求出对应的t的值;若不存在,请说明理由。
