反比例函数经典题型
(完整版)反比例函数基础练习题及答案

反比例函数练习一一.选择题(共22小题)1.(2015春•泉州校级期中)下列函数中,y是x的反比例函数的为()A.y=2x+1 B.C.D.2y=x2.(2015春•兴化市校级期中)函数y=k是反比例函数,则k的值是()A.﹣1 B.2 C.±2 D.±3.(2015春•衡阳县期中)若y=(m﹣1)x|m|﹣2是反比例函数,则m的值为()A.m=2 B.m=﹣1 C.m=1 D.m=04.(2014•汕尾校级模拟)若y与x成反比例,x与z成反比例,则y是z的()A.正比例函数B.反比例函数C.一次函数D.不能确定5.(2014春•常州期末)反比例函数(m为常数)当x<0时,y随x的增大而增大,则m的取值范围是()A.m<0 B.C.D.m≥6.(2015•贺州)已知k1<0<k2,则函数y=和y=k2x﹣1的图象大致是()A.B. C.D.7.(2015•滦平县二模)在同一直角坐标系中,函数y=kx+k与y=(k≠0)的图象大致为()A.B.C.D.8.(2015•上海模拟)下列函数的图象中,与坐标轴没有公共点的是()A.B.y=2x+1 C.y=﹣x D.y=﹣x2+19.(2015•宝安区二模)若ab>0,则函数y=ax+b与函数在同一坐标系中的大致图象可能是()A.B.C.D.10.(2015•鱼峰区二模)若方程=x+1的解x0满足1<x0<2,则k可能是()A.1 B.2 C.3 D.611.(2012•颍泉区模拟)如图,有反比例函数y=,y=﹣的图象和一个圆,则图中阴影部分的面积是()第11题图第12题图A.πB.2πC.4πD.条件不足,无法求12.(2010•深圳)如图所示,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A.y=B.y=C.y=D.y=13.(2014•随州)关于反比例函数y=的图象,下列说法正确的是()A.图象经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小14.(2014•昆明)如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k 的图象大致是()A.B.C.D.15.(2014•天水)已知函数y=的图象如图,以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.其中正确的个数是()A.4个B.3个C.2个D.1个16.(2014•杭州)函数的自变量x满足≤x≤2时,函数值y满足≤y≤1,则这个函数可以是()A.y=B.y=C.y=D.y=17.(2014•阜新)反比例函数y=在每个象限内的函数值y随x的增大而增大,则m的取值范围是()A.m<0 B.m>0 C.m>﹣1 D.m<﹣118.(2015•凉山州)以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=经过点D,则正方形ABCD的面积是()第18题图第19题图A.10 B.11 C.12 D.1319.(2015•眉山)如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D 点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()A.B.C.3 D.420.(2014•绥化)如图,过点O作直线与双曲线y=(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是()第20题图第21题图A.S1=S2B.2S1=S2C.3S1=S2D.4S1=S2 21.(2014•抚顺)如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小22.(2014•重庆)如图,反比例函数y=﹣在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1,﹣3,直线AB与x轴交于点C,则△AOC的面积为()A.8 B.10 C.12 D.24二.填空题(共4小题)23.(2015•锦江区一模)已知y=(a﹣1)是反比例函数,则a=.24.(2014•江西模拟)已知反比例函数的解析式为y=,则最小整数k=.25.(2013•路北区二模)函数y=,当y≥﹣2时,x的取值范围是(可结合图象求解).26.(2014•贵阳)若反比例函数的图象在其每个象限内,y随x的增大而增大,则k的值可以是.(写出一个符合条件的值即可)三.解答题(共4小题)27.(2014春•东城区校级期中)已知反比例函数y=﹣(1)说出这个函数的比例系数;(2)求当x=﹣10时函数y的值;(3)求当y=6时自变量x的值.28.(2013春•汉阳区校级期中)已知函数y=(5m﹣3)x2﹣n+(n+m),(1)当m,n为何值时是一次函数?(2)当m,n为何值时,为正比例函数?(3)当m,n为何值时,为反比例函数?29.(2013•德宏州)如图,是反比例函数y=的图象的一支.根据给出的图象回答下列问题:(1)该函数的图象位于哪几个象限?请确定m的取值范围;(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?30.(2014•苏州)如图,已知函数y=(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.(1)求△OCD的面积;(2)当BE=AC时,求CE的长.答案:一.选择题(共22小题)1.C 2.D 3.B 4.A 5.C 6.C 7.B 8.A 9.C 10.C 11.B 12.D 13.D 14.B 15.B 16.A 17.D 18.C 19.B20.B 21.C 22.C二.填空题(共4小题)23.-1 24.1 25.x≤-2或x>0 26.-1(答案不唯一)三.解答题(共4小题)27.28.29.30.。
反比例函数测试题(含答案)

反比例函数测试题(含答案)(时间90分钟 满分100分)班级 学号 姓名 得分一、选择题(每小题3分,共24分) 1.如果x 、y 之间的关系是10(0)ax y a -+=≠,那么y 是x 的 ( )A .正比例函数B .反比例函数C .一次函数D .二次函数 2.函数y =-4x 的图象与x 轴的交点的个数是( )A .零个B .一个C .两个D .不能确定3.反比例函数y =-4x 的图象在( )A .第一、三象限B .第二、四象限C .第一、二象限D .第三、四象限 4.已知关于x 的函数y =k (x +1)和y =-kx(k ≠0)它们在同一坐标系中的大致图象是(• )5.已知反比例函数y=x k 的图象经过点(m ,3m ),则此反比例函数的图象在 ( )A .第一、二象限B .第一、三象限C .第二、四象限D .第三、四象限6.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m 3) 的反比例函数,其图象如图所示.当气球内的气压大于120 kPa 时,气球发将爆炸.为了安全起见,气球的体积应 ( )A .不小于54m 3B .小于54m 3C .不小于45m 3D .小于45m 37.如果点P 为反比例函数x y 4=的图象上一点,PQ ⊥x 轴,垂足为Q ,那么△POQ的面积为 ( )A .2B . 4C .6D . 8 8.已知:反比例函数x my 21-=的图象上两点A (x 1,y 1),B (x 2, y 2)当x 1<0<x 2时,y 1<y 2,则m 的取值范围( )A .m <0B .m >0C .m <21 D .m >21二、填空题(每小题2分,共20分)9.有m 台完全相同的机器一起工作,需m 小时完成一项工作,当由x 台机器(x 为不大于m 的正整数)完成同一项工作时,所需的时间y 与机器台数x 的函数关系式是____.10.已知y 与x 成反比例,且当x 32=-时,y =5,则y 与x 的函数关系式为__________. 11.反比例函数xy 3=的图象在第一象限与第 象限. 3) 第6题12.某食堂现有煤炭500吨,这些煤炭能烧的天数y 与平均每天烧煤的吨数x 之间的函数关系式是 . 13.若nxm y ++=2)5(是反比例函数,则m 、n 的取值是 .14.两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数图象上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图象与直线y =x 有两个交点,你认为这两位同学所描述的反比例函数的解析式是 .15.在ABC △的三个顶点A (2,-3)、B (-4,-5)、C (-3,2)中,可能在反比例函数(0)ky k x=>的图象上的点是 .16.如果反比例函数4ny x-=的图象位于第二、四象限,则n 的取值范围是_______;如果图象在每个象限内,y 随x 的增大而减小,则n 的取值范围是 .17.如图,△P 1OA 1、△P 2A 1 A 2是等腰直角三角形,点P 1、P 2在函数4(0)y x x=>的图象上,斜边OA 1、A 1 A 2都在x 轴上,则点A 2的坐标是 .18.两个反比例函数k y x =和1y x=在第一象限内的图象如图所示,点P 在k y x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在ky x =的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA 与PB 始终相等; ④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分).三、解答题(共56分) 19.(4分)反比例函数xky =的图象经过点A (2 ,3). (1)求这个函数的解析式;(2)请判断点B (1 ,6)是否在这个反比例函数的图象上,并说明理由.20.(4分)已知三角形的一边为x ,这条边上的高为y ,三角形的面积为3,写出y 与x 的函数表达式,并画出函数的图象.OA 12第17题21.(4分)如图,一次函数y =kx +b 的图像与反比例函数xmy =的图像相交于A 、B 两点,(1)利用图中条件,求反比例函数和一次函数的解析式(2)根据图像写出使一次函数的值大于反比例函数的值的x 的取值范围.22.(6分)某蓄水池的排水管每时排水8 m 3,6h 可将满池水全部排空. (1)蓄水池的容积是多少?(2)如果增加排水管,使每时排水量达到Q (m 3),那么将满池水排空所需的时间t (h )将如何变化?(3)写出t 与Q 之间的函数关系式.(4)如果准备在5小时之内将满水池排空,那么每时的排水量至少为多少? (5)已知排水管的最大排水量为每时12m 3,那么最少多长时间可将满池水全部排空?23.(6分)双曲线5y x=在第一象限的一支上有一点C (1,5),过点C 的直线y =kx +b (k >0)与x 轴交于点A (a ,0).(1)求点A 的横坐标a 与k 之间的函数关系式;(2)当该直线与双曲线在第一象限内的另一交点D 的横坐标是9时,求△COA 的面积.第23题图第21题图24.(6分)已知反比例函数xmy 3-=和一次函数1-=kx y 的图象都经过点m P (,)3m -(1)求点P 的坐标和这个一次函数的解析式;(2)若点M (a ,1y )和点N (1+a ,2y )都在这个一次函数的图象上.试通过计算或利用一次函数的性质,说明1y 大于2y25.(6分)近视眼镜的度数y (度)与镜片焦距x (米)成反比例,已知800度近视眼镜镜片的焦距为0.125米, (1)求y 与x 的函数关系;(2)若张华同学近视眼镜镜片的焦距为0.25米,你知道他的眼睛近视多少度吗?26.(6分)对于取消市场上使用的杆秤的呼声越来越高,原因在于一些不法商贩在卖货时将秤砣挖空,或更换较小称砣,使砣较轻,从而欺骗顾客. (1)如图,对于同一物体,哪个图用的是标准秤砣,哪个用的是较轻的秤砣? (2)在称同一物体时,所称得的物体质量y (千克)与所用秤砣质量x (千克)之间满足 关系.(3)当砣较轻时,称得的物体变重,这正好符合哪个函数的哪些性质?图1图227.(6分)联想电脑公司新春期间搞活动,规定每台电脑0.7万元,交首付后剩余的钱数y 与时间t 的关系如图所示: (1)根据图象写出y 与t 的函数关系式. (2)求出首付的钱数.(3)如果要求每月支付的钱数不少于400元,那么还至少几个才能将所有的钱全部还清?28.(8分)如图,直线b kx y +=与反比例函数xk y '=(x <0)的图象相交于点A 、点B ,与x 轴交于点C ,其中点A 的坐标为(-2,4),点B 的横坐标为-4. (1)试确定反比例函数的关系式; (2)求△AOC 的面积.新人教八年级(下)第17章《反比例函数》答案一、选择题1.B ;2. A ;3. B ;4. A ;5. B ;6. C ;7.A ;8. C .二、填空题9.y =x m 2 10.152y x=- 11.三 12.y =x 50013.m ≠-5 n =-3 14.y=x315.B 16.n >4,n <4 17.(0) 18.①②④ 三、解答题19.(1)y =x6;(2)在 20. y =6x,图像略 21.(1)2y x=-,1y x =--;(2) 2x <-或0x <<122.(1)348m ;(2)t 将减小;(3)48t Q=;(4)4859.6Q Q==,;月)y ()(5)48412t ==23.(1)51a k=-+, (2) 25 24.(1)12--=x y ;(2)略 25.(1)100y x=,(2)400度 26.(1)图②是用与秤配套的秤砣,图①则使用较轻的秤砣.(2)反比例. (3)函数y =xk(k >0),当x 变小时,y 增大 27.(1)y =t 6000 ;(2)7000-6000=1000(元);(3)400=t6000,t =1528.(1)8xy =-;(2)126。
完整版)反比例函数经典习题及答案

完整版)反比例函数经典习题及答案反比例函数练题1.下列函数中,经过点(1.-1)的反比例函数解析式是()A。
y = 1/xB。
y = -1/xC。
y = 2/xD。
y = -2/x2.反比例函数y = -(k/ x)(k为常数,k ≠ 0)的图象位于()A。
第一、二象限B。
第一、三象限C。
第二、四象限D。
第三、四象限3.已知反比例函数y = (k - 2)/x的图象位于第一、第三象限,则k的取值范围是()A。
k。
2B。
k ≥ 2C。
k ≤ 2D。
k < 24.反比例函数y = k/x的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果三角形MON 的面积是2,则k的值为()A。
2B。
-2C。
4D。
-45.对于反比例函数y = 2/x,下列说法不正确的是()A。
点(-2.-1)在它的图象上B。
它的图象在第一、三象限C。
当x。
0时,y随x的增大而增大D。
当x < 0时,y随x的增大而减小6.反比例函数y = (2m - 1)x/(m^2 - 2),当x。
0时,y随x 的增大而增大,则m的值是()A。
±1B。
小于1的实数C。
-1D。
1/27.如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形P1A1O、P2A2O、P3A3O,设它们的面积分别是S1、S2、S3,则()。
A。
S1 < S2 < S3B。
S2 < S1 < S3C。
S3 < S1 < S2D。
S1 = S2 = S38.在同一直角坐标系中,函数y = -2与y = 2x的图象的交点个数为()A。
3B。
2C。
1D。
09.已知甲、乙两地相距s(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)与行驶速度v(km/h)的函数关系图象大致是()10.如图,直线y = mx与双曲线y = k/(x-2)交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若三角形ABM的面积为2,则k的值是()A。
反比例函数经典例题(有答案)

一、反比例函数的对称性1、直线y=ax (a>0)与双曲线y= 3/x 交于A (x i, y〔)、B (X2, y2)两点,贝U 4x i y2-3x2y i=2、如图1,直线y=kx (k>0)与双曲线y= 2/x交于A, B两点,若A B两点的坐标分别为A (x i, y i),B (x2, y2),贝U x i y2+x2y i 的值为( )A 、-8B 、4C 、-4D 、0解析:直线Y=KX和双曲线Y=2/X图象都关于原点对称因此两交点A、B也关于原点对称X2=-Xi, Y2=-Yi双曲线形式可变化为XY=2即双曲线上点的横纵坐标乘积为 2因此XiYi=2XiY2+X2Yi=Xi(-Yi) + (-Xi) Yi=-XiYi-XiYi=-4图i 图2 图3 图4二、反比例函数中“ K”的求法1、如图2,直线l是经过点(i, 0)且与y轴平行的直线.Rt△ ABC中直角边AC=4, BC=3将BC边在直线l上滑动,使A, B在函数y=k/x的图象上.那么k的值是( )A、3 B 、6 C 、i2 D 、i5/4解析:BC 在直线X=i 上,设B(i , M),贝U C(i, M-3), .••A(5, M-3), 又A B都在双曲线上,二i*M=5*(M-3) , M=i5/4 即K=i5/4 2、如图3,已知点A、B在双曲线y= k/x (x>0)上,Adx轴于点C, Bdy轴于点D, AC与BD交于点P, P是AC的中点,若△ ABP的面积为3,则k=解析:A(xi,k/xi),B(x2,k/x2)AC:x=xi BD:y=k/x2P(xi,k/x2)k/x2=k/2xi 2xi=x2BP=x2-xi=xiAP=k/xi-k/x2=k/2xiS=xi*k/(2xi)*i/2)=k/4=3 k=i23、如图4,双曲线y= k/x (k > 0)经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为3,则双曲线的解析式为( )A、y=i/xB、y=2/xC、y=3/xD、=6/解析:设E(x0,k/x0)E 是BC中点,二B(x0,2k/x0)B、D两点纵坐标相同,二D(x0/2,2k/x0)BD=x0/2,OC=x0,BC=2k/x0梯形面积=(BD+OC/ BC/2=3k/2=3•,- k=2 .•.双曲线的解析式为:y=2/x三、反比例函数“ K”与面积的关系1、如图5,已知双曲线y i=1/x(x >0) , y2=4/x(x >0),点P为双曲线y2=4/x上的一点,且PAlx 轴于点A, PBLy轴于点B, PA PB分别次双曲线y=/x于D C两点,则^ PCD的面积为( ) 图5 图6 图7解析:假设P的坐标为(a,b ),则C (a/4,b), D(a,b/4),PC=3/4*a PD=3/4*bS=1/2*3/4*a*3/4*b因为点P为双曲线y2=4/x上的一点所以a*b=4所以S=9/82、如图6,直线l和双曲线y=k/x(k >0)交于A B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为G D、E,连接OA OB 0P,设AAOC勺面积为S、△ BOD的面积为&、APOE的面积为S3,则( )A S I<S3B 、S I>S2>S3C 、S I=S2>&D 、S=S< S3解析:结合题意可得:AB者S在双曲线y=kx上,则有S1=S2而AB之间,直线在双曲线上方;故S1=SK S3.3、如图7,已知直线y=-x+3与坐标轴交于A、B两点,与双曲线y=k/x交于G D两点,且S3O C=&CO D=S\BOD 贝1J k=。
反比例函数精选练习题

反比例函数1.下列函数中,是反比例函数的为()A.y=B.y=C.y=2x+1 D.2y=x2.下列关系中,两个量之间为反比例函数关系的是()A.正方形的面积S与边长a的关系B.正方形的周长L与边长a的关系C.长方形的长为a,宽为20,其面积S与a的关系D.长方形的面积为40,长为a,宽为b,a与b的关系3.一司机驾驶汽车从甲地去乙地,他以平均80千米/小时的速度用了4个小时到达乙地,当他按原路匀速返回时.汽车的速度v千米/小时与时间t小时的函数关系是()A.v=320t B.v=C.v=20t D.v=4.如图,在同一平面直角坐标系中,反比例函数y=与一次函数y=kx﹣1(k为常数,且k >0)的图象可能是()A.B.C.D.5.反比例函数y=的图象如图所示,则一次函数y=kx+b(k≠0)的图象的图象大致是()A.B.C.D.6.如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=与y=﹣的图象均与正方形ABCD的边相交,则图中阴影部分的面积之和是()A.2 B.4 C.6 D.87.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(4a,a)是反比例函数y=(k>0)的图象上与正方形的一个交点,若图中阴影部分的面积等于16,则k的值为()A.16 B.1 C.4 D.﹣168.反比例函数y=的图象,当x>0时,y随x的增大而减小,则k的取值范围是()A.k<2 B.k≤2 C.k>2 D.k≥29.已知点A(x1,y1),(x2,y2)是反比例函数y=图象上的点,若x1>0>x2,则一定成立的是()A.y1>y2>0 B.y1>0>y2C.0>y1>y2D.y2>0>y110.反比例函数y=﹣(x<0)如图所示,则矩形OAPB的面积是()A.3 B.﹣3 C.D.﹣11.如图,在直角坐标系中,点A在函数y=(x>0)的图象上,AB⊥x轴于点B,AB的垂直平分线与y轴交于点C,与函数y=(x>0)的图象交于点D,连结AC,CB,BD,DA,则四边形ACBD的面积等于()A.2 B.2C.4 D.412.如图,点A是反比例函数(x>0)图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为()A.1 B.2 C.4 D.不能确定13.如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数y=经过另一条直角边AC的中点D,S△AOC=3,则k=()A.2 B.4 C.6 D.314.点A(1,y1)、B(3,y2)是反比例函数y=图象上的两点,则y1、y2的大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能确定15.反比例函数y=图象上三个点的坐标为(x1,y1)、(x2,y2)、(x3,y3),若x1<x2<0<x3,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y1<y3<y216.若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y3<y1C.y3<y2<y1D.y2<y1<y317.如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则该反比例函数的表达式为()A.y=B.y=C.y=D.y=18.如图,在同一平面直角坐标系中,直线y=k1x(k1≠0)与双曲线y=(k2≠0)相交于A,B两点,已知点A的坐标为(1,2),则点B的坐标为()A.(﹣1,﹣2)B.(﹣2,﹣1)C.(﹣1,﹣1)D.(﹣2,﹣2)19.如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b>的解集为()A.x<﹣6 B.﹣6<x<0或x>2 C.x>2 D.x<﹣6或0<x<220.如图,直线y=﹣x+b与x轴交于点A,与双曲线y=﹣(x<0)交于点B,若S△AOB=2,则b的值是()A.4 B.3 C.2 D.1二、解答题1.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x ≤10时,y与x成反比例).(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?2.如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数y=的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.(1)求反比例函数和一次函数的表达式;(2)求点C的坐标及△AOB的面积.3.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=.(1)求反比例函数的解析式;(2)连接OB,求△AOB的面积.4.如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.(1)求m、n的值并写出该反比例函数的解析式.(2)点E在线段CD上,S△ABE=10,求点E的坐标.5.在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=(k >0)图象与AC边交于点E.(1)请用k表示点E,F的坐标;(2)若△OEF的面积为9,求反比例函数的解析式.6.一次函数y=kx+b与反比例函数y=的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.(1)求一次函数与反比例函数的表达式;(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.。
初中数学千题解——反比例函数100题(练习版)

初中数学千题解——反比例函数100题(练习版)1.如图1.1所示,矩形ABCO中的顶点O与坐标原点重合,点A 在x轴上,点C在y轴上,反比例函数kyx(x≠0)的图像分布与BC、AB交于点E、F两点,连接AC.证明:(1)AC∥EF;(2)GE=FH2.如图1.2所示,矩形ABCO中的顶点O与坐标原点重合,点A 在x轴上,点C在y轴上,反比例函数kyx(x≠0)的图像分布与BC、BA的延长线交于点E、F两点,连接AC.证明:(1)AC∥EF;(2)GE=FH.图1.23.如图1.3所示,A 、B 是反比例函数1k y x第一象限图像上任意两点,射线OA 、OB 分别交反比例函数2 k yx的图像于C 、D 两点. 证明:(1)12k OAOC k ;(2)AB ∥CD .4.如图1.4所示,平行四边形ABCD 的顶点A 、B 位于反比例函数ky x第一象限的图像上,点C 、D 位于x 轴正半轴和y 轴正半轴上. 证明:(1)∠1=∠2,∠3=∠4.5.如图1.5所示,平行四边形ABCD的顶点A、B位于反比例函数kyx第一象限的图像上,点C、D分别位于y轴负半轴和x轴负半轴上,AD交y轴于点H,BC交x轴于点G.证明:(1)∠1=∠2,∠3=∠4;(2)四边形CDHG是菱形.6.如图1.6所示,A、B为反比例函数kyx第一象限图像上任意两点,连接AO并延长交反比例函数图像另一支于点C,连接BC交x轴于点G、交y轴于点F,连接AB并向两侧延长分别交x轴于点E、交y轴于点D.证明:∠1=∠2,∠3=∠4.7.如图1.7所示,在平面直角坐标系xOy中,点A、B在反比例函数4yx=(x>0)的图像上,延长AB交x轴于点C,且12BCAB=,连接OA交反比例函数1yx=(x>0)的图像于点D,则ABDS△=.8.如图1.8所示,双曲线4yx=(x>0)与直线EF交于点A、B,且AE=AB=BF,线段AO、BO 分别与双曲线2yx=(x>0)交于点C、D,则:(1)AB与CD的位置关系是;(2)四边形ABDC的面积为.9.如图1.9所示,直线y=-x与反比例函数kyx=的图像交于A、B两点,过点B作BD∥x轴,交y轴于点D,延长AD交反比例函数kyx=的图像于另一点C,则BCAC的值为.10.如图1.10所示,已知四边形ABCD是平行四边形,BC=2AB,A、B两点的坐标分别是(-1,0)和(0,2),C、D两点在反比例函数kyx的图像上,则k=.11.如图1.11所示,□ABCD的顶点A、B的坐标分别是A(-1,0)、B(0,-2),顶点C、D在双曲线y=kx上,边AD交y轴于点E,且四边形BCDE的面积是△ABE的面积的5倍,则k= ;12.如图1.12所示;A、B为反比例函数y=kx 第一象限图像上任意两点,连接B O并延长交反比例函数图像另一支于点C,连接AC交x轴于点F、交y轴于点G,连接BG,连接AB并向外两侧延长分别交x轴于点E、交y轴于点D;已知BEAB =12,S△GBO=1,则k= ;图1.1113. 如图1.13所示;在平面直角坐标系x O y 中,A (1,m )、B (n ,a )在反比例函数y =kx (k >0,x >0)的图像上,∠A O B =45°;(1)若a =12,已知∠A O B =∠O BA ,求k ;(2)若a =√63,求k14. 如图1.14所示;已知点A 、B 分别在反比例函数y =k x (x >0)和y =?4x (x >0)的图像上,且O A ⊥O B ,则OBOA 的值为;图1.12图1.1315. 如图1.15所示;已知点A (2,3)和点B (0,2),点A 在反比例函数y =kx的图像上,作AB ,再将射线AB 绕点A 按逆时针方向旋转45°,交反比例函数的图像于点C ,则点C 的坐标为;图1.14图1.1516.如图1.16所示,反比例函数y=kx的图像经过点(-1,-),点A是该图像第一象限分支上的动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当ADCDC的坐标为____________.图1.1617.如图1.17所示,点P在双曲线y=kx(x>0)的图像上,以点P为圆心的⊙P与两坐标轴都相切,点E为y轴负半轴上的一点,过点P作PF⊥PE交x轴于点F,若OF -OE=10,则k的值是___________.18.如图1.18所示,正方形A1B1P1P2的顶点P1、P2在反比例函数y=4x(x>0)的图像上,顶点A1、B1分别在x轴和y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=4x(x>0)的图像上,顶点A2在x轴的正半轴上,则点P2的坐标为__________,点P3的坐标为__________.图1.1819.如图1.19所示,在平面直角坐标系xOy中,△ABC为等边三角形,顶点C在y轴的负半轴上,点A(1)、点B在第一象限,经过点A的反比例函数y=kx(x>0)的图像恰好经过顶点B,求△ABC 的边长.20.如图1.20所示,反比例函数y 1=-1x的图像有一个动点A ,过点A 、O 作直线y 2=ax ,交图像的另一支于点B.若在第一象限内有一点C ,满足AC =BC ,当点A 运动时,点C 始终在反比例函数y =kx的图像上运动,且tan ∠CAB =2,求k 的值.21、如图1.21所示,点A 是双曲线xy 9-=第二象限分支上的一个动点,连接AO 并延长交另一分支于点B ,以AB 为底作等腰△ABC ,且∠ACB=1200,点C 在第一象限,随着点A 的运动,点C 的位置也不断变化,但点C 始终在双曲线xky =上运动,则k 的值为___________。
反比例函数十大经典题型

反比例函数十大经典题型(原创实用版)目录1.反比例函数的定义与性质2.反比例函数的图像与画法3.待定系数法在反比例函数中的应用4.反比例函数的比较大小问题5.反比例函数与直线的交点问题6.反比例函数的中点问题7.反比例函数的平行线问题8.反比例函数的内插法问题9.反比例函数的外插法问题10.反比例函数的实际应用问题正文一、反比例函数的定义与性质反比例函数是指两个变量之间的关系,当一个变量的值增大时,另一个变量的值会减小,而且它们的乘积保持不变。
反比例函数的一般形式为y=k/x,其中 k 是常数。
二、反比例函数的图像与画法反比例函数的图像是一条双曲线,它有两条渐近线,当 x 趋近于 0 时,y 趋近于无穷大;当 x 趋近于无穷大时,y 趋近于 0。
画反比例函数的图像时,可以先确定渐近线,然后在渐近线之间取一个点,以此点为起点,画出双曲线。
三、待定系数法在反比例函数中的应用待定系数法是求解反比例函数的常用方法,它的一般步骤是:先设反比例函数的关系式,然后根据题目的条件,列出方程组,解方程组得到 k 值,最后代入关系式求得函数的解析式。
四、反比例函数的比较大小问题比较反比例函数的大小问题通常是通过比较函数值的大小来解决的。
例如,若点 A(1, y1) 和点 B(2, y2) 在反比例函数 y=k/x 的图像上,则可以通过比较 y1 和 y2 的大小来判断 k 的取值范围。
五、反比例函数与直线的交点问题反比例函数与直线的交点问题可以通过解方程组来解决。
设反比例函数为 y=k/x,直线的解析式为 y=ax+b,将两个方程联立,解得 x 和 y 的值,即可得到交点。
六、反比例函数的中点问题反比例函数的中点问题通常是通过求解中点坐标来解决的。
设反比例函数为 y=k/x,已知两点 A(x1, y1) 和 B(x2, y2),则中点 M 的坐标为 ((x1+x2)/2, (y1+y2)/2)。
七、反比例函数的平行线问题反比例函数的平行线问题可以通过比较函数的斜率来解决。
反比例函数》测试题(含答案)

反比例函数》测试题(含答案)1、选择题(每小题5分,共50分)1、若点(x1.-1)、(x2.-2)、(x3.1)都在反比例函数y= k/x 上,则它们之间的大小关系是()A.x1<x3<x2B.x2<x1<x3C.x1<x2<x3D.x2<x3<x12、若反比例函数y=k/x的图象经过点(m,3m),其中m≠0,则此反比例函数的图象在()A.第一、二象限;B.第一、三象限;C.第二、四象限;D.第三、四象限3、在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=3/x上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小4、函数y=-kx与函数y=k/x的图象的交点个数是()A。
0B。
1C。
2D.不确定5、函数y=6-x与函数y=k/x的图象交于A、B两点,设点A的坐标为(x1,y1),则边长分别为x1、y1的矩形面积和周长分别为()A。
4,12B。
4,6C。
8,12D。
8,66、已知y1+y2=y,其中y1与x成反比例,且比例系数为k1,而y2与x2成正比例,且比例系数为k2,若x=-1时,y=0,则k1,k2的关系是( )A.k1+k2=0B.k1k2=1C.k1-k2=0D.k1k2=-17、正比例函数y=2kx与反比例函数y=k/(x-1)在同一坐标系中的图象不可能是()18、如图,直线y=mx与双曲线y=k/(x-1)交与A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是()A、2B、m-2C、mD、49、如图,点A在双曲线y=6/x上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )A.47B.5C.27D.2210、如图,反比例函数y= k/x的图象经过点(1,2),则k=()。
二、填空题(每小题5分,共20分)11、若y=k/x是反比例函数,且x1y1=x2y2,则k=______。
(完整版)反比例函数练习题集锦(含答案)

反比例函数练习题集锦(含答案)1、综合题1、如图,已知直线与双曲线交于两点,且点的横坐标为.(1)求的值;(2)若双曲线上一点的纵坐标为8,求的面积;(3)过原点的另一条直线交双曲线于两点(点在第一象限),若由点为顶点组成的四边形面积为,求点的坐标.2、已知一次函数与双曲线在第一象限交于A、B两点,A点横坐标为1.B点横坐标为4(1)求一次函数的解析式;(2)根据图象指出不等式的解集;(2) 点P是x轴正半轴上一个动点,过P点作x轴的垂线分别交直线和双曲线于M、N,设P点的横坐标是t(t>0),△OMN的面积为S,求S和t的函数关系式,并指出t的取值范围。
二、简答题3、.已知:如图,在平面直角坐标系中,直线AB 分别与轴交于点B、A,与反比例函数的图象分别交(1)求该反比例函数的解析式;(2)求直线AB的解析式.4、如图,已知正比例函数与反比例函数的图象交于两点.(1)求出两点的坐标;的范围;(2)根据图象求使正比例函数值大于反比例函数值的三、计算题5、为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒。
已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t 的函数关系为(为常数)。
如下图所示,据图中提供的信息,解答下列问题:(1)写出从药物释放开始,y与t之间的两个函数关系式及相应的自变量取值范围;(2)据测定,当空气中每立方米和含药量降低到0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?6、如图,在直角坐标系xOy中,一次函数y=k1x+b 的图象与反比例函数的图象交于A(1,4).B(3,m)两点。
(1)求一次函数的解析式;的面积。
(2)求△AOB7、如图,一次函数y=kx+b的图象与反比例函数y=图象交于A(-2,1)、B(1,n)两点.(1) 求反比例函数和一次函数的解析式.(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.(1)试确定上述反比例函数和一次函数的表达式;(2)求△AOB的面积。
反比例函数经典例题

反比例函数经典例题1.(北京模拟)如图,直线AB经过第一象限,分别与%轴、》轴交于A、B两点,P为线段AB 上任意一点(不与A、B重合),过点P分别向%轴、y轴作垂线,垂足分别为。
、。
.设OC=%,四边形OCPD的面积为S.(1)若已知4(4,0),B(0,6),求S与%之间的函数关系式;39(2)若已知4(a,0),B(0,b),且当%=彳时,S有最大值不,求直线AB的解析式;48(3)在(2)的条件下,在直线AB上有一点M,且点M到%轴、y轴的距离相等,点N在过M 点的反比例函数图象上,且■OAN是直角三角形,求点N的坐标.2.(北京模拟)已知点A是双曲线y=k(k1>0)上一点,点A的横坐标为1,过点A作平行于y轴的直线,与%轴交于点B,与双曲线y=k2(k2<0)交于点C.点D(m,0)是%轴上一点,且位于直线AC右侧,E是AD的中点.(1)如图1,当m=4时,求△ACD的面积(用含k1、k2的代数式表示);(2)如图2,若点E恰好在双曲线y=与(k1>0)上,求m的值;(3)如图3,设线段EB的延长线与y轴的负半轴交于点R当m=2时,若△BDF的面积为1,且CF//AD,求k1的值,并直接写出线段CF的长.图1图2图33.(上海模拟)Rt△ABC在直角坐标系中的位置如图所示,tan/BAC=1,反比例函数yk=~(k十0)在第一象限内的图象与BC边交于点D(4,m),与AB边交于点E(2,n),x△BDE的面积为2.(1)求反比例函数和直线AB的解析式;4.(安徽某校自主招生)如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在%轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD.(1)若直线y=kx+m(k十0)过B、D两点,求k的值;m(2)在(1)的条件下,反比例函数y=7的图象经过点B.xm①求证:反比例函数y=m的图象与直线AB必有两个不同的交点;x②已知点P(p,-n-1),Q(q,-n—2)在线段AB上,当点E落在线段PQ上时,求n的取值范围.5.(浙江杭州)在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).(1)当k=-2时,求反比例函数的解析式;(2)要使反比例函数与二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q,当A ABQ是以AB为斜边的直角三角形时,求k的值.6.(浙江义乌)如图,矩形OABC的顶点A、C分别在l、y轴的正半轴上,点D为对角线kOB的中点,点E(4,n)在边AB上,反比例函数y=-在第一象限内的图象经过点D、E,x 1且tan Z BOA=2.(1)求反比例函数的解析式;(2)若反比例函数的图象与矩形的边BC交于点F将矩形折叠,使点O与点F重合,折痕分别与%、y轴正轴交于点H、G,求线段OG的长.7.(浙江某校自主招生)已知点P的坐标为(m,0),在%轴上存在点Q(不与P重合),以PQ为边,Z PQM=60°作菱形PQMN,使点M落在反比例函数y=-2^的图象上.x(1)如图所示,若点P的坐标为(1,0),图中已经画出一个符合条件的菱形PQMN,若另一个菱形为PQ1M1N1,求点M1的坐标;(2)探究发现,当符合上述条件的菱形只有两个时,一个菱形的顶点M在第四象限,另一个菱形的顶点M1在第二象限.通过改变P点坐标,对直线MM1的解析式y=kx+b进行探究可得k=,若点P的坐标为(m,0),则k=(用含m的代数式表示);(3)继续探究:①若点P的坐标为(m,0),则m在什么范围时,符合上述条件的菱形分别为两个、三个、四个?②求出符合上述条件的菱形刚好有三个时,点M坐标的所有情况.备用图8 .(浙江模拟)如图,在平面直角坐标系中,△AOB 的顶点O 是坐标原点,点A 坐标为(1,k 3),A 、B 两点关于直线y =%对称,反比例函数y =-(%>0)图象经过点A ,点P 是直线y %9 .(浙江模拟)已知点P (m ,n )是反比例函数y =6(%>0)图象上的动点,PA 〃1轴,%3 PB 〃y 轴,分别交反比例函数y =-(%>0)的图象于点A 、B ,点C 是直线y =2%上的一点.%(1)请用含m 的代数式分别表示P 、A 、B 三点的坐标; (2)在点P 运动过程中,连接AB ,△PAB 的面积是否变化,若不变,请求出△PAB 的面积;若改变,请说明理由;(3)在点P 运动过程中,以点P 、A 、B 、C 为顶点的四边形能否为平行四边形,若能,请求出此时m 的值;若不能,请说明理由.=%上一动点.(1)填空:B 点的坐标为( ); (2)若点C 是反比例函数图象上一点,是否存在这样的点C ,使得以A 、B 、C 、P 四点为 顶点的四边形是平行四边形?若存在,求出点C 坐标; (3)若点Q 是线段OP 上一点(Q 不与O 、P 重合),分别作直线OA 和直线AP 的垂线,垂足分别为E 、F ,Q 点坐标. 若不存在,请说明理由;当四边形AOBP 为菱形时,过点Q 当QE +QF +QB 的值最小时,求出11.(江苏泰州)如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2c5=x的图象相交于B(-1,5)、C(2,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点. (1)求k、b的值;3c(2)设-1<m<5,过点P作x轴的平行线与函数y2=]的图象相交于点。
完整版)反比例函数练习题含答案

完整版)反比例函数练习题含答案测试1 反比例函数的概念一、填空题1.一般的,形如 y=k/x 的函数称为反比例函数,其中x是自变量,y是因变量。
自变量x的取值范围是x≠0.2.写出下列各题中所要求的两个相关量之间的函数关系式,并指出函数的类别。
1) 商场推出分期付款购电脑活动,每台电脑元,首付4000元,以后每月付y元,x个月全部付清,则y=(8000+)/x,是反比例函数。
2) 某种灯的使用寿命为1000小时,它的使用天数y与平均每天使用的小时数x之间的关系式为 y=1000/x,是反比例函数。
3) 设三角形的底边、对应高、面积分别为a、h、S。
当a=10时,S与h的关系式为 S=10h/2,是正比例函数;当S=18时,a与h的关系式为 h=36/a,是反比例函数。
4) 某工人承包运输粮食的总数是w吨,每天运x吨,共运了y天,则 y=w/x,是反比例函数。
3.下列各函数 y=1/(k2+1)、y=x/(x5+x12)、y=14-3x、y=2x和y=3x-1 中,是y关于x的反比例函数的有:①y=1/(k2+1)、② y=x/(x5+x12)、③ y=2x。
4.若函数 y=m/(x-1) (m是常数) 是反比例函数,则 m=1,解析式为 y=1/(x-1)。
5.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜片的焦距为0.25m,则 y=1000/x。
二、选择题6.已知函数 y=3x/(kx+1),当x=1时,y=-3,那么这个函数的解析式是 y=3x/(3k+1)。
(解析:由 y=-3=3/(3k+1) 可得 k=-1/3,代入原式得 y=3x/(3x-1)。
)7.已知 y 与 x 成反比例,当 x=3 时,y=4,那么 y=3 时,x 的值等于 4/3.三、解答题8.已知 y 与 x 成反比例,当 x=2 时,y=3.1) 求y 与x 的函数关系式:y=k/x,代入已知条件得k=6,因此函数关系式为 y=6/x。
反比例函数题型 专项练习

反比例函数题型专项练习专题一、反比例函数的图像1.反比例函数的定义域为x≠0,因此选项A中的x≥1是错误的。
应该改为x>0.2.由于y=kx+1与y=(k≠0)的图象大致是两条直线,因此它们交于点A(2,1)的横坐标应该在x>0的范围内。
因此选项B、C、D中的x<或x≤2都是错误的。
应该改为x>2.答案:A。
3.当ab>0时,函数y=ax+b与函数y=的图象大致是两条直线,其中一条斜率为a,另一条斜率为(1/a)。
因此选项D 中的图象是错误的。
应该改为y=。
答案:C。
4.方程x+1=0的解为x=−1,不在1<x<2的范围内,因此选项A、B、C都是错误的。
应该改为选项D,k=6.答案:D。
5.正比例函数y=kx的图象是一条直线,反比例函数y=的图象是一条双曲线。
因此选项A是错误的。
应该改为选项B、C、D。
答案:B、C、D。
6.函数y=的图象是一条双曲线,当y=a时,对应的x有两个不相等的值,即x=±(1/a)。
因此选项A、B、D都是错误的。
应该改为选项C。
答案:C。
7.函数y=k1x﹣1的图象是一条双曲线,函数y=的图象是一条直线。
因此选项A是错误的。
应该改为选项B、C、D。
答案:B、C、D。
8.函数y=的图象是一条双曲线,函数y=kx﹣k(k≠0)的图象是一条直线。
因此选项A、C、D都是错误的。
应该改为选项B。
答案:B。
9.函数y=ax+b的图象是一条直线,函数y=的图象是一条双曲线。
因此选项B、C、D都是错误的。
应该改为选项A。
答案:A。
10.函数y=的图象在第一、二象限,因为x>0,y>0.因此选项B是错误的。
应该改为选项A、C、D。
答案:A、C、D。
11.当k<0时,函数y1=kx﹣k的图象是一条双曲线,因此选项A、B、D都是错误的。
应该改为选项C。
答案:C。
12.图中反比例函数与一次函数的图象相交于A、B两点,使反比例函数的值小于一次函数的值的x的取值范围为x<﹣1,或1<x<2.因此选项B、C、D都是错误的。
反比例函数的应用六种题型

反比例函数实际应用的六种题型题型一:在面积中的应用 一:面积不变性(k 的几何意义)如图,设点P (a ,b )是反比例函数y=xk上任意一点,作PA ⊥x 轴于A 点,PB ⊥y 轴于B 点,则矩形PBOA 的面积是k (三角形PAO和三角形PBO 的面积都是k 21;面积是正数,所以k 要加绝对值) S 矩形PBOA =k ; S 三角形PAO =S 三角形PBO =k 21注意: (1)面积与P 的位置无关,即(0)ky k x=≠的面积不变性(2)当k 符号不确定的情况下须分类讨论S △ABC =︱K ︱; S ABCD =2︱K ︱二、曲直结合(一次函数与反比例函数)典型例题例1 如图,点P 是反比例函数xy 2=图象上的一点,PD ⊥x 轴于D.则△POD 的面积为 .例2 如图,已知,A,B 是双曲线)0(>=k xk y 上的两点,(1)若A(2,3),求K 的值;(2)在(1)的条件下,若点B 的横坐标为3,连接OA,OB,AB ,求△OAB 的面积。
(3)若A,B 两点的横坐标分别为a,2a ,线段AB 的延长线交X 轴于点C ,若6=∆AOC S ,求K 的值变式1 在双曲线)0(>=x xk y 上任一点分别作x 轴、y 轴的垂线段,与x 轴y 轴围成矩形面积为12,求函数解析式__________。
变式2 如图,在反比例函数2y x=(0x >)的图象上,有点1P ,2P ,3P ,4P 它们的横坐标依次为1,2,3,4.分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影部分的面积从左到右依次为1S ,2S ,3S ,求123S S S ++.S 3S 2S 11 2 3 4y=2xP 4P 3P 2xyO P 1变式3 如图,点P,Q是反比例函数y= 图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1,△QMN的面积记为S2,则S1________S2.(填“>”或“<”或“=”)变式4 已知A B C D E,,,,是反比例函数16yx=()0x>图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形,则这五个橄榄形的面积总和是__________(用含π的代数式表示)变式5 如图正方形OABC的面积为4,点O为坐标原点,点B在函数kyx=(0,0)k x<<的图象上,点P(m,n)是函数kyx=(0,0)k x<<的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F.(1)设矩形OEPF的面积为S l,判断S l与点P的位置是否有关(不必说理由).(2)从矩形OEPF的面积中减去其与正方形OABC重合的面积,剩余面积记为S2,写出S2与m的函数关系,并标明m的取值范围.(8分)总结:一个性质:反比例函数的面积不变性AB COyxy=16xEDCBAyx O两种思想:分类讨论和数形结合题型二:在工程与速度中的应用一、工程问题工作总量=工作效率×工作时间;合做的效率=各单独做的效率的和。
反比例函数经典例题(含详细解答)解析
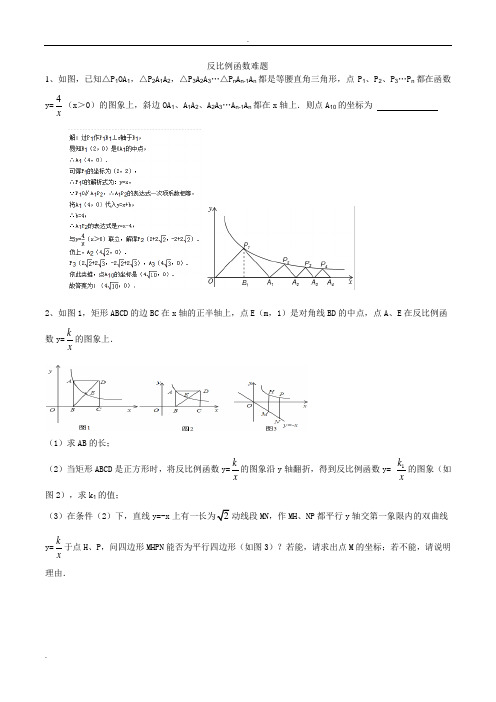
反比例函数难题1、如图,已知△P1OA1,△P2A1A2,△P3A2A3…△P n A n-1A n都是等腰直角三角形,点P1、P2、P3…P n都在函数2、如图1,矩形ABCD的边BC在x轴的正半轴上,点E(m,1)是对角线BD的中点,点A、E在反比例函数y=(1)求AB的长;(2)当矩形ABCD是正方形时,将反比例函数y=kx的图象沿y轴翻折,得到反比例函数y=1kx的图象(如图2),求k1的值;(3)在条件(2)下,直线y=-x上有一长为2动线段MN,作MH、NP都平行y轴交第一象限内的双曲线y=kx于点H、P,问四边形MHPN能否为平行四边形(如图3)?若能,请求出点M的坐标;若不能,请说明理由.1.已知反比例函数y=2kx和一次函数y=2x-1,其中一次函数的图象经过(a ,b ),(a+k ,b+k+2)两点.(1)求反比例函数的解析式;(2)求反比例函数与一次函数两个交点A 、B 的坐标: (3)根据函数图象,求不等式2kx>2x-1的解集; (4)在(2)的条件下,x 轴上是否存在点P ,使△AOP 为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由.1.如图,在平面直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象与反比例函数y =(m ≠0)的图象交于二、四象限内的A 、B 两点,与x 轴交于C 点,点B 的坐标为(6,n ),线段OA =5,E 为x 轴负半轴上一点,且s i n ∠AOE =45.(1)求该反比例函数和一次函数; (2)求△AOC 的面积.(1)过A 点作AD⊥x 轴于点D ,∵sin ∠AOE = 45,OA =5,∴在Rt△ADO 中,∵sin∠AOE=AD AO =AD 5= 45,xm∴AD=4,DO =OA2-DA2=3,又点A 在第二象限∴点A 的坐标为(-3,4),将A 的坐标为(-3,4)代入y = m x ,得4=m -3∴m=-12,∴该反比例函数的解析式为y =-12x ,∵点B 在反比例函数y =-12x 的图象上,∴n=-126=-2,点B 的坐标为(6,-2), ∵一次函数y =kx +b(k≠0)的图象过A 、B 两点,∴⎩⎨⎧-3k +b=4,6k +b =-2,∴⎩⎨⎧k =-23, b =2∴ 该一次函数解析式为y =-23x +2.(2)在y =-23x +2中,令y =0,即-23x +2=0,∴x=3,∴点C 的坐标是(3,0),∴OC =3, 又DA=4, ∴S△AOC=12×OC×AD=12×3×4=6,所以△AOC 的面积为6.练习1.已知Rt△ABC 的斜边AB 在平面直角坐标系的x 轴上,点C (1,3)在反比例函数y = k x的图象上,且sin∠BAC = 35.(1)求k 的值和边AC 的长; (2)求点B 的坐标.(1)把C (1,3)代入y = kx得k =3设斜边AB 上的高为CD ,则sin∠BAC =CD AC =35∵C (1,3) ∴CD=3,∴AC=5(2)分两种情况,当点B 在点A 右侧时,如图1有:AD=52-32=4,AO=4-1=3 ∵△ACD ∽ABC ∴AC 2=AD ·AB ∴AB=AC 2AD =254∴OB=AB -AO=254-3=134 图1此时B 点坐标为(134,0)图2 当点B 在点A 左侧时,如图2 此时AO=4+1=5 OB= AB -AO=254-5=54此时B 点坐标为(-54,0)所以点B 的坐标为(134,0)或(-54,0).1.如图,矩形ABOD 的顶点A 是函数与函数在第二象限的交点,轴于B ,轴于D ,且矩形ABOD 的面积为3.(1)求两函数的解析式.(2)求两函数的交点A 、C 的坐标. (3)若点P 是y 轴上一动点,且,求点P 的坐标.解:(1)由图象知k<0,由结论及已知条件得-k=3 ∴∴反比例函数的解析式为,一次函数的解析式为(2)由,解得,∴点A 、C 的坐标分别为(,3),(3,)(3)设点P 的坐标为(0,m ) 直线与y 轴的交点坐标为M (0,2)∵O xyB A CD∴∣PM∣=,即∣m-2∣=,∴或,∴点P的坐标为(0,)或(0,)1.如图,已知,是一次函数的图像和反比例函数的图像的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线与轴的交点的坐标及三角形的面积.解:(1)在上.反比例函数的解析式为:.点在上经过,,解之得一次函数的解析式为:(2)是直线与轴的交点当时,点1.(1)探究新知如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.(2)结论应用:①如图2,点M,N在反比例函数(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行。
(专题精选)初中数学反比例函数全集汇编含答案解析

(专题精选)初中数学反比例函数全集汇编含答案解析一、选择题1.已知1122(,),,)A x y Bx y (均在反比例函数2y x=的图像上,若120x x <<,则12,y y 的大小关系是( ) A .120y y << B .210y y <<C .120y y <<D .210y y <<【答案】D 【解析】 【分析】先根据反比例函数的性质判断出函数图象所在的象限,再根据反比例函数的性质即可作出判断. 【详解】解:∵反比例函数2y x=中k=2>0, ∴此函数的图象在一、三象限,且在每一象限内y 随x 的增大而减小, ∵0<x l <x 2,∴点A (x 1,y 1),B (x 2,y 2)均在第一象限, ∴0<y 2<y l . 故选:D . 【点睛】此题考查反比例函数图象上点的坐标特点,熟知反比例函数图象的增减性是解题的关键.2.已知点A (﹣2,y 1),B (a ,y 2),C (3,y 3)都在反比例函数4y x=的图象上,且﹣2<a <0,则( ) A .y 1<y 2<y 3 B .y 3<y 2<y 1C .y 3<y 1<y 2D .y 2<y 1<y 3【答案】D 【解析】 【分析】根据k >0,在图象的每一支上,y 随x 的增大而减小,双曲线在第一三象限,逐一分析即可. 【详解】 ∵反比例函数y=4x中的k=4>0, ∴在图象的每一支上,y 随x 的增大而减小,双曲线在第一三象限, ∵-2<a <0, ∴0>y 1>y 2,∵C (3,y 3)在第一象限,∴y 3>0, ∴213y y y <<, 故选D . 【点睛】本题考查了反比例函数的性质,熟练地应用反比例函数的性质是解题的关键.3.如图,点A 在双曲线4y x=上,点B 在双曲线(0)k y k x =≠上,AB x P 轴,交y 轴于点C .若2AB AC =,则k 的值为( )A .6B .8C .10D .12【答案】D 【解析】 【分析】过点A 作AD ⊥x 轴于D ,过点B 作BE ⊥x 轴于E ,得出四边形ACOD 是矩形,四边形BCOE 是矩形,得出ACOD S 矩形=4,BCOE S k =矩形,根据AB=2AC ,即BC=3AC ,即可求得矩形BCOE 的面积,根据反比例函数系数k 的几何意义即可求得k 的值. 【详解】过点A 作AD ⊥x 轴于D ,过点B 作BE ⊥x 轴于E , ∵AB ∥x 轴,∴四边形ACOD 是矩形,四边形BCOE 是矩形, ∵AB=2AC , ∴BC=3AC , ∵点A 在双曲线4y x=上, ∴ACOD S 矩形=4, 同理BCOE S k =矩形,∴矩形3BCOE ACOD S S =矩形矩形=12, ∴k=12, 故选:D .【点睛】本题考查了反比例函数图象上点的坐标特征,反比例系数k 的几何意义,作出辅助线,构建矩形是解题的关键.4.如图,点P 是反比例函数(0)ky k x=≠的图象上任意一点,过点P 作PM x ⊥轴,垂足为M . 连接OP . 若POM ∆的面积等于2. 5,则k 的值等于 ( )A .5-B .5C . 2.5-D .2. 5【答案】A 【解析】 【分析】利用反比例函数k 的几何意义得到12|k|=2,然后根据反比例函数的性质和绝对值的意义确定k 的值. 【详解】解:∵△POM 的面积等于2.5, ∴12|k|=2.5, 而k <0, ∴k=-5, 故选:A . 【点睛】本题考查了反比例函数系数k 的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数的性质.5.如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=﹣5x(x<0)的图象交于C,D两点,点C的横坐标为﹣1,过点C作CE⊥y轴于点E,过点D作DF ⊥x轴于点F.下列说法正确的是()A.b=5B.BC=ADC.五边形CDFOE的面积为35D.当x<﹣2时,y1>y2【答案】B【解析】【分析】根据函数值与相应自变量的关系,可得C点坐标,根据待定系数法,可得一次函数解析式,可判断A选项;根据解方程组,可得C、D点的坐标,根据全等三角形的判定与性质,可判断B选项;根据图形的分割,可得梯形、矩形,根据面积的和差,可判断C选项;根据函数与不等式的关系:函数图象在上方的函数值大,可判断D选项.【详解】解:由反比例函数y2=﹣5x(x<0)经过C,点C的横坐标为﹣1,得y=﹣51-=5,即C(﹣1,5).反比例函数与一次函数交于C、D点,5=﹣1+b,解得b=6,故A错误;CE⊥y轴于E点,E(0,﹣5),BE=6﹣5=1.反比例函数与一次函数交于C、D点,联立65y xyx=+⎧⎪⎨=-⎪⎩,x2+6x+5=0解得x1=﹣5,x2=﹣1,当x =﹣5时,y =﹣5+6=1, 即D (﹣5,1),即DF =1, 在△ADF 和△CBE 中,DAF BCE AFD CEB DF BE ∠=∠⎧⎪∠=∠⎨⎪=⎩, △ADF ≌△CBE (AAS ), AD =BC ,故B 正确; 作CG ⊥x 轴,S △CDFOE =S 梯形DFGC +S 矩形CGOE =()(15)422DF CG FG OG CG ++⨯+g +1×5=17,故C 错误;由一次函数图象在反比例函数图象上方的部分, 得﹣5<x <﹣1,即当﹣5<x <﹣1时,y 1>y 2,故D 错误; 故选:B . 【点睛】本题考查了反比例函数综合题,利用了自变量与函数值的对应关系,点的坐标与函数解析式的关系,全等三角形的判定与性质,图形分割法求图形的面积,函数图象与不等式的关系.6.如图,四边形OABF 中,∠OAB =∠B =90°,点A 在x 轴上,双曲线ky x=过点F ,交AB 于点E ,连接EF .若BF 2OA 3=,S △BEF =4,则k 的值为( )A.6 B.8 C.12 D.16【答案】A【解析】【分析】由于23BFOA=,可以设F(m,n)则OA=3m,BF=2m,由于S△BEF=4,则BE=4m,然后即可求出E(3m,n-4m),依据mn=3m(n-4m)可求mn=6,即求出k的值.【详解】如图,过F作FC⊥OA于C,∵23 BFOA=,∴OA=3OC,BF=2OC ∴若设F(m,n)则OA=3m,BF=2m ∵S△BEF=4∴BE=4 m则E(3m,n-4m)∵E在双曲线y=kx上∴mn=3m(n-4m)∴mn=6即k=6.故选A.【点睛】此题主要考查了反比例函数的图象和性质、用坐标表示线段长和三角形面积,表示出E点坐标是解题关键.7.如图,,A B是双曲线kyx=上两点,且,A B两点的横坐标分别是1-和5,ABO-∆的面积为12,则k 的值为( )A .3-B .4-C .5-D .6-【答案】C 【解析】 【分析】分别过点A 、B 作AD ⊥x 轴于点D ,BE ⊥x 轴于点E ,根据S △AOB =S 梯形ABED +S △AOD - S △BOE =12,故可得出k 的值. 【详解】分别过点A 、B 作AD ⊥x 轴于点D ,BE ⊥x 轴于点E ,∵双曲线ky x=的图象的一支在第二象限 ∴k<0,∵A ,B 两点在双曲线ky x =的图象上,且A ,B 两点横坐标分别为:-1,-5, ∴A (-1,-k ),B (-5, 5k-)∴S △AOB =S 梯形ABED +S △AOD - S △BOE=1||11||(||)(51)1||525225k k k k ⨯+⨯-+⨯⨯-⨯⨯=12||5k =12, 解得,k=-5 故选:C . 【点睛】本题考查反比例函数系数k 的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.8.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.﹣5 B.﹣4 C.﹣3 D.﹣2【答案】C【解析】分析:根据题意可以求得点B的坐标,从而可以求得k的值.详解:∵四边形ABCD是菱形,∴BA=BC,AC⊥BD,∵∠ABC=60°,∴△ABC是等边三角形,∵点A(1,1),∴OA=,∴BO=,∵直线AC的解析式为y=x,∴直线BD的解析式为y=-x,∵OB=,∴点B的坐标为(−,),∵点B在反比例函数y=的图象上,∴,解得,k=-3,故选C.点睛:本题考查反比例函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.9.如图,是反比例函数3yx=和7yx=-在x轴上方的图象,x轴的平行线AB分别与这两个函数图象相交于点,A B,点P在x轴上.则点P从左到右的运动过程中,APB△的面积是()A .10B .4C .5D .从小变大再变小【答案】C 【解析】 【分析】连接AO 、BO ,由AB ∥x 轴,得ABP ABO S S =V V ,结合反比例函数比例系数的几何意义,即可求解. 【详解】连接AO 、BO ,设AB 与y 轴交于点C . ∵AB ∥x 轴,∴ABP ABO S S =V V ,AB ⊥y 轴, ∵73522ABO BOC AOC S S S -=+=+=V V V , ∴APB △的面积是:5. 故选C .【点睛】本题主要考查反比例函数比例系数的几何意义,掌握反比例函数图象上的点与原点的连线,反比例函数图象上的点垂直于坐标轴的垂线段以及坐标轴所围成的三角形面积等于反比例函数比例系数绝对值的一半,是解题的关键.10.方程2x 3x 10+-=的根可视为函数3y x =+的图象与函数1y x=的图象交点的横坐标,则方程3x 2x 10+-=的实根x 0所在的范围是( ) A .010<x <4B .011<x <43C .011<x <32D .01<x <12【答案】C 【解析】 【分析】首先根据题意推断方程x 3+2x-1=0的实根是函数y=x 2+2与1y x=的图象交点的横坐标,再根据四个选项中x 的取值代入两函数解析式,找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程x 3+2x-1=0的实根x 所在范围. 【详解】解:依题意得方程3x 2x 10+-=的实根是函数2y x 2=+与1y x=的图象交点的横坐标,这两个函数的图象如图所示,它们的交点在第一象限.当x=14时,21y x 2216=+=,1y 4x ==,此时抛物线的图象在反比例函数下方; 当x=13时,21229y x =+=,1y 3x==,此时抛物线的图象在反比例函数下方; 当x=12时,21224y x =+=,1y 2x==,此时抛物线的图象在反比例函数上方; 当x=1时,2y x 23=+=,1y 1x==,此时抛物线的图象在反比例函数上方. ∴方程3x 2x 10+-=的实根x 0所在范围为:011<x <32. 故选C . 【点睛】此题考查了学生从图象中读取信息的数形结合能力.解决此类识图题,同学们要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.11.函数y =1-k x 与y =2x 的图象没有交点,则k 的取值范围是( ) A .k<0B .k<1C .k>0D .k>1【答案】D【解析】【分析】由于两个函数没有交点,那么联立两函数解析式所得的方程无解.由此可求出k 的取值范围.【详解】 令1-k x =2x ,化简得:x 2=1-2k ;由于两函数无交点,因此1-2k <0,即k >1. 故选D .【点睛】 函数图象交点坐标为两函数解析式组成的方程组的解.如果两函数无交点,那么联立两函数解析式所得的方程(组)无解.12.如图,在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积(mL)V 与气体对气缸壁产生的压强(kPa)P 的关系可以用如图所示的函数图象进行表示,下列说法正确的是( )A .气压P 与体积V 的关系式为(0)P kV k =>B .当气压70P =时,体积V 的取值范围为70<V<80C .当体积V 变为原来的一半时,对应的气压P 也变为原来的一半D .当60100V 剟时,气压P 随着体积V 的增大而减小 【答案】D【解析】【分析】A .气压P 与体积V 表达式为P=k V ,k >0,即可求解; B .当P=70时,600070V =,即可求解; C .当体积V 变为原来的一半时,对应的气压P 变为原来的两倍,即可求解;D.当60≤V≤100时,气压P随着体积V的增大而减小,即可求解.【详解】解:当V=60时,P=100,则PV=6000,A.气压P与体积V表达式为P= kV,k>0,故本选项不符合题意;B.当P=70时,V=600070>80,故本选项不符合题意;C.当体积V变为原来的一半时,对应的气压P变为原来的两倍,本选项不符合题意;D.当60≤V≤100时,气压P随着体积V的增大而减小,本选项符合题意;故选:D.【点睛】本题考查的是反比例函数综合运用.现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,进而根据字母代表的意思求解.13.若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y=kx(k>0)的图象上,则y1、y2、y3的大小关系是()A. y1>y2>y3B. y3>y1>y2C. y3>y2>y1D. y2>y1>y3【答案】B【解析】【分析】反比例函数y=kx(k>0)的图象在一、三象限,根据反比例函数的性质,在每个象限内y随x的增大而减小,而A(-3,y1)、B(-1,y2)在第三象限双曲线上的点,可得y2<y1<0,C(1,y3)在第一象限双曲线上的点y3>0,于是对y1、y2、y3的大小关系做出判断.【详解】∵反比例函数y=kx(k>0)的图象在一、三象限,∴在每个象限内y随x的增大而减小,∵A(-3,y1)、B(-1,y2)在第三象限双曲线上,∴y2<y1<0,∵C(1,y3)在第一象限双曲线上,∴y3>0,∴y3>y1>y2,故选:B.【点睛】此题考查反比例函数的图象和性质,解题关键在于当k>0,时,在每个象限内y随x的增大而减小;当k<0时,y随x的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.14.如图,点A 是反比例函数2(0)y x x=>的图象上任意一点,AB x P 轴交反比例函数3y x=-的图象于点B ,以AB 为边作ABCD Y ,其中C 、D 在x 轴上,则ABCD S Y 为( )A .2.5B .3.5C .4D .5【答案】D【解析】【分析】 过点B 作BH ⊥x 轴于H ,根据坐标特征可得点A 和点B 的纵坐标相同,由题意可设点A 的坐标为(2a,a ),点B 的坐标为(3a -,a ),即可求出BH 和AB ,最后根据平行四边形的面积公式即可求出结论.【详解】解:过点B 作BH ⊥x 轴于H∵四边形ABCD 为平行四边形∴//AB x 轴,CD=AB∴点A 和点B 的纵坐标相同由题意可设点A 的坐标为(2a ,a ),点B 的坐标为(3a -,a ) ∴BH=a ,CD=AB=2a -(3a -)=5a∴ABCD S Y =BH·CD=5 故选D .【点睛】此题考查的是反比例函数与几何图形的综合题,掌握利用反比例函数求几何图形的面积是解决此题的关键.15.已知反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限,该交点横坐标为1,抛物线2y ax bx c =++与x 轴只有一个交点,则一次函数b c y x a a =+的图象可能是( ) A . B . C . D .【答案】B【解析】【分析】根据题意得b <0,a+c <0,240b ac =>,可得a <0,c <0,进而即可判断一次函数b c y x a a=+的图象所经过的象限. 【详解】 ∵反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限, ∴反比例函数的图象在二、四象限,即b <0,∵该交点横坐标为1,∴y=a+c <0,∵抛物线2y ax bx c =++与x 轴只有一个交点, ∴240b ac -=,即:240b ac =>,∴a <0,c <0, ∴0b a>,0c a >, ∴b c y x a a=+的图象过一、二、三象限. 故选B .【点睛】 本题主要考查反比例函数与一次函数的图象和性质,掌握函数图象上点的坐标特征以及函数解析式的系数的几何意义,是解题的关键.16.如图,矩形ABCD 的顶点A ,B 在x 轴的正半轴上,反比例函数k y x =在第一象限内的图象经过点D ,交BC 于点E .若4AB =,2CE BE =,34AD OA =,则线段BC 的长度为( )A.1 B.32C.2 D.23【答案】B【解析】【分析】设OA为4a,则根据题干中的比例关系,可得AD=3a,CE=2a,BE=a,从而得出点D和点E 的坐标(用a表示),代入反比例函数可求得a的值,进而得出BC长.【详解】设OA=4a根据2CEBE=,34ADOA=得:AD=3a,CE=2a,BE=a∴D(4a,3a),E(4a+4,a)将这两点代入解析得;3444kaakaa⎧=⎪⎪⎨⎪=⎪+⎩解得:a=12∴BC=AD=32故选:B【点睛】本题考查反比例函数和矩形的性质,解题关键是用含有字母的式子表示出点D、E的坐标,然后代入解析式求解.17.如图,平行于x轴的直线与函数y=1kx(k1>0,x>0),y=2kx(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为()A .12B .﹣12C .6D .﹣6【答案】A【解析】【分析】 △ABC 的面积=12•AB•y A ,先设A 、B 两点坐标(其y 坐标相同),然后计算相应线段长度,用面积公式即可求解.【详解】 解:设:A 、B 点的坐标分别是A (1k m ,m )、B (2k m ,m ), 则:△ABC 的面积=12•AB•y A =12•(1k m ﹣2k m )•m =6, 则k 1﹣k 2=12.故选:A .【点睛】此题主要考查了反比例函数系数的几何意义,以及图象上点的特点,求解函数问题的关键是要确定相应点坐标,通过设A 、B 两点坐标,表示出相应线段长度即可求解问题.18.如图,A 、C 是函数1y x=的图象上任意两点,过点A 作y 轴的垂线,垂足为B ,过点C 作y 轴的垂线,垂足为D .记Rt AOB ∆的面积为1S ,Rt COD ∆的面积为2S ,则1S 和2S 的大小关系是( )A .12S S >B .12S S <C .12=S SD .由A 、C 两点的位置确定【答案】C【解析】【分析】 根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=12k|. 【详解】由题意得:S 1=S 2=12|k|=12. 故选:C .【点睛】 本题主要考查了反比例函数y =k x中k 的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=12|k|,是经常考查的一个知识点;这里体现了数形结合的思想.19.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA x ⊥轴,点C 在函数()0k y x x=>的图象上,若1AB =,则k 的值为( )A .1B .22C 2D .2【答案】A【解析】【分析】 根据题意可以求得 OA 和 AC 的长,从而可以求得点 C 的坐标,进而求得 k 的值,本题得以解决.【详解】Q 等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA ⊥x 轴,1AB =,45BAC BAO ︒∴∠=∠=,22OA OB ∴==,2AC =, ∴点C 的坐标为222⎛ ⎝,Q 点C 在函数()0k y x x=>的图象上,12k ∴==, 故选:A .【点睛】本题考查反比例函数图象上点的坐标特征、等腰直角三角形,解答本题的关键 是明确题意,利用数形结合的思想解答.20.在函数2y x=,3y x =+,2y x =的图象中,是中心对称图形,且对称中心是原点的图象共有( )A .0个B .1个C .2个D .3个【答案】B【解析】【分析】根据中心对称图形的定义与函数的图象即可求解.【详解】 y=x+3的图象是中心对称图形,但对称中心不是原点;y=x 2图象不是中心对称图形;只有函数2y x=符合条件. 故选:B .【点睛】 本题考查函数的图象性质与中心对称图形的性质,熟练掌握相关知识是解题的关键.。
(完整版)反比例函数试题及答案(最新整理)

反比例函数一、选择题1.(2016·黑龙江大庆)已知A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=上的三点,若x1<x2<x3,y2<y1<y3,则下列关系式不正确的是( )A.x1•x2<0 B.x1•x3<0 C.x2•x3<0 D.x1+x2<0【考点】反比例函数图象上点的坐标特征.【分析】根据反比例函数y=和x1<x2<x3,y2<y1<y3,可得点A,B在第三象限,点C在第一象限,得出x1<x2<0<x3,再选择即可.【解答】解:∵反比例函数y=中,2>0,∴在每一象限内,y随x的增大而减小,∵x1<x2<x3,y2<y1<y3,∴点A,B在第三象限,点C在第一象限,∴x1<x2<0<x3,∴x1•x2<0,故选A.【点评】本题考查了反比例函数图象上点的坐标特征,解答此题的关键是熟知反比例函数的增减性,本题是逆用,难度有点大.2.(2016·湖北十堰)如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C 是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=上(k>0,x>0),则k的值为( )A.25B.18C.9D.9【考点】反比例函数图象上点的坐标特征;平行线的性质;等边三角形的性质.【分析】过点A作AE⊥OB于点E,根据正三角形的性质以及三角形的边长可找出点A、B、E 的坐标,再由CD⊥OB,AE⊥OB可找出CD∥AE,即得出,令该比例=n,根据比例关系找出点D、C的坐标,利用反比例函数图象上点的坐标特征即可得出关于k、n的二元一次方程组,解方程组即可得出结论.【解答】解:过点A作AE⊥OB于点E,如图所示.∵△OAB为边长为10的正三角形,∴点A的坐标为(10,0)、点B的坐标为(5,5),点E的坐标为(,).∵CD⊥OB,AE⊥OB,∴CD∥AE,∴.设=n(0<n<1),∴点D的坐标为(,),点C的坐标为(5+5n,5﹣5n).∵点C、D均在反比例函数y=图象上,∴,解得:.故选C.【点评】本题考查了反比例函数图象上点的坐标特征、平行线的性质以及等边三角形的性质,解题的关键是找出点D、C的坐标.本题属于中档题,稍显繁琐,解决该题型题目时,巧妙的借助了比例来表示点的坐标,根据反比例函数图象上点的坐标特征找出方程组是关键.3. (2016·新疆)已知A(x1,y1),B(x2,y2)是反比例函数y=(k≠0)图象上的两个点,当x1<x2<0时,y1>y2,那么一次函数y=kx﹣k的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限【考点】反比例函数图象上点的坐标特征;一次函数图象与系数的关系.【分析】首先根据x1<x2<0时,y1>y2,确定反比例函数y=(k≠0)中k的符号,然后再确定一次函数y=kx﹣k的图象所在象限.【解答】解:∵当x1<x2<0时,y1>y2,∴k>0,∴﹣k<0,∴一次函数y=kx﹣k的图象经过第一、三、四象限,∴不经过第二象限,故选:B.【点评】此题主要考查了反比例函数图象上点的坐标特征以及一次函数图象与系数的关系,解决此题的关键是确定k的符号.4. (2016·云南)位于第一象限的点E在反比例函数y=的图象上,点F在x轴的正半轴上,O是坐标原点.若EO=EF,△EOF的面积等于2,则k=( )A.4 B.2 C.1 D.﹣2【考点】反比例函数系数k的几何意义.【分析】此题应先由三角形的面积公式,再求解k即可.【解答】解:因为位于第一象限的点E在反比例函数y=的图象上,点F在x轴的正半轴上,O 是坐标原点.若EO=EF,△EOF的面积等于2,所以,解得:xy=2,所以:k=2,故选:B【点评】主要考查了反比例函数系数k的几何意义问题,关键是由三角形的面积公式,再求解k.5. (2016·四川达州·3分)下列说法中不正确的是( )A.函数y=2x的图象经过原点B.函数y=的图象位于第一、三象限C .函数y=3x ﹣1的图象不经过第二象限D .函数y=﹣的值随x 的值的增大而增大【考点】正比例函数的性质;一次函数的性质;反比例函数的性质.【分析】分别利用正比例函数以及反比例函数的定义分析得出答案.【解答】解:A 、函数y=2x 的图象经过原点,正确,不合题意;B 、函数y=的图象位于第一、三象限,正确,不合题意;C 、函数y=3x ﹣1的图象不经过第二象限,正确,不合题意;D 、函数y=﹣的值,在每个象限内,y 随x 的值的增大而增大,故错误,符合题意.故选:D .6. (2016·四川乐山·3动时,点C 图象上运动,若tan ()A 2()C 6答案:D解析:连结CO 所以,CO ⊥AB ,因为tan 作AE ⊥x 轴,CD ⊥x 轴于则有△OCD ∽△OEA 设C (m ,n ),则有A 所以,k n m =解①②得:k =87. (2016·四川凉山州·4分)二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是( )A.B.C.D.【考点】反比例函数的图象;一次函数的图象;二次函数的图象.【分析】根据二次函数的图象找出a、b、c的正负,再结合反比例函数、一次函数系数与图象的关系即可得出结论.【解答】解:观察二次函数图象可知:开口向上,a>0;对称轴大于0,﹣>0,b<0;二次函数图象与y轴交点在y轴的正半轴,c >0.∵反比例函数中k=﹣a<0,∴反比例函数图象在第二、四象限内;∵一次函数y=bx﹣c中,b<0,﹣c<0,∴一次函数图象经过第二、三、四象限.故选C.8. (2016,湖北宜昌,15,3分)函数y=的图象可能是( )A.B.C.D.【考点】反比例函数的图象.【分析】函数y=是反比例y=的图象向左移动一个单位,根据反比例函数的图象特点判断即可.【解答】解:函数y=是反比例y=的图象向左移动一个单位,即函数y=是图象是反比例y=的图象双曲线向左移动一个单位.故选C【点评】此题是反比例函数的图象,主要考查了反比例函数的图象是双曲线,掌握函数图象的平移是解本题的关键.9. (2016吉林长春,8,3分)如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )A.减小B.增大C.先减小后增大D.先增大后减小【考点】反比例函数系数k的几何意义.【分析】首先利用m和n表示出AC和AQ的长,则四边形ACQE的面积即可利用m、n表示,然后根据函数的性质判断.【解答】解:AC=m﹣1,CQ=n,则S四边形ACQE=AC•CQ=(m﹣1)n=mn﹣n.∵P (1,4)、Q (m ,n )在函数y=(x >0)的图象上,∴mn=k=4(常数).∴S 四边形ACQE =AC •CQ=4﹣n ,∵当m >1时,n 随m 的增大而减小,∴S 四边形ACQE =4﹣n 随m 的增大而增大.故选B .【点评】本题考查了二次函数的性质以及矩形的面积的计算,利用n 表示出四边形ACQE 的面积是关键.10. (2016兰州,2,4分)反比例函数的图像在()。
反比例函数经典大题(有详细答案)
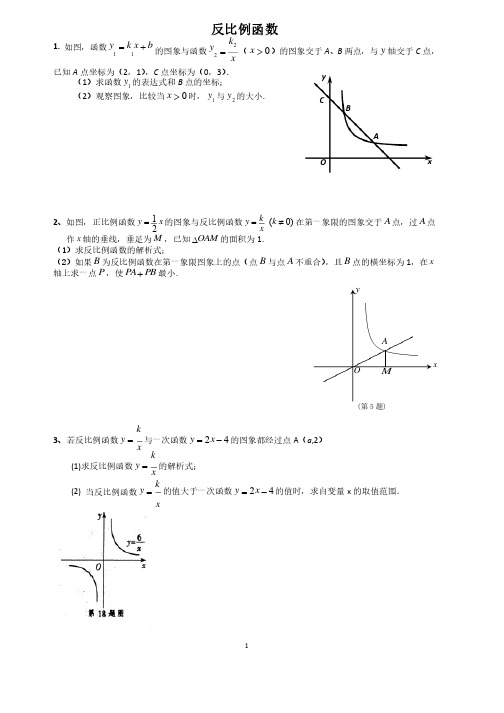
1 反比例函数1. 如图,函数b x k y +=11的图象与函数xk y22=(0>x )的图象交于A 、B 两点,与y 轴交于C 点,已知A 点坐标为(2,1),C 点坐标为(0,3).(1)求函数1y 的表达式和B 点的坐标;(2)观察图象,比较当0>x 时,1y 与2y 的大小. 2、如图,正比例函数12y x =的图象与反比例函数k y x =(0)k ¹在第一象限的图象交于A 点,过A 点作x 轴的垂线,垂足为M ,已知OAM D 的面积为1.(1)求反比例函数的解析式;(2)如果B 为反比例函数在第一象限图象上的点(点B 与点A 不重合),且B 点的横坐标为1,在x 轴上求一点P ,使PA PB +最小最小. .3、若反比例函数xk y =与一次函数42-=x y 的图象都经过点A (a ,2)(1)求反比例函数xky =的解析式;(2) 当反比例函数xk y =的值大于一次函数42-=x y 的值时,求自变量x的取值范围.ABOCxy OMxyA (第5题)4、如图,在直角坐标系中,O 为坐标原点. 已知反比例函数y= (k>0)的图象经过点A (2,m ),过点A 作AB ⊥x 轴于点B ,且△AOB 的面积为的面积为 . (1)求k 和m 的值;的值;(2)点C (x ,y )在反比例函数y= 的图象上,求当1≤x ≤3时函数值y 的取值范围;的取值范围;5、如图,四边形ABCD 为菱形,已知A (0,4),B (-3,0)。
⑴求点D 的坐标;的坐标;⑵求经过点C 的反比例函数解析式. 6、如图,一次函数3y kx =+的图象与反比例函数m y x=(x>0)的图象交于点P ,P A ⊥x 轴于点A ,PB ⊥y 轴于点B ,一次函数的图象分别交x 轴、y 轴于点C 、点D ,且S △DBP =27,12OC CA =。
(1)求点D 的坐标;的坐标;(2)求一次函数与反比例函数的表达式;)求一次函数与反比例函数的表达式;(3)根据图象写出当x 取何值时,一次函数的值小于反比例函数的值?取何值时,一次函数的值小于反比例函数的值?xkx k B O A21xyAO PBC D7、已知一次函数y =kx +b 的图象交反比例函数42m y x-=(x>0)图象于点A 、B ,交x 轴于点C .(1)求m 的取值范围;的取值范围;(2)若点A 的坐标是(2,-4),且13BC AB =,求m 的值和一次函数的解析式;的值和一次函数的解析式;(3)写出当x 取何值时,一次函数的值小于反比例函数的值?取何值时,一次函数的值小于反比例函数的值?8、如图,正比例函数11y k x =与反比例函数22k y x=相交于A 、B 点,已知点A 的坐标为(4,n ),BD ⊥x 轴于点D ,且S △BDO =4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)请写的日销售利润为1800元,则其售价应为多少元?
课后练习
1.对与反比例函数 ,下列说法不正确的是( )
3.如果矩形的面积为6cm2,那么它的长 cm与宽 cm之间的函数图象大致为( )
4.某气球内充满了一定质量的气体,当温度不变时,
气球内气体的气压P ( kPa ) 是气体体积V ( m3)
的反比例函数,其图象如图所示.当气球内气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A、不小于 m3B、小于 m3C、不小于 m3D、小于 m3
反比例函数经典题型
【例1】如果函数 的图像是双曲线,且在第二,四象限内,那么的值是多少?
对应练习
1.反比例函数 的图像位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.若 与 成反比例, 与 成正比例,则 是 的( )
A、正比例函数 B、反比例函数 C、一次函数 D、不能确定
A. + =0B. · <0C. · >0D. =
4. 反比例函数y=的图象过点P(-1.5,2),则k=________.
5. 点P(2m-3,1)在反比例函数y=的图象上,则m=__________.
6. 已知反比例函数的图象经过点(m,2)和(-2,3)则m的值为__________.
7. 已知反比例函数 的图象上两点 ,当 时,有 ,则 的取值范围是?
(1)蓄水池的容积是多少?
(2)如果增加排水管,使每小时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
(3)写出t与Q的关系式.
(4)如果准备在5小时内将满池水排空,那么每小时的排水量至少为多少?
(5)已知排水管的最大排水量为每小时12m3,那么最少需多长时间可将满池水全部排空?
【例2】在反比例函数 的图像上有三点 , , , , , 。若 则下列各式正确的是( )
A. B. C. D.
对应练习
1、在函数 (a为常数)的图象上有三个点 , , ,则函数值 、 、 的大小关系是( ).
A. < < B. < <
C. < < D. < <
【例3】如果一次函数 相交于点( ),那么该直线与双曲线的另一个交点坐标是多少?
A.S1>S2B. S1<S2
C. S1=S2D. S1与S2的大小关系不能确定
2.如图,在直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数 的图象交于A(-2,1)、B(1,n)两点。
(1)求上述反比例函数和一次函数的表达式;
(2)求△AOB的面积。
反比例函数的应用
8. 某蓄水池的排水管每小时排水8m3,6小时可将满池水全部排空.
对应练习
1.关于x的一次函数y=-2x+m和反比例函数y= 的图象都经过点A(-2,1).
求:(1)一次函数和反比例函数的解析式;(2)两函数图象的另一个交点B的坐标;
(3)△AOB的面积.
2. 如图所示,一次函数y=ax+b的图象与反比例函数y=的图象交于A、B两点,与x轴交于点C.已知点A的坐标为(-2,1),点B的坐标为(,m).
8.已知y与x-1成反比例,并且x=-2时y=7,求:
(1)求y和x之间的函数关系式; (2)当x=8时,求y的值;
(3)y=-2时,x的值。
9. 已知 ,且反比例函数 的图象在每个象限内, 随 的增大而增大,如果点 在双曲线上 ,求a是多少?
A.点( )在它的图像上B.它的图像在第一、三象限
C.当 时, D.当 时,
2.已知反比例函数 的图象经过点(1,-2),则这个函数的图象一定经过( )
A、(2,1) B、(2,-1) C、(2,4) D、(-1,-2)
3在同一直角坐标系内,如果直线 与双曲线 没有交点,那么 和 的关系一定是( )
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
【例4】 如图,在 中,点 是直线 与双曲线 在第一象限的交点,且 ,则 的值是多少.
对应练习
1.如图 ,A、C是函数 的图象上的任意两点,过A作 轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面积为S2则 ( )
